Dane:
Obliczenia i szkice:
Wyniki:
Q=60
kN
H =310
mmm
h=50
mm
μ
w
=
2
Podnoszona masa: Q = 60 kN
Wysokość podnoszenia: H = 310 mm
1.0 Śruba
Materiał jaki przyjmuję na śrubę to stal niestopowa
konstrukcjyjna ogólnego przeznaczenia St5
R
m
= 500 MPa
R
e
= 300 Mpa
k
r
= 145 Mpa
1.1 Swobodna długość wyboczeniowa.
l=H + 0,5 h+ ∆
l=310+ 0,5⋅50+ 1,2⋅50=395
h−orientacyjna wysokość nakrętki[mm ].
∆−suma wysokości mechanizmu zapadkowego
i części śruby wchodzącej w otwór głowicy. ∆=(1,2 ÷ 1,5)h
l
w
=
l⋅μ
w
l
w
=
395⋅2=790 mm
μ
w
−
współczynnik wyboczeniowy uwzględniający
charakter wyboczenia
(ź) "Podnośniki i prasy śrubowe PKM projektowanie" Zbiegniew
Skrzyszowski
l=395
mm
l
w
=
790
mm
Dane:
Obliczenia i szkice:
Wyniki:
Q=60kN
β=
1,3
K
c
=
R
3
3
l
w
=
790
mm
d
3
=
27
mm
E=2,1⋅10
5
1.2 Średnica rdzenia śruby.
Wewnętrzna średnica gwintu d
3
z umowy wytrzymałości trzpienia
śruby na ściskanie z uwzględnieniem skręcania.
d
3
=
√
4β
Q
(π
k
c
)
=
26,2 mm
β−
współczynnik uwzględniający wpływ naprężeń
skręcających w przekroju śruby β=1,3
K
c
−
napręzenia dopuszczalne na ściskanie K
c
=
R
3
3
[
MPa]
(ź) Leonid W. Kurmaz "Projektowanie z podstaw konstrukcji
maszyn" 1995 (s. 18)
Przyjmuję gwint Tr 34 x 6 [d
3
=27 mm]
Obliczam smukłość graniczną śruby
Naprężenia krytyczne należy wyznaczyć wykorzystująć wzór :
−
Eulera dla zakresu sprężężystego lub
−
Johnsona−Ostenfelda dla zakresu sprężysto plastycznego , tzn.
σ
kr
=π
2
E
λ
2,
dla λ≥λ
t
σ
kr
=
R
e
−
B λ
2,
dla λ< λ
t
λ =
(
4⋅l
w
)
d
3
=
117,03
λ
t
=
π
√
2
E
R
e
=
π
√
(
2⋅2,1⋅10
5
300
)=
117,55
Ponieważ λ < λ
t
naprężenia krytyczne należy wyznaczyć
wykorzystując wzór Johnsona−Ostenfelda dla zakresu
plastyczno−sprężystego.
B=
R
e
2
(
4 π
2
E)
=
300
2
(
4 π
2
2⋅10
5
)
=
0,01085
σ
kr
=
R
e
−
B⋅λ
2
=
300−0,010855⋅117,03
2
=
151,4 MPa
(ź) "Sprawdzenie wymiarów śruby na wyboczenie" Henryk Sanecki
d
3
=
26,2
mm
Tr 34 x 6
d
3
=
27 mm
λ=
117,03
λ
t
=
117,55
B=0,01085
σ
kr
=
151,4
MPa

Dane:
Obliczenia i szkice:
Wyniki:
Q
c
=
60
kN
d
3
=
27
mm
l
w
=
790
mm
d
3
=
41
mm
B=0,01085
R
e
=
300
MPa
Średnicę rdzenia śruby d
3
należy sprawdzić
z warunku na
wyboczenie siłą sciskającą Q. Warunek ten można zapisać w postaci
nierówności:
σ
c
≤
k
w
=
σ
c
x
w
σ
c
−
napężenia ściskające działające w przekroju rdzenia śruby
k
w
−
naprężenia dopuszczalne na wyboczenie
x
w
−
współczynnik bezpieczeństwa na wyboczenie
σ
r
−
naprężeani krytyczne
(ź) "Sprawdzenie wymiarów śruby na wyboczenie" Henryk Sanecki
Obliczam naprężenia ściskające działające w rdzeniu śruby
Q
c
=
4Q
( π
d
3
2
)
=
104,8 MPa
(ź) "Sprawdzenie wymiarów śruby na wyboczenie" Henryk Sanecki
104,8>
151,4
7
=
21,63
Warunek nie został spełniony. Przyjmuję kolejny gwint gwint Tr 36 x
6 [d
3
=29 mm]
λ =
(
4⋅l
w
)
d
3
=
108,97
σ
kr
=
R
e
−
B⋅λ
2
=
300−0,010855⋅108,97
2
=
171,1 MPa
Q
c
=
4Q
(π
d
3
2
)
=
90,84 MPa
90,84>
171,1
7
=
24,43
Warunek nie został spełniony.
Po kilkukrotnym przeliczeniu przyjmuję gwint gwint Tr 60 x 9 [d
3
=50 mm]
Q
c
=
104,8
MPa
Tr 36x6
λ=
108,97
Q
c
=
90,84
MPa
Tr 60 x 9
Dane:
Obliczenia i szkice:
Wyniki:
l
w
=
790
mm
d
3
=
50
mm
B=0,01085
R
e
=
300
MPa
R
w
=
164,65
d
r
=
50
mm
Q=60
kN
λ =
(
4⋅l
w
)
d
3
=
(
4⋅l
w
)
50
=
63,3
σ
kr
=
R
e
−
B⋅λ
2
=
300−0,010855⋅73,48
2
=
256,5 MPa
Q
c
=
4Q
( π
d
r
2
)
=
30,55 MPa
30,55<
256,5
7
=
36,64
Warunek został spełniony.
1.3 Obliczenie rzeczywistego współczynnika bezpieczeństwa X
X =
(
R
w
π
d
r
2
)
4Q
=
(
164,65⋅π 50
2
)
(
4⋅60⋅1000)
=
5.38
R
w
=
(
π
2
E )
λ
2
=
164,65
Wymagany współczynnik bezpieczeństwa na wyboczenie nie został
osiągnięty. Należy dobrać kolejną wiekszą średnicę rdzenia
d
3
= 54
λ=
(
4 μ l
w
)
d
r
=
58,51
X
w
=
(
R
w
π
d
r
2
)
4Q
=
(
192,71⋅π 54
2
)
(
4⋅60⋅1000)
=
7.35
R
w
=
(
π
2
E)
λ
2
=
192,71
Wymagany współczynnik bezpieczeństwa: X
w
=7 został osiągnięty.
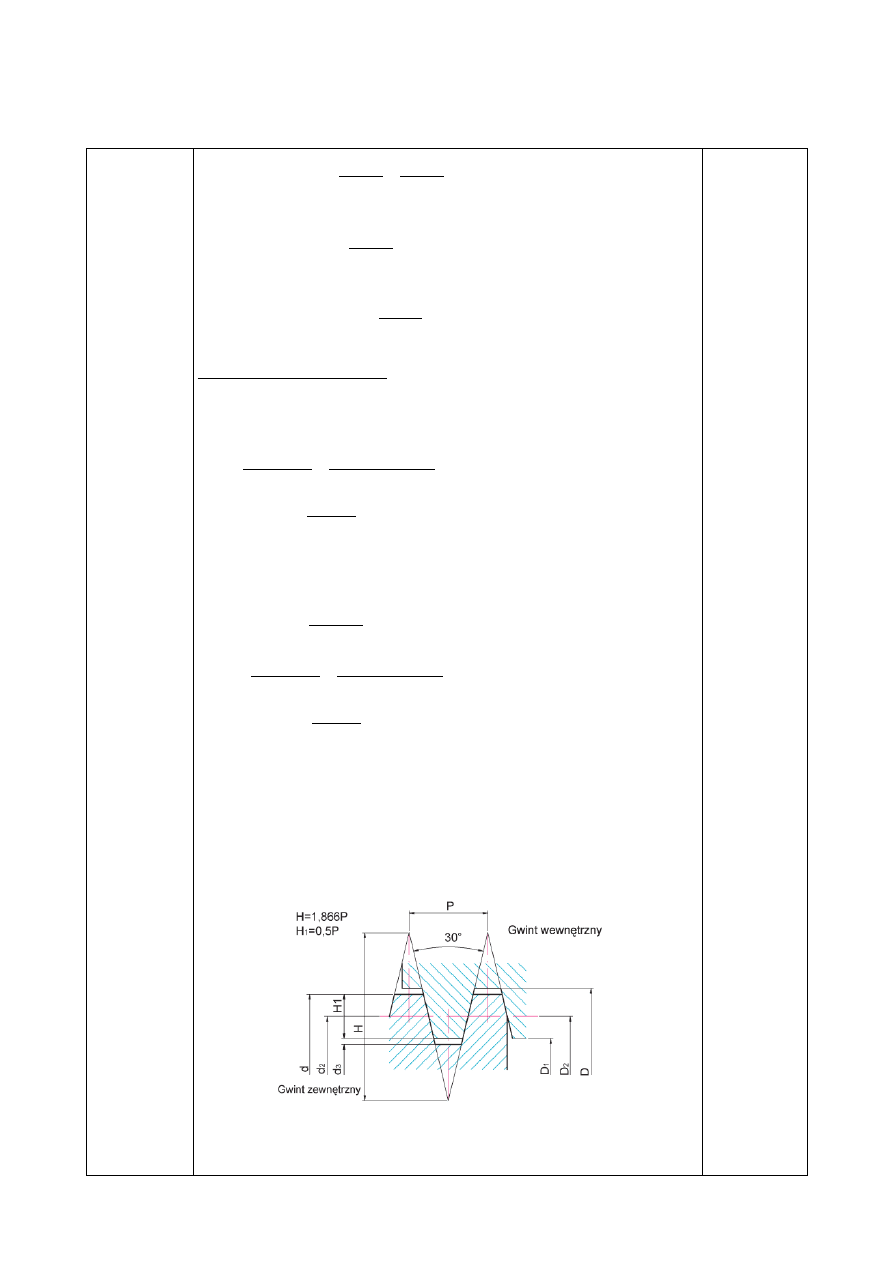
1.4 ostateczne przyjęcie gwintu:
Przyjmuje się gwint: metryczny trapezowy Tr 65 x 10
o średnicy rdzenia d
3
=
54 mm
R
w
=
164,65
d
3
=
54
mm
λ=
58,51
X
w
=
7
R
w
=
192,71
Tr 65 x 10
d
3
=
54 mm

Dane:
Obliczenia i szkice:
Wyniki:
2.0
Sprawdzenie samohamowności dobranego gwintu.
2.1 Kąt wzniosu lini śrubowej.
tg γ =
P
(π⋅
d
2
)
=
10
(π⋅
60)
=
0,053
γ =
3° 2 '
"Podstawy konstrukcji maszyn zbiór zadań" B. Malik
2.2 Obliczenie pozornego współczynnika tarcia.
ρ
'=
μ
(
cos α
2
)
=
0,62
ρ
'=3 ° 34 '
"Podstawy konstrukcji maszyn zbiór zadań" B. Malik
2.3 Warunek samohamowności
ρ
'=3 ° 34 '> γ =3 ° 2 '
"Podstawy konstrukcji maszyn zbiór zadań" B. Malik
Gwint jest samohamowny
3.0 Nakrętka
3.1 Przyjęcie materiału na nakrętkę.
Na meteriał nakrętki dobieram Brąz B10 przeznaczony do silnie
obciążonych części maszyn.
R
m
=270 MPa
k
r
=90
γ=
3,2
ρ
'=3 ° 34 '
Dane:
Obliczenia i szkice:
Wyniki:
Brąz B10
R
m
=
270
270
MPa
k
r
=
90
μ=
0,13
3.2 Obliczenie pozornego kąta tarcia
tg ρ '=
μ
(
cosα )
=
0,13
(
cos 30)
=
0,1501
tg ρ ' =8° 40 '
μ−
współczynnik tarcia 0,13 średnia jakość materiałów
i obróbki , średnie warunki pracy
Podnośniki i Prasy Śrubow tab.14 Zbigniew Skrzyszowski
3.3 Moment tarcia na gwincie.
M
s
=
(
Qd
s
tg(γ + ρ ' ))
2
(
60⋅1000⋅0,060⋅tg(6° 36 ' ))
2
=
208,3 N⋅m
(1) s.132 [2.52]
3.4 Naprężenia skręcające.
τ =
(
1
2
d
s
F tg(γ + ρ ' ))
(
1
5
d
r
3
)
=
(
1
2
0,06⋅60⋅1000⋅18,78)
(
1
5
0,054
3
)
=
1073,3 MPa
(1) s. 136 [2.64]
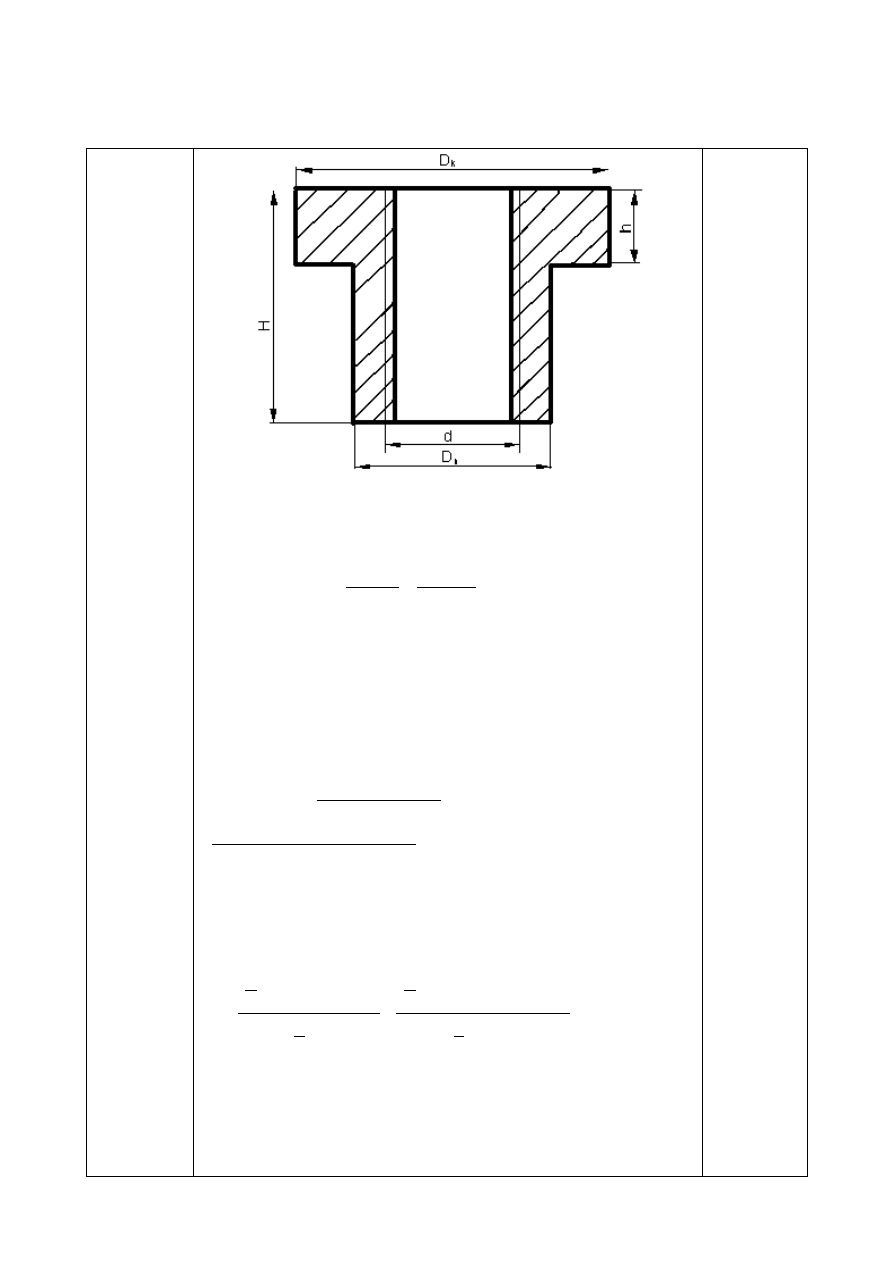
3.5 Wysokość nakętki.
tg ρ ' =8° 40'
M
s
=
208,3
N⋅m
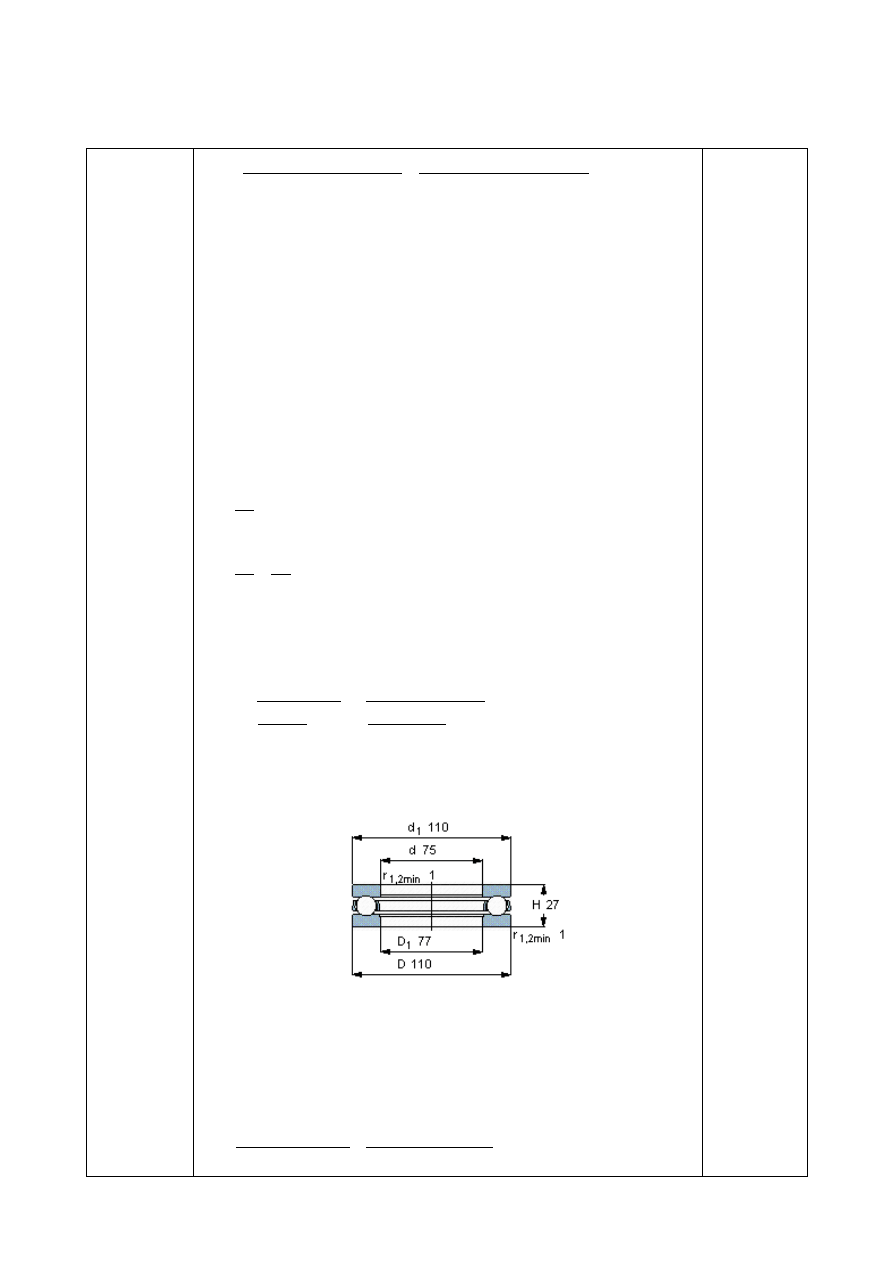
Dane:
Obliczenia i szkice:
Wyniki:
P=10
Q=60 kN
d =65
D
1
=
55
k
0
=
90
MPa
Q=60 kN
k
r
=
90
MPa
d =65
mm
H =
4⋅P⋅Q
(
π⋅(
d
2
−
D
1
2
)⋅
0,15⋅k
o
)
=
4⋅10⋅60⋅1000
(
π⋅(
65
2
−
55
2
)⋅
0,15⋅90)
H =47,15 mm
k
o
= (0,1-0,2) k
c
k
c
=90 MPa
(2) s. 26 [7.2]
Ze względów konstrukcyjnych przyjmuje się wysokość nakrętki
H=80 mm wg PN-78/M-02041
"Podstawy konstrukcji maszyn" Zbiór zadań Bronisław Malik s. 126
tab. 44.
3.6 Sprawdzenie czynnej liczby zwojów nakrętki. (tzn. czy
z =
H
P
=
6−10 zwojów )
z =
H
P
=
80
10
=
8
liczba zwojów mieści się w wartości zalecanej
3.7 Średnica zewnętrzna nakrętki
D
n
≥
√
4⋅Q
(
π⋅
k
r
)
+
d
2
=
√
4⋅60⋅1000
(π⋅
90)
+
65
2
=
71,2 mm
Ze względu na średnicę lożyska przyjmuje się D
n
= 77 mm
"Podstawy konstrukcji maszyn" Zbiór zadań Bronisław Malik
3.5 Wyskokość kołnierza nakrętki
h≥
Q
(
π⋅
D
n
⋅
0,65⋅k
r
)
=
60⋅1000
(
π⋅
80,9⋅0,65⋅90)
≥
4 mm
τ
=
1073,3
MPa
H =80
mm
z =8
D
n
=
77
mm
Dane:
Obliczenia i szkice:
Wyniki:
Q=60 kN
D
n
=
80,9
k
r
=
90
MPa
3.6 Średnica zewnętrzna kołnierza nakrętki
D
k
=
√
4Q
(
π⋅
0,15⋅k
c
)
+
D
n
2
=
√
4⋅60⋅1000
(
π⋅
0,15⋅90)
+
80,9
2
=
110 mm
3.7 Obliczenia sprawności pary śrubowej urządzenia.
η=
(
tg γ )
(
tg (γ + ρ ' ))
=
0,16
"Podstawy konstrukcji maszyn" Praca zbiorowa pod redakcją
Zbigniewa Osińskiego Wydawnictwko Naukowe PWN Warszawa
1999 s. 131 [2.49]
4. Obliczenie wymiarów karpusu.
4.1 Schemat korpusu i jego podstawowe wymiary
Przyjmuję się konstrukcję rurową z podstawą i wspornikami
usztywniającymi, spawaną
4.2 Średnica zewnętrzna rury
D
z
=
D
n
+
2⋅g =88,9 mm
"Podstawy konstrukcji maszyn" Zbiór zadań Bronisław Malik
4.3 Sprawdzenie grubości ścianki rury
Materiał rury St4S
Warunek wytrzymałościowy
σ=
4Q
(π⋅(
D
z
2
−
D
n
2
))
≤
k
c
σ=
56,2≤k
c
=
130 [MPa ]
Warunek wytrzymałościowy został spełniony.
4.4 Średnica podstawy podnośnika. (Obliczona z warunku na
nacisk powierzchniowy )
D
p
≥
√
4Q
(π⋅
p
g
)
=
√
4⋅60⋅1000
(π⋅
4)
=
138,19=140 mm
h≥4 mm
D
k
=
110
mm
η=
0,16
Dane:
Obliczenia i szkice:
Wyniki:
4.5 Grubość podstawy podnośnika
Uwzględniając sposób połączenia podstawy z rurą, ustala się
grubość podstawy na podstawie minimalnej grubości spoiny
pachwinowej (tzn. a
min
=0,7 g
p
= 3mm)
g
p
≥
a
min
0,7
=
4,3 mm=5 mm
4.6 Średnica pierścienia przyspawanego do górnej części rury.
Średnicę pierścienia oblicza się z warunku wytrzymałościowego na
nacisk powierzchniowy, którą następnie przyrównuje się do srednicy
kołnierza nakrętki i ostatecznie dobiera większą średnicę.
D
k
=
√
4Q
(π⋅
0,15⋅k
c
)
+
D
n
2
=
√
4⋅60⋅1000
(π⋅
0,15⋅130)
+
80,9
2
=
102,3 mm
Ostatecznie przyjmuje się średnicę kołnierza nakrętki = 110,5 mm
4.7 Grubość pierścienia przyspawanego do górnej częsci rury.
Ustala się minimalną grubość pierścienia jak w punkcie 5.5
g
k
≥
a
min
0,7
=
4,3 mm
4.8 Wysokość korpusu
H
k
=
h
p
+
g
p
+
h
1
+ (
H −h)=340 mm
h
p
= grubość podkładki ograniczającej ruch śruby oraz luz miedzy tą
podkładką oraz podstawą h
p
przyjmuje się 10 mm
5. Wymiary korony
5.1 Średnica zewnętrzna koronki
Zakłada się że 50% powierzchni korony przenosi obciążenie (rowki
na powierzchni korony)
D
k
=
√
4⋅Q
(
0,3 π⋅0,8⋅k
c
)
=
√
4⋅60⋅1000
(
0,3 π⋅0,8⋅25)
=
97,7 mm
Zgodnie z PN D
kPN
=
120 mm
Dane:
Obliczenia i szkice:
Wyniki:
k
c
= dopuszczalny nacisk przedmiotów podnoszonych = 25 MPa
5.2 Wysokość korony
Przyjmuję sie wysokość korony 0,5 D
k
h
k
= 50 mm
h
k PN
= 50 mm
6
.0 Mechanizm zapdkowy.
Materiał na koło zapadkowe dobieram material stal 10 poddaną
nawęglaniu i hartowaniu.
k
r
=125 MPa
Materiał na zapadkę doboieram Brąz B10
k
r
=90 MPa
Średnica śruby pod kołem zapadkowym.
d
0
=d=65 mm
Średnica stóp kóła zapadkowego
d
s
=
1,6⋅d
0
=
1,6⋅65=104 mm
Minimalna i maksymalna wysokość ząbka - wartość przyjęta
konstrukcyjnie.
h
z
=
((
0,25−0,5)π d
S
)
12
h
zMIN
=
6,8
h
zMAX
=
13,6
h
z
=
10 mm
Średnica podziałowa koła zapadkowego.
d
p
=
d
s
+
h
z
=
114 mm
Promień wierzchołków ząbków
r
z
=
d
z
2
=
d
s
2
+
h
z
=
62 mm
Wysokość (grubość) koła zapadkowego

Dane:
Obliczenia i szkice:
Wyniki:
l
k
=(
0,8−1,5)d
0
l
kMIN
=
52
l
kMAX
=
97,5
l
k
=
75 mm
Grubość widełek
g
w
=(
0,1−0,3)l
k
g
wMIN
=
7,5 mm
g
wMAX
=
22,5 mm
g
w
=
15 mm
http://www.stal-inox.pl/blachy_nierdzewne_kwasoodporne.html
Grubość podkładek lub osadzeń na zapadce
g
podkł
= 1 mm
Wysokość zapadki i ząbków koła zapadkowego
g
k
=
l
z
=
l
k
−
2g
w
−
2g
podkł
=
75−2⋅15−2⋅1=43 mm
Grubość piasty koła zapadkowego
g
p
=
(
d
s
−
d
0
)
2
=
(
104−65)
2
=
19,5 mm
Obliczenie wysokości koła zapadkowego
l
k
'=l
k
−
2g
w
=
75−2⋅15=45 mm
Obliczenia Wpsutu (Progrma)
całkowity moment obrotowy potrzebny do podniesienia ciężaru Q
M =0,25⋅Q⋅[(d + d
3
)⋅
tg (γ+ ρ ' )+ μ⋅(D
k
+
D
n
)]=
379 Nm
Obliczenie połączenia wielowypustowego
Warunek wytrzymałościowy na nacisk powierzchniowy

Dane:
Obliczenia i szkice:
Wyniki:
p=
F
(
0,75⋅z⋅h
0
⋅
l
0
)
≤
k
0
F −siła działająca na wpust
z−liczba wpustów
h
0
−
prowmieniowa wysokość wpustu
l
0
−
długość obliczeniowa wpustu
l
0
=
F
(
0,75⋅z⋅h
0
⋅
k
0
)
≤
14,18
l
0PN
=
16 mm
2 Rodziaj i wymiar połączenia wielowypustowego - tablica 5
3 Siła działająca na wpusty
F =
2⋅M
(
D
s
)
=
4⋅M
(
D+ d )
=
4⋅378
(
0,58+ 52)
=
13745,45 N
d −średnica wewnętrzna wpustów
D−średnica zewnętrzna wpustów
M −moment obrotowy
D
s
−
(
D+ d )
2
4 Promieniowa wysokość wpustu
h
0
=
(
D−d )
2
=
(
58−52)
2
=
3 mm
5 Dopuszczalne naciski powiechniowe
k
0
=
z
1
⋅
k
c
=
0,6⋅90=54 MPa
z
1
−
współczynnik zależny od warunków pracy
k
c
−
napreżenia rozrywające dla materiału słabszego
6 Grubość piastu w miejscu osadzenia wpustów
g =c⋅
3
√
M
Nm
=
3,2⋅
3
√
379=23,16
c−współczynnik przyjmowany dla piasty stalowej c=3,2
Ostatecznie ustalono:
wałek: 8 x 52 x 58 PN-ISO 14:1994
otwór: 8 x 52 x 58 PN-ISO 14:1994

Dane:
Obliczenia i szkice:
Wyniki:
Obliczenia sprawdzające koła zapadkowego
Naciski dopuszczalne koło zapadkowe - zapadka
p
dopZAP
=
0,8⋅k
c
=
0,8⋅90=72 MPa
Sprawdzam nacisk koło zapadkowe - zapadka.
p
zap
=
2M
c
(
d
s
g
k
h
z
)
=
379
(
104⋅43⋅10)
=
84 MPa
P
dopZAP
<
p
zap
Warunek nie został spełniony.
Ponownie dobieram materiał zapadki - przyjmuję Brąz BK331
k
r
=120 MPa
Naciski dopuszczalne koło zapadkowe - zapadka
p
dopZAP
=
0,8⋅k
c
=
0,8⋅120=96 MPa
Sprawdzam nacisk koło zapadkowe - zapadka.
p
zap
=
2M
c
(
d
s
g
k
h
z
)
=
379
(
104⋅43⋅10)
=
84 MPa
P
dopZAP
<
p
zap
Warunke został spełniony.
Naprężenia rozrywające piastę koła zapadkowego.
σ=
(
2β M
c
)
(
d
s
l
k
' ( g
p
−
h
0
))
=
(
2⋅2⋅379)
(
104⋅45⋅(19,5−3))
=
196 Mpa
Literatura:
(1) "Podstawy konstrukcji maszyn" Praca zbiorowa pod redakcją
Zbigniewa Osińskiego Wydawnictwko Naukowe PWN Warszawa
1999
(2) "Podstawy konstrukcji maszyn" Zbiór zadań Bronisław Malik
(3) "Projektowanie węzłów i części maszyn" Leonid W. Kurmaz,
Oleg L. Kurmaz Kielce 2007

Dane:
Obliczenia i szkice:
Wyniki:
(4) Zbigniew Skrzyszowski
Document Outline
Wyszukiwarka
Podobne podstrony:
Podnosnik(O) verUproszczona id Nieznany
dobry poprawiony id 138426 Nieznany
podnosnik A2 by Arti id 365542 Nieznany
Abolicja podatkowa id 50334 Nieznany (2)
4 LIDER MENEDZER id 37733 Nieznany (2)
katechezy MB id 233498 Nieznany
metro sciaga id 296943 Nieznany
perf id 354744 Nieznany
interbase id 92028 Nieznany
Mbaku id 289860 Nieznany
Probiotyki antybiotyki id 66316 Nieznany
miedziowanie cz 2 id 113259 Nieznany
LTC1729 id 273494 Nieznany
D11B7AOver0400 id 130434 Nieznany
analiza ryzyka bio id 61320 Nieznany
pedagogika ogolna id 353595 Nieznany
Misc3 id 302777 Nieznany
więcej podobnych podstron