1

Rzut równoległy

Dana jest płaszczyzna

π (rzutnia)

i nierównoległa do niej prosta k określająca

kierunek rzutowania.

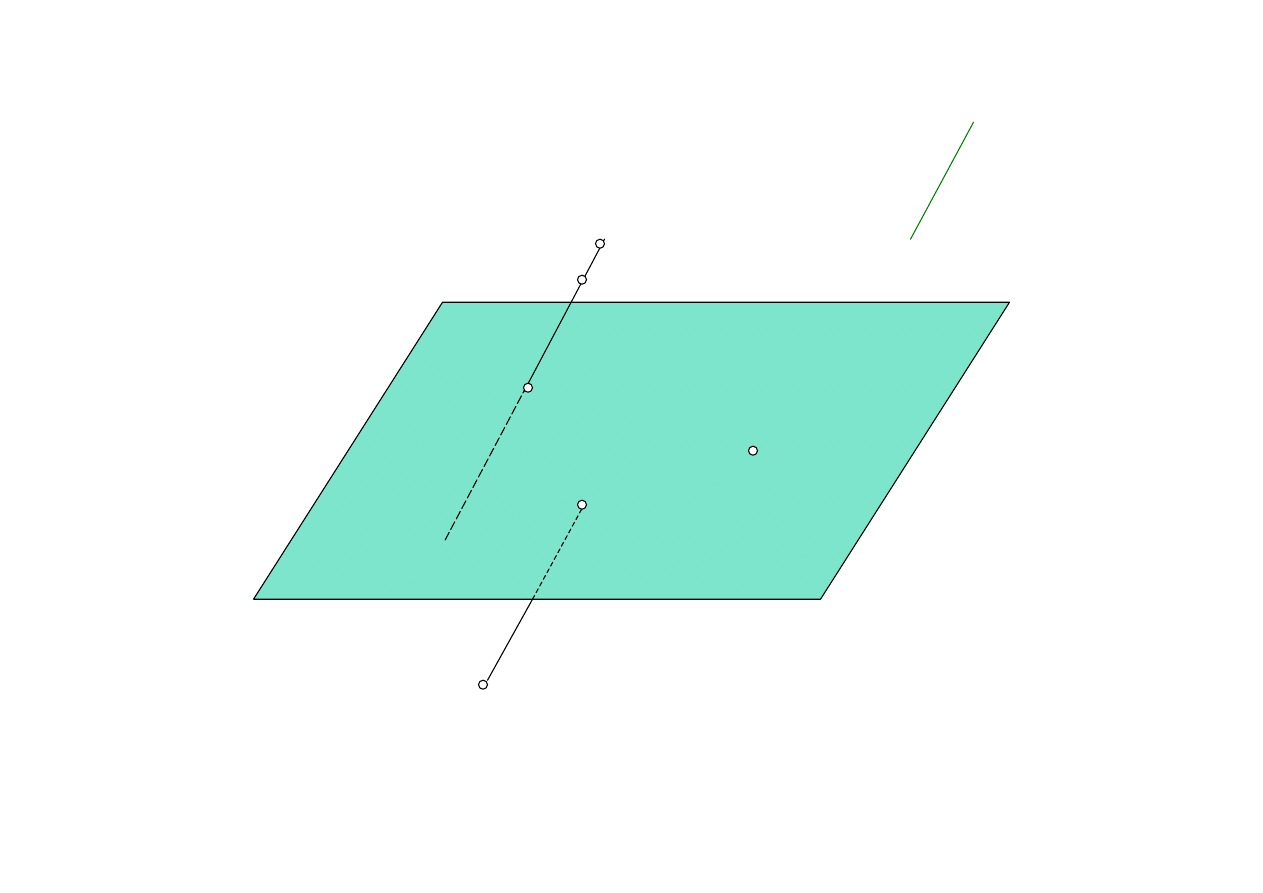
Rzutem równoległym punktu A na płaszczyznę

π

nazywamy punkt A’, w którym prosta rzutująca
m||k, poprowadzona przez punkt A, przebija

rzutnię

π.

2

A

A’

B

C

B’=C’

k

D=D’

Π

Rzut równoległy

3

Niezmienniki rzutowania

równoległego

4

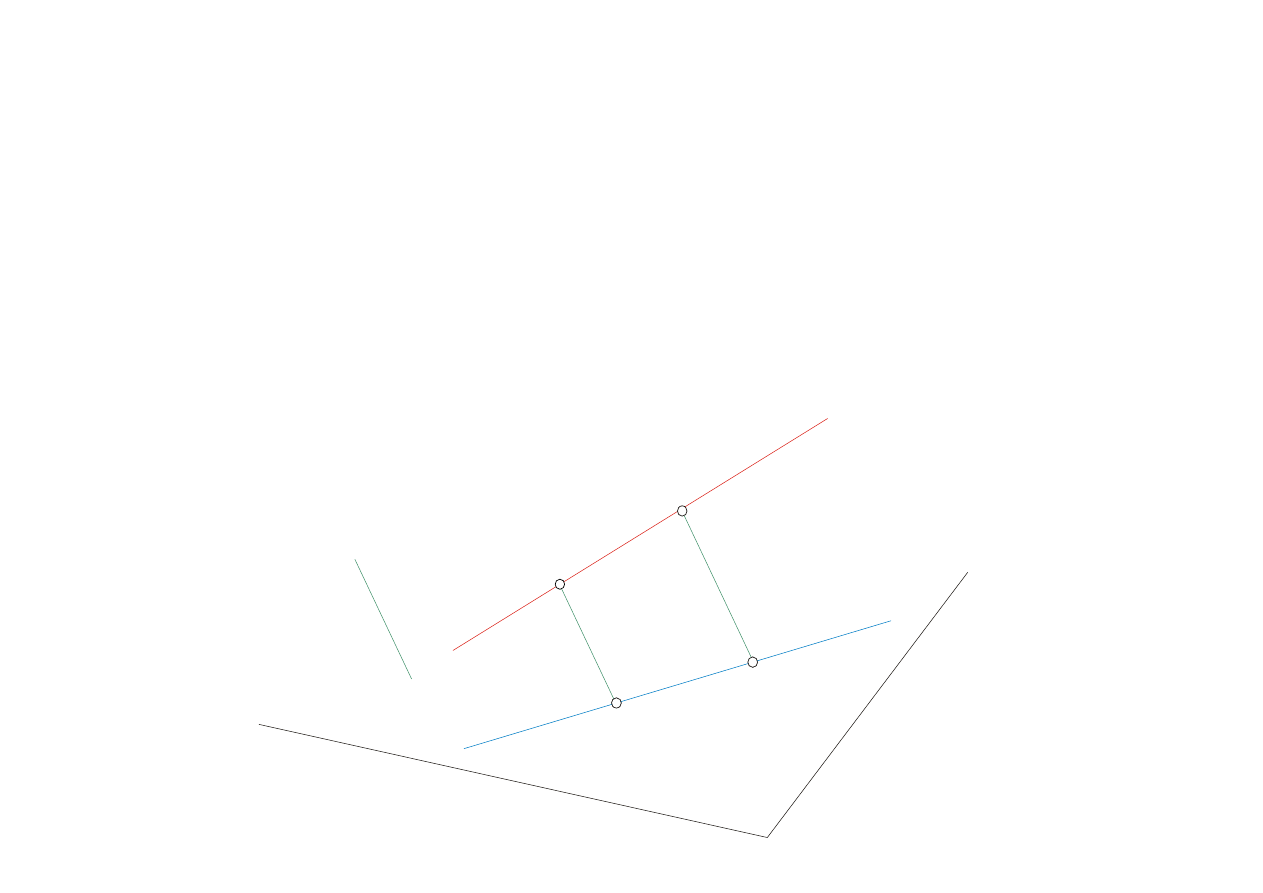
Niezmiennik 1

(N1) Przynależność

Jeżeli punkt

A

należy do prostej

n

to rzut

A

’ punku

A

należy do rzutu

n

’ prostej

n

A

A’

n

n’

k

π

B

B’

5

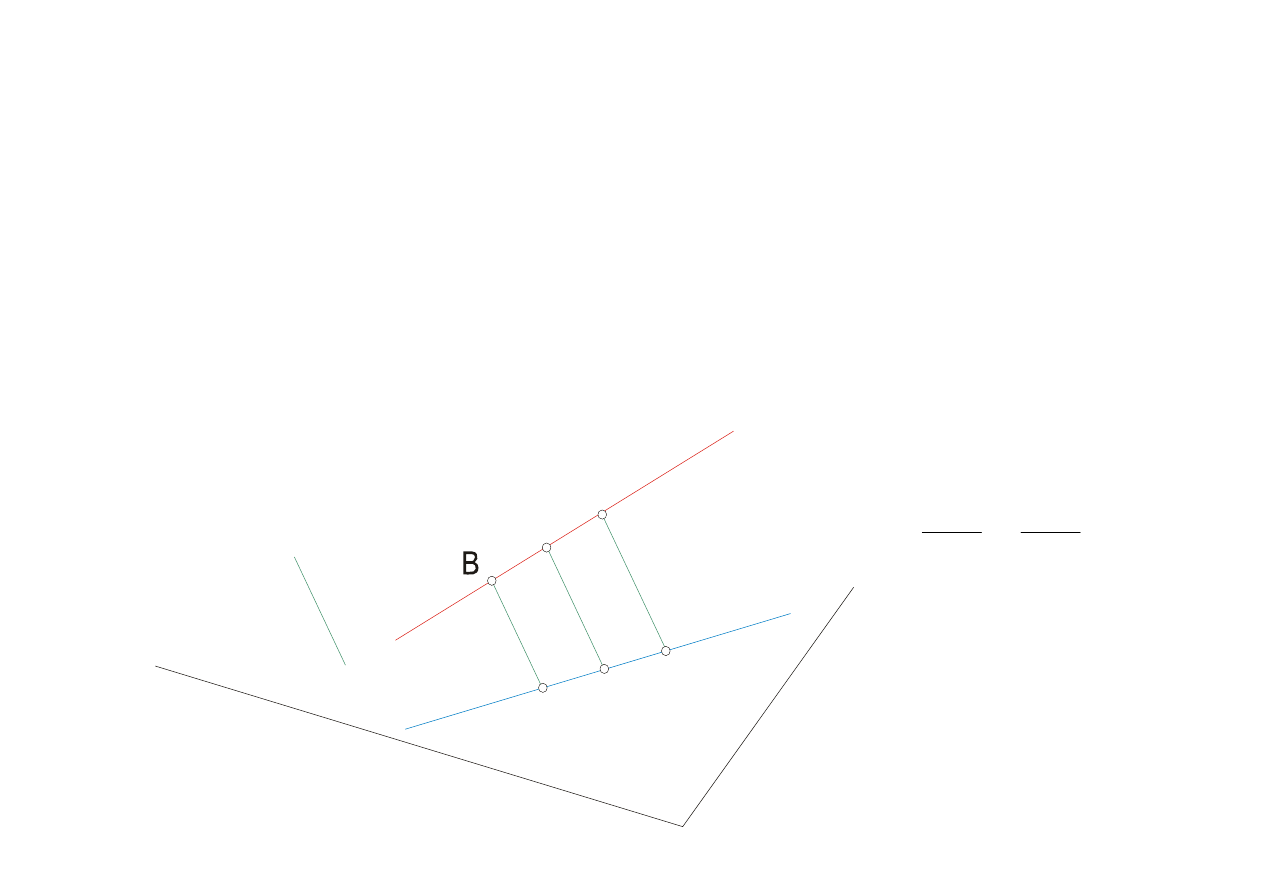
Niezmiennik 2

(N2) Stosunek podziału odcinka

Rzutowanie równoległe nie zmienia stosunku

podziału odcinka

A

A’

n

n’

k

B’

C

C’

π

AC
BC

A’C’
B’C’

=

6

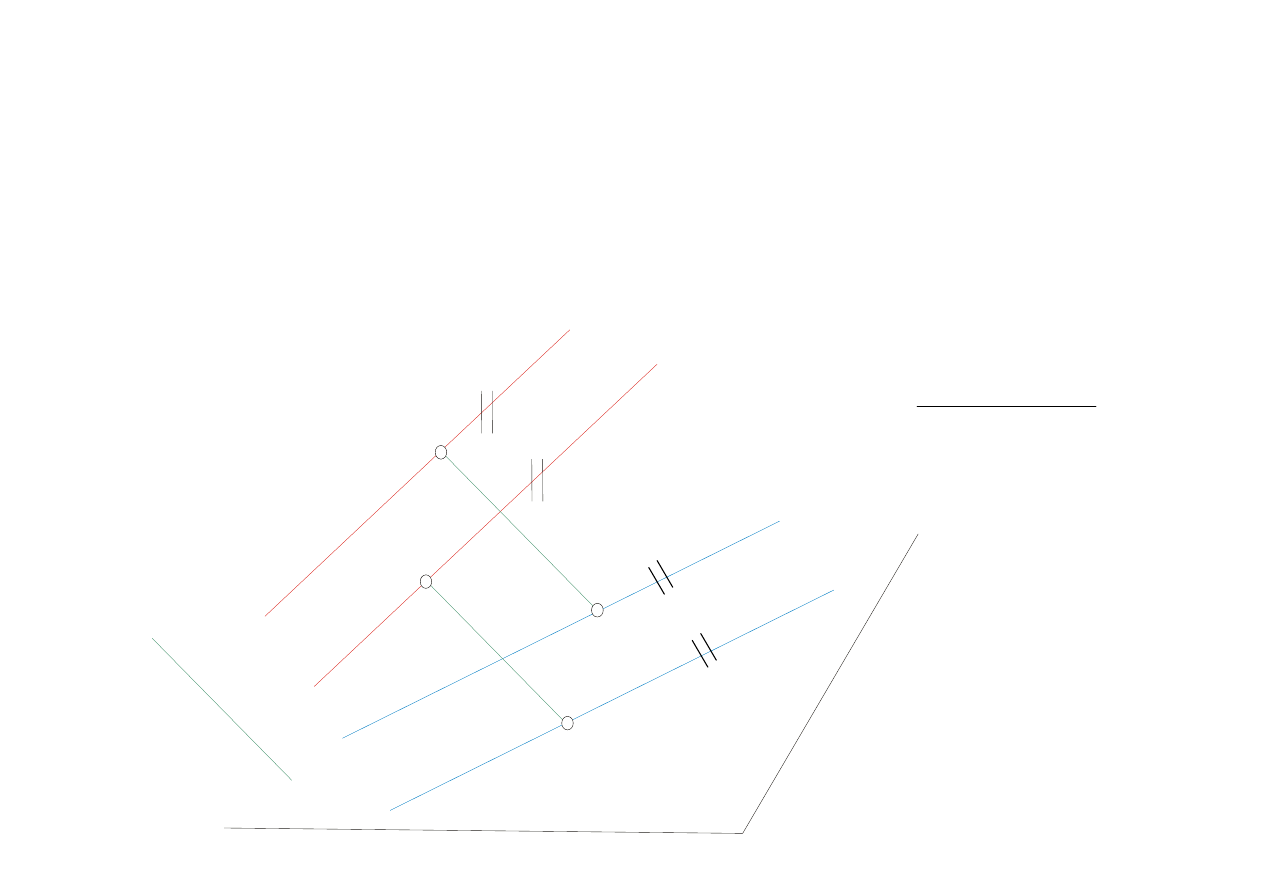
Niezmiennik 3

(N3) Równoległość prostych

m

n

m’

n’

k

π

A

B

A’

B’

m’||n’

Rzutowanie równoległe zachowuje równoległość

prostych

m||n

7

Niezmiennik 4

(N4) Metryka figur płaskich

równoległych do rzutni

Jeżeli figura płaska leży w płaszczyźnie

równoległej do rzutni, to rzut tej figury jest

do niej przystający.

A

B

C

A’

B’

C’

π

k

ABC ||

π

A’B’C’

≡ ABC

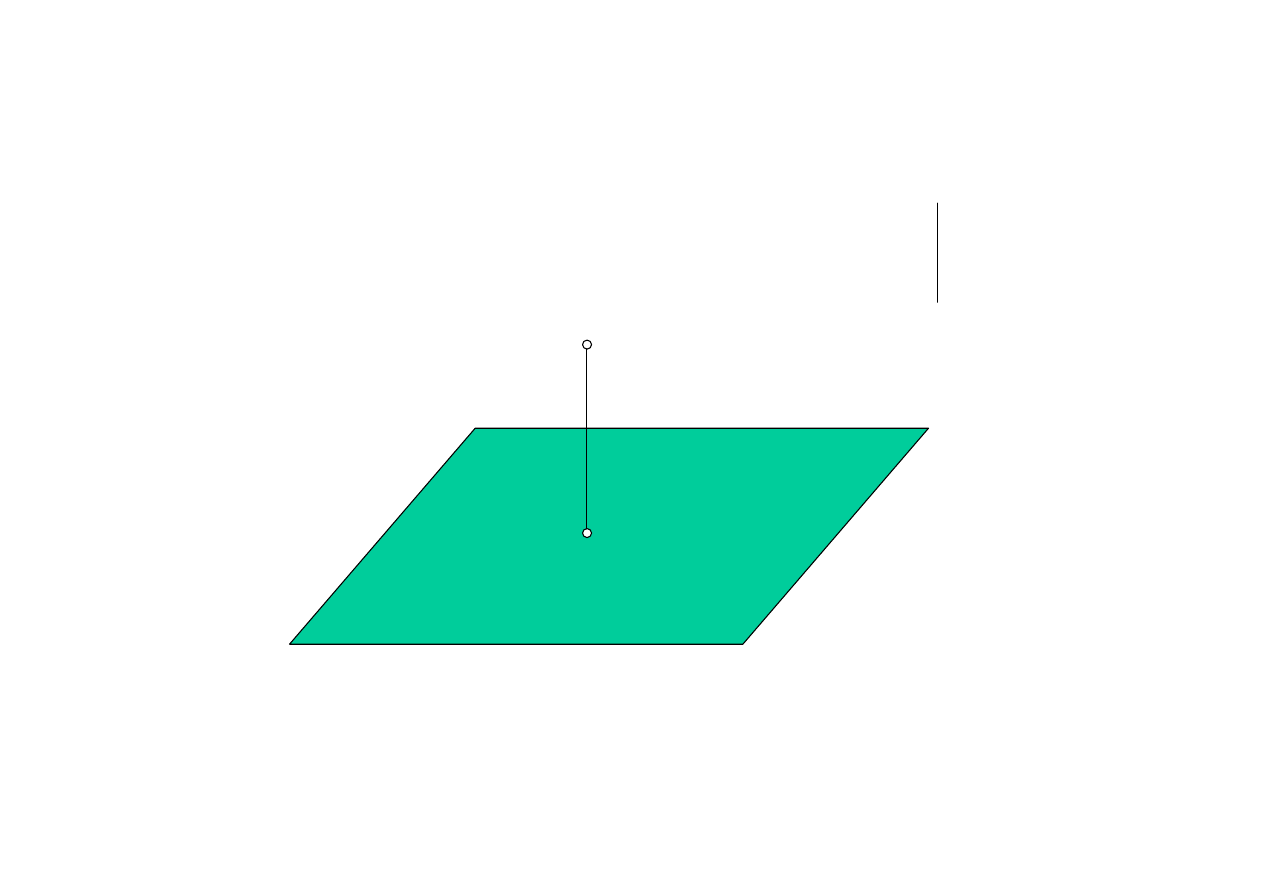
8

A

A’

π

k

⊥ π

Rzut prostokątny

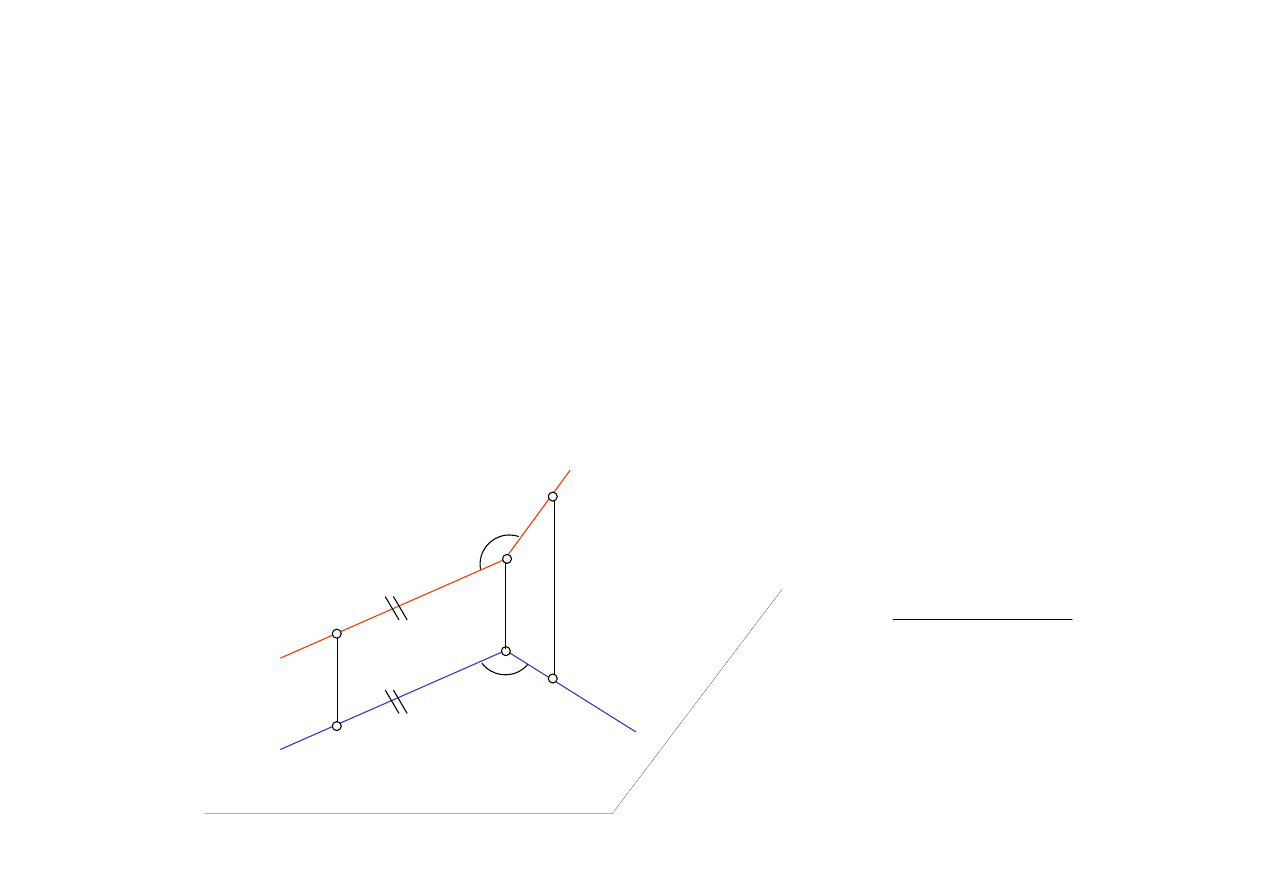
9

(N5) Kąt prosty

(niezm. rzut. prostokątnego)

Niezmiennikiem rzutowania prostokątnego

jest kąt prosty, którego jedno ramię jest do

rzutni równoległe.

π

A

B

B’

A’

W

W’

.

.

a

⊥ b

a ||

π

b

b’

a’

⊥ b’