Metrologia Techniczna

wyk.3

29.03.2011

METROLOGIA TECHNICZNA

WYKŁAD 3

Zakres wykładu:

–

Płytki wzorcowe

•

Wymagania

•

Klasyfikacja

•

Pomiary

–

Czujniki pomiarowe

–

Działania na wymiarach tolerowanych

–

Analiza wymiarowa

1. Wzorce

Wzorce kreskowe:

–

Zwykłe

–

Inkrementalne

–

Kodowe

Przyrządy pomiarowe wykorzystujące wzorce kreskowe:

–

suwmiarki

–

mikroskopy uniwersalne

–

długościomierze

–

przyrządy fotooptyczne

–

maszyny pomiarowe

1

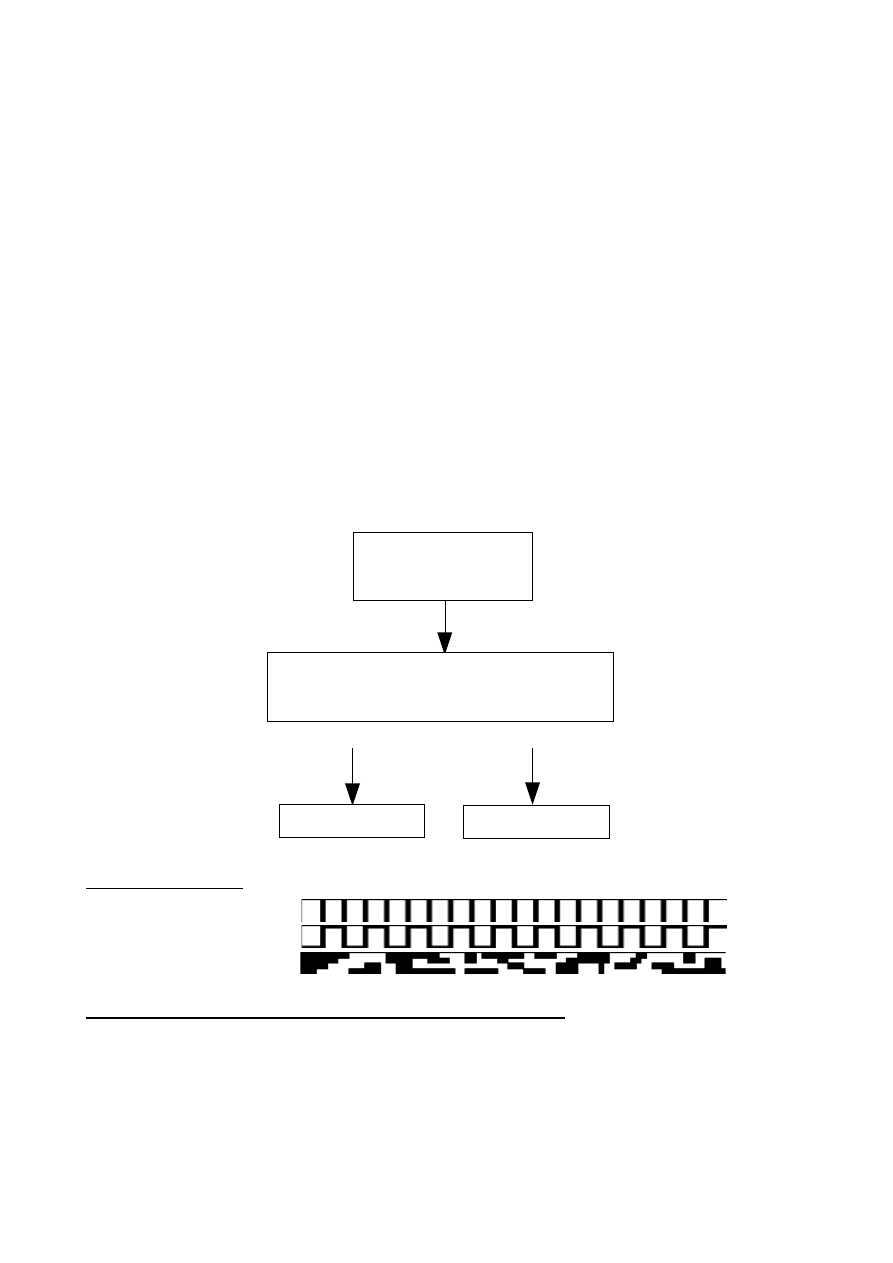
Etalon – Metra

(metoda etalonowa)

Laser stabilizowany

Metr – jest to odległość, jaką pokonuje

światło w próżni w czasie 1/299 792 458 s

Wzorce kreskowe

Wzorce końcowe

Metrologia Techniczna

wyk.3

29.03.2011

Wzorce końcowe:

–

reprezentują je płytki wzorcowe wykonane w różnych klasach dokładności 0, 1, 2 (k)

Przyrządy pomiarowe wykorzystujące wzorce końcowe:

–

mikrometry

–

projektory

–

mikroskopy warsztatowe

–

czujniki pomiarowe (mechaniczne, elektryczne, pneumatyczne)

2. Płytki wzorcowe

Płytki wzorcowe stanowią najczęściej używane wzorce końcowe w laboratoriach
pomiarowych. Informacje o płytkach i wymaganiach ich dotyczących można znaleźć w
normie PN-EN ISO3650.

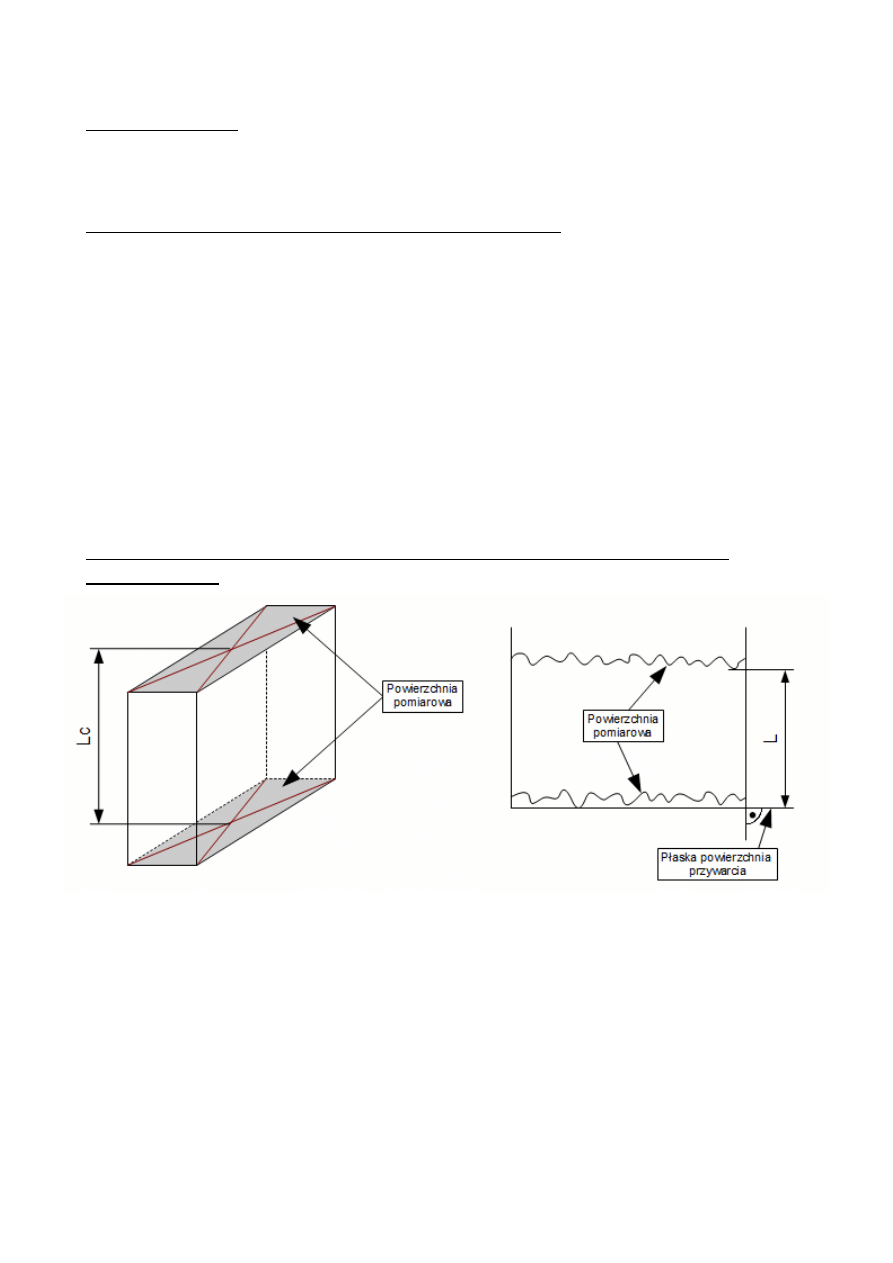
Płytki wzorcowe charakteryzowane są za pomocą następujących wymiarów
długościowych:

–

długości nominalnej Ln

–

długości środkowej Lc

–

długości L

Płytki wzorcowe są jednowymiarowymi końcowymi wzorcami długości i mają
najczęściej kształt prostopadłościanów. Długość nominalna Lc płytki wzorcowej jest
wymiarem odniesienia, względem którego określa się odchyłki graniczne długości płytki.

2

Metrologia Techniczna

wyk.3

29.03.2011

Płytki wzorcowe stopniowane są według następujących wymiarów (przykładowe wymiary
stanowią długości nominalne):

–

mm: 0,01 ; 0,1 ; 0,5 ; 1 ; 10 ; 25 ; 100

–

μm: 0,5 ; 1 ; 10 ; 100 ; 500 ; 10mm

Standardowe komplety płytek wzorcowych składają się z następujących liczb płytek:

–

komplet mały (47 sztuk)

–

komplet średni (76 sztuk)

–

komplet duży (103 sztuki)

Stos płytek wzorcowych o dowolnej wysokości zawsze zaczynamy składać od ostatniej
liczby po przecinku, np. składając stos płytek o wysokości 43,735mm, z kompletu
wybieramy następujące płytki:

–

1,005 mm

–

1,03 mm

–

1,7 mm

–

40,0 mm
Suma – 43,735 mm

Materiały stosowane na płytki wzorcowe:

–

stal odporna na ścieranie i korozję o współczynniku rozszerzalności cieplnej

=

11,5±1,0⋅10

−

6

1 /

o

C

w zakresie temp. 10 – 30ºC, twardość większa lub równa

od 62HRC (stal chromowa ŁH15, stal stopowa narzędziowa)

–

ceramika (ma jasną barwę i nie jest przeźroczysty)

–

węgliki spiekane o współczynniku

=

5,5±0,5⋅10

−

6

1 /

o

C

Wymagania stawiane materiałom przeznaczonym na płytki wzorcowe:

–

niezmienność wymiarów w czasie

–

odporność na ścieranie

–

odporność na korozję

–

współczynnik rozszerzalności cieplnej

Podstawowe klasy dokładności płytek:

–

Klasa K – w laboratoriach pomiarowych do wzorcowania innych płytek wzorcowych

–

Klasa 0 – jako płytki wzorcowe podstawowe do sprawdzania płytek
podporządkowanych (o niższej klasie dokładności), do wzorcowania przyrządów
pomiarowych o dużej dokładności.

3

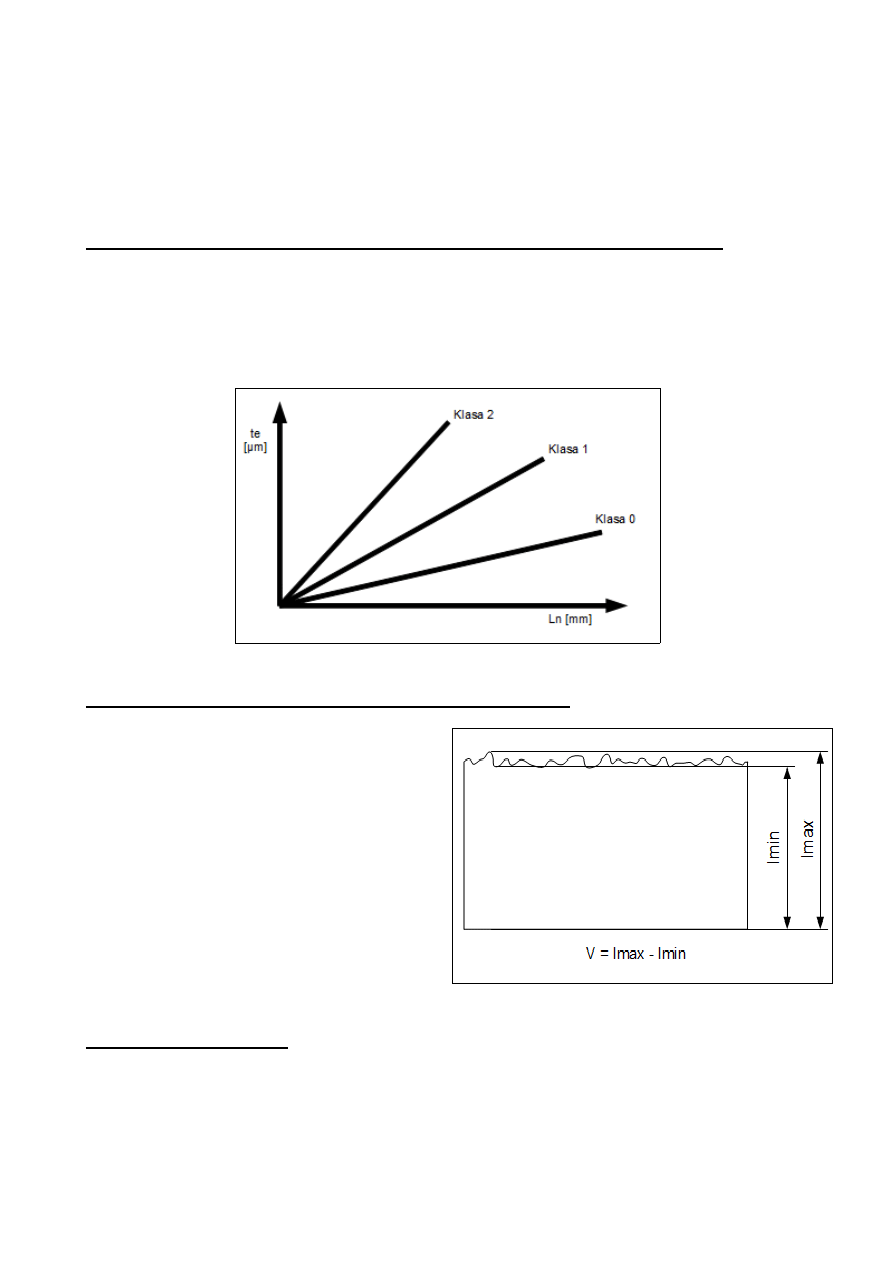
Metrologia Techniczna

wyk.3

29.03.2011

–

Klasa 1 – do pomiarów wzorców kontrolnych i sprawdzianów, do wzorcowania
długościomierzy i pomiarów w laboratoriach pomiarowych

–

Klasa 2 – jako wzorce nastawcze i kontrolne przyrządów pomiarowych niższej
dokładności (wzorce zastępujące sprawdziany szczękowe)

Odchyłki graniczne płytek wzorcowych w zależności od klasy dokładności:

–

klasa 0 -

te≈0,10,002ln

np. dla

ln=100mm

te=±0,3  m

–

klasa 1 -

te≈0,20,004 ln

np. dla

ln=100mm

te=±0,3  m

–

klasa 2 -

te≈0,40,008 ln

np. dla

ln=100mm

te=±1,2  m

Tolerancja zmienności długości płytek wzorcowych (Tv):

–

klasa 0 – Tv od 0,1 do 0,4 μm

–

klasa 1 – Tv od 0,16 do 0,6 μm

–

klasa 2 – Tv od 0,3 do 1 μm

Odchyłka płaskości (fd) – jest to najmniejsza odległość między dwiema płaszczyznami,
między którymi leżą punkty powierzchni pomiarowej.

4

Metrologia Techniczna

wyk.3

29.03.2011

Tolerancja płaskości (Td):

Długość nominalna ln

[mm]

Tolerancja płaskości tf [μm]

k

0

1

2

0,5 ≤ ln ≤ 150

0,05

0,1

0,15

0,25

150 < ln ≤ 500

0,1

0,15

0,18

0,25

500 < ln ≤ 1000

0,15

0,18

0,2

0,25

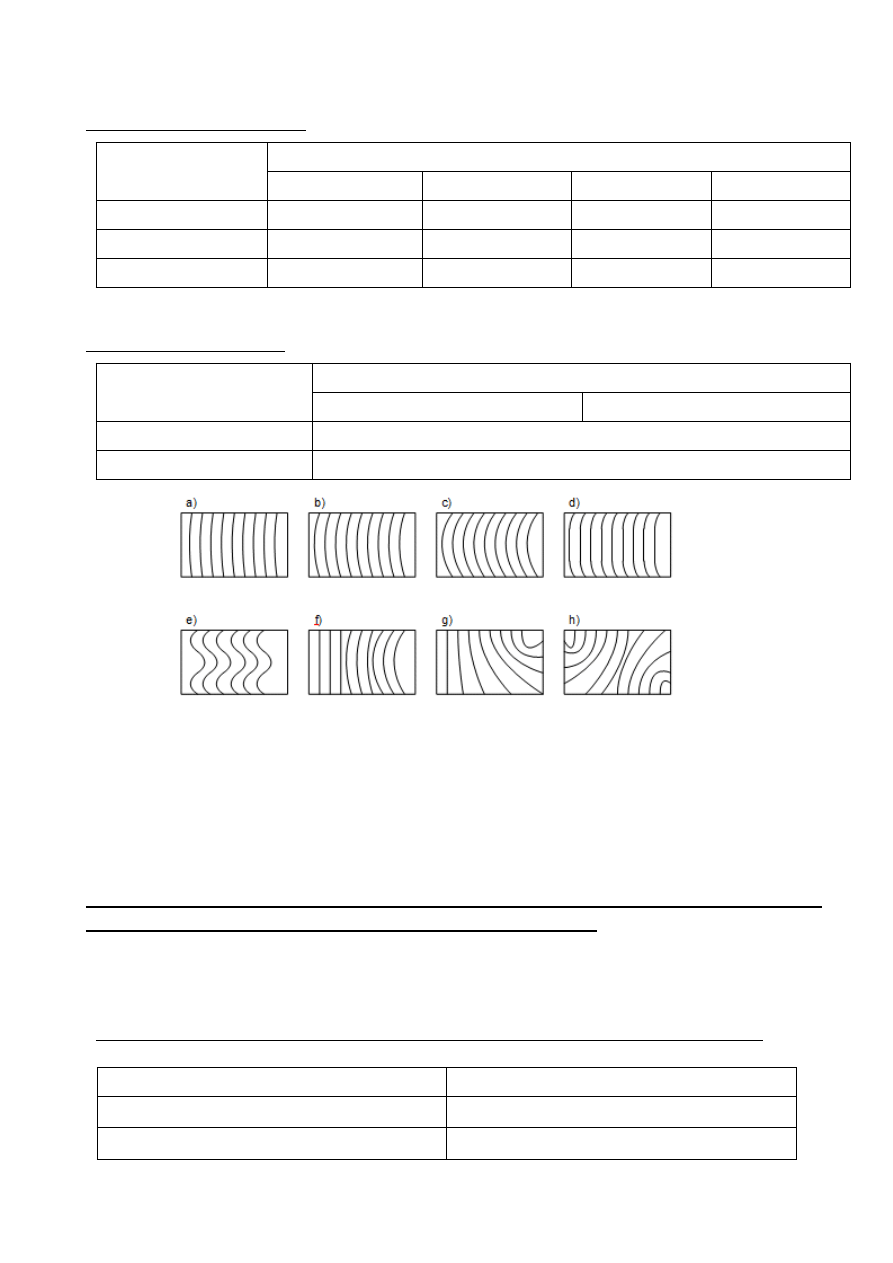
Ocena przywieralności:

Klasa dokładności

Obraz interferencyjny

Prążki interferencyjne

odcienie

K, 0

Nie dopuszcza się

1, 2

Jasne plamy lub szare odcienie

a, b, c – powierzchnie wypukłe
d – powierzchnia płaska z zaokrąglonymi krawędziami
e, f, g – powierzchnie z wklęsłością wzdłużną
h -

Powierzchnie wklęsłe od wypukłych odróżnić można jedynie przez celowe dociśnięcie
płytki do przedmiotu co powoduje przesunięcie się prążków:

–

od środka – wypukła

–

do środka – wklęsła

Stabilność wymiarów – w ciągu roku powinna spełnić następujące wymagania:

Klasa dokładności

∆L [μm]

K, 0

±

0,020,25⋅10

−

6

⋅

ln

1, 2

±

0,050,5⋅10

−

6

⋅

ln

5

Metrologia Techniczna

wyk.3

29.03.2011

Pomiary płytek wzorcowych:

Pomiary płytek wzorcowych przeprowadza się dwoma metodami:

–

metoda bezwzględna – (interferencyjna) tą metodą mierzone są płytki o klasach
dokładności 0 lub K

–

metoda porównawcza – tą metodą mierzy się płytki klasy 1 lub 2. Płytki porównuje
się z płytkami klasy wyższej (K lub 0)

Podczas mierzenia należy przestrzegać zasady, że płytki o wysokości 100mm mierzymy
w położeniu pionowym, natomiast powyżej 100mm w położeniu poziomym.

2. Czujniki pomiarowe

Wyróżniamy następujące czujniki pomiarowe:

–

mechaniczne
- dźwigniowe
- zębate (zegarowe)
- dźwigniowo zębate
- sprężynowe

–

mechaniczno-optyczne

–

indukcyjne

–

pojemnościowe

–

pneumatyczne

–

optoelektroniczne

3. Analiza Wymiarowa

Analiza zajmuje się badaniem zależności między niedokładnością wymiarów składowych

a wymiarem wynikowym. Obejmuje ona tak że zagadnienia związane z optymalizacją doboru
wymiarów składowych.

Celem prowadzenia analizy wymiarowej jest wyznaczenie wartości wymiaru

wynikowego (zależnego) lub jednego z wymiarów składowych (niezależnych).

W celu poprawnego przeprowadzenia analiz wymiarowych należy poznać zasady

matematyczne obowiązujące przy wykonywaniu działań wymiarowych tolerowanych.

Działania matematyczne na wymiarach tolerowanych polegają na wyznaczeniu wartości

nominalnej wymiaru wynikowego X i jego odchyłek, górnej x

2

i dolnej x

1

w oparciu o znane

wymiary:

A

i

a

2i

a

1i

6

Metrologia Techniczna

wyk.3

29.03.2011

Do podstawowych działań matematycznych na wymiarach tolerowanych zaliczamy:

–

dodawanie i odejmowanie wymiarów tolerowanych

–

mnożenie lub dzielenie wymiarów tolerowanych
- przez stałą K
- wymiaru przez wymiar

–

podnoszenie do kwadratu lub pierwiastkowanie

–

działania złożone

Działania na wymiarach tolerowanych można prowadzić podstawowymi metodami:

–

metoda rachunku różniczkowego – polega na obliczeniu wymiaru nominalnego z
zależności:

x= f  A

1

, A

2

,... , A

n

, B

k1

, ... , P

n



, następnie wyznaczamy wartości

odchyłek dolnych i górnych.

–

Metoda wymiarów granicznych - polegająca na obliczeniu wymiaru nominalnego
oraz wymiarów granicznych, a następnie odchyłek.

Wartość odchyłki wyznaczamy z zależności:

–

odchyłka górna:

x

2

=

∑

i=1

k

∂

x

∂

A

i

⋅

a

2i



∑

i= k1

n

∂

x

∂

B

i

⋅

b

2i

–

odchyłka dolna:

x

1

=

∑

i =1

k

∂

x

∂

A

i

⋅

a

1i



∑

i=k 1

n

∂

x

∂

B

i

⋅

b

1i

gdzie:

A

i

- wymiary zwiększające

B

i

- wymiary zmniejszające

a

2i

, b

2i

- odchyłki górne

a

1i

, b

1i

- odchyłki dolne

Wymiary zwiększające i zmniejszające wyznaczamy w oparciu o następujące kryteria:

∂

x

∂

A

i



0

∂

x

∂

B

i



0

Dodawanie wymiarów tolerowanych:

X x

2

x

1

=

A a

2

a

1



B b

2

b

1

Wymiar nominalny wyznaczamy z zależności:

X =A B

7

Metrologia Techniczna

wyk.3

29.03.2011

Wymiary graniczne wyznaczamy z zależności:

X

max

=

A

max



B

max

=

Aa

2



Bb

2

X

min

=

A

min



B

min

=

Aa

1



Bb

1

Odchyłki graniczne wyznaczamy z zależności:

x

2

=

Aa

2



Bb

2

−

AB=a

2



b

2

x

1

=

Aa

1



Bb

1

−

AB=a

1



b

1

Wynik możemy zapisać jako:

X x

2

x

1

=

AB a

2



b

2

a

1



b

1

Przykład dodawania:

X x

2

x

1

=

150,25



0,10



250,1

−

0,1

=

400,35

0

Odejmowanie wymiarów tolerowanych:

X x

2

x

1

=

A a

2

a

1

−

B b

2

b

1

Wymiar nominalny:

X =A− B

Wymiary graniczne:

X

max

=

A

max

−

B

min

=

Aa

2

−

Bb

1



X

min

=

A

min

−

B

max

=

Aa

1

−

Bb

2



Odchyłki graniczne wyznaczamy z zależności:

x

2

=

Aa

2

−

B−b

1

−

A− B=a

2

−

b

1

x

1

=

Aa

1

−

B−b

2

−

A−B=a

1

−

b

2

Wynik można zapisać jako:

X x

2

x

1

=

A−B a

2

−

b

1

a

1

−

b

2

Przykład odejmowania:

X x

2

x

1

=

350,2



0,1

−

50,05

−

0,05

=

300,25

0,05

* jeżeli przed kolejnym wymiarem znajduje się znak minus, bierzemy pod uwagę przeciwny wymiar w

stosunku do tego który aktualnie liczymy z uwzględnieniem minusa przed wymiarem.

8