Materiały półprzewodnikowe 

 

 

1

 

 

Materiały półprzewodnikowe

 

 
 
 

Zad. 2.1 

 

 
Przyjmując szerokość przerwy energetycznej dla germanu              

W

go1

 

= 0.78 eV  i  krzemu W

go2

  = 1.21 eV oszacować stosunek 

2

i

1

i

n

n

 

koncentracji samoistnych w tych materiałach w temperaturze 

300 K.  

 

Zad. 2.2 

 

 

Wyznaczyć temperaturowy współczynnik względnych zmian 
koncentracji nośników samoistnych w krzemie i germanie. Obliczyć 
wartość tego współczynnika w temperaturze 

300 K dla obu 

pierwiastków. 
 

Zad. 2.3 

 

 

Obliczyć wartości temperaturowych współczynników względnych 
zmian koncentracji elektronów i dziur w krzemie typu n o 
koncentracji 

3

13

D

cm

10

N

−

=

 w dwóch temperaturach 

K

300

T

1

=

 i 

K

500

T

2

=

. 

 

 

Zad. 2.4 

 

 

 

Do 

100 g krzemu samoistnego dodano 10

-6 

g boru. Przy założeniu 

równomiernego rozmieszczenia atomów domieszki w sieci 
krystalicznej, znaleźć: 
a)  typ półprzewodnika 
b)  koncentrację nośników większościowych i mniejszościowych w 

temperaturze 

T = 300 K  

 
Dane: 

 

ciężar atomowy boru – 

10.82 g/mol 

gęstość krzemu – 

2.33 g/cm³ 

Materiały półprzewodnikowe 

 

 

2

 

Zad. 2.5 

 

Dysponując wykresem przedstawionym na rys. 2.3 wyznaczyć 
występujący w zależności 

( )

T

i

σ

 czynnik przedeksponencjalny 

(niezależny od temperatury) oraz parametr charakteryzujący materiał 
półprzewodnikowy. 
 

1/T

0,003

5

i

ln

σ

 

 

Zad. 2.6 

 

 

Wyznaczyć temperaturowy współczynnik względnych zmian 
konduktywności silnie domieszkowanego krzemu typu 

p. Obliczyć 

wartość tego współczynnika w temperaturze 

T = 300 K 

 

Zad. 2.7 

 

O ile procent wzrośnie konduktywność próbki germanu samoistnego 
przy zmianie temperatury 

od 300 K do 300.5 K oraz od 300 K do  

350 K? 

 

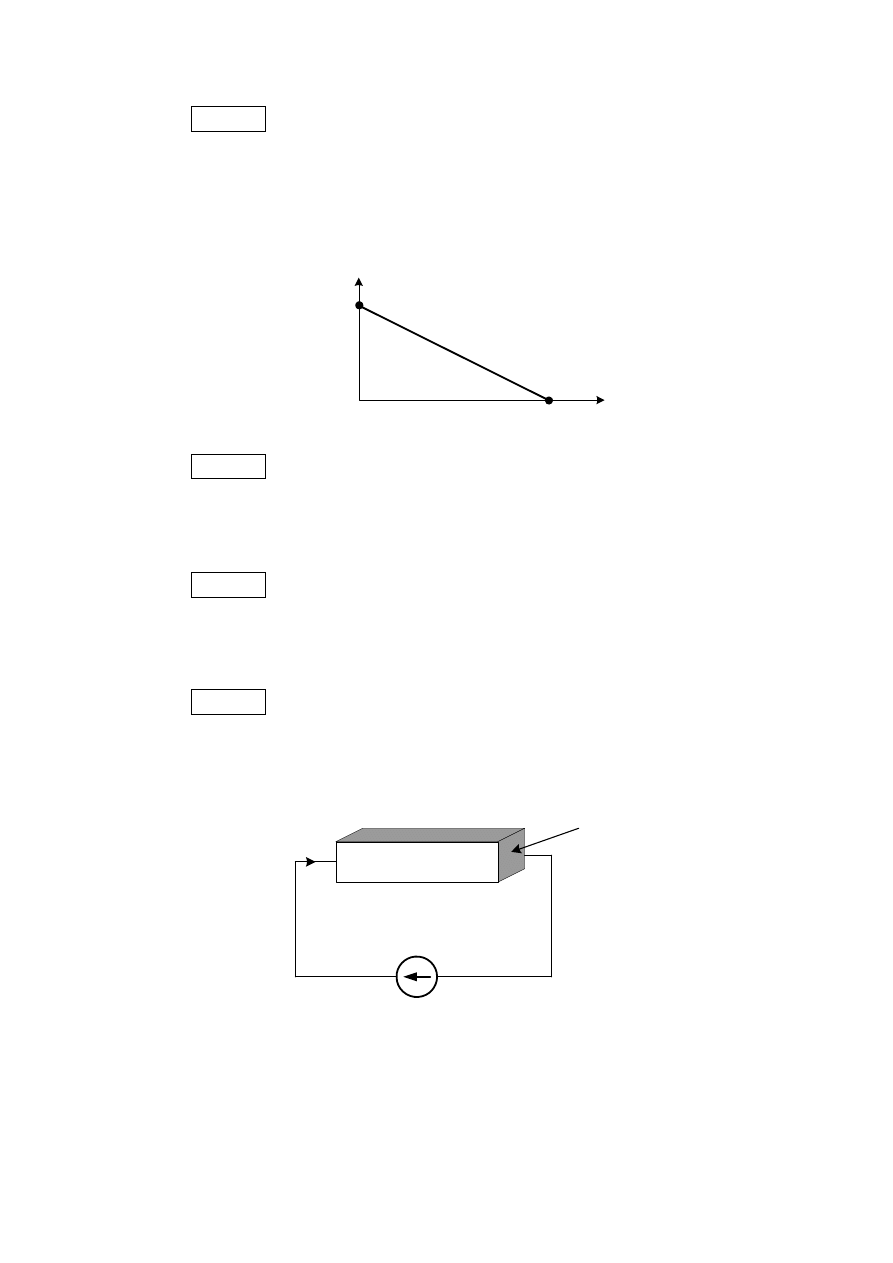
Zad. 2.8 

 

Rezystor półprzewodnikowy o wymiarach podanych na rysunku 
połączono szeregowo ze źródłem 

E = 10 V. 

 

E=10V

S=1cm

2

l=10cm

i

 

W temperaturze  

K

300

T

1

=

, w której półprzewodnik jest silnie 

domieszkowany, płynie prąd 

mA

100

i

1

=

. Oblicz prąd w obwodzie 

w temperaturze 

K

290

T

2

=

. 

Rys. 2.4

 

Rys. 2.3 

Materiały półprzewodnikowe 

 

 

3

 

Zad. 2.9 

 
Powierzchnia półnieskończenie wielkiej bryły krzemu typu 

n jest 

oświetlana w  sposób ciągły ze stałą  wydajnością, tak że koncentracja 
dziur na powierzchni  wynosi 

p

n

(x = 0) = 5.5 · p

no

, 

zaś koncentracja 

dziur w odległości w od  powierzchni  wynosi  

p

n

(x = w

1

) = p

no

.  

Wyznaczyć    rezystywność  próbki dla 

T = 300 K,  τ

p 

= 200 μs,          

w

1

 = 0.1 cm. 

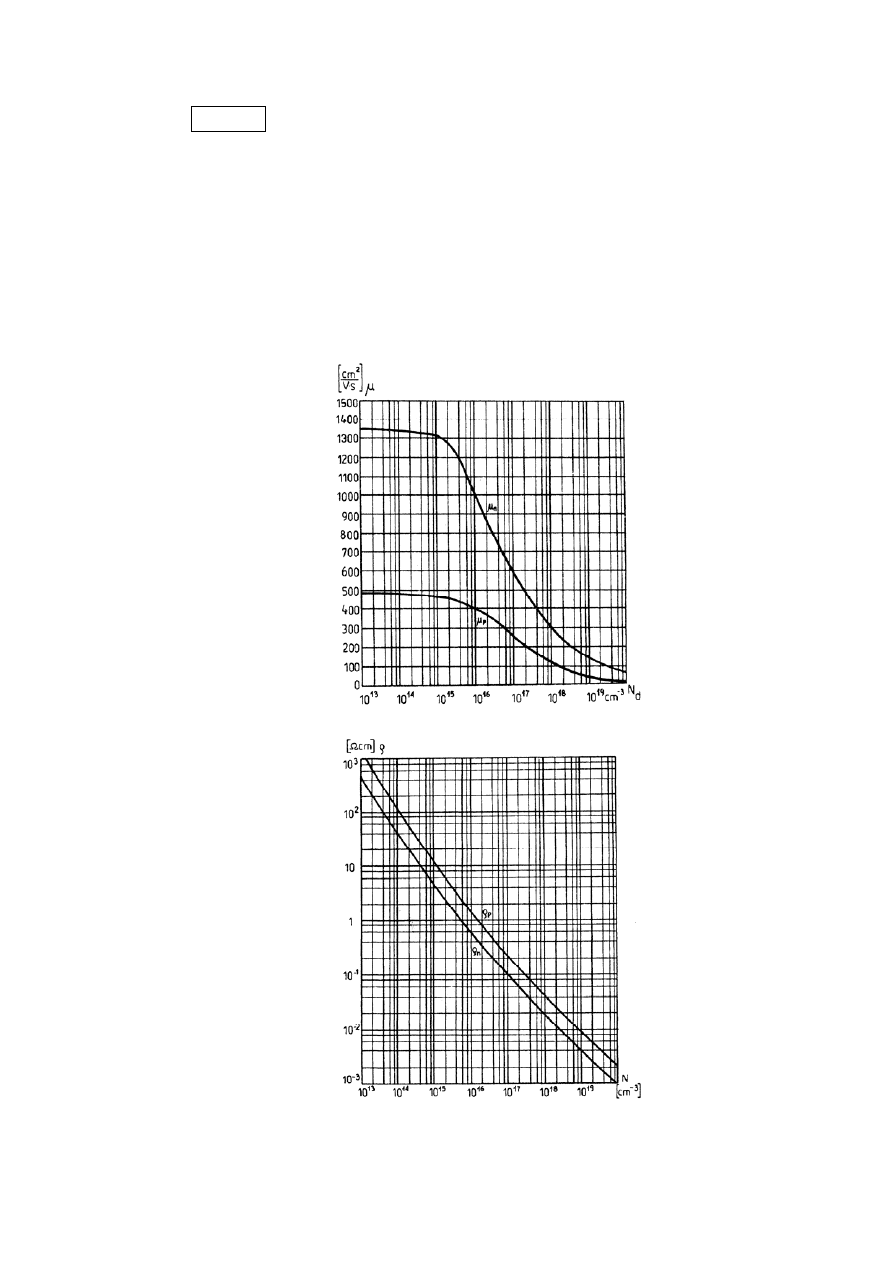
Zależność  

( )

D

N

μ

 oraz 

( )

D

N

ρ

 przedstawiono na rys 2.5 

 

 

 

 

a)

 

b)

 

Rys. 2.5