Fizyka Ogólna

W yk³ad IV

1

Drgania nieliniowe

Najprostsze uogólnienie równania ruchu dla oscylatora
harmonicznego da siê zapisaæ:

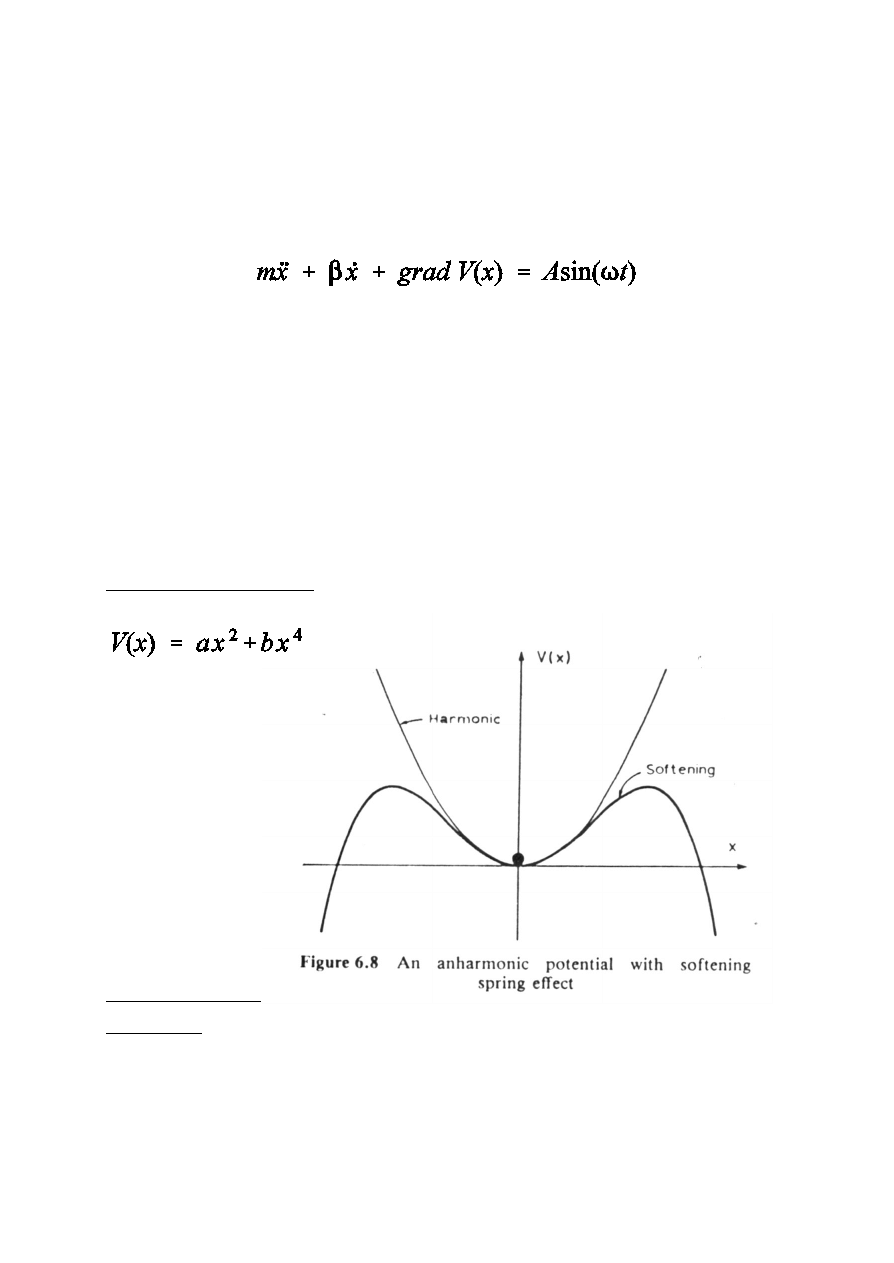
gdzie V(x) jest energi¹ potencjaln¹ w jakiej porusza siê
oscylator. Oczywiœcie oscylator harmoniczny porusza siê w
potencjale V(x) = 2 a x2.

Gdy wychylenia uk³adu s¹ du¿e zaczynaj¹ odgrywaæ coraz to
dalsze wyrazy rozwiniêcia potencja³u V(x) na szereg. Potencja³
zawieraj¹cy co najwy¿ej 4-t¹ potêgê nazywa siê potencja³em
anharmonicz-nym.
“Miêkka” sprê¿yna
P o t e n c j a ³

dla b < 0 to
p r z y p a d e k
s p r ê ¿ y n y
niel iniowej ,
k t ó r e j
s p r ê ¿ ys t o œ æ
ma l e j e d l a
w i ê k s z y c h
drgañ x.

“ T w a r d a ”
sprê¿yna
Odwrotny przypadek zachodzi gdy b > 0. Wtedy sprê¿ystoœæ
sprê¿yny roœnie w miarê wzrostu wychylenia x.

Fizyka Ogólna

W yk³ad IV

2

Obecnoœæ nieliniowoœci w równaniu ruchu prowadzi do szeregu
ciekawych efektów:
‚

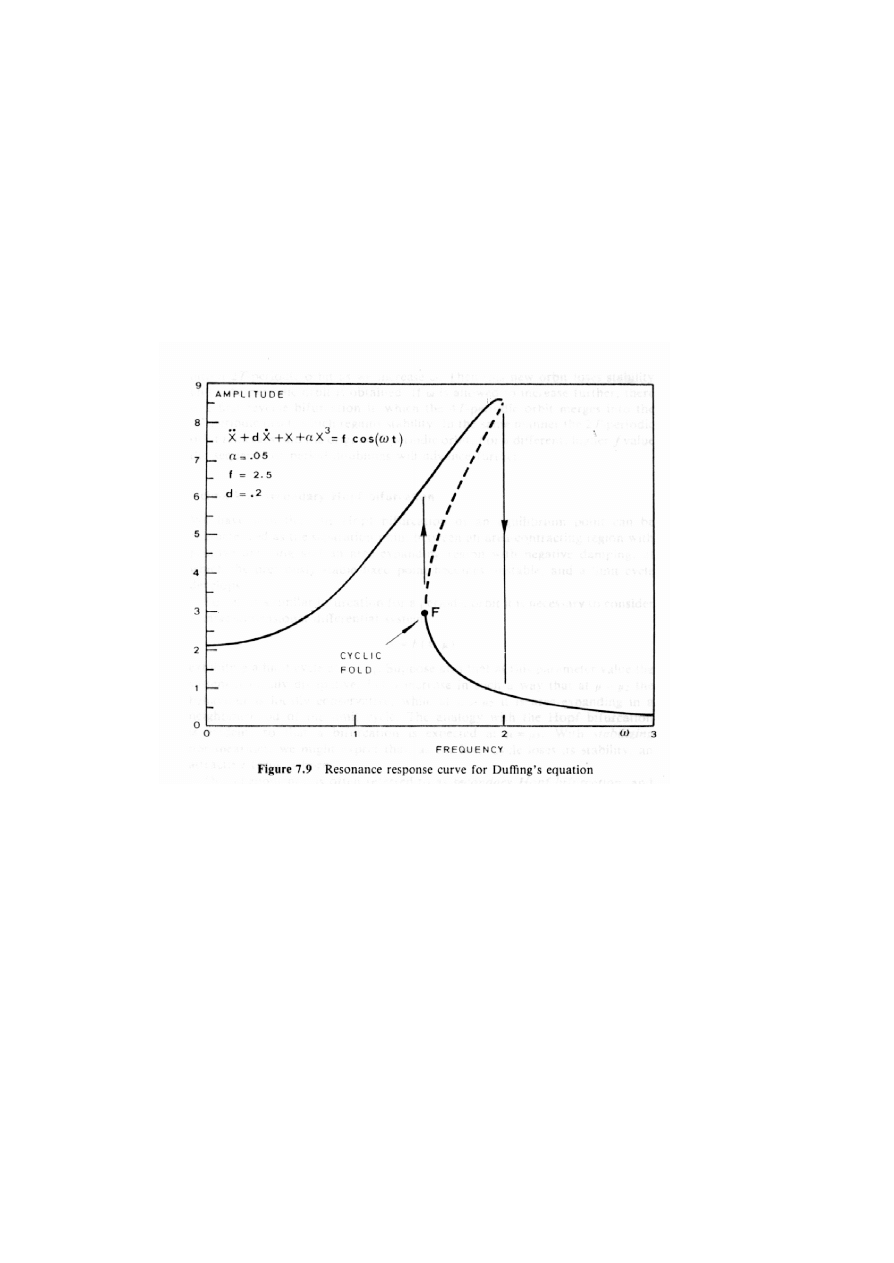
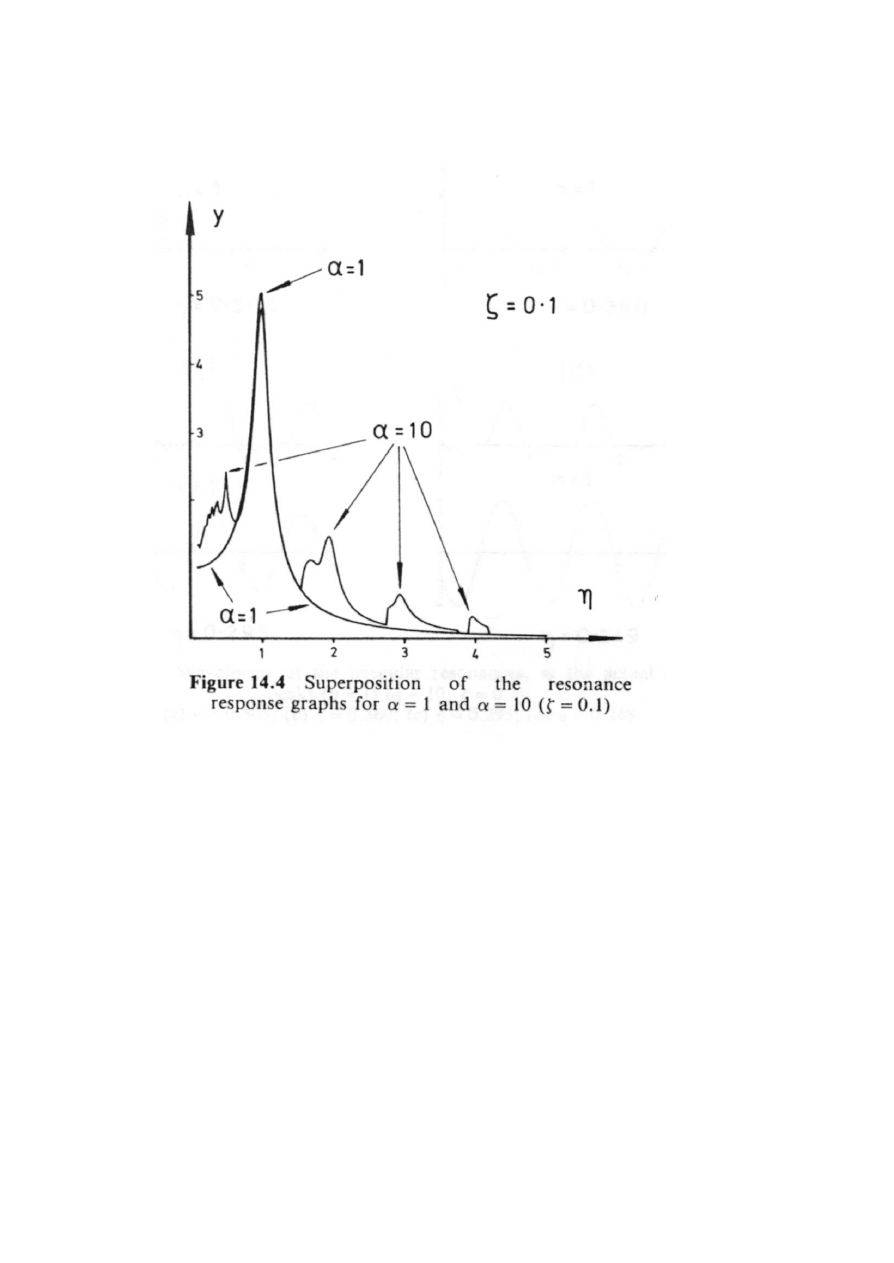
Nieliniowy rezonans
Krzywa rezonansowa ulega zniekszta³ceniu. Wygina siê

ona w lewo, gdy potencja³u typu miêkka sprê¿yna oraz w prawo
dla potencja³u sprê¿yny twardej

Jednoczeœnie pojawiaj¹ siê nowe zjawiska:
!

multistabilnoœæ - istniej¹ pewne zakresy parametrów
kontrolnych uk³adu (na rys. obok jest to czêstoœæ), dla
których w zale¿noœci od warunków pocz¹tkowych
otrzymaæ mo¿na 2 (czasami wiêcej ) rozwi¹zañ.

Fizyka Ogólna

W yk³ad IV

3

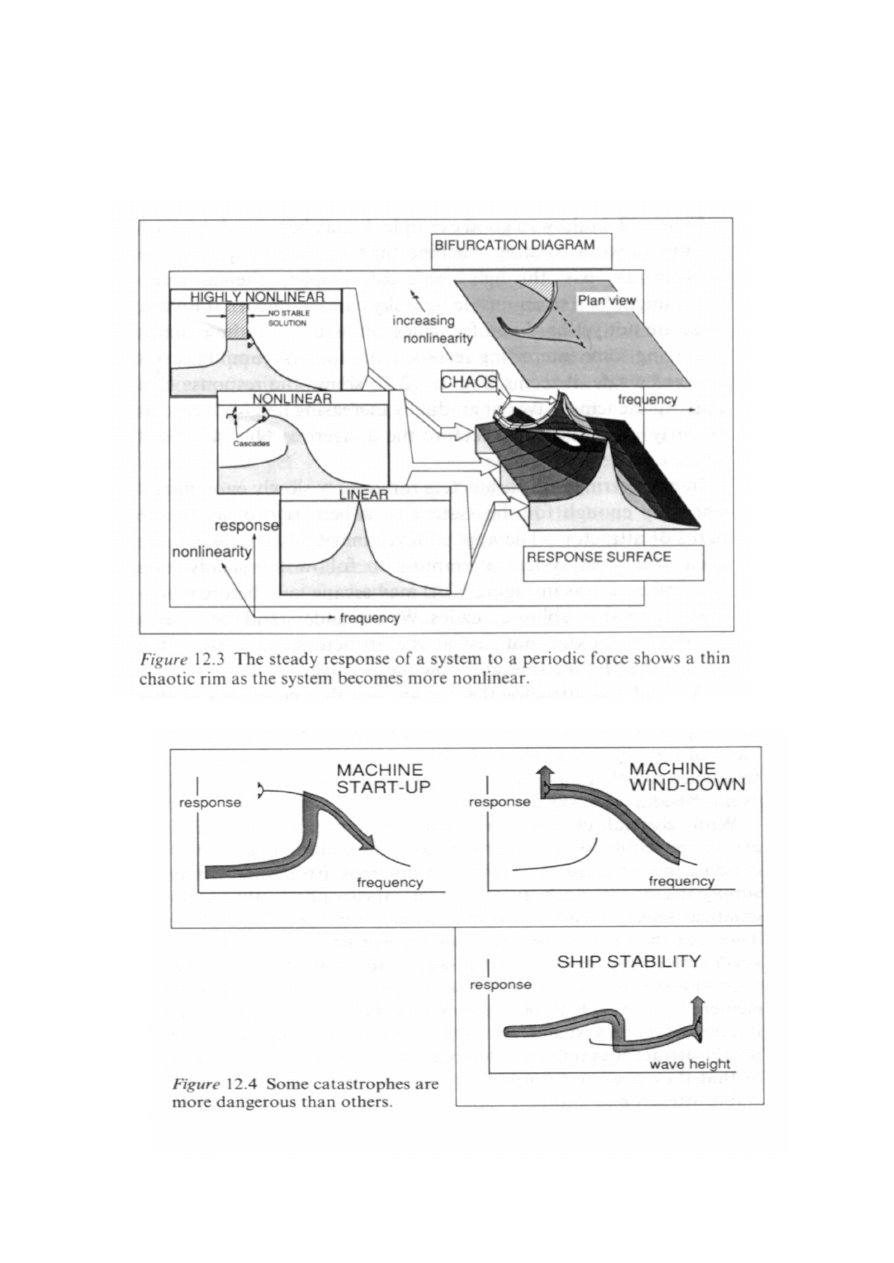
Ju¿ nieliniowoœæ czwartego stopnia w potencjale (tj. 3-go
stopnia w sile) mo¿e prowadziæ do bardzo z³o¿onych trajektorii
w tym równie¿ chaotycznych.

Fizyka Ogólna

W yk³ad IV

4

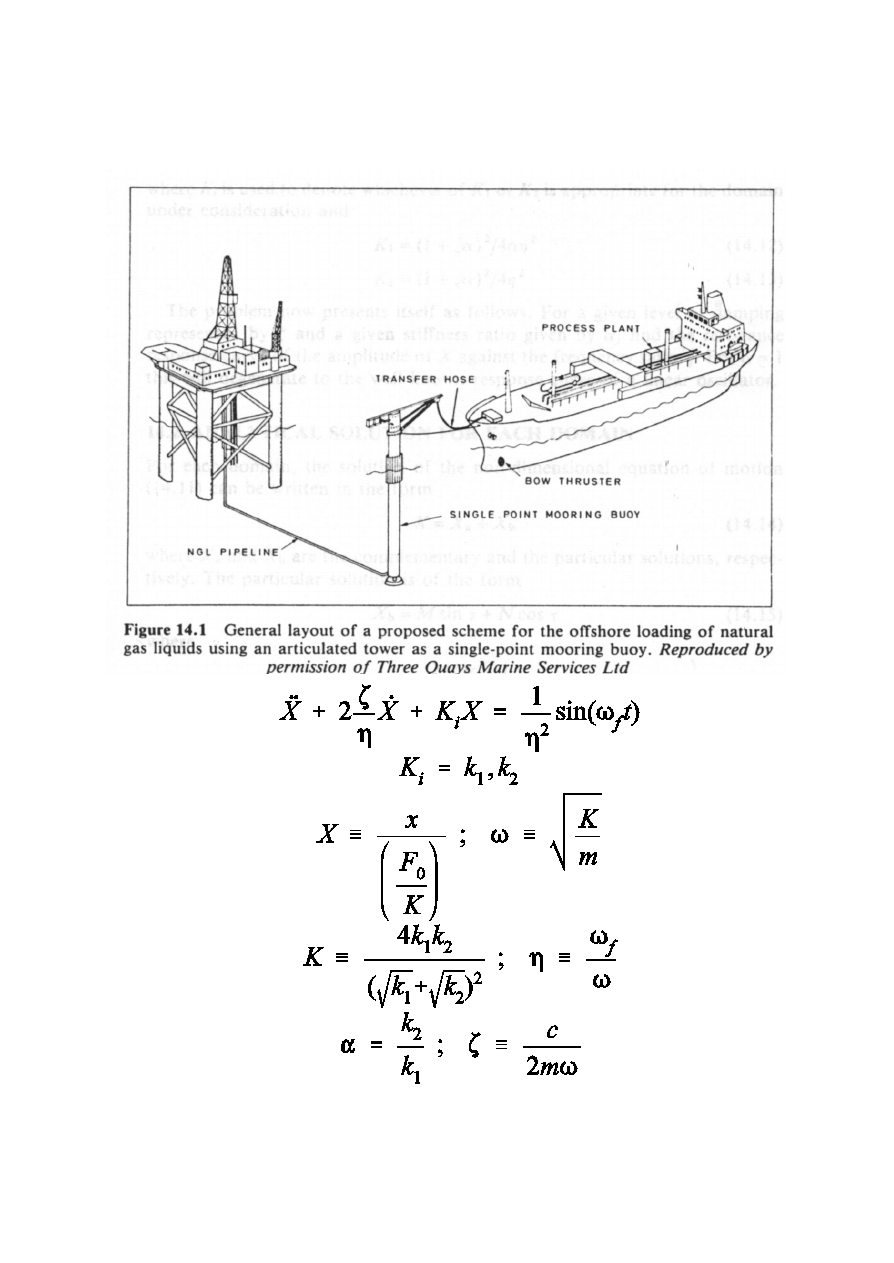
Inne proste nieliniowosci prowadz¹ do wielu zjawisk jak np.
!

rezonans podharmoniczny

Fizyka Ogólna

W yk³ad IV

5

W powy¿szym przyk³adzie Tf jest czêstoœcia wymuszenia (tj. fal

morskich).

!

ruch chaotyczny

Czu³oœæ na warunki pocz¹tkowe

Powy¿ej widzieliœmy, ¿e w miarê zmiany parametru

kontrolnego (np. zmiany amplitudy si³y zewnetrznej lub jej
czêstoœci) proste drgania harmoniczne trac¹ stabilnoœæ i s¹
zastêpowane innymi rozwi¹zaniami o bardziej z³o¿onym
charakterze.
Typowym objawem takiego zachowania jest np. podwajanie
okresu gdy uk³ad - dotychczas poruszaj¹cy siê z czêstoœci¹ T
porusza siê z czêstoœci¹ T/2 . Zazwyczaj przejœcie takie polega
na tym, ¿e co druga amplituda drgania ma inn¹ wysokoœæ.

Fizyka Ogólna

W yk³ad IV

6

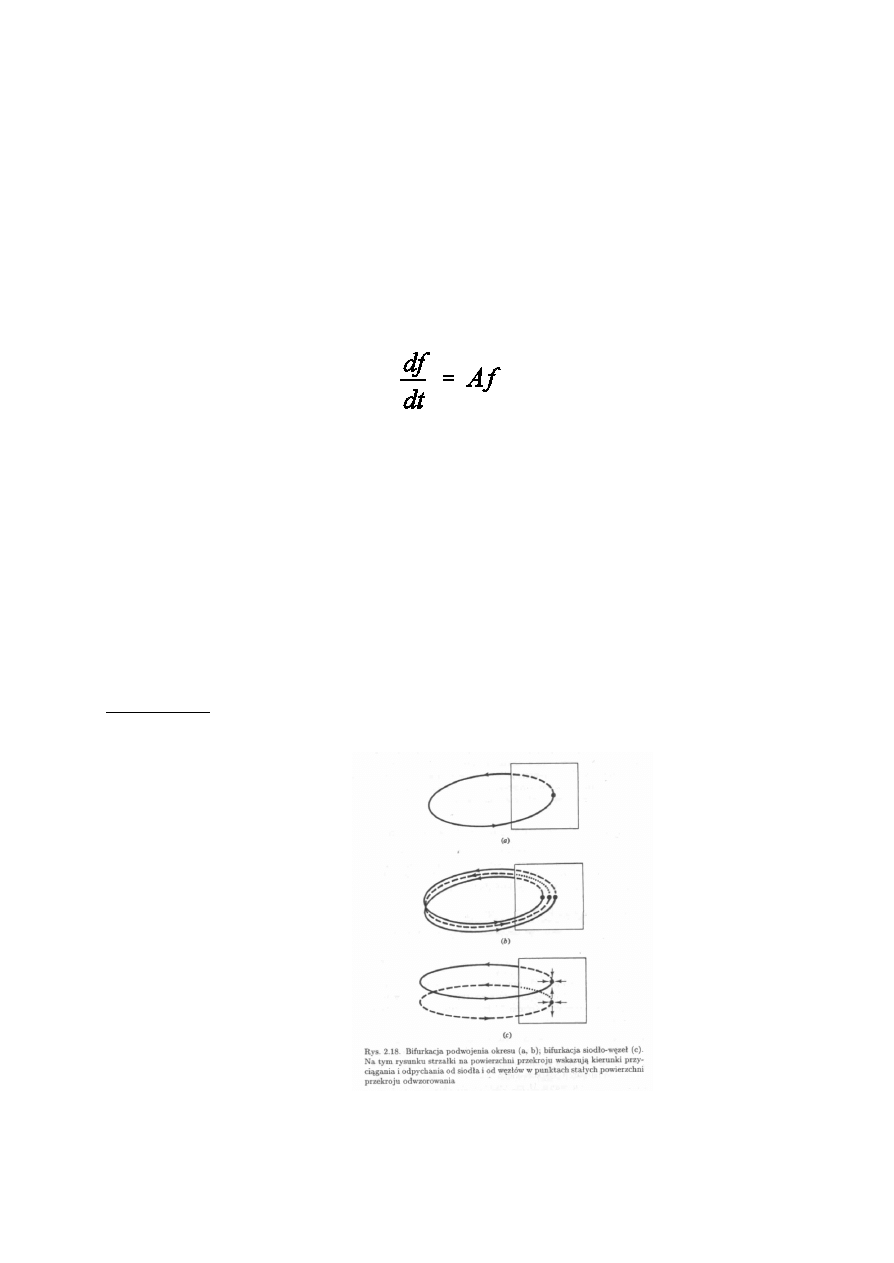
Mówimy, ¿e wyst¹pi³a bifurkacja. Klasyfikacjê bifurkacji

uzyskuje siê linearyzuj¹c równanie ró¿niczkowe w pobli¿u
punktu bifurkacji

rozwijaj¹c rozwi¹zanie dla parametru kontrolnego równego
punktowi bifurkacji i zachowuj¹c tylko wyrazy liniowe

a nastêpnie badaj¹c wartoœci w³asne macierzy jakie siê z takiej
linearyzacji wy³oni¹. Zlinearyzowane równanie ruchu przyjmuje
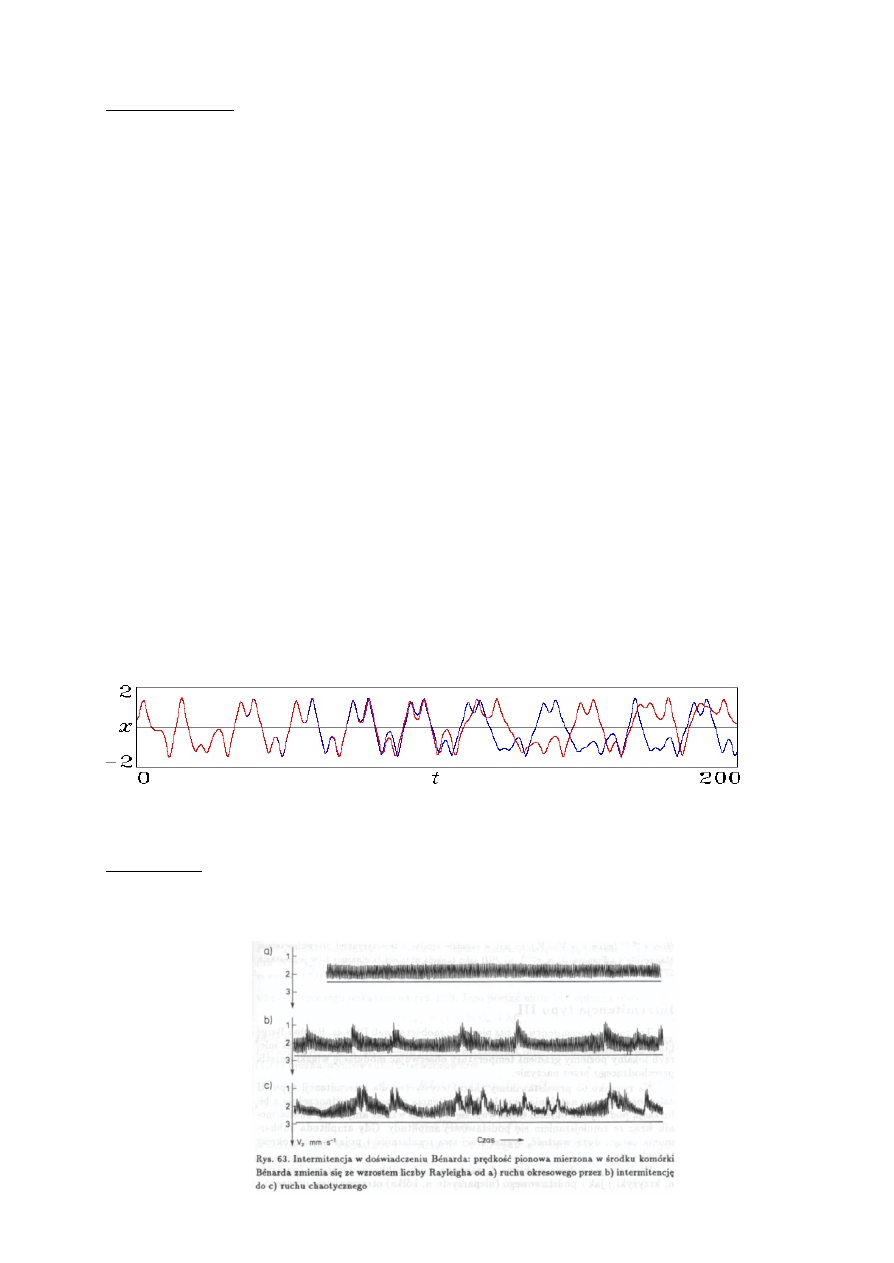
wtedy postaæ:

gdzie f jest rozwi¹zaniem równania zlinearyzowanego zaœ A jest
macierz¹ charakterystyczn¹.

Zmiana znaku i/lub zmiana wartoœci rzeczywistej na

urojon¹ czy te¿ przekroczenie okrêgu jednostkowego na
p³aszczyŸnie zespolonej przez wartoœci w³aœciwe macierzy
charakterystycznych odpowiadaj¹ ró¿nego rodzjau bifurkacjom
rozwi¹zañ nieliniowego równania.
Przyk³ad:
Bifurkacja podwajania okresu prostego drgania harmonicznego

Bywaj¹ takie uk³ady fizyczne, w których nastêpuje ci¹g
bifurkacji: kolejne roziw¹zania trac¹ stabilnoœæ na rzecz
nastêpnych.

Fizyka Ogólna

W yk³ad IV

7

Przyk³adem jest tzw. droga do chaosu przez podwajanie okresu,
w której odstêpy pomiêdzy kolejnymi podwojeniami okresu
malej¹ w postêpie geometrycznym. Gdy parametr kontrolny
uk³adu osi¹gnie tzw. punkt akumulacji okres trajektorii staje siê
nieskoñczony. Oznacza to trajektoriê, która siê nie powtarza.
Mówimy wtedy, ¿e uk³ad osi¹gn¹³ stan chaosu
deterministycznego.

Stan chaotyczny jest to dope³nienie zbioru wszystkich
niestabilnych trajektorii okresowych uk³adu w takim obszarze
przestrzeni parametrów kontrolnych, gdzie ¿aden stan okresowy
nie jest stabilny.

Wprowadza siê rózró¿nienie pomiêdzy stanami chaotycznymi a
zachowaniem przypadkowym
Chaotycznoœæ trajektorii uk³adów deterministycznych wynika z
czu³oœci na warunki pocz¹tkowe uk³adu w stanie niestabilnym
a nie z dzia³ania czynników przypadkowych

Dróg do chaosu jest wiêcej.
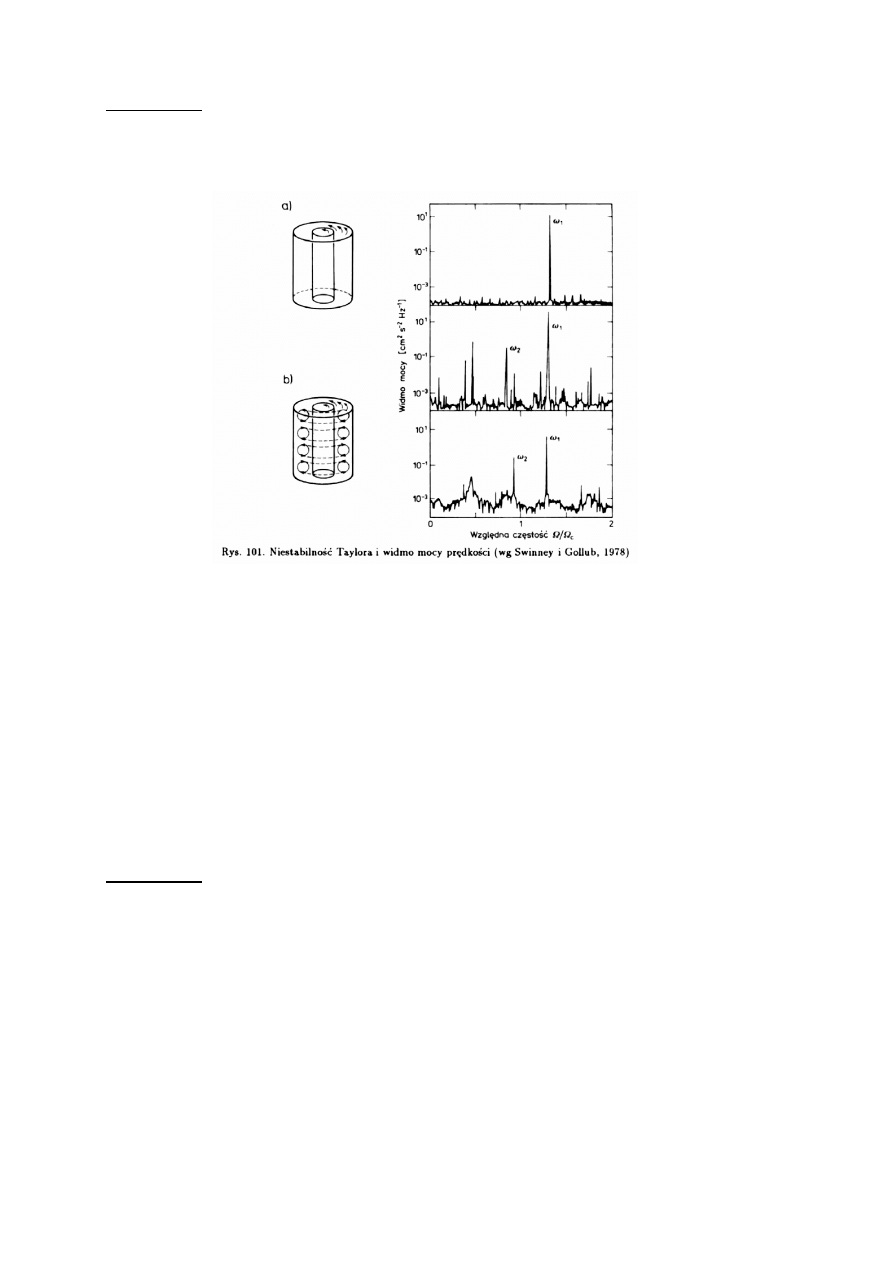
Przyk³ad
Droga do chaosu poprzez intermitencjê

Fizyka Ogólna

W yk³ad IV

8

Przyk³ad
Droga do chaosu poprzez kwazi-okresowoϾ

W widmie mocy pojawiaja siê nowe niewspó³mierne czêstoœci

UniwersalnoϾ zjawisk chaotycznych

Znaczenie zarówno poznawcze jak i praktyczne ma to, ¿e

cechy ruchu chaotycznego s¹ w du¿ym stopniu uniwersalne.
Rozumiemy tu fakt, ¿e fizycznie bardzo ró¿ne uk³ady wykazuj¹
bardzo podobne zachowania dynamiczne.

Przyk³ad
Drogê do chaosu poprzez kwazi-okresowoœæ znaleziono w
!

uk³adzie wahad³a nieliniowego
(wahad³o matematyczne o du¿ych k¹tach wychylenia),

!

w przep³ywach ciep³a

!

w przewodnictwie niektórych substancji (nioban barowo-
sodowy - rodzaj ceramiki przewodz¹cej).

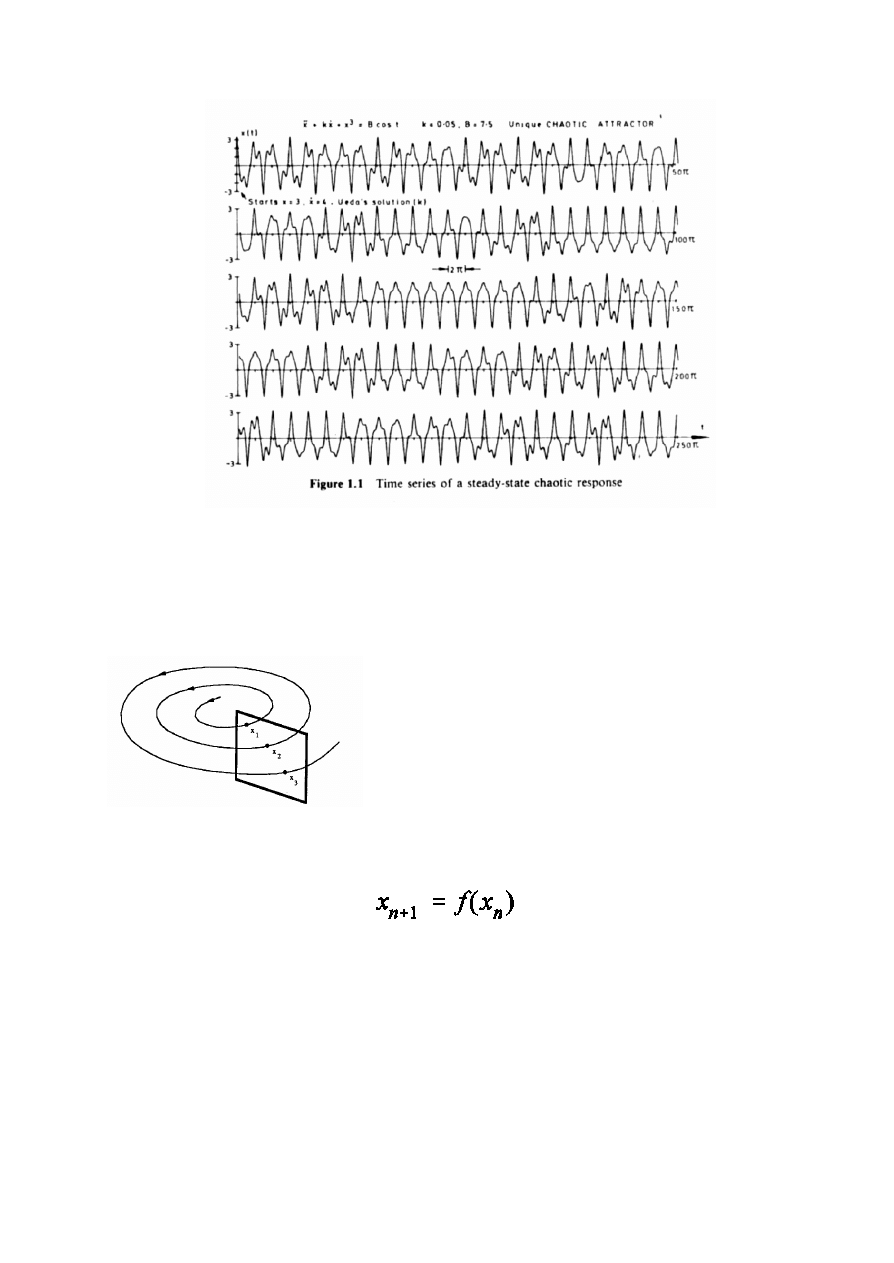
Cech¹ wspóln¹ uk³adów dynamicznych w ruchu chaotycznym
jest samo-podobieñstwo zachowania (ewolucji w czasie) w
ró¿nych okresach czasu:

Fizyka Ogólna

W yk³ad IV

9

Uniwersalnoœæ ta wynika z w³asnoœci równañ ró¿niczkowych,
które s¹ równaniami ruchu uk³adu.

Je¿eli rozpatrzeæ przeciêcie

trajektorii fazowej uk³adu p³aszczyzn¹
to oka¿e siê, ¿e w trakcie jednego
obiegu przestrzeni fazowej uk³ad
dokonuje

odwzorowania n-tego punktu przeciêcia trajektorii z
p³aszczyzn¹ przekroju w n+1 punkt przekroju:

gdzie xn jest n-tym punktem na przekroju trajektorii

!

Czêsto te odwzorowania okazuj¹ siê jednowymiarowe i
mo¿na je zapisaæ postaci g³adkich fun kcji
jednoparametrowych.

Fizyka Ogólna

W yk³ad IV

10

To w³aœnie te odwzorowania - niejako ukryte w dzia³aniu uk³adu
- s¹ uniwersalne:

Ich postaæ funkcyjna okazuje wspólna dla wielu ró¿nych
uk³adów.

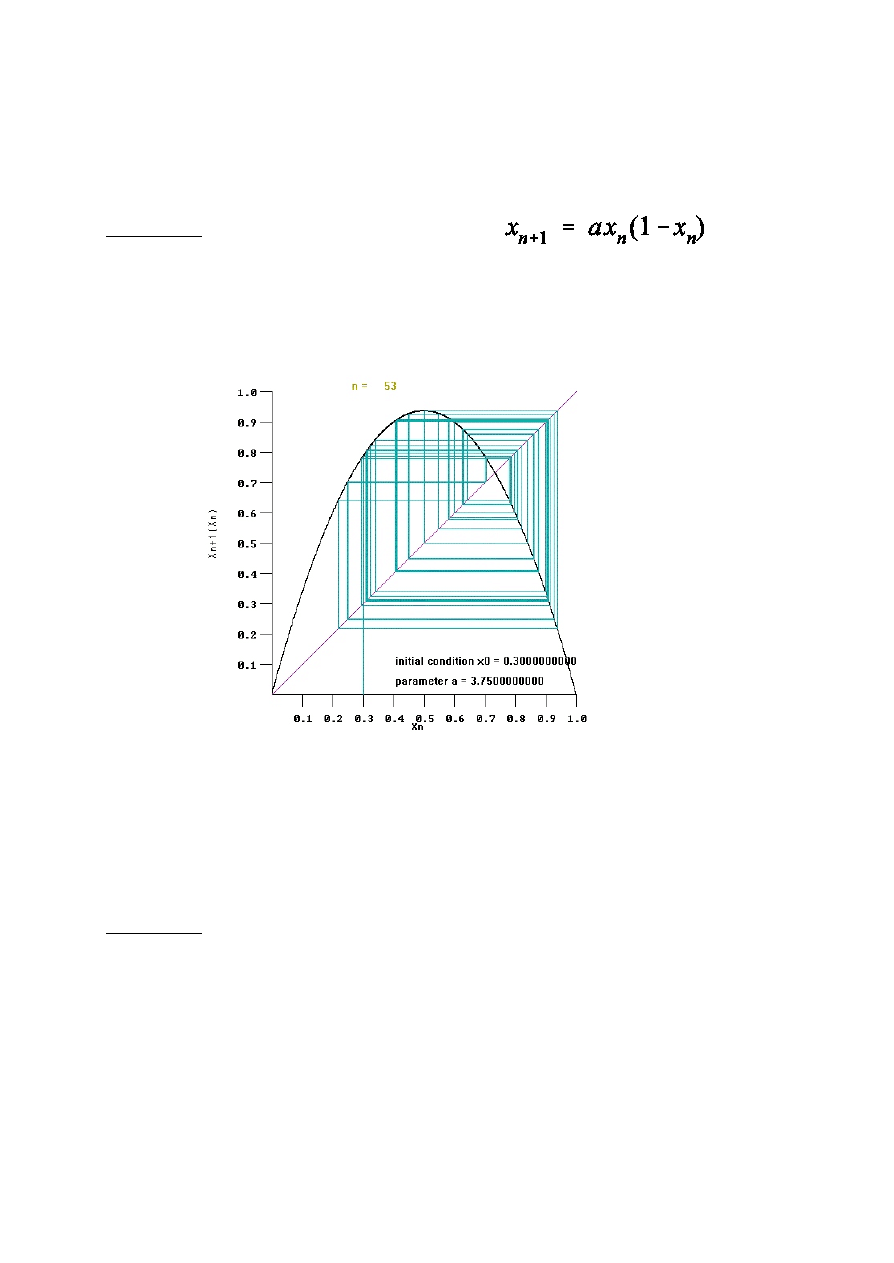
Przyk³ad odwzorowanie logistyczne
jest jednym z najbardziej rozpowszechnionych typów
odwzorowañ dyskretnych otrzymywanych z przekroju trajektorii
fazowej. Nale¿y ono do klasy odwzorowañ unimodalnych tj. z
jednym g³adkim maximum.

Uniwersalnoœæ zachowañ uk³adów dynamicznych spowodowa³a,
¿e teoria chaosu deterministycznego znalaz³a zastosowanie w
bardzo wielu dziedzinach nauki i techniki.

Przyk³ad
Zbiór warunków pocz¹tkowych prowadz¹cy do danego atraktora
nazywamy basenem atrakcji.

Baseny atrakcji wielu atraktorów nie s¹ prostymi obiektami
geometrycznymi - czêsto s¹ fraktalami:

Fizyka Ogólna

W yk³ad IV

11

Po lewej pokazano kilka ró¿nych przyk³¹dów uk³adów maj¹cych
z³o¿one baseny atrakcji.
Na tych rysunkach kolorem ¿ó³tym oznaczono rozwi¹zania
(atraktory) porz¹dane a niebieskim - nieporz¹dane.
Po prawej pokazane s¹ baseny atrakcji dla stanów statku na
sfalowanym morzu. Widaæ, ¿e niebieski (stan “stêpk¹ do góry”)
w funkcji stanu morza wtargn¹³ do basenu atrakcji statku
stabilnego. Fraktalnoœc tych basenów atrakcji œwiadczy o
niestablinoœci statku: bardzo ma³a zmiana warunku
pocz¹tkowego prowadzi do wywrotki.