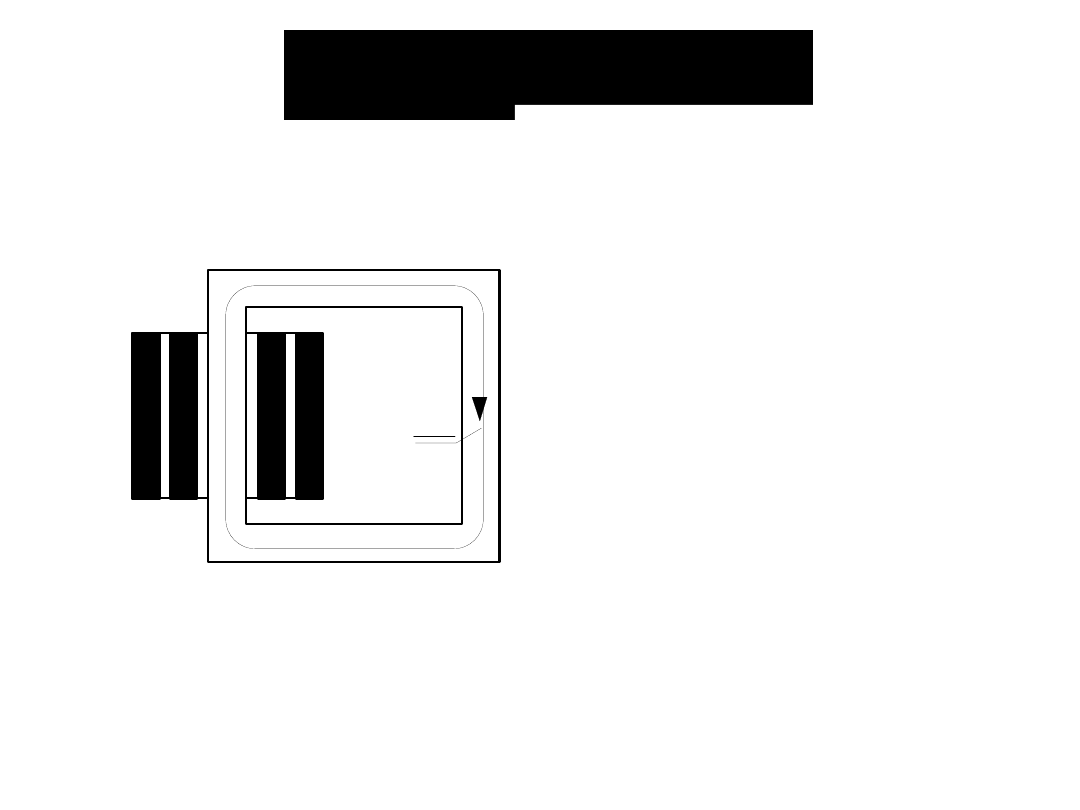
Transformatory

Transformatory

trójfazowe

trójfazowe

R



S



T





R

+ 

S

+ 

T

= 0

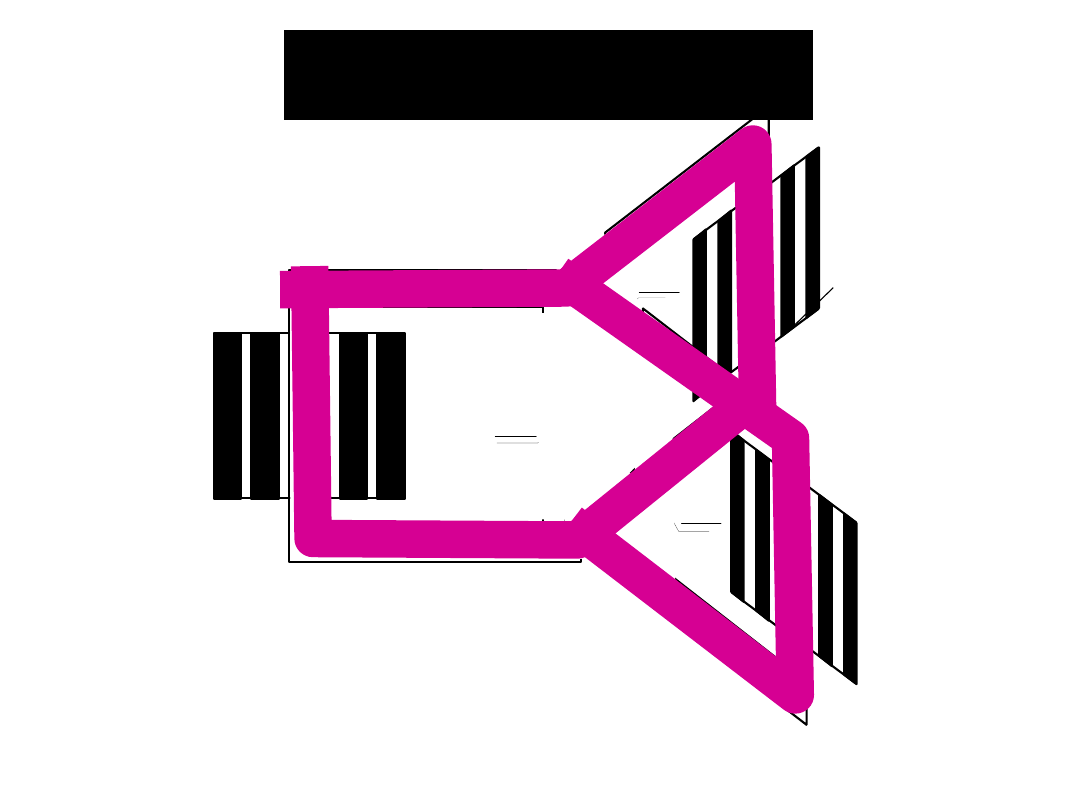
Transformatory

Transformatory

trójfazowe

trójfazowe

R



S



T





R

+ 

S

+ 

T

= 0

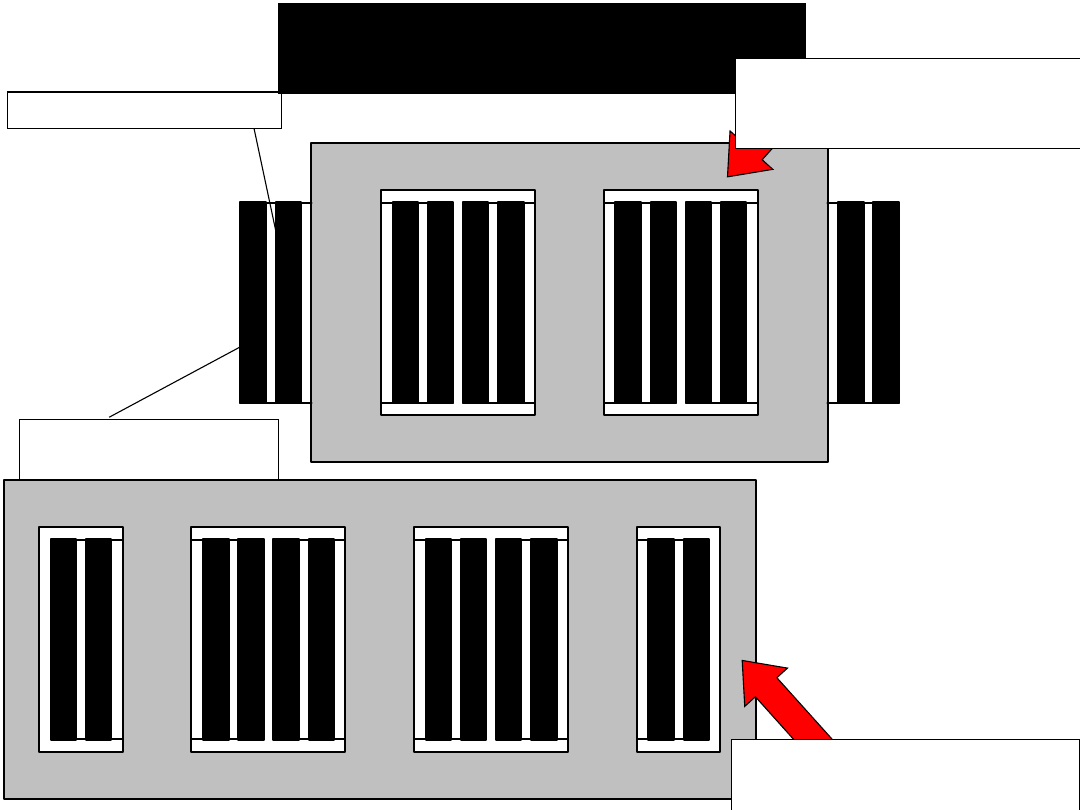
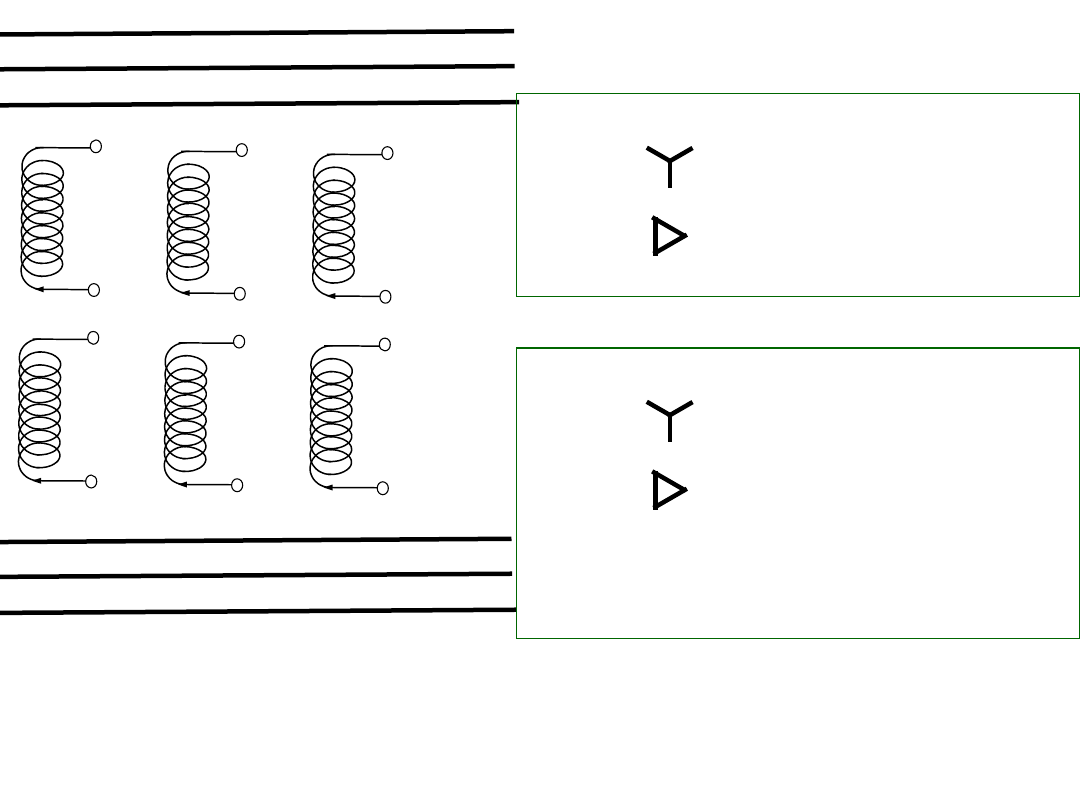
Uzwojenie dolne

Uzwojenie

górne

Transformatory

Transformatory

trójfazowe

trójfazowe

Struktura 3
kolumnowa

Struktura 5
kolumnowa

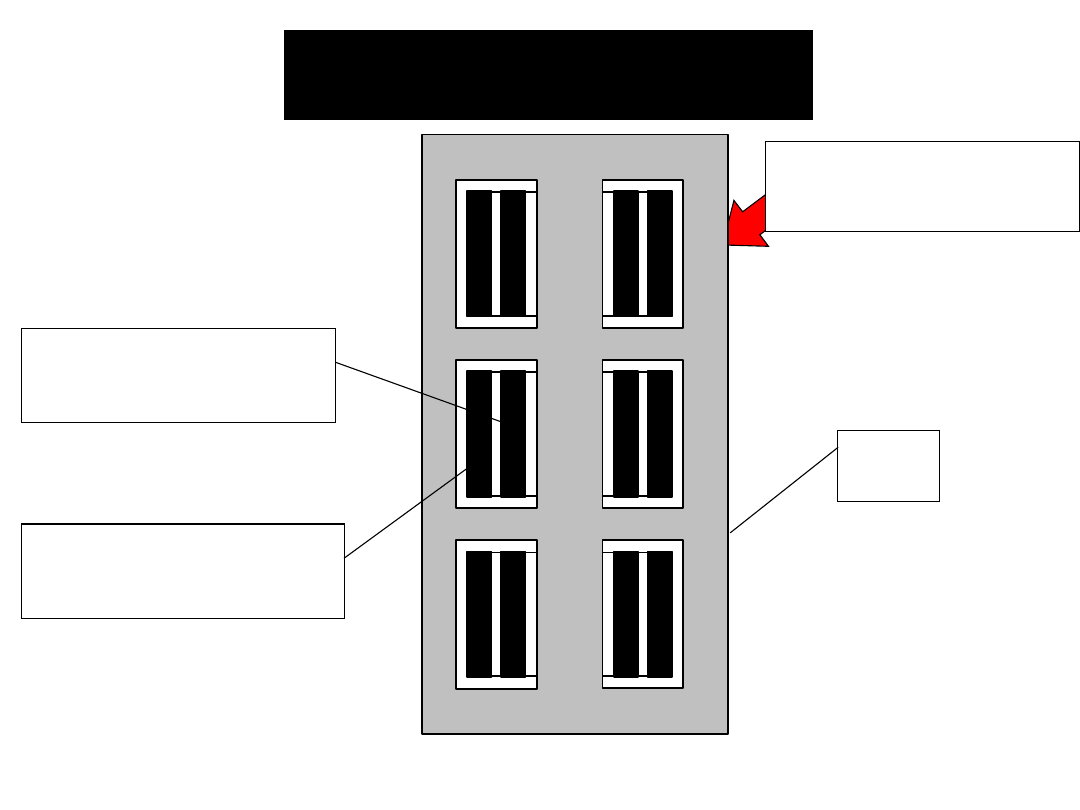
Rdze
ń

Uzwojenie dolne

(zwykle

niskiego

napięcia)

Uzwojenie górne

(zwykle

wysokiego

napięcia)

Transformatory

Transformatory

trójfazowe

trójfazowe

Struktura
płaszczowa

u

A

u

B

u

C

u

R

u

S

u

T

u

r

u

s

u

t

u

a

u

b

u

c

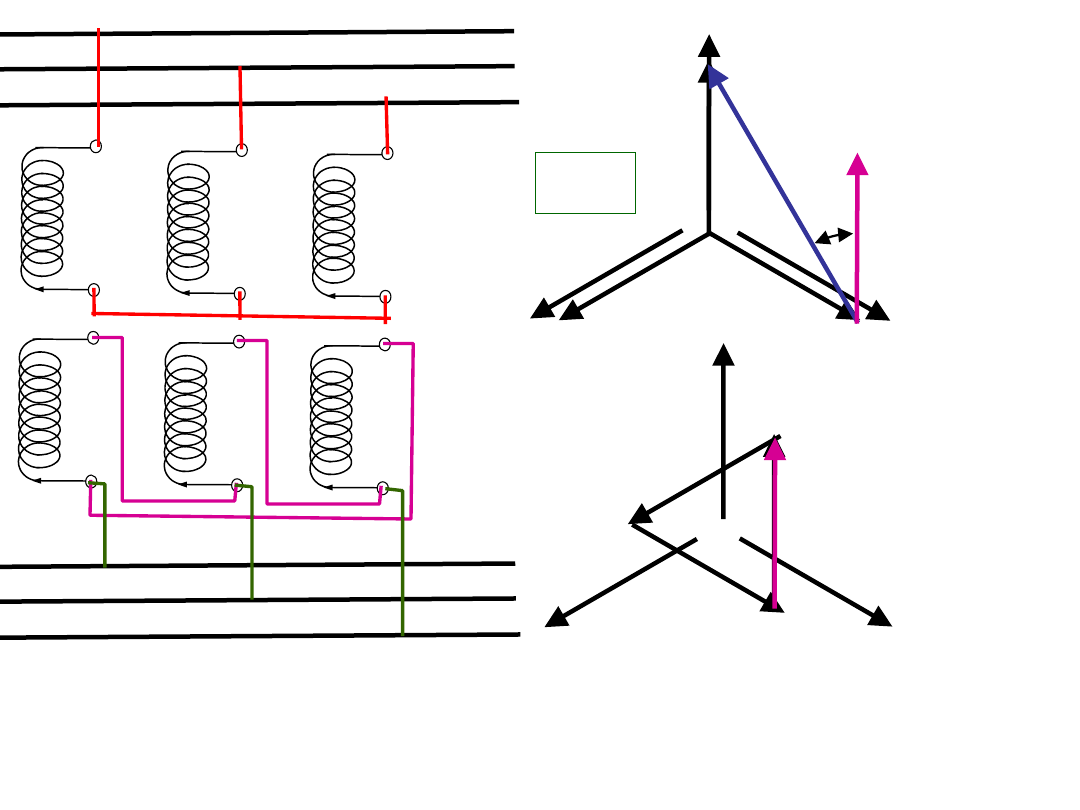
Uzwojenie pierwotne

połączone w:

gwiazdę , Y

trójkąt , , D

Uzwojenie wtórne połączone

w:

gwiazdę , y lub y

0

(z przew.

zerowym)

trójkąt , , d
zygzak

(gwiazda łamana)

u

A

u

B

u

C

u

R

u

S

u

T

u

r

u

s

u

t

u

a

u

b

u

c

u

c

u

a

u

b

u

C

u

A

u

B

u

A

u

B

u

C

u

R

u

S

u

T

u

r

u

s

u

t

u

a

u

b

u

c

u

c

u

a

u

b

u

C

u

A

u

B

X

Y

Z

(

R

)

(

S

)

(

T

)

x

y

z

A

B

C

(X,Y,Z
)

a

b

c

u

c

u

a

u

b

(x,b)

s

(z,a)

r

(y,c)

t

(r,s)

(R,S)

(r,s)

Yd1

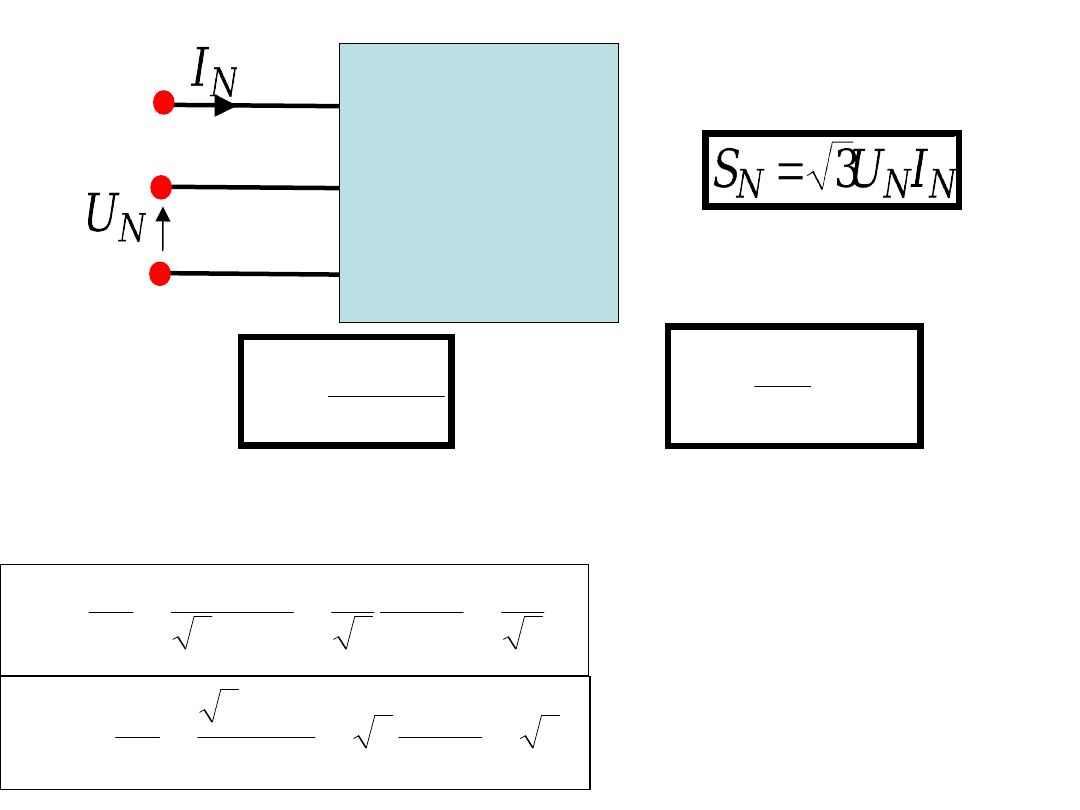
N

N

z

z

S

U

u

Z

100

2

%



CuN

N

N

z

P

S

U

R





2

2

Ważne

W transformatorach 3-fazowych przekładnia zwojowa może
różnić się od przekładni napięciowej

Dy;









3

1

3

1

3

2

1

2

1

2

1

faz

faz

faz

faz

U

U

U

U

U

U









3

3

3

2

1

2

1

2

1

faz

faz

faz

faz

U

U

U

U

U

U

Yd;

2

2

1I

I







2

1

2

1

,

,

L

L







2

2

E

E







2

2

U

U







2

2

2

R

R 





2

2

2

r

r

X

X







1

2

0

I

I

I







2

1

2

1

,

,

X

X

X

g











1

R

2

R

1

r

jX

2

r

X

j 

g

jX

1

I

2

I

2

U

1

U

0

I

o

I

2

I

o

I



o

U

o

U



2

U

c

0

I

0

I



E

E



Fe

R

c

0

I

1

g

jX

E



0

I



1

1

o

Z

o

Z



o

Z

2



2

1

2

1

12

11

1

)

(

r

r

z

j

L

L

j

jX















2

2

1

12

22

2

)

(

r

r

z

j

L

L

j

X

j



















g

g

z

j

L

j

jX













2

1

12

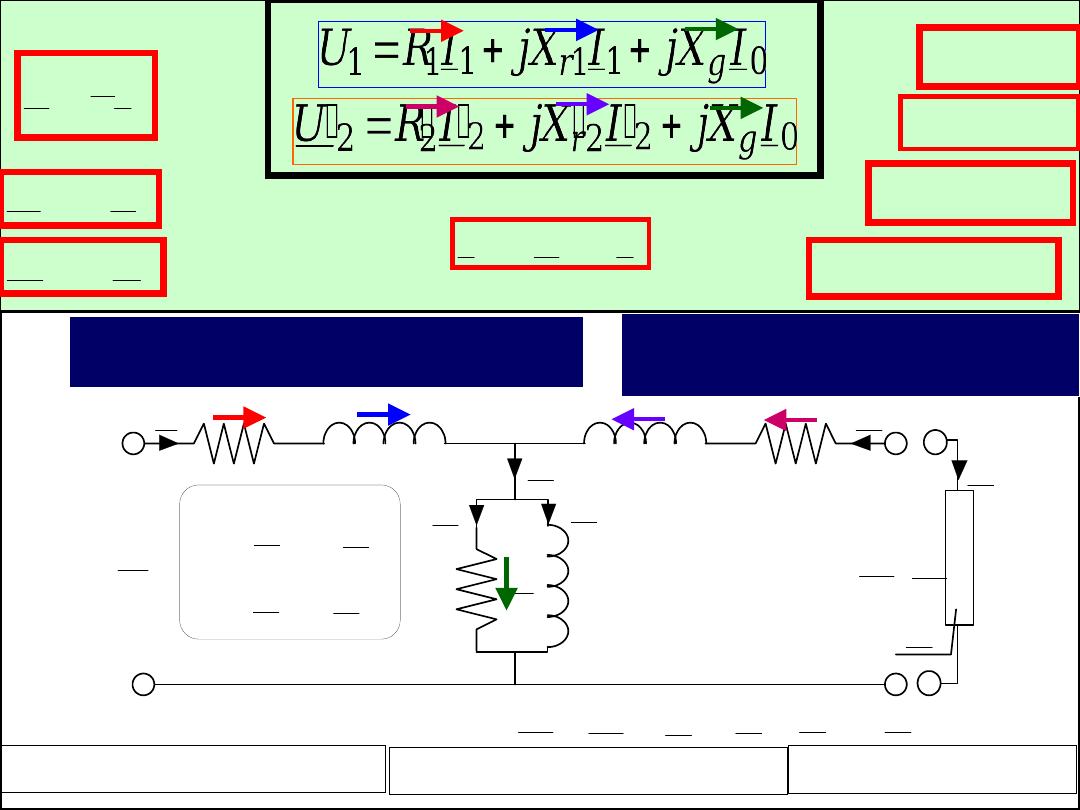
Schemat zastępczy

Schemat zastępczy

transformatora

transformatora

Nie należy mylić schematu

Nie należy mylić schematu

zastępczego ze schematem

zastępczego ze schematem

rdzenia lub uzwojeń

rdzenia lub uzwojeń

1

R

2

R

1

r

jX

2

r

X

j 

g

jX

1

I

2

I

2

U

1

U

0

I

o

I

2

I

o

I



o

U

o

U



2

U

c

0

I

0

I



E

E



Fe

R

c

0

I

1

g

jX

E



0

I



1

1

o

Z

o

Z



o

Z

2



2

1

2

1

12

11

1

)

(

r

r

z

j

L

L

j

jX















2

2

1

12

22

2

)

(

r

r

z

j

L

L

j

X

j



















g

g

z

j

L

j

jX













2

1

12

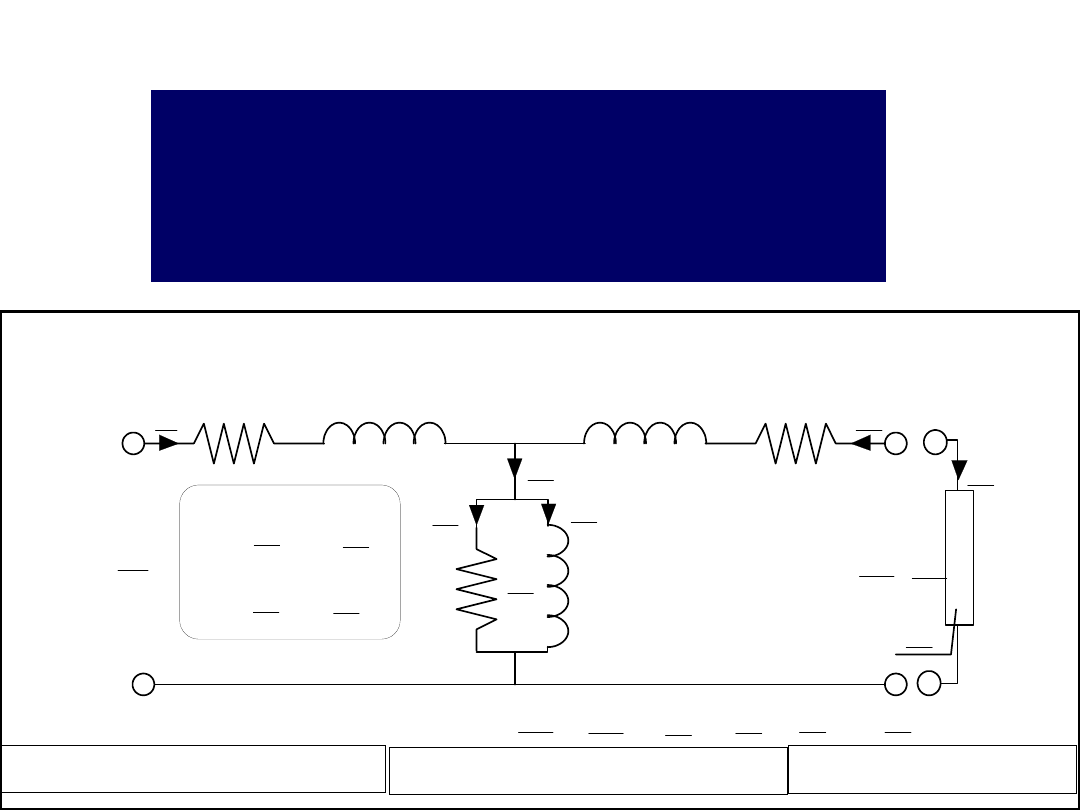
Przy pracy symetrycznej

Przy pracy symetrycznej

trójfazowej można posługiwać się

trójfazowej można posługiwać się

schematem zastępczym jak dla

schematem zastępczym jak dla

transformatora jednofazowego (dla

transformatora jednofazowego (dla

wielkości fazowych)

wielkości fazowych)

U

1

U

2

a)Nie powinny występować prądy wyrównawcze,

b)Moce powinny sumować się algebraicznie,

c)Transformatory powinny obciążać się

równomiernie (w jednakowej proporcji do mocy
znamionowej S

1

/S

N1

=S

2

/S

N2

)

Prąd wyrównawczy może
wystąpić nawet w stanie
jałowym

„Oczko”

dla

prądu

wyrównawczeg

o

0

2

1

2

2

1

2











cze

wyrównaw

I

U

U

c

wię

a

)

(

)

(

zy

Pr

1

2

)

(U

2

2

)

(U



2



1

Praca
równoległa
transformatoró
w

a)Nie powinny występować prądy wyrównawcze,
b)Moce powinny sumować się algebraicznie,
c)Transformatory powinny obciążać się

równomiernie (w jednakowej proporcji do mocy

znamionowej S

1

/S

N1

=S

2

/S

N2

)

U

1

R

z

=

R

1

+

R

2

′

L

z

=L

r1

+

L

r2

′

I

1

=

I

2

′

U

2

′

U

1

Z

z

=R

z

+j

X

z

I

1

=

I

2

′

U

2

′

U

1

(Z

z

)

1

(I

1

)

1

U

2

′

(Z

z

)

2

(I

1

)

2

2

2

1

2

2

2

1

1

1

1

)

(

)

(

)

(

)

(

I

I

I

I

I

I

wyp

wyp









Moce będą się

sumować

algebraicznie

jeśli prądy

będą się

sumować

algebraicznie,

tj. będą w

fazie

e

rzeczywist

Z

Z

e

rzeczywist

I

I

z

z





2

1

2

1

1

1

)

/(

)

(

)

/(

)

(

traf

z

z

traf

z

z

X

R

X

R

2

1



























1

2

I

I

I

o











z

R

I

1



z

X

I

j

1

1

U

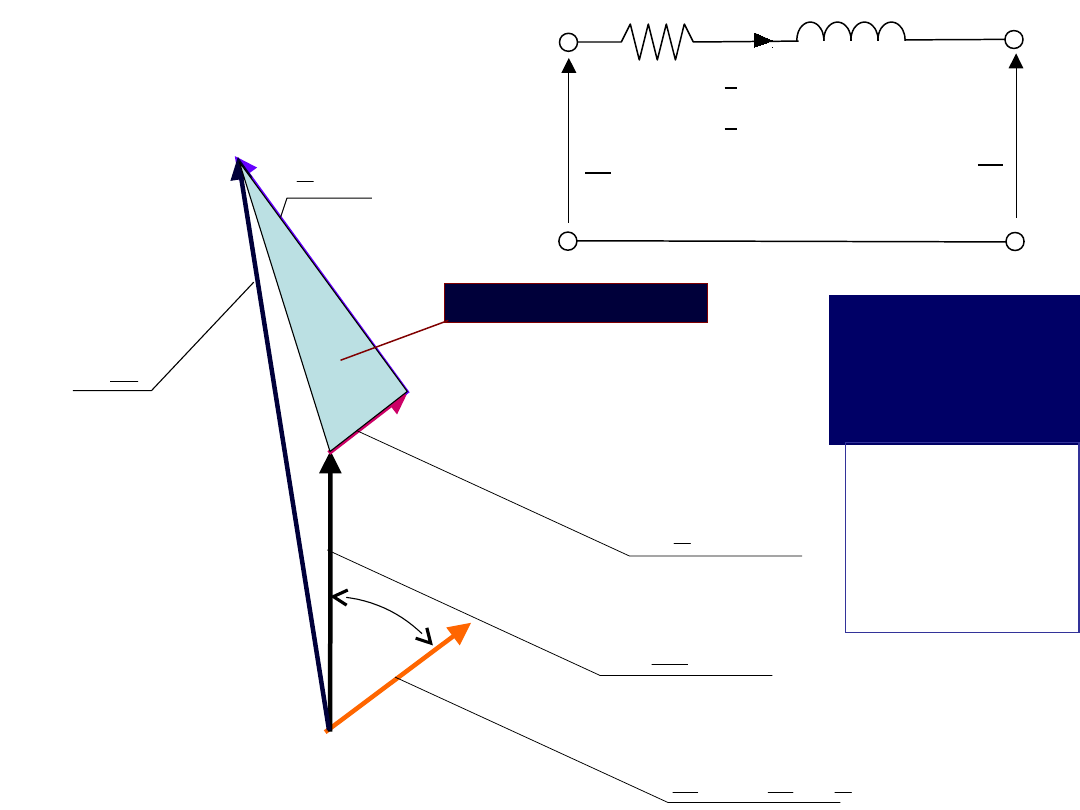
Wykres fazorowy

Wykres fazorowy

(wskazowy)

(wskazowy)

transformatora

transformatora

bez gałęzi

bez gałęzi

poprzecznej

poprzecznej

2

U

U

1

R

z

=

R

1

+

R

2

′

L

z

=L

r1

+

L

r2

′

I

1

=

I

2

′

U

2

′

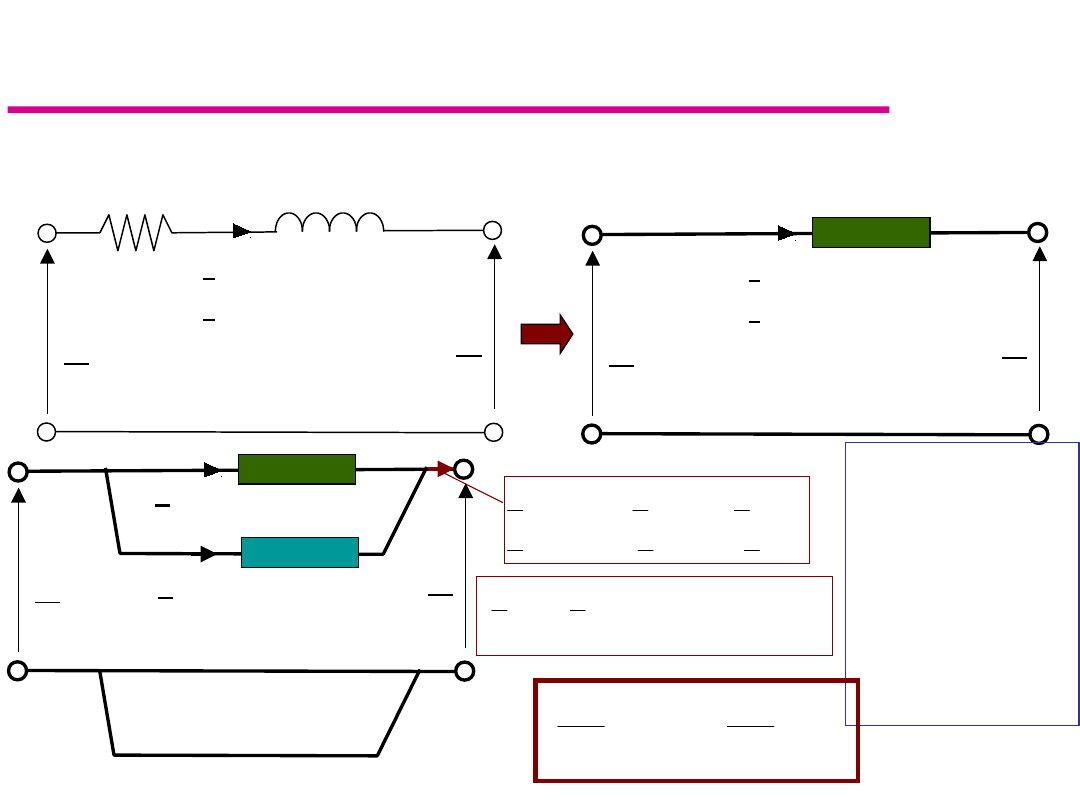
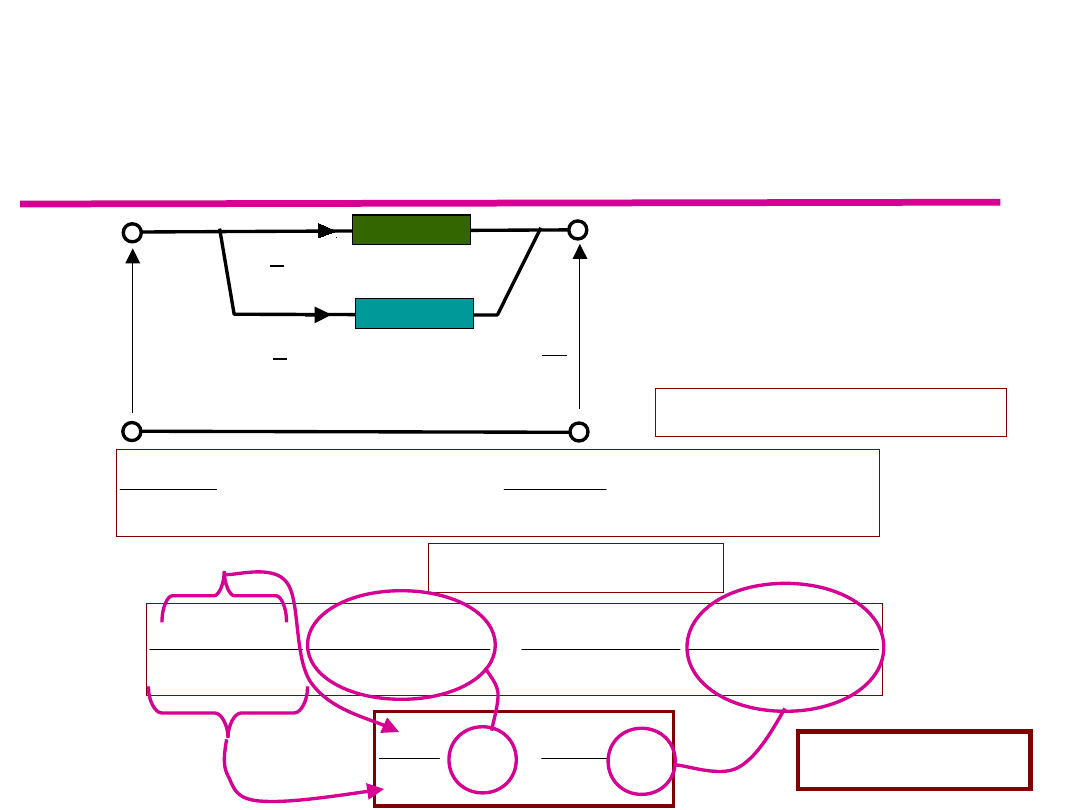
Trójkąt zwarcia

Trójkąt zwarcia

Moce będą się

sumować

algebraicznie

jeśli trójkąty

zwarcia będą

podobne

a)Nie powinny występować prądy wyrównawcze,
b)Moce powinny sumować się algebraicznie,
c)Transformatory powinny obciążać się

równomiernie (w jednakowej proporcji do mocy

znamionowej S

1

/S

N1

=S

2

/S

N2

)

U

1

(Z

z

)

1

(I

1

)

1

U

2

′

(Z

z

)

2

(I

1

)

2

2

2

1

1

1

1

)

(

)

(

)

(

)

(

z

z

Z

I

Z

I



2

2

1

2

1

2

1

1

1

1

1

1

1

1

1

1

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

z

N

N

z

N

N

Z

I

I

I

Z

I

I

I



N

z

N

N

N

N

N

z

N

N

N

N

U

Z

I

U

I

I

U

U

Z

I

U

I

I

U

2

2

1

2

1

2

1

1

1

1

1

1

1

1

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(



N

U

U

U

1

2

1

1

1





)

(

)

(

2

2

2

1

1

1

z

N

z

N

u

S

S

u

S

S



N

U

1

%

%

2

1

z

z

u

u



a) Nie powinny występować prądy wyrównawcze,

b) Moce powinny sumować się algebraicznie,

c)Transformatory powinny obciążać się

równomiernie (w jednakowej proporcji do mocy

znamionowej S

1

/S

N1

=S

2

/S

N2

)

%

%

2

1

z

z

u

u



2

1







w 3-fazowych, jednakowe przesunięcia fazowe,
grupy połączeń

traf

z

z

traf

z

z

X

R

X

R

2

1



























U

1

/

k

Z

zk

I

k

U

2



















2

1

1

U

U

Z

I

k

zk

k





























n

k

k

zk

n

k

k

obc

U

U

Z

I

I

1

2

1

1

1























n

k

k

zk

obc

U

U

Y

I

1

2

1















n

k

k

zk

obc

n

k

zk

Y

I

Y

U

U

1

1

2

1

























k

r

k

k

r

k

k

k

zk

X

X

j

R

R

Z

)

(

)

(

)

(

)

(

2

2

1

2

2

1

zk

zk

Y

Z 

1

Praca równoległa

transfor-matorów,

opis analityczny

k-ty

transformator

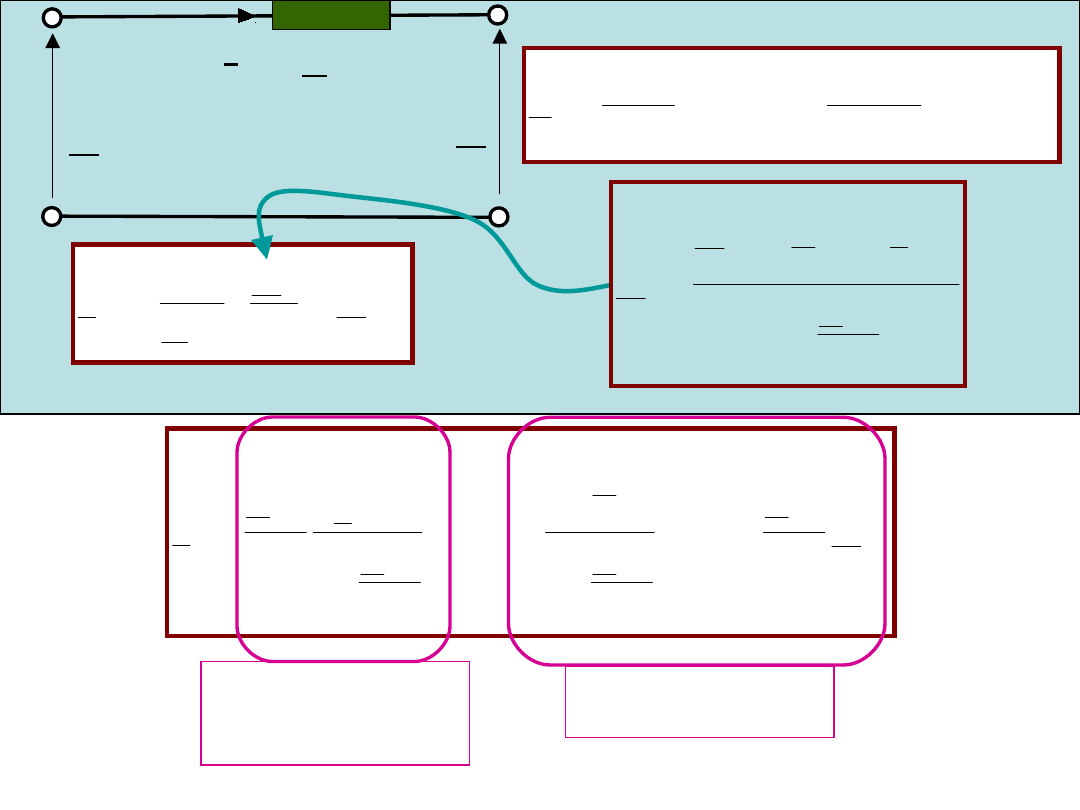
U

1

/

q

Z

zq

I

q

U

2

























q

r

q

q

r

q

q

q

zq

X

X

j

R

R

Z

)

(

)

(

)

(

)

(

2

2

1

2

2

1



















2

1

1

U

U

Z

I

q

zq

q

2

1

1

1

U

Y

Y

Y

Y

I

Y

I

q

zq

q

n

k

k

zk

n

k

zk

n

k

k

zk

obc

q

zq

q

















































prąd

wynikający z

obciążenia

prąd

wyrównawczy















n

k

k

zk

obc

n

k

zk

Y

I

Y

U

U

1

1

2

1

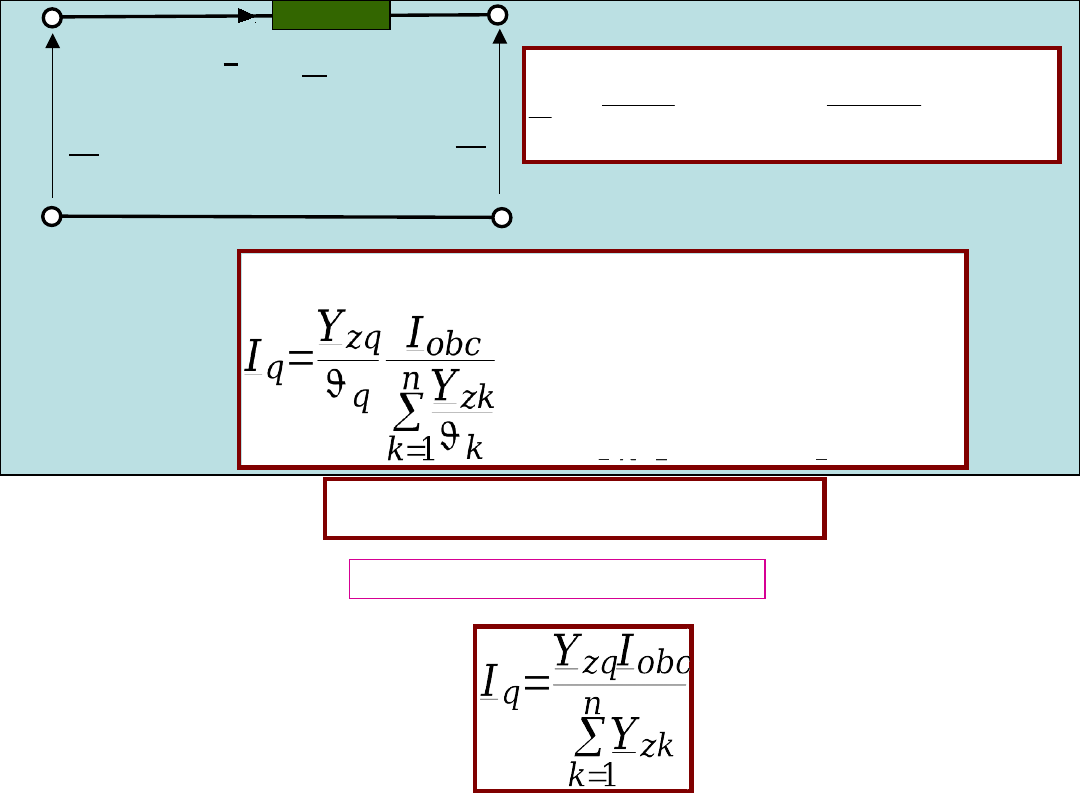
U

1

/

q

Z

zq

I

q

U

2

























q

r

q

q

r

q

q

q

zq

X

X

j

R

R

Z

)

(

)

(

)

(

)

(

2

2

1

2

2

1

n

k

q































2

1

prąd wyrównawczy=0

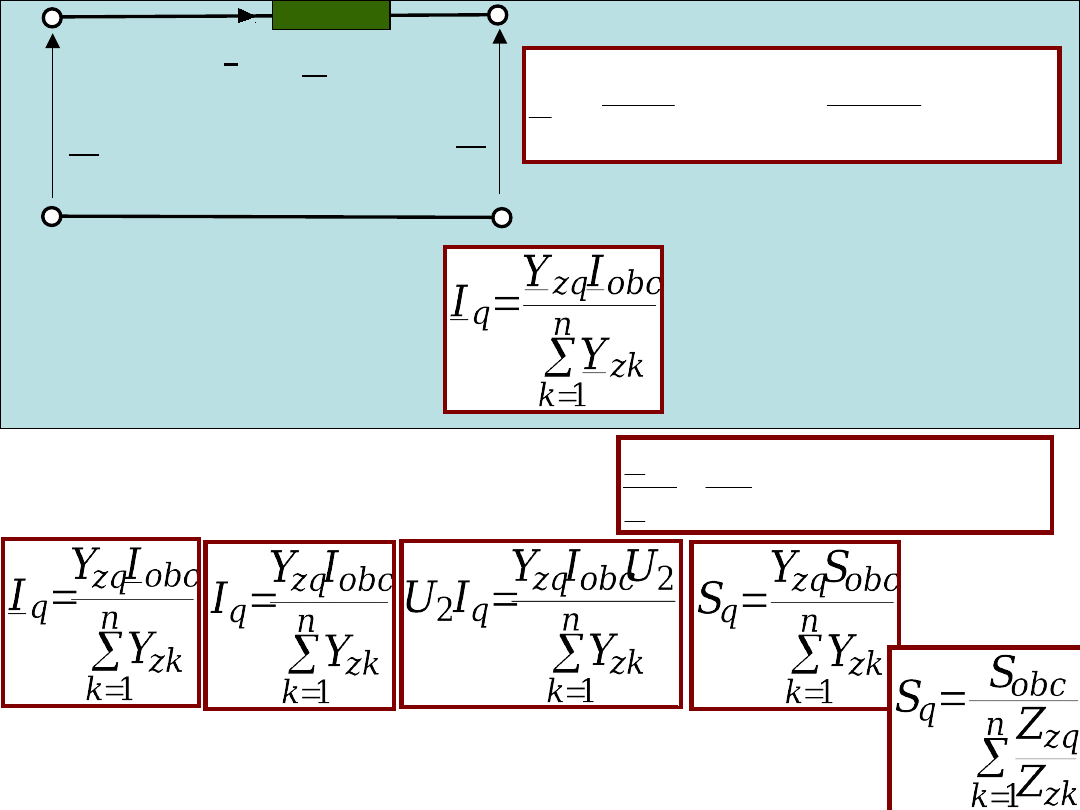
U

1

/

q

Z

zq

I

q

U

2

























q

r

q

q

r

q

q

q

zq

X

X

j

R

R

Z

)

(

)

(

)

(

)

(

2

2

1

2

2

1

Prądy sumują się
algebraicznie

a

rzeczywist

liczba

Y

Y

Y

Y

zk

zq

zk

zq





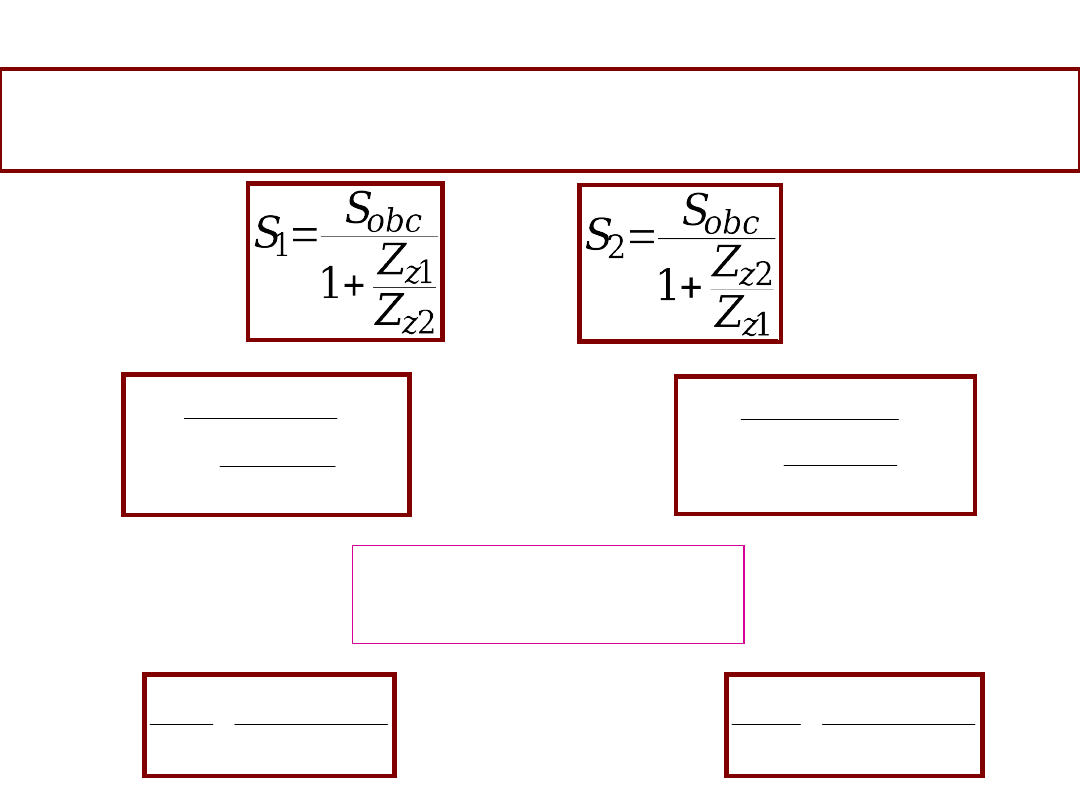
obc

N

z

N

z

S

S

u

S

u

S

1

2

2

1

1

1

1





obc

N

z

N

z

S

S

u

S

u

S

2

1

1

2

2

1

1





Rozkład mocy pomiędzy 2 transformatory obciążone mocą

sumaryczną

S

obc

%

%

2

1

z

z

u

u



Jeśli
to

2

1

1

1

N

N

obc

N

S

S

S

S

S





2

1

2

2

N

N

obc

N

S

S

S

S

S





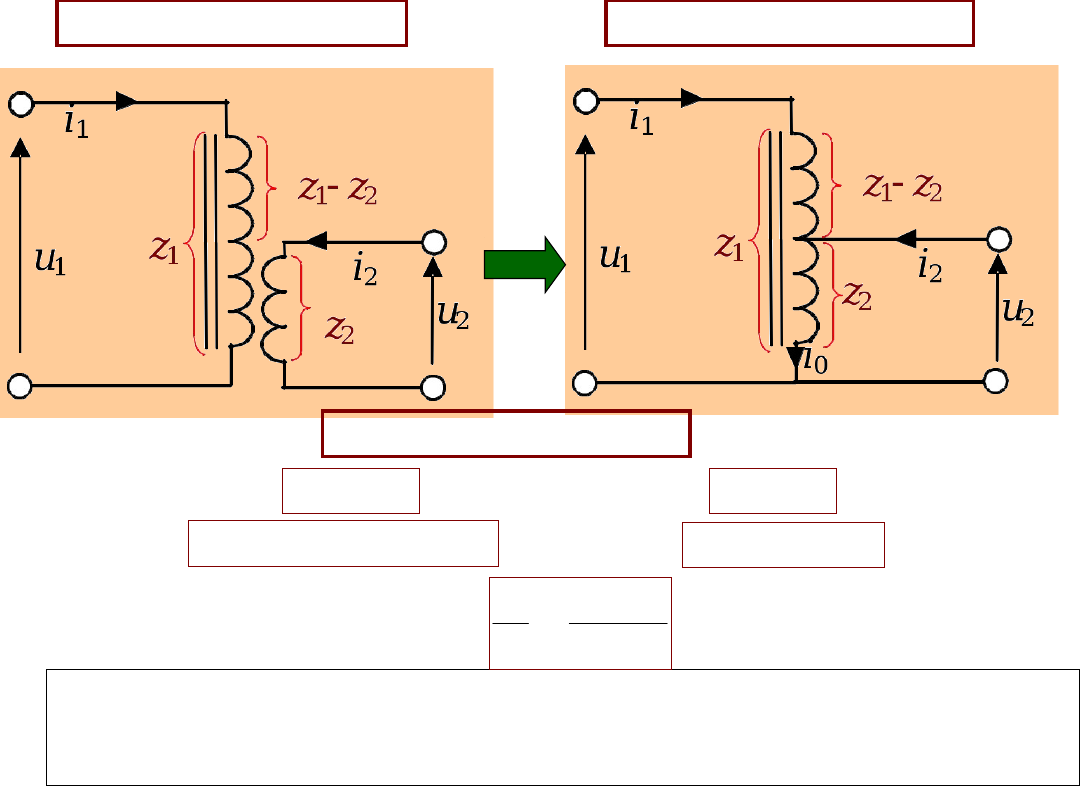
Autotransformator

1

2

i

i







W autotransformatorze występuje tylko

z

1

-z

2

zwojów z

prądem

i

1

i

z

2

przewodów z mniejszym niż w

transformatorze prądem

i

0

.

Mniej zwojów z prądem

i

1

i mniejszy prąd w zwojach

z

2

Transformator

1

2

I

I





1

2

1

0

1

i

i

i

i

)

(











1

0

1 I

I

)

( 





Autotransformator









)

(

1

2

0

I

I

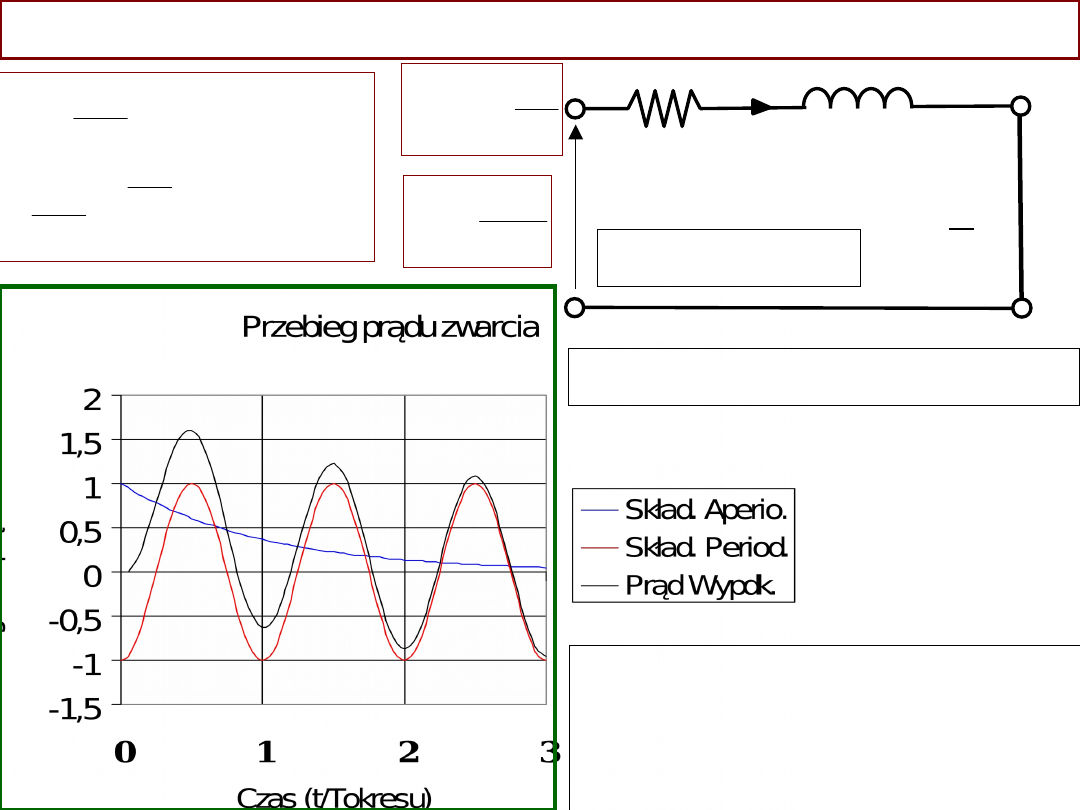
Zwarcie transformatora stan przejściowy

u

R

z

=

R

1

+

R

2

′

L

z

=L

r1

+

L

r2

′

U

2

=

0

′

u=U

m

sin(t)

w

chwili

zwarcia

t

=0,

u=



U

m

sin

)

sin(

)

sin(

)

(

























z

T

t

z

m

z

z

m

zw

e

Z

U

t

Z

U

t

i

z

z

z

Z

R





cos

z

z

zw

R

X

T





w dużych transformatorach

R

z

0



z

/

2,

zwarcie jest

najgroźniejsze jeśli

u=0

w chwili

zwarcia

t=0.

Występuje wtedy

składowa aperiodyczna

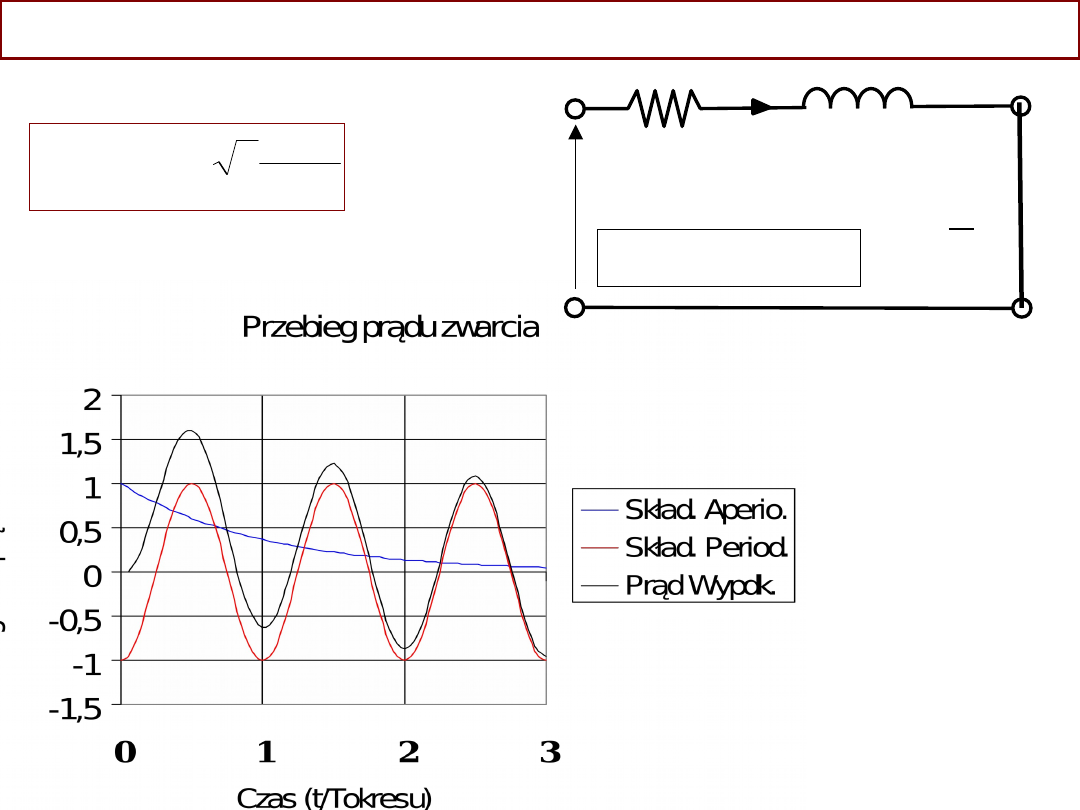
Zwarcie transformatora stan przejściowy

u

R

z

=

R

1

+

R

2

′

L

z

=L

r1

+

L

r2

′

U

2

=

0

′

u=U

m

sin(t



)

%

max

/

zw

N

u

I

i

100

2

2



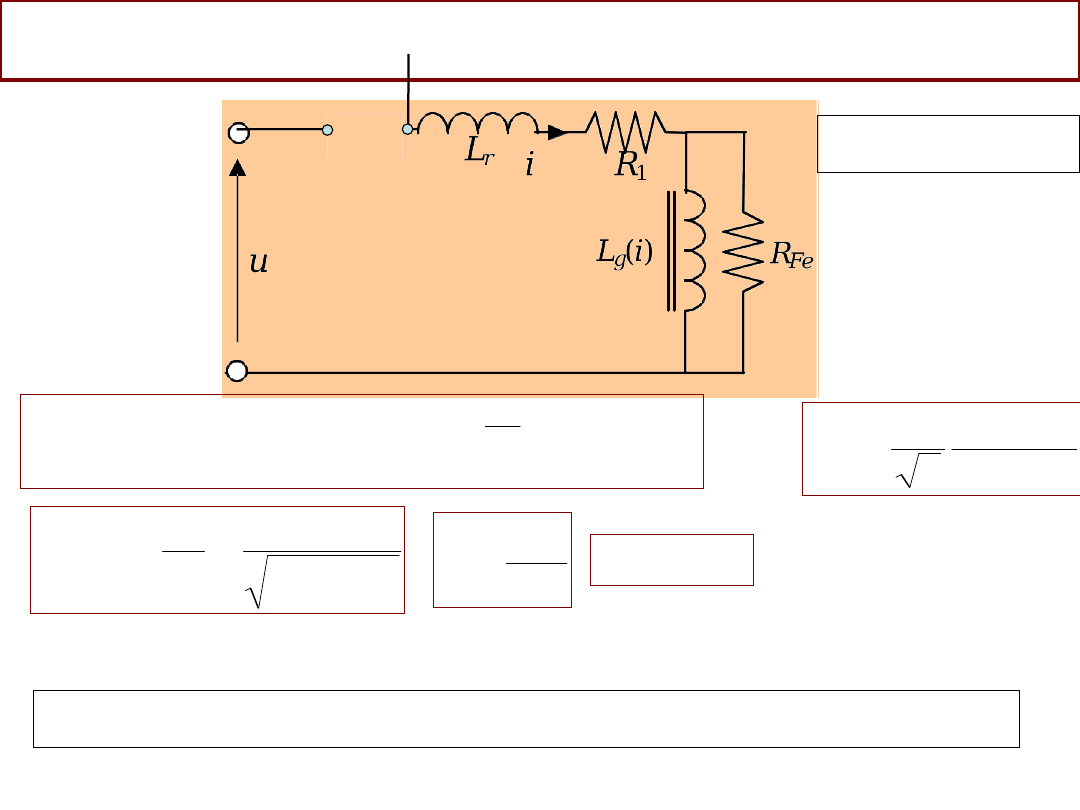
Włączenie transformatora stan przejściowy

(transformator

nieobciążony)

)

sin(

)

sin(

)

(





























sj

T

t

m

sj

m

sj

e

t

t

u=U

m

sin(t



)

2

2

1

1

0

0

g

sj

X

R

R

Z

R









cos

1

R

X

T

g

sj





g

g

L

X





f

z

U

m

m

1

44

4

1

2 .





Jeśli

u

(t

=0)

=0,

to

=0.

Ponieważ , to

2

/







sj

m

t







2

max

)

(

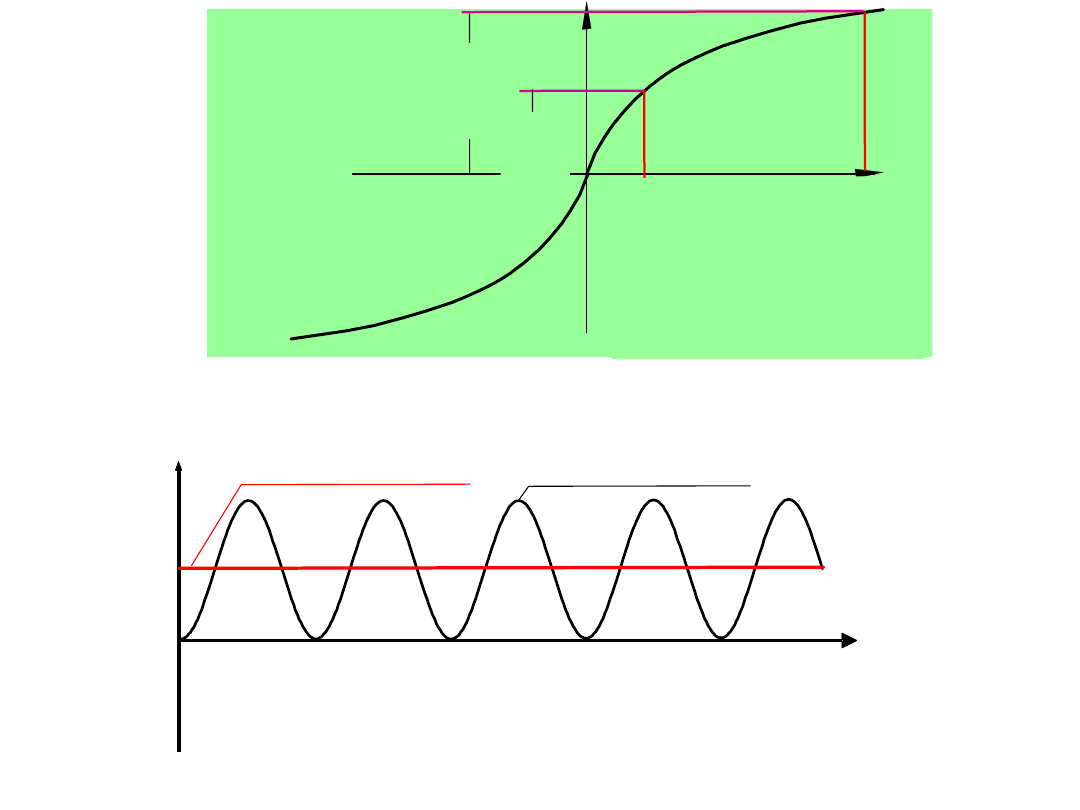
B

H

S

s



B

l

s



H

l

s



H

i

z

zmiana skali

zmiana skali

zmiana skali

Charakterystyka
magnesowania

i



czas



0

Składowa periodyczna +aperiodyczna

Składowa aperiodyczna



ma

x

2

ma

x

√2I

0

N

k√2I

0

N