Zazębienie

Jak już wzmiankowano, kształt zarysu zęba
może być dowolny.

Jednakże nie wszystkie zarysy spełniają
podstawową zasadę zazębienia (zasadę
Willis’a),
‘prosta normalna do boku zęba w punkcie styku
zębów kół współpracujących musi przechodzić
przez punkt styku kół tocznych’.

Aby dwa zarysy współpracujących ze sobą
zębów miały wspólną normalną w punkcie ich
styku to muszą być one utworzone przez to
samo koło odtaczające.

Warunek te spełniają zarysy utworzone przez
krzywe cykliczne, tj. różnego rodzaju

cykloidy

oraz

ewolwenta

koła.

Z zasady zazębienia wynika, że współpracujące części
zębów, a więc zarys stopy zęba koła 1 i zarys głowy
zęba koła współpracującego 2, muszą posiadać
wspólną normalną do ich zarysów przechodzącą przez
centralny biegun zazębienia

C

.

Oznacza to, że obie odpowiadające sobie części boków
zęba muszą być utworzone przez to samo koło
odtaczające. Tylko w takim przypadku obie normalne
będą się pokrywać.

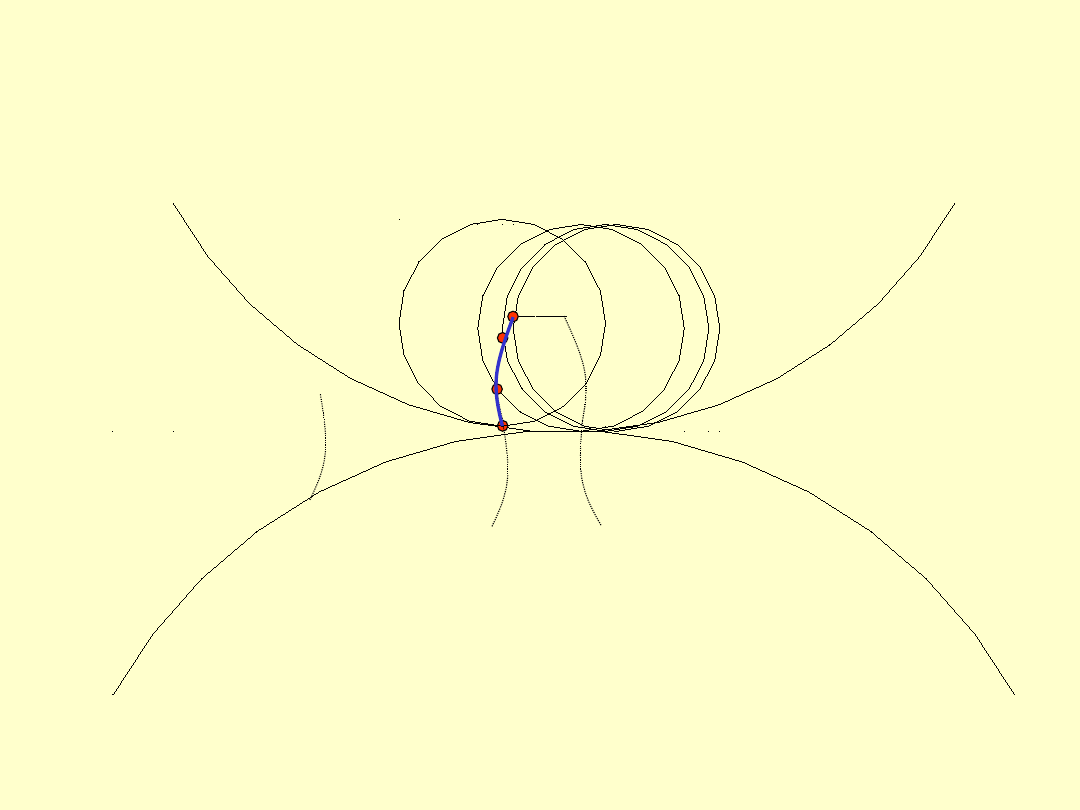
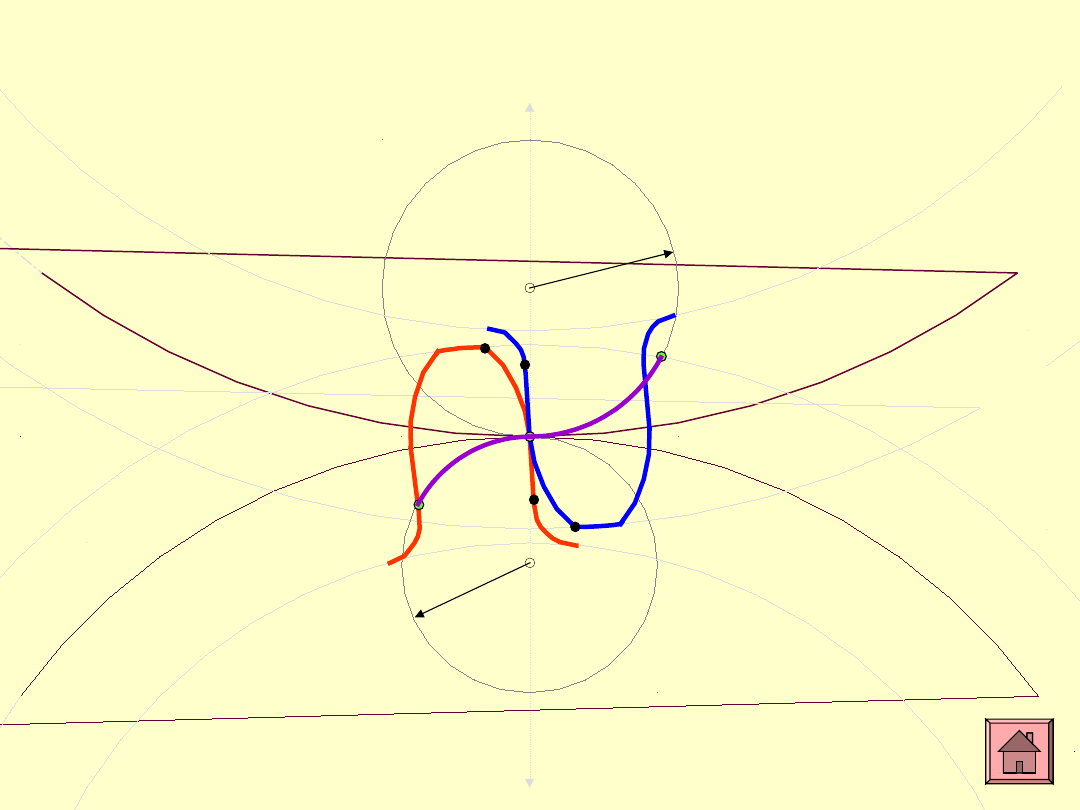
W zazębieniu cykloidalnym epicykloida i hipocykloida
są utworzone przez to samo koło odtaczające. Tworzą
one zarysy odpowiednio stopy zęba koła 1 i zarys głowy
zęba koła współpracującego 2.

Zazębienie cykloidalne

O

1

O

2



1



2

KP

1

=KZ

1

=KT

1

KP

2

=KZ

2

=KT

2

E

1

E

2

C

W

1

W

2

D

2

D

2

Koło 1

Koło 2

Koło odtaczające o promieniu



1

toczy się kolejno

po dwóch kołach zasadniczych, tj.:

 po wewnętrznym torze koła zasadniczego KZ1

tworzy hipocykloidę CD1 stanowiącą część
zarysu stopy koła 1,

 po zewnętrznym torze koła zasadniczego KZ2

tworzy epicykloidę CW2, tj. zarys głowy zęba
koła drugiego.

W podobny sposób tworzy się pozostałe części
zarysów zębów, a więc głowę zęba w kole 1
(epicykloida) CW1 oraz stopę zęba w kole 2
(hipocykloidę) CD2 poprzez przetoczenie innego
koła odtaczającego o promieniu



1

kolejno po

wewnętrznym torze KZ2 i zewnętrznym KZ1.

W zazębieniu cykloidalnym koła toczne

KT

są równocześnie kołami podziałowymi

KP

, a także kołami zasadniczymi

KZ

, tzn.

kołami stanowiącymi tor, po którym
obtaczają się koła odtaczające tworzące
zarysy zębów.

Linia przyporu składa się z dwóch łuków
kół odtaczających.

Większy promień kół odtaczających



daje

lepszą

współpracę

zębów

„większy

promień krzywizny”, ale ząb staje się
cięższy przez to mniej wytrzymały.

Do

najistotniejszych

zalet

zazębienia

cykloidalnego należy zaliczyć to, że wklęsła
powierzchnia koła 1 współpracuje z wypukłą
powierzchnią zęba koła 2 i na odwrót, przez co:

 występuje duże pole dolegania,
 zmniejszają się naciski powierzchniowe,
 zmniejsza się zużycie zębów,
 występują niższe poślizgi jednostkowe,
 zwiększa się sprawność zazębienia.

Najistotniejsze wady to:

 wrażliwość na przesunięcie osi, spowodowane

koniecznością współpracy ściśle określonych
wypukłych powierzchni zęba ze ściśle określonymi
wklęsłymi powierzchniami zęba,

 mniejsza się dokładność wykonania ze względu na

niemożność zastosowania metody obwiedniowej,

 obróbka zębów musi być przeprowadzona za

pomocą metody kształtowej, która nie daje dużej
dokładności wykonania,

 utrudniony pomiar zarysu zęba i jego grubości,
 linia przyporu jest krzywoliniowa, co powoduje

zmianę wielkości sił zazębienia, a więc powstawanie
drgań.

Wymienione wady powodują, że
zazębienie cykloidalne nie może być
stosowane do przenoszenia dużych
obciążeń

z

dużymi

prędkościami

obrotowymi. Znalazło ono natomiast
zastosowanie w mechanice precy-zyjnej.

ZAZĘBIENIE EWOLWENTOWE

W zazębieniu ewolwentowym zarysy boków
współpracujących zębów są utworzone przez
odtaczanie linii prostej po kole zasadniczym.

Oznacza

to,

że

zarysy

boków

współpracujących zębów są utworzone przez
to samo koło odtaczające (o promieniu



=



),

a więc mają one wspólną normalną w punkcie
ich styku.

W ten sposób został spełniony warunek podstawowej
zasady zazębienia:
‘prosta normalna do boku zęba w punkcie styku
zębów kół współpracujących musi przechodzić przez
punkt styku kół tocznych’.

CECHY ZAZĘBIENIA

EWOLWENTOWEGO

1. Zarys boku zęba

 jako zarys boku zęba wykorzystywany jest odcinek

ewolwenty,

 początek łuku ewolwenty możliwy do

wykorzystania jako zarys ewolwentowy znajduje
się na kole zasadniczym,

 współpracujące części ewolwenty powstają tylko

na odcinku zarysu ponad okręgami zasadniczymi,

 część zarysu poniżej okręgu zasadniczego

wykonywana jest jako krzywa przejściowa (może
ona być dowolna, ale taka aby umożliwiła przejście
wierzchołka zęba i jednocześnie nie powodowała
zmniejszenia grubości zęba i jego osłabienia przy
podstawie).

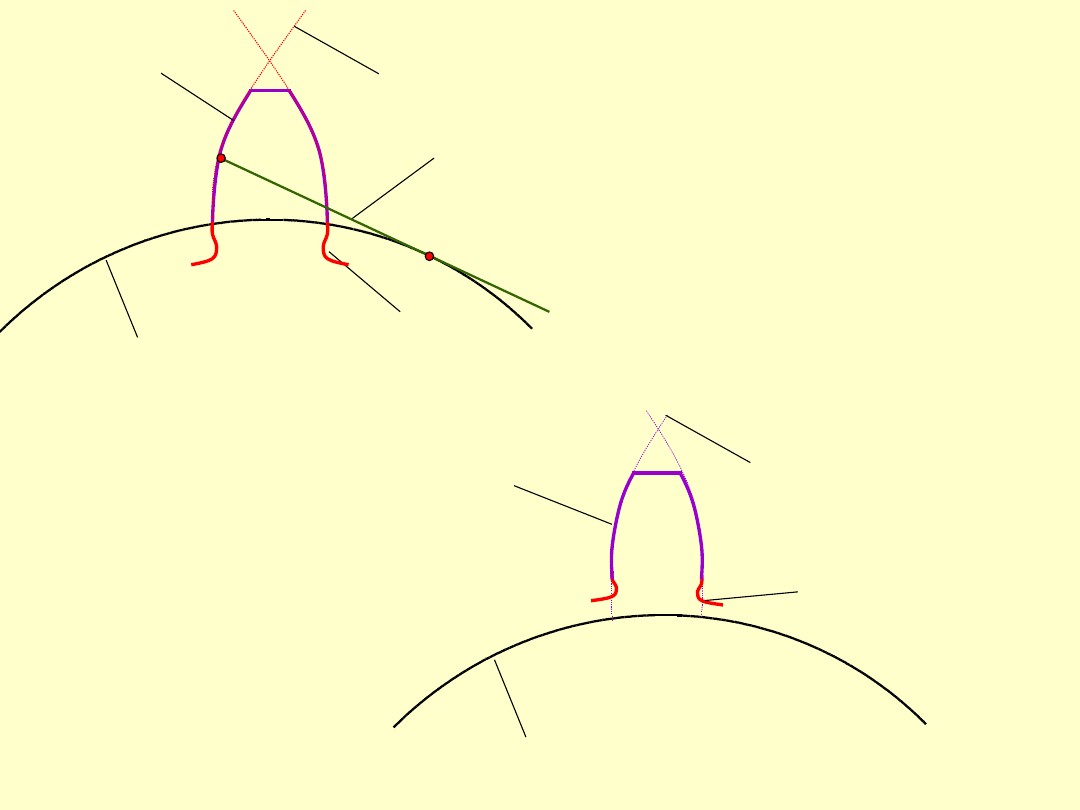
koło odtaczające

koło zasadnicze

ewolwenta

odcinek
ewolwenty
wykorzystan
y jako zarys

krzywa
przejściowa

koło zasadnicze

ewolwenta

odcinek
ewolwenty
wykorzystan
y jako zarys

krzywa
przejściowa

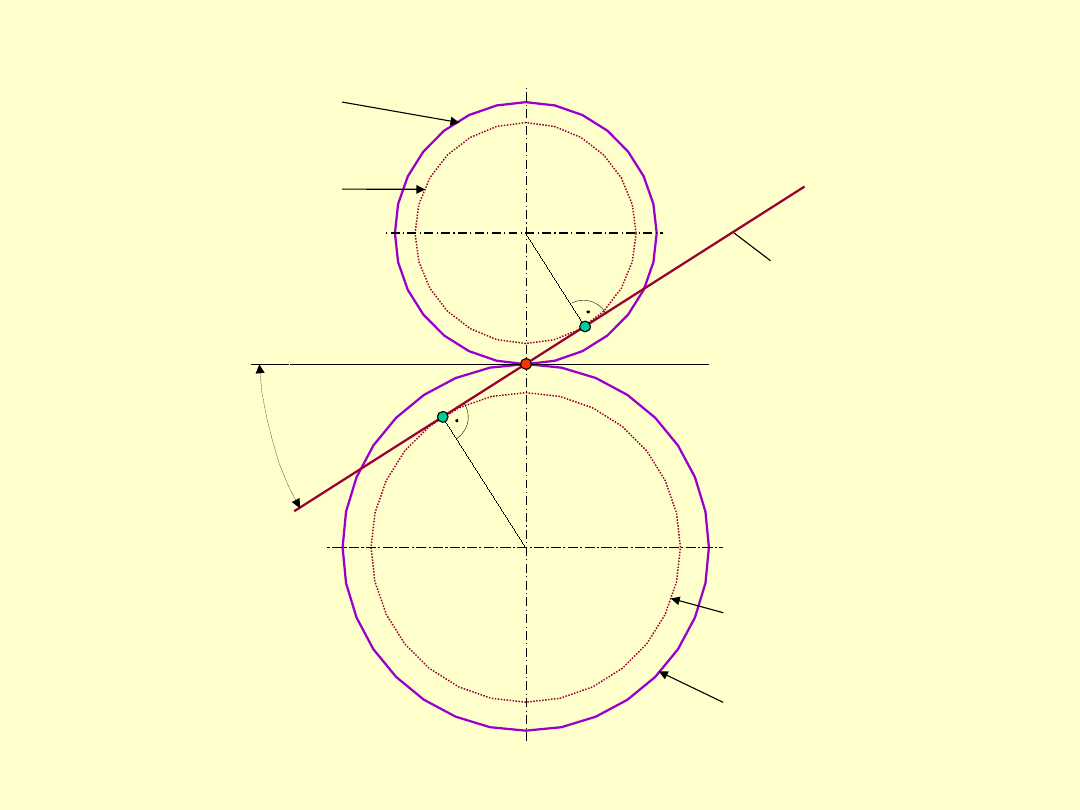
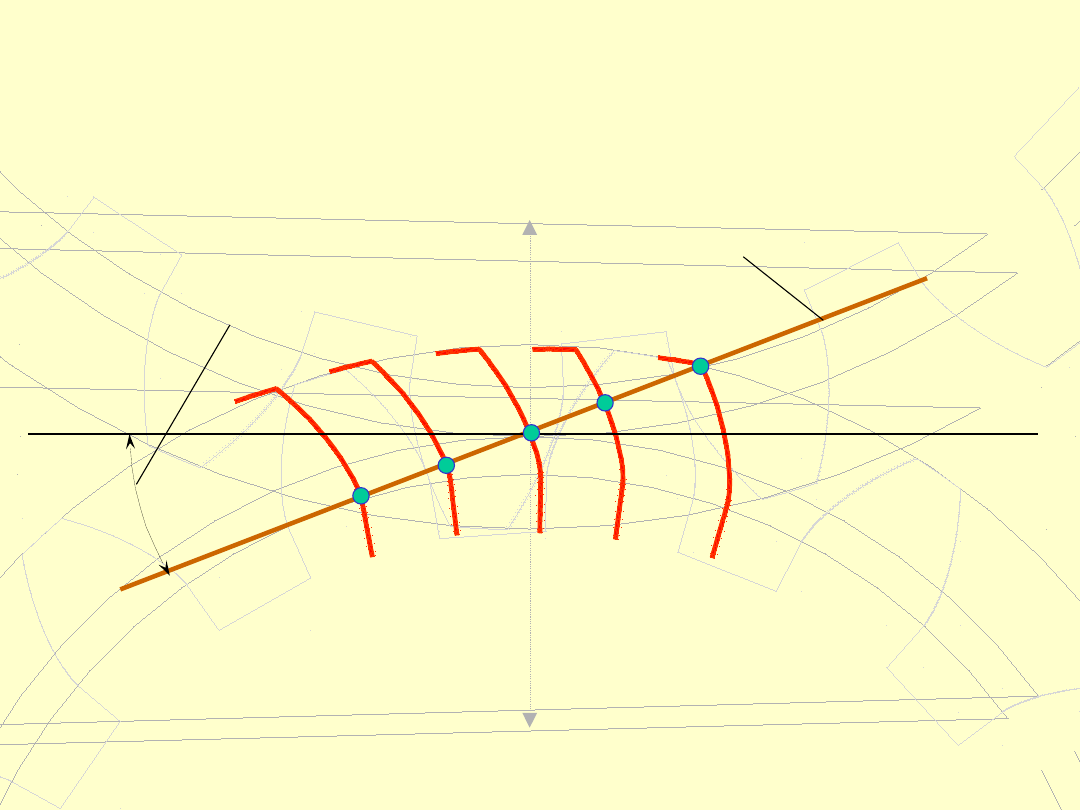
2. Linia przyporu

 linia przyporu jest linią prostą,
 linia przyporu jest styczną do kół zasadniczych,

przechodzącą przez centralny biegun zazębienia

C

,

 linia przyporu jest nachyloną do stycznej

poprowadzonej w punkcie styku kół tocznych pod
kątem



.

O

1

O

2

N

1

N

2



KT1

KT2

KZ1

KZ2

C

linia przyporu

linia przyporu

3. Kąt przyporu

 kąt przyporu ma stałą wartość.
 gdy koła toczne pokrywają się z kołami

podziałowymi, to mamy do czynienia z tzw.
zazębieniem zerowym i w takim przypadku kąt
przyporu nosi nazwę nominalnego kąta przyporu
(zerowego kąta przyporu),

 w przypadku, gdy koła toczne nie pokrywają się z

kołami podziałowymi, kąt przyporu zmienia swoją
wartość i powstaje wówczas toczny kąt przyporu
różny od nominalnego kąta przyporu .

 kąt przyporu nazywany jest kątem zarysu

ponieważ określa on punkt oddziaływania siły
miedzyzębnej na zarys zęba.

a

0



0

O

1

O

2

KT1=KP1

KT2=KP2

r

1

r

2

r

z2

r

z1

a
)

C

N

1

N

2

KZ2

O’

1

O’

2

C





w



w

N’

1

N’

2

r

w1

r

w2

KT1

KT2

KZ1

KP1

KP2

r

z1

r

z2

b
)

a

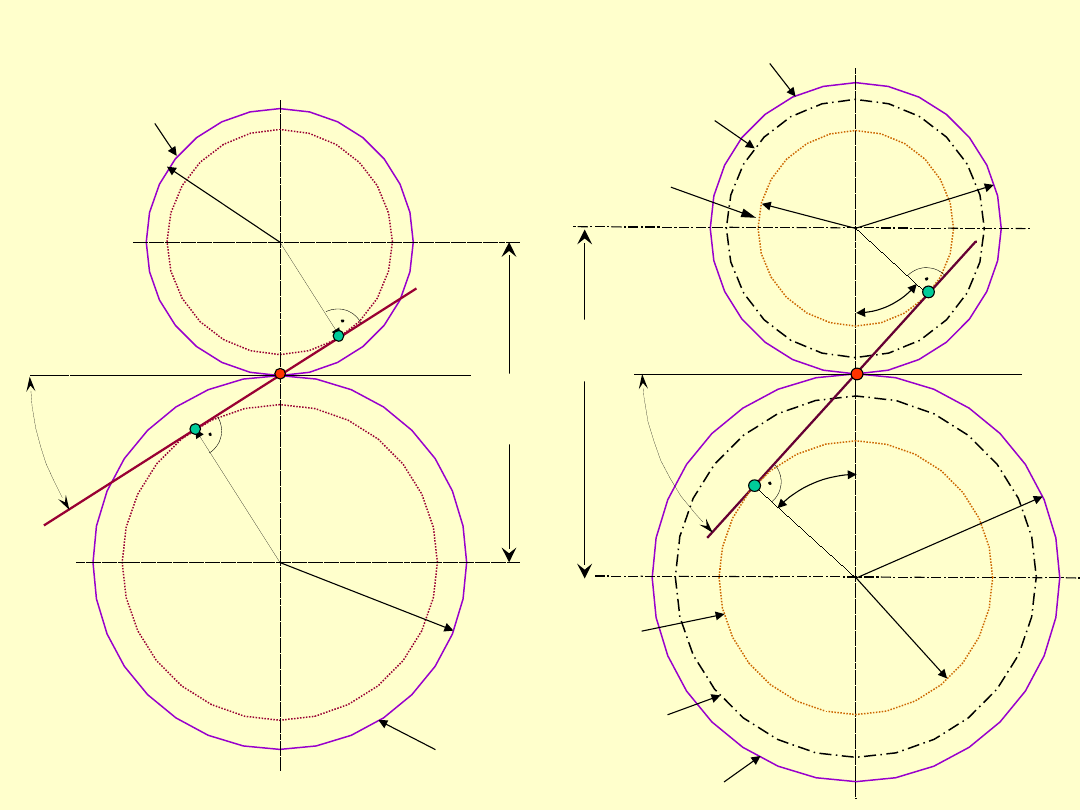
Zależność między nominalnym kątem przyporu



0

a tocznym kątem przyporu



znajdziemy

rozpatrując następujące trójkąty:

a)

b)

O

1

N

1

C

O

2

N

2

C

O

1

’N

1

’C

O

2

’N

2

’C

C

O

N

O

cosα

1

1

1

0



'C

O

'

'N

O

α

cos

1

1

1







C

'

O

'

N

'

O

2

2

2





C

O

N

O

2

2

2

r

r

r

r

r

r

z

z

z







2

2

1

1

w

z

w

z

w

z

r

r

r

r

r

r







2

2

1

1

r

r

α

cos

z



0

w

z

r

r

α

cos 

0





cos

r

r

cos

w







O

2

O

1



2



1

linia przyporu

kąt zarysu = kąt przyporu

4. Odległość międzyosiowa

 koła o ewolwentowych zarysach zębów mogą

poprawnie pracować przy zmianie odległości osi,
gdyż w punkcie przyporu normalne do ich zarysów
pokrywają się,

 przesunięcie osi dopuszcza się tylko w pewnych

granicach, ponieważ zmieniają się luzy
międzyzębne,

 nominalna (zerowa odległość międzyosiowa)

równa się:

a

0

= r

1

+ r

2

 rzeczywista odległość osi będzie wynosiła:







2

1

0

r

r

a







w2

w1

r

r

a

1

1

0

r

r

α

cos

z



2

2

0

r

r

α

cos

z



0

1

1

α

cos

r

r

z



0

2

2

α

cos

r

r

z



0

2

2

α

cos

r

r

z

w



0

1

1

α

cos

r

r

z

w



1

1

w

z

w

r

r

α

cos 

2

2

w

z

w

r

r

α

cos 

0

2

1

α

cos

r

r

z

z





w

z

z

α

cos

r

r

2

1





w

0

0

cosα

cosα

a

a





w

0

0

cosα

a

cosα

a







5. Przełożenie

 przełożenie nie zależy od odległości międzyosiowej

bowiem niezależnie od tego, które odcinki
ewolwenty ze sobą współpracują, promienie kół
zasadniczych nie ulegają zmianie (pozostają
zawsze te same).

Jak już wzmiankowano, z zasady zazębienia wynika,

że:

1

2

2

1

z

z

r

r

ω

ω

i





Oznacza to, że stosunek prędkości kątowych jest
równy stosunkowi promieni kół zasadniczych.

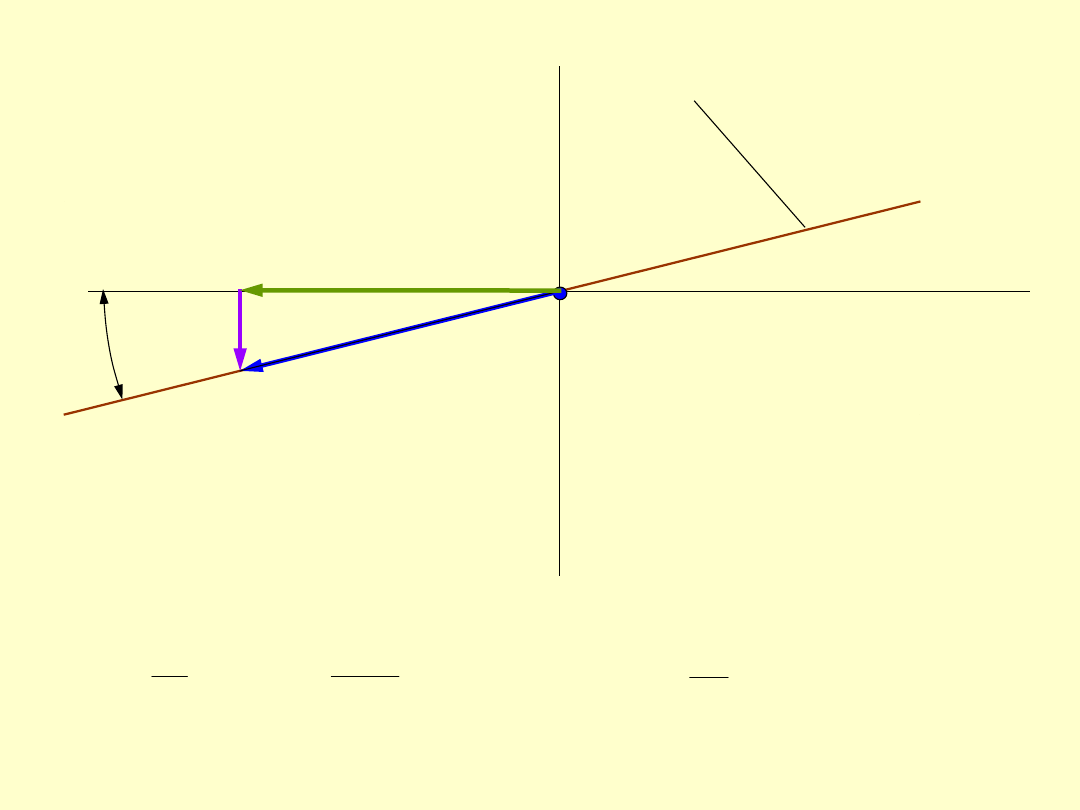
6. Siły w zazębieniu

 z własności prostej przyporu wynika korzystna

właściwość przekładni o zazębieniu
ewolwentowym: stały kierunek siły międzyzębnej.

 przyczynia się to do tego, że zmiany położenia

punktu przyporu nie wpływają na stan obciążenia
łożysk i wałów.

C

O

2

O

1

linia przyporu

P

P

R

P

N







cos

P

P

P

P

cos

N

N











tg

P

P

P

P

tg

R

R









Zalety zazębienia ewolwentowego

zazębienie ewolwentowe jest zupełnie

nieczułe na zmianę odległości osi,

obróbka może być przeprowadzana bardzo

dokładnie uniwersalnymi narzędziami, tj.
jednym, tym samym narzędziem można
obrabiać koła o różnych liczbach zębów (ale
tym samym



,

y

i

m

),

sprawdzenie wielkości koła i uzębienia odbywa

się łatwo przy użyciu bardzo prostych narzędzi
(suwmiarka modułowa),

kierunek i wielkość sił promieniowych są stałe,

a więc z tego powodu podczas pracy nie
występują dodatkowe wahania obciążenia i
drgania.

Wady zazębienia ewolwentowego

Współpraca w zazębieniu zewnętrznym odbywa się
między dwoma zębami o wypukłych bokach, a przez
to:

 występuje małe pole dolegania,
 występują dość duże jednostkowe naciski

powierzchniowe,

 występują nieco większe poślizgi niż w

zazębieniu cykloidalnym.

Pomimo tych wad, zazębienie ewolwentowe uzyskało
powszechne zastosowanie w przekładniach zębatych
stosowanych w budowie maszyn i okrętownictwie do
przenoszenia dużych mocy z dużymi prędkościami
obrotowymi.