
POLITECHNIKA GDAŃSKA
Wydział Elektrotechniki i Automatyki
Katedra Energoelektroniki i Maszyn Elektrycznych
MATERIAŁY POMOCNICZE DO LABORATRIUM
M A S Z Y N Y E L E K T R Y C Z N E I I
PODSTAWY DYNAMIKI MASZYN ELEKTRYCZNYCH
Kier. Elektrotechnika, studia mgr, sem. V
TEMATYKA ĆWICZENIA
BADANIE DYNAMIKI SILNIKA PRĄDU STAŁEGO
WSPOMAGANE SYMULATOREM OBWODÓW PSPICE
(wersja 2)
Mieczysław RONKOWSKI
GDAŃSK 2002

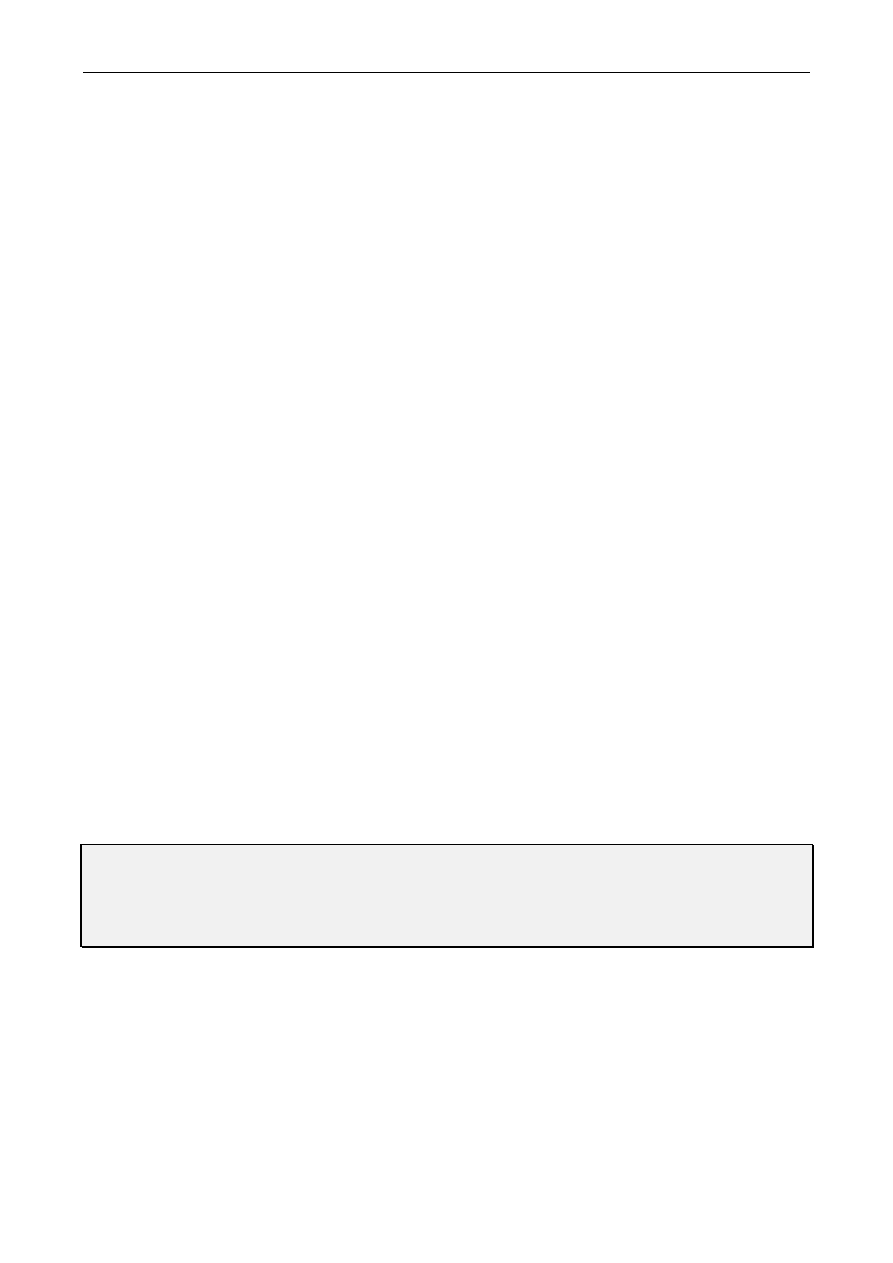
Mieczysław RONKOWSKI
1
ĆWICZENIE
BADANIE DYNAMIKI SILNIKA PRĄDU STAŁEGO
WSPOMAGANE SYMULATOREM OBWODÓW PSPICE
Program ćwiczenia
1. CEL
ĆWICZENIA ........................................................................................................................................1
2. MASZYNA
PRĄDU STAŁEGO JAKO WZORCOWE SPRZĘŻENIE ELEKTROMECHANICZNE ..............1
3. DYNAMICZNY MODEL OBWODOWY WZORCOWEGO SPRZĘŻENIA ELEKTROMECHANICZNEGO.3
4. ZASTOSOWANIE PROGRAMU SYMULACYJNEGO PSPICE DO BADANIA WŁAŚCIWOŚCI
DYNAMICZNYCH SILNIKA PRĄDU STAŁEGO.................................................................................................9
5. PYTANIA
(TEORIA/SYMULACJA)............................................................................................................16
6. ZADANIE ...................................................................................................................................................17
7. SPRAWOZDANIE .....................................................................................................................................17
8. LITERATURA ............................................................................................................................................18
9. ZAŁĄCZNIK...............................................................................................................................................18
9.1. Wyznaczanie
wartości parametrów modelu liniowego na podstawie danych katalogowych .............19
9.2. Wyznaczanie
wartości parametrów modelu nieliniowego na podstawie danych doświadczalnych ...20
9.3. PYTANIA
(POMIARY) ........................................................................................................................26
1. CEL
ĆWICZENIA
Celem ćwiczenia jest:
•
zapoznanie się z dynamicznym modelem obwodowym maszyny prądu stałego — wzorcowego
sprzężenia elektromechanicznego;
•
opanowanie zastosowania programu symulacyjnego PSPICE do badania właściwości dynamicznych
silnika prądu stałego;
•
wykonanie badań symulacyjnych typowych stanów pracy dynamicznej silnika prądu stałego o
zadanych wartościach parametrów modelu oraz wymuszeniach elektrycznych i mechanicznych;
•
porównanie wyników badań symulacyjnych z wynikami badań eksperymentalnych.
2. MASZYNA
PRĄDU STAŁEGO JAKO WZORCOWE SPRZĘŻENIE
ELEKTROMECHANICZNE
Schemat układu elektromechanicznego na rys. 1 przedstawia podstawowy model fizyczny maszyny
prądu stałego wraz z ilustracją zasady jej działania — generacji momentu elektromagnetycznego. Na
podstawowy model fizyczny maszyny prądu stałego składają się następujące elementy czynne: magneśnica
(uzwojenie wzbudzenia, bieguny główne, nabiegunniki, jarzmo); twornik (uzwojenie twornika, rdzeń
twornika, komutator, szczotki, wał).
Uwaga: W rzeczywistej maszynie prądu stałego stosuje się dodatkowo: a) bieguny komutacyjne wraz z
uzwojeniem (uzwojenie połączone szeregowo z uzwojeniem twornika) — umieszczone między
biegunami głównymi — celem poprawy komutacji (eliminacja iskrzenia szczotek); c) uzwojenie
kompensacyjne — umieszczone w żłóbkach nabiegunników biegunów głównych — celem
eliminacji oddziaływania twornika.
Przyjęte na rys. 1 symbole a, f oznaczają umowne początki uzwojeń odpowiednio twornika i
wzbudzenia, a litery a', f' — umowne końce tych uzwojeń. Płynące prądy w uzwojeniach maszyny
wytwarzają pola magnetyczne (przepływy, siły magnetomotoryczne -SMM), których osie są skierowane
zgodnie z osiami (magnetycznymi) tych uzwojeń: np. oś d dla uzwojenia wzbudzenia f - f’; oś q dla
uzwojenia twornika a - a’. Dla rozpatrywanej maszyny układ osi magnetycznych d oraz q jej uzwojeń
stanowi układ współrzędnych naturalnych.
Maszyna prądu stałego będzie rozpatrywana jako układ elektromechaniczny w którym moce:
elektryczna (dostarczana) i mechaniczna (odbierana), ulegają przemianie za pośrednictwem pola
magnetycznego. Zatem podstawowym stanem pracy jest stan silnikowy. Moc pola magnetycznego jest mocą
wewnętrzną maszyny, gdyż układ nie ma możliwości wymiany tej mocy z otoczeniem. Pole magnetyczne
2
Ćwiczenie: BADANIE DYNAMIKI SILNIKA PRĄDU STAŁEGO
wyraża się zależnościami strumieniowo-prądowymi. Stąd stan maszyny będzie opisany układem równań
napięciowo-prądowych dla strony elektrycznej i momentowo-prędkościowych dla strony mechanicznej.
Maszyna na rys. 1 może być przedstawiona jako wielowrotnik elektromechaniczny o trzech parach
zacisków (wrotach), które stanowią: dwa „wejścia elektryczne” — zaciski kolejnych uzwojeń i jedno
„wyjście mechaniczne” — koniec wału (sprzęgło). Dynamika (ruch) maszyny jest określona dwoma
parametrami mocy na każdej parze zacisków. Jej formalnym opisem będzie układ równań różniczkowych
zwyczajnych nieliniowych przy trzech zadanych wymuszeniach. Układ ten opisuje, m.in., związki między
napięciami, prądami i strumieniami magnetycznymi maszyny.
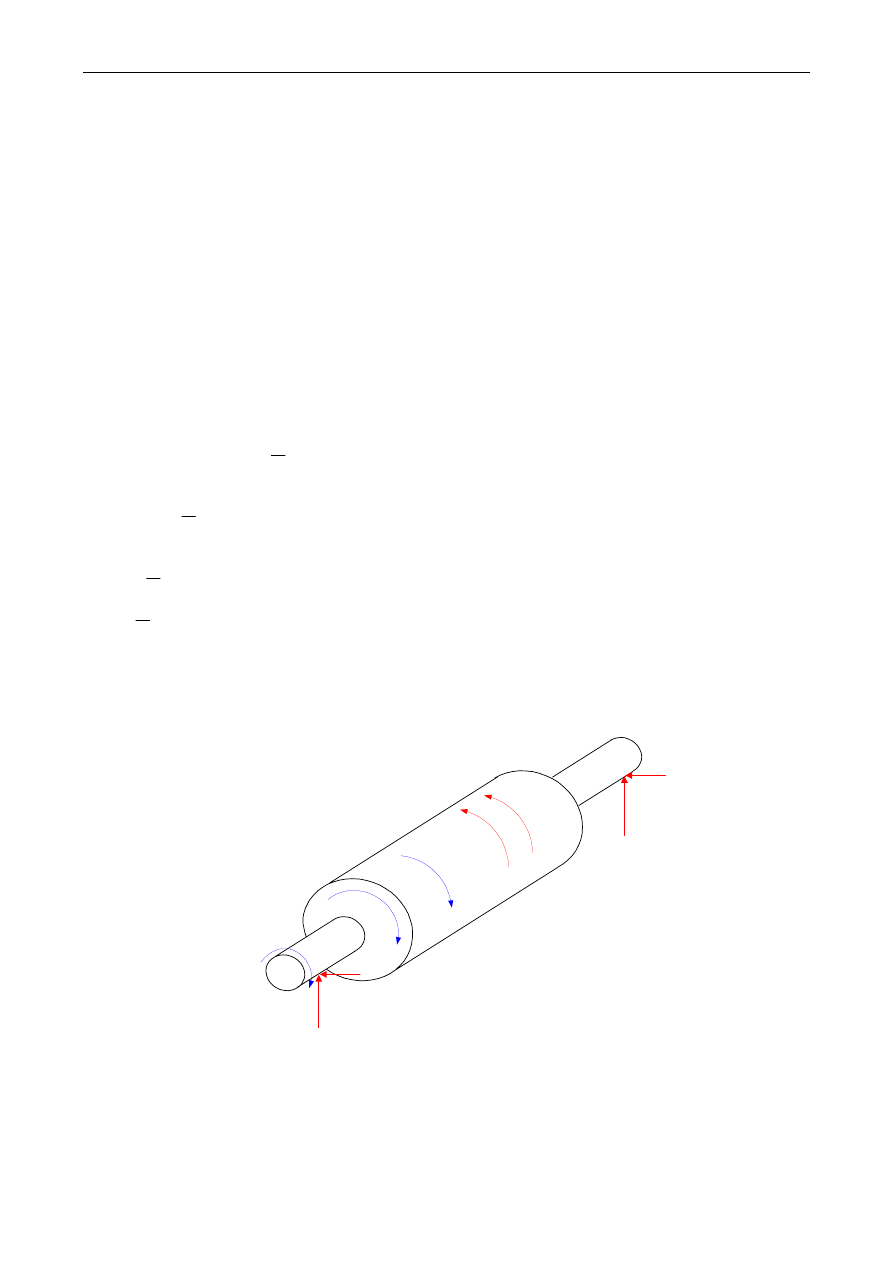
a'
a
F
a
T
e
F
f
ω
r
_
+
γ
i
a-a'
oś uzwojenia wzbudzenia
oś cewki a-a'
a'
a
u
a
F
a
T
e
F
f
ω
r
_
+
i
a-a'
f
a)
b)
i
a
+
_
u
a
F
a
T
e
F
f
i
f
ω
r
_
+
d - oś uzwojenia wzbudzenia
q - oś szczotek
F
f
F
a
γ
π
=
2
T
e
Zasada generacji momentu elektromagnetycznego
c)
d)
γ
= const
T
e
~ |F
f
||F
a
|
φ
f
φ
a
u
a
oś uzwojenia wzbudzenia
oś cewki a-a'
u
f
i
f
f
f'
u
f
i
f
f'
i
a
i
a
+
+
a
a'
u
f
f
f'
Rys. 1. Podstawowy model fizyczny maszyny prądu stałego z ilustracją zasady jej działania —generacji
momentu elektromagnetycznego:
a) oraz b) model elementarnego elektromechanicznego regulatora położenia pola wirnika — generacja
„prawie nieruchomej” SMM twornika (wirnika) Fa;
c) model fizyczny wzorcowego sprzężenia elektromechanicznego — generacja nieruchomej SMM twornika
Fa w osi q prostopadłej do osi d — osi pola magneśnicy (wzbudzenia),
d) zasada generacji momentu elektromagnetycznego — pewnej skłonności pola sił do zwiększania
całkowitego strumienia magnetycznego sprzężonego z układem elektromagnetycznym maszyny
W dalszych rozważaniach przyjęto następujące założenia upraszczające:
•
uzwojenia stojana i wirnika maszyny są układem symetrycznym a przewody uzwojenia wirnika są
równomiernie rozmieszczone w żłobkach;
Mieczysław RONKOWSKI
3
•
płynące w uzwojeniach prądy o dowolnych przebiegach wzbudzają SMM stojana i wirnika o rozkładzie
przestrzennym zbliżonym do sinusoidalnego (odwzorowane wektorami przestrzennymi);
•
wpływ pola elektrycznego między elementami maszyny, zjawisk anizotropii, histerezy i nasycenia
obwodu magnetycznego, strat w żelazie i wypierania prądu w przewodach uzwojeń jest pomijalnie mały
(odpowiada to przyjęciu liniowych obwodów magnetycznych i elektrycznych maszyny);
•
układ mechaniczny maszyny jest idealnie sztywny, a jego stałymi skupionymi są moment bezwładności i
współczynnik tarcia lepkiego.
Uwaga: Przyjęty na rys. 1 sposób strzałkowania napięć, prądów, SMM, prędkości kątowej i momentów
obrotowych dotyczy pracy silnikowej. Pokazany zwrot prędkości kątowej wirnika przyjęto jako
zwrot odniesienia — odpowiada wartości chwilowej dodatniej (
ω
r > 0). Analogicznie zwroty
prądów uzwojenia twornika i wzbudzenia odpowiadają ich wartościom chwilowym dodatnim (np.
dodatni prąd twornika dopływa do zacisku a, natomiast wypływa zaciskiem a’).
Maszyna prądu stałego jest fizycznym przykładem tzw. wzorcowego sprzężenia
elektromechanicznego, tzn. układu elektromechanicznego, w którym można wyróżnić dwa
obwody „jakby nieruchome” względem siebie o osiach magnetycznych wzajemnie
prostopadłych — tworzących kąt momentu
γ
=
π
/2. Osie te przyjęto oznaczyć symbolami d i q.
Wzajemnie prostopadłe położenie osi sił SMM uzwojenia wirnika (twornika) względem osi SMM
uzwojenia stojana (wzbudzenia) — tworzących kąt momentu
γ
=
π
/2, generuje moment elektromagnetyczny
(jako efekt interakcji dwóch pól) proporcjonalny do iloczynu:
•
modułów wektorów SMM stojana |Ff|i wirnika |Fa|
(przy pomięciu efektu nasycenia żelaza i reakcji
twornika);
•
strumienia w szczelinie przytwornikowej bieguna głównego i prądu wirnika (przy uwzględnieniu
efektu nasycenia żelaza i reakcji twornika).
Stwarza to szczególnie korzystne warunki kształtowania charakterystyki zewnętrznej maszyny
zarówno dla stanu statycznego jak i dynamicznego. Składają się na nie:
•
wyodrębnienie sterowanego źródła napięcia zasilania obwodu stojana, kształtującego strumień
wzbudzenia maszyny;
•
wyodrębnienie sterowanego napięcia zasilania obwodu wirnika, kształtującego prąd wirnika.
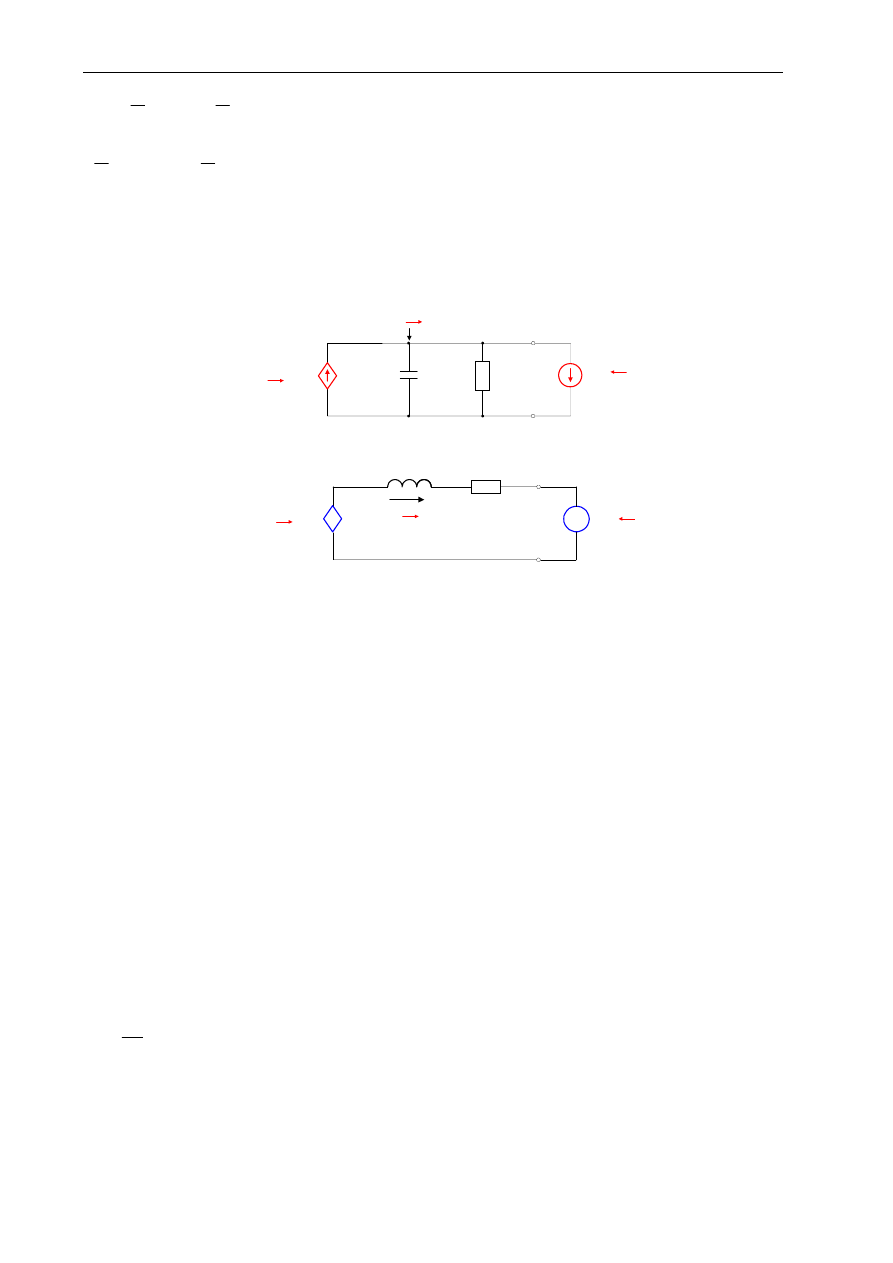
3.
DYNAMICZNY MODEL OBWODOWY WZORCOWEGO SPRZĘŻENIA
ELEKTROMECHANICZNEGO
♦
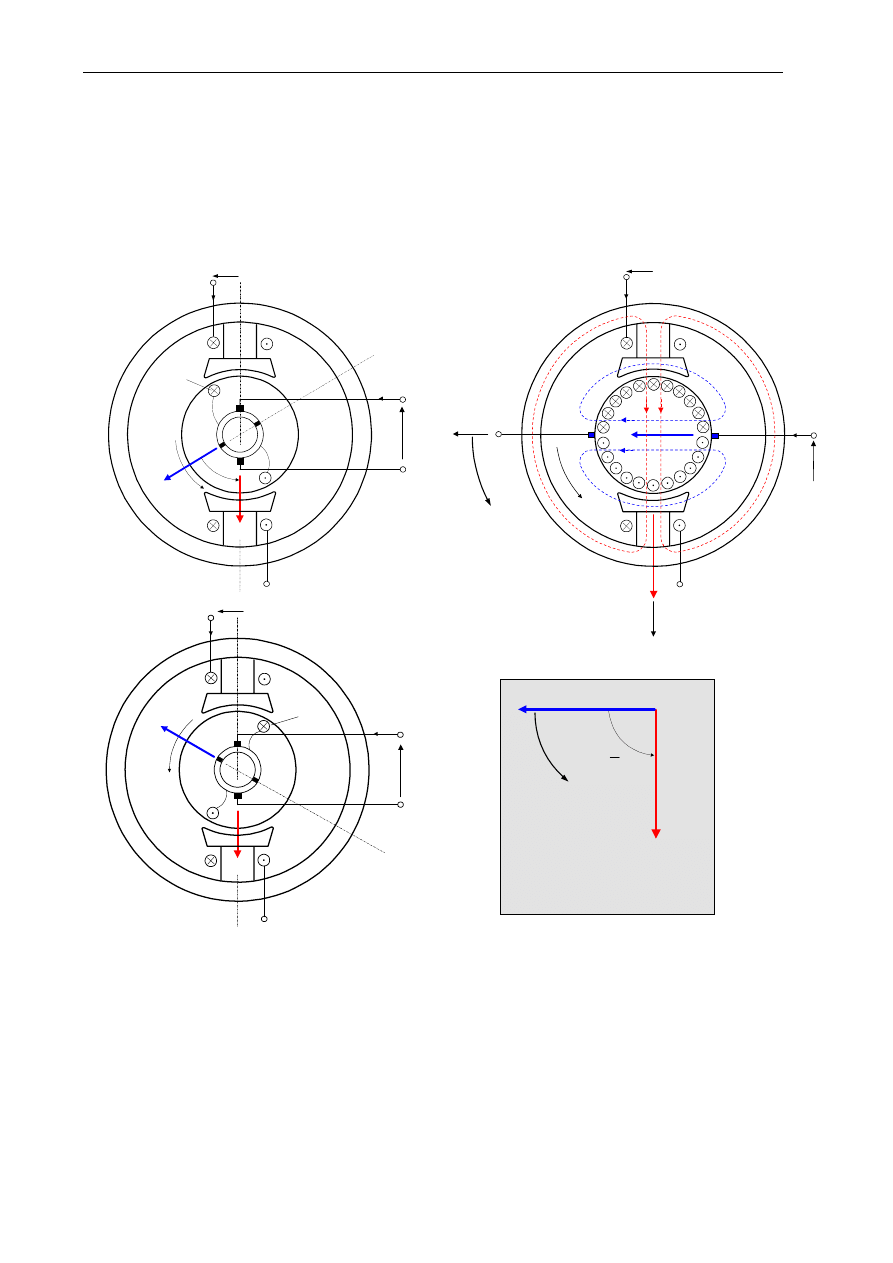
Wielkości oraz parametry modelu fizycznego sprzężenia
Do opisu modelu fizycznego wzorcowego sprzężenia elektromechanicznego — maszyny prądu
stałego (podanego na rys. 2), przyjęto układ współrzędnych dq i następujące wielkości oraz parametry (stałe
skupione):
a) wielkości i parametry elektryczne:
•
napięcia twornika ua i wzbudzenia uf,
•
prądy twornika ia oraz wzbudzenia if;
•
rezystancje uzwojenia twornika Ra oraz wzbudzenia Rf;
b) wielkości i parametry elektromagnetyczne:
•
strumienie skojarzone obwodu wzbudzenia
λ
df, obwodu twornika
λ
da w osi d, obwodu twornika
λ
qa
w osi q,
•
indukcyjność własną obwodu wzbudzenia Lff, indukcyjnością własną obwodu twornika Laa oraz
indukcyjnością wzajemną Laf obwodów twornika i wzbudzenia o charakterze sprzężenia
elektromechanicznego (rotacyjnego);
c)
wielkości elektromechaniczne:
•
kąt momentu
γ
,
•
sem rotacji ea,
4
Ćwiczenie: BADANIE DYNAMIKI SILNIKA PRĄDU STAŁEGO
•
moment elektromagnetyczny Te;
d) wielkości i parametry mechaniczne:
•
prędkość kątowa elektryczna wirnika
ω
r (równoznaczna prędkości mechanicznej dla maszyny
dwubiegunowej — P = 2),
•
moment obciążenia TL,
•
sumaryczny moment bezwładności wirnika i obciążenia J,
•
współczynnik tarcia lepkiego Bm.
u
f
i
f
λ
df
u
a
i
a
λ
qa
λ
da
e
a
T
e
ω
r
d
q
+
T
L
λ
df
ff f
L i
=
λ
da
af f
L i
=
λ
qa
aa a
L i
=
e
a
r
da
= ω λ
T
i
e
a
da
=
λ
B)
(V
q
F
e
×
=
T
B)
(V
q
F
e
×
=
a
J'
B
m
'
Rys. 2. Podstawowy model fizyczny wzorcowego sprzężenia elektromechanicznego — układ obwodów
stojana i wirnika „jakby nieruchomych” względem siebie o osiach magnetycznych q oraz d wzajemnie
prostopadłych
Uwaga: Podstawy fizyczne wyprowadzenia równania momentu elektromagnetycznego i sem rotacji podano
na rys. 2, odwołując się do wzoru Lorentza — wzoru na siłę działającą na ładunek q poruszający się
z prędkością V w polu magnetycznym o indukcji B. Proszę pamiętać, że ważny jest ruch względny
ładunku i pola!.
Regulator elektromechaniczny (komutator i szczotki) położenia pola twornika sprawia, że prąd
zmienny w prętach uzwojenia twornika wzbudza strumień
λ
qa nieruchomy i prostopadły względem
strumienia głównego (szczelinowego)
λ
da — strumienia wzbudzanego prądem if. Zatem wirujące uzwojenie
Mieczysław RONKOWSKI
5
twornika można odwzorować obwodem "jakby nieruchomym" — obwodem w którym płynie także prąd
stały, który jest równy prądowi ia dopływającemu do zacisków szczotek.
♦
Równania równowagi dynamicznej sprzężenia
Konsekwencją powyższych warunków i założeń są proste równania równowagi dynamicznej
obwodu twornika i wzbudzenia wzorcowego sprzężenia elektromechanicznego:
df
p
f
i
f
R
f
u
λ
+
=
(1)
a
e
qa
p
a
i
a
R
a
u
+
λ
+
=
(2)
gdzie: p = d/dt - operator różniczkowania.
Przy tworzeniu modelu sprzężenia, wpływ wielkości magnetycznych (strumieni sprzężonych) na
właściwości sprzężenia odwzorowano wielkościami obwodowymi: indukcyjnością własną obwodu
wzbudzenia Lff, indukcyjnością własną obwodu twornika Laa, indukcyjnością wzajemną Laf o charakterze
sprzężenia rotacyjnego (elektromechanicznego) obwodów twornika i wzbudzenia. Relacje te opisują
odpowiednie zależności dla strumieni sprzężonych podane na rys. 2.
Z kolei dla maszyny P- biegunowej zależności podane na rys. 2 przyjmują następującą postać:
dla sem rotacji
rm
f
i
af
G
rm
P
f
i
af
L
r
f
i
af
L
a
e
ω
ω
ω
====
====
====
)
2
(
(3)
dla momentu elektromagnetycznego (każda para biegunów zwiększa P/2 razy moment)
a
i
f
i
af
G
a
i
P
f
i
af
L
e
T
====
====
)
2
(
(4)
gdzie:
af
L
P
af
G
)
2
(
====
(5)
mr
P
r
ω
ω
)
2
(
====
(6)
Gaf - indukcyjność rotacji,
ω
rm - mechaniczna prędkość kątowa wirnika; P - liczba biegunów.
Celem sformułowania równania równowagi dynamicznej układu mechanicznego wzorcowego
sprzężenia elektromechanicznego rozważono odpowiednie siły działające na wirnik maszyny prądu stałego
(rys. 3).
B
m
ω
rm
T
e
Jp
ω
rm
T
L
ω
rm
Rys. 3. Siły działające na wirnik maszyny prądu stałego: sformułowanie równania równowagi dynamicznej
układu mechanicznego
Na podstawie rys. 3 można sformułować następujące równanie równowagi:
L
T
rm
m
B
rm
p
J
e
T
+
+
=
ω
ω
(7)
lub
6
Ćwiczenie: BADANIE DYNAMIKI SILNIKA PRĄDU STAŁEGO
L
T
r
m
B
P
r
Jp
P
e
T
+
+
=
ω
ω
)
2
(
)
2
(
(8)
gdzie:
m
B
m
B
P
J
J
P
′
=
′
=
)
2
(
;
)
2
(
J’ - moment bezwładności oraz B’m - współczynnik tarcia lepkiego, zredukowane do elektrycznej prędkości
kątowej wirnika
ω
r, tzn. prędkości odpowiadającej maszynie dwubiegunowej (P=2).
♦
Analog elektryczny sprzężenia
Możliwe analogie elektryczne równania ruchu (7) układu mechanicznego pokazuje rys. 4.
-
+
T
e
L = J
R = B
m
T
L
T
e
G = B
m
T
L
u
C
i
C = J
ω
rm
i
u
ω
rm
m
m
_+
u
i
a)
b)
Rys. 4. Możliwe analogie elektryczno-mechaniczne równania ruchu: a) analogie: napięcie — prędkość
kątowa, prąd — moment obrotowy, pojemność — moment bezwładności, przewodność — współczynnik
tarcia; b) analogie: prąd: — prędkość kątowa, napięcie — moment obrotowy, indukcyjność — moment
bezwładności, rezystancja — współczynnik tarcia
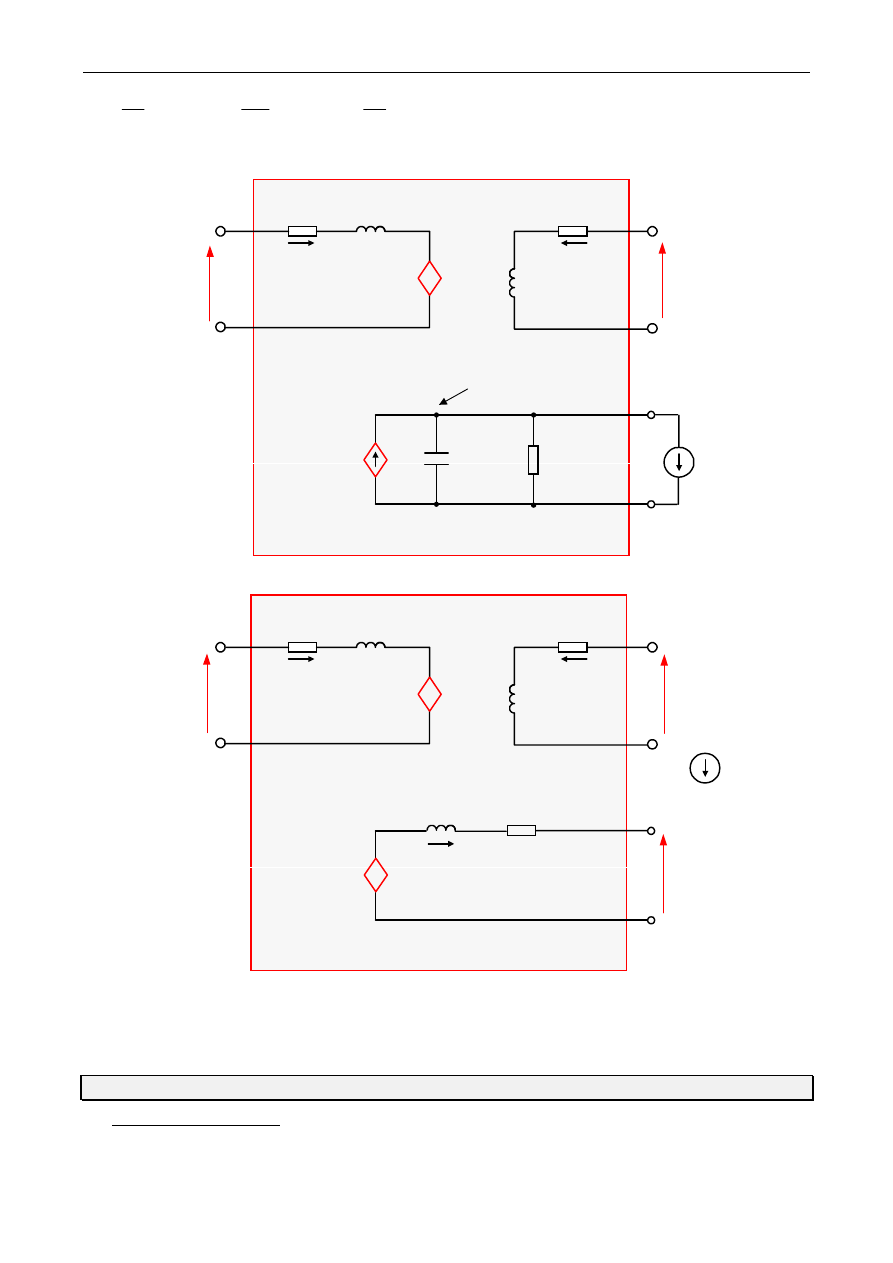
Równania (1)-(4) i (7) dla wzorcowego sprzężenia elektromechanicznego (P - biegunowego) można
odwzorować dynamicznym modelem obwodowym pokazanym na rys. 5, gdzie sem rotacji modelowane jest
sterowanym źródłem napięciowym, a dla modelu obwodowego równania ruchu (7) przyjęto analogie
odpowiednie podane na rys. 4a (moment elektromagnetyczny modelowany jako sterowane źródło prądowe) i
na rys. 4b (moment elektromagnetyczny modelowany jako sterowane źródło napięciowe).
♦
Redukcja analogu elektrycznego sprzężenia
Celem redukcji analogu elektrycznego (obwodu) układu mechanicznego do obwodu twornika
założono: if = const, zatem
rm
v
k
rm
f
i
af
G
a
e
ω
ω
=
=
(9)
a
i
v
k
a
i
f
i
af
G
e
T
=
=
(10)
gdzie, stała maszyny
f
i
af
G
v
k
=
Następnie po przekształceniu równania (10) do postaci:
v
k
e
T
a
i
=
oraz założeniu:
rm
v
k
a
e
c
u
ω
=
=
równanie układu (obwodu) mechanicznego (7) można przekształcić do postaci:
Mieczysław RONKOWSKI
7
)
(
2
)
(
2
v
k
L
T
rm
v
k
v
k
m
B
rm
v
k
p
v
k
J
a
i
+
+
=
ω
ω
(11)
a)
u
a
a
R
a
L
aa
i
a
e
a
e
a
= G
af
i
f
ω
rm
L
ff
i
f
R
f
u
f
f
+
_
+
_
+
_
T
e
= G
af
i
f
i
a
+
_
T
L
m
u
c
=
ω
rm
G = B
m
T
e
C = J
b)
u
a
a
R
a
L
aa
i
a
e
a
e
a
= G
af
i
f
ω
rm
L
ff
i
f
R
f
u
f
f
+
_
+
_
+
_
T
e
= G
af
i
f
i
a
+
_
T
L
m
i
L
=
ω
rm
R = B
m
T
e
L = J
+
_
Rys.5. Dynamiczny model obwodowy (analog elektryczny) maszyny (silnika) prądu stałego — wzorcowego
sprzężenia elektromechanicznego: a) analog elektryczny układu mechanicznego wg rys. 4a; b) analog
elektryczny układu mechanicznego wg rys. 4b
Uwaga: Strzałkowanie na rys. 5. przyjęto wg konwencji silnikowej (odbiornikowej).
1. Wielkości modelu na rys. 5.
ua
- napięcie twornika
uf
-
napięcie wzbudzenia
8
Ćwiczenie: BADANIE DYNAMIKI SILNIKA PRĄDU STAŁEGO
ia
-
prąd twornika
if
-
prąd wzbudzenia
ea
- sem rotacji
Te
- moment elektromagnetyczny (wewnętrzny)
ω
rm
- prędkość kątowa (mechaniczna) wirnika
TL
- moment obciążenia (zewnętrzny)
2. Parametry modelu na rys. 5.
Ra
- rezystancja obwodu twornika
Rf
- rezystancja obwodu wzbudzenia
Laa
- indukcyjność obwodu twornika
Lff
- indukcyjność obwodu wzbudzenia
Gaf
- indukcyjność rotacji (sprzężenia elektromechanicznego)
J
- moment bezwładności
Bm
- współczynnik tarcia lepkiego
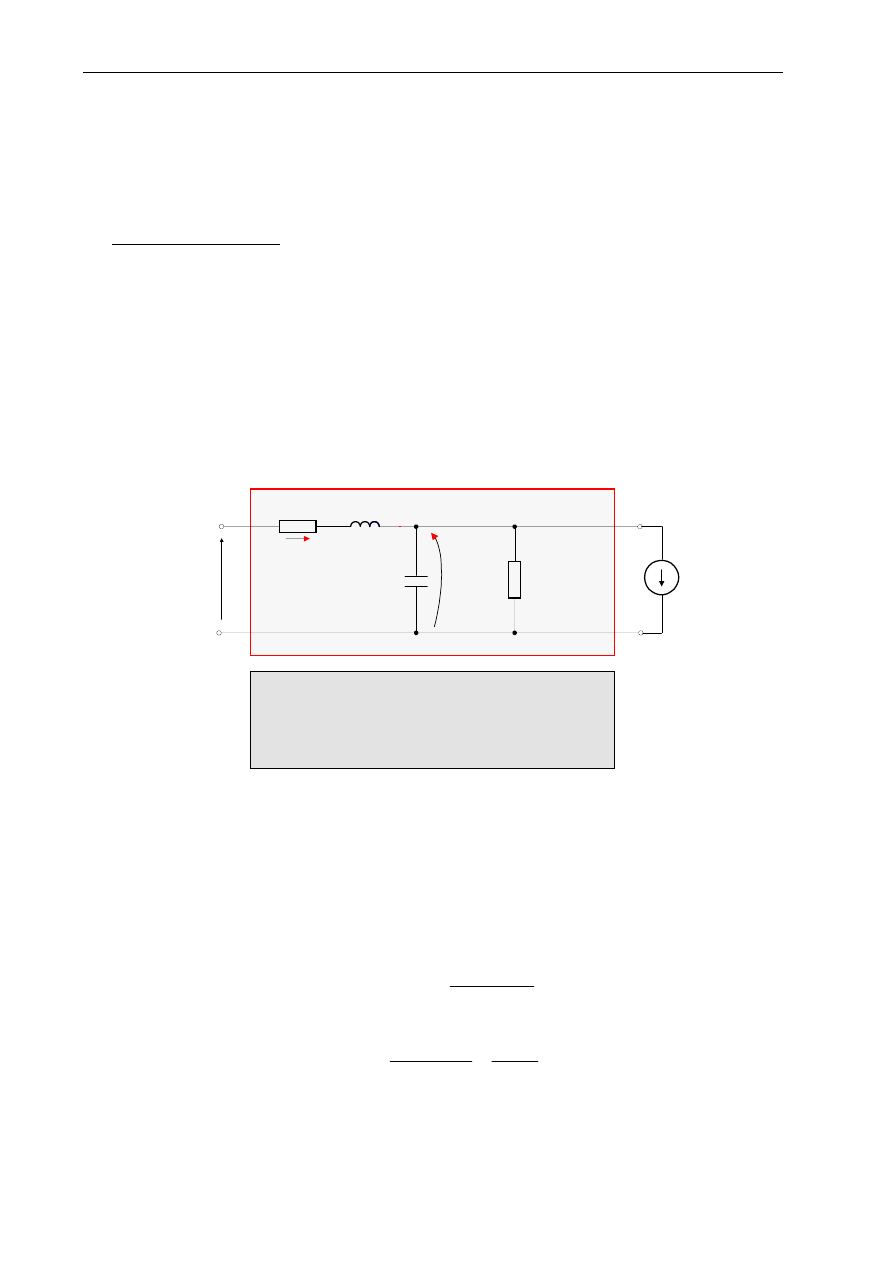
Taka postać równania ruchu (umożliwia połączenie galwaniczne zacisków sem rotacji ea obwodu
twornika z zaciskami źródła momentu elektromagnetycznego (o wydajności równej ia) analogu
elektrycznego układu mechanicznego (rys 5a). Otrzymujemy zatem analog RLC wzorcowego sprzężenia
elektromechanicznego, pokazany na rys. 6.
u
a
a
R
a
L
aa
i
a
m'
J
k
v
2
B
k
m
v
2
e
a
e
k
a
v
rm
=
ω
- pojemność dynamiczna
_
_
T
k
L
v
_
J
k
v
2
_
v
=
T
k
i
e
a
_
k
G
v
af f
=
I
Rys. 6. Maszyna (silnik) prądu stałego — wzorcowe sprzężenie elektromechaniczne: zredukowany
dynamiczny model obwodowy: analog RLC przy założeniu if = const
Dla analogu RLC na rys. 6, przy założeniu Bm
≈
0, można zdefiniować następujące stałe czasowe
silnika prądu stałego:
•
stała czasowa elektromagnetyczna
/ a
r
aa
L
a
=
τ
•
stała czasowa elektromechaniczna
2
)
(
f
I
af
G
a
r
J
C
a
r
m
=
=
τ
gdzie, pojemność
2
)
(
2
)
(
v
k
J
f
I
af
G
J
C
=
=
nazywa się pojemnością dynamiczną silnika prądu stałego.
Dla tak zdefiniowanych stałych czasowych można podać następujące warunki stabilności
przebiegów dynamicznych silnika prądu stałego:

Mieczysław RONKOWSKI
9
τ
τ
m
a
>
4
przebiegi
aperiodyczne;
τ
τ
m
a
=
4
przebiegi aperiodyczne krytyczne;
τ
τ
m
a
<
4
przebiegi
oscylacyjne.
4.
ZASTOSOWANIE PROGRAMU SYMULACYJNEGO PSPICE DO BADANIA
WŁAŚCIWOŚCI DYNAMICZNYCH SILNIKA PRĄDU STAŁEGO
♦
Stany dynamiczne silnika prądu stałego
Stany dynamiczne silnika prądu stałego określone są przez następujące czynniki:
•
warunki zasilania (wymuszenia elektryczne);
•
przebiegi napięć, prądów i strumieni sprzężonych poszczególnych uzwojeń stojana i wirnika;
•
rozwijany przez maszynę moment elektromagnetyczny (wewnętrzny) jako wynik wzajemnego
oddziaływania odpowiednich prądów i strumieni sprzężonych;
•
warunki obciążenia na wale maszyny (moment obciążenia - zewnętrzny, prędkość kątowa
wirnika)
•
wypadkowy moment bezwładności (silnika i maszyny napędzanej).
Silnik prądu stałego może być zasilany w warunkach sieci sztywnej lub elastycznej, napięcia
zasilania mogą mieć przebieg stały („gładki”) lub odkształcony (np. zasilanie z prostownika).
Warunki obciążenia na wale silnika prądu stałego — „zaciskach mechanicznych” — mogą być stałe
lub zmienne: np. zależne od czasu lub prędkości kątowej maszyny (liniowo lub kwadratowo).
Typowe stany pracy dynamicznej silnika prądu stałego, pracującej w układzie napędu
elektrycznego, mogą być następujące:
•
rozruch (bezpośredni, z opornikiem w obwodzie twornika, za pomocą układu typu „chopper” lub
prostownika sterowanego);
•
hamowanie;
•
nawrót;
•
skokowa (lub inna) zmiana momentu obciążenia.
•
wybieg grupowy (np. zanik napięcia w sieci zasilającej kilka silników)
•
stany zwarcia w sieci zasilającej silnik (np. zwarcie chwilowe na zaciskach uzwojenia twornika).
Właściwa analiza wymienionych wyżej stanów pracy dynamicznej — stanów nieustalonych —
silnika prądu stałego, ze względu na nieliniowość zachodzących procesów elektromechanicznych w
maszynie, wymaga zastosowania zaawansowanych technik symulacyjnych. Opracowany w p. 3 niniejszego
ćwiczenia model obwodowy maszyny prądu stałego, zawierający m.in. źródła sterowane, stanowi wygodną
bazę do obliczeń komputerowych, wykorzystujących programy symulacyjne obwodów elektrycznych typu:
NAP, PSPICE, TUTSIM, itp. Program PSPICE wydaję się być zarówno programem najbardziej
zaawansowanym jak i przyjaznym dla użytkownika, w klasie programów symulacyjnych obwodów
elektrycznych.
♦
Budowa modelu symulacyjnego w programie PSPICE
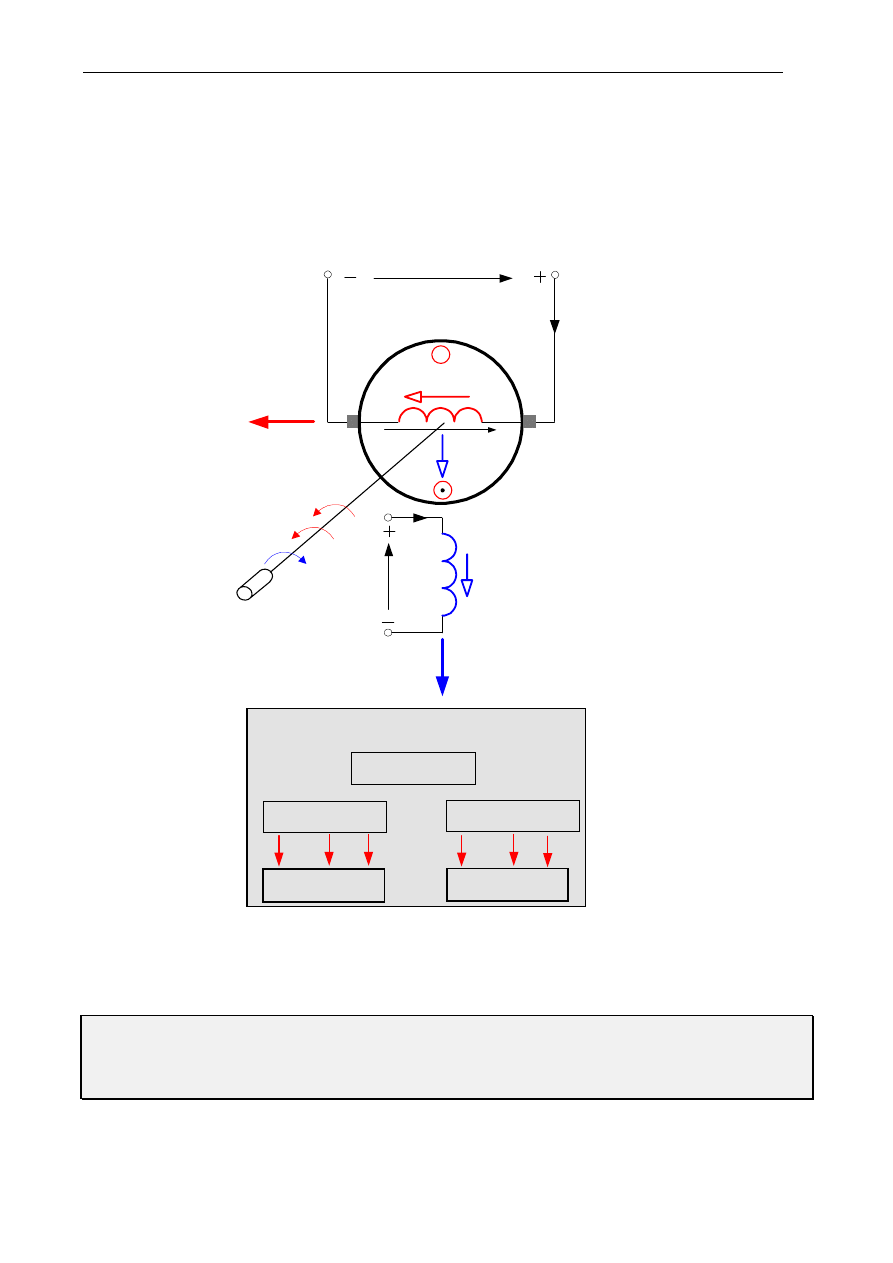
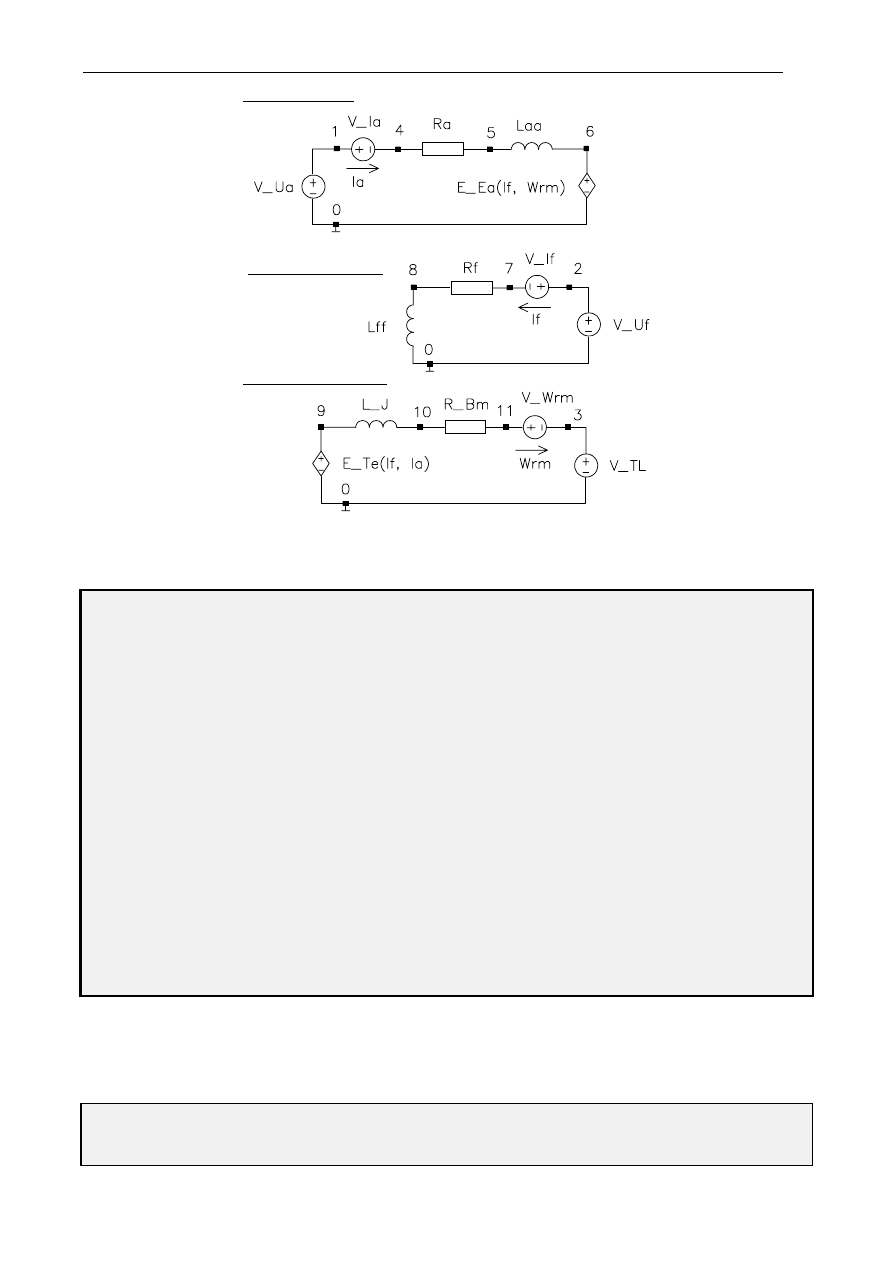
Opierając się na modelu obwodowym maszyny prądu stałego przedstawionym na rys. 5b oraz
zasadach formułowania modelu symulacyjnego obowiązujących dla programu PSPICE zbudowano analog
elektryczny maszyny, pokazany na rys. 7, przystosowany do analizy za pomocą programu PSPICE. Każdy
element jest włączony w obwód w dokładnie zdefiniowanych węzłach. Definicja węzłów polega na
nazwaniu każdego z nich kolejną liczbą lub literami. Nie obowiązuje żadna hierarchia tych oznaczeń.
Jedynym warunkiem jest umieszczenie na liście węzłów, węzła oznaczonego numerem „0”.
W badaniach stanów nieustalonych — silnika prądu stałego należy określić wartości parametrów dla
jej modelu obwodowego, charakter wymuszeń elektrycznych i mechanicznych.
Wartości parametrów modelu silnika można obliczyć z wystarczającą dokładnością dla obliczeń
inżynierskich na podstawie jej danych katalogowych lub danych pomiarowych (szczegóły w załączniku do
instrukcji). Z kolei do wprowadzenia wartości tych parametrów do programu PSPICE wykorzystuje się
instrukcję .PARAM, którą ilustruje następujący przykład:
10
Ćwiczenie: BADANIE DYNAMIKI SILNIKA PRĄDU STAŁEGO
Obwód twornika
Obwód wzbudzenia
Obwód mechaniczny
Rys. 7. Analog elektryczny silnika prądu stałego dla sformułowania pliku wejściowego PSPICE (podstawa
sformułowania — model obwodowy silnika na rys. 5b)
*Dane znamionowe (indeks n oznacza wartosci znamionowe) silnika:
* Pn=13kW - moc; Uan=220V - napiecie twronika;
* Ian=67.7A - prad twornika; Pfn=186W - moc wzbudzenia;
* Ufn=110V - napiecie wzbudzenia; Ra=0.33 ohm - rezystancja twronika
* Laa=0.204H - indukcyjnosc twronika; nn=1500obr/min - predkosc obrotowa;
* J=0.11kgm2 - moment bezwladnosci
* wprowadzanie danych poprzez paramerty globalne
.PARAM Pn=13e3 Uan=220 Ian=67.7 Pfn=186 Ufn=110
.PARAM Ra=0.4 Laa=0.02 nn=1500 J=0.11
*stale
.PARAM pi=3.14159
*Obliczenia brakujacych danych i parametrow modelu silnika
.PARAM Ifn={Pfn/Ufn} Rf={Ufn/Ifn} Wrmn={2*pi*nn/60}
*znamionowy moment obciazenia
.PARAM TLn={Pn/Wrmn}
* obliczanie indukcyjnosci rotacji
.PARAM Gaf={(Uan - Ian*Ra)/Ifn/Wrmn}
*przyjeto indukcyjnosc obwodu wzbudzenia Lff>=20*Laa*Rf/Ra
.PARAM Lff={20*Laa*Rf/Ra}
*przyjeto wspolczynnik tarcia Bm=(0.01*Pn/Wrmn/Wrmn) Nms/rad
.PARAM Bm={(0.01*Pn/Wrmn/Wrmn)}
Klasyczne wymuszenia elektryczne dla silnika prądu stałego mają charakter napięciowy o stałej
wartości. Do wprowadzenia wartości tych napięć do programu PSPICE wykorzystuje się instrukcję
definiującą źródła napięciowe niezależne. Wydajność tych źródeł można zmieniać za pomocą odpowiednich
współczynników, ilustruje to następujący przykład:
*wspolczynniki do okreslenia napiecie zasilania twornika i wzbudzenia,
.PARAM kUa=1 kUf=1
*************************************

Mieczysław RONKOWSKI
11
*napiecie zasilania twornika
V_Ua 1 0 DC {Uan*kUa}
* dla nawrotu przyjac napiecie o przebiegu impulsowym
*V_Ua 1 0 PULSE({Uan*kUa} {-Uan*kUa} 0.6 0 0 0.8 5)
* gdzie: V1=Ua; V2=-Ua; td=0.6s; trise=0s; tfall=0s; pw=0.8; per=5s
**********************************
*napiecie zasilania wzbudzenia
V_Uf 2 0 {Ufn*kUf}
Klasyczne wymuszenia mechaniczne (obciążenia na wale) dla maszyny prądu stałego mogą być o
charakterze stałego lub zmiennego momentu obciążenia TL : np. zależnego od czasu lub prędkości kątowej
maszyny (liniowo lub kwadratowo). Przykładowe momenty obciążenia można zapisać następująco:
•
stały moment obciążenia o wartości zerowej
TL = 0
•
stały moment obciążenia o wartości momentu znamionowego lub innej
TL = TLn
lub
TL = kTL*TLn
gdzie, dla danej znamionowej mocy Pn i prędkości obrotowej nn
T
P
Ln
n
rmn
=
/
ω
ω
π
rmn
=
2
60
n
n
/
kTL
≠
1
•
moment obciążenia zależny liniowo od prędkości kątowej
rm
TL
k
L
T
ω
====
rmn
Ln
T
TL
k
ω
/
====
•
moment obciążenia zależny kwadratowo od prędkości kątowej
rm
rm
TL
k
L
T
ω
ω
====
)
/(
rmn
rmn
Ln
T
TL
k
ω
ω
====
•
moment obciążenia zależny od czasu, np. zmieniający się skokowo (impulsowo)
od wartości TL = 0 do TL = TLn
Do wprowadzenia wartości tych momentów obciążenia do programu PSPICE wykorzystuje się
instrukcję definiującą źródła napięciowe niezależne lub zależne (jako analog momentu), którą ilustrują
następujące przykłady:
*wspolczynniki do okreslenia momentu obciazenia
.PARAM kTL=0 ; wspolczynnik dla stalego momentu
*.PARAM kTL={TLn/Wrmn} ;wspolczynnik dla TL=kTL*Wrm
*.PARAM kTL={TLn/Wrmn/Wrmn } ;wspolczynnik dla TL=kTL*Wrm*Wrm
****************************
V_TL 3 0 DC {TLn*kTL} ; staly moment obciazenia na wale TL
*moment obciazenia TL=kTL*Wrm
*E_TL TL 0 VALUE={kTL*I(V_Wr)}
*moment obciazenia TL=kTL*Wrm*Wrm
*E_TL TL 0 VALUE={kTL*I(V_Wr)*I(V_Wr)}
*Uwaga: dla skokowej zmiany momentu TL przyjac
*V_TL 3 0 PULSE(0 {TLn*kTL} 0.6 0 0 0.3 0.6)
* gdzie: V1=0 Nm; V2=TL Nm; td=0.6s; trise=0s; tfall=0s; pw=0.3; per=0.6s
W badaniach stanów nieustalonych za pomocą programu PSPICE wykorzystuje się instrukcję
analizy czasowej o następującym formacie:
.TRAN <krok wydruku (HWYDR)> <czas końca analizy (TSTOP) <czas opóźnienia drukowania
+wyników (HNDR)> < maks. krok obliczeń (HMAX)> [UIC]
gdzie,
HWYDR - krok wydruku czyli odstęp czasowy wyprowadzania wyników obliczeń do zbioru
wynikowego z rozszerzeniem .OUT (jeżeli zostanie użyta instrukcja .PRINT);

12
Ćwiczenie: BADANIE DYNAMIKI SILNIKA PRĄDU STAŁEGO
TSTOP - czas analizy od czasu t = 0 s do t = TSTOP s określającego koniec obliczeń;
HNDR - czas określający rozpoczęcie zapisu wyników do zbioru wynikowego z rozszerzeniem
.OUT (jeżeli zostanie użyta instrukcja .PRINT) i zbioru wynikowego z rozszerzeniem
.DAT (jeżeli zostanie użyta instrukcja .PROBE);
HMAX - maks. krok obliczeń o wartości domyślnej = TSTOP/50 s - faktyczny krok obliczeń jest
dobierany automatycznie w trakcie trwania obliczeń;
UIC - parametr oznacza, że do obliczeń będą brane warunki początkowe zapisane za pomocą
oddzielnej instrukcji .IC (INITIAL CONDITIONS) lub za pomocą wyrażenia IC= , które
jest podane w liniach określających indukcyjność (IC= prąd początkowy) lub pojemność
(IC=napięcie początkowe).
Uwaga: W analizie maszyny elektrycznych, ze względu na możliwość wystąpienia oscylacji numerycznych
(niestabilności rozwiązania w fazie obliczeń, kiedy maszyna wchodzi w stan pracy ustalonej),
niedopuszczalne jest pomijanie w instrukcji .TRAN maks. kroku obliczeń HMAX. Szacowanie jego
wartości należy przeprowadzić w oparciu o stałe czasowe modelu obwodowego maszyny i okres
wymuszeń na zaciskach maszyny (należy zajrzeć do notatek z metod numerycznych!!!).
W badaniach stanów nieustalonych maszyny prądu stałego za pomocą programu PSPICE warunki
początkowe ustala się dla wartości prądów i prędkości kątowej wirnika, odpowiadające wyjściowemu
stanowi ustalonemu maszyny. Najłatwiej można je ustalić dla analizy rozruchu maszyny — wartości prądów
i prędkości kątowej wirnika są wtedy zerowe. Warunki początkowe zapisane w programie PSPICE ilustrują
następujące przykłady:
*obwod twornika
Laa 5 6 {Laa} IC=0
*************************
*obwod wzbudzenia
Lff 8 0 {Lff} IC={Ufn*kUf/Rf} ;If=(Uf/Rf) ustalony prad wzbudzenia
* dla silnika obcowzbudnego
*Uwaga: dla silnika bocznikowego IC=0 bo If=0
*****************************
*obwod mechaniczny
L_J 9 10 {J} IC=0 ; predkosc poczatkowa zerowa
Dla analizy innych stanów dynamicznych maszyny można wykonać najpierw obliczenia dla
rozruchu aż do wejścia maszyny w stan ustalony — od tego momentu zapisywać wyniki obliczeń do pliku
.DAT. Możliwe jest także obliczenie ręczne warunków początkowych dla zadanego stanu ustalonego
wyjściowego maszyny. Dla analizy hamowania i nawrotu można przyjąć wartość prędkości kątowej wirnika
równą znamionowej lub idealnego biegu jałowego i założyć zerowe wartości prądu twornika.
Analiza stanów dynamicznych maszyny za pomocą programu PSPICE wymaga określenia czasu
trwania obliczeń TSTOP — czasu określającego koniec obliczeń. Czas ten — w przypadku rozruchu
bezpośredniego bez obciążenia — można w przybliżeniu oszacować w oparciu o tzw. stałą rozruchową
maszyny
τ
r :
TSTOP
≥
=
τ
ω
r
n
rm
J T
( /
)
0
która jak widać określa czas rozruch maszyny (układu) o momencie bezwładności J pod wpływem momentu
znamionowego maszyny Tn od zera do prędkości biegu jałowego
ω
rm0 .
Do wyprowadzania wyników analizy w programie PSPICE służy instrukcja .PROBE. Przykłady
użycia instrukcji .TRAN oraz .PROBE w programie PSPICE ilustrują następujące przykłady:
*symulacja charakterystyk rozruchowych
.TRAN 0.004 0.6 0 0.002 UIC
*obliczone przebiegi do obserwacji na ekranie
.PROBE V(1) I(Ra) V(6) V(2) I(Rf) V(9) I(R_Bm) V(3)
♦
Plik wsadowy programu PSPICE: cw3-2.cir
W oparciu o analog elektryczny silnika prądu stałego na rys. 7 oraz powyższe rozważania,
sformułowano następujący plik wsadowy programu PSPICE.

Mieczysław RONKOWSKI
13
ROZRUCH SILNIKA PRADU STALEGO (OBCOWZBUDNEGO) przy TL=0
*Dane znamionowe (indeks n oznacza wartosci znamionowe) silnika:
* Pn=13kW - moc; Uan=220V - napiecie twronika;
* Ian=67.7A - prad twornika; Pfn=186W - moc wzbudzenia;
* Ufn=110V - napiecie wzbudzenia; Ra=0.33 ohm - rezystancja twronika
* Laa=0.204H - indukcyjnosc twronika; nn=1500obr/min - predkosc obrotowa;
* J=0.11kgm2 - moment bezwladnosci
* wprowadzanie danych poprzez paramerty globalne
.PARAM Pn=13e3 Uan=220 Ian=67.7 Pfn=186 Ufn=110
.PARAM Ra=0.4 Laa=0.02 nn=1500 J=0.11
*stale
.PARAM pi=3.14159
*Obliczenia brakujacych danych i parametrow modelu silnika
.PARAM Ifn={Pfn/Ufn} Rf={Ufn/Ifn} Wrmn={2*pi*nn/60}
*znamionowy moment obciazenia
.PARAM TLn={Pn/Wrmn}
* obliczanie indukcyjnosci rotacji
.PARAM Gaf={(Uan - Ian*Ra)/Ifn/Wrmn}
*przyjeto indukcyjnosc obwodu wzbudzenia Lff>=20*Laa*Rf/Ra
.PARAM Lff={20*Laa*Rf/Ra}
*przyjeto wspolczynnik tarcia Bm=(0.01*Pn/Wrmn/Wrmn) Nms/rad
.PARAM Bm={(0.01*Pn/Wrmn/Wrmn)}
*wspolczynniki do okreslenia napiecie zasilania twornika i wzbudzenia,
.PARAM kUa=1 kUf=1
*wspolczynniki do okreslenia rezystancji twornika
.PARAM kRa=1
*wspolczynniki do okreslenia momentu obciazenia
.PARAM kTL=0 ; wspolczynnik dla stalego momentu
*.PARAM kTL={TLn/Wrmn} ;wspolczynnik dla TL=kTL*Wrm
*.PARAM kTL={TLn/Wrmn/Wrmn } ;wspolczynnik dla TL=kTL*Wrm*Wrm
*obwod twornika
*napiecie zasilania twornika
V_Ua 1 0 DC {Uan*kUa}
* dla nawrotu przyjac napiecie o przebiegu impulsowym
*V_Ua 1 0 PULSE({Uan*kUa} {-Uan*kUa} 0.6 0 0 0.8 5)
* gdzie: V1=Ua; V2=-Ua; td=0.6s; trise=0s; tfall=0s; pw=0.8; per=5s
V_Ia 1 4 DC 0V ;pomiar pradu Ia
Ra 4 5 {Ra*kRa}
Laa 5 6 {Laa} IC=0
*SEM rotacji
E_Ea 6 0 VALUE={Gaf*I(V_If)*I(V_Wrm)} ;bo Ea=Gaf*If*Wrm
*obwod wzbudzenia
*napiecie zasilania wzbudzenia
*tylko dla silnika obcowzbudnego mozna pominac cztery kolejne linie
V_Uf 2 0 {Ufn*kUf}
V_If 2 7 DC 0V ;pomiar pradu If
Rf 7 8 {Rf}
Lff 8 0 {Lff} IC={Ufn*kUf/Rf} ;If=(Uf/Rf) ustalony prad wzbudzenia
* dla silnika obcowzbudnego
*Uwaga: dla silnika bocznikowego IC=0 bo If=0
*obwod mechaniczny
*analog momentu elektromagnetycznego
E_Te 9 0 VALUE={Gaf*I(V_If)*I(V_Ia)}; bo Te=Gaf*If*Ia
L_J 9 10 {J} IC=0 ; predkosc poczatkowa zerowa
R_Bm 10 11 {Bm}
V_Wrm 11 3 DC 0V ;pomiar predkosci katowej Wrm
V_TL 3 0 DC {TLn*kTL} ; staly moment obciazenia na wale TL
14
Ćwiczenie: BADANIE DYNAMIKI SILNIKA PRĄDU STAŁEGO
*moment obciazenia TL=kTL*Wrm
*E_TL TL 0 VALUE={kTL*I(V_Wr)}
*moment obciazenia TL=kTL*Wrm*Wrm
*E_TL TL 0 VALUE={kTL*I(V_Wr)*I(V_Wr)}
*Uwaga: dla skokowej zmiany momentu TL przyjac
*V_TL 3 0 PULSE(0 {TLn*kTL} 0.6 0 0 0.3 0.6)
* gdzie: V1=0 Nm; V2=TL Nm; td=0.6s; trise=0s; tfall=0s; pw=0.3; per=0.6s
*Uwaga: dla analizy .DC pominac V_TL
* dla analizy .DC :charakterystyka Te=Te(Wrm)
* podstawic I_Wrm zamiast V_TL
*I_Wrm 3 0 DC 0A
*analiza wplywu momentu bezwladnosci dla J=0.11 J=3*0.11 J=6*0.11
* na dynamike silnika
.STEP PARAM J LIST 0.11 0.33 0.66
.PROBE V(1) I(Ra) V(6) V(2) I(Rf) V(9) I(R_Bm) V(3)
*analiza .TRAN dla wyznaczenia charakterystyk rozruchowych
.TRAN 0.004 0.6 0 0.002 UIC
*krok druku, czas koncowy, czas poczt. druku, max krok calkowania, wyk. war. *pocz.
*analiza .DC :wyznaczenie charakterystyki Te=Te(Wrm) dla Ua=180V i Ua=220;
*.DC LIN I_Wrm 0 200 10 V_Ua 140 220 40
*skala liniowa, zmienna, zakres dolny, zakres gorny, krok, druga zmienna, zakres dolny, zakres
*gorny, krok
.END
♦
Wyniki symulacji wybranych stanów dynamicznych silnika
•
Stan ustalony
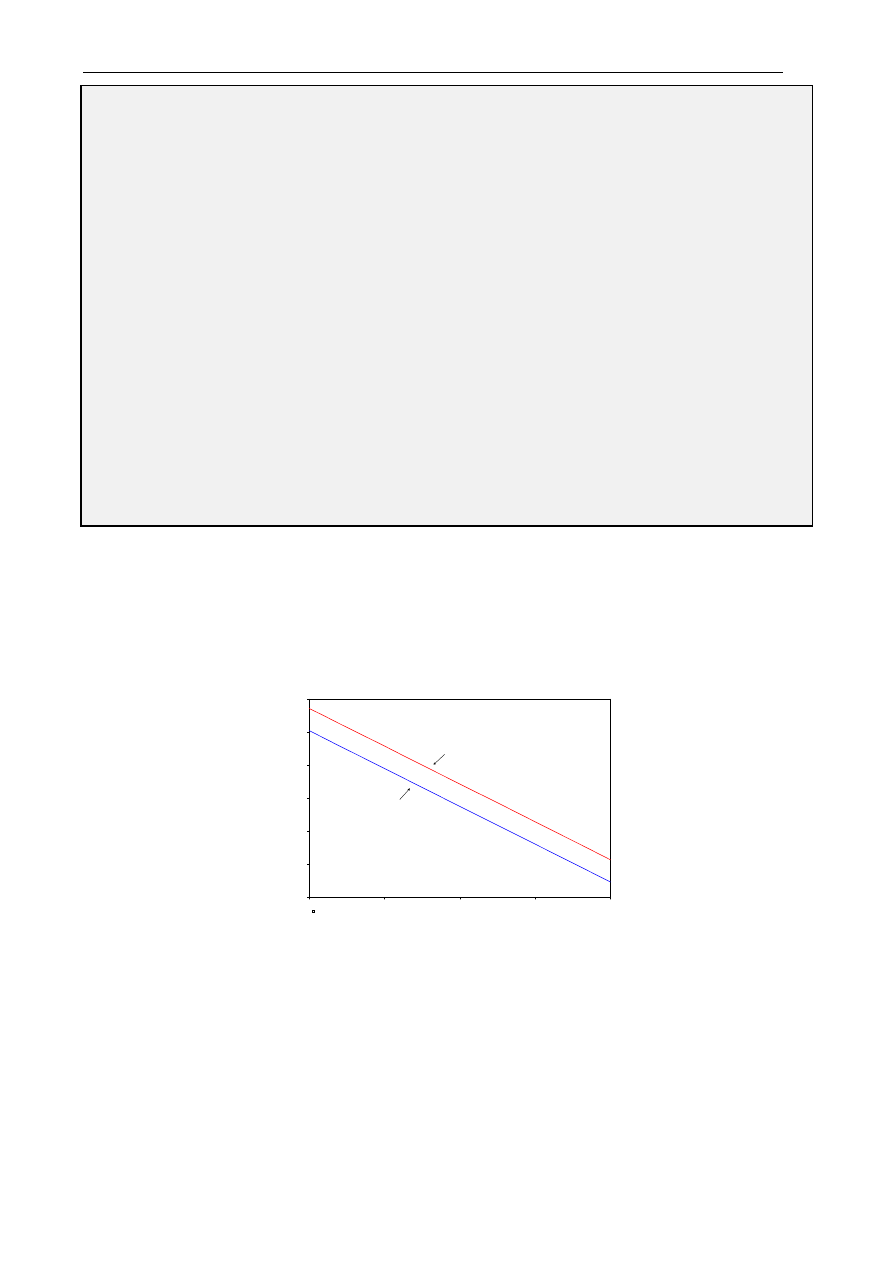
Interesującą charakterystyką stanu ustalonego jest charakterystyka mechaniczna Te=Te(
Ω
rm).
Można ją wyznaczyć za pomocą analizy stałoprądowej .DC symulatora PSPICE. Jej przebieg pokazano na
rys. 8.
Wyniki analizy .DC (postprocesor graficzny .PROBE)
0
50
100
150
200
I_Wrm
V(9)
800
600
400
200
0
-200
-400
Ua=180 [V]
Ua=220 [V]
Wrm [rad/s]
Te [Nm]
CHARAKTERYSTYKI SILNIKA PRADU STALEGO (OBCOWZBUDNEGO) Te=Te(Wrm)
Date/Time run: 03/17/93 21:12:17
Temperature: 27.0
Rys.8. Wyniki analizy .DC: charakterystyka mechaniczna Te=Te(
Ω
rm) silnika
•
Stan nieustalony
Interesującą charakterystyką stanu nieustalonego jest charakterystyka rozruchowa. Można ją
wyznaczyć za pomocą analizy stanu nieustalonego .TRAN symulatora PSPICE. Jej przykładowe przebiegi
pokazano na rys.9. Charakterystykę dynamiczną Te=Te(
ω
rm) pokazano na rys.10.
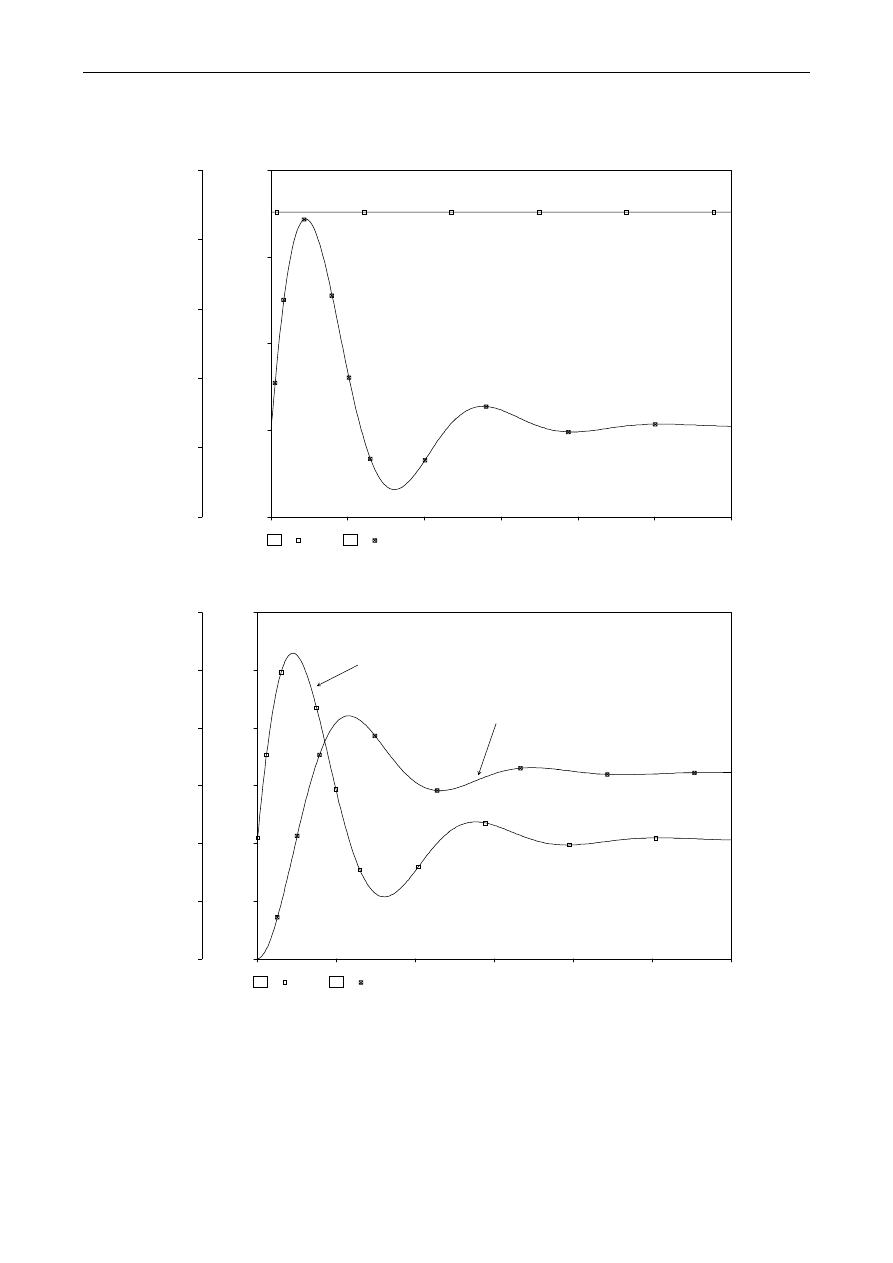
Mieczysław RONKOWSKI
15
Wyniki analizy .TRAN (postprocesor graficzny .PROBE)
a)
0s
100ms
200ms
300ms
400ms
500ms
600ms
Time
1
2
1
V(1)
2
I(Ra)
250V
200V
150V
100V
50V
0V
1
300A
200A
100A
0A
-100A
2
>>
ROZRUCH SILNIKA PRADU STALEGO (OBCOWZBUDNEGO) DLA Tl=0
Date/Time run: 03/17/93 20:29:50
Temperature: 27.0
b)
0s
100ms
200ms
300ms
400ms
500ms
600ms
Time
1
2
1
V(9)
2
I(R_Bm)
400
300
200
100
0
-100
-200
1
300
250
200
150
100
50
0
2
>>
Wrm [rad/s]
Te [Nm]
ROZRUCH SILNIKA PRADU STALEGO (OBCOWZBUDNEGO) DLA Tl=0
Date/Time run: 03/17/93 20:29:50
Temperature: 27.0
Rys.9. Wyniki analizy .TRAN: rozruch bezpośredni silnika prądu stałego:
a) przebieg napięcia u
a
oraz prądu i
a
twornika
b) przebieg prędkości kątowej
ω
rm oraz momentu elektromagnetycznego Te

16
Ćwiczenie: BADANIE DYNAMIKI SILNIKA PRĄDU STAŁEGO
0
40
80
120
160
200
240
I(R_Bm)
V(9)
400
300
200
100
0
-100
-200
Wrm [rad/s]
Te [Nm]
ROZRUCH SILNIKA PRADU STALEGO (OBCOWZBUDNEGO) DLA Tl=0
Date/Time run: 03/17/93 20:29:50
Temperature: 27.0
Rys.10. Wyniki analizy .TRAN: charakterystyka dynamiczna Te=Te(
ω
rm) silnika prądu stałego dla rozruchu
bezpośredniego
5. PYTANIA
(TEORIA/SYMULACJA)
1. Podaj elementarny (podstawowy) model fizyczny maszyny prądu stałego z ilustracją zasady jej działania
— generacji momentu elektromagnetycznego (rys. 1 wg instrukcji ćw. 2A). Nazwij elementy i wielkości
modelu. Wykaż, że w stanie ustalonym siły magnetomotoryczne (SMM) stojana i wirnika są nieruchome
względem siebie oraz nieruchome względem stojana.
2. Podaj podstawowy model fizyczny wzorcowego sprzężenia elektromechanicznego — maszyny prądu
stałego (rys. 2 wg instrukcji ćw. 2A). Nazwij i uzasadnij sens fizyczny wielkości i parametrów modelu.
3. Podaj elementarny (podstawowy) model fizyczny układy mechanicznego maszyn elektrycznych (rys. 2
wg instrukcji ćw. 2A). Wymień i nazwij siły działające na wirnik maszyny. Podaj analogie elektryczno-
mechaniczne równania ruchu stosowane w modelowaniu obwodowym układu mechanicznego maszyn
(rys. 4 wg instrukcji ćw. 2A).
4. Podaj dynamiczny model obwodowy (analog elektryczny) maszyny (silnika) prądu stałego —
wzorcowego sprzężenia elektromechanicznego (rys. 5 wg instrukcji ćw. 2A). Nazwij i uzasadnij sens
fizyczny wielkości i parametrów modelu.
5. Podaj zredukowany dynamiczny model obwodowy (analog elektryczny) maszyny (silnika) prądu stałego
— wzorcowego sprzężenia elektromechanicznego przy i
f
=const (rys. 6 wg instrukcji ćw. 2A). Nazwij i
uzasadnij sens fizyczny wielkości i parametrów modelu. Podaj stałe czasowe i warunki stabilności
przebiegów dynamicznych silnika prądu stałego.
6. Podaj analog elektryczny silnika prądu stałego (rys. 7 wg instrukcji ćw. 2A), który służy do
sformułowania pliku wsadowego programu PSPICE’a, celem symulacji rozruchu silnika indukcyjnego.
Nazwij wielkości i parametry analogu
7. Podaj sposób wprowadzania w pliku wsadowym programu PSPICE’a wartości parametrów analogu
elektrycznego silnika prądu stałego (rys. 7 wg instrukcji ćw. 2A), celem symulacji rozruchu silnika.
8. Podaj sposób odwzorowania w pliku wsadowym programu PSPICE’a równania napięcia rotacji i
równania momentu elektromagnetycznego analogu elektrycznego silnika prądu stałego (rys. 7 wg
instrukcji ćw. 2A), celem symulacji rozruchu silnika.
9. Podaj sposób wprowadzania w pliku wsadowym programu PSPICE’a warunków początkowych analogu
elektrycznego silnika prądu stałego (rys. 7 wg instrukcji ćw. 2A), celem symulacji rozruchu silnika.
10. Podaj sposób wprowadzania w pliku wsadowym programu PSPICE’a wymuszeń elektrycznych analogu
elektrycznego silnika prądu stałego (rys. 7 wg instrukcji ćw. 2A), celem symulacji rozruchu silnika.
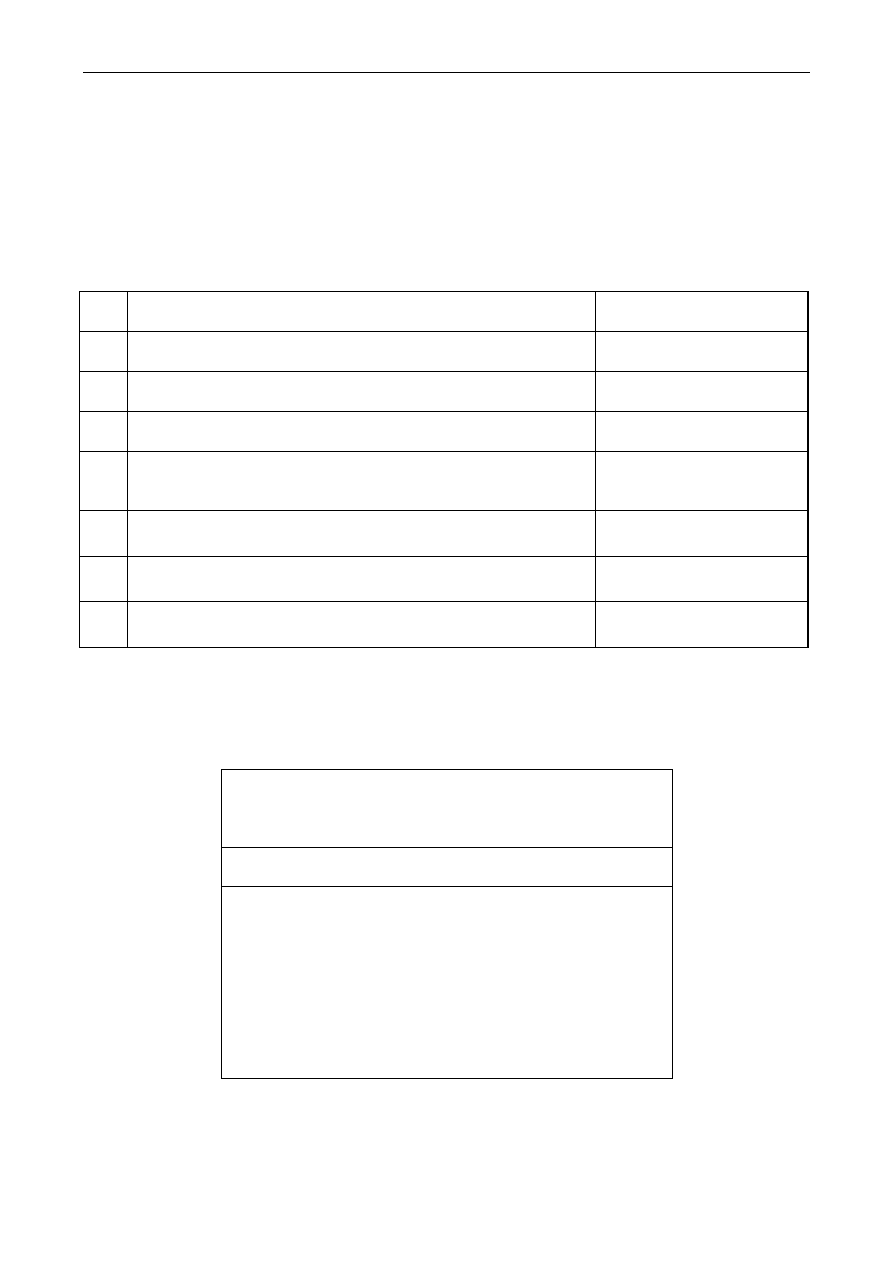
Mieczysław RONKOWSKI
17
11. Podaj sposób wprowadzania w pliku wsadowym programu PSPICE’a wymuszeń mechanicznych analogu
elektrycznego silnika prądu stałego (rys. 7 wg instrukcji ćw. 2A), celem symulacji rozruchu silnika.
12. Podaj sposób doboru maksymalnego kroku całkowania i czasu trwania obliczeń (maksymalnego kroku
obliczeń HMAX i czasu TSTOP w komendzie .TRAN) w pliku wsadowym programu PSPICE’a dla
analogu elektrycznego silnika prądu stałego (rys. 7 wg instrukcji ćw. 2A), celem symulacji rozruchu
silnika.
6. ZADANIE
Dla danych silnika prądu stałego (z katalogu lub silnika badanego) wykonać analizę .TRAN:
Nr
zada.
Stan pracy dynamicznej silnika i warunki obciążenia
Warunki początkowe
1
rozruch bezpośredni dla J = 1.5Jn oraz Jn przy TL = 0
zerowe wartości prądów i
prędkości wirnika dla t = 0
2
rozruch bezpośredni dla J = 1.5Jn oraz Jn przy TL = kTL*
ω
rm
zerowe wartości prądów i
prędkości wirnika dla t = 0
3
rozruch bezpośredni dla J = 1.5Jn oraz Jn przy TL = kTL*
ω
rm*
ω
rm zerowe wartości prądów i
prędkości wirnika dla t = 0
4
skokowa zmiana TL = 0 do TL = TLn dla J = 1.5Jn oraz Jn
wartości prądów maszyny
i prędkości wirnika jak dla
stanu biegu jałowego dla t = 0
5
hamowanie i nawrót dla J = 1.5Jn oraz Jn przy TL = 0
zerowe wartości prądów oraz
ω
rm
=
ω
rmn dla t = 0
6
hamowanie i nawrót dla J = 1.5Jn oraz Jn przy TL = kTL *
ω
rm
zerowe wartości prądów oraz
ω
rm
=
ω
rmn dla t = 0
7
hamowanie i nawrót dla J = 1.5Jn oraz Jn przy TL = k*
ω
rm*
ω
rm
zerowe wartości prądów
oraz
ω
rm
=
ω
rmn dla t = 0
Założyć znamionowe warunki zasilania lub podane przez prowadzącego ćwiczenie.
7. SPRAWOZDANIE
Opracowanie sprawozdania powinno zawierać:
•
stronę tytułową wg następującego układu:
POLITECHNIKA GDAŃSKA
WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI
KATEDRA ENERGOELEKTRONIKI I MASZYN
ELEKTRYCZNYCH
MASZYNY ELEKTRYCZNE II
LABORATORIUM KOMPUTEROWE
ĆWICZENIE 2A
BADANIE DYNAMIKI SILNIKA PRĄDU STAŁEGO
WSPOMAGANE SYMULATOREM OBWODÓW PSPICE
Opracował:
Imię i nazwisko
nr grupy laboratoryjnej
(podać nr grupy laboratoryjnej wg lab. MEII)
data oddania sprawozdania
•
nr, dane znamionowe (katalogowe) i dane obwodowe badanego silnika prądu stałego;
•
nr i treść zadania;
•
określenie wymuszeń elektrycznych i mechanicznych (należy podać odpowiadające im fragmenty
programu PSPICE);
18
Ćwiczenie: BADANIE DYNAMIKI SILNIKA PRĄDU STAŁEGO
•
określenie warunków początkowych (wartości prądów indukcyjności i napięć na pojemnościach,
należy podać odpowiadające im fragmenty programu PSPICE);
•
obliczenia stałych czasowych modelu obwodowego dla danego silnika indukcyjnego;
•
oszacowanie maks. kroku obliczeń HMAX i czasu końca analizy TSTOP;
•
„ręczne” oszacowanie wartości udarowych prądów, momentu elektromagnetycznego i prędkości
obrotowej oraz porównanie ich wartości z wynikami otrzymany na drodze symulacyjnej;
•
wybrane przebiegi wielkości, które są istotne (wg piszącego sprawozdanie) dla przeprowadzenia
analizy zadanego stanu pracy dynamicznej maszyny prądu stałego;
•
uzasadnienie fizyczne uzyskanych wyników (powinno być napisane w stylu inżynierskim !!!
—- tzn. minimum języka tekstowego a maksimum języka graficznego i symbolicznego);
•
krótka dyskusja wpływu założeń upraszczających modelu maszyny na uzyskane wyniki obliczeń;
•
wykaz literatury wykorzystanej przy pisaniu sprawozdania;
•
załącznik w postaci dyskietki, zawierającej sformułowany plik wsadowy programu PSPICE.
8. LITERATURA
1. P.C. Krause i O. Wasynczuk: Electromechanical Motion Devices, Mc Graw -Hill Book Comp.. New
York, 1989. Purdue University, USA.
2. P.C. Krause: Analysis of Electric Machinery. Mc Graus - Hill Book Comp. New York, 1986.
3. W. Latek: Teoria maszyn elektrycznych. WNT, Warszawa, 1982.
4. Z. Manitius: Maszyny elektryczne cz. I, II. Skrypt PG, 1982, 1984.
5. W. Paszek: Stany nieustalone maszyn elektrycznych prądu przemiennego. WNT, Warszawa, 1986.
6. S. Roszczyk: Teoria maszyn elektrycznych. WNT, Warszawa, 1979.
7. P. Zimny, K. Karwowski: SPICE klucz do elektrotechniki. Instrukcja, program, przykłady. Skrypt
PG, 1993.
9. ZAŁĄCZNIK
WYZNACZANIE WARTOŚCI PARAMETRÓW DYNAMICZNEGO MODELU OBWODOWEGO
SILNIKA PRĄDU STAŁEGO
Metody wyznaczania wartości parametrów dynamicznego modelu obwodowego silnika prądu stałego
(podanego na rys. Z1) opisano poniżej.
u
a
a
R
a
L
aa
i
a
e
a
e
a
= G
af
i
f
ω
rm
L
ff
i
f
R
f
u
f
f
+
_
+
_
+
_
T
e
= G
af
i
f
i
a
+
_
T
L
m
u
c
=
ω
rm
G = B
m
T
e
C = J
Rys.Z1. Dynamiczny model obwodowy (analog elektryczny) maszyny (silnika) prądu stałego — wzorcowego sprzężenia
elektromechanicznego
1. Wielkości modelu na rys. Z1.
ua
- napięcie twornika
Mieczysław RONKOWSKI
19
uf
-
napięcie wzbudzenia
ia
-
prąd twornika
if
-
prąd wzbudzenia
ea
- sem rotacji
Te
- moment elektromagnetyczny (wewnętrzny)
ω
rm
-
prędkość kątowa (mechaniczna) wirnika
TL
- moment obciążenia (zewnętrzny)
2. Parametry modelu na rys. Z1.
Ra
- rezystancja obwodu twornika
Rf
- rezystancja obwodu wzbudzenia
Laa
- indukcyjność własna obwodu twornika
Lff
- indukcyjność własna obwodu wzbudzenia
Gaf
- indukcyjność rotacji (sprzężenia elektromechanicznego)
J
- moment bezwładności
Bm
- współczynnik tarcia lepkiego
Wyróżniono dwa przypadki wyznaczania wartości parametrów dynamicznego modelu obwodowego
silnika prądu stałego:
♦
modelu liniowego (modelu o parametrach stałych) na podstawie danych katalogowych;
♦
modelu nieliniowego (modelu o parametrach zmiennych) na podstawie danych doświadczalnych.
9.1. Wyznaczanie
wartości parametrów modelu liniowego na podstawie
danych katalogowych
Wartości parametrów modelu obwodowego silnika można obliczyć z wystarczającą dokładnością dla
obliczeń inżynierskich na podstawie jej danych katalogowych. Przykład takich danych podano poniżej w
tablicy Tab. Z.1.
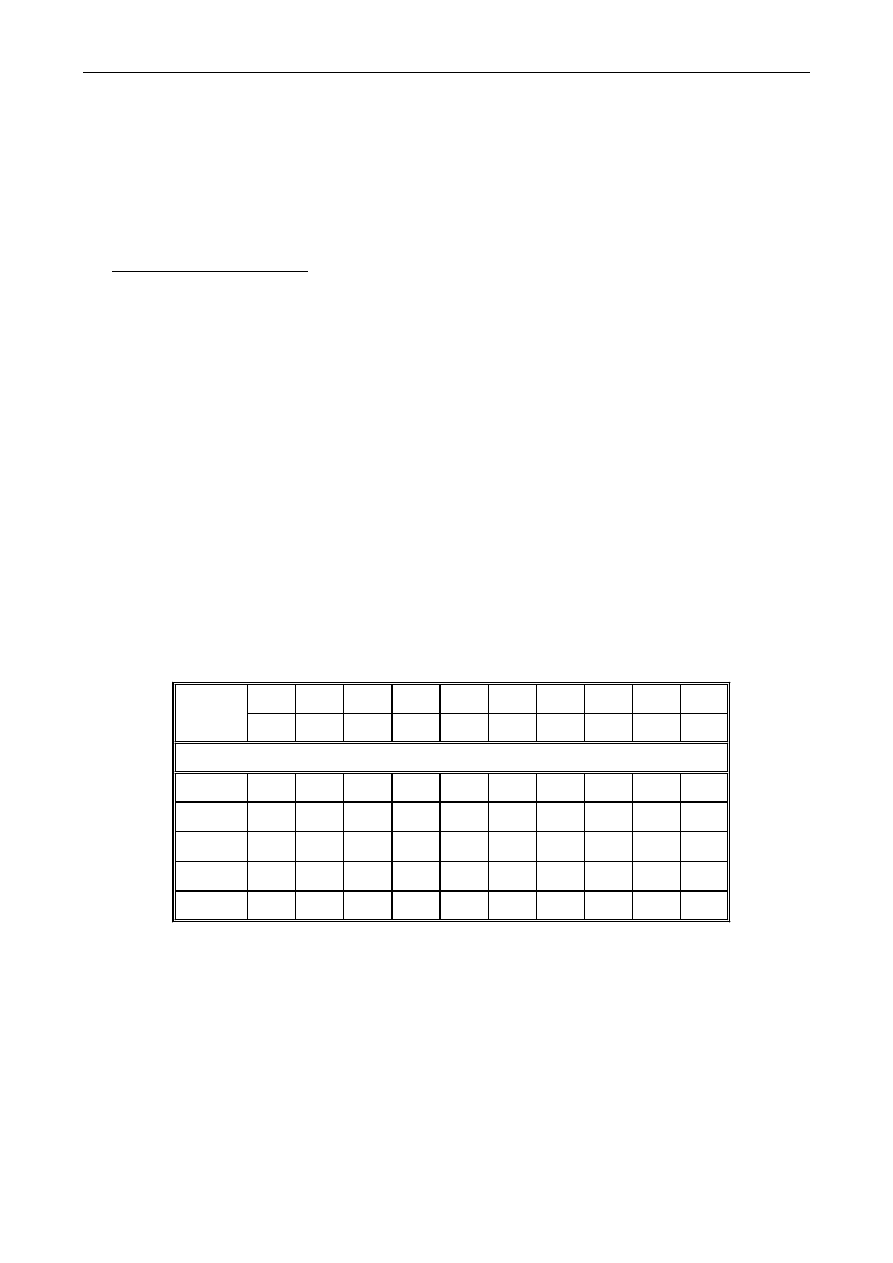
Tablica Z.1. Dane katalogowe silników prądu stałego – producent firma SIEMES
Wielkość
U
an
n
n
P
n
J
I
an
η
n
P
fn
U
fn
R
a
L
aa
mechaniczna
V
obr/min
kW
kgm
2
A
%
W
V
Ω
mH
100L
300
1850
1,25
0,0115
5
75
145
180
4,6
42
112L
400
2700
4,6
0,0301
13,5
83
130
180
1,97
16
160M
400
3500
19,2
0,121
54,0
86
480
180
0,13
2
225L
440
2300
38,0
0,65
94,0
90,4
650
310
0,15
2,3
225L
600
2950
136,0
0,75
245
91,1
800
310
0,12
1,5
W powyższej tabeli producent podał wartości tylko dla części parametrów (J, R
a
, L
aa
) - wartości pozostałych
parametrów wyznacza się wg podanych niżej zależności.
Indukcyjność rotacji
wyznacza się z równania równowagi dla obwodu twornika przy warunkach znamionowych:
an
a
mn
r
fn
af
an
I
R
I
G
U
+
=
)
(
Ω
[V]
(1)
po przekształceniu otrzymuje się
)
/(
)
(
mn
r
fn
an
a
an
af
I
I
R
U
G
Ω
−
=
[H]
(2)
gdzie, znamionowy prąd wzbudzenia

20
Ćwiczenie: BADANIE DYNAMIKI SILNIKA PRĄDU STAŁEGO
fn
fn
fn
U
P
I
/
====
[A]
(3)
oraz znamionowa prędkość kątowa [rad/s]
Ω
r mn
n
n
=
2
60
π
/
[rad/s]
(4)
Rezystancja obwodu wzbudzenia
fn
fn
f
P
U
R
/
2
=
[
Ω
] (5)
Współczynnik tarcia lepkiego
2
mn
r
mn
m
P
B
Ω
∆
≅
[Nm
.
s]
(6)
gdzie, znamionowe strat mechaniczne szacuje się następująco
n
mn
P
P
100
)%
1
...
3
,
0
(
≅
∆
[W]
(7)
Elektromagnetyczna stała czasowa (stała czasowa obwodu twornika)
a
aa
a
R
L /
====
τ
[s]
(8)
Elektromechaniczna stała czasowa
2
)
(
fn
af
a
m
I
G
J R
=
τ
[s]
(9)
Indukcyjności obwodu wzbudzenia
ze względu na jej brak w danych katalogowych, szacuje się z następującej relacji między stałą czasową
obwodu wzbudzenia (
f
ff
f
R
L /
====
τ
) a elektromagnetyczną stałą czasową (stała czasowa obwodu
twornika)
τ
τ
f
a
≥
20
lub
a
aa
f
ff
R
L
R
L
/
20
/
=
(10)
zatem
a
f
a
a
ff
R
R
L
L
/
20
≥
[H]
(11)
Uwaga:
Powyższa relacja jest słuszna dla silnika o napięciu twornika takim samym jak napięcie
wzbudzenia. W przypadku różnych napięć należy wyznaczyć wartość indukcyjności wg
relacji (11), a następnie skorygować jej wartość do poziomu danego napięcia wzbudzenia,
zakładając, że energia pola magnetycznego obwodu wzbudzenia jest taka sama w obu
przypadkach.
Indukcyjność obwodu twornika
w przypadku braku jej wartości w danych katalogowych, można oszacować następująco:
n
an
an
a
aa
n
P
I
U
c
L
120
≅
[H]
(12)
gdzie, stała ca
przyjmuje wartości:
•
w przedziale 0,05...0,07 - dla maszyn bez uzwojenia kompensacyjnego;
•
około 0,032 - dla maszyn z uzwojeniem kompensacyjnym.
Uwaga: P – oznacza liczbę biegunów maszyny!.
9.2. Wyznaczanie
wartości parametrów modelu nieliniowego na podstawie
danych doświadczalnych
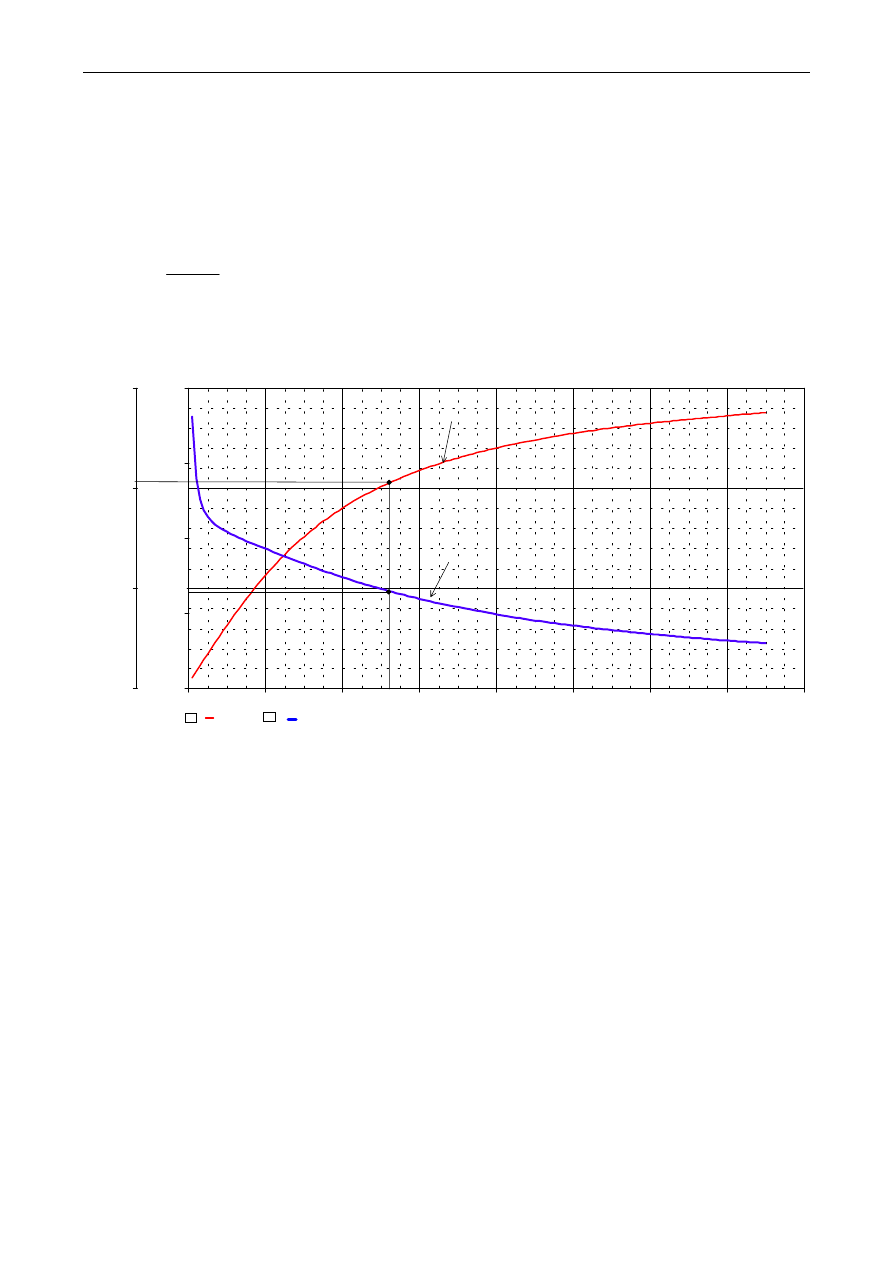
Indukcyjność rotacji
wyznacza się na podstawie charakterystyki biegu jałowego (w innej skali charakterystyka magnesowania)
badanego silnika prądu stałego w stanie pracy prądnicowej. Sposób pomiaru charakterystyki opisano w
instrukcji do ćwiczenia pt. „Maszyny prądu stałego – silniki” Laboratorium Maszyny Elektryczne I.
Charakterystykę biegu jałowego, czyli relację między SEM rotacji a prądem wzbudzenia silnika, opisuje
następująca zależność:
Mieczysław RONKOWSKI
21
rm
)
(
)
(
Ω
f
f
af
f
a
I
I
G
I
E
=
[V]
(13a)
gdzie, iloczyn
)
(
f
f
af
I
I
G
przedstawia strumień wzbudzenia sprzężony z uzwojeniem twornika na
przestrzeni P/2 podziałek biegunowych.
Wpływ nasycenia drogi strumienia wzbudzenia na wartość indukcyjności rotacji G
af
wyraża zapis G
af
(I
f
),
który odwzorowuje jej zależność od prądu wzbudzenia I
f
. Po odpowiednim przekształceniu relacji (13a)
otrzymuje się:
rm
)
(
)
(
Ω
f
f
a
f
af
I
I
E
I
G
=
[H]
(13b)
Przykładowe przebiegi charakterystyk wg relacji (13a) i (13b) przy
Ω
rm
= const. pokazano na rys. Z2.
Wartość G
af
wyznacza się dla znamionowego prądu wzbudzenia I
fn
.
If
0A
0.2A
0.4A
0.6A
0.8A
1.0A
1.2A
1.4A
1.6A
1 V(Ea) 2
V(3)
0V
100V
200V
300V
1
>>
0H
2.0H
4.0H
6.0H
8.0H
2
Ean
Ifn
Gaf
Ea
Gafn
Rys. Z2. Przykładowe charakterystyki biegu jałowego (w innej skali charakterystyka magnesowania) i indukcyjności
rotacji maszyny prądu stałego
Rezystancje
obwodu wzbudzenia R
f
oraz twornika R
a
można wyznaczyć metodą techniczną (patrz instrukcja do
ćwiczenia pt. „Maszyny prądu stałego – silniki” Laboratorium Maszyny Elektryczne I).
Indukcyjności
obwodów twornika i wzbudzenia wyznacza się doświadczalnie metodą stałych czasowych, polegającej na
odpowiednim pomiarze przebiegu czasowego narastania lub zanikania prądu w obwodzie typu RL lub RC.
Indukcyjność obwodu twornika
ze względu na jej stosunkowo małą wartość, wyznacza się na podstawie przebiegu czasowego zanikania
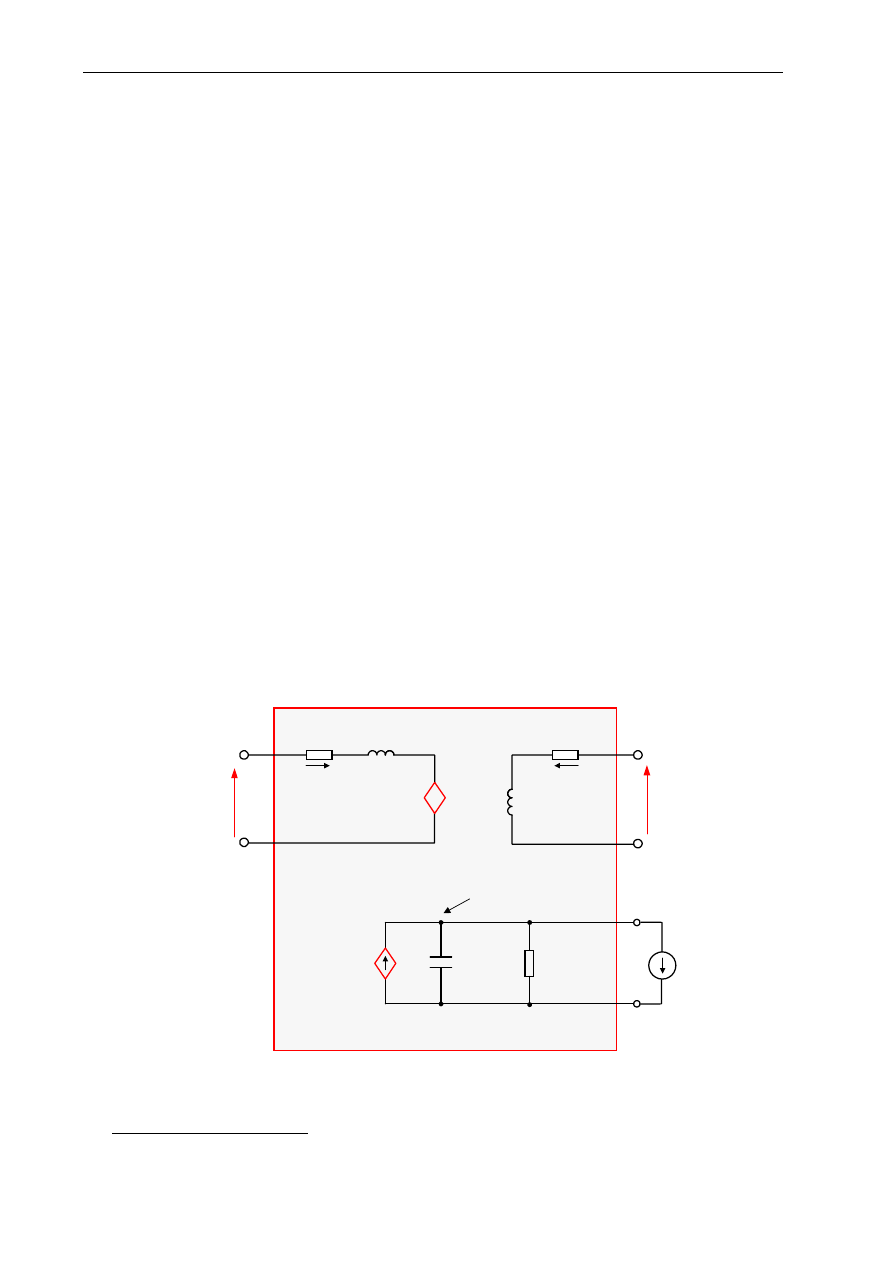
prądu w obwodzie twornika. Przykładowy układ pomiarowy przedstawiono na rys. Z3, w którym obwód
twornika początkowo jest zasilany ze źródła napięci stałego, a następnie zwarty stycznikiem ST, co
powoduje zanik prądu i
a
w obwodzie. Jeśli założy się jednowykładniczy zanik prądu i
a
, to jego przebieg jest
opisany relacją:
a
t
a
a
e
I
i
τ
/
)
0
(
−
=
(14)
gdzie, I
a
(0) – początkowy prąd twornika, t – czas,
τ
a
– stała czasowa obwodu twornika.
Sposób wyznaczania wartości indukcyjność obwodu typu RL zilustrowano na przykładzie teoretycznego
przebiegu wg rów. (14) pokazanego na rys. Z4. Jego przebieg wyznaczono za pomocą programu PSPICE dla
obwodu o danych R=1
Ω
oraz L=0,5 H, przyjmując wartość początkową prądu I(0)=Ip=10 A. Punktem
wyjścia do wyznaczenia wartości L jest określenie stałej czasowej rozważanego obwodu. Jest kilka
sposobów jej wyznaczenia. Tutaj, ze względu na dostępną w postprocesorze graficznym PROBE programu
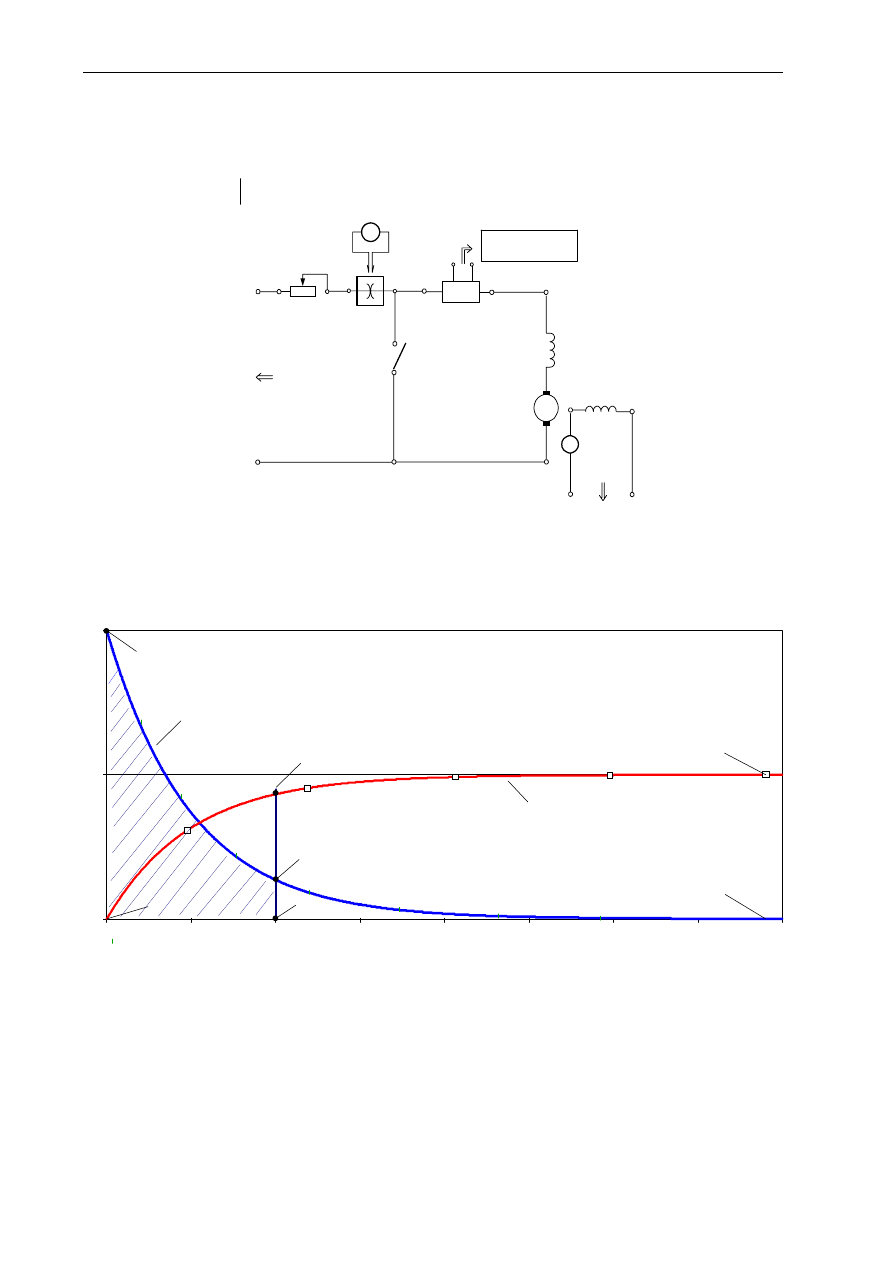
22
Ćwiczenie: BADANIE DYNAMIKI SILNIKA PRĄDU STAŁEGO
PSPICE opcję całkowania krzywej, wybrano sposób wyznaczania na podstawie pola powierzchni pod
krzywą zanikania prądu.
Pole powierzchni pod krzywą wg wyrażenia (14), w przedziale czasu od 0 do t
x
, wyznacza następujące
wyrażenie:
x
t
t
a
x
t
a
e
I
dt
i
0
/
0
)
0
(
τ
τ
−
−
=
∫
(15a)
R
d
i
a
ST
B2
A1
F1
F2
I
f
A
LEM(I)
Karta pomiarowa
(oscyloskop)
A
Do źródła napięcia
stałego
Do
źród
ła napi
ęcia
sta
łego
M
Rys. Z3. . Przykładowy układ pomiarowy do wyznaczania indukcyjność obwodu twornika maszyny prądu stałego na
podstawie przebiegu czasowego zanikania prądu w obwodzie twornika
Time
0s
0.5s
1.0s
1.5s
2.0s
2.5s
3.0s
3.5s
4.0s
I(R_A) S(I(R_A))
0
5
10
s(Ik)
s(Ip)
Ik
Ip
(3.9018,4.0826m)
(3.9018,4.9979)
(20.000u,99.997u)
(10.000u,10.000)
s(Ix)
tx
i [A]
Ix
i
s(i)
Rys. Z4. Ilustracja sposobu wyznaczania wartości indukcyjność obwodu RL na podstawie pola powierzchni pod krzywą
zanikania prądu – tzw. metodą zastępczej stałej czasowej
Na rys. Z4 krzywą pierwotną jest przebieg i, a po jego scałkowaniu przebieg s(i). Wartość pola pod krzywą i
w przedziale czasu od 0 do tx określa wartość rzędnej s(Ix). Natomiast wartość całego pola pod krzywą i dla
czasu
∞
→
t
praktycznie określa wartość rzędnej s(Ik). Zatem, biorąc pod uwagę wyrażenie (15a), można
łatwo wykazać, że wartość stałej czasowej przebiegu określona jest następująco:
Mieczysław RONKOWSKI
23
5
,
0
10
9979
,
4
)
(
≅
=
≅
Ip
Ik
s
τ
[s]
(15b)
co odpowiada wartości
5
,
0
1
5
,
0
=
=
=
R
L
τ
[s]
(16)
dla przyjętych wartości parametrów rozważanego obwodu.
Stąd, przy znanej wartość rezystancji R obwodu, można wyznaczyć wartość indukcyjność L z relacji:
0,5
5
,
0
1
=
⋅
=
=
τ
R
L
[H]
(17)
Uwaga:
Przedstawiony sposób wyznaczania stałej czasowej w literaturze znany jest pod nazwą
metody zastępczej stałej czasowej, gdyż metodę tą można stosować do wyznaczania stałej
czasowej przebiegów dwu lub więcej wykładniczych – takimi są przebiegi zanikania prądu
w obwodach rzeczywistych (efekt zjawiska nasycenia obwodu magnetycznego, zjawisko
indukowania prądów wirowych, itp.).
Poniżej przedstawiono zastosowanie, powyżej opisanej metody, do wyznaczania wartości indukcyjności
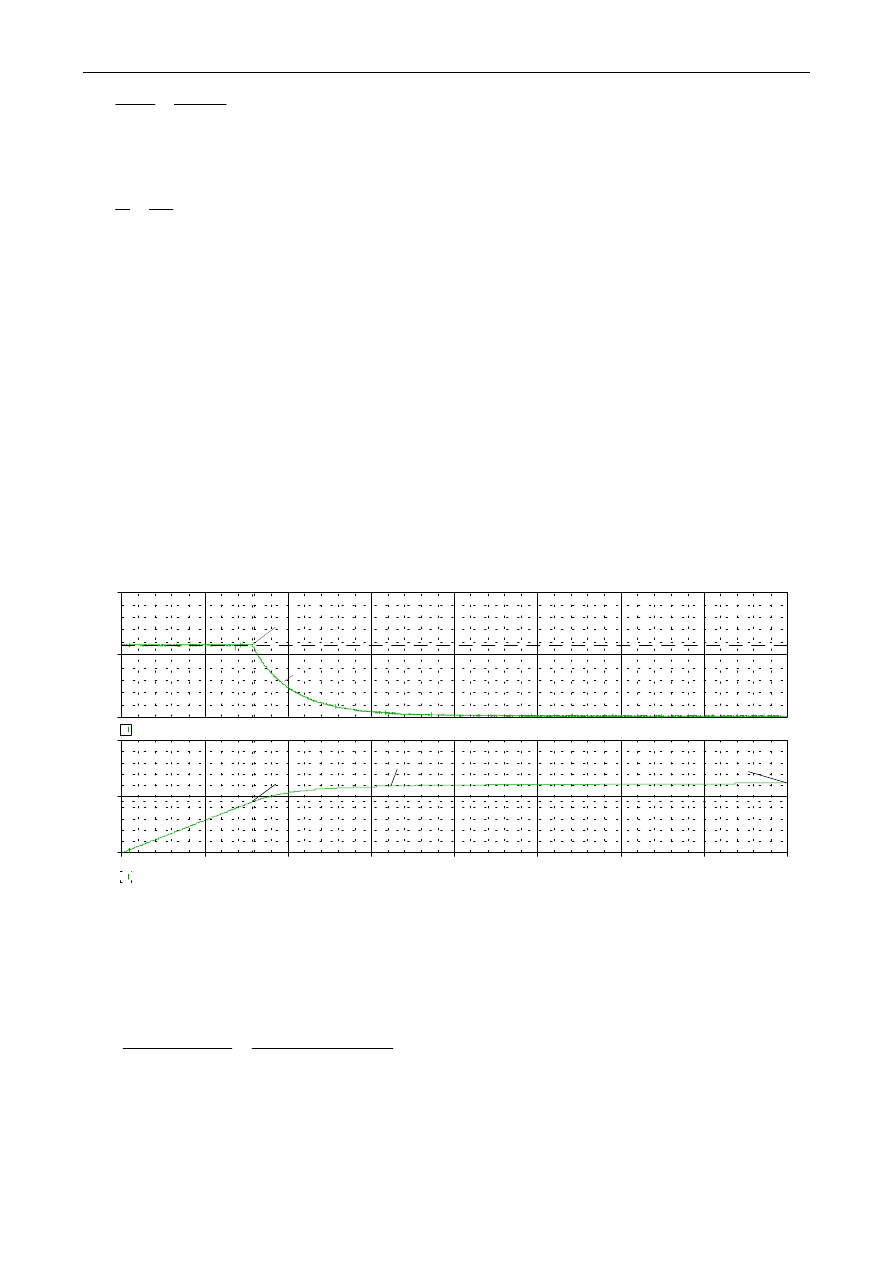
obwodu twornika na podstawie pomierzonego przebiegu zanikania prądu twornika (patrz rys. Z5).
Time
0s
50ms
100ms
150ms
200ms
250ms
300ms
350ms
400ms
S(Chan0)
0
5m
10m
SEL>>
s(Iak)
s(Iap)
(400.200m,6.1984m)
(78.505m,4.5286m)
Chan0
0
50m
100m
Iap
(78.505m,57.619m)
Ia
s(Ia)
tp
tp
tp
a)
b)
Rys. Z5. Przykładowe przebiegi do wyznaczenia indukcyjności obwodu twornika metodą zastępczej stałej
czasowej: a) pomierzone zanikanie prądu twornika i
a
; b) przebieg s(i
a
)otrzymany po scałkowaniu krzywej i
a
Łatwo wykazać, że zastępcza stała czasowa przebiegu określona jest następująco:
98
,
28
619
,
57
5286
,
4
1984
,
6
)
(
)
(
≅
−
=
−
≅
m
m
m
Iap
Iap
s
Iak
s
a
τ
[ms]
(18)
Wartość pomierzonej rezystancji obwodu twornika dla badanego silnika wyniosła R
a
= 3,72
Ω
, zatem
indukcyjność obwodu twornika wynosi:
81
,
107
72
,
3
98
,
28
≅
Ω
⋅
=
=
ms
R
L
a
a
aa
τ
[mH]
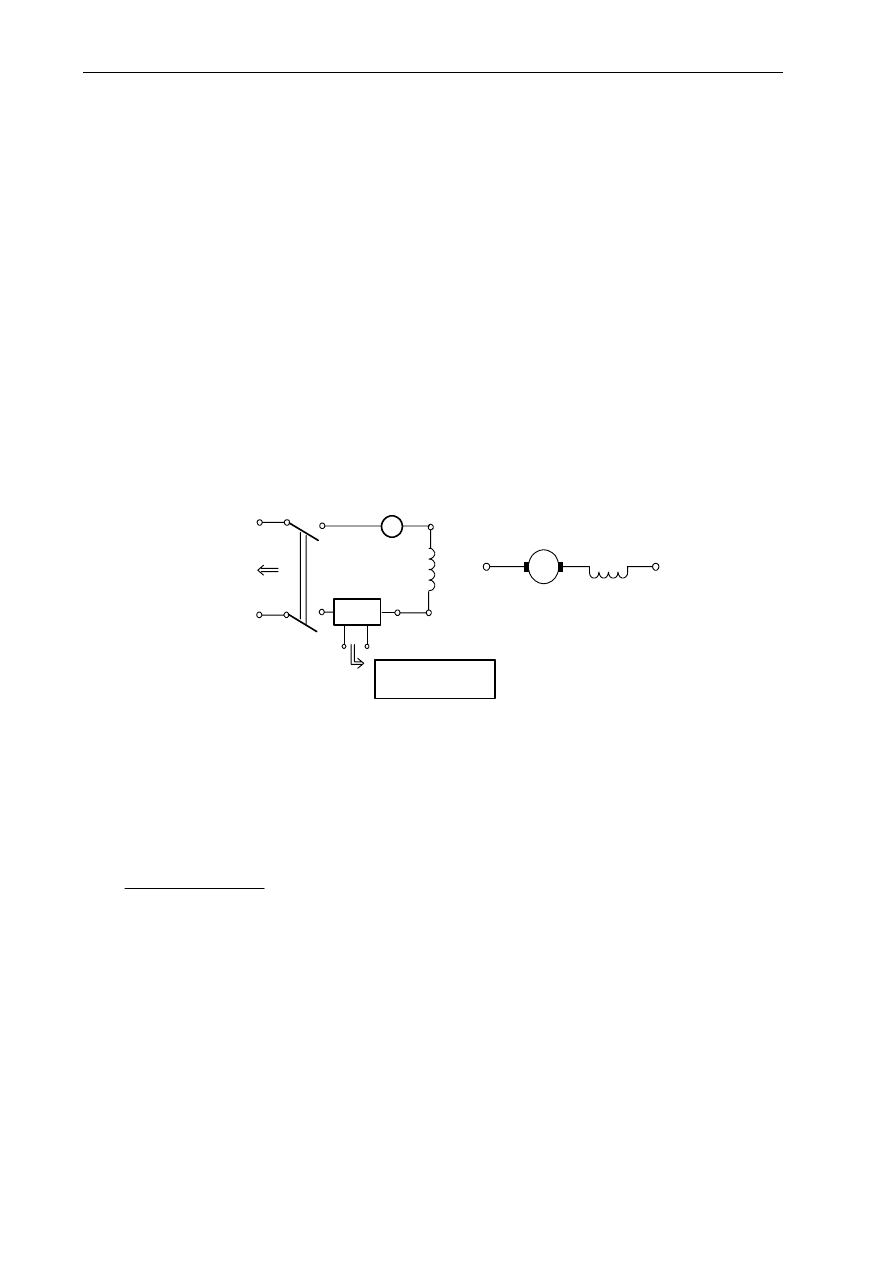
24
Ćwiczenie: BADANIE DYNAMIKI SILNIKA PRĄDU STAŁEGO
Uwaga:
Błąd obliczeń wynika głównie z pomięcia rezystancji łącznika ST w układzie pomiarowym.
Uwaga:
Indukcyjność obwodu twornika wyznacza się dla następujących warunków zasilania:
I
a
(0) = 0,2 I
an
przy I
f
= I
fn
I
a
(0) = 0,2 I
an
przy I
f
= 0.4I
fn
przy zablokowanym wirniku.
Indukcyjność obwodu wzbudzenia
ze względu na jej stosunkowo dużą wartość, można wyznaczyć na podstawie przebiegu czasowego
narastania prądu w obwodzie wzbudzenia. Przykładowy układ pomiarowy przedstawiono na rys. Z6, w
którym obwód wzbudzenia jest skokowo załączony do zasilania ze źródła napięcia stałego za pomocą
stycznika ST, co powoduje wzrost prądu i
f
w obwodzie. Jeśli założy się jednowykładniczy wzrost prądu i
f
, to
jego przebieg jest opisany relacją:
)
1
)(
(
/
f
t
f
f
e
I
i
τ
−
−
∞
=
[A]
(19)
gdzie, I
f
(
∞
) – ustalona wartość prądu wzbudzenia, t – czas,
τ
f
– stała czasowa obwodu wzbudzenia.
ST
F1
F2
I
f
LEM(I)
Karta pomiarowa
(oscyloskop)
A
Do
źród
ła napi
ęcia
sta
łego
B2
A1
M
Rys. Z6. . Przykładowy układ pomiarowy do wyznaczania indukcyjność obwodu wzbudzenia maszyny prądu stałego na
podstawie przebiegu czasowego narastania prądu w obwodzie wzbudzenia
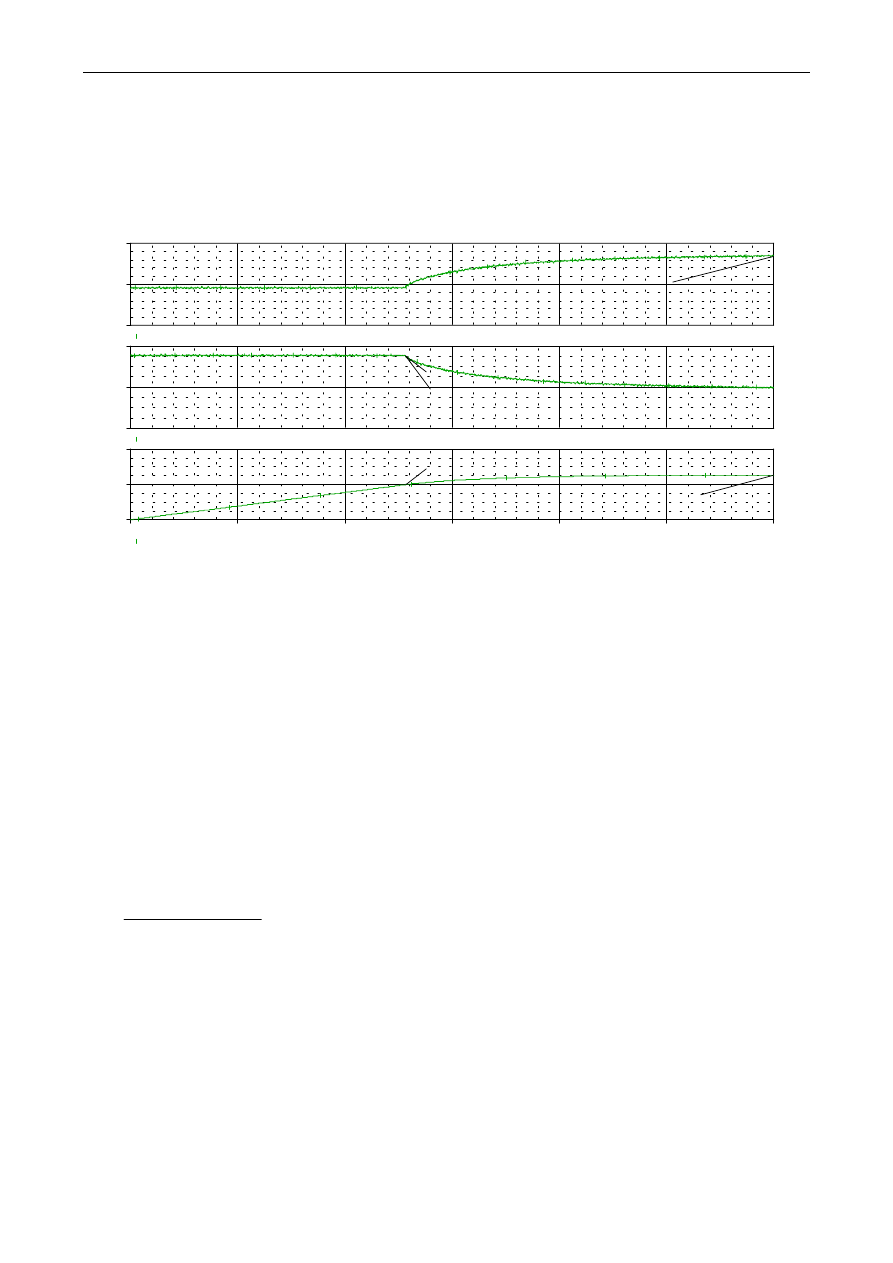
Na rys. Z7a przedstawiono przykładowy przebieg narastania prądu w obwodzie wzbudzenia a następnie
wykreślone kolejno przebiegi niezbędne do wyznaczenia indukcyjności obwodu wzbudzenia metodą
zastępczej stałej czasowej.
Zastępcza stałą czasowa przebiegu na rys. Z7a została określona analogicznie jak dla przebiegu na rys. Z5a:
64
,
347
332
,
15
789
,
19
119
,
25
≅
−
≅
m
m
m
f
τ
[ms]
(20)
Wartość pomierzonej rezystancji obwodu wzbudzenia dla badanego silnika wyniosła R
f
= 621,25
Ω
, zatem
indukcyjność obwodu wzbudzenia wynosi:
97
,
215
25
,
621
64
,
347
≅
Ω
⋅
=
=
ms
R
L
f
f
ff
τ
[H]
(21)
Uwaga:
Błąd obliczeń wynika głównie z pomięcia rezystancji łącznika ST i źródła napięcia zasilania
w układzie pomiarowym.
Mieczysław RONKOWSKI
25
Uwaga:
Indukcyjność obwodu wzbudzenia wyznacza się dla następujących warunków zasilania:
I
f
(
∞
) = I
fn
przy I
a
= 0
I
f
(
∞
) = 0,4 I
fn
przy I
a
= 0
przy otwartym obwodzie twornika.
Time
0s
0.5s
1.0s
1.5s
2.0s
2.5s
3.0s
S(13.7m - Chan0)
0
20m
40m
SEL>>
(3.0010,25.119m)
(1.2825,19.789m)
13.7m- Chan0
-20m
0
20m
(1.2825,15.332m)
Chan0
-20m
0
20m
(3.0010,13.700m)
Rys. Z7. Przykładowe przebiegi do wyznaczenia indukcyjności obwodu wzbudzenia metodą zastępczej stałej
czasowej: a) pomierzone narastanie prądu wzbudzenia i
f
; b) wyznaczone zanikanie prądu wzbudzenia
(I
f
(
∞
) - i
f
); c) przebieg s(I
f
(
∞
) - i
f
) otrzymany po scałkowaniu krzywej (I
f
(
∞
) - i
f
)
Moment bezwładności
zwykle wyznacza się metodą wybiegu. Układ pomiarowy jest analogiczny jak przy wyznaczaniu
charakterystyki magnesowania silnika. Badany silnik biegnie jałowo i jest zasilany z dwóch niezależnych
źródeł napięcia, tzn. oddzielnie obwód wzbudzenia i obwód twornika (napięciem znamionowym). Regulując
wartość prądu wzbudzenia ustalamy znamionową prędkość obrotową silnika, a następnie odłączamy
zasilanie, ale tylko obwodu twornika, rejestrując jednocześnie przebieg czasowy zanikania prędkości
obrotowej.
Na rys. Z8a przedstawiono przykładowy przebieg czasowy zanikania prędkości obrotowej silnika, a
następnie wykreślone kolejno przebiegi niezbędne do wyznaczenia moment bezwładności układu
mechanicznego silnika metodą zastępczej stałej czasowej.
Zastępcza stałą czasowa przebiegu na rys. Z8a została określona analogicznie jak dla przebiegu na rys. Z5a:
574
,
4
300
,
260
992
,
823
0147
,
2
≅
−
≅
m
m
J
τ
[s]
(22)
Uwaga:
Jeżeli w czasie pomiaru zanikania prędkości obrotowej nie odłączono maszyny służącej do
obciążenia silnika, to wyznaczona wartość momentu bezwładności jest łączna dla całego
zespołu maszynowego.
Przed wyłączeniem zasilania twornika, celem oszacowania strat mechanicznych maszyny, należy pomierzyć
napięcie twornika, prąd twornika i prędkość obrotową. Ich wartości dla rozważanej maszyny wyniosły:
U
a
=217,5V oraz I
a
=0,72A, n=1550 obr/min
zatem starty mechaniczne:
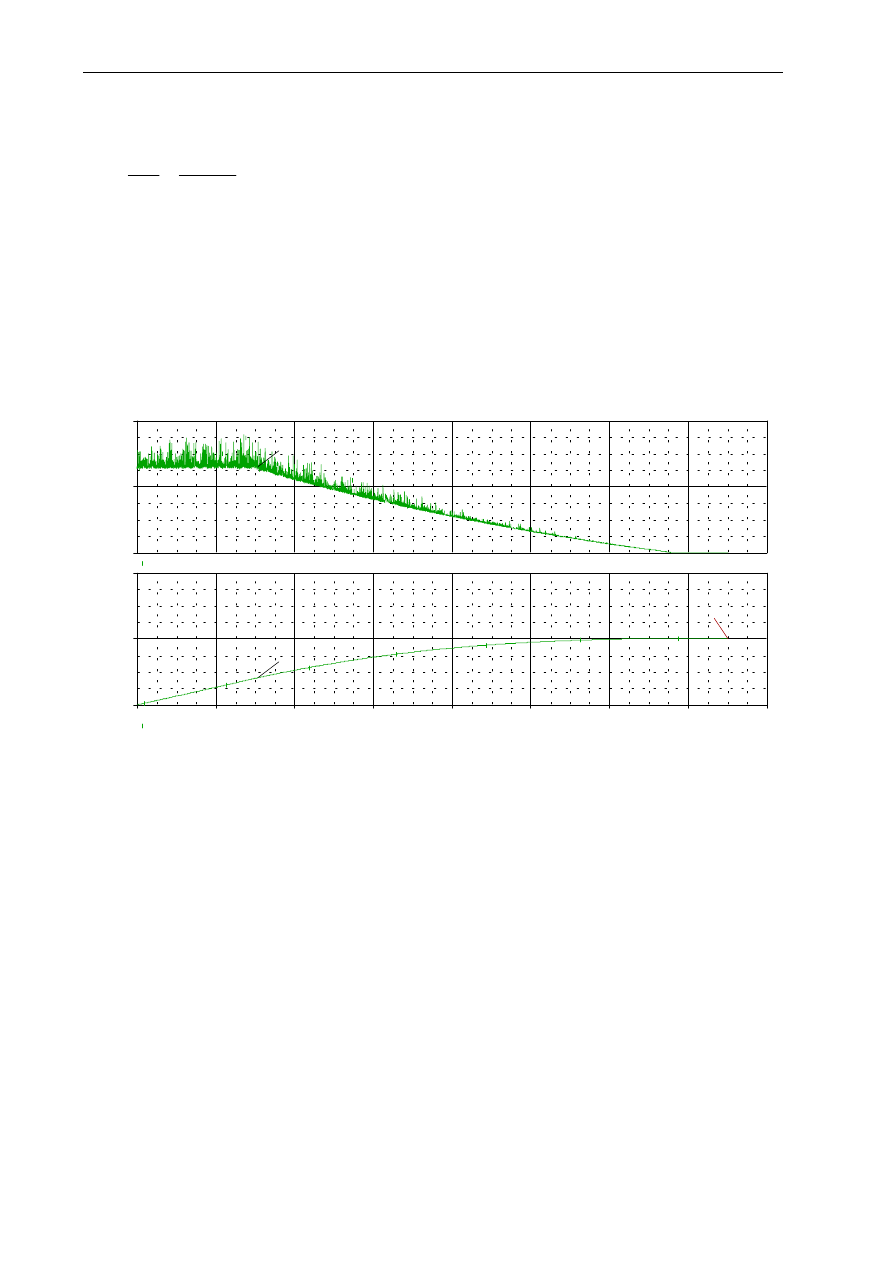
26
Ćwiczenie: BADANIE DYNAMIKI SILNIKA PRĄDU STAŁEGO
82
,
110
)
72
,
0
(
72
,
3
72
,
0
5
,
217
2
2
=
⋅
−
⋅
=
−
≅
∆
a
a
a
a
m
I
R
I
U
P
[W]
(23)
a stąd współczynnik tarcia lepkiego
3
2
2
10
206
,
4
32
,
162
82
,
110
−
⋅
=
=
Ω
∆
≅
m
r
m
m
P
B
[Nm
.
s]
(24)
gdzie
32
,
162
60
/
1550
2
60
/
2
=
⋅
=
=
Ω
π
π
n
mn
r
[rad/s]
zatem moment bezwładności
01924
,
0
s
Nm
10
206
,
4
s
574
,
4
3
≅
⋅
⋅
⋅
=
=
−
m
J
B
J
τ
[kgm
2
]
(25)
Uwaga:
Wyznaczone straty mechaniczne wg wzoru (23) zawierają także straty w żelazie twornika
silnika i straty mechaniczne maszyny służącej do obciążenia.
Time
0s
2s
4s
6s
8s
10s
12s
14s
16s
S(Chan1)
0
2.0
4.0
SEL>>
(15.000,2.0147)
(3.0783,823.992m)
Chan1
0
200m
400m
(3.0775,260.300m)
Rys. Z8. Przykładowe przebiegi do wyznaczenia momentu bezwładności silnika metodą zastępczej stałej
czasowej: a) pomierzony zanik prędkości obrotowej
Ω
rm
; b) przebieg s(
Ω
rm
) otrzymany po scałkowaniu
krzywej
Ω
rm
9.3.
PYTANIA (POMIARY)
1.
Podaj sposób wyznaczania wartości parametrów dynamicznego modelu obwodowego silnika prądu stałego —
wzorcowego sprzężenia elektromechanicznego (rys. 5 wg instrukcji ćw. 2A) na podstawie jego danych
katalogowych.
2.
Wymień, nazwij i opisz metody pomiaru wartości parametrów dynamicznego modelu obwodowego maszyny
(silnika) prądu stałego — wzorcowego sprzężenia elektromechanicznego (rys. 5 wg instrukcji ćw. 2A).
3.
Narysuj układ pomiarowy do wyznaczania indukcyjność rotacji maszyny prądu stałego na podstawie
charakterystyki magnesowania. Podaj zasady doboru elementów układu.
4.
Narysuj układ pomiarowy do wyznaczania indukcyjność obwodu wzbudzenia maszyny prądu stałego na
podstawie przebiegu czasowego narastania prądu w obwodzie wzbudzenia. Podaj zasady doboru elementów
układu.
5.
Narysuj układ pomiarowy do wyznaczania indukcyjność obwodu twornika maszyny prądu stałego na podstawie
przebiegu czasowego narastania prądu w obwodzie twornika. Podaj zasady doboru elementów układu.
6.
Narysuj układ pomiarowy do wyznaczania momentu bezwładności silnika metodą wybiegu. Podaj zasady
doboru elementów układu.
Wyszukiwarka
Podobne podstrony:
Me2 oscyloskop
me2 cw1a
ćw2a
me2 cw2b
me2 trafo
Ćw2a
cw2A, Politechnika Wrocławska, Automaty lab
Wykresy ME2 CW3
me2
Egzamin1MaszynyElektryczne15.06.2009, Studia, semestr 4, Maszyny elektryczne, Maszyny elektryczne I,
me, Studia, semestr 4, Maszyny elektryczne, Maszyny elektryczne I, ME2
Me2
CW2a
cw2A
kolokwium 1, Studia, semestr 4, Maszyny elektryczne, Maszyny elektryczne I, ME2
Me2
me2 cw4b
cw2a
cw2a
więcej podobnych podstron