POLITECHNIKA GDAŃSKA

Wydział Elektrotechniki i Automatyki

Katedra Energoelektroniki i Maszyn Elektrycznych

MATERIAŁY POMOCNICZE DO LABORATORIUM

M A S Z Y N Y E L E K T R Y C Z N E I I

PODSTAWY DYNAMIKI MASZYN ELEKTRYCZNYCH

Kier. Elektrotechnika, studia mgr, sem. V

TEMATYKA ĆWICZENIA

BADANIE DYNAMIKI TRANSFORMATORA

WSPOMAGANE SYMULATOREM OBWODÓW PSPICE

© Mieczysław RONKOWSKI

GDAŃSK 2003

Mieczysław RONKOWSKI

1

ĆWICZENIE

BADANIE DYNAMIKI TRANSFORMATORA

WSPOMAGANE SYMULATOREM OBWODÓW PSPICE

Program ćwiczenia

1. CEL ĆWICZENIA .......................................................................................................................................1
2. TRANSFORMATOR JAKO WZORCOWE SPRZĘŻENIE TRANSFORMATOROWE...................1
3. DYNAMICZNY MODEL OBWODOWY WZORCOWEGO SPRZĘŻENIA

TRANSFORMATOROWEGO..................................................................................................................2

4. ZASTOSOWANIE PROGRAMU SYMULACYJNEGO PSPICE DO BADANIA WŁAŚCIWOŚCI

DYNAMICZNYCH TRANSFORMATORA............................................................................................3

5. WYNIKI SYMULACJI WYBRANYCH STANÓW DYNAMICZNYCH TRANSFORMATORA.....7
6. LITERATURA ...........................................................................................................................................10
7. ZADANIE....................................................................................................................................................10
8. SPRAWOZDANIE .....................................................................................................................................11
9. ZAŁĄCZNIK ..............................................................................................................................................12

1. CEL

ĆWICZENIA

Celem ćwiczenia jest:

• zapoznanie się z dynamicznym modelem obwodowym transformatora — wzorcowego sprzężenia

transformatorowego;

• opanowanie zastosowania programu symulacyjnego PSPICE do badania właściwości dynamicznych

transformatora;

• wykonanie badań symulacyjnych typowych stanów pracy dynamicznej transformatora o zadanych

wartościach parametrów modelu oraz wymuszeniach elektrycznych;

• porównanie wyników badań symulacyjnych z wynikami badań eksperymentalnych.

2.

TRANSFORMATOR JAKO WZORCOWE SPRZĘŻENIE TRANSFORMATOROWE
Schemat układu elektromagnetycznego na rys.

1 przedstawia podstawowy model fizyczny

transformatora wraz z ilustracją zasady jego działania — generacji SEM transformacji. Na podstawowy
model fizyczny transformatora składają się:

• elementy czynne: rdzeń, uzwojenia pierwotne i wtórne;
• wielkości fizyczne: napięcia na zaciskach uzwojeń, prądy płynące w uzwojeniach, strumień

magnesowania (główny), strumienie rozproszenia uzwojeń, straty w żelazie i straty w miedzi uzwojeń.

Przyjęte na rys. 1 symbole a1, a3 oznaczają umowne początki uzwojeń odpowiednio pierwotnego i

wtórnego, a symbole a2, a4 — umowne końce tych uzwojeń. Płynące prądy w uzwojeniach transformatora
wytwarzają pola magnetyczne (przepływy, siły magnetomotoryczne -SMM: F

1

oraz F

2

), których osie są

skierowane zgodnie z osiami magnetycznymi tych uzwojeń (osiami kolumn).

Transformator będzie rozpatrywany jako układ elektromagnetyczny w którym moc elektryczna

dostarczana i moc elektryczna odbierana, ulegają przemianie za pośrednictwem pola magnetycznego. Moc
pola magnetycznego jest mocą wewnętrzną transformatora, gdyż układ nie ma możliwości wymiany tej
mocy z otoczeniem. Pole magnetyczne wyraża się zależnościami strumieniowo-prądowymi. Stąd, stan
transformatora będzie opisany układem równań napięciowo-prądowych dla obu stron elektrycznych.

Transformator na rys. 1 może być przedstawiony jako wielowrotnik elektromagnetyczny o dwóch

parach zacisków (wrotach), które stanowią „wejście i wyjście elektryczne” — zaciski kolejnych uzwojeń.
Dynamika (ruch) transformatora jest określona dwoma parametrami mocy na każdej parze zacisków. Jej
formalnym opisem będzie układ równań różniczkowych zwyczajnych nieliniowych przy dwóch zadanych
wymuszeniach. Układ ten opisuje, m.in., związki między napięciami, prądami i strumieniami
magnetycznymi transformatora.

2

Ćwiczenie: BADANIE DYNAMIKI TRANSFORMATORA

∆ P

Cu 1

∆P

Cu 2

∆P

Fe

Φ

m

u

2

z

1

z

2

i

2

Φ

1

l

Φ

2

l

i

1

u

1

F

1

F

2

a1

a2

a3

a4

Rys. 1. Podstawowy model fizyczny transformatora jednofazowego: rdzeń; układ uzwojeń pierwotnego

i wtórnego; rozpływ strumienia magnesującego (głównego)

Φ

m

oraz strumieni rozproszenia

Φ

l1

i

Φ

l2

; straty

w żelazie

∆

P

Fe

; straty w miedzi uzwojeń

∆

P

Cu1

oraz

∆

P

Cu2

W dalszych rozważaniach przyjęto następujące założenia upraszczające:

• uzwojenia transformatora są układem symetrycznym;
• płynące w uzwojeniach prądy o dowolnych przebiegach wzbudzają SMM odwzorowane wektorami

przestrzennymi F

1

oraz F

2

;

• wpływ pola elektrycznego między elementami maszyny, zjawisk anizotropii, histerezy, strat w żelazie i

wypierania prądu w przewodach uzwojeń są pomijalnie małe.

Uwaga: Przyjęty na rys. 1 sposób strzałkowania napięć, prądów, SMM, dotyczy konwencji odbiornikowej.

Zwroty prądów uzwojenia pierwotnego i wtórnego odpowiadają ich wartościom chwilowym
dodatnim (np. dodatni prąd pierwotny dopływa do zacisku a1, natomiast wypływa zaciskiem a2;
analogicznie jest dla prądu wtórnego — dodatni prąd wtórny dopływa do zacisku a3, natomiast
wypływa zaciskiem a4).

Transformator jednofazowy jest fizycznym przykładem tzw. wzorcowego
sprzężenia transformatorowego, tzn. układu elektromagnetycznego, w którym
można wyróżnić dwa obwody magnetycznie sprzężone, które są nieruchome
względem siebie i mają wspólną oś magnetyczną.

3.

DYNAMICZNY MODEL OBWODOWY WZORCOWEGO SPRZĘŻENIA
TRANSFORMATOROWEGO
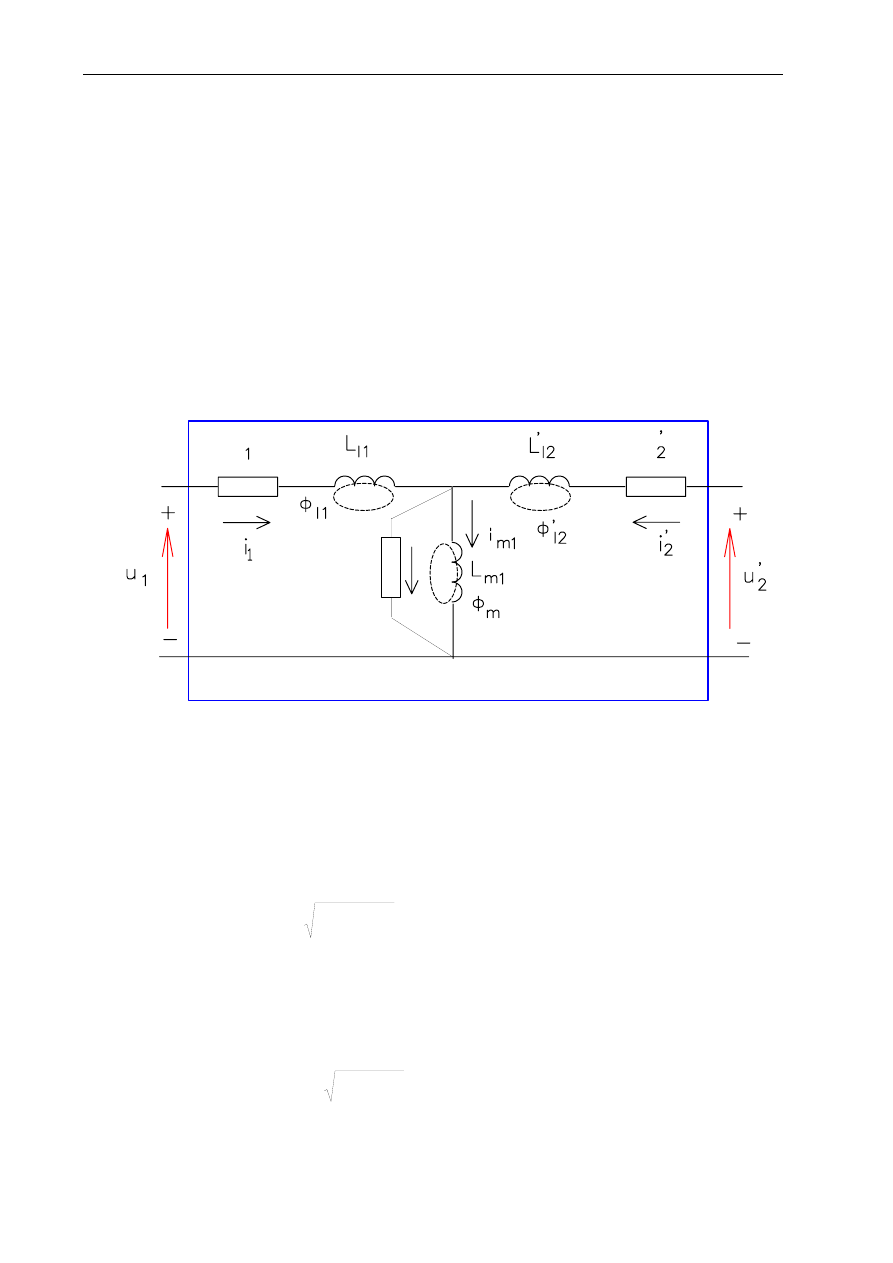
Do opisu modelu fizycznego wzorcowego sprzężenia transformatorowego — transformatora

jednofazowego, przyjęto następujące wielkości oraz parametry (stałe skupione):
a) wielkości i parametry elektryczne:

• napięcia i prądy strony pierwotnej u1, i1 oraz strony wtórnej u2, i2,
• rezystancje uzwojeń pierwotnego R1 i wtórnego R2,

b) wielkości i parametry elektromagnetyczne:

• strumień magnesujący (główny)

φ

m,

• strumienie rozproszenia uzwojenia pierwotnego

φ

l1 i wtórnego

φ

l2,

• indukcyjność magnesowania (główna) Lm1,
• indukcyjności rozproszenia uzwojenia pierwotnego Ll1 i wtórnego Ll2.

Tworząc model obwodowy sprzężenia przyjęto, że wpływ zmiennych magnetycznych (strumieni

magnesującego

φ

m

i rozproszenia

φ

l1

,

φ

l2

) na zachowanie sprzężenia odwzorowują wielkości obwodowe:

indukcyjności magnesowania L

m1

, oraz rozproszenia L

l1

i L

l2

. Następnie, po redukcji uzwojenia wtórnego do

pierwotnego, czyli zamianie liczby zwojów z

2

na z'

2

= z

1

, model obwodowy sprzężenia przyjmie postać jak

na rys. 2 (pominięto odwzorowanie wpływu strat w żelazie na właściwości dynamiczne sprzężenia).

Mieczysław RONKOWSKI

3

R

R

Rys. 2. Model obwodowy (schemat zastępczy) wzorcowego sprzężenia transformatorowego —

transformatora jednofazowego

4.

ZASTOSOWANIE PROGRAMU SYMULACYJNEGO PSPICE DO BADANIA
WŁAŚCIWOŚCI DYNAMICZNYCH TRANSFORMATORA

♦ Stany dynamiczne (nieustalone) transformatora

Stany dynamiczne transformatora określone są przez następujące czynniki:

• warunki zasilania (wymuszenia elektryczne);
• przebiegi napięć, prądów i strumieni sprzężonych poszczególnych uzwojeń transformatora;
• siły elektrodynamiczne, jako wynik wzajemnego oddziaływania odpowiednich prądów i strumieni

sprzężonych;

• warunki obciążenia strony wtórnej transformatora.

Najbardziej interesujące z punktu widzenia eksploatacji transformatorów przemysłowych są

następujące przebiegi:

• prądu jałowego (łączeniowego) przy załączaniu transformatora,
• prądu zwarcia udarowego,

w warunkach zasilania napięciem sinusoidalnie zmiennym.
Interesujące jest także poznanie właściwości dynamicznych sprzężenia transformatorowego
(transformatora) w warunkach zasilania napięciem stałym.

Właściwa analiza wymienionych wyżej stanów pracy dynamicznej — stanów nieustalonych —

transformatora, ze względu na nieliniowość zachodzących procesów elektromagnetycznych w
transformatorze, wymaga zastosowania zaawansowanych technik symulacyjnych. Przedstawiony w p. 3
niniejszego ćwiczenia model obwodowy transformatora stanowi wygodną bazę do obliczeń komputerowych,
wykorzystujących programy symulacyjne obwodów elektrycznych typu: NAP, PSPICE, TUTSIM, itp. W
klasie programów symulacyjnych obwodów elektrycznych, program PSPICE wydaję się być zarówno
programem najbardziej zaawansowanym jak i przyjaznym dla użytkownika.

♦ Budowa modelu symulacyjnego w programie PSPICE

a) Model liniowy
Opierając się na modelu obwodowym transformatora przedstawionym na rys. 2 oraz na zasadach

formułowania modelu symulacyjnego, obowiązujących dla programu PSPICE, zbudowano analog
elektryczny transformatora (pokazany na rys. 3) przystosowany do analizy za pomocą programu PSPICE.
Każdy element jest włączony w obwód w dokładnie zdefiniowanych węzłach. Definicja węzłów polega na
nazwaniu każdego z nich kolejną liczbą lub literami. Nie obowiązuje żadna hierarchia tych oznaczeń.
Jedynym warunkiem jest umieszczenie na liście węzłów, węzła oznaczonego numerem „0”.

W badaniach stanów nieustalonych transformatora należy określić wartości parametrów jego modelu

obwodowego, charakter wymuszeń elektrycznych i warunki początkowe.

Wartości parametrów modelu transformatora można obliczyć z wystarczającą dokładnością dla

obliczeń inżynierskich na podstawie jej danych katalogowych lub danych pomiarowych (szczegóły w
załączniku do niniejszej instrukcji). Z kolei do wprowadzania wartości tych parametrów do programu
PSPICE wykorzystuje się instrukcję .PARAM, którą ilustruje następujący przykład.

4

Ćwiczenie: BADANIE DYNAMIKI TRANSFORMATORA

a)

b)

4

R2

Ll2

i2

Rys. 3. Liniowy analog elektryczny transformatora do sformułowania pliku wejściowego PSPICE (podstawa

sformułowania — model obwodowy transformatora na rys. 2)

a) do analizy prądu łączeniowego b) do analizy prądu zwarcia udarowego

* Dane katalogowe transformatora
.PARAM Sn=1E3 U1n=220 U2n=133 Po=50 Pu=35 Uz=4.1 Io=14 fen=50
.PARAM pi=3.14159
* Obliczenia parametrow modelu obwodowego (patrz wzory w zalaczniku!)
* galaz magnesujaca
.PARAM I1n={Sn/U1n} IFe1={Po/U1n} RFe1={U1n/IFe1} Io1={(Io/100)*I1n}
.PARAM Im1={SQRT(Io1*Io1-IFe1*IFe1)} Xm1={U1n/Im1} Lm1={Xm1/(2*pi*fen)}
* galaz zwarciowa
.PARAM Rz={Pu/(I1n*I1n)} R1={Rz/2} R2={R1} Zz={(Uz/100)*(U1n/I1n)}
.PARAM Xz={SQRT(Zz*Zz-Rz*Rz)} Xl1={Xz/2} Xl2={Xl1} Ll1={Xl1/(2*pi*fen)} Ll2={Ll1}

♦ Pliki wsadowe programu PSPICE

W oparciu o analog elektryczny transformatora na rys. 3 oraz powyższe rozważania, sformułowano

następujące pliki wsadowe programu PSPICE.

•

Plik cw1a-a.cir: symulacja prądu łączeniowego transformatora - model liniowy

Symulacja prądu łaczeniowego transformatora - model liniowy
* Dane katalogowe transformatora
.PARAM Sn=1E3 U1n=220 U2n=133 Po=50 Pu=35 Uz=4.1 Io=14 fen=50
.PARAM pi=3.14159
* Obliczenia parametrow modelu (patrz wzory w zalaczniku!)
* galaz magnesujaca
.PARAM I1n={Sn/U1n} IFe1={Po/U1n} RFe1={U1n/IFe1} Io1={(Io/100)*I1n}
.PARAM Im1={SQRT(Io1*Io1-IFe1*IFe1)} Xm1={U1n/Im1} Lm1={Xm1/(2*pi*fen)}
* galaz zwarciowa
.PARAM Rz={Pu/(I1n*I1n)} R1={Rz/2} R2={R1} Zz={(Uz/100)*(U1n/I1n)}
.PARAM Xz={SQRT(Zz*Zz-Rz*Rz)} Xl1={Xz/2} Xl2={Xl1} Ll1={Xl1/(2*pi*fen)} Ll2={Ll1}
************************************
*1. ANALIZA .TRAN (zasilanie DC)
* amplituda napiecia zasilania
.PARAM U1m={SQRT(2)*U1n}
V1 1 0 DC {U1m} ;V

Mieczysław RONKOWSKI

5

* nazwa, N+, N-, zrodlo DC, wartosc [V]
R1 1 2 {R1} ;ohm
Ll1 2 3 {Ll1} IC=0
Lm1 3 0 {Lm1} IC=0
.TRAN 0.002 3 0 0.002 UIC
* analiza TRAN, krok druku, czas koncowy, czas poczat. druku, max krok analizy, wyk. war. pocz.
.PROBE V(1) I(R1) V(3)
.END
*2. ANALIZA .TRAN (zasilanie AC)
************************************
.PARAM Sn=1E3 U1n=220 U2n=133 Po=50 Pu=35 Uz=4.1 Io=14 fen=50
.PARAM pi=3.14159
* Obliczenia parametrow modelu (patrz wzory w zalaczniku!)
* galaz magnesujaca
.PARAM I1n={Sn/U1n} IFe1={Po/U1n} RFe1={U1n/IFe1} Io1={(Io/100)*I1n}
.PARAM Im1={SQRT(Io1*Io1-IFe1*IFe1)} Xm1={U1n/Im1} Lm1={Xm1/(2*pi*fen)}
* galaz zwarciowa
.PARAM rz={Pu/(I1n*I1n)} R1={Rz/2} R2={R1} Zz={(Uz/100)*(U1n/I1n)}
.PARAM Xz={SQRT(Zz*Zz-Rz*Rz)} Xl1={Xz/2} Xl2={Xl1} Ll1={Xl1/(2*pi*fen)} Ll2={Ll1}
* amplituda napiecia zasilania
.PARAM U1m={SQRT(2)*U1n}
V1 1 0 SIN (0 {U1m} {fen} 0 0 0)
* nazwa, N+, N-, skl. stala, amplit., czestot.[Hz], opoznienie, wsp. tl., faza[stop]
R1 1 2 {r1} ;ohm
Ll1 2 3 {Ll1} IC=0
Lm1 3 0 {Lm1} IC=0
.TRAN 0.002 3 0 0.002 UIC
.PROBE V(1) I(R1) V(3)
.END

•

Plik cw1a-b.cir: symulacja prądu zwarcia udarowego transformatora - model liniowy

Symulacja pradu zwarcia udarowego transformatora - model liniowy
*Dane katalogowe transformatora
.PARAM Sn=1E3 U1n=220 U2n=133 Po=50 Pu=35 Uz=4.1 Io=14 fen=50
.PARAM pi=3.14159
* Obliczenia parametrow modelu obwodowego (patrz wzory w zalaczniku!)
* galaz magnesujaca
.PARAM I1n={Sn/U1n} IFe1={Po/U1n} RFe1={U1n/IFe1} Io1={(Io/100)*I1n}
.PARAM Im1={SQRT(Io1*Io1-IFe1*IFe1)} Xm1={U1n/Im1} Lm1={Xm1/(2*pi*fen)}
* galaz zwarciowa
.PARAM Rz={Pu/(I1n*I1n)} R1={Rz/2} R2={R1} Zz={(Uz/100)*(U1n/I1n)}
.PARAM Xz={SQRT(Zz*Zz-Rz*Rz)} Xl1={Xz/2} Xl2={Xl1} Ll1={Xl1/(2*pi*fen)} Ll2={Ll1}
* 1. ANALIZA .TRAN (zasilanie DC)
* amplituda napiecia zasilania
.PARAM U1m={SQRT(2)*U1n}
V1 1 0 DC {U1m} ;V
* nazwa, N+, N-, zrodlo DC, wartosc [V]
R1 1 2 {R1} ;ohm
Ll1 2 3 {Ll1} IC=0
Lm1 3 0 {Lm1} IC=0
Ll2 4 3 {Ll2} IC=0
R2 0 4 {R2} IC=0
.TRAN 0.002 4 0 0.002 UIC
* analiza TRAN, krok druku, czas koncowy, czas poczat. druku, max krok analizy, wyk. war. pocz.
.PROBE V(1) I(R1) I(Lm1) I(R2)

6

Ćwiczenie: BADANIE DYNAMIKI TRANSFORMATORA

.END
*2. ANALIZA .TRAN (zasilanie AC)
*Dane katalogowe transformatora
.PARAM Sn=1E3 U1n=220 U2n=133 Po=50 Pu=35 Uz=4.1 Io=14 fen=50
.PARAM pi=3.14159
* Obliczenia parametrow modelu obwodowego (patrz wzory w zalaczniku!)
* galaz magnesujaca
.PARAM I1n={Sn/U1n} IFe1={Po/U1n} RFe1={U1n/IFe1} Io1={(Io/100)*I1n}
.PARAM Im1={SQRT(Io1*Io1-IFe1*IFe1)} Xm1={U1n/Im1} Lm1={Xm1/(2*pi*fen)}
* galaz zwarciowa
.PARAM Rz={Pu/(I1n*I1n)} R1={Rz/2} R2={R1} Zz={(Uz/100)*(U1n/I1n)}
.PARAM Xz={SQRT(Zz*Zz-Rz*Rz)} Xl1={Xz/2} Xl2={Xl1} Ll1={Xl1/(2*pi*fen)} Ll2={Ll1}
* amplituda napiecia zasilania
.PARAM U1m={SQRT(2)*U1n}
V1 1 0 SIN (0 {U1m} {fen} 0 0 0)
* nazwa, N+, N-, skl. stala, amplit., czestot.[Hz], opoznienie, wsp. tl., faza[stop]
R1 1 2 {R1} ;ohm
Ll1 2 3 {Ll1} IC=0
Lm1 3 0 {Lm1} IC=0
Ll2 4 3 {Ll2} IC=0
R2 0 4 {R2} IC=0
.TRAN 0.002 4 0 0.002 UIC
.PROBE V(1) I(R1) I(Lm1) I(R2)
.END

b) Model nieliniowy
Opierając się na modelu obwodowym transformatora, przedstawionym na rys.

2, można

sformułować następujące równanie różniczkowe dla stanu jałowego:

1

1

1

1

1

1

m

m

l

m

p

pi

L

i

R

u

λ

+

+

=

(1)

gdzie,

λ

m1

- strumień magnesujący sprzężony z uzwojeniem pierwotnym i wtórnym, p=d/dt- operator

różniczkowania.

Strumień magnesujący

λ

m1

jest nieliniową funkcją prądu magnesującego i

m1

, która odwzorowuje

charakterystykę magnesowania:

)

(

1

1

1

m

m

m

i

λ

λ

=

(2)

Celem rozwiązania numerycznego rów. (1), jako zmienną stanu przyjęto strumień

λ

m1

, wymaga to

przekształcenia rów. (2) w funkcję odwrotną:

)

(

1

1

1

m

m

m

i

i

λ

=

(3)

Zatem rów. (1), po pominięciu indukcyjności rozproszenia (pomijalnie mały wpływ w bilansie

napięć), można przekształcić do następującej postaci normalnej:

)

(

1

1

1

1

m

m

i

R

u

p

−

=

λ

(4)

Sposób wyznaczania charakterystyki magnesowania wg rów. (3) podano w załączniku do niniejszej

instrukcji. Do rozwiązania rów. (4) przyjęto aproksymację dwuodcinkową charakterystyki magnesowania.

Jako analogi elektryczne rów. (4) i (3) przyjęto obwody pokazane na rys. 4.
W oparciu o analog elektryczny transformatora na rys. 4 oraz powyższe rozważania, sformułowano

następujący plik wsadowy programu PSPICE.

•

Plik cw1a-c.cir: symulacja prądu łączeniowego transformatora - model nieliniowy

Symulacja prądu laczeniowego transformatora - model nieliniowy
*ANALIZA .TRAN (zasilanie AC)
************************************
* Dane katalogowe transformatora
.PARAM Sn=1E3 U1n=220 U2n=133 Po=50 Pu=35 Uz=4.1 Io=14 fen=50
.PARAM pi=3.14159
* Obliczenia parametrow modelu (patrz wzory w zalaczniku!)

Mieczysław RONKOWSKI

7

* galaz magnesujaca
.PARAM I1n={Sn/U1n} IFe1={Po/U1n} RFe1={U1n/IFe1} Io1={(Io/100)*I1n}
.PARAM Im1={SQRT(Io1*Io1-IFe1*IFe1)} Xm1={U1n/Im1} Lm1={Xm1/(2*pi*fen)}
* galaz zwarciowa
.PARAM Rz={Pu/(I1n*I1n)} R1={Rz/2} R2={R1} Zz={(Uz/100)*(U1n/I1n)}
.PARAM Xz={SQRT(Zz*Zz-Rz*Rz)} Xl1={Xz/2} Xl2={Xl1} Ll1={Xl1/(2*pi*fen)} Ll2={Ll1}
************************************
* amplituda napiecia zasilania
.PARAM U1m={SQRT(2)*U1n}
*faza napiecia zasilania
.PARAM fi_U1=0
*wykonanie analizy przy fazie napiecia zasilania = 0 i 90 stopni
.STEP PARAM fi_U1 LIST 0 90

*napiecie zasilania
V_U1 1 0 SIN(0 {U1m} {fen} 0 0 {fi_U1})
R_U1 1 0 1

* Calkowanie strumienia magnesowania lambda_m1 - row. (4)
G_lambda_m1 0 2 VALUE={V(1) - R1*V(3)}
C_lambda_m1 2 0 1 IC=0
R_lambda_m1 2 0 1E6

* Aproksymacja 2-odcinkowa
* charakterystyki magnesowania im1=im1(lamba_m1) - row. (3)
G_im1 0 3 TABLE={V(2)} (-2.0,-18) (-0.99,-0.905) (0,0) (0.99,0.905) (2.0,18)
R_im1 3 0 1
*V(2) - wielkosc sterujaca - strumien lambda_m1
* -2.0 - wartosc wejsciowa; -18 - wartosc wyjsciowa, itp.
*Wyprowadzenie wynikow analizy
.PROBE V(1) V(2) I(G_im1)
.TRAN 0.001 0.1 0 0.0001 UIC
.END

V_U1

1

R_U1 = 1

V(2)=

λ

m1

G_lambda_m1

Napięcie zasilania

~

0

R_lambda_m1 = 1e6

C_lambda_m1 = 1

2

0

Całkowanie strumienia - rów. (4)

G_im1

3

R_im1 = 1

Charakterystyka magnesowania - rów. (3)

0

V(1) = u

1

V(3) = i

m1

Rys. 4. Analog elektryczny transformatora do sformułowania pliku wejściowego PSPICE

(podstawa sformułowania — rów. (3) i (4)): nieliniowa analiza prądu łączeniowego

5.

WYNIKI SYMULACJI WYBRANYCH STANÓW DYNAMICZNYCH TRANSFORMATORA

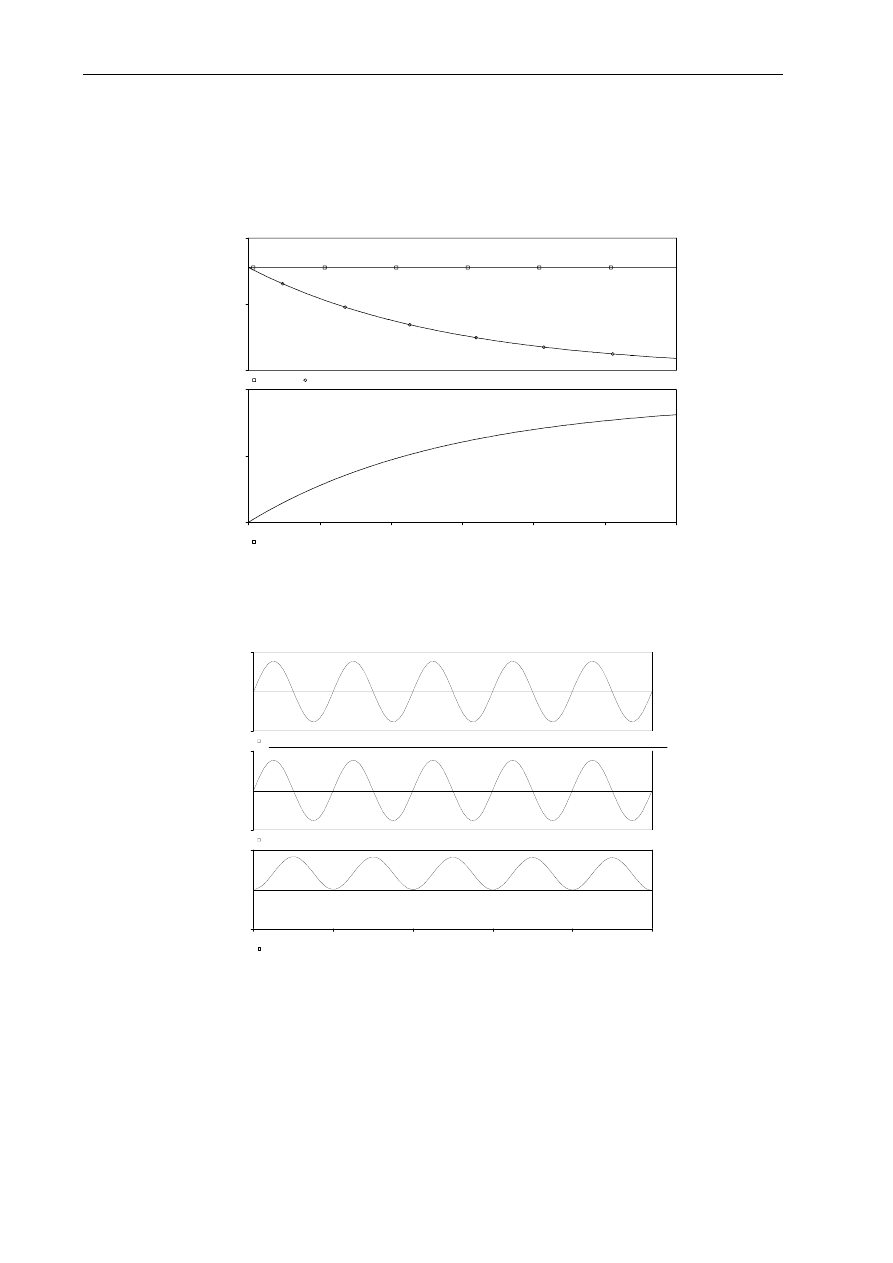
♦ Przebiegi czasowe prądu łączeniowego transformatora - model liniowy

8

Ćwiczenie: BADANIE DYNAMIKI TRANSFORMATORA

Przykładowe przebiegi czasowe napięcia zasilania V(1), SEM transformacji V(3) i prądu

łączeniowego transformatora I(R1) — model liniowy (stała wartość indukcyjności magnesowania), pokazano
na rys. 5.

WYNIKI SYMULACJI (POSTPROCESOR GRAFICZNY .PROBE)

a)

0s

0.5s

1.0s

1.5s

2.0s

2.5s

3.0s

Time

I(R1)@1

400A

200A

0A

V(1)@1

V(3)@1

400V

200V

0V

* 1. ANALIZA .TRAN (zasilanie DC)

Date/Time run: 10/06/99 11:57:42

Temperature: 27.0

b)

0s

20ms

40ms

60ms

80ms

100ms

Time

I(R1)@2

2.0A

-2.0A

V(3)@2

400V

-400V

V(1)@2

400V

-400V

*2. ANALIZA .TRAN (zasilanie AC)

e/Time run: 11/13/100 13:29:51

Temperature: 27.0

Rys.5. Wyniki analizy .TRAN załączania transformatora — model liniowy(stała wartość indukcyjności

magnesowania) — przebiegi czasowe napięcia zasilania V(1), SEM transformacji V(3) i prądu łączeniowego

transformatora I(R1)

a) załączanie napięcia stałego b) załączanie napięcia przemiennego - w chwili włączenia napięcie zasilania

miało wartość zerową

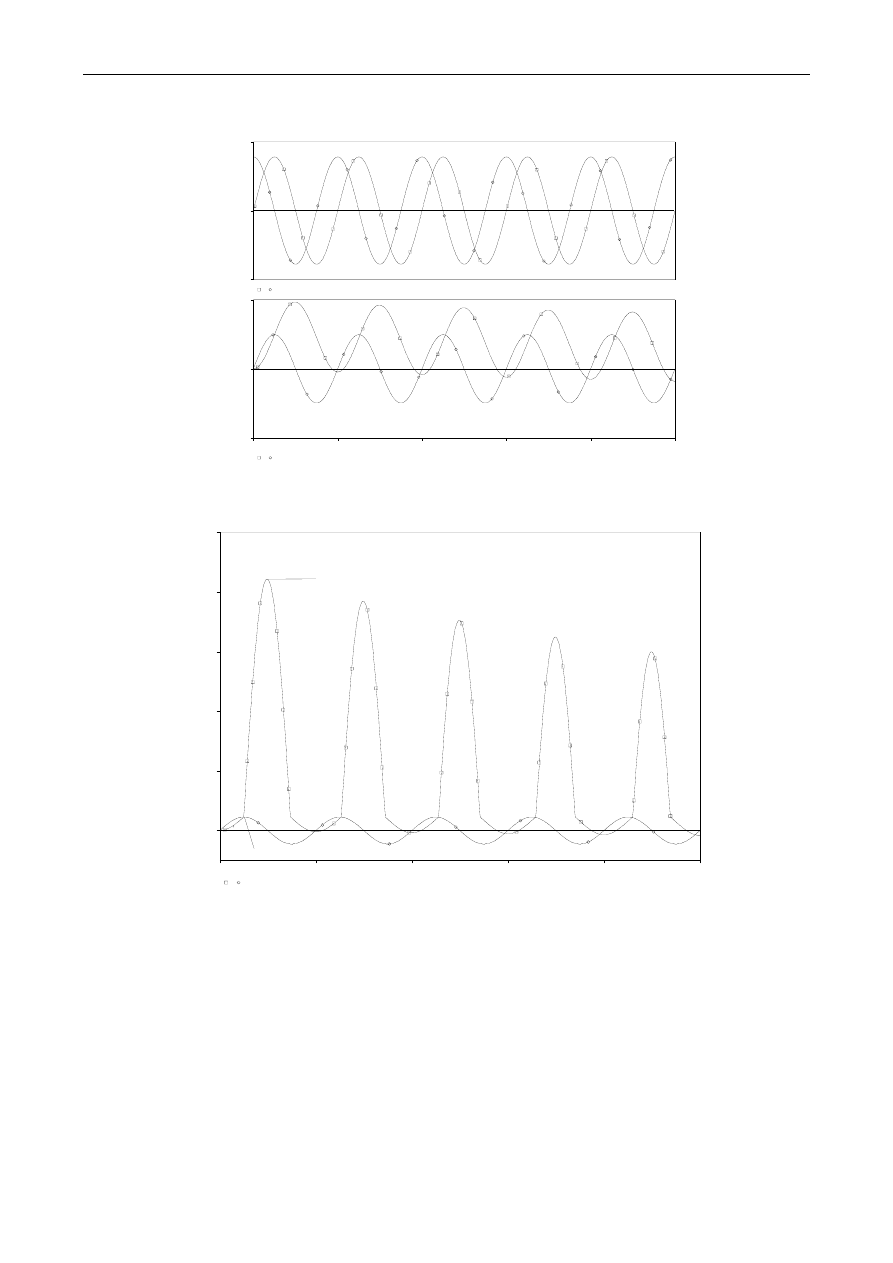
♦ Przebiegi czasowe prądu łączeniowego transformatora - model nieliniowy

Przykładowe przebiegi czasowe napięcia zasilania V(1), sprzężonego strumienia magnesowania V(2)

i prądu łączeniowego transformatora I(G_im1) pokazano na rys. 6.

Mieczysław RONKOWSKI

9

0s

20ms

40ms

60ms

80ms

100ms

Time

V(2)

2.0

0

-2.0

V(1)

400V

0V

-400V

WLACZANIE TRAFO - MODEL NIELINIOWY

Date/Time run: 11/13/100 22:50:24

Temperature: 27.0

0s

20ms

40ms

60ms

80ms

100ms

Time

I(G_im1)

20A

16A

12A

8A

4A

0A

(5.1149m,902.224m)

(9.739m,16.855)

WLACZANIE TRAFO - MODEL NIELINIOWY

Date/Time run: 11/13/100 22:40:32

Temperature: 27.0

Rys.6. Wyniki analizy .TRAN załączania transformatora — model nieliniowy (zmienna wartość

indukcyjności magnesowania) — przebiegi czasowe:

napięcia zasilania V(1), sprzężonego strumienia magnesowania V(2) i prądu łączeniowego I(G_im1)

przebieg oznaczony — w chwili włączenia napięcie zasilania miało wartość zerową

przebieg oznaczony

◊— w chwili włączenia napięcie zasilania miało wartość maksymalną

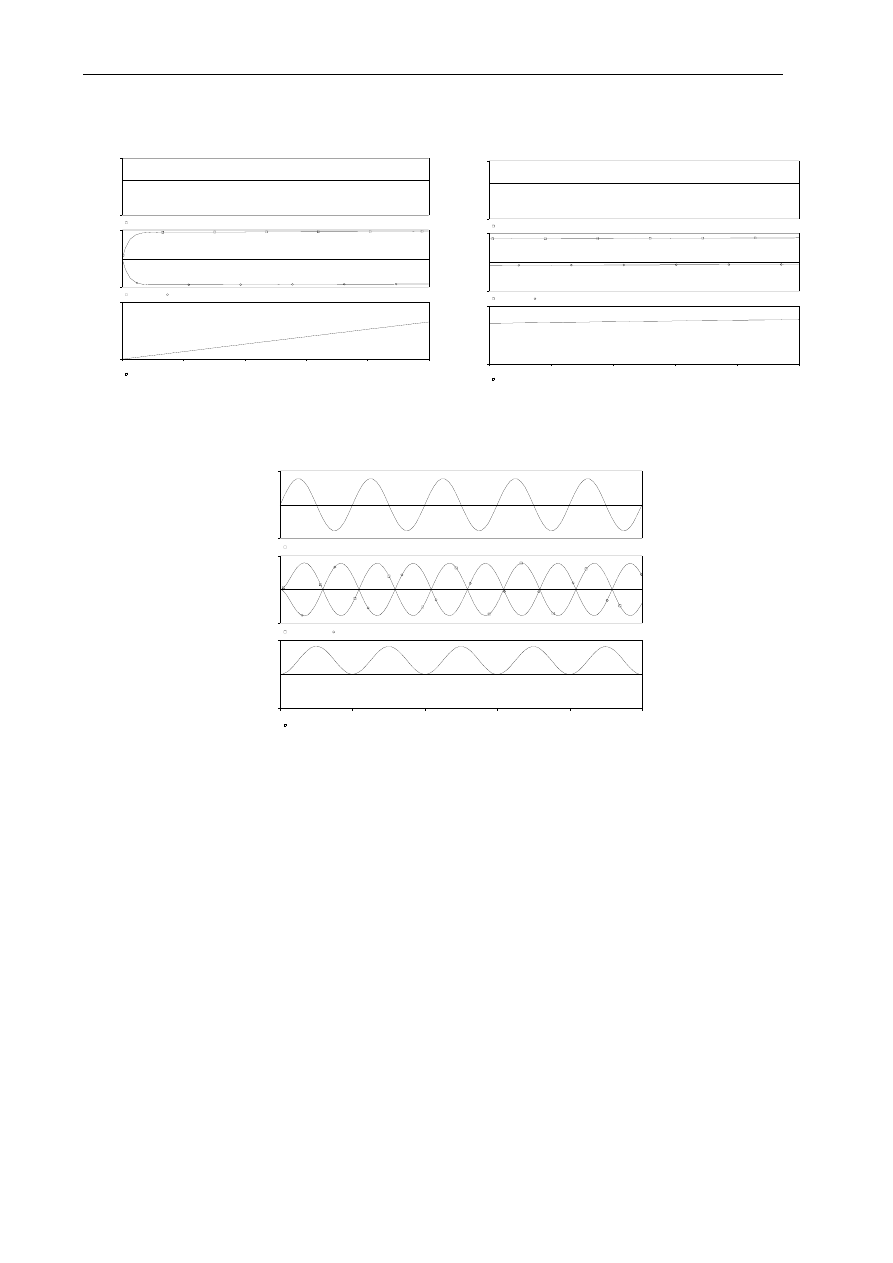
♦ Przebiegi czasowe zwarcia udarowego transformatora - model liniowy

Przebiegi napięcia zasilania transformatora V(1), pierwotnego prądu zwarciowego I(R1), wtórnego

prądu zwarciowego I(R2), prądu magnesowania I(Lm1) pokazano na rys. 7.

10

Ćwiczenie: BADANIE DYNAMIKI TRANSFORMATORA

WYNIKI SYMULACJI (POSTPROCESOR GRAFICZNY .PROBE)

a)

0s

20ms

40ms

60ms

80ms

100ms

Time

I(Lm1)@1

20A

0A

I(R1)@1

I(R2)@1

200A

-200A

V(1)@1

500V

0V

*1. ANALIZA .TRAN (ZASILANIE DC)

Date/Time run: 11/13/100 15:04:12

Temperature: 27.0

0

czas od 0 do 100ms

4.0s

4.2s

4.4s

4.6s

4.8s

5.0s

Time

I(Lm1)@1

400A

0A

I(R1)@1

I(R2)@1

400A

-400A

V(1)@1

500V

0V

*1. ANALIZA .TRAN (ZASILANIE DC)

Date/Time run: 11/13/100 15:42:09

Temperature: 27.0

0

czas od 4 do 5s

b)

0s

20ms

40ms

60ms

80ms

100ms

Time

I(Lm1)@2

1.0A

-1.0A

I(R1)@2

I(R2)@2

200A

-200A

V(1)@2

400V

-400V

*2. ANALIZA .TRAN (ZASILANIE AC)

Date/Time run: 11/13/100 15:04:12

Temperature: 27.0

0

0

0

Rys. 7. Wyniki analizy .TRAN zwarcia udarowego transformatora — model liniowy (stała wartość

indukcyjności magnesowania) — przebiegi czasowe:

napięcia zasilania transformatora V(1), pierwotnego prądu zwarciowego I(R1), wtórnego prądu

zwarciowego I(R2), prądu magnesowania I(Lm1)

a) załączanie napięcia stałego b) załączanie napięcia przemiennego — w chwili włączenia wartość napięcia

zasilania była równa zero

6. LITERATURA

1. P.C. Krause i O. Wasynczuk: Electromechanical Motion Devices, Mc Graw -Hill Book Comp.. New

York, 1989. Purdue University, USA.

2. P.C. Krause: Analysis of Electric Machinery. Mc Graus - Hill Book Comp. New York, 1986.
3. W. Latek: Teoria maszyn elektrycznych. WNT, Warszawa, 1982.
4. Z. Manitius: Maszyny elektryczne cz. I, II. Skrypt PG, 1982, 1984.
5. W. Paszek: Stany nieustalone maszyn elektrycznych prądu przemiennego. WNT, Warszawa, 1986.
6. S. Roszczyk: Teoria maszyn elektrycznych. WNT, Warszawa, 1979.
7. P. Zimny, K. Karwowski: SPICE klucz do elektrotechniki. Instrukcja, program, przykłady. Skrypt PG,

1993.

7. ZADANIE

Dla danych transformatora (z katalogu lub pomiaru) wykonać analizę .TRAN:

Mieczysław RONKOWSKI

11

Nr

zada.

Stan pracy dynamicznej transformatora

Warunki początkowe

1

model liniowy i nieliniowy (aproksymacja 3-odcinkowa):
załączanie napięcia stałego - obwód wtórny otwarty

zerowe wartości prądów

2

model liniowy i nieliniowy (aproksymacja 4-odcinkowa):
załączanie napięcia przemiennego - obwód wtórny otwarty

zerowe wartości prądów

3

model liniowy i nieliniowy (aproksymacja 5-odcinkowa):
załączanie napięcia stałego - obwód wtórny otwarty

zerowe wartości prądów

4

model nieliniowy - aproksymacja 6-odcinkowa:
załączanie napięcia przemiennego - obwód wtórny otwarty

zerowe wartości prądów

5

model liniowy i nieliniowy - aproksymacja 7-odcinkowa:
załączanie napięcia stałego - obwód wtórny otwarty

zerowe wartości prądów

6

model liniowy i nieliniowy - aproksymacja 8-odcinkowa:
załączanie napięcia przemiennego - obwód wtórny otwarty

zerowe wartości prądów

7

model liniowy:
załączanie napięcia stałego - obwód wtórny zwarty,
analizę wykonać dla rezystancji zwarciowej znamionowej i 10 razy
mniejszej

zerowe wartości prądów

8

model liniowy:
załączanie napięcia przemiennego - obwód wtórny zwarty,
analizę wykonać dla rezystancji zwarciowej znamionowej i 10 razy
mniejszej

zerowe wartości prądów

Założyć znamionowe warunki zasilania lub podane przez prowadzącego ćwiczenie.

8. SPRAWOZDANIE

Opracowanie sprawozdania powinno zawierać:
• stronę tytułową wg następującego układu:

POLITECHNIKA GDAŃSKA

WYDZIAŁ ELEKTROTECHNIKI I AUTOMATYKI

KATEDRA ENERGOELEKTRONIKI I MASZYN

ELEKTRYCZNYCH

MASZYNY ELEKTRYCZNE II

LABORATORIUM KOMPUTEROWE

ĆWICZENIE 1A

BADANIE DYNAMIKI TRANSFORMATORA
WSPOMAGANE SYMULATOREM OBWODÓW PSPICE

Opracował:
Imię i nazwisko
nr grupy laboratoryjnej:
(podać nr grupy laboratoryjnej wg lab. MEII)
data oddania sprawozdania:

• dane znamionowe (wg katalogu lub wg pomiarów) i dane obwodowe badanego transformatora;
• nr i treść zadania;
• określenie wymuszeń elektrycznych (należy podać odpowiadające im fragmenty programu

PSPICE);

• określenie warunków początkowych (wartości prądów indukcyjności i napięć na pojemnościach,

należy podać odpowiadające im fragmenty programu PSPICE);

• obliczenia stałych czasowych modelu obwodowego dla danego transformatora;
• oszacowanie maks. kroku obliczeń HMAX i czasu końca analizy TSTOP;
• „ręczne” oszacowanie wartości prądów udarowych oraz porównanie ich wartości z wynikami

otrzymanymi na drodze symulacyjnej;

12

Ćwiczenie: BADANIE DYNAMIKI TRANSFORMATORA

• wybrane przebiegi wielkości, które są istotne (wg piszącego sprawozdanie) dla przeprowadzenia

analizy zadanego stanu pracy dynamicznej transformatora;

• uzasadnienie fizyczne uzyskanych wyników (powinno być napisane w stylu inżynierskim !!!

—- tzn. minimum języka tekstowego a maksimum języka graficznego i symbolicznego);

• krótka dyskusja wpływu założeń upraszczających modelu transformatora na uzyskane wyniki

obliczeń;

• wykaz literatury wykorzystanej przy pisaniu sprawozdania;
• załącznik w postaci dyskietki, zawierającej sformułowany plik wsadowy programu PSPICE.

9. ZAŁĄCZNIK

WYZNACZANIE WARTOŚCI PARAMETRÓW MODELU OBWODOWEGO

TRANSFORMATORA JEDNOFAZOWEGO

♦ Model liniowy

Metodę wyznaczania wartości parametrów modelu obwodowego transformatora jednofazowego

(podanego na rys. Z1),

R

R

R

Fe1

i

Fe1

Rys. Z1. Model obwodowy (schemat zastępczy) wzorcowego sprzężenia transformatorowego —

transformatora jednofazowego

przedstawiają następujące zależności:
a) na podstawie danych katalogowych

• gałąź magnesująca:

1

/

1

m1

X

2

1

2

01

1

1

)

100

/

%

0

(

01

I

1

/

1

1

1

/

0

1

1

/

1

m

I

n

U

Fe

I

I

m

I

n

I

I

Fe

I

n

U

Fe

R

n

U

P

Fe

I

n

U

n

S

n

I

≅

−

=

=

≅

≅

=

• gałąź zwarciowa

2

l2

X

l1

X

2

2

1

1

100

2

2

1

R

2

1

/

z

X

z

R

z

Z

z

X

)

n

I

/

n

U

)(

/

%

z

U

(

z

Z

/

z

R

R

n

I

/

u

P

z

R

≅

′

≅

−

=

=

≅

≅

≅

przy czym dana indukcyjność L=X / (2

π

fen)

gdzie:

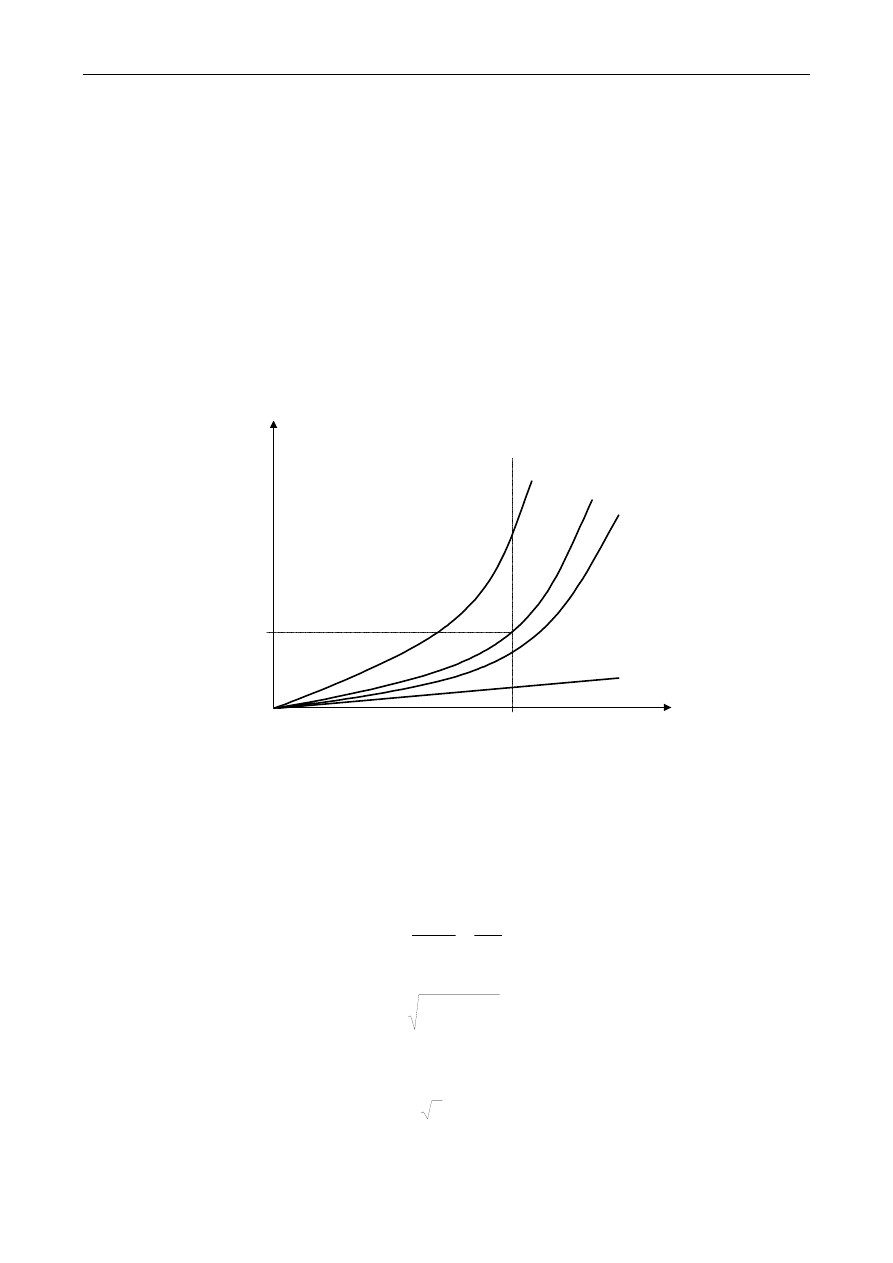
Mieczysław RONKOWSKI

13

P

0

- moc pobierana w stanie jałowym [W] - praktycznie równa stratom w żelazie,

P

u

- moc strat w uzwojeniach [W] - praktycznie równa mocy pobieranej w stanie zwarcia,

fen - częstotliwość znamionowa napięcia zasilania.
Uwaga:

Do obliczeń parametrów transformatora trójfazowego należy przyjąć, że podane w powyższych
zależnościach wielkości są wielkościami fazowymi: dotyczy to napięć, prądów i mocy transformatora.

b) na podstawie wyników prób stanu jałowego i zwarcia

Uwaga:

Szczegóły podano w instrukcji do Ćw. 1 „Badanie transformatora”. Laboratorium ME I sem.
IV.

♦ Model nieliniowy

Model nieliniowy dotyczy nieliniowości indukcyjności (reaktancji) magnesowania. Podstawą jej

wyznaczenia jest charakterystyka biegu jałowego transformatora (przykład podano na rys. Z2).

U

1

[V]

0

P

0

[W]

I

m1

I

01

I

Fe1

[A]

P

0

I

01

I

m1

I

Fe1

U

1n

I

01n

Rys. Z2. Charakterystyki stanu jałowego transformatora

Należy dokonać rozkładu prądu stanu jałowego transformatora na składową magnesującą i składową
pokrywająca w straty w żelazie wg następującej procedury:
• straty w żelazie przy założeniu:

[W]

0

Fe

P

P

≈

∆

• składowa czynna prądu stanu jałowego:

[A]

1

0

1

Fe1

I

U

P

E

Fe

P

≈

∆

=

• prąd magnesujący

[A]

2

1

2

01

1

I

Fe

I

I

m

−

=

Uwaga:

• prąd magnesujący należy przeliczyć na wartości maksymalne

[A]

1

2

1

m

I

m

i

=

• sprzężony strumień magnesujący należy wyznaczyć w następujący sposób

14

Ćwiczenie: BADANIE DYNAMIKI TRANSFORMATORA

[Wb]

2

1

2

2

1

2

1

en

f

U

en

f

E

m

π

≈

π

=

λ

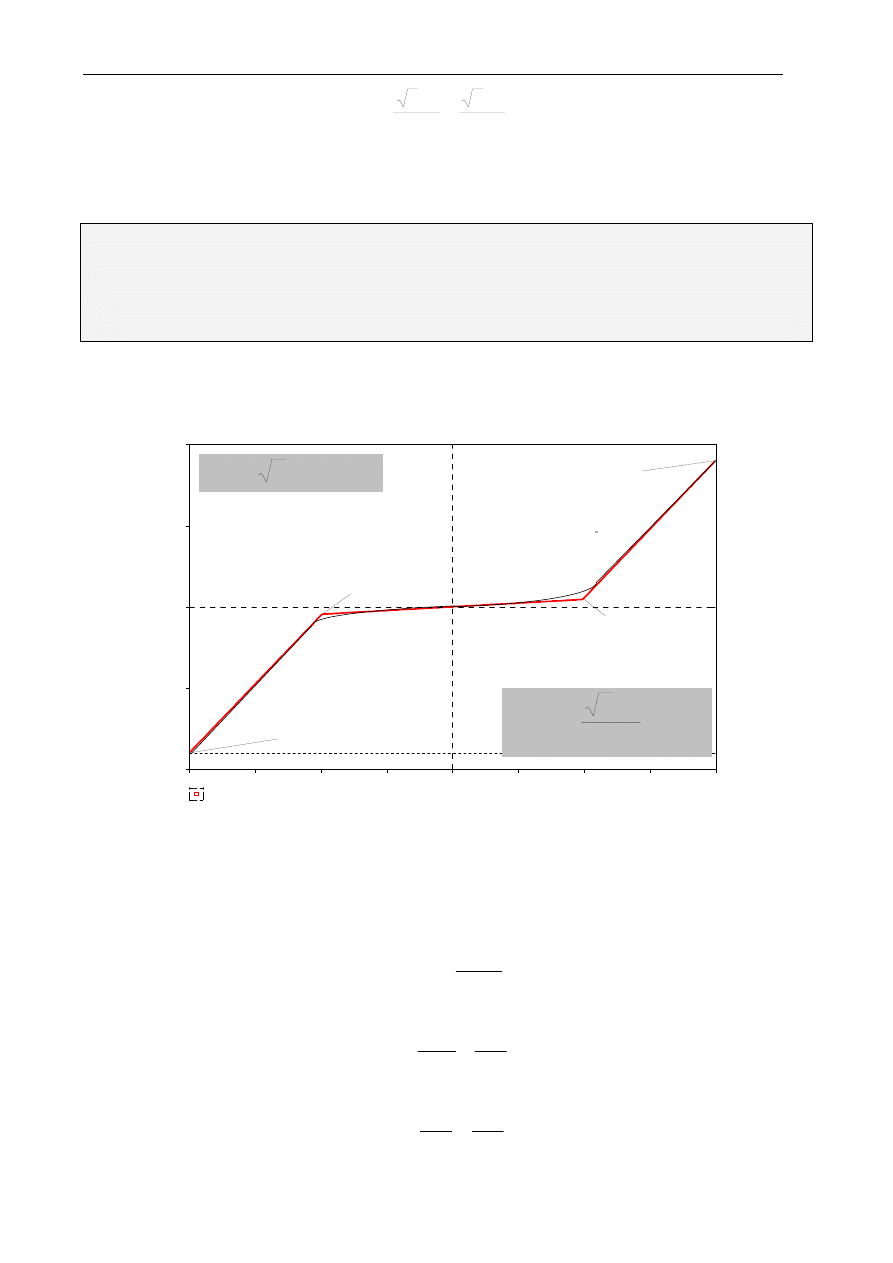
Przykład dwuodcinkowej aproksymacji odwrotnej charakterystyki magnesowania transformatora

)

m

(

m

i

m

i

1

1

1

λ

=

podano na rys. Z3.

Przykład instrukcji w programie PSPICE, który realizuje tą charakterystykę podano niżej.

* Aproksymacja 2-odcinkowa
* charakterystyki magnesowania im1=im1(lambda_m1) - row. (3)
G_im1 0 3 TABLE={V(2)} (-2.0,-18) (-0.99,-0.905) (0,0) (0.99,0.905) (2.0,18)
*V(2) - wielkosc sterujaca to strumien lambda_m1
* -2.0 - wartosc wejsciowa; -18 - wartosc wyjsciowa, itp.
R_im1 3 0 1

-2.0

-1.5

-1.0

-0.5

0

0.5

1.0

1.5

2.0

V_lambda_m1

V(2)

20

10

0

-10

-20

(0.99,0.905)

(2.0,18)

(-2.0,-18)

CHARAKTERYTYKA MAGNESOWANIA im1=im1(lambda_m1)

Date/Time run: 11/13/100 22:20:48

Temperature: 27.0

(-0.99,-0.905)

[Wb]

2

1

2

1

en

f

U

m

π

≈

λ

[A]

1

2

1

m

I

m

i

=

Rys. Z3. Przykład dwuodcinkowej aproksymacji odwrotnej charakterystyki magnesowania transformatora

)

m

(

m

i

m

i

1

1

1

λ

=

Dalsze obliczenia to:
• współczynnik mocy stanu jałowego

01

1

0

0

cos

I

U

P

=

ϕ

• rezystancja modelującą straty w żelazie

]

[

1

1

1

Fe1

R

Ω

≈

=

Fe

I

U

Fe

I

E

• reaktancja magnesująca

]

[

1

1

1

1

1

X

Ω

≈

=

m

I

U

m

I

E

m