Ogłoszenia:

e-portal

Przezrocza z aktualnych wykładów, listy zadań, podręczniki,

zasady zaliczania, symulacja ocen, terminy kolokwiów i

egzaminów, zapisy na kolokwia i egzaminy itp.

W.2

Podstawy chemii fizycznej

(biotechnologia)

prof. Ludwik Komorowski

pok. 315 A-3. pon., czw. 13-15

1

Plan W.2

1. Dowiadczenie Joule’A: gaz doskonały, gazy

rzeczywiste.

2. Praca adiabatyczna
3. Entalpia, C

p

oraz C

v

4. Wielkości cząstkowe, liczba postępu reakcji
5. Ciepło reakcji
6. Prawo Hessa, prawo Kirchhoffa
7. Samorzutność procesów

2

V

T

U

U

dU

dT

dV

T

V





































0

T

V

V

U

V

U

dU

dT

C dT

T





 































3

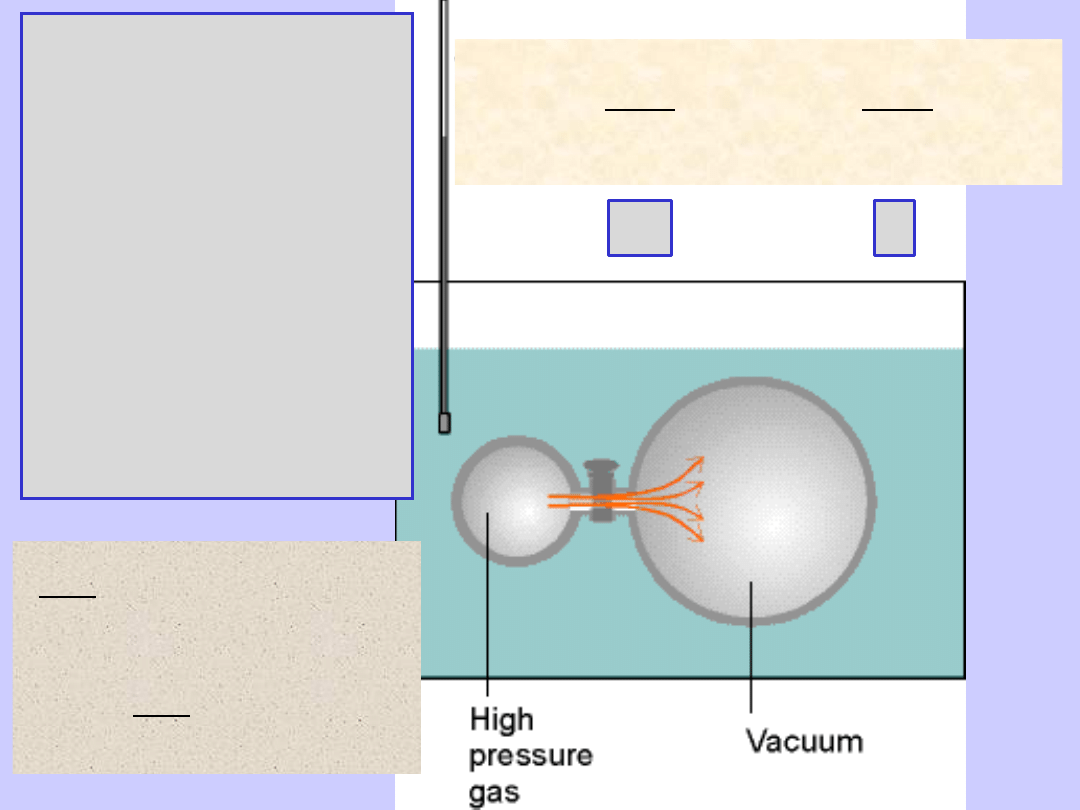
Doświadczenie Joule’a

Gaz doskonały

rozprężany do próżni

nie zmienia temperatury

W==-pdV=0 bo p=0



T=0



Q=0,

czyli



U=Q+W

C

V

0

Adiabata odwracalna czyli kwazystatyczna

(Poissona) dla gazu doskonałego.

Gaz w osłonie adiabatycznej zmienia p, V, i T.

Q = 0, dU = W

el

2

2

1

1

(

1)

(

1)

2 2

2

2

1

1

1 1

zał:

ln

ln

gdzie

1

V

el

T

V

V

V

T

V

V

V

nRT

dU

C dT

dV

W

V

nRT

C dT

dV

C

const

V

T

V

C

nR

T

T

TV

R

V

V

n

C













 



 



 

 







4

Adiabata kwazystatyczna (odwracalna)

1

2

2

1

1

2

1

1

2

1

1

(

)

1

V

V

V

V

T

T

V

W

C

T

C T

T

V

W

C T

V













  







 



































V

V

V

V

R

C

nR

C











C

C

5

Krok 1: obliczenie temperatury końcowej

Krok 2: obliczenie pracy

Entalpia H

W realnym procesie



U = Q + W = Q – p



V



U=Q gdy V=const i W=0

Wartość ciepła Q jest zależna od

warunków (izochora, izobara)

Czy istnieje funkcja H, taka że



H=Q gdy p=const

???

6

Entalpia H

Czy istnieje funkcja H, taka że



H=Q gdy p=const

(izobara)

Wykorzystamy I zasadę:



U=Q-p



V



H=Q=



U+p



V=



(U+pV)

Wniosek:

H=U+pV pV>0

I zasada dla entalpii



H=



U-p



V+



(Vp)=Q+V



p

7

Pojemność cieplna

w stałej objętości

V

V

C

























T

U

Q

U

const.

V

Gdy

V

Pojemność cieplna

pod stałym ciśnieniem

p

p

p

p

C











































T

Q

T

H

Q

H

const.

p

Gdy

8

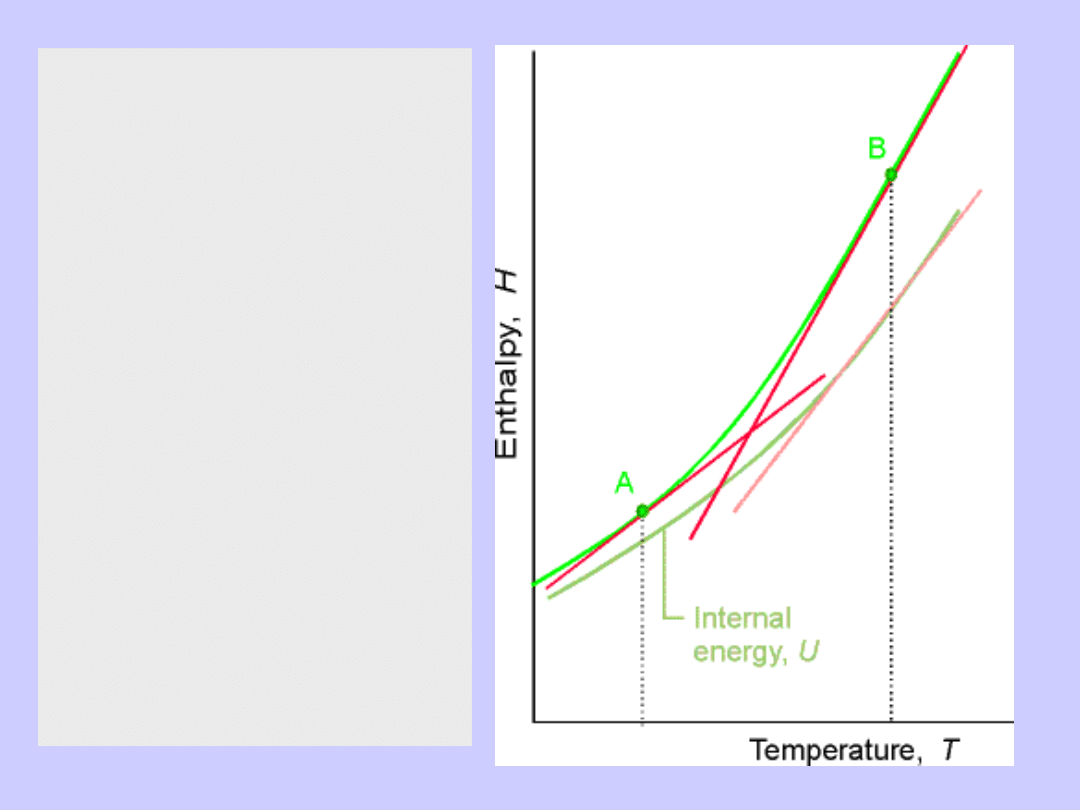
pV=nRT

H-U=pV=nRT>0

Gdy T rośnie

H-U także rośnie

Skąd wniosek
C

p

>C

V

>0

Większe nachylenie!

H(T)

U(T)

9

Dla gazu doskonalego

(

)

p

V

p

V

p

V

p

V

H

U

pV

dH

dU

d(pV)

C dT

C dT d nRT

C dT

C dT nRdT

C

C

nR

R

 





















C

C

Gaz doskonały

p

V

V

V

R









C

C

C

C

10

i

p

V

C

C

i

p

V

C

C

Po podstawieniu

Ponieważ

0, zatem

0

p

T

V

T

T

T

dH

dU

d(pV)

dU

nRdT

H

dH

C dT

dp

p

U

dU

C dT

dV

V

U

H

V

p

















 

















 



















 























Własności entalpii: gaz doskonały

11

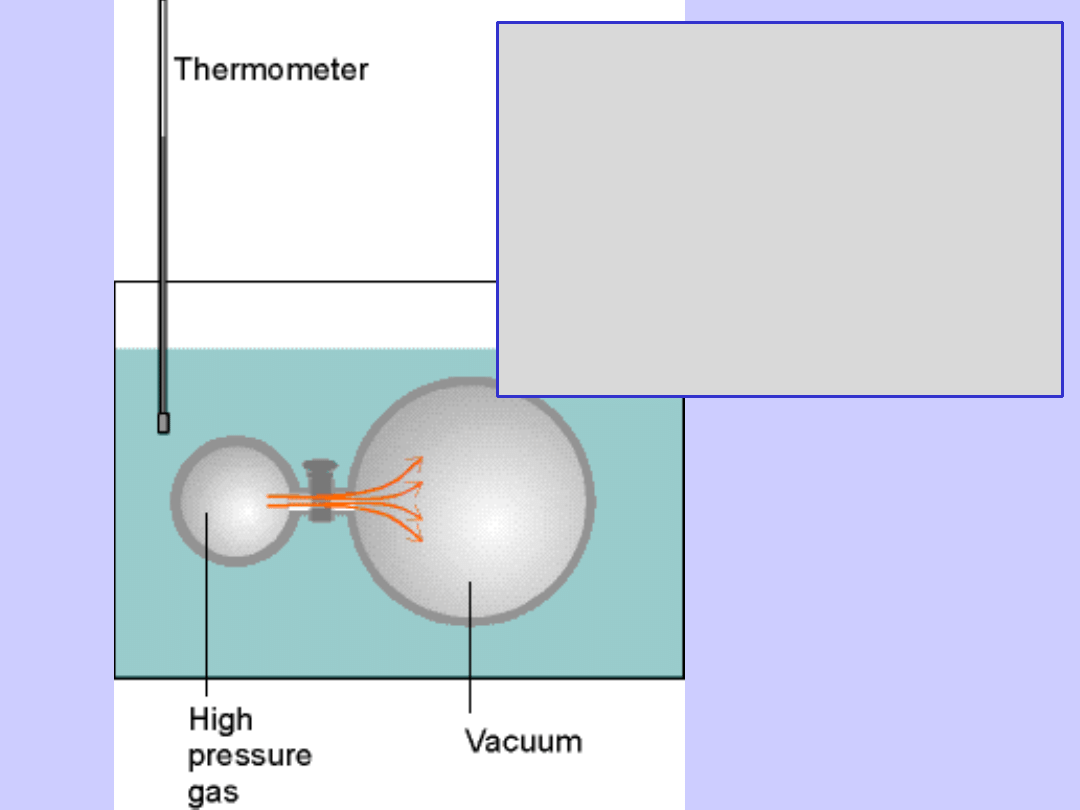
Doświadczenie Joule’a dla gazów

rzeczywistych

• Rozprężanie do próżni (W=0)
• Zmiana temperatury ∆T<0
• Ciepło pobrane z kąpieli
• Zmiana energii wewnętrznej gazu

∆U=Q+W=0 bo Q=0 i W=0

0

0

0

V

T

V

T

T

J

U

V

V

J

T

U

U

dU

dT

dV

T

V

U

dU

C dT

dV

V

U

T

V

V

C

U

C

V























































































 

















  













0

V

J

T

U

C

V







 













Gaz rzeczywisty

Współczynnik Joule’a

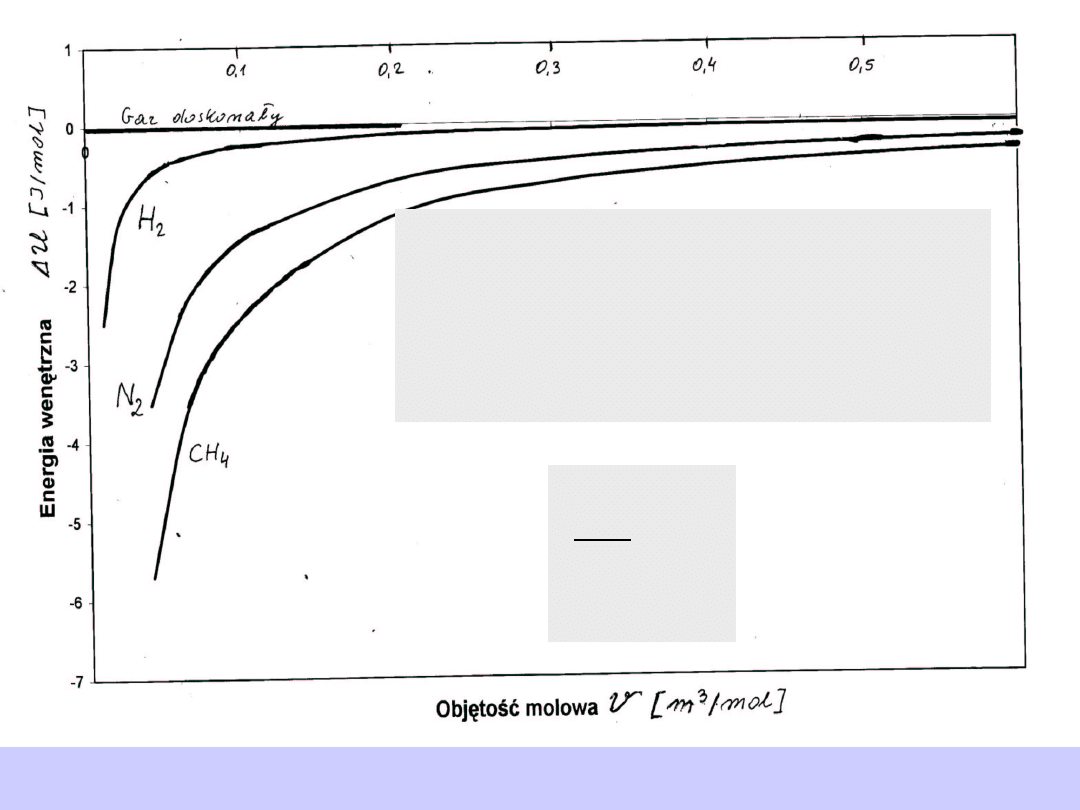
Doświadczenie Joule’a dla

gazów rzeczywistych

WNIOSKI

0

T

U

V





 











2

2

.

2

(

)

0

0

0

J

V

g dosk

T

a

p

b

RT

T

a

V

C

a

U

U

V

U

a

a

V

V

























   





















   













Gaz van der

Waalsa

b = objętość własna

a/V

2

= miara oddziaływań

przyciągających

Współczynnik Joule’a

otrzymany

przez różniczkowanie

Ze wzrostem objętości energia

wewnętrzna gazu rośnie. Jest zużywana na

pokonywanie oddziaływań

przyciągających między cząsteczkami

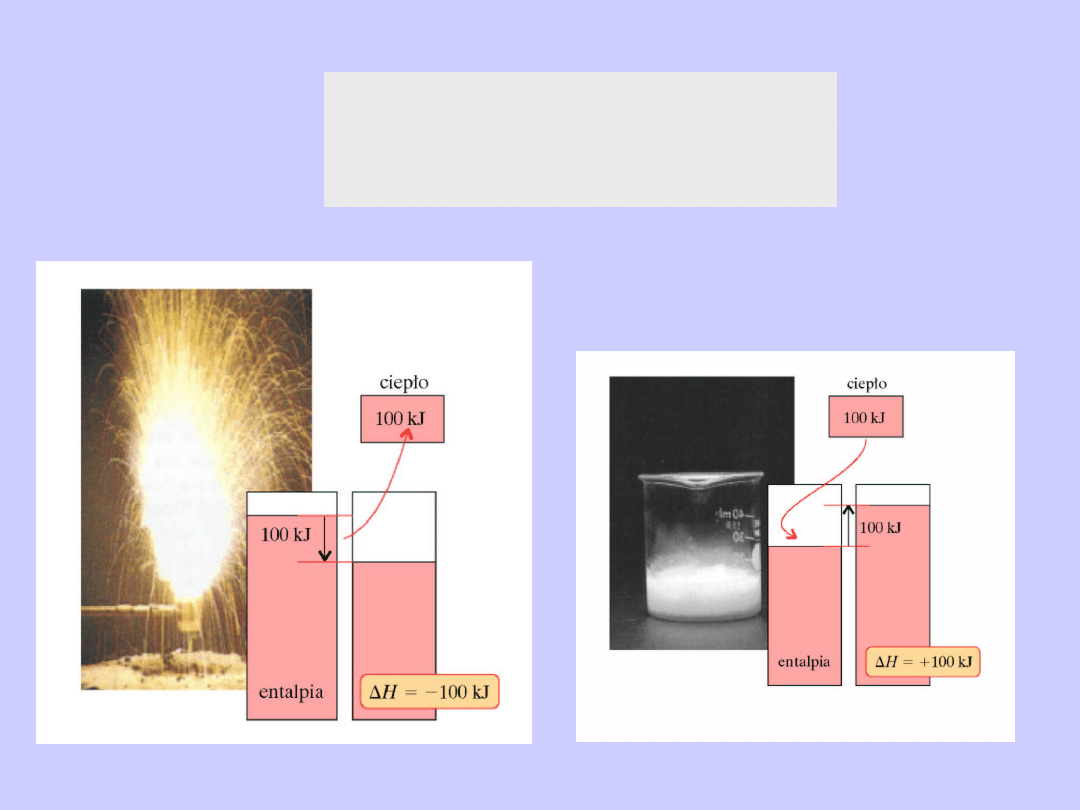
Egzo- i endo-

Wielkości cząstkowe molowe

czyli

„parcjalne”

w mieszaninach

Objętość mieszaniny (roztworu) V

V



n

A

A

+ n

B

B

Załóżmy jednak że

V = n

A

V

A

+n

B

V

B

Czyli w roztworze V

A



A

oraz V

B



B

V (

n

A

,n

B

) znane z doświadczenia !!!

V

A



(



V/



n

A

)

T,p

Cząstkowa molowa objętość w roztworze

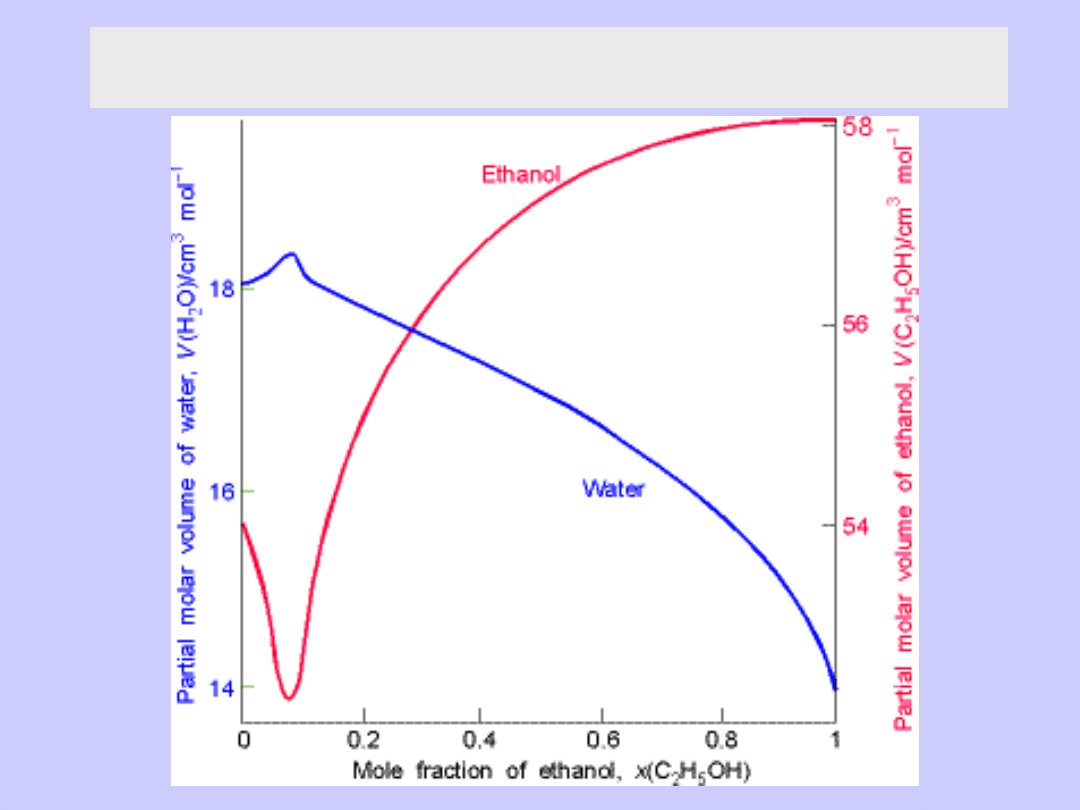
Cząstkowe objętości molowe

Cząstkowa, molowa

pojemność cieplna

w stałej objętości

,

,

,

,

T

T

j

j

j

V

V i

V

i

i

T n

T n

i

V

i

T n

V

C

U

n

n

U

T

n















































































































i

i

T

U

n







 









Mieszanina gazów

Liczba postępu

reakcji „



”

2 H

2

+O

2



2 H

2

O

0

2

1

2

2

2

2























O

H

O

H

n

n

n

i

i

v

dn

d







d

v

dn

i

i



Współczynniki

stechiometryczne ν

i

Obliczanie pracy i ciepła w przemianach gazowych

Liczba moli substancji jest stała.

V

T

U

U

dU

dT

dV

T

V





































( , )

U V T

Q

U W

  

0

T

U

V





 











V

V

U

C

T





 











Obliczanie pracy i ciepła w przemianach gazowych

Liczba moli substancji jest stała.

( , )

H p T

p

p

H

C

T





 











p

T

H

H

dH

dT

dp

T

p















 



















Q

H V p

   

0

T

H

p



















,

,

,

,

.;

.

p

p T

T

r

p T

H

H

H

dH

d

dT

dp

T

p

p

const

T

const

H

dH

d

H d





































 









































 











Entalpia procesu

izotermiczno-izobarycznego

gdy zachodzi reakcja chemiczna

,

,

,

.

,

.

Gaz doskonaly

r

p T

r

V T

r

r

i

gaz

H

T p

const

H

U

T V

const

U

H

U

RT

















 



















 











 





Ciepło reakcji pod stałym ciśnieniem

oraz w stałej objętości

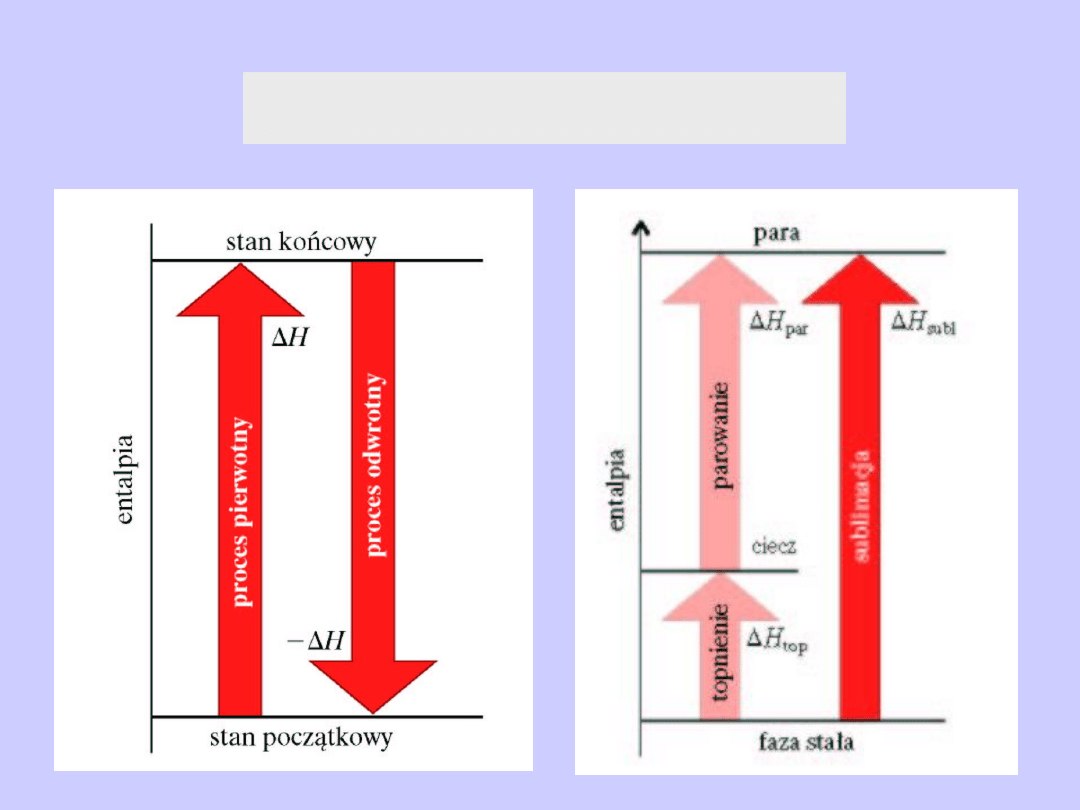
Ciepło procesu

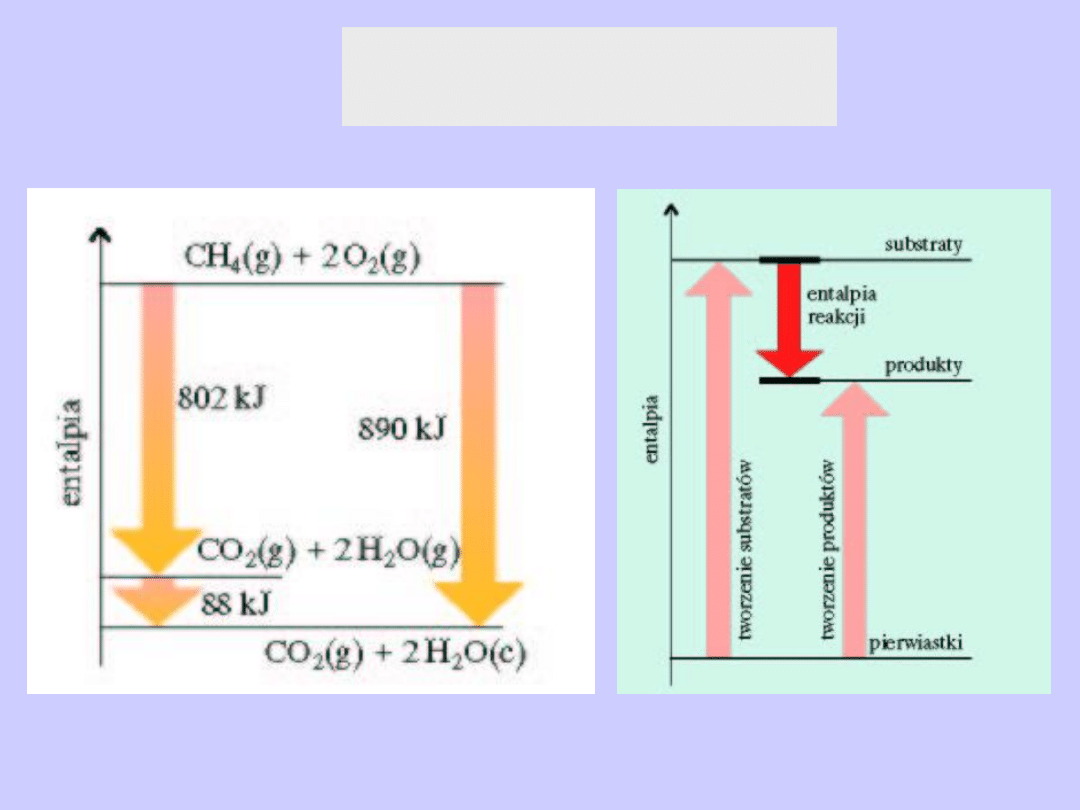
Prawo Hessa

Prawo Hessa -zastosowanie



H

tw

– ciepło tworzenia



H

sp

– ciepło spalania

0

doskonaly

Gaz

































































T

T

T

r

p

H

H

p

p

H





,

,

,

,

p

r

p

p

p

p

o

p

i

p i

i

o

p

i

p i

o

o

r

i

p i

p i

i

i

i

i

p

p

p

p

C

H

H

H

T

T

T

C

n

C

n

H

n

T































 

 



 























 

 











































 























































C

C

C

C

Zależność od ciśnienia oraz temperatury

Prawo Kirchhoffa

,

2

,

1

,

2

1

2

2

( )

( )

( )

( )

( )

p i

p i

p i

o

r

i

i

p

T

o

r

r

i

i

T

o

i

i

i

i

H

T

T

T

T

T

T

a

b T

c T

d T











 













 



 









H

H

C

C

C

Standardowe ciepło reakcji

Czyste, rozdzielone substraty



czyste, rozdzielone produkty

w warunkach standardowych



H

o

,



U

o

o

o





H

U