1

BUDOWA I WŁASNOŚCI CZĄSTECZKOWE GAZÓW

ATOMY I CZĄSTECZKI

• Jednostka masy

1 u (unit) =

12

1

masy izotopu

kg

C

27

12

6

10

66

.

1

−

⋅

=

• Masa atomowa lub cząsteczkowa

µ = (masa atomu lub molekuły) / 1u, wielkość bezwymiarowa

• Gramoatom lub gramocząsteczka (inaczej mol): µ wyrażone w gramach

• Stała Avogadro = liczba atomów lub cząsteczek w 1 molu substancji

1

23

1

27

1

10

023

.

6

10

66

.

1

12

012

.

0

12

12

−

−

−

−

⋅

=

⋅

⋅

=

=

mol

mol

kg

kg

mol

u

g

N

A

• Masa 1 mola substancji wyrażona w kg

u

N

m

A

⋅

⋅

=

µ

µ

• Koncentracja molekuł

n = liczba molekuł w jednostce objętości

µ

ρ

=

m

N

n

A

w jednostkach cm

-3

, m

-3

ρ = gęstość masowa substancji w jednostkach

3

cm

g

,

3

m

kg

• Siły międzyatomowe w cząsteczkach oraz międzycząsteczkowe są siłami

elektromagnetycznymi. Atomy, cząsteczki oddziaływują poprzez trwałe lub

indukowane elektryczne momenty dipolowe. Są to tzw. siły van der Waalsa

2

(siły odpychające przy małych odległościach między atomami, cząsteczkami

oraz przyciągające na odległościach dużych).

CIŚNIENIE GAZU NA ŚCIANKI NACZYNIA

(MODEL GAZU DOSKONAŁEGO)

• Gaz idealny jest modelowym przybliżeniem gazu doskonałego. W gazie

idealnym atomy (molekuły) zachowują się jak ciała doznające nieustannie

zderzeń sprężystych ze sobą i ściankami naczynia. W jednorodnym gazie

wszystkie molekuły posiadają tę sama masę m.

• Ciśnienie p jest równe liczbowo sile działającej na jednostkę powierzchni

naczynia, ciała.

Jednostki ciśnienia:

1 Pa (pascal) = 1N/m

2

(1 N = 1 niuton)

1 atm (atmosfera techniczna) = 1 Atm = 10

5

Pa = 1000 hPa (zależność

przybliżona)

U (r)

0

r

SIŁY ODPYCHAJĄCE

SIŁY PRZYCIĄGAJĄCE

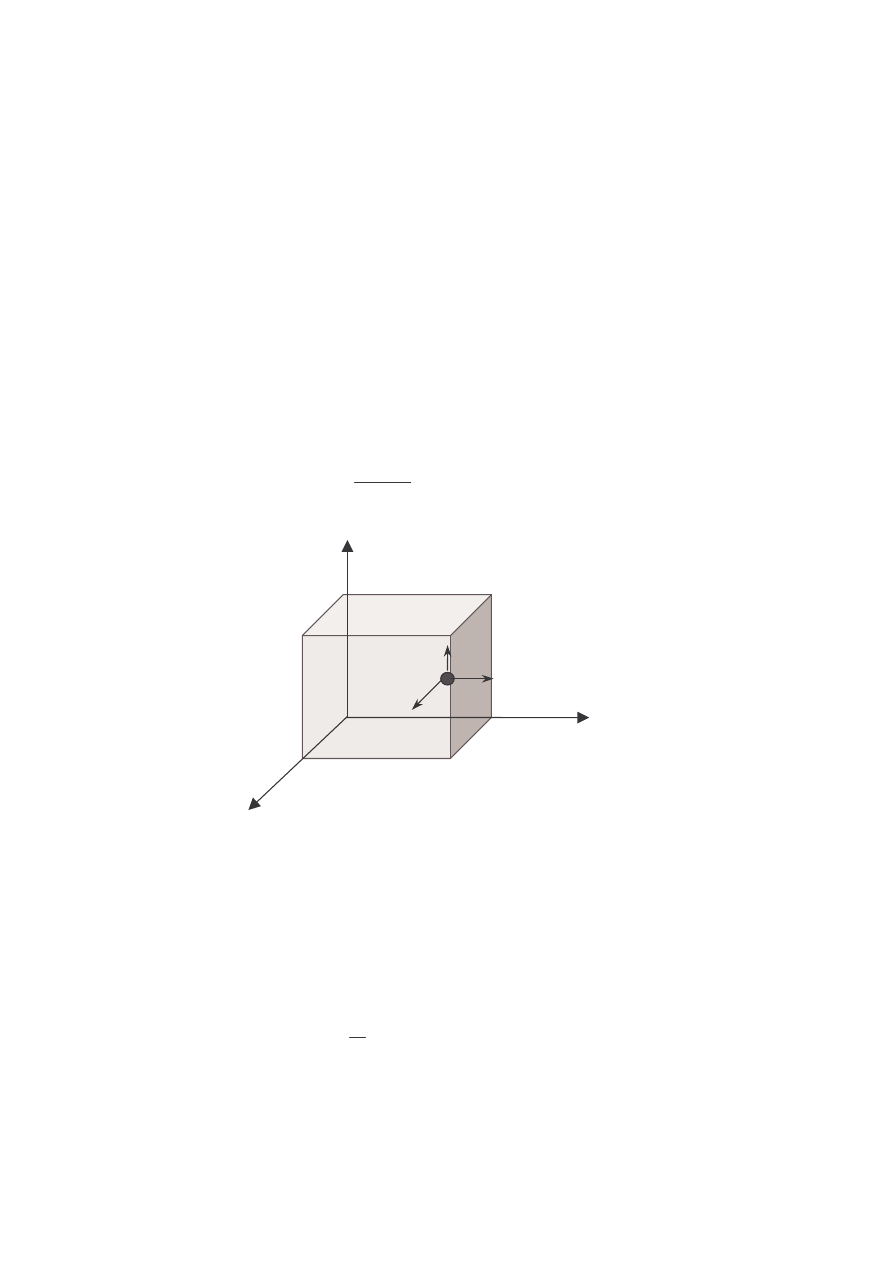
3

1 Atm (atmosfera normalna) = ciśnienie hydrostatyczne słupa rtęci o

wysokości h = 760 mm = 0.76 m

gh

p

ρ

=

ρ = 13.6 g/cm

3

= 13 600 kg/m

3

gęstość rtęci

g = 9.81 m/s

2

przyspieszenie ziemskie

• Podczas zderzenia ze ścianką naczynia i – ta molekuła posiadająca pęd (mv

i

)

oddziałuje na ściankę siłą doznając zmiany pędu w czasie ∆t

t

)

mv

(

F

i

i

∆

∆

=

• Ciśnienie p wywierane przez gaz na ścianki naczynia, zawierający liczbę N

molekuł, jest równe sumie ciśnień cząstkowych p

i

wywieranych przez

pojedyncze molekuły. Koncentracja molekuł wynosi

V

N

n

=

0

x

y

z

v

x

v

y

v

z

N

4

• Można udowodnić, że

N

v

N

v

v

nm

3

1

N

3

v

N

nm

S

F

p

p

i

i

2

2

2

i

i

i

i

N

1

i

i

∑

>=

<

>

<

=

∑

=

∆

∑

=

∑

=

=

N

i

liczba molekuł o prędkościach v

i

<v

2

>

średnia kwadratu prędkości

>

<

2

v

średnia prędkość kwadratowa ruchu postępowego molekuł

• Ciśnienie można wyrazić poprzez średnią energię kinetyczną pojedynczej

molekuły gazu

>

<

>=

<

⋅

=

>

<

>=

<

=

ε

n

mv

n

v

m

n

v

nm

p

3

2

2

1

3

2

2

3

2

3

1

2

2

2

>

<

ε

średnia energia kinetyczna ruchu postępowego

pojedynczej molekuły

RÓWNANIE STANU GAZU DOSKONAŁEGO

• Dla 1 mola gazu

pV = RT

p – ciśnienie gazu na ścianki naczynia

V – objętość gazu (naczynia)

T – temperatura gazu (w K)

R – uniwersalna stała gazowa R = 8.31 J · K

-1

mol

-1

5

• Dla masy M gazu (liczby molekuł N)

kT

2

3

k

N

R

N

3

2

RT

N

N

N

3

2

nV

3

2

pV

RT

N

N

RT

M

pV

A

A

A

>=

ε

<

=

>

ε

<

=

>

ε

<

>=

ε

<

=

=

µ

=

Stała Boltzmanna

A

N

R

k

=

ZASADA EKWIPARTYCJI ENERGII

(ZASADA RÓWNEGO PODZIAŁU ENERGII POMIĘDZY STOPNIE

SWOBODY MOLEKUŁ)

• Stopnie swobody – sposoby magazynowania energii przez molekułę

• Gaz 1 – atomowy (cząsteczka 1-atomowa).

x

y

z

PUNKT MATERIALNY

(GAZ 1- ATOMOWY)

6

Cząsteczka gazu przedstawia sobą punkt materialny, który wykonuje ruch

postępowy w trzech kierunkach przestrzeni: x, y, z i posiada w tych kierunkach

trzy składowe prędkości. Ze składowymi tymi związane są odpowiednio 3

wartości energii kinetycznej ruchu postępowego. Cząsteczka taka posiada 3

stopnie swobody ruchu postępowego (i = 3).

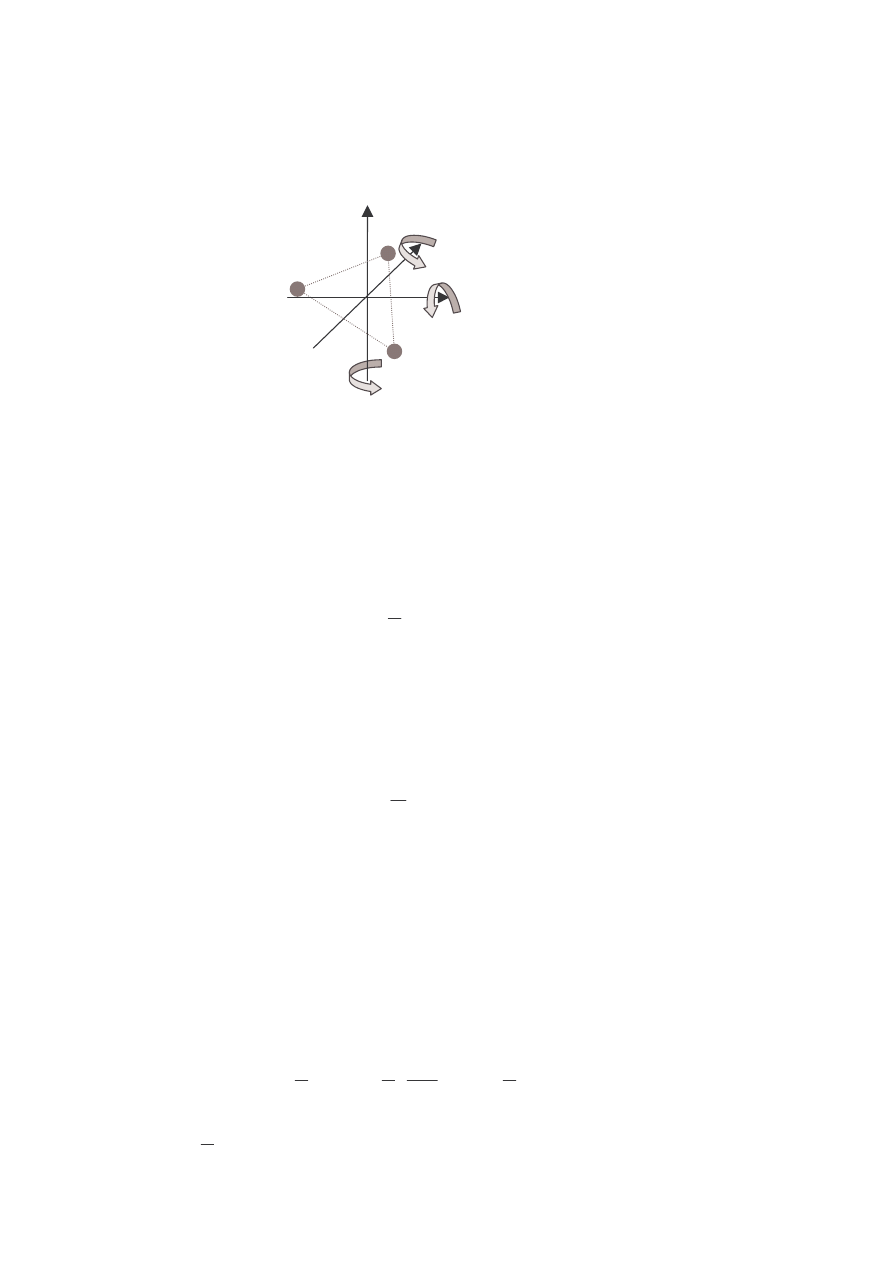
• Gaz 2 – atomowy. Cząsteczka prezentuje sobą układ dwóch punktów

materialnych (bryła sztywna), które oprócz ruchu postępowego mogą

wykonywać ruch obrotowy wokół dwóch, wzajemnie prostopadłych, osi

obrotu. Z ruchem tym związane są 2 wartości energii ruchu obrotowego, 2

stopnie swobody ruchu obrotowego.

Gaz 2 – atomowy posiada

i = 3 + 2 = 5

stopni swobody

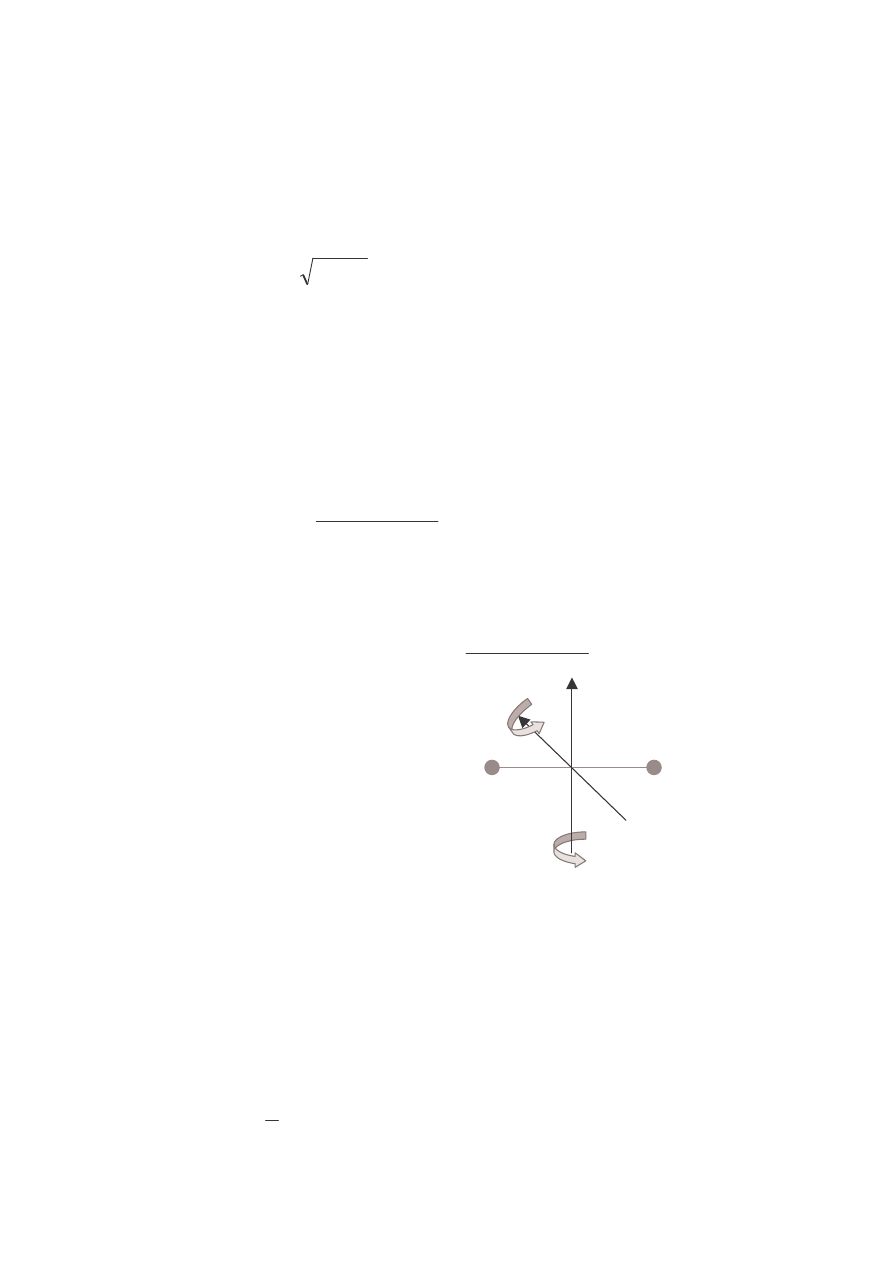
• Gaz 3- lub więcej atomowy (układ 3 lub więcej punktów materialnych)

Molekuła gazu (bryła sztywna) posiada 3 stopnie swobody ruchu

postępowego oraz 3 stopnie swobody ruchu obrotowego, związane z

możliwością ruchu obrotowego wokół trzech osi obrotu.

2 MOśLIWE OSIE OBROTU

7

Gaz 3- lub więcej atomowy posiada

i = 3 + 3 = 6

stopni swobody

• Zasada ekwipartycji brzmi: na każdy, pojedynczy stopień swobody molekuły

przypada jednakowa wartość energii, wynosząca

kT

2

1

1

>=

ε

<

• Całkowita energia kinetyczna ruchu postępowego (ruchu cieplnego)

pojedynczej molekuły wynosi

kT

2

i

>=

ε

<

i – liczba stopni swobody

ENERGIA WEWNĘTRZNA GAZU DOSKONAŁEGO

(ENERGIA RUCHÓW CIEPLNYCH WSZYSTKICH MOLEKUŁ GAZU)

• Energia wewnętrzna 1 mola gazu

RT

i

U

RT

i

T

N

N

R

i

kTN

i

N

U

A

A

A

A

2

2

2

2

=

=

⋅

=

>=

<

=

ε

3 MOśLIWE OSIE OBROTU

8

• Energia wewnętrzna dowolnej masy gazu

RT

m

2

i

U

µ

=

m – masa wszystkich molekuł

µ – masa 1 mola gazu (gramocząsteczka, gramoatom)

PRZEMIANY GAZU DOSKONAŁEGO

???????????????????????????????????????

CIEPŁO WŁAŚCIWE MOLOWE GAZÓW

(CIEPŁO POTRZEBNE DO OGRZANIA 1 MOLA GAZU)

• Ciepło właściwe molowe w stałej objętości

R

2

i

dT

dU

C

V

=

=

• Ciepło właściwe przy stałym ciśnieniu

R

2

2

i

R

C

C

V

p

+

=

+

=

• C

p

i C

V

gazu doskonałego nie zależą od temperatury

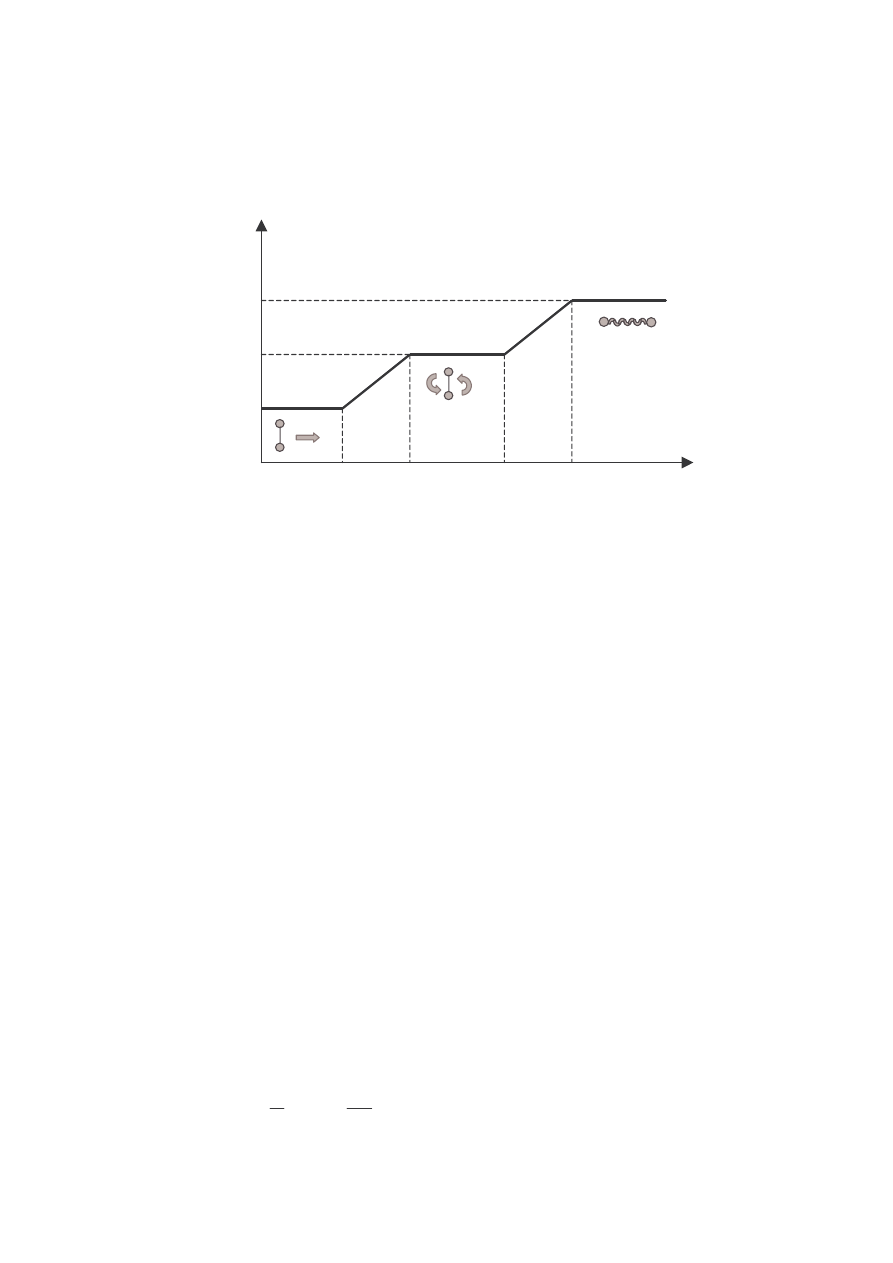
CIEPŁO WŁAŚCIWE GAZÓW WIELOATOMOWYCH

• W miarę wzrostu temperatury gazu molekuły wykonują coraz bardziej

złożone ruchy cieplne. Oznacza to zwiększanie się liczby stopni swobody

9

i w związku z tym, wzrost wartości ciepła właściwego gazu przy stałym

ciśnieniu i w stałej objętości.

Doświadczenie: zależność C

V

od temperatury dla wodoru cząsteczkowego H

2

(najprostsze molekuły gazu)

• Widmo energii molekuł dla ruchu postępowego jest widmem ciągłym, dla

ruchu rotacyjnego i drgającego – widmem dyskretnym. Oznacza to, że

energia tych dwóch ostatnich ruchów podlega kwantowaniu (inaczej –

molekuły posiadają kwantowe stopnie swobody. W miarę wzrostu

temperatury wodoru rośnie liczba stopni swobody molekuł.

KWANTOWANIE ENERGII ROTACJI MOLEKUŁ

• Energia rotacji molekuly

)

I

J

(

I

2

J

I

2

1

E

2

2

R

ω

=

=

ω

=

3/2 R

5/2 R

7/2 R

H

2

GAZ

10

∼50

∼200

∼2000

5000

30

20

10

C

v

[J/(mol

.

K)]

T

[K]

DOŚWIADCZALNA ZALEśNOŚĆ C

v

OD TEMPERATURY DLA H

2

10

I – moment bezwładności molekuły ; J- moment pędu (kręt)

ω – prędkość kątowa rotacji

• Kwantowa wartość momentu pędu J

n

,...,

2

,

1

,

0

l

2

/

h

)

1

l

(

l

J

=

π

+

=

h – stała Plancka

l – liczba kwantowa rotacji

• Kwantowe wartości energii rotacji wynoszą

I

2

)

2

/

h

)(

1

l

(

l

E

2

R

π

+

=

• Odległość poziomów energetycznych (zmiana energii rotacji)

I

)

2

/

h

)(

1

l

(

)

l

(

E

)

1

l

(

E

E

2

R

π

+

=

−

+

=

∆

Układ rotacyjnych

poziomów energetycznych molekuły

TERMICZNE WZBUDZENIA STANÓW ROTACYJNYCH MOLEKUŁ

• Molekuła 2 – atomowa posiada i =2 stopnie swobody ruchu rotacyjnego

(oraz 3 stopnie swobody ruchu postępowego). Energia rotacji molekuły

wynosi

kT

kT

2

i

E

R

=

=

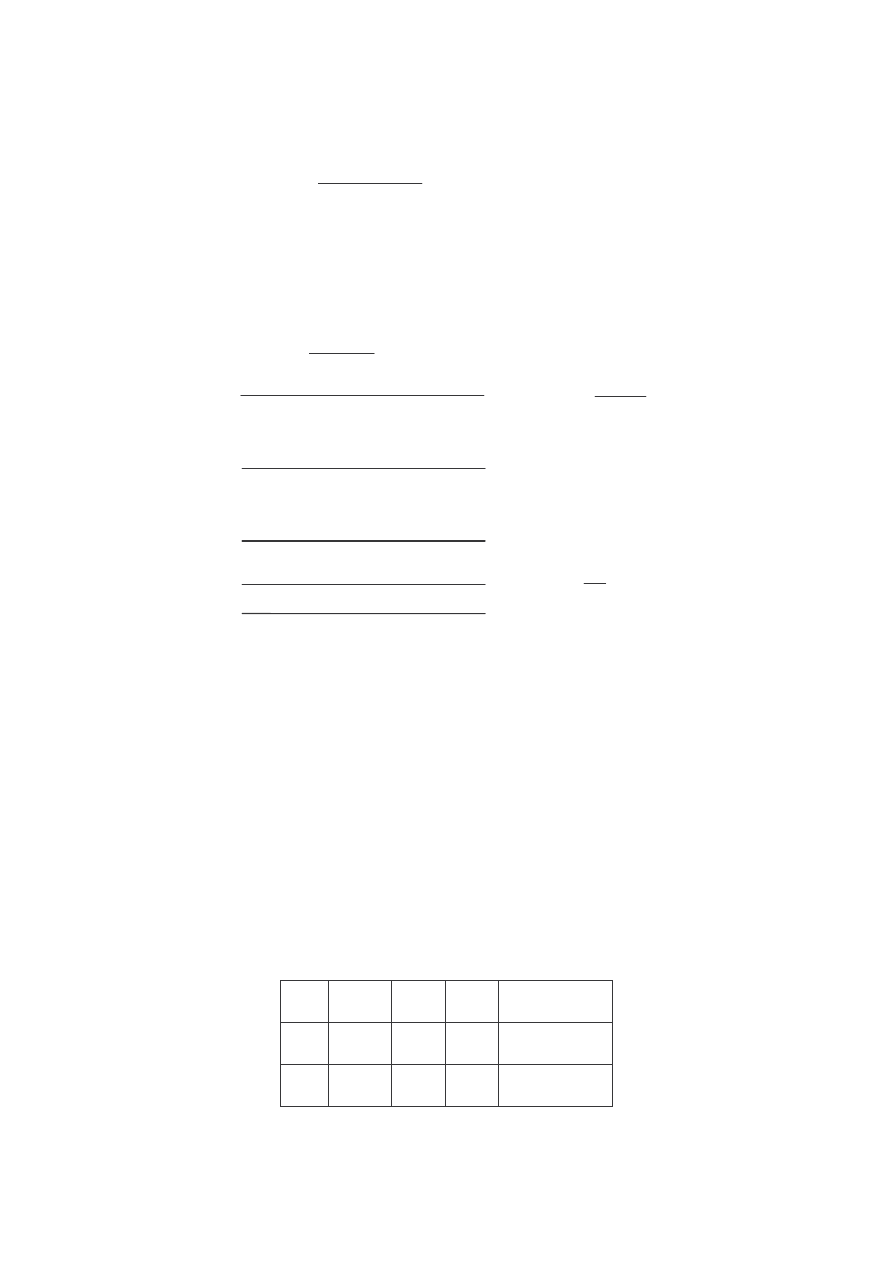
11

• Zmiana energii rotacji

I

)

2

/

h

)(

1

l

(

T

k

E

2

R

π

+

=

∆

=

∆

Przejście między stanami energetycznymi o l = 0 i l = 1 wymaga zmiany energii

cieplnej, tj. Zmiany temperatury gazu o

kI

)

2

/

h

(

T

2

π

=

∆

Wymagana zmiana temperatury zależy od różnicy wartości liczb kwantowych

oraz momentu bezwładności molekuły. Dla molekuł o różnych momentach

bezwładności kolejne zmiany stanu energetycznego wymagają dostarczenia

różnej ilości ciepła, tj. Różnej zmiany temperatury gazu.

H

2

HCl

O

2

I

4.72

26.8

194

[10

-45

kg*m

2

]

∆T

170

30

4

[K]

4

3

2

1

0

I

E

2

10 h

=

I

E

2

h

=

E

N

E

R

G

I

A

ROTACYJNE POZIOMY ENERGETYCZNE MOLEKUŁY

12

KWANTOWANIE ENERGII DRGAŃ (ENERGII OSCYLACJI)

• Kwantowa wartość energii drgań oscylatora harmonicznego prostego wynosi

ν

+

=

h

)

2

1

n

(

E

osc

n = 0, 1, 2, ... – liczba kwantowa drgań

h – stała Plancka

ν – częstość drgań

• Różnica energii kolejnych stanów oscylacyjnych

ν

=

+

ν

−

+

+

ν

=

∆

h

)

2

1

n

(

h

)

1

2

1

n

(

h

E

osc

Poziomy oscylacyjne są jednakowo odległe o wartość hν (Inaczej: różnica

energii kolejnych stanów ruchu drgającego oscylatora harmonicznego wynosi

zawsze hν).

Widmo stanów oscylacyjnych molekuły

n

3

2

1

0

E

7/2

.

h

ν

1/2

.

h

ν

13

TERMICZNE WZBUDZENIE STANÓW OSCYLACYJNYCH MOLEKUŁ

• Molekuła 2-atomowa posiada i = 3 stopnie swobody

K

1000

k

3

h

2

T

T

k

2

3

h

E

osc

≈

ν

=

∆

∆

=

ν

=

∆

RUCHY CIEPLNE MOLEKUŁ GAZU

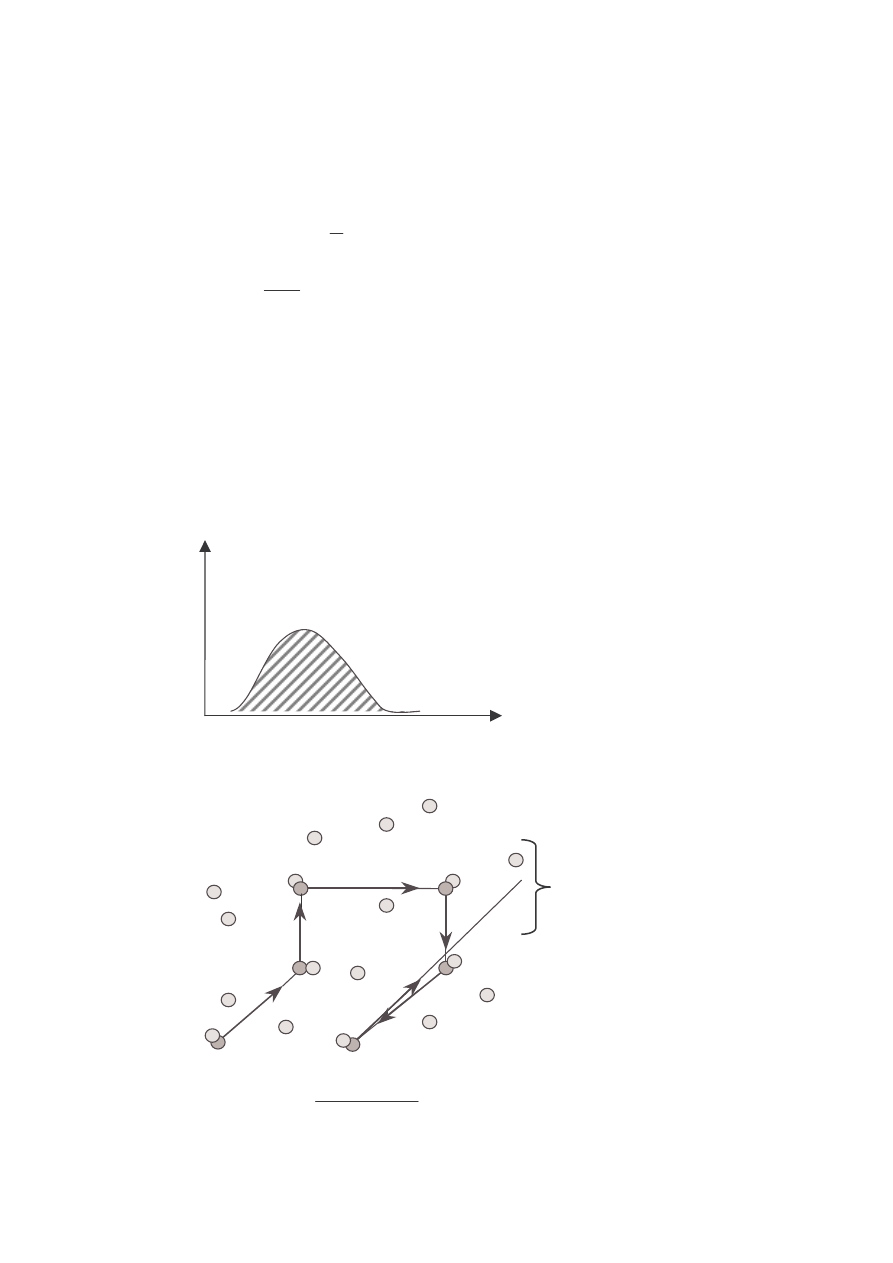
• Molekuły gazu wykonują chaotyczne (nieuporządkowane) ruchy cieplne

doznając nieustannych zderzeń

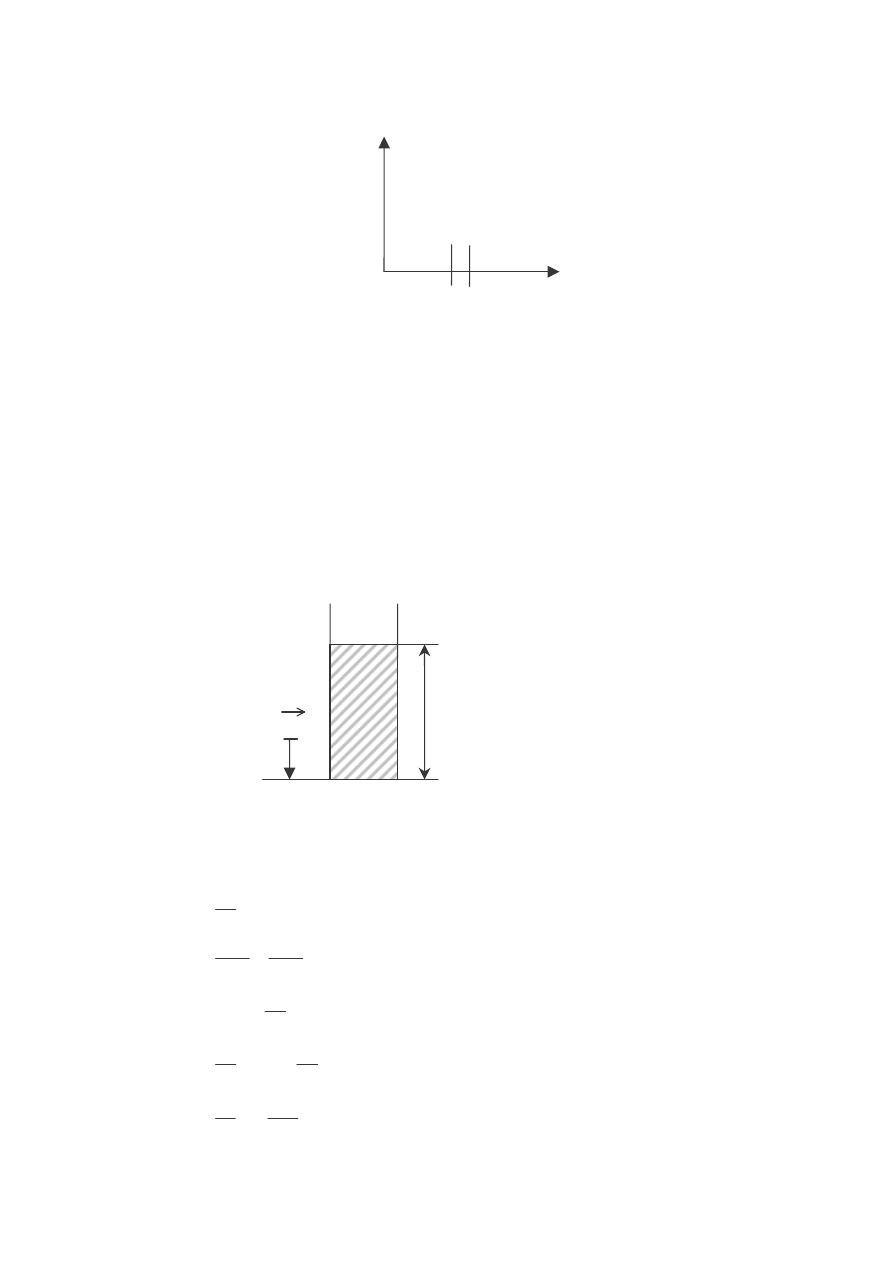
ŚREDNIA DROGA SWOBODNA MOLEKUŁ

• Średnia droga swobodna molekuły jest równa średniej odległości między

zderzeniami

k

...

l

l

l

l

3

2

1

+

+

+

>=

<

k – liczba zderzeń w pewnym przedziale czasu

n

i

v

i

l

1

l

2

l

3

KOLEJNE ZDERZENIA
WYBRANEJ MOLEKUŁY
GAZU

14

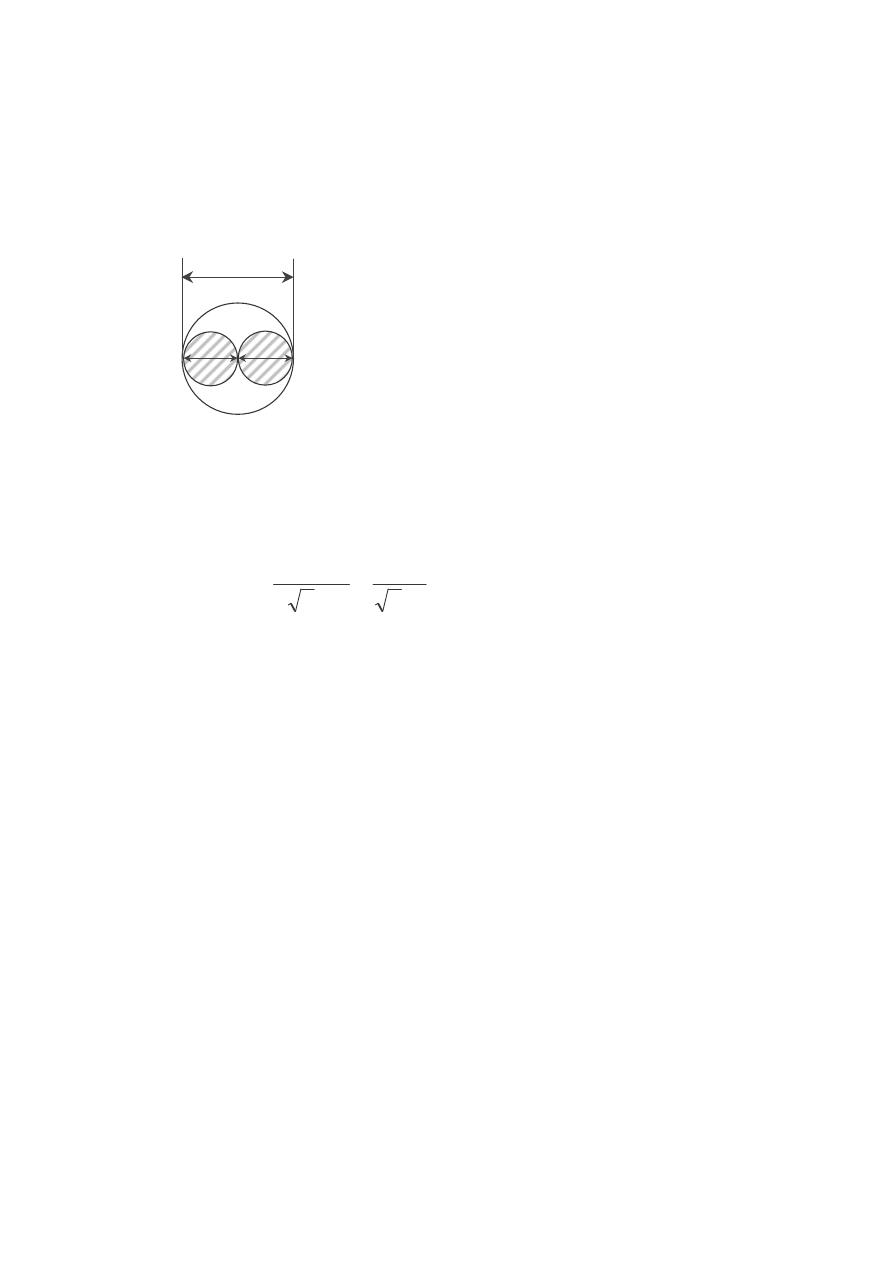
• Prawdopodobieństwo zderzenia dwóch molekuł określone jest poprzez tzw.

przekrój czynny na zderzenie σ. Molekuła w czasie zderzenia przedstawia

sobą tarczę o średnicy d równej średnicy molekuły

2

d

π

=

σ

• Z rozważań statystycznych dla dużej liczby zderzeń wynika wzór na średnią

drogę swobodną

σ

=

π

>=

<

n

2

1

nd

2

1

l

2

n – koncentracja molekuł

• Przykład: średnia droga swobodna molekuł powietrza (praktycznie azotu

cząsteczkowego N

2

)

T = 273 K, p = 1 atm, co odpowiada n = 3·10

19

cm

-3

d = 2·10

-10

m

typowy rozmiar prostych molekuł

<l> = 2·10

-7

m

• Przekrój czynny na zderzenie

σ = 1.2·10

-19

m

2

Jednostka przekroju czynnego

1 barn = 1 b = 10

-24

cm

2

= 10

-28

m

2

; σ (N

2

) = 10

9

b

• Częstość zderzeń (liczba zderzeń w jednostce czasu, np. w ciągu 1 sekundy)

d

d

2 d

MOLEKUŁA

„TARCZA” O ŚREDNICY

d

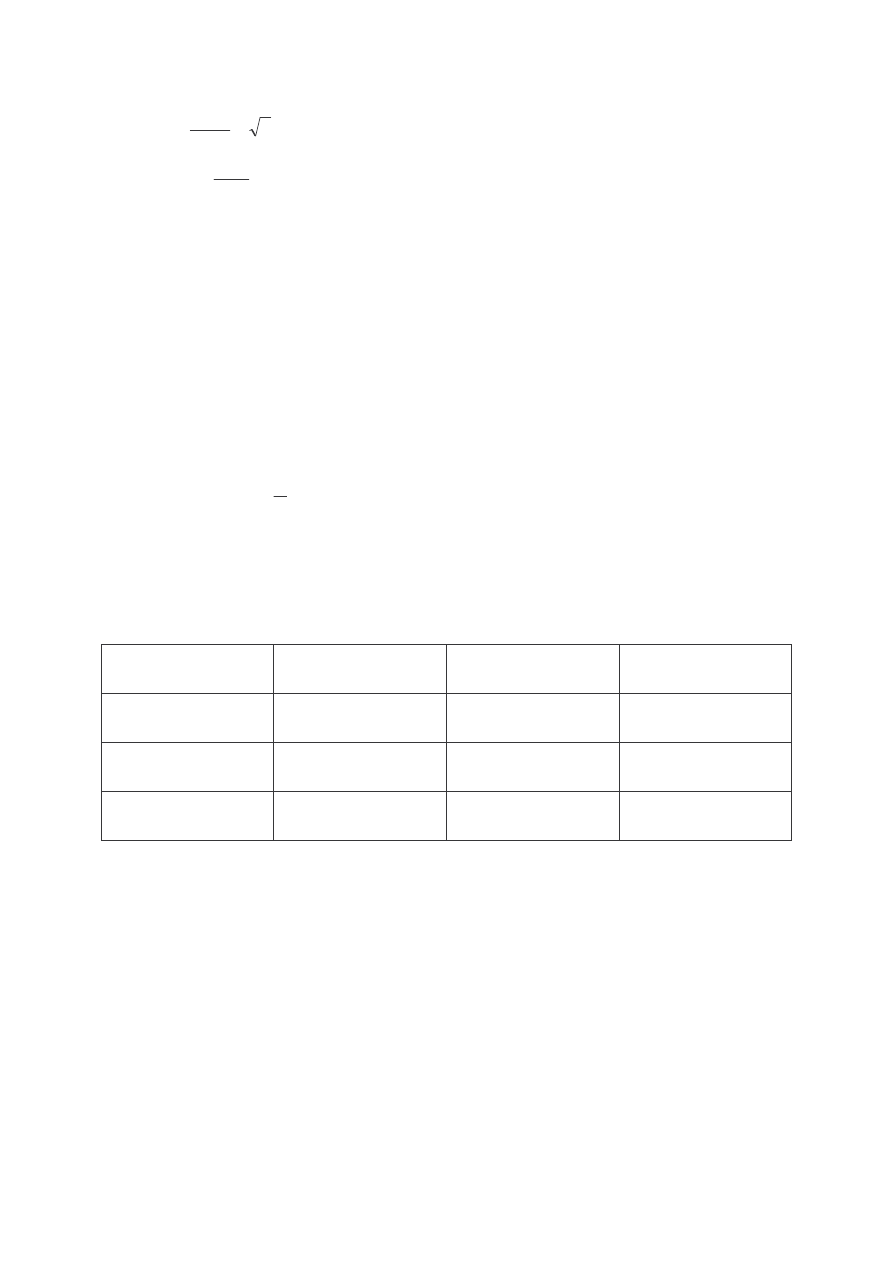
15

N

v

v

n

2

l

v

i

∑

>=

<

σ

=

>

<

>

<

=

ν

<v> - prędkość średnia (średnia arytmetyczna)

N - całkowita liczba molekuł

ν = 5·10

9

s

-1

(pięć miliardów zderzeń w ciągu 1 sekundy doznają molekuły

powietrza w warunkach normalnych)

• średni czas między zderzeniami

s

10

10

2

1

−

⋅

=

>=

<

ν

τ

ATMOSFERA ZIEMSKA

• Zmiany własności atmosfery ziemskiej z wysokością nad poziomem morza

h[m]

P[atm]

<l> [m]

N [cm

-3

]

0

1

10

-7

3·10

19

100

10

-6

1

3·10

13

300

10

-9

10

3·10

10

Duże h – pojęcie średniej drogi swobodnej traci sens. Działanie pola

grawitacyjnego powoduje, że molekuły poruszają się po torach

balistycznych i mogą uciekać z atmosfery

16

ZMIANA CIŚNIENIA Z WYSOKOŚCIĄ W ATMOSFERZE ZIEMSKIEJ

Poziom morza x = 0

• Ciśnienie hydrostatyczne gazu, cieczy o gęstości ρ i wysokości słupa h, g –

przyspieszenie ziemskie. Dla wysokości h = 0 (na poziomie morza) ciśnienie

wynosi p

0

, a gęstość powietrza ρ

0

dx

p

g

p

dp

p

p

g

dx

dp

p

p

p

)

x

(

p

)

x

(

g

dx

dp

gdx

)

x

(

)

x

(

dp

gh

p

0

0

0

0

0

0

0

0

ρ

−

=

ρ

−

=

ρ

=

ρ

=

ρ

ρ

ρ

−

=

ρ

−

=

ρ

=

p

x

dx

x = 0

POZIOM MORZA

ρρρρ

p

h

17

Powyższe równanie różniczkowe jest równaniem o zmiennych rozdzielonych,

które całkujemy w granicach od p

0

do p(x) i od 0 do x

1

1

4

2

5

0

3

0

2

0

0

0

0

0

0

0

0

0

0

0

0

116

.

0

10

16

.

1

/

10

01

.

1

20

/

2

.

1

/

81

.

9

exp

ln

0

−

−

−

−

=

⋅

=

⋅

=

=

=

=

≡

=













−

=

−

=

−

=

∫

∫

km

m

m

N

p

C

t

m

kg

s

m

g

p

g

e

p

x

p

g

p

p

x

p

g

p

p

p

g

p

dp

o

x

x

p

p

α

ρ

ρ

α

ρ

ρ

ρ

α

GŁĘBOKOŚĆ [km]

WYSOKOŚĆ [km]

5 10 15 20 25 30

15 10 5

1,0

0,5

100

500

p [atm]

POZIOM

MORZA

p (x) =

ρρρρgx

p (x) = p

o

e

-dx

WZÓR BAROMETRYCZNY

UWZGLĘDNIA ZMIANY g i T z WYSOKOŚCIĄ

dx

o

e

p

g

dx

dp

−

⋅

=

⋅

−

=

α

ρ

x

g

p

const

g

dx

dp

⋅

⋅

=

=

⋅

=

ρ

ρ

18

ROZKŁAD PRĘDKOSCI MOLEKUŁ W GAZIE

FUNKCJA ROZKŁADU PRĘDKOŚCI

• Funkcja rozkładu prędkości pozwala określić ile molekuł posiada prędkości

zawarte w przedziale (v, v+dv)

• Funkcja rozkładu oznacza prawdopodobieństwo tego, że w układzie

złożonym z bardzo dużej liczby molekuł znajdziemy molekułę o prędkości z

przedziału (v, v+dv)

• Funkcja rozkładu pozwala wyznaczać wartości średnie, np. <v>, <v

2

>

• Postać funkcji rozkładu jest określany na gruncie fizyki statystycznej

ROZKŁAD MAXWELLA

• Gaz składa się z cząsteczek o różnych prędkościach w danej temperaturze i

danym ciśnieniu. Stan taki jest spowodowany nieustającymi zderzeniami

molekuł i przekazem pędu.

• Najbardziej prawdopodobny rozkład prędkości wielkiej liczby cząstek

• Funkcja rozkładu Maxwella ma postać

kT

2

mv

2

2

3

2

e

v

kT

2

m

N

4

)

v

(

N

−













π

π

=

N – całkowita liczba cząsteczek w próbce gazu

k – stała Boltzmanna

T – temperatura gazu

19

m – masa pojedynczej cząsteczki

N(v)dv – liczba cząsteczek w próbce gazu o prędkościach z przedziału

(v, v+dv)

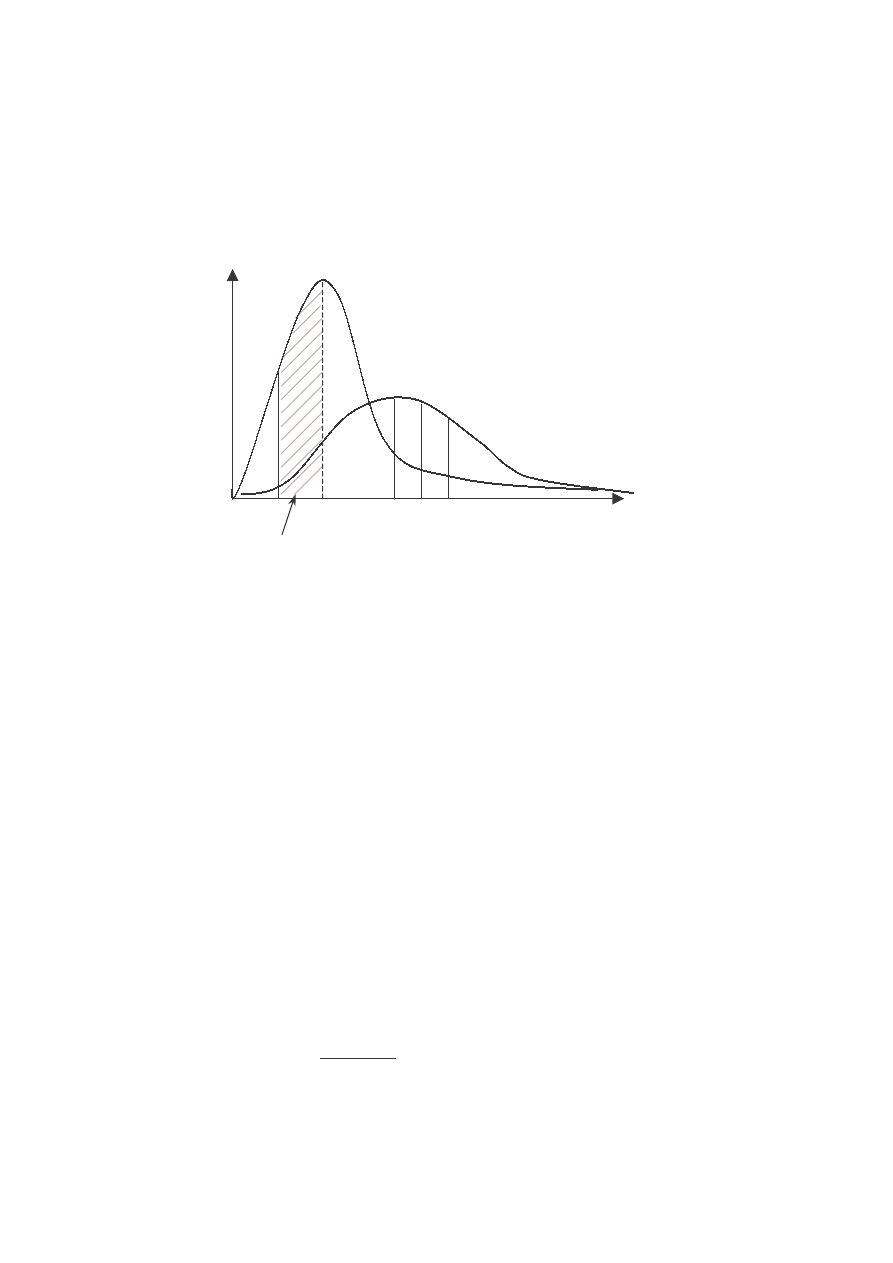
Kształt funkcji Maxwella dla dwóch różnych temperatur gazu T

1

< T

2

.

N(v ) oznacza liczbę cząsteczek przypadających na jednostkowy przedział

prędkości.

• Pole powierzchni pod krzywą jest równe całkowitej liczbie cząsteczek

∫

=

∞

0

dv

)

v

(

N

N

• Funkcja rozkładu prędkości pozwala wyznaczyć wartości średnie prędkości

Prędkość średnia (arytmetyczna)

N

vdv

)

v

(

N

v

0

∫

>=

<

∞

T

2

N(v)

N(v)dv

v

T

1

v

p

<v> v

kw

20

Prędkość średnią kwadratową

N

dv

v

)

v

(

N

v

0

2

2

∫

=

>

<

∞

oraz prędkość najbardziej prawdopodobną v

p

, która oznacza położenie

maksimum funkcji rozkładu na osi prędkości

• Relacje liczbowe między poszczególnymi prędkościami

m

kT

m

kT

v

59

.

1

8

=

>=

<

π

,

m

kT

v

73

.

1

2

=

>

<

,

m

kT

m

kT

v

p

41

.

1

2

=

=

v

p

< <v> <

>

<

2

v

inaczej

(v

p

< <

v

> <

>

<

2

v

)

>

≡<

>

≡<

l

v

v

λ

• Im mniejsza masa, tym większa liczba molekuł o dużych prędkościach w

danej temperaturze, np.:

H

2

, N

2

, O

2

w górnych warstwach atmosfery

Ucieka łatwiej z górnych warstw niż O

2

i N

2

21

n

0

z

dz

dn

j

D

= grad n

z

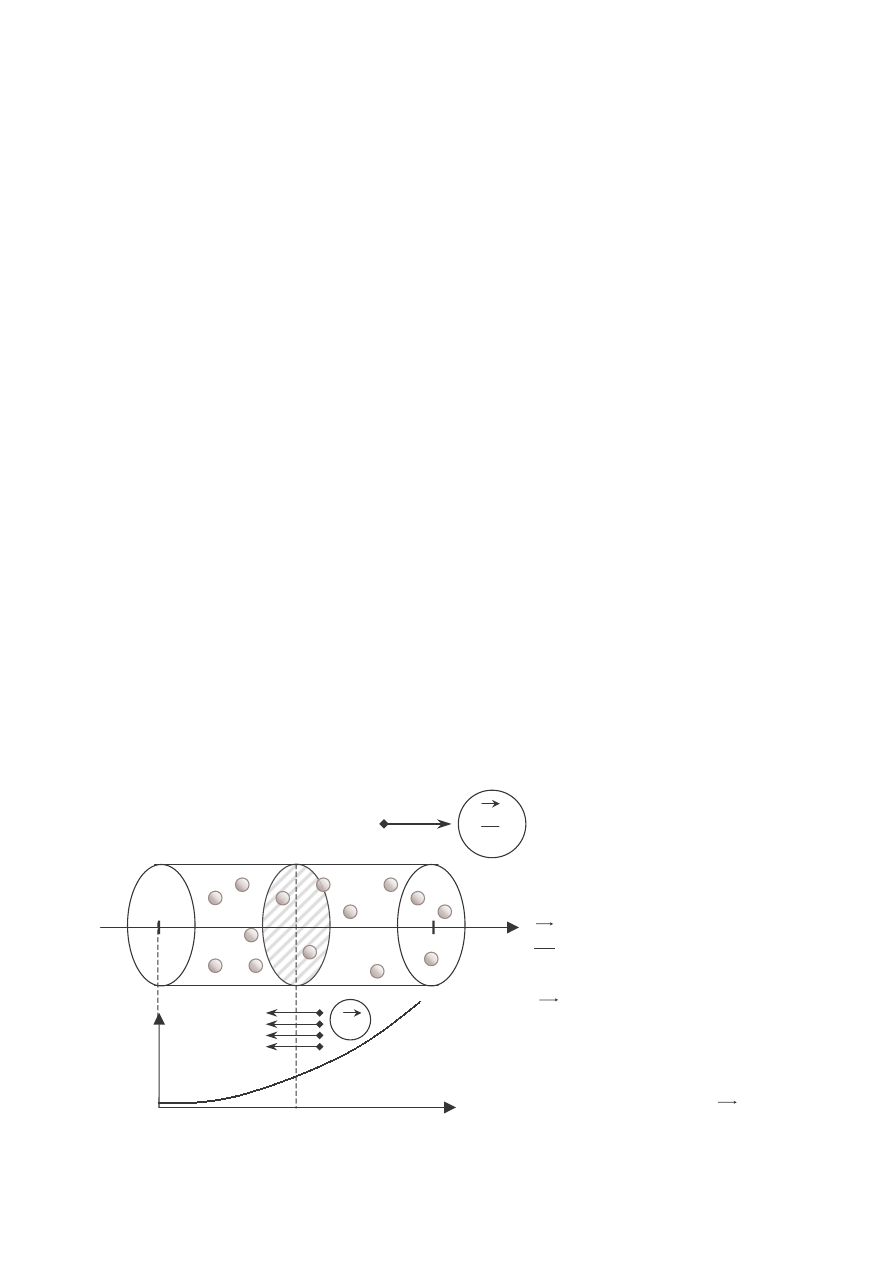
ZJAWISKA TRANSPORTU W GAZACH

- DYFUZJA

- TRANSPORT MASY

- PRZEWODNICTWO CIEPLNE

- TRANSPORT ENERGII

- LEPKOŚĆ

- TRANSPORT PĘDU

DYFUZJA

• Samorzutnie przebiegający proces wyrównywania koncentracji molekuł

na skutek ich ruchu cieplnego

• Układ (gaz) nie jest w stanie równowagi, ale do niej dąży

• (może być TERMODYFUZJA = przemieszczanie się molekuł

spowodowane różnicą temperatur objętości gazu)

Możliwe zjawiska dyfuzyjne:

- autodyfuzja (samodyfuzja)

- dyfuzja wzajemna

- termodyfuzja

n - koncentracja molekuł

dz

dn

- gradient koncentracji

D

j

- gęstość prądu dyfuzji

(liczba molekuł na jednostkę

powierzchni prostopadłej do

D

j

na sekundę)

22

• |

D

j

|=

dz

dn

D

j

D

−

=

równanie dyfuzji

v

D

⋅

=

λ

3

1

współczynnik dyfuzji D~10

-5

2

s

m

, w gazach

(model gazu doskonałego)

(

λ

,

v

- średnia droga swobodna, średnia prędkość)

• równanie dyfuzji inaczej

dz

d

D

mn

dz

d

D

j

M

ρ

−

=

−

=

)

(

gęstość strumienia masy

(m = masa molekuły)

• współczynnik dyfuzji

m

kT

p

kT

D

π

σ

8

2

3

1

⋅

⋅

⋅

=

T = const, D~

p

1

p = const, D~

2

3

T

np.: H

2

D=6.6·10

-5

m

2

/s

O

2

D=0.93·10

-5

m

2

/s

dla danego gazu

współczynnik samodyfuzji

w warunkach normalnych

23

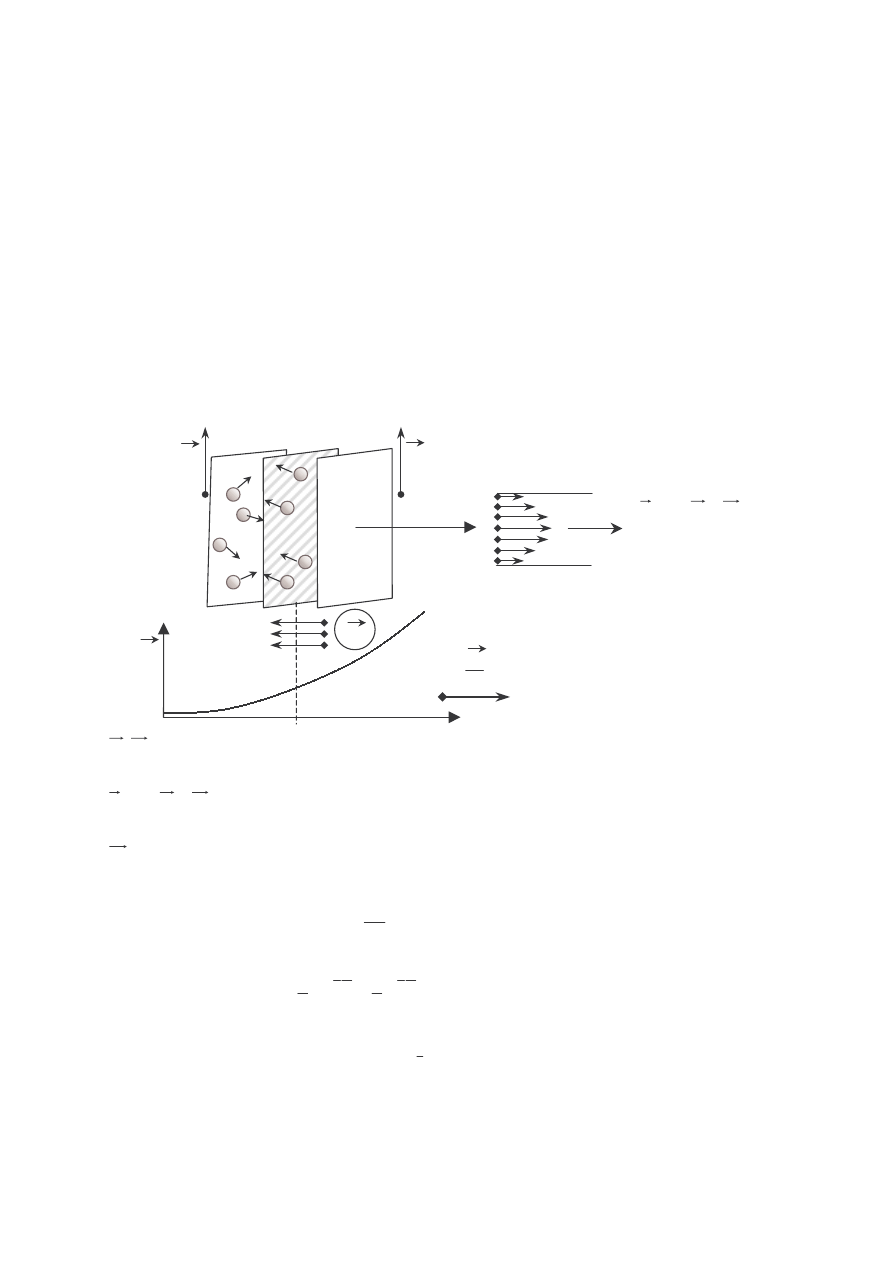
PRZEWODNICTWO CIEPLNE

• ρ=const, zmienne T w objętości gazu

T=T(z)

dZ

dT

j

Q

κ

−

=

[j

Q

]=J/(m

2

s), [κ]=W/(mK)

2

3

1

f

k

v

n

⋅

⋅

⋅

⋅

=

λ

κ

k - stała Boltzmana, f - liczba stopni swobody

V

c

v

⋅

⋅

=

λ

κ

3

1

)

~

(

2

1

T

v

,

2

1

~ T

κ

κ - nie zależy od n a więc i p

j

Q

z

T

0

z

dz

dT

= grad T;

dz

dT

> 0

równanie transportu ciepła (energii)

= gęstość prądu energii

współczynnik przewodnictwa cieplnego

(model gazu doskonałego)

c

V

- odniesione do jednostki objętości

24

np.:

H

2

κ=16.8·10

-2

W/(m/K)

O

2

κ=2.4·10

-2

W/(m/K)

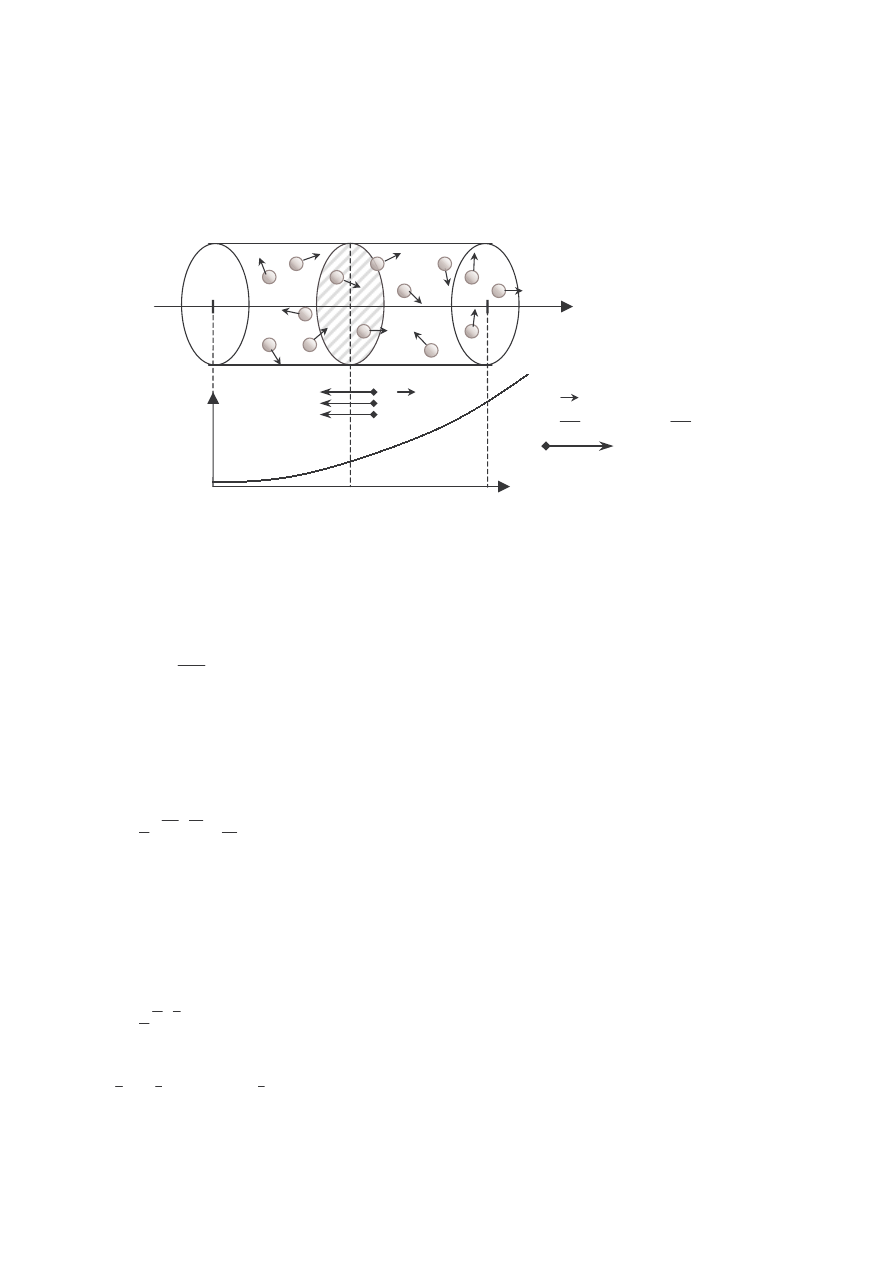
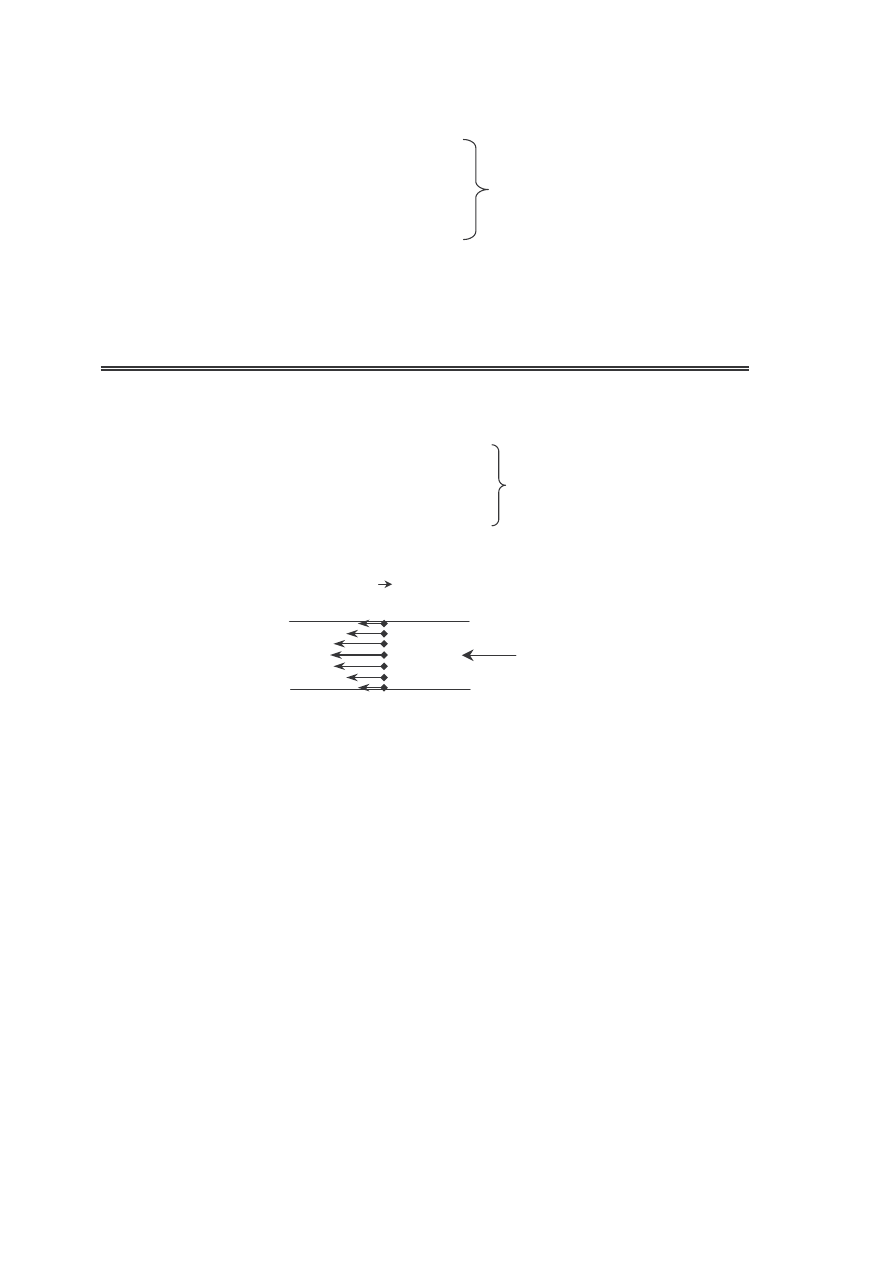
TRANSPORT PĘDU (LEPKOŚĆ, TARCIE WEWNĘTRZNE)

Przekaz pędu między warstwami gazu o różnej prędkości

(w ruchu uporządkowanym)

)

(

2

1

u

u

m

p

−

=

2

1

, u

u

- prędkości warstw

)

(

2

1

u

u

m

p

−

=

- zmiana pędu molekuły

p

j

- gęstość strumienia pędu ( pęd/(m

2

s) )

dz

du

j

p

η

−

=

λ

ρ

λ

η

v

v

nm

3

1

3

1

=

=

współczynnik lepkości

2

1

~ T

η

; η- nie zależy od p

u

0

z

j

p

dz

du

= grad u

z

u

1

u

2

równanie lepkości

[η]=kg/(ms)

25

np

.:

H

2

η=0.84·10

-5

kg/(ms)

O

2

η=1.40·10

-5

kg/(ms)

UWAGA:

Pomiar współczynnika lepkości cieczy

Pomiar współczynnika lepkości powietrza

Ćwiczenia

na pracowni fizycznej

v

GAZ, CIECZ

w warunkach
normalnych