NAUCZANIE FIZYKI

O trajektoriach chaotycznych

∗

Hieronim Lalek∗∗, Andrzej Bożek∗∗

Liceum Ogólnokształcące w Rymanowie

On chaotic trajectories

Abstract: A computer program for simulations of deterministic chaos in a simple ballistic experiment is
presented.

1. Wstęp

Do modnych zagadnień w fizyce współczesnej

należy chaos. Tematyka ta wiąże się z fundamen-
talnymi problemami fizyki klasycznej i kwanto-
wej, lecz jej znajomość przydaje się też w ży-
ciu codziennym. Chaos w potocznym rozumie-
niu oznacza zamieszanie, bezład. Bywa on właści-
wością procesów fizycznych, ekonomicznych, spo-
łecznych, medycznych itd. Z pobłażliwością na-
leży przyjmować pewność siebie, z jaką prezente-
rzy radiowi i telewizyjni przedstawiają długoter-
minowe prognozy pogody. Można się nieraz prze-
konać, że ich trafność jest chaotyczna, co wynika
z natury problemu. Ponieważ chaos może także
być cechą prostych sytuacji, już w szkole średniej
można przedstawić niektóre zagadnienia tej pro-
blematyki.

2. Model fizyczny

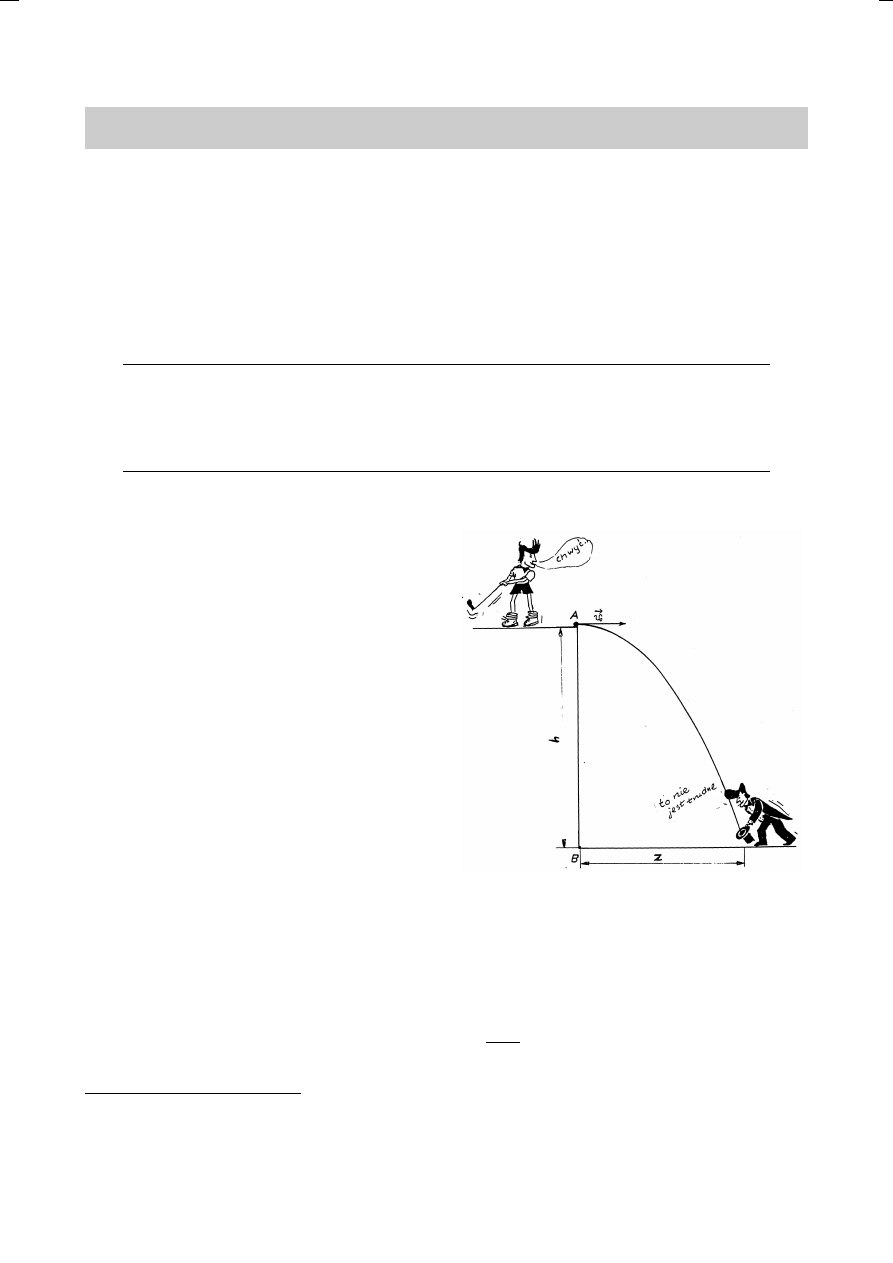
Rozważmy dwie sytuacje przedstawione na

rys. 1 i 2. W obu przypadkach zadaniem czło-
wieka znajdującego się na dole jest przewidzenie
toru kulek, które wystrzeliwuje poziomo z pręd-
kością v

0

człowiek stojący u góry.

Rys. 1.

W pierwszym przypadku, przy zadanej pręd-

kości v

0

i określonej geometrii układu człowiek

stojący u dołu nie ma większych problemów
z wyłapaniem kulki. Czeka po prostu z kapelu-
szem w pobliżu miejsca, gdzie zasięg rzutu z =
v

0

p

2h/g, gdzie h jest różnicą wysokości, a g

– przyspieszeniem ziemskim. Niewielkie różnice

∗

Rozszerzona wersja artykułu, opublikowanego w zesz. 5/2001 (Postępy Fizyki 52, 255 (2001)).

∗∗

Jeden z autorów (H.L.) jest nauczycielem fizyki, a drugi (A.B.) tegorocznym absolwentem (trzykrotnym finalistą

Olimpiady Fizycznej) Liceum Ogólnokształcącego w Rymanowie (przyp. Red.).

POSTĘPY FIZYKI

TOM 52

ROK 2001

MATERIAŁY DODATKOWE

[1]

H. Lalek, A. Bożek – O trajektoriach chaotycznych

prędkości nie mają dużego wpływu na miejsce
upadku kulki. W każdym razie ustawienie kape-
lusza może być skorygowane w trakcie lotu kulki.

W drugim przypadku sytuacja znacznie się

komplikuje. Na walcowej ścianie o promieniu
r = h, której oś dla uproszczenia rozważań niech
będzie prostopadła do płaszczyzny lotu, wyróż-
niamy punkty C, Y, R i K. Zderzenia kulki ze ścia-
nami traktujemy jako doskonale sprężyste, a jej
masę uważamy za dużo mniejszą od masy ściany.

Rys. 2.

O osobliwych cechach wyróżnionych punktów

decydują czynniki opisane dalej. Punkt C jest naj-
niższym punktem ściany. Przez punkt Y przecho-
dzi tor, którego pierwszy odcinek (między punk-
tem wystrzelenia a punktem pierwszego odbicia)
przy minimalnej prędkości v

0

leży w całości nad

prostą AO. Przez punkt R przechodzi trajektoria,
która ma tę właściwość, że styczna do paraboli
w tym punkcie pokrywa się z kierunkiem promie-
nia OR. Dzięki temu kulka trafiająca w ten punkt
po odbiciu wraca do miejsca wystrzelenia. Następ-
nym wyróżnionym punktem jest K. Kulka trafia-
jąca w ten punkt po odbiciu leci pionowo w górę.
Podobnie jak dla kulki odbitej w punkcie R, jej
ruch jest odwracalny, ale w bardziej skompliko-
wany sposób.

Teraz proponujemy czytelnikom orientacyjne

wyznaczenie trajektorii dla różnych wartości v

0

.

Wyróżnienie punktów ułatwia przeprowadzenie
takiej dyskusji. Jeden z wyników przewidywań
przedstawia rys. 3.

Oczywiście takie przewidywania, aczkolwiek

bardzo pouczające, mogą wpuścić czytelników
w przysłowiowe maliny. Takie sytuacje wciąż nam
się zdarzały, co skłoniło nas do rozstrzygania po-
wstałych problemów za pomocą techniki kompu-
terowej. Przyjęliśmy, że ponad wszelką wątpliwość
mamy do czynienia z chaosem deterministycznym.

Rys. 3.

3. Wprowadzenie do metody numerycznej

analizy problemu

Istota opisu matematycznego chaosu deter-

ministycznego nie jest zagadnieniem szczególnie
złożonym. W większości przypadków zachowanie
układów chaotycznych podlega klasycznym pra-
wom mechaniki czy termodynamiki, wyrażonym
równaniami znanymi w fizyce od kilku stuleci.
Problem w tym, że dla parametrów odpowiada-
jących stanom chaotycznym równania te przyj-
mują postać bardzo trudną lub niemożliwą do
analitycznej obróbki matematycznej. Chodzi tu
przede wszystkim o nieliniowe równania różnicz-
kowe, ale można to również odnieść do naszego
zjawiska (wielokrotnych odbić punktu material-
nego między prostą a okręgiem), gdzie zacho-
dzi potrzeba rozwiązywania sporej ilości nielinio-
wych równań algebraicznych z dość dużą dokład-
nością, wyznaczoną rozdzielczością pomiarów pa-
rametrów układu, zależną od technicznych moż-
liwości przyrządów. Dopiero bardzo precyzyjne
obliczenia, przewyższające dokładnością rozdziel-
czość pomiarów, pozwalają udowodnić, że nie-

[2]

POSTĘPY FIZYKI

TOM 52

ROK 2001

MATERIAŁY DODATKOWE

H. Lalek, A. Bożek – O trajektoriach chaotycznych

wykrywalne zmiany parametrów początkowych,
prowadzą do nieprzewidywalnych zmian w ewo-
lucji układu – co jest istotą chaosu determini-
stycznego. Realizacja wspomnianych obliczeń wy-
maga przeprowadzenia ogromnej liczby elemen-
tarnych działań, co jest w zasadzie niemożliwe
(zwłaszcza na większą skalę, dla różnych parame-
trów układu itp.) nawet dla człowieka dysponu-
jącego nieograniczonym zapasem papieru i dłu-
gopisów oraz kilkudziesięcioma latami wolnego
czasu. Dlatego też badania nad chaosem determi-
nistycznym rozwinęły się dopiero stosunkowo nie-
dawno, po pojawieniu się komputerów. Urządze-
nia te umożliwiają bardzo szybkie wykonywanie
algorytmów numerycznych, złożonych z wielkiej
liczby prostych działań arytmetycznych. W ten
sposób można w krótkim czasie zebrać mate-
riał badawczy, nieosiągalny dawniej innymi spo-
sobami.

Powyższe argumenty wskazują, że symulacja

komputerowa jest obecnie najlepszą metodą obra-
zowania zachowań chaotycznych. Z tego względu
napisaliśmy program komputerowy symulujący
zachowanie analizowanego układu. Wprowadza
się do niego dane określające parametry geo-
metryczne ścian odbijających kulkę (traktowaną
jako punkt materialny) oraz składowe prędko-
ści początkowej, przy czym składowa pozioma
może być wybierana ze znaczną dokładnością.
Jako dane wyjściowe otrzymujemy tor punktu
materialnego, odpowiadający założonym parame-
trom. Program uwzględnia odpowiednie skalowa-
nie odległości i normalną wartość przyspieszenia
ziemskiego (g = 9,81 m/s

2

). Zachęcamy Czy-

telników do skorzystania z możliwości skopiowa-
nia (za pomocą ftp, np. bezpośrednio z przeglą-
darki WWW) pliku wykonywalnego Chaos.exe
oraz kodu źródłowego programu i przeprowadze-
nia eksperymentów numerycznych we własnym
zakresie na domowym komputerze.

4. Obsługa programu

Po uruchomieniu programu Chaos.exe na

ekranie ukazuje się kontur przeszkody o domyśl-
nych wymiarach, a nad nim dwa paski z ele-
mentami obsługi. Najważniejszy jest element słu-
żący do zmiany składowej poziomej prędkości po-
czątkowej. Przyciski umieszczone pod każdą cy-
frą umożliwiają dowolną zmianę każdej z pozycji

dziesiętnych, przy czym wartość musi mieścić się
w zakresie 0,010 000–9,999 999 m/s.

Bardziej na prawo znajduje się przycisk Ry-

suj tor, którego naciśnięcie wyzwala obliczenie
i narysowanie trajektorii dla ustawionych para-
metrów. Dodatkowo, ustawienie znacznika Rysuj
po zmianie powoduje automatyczną aktualizację
toru po każdej zmianie v

0

, co jest bardzo prak-

tyczne, gdyż ułatwia obserwację zmian zachowa-
nia układu przy zmianach v

0

.

Włączenie przycisku Podwójna grubość po-

woduje pogrubienie linii odwzorowującej tor, co
często zwiększa przejrzystość rysunku, ale przy-
czynia się także do spowolnienia rysowania.

Liczba odcinków stanowiących całość toru

(od punktu początkowego do ucieczki poza prze-
szkodę) wyświetlana jest na zielono obok ety-
kiety Liczba wszystkich odcinków toru. Pro-
gram umożliwia odwzorowanie maksymalnie 999
odcinków toru. Jeżeli taka ich liczba zostanie osią-
gnięta, to liczba 999 jest wyświetlana na czer-
wono, przestrzegając, że dalszy przebieg ruchu nie
jest symulowany. Niezależnie od tego, ostatni ob-
liczony odcinek trajektorii znaczony jest dla wy-
różnienia kolorem niebieskim.

W polu Liczba rysowanych odcinków toru

można zadeklarować dowolną liczbę nie większą
od maksymalnej (999); tylko taka liczba odcin-
ków będzie pokazywana graficznie (choć oblicze-
nia przeprowadzane są zawsze do 999), co po-
zwala w wielu wypadkach na poprawę przejrzy-
stości i przyspieszenie rysowania.

Pole umieszczone w prawym górnym rogu

służy do wyróżniania wybranych odcinków toru.
Wpisanie w okienku Wyróżnij odcinek toru nr
pewnej liczby i naciśnięcie OK spowoduje naryso-
wanie (przerysowanie) na kolor czerwony odcinka
trajektorii o podanym numerze (jeżeli podana
zostanie liczba większa niż Liczba wszystkich
odcinków toru, to jej wartość zostanie zmieniona
na numer ostatniego odcinka trajektorii). Po na-
ciśnięciu, etykieta przycisku zmienia się z OK na +;
od tej pory kolejne naciśnięcia będą zwiększać
o jeden wartość liczby wpisanej w polu i wyróżniać
kolejne odcinki – taka pseudoanimacja może po-
zwolić dokładniej zanalizować przebieg kolejnych
odbić.

Włączenie opcji Za każdym razem powoduje,

że odcinek o wpisanym numerze będzie wyróż-
niany po każdej zmianie parametrów ruchu, co

POSTĘPY FIZYKI

TOM 52

ROK 2001

MATERIAŁY DODATKOWE

[3]

H. Lalek, A. Bożek – O trajektoriach chaotycznych

umożliwia badanie zachowania się wybranego od-
cinka w zależności od zmian parametrów (w szcze-
gólności v

0

).

Wszystkie potrzebne wnioski można uzyskać

wykorzystując domyślną (wprowadzaną po uru-
chomieniu programu) wartość v

y

i parametrów

geometrycznych przeszkody. Jednak dla zwiększe-
nia możliwości programu i jego uelastycznienia
istnieje opcja zmiany tych parametrów w pew-
nych zakresach. Służy do tego dolny pasek narzę-
dziowy.

Znaczenia i dozwolone przedziały wartości

w poszczególnych polach są następujące:

v

y

– składowa pionowa wektora prędkości po-

czątkowej – zakres: od −9,999 do 9,9999 m/s;

h – wysokość pionowej ściany – zakres: od

0,5000 do 2,0000 m;

d – odległość BC ściany walcowej od ściany

pionowej (u ich podnóża) – zakres: od 0,5000 do
1,5000 m;

r – promień walca – zakres: od 0,5000 do

1,5000 m.

Podczas modyfikacji tych wielkości, aż do ich

akceptacji przyciskiem Zastosuj, blokowane jest
rysowanie toru.

Obsługa programu ma charakter naturalny

i nie powinna nastręczyć żadnych problemów.

5. Opis użytego algorytmu

Analiza przebiegu ruchu polega w rozwa-

żanym modelu na odpowiednim wyznaczaniu
kształtów trajektorii, punktów odbicia i nowych
wektorów prędkości po odbiciu; wszystko to musi
odbywać się zgodnie z prawami fizyki. W uję-
ciu matematycznym zagadnienie sprowadza się do
wielokrotnie powtarzanych serii działań; na każdą
serię składa się:

a) wyznaczenie równania paraboli na podsta-

wie danych – składowych położenia i prędkości
początkowej;

b) wyznaczenie punktów przecięcia paraboli

z konturem przeszkody (tzn. ściany walcowej i pio-
nowej) i decyzja, który z nich jest punktem odbi-
cia;

c) przeliczenie składowych wektora prędkości

w punkcie odbicia zgodnie z prawem odbicia sprę-
żystego;

d) przepisanie nowo wyznaczonych parame-

trów na miejsce parametrów początkowych.

Skomplikowany matematycznie kształt ściany

sprawia, że realizacja czynności z podpunktu b)
jest sprawą złożoną, stanowiącą sedno symulacji.
Ta faza obliczeń jest wykonywana wieloetapowo,
z zastosowaniem działań warunkowych, a „ ją-
drem”, które nimi rozporządza, jest procedura
router.

Do obliczeń niezbędne są procedury rozwią-

zujące równania stopnia drugiego (przecięcie pa-
raboli z prostą) oraz trzeciego i czwartego (prze-
cięcie paraboli z okręgiem). Procedury te zre-
alizowano w oparciu o tzw. wzory pierwiastni-
kowe, rezygnując z metod numerycznych, dają-
cych wartości przybliżone (poza tym procedury
numeryczne traciły zbieżność dla niektórych ze-
stawów parametrów). Procedury starano się uło-
żyć w ten sposób, aby wyeliminować negatywny
wpływ nieoznaczoności liczbowych, mogących wy-
stąpić dla niektórych wartości parametrów.

Przebieg

nadrzędnej

procedury

liczącej

(router) przedstawia się w zarysie następująco:

1) jeżeli ruch odbywa się od strony lewej

do prawej (dodatnia wartość poziomej składowej
prędkości) i ostatnio nastąpiło odbicie od ściany
pionowej lub „podłoża”, to następuje sprawdze-
nie, czy parabola przetnie się z podłożem przed
podnóżem ściany walcowej (równanie 2. stopnia):

a) jeśli tak, to następuje podjęcie decyzji,

który z punktów przecięcia jest punktem odbicia
(na podstawie kierunku ruchu), i przejście do na-
stępnej procedury (NEXT);

b) jeśli nie, to następuje sprawdzenie, czy

parabola przetnie się z okręgiem (równanie 4.
stopnia):

i) jeśli tak, to następuje podjęcie decy-

zji, który z dwóch punktów przecięcia jest punk-
tem odbicia (na podstawie kierunku ruchu i szcze-
gółów geometrii układu), i przejście do następnej
procedury (NEXT);

ii) jeśli nie, to znaczy, że trajektoria

ucieka z układu odbijającego, co oznacza koniec
działania algorytmu (END);

2) jeżeli ruch odbywa się od strony lewej do

prawej i ostatnio nastąpiło odbicie od ściany wal-
cowej, to następuje sprawdzenie, czy tor przetnie
się ponownie z konturem tej ściany (w tym przy-
padku mogą wystąpić cztery punkty przecięcia,
przy czym jeden – z poprzedniego odbicia – jest
znany, co umożliwia redukcję stopnia równania do
równania 3. stopnia);

[4]

POSTĘPY FIZYKI

TOM 52

ROK 2001

MATERIAŁY DODATKOWE

H. Lalek, A. Bożek – O trajektoriach chaotycznych

a) jeśli tak, to następuje podjęcie decyzji,

który z punktów przecięcia jest punktem odbicia
(na podstawie kierunku ruchu, danych z poprzed-
niego odbicia i szczegółów geometrii układu),
i przejście do następnej procedury (NEXT);

b) jeśli nie, to znaczy, że trajektoria ucieka

z układu odbijającego, co oznacza koniec działa-
nia algorytmu (END);

3) jeżeli ruch odbywa się od strony prawej do

lewej i ostatnio nastąpiło odbicie od ściany wal-
cowej, to następuje sprawdzenie, czy tor przetnie
się ponownie z konturem tej ściany (szczegóły jak
w p. 2);

a) jeśli tak, to następuje podjęcie decyzji,

który z punktów przecięcia jest punktem odbi-
cia (na podstawie kierunku ruchu, danych z po-
przedniego odbicia i szczegółów geometrii układu)
(NEXT);

b) jeśli nie, to następuje sprawdzenie, czy

parabola przetnie się z „podłożem” przed podnó-
żem ściany pionowej (równanie 2. stopnia):

i) jeśli tak, to następuje podjęcie decyzji,

który z punktów przecięcia jest punktem odbicia
(na podstawie kierunku ruchu) (NEXT);

ii) jeśli nie, to następuje sprawdzenie, czy

tor odbije się od ściany:

(1) jeśli tak, to następuje przeliczenie

parametrów odbicia (NEXT);

(2) jeśli nie, to znaczy, że punkt ucieka

z układu ponad ścianą (END);

4) jeżeli ruch odbywa się ze strony prawej

do lewej i ostatnio nastąpiło odbicie od „pod-
łoża” to następuje ciąg działań analogicznych jak
w p. 3b, czyli sprawdzenie, czy parabola przetnie
się z „podłożem” przed podnóżem ściany piono-
wej (równanie 2. stopnia):

a) jeśli tak, to następuje decyzja który

z punktów przecięcia jest punktem odbicia (na
podstawie kierunku ruchu) (NEXT);

b) jeśli nie, to następuje sprawdzenie, czy

tor odbije się od ściany:

i) jeśli tak, to następuje przeliczenie pa-

rametrów odbicia (NEXT);

ii) jeśli nie, to znaczy, że punkt ucieka

z układu ponad ścianą (END);

Po dojściu programu do linii oznaczonej ety-

kietą (NEXT), wywoływane są procedury, które
na podstawie dostępnych danych (współrzędnych
punktu odbicia i składowych prędkości w tym
punkcie oraz równania powierzchni odbijającej)

wyliczają składowe wektora prędkości po odbiciu.
W ten sposób zamyka się cykl repetycji i program
wraca do początku pętli. Dojście do linii ozna-
czonej etykietą END, które oznacza, że tor ucieka
z pułapki odbijającej, powoduje opuszczenie pętli
przeliczającej trajektorię.

Kod programu zawarty jest w dwóch modu-

łach: Unit1.pas i Unit2.pas. Pierwszy z nich jest
modułem głównym, zawierającym przeważającą
liczbę procedur. Drugi zawiera dodatki, odpowie-
dzialne za rozwiązywanie równań 3. i 4. stop-
nia. W module głównym w pierwszej kolejności
umieszczone są procedury obliczeniowe, a po nich
znajdują się procedury odpowiedzialne za wypro-
wadzanie grafiki i sterowanie elementami inter-
fejsu użytkownika.

Program został napisany i skompilowany przy

użyciu platformy Delphi 3. W celu zaznajomienia
się z jego szczegółami technicznymi odsyłamy do
kodu źródłowego.

6. Wnioski wynikające z symulacji

Symulacja komputerowa weryfikuje wysu-

nięte wcześniej przypuszczenia teoretyczne i po-
twierdza większość z nich. Na przykład, przy uży-
ciu programu bez trudu można znaleźć wartości
v

0

, dla których realizuje się postulowana odwra-

calność ruchu, co odpowiada odbiciu od punktów
umownie określonych jako R i K; co więcej, oka-
zuje się, że mogą istnieć także inne tory o analo-
gicznej właściwości (np. dla v

0

= 2,960 000 m/s

lub v

0

= 3,680 000 m/s). Ale nie to jest naj-

ważniejsze. Ograniczając liczbę rysowanych od-
cinków toru do dwóch lub trzech, możemy anali-
zować przebieg ruchu w zakresie odpowiadającym
uprzednim przewidywaniom, lecz już na podsta-
wie konkretnych, dokładnych obliczeń, przy od-
powiednim wymiarowaniu i dla „prawdziwego”
pola grawitacyjnego. To jednak również nie jest
źródłem żadnych nowych spostrzeżeń i niczego
dodatkowego nie udowadnia. Sednem symulacji
jest to, iż potrafi ona przewidzieć ruch w za-
kresie tysiąca odbić – człowiek nigdy nie doko-
nałby tego „na piechotę”. Dopiero ta możliwość
pozwala na potwierdzenie chaotycznych właści-
wości ruchu, które w rozważaniach teoretycznych
pozostawały postulatem. Program ukazuje chaos
deterministyczny w rozważanym modelu poprzez
dwie jego specyficzne cechy:

POSTĘPY FIZYKI

TOM 52

ROK 2001

MATERIAŁY DODATKOWE

[5]

H. Lalek, A. Bożek – O trajektoriach chaotycznych

1. Zmiana wartości v

0

o 10

−6

m/s (co wy-

daje się rzędem wielkości niewykrywalnym i nie
dającym się kontrolować) może powodować dia-
metralne zmiany w przebiegu ruchu, które łatwo
dostrzec poprzez obraz rysowanego toru; jest to
istota chaosu, jego fundamentalna, charaktery-
styczna właściwość.

2. Zachowania chaotyczne ujawniają się tylko

dla pewnych przedziałów parametrów. W naszym
modelu są one wywołane wielokrotnymi odbiciami
od zakrzywionej powierzchni, a wielokrotnym od-
biciom sprzyja długie przebywanie w studni po-
tencjału grawitacyjnego, dlatego najgęstsze sku-
pisko stanów chaotycznych przypada w przybliże-
niu dla v

0

< 1,5 m/s. Z tej samej przyczyny dla

v

0

> 5,0 m/s zachowania chaotyczne są znacz-

nie rzadsze i „słabsze” (cudzysłów bierze się stąd,
że nie wprowadziliśmy formalnej miary chaosu),
a dla v

0

większego od ok. 8,8 m/s ruch jest pro-

sty i całkowicie przewidywalny („zero chaosu”).
Warto jeszcze wspomnieć, iż przebieg ruchu jest
stabilny (nie chaotyczny) w otoczeniu wartości pa-
rametrów, dla których zachodzi jego odwracalność
(chodzi tu np. o odbicie w punkcie R lub K). Wy-
jaśnienie tego faktu jest stosunkowo proste; niech
pozostanie ono zadaniem dla Czytelnika.

7. Podsumowanie: walory dydaktyczne

symulacji

Cały przedstawiony tok myślenia oraz pro-

gram symulacyjny mogą stanowić bazę dydak-
tyczną dla krótkiego i przystępnego wprowadzenia
pojęcia chaosu. Niech np. na początku zajęć na-
uczyciel rzuci (z rozmachem!) w klasie elastyczną
piłeczką (np. kauczukową), a potem poleci powtó-

rzyć ten eksperyment uczniom – jeżeli nauczy-
ciel obawia się o cenne zasoby swojej pracowni,
może ograniczyć się do doświadczenia myślowego.
W każdym razie chodzi o to, aby uczniowie uświa-
domili sobie, że wyniki kolejnych rzutów są na
ogół niepowtarzalne. Po takim wstępie należałoby
zaprezentować im program komputerowy. Ma on
wskazać uczniom, iż przebieg ruchu bywa niepo-
wtarzalny i niemożliwy do jednoznacznego, do-
kładnego określenia także w przypadku wyideali-
zowanego, symulowanego komputerowo układu fi-
zycznego. Na tej podstawie, bez dodatkowych ści-
słych rozważań, uczniowie powinni sobie uświado-
mić, że niemożliwość przewidzenia ewolucji dyna-
micznej niektórych układów nie wynika tylko z za-
kłóceń wprowadzanych przez warunki rzeczywi-
ste, ale tkwi głębiej – jest integralną cechą samej
sytuacji, samego układu fizycznego. Na końcu roz-
ważań nauczyciel może wyjaśnić, że cechę tę okre-
śla się mianem chaosu deterministycznego. Jeżeli
potem hasło „chaos deterministyczny” wywoła
u ucznia refleksję typu „gdy rzucimy kulkę, która
lata szybko tu i tam, odbijając się wiele razy, to
w niektórych sytuacjach przewidzenie jej toru na
podstawie parametrów samego rzutu jest niemoż-
liwe nie tylko z przyczyn praktycznych (technicz-
nych), ale i teoretycznych”, to nauczyciel będzie
mógł powiedzieć, że odniósł dydaktyczny sukces.

Lektura uzupełniająca

A. Fuliński, Fizyka w Szkole, z. 2/1994.
I. Stewart, Czy Bóg gra w kości (Wydawnictwo Na-
ukowe PWN, Warszawa 1994).
G.L. Baker, J.P. Gollub, Wstęp do dynamiki ukła-
dów chaotycznych (Wydawnictwo Naukowe PWN,
Warszawa 1998).

[6]

POSTĘPY FIZYKI

TOM 52

ROK 2001

MATERIAŁY DODATKOWE