Uwagi ogólne dotyczące wyznaczania sił przekrojowych
Aby wyznaczyć siły wewnętrzne w wybranych przekrojach (siły przekrojowe) ustroju
prętowego należy:
1. podzielić cały ustrój na punkty i przedziały charakterystyczne (punktami
charakterystycznymi ustroju są: miejsca załamań pręta, punkty przyłożenia obciążeń
skupionych, miejsca skoków funkcji i pochodnych obciążeń, przedział
charakterystyczny to część belki między sąsiednimi punktami charakterystycznymi),
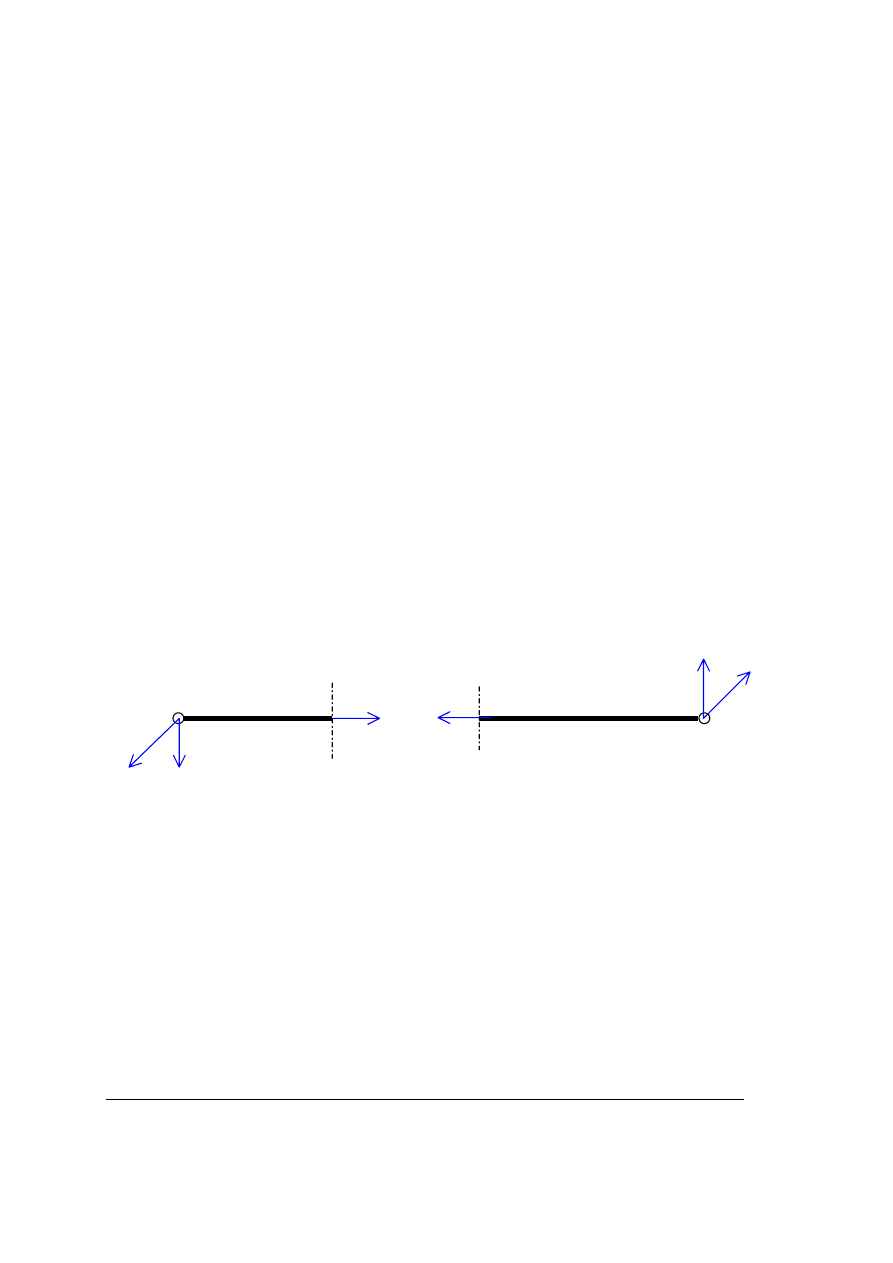
2. wprowadzić w każdej części rozciętego przekrojem
α-α
przedziału „i – j” układy
współrzędnych:
- o początku w punkcie charakterystycznym -i- układ współrzędnych (x
i
, y
i
, z
i
),
tak aby oś x
i
– pokrywała się z osią pręta i była normalna do przekroju pręta,
zaś osie y
i
i z
i
były zorientowane wzdłuż osi głównych centralnych bezwładności
przekroju poprzecznego
- o początku w
punkcie charakterystycznym –j-. układ współrzędnych (x
j
, y
j
, z
j
),
tak aby oś x
j
– pokrywała się z osią pręta i była normalna do przekroju pręta,
zaś osie y
j
i z
j
były zorientowane wzdłuż osi głównych centralnych bezwładności
przekroju poprzecznego
Dla części pręta po lewej stronie przekroju
α - α przyjmujemy lewostronny
układ współrzędnych, zaś dla części pręta po prawej stronie przekroju
α - α
przyjmujemy prawostronny układ współrzędnych.
Kolejne układy osi współrzędnych w następnych przedziałach charakterystycznych
powinny tworzyć jeden układ współrzędnych przemieszczający się po pręcie.
Zaleca się jak w układach prętowych płaskich usytuowanych w płaszczyźnie
osi „x” i „y” zwrot osi „y” ustalać po stronie rozciąganych włókien przy zginaniu
pręta.
y
j
i
α
α
z
j
x
i
x
j
α
α
j
y
i
z
i
3. Sześć nieznanych funkcji sił wewnętrznych w dowolnym przekroju
α - α k- tego
przedziału charakterystycznego (siłę normalną, dwie składowe sił tnących, moment
skręcający i dwie składowe momentu zginającego) wyznaczamy z analizy sześciu
warunków równowagi dowolnej części ustroju prętowego rozdzielonego badanym
przekrojem
α - α (trzech sum rzutów sił i trzech sum rzutów momentów).
4. Znaki sił wewnętrznych w przekroju
α - α przyjmujemy zgodne ze znakami układów
współrzędnych wprowadzonych dla danej części. Dodatkowo musimy pamiętać, że
wyznaczenia funkcji sił wewnętrznych wymaga znajomości nie tylko zadanych sił
zewnętrznych ale również reakcji występujących w badanej części pręta. W przypadku
rozpatrywania wspornikowej części pręta, wcześniejsze wyznaczenie reakcji nie jest
konieczne.
Uproszczenia w wyznaczaniu sił wewnętrznych "metoda punktów charakterystycznych"
1. Zazwyczaj dla „typowych inżynierskich obciążeń” zamiast obliczać funkcje sił
wewnętrznych w dowolnych przekrojach każdego przedziału charakterystycznego
1
wyznaczamy tylko wartości sił wewnętrznych na brzegach przedziałów
charakterystycznych, z prawej strony na początku przedziału i lewej strony na końcu
przedziału.
2. Jeżeli na początku przedziału siły przekrojowe są znane to wartości na końcu
przedziału możemy obliczyć ze znajomości funkcji siły przekrojowej we wnętrzu
przedziału charakterystycznego. Wartość ta zależy od sił na początku przedziału i
obciążeń we wnętrzu przedziału charakterystycznego ( patrz: zależności różniczkowe
między siłami wewnętrznymi i obciążeniami).
3. Dla najbardziej typowych przypadków mają one postać:
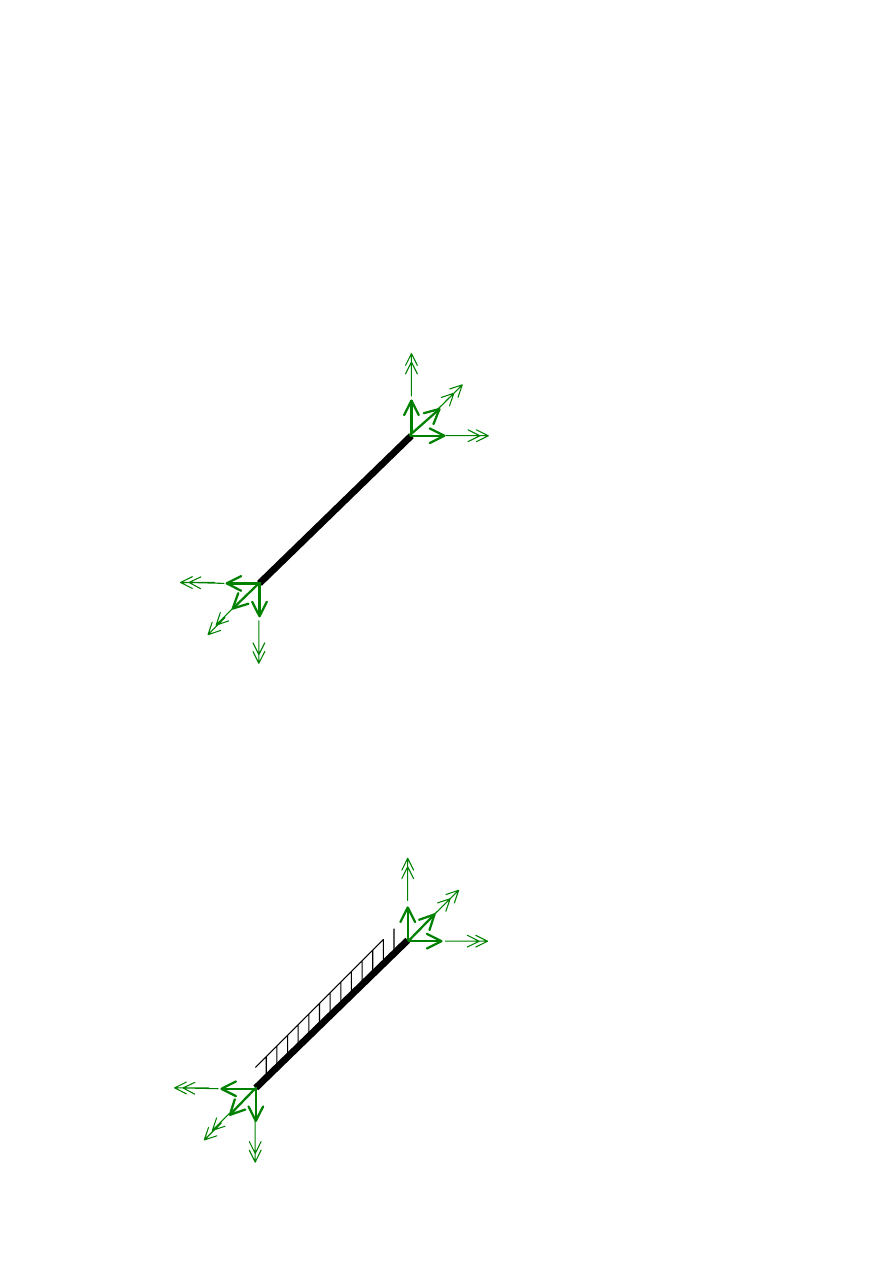
Przypadek I - przedział charakterystyczny i - j pręta jest nieobciążony:
M
gzj
M
sj
T
zj
N
j
T
yj
M
gyj
l
ij
N
j
= N
i
M
sj
= M
si
T
yj
= T
yi
T
zj
= T
zi
M
gyj
= M
gyi
- T
zi
⋅ l
ij
M
gyi
T
yi
M
gzj
= M
gzi
+ T
yi
⋅ l
ij
N
i
T
zi
M
si
M
gzi
UWAGA. W punkcie „i” narysowane siły wewnętrzne mają znaki zgodne z prawoskrętnym
układem współrzędnych ponieważ są po prawej stronie przekroju
α - α usytuowanego
nieskończenie blisko punktu „i”. Analogicznie w punkcie „j” kierunki sił wewnętrznych mają
kierunki zgodne z układem lewoskrętnym.
Przypadek II - przedział charakterystyczny i - j pręta obciążony na długości pręta
obciążeniem ciągłym stałym q = (q
x
, q
y
, q
z
), m = (m
x
, m
y
, m
z
)
M
gzj
M
sj
N
j
T
zj
T
yj
M
gyj
l
ij
N
j
= N
i
+ q
x
⋅ l
ij
M
sj
= M
si
+ m
x
⋅ l
ij
T
yj
= T
yi
+ q
y
⋅ l
ij
M
gyi
T
yi
M
gzj
= M
gzi
– T
yi
⋅ l
ij
- ½ q
y
⋅ l
ij
2
N
i
T
zi
T
zj
= T
zi
+ q
z
⋅ l
ij
M
si
M
gyj
= M
gyi
+ T
zi
⋅ l
ij
+ ½ q
z
⋅ l
ij
2
M
gzi
2
3
gdzie wprowadzono oznaczenia:
-i-
początek przedziału charakterystycznego,
-j-
koniec przedziału charakterystycznego,
N
i
(N
j
) siła normalna na początku (końcu) przedziału,
M
si
(M
sj
) moment
skręcający na początku (końcu) przedziału,
T
yi
(T
yj
) siła tnąca w kierunku osi -y- na początku (końcu) przedziału,
T
zi
(T
zj
) siła tnąca w kierunku osi -z- na początku (końcu) przedziału,
M
gyi
(M
gyj
) moment
gnący w kierunku osi -y- na początku (końcu) przedziału,
M
gzi
(M
gzj
) moment
gnący w kierunku osi -y- na początku (końcu) przedziału,
Uwagi dotyczące funkcji sił przekrojowych
1. Funkcje sił wewnętrznych mają skoki w miejscach występowania obciążeń
skupionych (przyłożenie siły wzdłuż osi pręta wywołuje skok siły normalnej,
przyłożenie siły prostopadłej do osi pręta wywołuje skok siły poprzecznej w kierunku
linii działania siły, przyłożenie momentu skupionego równoległego do osi pręta
wywołuje skok momentu skręcającego, przyłożenie momentu skupionego o linii
działania prostopadłej do osi pręta skutkuje powstaniem skoków momentów gnących).
2. W miejscach załamań pręta następuje zamiana sił wewnętrznych na inne. Ich rodzaj
ustalamy z warunków równowagi wyciętego z ustroju prętowego węzła.
3. Przyłożone w danym przedziale charakterystycznym pręta obciążenia o stałej
intensywności powoduje powstanie liniowych funkcji sił wewnętrznych.