
2. WYZNACZENIE ZBROJENIA W SLUPACH ZELBETOWYCH:
fcd
13.3MPa
:=
Ecm
30GPa
:=
Beton C25/30(B25):
fyd
310MPa
:=
Es
200GPa
:=
ξ
eff.lim
0.55
:=
Stal zbrojeniowa A-II:
lcol
390cm
:=
Dlugosc slupa:
Wymiar poprzeczny slupa:
hs
30cm
:=
bs
30cm
:=
Dlugosc podciagu:
leff
620cm
:=
Wymiary podciagu:
bp
30cm
:=
hp
60cm
:=
Odsuniecie zbrojenia od krawedzi:
a1
4cm
:=
a2
4cm
:=
2.1. Wymiarowanie zbrojenia slupa skrajnego na najnizszej kondygnacji:
wyniki obliczen statycznych z programu RM-WIN:
Wezel 1:
N1.max
435
209
+
10
+
(
)kN
:=
M1.odp
16
10
+
(
)kN m
⋅
:=
N1.max 654 kN
=
M1.odp 26 kN m
⋅
=
N1.odp
435
125
+
(
)kN
:=
M1.max
16
13
+
(
)kN m
⋅
:=
N1.odp 560 kN
=
M1.max 29 kN m
⋅
=
Wezel 3:
N3.max
435
209
+
10
+
(
)kN
:=
M3.odp
30
19
+
(
)kN m
⋅
:=
N3.max 654 kN
=
M3.odp 49 kN m
⋅
=
N3.odp
435
125
+
(
)kN
:=
M3.max
30
26
+
(
)kN m
⋅
:=
N3.odp 560 kN
=
M3.max 56 kN m
⋅
=
2.1.1. Wymiarowanie zbrojenia slupa w przekroju
α
α
α
α1-α
α
α
α1:
A) Na maksymalna sile osiowa i odpowiadajacy moment gnacy
N1.max 654 kN
=
M1.odp 26 kN m
⋅
=
Obliczanie wspolczynnika wyboczeniowego z uwzglednieniem sztywnosci wezlow A i B:
••••
moment bezwl. slupa
moment bezwl podciagu
Jcol
bs hs
3
⋅
12
:=
bs hs
3
⋅
12
30 cm
⋅
30 cm
⋅
(
)
3
⋅
12
=
0.0007 m
4
=
Jp
bp hp
3
⋅
12
:=
bp hp
3
⋅
12
30 cm
⋅
60 cm
⋅
(
)
3
⋅
12
=
0.0054 m
4
=
6

kA
Jp
leff
lcol
2 Jcol
⋅
⋅
:=
Jp
leff
lcol
2 Jcol
⋅
⋅
0.0054 m
4
⋅
620 cm
⋅
390 cm
⋅
2 0.0007 m
4
⋅
⋅
⋅
=
2.43
=
wzor z [PN-03264] zal C, tab C2
kB "nieskonczonosc"
=
-slup utwierdzony w sztywnym fundamencie
β
1
1
5 kA
⋅
1
+
+
:= 1
1
5 kA
⋅
1
+
+
1
1
5 2.43
⋅
1
+
+
=
1.08
=
Wysokosc wyboczeniowa slupa:
l0
β l
col
⋅
:=β l
col
⋅
1.08 390 cm
⋅
⋅
=
4.21 m
=
Wspolczynnik smuklosci:
λ
l0
hs
:=
l0
hs
4.21 m
⋅
30 cm
⋅
=
14.03
=
λ
7
>
1
=
Mimosrody:
- mimosrod konstrukcyjny:
ee
M1.odp
N1.max
:=
M1.odp
N1.max
26 kN
⋅
m
⋅
654 kN
⋅
=
39.8 mm
=
- mimosrod przypadkowy:
ea
max 10mm
lcol
600
,
hs
30
,
:= max 10mm
lcol
600
,
hs
30
,
max 10 mm
⋅
390 cm
⋅
600
,
30 cm
⋅
30
,
=
10.0 mm
=
Calkowity mimosrod poczatkowy:
e0
ee ea
+
:= e
e
ea
+
40 mm
⋅
10 mm
⋅
+
=
50 mm
=
Ustroj o wezlach nieprzesownych!
η
1.0
:=
Mimosrod ostateczny:
etot
η e
0
⋅
:= η e
0
⋅
1.0 50 mm
⋅
⋅
=
50.0 mm
=
Sumaryczne zbrojenie minimalne:
As.min
max 0.003 bs
⋅
hs
⋅
0.15
N1.max
fyd
⋅
,
:= max 0.003 b
s
⋅
hs
⋅
0.15
N1.max
fyd
⋅
,
3.16 cm
2
=
d
hs a1
−
:= h
s
a1
−
30 cm
⋅
4 cm
⋅
−
=
26.0 cm
=
odleglosc sily sciskajacej od zbr A
s1
es1
etot
hs
2
+
a1
−
:=e
tot
hs
2
+
a1
−
50 mm
⋅
30 cm
⋅
2
+
4 cm
⋅
−
=
160.0 mm
=
ξ
eff
N1.max
bs d
⋅ f
cd
⋅
:=
N1.max
bs d
⋅ f
cd
⋅
654 kN
⋅
30 cm
⋅
26 cm
⋅
⋅
13.3 MPa
⋅
⋅
=
0.630
=
ξ
eff.lim
0.55
=
ξ
eff
ξ
eff.lim
<
(
)
0
=
war. nie spelniony:
|TAK= DUZY MIMOSROD
|NIE= MALY MIMOSROD
Korekta zasiegu strefy sciskanej:
Parametry do rownania:
B
N1.max d a2
−
(
)
⋅
bs d
2
⋅
fcd
⋅
:=
B
0.533
=
A
2 N1.max
⋅
es1
⋅
bs d
2
⋅
fcd
⋅
:=
A
0.776
=
7
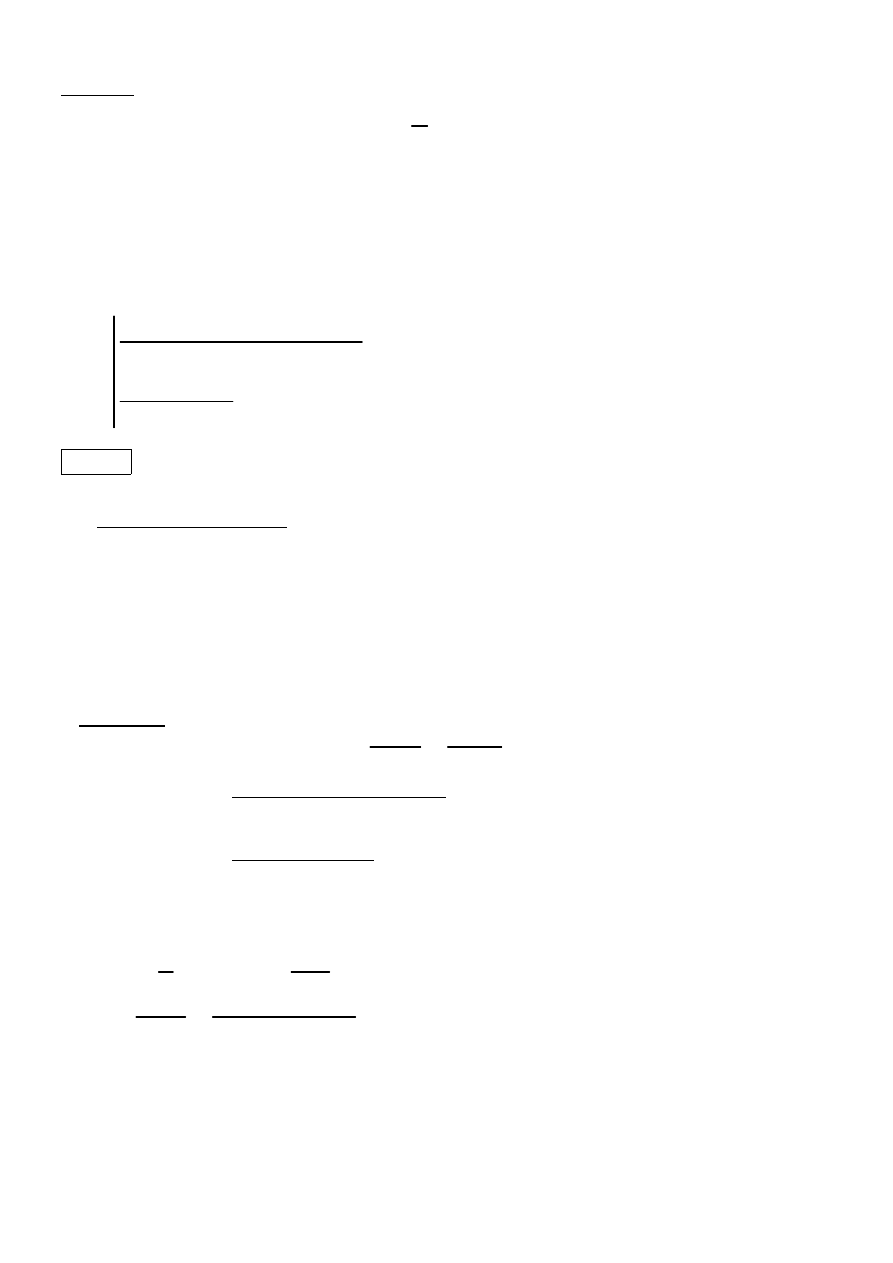
Rownanie:
W ξeff
( )
ξ
eff
3
2
ξ
eff.lim
+
(
)
ξ
eff
2
⋅
−
1
ξ
eff.lim
+
a2
d
1
ξ
eff.lim
−
(
)
⋅
−
A
+
ξ
eff
⋅
+
A ξeff.lim
⋅
−
B 1
ξ
eff.lim
−
(
)
⋅
−
:=
W ξeff
( )
0
=
ξ
eff
1
:=
root W ξeff
( )
ξ
eff
,
(
)
0.663
=
Zatem zasieg strefy sciskanej be. po korekcie:
ξ
eff
0.6630
:=
ξ
eff
1
<
1
=
As1
N1.max ξeff bs
⋅
d
⋅ f
cd
⋅
−
(
)
1
ξ
eff.lim
−
(
)
⋅
2 ξeff ξeff.lim
−
(
)
⋅
fyd
⋅
ξ
eff
1
<
if
N1.max bs d
⋅ f
cd
⋅
−
2 fyd
⋅
ξ
eff
1
>
if
:=
As1
2.171
−
cm
2
=
As2
As1
:=
As1 As2
+
As.min
>
0
=
As.min 3.16 cm
2
=
Przyjeto minimalne zbrojenia:
As1.prov
4.02cm
2
:=
(2 prety
φ16 )
As1.prov 0.5 As.min
⋅
>
1
=
As.min 3.165 cm
2
=
As2.prov
4.02cm
2
:=
(2 prety
φ16 )
As2.prov 0.5 As.min
⋅
>
1
=
B) Na maksymalny moment i odpowiadajaca mu sile osiowa:
N1.odp 560 kN
=
M1.max 29 kN m
⋅
=
Mimosrody:
- mimosrod konstrukcyjny:
ee
M1.max
N1.odp
:=
M1.max
N1.odp
29 kN m
⋅
⋅
560 kN
⋅
=
52 mm
=
Calkowity mimosrod poczatkowy:
e0
ee ea
+
:= e
e
ea
+
52 mm
⋅
10 mm
⋅
+
=
62 mm
=
Mimosrod ostateczny:
η
1.0
:=
etot
η e
0
⋅
:= η e
0
⋅
1.0 62 mm
⋅
⋅
=
62.0 mm
=
odleglosc sily sciskajacej od zbr A
s1
es1
etot
hs
2
+
a1
−
:=e
tot
hs
2
+
a1
−
62 mm
⋅
30 cm
⋅
2
+
4 cm
⋅
−
=
172.0 mm
=
ξ
eff
N1.odp
bs d
⋅ f
cd
⋅
:=
N1.odp
bs d
⋅ f
cd
⋅
560 kN
⋅
30 cm
⋅
26 cm
⋅
⋅
13.3 MPa
⋅
⋅
=
0.540
=
ξ
eff.lim
0.55
=
ξ
eff
ξ
eff.lim
<
(
)
1
=
war. spelniony:
|TAK= DUZY MIMOSROD
|NIE= MALY MIMOSROD
8

2 a2
⋅
d
0.308
=
ξ
eff
2 a2
⋅
d
>
1
=
warunek wspolpracy betonu ze zbrojeniem sciskanym; spelniony
odleglosc sily sciskajacej od zbr A
s2
es2
etot 0.5 hs
⋅
−
a2
+
:=
es2
48
−
mm
=
As1
N1.odp es2
⋅
fyd d a2
−
(
)
⋅
ξ
eff
2
a2
d
⋅
<
if
N1.odp es1
⋅
ξ
eff
1
ξ
eff
2
−
⋅
hs
⋅
d
2
⋅
fcd
⋅
−
d
a2
−
(
)
fyd
⋅
ξ
eff
2
a2
d
⋅
>
if
:=
As1
1.467
−
cm
2
=
As2
As1
:=
As1 As2
+
As.min
>
0
=
As.min 3.16 cm
2
=
Przyjeto minimalne zbrojenia:
As1.prov
4.02cm
2
:=
(2 prety
φ16 )
As1.prov 0.5 As.min
⋅
>
1
=
As.min 3.165 cm
2
=
As2.prov
4.02cm
2
:=
(2 prety
φ16 )
As2.prov 0.5 As.min
⋅
>
1
=
Zatem w przekroju
α1
α1
α1
α1-α1
α1
α1
α1 przyjeto zbrojenia:
As1.prov
4.02cm
2
:=
(2 prety
φ16 )
As1.prov 0.5 As.min
⋅
>
1
=
As.min 3.165 cm
2
=
As2.prov
4.02cm
2
:=
(2 prety
φ16 )
As2.prov 0.5 As.min
⋅
>
1
=
2.1.2. Wymiarowanie zbrojenia slupa w przekroju
α2
α2
α2
α2-α2
α2
α2
α2:
A) Na maksymalna sile osiowa i odpowiadajacy moment gnacy
N2.max
N1.max N3.max
+
2
:=
N2.max 654 kN
=
Mimosrody:
- mimosrod konstrukcyjny: e
e
0.6 M1.odp
⋅
0.4 M3.odp
⋅
+
N2.max
:=
0.6 M1.odp
⋅
0.4 M3.odp
⋅
+
N2.max
0.6 26 kN
⋅
m
⋅
⋅
0.4 49 kN
⋅
m
⋅
⋅
+
654 kN
⋅
=
54 mm
=
Calkowity mimosrod poczatkowy:
e0
ee ea
+
:= e
e
ea
+
54 mm
⋅
10 mm
⋅
+
=
64 mm
=
9
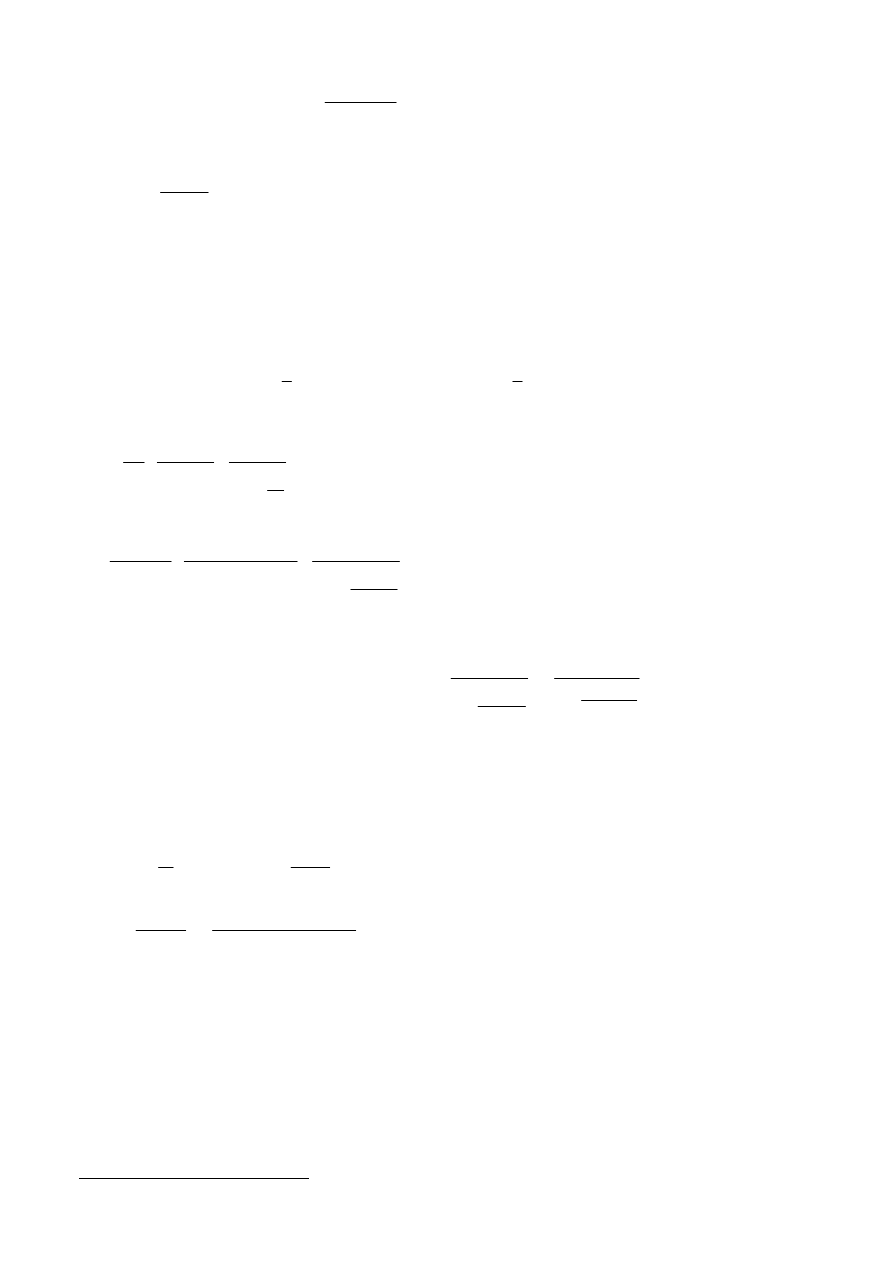
Wyznaczenie sily krytycznej:
wymiar miarodajny przekroju:
h0
2 bs
⋅
hs
⋅
2 bs
⋅
2 hs
⋅
+
:=
2 bs
⋅
hs
⋅
2 bs
⋅
2 hs
⋅
+
150 mm
=
==>>
φ
oo.t0
1.7
:=
wsp. uwzgledniajacy czesc obc.dlugotrwalego:
NSd.1
100% N2.max
⋅
:=
k1t
1
0.5
NSd.1
N2.max
⋅
φ
oo.t0
⋅
+
:=
k1t 1.85
=
Moment bezwladnosci zginanego przekroju betonowego:
Jcol 7 10
4
−
×
m
4
=
Moment bezwladnosci pola przekroju zbrojenia wzgledem srodka ciezkosci przekroju przy wstepnym zalozeniu
sumarycznego stopnia zbrojenia
ρ
0
1.1%
:=
Js
ρ
0 bs
⋅
hs
⋅
1
2
bs
⋅
a1
−
2
⋅
:= ρ
0 bs
⋅
hs
⋅
1
2
hs
⋅
a1
−
2
⋅
1.1 %
⋅
30 cm
⋅
⋅
30 cm
⋅
⋅
1
2
30 cm
⋅
⋅
4 cm
⋅
−
2
⋅
=
1198 cm
4
=
Sila krytyczna:
Ncrit
9
l0
2
Jcol Ecm
⋅
2 k1t
⋅
0.11
0.1
e0
hs
+
0.1
+
⋅
Es Js
⋅
+
⋅
:=
Ncrit
9
3.38 m
⋅
(
)
2
0.0007 m
4
⋅
30 GPa
⋅
⋅
2 1.85
⋅
0.11
0.1
ee ea
+
30 cm
⋅
+
0.1
+
⋅
200 GPa
⋅
1198 cm
4
⋅
⋅
+
⋅
=
Ncrit 2.52 MN
=
η
1
1
N1.max
Ncrit
−
:=
1
1
N1.max
Ncrit
−
1
1
654 kN
⋅
2.52 MN
⋅
−
=
1.35
=
wsp zwiekszajacy sumaryczny mimosrod:
mimosrod ostateczny:
etot
η e
0
⋅
:= η e
0
⋅
1.35 64 mm
⋅
⋅
=
86 mm
=
odleglosc sily sciskajacej od zbr A
s1
es1
etot
hs
2
+
a1
−
:=e
tot
hs
2
+
a1
−
86 mm
⋅
30 cm
⋅
2
+
4 cm
⋅
−
=
196.0 mm
=
ξ
eff
N2.max
bs d
⋅ f
cd
⋅
:=
N2.max
bs d
⋅ f
cd
⋅
654 kN
⋅
30 cm
⋅
26 cm
⋅
⋅
13.3 MPa
⋅
⋅
=
0.630
=
ξ
eff.lim
0.55
=
ξ
eff
ξ
eff.lim
<
(
)
0
=
war. nie spelniony:
|TAK= DUZY MIMOSROD
|NIE= MALY MIMOSROD
Korekta zasiegu strefy sciskanej:
10
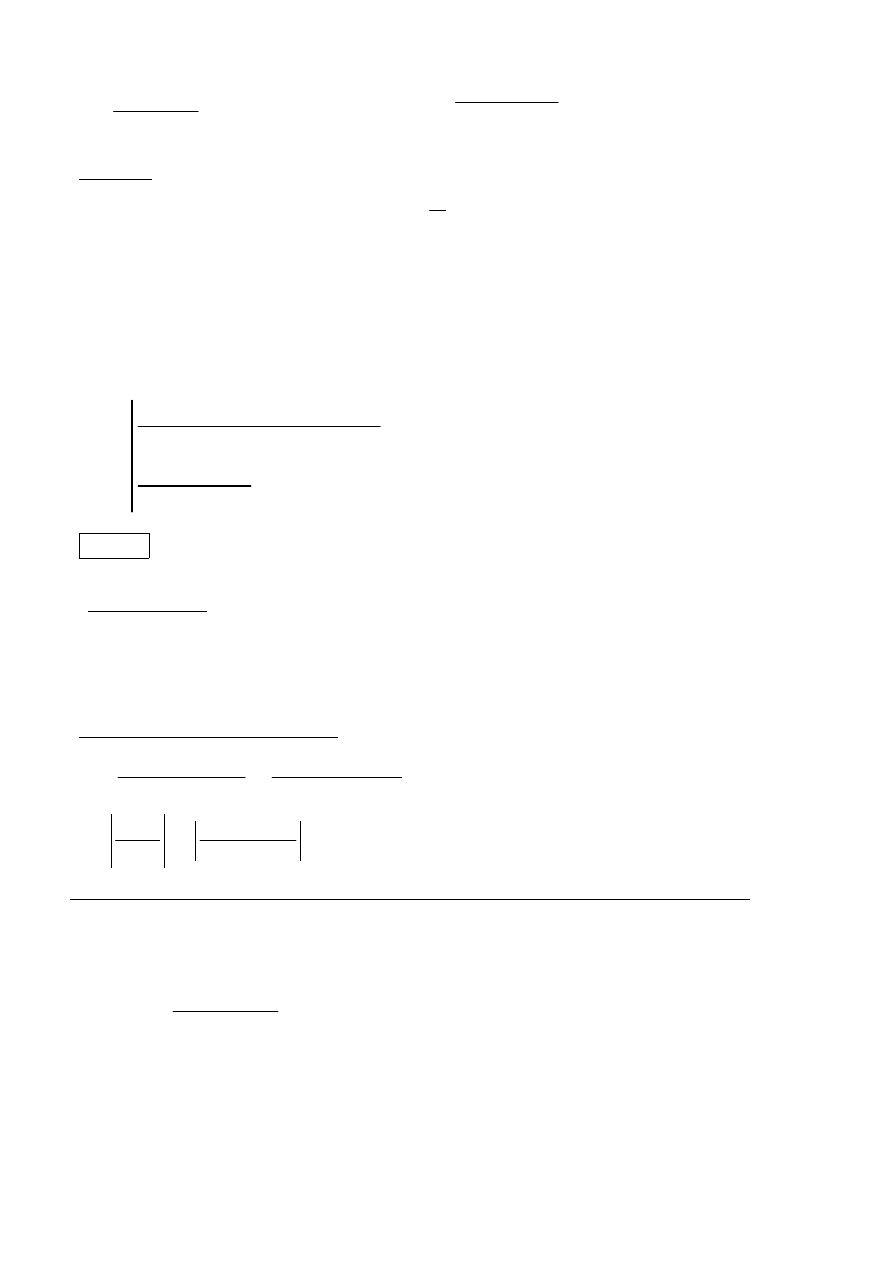
Parametry do rownania:
B
N1.max d a2
−
(
)
⋅
bs d
2
⋅
fcd
⋅
:=
B
0.533
=
A
2 N1.max
⋅
es1
⋅
bs d
2
⋅
fcd
⋅
:=
A
0.95
=
Rownanie:
W ξeff
( )
ξ
eff
3
2
ξ
eff.lim
+
(
)
ξ
eff
2
⋅
−
1
ξ
eff.lim
+
a2
d
1
ξ
eff.lim
−
(
)
⋅
−
A
+
ξ
eff
⋅
+
A ξeff.lim
⋅
−
B 1
ξ
eff.lim
−
(
)
⋅
−
:=
W ξeff
( )
0
=
ξ
eff
1
:=
root W ξeff
( )
ξ
eff
,
(
)
0.614
=
Zatem zasieg strefy sciskanej be. po korekcie:
ξ
eff
0.614
:=
ξ
eff
1
<
1
=
As1
N1.max ξeff bs
⋅
d
⋅ f
cd
⋅
−
(
)
1
ξ
eff.lim
−
(
)
⋅
2 ξeff ξeff.lim
−
(
)
⋅
fyd
⋅
ξ
eff
1
<
if
N1.max bs d
⋅ f
cd
⋅
−
2 fyd
⋅
ξ
eff
1
>
if
:=
As1 1.932 cm
2
=
As2
As1
:=
As1 As2
+
As.min
>
1
=
As.min 3.16 cm
2
=
Przyjeto zbrojenia:
As1.prov
4.02cm
2
:=
(2 prety
φ16 )
As1.prov As1
>
1
=
As2.prov
4.02cm
2
:=
(2 prety
φ16 )
2 As1.prov
⋅
As.min
>
1
=
Kontrola minimalnego stopnia zbrojenia:
ρ
As1.prov As2.prov
+
d hs
⋅
:=
As1.prov As2.prov
+
d hs
⋅
4.02 cm
2
⋅
4.02 cm
2
⋅
+
26 cm
⋅
30 cm
⋅
⋅
=
1.03 %
=
ε
ρ
0
ρ
−
ρ
0
:=
ρ
0
ρ
−
ρ
0
1.1 %
⋅
1.03 %
⋅
−
1.1 %
⋅
=
6.36 %
=
ε
10%
<
1
=
zatem wstepne oszacowanie stopnia zbrojenia bylo wystarczajaco dobre aby zakonczyc iteracje!
B) Na maksymalny moment i odpowiadajaca sile:
N2.odp
N1.odp N3.odp
+
2
:=
N2.odp 560 kN
=
11
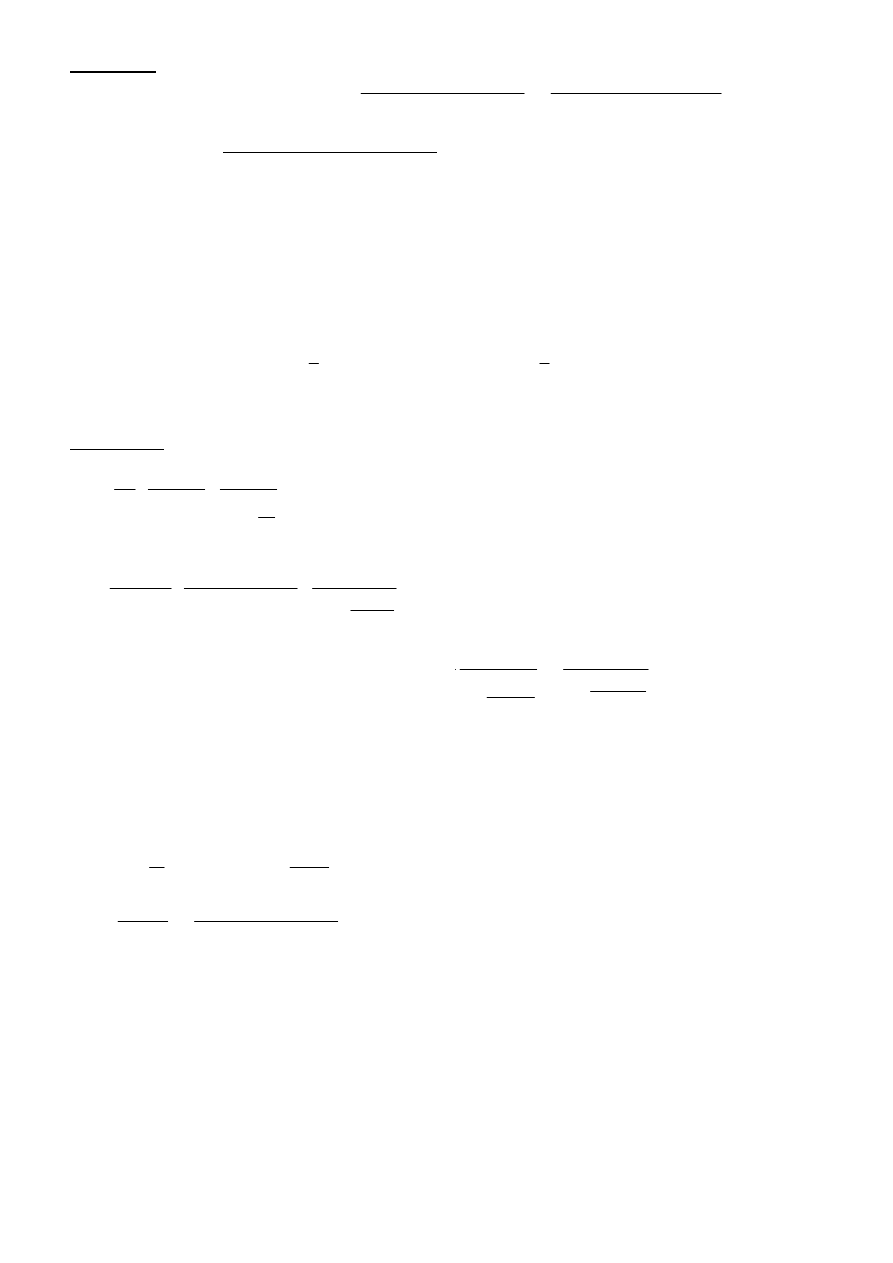
Mimosrody:
- mimosrod konstrukcyjny:
ee
0.6 M1.max
⋅
0.4 M3.max
⋅
+
N2.odp
:=
0.6 M1.max
⋅
0.4 M3.max
⋅
+
N2.odp
0.6 29 kN m
⋅
⋅
⋅
0.4 56 kN
⋅
m
⋅
⋅
+
N2.odp
=
71 mm
=
Calkowity mimosrod poczatkowy:
e0
ee ea
+
:= e
e
ea
+
71 mm
⋅
10 mm
⋅
+
=
81 mm
=
Moment bezwladnosci zginanego przekroju betonowego:
Jcol 7 10
4
−
×
m
4
=
Moment bezwladnosci pola przekroju zbrojenia wzgledem srodka ciezkosci przekroju przy wstepnym zalozeniu
sumarycznego stopnia zbrojenia
ρ
0
1.4%
:=
Js
ρ
0 bs
⋅
hs
⋅
1
2
bs
⋅
a1
−
2
⋅
:= ρ
0 bs
⋅
hs
⋅
1
2
hs
⋅
a1
−
2
⋅
1.4 %
⋅
30 cm
⋅
⋅
30 cm
⋅
⋅
1
2
30 cm
⋅
⋅
4 cm
⋅
−
2
⋅
=
1525 cm
4
=
Sila krytyczna:
Ncrit
9
l0
2
Jcol Ecm
⋅
2 k1t
⋅
0.11
0.1
e0
hs
+
0.1
+
⋅
Es Js
⋅
+
⋅
:=
Ncrit
9
3.38 m
⋅
(
)
2
0.0007 m
4
⋅
30 GPa
⋅
⋅
2 1.85
⋅
0.11
0.1
73 mm
⋅
30 cm
⋅
+
0.1
+
⋅
200 GPa
⋅
1633 cm
4
⋅
⋅
+
⋅
=
Ncrit 2.69 MN
=
η
1
1
N1.max
Ncrit
−
:=
1
1
N1.max
Ncrit
−
1
1
654 kN
⋅
2.69 MN
⋅
−
=
1.32
=
wsp zwiekszajacy sumaryczny mimosrod:
mimosrod ostateczny:
etot
η e
0
⋅
:= η e
0
⋅
1.32 81 mm
⋅
⋅
=
107 mm
=
odleglosc sily sciskajacej od zbr A
s1
es1
etot
hs
2
+
a1
−
:=e
tot
hs
2
+
a1
−
107 mm
⋅
30 cm
⋅
2
+
4 cm
⋅
−
=
217.0 mm
=
ξ
eff
N2.odp
bs d
⋅ f
cd
⋅
:=
N2.odp
bs d
⋅ f
cd
⋅
560 kN
⋅
30 cm
⋅
26 cm
⋅
⋅
13.3 MPa
⋅
⋅
=
0.540
=
ξ
eff.lim
0.55
=
ξ
eff
ξ
eff.lim
<
(
)
1
=
war. nie spelniony:
|TAK= DUZY MIMOSROD
|NIE= MALY MIMOSROD
12

Korekta zasiegu strefy sciskanej:
Parametry do rownania:
B
N1.max d a2
−
(
)
⋅
bs d
2
⋅
fcd
⋅
:=
B
0.533
=
A
2 N1.max
⋅
es1
⋅
bs d
2
⋅
fcd
⋅
:=
A
1.052
=
Rownanie:
W ξeff
( )
ξ
eff
3
2
ξ
eff.lim
+
(
)
ξ
eff
2
⋅
−
1
ξ
eff.lim
+
a2
d
1
ξ
eff.lim
−
(
)
⋅
−
A
+
ξ
eff
⋅
+
A ξeff.lim
⋅
−
B 1
ξ
eff.lim
−
(
)
⋅
−
:=
W ξeff
( )
0
=
ξ
eff
1
:=
root W ξeff
( )
ξ
eff
,
(
)
0.602
=
Zatem zasieg strefy sciskanej be. po korekcie:
ξ
eff
0.602
:=
ξ
eff
1
<
1
=
As1
N1.max ξeff bs
⋅
d
⋅ f
cd
⋅
−
(
)
1
ξ
eff.lim
−
(
)
⋅
2 ξeff ξeff.lim
−
(
)
⋅
fyd
⋅
ξ
eff
1
<
if
N1.max bs d
⋅ f
cd
⋅
−
2 fyd
⋅
ξ
eff
1
>
if
:=
As1 4.115 cm
2
=
As2
As1
:=
As1 As2
+
As.min
>
1
=
As.min 3.16 cm
2
=
Przyjeto zbrojenia:
As1.prov
6.03cm
2
:=
(3 prety
φ16 )
As1.prov As1
>
1
=
As2.prov
6.03cm
2
:=
(3 prety
φ16 )
2 As1.prov
⋅
As.min
>
1
=
Kontrola minimalnego stopnia zbrojenia:
ρ
As1.prov As2.prov
+
d hs
⋅
:=
As1.prov As2.prov
+
d hs
⋅
6.03 cm
2
⋅
6.03 cm
2
⋅
+
26 cm
⋅
30 cm
⋅
⋅
=
1.55 %
=
ε
ρ
0
ρ
−
ρ
0
:=
ρ
0
ρ
−
ρ
0
1.4 %
⋅
1.5 %
⋅
−
1.4 %
⋅
=
7.14 %
=
ε
10%
<
1
=
zatem wstepne oszacowanie stopnia zbrojenia bylo wystarczajaco dobre aby zakonczyc iteracje!
Zatem w przekroju
α2
α2
α2
α2-α2
α2
α2
α2 przyjeto zbrojenia:
As1.prov 0.5 As.min
⋅
>
1
=
As.min 3.165 cm
2
=
As1.prov
6.03cm
2
:=
(3 prety
φ16 )
As2.prov
6.03cm
2
:=
(3 prety
φ16 )
As2.prov 0.5 As.min
⋅
>
1
=
13
2.1.3. Wymiarowanie zbrojenia slupa w przekroju
α3
α3
α3
α3-α3
α3
α3
α3:
A) Na maksymalna sile osiowa i odpowiadajacy moment gnacy
N3.max 654 kN
=
M3.odp 49 kN m
⋅
=
Mimosrody:
- mimosrod konstrukcyjny:
ee
M3.odp
N3.max
:=
M3.odp
N3.max
49 kN
⋅
m
⋅
654 kN
⋅
=
75 mm
=
Calkowity mimosrod poczatkowy:
e0
ee ea
+
:= e
e
ea
+
75 mm
⋅
10 mm
⋅
+
=
85 mm
=
Mimosrod ostateczny:
η
1.0
:=
etot
η e
0
⋅
:= η e
0
⋅
1.0 85 mm
⋅
⋅
=
85.0 mm
=
odleglosc sily sciskajacej od zbr A
s1
es1
etot
hs
2
+
a1
−
:=e
tot
hs
2
+
a1
−
85 mm
⋅
30 cm
⋅
2
+
4 cm
⋅
−
=
195.0 mm
=
ξ
eff
N1.max
bs d
⋅ f
cd
⋅
:=
N3.max
bs d
⋅ f
cd
⋅
654 kN
⋅
30 cm
⋅
26 cm
⋅
⋅
13.3 MPa
⋅
⋅
=
0.630
=
ξ
eff.lim
0.55
=
ξ
eff
ξ
eff.lim
<
(
)
0
=
war. nie spelniony:
|TAK= DUZY MIMOSROD
|NIE= MALY MIMOSROD
Korekta zasiegu strefy sciskanej:
Parametry do rownania:
B
N1.max d a2
−
(
)
⋅
bs d
2
⋅
fcd
⋅
:=
B
0.533
=
A
2 N1.max
⋅
es1
⋅
bs d
2
⋅
fcd
⋅
:=
A
0.946
=
Rownanie:
W ξeff
( )
ξ
eff
3
2
ξ
eff.lim
+
(
)
ξ
eff
2
⋅
−
1
ξ
eff.lim
+
a2
d
1
ξ
eff.lim
−
(
)
⋅
−
A
+
ξ
eff
⋅
+
A ξeff.lim
⋅
−
B 1
ξ
eff.lim
−
(
)
⋅
−
:=
W ξeff
( )
0
=
ξ
eff
1
:=
root W ξeff
( )
ξ
eff
,
(
)
0.614
=
Zatem zasieg strefy sciskanej be. po korekcie:
ξ
eff
0.614
:=
ξ
eff
1
<
1
=
As1
N1.max ξeff bs
⋅
d
⋅ f
cd
⋅
−
(
)
1
ξ
eff.lim
−
(
)
⋅
2 ξeff ξeff.lim
−
(
)
⋅
fyd
⋅
ξ
eff
1
<
if
N1.max bs d
⋅ f
cd
⋅
−
2 fyd
⋅
ξ
eff
1
>
if
:=
As1 1.932 cm
2
=
14

As2
As1
:=
As1 As2
+
As.min
>
1
=
As.min 3.16 cm
2
=
Przyjeto zbrojenia:
As1.prov
4.02cm
2
:=
(2 prety
φ16 )
As1.prov As1
>
1
=
As2.prov
4.02cm
2
:=
(2 prety
φ16 )
As1.prov As.min
>
1
=
B) Na maksymalny moment i odpowiadajaca sile:
N3.odp 560 kN
=
M3.max 56 kN m
⋅
=
Mimosrody:
- mimosrod konstrukcyjny:
ee
M3.max
N3.odp
:=
M3.max
N3.odp
56 kN
⋅
m
⋅
560 kN
⋅
=
100 mm
=
Calkowity mimosrod poczatkowy:
e0
ee ea
+
:= e
e
ea
+
100 mm
⋅
10 mm
⋅
+
=
110 mm
=
Mimosrod ostateczny:
η
1.0
:=
etot
η e
0
⋅
:= η e
0
⋅
1.0 110 mm
⋅
⋅
=
110.0 mm
=
odleglosc sily sciskajacej od zbr A
s1
es1
etot
hs
2
+
a1
−
:=e
tot
hs
2
+
a1
−
110 mm
⋅
30 cm
⋅
2
+
4 cm
⋅
−
=
220.0 mm
=
ξ
eff
N3.odp
bs d
⋅ f
cd
⋅
:=
N3.odp
bs d
⋅ f
cd
⋅
560 kN
⋅
30 cm
⋅
26 cm
⋅
⋅
13.3 MPa
⋅
⋅
=
0.540
=
ξ
eff.lim
0.55
=
ξ
eff
ξ
eff.lim
<
(
)
1
=
war. spelniony:
|TAK= DUZY MIMOSROD
|NIE= MALY MIMOSROD
2 a2
⋅
d
0.308
=
ξ
eff
2 a2
⋅
d
>
1
=
warunek wspolpracy betonu ze zbrojeniem sciskanym; spelniony
odleglosc sily sciskajacej od zbr A
s2
es2
etot 0.5 hs
⋅
−
a2
+
:=
es2 6.9 10
15
−
×
mm
=
As1
N1.odp es2
⋅
fyd d a2
−
(
)
⋅
ξ
eff
2
a2
d
⋅
<
if
N1.odp es1
⋅
ξ
eff
1
ξ
eff
2
−
⋅
hs
⋅
d
2
⋅
fcd
⋅
−
d
a2
−
(
)
fyd
⋅
ξ
eff
2
a2
d
⋅
>
if
:=
As1 2.474 cm
2
=
As2
As1
:=
As1 As2
+
As.min
>
1
=
As.min 3.16 cm
2
=
15

Przyjeto minimalne zbrojenia:
As1.prov
4.02cm
2
:=
(2 prety
φ16 )
As1.prov 0.5 As.min
⋅
>
1
=
As.min 3.165 cm
2
=
As2.prov
4.02cm
2
:=
(2 prety
φ16 )
As2.prov 0.5 As.min
⋅
>
1
=
Zatem w przekroju
α3
α3
α3
α3-α3
α3
α3
α3 przyjeto zbrojenia:
As1.prov
4.02cm
2
:=
(2 prety
φ16 )
As1.prov 0.5 As.min
⋅
>
1
=
As.min 3.165 cm
2
=
As2.prov
4.02cm
2
:=
(2 prety
φ16 )
As2.prov 0.5 As.min
⋅
>
1
=
2.1.4. Podsumowanie slupa skrajnego:
Przyjete wymiary slupa:
•
bs 30 cm
=
hs 30 cm
=
W celu ujednolicenia zbrojenia na calej jego dlugosci, przyjmujemy zbrojenia:
•
As1.prov 0.5 As.min
⋅
>
1
=
As.min 3.16 cm
2
=
As1.prov
6.03cm
2
:=
(3 prety
φ16 )
As2.prov
6.03cm
2
:=
(3 prety
φ16 )
As2.prov 0.5 As.min
⋅
>
1
=
Na calej dlugosci slupa przyjeto 6 pretow
φ16.
•
Maksymalny rostaw strzemion:
•
smax
16mm 15
⋅
:=
smax 24 cm
=
Zastosowano strzemiona dwuciete, srednicy
φ8 rostawione w odleglosci:
•
s
20cm
:=
16
Wyszukiwarka
Podobne podstrony:
03 slup wew 30x30
02 slup
Guy N Smith Kraby 02 Zew krabów
Arthur Keri Zew Nocy 02 Całując grzech
Wyk 02 Pneumatyczne elementy
02 OperowanieDanymiid 3913 ppt
02 Boża radość Ne MSZA ŚWIĘTAid 3583 ppt
OC 02
PD W1 Wprowadzenie do PD(2010 10 02) 1 1
02 Pojęcie i podziały prawaid 3482 ppt
WYKŁAD 02 SterowCyfrowe
02 filtracja
więcej podobnych podstron