Teoria liczb 2010, sem.IV,

B.Bajorska, O.Macedońska

Wykład 13.

Liczby Fibonacci

Potrzebne: (i). Jeśli b

|c, to NW D(a + c, b) = NW D(a, b).

(ii). Jeśli N W D(a, c) = 1, to N W D(a, bc) = N W D(a, b).

Leonardo Fibonacci (1170-1250). Wiadomo, że Leonardo urodził się w

1170 w Pizie. Należał do rodu Bonacci (Fibonacci = ”syn dobrotliweg”).
W roku 1192 Ojciec pełniąc obowiązki sekretarza Republiki Piza, wyjechał
do terazniejszej Algerii i zabrał syna, by nauczył sie rachunków i mógł być
kupcem. Właśnie tam Leonardo zainteresował się matematyką i nauczył
się nowych metod z użyciem cyfr pochodzących z Indii, ale znanych jako
arabskie.

W 1202 roku Fibonacci napisał słynną ksęgę ”Liber Abaci”. Słowo ”aba-

cus” (z greckiego ”abax”) oznacza deskę posiadającą rowki z wgłębieniami,
gdzie przesuwano kamyczki do liczenia. Używano abacus do XVIII wieku,
do powstania liczydła, gdy zamieniono rowki drutami z przesuwanymi kora-
likami.

Wielu historyków uważa, że w nazwa ”Liber abbaci” ma być tłumaczona

jako ”Księga rachunków”.

Ksęga ”Liber Abaci” była napisana ręcznie i systematycznie przedstaw-

iała wiedzę matematyki arabskiej. Była to pierwsza encyclopedia mate-
matyki, w ciągu stuleci służyła jako podstawowy podręcznik aryt-
metyki i algebry na terenie Europy Zachodniej.

W książce ”Liber Abaci” 1202, Leonardo Fibonacci wprowadził arab-

skie (ale wcześniej hinduskie) cyfry, których używamy do dziś.

1

Ciąg Fibonacci

Leonardo Fibonacci zajmował się zagadnieniem, które doprowadziło go do
rekurencyjnego określenia pewnego ci¸

agu liczb, które na jego cześć zostały

nazwane liczbami Fibonacciego. Konkretnie chodziło o obliczenie, jak szybko
powiększać się będzie populacja królików pochodzących od jednej pary.

Ile par królików może spłodzić jedna para w ciągu roku jeśli:

(i) każda para rodzi nową parę pod koniec każdego miesiąca zaczynając od
drugiego miesiąca. życia;
(ii) króliki nie zdychają.

Wzrost populacji królików opisuje ciąg Fibonacci 0, 1, 1, 2, 3, 5, 8, 13, 21, ...

w którym każdy wyraz jest sumą dwóch poprzednich: f

1

= f

2

= 1, f

n

=

f

n

−1

+ f

n

−2

, n

≥ 3.

1

Na tarczy słonecznika znajdują się dwa układy linii spiralnych.

Jeśli

policzymy spirale zgodne z ruchem wskazówek zegara i spirale przeciwne do
nich, to otrzymamy liczby Fibonacciego. 34 i 55 lub 55 i 89.

Spirale Fibonacciego występują w szyszkach sosnowych z liczbami 8 i 13.

Liczby Fibonacciego można odczytać z ananasa: 8 i 13.

Liczba płatków stokrotki jest liczbą Fibonacciego: 13 21 34 55 89.

Jedno z najstarszych twierdzeń dotyczących liczb Fibonacci po raz pier-

wszy opublikowano w roku 1680 przez włoskiego astronoma Jean-Dominique
Cassiniego.

Twierdzenie 1. (Cassini, 1680) Dla liczb Fibonacci zachodzi tożsamość

f

2

n+1

= f

n

f

n+2

+ (

−1)

n

.

Dowód. Zastosujmy indukcje względem n. Dla n = 1 mamy f

2

2

= f

1

f

3

−1 =

2

− 1 = 1. Załóżmy, że f

2

k+1

= f

k

f

k+2

+ (

−1)

k

. Dodajemy do obu stron

f

k+1

f

k+2

. Mamy

f

2

k+1

+ f

k+1

f

k+2

= f

k

f

k+2

+ f

k+1

f

k+2

+ (

−1)

k

,

f

k+1

(f

k+1

+ f

k+2

) = f

k+2

(f

k

+ f

k+1

) + (

−1)

k

,

f

k+1

f

k+3

= f

2

k+2

+ (

−1)

k

,

f

2

k+2

= f

k+1

f

k+3

+ (

−1)

k+1

.

Na przyklad 8

· 8 = 5 · 13 − 1 powoduje powstanie łamigłówki.

Twierdzenie 2. Niech f

n

będzie n-tą liczbą Fibonacciego. Wtedy N W D(f

n

, f

n+1

) =

1 dla n

≥ 1.

Dowód. Jeśli d

|f

n+1

i d

|f

n

, to d

|f

n

−1

. Rozumując tak samo, otrzymamy

d

|f

n

−2

, d

|f

n

−3

,..., i w końcu d

|f

1

. Stąd d = 1.

2

Twierdzenie 3. Dla liczb Fibonnaciego zachodzi równość:

f

m+n

= f

m

−1

f

n

+ f

m

f

n+1

.

Dowód. Stosujemy indukcję ze względu na n, przy ustalonym m. Dla n = 1
f

m+1

:= f

m

−1

+ f

m

= f

m

−1

f

1

+ f

m

f

2

bo f

1

= f

2

= 1 więc OK.

Zakładamy, że wzór jest prawdziwy dla n i n

−1 : f

m+n

= f

m

−1

f

n

+f

m

f

n+1

oraz f

m+(n

−1)

= f

m

−1

f

n

−1

+ f

m

f

n

. Sprawdzamy czy równość zachodzi dla

n + 1:

f

m+n+1

:= f

m+n

+ f

m+n

−1

= (f

m

−1

f

n

+ f

m

f

n+1

) + (f

m

−1

f

n

−1

+ f

m

f

n

) =

f

m

−1

(f

n

+ f

n

−1

) + f

m

(f

n+1

+ f

n

) = f

m

−1

f

n+1

+ f

m

f

n+2

= f

m+(n+1)

.

Uwaga Liczba 12 jest podzielna przez 6, 4, 3, 2 i 1 a f

12

= 144 jest podzielne

przez: f

6

= 8, f

4

= 3, f

3

= 2, f

2

= f

1

= 1.

Twierdzenie 4. Liczba f

mn

jest podzielna przez f

m

dla m, n

≥ 1 .

Dowód. Stosujemy indukcję ze względu na n przy ustalonym m dla n = 1 :
f

m

|f

m

. Zakładamy: f

m

|f

mn

. Pokazemy, że f

m

|f

m(n+1)

.

Na podstawie Twierdzenia 3, f

m(n+1)

= f

mn+m

= f

mn

−1

f

m

+ f

mn

f

m+1

.

Zauważmy, ze f

m

dzieli każdy składnik. Czyli dzieli też ich sumę.

Lemat 1. Jeśli m = qn + r, to N W D(f

m

, f

n

) = N W D(f

r

, f

n

).

Dowód. Korzystając z Twierdzenia 3 mamy f

qn+r

= f

qn

−1

f

r

+ f

qn

f

r+1

,

N W D(f

m

, f

n

) = N W D(f

qn+r

, f

n

) = N W D(f

qn

−1

f

r

+f

qn

f

r+1

, f

n

).

Jeśli b

|c, to NW D(a + c, b) = NW D(a, b); z warunku f

n

|f

qn

otrzymujemy

N W D(f

m

, f

n

) = N W D(f

qn

−1

f

r

+ f

qn

f

r+1

, f

n

) = N W D(f

qn

−1

f

r

, f

n

).

Wystarczy więc wykazać, że N W D(f

qn

−1

, f

n

) = 1. Niech N W D(f

qn

−1

, f

n

) =

d. Ponieważ d

|f

n

i f

n

|f

qn

, więc d

|f

qn

, a jednocześnie d

|f

qn

−1

, czyli d dzieli

kolejne liczby Fibonacciego i zgodnie z Twierdzenia 2, d = 1, co kończy
dowód.

Twierdzenie 5. Dla liczb Fibonacci’ego N W D(f

m

, f

n

) = f

d

, gdzie d =

N W D(m, n).

Dowód. Przyjmijmy, że m

≥ n. Z algorytmu Euklidesa:

m = q

1

n + r

1

gdzie 0 < r

− 1 < n,

n = q

2

r

1

+ r

2

gdzie 0 < r

2

< r

1

,

...............................................
r

k

−2

= q

k

r

k

−1

+ r

k

gdzie 0 < r

k

< r

k

−1

,

r

k

−1

= qk + 1r

k

+ 0.

Z Lematu 1 wynika, że:

N W D(f

m

, f

n

) = N W D(f

n

, f

r

1

) = N W D(f

r

1

, f

r

2

) = . . . = N W D(f

r

k

−1

, f

r

k

) = f

r

k

.

Z drugiej strony r

k

= N W D(m, n), co kończy dowód.

3

Przykład N W D(2584, 610) = N W D(f

18

, f

15

) = f

N W D(18,15)

= f

3

= 2.

Wniosek 1. Jeśli m, n > 2, to dla liczb Fibonacciego f

m

|f

n

wtedy i tylko

wtedy, gdy m

|n, bo: f

m

|f

n

⇒ NW D(f

m

, f

n

) = f

m

⇒ NW D(m, n) = m ⇒

m

|n.

Wzór Bineta (1843)

f

n

=

1

√

5




(

1 +

√

5

2

)

n+1

−

(

1

−

√

5

2

)

n+1


 , n ∈ N.

2

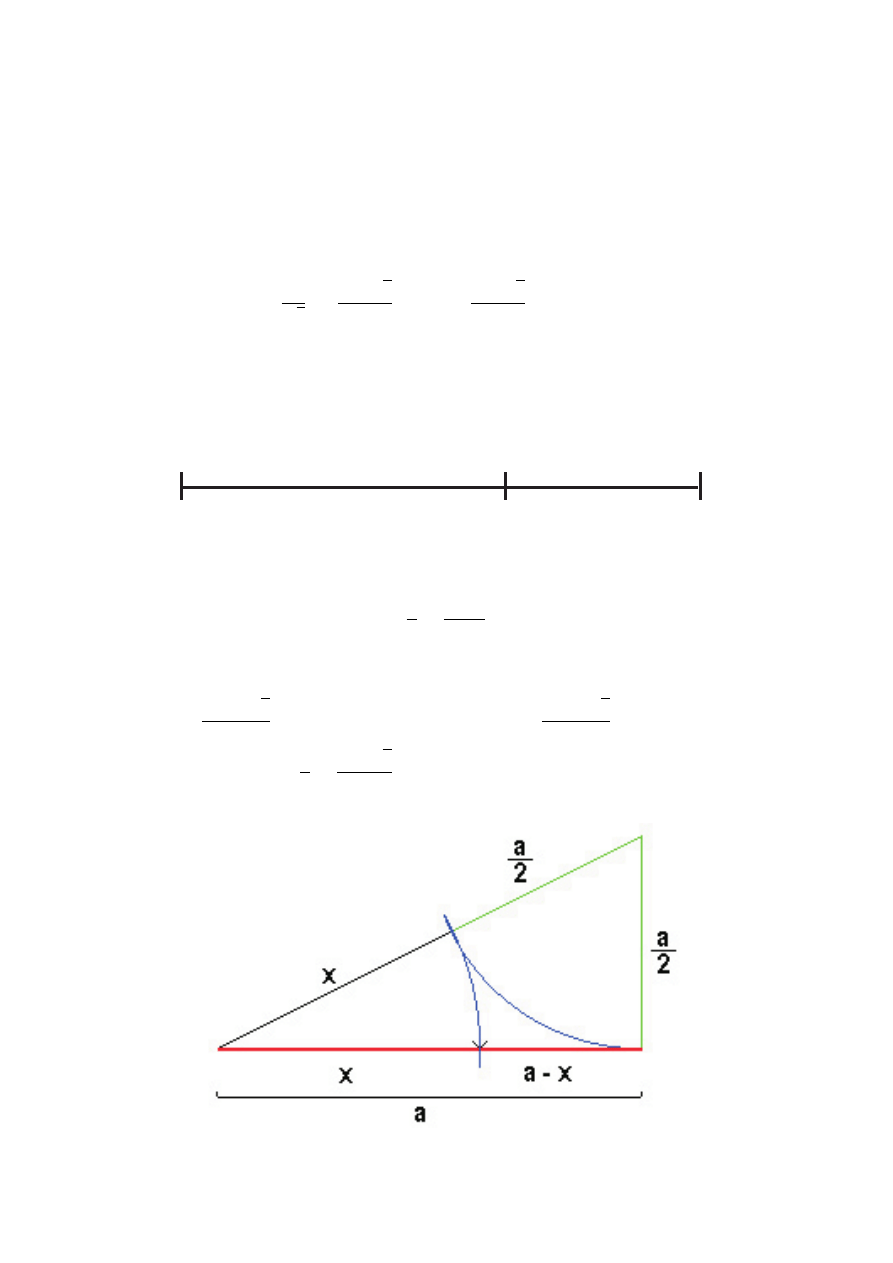
Złoty podział

a

a - x

x

a

x

=

x

a

− x

x

2

+ ax

− a

2

= 0

x

1

=

−1 −

√

5

2

a =

−a · 1, 618... < 0,

x = x

2

=

−1 +

√

5

2

a = a

· 0, 618... .

a

x

=

1 +

√

5

2

:= φ naz.ZOTALICZBA

Konstrukcja złotej liczby

4

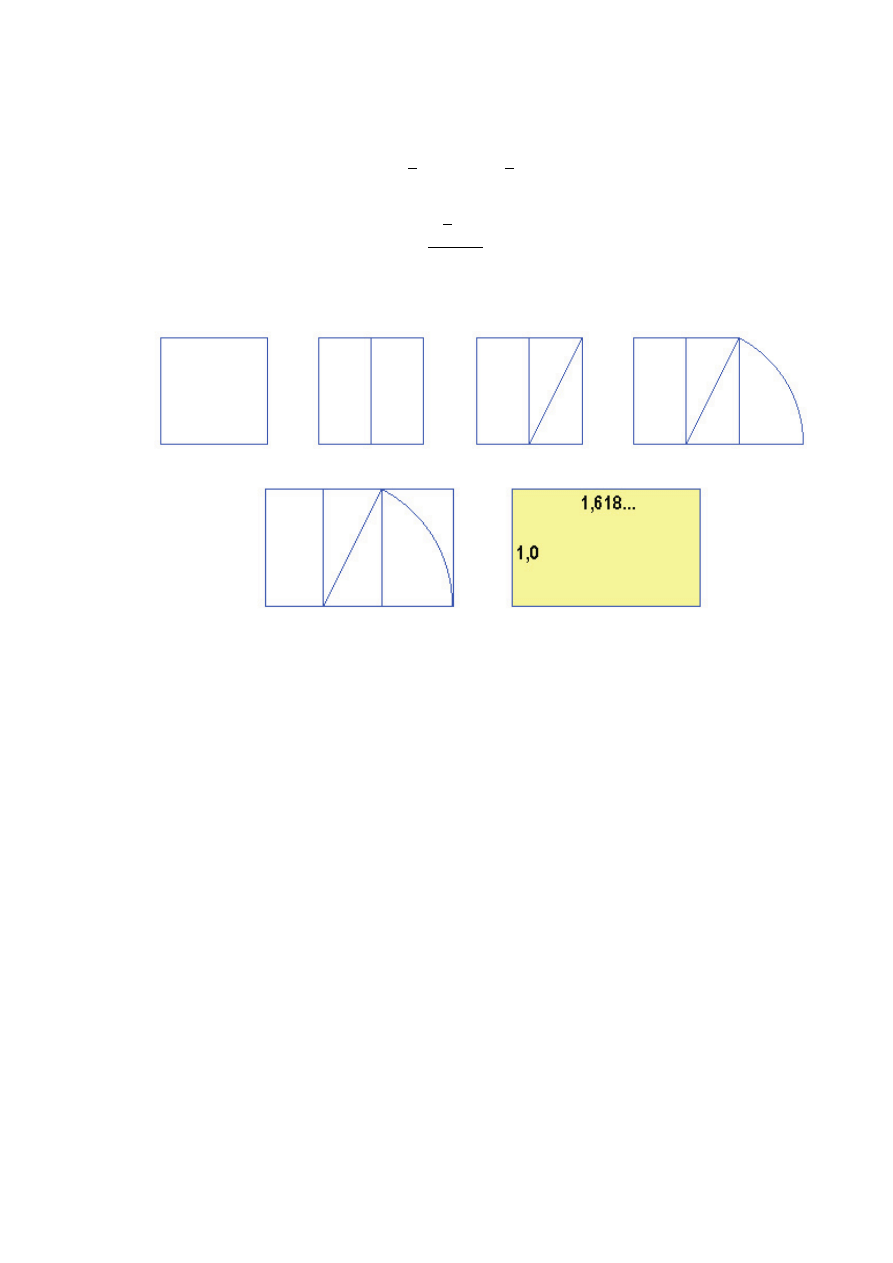
a

2

+

(

a

2

)

2

=

(

x +

a

2

)

2

x

2

+ ax

− a

2

= 0

x =

√

5

− 1

2

a.

Konstrukcja złotego prostokąta

5