1

Inżynieria Chemiczna - Laboratorium

Ćwiczenie VIII

BADANIE MODELOWE PROCESU SEDYMENTACJI

8.1 Wprowadzenie teoretyczne

Rozdzielanie

układów wieloskładnikowych można prowadzić dwoma sposobami.

Zgodnie z pierwszym wykorzystuje się operacje dyfuzyjne, podczas których występują

przemiany fazowe lub ruch masy między fazami. Drugi sposób – to stosowanie operacji

mechanicznych, które powodują wydzielanie cząsteczek ciała stałego lub kropel cieczy z

układu heterogenicznego. Technika rozdziału oparta jest na różnicach własności fizycznych

składników układu, takich jak: wielkość cząstek, ich kształt oraz gęstość składników układu.

Dzięki temu możliwe jest oddzielenie jednych cząstek od innych lub wydzielenie cząstek

ciała stałego z gazu, kropel cieczy z gazu oraz cząstek ciała stałego z cieczy. Do tych

ostatnich operacji mechanicznych zalicza się: filtrację, flotację, odwirowanie i sedymentację.

Sedymentacja, czyli zjawisko zakłóconego opadania cząstek ciała stałego w cieczy,

służy do zagęszczania zawiesiny pod wpływem działania pola grawitacyjnego. Zaistnienie

różnicy gęstości ciała stałego i cieczy jest w tym przypadku warunkiem koniecznym [1].

Zawiesina jest układem dwufazowym składającym się z cząsteczek ciała stałego

zawieszonych w cieczy. Jeżeli cząstki ciała stałego rozmieszczone są równomiernie w

objętości zawiesiny, to uważa się ją za jednorodną, a w przeciwnym przypadku – za

niejednorodną. Zawartość ciała stałego w zawiesinie (stężenie ciała stałego) może być różna.

Zawiesiny zawierające poniżej 10% objętości ciała stałego uważa się zazwyczaj za

rozcieńczone, natomiast powyżej ok. 7-% objętości – za zagęszczone. Stężenie zawiesiny

może być wyrażone w różny sposób, często stosuje się w tym celu pojęcie porowatości

zawiesiny. Porowatość zawiesiny może być stała lub może ulegać zmianie podczas

sedymentacji.

Cząstki ciała stałego w zawiesinie mogą mieć różne kształty, np. kuli, walca,

prostopadłościanu lub innych brył geometrycznych bądź rzeczywistych. Kształt cząstki może

być izomeryczny, czyli współmierny, a więc o rozmiarach wzajemnie współmiernych w

trzech wzajemnie prostopadłych kierunkach, bądź nieizomeryczny. Wielkość rozmiarów

cząstek ciała stałego określa się za pomocą średnicy (dla cząstek kulistych) lub odpowiednio

2

zdefiniowanej średnicy zastępczej. Cząstki ciała stałego o rozmiarach powyżej 100 µm noszą

nazwę gruboziarnistych, a poniżej 30 µm – drobnoziarnistych. Cząstki drobnoziarniste w

zawiesinie mogą wykazywać skłonność do flokulacji, czyli łączenia się w większe zespoły.

Ponadto niekuliste cząstki ciała stałego mogą opadać zabierając ze sobą pewną objętość

cieczy zatrzymanej w nieregularnościach ich powierzchni.

Zawiesiny zawierające cząstki ciała stałego o takim samym kształcie i takich samych

rozmiarach nazywane są modyspersyjnym, a w innych przypadkach – polidyspersyjnym.

Cząstki ciała stałego w zawiesinie polidyspersyjnej traktuje się jako zbiory i opisuje za

pomocą tzw. charakterystyk zbioru. Na ich podstawie określa się m.in. średnią średnicę

cząstek w zawiesinie. Jeśli stosunek rozmiarów największej cząstki do najmniejszej jest

mniejszy niż 6: l, to w praktyce można uważać zawiesinę za monodyspersyjną.

Ze względu na własności reologiczne zawiesiny mogą zachowywać się jak płyny

newtonowskie bądź też - jak płyny nienewtonowskie. Niektóre związki chemiczne dodane do

zawiesiny mogą wpłynąć na jej własności poprzez zmianę oddziaływania między cząstkami

ciała stałego lub między cieczą a cząstkami ciała stałego.

Związki ilościowe pomiędzy ciałem stałym, cieczą i zawiesiną są wyrażane w postaci

udziałów masowych lub objętościowych. Udział masowy ciała stałego, zwany również

stężeniem masowym, ciała stałego, jest to stosunek masy ciała stałego m

s

do masy zawiesiny

m

z

:

gdzie:

Udział masowy cieczy (stężenie masowe cieczy) jest to stosunek masy cieczy me do masy

zawiesiny m

z

:

Suma udziałów masowych ciała stałego i cieczy w zawiesinie wynosi:

Udział objętościowy ciała stałego (stężenie objętościowe ciała stałego) jest to stosunek

objętości ciała stałego V

s

do objętości zawiesiny V

z

:

3

gdzie:

Udział objętościowy cieczy (stężenie objętościowe cieczy) jest to stosunek objętości cieczy

do objętości zawiesiny:

Wielkość ta znana jest pod nazwą porowatości. Suma udziałów objętościowych ciała stałego i

cieczy w zawiesinie wynosi:

Pojęcie porowatości wywodzi się z dziedziny przepływów przez warstwy porowate.

Porowatość może zmieniać się w granicach 0 ≤ ε ≤ 1. Porowatość ε = 0 oznacza zupełny brak

swobodnej przestrzeni (φ= 1) między cząstkami, co odpowiada ciągłej fazie stałej, a

porowatość ε =1 - brak fazy stałej (φ = 0). Poza wymienionymi wyżej rodzajami stężeń często

stosuje się stężenia wyrażane stosunkiem masy ciała stałego lub masy cieczy do objętości

zawiesiny:

Sumę tych stężeń można przedstawić w postaci:

gdzie p

z

oznacza gęstość zawiesiny. Każde z wymienionych stężeń może mieć charakter

lokalny lub uśredniony w czasie i miejscu.

Gęstość zawiesiny zależy od gęstości cząstek ciała stałego w zawiesinie. Stosuje się

następujące pojęcia gęstości cząstek ciała stałego:

• gęstość materiałowa,
• gęstość rzeczywista,
• gęstość pozorna,

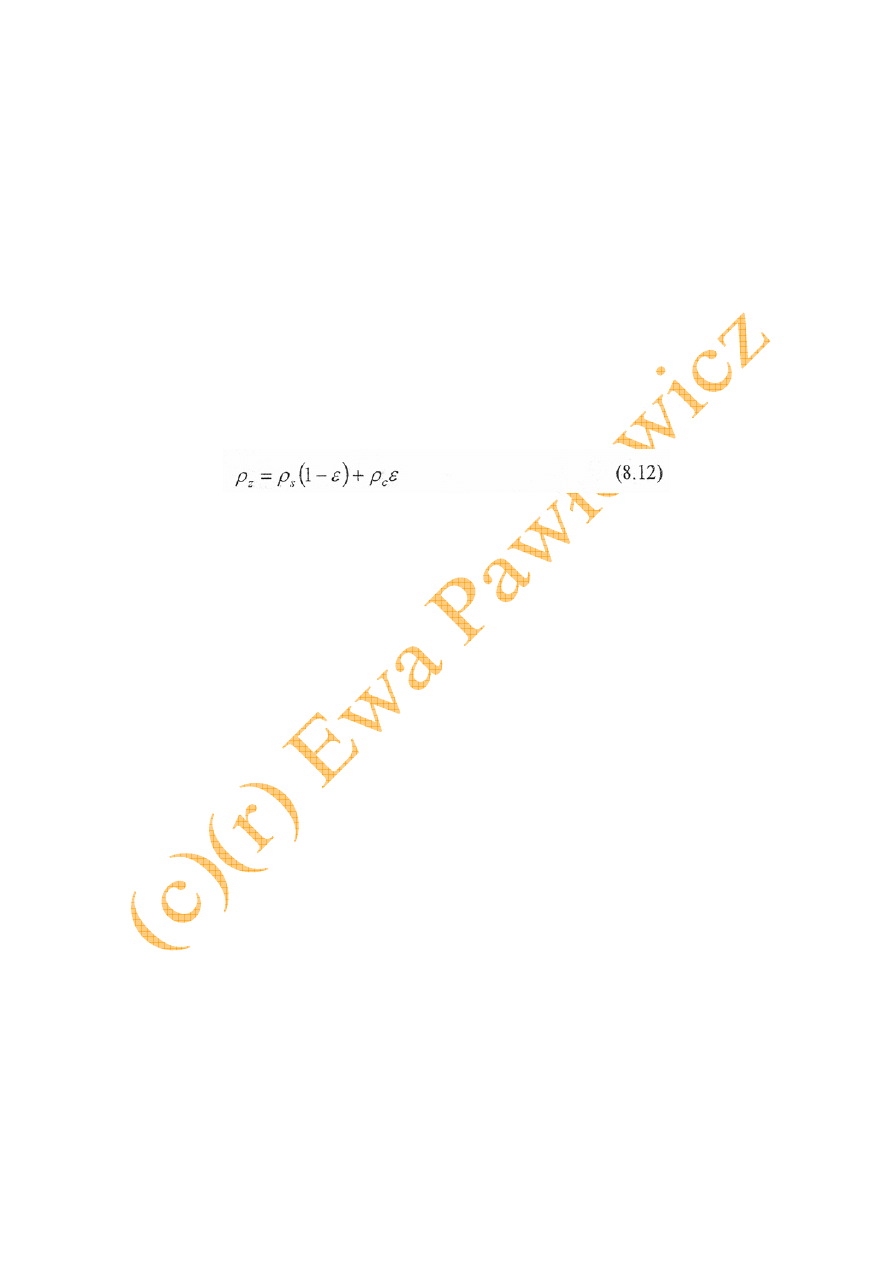
4

• gęstość nasypowa.

Gęstość materiałowa jest to stosunek masy cząstki ciała stałego do jej objętości. Jeżeli

ciało stałe jest porowate, to objętość porów odejmuje się od objętości cząstki ciała stałego.

Gęstość rzeczywista jest to stosunek masy cząstki do jej objętości zmniejszonej o objętość

porów otwartych. Gęstość pozorna cząstki jest to stosunek masy cząstki do jej objętości,

łącznie z porami otwartymi i zamkniętymi. Gęstość nasypowa jest to stosunek masy cząstek

do całkowitej objętości zajmowanej przez złoże. Objętość warstwy cząstek zależy od ich

upakowania. Spośród podanych wyżej pojęć gęstości cząstek w sedymentacji stosowana jest

głównie gęstość rzeczywista cząstki ps. Gęstość zawiesiny oblicza się z różnych wzorów, w

zależności od sposobu wyrażania stężenia ciała stałego i cieczy w zawiesinie. Na przykład,

jeżeli wykorzysta się porowatość E, to gęstość zawiesiny będzie wyrażona wzorem:

Lepkość zawiesiny zależy od stężenia ciała stałego, obecności innych. substancji

zmieniających oddziaływanie między cząstkami ciała stałego i między cieczą a cząstkami

ciała stałego, oraz od lepkości cieczy [l].

Najprostszym przypadkiem opadania cząstek ciał stałych w płynach pod wpływem

pola grawitacyjnego jest opadanie swobodne pojedynczej cząstki. Może ona opadać w sposób

ustalony bądź nieustalony. Prędkość swobodnego opadania cząstki zależy od własności

fizycznych płynu i cząstki, a w szczególności od różnicy gęstości cząstki i płynu, od jego

lepkości oraz od rozmiaru i kształtu cząstki. Opadająca cząstka może poruszać się ruchem

uwarstwionym, przejściowym lub burzliwym, w zależności od wartości liczby Reynoldsa,

określającej podobieństwo hydrodynamiczne (stosunek siły bezwładności do siły lepkości).

Jeżeli prędkość cząstki względem płynu jest mała, to warstwy płynu opływającego cząstkę nie

mieszają się i układają się w sposób przedstawiony na rys. 8.la. Cząstki płynu w pobliżu

powierzchni ciała stałego mają taki sam czas na jego opłynięcie jak pozostałe cząstki płynu.

Wynika z tego, że wokół cząstki tworzą się warstwy płynu, które przemieszczają się

względem siebie z różnymi prędkościami. Ten rodzaj ruchu nosi nazwę uwarstwionego.

Miarą tarcia wewnętrznego warstwy płynu jest jego lepkość.

5

Rys. Opływ cząstki przez płyn: a) zakres uwarstwiony, b) zakres przejściowy, c) zakres

burzliwy [1]

Jeżeli prędkość cząstki względem płynu rośnie, to układ warstw ulega zakłóceniu i

zaczynają tworzyć się wiry (rys. 8.lb), a ruch nazywa się ruchem przejściowym. Dalszy

wzrost prędkości cząstki, bardziej nieregularny jej kształt lub większa chropowatość jej

powierzchni powodują.. powiększenie obszaru zawirowań wokół cząstki i poza nią. Zachodzi

wówczas burzliwy opływ cząstki (rys. 8.lc).

Bardziej złożony jest proces opadania cząstek ciała stałego w zawiesinie. Jest on nazywany

opadaniem zakłóconym lub sedymentacją zawiesiny. Proces ten wykorzystywany jest w

praktyce przemysłowej do zagęszczania zawiesin w aparatach zwanych osadnikami.

Ponieważ na ruch każdej cząstki w zawiesinie wpływa obecność opadających cząstek

sąsiednich, więc prędkość opadania cząstek zależeć będzie od stężenia ciała stałego w

zawiesinie.

Podstawy teoretyczne i analizę procesu sedymentacji omówiono szczegółowo w

monografii [1].

Sedymentacja zawiesin cząstek ciała stałego o jednakowych rozmiarach i gęstości przebiega

w ten sposób, że cząstki opadają z taką samą prędkością. Wpływ stężenia na prędkość

opadania cząstek w zawiesinie monodyspersyjnej określa się, modyfikując równania

opisujące prędkość swobodnego opadania lub stosując inne modele procesu, jak np. model

przepływu cieczy przez warstwę ziarnistą, model komórkowy i inne. Uwzględnia się w ten

sposób oddziaływanie hydrostatyczne, lepkościowe, efekt tarcia oraz oddziaływanie

strumienia cieczy.

Sedymentację zawiesin można prowadzić jako proces okresowy lub ciągły.

Sedymentacja okresowa cząstek ciała stałego w cieczy zachodzi wtedy, gdy zawiesina

6

znajduje się w naczyniu, a natężenie dopływającej zawiesiny oraz natężenie wypływającego

osadu (zagęszczonej zawiesiny) są równe zeru.

Sedymentacja okresowa cząstek ciała stałego w cieczy zachodzi wtedy, gdy zawiesina

znajduje się w naczyniu, a natężenie dopływającej zawiesiny oraz natężenie wypływającego

osadu (zagęszczonej zawiesiny) są równe zeru.

Sedymentacja okresowa cząstek ciała stałego w cieczy zachodzi wtedy, gdy zawiesina

znajduje się w naczyniu, a natężenie dopływającej zawiesiny oraz natężenie wypływającego

osadu (zagęszczonej zawiesiny są równe zeru.

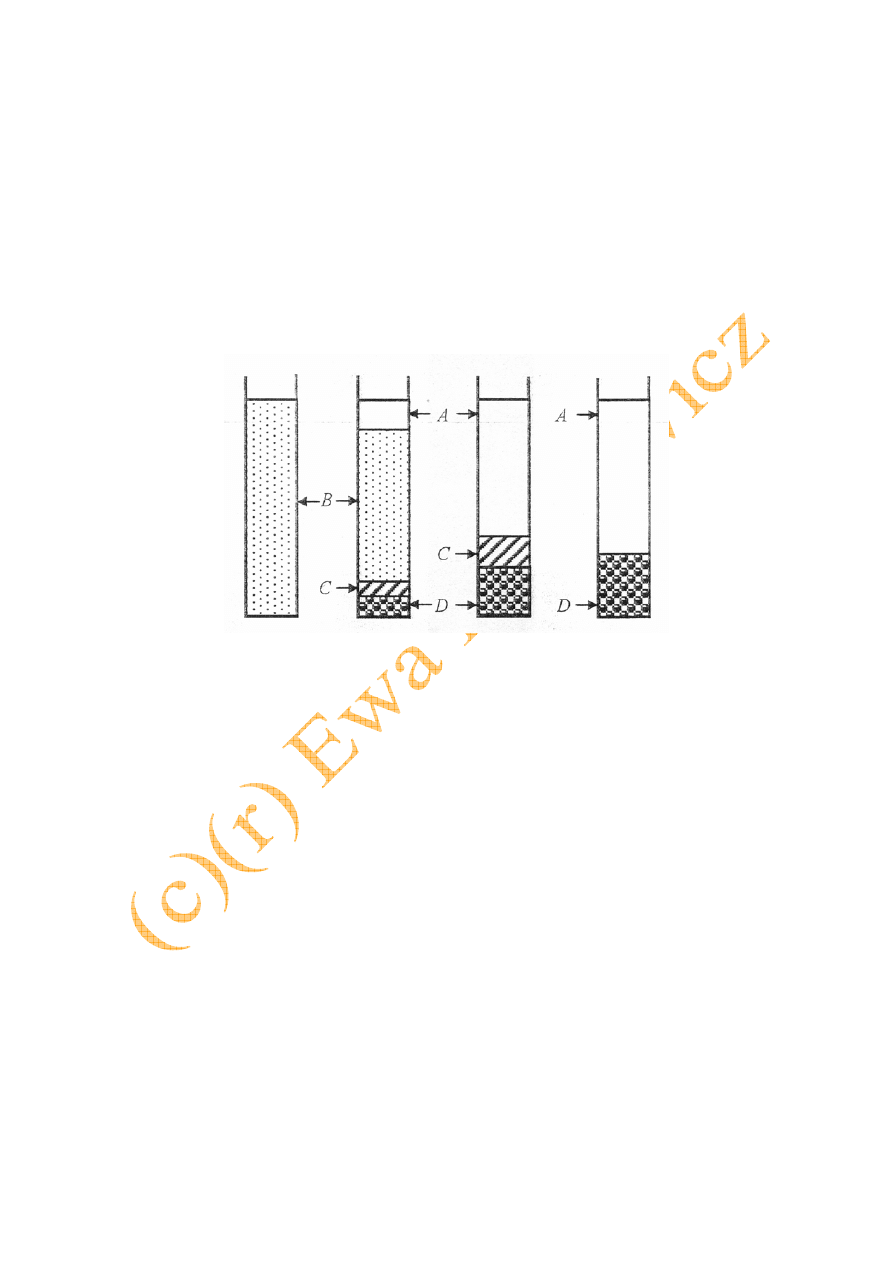
Rys. 8.2. Przebieg testu sedymentacyjnego [1]

Przebieg tego procesu można obserwować, wykonując doświadczenie nazywane

testem sedymentacyjnym zawiesiny. Badanie to polega na obserwacji zachowania się

zawiesiny umieszczonej w przeźroczystym cylindrze. Początkowa wysokość słupa zawiesiny

wynosi ho, a jej początkowe stężenie, jednakowe w każdym miejscu, równe jest φ

0

. Ten stan

początkowy dotyczy czasu t = 0. Od tego momentu rozpoczyna. się. sedymentacja zawiesiny.

Przebieg. tego procesu przedstawiono w sposób uproszczony na rys. 8.2. U góry cylindra

pojawia się granica między cieczą a zawiesiną i równocześnie na dnie naczynia zaczyna

narastać osad. Powstają zatem trzy strefy: ciecz czysta A, zawiesina B i osad D. Podczas

sedymentacji niektórych zawiesin strefa zawiesiny może składać się z dwóch części: górnej

B - o stałym stężeniu φ

0

i dolnej C - o zmiennym stężeniu. Z upływem czasu górna część

zawiesiny B zanika, a strefa osadu D narasta. W pewnym momencie granica między cieczą a

zawiesiną i granica między zawiesiną a osadem stykają się ze sobą i powstaje granica między

cieczą a osadem. Osad ulega dalszemu zagęszczeniu, aż do osiągnięcia stężenia φ

max

. Ze

względu na fakt, że na granicach między strefami następuje skok stężenia ciała stałego, noszą

7

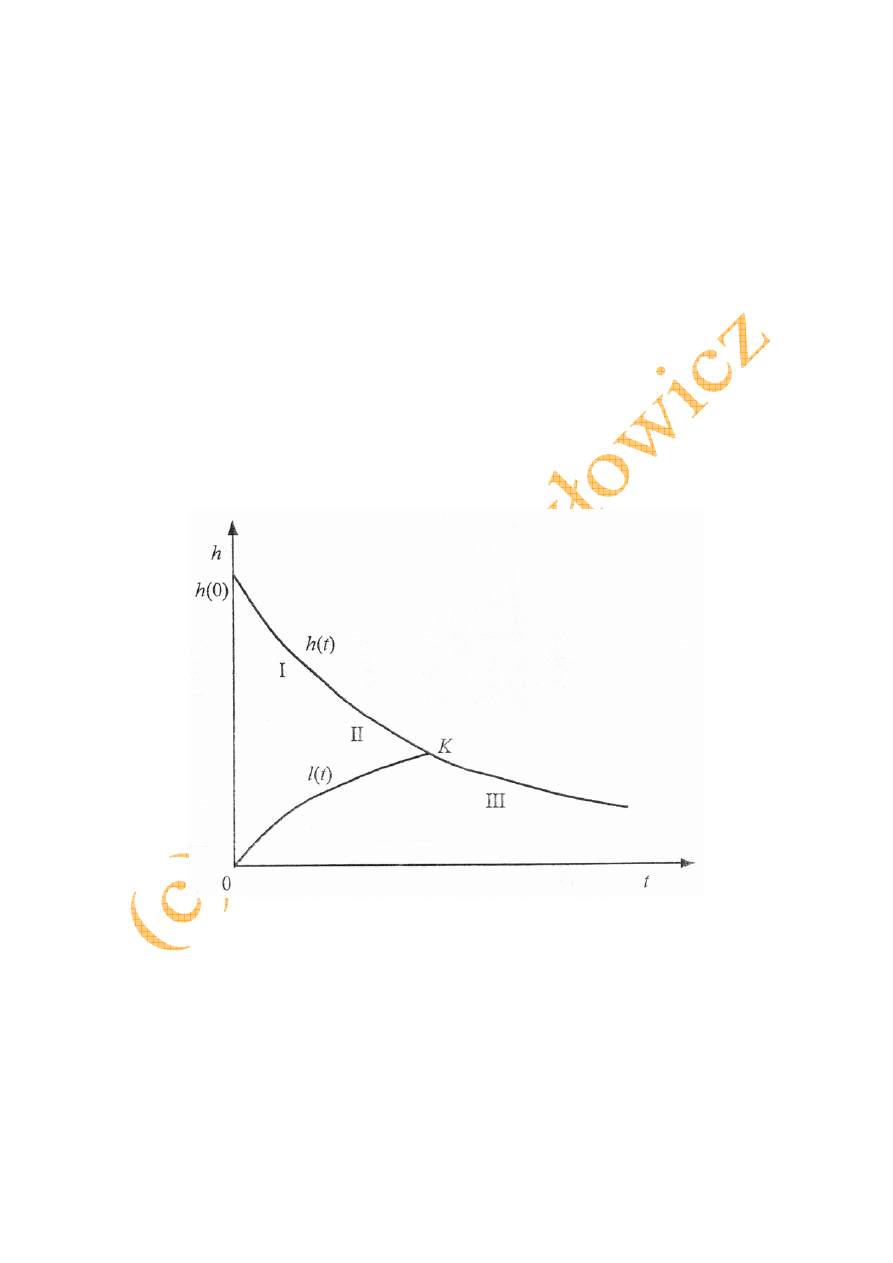
one również nazwę górnej i dolnej nieciągłości. Na podstawie odczytywanych wysokości

położenia górnej nieciągłości h i dolnej nieciągłości l, w zależności od czasu t, sporządza się

Wrykres przedstawiony na rys. 8.3. Krzywa h(t) nosi nazwę krzywej sedymentacji zawiesiny,

natomiast krzywa l(t) nazywa się krzywą narastania osadu. Na krzywej sedymentacji można

wyróżnić trzy charakterystyczne części: część prostoliniową i dwie części krzywoliniowe,

rozdzielone punktem przecięcia krzywej sedymentacji z krzywą narastania osadu. Punkt ten

nosi nazwę punktu krytycznego krzywej sedymentacji. Część prostoliniowa krzywej

sedymentacji odzwierciedla fakt występowania w cylindrze strefy zawiesiny o stałym

stężeniu φ

0

. Pierwsza część krzywoliniowa wskazuje na występowanie strefy zawiesiny o

zmiennym stężeniu, a druga część krzywoliniowa krzywej sedymentacji przedstawia

zagęszczenie osadu do stężenia φ

max

, któremu odpowiada wysokość h

min

.

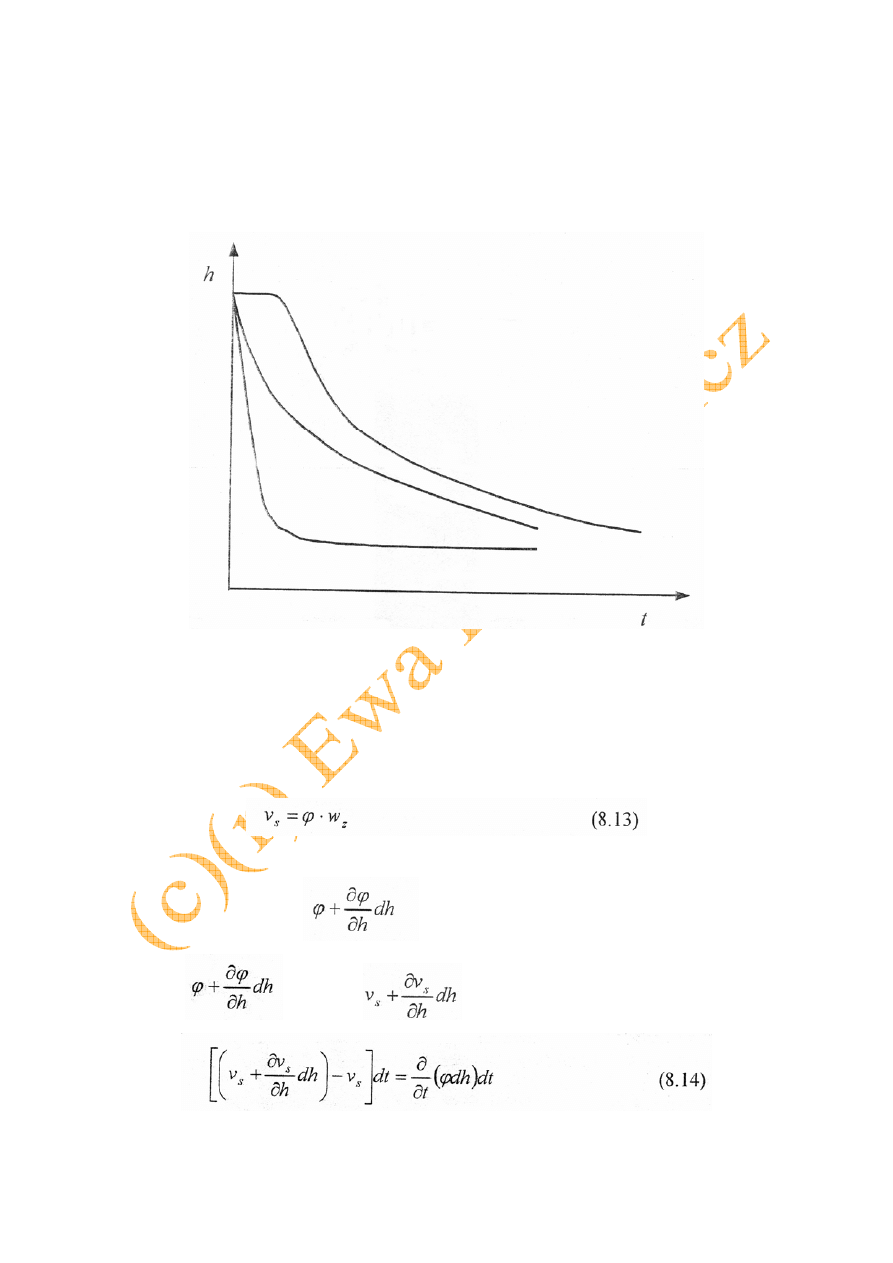
W zależności od rodzaju zawiesiny krzywe sedymentacji mogą mieć również inny kształt

(rys. 8.4).

Rys. 8.3. Krzywa sedymentacji i linia narastania osadu [1]

Kynch [4] przeprowadził analizę sedymentacji zawiesiny, Opierając się na

następujących założeniach [l]:

• stężenie ciała stałego φ w dowolnej poziomej warstwie jest takie samo,
• wpływa ścian naczynia można pominąć,
• różnice kształtu, rozmiaru i układu cząstek nie mają wpływu na prędkość opadania,
• prędkość opadania cząstek zależy tylko od ich lokalnego stężenia,

8

• początkowe stężenie zawiesiny φ

0

jest jednakowe w całej objetości bądź też rośnie w

kierunku dna naczynia,

• prędkość sedymentacji w

z

dąży do zera gdy stężenie zbliża się do wartości

odpowiadającej stężeniu warstwy osadu powstałej na dnie naczynia

Rys. 8.4. Kształty krzywej sedymentacji [1]

Objętościowe natężenie przepływu ciała stałego przypadające na jednostkę przekroju

poprzecznego, czyli gęstość strumienia ciała stałego w dowolnej poziomej warstwie o

stężeniu φ i prędkości w

z

, wyraża się zależnością:

Bilans masowy ciała stałego dla warstwy dh znajdującej się między poziomem h od dna,

gdzie stężenie jest równe

i strumień v

s

, a poziomem h + dh, gdzie stężenie

jest równe

i strumień

, prowadzi do równania:

9

którego prawa strona wyraża akumulację cząstek w czasie dt. Równanie (8.14) po

przekształceniu otrzymuje postać:

Ponieważ v

s

zależy tylko od φ, więc:

zatem:

Stężenie ciała stałego ciała stałego jest funkcją położenia i czasu, czyli:

Po spełnieniu warunku stałego stężenia, tzn. dφ = 0, równanie (8.18) przybierze formę:

Podstawienie wzoru (8.19) do równania (8.17) daje zależność:

Ponieważ równanie (8.20) odnosi się do określonego stężenia ciała stałego φ, więc dv

s

/dφ jest

stałe, a stąd również dh/dt jest stałe dla tego stężenia, czyli stała jest prędkość u

przemieszczania się strefy o tym stężeniu:

Gdy pochodna dv

s

/dφ ma wartość ujemną prędkość przemieszczania się strefy jest dodatnia,

zatem fala rozchodzi się ku górze, a w przypadku przeciwnym - ku dołowi. Rozpatrując fale

tworzące się przy dnie cylindra sedymentacyjnego, można stwierdzić, że fale, dla których

pochodna dv

s

/dφ jest ujemna, przemieszczają się do góry, w kierunku. powierzchni

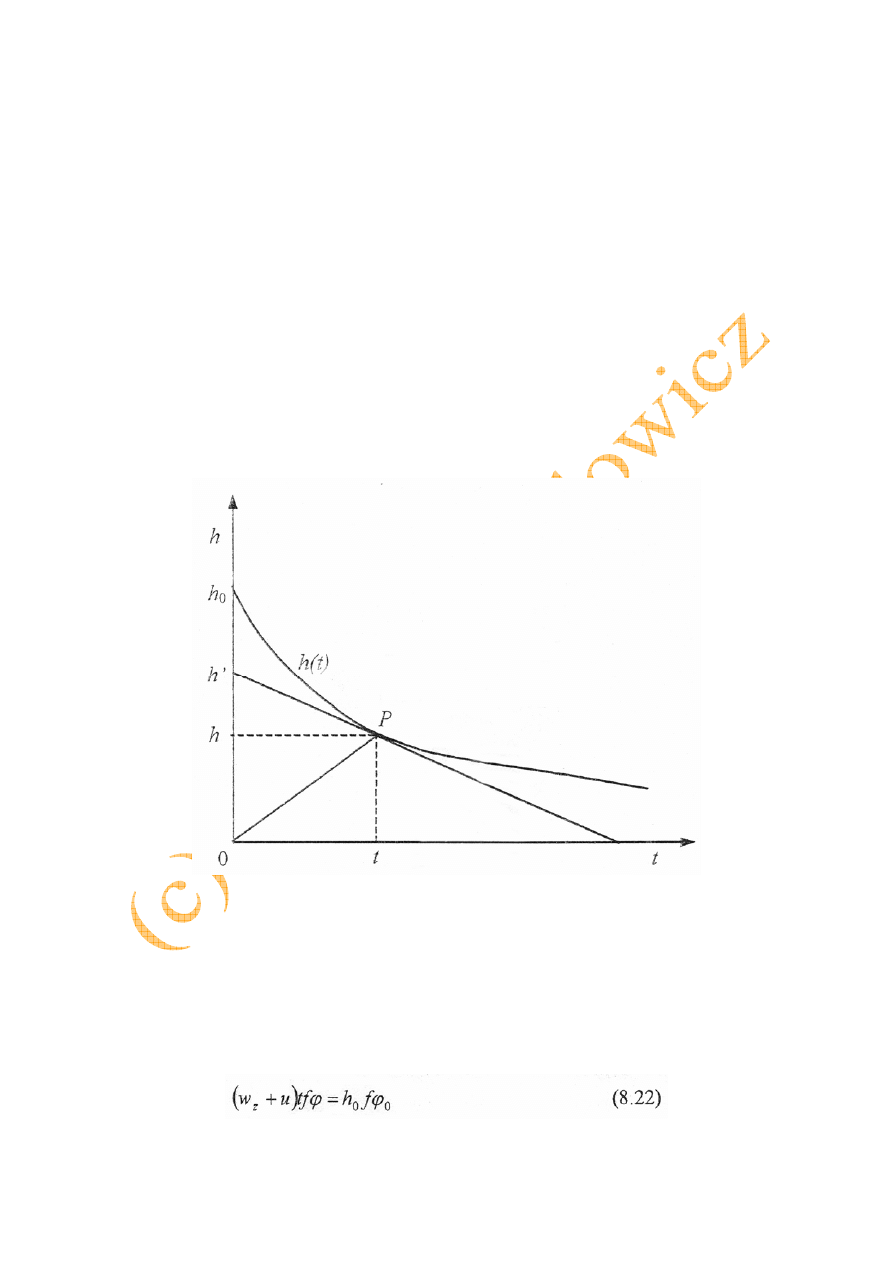
10

zawiesiny, a fale, dla których pochodna dv

s

/dφ jest dodatnia, nie będą powstawały ze względu

na obecność dna.

Jakkolwiek teoria Kyncha może być zastosowana do dowolnej zawiesiny, której

stężenie w chwili początkowej rośnie w kierunku dna naczynia, to jednak dalsze rozważania

ograniczone zostaną do przypadku, gdy początkowe stężenie zawiesiny jest jednakowe w

całej objętości i wynosi φ

0

. Wówczas granica między zawiesiną a cieczą opada ze stałą

prędkością aż do chwili, gdy strefa o stężeniu większym niż φ

0

przemieści się od dna do

powierzchni zawiesiny. Prędkość sedymentacji będzie stale się zmniejszała, w miarę jak

strefy o większym stężeniu będą osiągały powierzchnię zawiesiny i sedymentacja zakończy

się, gdy strefa o stężeniu φ

max

osiągnie powierzchnię. Powyższe rozważania można

wykorzystać w celu interpretacji krzywej sedymentacji otrzymanej na podstawie testu

sedymentacyjnego (rys. 8.5).

Rys. 8.5. Interpretacja krzywej sedymentacji według Kyncha[1]

Całkowita objętość ciała stałego w cylindrze testowym o przekroju poprzecznym f

wynosi h

0

fφ

0

. Jeżeli strefa o stężeniu φ, przemieszczając się od dna cylindra, osiągnęła

powierzchnię zawiesiny po czasie t, to musiały przejść przez nią wszystkie cząstki ciała

stałego. Wówczas:

11

Kynch przyjął, że prędkość przemieszczania się stref o stałym stężeniu jest stała, a więc

równanie (8.21) można zastąpić zależnością:

Równanie (8.23) przedstawia linię prostą wychodzącą z początku układu współrzędnych

(rys. 8.5). Po podstawieniu zależności (8.23) do wzoru (8.22) otrzymuje się równanie:

Z kolei prędkość sedymentacji w

z

określona jest pochyleniem stycznej do krzywej

sedymentacji:

Na podstawie zależności (8.24) i (8.25) można napisać że:

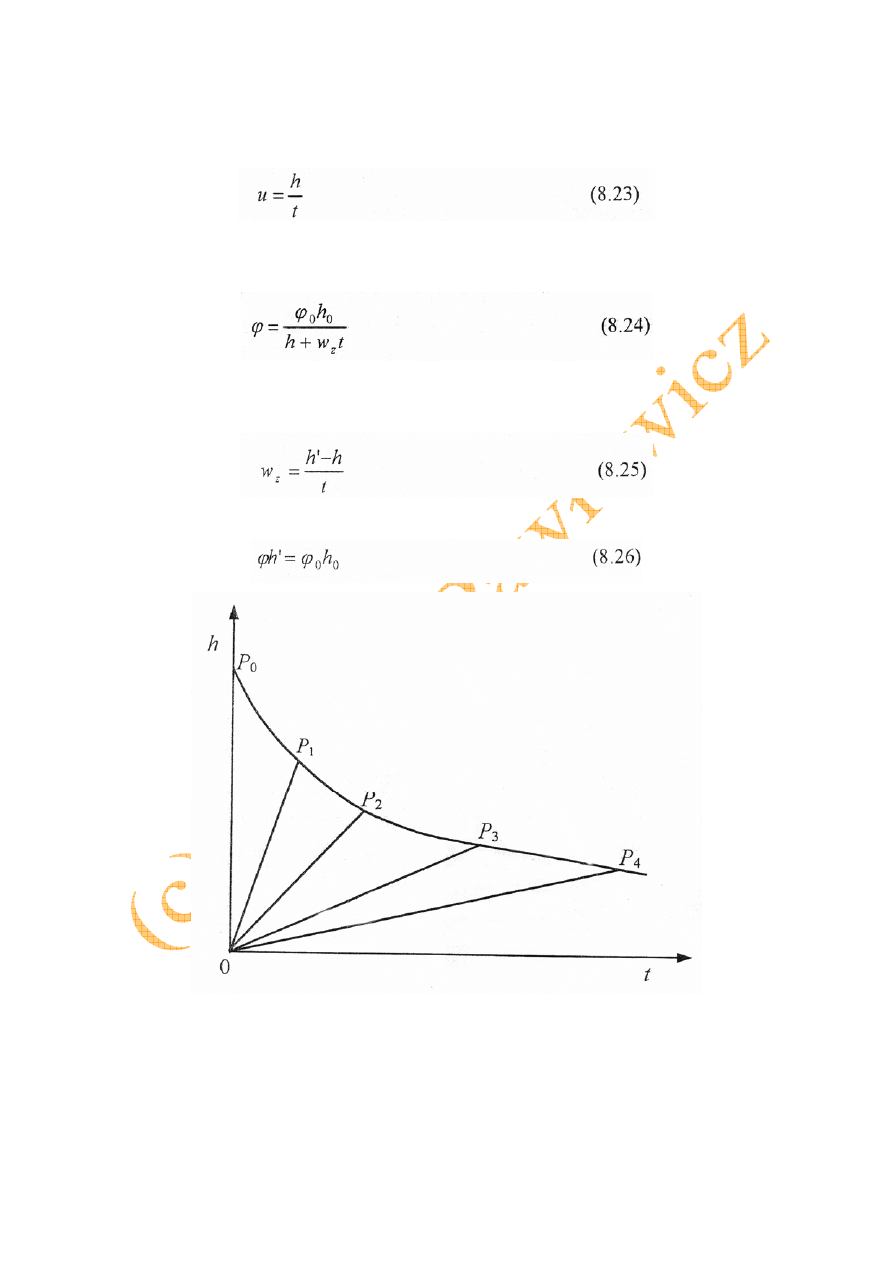
Rys. 8.6. Odcinki odpowiadające strefom o różnych stężeniach ciała stałego [1]

Wielkość rzędnej h' określa wysokość słupa zawiesiny o stężeniu φ, która zawiera taką

samą objętość ciała stałego jak początkowa zawiesina. Na podstawie sedymentacyjnej teorii

Kyncha można wyznaczyć stężenia w dowolnych punktach krzywej sedymentacji (rys. 8.6),

12

korzystając ze wzoru (8.24). Przez te punkty oraz przez początek układu współrzędnych

prowadzi się pęk linii prostych o różnym pochyleniu. Każda z nich odnosi się do strefy o

określonym stężeniu, która przemieszcza się od dna cylindra w kierunku górnej nieciągłości

(granica między cieczą a zawiesiną) z prędkością określoną wzorem (8.23). Jeśli początkowy

odcinek krzywej sedymentacji P

0

P

1

jest prostoliniowy, to prędkość sedymentacji jest stała i

zgodnie z równaniem (8.24) - stałe jest również stężenie, równe stężeniu początkowemu φ

0

.

Prędkość przemieszczania się strefy o stężeniu φ

0

jest największa, a jej miarą jest tangens kąta

pochylenia odcinka OP

1

. Każda następna strefa o większym stężeniu przemieszcza się z

prędkością odpowiednio mniejszą. W punkcie P

4

stężenie osiąga wartość φ

max

.

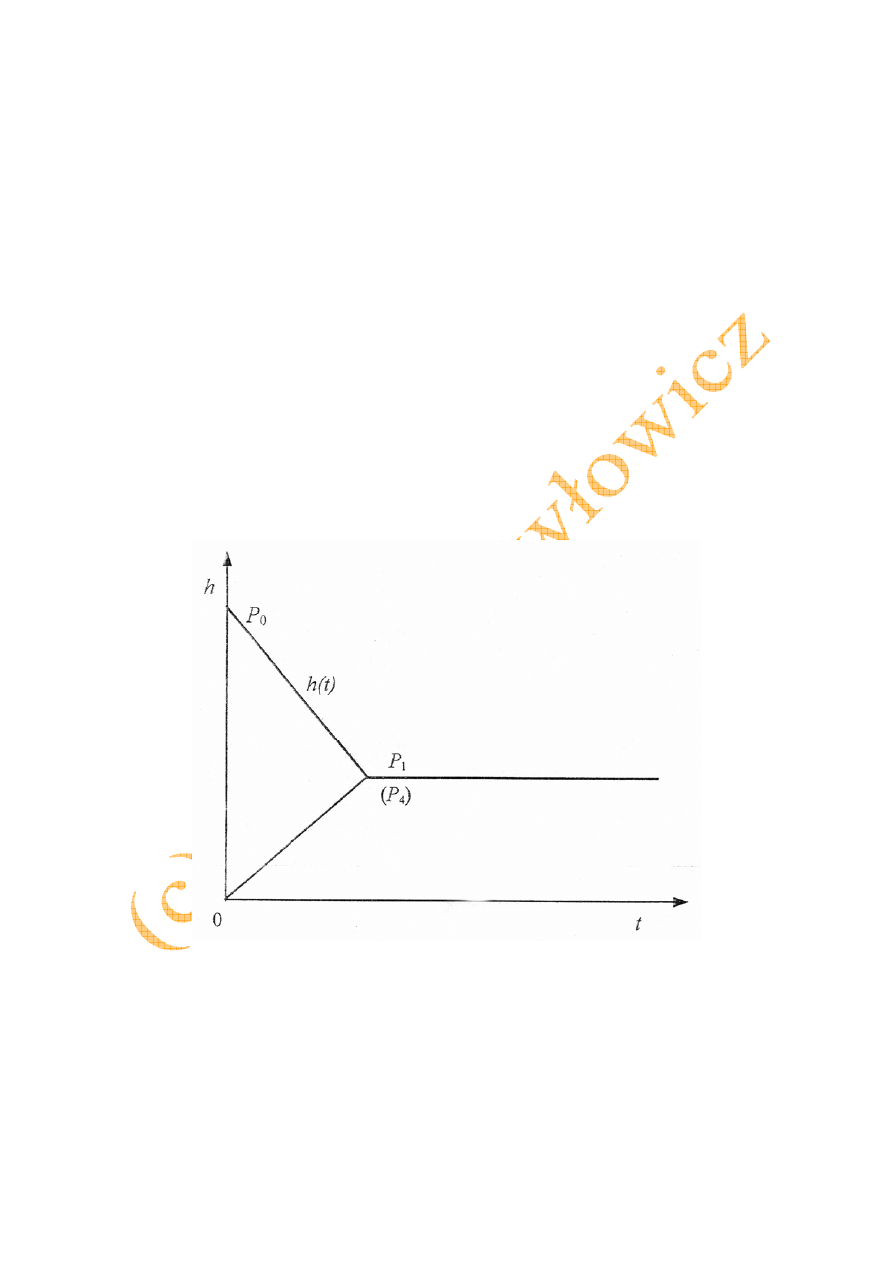
Szczególny przypadek krzywej sedymentacji przedstawiono na rys. 8.7. Składa się ona z dwu

części prostoliniowych, brak jest natomiast środkowej części krzywoliniowej. Odpowiada to

skokowej zmianie stężenia zawiesiny od wartości początkowej φ

0

do końcowej φ

max

. Górna

nieciągłość porusza się z prędkością równą ujemnemu tangensowi kąta pochylenia odcinka

P

0

P

1

, a dolna z prędkością równą tangensowi kąta pochylenia odcinka OP

1

[l].

Rys. 8.7. Krzywa sedymentacji odpowiadająca skokowej zmianie stężenia [1]

W podstawach teoretycznych sedymentacji Kynch. [4] nie uwzględnił jednak wpływu

tworzenia się osadu na przebieg procesu, co stanowi istotną cechę sedymentacji okresowej.

Zagadnienie to zostało szczegółowo przeanalizowane w pracy Tillera [5].

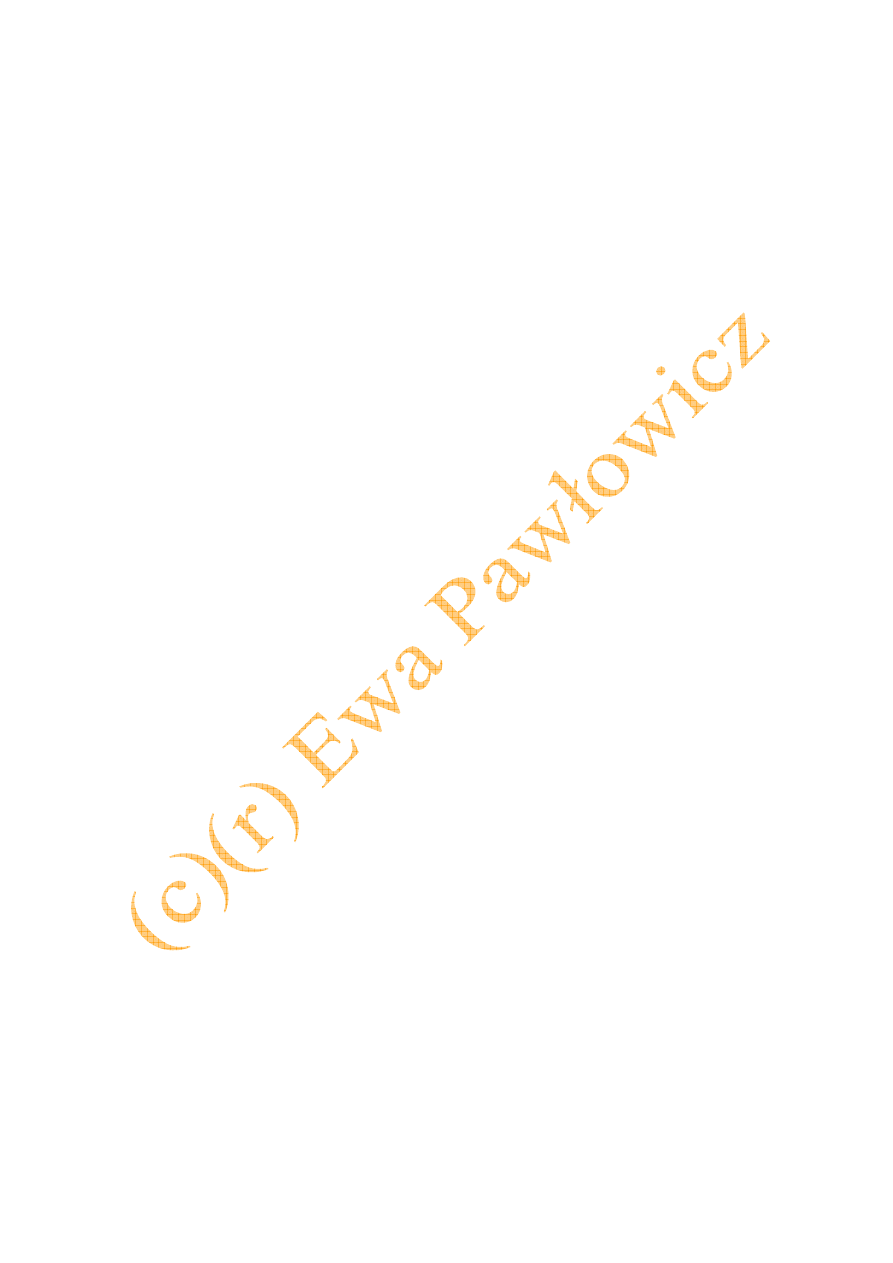
13

Sedymentacja zawiesin znajduje szerokie zastosowanie w technologiach wielu gałęzi

przemysłu oraz w ochronie środowiska naturalnego. Chodzi tu zwłaszcza o zakłady

przemysłowe uciążliwe dla środowiska, jak cukrownie, przetwórnie ziemniaków, zakłady

mięsne i drobiarskie. Ponadto tradycyjne osadniki pracują w górniczych zakładach przeróbki

kopalin oraz w komunalnych oczyszczalniach ścieków [l].

Sedymentacja ciągła polega na stworzeniu w osadniku takich warunków, które

pozwoliłyby doprowadzić do ciągłego rozdziału na czystą ciecz i osad. Przyjmuje się, że w

procesie sedymentacji ciągłej decydują warunki panujące w tzw. warstwie granicznej, której

odpowiada graniczna wartość strumienia ciała stałego. Stanowi ona podstawę do wyznaczenia

powierzchni osadnika. Podczas sedymentacji zawiesiny w osadniku ciągłym można

stwierdzić występowanie stref o różnych stężeniach. Wysokości stref nie zmieniają się; przy

niezmiennych natężeniach przepływu suma tych wysokości określa głębokość odstojnika [l].

Proces zagęszczania zawiesiny prowadzi się w aparatach zwanych odstojnikami.

Urządzenia te pracują w sposób okresowy, półciągły lub ciągły.

Odstojniki o działaniu okresowym są to aparaty typu zbiornikowego o przekroju

kołowym, zaopatrzone w szkła wzierne i króćce równomiernie rozmieszczone w pewnych

odległościach na odpowiedniej wysokości. Zawiesinę o objętości równej pojemności

odstojnika doprowadza się do nich jednorazowo. W miarę opadania cząstek ciała stałego pod

działaniem siły ciężkości wzrasta wysokość warstwy cieczy klarownej w górnej części

odstojnika. Ciecz klarowną odprowadza się okresowo króćcami umieszczonymi w ścianie

odstojnika, zaopatrzonymi w zawory. Osad w postaci szlamu odprowadza się króćcem

umieszczonym w dnie odstojnika po odprowadzeniu całkowitej objętości cieczy klarownej.

W odstojnikach o działaniu półciągłym doprowadzenie zawiesiny i odprowadzenie

cieczy klarownej odbywa się w sposób ciągły, natomiast osad odprowadza się w sposób

okresowy.

14

W odstojnikach o działaniu ciągłym zarówno doprowadzenie zawiesiny, jak i

odprowadzenie cieczy klarownej i osadu odbywa się w sposób ciągły.

Rys. 8.8. Odstojnik Dorra o działaniu ciągłym [2]: 1 – rynna, 2- wał, 3 – płyty zgarniacza

osadu, 4 – rura dopływowa zawiesiny, 5 – króciec odpływowy osadu w postaci

szlamu, 6 – króciec odpływowy cieczy klarownej

Na rysunku 8.8 przedstawiono schemat odstojnika o działaniu ciągłym zwanego

odstojnikiem Dorra. Jest to aparat cylindryczny, zamknięty dnem stożkowym o dużym kącie

rozwarcia. W górnej części cylindrycznej na całym jej obwodzie znajduje się prostokątna

rynna (1) służąca do odprowadzania cieczy klarownej. Do wału (2) wewnątrz aparatu są

przymocowane ramiona zaopatrzone w prostokątne płyty (3), które zgarniają osad ze

stożkowatego dna. Zawiesinę doprowadza się rurą (4), której dolna część znajduje się poniżej

powierzchni cieczy w odstojniku. Zawiesina rozpływa się na. całą powierzchnię odstojnika

poniżej powierzchnii cieczy i cząstki ciała stałego opadają na powierzchnię dna stożkowego,

skąd w postaci :szlamu są zgarniane do króćca (5) odprowadzającego osad. Ciecz klarowna

natomiast przepływa do góry, przelewa się na całym obwodzie do rynny (l) i króćcem (6)

odpływa z odstojnika.

Odstojniki o działaniu ciągłym mają średnice, których wielkość dochodzi do 200 mm,

a wysokość - do 7 m. Wadą odstojników jako aparatów do rozdzielania zawiesin jest to, że

zajmują one dużo miejsca. W celu lepszego wykorzystania miejsca w budynkach fabrycznych

buduje się odstojniki wielokomorowe. składające się z kilku odstojników o małej wysokości,

umieszczonych jeden na drugim.

15

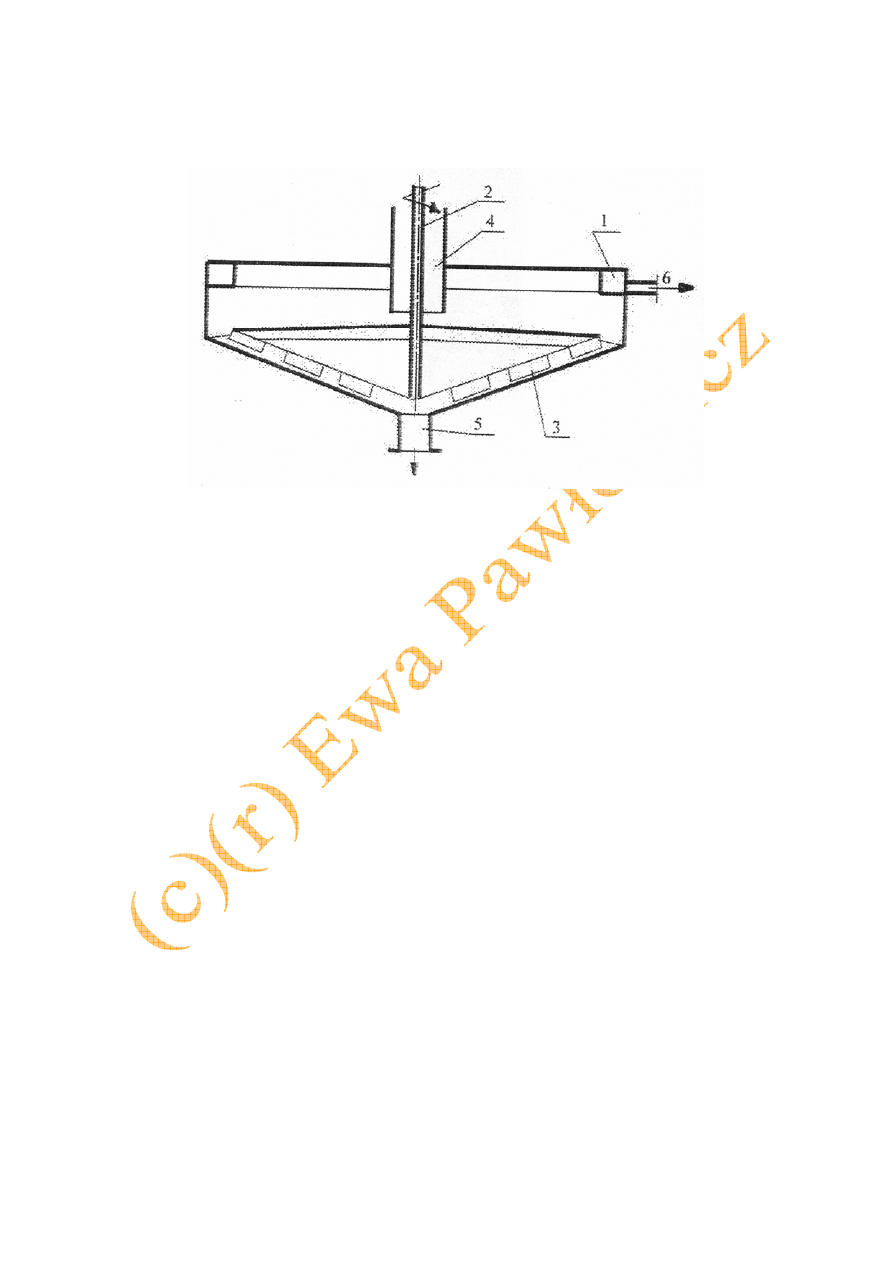
W odstojniku dwukomorowym (rys. 8.9), składającym się z odstojnika - komory (1) i

(2) - zawiesina dopływa ze wspólnego przewodu (3) przewodami (3a) i (3b). Osad z górnego

odstojnika spływa do odstojnika dolnego i razem z osadem otrzymanym z zawiesiny

doprowadzanej do tego odstojnika jest odprowadzany w postaci szlamu przewodem (4). Ciecz

klarowna przewodami (5a) i (5b) przepływa do jednego wspólnego przewodu (5).

Rys. 8.9. Odstojnik dwukomorowy [2]: 1, 2 – komory odstawiania, 3, 3a, 3b – przewody

dopływowe zawiesiny, 4 – odpływ szlamu, 5, 5a, 5b – przewody odpływowe

cieczy klarownej

Jeżeli zachodzi potrzeba nie tylko oddzielenia cząstek od fazy ciekłej, ale rozdzielenia

ich na pewne frakcje w zależności od wielkości, to proces ten, zwany klasyfikacją

hydrauliczną, prowadzi się w klasyfikatorach hydraulicznych.

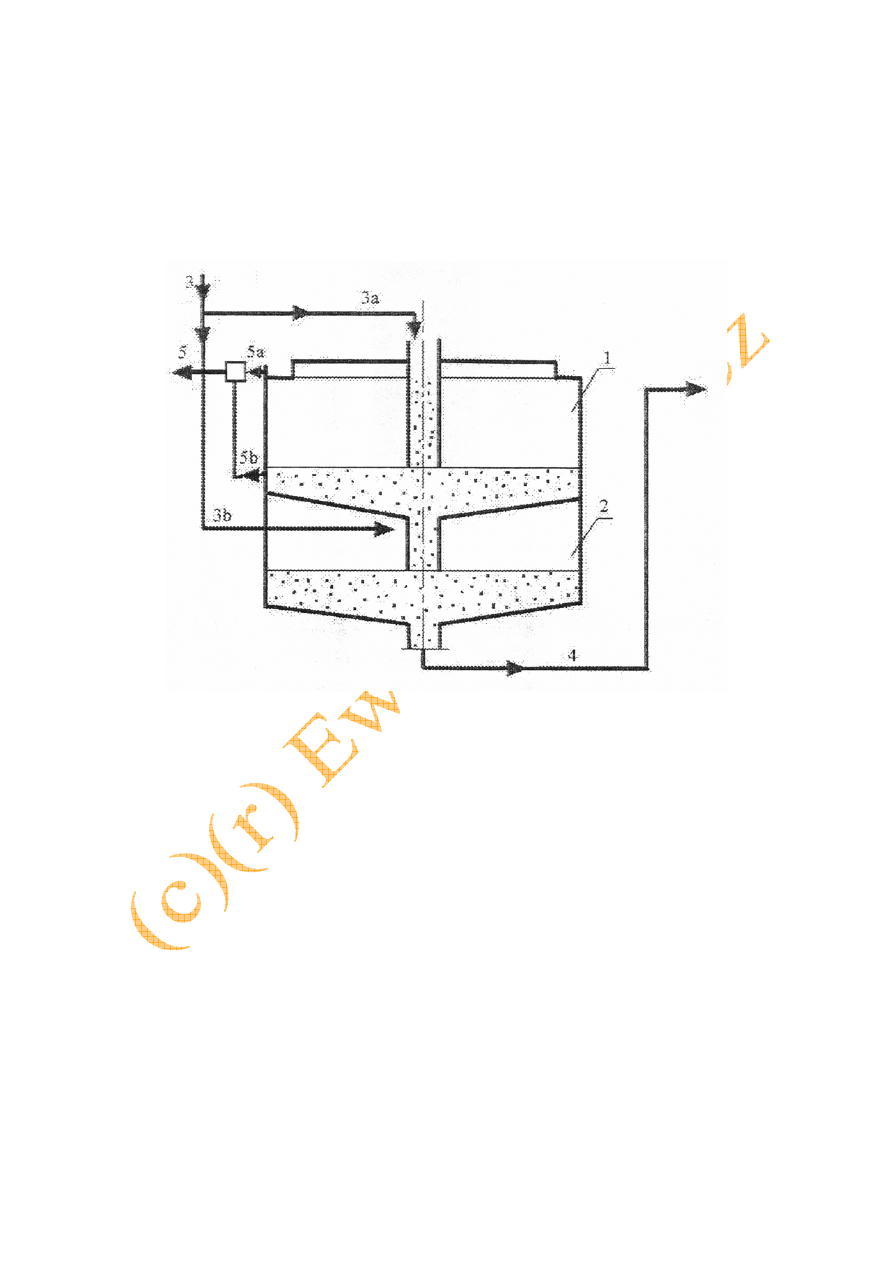
Klasyfikator hydrauliczny (rys. 8.10) składa się z kilku skrzyń w kształcie

odwróconych ostrosłupów o podstawie prostokątnej połączonych ze sobą szeregowo.

Zawiesina dopływa przewodem (l) do skrzyni (2), której przekrój prostopadły do kierunku

przepływu jest najmniejszy w porównaniu z przekrojami skrzyń dalszych, ale jest większy od

przekroju przewodu doprowadzającego. W wyniku zwiększenia się przekroju przewodu

maleje prędkość i w skrzyni (2) opadają cząstki największe. W miarę przepływu w

następnych skrzyniach (3) i (4) stopniowo opadają coraz to mniejsze cząstki. Ciecz klarowna

16

odpływa z ostatniej skrzyni przewodem (5), a osad - indywidualnie z każdej skrzyni

przewodami (2a), (3a);:1(4a) stanowiącymi zamknięcia hydrauliczne.

Rys. 8.10. Klasyfikator hydrauliczny [2]: 1 – przewód dopływowy zawiesiny, 2, 3,

4 – skrzynie klasyfikatora, 2a, 3a, 4a – odpływ szlamu, 5 – króciec odpływowy

cieczy klarownej

W klasyfikatorach hydraulicznych osad można rozdzielać, wykorzystując różnicę

gęstości cząstek ciała stałego, jeżeli ten osad stanowi mieszaninę dwóch lub kilku składników

ciała stałego, a więc można prowadzić proces sortowania hydraulicznego [2].

17

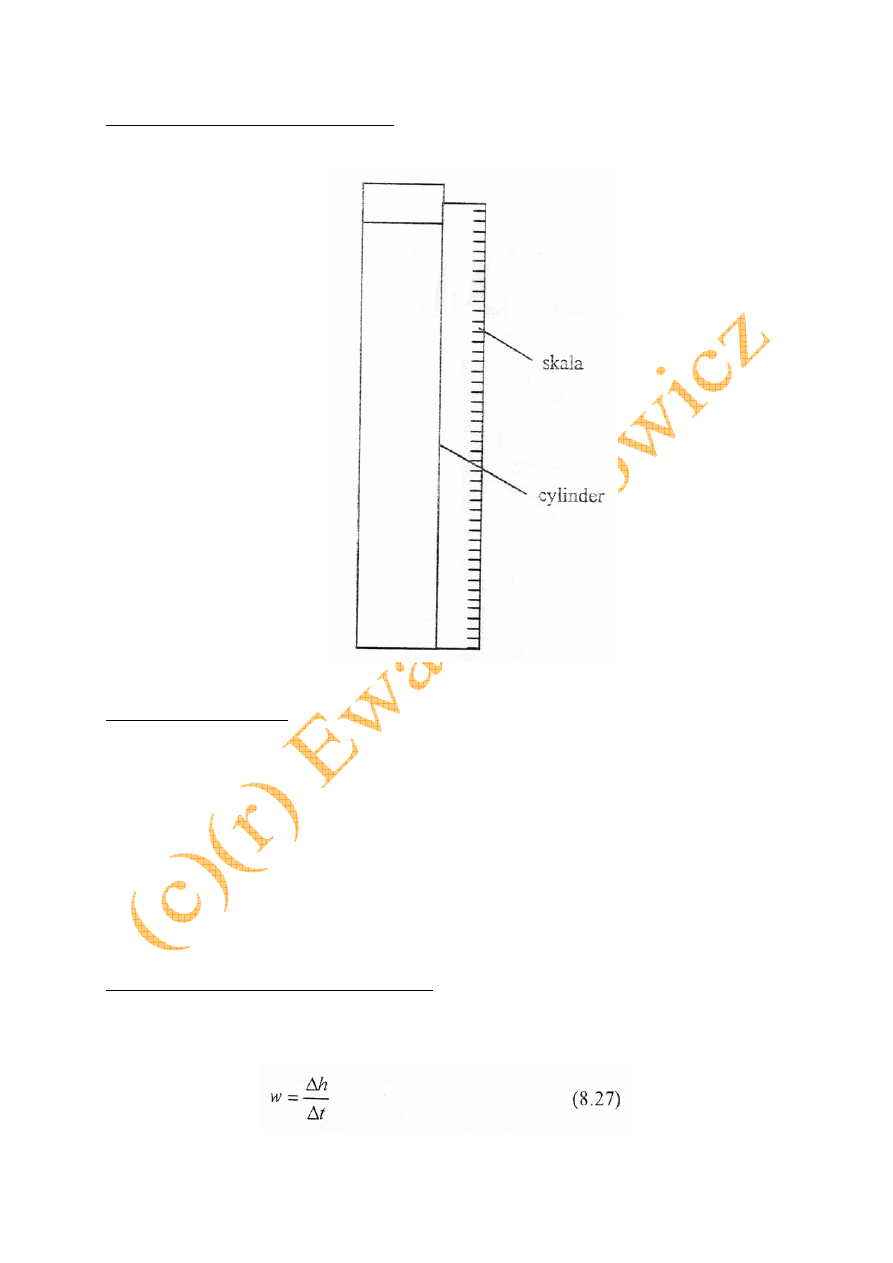
8.2. Schemat i opis instalacji badawczej

Zestaw do wykonywania testu okresowego przedstawiono na rys. 8.11.

8.3. Metodyka pomiarów

Badania procesu sedymentacji polegają na wyznaczaniu zależności wysokości.

warstwy zawiesiny od czasu. Pomiary te wykonuje się w cylindrze o pojemności l dm

3

.

Zadane naważki substancji stałej odważa się na wadze szalkowo-uchylnej, wprowadza się do

cylindra i uzupełnia wodą do objętości 1 dm

3

. Z różnicy mas cylindra z zawiesiną i cylindra

pustego wyznacza się średnią gęstość zawiesiny. Po dokładnym wymieszaniu układu ciecz-

ciało stałe odczytuje się wysokości warstwy zawiesiny w odstępach jednominutowych.

8.4. Opracowanie i korelacja wyników badań

Uzyskane wyniki badań przedstawia się najpierw graficznie w postaci zależności

h = f(t), a następnie wyznacza się prędkości sedymentacji ze wzoru:

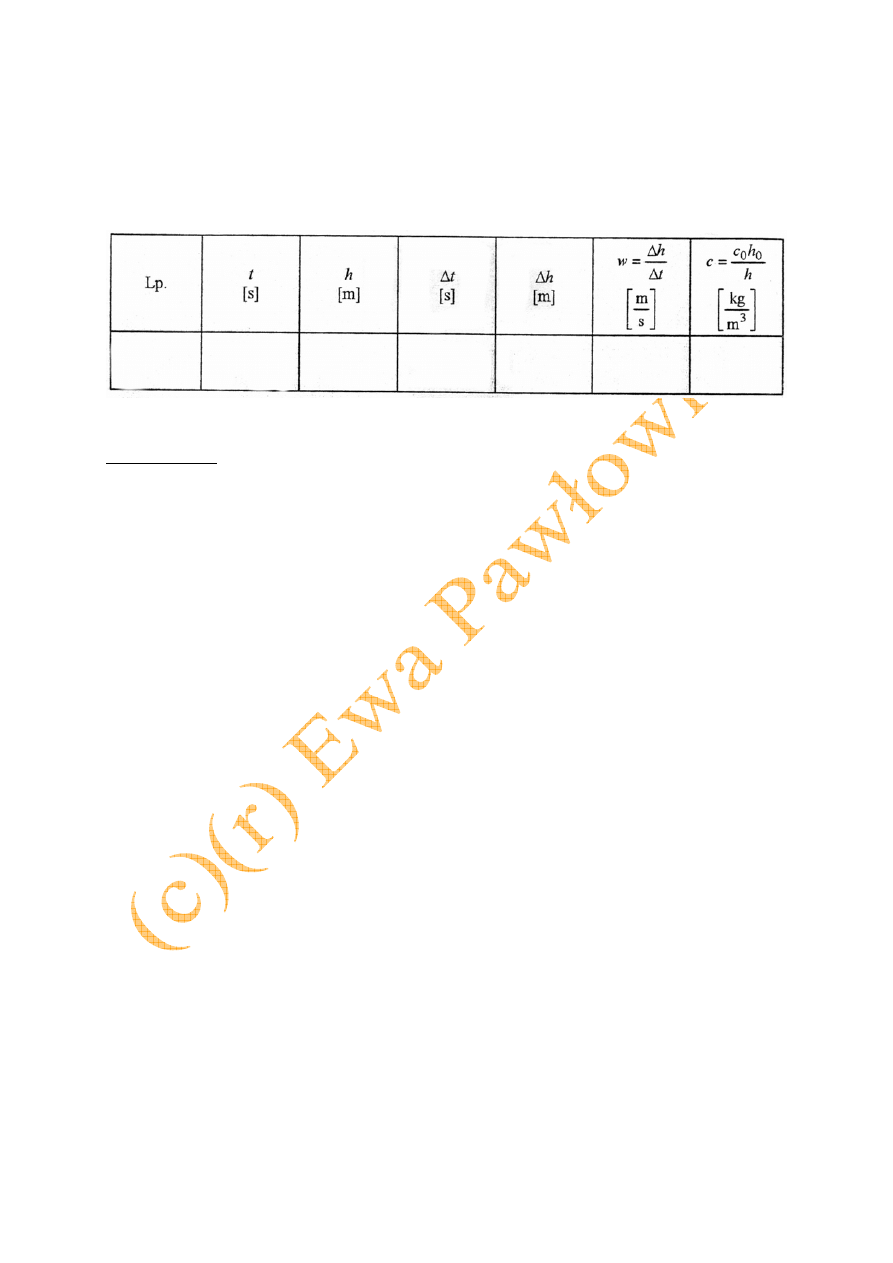
18

Następnie przeprowadza się analizę zależności zmian prędkości od czasu oraz od stężenia

zawiesiny.

Tabela 8.1

Tabela pomiarowo – obliczeniowa (wzór)

8.5. Literatura

[1] BandrowskiJ., Merta H., Zioło J., Sedymentacja zawiesin. Zasady i projektowanie,

Gliwice, Wydawnictwo Politechniki Śląskiej 1995.

[2] Błasiński H., Młodziński B., Aparatura przemysłu chemicznego, Warszawa,

WNT 1971.

[3] Broniarz – Press L., Borowski J., Wesołowski P., Różański J., Inzynieria

chemiczna i procesowa. Materiały pomocnicze, Poznań Wydawnictwo Politechniki

Poznańskiej 1999.

[4] Kynch G.J., A theory of sedimentation, Trans. Faraday Soc., 1952, 48, s. 166.

[5] Tiller F.M., Revision of Kynch sedimentation theory, AIChE Journal, 1981,27,5,

s.823-829