We wszystkich zagadnieniach rozpatrywanych w poprzednich rozdziałach

związki geometryczne były zadawane w swej ścisłej postaci, natomiast w czasie

rozwiązywania wprowadzono przybliżenia. W klasycznej teorii płyt wprowadza się

założenie o liniowej zmienności odkształceń i naprężeń na prostych prostopadłych do

płaszczyzny płyty, w celu sprowadzenia do zagadnienia dwuwymiarowego. Założenie to

dotyczy tzw. płyt cienkich przy małych ugięciach.

Stan odkształceń płyty może być całkowicie opisany za pomocą jednej

wielkości. Jest nią poprzeczne przemieszczenie u

z

powierzchni środkowej płyty. Warunki

ciągłości pomiędzy elementami są teraz nałożone nie tylko na u

z

, lecz również na jej

pochodne. Funkcje kształtu, które nie zapewniają ciągłości nachylenia między

elementami nazywamy niedostosowanymi. Te, które zapewniają tę ciągłość –

nazywamy dostosowanymi. Najprostszym elementem do opisu jest element prostokątny.

PŁYTY

Wstęp

Przemieszczenia płyty według teorii płyt cienkich są jednoznacznie określone przez ugięcia u

z

.

Ugięcie to zapiszemy w postaci:

 

 



N

u

z



gdzie

 



























l

k

j

i











Ponieważ odkształcenia w płycie są definiowane przez drugie pochodne, jako parametry

węzłowe przyjmujemy przemieszczenia

)

(i

z

u

, obroty

)

(i

x



wokół osi x i obrót

)

(i

y



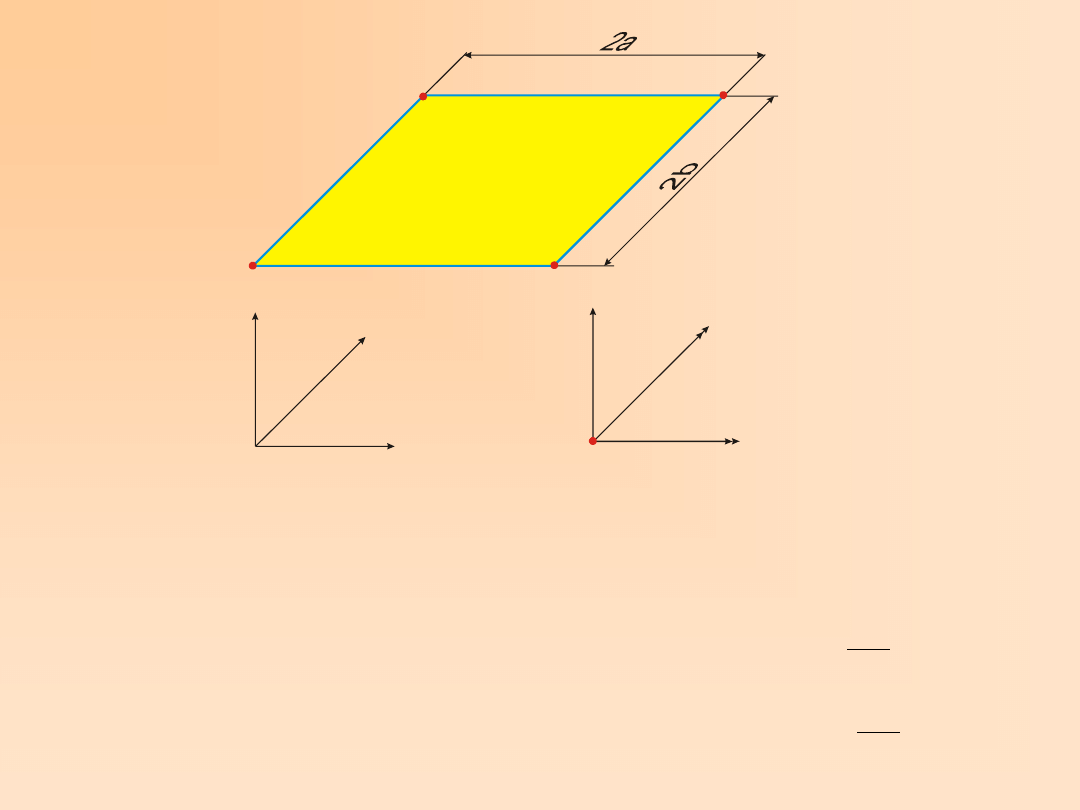
wokół osi y (rys. 5.1).

Funkcje przemieszczeń

(5.1)

i

k

l

x

y

z

j



x

x

(M )



y

y

(M )

u (F )

z

z

Możemy, więc zapisać, zgodnie z teorią płyt cienkich

 



































































































)

(

)

(

)

(

)

(

)

(

)

(

i

z

i

z

i

z

i

y

i

x

i

z

i

x

u

y

u

u

u



(5.2)

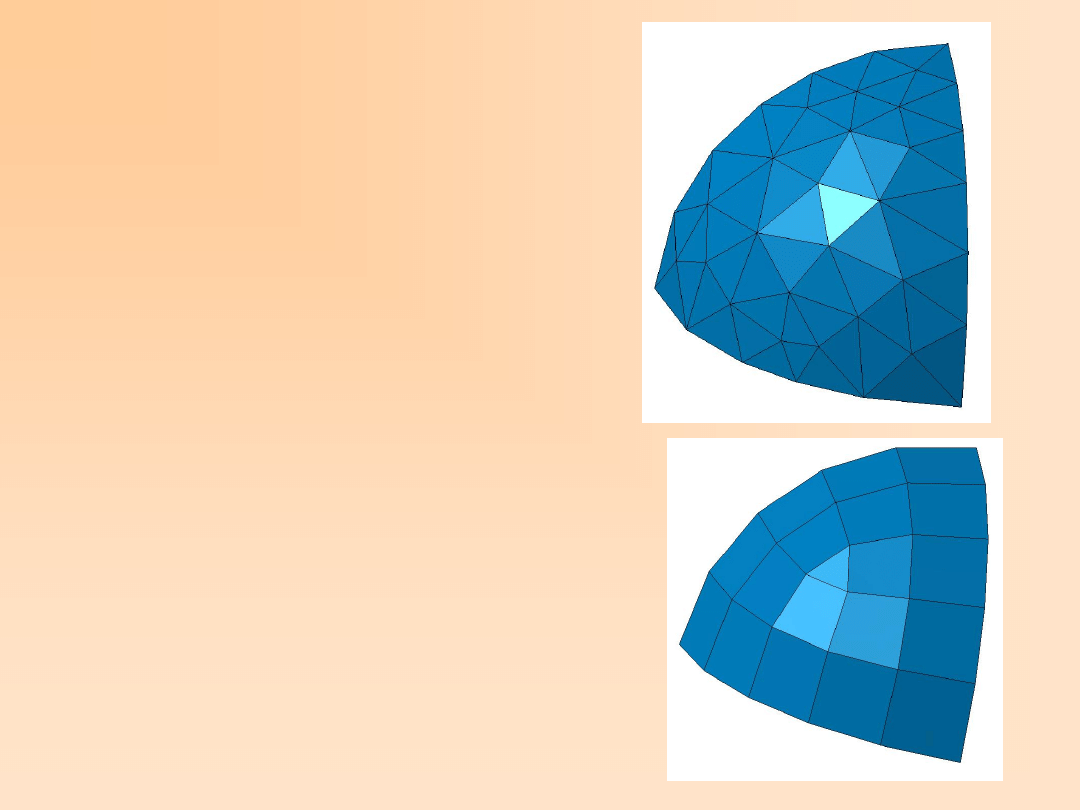
Element płytowy prostokątny

Rys. 5.1.

W elemencie prostokątnym występuje wobec tego dwanaście parametrów. Przyjmujemy następującą
aproksymację

3

12

3

11

3

10

2

9

2

8

3

7

2

6

5

2

4

3

2

1

xy

y

x

y

xy

y

x

x

y

xy

x

y

x

u

z

















































inaczej

 

 



P

u

z



gdzie

]

,

,

,

,

,

,

,

,

,

,

,

1

[

]

[

3

3

3

2

2

3

2

2

xy

y

x

y

xy

y

x

x

y

xy

x

y

x

P



(5.5)

T

}

,...,

,

,

{

}

{

12

3

2

1













Stałe

1



do

12



można określić pisząc dwanaście równań wiążących wielkości u

z

i jej pochodnych w węzłach

i

i

i

i

i

i

i

i

i

yi

i

z

i

i

i

i

i

i

i

i

i

xi

i

z

i

i

i

i

i

i

i

i

i

z

y

x

y

x

y

x

y

y

y

x

u

y

x

x

y

y

x

x

y

x

y

u

y

x

y

y

x

x

y

x

u

2

11

3

12

2

7

8

2

9

5

4

2

2

12

3

11

2

10

9

2

8

6

5

3

3

12

2

6

5

2

4

3

2

1

3

3

2

2

3

3

2

2

...











































































































































(5.7)

(5.3)

(5.4)

(5.6)

Te dwanaście równań możemy zapisać w postaci macierzowej

 

 





]

[C

e



gdzie
[C] – macierz 12x12 zależna od współrzędnych węzłów.
Odwracając to równanie mamy

e

C

}

{

]

[

}

{

1









Teraz możemy zapisać wyrażenie na przemieszczenia wewnątrz elementu w postaci standardowej

e

e

z

C

P

N

u

}

{

]

][

[

}

]{

[

1











Jawną postać powyższego wyrażenia wyprowadził Melosh w 1963r. We współrzędnych
znormalizowanych macierz funkcji kształtu

]

[

]

[

m

k

j

i

N

N

N

N

N



(5.11)













 









 



]

1

1

1

,

1

1

1

,

2

1

1

[

8

1

]

[

0

2

0

0

0

0

2

0

2

2

0

0

0

0























































i

i

i

b

a

N

gdzie

i

i

C

C

b

y

y

a

x

x

























0

0

(5.13)

(5.8)

(5.9)

(5.10)

(5.12)

Zależność między odkształceniami {

e

}, a ugięciem płyty u

z

zgodnie z teorią cienkich płyt płaskich

ma postać

 

















































































y

x

u

y

u

x

u

z

z

z

xy

y

x

2

2

2

2

2







e

Uwzględniając (5.10) i (5.11) znajdujemy macierz [B] występującą w

 

 

 

e

B



e



w której



























































]

[

]

[

]

[

]

[

2

2

2

2

2

i

i

i

i

N

y

x

N

y

N

x

B

(5.15)

Odkształcenia

(5.14)

Naprężenia odpowiadające zdefiniowanym wcześniej odkształceniom są w istocie
momentami zginającymi i skręcającymi na jednostkę długości























xy

y

x

M

M

M

}

{



Zgodnie z teorią płyt cienkościennych

y

x

u

D

M

x

u

y

u

D

M

y

u

x

u

D

M

z

xy

z

z

y

z

z

x

































































2

2

2

2

2

2

2

2

2

)

1

(







Macierz sprężystości [D] określa się ze związku

   





0

]

[

}

{

e

e







D

Dla płyty izotropowej



































1

0

0

0

1

0

1

)

1

(

12

]

[

2

3

Et

D

(5.18)

Naprężenia

(5.16)

(5.17)

Macierz sztywności, wiążącą siły węzłowe z odpowiadającymi im
przemieszczeniami węzłów, można zapisać w postaci





dxdy

B

D

B

k

T

]

][

[

]

[

]

[

Jeśli obciążenie ciągłe q działa na jednostkę pola elementu w kierunku u

z

,

wówczas udział tego obciążenia w siłach węzłowych wynosi

 







qdxdy

N

F

T

e

p

]

[

Całkę tę można łatwo wyznaczyć. Należy zauważyć, że w przypadku ogólnym wszystkie trzy
składowe sił zewnętrznych w każdym węźle nie będą mieć wartości zerowych. Dla elementu
prostokątnego pod obciążeniem równomiernym q otrzymamy:

Macierz sztywności

(5.19)

Siły węzłowe od obciążenia ciągłego

(5.20)



































































































































































12

/

12

/

4

/

1

12

/

12

/

4

/

1

12

/

12

/

4

/

1

12

/

12

/

4

/

1

4

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

a

b

a

b

a

b

a

b

qab

M

M

F

M

M

F

M

M

F

M

M

F

m

y

m

x

m

z

k

y

k

x

k

z

j

y

j

x

j

z

i

y

i

x

i

z

(5.21)

W wyniku rozwiązania podstawowego układu równań

}

{

}

]{

[

F

K





otrzymujemy wektor przemieszczeń węzłowych. Dalej na podstawie związków geometrycznych
wyznaczamy składowe odkształceń płytowych

}

{

xy

y

x







A ze związków fizycznych określimy momenty zginające i skręcające

}

{

xy

y

x

M

M

M

Dalej wiedząc, że







2

/

2

/

.

t

t

x

x

itd

zdz

M



i że

x



zmieniają się liniowo na grubości płyty, można znaleźć takie wyrażenia jak

.

12

3

itd

z

t

M

x

x





W celu określenia wytężenia płyty wyznacza się naprężenia dla górnej (z=t/2) i dla dolnej warstwy (z=-t/2).
Ponadto w znany sposób oblicza się naprężenia główne







,

,

2

1

i naprężenia zredukowane według Hubera-Misesa

zred



.

Obliczenie naprężeń

(5.22)

(5.23)

(5.24)

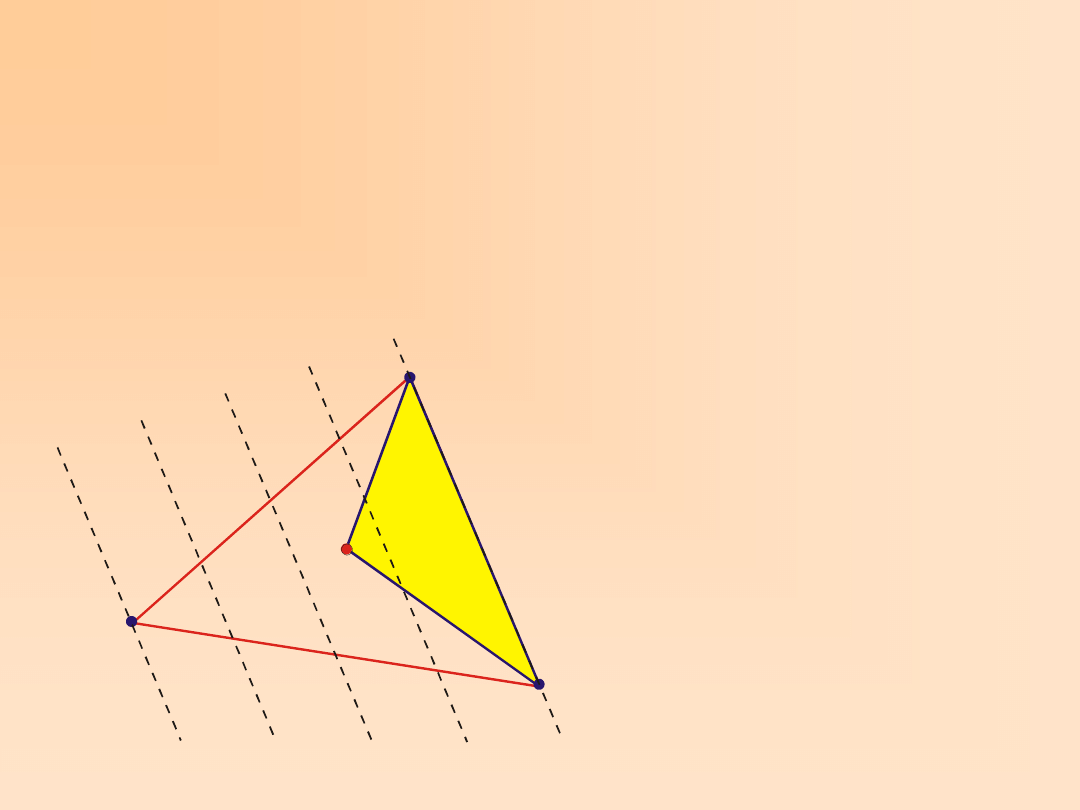
Wprowadza się znormalizowane współrzędne dla trójkątów, są to tzw. współrzędne

powierzchniowe L

1

, L

2

, L

3

określone następującą zależnością liniową między tymi

współrzędnymi a współrzędnymi kartezjańskimi

3

2

1

3

3

2

2

1

1

3

3

2

2

1

1

1

L

L

L

y

L

y

L

y

L

y

x

L

x

L

x

L

x



















Miejscem geometrycznym dla L

1

=const są

proste równoległe do boku 2-3. W punkcie
1 jest L

1

=1, a w punktach 2 i 3 jest

L

2

=L

3

=0.

P(L , L , L )

1

2

3

L =1

1

L =0,75

1

L =0,5

1

L =0,25

1

L =0

1

1

2

3

(x ,y )

1

1

(x ,y )

2

2

(x ,y )

3

3

Rys. 5.2. Współrzędne powierzchniowe trójkąta

Element płytowy trójkątny

(5.25)

Odmienna definicja współrzędnej L

1

punktu P może być wyrażona przez stosunek

pola trójkąta

D

P23 do pola całego trójkąta

D

123

123

23

1

D

D



A

A

L

P

P

Rozwiązując (5.25) względem x i y otrzymamy













y

c

x

b

a

L

y

c

x

b

a

L

y

c

x

b

a

L

3

3

3

3

2

2

2

2

1

1

1

1

2

1

2

1

2

1





D







D







D



gdzie

3

3

2

2

1

1

1

1

1

det

2

y

x

y

x

y

x



D

2

3

1

3

2

1

2

3

3

2

1

x

x

c

y

y

b

y

x

y

x

a













(5.26)

(5.27)

Tutaj podobnie przy aproksymacji przemieszczeń stosujemy rozwinięcia w wielomiany, np.:

3

3

2

2

1

1

L

L

L











jest wielomianem liniowym, a

2

3

6

2

2

5

2

1

4

1

3

3

3

2

2

2

1

1

L

L

L

L

L

L

L

L

L























zawiera wszystkie sześć wyrazów rozwinięcia kwadratowego (w tym także i
rozwinięcie liniowe). Dziewięć wyrazów sześciennych jest ukształtowanych z
iloczynów wszystkich możliwych kombinacji, tj.:

]

,

,

,

,

,

,

,

,

,

[

3

2

1

3

2

1

2

2

3

1

2

2

1

2

3

3

2

2

2

2

1

3

3

3

2

3
1

L

L

L

L

L

L

L

L

L

L

L

L

L

L

L

L

L

L

Dla elementu o dziewięciu stopniach swobody każdy z tych wyrazów może być użyty w dowolnej
kombinacji. Przemieszczenia płyty opisuje się w następujący sposób









































3

2

1

2

2

1

9

3

2

1

1

2

2

4

3

3

2

2

1

1

2

1

2

1

L

L

L

L

L

L

L

L

L

L

L

L

L

u

z













i podstawiając wartości:

i

z

i

y

i

z

i

x

i

z

x

u

oraz

y

u

u











































)

(

)

(

)

(

,

można obliczyć stałe



, a zatem i funkcje kształtu.

(5.28)

(5.29)

(5.30)

(5.31)

W celu wyznaczenia macierzy [B] należy liczyć drugie pochodne od [N], względem
współrzędnych kartezjańskich x i y. Jest to proste zważywszy, że





























D





































3

3

2

2

1

1

3

3

2

2

1

1

2

1

L

b

L

b

L

b

L

x

L

L

x

L

L

x

L

x

Wszystkie wyrażenia pozostają wielomianami we współrzędnych powierzchniowych i można je łatwo
scałkować w sposób ogólny. Istnieje wyrażenie







D

D











2

!

2

!

!

!

3

2

1

c

b

a

c

b

a

dxdy

L

L

L

c

b

a

Prościej jednak jest wykonać program na maszynę cyfrową, stosując całkowanie numeryczne.

(5.33)

(5.34)

Elementy opisane za pomocą powyższych funkcji przedstawione były po raz pierwszy w pracy z 1965r.

 











































































































3

2

1

3

2

1

2

3

2

1

2

2

1

3

3

2

1

3

2

1

2

3

2

1

2

2

1

3

2

3

1

2

2

1

3

2

1

2

2

1

1

1

2

1

2

1

2

1

2

1

L

L

L

L

L

c

L

L

L

L

L

c

L

L

L

L

L

b

L

L

L

L

L

b

L

L

L

L

L

L

L

L

L

N

T

(5.32)

Typowa funkcja kształtu

w odniesieniu do węzła

1 ma postać

Przyjmuje się aproksymację powierzchni

zakrzywionej w sposób ciągły za pomocą

powierzchni utworzonej z małych płaskich

elementów.

W powłokach element poddany jest, w

ogólnym przypadku, zarówno zginaniu jak i

działaniu sił w „płaszczyźnie”.

W praktyce stosujemy elementy trójkątne

i czworokątne. Możliwości obliczania powłok

za pomocą MES są duże, łatwo można

obliczać powłoki z otworami, o zmiennej

grubości, powłoki o strukturze anizotropowej.

POWŁOKA JAKO ZBIÓR PŁASKICH

ELEMENTÓW

Wstęp

Rozpatrzmy typowy element poddany działaniu sił „w płaszczyźnie” i zginaniu.
Należy odnotować dwa fakty. Pierwszy, że przemieszczenia powodowane działaniem

sił stanu tarczowego nie wpływają na odkształcenia gięte i odwrotnie. Drugi, że obrót



z

nie

może występować jako parametr przy określaniu deformacji. Wprowadzamy ten obrót do
rozważań i połączymy z nim fikcyjny moment M

z

.

Przemieszczenia węzłów definiujemy jako:

 









































































)

(

)

(

)

(

)

(

)

(

)

(

)

(

i

z

b

i

p

i

i

z

i

y

i

x

i

z

i

y

i

x

i

u

u

u







a odpowiednie siły węzłowe

 

































































)

(

)

(

)

(

)

(

)

(

)

(

)

(

i

z

b

i

p

i

i

z

i

y

i

x

i

z

i

y

i

x

i

M

F

F

M

M

M

F

F

F

F

przy czym mamy

 

 

 

 

 

 

b

b

b

p

p

p

k

F

k

F









(6.1)

(6.2)

Sztywność elementu płaskiego we współrzędnych lokalnych

Macierz

sztywności

elementu

powłokowego może być zapisana w
postaci

 

 

 

e

e

e

k

F





i składa się z następujących podmacierzy

 

 

 























0

0

0

0

0

0

0

b

rs

p

rs

rs

k

k

k

(6.4)

(6.3)

x

y

z

i

u

x

(i)

u

y

(i)

m

j

+

=



x

(i)



y

(i)

m

i

j

u

z

(i)

u

x

(i)



x

(i)



z

(i)

u

y

(i)



y

(i)

m

i

j

u

z

(i)

Element

tarczowy

Element

płytowy

Element

powłokowy

Macierz sztywności, wyprowadzona w poprzednich rozważaniach, odniesiona była

do układu współrzędnych lokalnych w płaszczyźnie elementu.

W celu połączenia elementów w całość i wypisania równań równowagi niezbędna

jest transformacja tego układu do globalnego układu współrzędnych. Układ lokalny
oznaczamy przez x’, y’, z’, układ zaś globalny przez x, y, z.

Z drugiej strony bardziej dogodne jest przyporządkowanie węzłów elementów

współrzędnym globalnym i wyrażenie za ich pomocą współrzędnych lokalnych, temu
celowi służyć będzie transformacja odwrotna.

Siły i przemieszczenia węzłów transformuje się z układu globalnego na lokalny

poprzez macierz [L] w następujący sposób

 

 

}

]{

[

};

]{

[

'

'

i

i

i

i

F

L

F

L









gdzie



















0

0

]

[L

(6.6)

(6.5)

Transformacja współrzędnych

x

y

z

x’

y’

z’

x’x

Tutaj [



] jest macierzą rzędu 3x3 kosinusów kierunkowych kątów pomiędzy dwoma układami tj.























z

z

y

z

x

z

z

y

y

y

x

y

z

x

y

x

x

x

'

'

'

'

'

'

'

'

'

]

[





















gdzie

x

x'



jest kosinusem kierunkowym kąta pomiędzy osiami x oraz x’.

(6.7)

Dla całego układu sił działających w węzłach na dany element można, zatem napisać

 

 

 

 

e

e

e

e

F

T

F

T

]

[

'

;

]

[

'









Jeśli macierz sztywności została zapisana w lokalnych współrzędnych (primowanych), to równanie

 

e

e

p

e

e

e

F

F

k

F

0

}

'

{

}

'

{

}

'

{

]

'

[

'

e









w ogólnych współrzędnych (nieprimowanych) ma postać

e

e

p

e

e

e

e

F

T

F

T

T

k

T

F

T

F

0

}

'

{

]

[

}

'

{

]

[

}

]{

[

]

'

[

]

[

}

'

{

]

[

}

{

1

1

1

1

e



















(6.10)

(6.9)

(6.8)

Macierz sztywności w globalnych współrzędnych wyraża się, zatem następująco

]

[

]

'

[

]

[

]

[

1

T

k

T

k

e

e





Ponieważ, macierz transformacji jest ortogonalna, to transpozycja macierzy równa się jej
odwrotności, mamy

T

T

T

]

[

]

[

1





a więc

]

][

'

[

]

[

]

[

T

k

T

k

T

e



W powyższych równaniach [T] oznacza





















































L

L

L

L

T

0

0

0

0

0

0

0

0

0

0

0

0

]

[

jest macierzą quasidiagonalną zbudowaną z macierzy [L] w liczbie odpowiadającej liczbie
węzłów elementu. Łatwo pokazać, że typowa podmacierz macierzy sztywności jest teraz równa

T

rs

T

rs

L

k

L

k

]

][

'

[

]

[

]

[



gdzie

]

'

[

rs

k

jest określone za pomocą równania (6.4) we współrzędnych lokalnych.

(6.11)

(6.12)

(6.13)

(6.14)

(6.15)

Współrzędne lokalne określa się według podobnego schematu. Jeśli początki układów
lokalnego i globalnego pokrywają się, wówczas































































z

y

x

z

y

x

z

z

y

z

x

z

z

y

y

y

x

y

z

x

y

x

x

x

'

'

'

'

'

'

'

'

'

'

'

'



















Ponieważ przy obliczaniu macierzy sztywności położenie początku układu jest nieistotne,
transformacja ta wystarczy do określenia lokalnych współrzędnych w płaszczyźnie elementu.
Przemieszczenia obliczone z rozwiązania podstawowego układu równań odniesione są do
globalnego układu współrzędnych. Zanim więc przystąpimy do obliczania naprężeń, konieczna
jest transformacja przemieszczeń węzłowych elementu do układu lokalnego elementu.

(6.16)

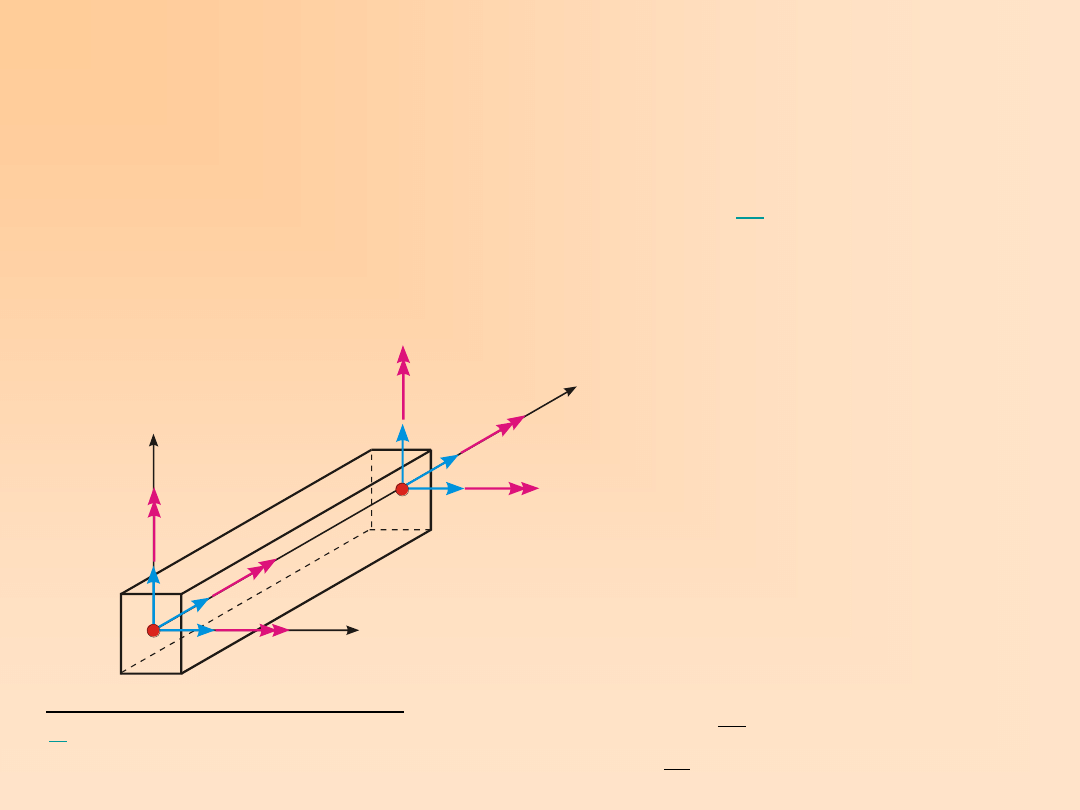
Rozważmy element belkowy (rys. 8.1) prosty o długości l, stałym przekroju A,

wykonany z jednorodnego materiału o module Younga E, liczbie Poissona



i gęstości

r

.

Znane są także: I

s

, I

y

, I

z

– wskaźnik sztywności pręta na skręcanie

[1]

i główne momenty

bezwładności przekroju poprzecznego odpowiednio na zginanie względem osi y

e

oraz z

e

, które

dla elementu przyjmujemy jako stałe. W elemencie przyjmujemy dwa węzły i oraz j
znajdujące się na jego końcach. Oś układu lokalnego x

e

pokrywa się z osią obojętną zginania

pręta, a początek układu znajduje się w węźle i (rys. 8.1)



x

(i)

u

z

(i)

u

z

(j)

u

x

(i)

u

x

(j)

u

y

(i)

u

y

(j)



z

(i)



z

(j)



x

(j)



y

(i)



y

(j)

z

e

y

e

x

e

i

j

Rys. 8.1. Element belkowy o
12 stopniach swobody w
układzie lokalnym x

e

, y

e

, z

e

.

Osie y

e

i z

e

pokrywają się z

głównymi centralnymi osiami
bezwładności przekroju.

[1]

Kąt skręcenia pręta pryzmatycznego o długości l obciążonego momentem M określa zależność

s

GI

Ml





a naprężenie styczne przy skręcaniu w odległości r od osi -

s

I

Mr





ELEMENT BELKOWY

Przemieszczenia i siły uogólnione

Przemieszczeniami uogólnionymi węzłów elementu są przemieszczenia translacyjne oraz trzy
rotacyjne. Wektor przemieszczeń węzłowych elementu ma postać:

 















j

i

e







gdzie

 





)

(

)

(

)

(

)

(

)

(

)

(

i

z

i

y

i

x

i

z

i

y

i

x

T

i

u

u

u











)

(

)

(

)

(

,

,

i

z

i

y

i

x

u

u

u

- przemieszczenia translacyjne i-tego węzła w kierunku osi x

e

, y

e

, z

e

.

)

(

)

(

)

(

,

,

i

z

i

y

i

x







Siły uogólnione węzłowe są siłami i momentami sił działającymi w kierunkach zgodnych z
przemieszczeniami uogólnionymi (rys. 8.1). Wektor sił uogólnionych ma postać

 















j

i

e

F

F

F

gdzie

 





)

(

)

(

)

(

)

(

)

(

)

(

i

z

i

y

i

x

i

z

i

y

i

x

T

i

M

M

M

F

F

F

F



)

(

)

(

)

(

,

,

i

z

i

y

i

x

F

F

F

-siły działające w i-tym węźle w kierunku osi x

e

, y

e

, z

e

.

)

(

)

(

)

(

,

,

i

z

i

y

i

x

M

M

M

- momenty sił w i-tym węźle względem osi x

e

, y

e

, z

e.

- przemieszczenia rotacyjne i-tego węzła względem osi xe, ye, ze.

(8.2)

(8.1)

Przemieszczenia przekroju elementu belkowego dla punktu leżącego na osi obojętnej elementu
określamy za pomocą trzech składowych translacyjnych oraz trzech składowych rotacyjnych,
będących obrotami względem osi x

e

, y

e

, z

e

. Wektor przemieszczeń dowolnego przekroju ma, zatem

postać

 





z

y

x

z

y

x

T

u

u

u

u









Dla elementu belkowego przyjmujemy wielomiany aproksymujące przemieszczenia zgodnie z
elementarną teorią belek

e

x

e

e

e

z

e

e

e

y

e

x

x

x

x

x

u

x

x

x

u

x

u

12

11

3

10

2

9

8

7

3

6

2

5

4

3

2

1



















































natomiast obroty względem osi y

e

i z

e

zgodnie z klasyczną teorią belek są równe

2

6

5

4

2

10

9

3

3

2

3

2

e

e

e

y

z

e

e

e

z

y

x

x

x

u

x

x

x

u













































(8.5)

(8.3)

(8.4)

Stałe



1

,



2

,…,



12

wyznaczymy z warunków

   

 

 

j

i

l

u

u









)

(

)

0

(

W ten sposób otrzymamy zależność wektora przemieszczeń od wektora przemieszczeń węzłowych

 

 

 

e

e

N

u





gdzie macierz funkcji kształtu jest równa

(8.6)

(8.7)

 











































































































)

2

3

(

0

0

0

)

1

(

6

0

1

4

3

0

0

0

)

1

(

6

0

0

)

2

3

(

0

)

1

(

6

0

0

0

1

4

3

0

)

1

(

6

0

0

0

0

0

0

0

0

0

1

0

0

0

0

)

1

(

0

)

3

2

(

0

0

0

)

1

2

(

0

1

3

2

0

0

)

1

(

0

0

0

)

3

2

(

0

)

1

2

(

0

0

0

1

3

2

0

0

0

0

0

0

0

0

0

0

0

1

2

2

2

2

2

2

3

2

2

2

2

3













































































l

l

l

l

l

l

l

l

N

e

przy czym przyjęto współrzędną bezwymiarową

l

x

e





(8.8)

Pomijając odkształcenia belki wywołane siłami porzecznymi, wektor odkształceń jednostkowych
wygodnie jest przyjąć w postaci

 

 

 

u

L

z

y

x

x



































e

e

e

x

- wydłużenie jednostkowe osi obojętnej

x

u

x

x







e



x

- jednostkowy kąt skręcenia

x

x

x













y

- jednostkowy kąt ugięcia względem osi y

e

2

2

x

u

x

z

y

y





















z

- jednostkowy kąt ugięcia względem osi z

e

2

2

x

u

x

z

z

y

















stąd mamy liniowy operator różniczkowy

 





























































x

x

x

x

l

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

(8.14)

Odkształcenia

(8.9)

gdzie

(8.10)

(8.11)

(8.12)

(8.13)

Macierz [B] uzależniająca odkształcenia od współrzędnych uogólnionych
elementu, otrzymamy podstawiając (8.8) do (8.9). Ma ona postać









































































)

4

6

(

1

0

0

0

)

1

2

(

6

0

0

)

4

6

(

1

0

)

1

2

(

6

0

0

0

0

1

0

0

0

0

0

0

0

0

1

]

][

[

]

[

2

2









l

l

l

l

l

l

N

B

e

(8.15)

Tworzymy wektor naprężeń (sił) przekrojowych

 



























z

y

x

x

M

M

M

F



gdzie

Związki fizyczne pomiędzy wektorem sił przekrojowych a wektorem odkształceń
jednostkowych zapisujemy w postaci











































































z

y

x

x

z

y

s

z

y

s

x

EI

EI

GI

EA

M

M

M

F







e

lub krótko

}

]{

[

}

{

e



D



(8.19)

Naprężenia

(8.16)

(8.17)

(8.18)

dz

y

M

dz

z

M

r

I

M

A

F

x

z

x

y

s

s

x

x





















Macierz sztywności elementu belkowego w układzie lokalnym jest równa





l

e

T

dx

B

D

B

k

0

]

][

[

]

[

]

'

[

W postaci jawnej





































































































l

EI

l

EI

l

EI

l

EI

l

GI

l

EI

l

EI

l

EI

l

EI

l

EA

k

y

z

y

y

s

y

y

z

z

4

0

0

0

6

0

0

4

0

6

0

0

0

0

0

0

0

0

6

0

12

0

0

6

0

0

0

12

0

0

0

0

0

0

]

'

[

2

2

2

3

2

3

(8.21)

Macierz sztywności

(8.20)

Transformacja z układu lokalnego (primowanego) do globalnego przemieszczeń i sił

węzłowych odbywa się za pomocą zależności

e

e

e

e

F

T

F

T

}

]{

[

}

'

{

}

]{

[

}

'

{









Po uwzględnieniu ich macierz sztywności w globalnych współrzędnych możemy przedstawić w postaci

]

][

'

[

]

[

]

[

T

k

T

k

T

e



Jednoznaczne określone jest położenie osi x

e

wynikające z kolejności podania węzłów

ograniczających element. Osie y

e

i z

e

pokrywają się z głównymi centralnymi osiami bezwładności

przekroju elementu belkowego tworząc układ prawoskrętny.

W programach MES wprowadzając charakterystyki elementu belkowego tj. momenty

bezwładności przekroju I

y

i I

z

należy określić położenie osi względem, których obliczono te

momenty bezwładności. Osi te, jak podano powyżej, są osiami y

e

i z

e

lokalnego układu

współrzędnych elementu. Ponieważ oś x

e

jest jednoznacznie określona przez kolejność podawania

węzłów opisujących element belkowy, wystarczy podać orientację osi y

e

. Oś z

e

wynika z faktu, że

układ ma być kartezjański prawoskrętny.

Transformacja układów współrzędnych

(8.22)

(8.23)

Typowy program MES zbudowany jest z szeregu bloków (podprogramów). Na rys. 9.1

pokazano schemat blokowy programu MES.

Typowe bloki to:
- wprowadzanie danych,
- budowanie macierzy sztywności elementu i układu
- procedura rozwiązywania równań,
- obliczenie naprężeń
- wydruk wyników (tabele lub graficznie w postaci warstwic).

Na początku rozwoju MES dane wprowadzało się w tzw. sposób wsadowy, tj.

przygotowywało się listę węzłów z ich współrzędnymi, listę elementów z węzłami, pomiędzy
którymi się te elementy znajdują, własności materiałowe, listę obciążonych węzłów, listę węzłów,
w których występują zerowe przemieszczenia, (czyli podparcia, utwierdzenia). Obecnie przy
wprowadzaniu danych bazuje się na geometrii modelu, tj. na liniach, powierzchniach lub bryłach.
Węzły i elementy są w określony sposób generowane na geometrii zakładając ich wielkość lub
liczbę, typ elementu i rząd elementu. Również obciążenia węzłowe wprowadzane są posiłkując
się geometrią, czyli siły przykłada się do punktu, linii czy powierzchni. Podobnie jest z
podparciami.

STRUKTURA PROGRAMÓW MES

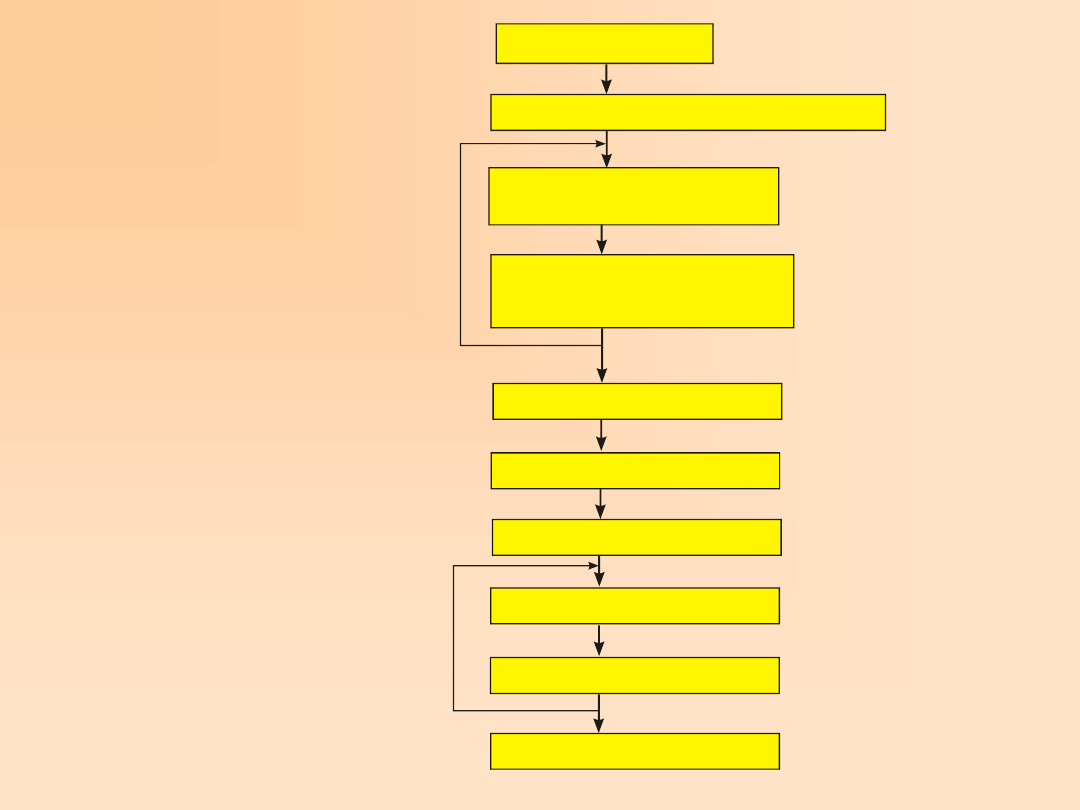
CZYTANIE ZBIORU DANYCH

- geometria (węzły i elementy),
- własności materiału,
- obciążenia,
- podparcia.

- metody bezpośrednie
- metody iteracyjne

BUDOWANIE WEKTORA OBCIĄŻEŃ ZEWNĘTRZNYCH

Obliczanie macierzy sztywności elementu

w układzie lokalnym

i transformacja do układu globalnego

Uwzględnienie zerowych przemieszczeń

(podparcia, utwierdzenia)

Rozwiązanie układu równań

Wydruk przemieszczeń

tabelarycznie lub graficznie

Wydruk naprężeń

tabelarycznie lub graficznie

Transformacja przemieszczeń
do układu lokalnego elementu

Obliczenie naprężeń w elemencie

{F}

[k’]

[k]=[T] [k’][T]

T

AGREGACJA

Wprowadzenie macierzy sztywności elementu

do macierzy sztywności układu

P

ęt

la

p

o

el

em

en

ta

ch

P

ęt

la

p

o

el

em

en

ta

ch

[K] { }={F}



[K]

{ ’} =[T]{ }





e

e

{ ’} =[D] [B]{ ’}





e

e

Schemat blokowy programu MES