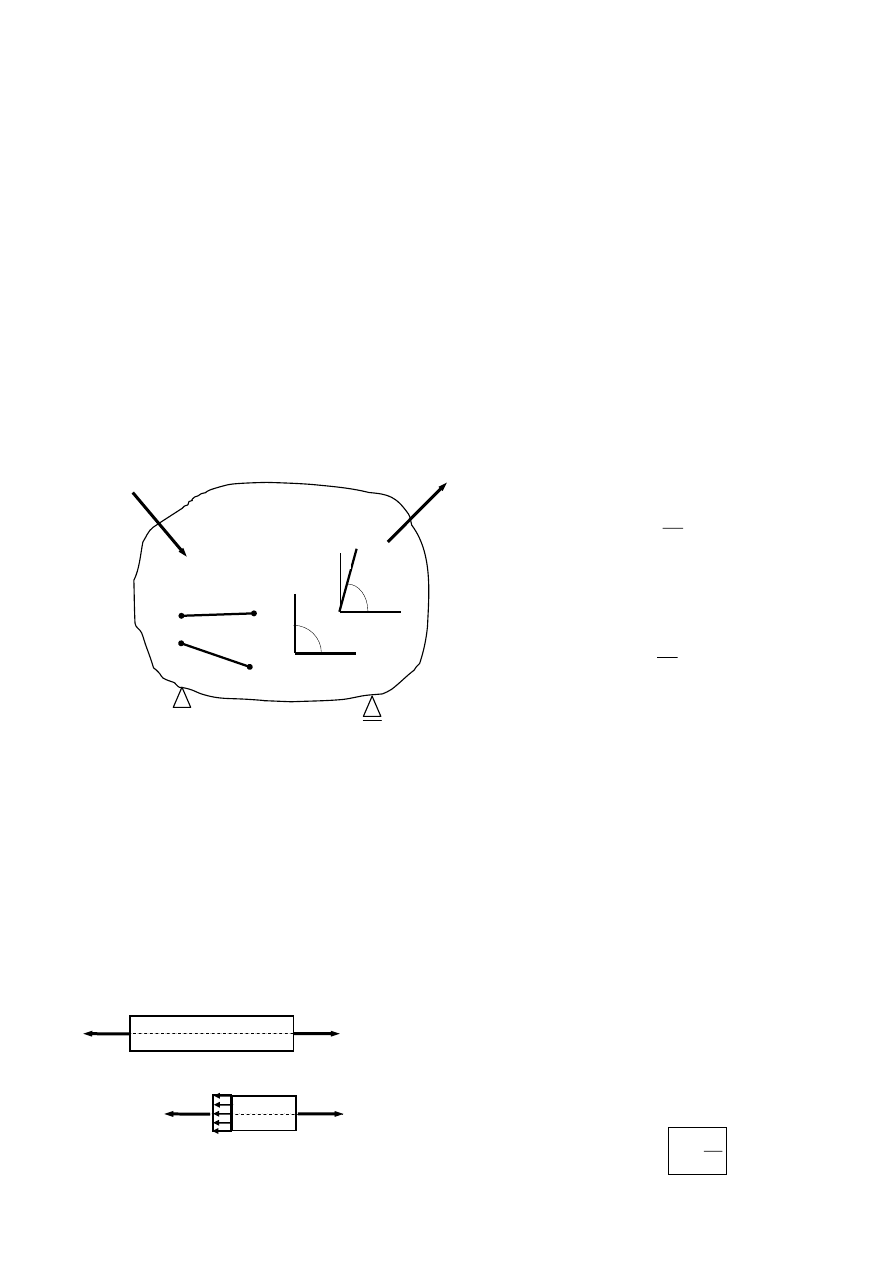
ODKSZTAŁCENIE
Materiały rzeczywiste są materiałami odkształcalnymi – pod wpływem sił lub innych czynników
zewnętrznych ulegają odkształceniom (zmianie wymiarów i postaci).
Rozróżniamy:
-
odkształcenia sprężyste
-
ustępują po odciążeniu,
-
odkształcenia plastyczne (trwałe) - pozostają.
Materiały rzeczywiste zależnie od sposobu zachowania dzielimy na:
-
materiały w stanie sprężysto-plastycznym
-
materiały w stanie sprężysto-kruchym.
Pod względem geometrycznym odkształcenia dzielimy na:
-
liniowe
– wydłużenie, skrócenie, wzajemne przesunięcie,
-
kątowe (postaciowe) – kąt obrotu, kąt skręcenia.
O charakterze odkształceń przekonać się możemy badając zmianę jakiej dozna pod wpływem
obciążenia wybrany odcinek AB lub kąt prosty CDE
AB = l
A’B’ = l +
l
Średnie wydłużenie względne AB
l
l
średnie
Graniczna wartość jest lokalną
intensywnością zmiany wymiarów
liniowych w bezpośrednim otoczeniu
punktu A
l
l
l
0
lim
i nosi nazwę wydłużenia względnego.
Zależy ono nie tylko od obciążenia ale
także od kierunku jego wyznaczania.
Drugą niezależną od wydłużenia względnego miarą intensywności odkształcenia jest zmiana
kąta prostego CDE. Jest nim kąt
zwany
kątem odkształcenia postaciowego
'
'
'
lim
0
,
0
E
D
C
CDE
DE
CD
Zbiór wydłużeń względnych
x
,
y
,
z
i
odkształceń postaciowych
w określonym punkcie ciała,
we wszystkich możliwych kierunkach, nazywamy stanem odkształcenia w danym punkcie.
ROZCIĄGANIE I ŚCISKANIE PRĘTA PROSTEGO O STAŁYM PRZEKROJU
A.
Warunki równowagi
Na pręt działa siła P wywołująca w dowolnym
normalnym przekroju siłę N=P. Siła normalna N jest
wypadkową sił wewnętrznych (tu naprężeń
normalnych
)
A
dA
N
gdy
nie zależy od obioru punktu A na przekroju
tzn.
= const
A
dA
N
A
N
P
2
A
P
1
A’
B
B’
l
l+
l
C’
E’
D’
D
E
C
90-
N
P
P
P
B. Warunki geometryczne
Wydłużenie względne odcinka dx
dx
du
u
– przemieszczenie przekroju A-A,
u + du - przemieszczenie przekroju B
– B
W przypadku gdy
=const. mamy przypadek
2
1
)
(
1
2
x
x
x
x
dx
u
dx
du
Jeżeli x
2
-x
1
=l to u=
l=
l i
l
l
Zmieniają się nie tylko wymiary wzdłużne lecz również wymiar poprzeczny pręta d.
Zakładając, że materiał jest izotropowy to zmiany te są jednakowe we wszystkich kierunkach:
d
d
d
z
y
'
odkształcenie poprzeczne
’ =
y
=
z
dla rozciągania d > d’
zatem
’ < 0
C.
Związki fizyczne – określają zależności między odkształceniami a naprężeniami.
Związek ten nazywa się prawem Hooke’a – wydłużenie jest
proporcjonalne do naprężenia które je spowodowało. Jest ono
słuszne dla naprężeń niższych od pewnej wartości granicznej.
E
– moduł Younga (moduł sprężystości wzdłużnej). Charakteryzuje odkształcalność
materiałów. Ma wymiar naprężenia czyli N/m
2
= [Pa] lub [MPa] = 10
6
Pa
Graficznie zależność ta przedstawia się jako:
gdzie
E
tg
Pomiędzy
i
’ istnieje związek:
'
gdzie
-
współczynnik (ułamek, liczba) Poissona,
'
o <
< 0,5
dla
l
l
dx
EA
N
dx
l
EA
N
A
N
,
,
jeżeli N = P = const,
A = const,
E = const
EA
Pl
l
EA
– sztywność pręta rozciąganego (ściskanego)
Warunek wytrzymałościowy na rozciąganie:
r
k
A
P
1
n
n
k
nieb
r
E
1
P
P
x
A
B
A
B
x
1
dx
x
2
d
nieb
R
e
R
m
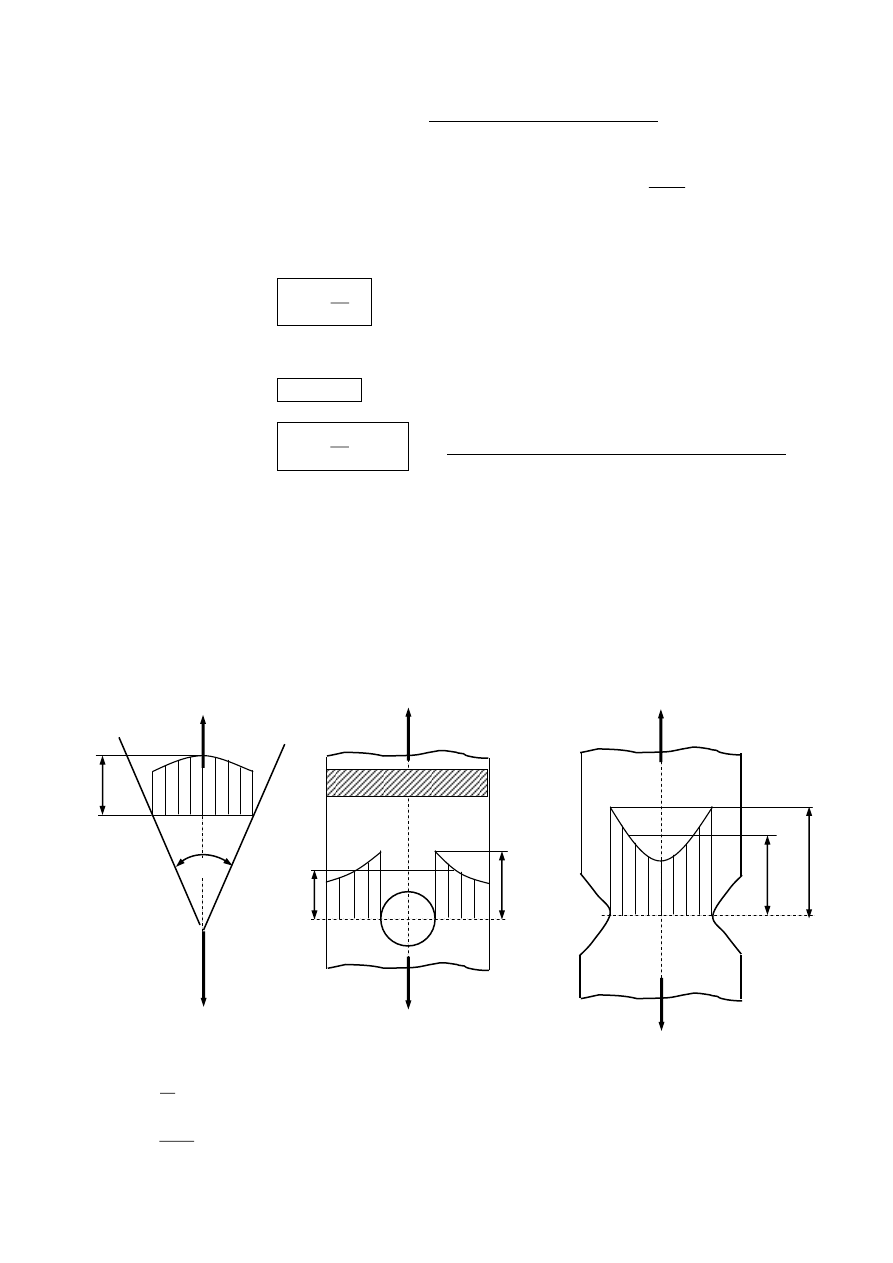
Obliczenia wytrzymałościowe prętów na rozciąganie (ściskanie)
Próba rozciągania pozwala na wyznaczenie naprężenia niebezpiecznego R
e
lub R
m
.
W poprawnie zaprojektowanej konstrukcji max. naprężenie robocze (inaczej-dopuszczalne)
dop
<
nieb
a ściślej
n
nieb
dop
n>1 -
współczynnik bezpieczeństwa
Podstawą obliczeń wytrzymałościowych jest równanie:
A
N
gdzie: N
– siła osiowa;
A
– pole przekroju poprzecznego;
-
naprężenie normalne
i warunek
dop
przy rozciąganiu
dop
= k
r
łącząc je otrzymamy
r
k
A
N
-
warunek wytrzymałościowy na rozciąganie
Zależnie od tego co jest w tym równaniu nieznane, mamy:
a.
obliczenia sprawdzające;
b.
wyznaczenie naprężenia dopuszczalnego;
c.
wyznaczenie wymiarów.
Spiętrzenie naprężeń
Powstają w prętach o zmiennym przekroju np.:
a)
b)
c)
A
P
n
-
naprężenie nominalne
n
k
max
-
współczynnik kształtu
max
P
max
P
P
max
n
P
P
n
P
max
tym
większe im
większy kąt
PRZYPADKI STATYCZNIE NIEWYZNACZALNE PRZY ROZCIĄGANIU (ŚCISKANIU)
- wtedy gdy siły osiowe w prętach nie mogą być wyznaczone z samych tylko równań równowagi.
Brakujące równania uzyskuje się rozpatrując sprężyste odkształcenie układu.
Przykład. Pręty 1 i 2 o jednakowej długości,
różnych przekrojach i różnych E.
Wyznaczyć: – siły wzdłużne N
1
,N
2
– naprężenia
1
,
2
A. Warunki równowagi
0
2
1
N
N
P
- zadanie 1-krotnie statycznie niewyznaczalne
B. Warunki geometryczne
1
=
2
-
warunek
nierozdzielczości przemieszczeń
C. Warunki fizyczne
2
2
2
2
1
1
1
1
;
A
E
l
N
A
E
l
N
-
prawo Hooke’a
2
2
1
1
1
1
1
1
2
2
2
1
1
1
1
1
1
1
2
2
2
2
1
1
1
....;
;
A
E
A
E
E
P
A
N
N
A
E
A
E
A
E
P
N
N
P
N
i
A
E
N
A
E
N
Przykład Pręt AB umocowano na dwóch nieprzesuwnych podporach i podgrzano o 30 K.
Wyznaczyć naprężenia powstałe w pręcie.
B
t
=1,2 10
-5
1/K, E=2,1 10
5
MPa,
T=30 K
A. Warunki równowagi
R
A
– R
B
= 0
B. Warunki geometryczne
= 0
C. Warunki fizyczne
=
t
T odkształcenie wywołane zmiana temperatury
lub
l=
t
T l
gdy wraz ze wzrostem temperatury pojawi się naprężenie to:
l
T
EA
Nl
l
T
E
t
t
lub
B
A
t
R
R
N
T
EA
Nl
;
0
MPa
TE
A
N
TEA
R
R
t
t
t
B
A
6
,
75
10
1
,
2
30
10
2
,
1
;
5
5
Przykład
A.
Warunek równowagi
R
2
+R
1
-P=0
B. Warunek geometryczny
l
1
=
+
l
C. Warunki fizyczne
EA
l
R
l
EA
l
P
l
1
1
;
5
,
0
A
R
A
R
B
l
B
P
R
2
R
1
l/2
l
l
l
1
l/2
1
2
N
2
N
1
P
P
l
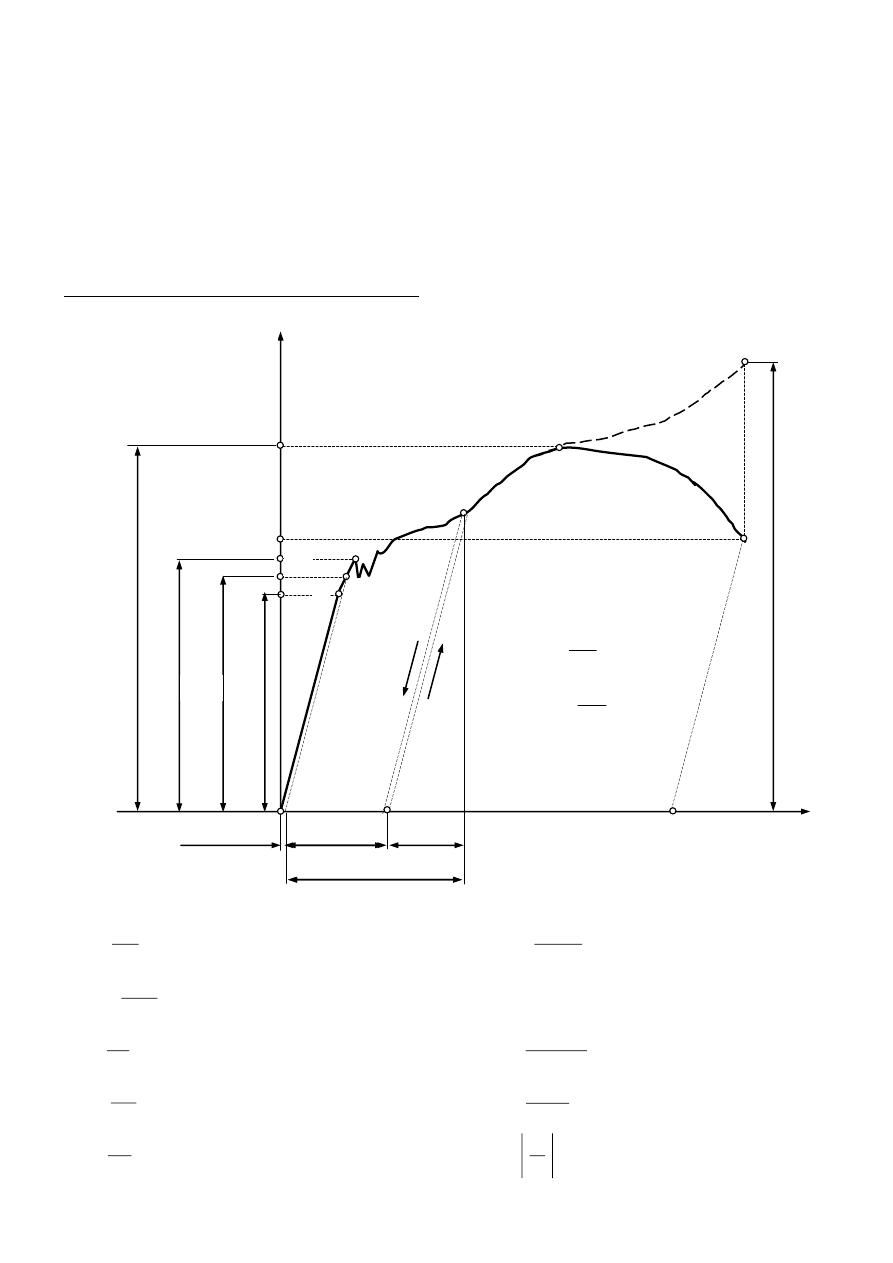
Doświadczalne podstawy określania własności mechanicznych
Badania
– podstawowe, znormalizowane np. próba rozciągania,
- specjalistyczne
– cel określenie zachowania się elementu pod obciążeniem
np. tensometryczne, ultradzwiękowe, zmęczeniowe, udarowe, elastooptyczne
Statyczna próba rozciągania metali (PN-EN 10002-1+AC 1).
Norma określa sposób, warunki, kształt i wymiary próbek, definicje wyznaczanych wielkości.
Przebieg próby rejestrowany jest w układzie F-
l
(siła - wydłużenie).
Często przedstawia się go później w układzie
-
(naprężenie - odkształcenie).
Typowy wykres rozciągania dla stali 0,15%C (wyraźna granica plastyczności)
Podstawowe wielkości:
0
A
F
R
H
H
[MPa] -
granica proporcjonalności
0
0
l
l
l
A
u
p
100%
wydłużenie względne
0
05
,
0
05
,
0
A
F
R
[MPa] -
granica sprężystości
p
– krotność próbki (5 lub 10)
0
A
F
R
e
e
[MPa] -
granica plastyczności
%
100
0
0
A
A
A
Z
u
przewężenie
0
A
F
R
m
m
[MPa] -
wytrzymałość na rozciąganie
l
A
l
F
E
moduł Younga
u
u
u
A
F
R
[MPa] -
naprężenie zerwania
'
liczba Poissona
R
u
R
m
R
e
R
0,05
R
H
H
F
D
A
B
C
G
A
E
0
l
pl
l
spr
l
całk
X=0,05%
l
[%]
[MPa]
F [N]
F
m
F
u
F
e
F
0,05
F
H
u
u
u
A
F
R
A
F
R
0
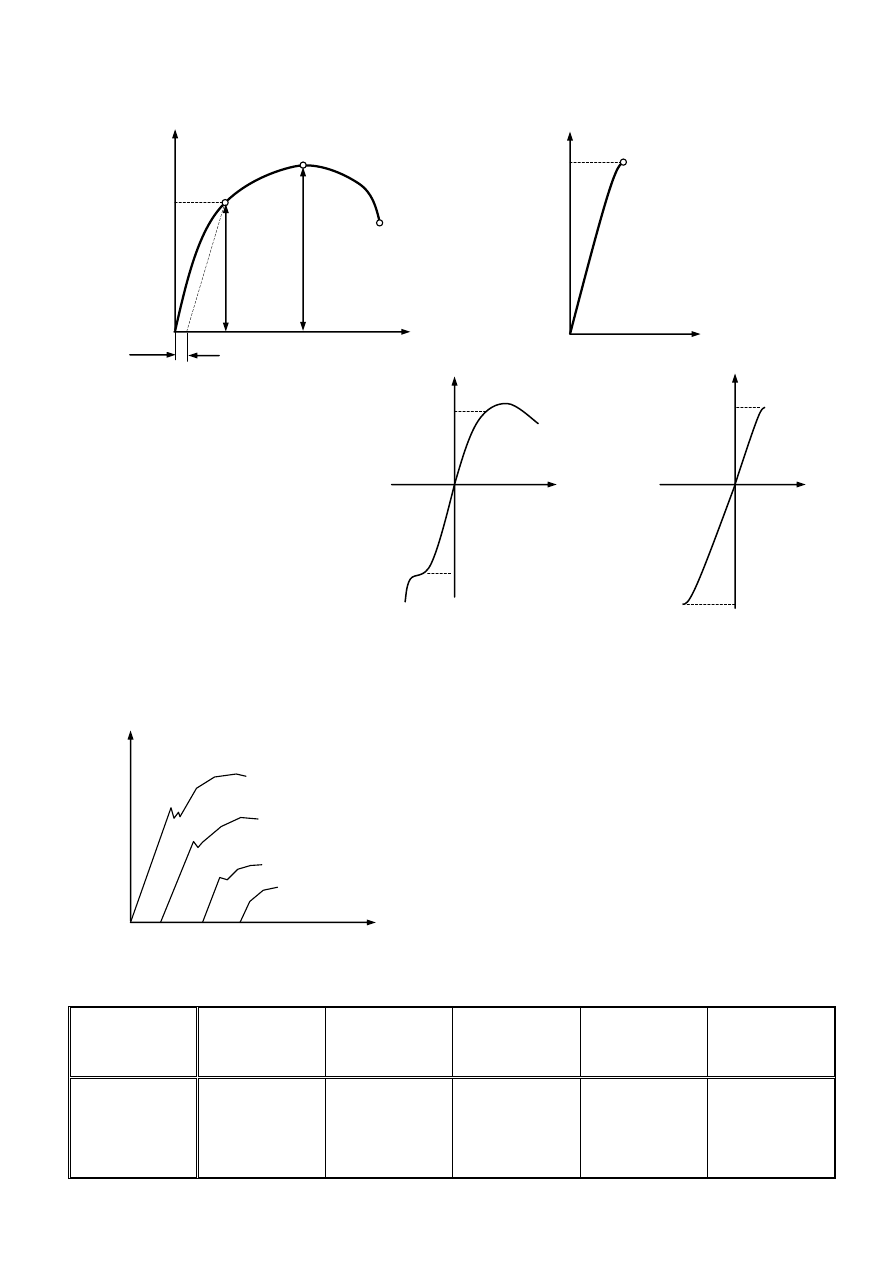
Wykres bez wyraźnej granicy plastyczności
Wykres materiału sprężysto-kruchego
Wykresy ściskania:
a)
materiał sprężysto-plastyczny
b)
materiał sprężysto-kruchy
Wpływ na wykresy rozciągania:
a) czasu-
szybkości rozciągania
b) temperatury
T - wzrost temperatury powoduje
przesuwanie się zachowania materiału
ze stanu kruchego w plastyczny
T - z plastycznego w kruchy
Własności mechaniczne wybranych materiałów
Materiał
E
[MPa]
R
e
[Mpa]
R
m
[Mpa]
A
5
[%]
stal St 3
żeliwo zwykłe
miedź
2,06 10
5
1,2 10
5
1,17 10
5
0,29
0,23-0,27
0,32-0,35
235
-
-
370-460
120-200
224
25
-
60
F
F
F
0,2
F
u
=F
m
l
R
m
l
F
=0,2%
R
0,2
F
F
l
l
F
0,2
F
0,2
F
u
F
m
F
l
V
1
V
1
> V
4
V
4