Temat 1

Obliczanie wielomianu metodą klasyczną i

metodą Hornera

Tomasz Walocha

Akademia Górniczo-Hutnicza w Krakowie

Kierunek Metalurgia

Wydział odlewnictwa

Rok I

Grupa VI

Spis treści

1. Metoda Hornera

2. Wykonywanie obliczeń metodą

klasyczną i Hornera

3. Przedstawienie różnicy czasu

wykonywania obliczeń obiema
metodami (tabelka)

4. Przedstawienie różnicy czasu

wykonywania obliczeń obiema
metodami (wykres)

5. Wnioski

1. Metoda Hornera

Metoda Hornera: Schemat Hornera – sposób obliczania wartości wielomianu dla danej
wartości argumentu wykorzystujący minimalną liczbę mnożeń, jest to również algorytm
dzielenia wielomianu W(x) przez dwumian x-C. Schemat ten wiązany jest z nazwiskiem
Hornera, był jednak już znany Newtonowi, Ruffiniemu i matematykom chińskim w XII
wieku.

Przy dzieleniu wielomianów schemat Hornera można stosować tylko wtedy gdy w dwumianie
nie ma przy x żadnej potęgi i współczynnika. Dla przykładu: dla dzielenia przez dwumian
x-5 można stosować schemat Hornera. Jednak dla dzielenia przez dwumian 4x

2

-1 schematu

Hornera stosować już nie wolno. Dla dzielenia wielomianu przez dwumian 3x-6 można
stosować schemat Hornera, jeżeli najpierw podzieli się dwumian i wielomian, przez 3.

2. Wykonywanie obliczeń metodą klasyczną i

Hornera

Metoda klasyczna:
W(x)= 2x

2

+3x-5 W(x)=5

W(5)=2*5*5+3*5-5
W(5)=60


Metoda hornera:
W(x)=(2x+3)x-5
W(5)=(2*5+3)5-5
W(5)=13*5-5
W(5)=60

Metoda klasyczna:
W(x)=3x

3

+4x

2

+3x+6 W(x)=3

W(3)=3*3*3+4*3*3+3*3+6
W(3)=81+36+9+6
W(3)=132


Metoda hornera:
W(x)=(3x

2

+4x+3)x+6

W(3)=((3x+4)x+3)x+6
W(3)=((3*3+4)3+3)3+6
W(3)=((9+4)3+3)3+6
W(3)=(13*3+3)3+6
W(3)=(39+3)3+6
W(3)=42*3+6
W(3)=126+6
W(3)=132


Metoda klasyczna:
W(x)=2x

4

+4x

3

+5x

2

+2x-4 W(x)=2

W(2)=2*2*2*2*2+4*2*2*2+5*2*2+2*2-4
W(2)=32+32+20+4-4
W(2)=84


Metoda Hornera:
W(x)=(2x

3

+4x

2

+5x+2)x-4

W(2)=((2x

2

+4x+5)x+2)x-4

W(2)=(((2x+4)x+5)x+2)x-4
W(2)=(((2*2+4)2+5)2+2)2-4
W(2)=((8*2+5)2+2)2-4
W(2)=(21*2+2)2-4
W(2)=44*2-4
W(2)=88-4
W(2)=84

Metoda klasyczna:
W(x)=3x

5

+2x

4

+3x

3

+5x

2

+2x-10 W(x)=1

W(1)=3*1+2*1+3*1+5*1+2*1-10
W(1)=3+2+3+5+2-10
W(1)=15-10
W(1)=5


Metoda Hornera:
W(x)=(3x

4

+2x

3

+3x

2

+5x+2)x-10

W(1)=((3x

3

+2x

2

+3x+5)x+2)x-10

W(1)=(((3x

2

+2x+3)x+5)x+2)x-10

W(1)=((((3x+2)x+3)x+5)x+2)x-10
W(1)=((((3*1+2)1+3)1+5)1+2)1-10
W(1)=(((5*1+3) 1+5)1+2)1-10
W(1)=((8*1+5)1+2)1-10
W(1)=13*1+2)1-10
W(1)=15*1-10
W(1)=5

Metoda klasyczna:
W(x)=2x

6

+3x

5

+4x

4

+2x

3

+3x

2

+5x-120 W(x)=2

W(2)=2*2*2*2*2*2*2+3*2*2*2*2*2+4*2*2*2*2+2*2*2*2+3*2*2+5*2-120
W(2)=128+96+64+16+12+10-120
W(2)=326-120
W(2)=206

Metoda hornera:
W(x)=(2x

5

+3x

4

+4x

3

+2x

2

+3x+5)x-120

W(2)=((2x

4

+3x

3

+4x

2

+2x+3)x+5)x-120

W(2)=(((2x

3

+3x

2

+4x+2)x+3)x+5)x-120

W(2)=((((2x

2

+3x+4)x+2)x+3)x+5)x-120

W(2)=(((((2x+3)x+4)x+2)x+3)x+5)x-120
W(2)=(((((2*2+3)2+4)2+2)2+3)2+5)2-120
W(2)=((((7*2+4)2+2)2+3)2+5)2-120
W(2)=(((18*2+2)2+3)2+5)2-120
W(2)=((38*2+3)2+5)2-120
W(2)=(79*2+5)2-120
W(2)=163*2-120
W(2)=206

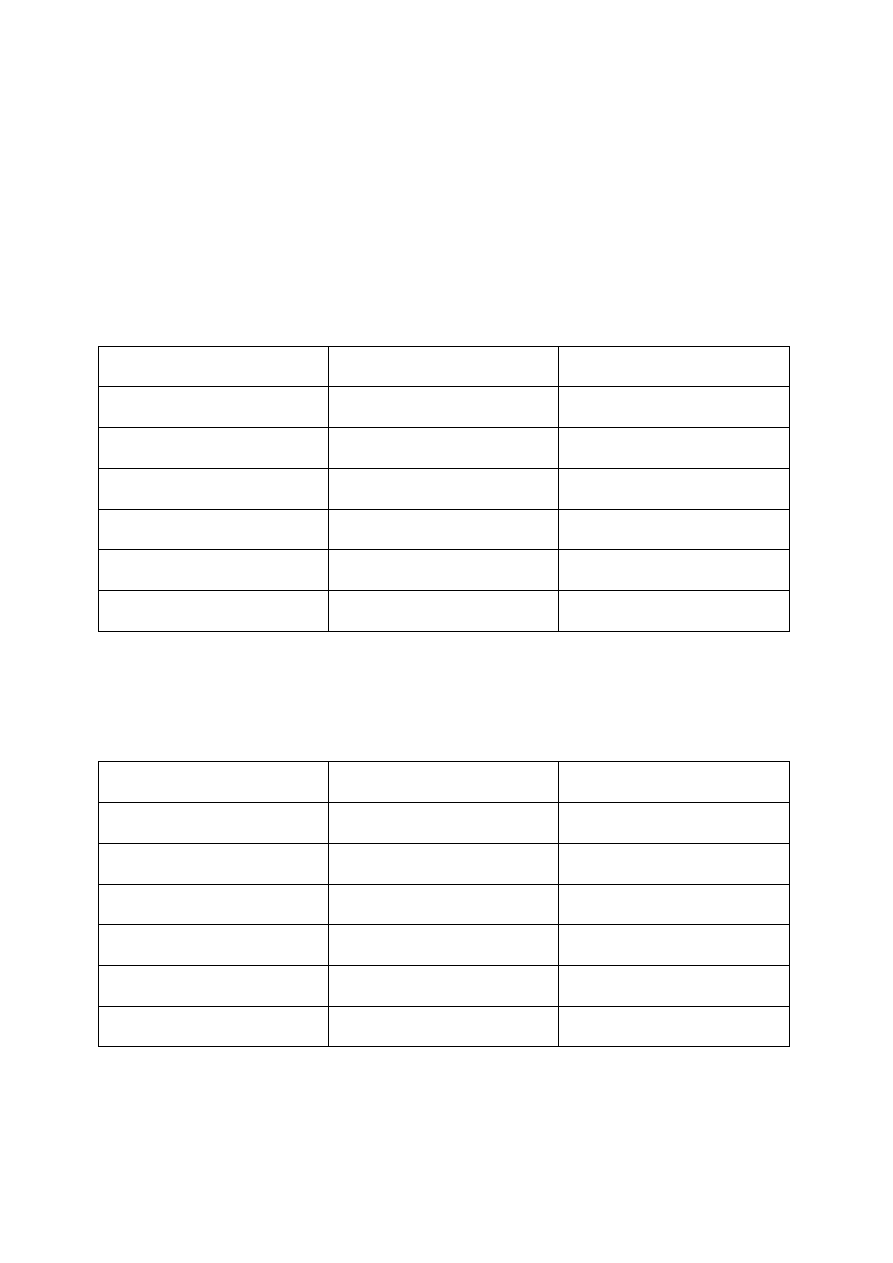
3.

Przedstawienie różnicy czasu wykonywania

obliczeo obiema metodami (tabelka)

Liczba 7-12 (9)

Czas hornera

Czas klasyczny

1000

0

1

10000

0

4

100000

6

45

1000000

59

447

10000000

589

4473

100000000

5885

44732

Liczba 15-19 (17)

Czas hornera

Czas klasyczny

1000

0

1

10000

1

14

100000

11

137

1000000

107

1374

10000000

1070

13742

100000000

10699

137420

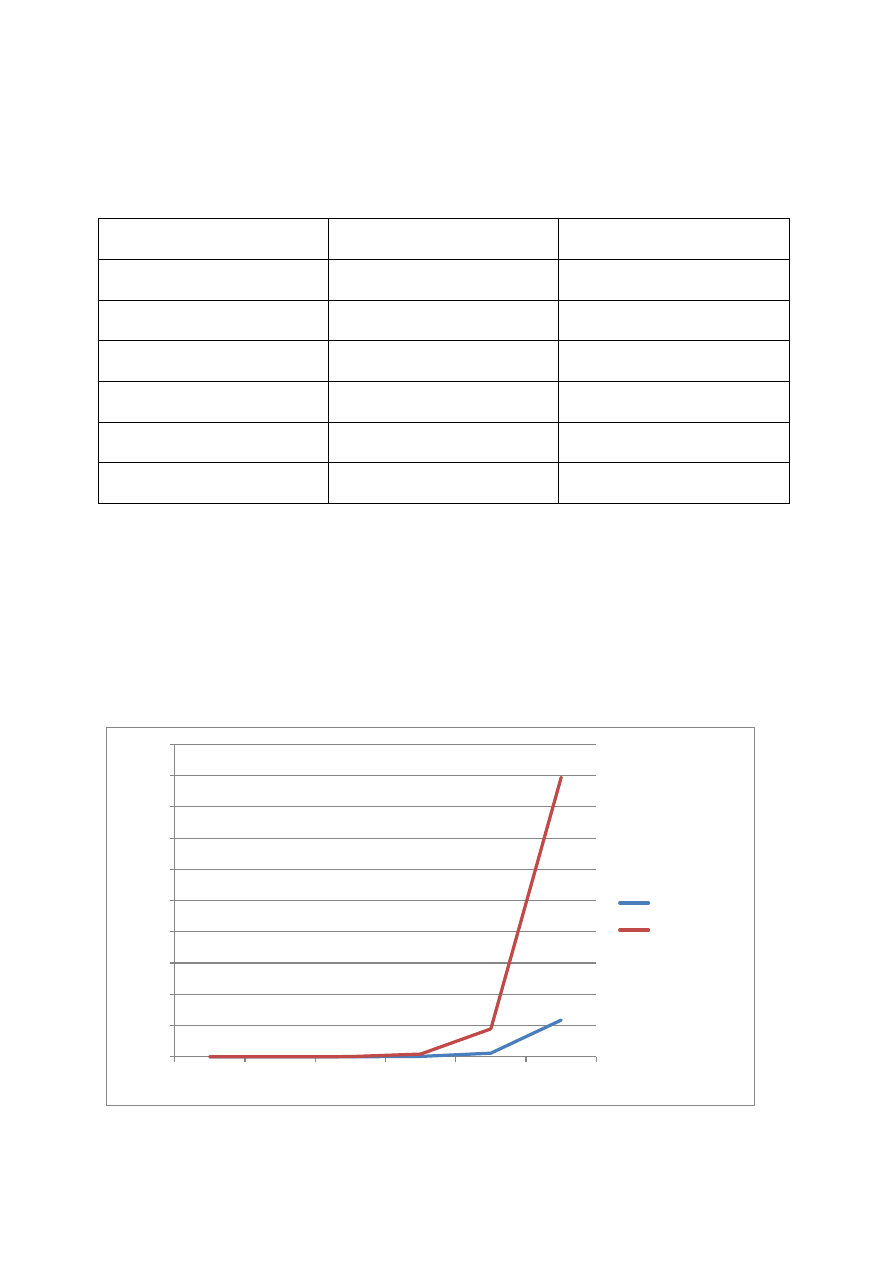
Liczba 20-25 (22)

Czas hornera

Czas klasyczny

1000

0

3

10000

1

22

100000

14

221

1000000

137

2209

10000000

1372

22095

100000000

13725

220952

4. Przedstawienie różnicy czasu wykonywania

obliczeo obiema metodami (wykres)

Wykres liczb o potędze 9

0

5000

10000

15000

20000

25000

30000

35000

40000

45000

50000

1000

10000

100000

1000000 10000000 100000000

Czas hornera

Czas klasyczny

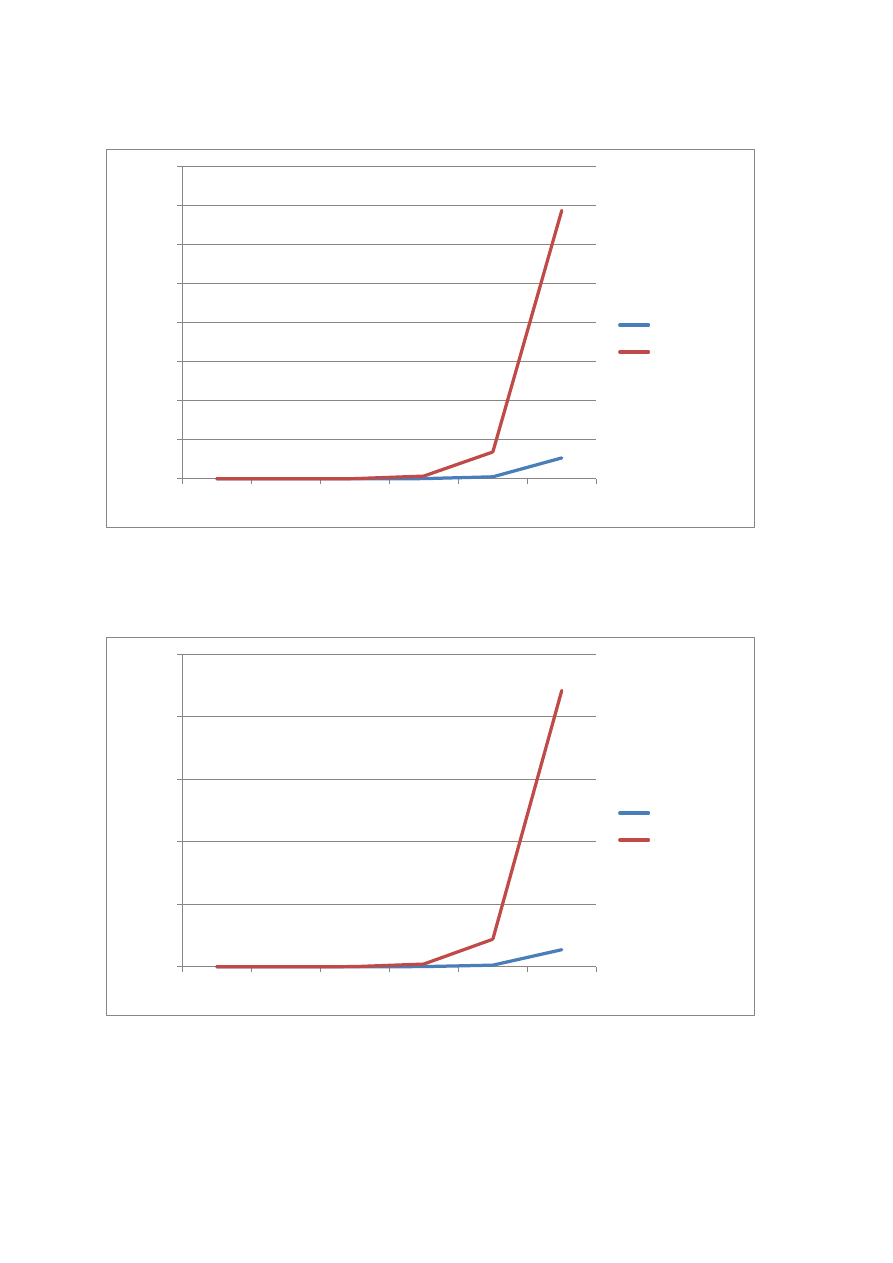
Wykres liczby o potędze 17

Wykres liczby o potędze 22

0

20000

40000

60000

80000

100000

120000

140000

160000

1000

10000

100000

1000000 10000000 10000000

Czas hornera

Czas klasyczny

0

50000

100000

150000

200000

250000

1000

10000

100000

1000000 10000000 100000000

Czas hornera

Czas klasyczny

5. Wnioski

Na podstawie zaobserwowanych wyników przedstawionych w tabelach oraz
wykresach możemy stwierdzid iż metoda hornera jest dużo szybsza i
skuteczniejsza od metody klasycznej. Przy porównaniu czasów wykonania
działania obiema metodami widzimy że metoda hornera jest przy dużych
liczbach nawet 12x szybsza od metody klasycznej a przy dokładniejszej
obserwacji wykresu widzimy ze przy liczbie 10000000 czas obliczeo metoda
klasyczna gwałtownie wzrasta i z większymi liczbami staje się coraz większy

Bibliografia:

www.wikipedia.pl

Doświadczenie przeprowadzono na programie:

TurboDelphii