1

Szybko reakcji chemicznej definiowana jest

jako ubytek st enia substratu lub przyrost

st enia produktu w jednostce czasu.
W definicjach szybko ci innych zjawisk wa na

jest wielko okre laj ca kinetyk w danej chwili,

tzn. wielko rzeczywista a nie rednia.

v= - dc/ dt = + dx/dt

Rzeczywista szybko

jest pochodn st enia

substratu wzgl dem czasu (ze znakiem minus,

poniewa szybko ma sens fizyczny jako

wielko dodatnia) lub pochodn st enia

produktu wzgl dem czasu

.

Szybko reakcji jest funkcja st enia reagentów. Funkcj t

zapisujemy w formie ogólnie stosowanego równania

kinetycznego.

Je eli w reakcji bior udział substraty A,B,C i reakcja jest

prosta,tzn. przebiega tylko w jednym kierunku,wówczas

v = k•[A]

a

•[B]

b

•[C]

c

Gdzie : k jest tzw. stał szybko ci reakcji, jest dla danej

reakcji wielko ci stał w danej temperaturze,zale y bardzo

silnie od temperatury.
Symbole w nawiasach kwadratowych oznaczaj st enia

poszczególnych substratów.
Współczynniki pot gowe przy st eniach poszczególnych

substratów okre laj rz d reakcji.

Rz d reakcji – odró niamy rz d reakcji sumaryczny

od rz dów reakcji wzgl dem poszczególnych

substratów.
Współczynniki pot gowe przy st eniach w

równaniach kinetycznych nie zawsze pokrywaj si

ze współczynnikami stechiometrycznymi.

Cz steczkowo reakcji – liczba cz stek

bior cych udział w elementarnej przemianie.
Zapis równania kinetycznego mówi, ze dana reakcja

jest rz du a wzgl dem substratu A, rz du b

wzgl dem B, i c wzgl dem C, a sumaryczny rz d

reakcji wynosi a+b+c.

Je eli reakcja chemiczna przebiega przez tylko jedna

elementarna przemian , wówczas wszystkie trzy wielko ci,a

wi c rz d reakcji, cz steczkowo i suma współczynników

stechiometrycznych pokrywaj si .

W reakcjach przebiegaj cych poprzez kilka stadiów przemian

elementarnych te trzy wielko ci mog by zupełnie ro ne.

Rz d reakcji stosuje si do eksperymentalnego równania

szybko ci, natomiast cz steczkowo okre la teoretyczny

mechanizm przemiany elementarnej.

Równania kinetyczne prostych reakcji.
Dla reakcji pierwszego rz du, szybko mo emy zapisa

w sposób :

-dc/dt = k•c lub dx/dt = k(a-x)

w drugim zapisie a oznacza st enie pocz tkowe

substratu, natomiast x aktualne st enie produktu.
Po scałkowaniu – dc/c = k dt + const
Otrzymujemy –lnc = kt + const. Stał całkowania

znajdziemy z warunków pocz tkowych; bior c za t=0,

const= -ln c

0

Po scałkowaniu otrzymujemy

ln a/a-x = kt

Czas połówkowy reakcji to czas, po upływie którego

st enie substratu spada do połowy pocz tkowej warto ci.

Podstawiaj c do wcze niejszego równania c=1/2c

0

otrzymujemy, e czas połówkowy I rz d = ln2/k
wynika st d, e czas ten nie zale y od st enia

pocz tkowego substratu.
W przypadku reakcji drugiego rz du równanie kinetyczne

ma posta dx/dt =k(a-x)(b-x)
Gdzie : a i b- st enia pocz tkowe substratów

a x - st enie aktualne produktu

2

W przypadku reakcji trzeciego rz du, kiedy bierze

udział w reakcji tylko jeden substrat, lub gdy st enia

substratów s jednakowe, równanie kinetyczne ma

posta - dc/dt = kc

3

po scałkowaniu przechodzi w

c

0

2

– c

2

/ 2c

2

•c

0

2

= k t

Wyznaczanie rz du reakcji

Najprostszy sposób wyznaczenia rz du reakcji, to

sprawdzanie stało ci k w równaniach kinetycznych

odpowiednich rz dów. O warto ci rz du reakcji

informuje nas tak e zachowanie si czasu

połówkowego reakcji.
Dla reakcji pierwszego rz du czas ten nie zale y od

st enia pocz tkowego. Dla innych rz dów czas ten

zale y od c

0.

ogólnie ~ 1/c

0

n-1

n-rz d reakcji

Najdokładniejsz metod wyznaczenia rz du reakcji jest

porównywanie pocz tkowej szybko ci reakcji dla
okre lonych st e pocz tkowych.

Przez zastosowanie du ego nadmiaru wszystkich

pozostałych substratów w stosunku do badanego

składnika mo na okre li rz d reakcji wzgl dem

konkretnych składników.
Badanie szybko ci reakcji w stadium pocz tkowym jest

wa ne, e eliminujemy ewentualny wpływ reakcji

odwrotnych. Trzeba podkre li ze wszystkie reakcje s

dwukierunkowe, d

do osi gni cia równowagi

termodynamicznej, w której szybko ci reakcji w obu

kierunkach si zrównuj .

Reakcje zło one

Reakcje odwrotne

S to najcz ciej spotykane reakcje zło one. Niemal wszystkie

reakcje s odwracalne i po pewnym czasie, od chwili rozpocz cia

reakcji, szybko jest ich wypadkow z reakcji w jednym i drugim

kierunku.

A

B

Tylko dla reakcji o prostym mechanizmie i niskiej całoliczbowej

rz dowo ci mo liwe jest cisłe ilo ciowe uj cie sumarycznej

kinetyki procesu.

Reakcje odwrotne

Je eli reakcje zachodz ce zarówno w prawo jak i w lewo s

pierwszego rz du, to wówczas mo na zapisa dla tej reakcji

nast puj ce równanie kinetyczne:

dx/dt = k

1

(a – x) – k

–1

x = k

1

a – (k

1

+ k

-1

)x

gdzie:
a- st enie pocz tkowe substratu k- stała szybko ci
x- aktualne st enie produktu

Reakcje odwrotne

Po scałkowaniu tego równania kinetycznego, otrzymuje si

nast puj c zale no :

ln z/z-x = (k

1

+ k

-1

)t

gdzie: z = k

1

a/(k

1

+ k

-1

)

Stosunek k

-1

/k

1

= K , gdzie K jest stał równowagi reakcji

chemicznej.

3

Reakcje równoległe

A

B

C

k

1

k

2

Je eli obie reakcje s pierwszego rz du, wówczas równanie

kinetyczne mo na przedstawi w postaci:

dx/dt = k

1

(a-x) + k

2

(a-x)= (k

1

+ k

2

) (a-x)

Gdzie: x oznacza ubytek st enia substratu (sum st e

produktów)

Reakcje równoległe

Po scałkowaniu otrzymuje si nast puj ce wyra enie:

ln a/a –x = (k

1

+ k

2

)t

Sumaryczna szybko reakcji jest zwykle uwarunkowana jedn z

dwu równoległych reakcji je eli k

1

>>

k

2

lub k

1

<<

k

2

.

Reakcje nast pcze
O reakcjach nast pczych mówimy wtedy gdy produkt

reakcji staje si substratem dla dalszej reakcji a stałe

szybko ci tych reakcji s porównywalne.

A

B

C

(a-x)

(x-y)

y

k

1

k

1

`

a-x, x-y,y oznaczaj aktualne st enia reagentów A, B, C
a- st enie pocz tkowe wyj ciowego substratu A

Reakcje nast pcze

Równania kinetyczne tych reakcji s nast puj ce:

dx/dt = k

1

(a – x)

dy/dt = k

1

`

(x – y)

Reakcje nast pcze

Rys. 1. Zmiany st e reagentów w reakcji nast pczej dla przypadku k

1

=k

1

`

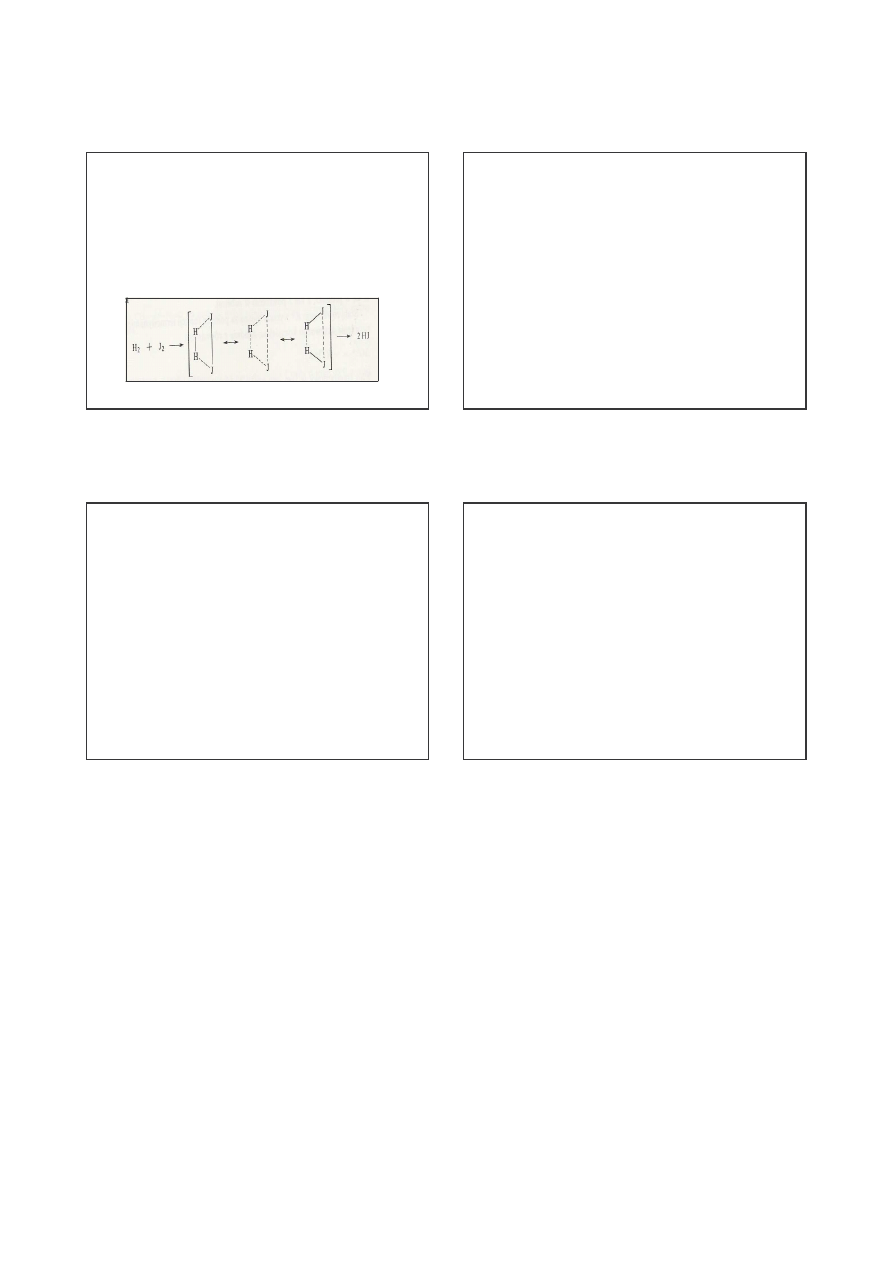
Teoria zderze aktywnych

Efektywne w sensie chemicznym s zderzenia tylko mi dzy

cz steczkami maj cymi wystarczaj cy zasób energii.
Z teorii kinetycznej gazów wiemy, e ułamek cz steczek o energii

równej lub przewy szaj cej pewn warto

a

wynosi

x = e

- a/kT

lub

x = e

-Ea/RT

je eli energi liczy na 1 mol

4

Je eli przez Z

0

oznaczymy liczb wszystkich zderze mi dzy

reaguj cymi cz steczkami, to liczba zderze aktywnych wyniesie

Z = Z

0

e

-Ea/RT

gdzie:
Z- ma wymiar szybko ci reakcji; wyra a liczb cz steczek

reaguj cych w przeci gu sekundy
Ea- energia aktywacji

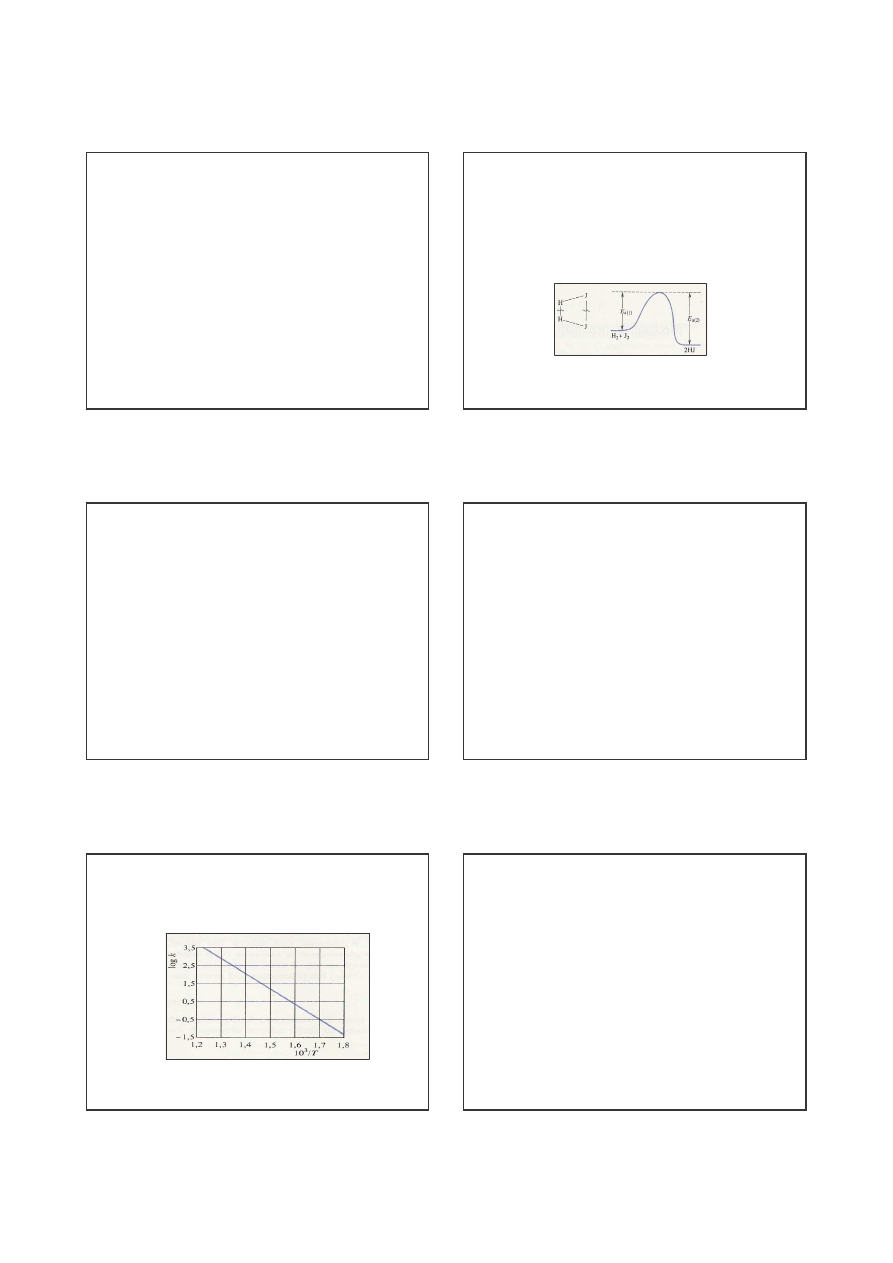
Energia aktywacji

H

2

+ J

2

= 2 HJ

Rys. 2. Bariera energetyczna reakcji chemicznej H

2

+ J

2

= 2 HJ

Równanie Arrheniusa

Równanie Z = Z

0

e

-Ea/RT

poci ga za sob fakt, e ten sam typ

zale no ci wyst pi w wyra eniu na stał szybko ci

k = Ae

-Ea/RT

gdzie:
A- czynnik cz sto ci (przedekspotencjalny), wielko stała,

niezale na od temperatury

Równanie Arrheniusa

Je eli równanie zlogarytmujemy, otrzymamy:

ln k = - E

a

/RT + ln A

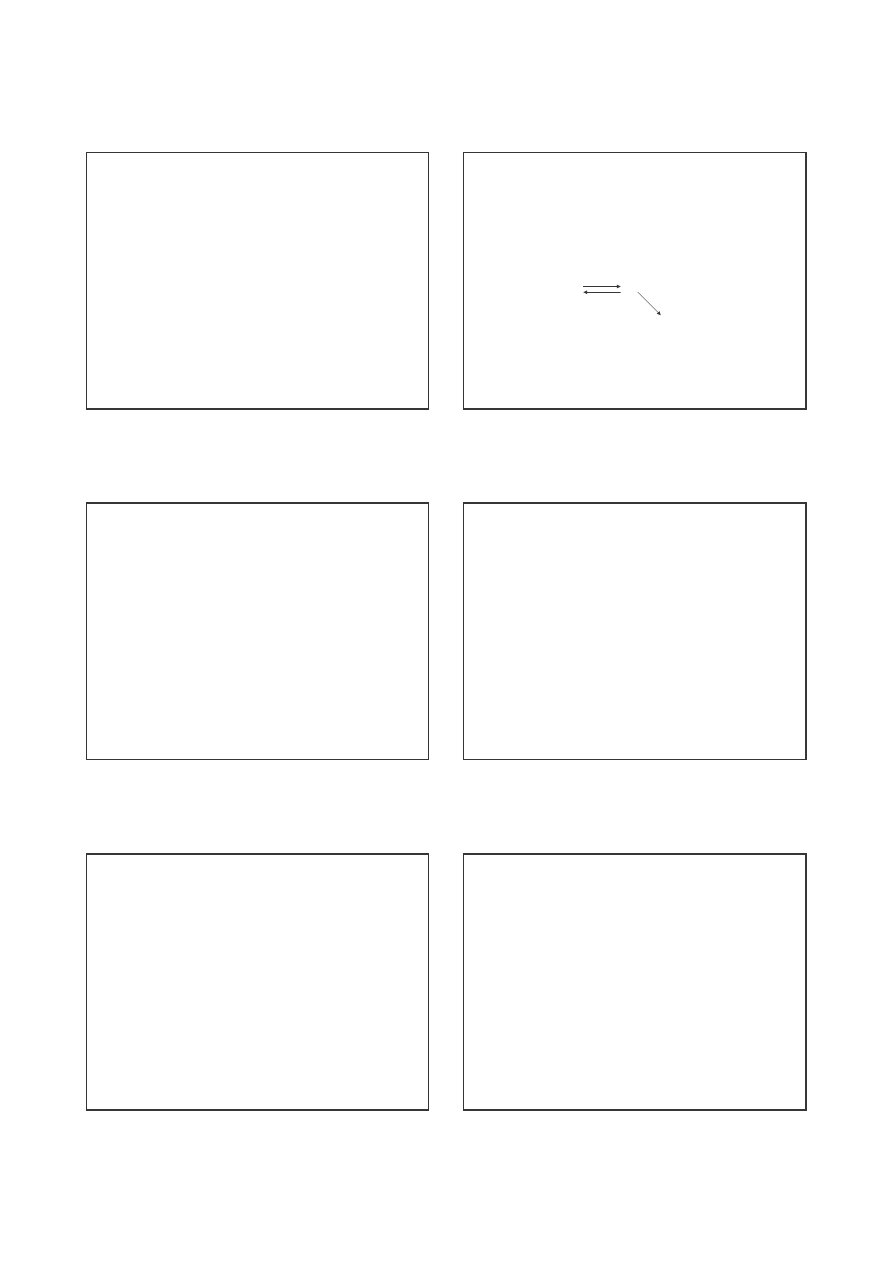
Wykre laj c zale no ln k od odwrotno ci temperatury,

otrzymujemy lini prost , której tangens k ta nachylenia okre la

warto E

a

/R

Rys. 3. Zale no logarytmu stałej szybko ci reakcji syntezy

jodowodoru od odwrotno ci temperatury.

Równanie Arrheniusa

Równanie Arrheniusa mo na ogólniej zapisa w postaci

ró niczkowej

ln k/ T = E

a

/RT

2

Po scałkowaniu w granicach T

1

od T

2

otrzymujemy przy zało eniu,

e E

a

= const jedn z najbardziej znanych postaci równania

Arrheniusa:

ln k

2

/k

1

= E

a

/R (1/T

1

– 1/T

2

)

5

Przykład

Ile razy zwi kszy si szybko reakcji chemicznej, je eli

zwi kszymy temperatur od 0 do 10°C. Energia aktywacji wynosi 40

kcal/mol.
Zgodnie z równaniem Arrheniusa:

log k

2

/k

1

= E

a

/2,303 R (1/T

1

– 1/T

2

)

log k

2

/k

1

= 4 10

4

/4,576 10/273 283 = 1,131

k

2

/k

1

= 13,5

Teoria reakcji jednocz steczkowych

W reakcji jednocz steczkowej A

→ B + C, pierwszym etapem jest

aktywacja, tj. wzbudzenie energetyczne cz steczek na drodze

zderze

A + A

A

‡

+ A

k

2

k

-2

B + C

k

1

Proces aktywacji jest procesem odwracalnym, tzn. zderzenie

cz steczki zaktywowanej ze zwykł cz steczk mo e prowadzi do

dezaktywacji.

Wymienione przemiany mo na uj za pomoc nast puj cych

równa kinetycznych

d[B]/dt = k

1

[A

‡

]

d[A

‡

]

/dt

=

k

2

[A]

2

– k

-2

[A

‡

]

[A] – k

1

[A

‡

]

Model stanu stacjonarnego

Podczas przebiegu reakcji szybko powstawania cz steczek

aktywnych równa si szybko ci ich dezaktywacji.

Stosuj c model stanu stacjonarnego do wcze niejszych rozwa a

kinetycznych mo emy stwierdzi , e [A

‡

]

jest stałe. Zatem

d[A

‡

]

/dt

= 0.

Zało enie to jest słuszne dla niedu ego przedziału

czasowego. Ponadto trzeba wzi pod uwag , e wielko [A

‡

]

jest bardzo mała, a wi c i zmiany w czasie b d małe. Mo na

wi c bez wi kszego bł du przyj pochodn równ zeru.

Poci ga to za sob :

[A

‡

] =

k

2

[A]

2

/k

-2

[A]+k

1

Szybko reakcji definiowanej jako d[B]/dt wynosi:

d[B]/dt = k

1

[A

‡

]

= k

1

k

2

[A]

2

/k

-2

[A]+k

1

Zakładaj c, e k

1

>>k

-2

[A]

2

otrzymujemy wyra enie:

d[B]/dt = k

2

[A]

2

dla zwykłej reakcji drugiego rz du.

Je eli natomiast k

-2

A>>k

1

wówczas:

d[B]/dt = k

1

k

2

/k

-2

[A] = k [A]

Otrzymujemy równanie kinetyczne reakcji pierwszego rz du.

6

Teoria stanów przej ciowych

Szczyt bariery energetycznej, która musi by pokonana podczas

przemiany, nie jest równowa ny stanowi dysocjacji. Jest to stan, w

którym działaj w równym stopniu pierwotne jak i nowe wi zania.

Stan taki nazywamy aktywnym stanem przej ciowym.

A + B

(AB)

‡

C + D

(AB)

‡

- aktywny stan przej ciowy.

Szybko tej reakcji jest proporcjonalna do st enia stanów

przej ciowych:

d[C]/dt = b[(AB)

‡

]

b- czynnik cz sto ci, okre la szybko z jak aktywny kompleks

przej ciowy przechodzi do stanu ko cowego, lub pocz tkowego

reakcji; jest odwrotno ci czasu ycia kompleksu.

b = kT/h

k- stała Boltzmana, h- stała Planca, – współczynnik transmisji

Aktywny kompleks (AB)

‡

jest w równowadze z substratami.

Stała równowagi tej reakcji wynosi:

K

‡

= [(AB)

‡

]/[A][B]

st d:

[(AB)

‡

] = K

‡

[A][B]

Szybko reakcji b dzie zatem okre lona wzorem:

d[C]/dt = bK

‡

[A][B]

Stał równowagi K

‡

wyrazi mo na za pomoc funkcji

termodynamicznych tworzenia aktywnego kompleksu, zgodnie z

równaniem:

G

0‡

= -RTlnK

c

‡

Poniewa G

0‡

= H

0‡

- T S

0‡

otrzymujemy:

k = be

S

º

/R

e

- H

º

/R

Wielko ci S

0‡

i H

0‡

nosz nazw entropii i entalpii aktywacji.