MECHANIKA BUDOWLI

I KONSTRUKCJI

wykład nr11

•

Wyznaczanie

przemieszczeń

w

belce

statycznie wyznaczalnej. Metoda Clebscha.

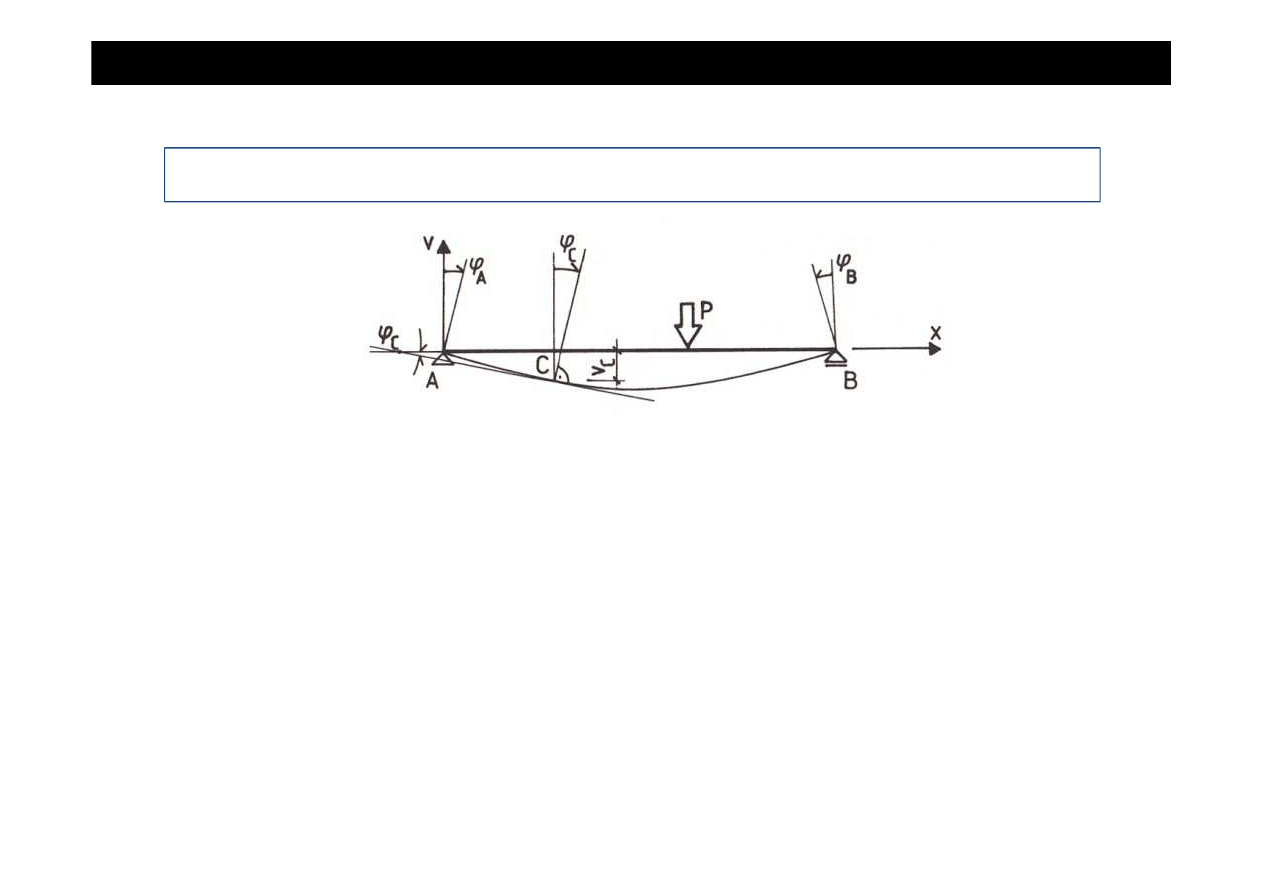
ODKSZTAŁCENIA BELEK ZGINANYCH

Je

ż

eli belka jest poddawana zginaniu, to jej o

ś

zakrzywia si

ę

w płaszczy

ź

nie

obci

ąż

enia,

ś

rodki

ci

ęż

ko

ś

ci

poszczególnych

przekrojów

poprzecznych

(wyznaczaj

ą

ce o

ś

belki) przemieszczaj

ą

si

ę

w pionie (równolegle do osi pionowej),

oraz przekroje poprzeczne obracaj

ą

si

ę

dookoła osi oboj

ę

tnej.

Przemieszczenia

ś

rodka ci

ęż

ko

ś

ci przekroju poprzecznego belki w pionie nazywa si

ę

ugi

ę

ciem

i oznacza liter

ą

v.

Obroty poszczególnych przekrojów poprzecznych w stosunku do swoich pierwotnych

poło

ż

e

ń

okre

ś

la si

ę

jako

k

ą

t obrotu

oznacza liter

ą

.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

RÓWNANIE RÓ

Ż

NICZKOWE OSI ODKSZTACONEJ

Mi

ę

dzy ugi

ę

ciem

v

belki oraz jej momentem zginaj

ą

cym i sztywno

ś

ci

ą

, tj. iloczynem

EI, zachodzi zale

ż

no

ść

ró

ż

niczkowa:

= EI

``

= ± ,

całkuj

ą

c raz powy

ż

sze równanie, otrzymuje si

ę

zale

ż

no

ść

okre

ś

laj

ą

c

ą

k

ą

t obrotu:

= EI

`

= +

,

a całkuj

ą

c dwa razy – zale

ż

no

ść

okre

ś

laj

ą

c

ą

ugi

ę

cie:

=

+ + [

dx],

gdzie: C,D – stałe całkowania zale

ż

ne od warunków brzegowych.

Stałe całkowania maj

ą

nast

ę

puj

ą

ce jednostki: C

∙ !" ,

D

∙ !"

#

.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

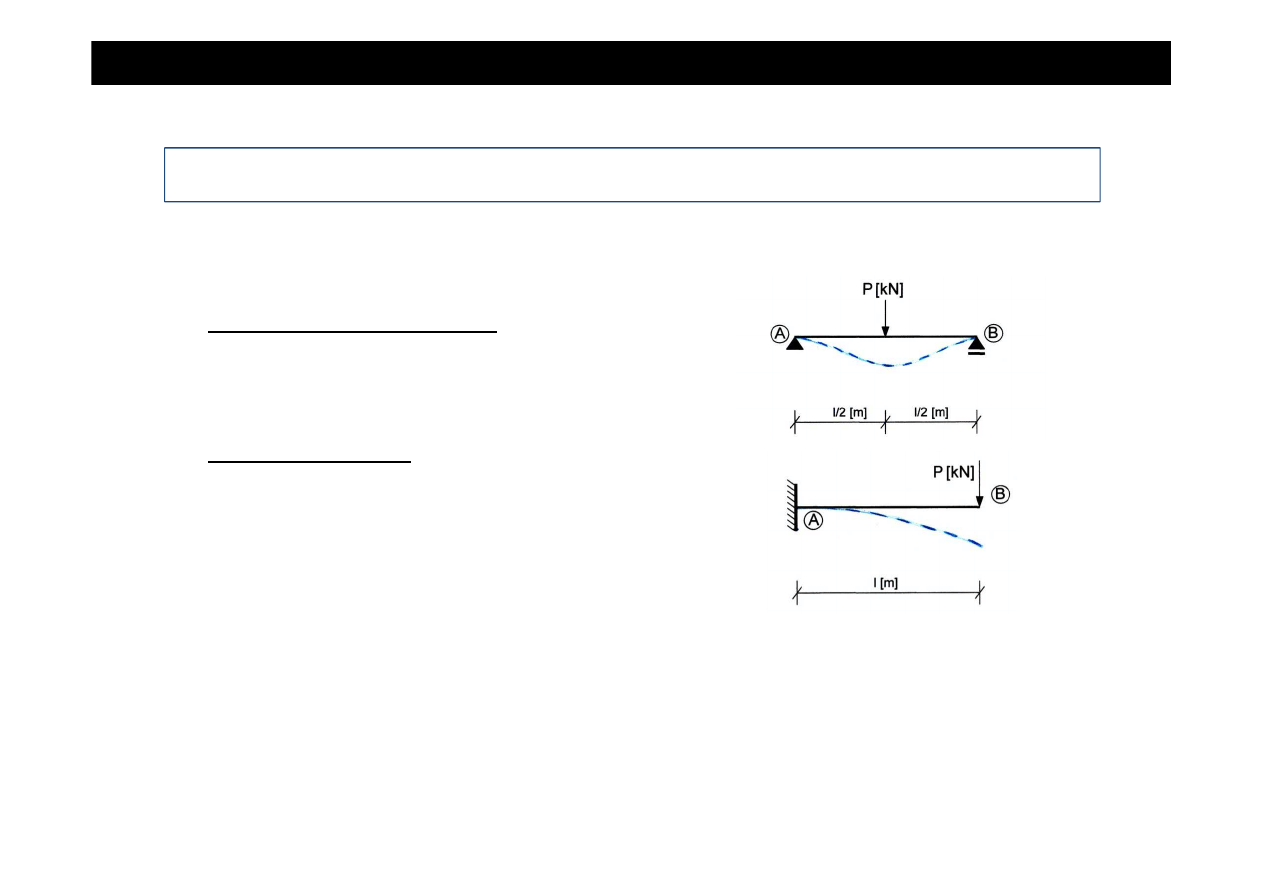
WARUNKI BRZEGOWE

Warunki brzegowe zale

żą

od rodzaju podpór oraz ogólnego warunku ci

ą

gło

ś

ci osi

odkształconej.

•

Belka swobodnie podparta:

ugi

ę

cie na ka

ż

dej podporze równa si

ę

zeru

%

= 0,

'

= 0

.

•

Belka utwierdzona:

ugi

ę

cie w utwierdzeniu równa si

ę

zeru

%

= 0,

k

ą

t obrotu w utwierdzeniu równa si

ę

zeru

%

= 0.

•

K

ą

t obrotu

przekroju poprzecznego równa si

ę

zeru (

= 0)

w połowie długo

ś

ci

belki przy jej symetrycznym obci

ąż

eniu.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

METODA CLEBSCHA

•

Ugi

ę

cie

obliczone z równania dla lewego przedziału obci

ąż

enia równa si

ę

ugi

ę

ciu

obliczonemu dla przedziału prawego na ka

ż

dej granicy przedziału.

•

K

ą

t obrotu

obliczony z równania dla lewego przedziału obci

ąż

enia równa si

ę

k

ą

towi obrotu przekroju obliczonemu z równania dla przedziału prawego na ka

ż

dej

granicy przedziału.

Równanie

ma ró

ż

n

ą

posta

ć

na poszczególnych przedziałach belki o ró

ż

ni

ą

cych si

ę

obci

ąż

eniach. Je

ż

eli jest wi

ę

c n takich przedziałów, to otrzymuje si

ę

n równa

ń

ró

ż

niczkowych oraz 2n stałych całkowania. Wyznaczenie tych stałych jest bardzo

pracochłonne. Obliczenia znacznie ułatwia si

ę

(ogranicza si

ę

do 2 liczba stałych

całkowania), przyjmuj

ą

c specjalny sposób zapisu wyra

ż

enia okre

ś

laj

ą

cego moment

zginaj

ą

cy

, nazywany metod

ą

Clebscha.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

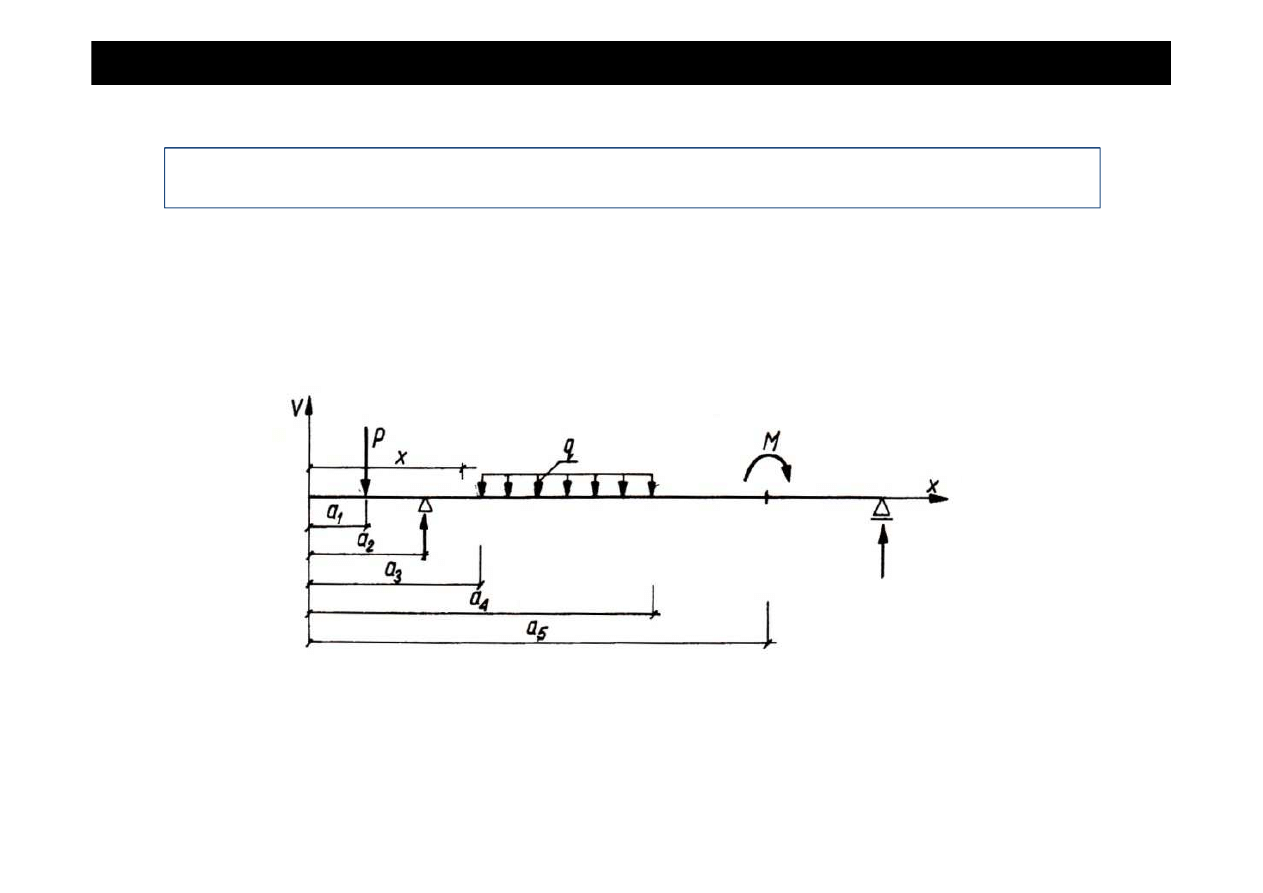
METODA CLEBSCHA

Warunki, jakie powinny by

ć

spełnione dla metody Clebscha w przypadku belek

o stałej sztywno

ś

ci EI:

1. Pocz

ą

tek układu współrz

ę

dnych przyjmuje si

ę

na jednym z ko

ń

ców belki.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

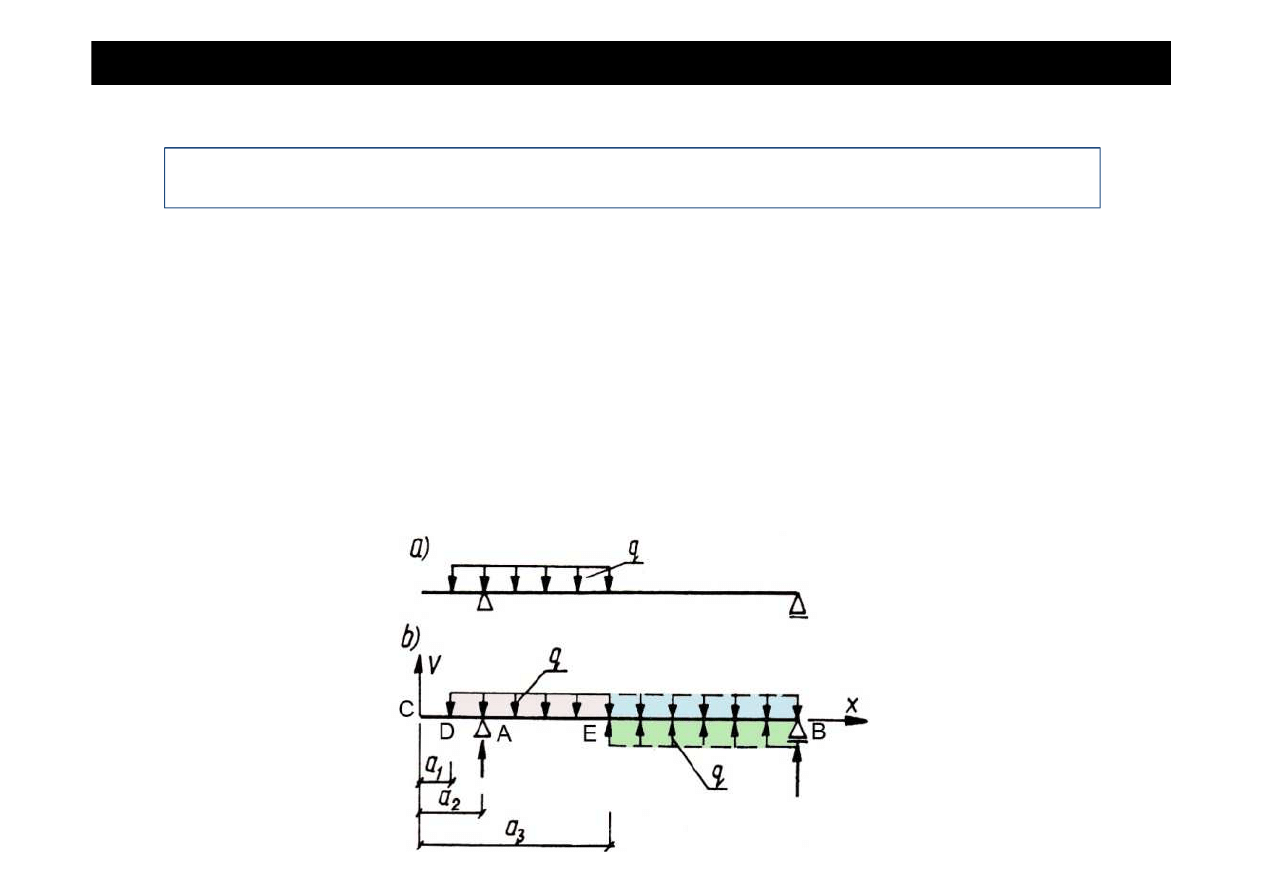
METODA CLEBSCHA

2. Równanie momentu zginaj

ą

cego

na wszystkich odcinkach belki zapisuje si

ę

uwzgl

ę

dniaj

ą

c siły działaj

ą

ce po jednej stronie przekroju. Zatem

wszystkie wyrazy

z równania

poprzedniego przedziału musz

ą

by

ć

wprowadzone bez zmian do

równania momentu zginaj

ą

cego nast

ę

pnego przedziału.

W przypadku obci

ąż

enia ci

ą

głego belk

ę

, ko

ń

cz

ą

cego si

ę

w okre

ś

lonym punkcie belki,

niezb

ę

dne jest „przedłu

ż

enie” tego odcinka do ko

ń

ca belki i jednoczesne dodanie na

tym odcinku obci

ąż

enia równowa

żą

cego (o zwrocie przeciwnym).

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

METODA CLEBSCHA

3. Wszystkie nowe wyra

ż

enia wchodz

ą

ce do równania

rozpatrywanego

przedziału musz

ą

zawiera

ć

mno

ż

nik

( − +

,

),

gdzie:

– odci

ę

ta danego przekroju,

+

,

– odci

ę

ta punktu pocz

ą

tkowego danego odcinka.

4.Całkowanie wyra

ż

e

ń

zawieraj

ą

cy dwumiany

( − +

,

) nale

ż

y wykona

ć

wzgl

ę

dem

nowej zmiennej

( − +

,

), czyli bez otwierania nawiasów, zgodnie z reguł

ą

:

( − +

,

)

-

= ( − +

,

)

-

( − +

,

)

=

( ./

0

)

123

-45

+ C

.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

METODA CLEBSCHA

Zasada całkowania:

( − +

,

)

-

= ( − +

,

)

-

( − +

,

)

=

( − +

,

)

-45

" + 1

+ C.

− +

,

5

=

./

0 8

+ C

− +

,

=

./

0 9

#

+ C →

./

0 8

=

./

0 9

∙#

+ C =

./

0 9

;

+ C

− +

,

#

=

./

0 <

=

+ C →

./

0 9

;

=

./

0 <

;∙=

+ C =

./

0 <

=

+ C

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

METODA CLEBSCHA

5. Stałe całkowania, jako wspólne dla wszystkich odcinków, pisze si

ę

na pocz

ą

tku

prawej strony równa

ń

.

6. Równanie

zapisuje si

ę

od razu w odniesieniu do całej belki w takiej postaci, aby

pionowymi kreskami z odpowiednimi indeksami były zaznaczone granice przedziału

zmienno

ś

ci

.

7. Je

ż

eli w równaniu

wyst

ę

puje moment skupiony M, to przy tym momencie

zapisuje si

ę

mno

ż

nik

( − +

,

)

>

, gdzie

+

,

- odci

ę

ta punktu przyło

ż

enia momentu

skupionego M.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

METODA CLEBSCHA

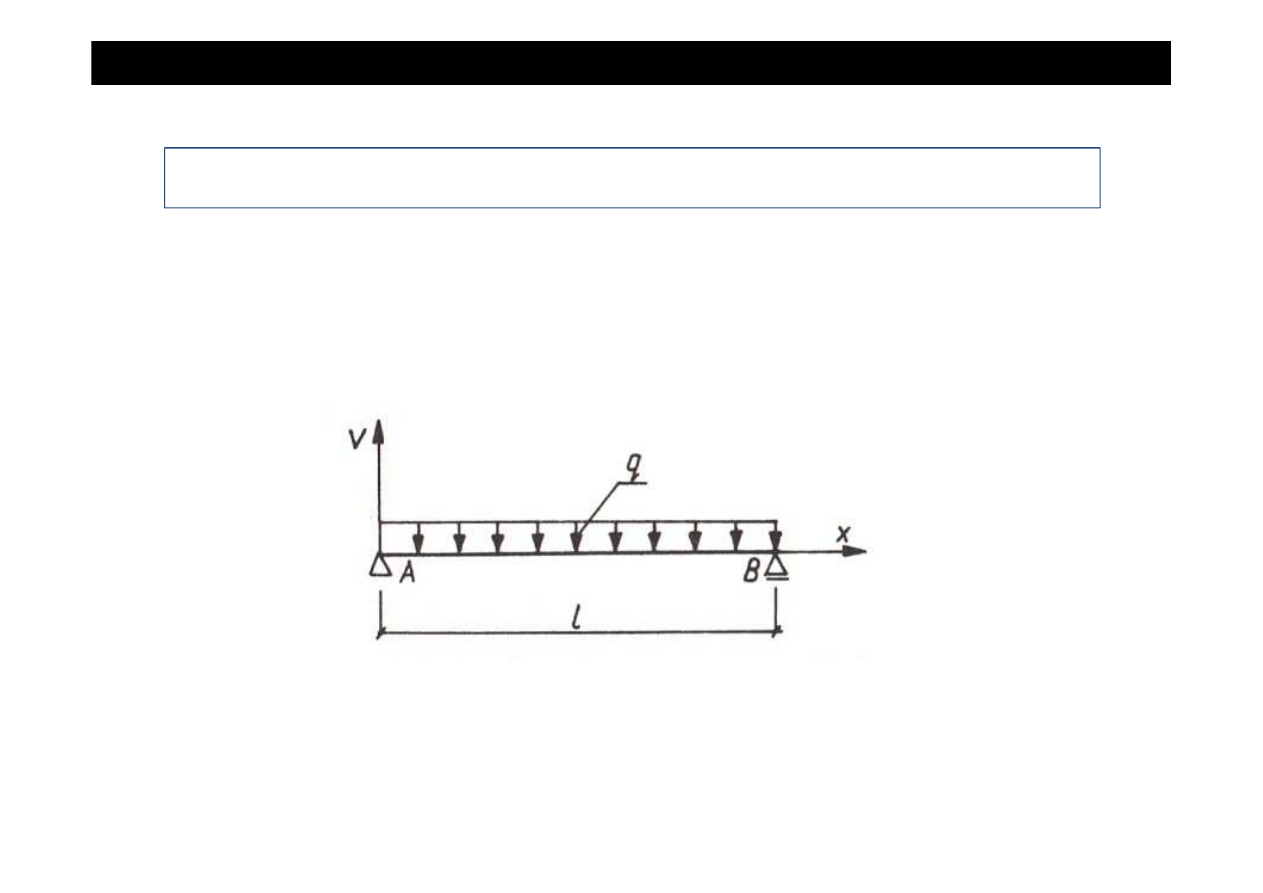
Zadanie

Dana jest belka swobodnie podparta, obci

ąż

ona równomiernie na całej długo

ś

ci. Wyznaczy

ć

ugi

ę

cie oraz k

ą

t obrotu w połowie rozpi

ę

to

ś

ci belki.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

METODA CLEBSCHA

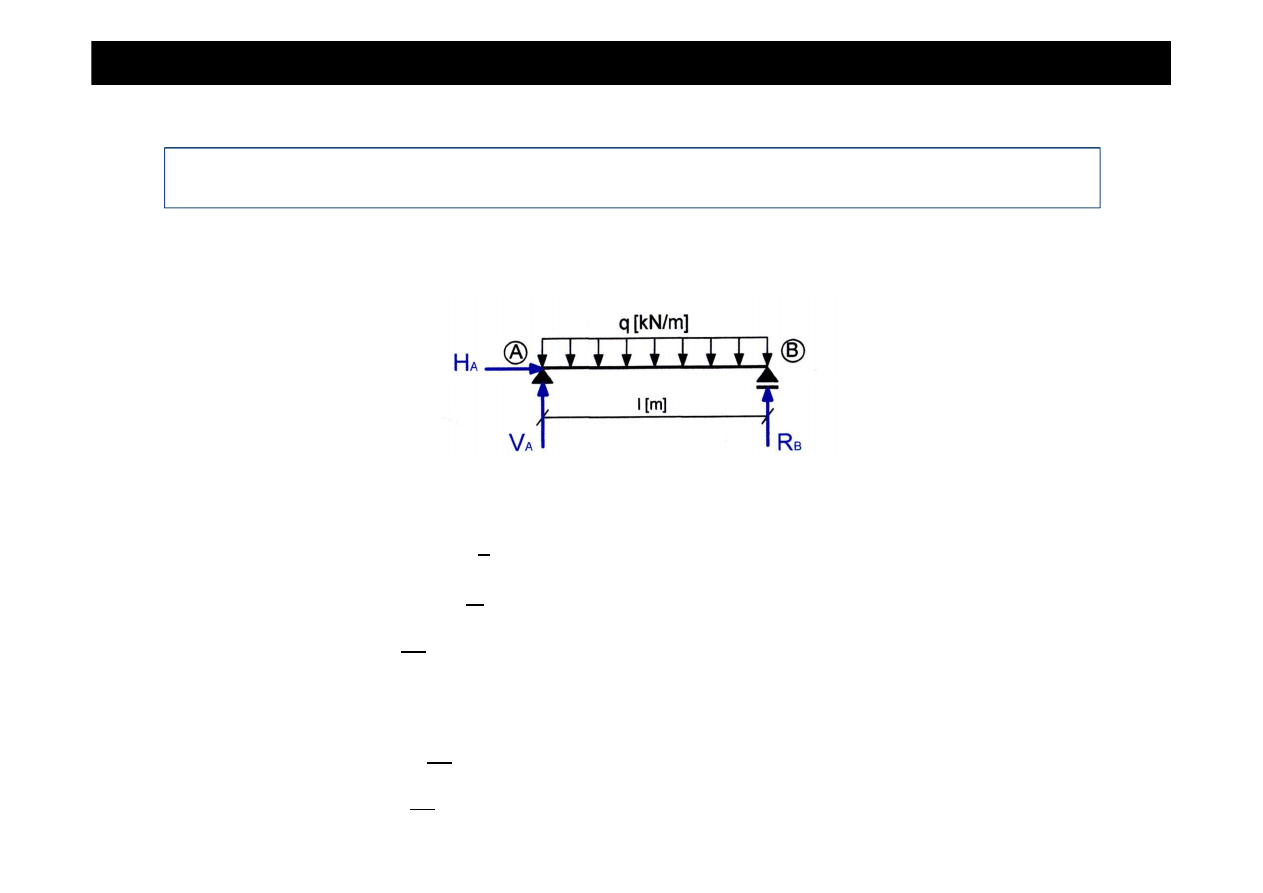
Zadanie cd

•

Wyznaczamy warto

ś

ci reakcji podporowych

1.

∑ @ = 0 A

%

= 0 [kN]

2.

∑ C = 0 D

%

+

E

'

- q

∙

l = 0

→ F GH" IóFK+KLM Ną FLP KLPFL+ Q"P

3.

∑

'

=0

D

%

∙ S

- q

∙ S ∙

T

= 0

D

%

∙ l = q ∙

T

8

/:l

D

%

=

W∙T

[kN]

4. powracamy do równania nr2

∑ C

= 0

→ E

'

= -

D

%

+ q

∙

l

E

'

= -

W∙T

+ q

∙

l

E

'

=

W∙T

[kN

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

METODA CLEBSCHA

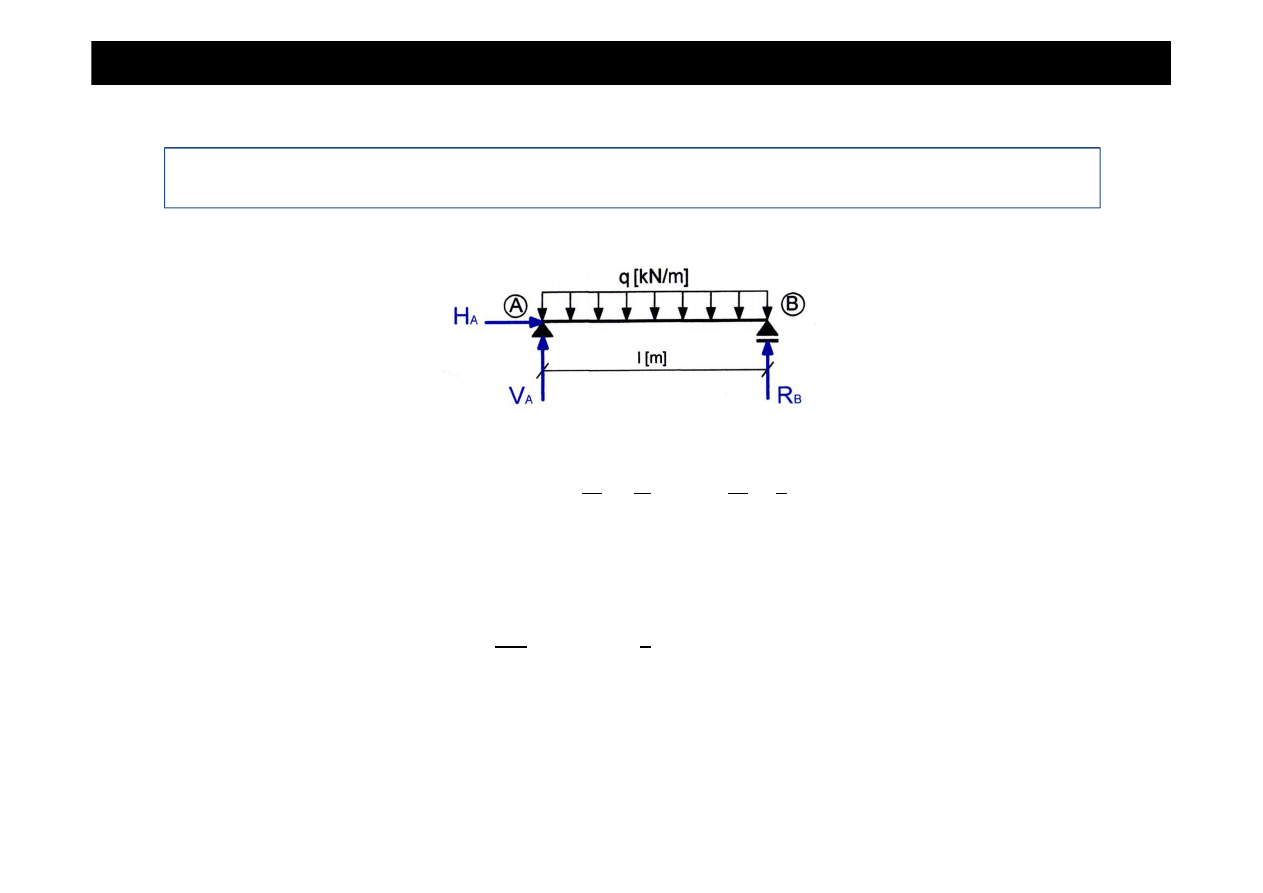
Zadanie cd

Moment zginaj

ą

cy w dowolnym przekroju

X − X

o odci

ę

tej x wyra

ż

a si

ę

zale

ż

no

ś

ci

ą

:

%'

X

=

D

%

∙ x

- q

∙

8

=

WT

∙

- q

∙

8

=

W

(l

∙

x -

).

1.Mi

ę

dzy ugi

ę

ciem

belki oraz jej momentem zginaj

ą

cym zachodzi zale

ż

no

ść

ró

ż

niczkowa:

8

=

``

=

W

(l

∙

x -

)

|

%'

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

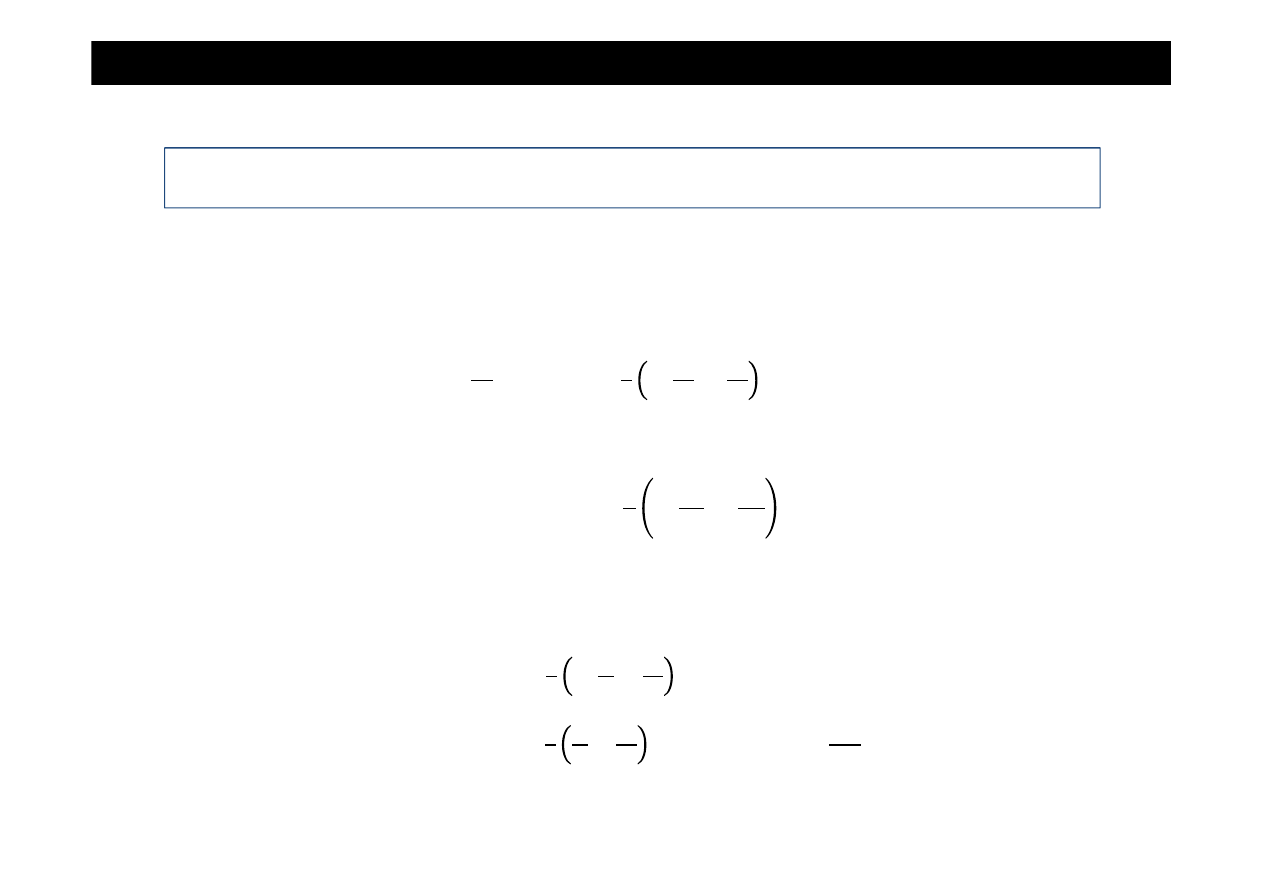
METODA CLEBSCHA

Zadanie cd

2.Pierwsza całka równania – k

ą

t obrotu:

=

`

= C +

W

S ∙

8

−

9

#

|

%'

.

3.Druga całka równania – linia ugi

ę

cia:

= + ∙ +

Z

2 S ∙

#

6 −

=

12 |

%'

Stałe całkowania C i D okre

ś

la si

ę

z warunków brzegowych:

•

dla x=0

→

%

=0, st

ą

d D=0,

•

dla x=l

→

'

=0, st

ą

d

∙ S +

W

S ∙

T

9

;

−

T

<

5

=0

∙ S +

W T

<

;

−

T

<

5

=0, st

ą

d

= −

W∙T

9

=

.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

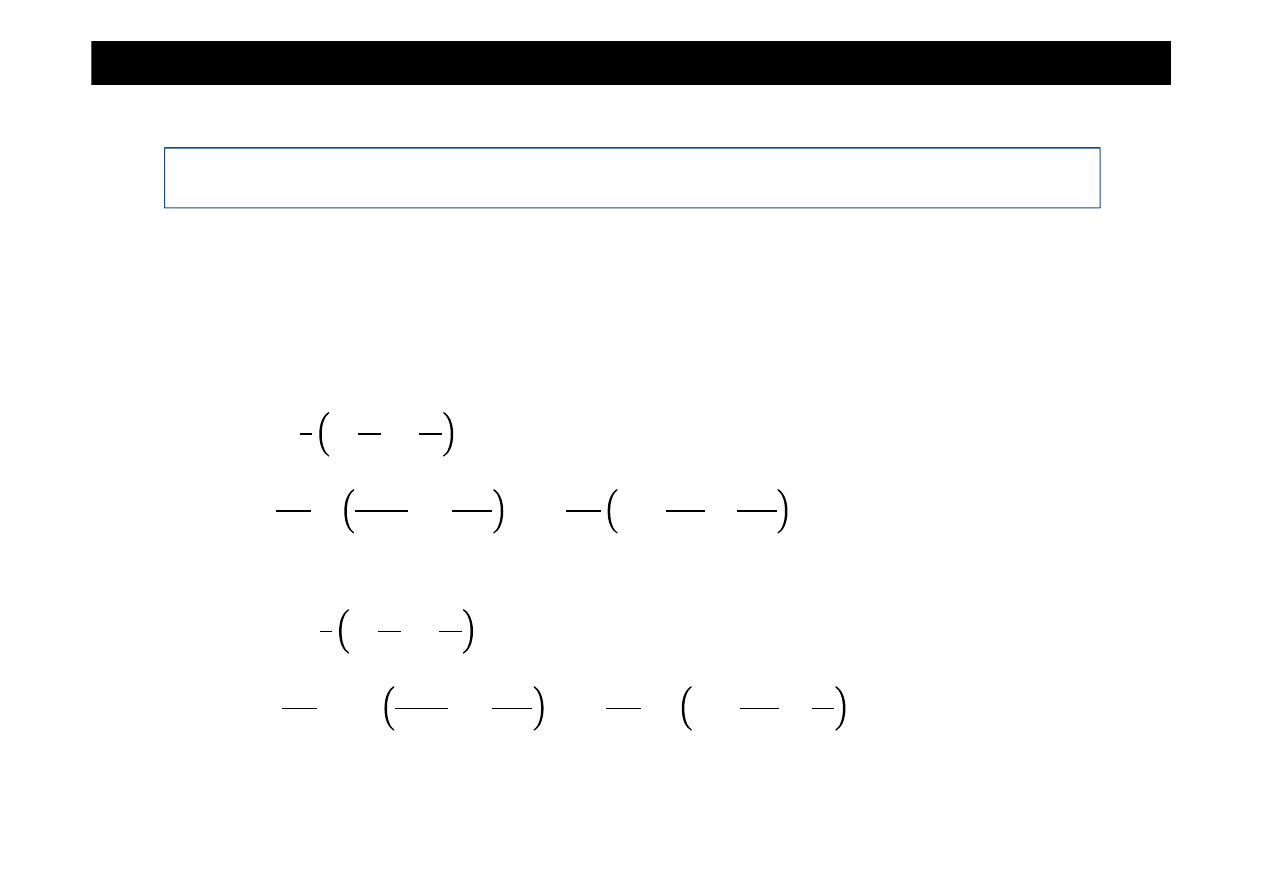
METODA CLEBSCHA

Zadanie cd

Po podstawieniu stałych całkowania C i D równania odkształce

ń

przyjmuj

ą

posta

ć

:

•

równanie k

ą

ta obrotu

`

= C +

W

S ∙

8

−

9

#

|

%'

=

= −

W∙T

9

=

+

W∙T∙

8

=

−

W∙

9

;

= −

W∙T

9

=

1 −

;∙

8

T

8

+

=∙

9

T

9

,

•

równanie linii ugi

ę

cia

= C∙ +

W

S ∙

9

;

−

<

5

|

%'

=

= −

W∙T

9

=

∙

+

W∙T∙

9

5

−

W∙

<

=

= −

W∙T

9

=

∙ 1 −

∙

8

T

8

+

9

T

9

.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

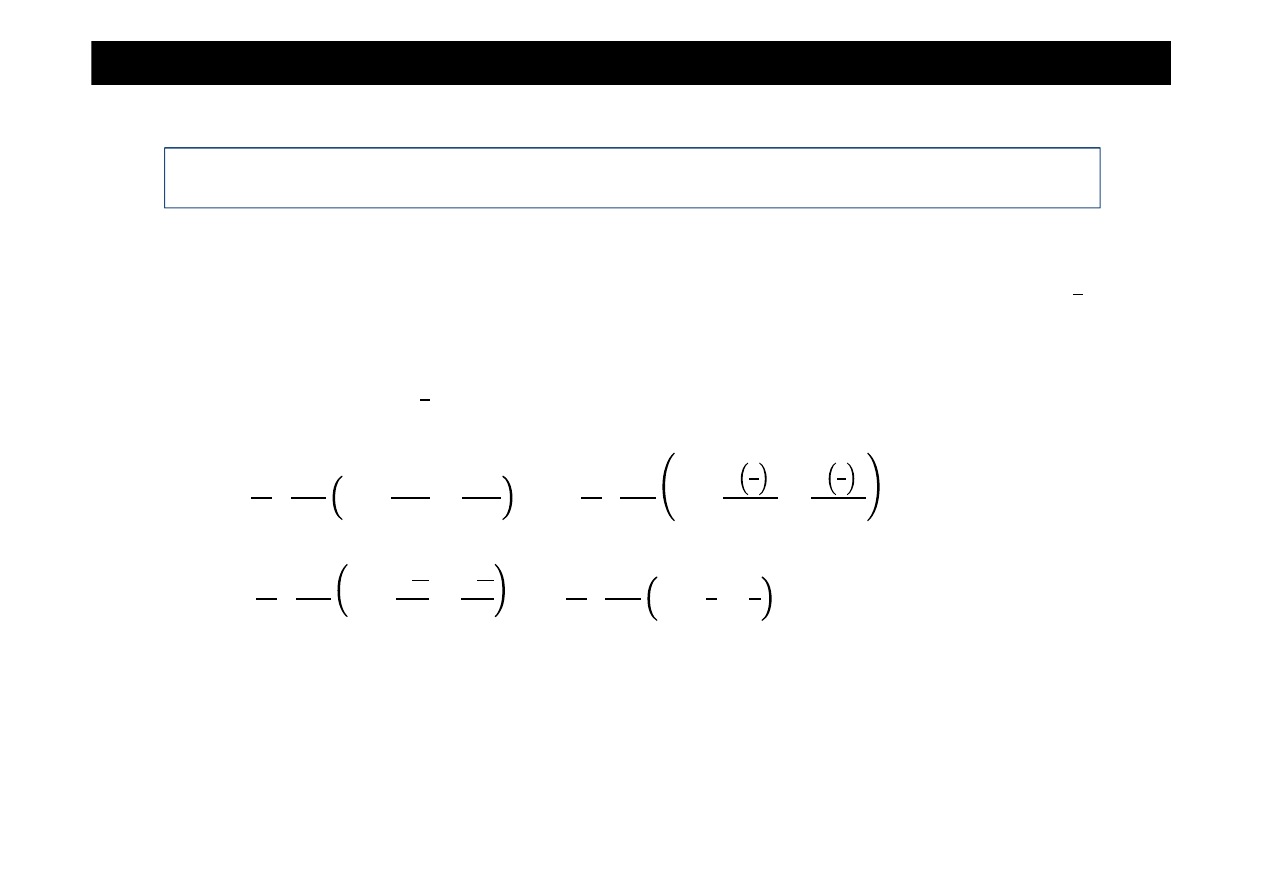
METODA CLEBSCHA

Zadanie cd

Wyznaczanie warto

ś

ci k

ą

ta obrotu i ugi

ę

cia w połowie rozpi

ę

to

ś

ci belki, czyli dla

=

T

•

k

ą

ta obrotu dla

=

T

:

`

= −

5

\]

∙

W∙T

9

=

1 −

;∙

8

T

8

+

=∙

9

T

9

= −

5

\]

∙

W∙T

9

=

1 −

;∙

^

8

8

T

8

+

=∙

^

8

9

T

9

=

−

5

\]

∙

W∙T

9

=

1 −

;∙

^8

<

T

8

+

=∙

^9

_

T

9

= −

5

\]

∙

W∙T

9

=

1 −

#

+

5

= 0 rad = 0°,

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

METODA CLEBSCHA

Zadanie cd

Dla belki stalowej o długo

ś

ci l=4,0 m, obci

ąż

eniu q=3,0 kN/m o przekroju dwuteowym

I180

o warto

ś

ci momentu bezwładno

ś

ci

=1450

!"

=

oraz warto

ś

ci współczynnika spr

ęż

ysto

ś

ci

podłu

ż

nej E=210 000 MPa – warto

ść

ugi

ę

cia wynosi:

= −

c∙W∙T

<

#d=∙\]

= −

c∙#

ef

1

∙ =-

<

#d=∙ ,5∙5>

_ef

18

∙5=c>∙5>

g_

-

<

= −

c∙#

ef

1

∙ c;-

<

#d=∙ ,5∙5>

_ef

18

∙5=c>∙5>

g_

-

<

=

= −

3840

∙ "

#

1169280 "

= −0,0033 " = −0,33 !"

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

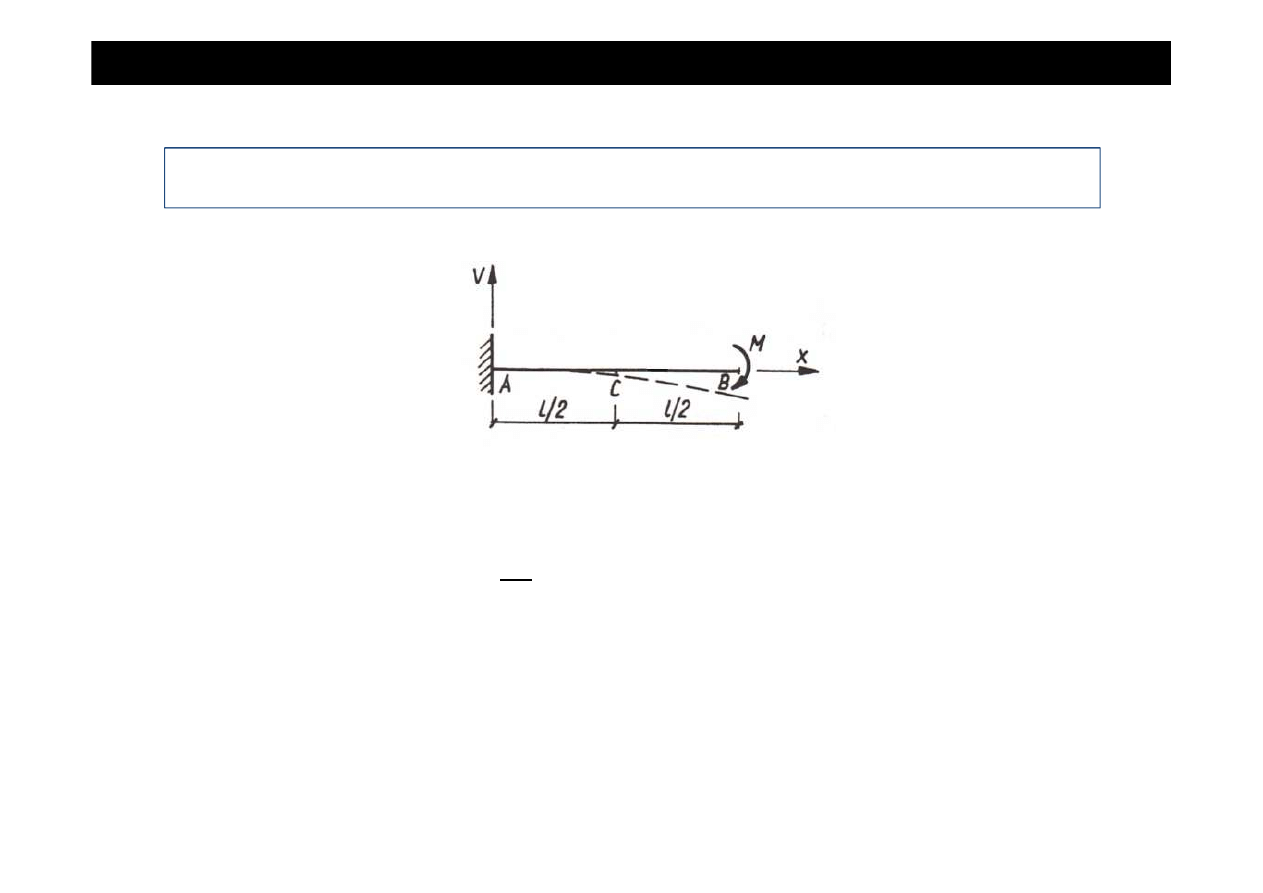
METODA CLEBSCHA

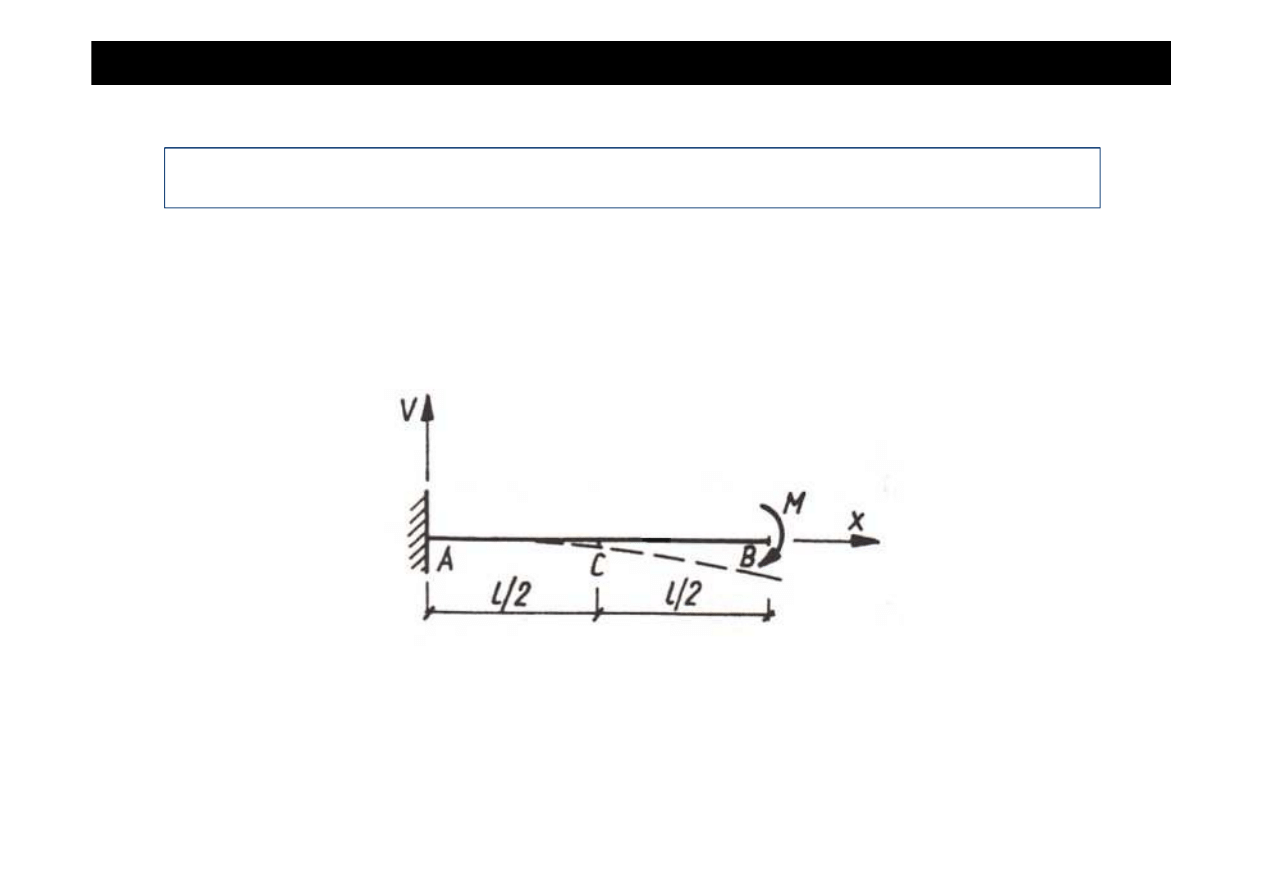
Zadanie

Dana jest belka utwierdzona obci

ąż

ona momentem skupionym M przyło

ż

onym na jej ko

ń

cu.

Wyznaczy

ć

odkształcenia: k

ą

t obrotu i ugi

ę

cie w punkcie przyło

ż

enia obci

ąż

enia.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

METODA CLEBSCHA

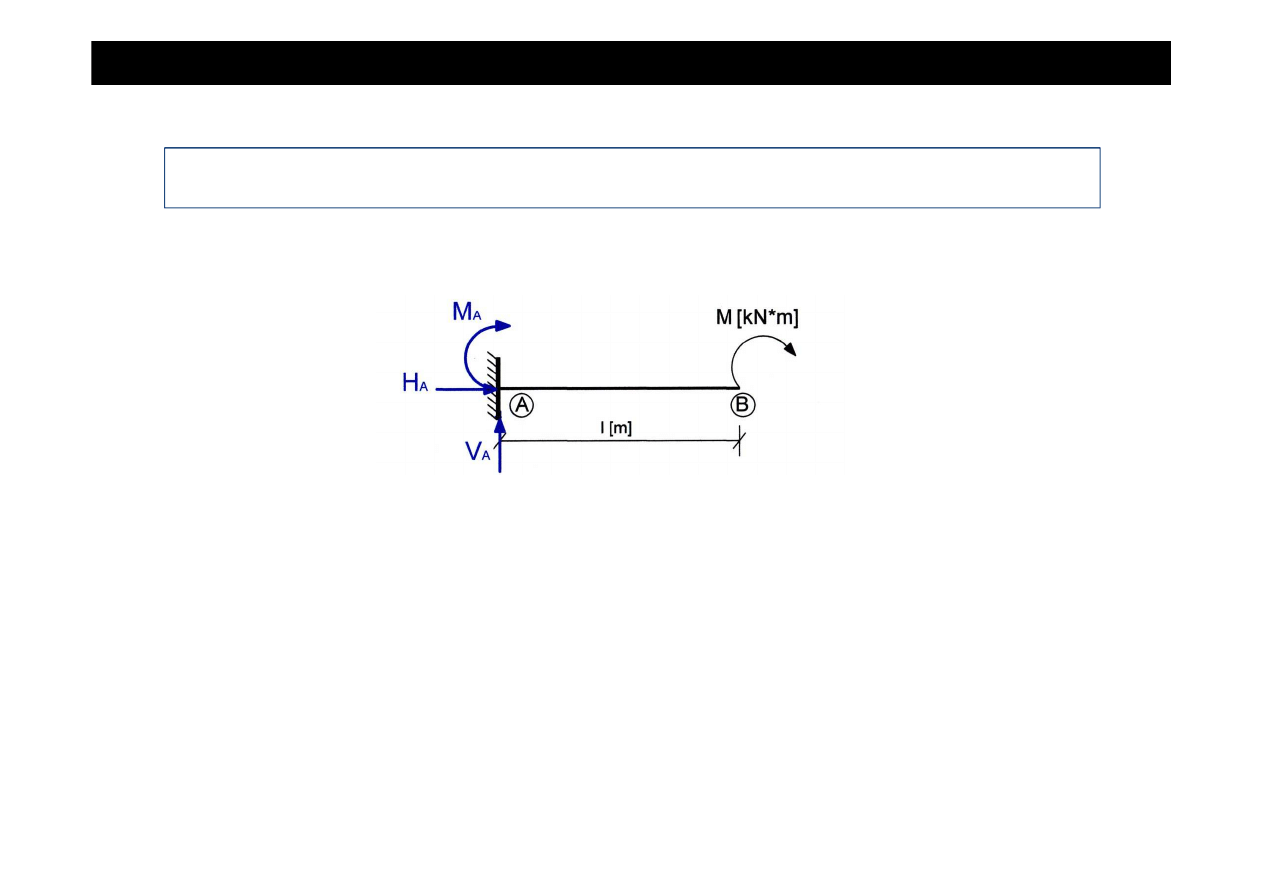
Zadanie cd

•

Wyznaczamy warto

ś

ci reakcji podporowych

1.

∑ @ = 0 A

%

= 0 [kN]

2.

∑ C = 0 D

%

= 0 [kN]

3.

∑

%

=0

%

+

= 0

%

= −M [kN ∙ "]

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

METODA CLEBSCHA

Zadanie cd

1.Mi

ę

dzy ugi

ę

ciem

belki oraz jej momentem zginaj

ą

cym zachodzi zale

ż

no

ść

ró

ż

niczkowa:

8

=

``

= − ∙

>

|

%'

.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

METODA CLEBSCHA

Zadanie cd

2.Pierwsza całka równania – k

ą

t obrotu:

=

`

= C − ∙

5

|

%'

.

3.Druga całka równania – ugi

ę

cie:

= + ∙ − ∙

8

|

%'

.

Stałe całkowania C i D okre

ś

la si

ę

z warunków brzegowych:

•

dla x=0

→

%

=0, st

ą

d D=0,

•

dla x=0

→

`

%

=0, st

ą

d C=0.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11

METODA CLEBSCHA

Zadanie cd

Po podstawieniu stałych całkowania C i D równania odkształce

ń

przyjmuj

ą

posta

ć

:

•

równanie k

ą

ta obrotu

`

= −

5

\]

∙

5

|

%'

,

•

równanie linii ugi

ę

cia

= −

5

\]

∙

8

|

%'

.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr11