MECHANIKA BUDOWLI

I KONSTRUKCJI

wykład nr7 i 8

•

Pojęcie

momentu

zginającego,

siły

poprzecznej, siły podłużnej.

•

Analityczne wyznaczanie sił wewnętrznych

w

belce

prostej

i

sporządzanie

ich

wykresów.

SIŁY WEWN

Ę

TRZNE W UKŁADACH PR

Ę

TOWYCH PŁASKICH

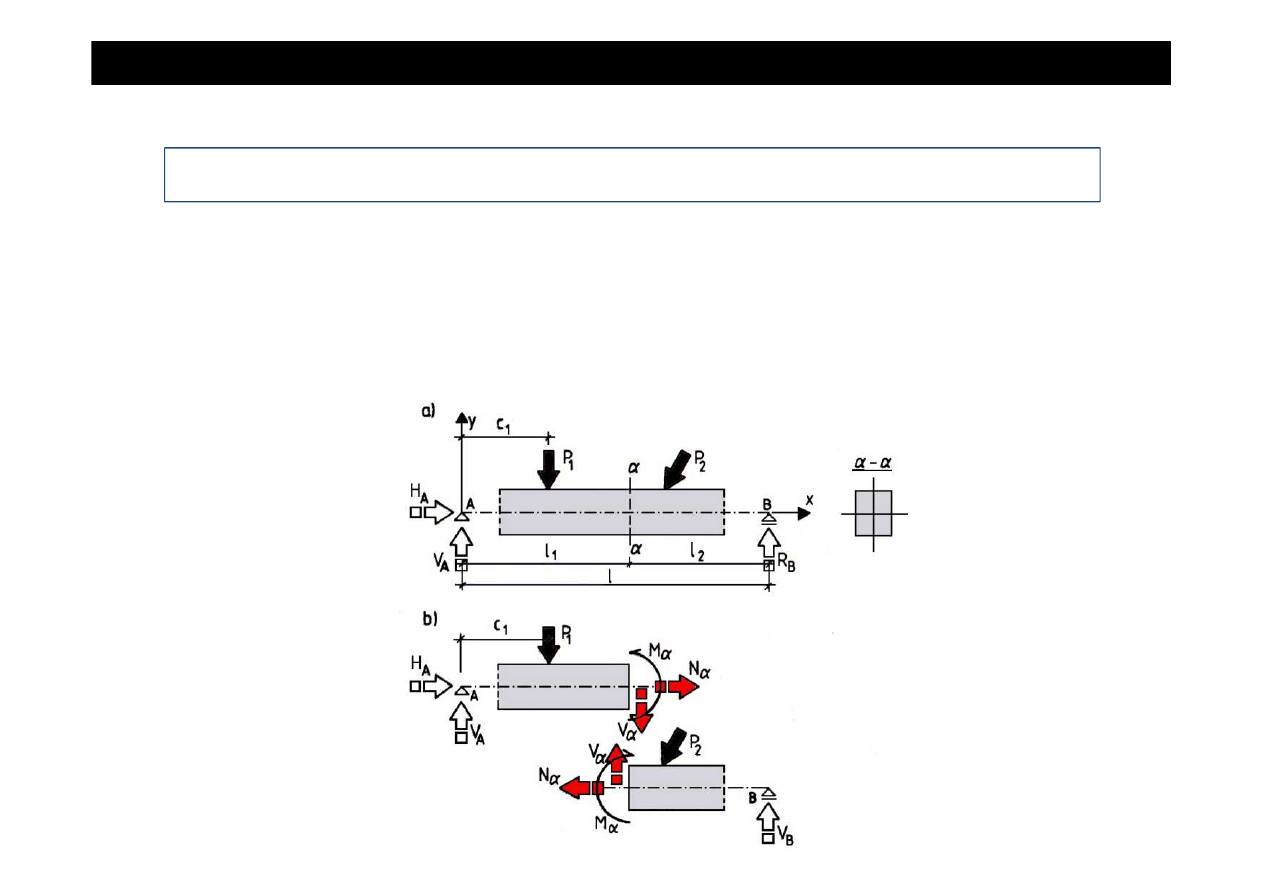
Przez pr

ę

t, w dowolnym jego miejscu na jego długo

ś

ci, mo

ż

na poprowadzi

ć

przekrój

∝−∝.

Je

ż

eli pr

ę

t przetniemy przekrojem

∝−∝

na dwie cz

ęś

ci, to w celu zapewnienia równowagi obu

cz

ęś

ci wzajemne ich oddziaływanie trzeba zast

ą

pi

ć

odpowiednimi siłami zaczepionymi w tym

przekroju, zwanymi siłami wewn

ę

trznymi.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

SIŁY WEWN

Ę

TRZNE W UKŁADACH PR

Ę

TOWYCH PŁASKICH

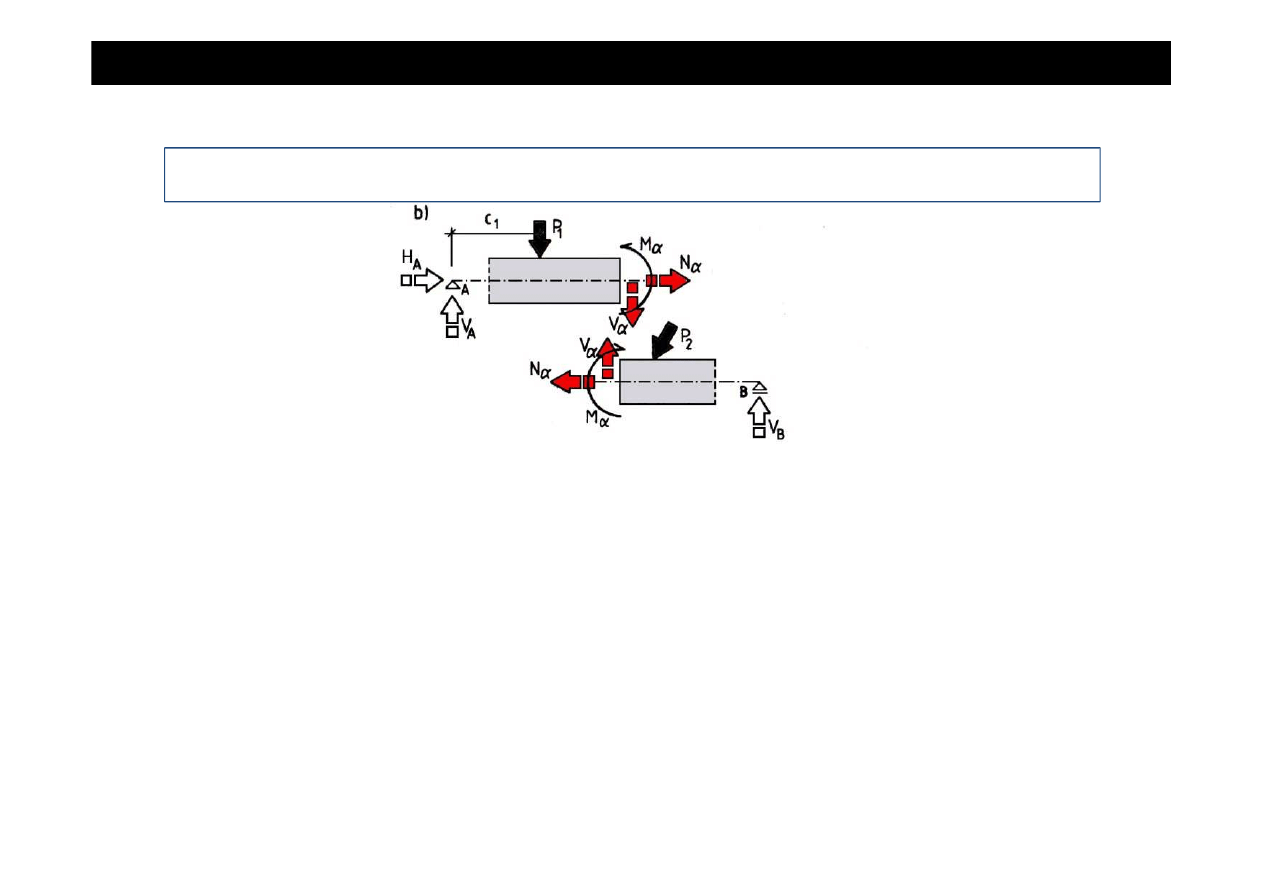
W dowolnym przekroju pr

ę

ta, którego o

ś

le

ż

y w płaszczy

ź

nie oraz obci

ąż

enia działaj

ą

w tej

płaszczy

ź

nie, wyst

ę

puj

ą

trzy rodzaje sił wewn

ę

trznych:

•

siła podłu

ż

na

∝

,

•

siła poprzeczna

∝

(

∝

),

•

moment zginaj

ą

cy

∝

.

Ka

ż

da z wydzielonych cz

ęś

ci znajduje si

ę

w równowadze pod działaniem sił zewn

ę

trznych

działaj

ą

cych na dan

ą

cz

ęść

i sił wewn

ę

trznych w przekroju

∝−∝

.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

SIŁY WEWN

Ę

TRZNE W UKŁADACH PR

Ę

TOWYCH PŁASKICH

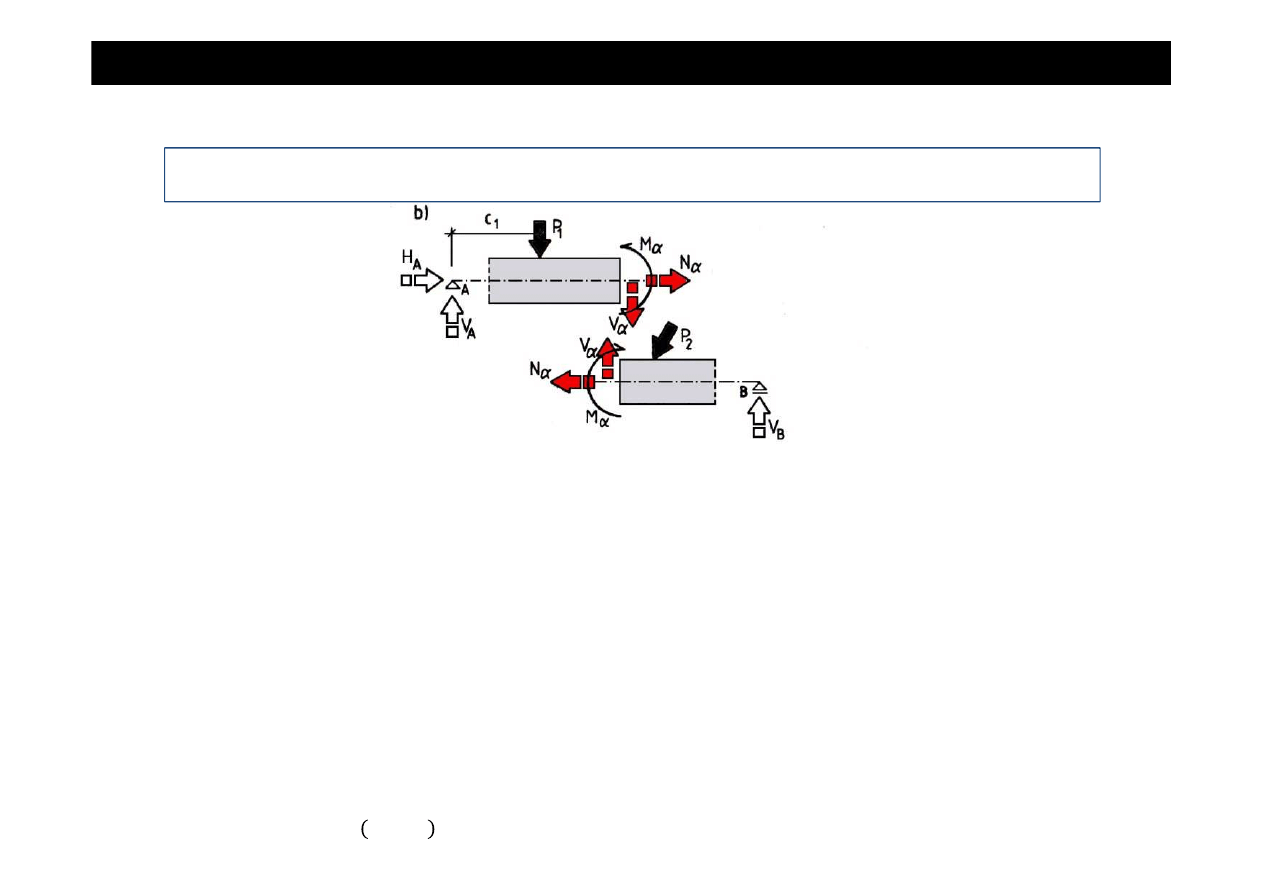
Siła podłu

ż

na w my

ś

lowym przekroju

∝−∝

równa si

ę

sumie algebraicznej rzutów wszystkich sił

działaj

ą

cych po jednej stronie przekroju na kierunek stycznej do osi pr

ę

ta w tym przekroju.

∑

= 0

+

∝

=0

(lewa strona przekroju)

Siła poprzeczna w my

ś

lowym przekroju

∝−∝

równa si

ę

sumie algebraicznej rzutów wszystkich sił

działaj

ą

cych po jednej stronie przekroju na kierunek prostopadły do osi pr

ę

ta w tym przekroju.

∑

= 0

−

−

∝

=0

(lewa strona przekroju)

Moment zginaj

ą

cy w my

ś

lowym przekroju

∝−∝

równa si

ę

sumie algebraicznej momentów

statycznych wszystkich sił poło

ż

onych po jednej stronie przekroju wzgl

ę

dem

ś

rodka ci

ęż

ko

ś

ci tego

przekroju.

∑

= 0

−

−

−

∝

= 0

(lewa strona przekroju)

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

SIŁY WEWN

Ę

TRZNE W UKŁADACH PR

Ę

TOWYCH PŁASKICH

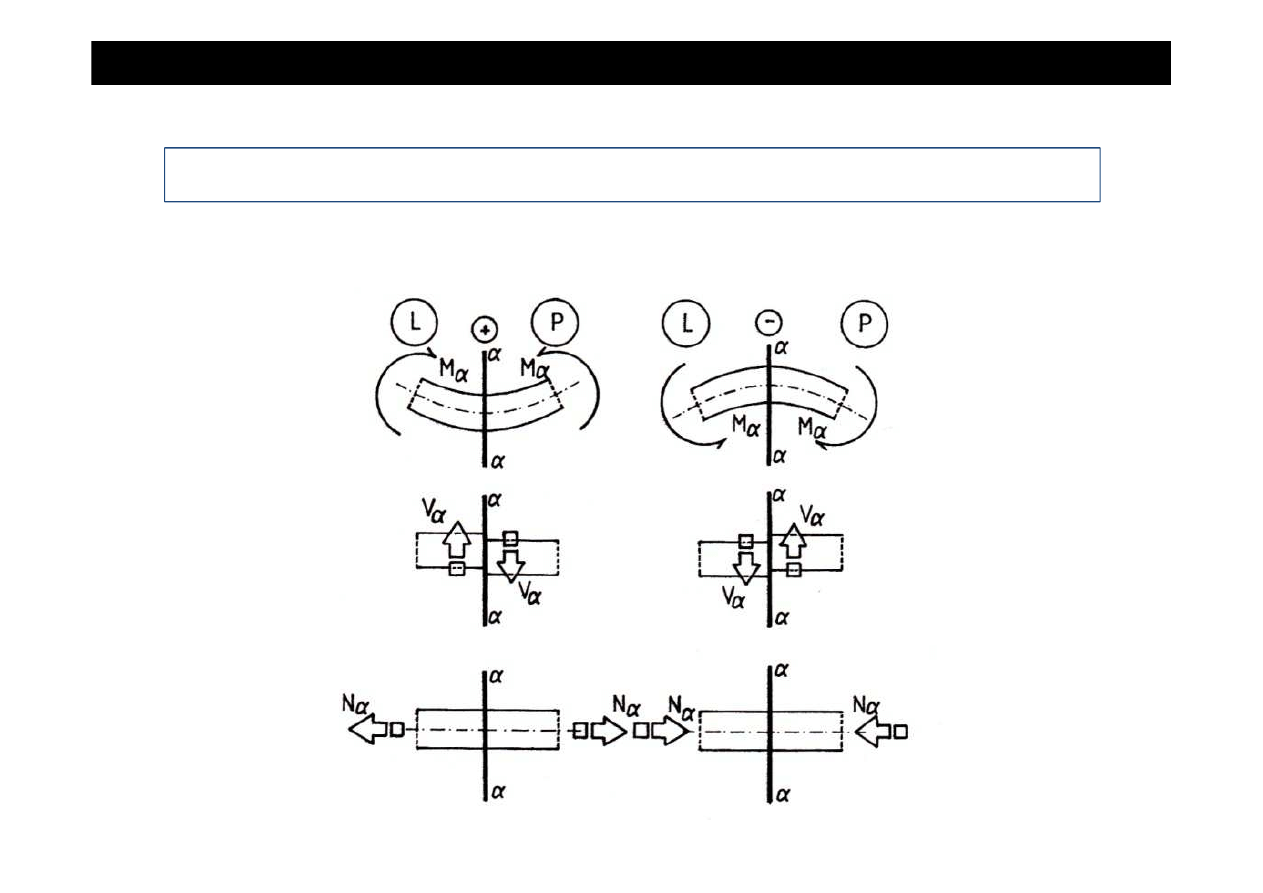
Zasada znakowania sił wewn

ę

trznych

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

ZALE

Ż

NO

Ś

CI RÓ

Ż

NICZKOWE MI

Ę

DZY SIŁMI WEWNETRZNYMI

I OBCI

ĄŻ

ENIEM

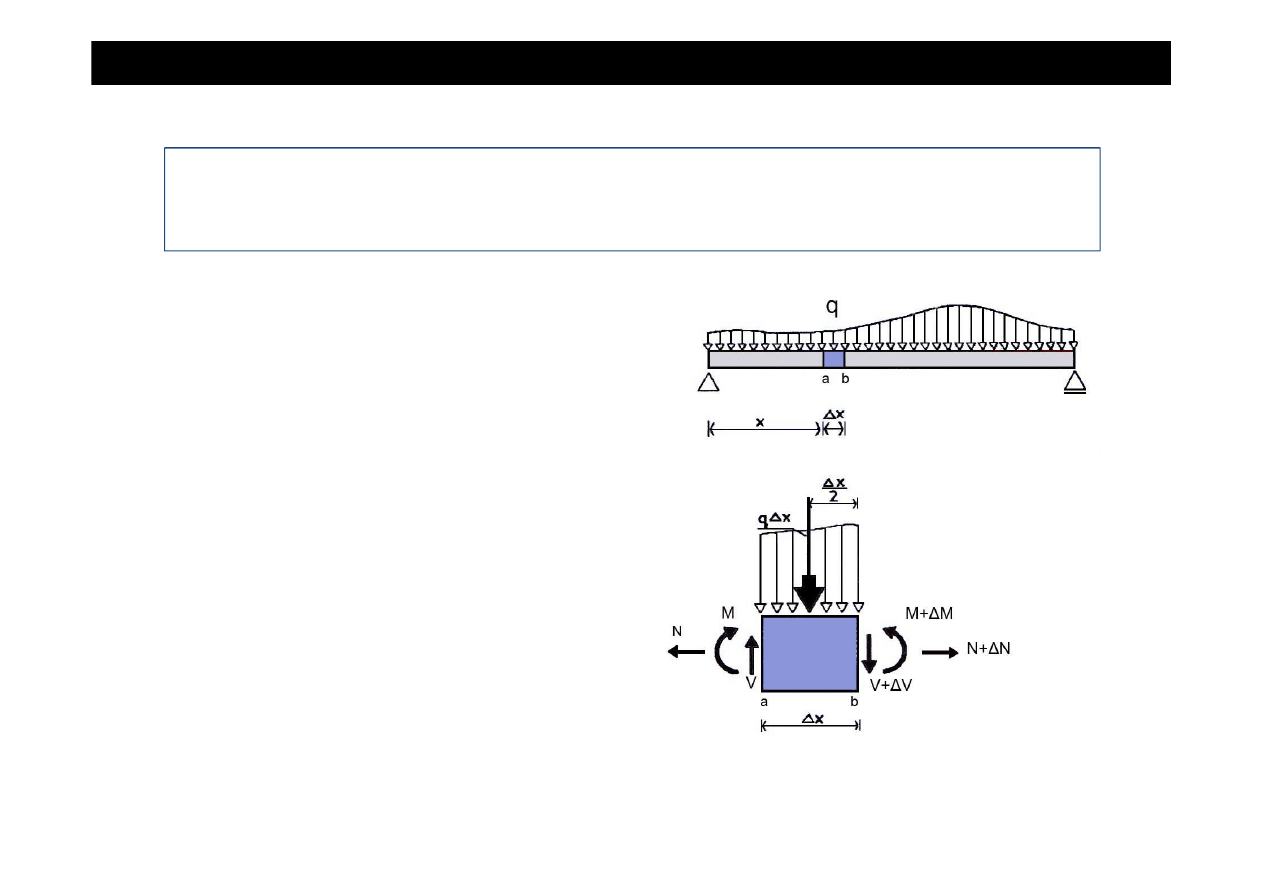
Belka obci

ąż

ona jest obci

ąż

eniem rozło

ż

onym

liniowo q [kN/m].

Z belki tej mo

ż

na wyci

ąć

elementarny odcinek

o długo

ś

ci

∆

x le

żą

cy mi

ę

dzy przekrojami a i b.

W przekroju a wyst

ą

pi

ą

: moment zginaj

ą

cy M, siła

poprzeczna V i siła podłu

ż

na N.

W

przekroju

b

wyst

ą

pi

ą

natomiast:

moment

zginaj

ą

cy M+

∆

M, siła poprzeczna V+

∆

i siła

podłu

ż

na N+

∆

N.

Wypadkowa obci

ąż

eniem znajduje si

ę

w połowie

odcinka

∆

x i ma warto

ść

q

∆

x.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

ZALE

Ż

NO

Ś

CI RÓ

Ż

NICZKOWE MI

Ę

DZY SIŁMI WEWNETRZNYMI

I OBCI

ĄŻ

ENIEM

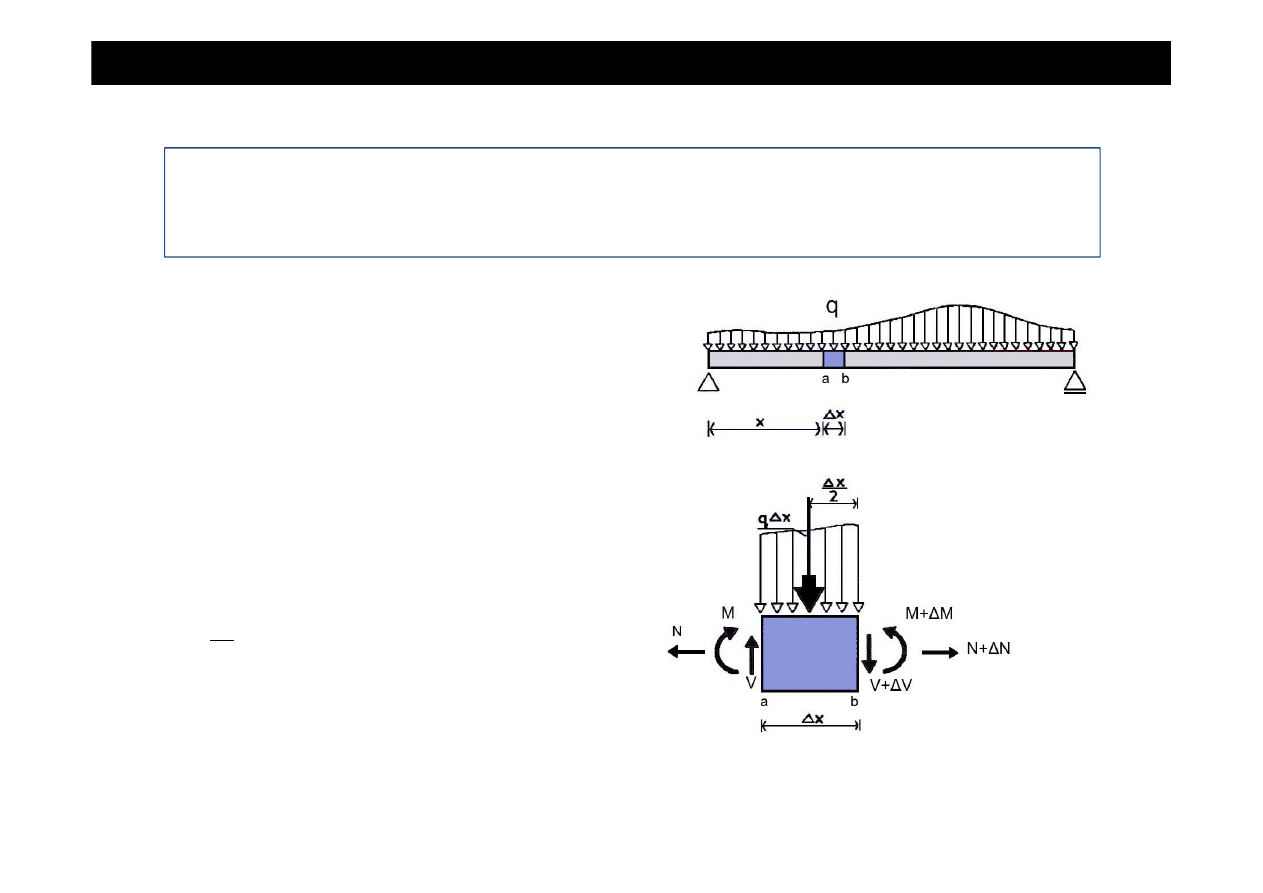
Wszystkie

siły:

zewn

ę

trzne

(obci

ąż

enia)

i wewn

ę

trzne, działaj

ą

ce na wyci

ę

tej cz

ęś

ci belki

musz

ą

spełnia

ć

warunki równowagi.

•

Z warunków rzutów na o

ś

pionow

ą

wynika:

V - (V+

∆

V) - q

∆

x = 0

∆

V = - q

∆

x,

gdy

∆

x d

ąż

y do zera (

∆

x

→

0), to otrzymuje si

ę

zale

ż

no

ść

:

= - q .

Jest

to

zale

ż

no

ść

ró

ż

niczkowa

mi

ę

dzy

sił

ą

poprzeczn

ą

a obci

ąż

eniem. Zale

ż

no

ść

ta oznacza,

ż

e pierwsza pochodna siły poprzecznej równa si

ę

obci

ąż

eniu

jednostkowemu

w

tym

przekroju

wzi

ę

tym z odwrotnym znakiem.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

ZALE

Ż

NO

Ś

CI RÓ

Ż

NICZKOWE MI

Ę

DZY SIŁMI WEWNETRZNYMI

I OBCI

ĄŻ

ENIEM

•

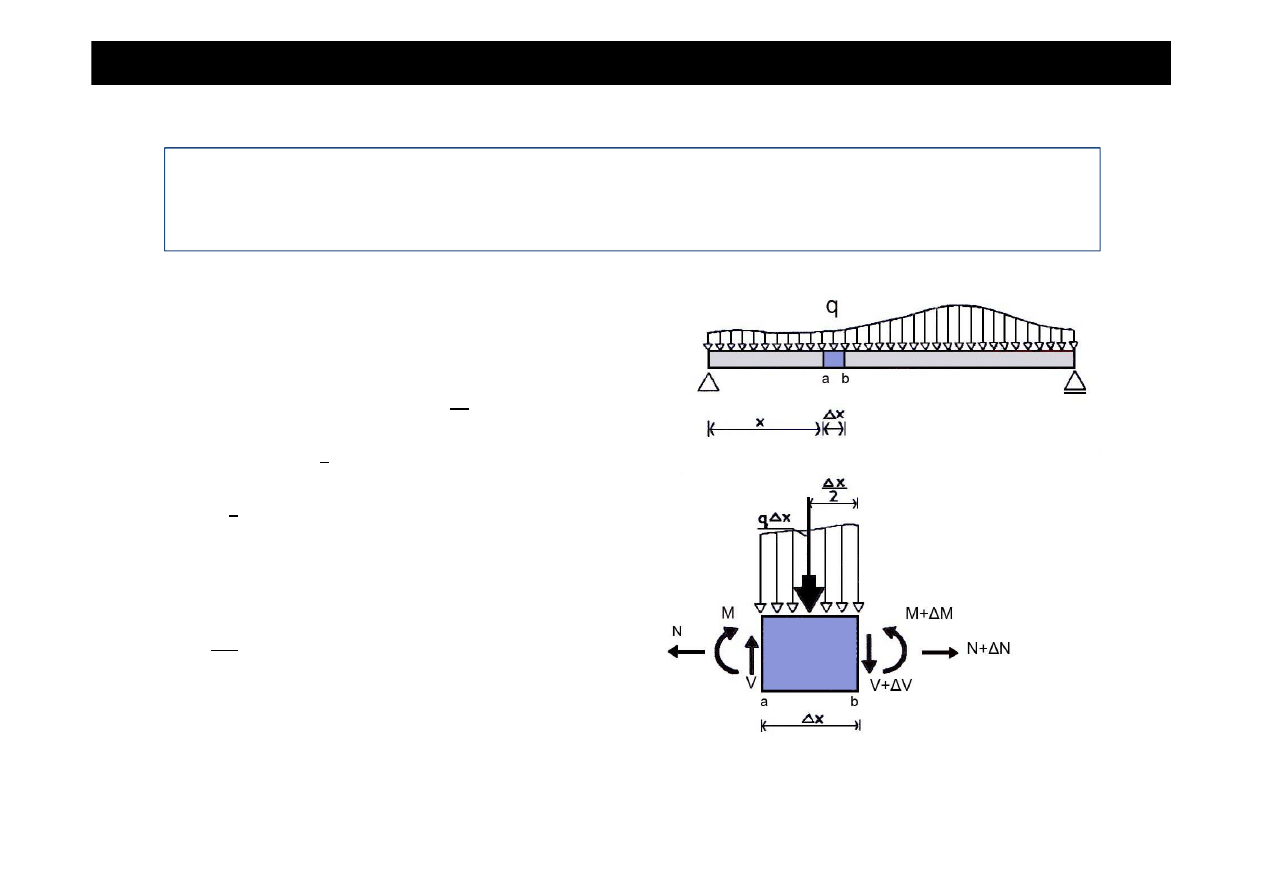
Warunek

równowagi

momentów

wzgl

ę

dem

przekroju b:

M - (M+

∆

M) +V

∆

x - q

∆

x

∙

∆

= 0

∆

M = V

∆

x -

q

(∆

x

)

,

(

q

(∆

x

)

- mała warto

ść

, dlatego jest pomijana)

gdy

∆

x d

ąż

y do zera (

∆

x

→

0), to otrzymuje si

ę

zale

ż

no

ść

:

"

= V .

Jest to zale

ż

no

ść

ró

ż

niczkowa mi

ę

dzy momentem

zginaj

ą

cym

a

sił

ą

poprzeczn

ą

.

Zale

ż

no

ść

ta

oznacza,

ż

e

siła

poprzeczna

jest

pochodn

ą

momentu zginaj

ą

cego.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

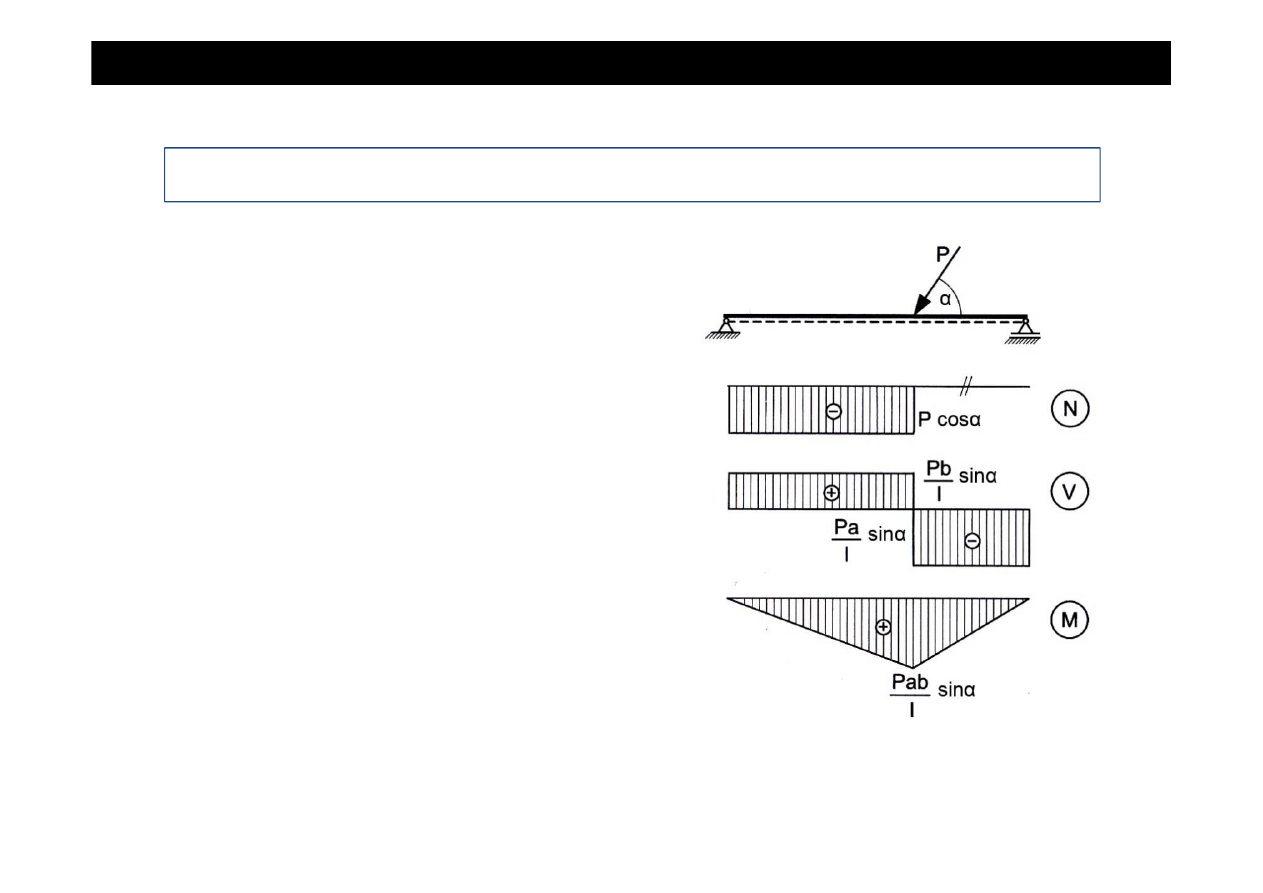
GRAFICZNE PRZEDSTAWIENIE SIŁ WEWN

Ę

TRZNYCH

Siły wewn

ę

trzne przedstawia si

ę

w sposób

graficzny – za pomoc

ą

wykresów.

Zgodnie

z

przyj

ę

t

ą

konwencj

ą

,

warto

ś

ci

dodatnie momentów zginaj

ą

cych umieszcza

si

ę

u spodu pr

ę

ta, a ujemne po stronie

przeciwnej.

Wykresy

sił

poprzecznych

(równie

ż

sił

podłu

ż

nych)

o

warto

ś

ciach

dodatnich

zaznacza

si

ę

u

góry

pr

ę

ta,

natomiast

warto

ś

ci ujemne u spodu pr

ę

ta.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

GRAFICZNA INTERPRETACJA ZALE

Ż

NO

Ś

CI RÓ

Ż

NICZKOWYCH

•

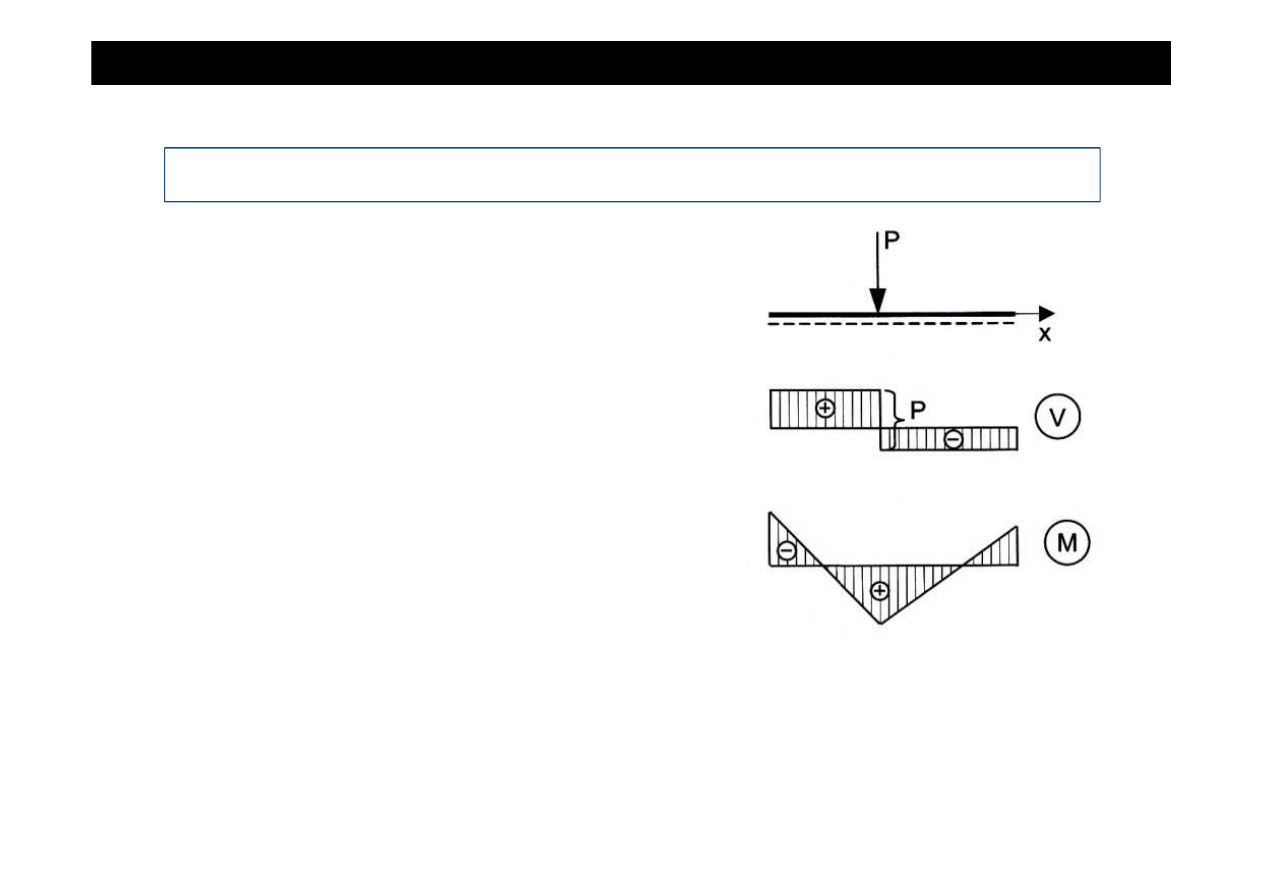
Obci

ąż

enie sił

ą

skupion

ą

P

Je

ż

eli wykres sił poprzecznych jest prost

ą

poziom

ą

,

to wykres momentów zginaj

ą

cych jest opisany

równaniem prostej nachylonej.

W przypadku obci

ąż

enia sił

ą

skupion

ą

P w miejscu

jej przyło

ż

enia wyst

ą

pi nieci

ą

gło

ść

w wykresie sił

poprzecznych.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

GRAFICZNA INTERPRETACJA ZALE

Ż

NO

Ś

CI RÓ

Ż

NICZKOWYCH

•

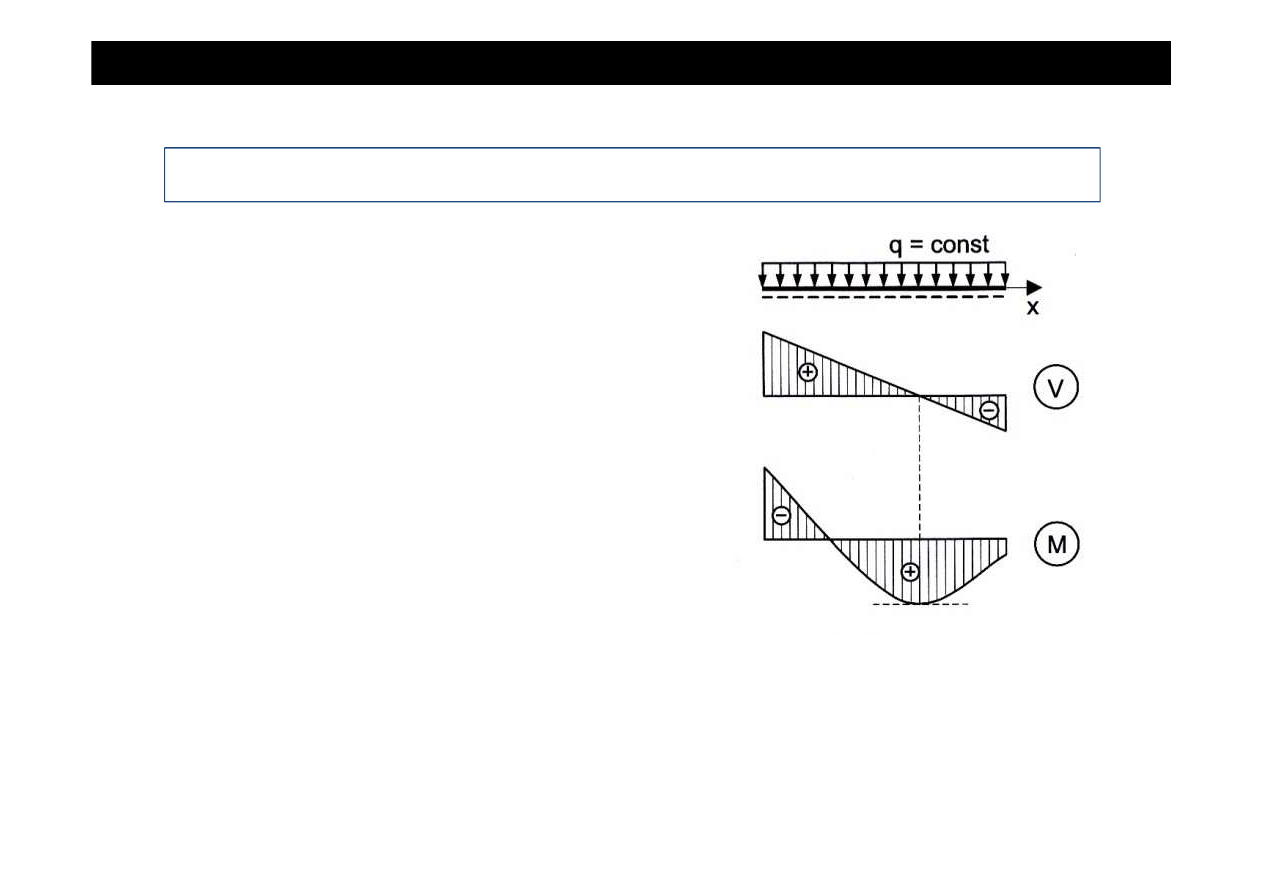
Obci

ąż

enie rozło

ż

one liniowo q

Je

ż

eli

wykres

sił

poprzecznych

jest

prost

ą

o

współczynniku

kierunkowym,

to

wykres

momentów zginaj

ą

cych jest opisany parabol

ą

.

W celu znalezienia ekstremum dowolnej funkcji,

przyrównuje si

ę

pochodn

ą

do zera, a wi

ę

c ekstrema

momentu zginaj

ą

cego znajduj

ą

si

ę

w miejscach

zerowania siły poprzecznej.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

GRAFICZNA INTERPRETACJA ZALE

Ż

NO

Ś

CI RÓ

Ż

NICZKOWYCH

•

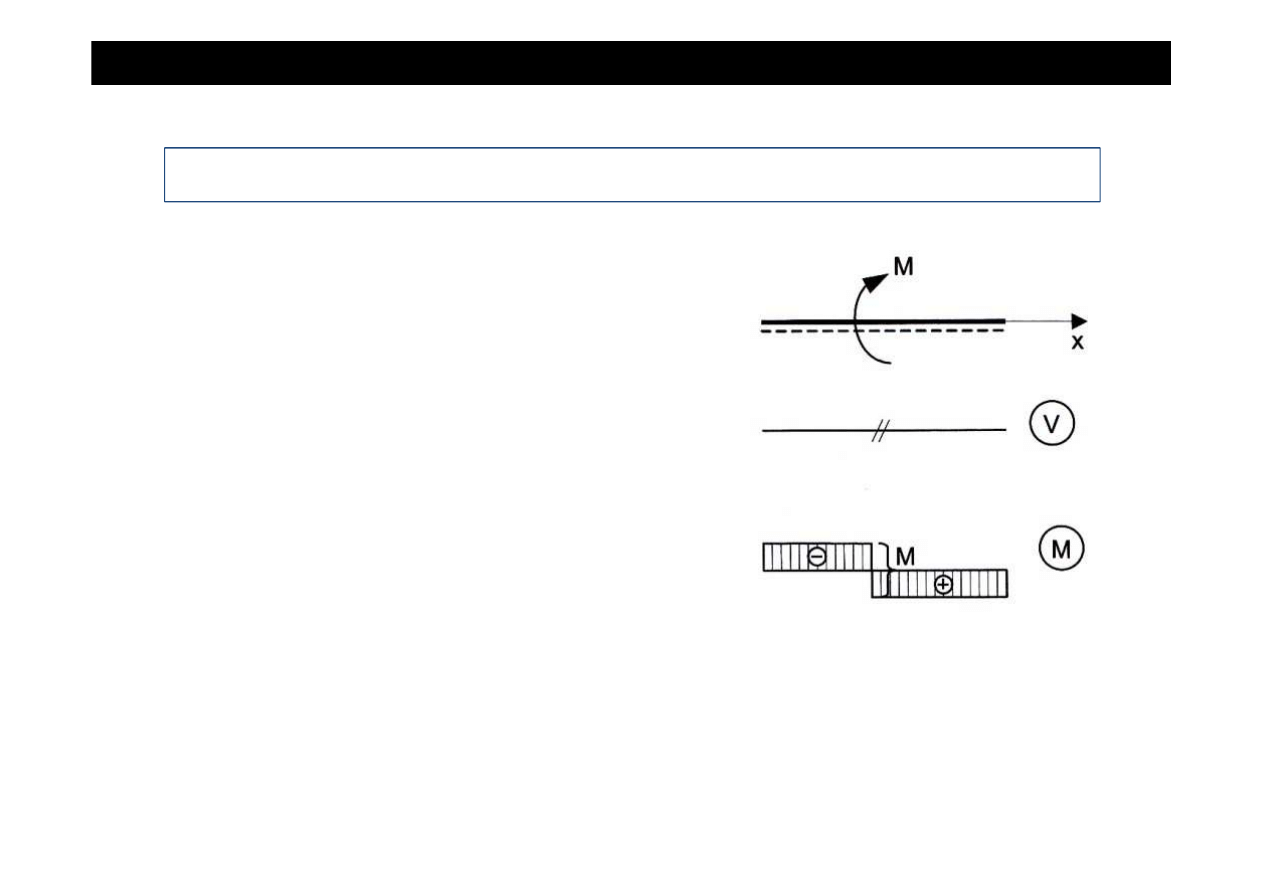
Obci

ąż

enie momentem skupionym M

W przypadku działania momentu skupionego M,

w miejscu jego przyło

ż

enia wyst

ą

pi nieci

ą

gło

ść

na

wykresie momentów zginaj

ą

cych.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

WYZNACZANIE SIŁ WEWN

Ę

TRZNYCH I SPORZ

Ą

DZANIE ICH WYKRESÓW

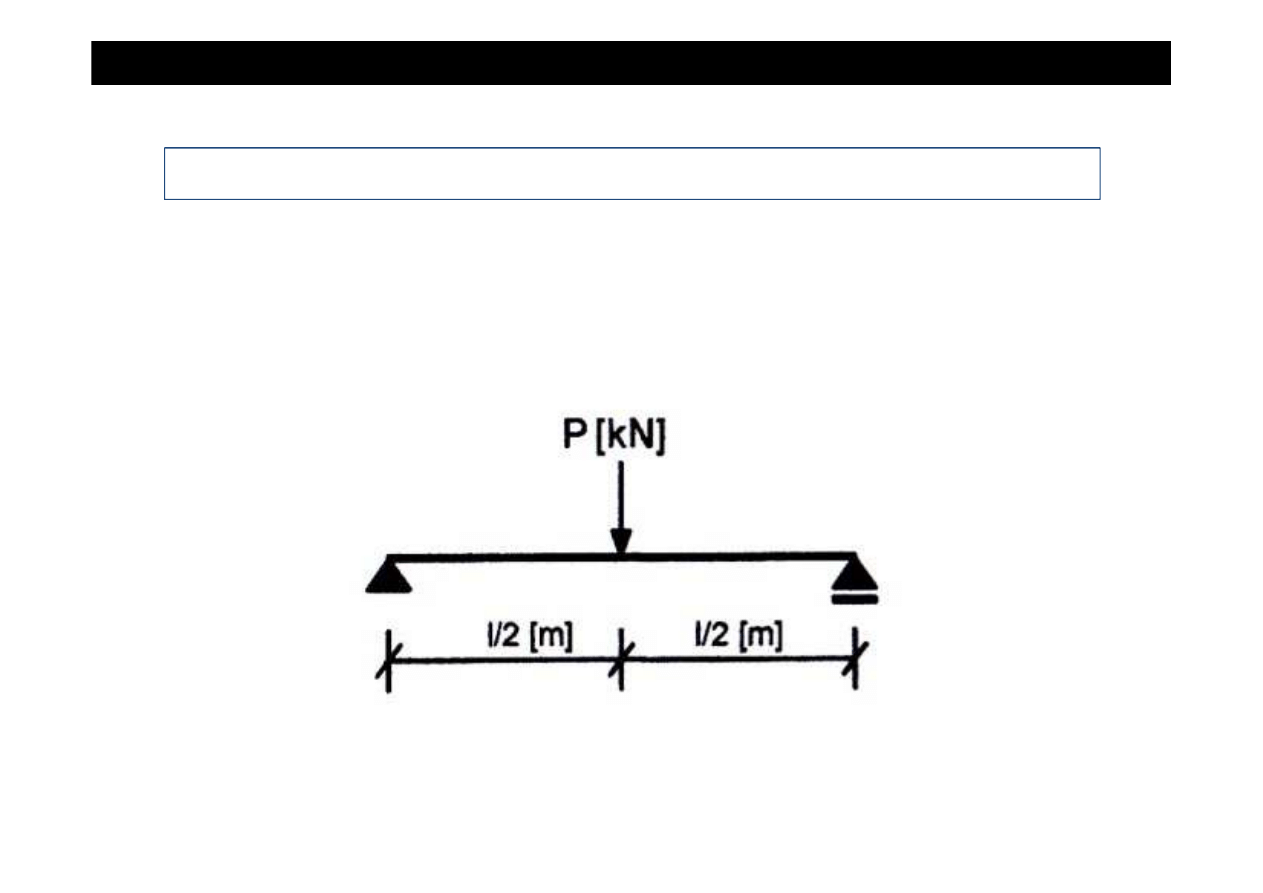
Zadanie

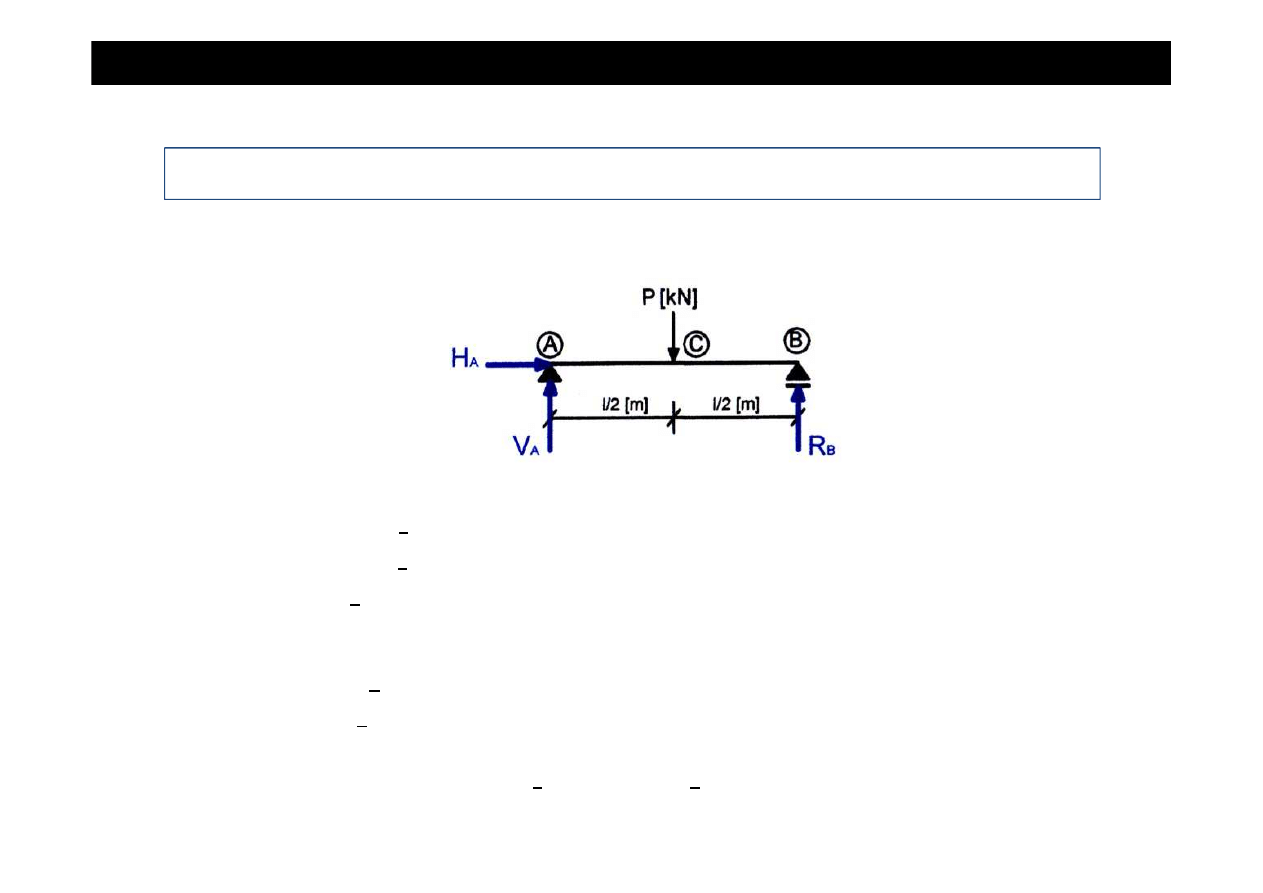
Wyznaczy

ć

warto

ś

ci sił wewn

ę

trznych i sporz

ą

dzi

ć

ich wykresy w belce jak na rysunku.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

WYZNACZANIE SIŁ WEWN

Ę

TRZNYCH I SPORZ

Ą

DZANIE ICH WYKRESÓW

Zadanie cd

•

Wyznaczamy warto

ś

ci reakcji podporowych

1.

∑

= 0

= 0 [kN]

2.

∑

= 0

+

%

&

- P = 0

→ ' ()* +ó'-.-/0 1ą 3'/4 -/4'/.35*4

3.

∑

&

=0

∙

- P

∙

7

= 0

∙ l =

P

∙

7

/:l

=

9

[kN]

4.

powracamy do równania nr2

∑

= 0

→ %

&

= -

+ P

%

&

= -

9

+ P

%

&

=

9

[kN]

5. sprawdzenie

∑

=0 -

%

&

∙

+ P

∙

7

= 0

→

%

&

=

9

[kN]

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

WYZNACZANIE SIŁ WEWN

Ę

TRZNYCH I SPORZ

Ą

DZANIE ICH WYKRESÓW

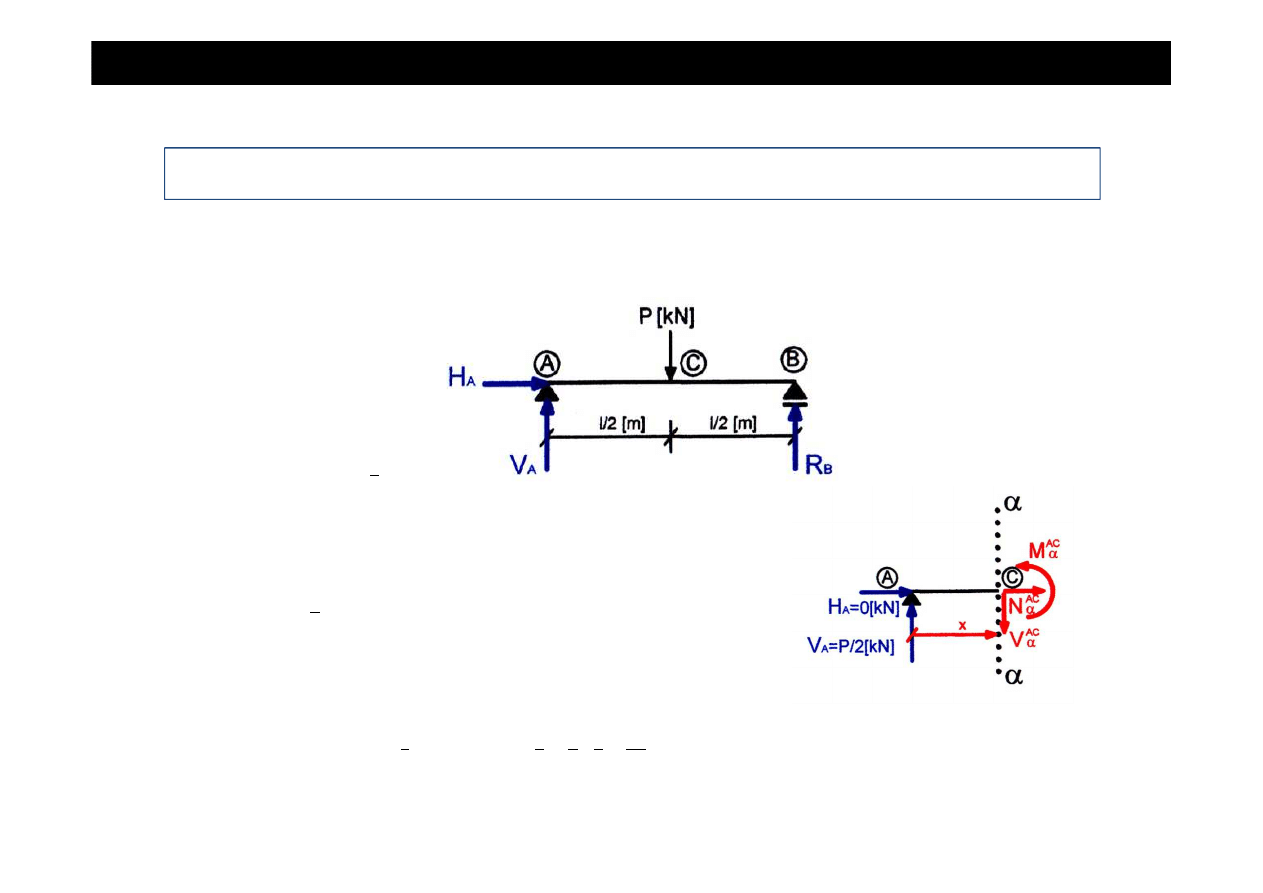
Zadanie cd

•

Wyznaczamy warto

ś

ci sił wewn

ę

trznych (sił podłu

ż

nych, sił poprzecznych i momentów

zginaj

ą

cych) w poszczególnych przedziałach belki.

Przedział AC

, x

∈

(0,

7

)

siły podłu

ż

ne

;

<

+

= 0

→

;

< = −

= 0 [kN]

siły poprzeczne

−

;

<

+

= 0

;

<

=

=

9

[kN]

momenty zginaj

ą

ce

−

;

<

+

∙ x

= 0

;

<

=

∙ x

dla x=0

;

A

=

∙

0 = 0 [kN

∙

m]

dla x=

7

;

C

=

∙

7

=

9

∙

7

=

9∙7

@

[kN

∙

m]

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

WYZNACZANIE SIŁ WEWN

Ę

TRZNYCH I SPORZ

Ą

DZANIE ICH WYKRESÓW

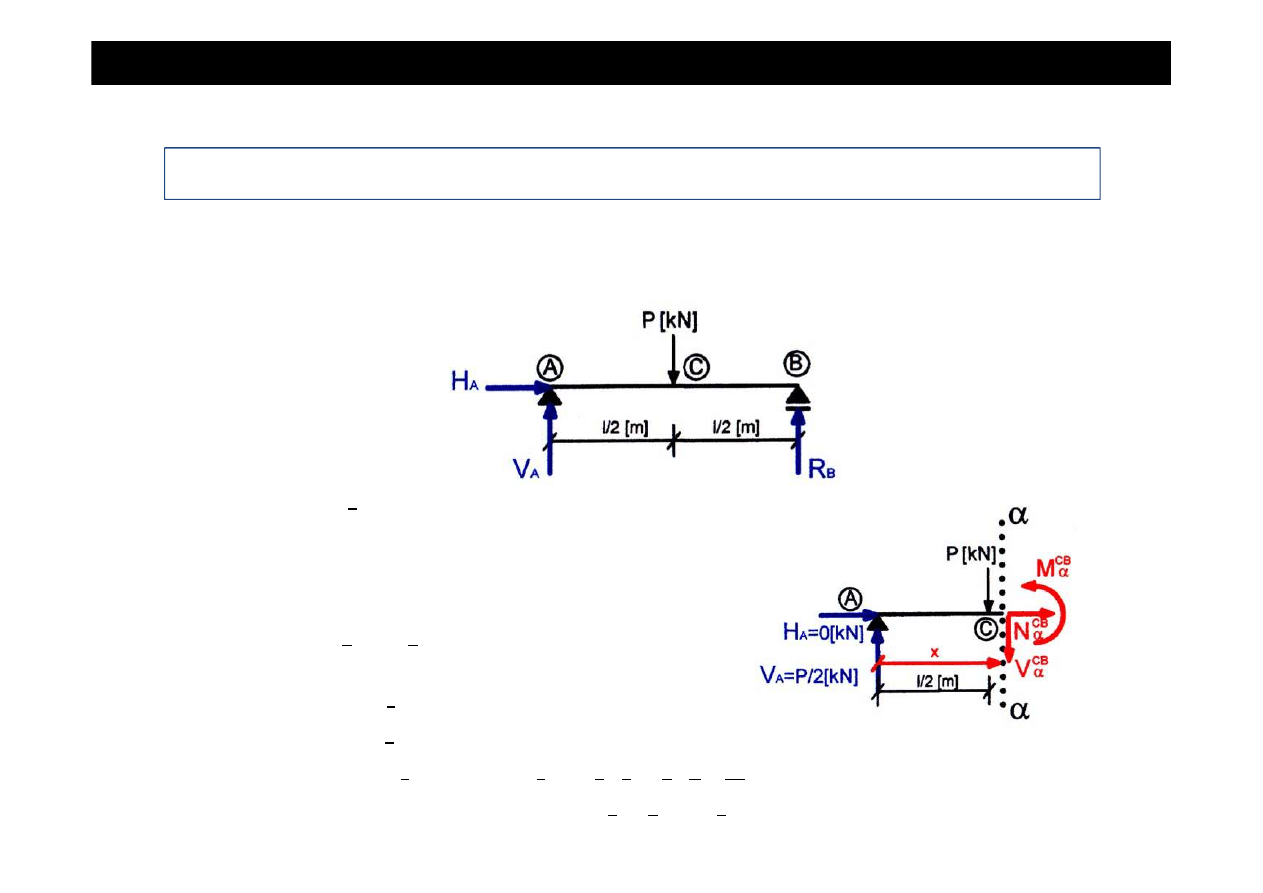
Zadanie cd

•

Wyznaczamy warto

ś

ci sił wewn

ę

trznych (sił podłu

ż

nych, sił poprzecznych i momentów

zginaj

ą

cych) w poszczególnych przedziałach belki.

Przedział CB

, x

∈

(

7

,l)

siły podłu

ż

ne

;&

<

+

= 0

→

;&

< = −

= 0 [kN]

siły poprzeczne

−

;&

<

+

- P = 0

;&

<

=

- P =

9

- P =

9

[kN]

momenty zginaj

ą

ce

−

;&

<

+

∙ x

- P

∙

(x -

7

) = 0

;&

<

=

∙ x

- P

∙

(x -

7

)

dla x=

7

;&

=

∙

7

- P

∙

(

7

-

7

) =

9

∙

7

=

9∙7

@

[kN

∙

m]

dla x=l

;&

B

=

∙

l - P

∙

(l -

7

) =

9

∙

l - P

∙

7

= 0 [kN

∙

m]

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

WYZNACZANIE SIŁ WEWN

Ę

TRZNYCH I SPORZ

Ą

DZANIE ICH WYKRESÓW

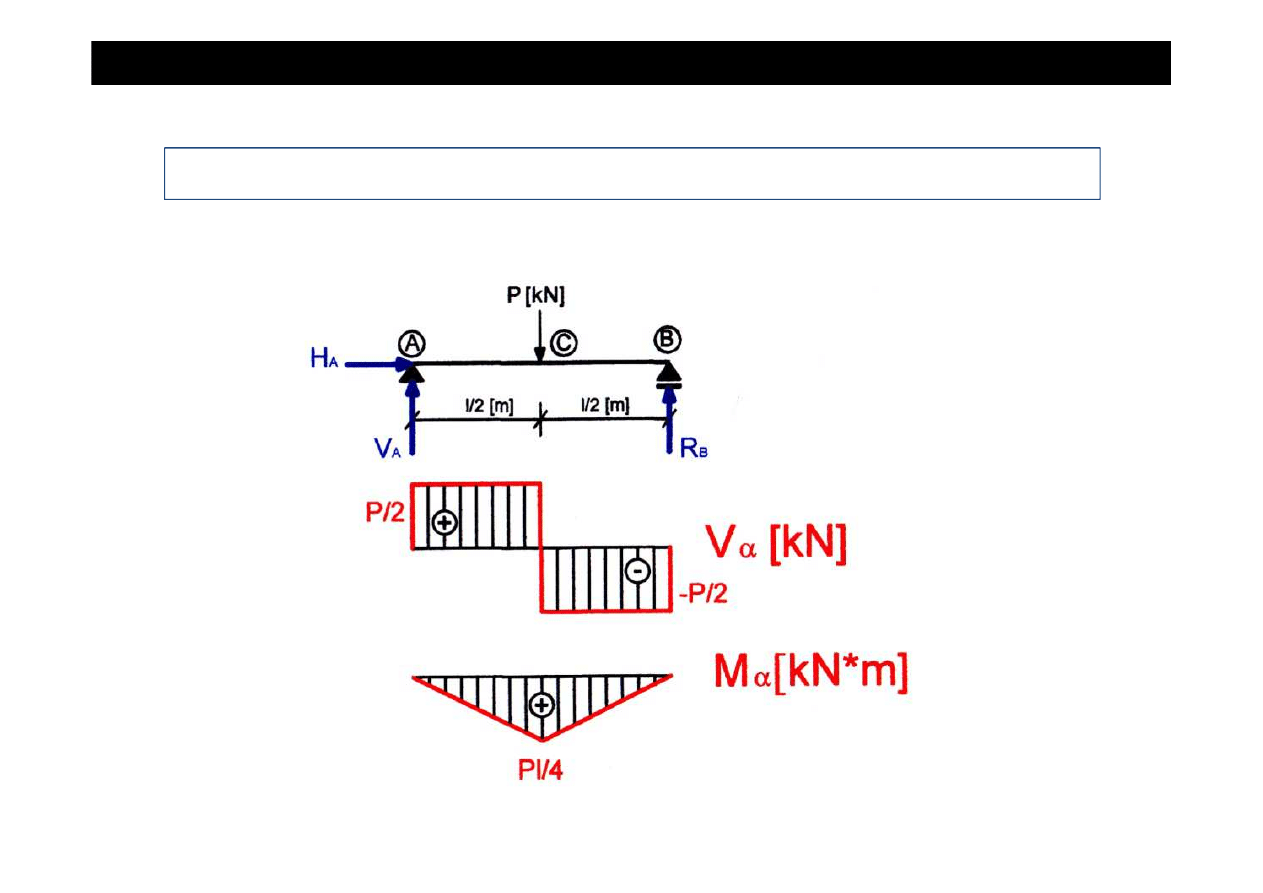
Zadanie cd

•

sporz

ą

dzamy wykresy sił wewn

ę

trznych

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

WYZNACZANIE SIŁ WEWN

Ę

TRZNYCH I SPORZ

Ą

DZANIE ICH WYKRESÓW

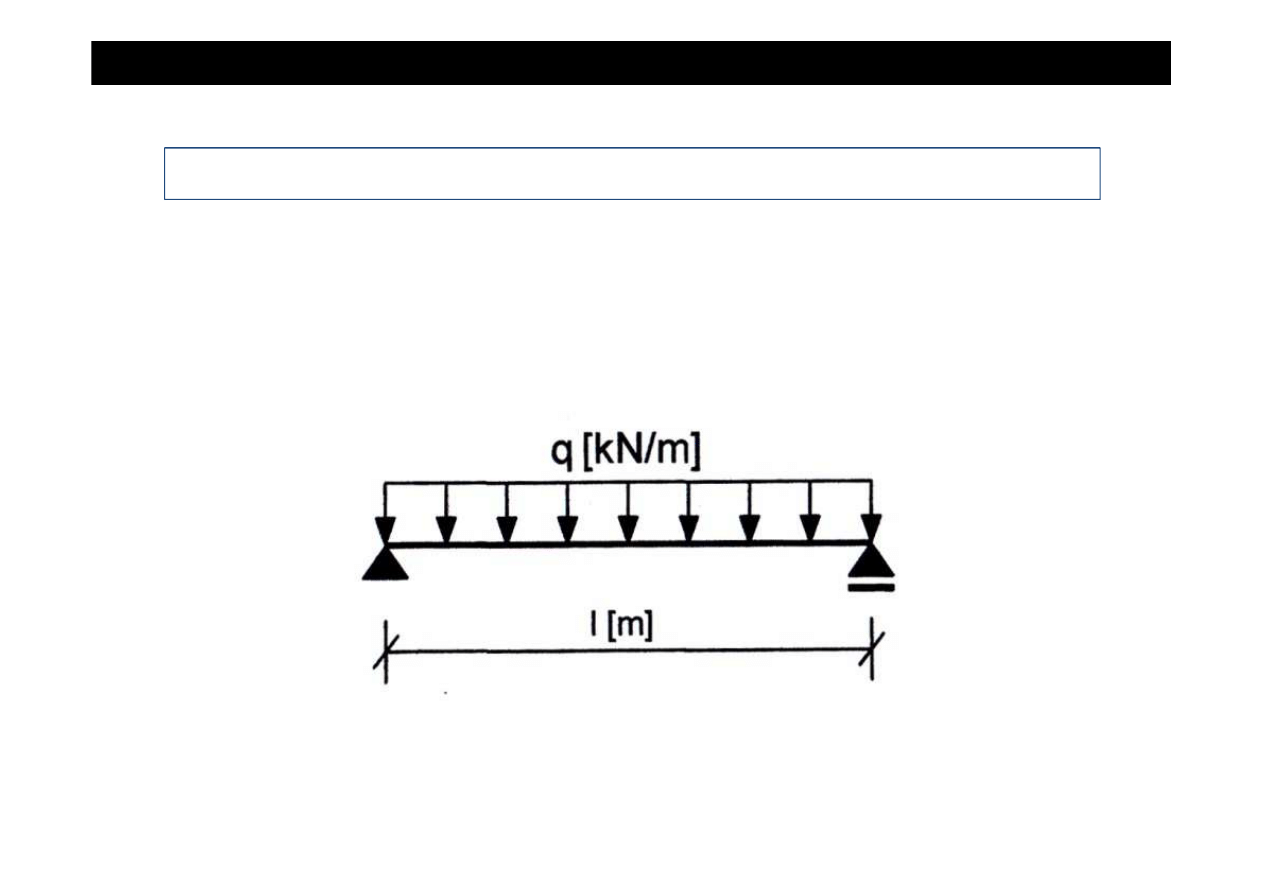
Zadanie

Wyznaczy

ć

warto

ś

ci sił wewn

ę

trznych i sporz

ą

dzi

ć

ich wykresy w belce jak na rysunku.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

WYZNACZANIE SIŁ WEWN

Ę

TRZNYCH I SPORZ

Ą

DZANIE ICH WYKRESÓW

Zadanie cd

•

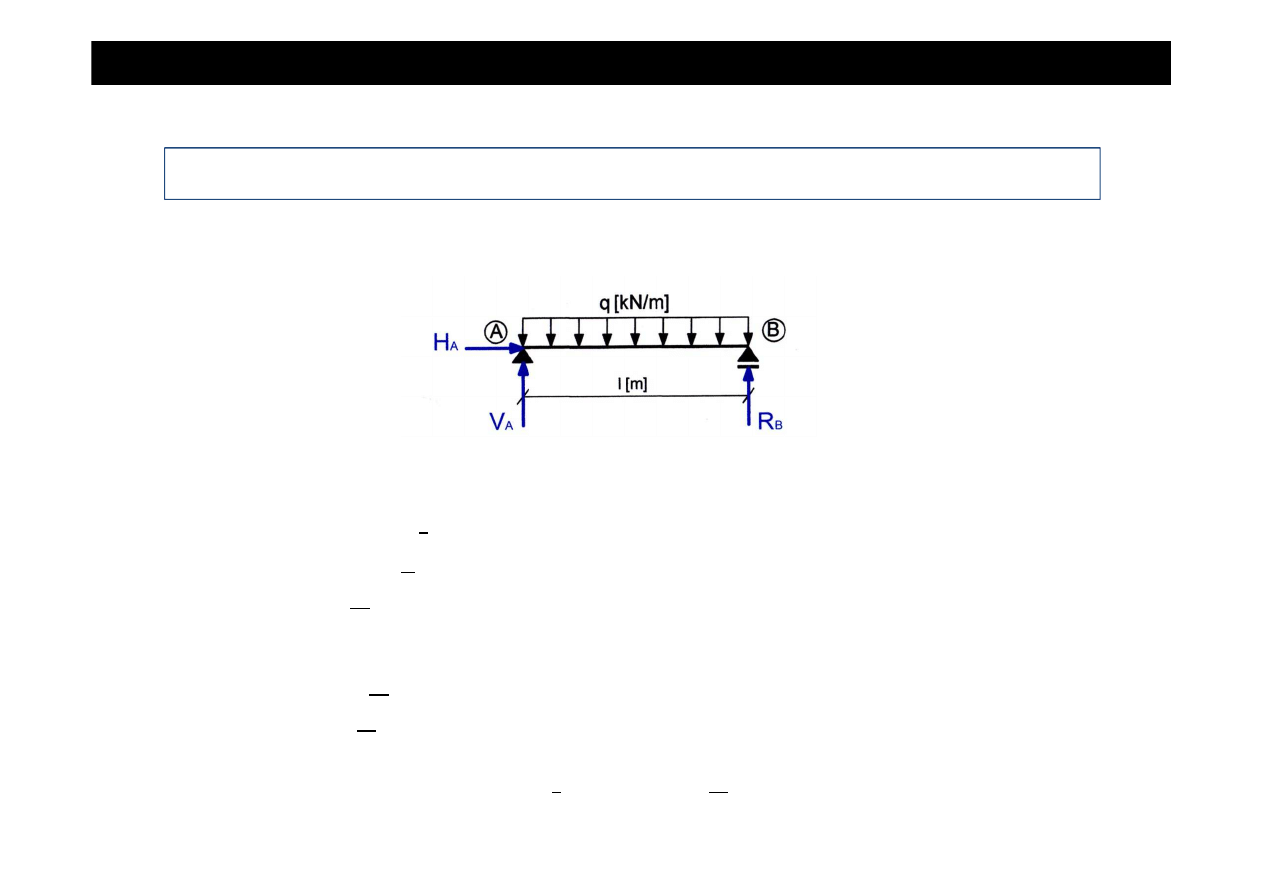
Wyznaczamy warto

ś

ci reakcji podporowych

1.

∑

= 0

= 0 [kN]

2.

∑

= 0

+

%

&

- q

∙

l = 0

→ ' ()* +ó'-.-/0 1ą 3'/4 -/4'/.35*4

3.

∑

&

=0

∙

- q

∙ ∙

7

= 0

∙ l = q ∙

7

C

/:l

=

D∙7

[kN]

4.

powracamy do równania nr2

∑

= 0

→ %

&

= -

+ q

∙

l

%

&

= -

D∙7

+ q

∙

l

%

&

=

D∙7

[kN]

5. sprawdzenie

∑

=0 -

%

&

∙

+ q

∙ ∙

7

= 0

→

%

&

=

D∙7

[kN]

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

WYZNACZANIE SIŁ WEWN

Ę

TRZNYCH I SPORZ

Ą

DZANIE ICH WYKRESÓW

Zadanie cd

•

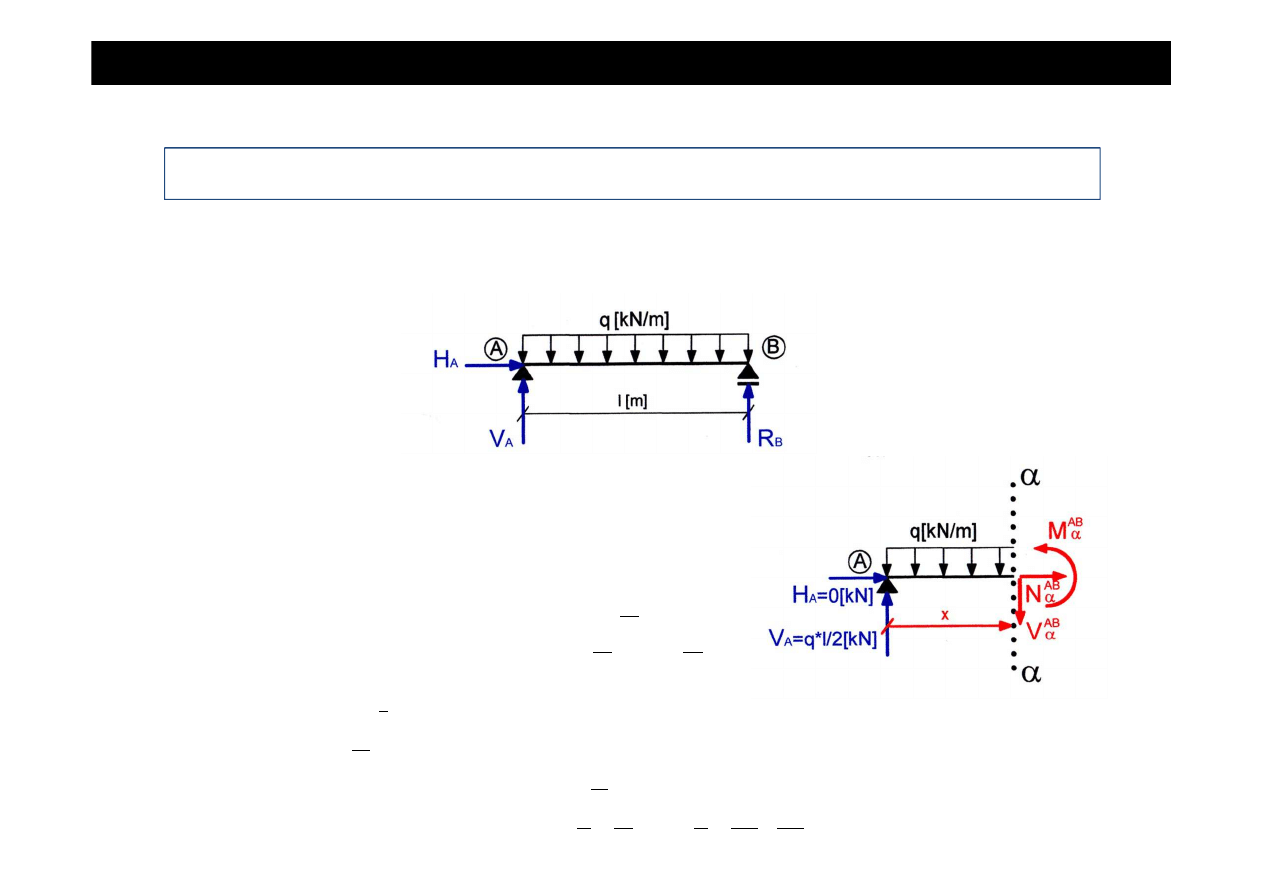
Wyznaczamy warto

ś

ci sił wewn

ę

trznych (sił podłu

ż

nych, sił poprzecznych i momentów

zginaj

ą

cych) w poszczególnych przedziałach belki.

Przedział AB

, x

∈

(0,l)

siły podłu

ż

ne

&

<

+

= 0

→

&

< = −

= 0 [kN]

siły poprzeczne

−

&

<

+

- q

∙ x

= 0

&

<

=

- q

∙ x

dla x=0

&

A

=

- 0 =

=

D∙7

[kN]

dla x=l

&

B

=

- q

∙

l =

D∙7

- q

∙

l= -

D∙7

[kN]

momenty zginaj

ą

ce

−

&

<

+

∙ x

- q

∙ x ∙

= 0

&

<

=

∙ x

- q

∙

C

dla x=0

&

A

=

∙

0 - q

∙

E

C

= 0 [kN

∙

m]

dla x=l

&

B

=

∙

l - q

∙

7

C

=

D∙7

∙

l - q

∙

7

C

=

D∙7

C

-

D∙7

C

= 0 [kN

∙

m]

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

WYZNACZANIE SIŁ WEWN

Ę

TRZNYCH I SPORZ

Ą

DZANIE ICH WYKRESÓW

Zadanie cd

•

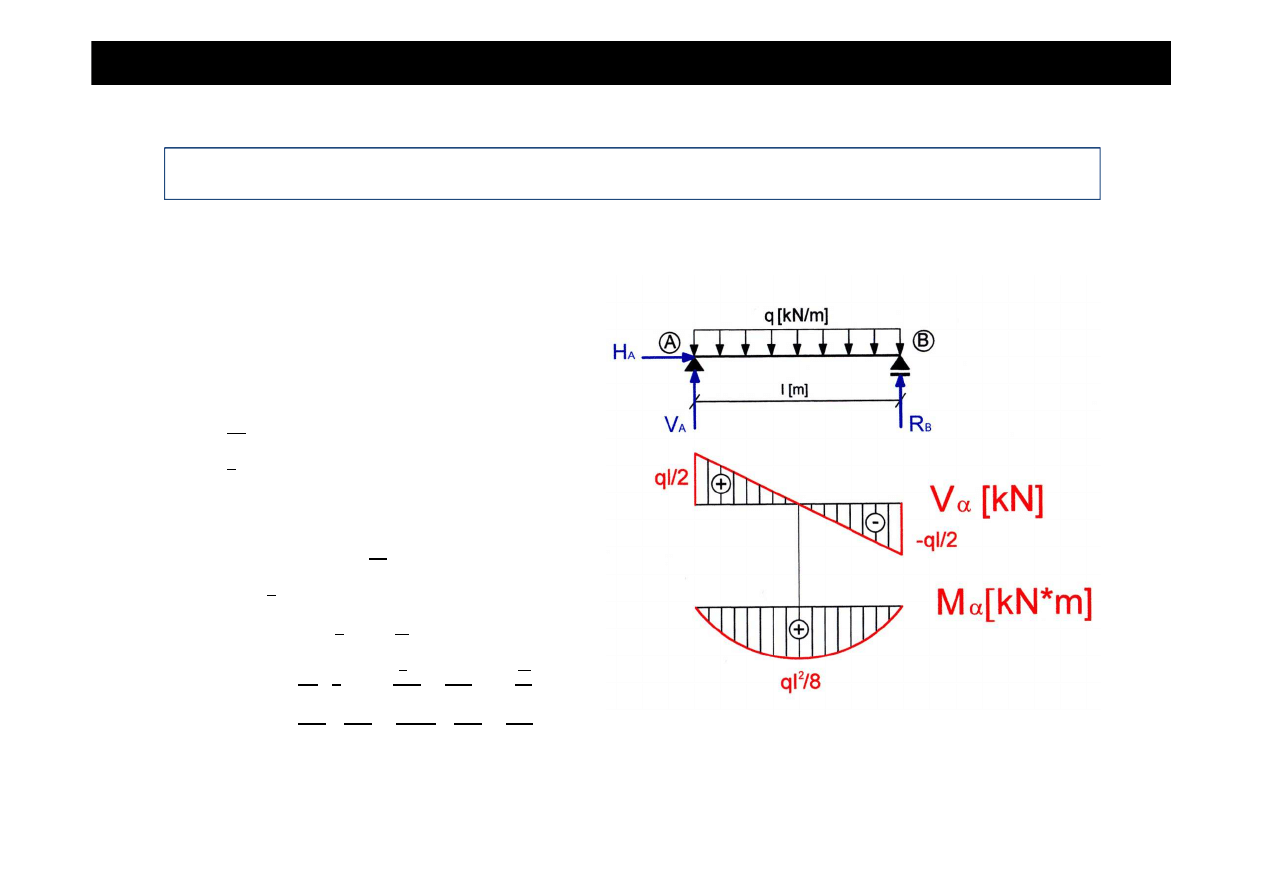
sporz

ą

dzamy

wykresy sił wewn

ę

trznych

ekstremum w przedziale AB

&

<

= 0

&

<

=

- q

∙

x

- q

∙

x = 0

q

∙

x =

q

∙

x =

D∙7

/:q

x =

7

[m]

&

<

=

∙ x

-

F ∙

C

dla x =

7

[m]

&

*.G

=

∙

7

-

F ∙

7

C

=

=

D∙7

∙

7

– q

∙

(

H

C

)

C

=

D∙7

C

@

- q

∙

HC

I

=

=

D∙7

C

@

-

D∙7

C

J

=

∙D∙7

C

J

-

D∙7

C

J

=

D∙7

C

J

[kN

∙

m]

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

WYZNACZANIE SIŁ WEWN

Ę

TRZNYCH I SPORZ

Ą

DZANIE ICH WYKRESÓW

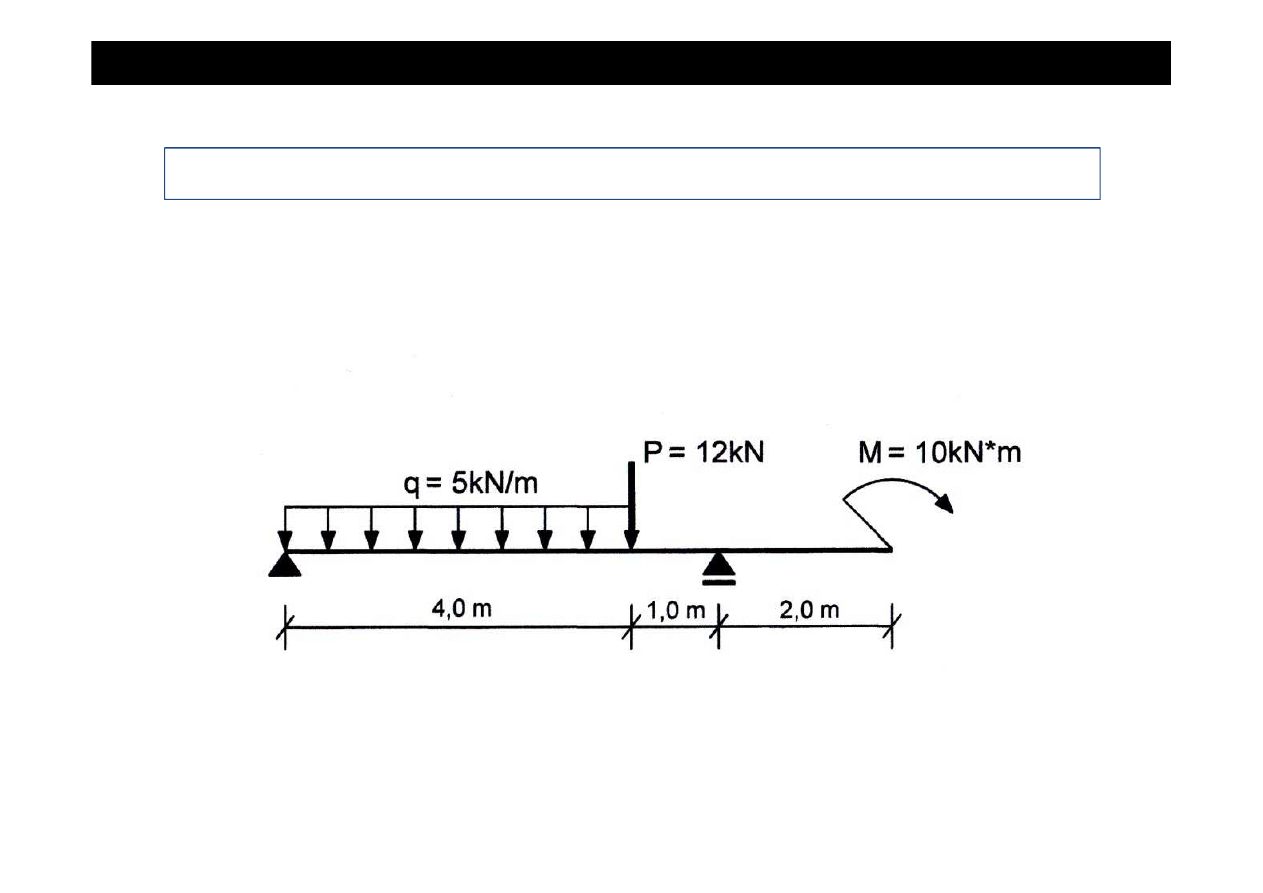
Zadanie

Wyznaczy

ć

warto

ś

ci sił wewn

ę

trznych i sporz

ą

dzi

ć

ich wykresy w belce jak na rysunku.

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

WYZNACZANIE SIŁ WEWN

Ę

TRZNYCH I SPORZ

Ą

DZANIE ICH WYKRESÓW

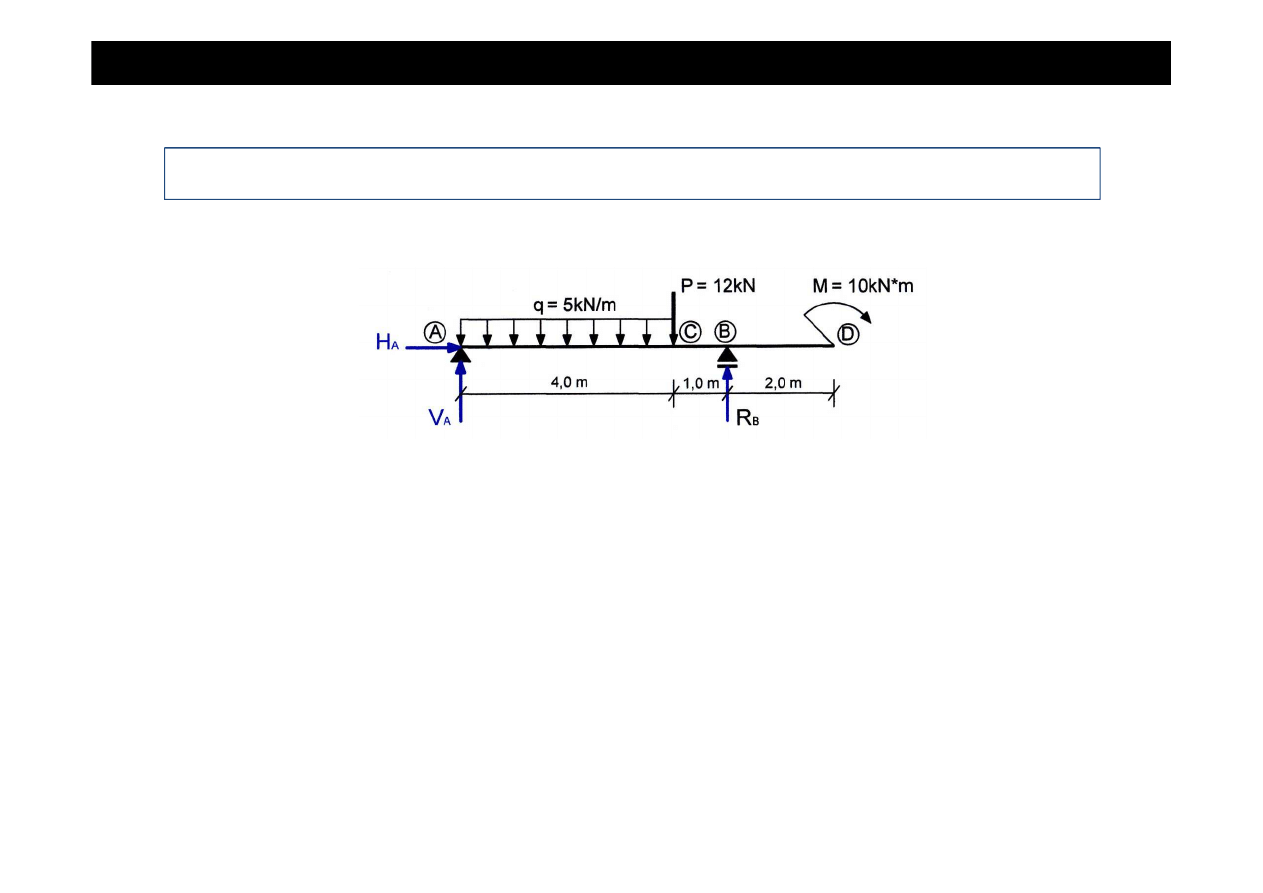
Zadanie cd

•

Wyznaczamy warto

ś

ci reakcji podporowych

1.

∑

= 0

= 0 [kN]

2.

∑

= 0

+

%

&

- q

∙ 4

– P = 0

→ ' ()* +ó'-.-/0 1ą 3'/4 -/4'/.35*4

3.

∑

&

=0

∙ 5

- q

∙ 4 ∙ 3

- P

∙

1 + M = 0

∙ 5 =

q

∙ 4 ∙ 3

+ P

∙

1 – M

∙ 5

= 5

∙ 4 ∙ 3

+ 12

∙

1 – 10

∙ 5

= 62

=

12,4 [kN]

4.

powracamy do równania nr2

∑

= 0

→ %

&

= -

+ q

∙ 4

+ P

%

&

= - 12,4 + 5

∙ 4

+ 12

%

&

= 19,6 [kN]

5. sprawdzenie

∑

=0 -

%

&

∙ 5

+ q

∙ 4 ∙ 2

+ P

∙ 4

+ M = 0

→

%

&

= 19,6 [kN]

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

WYZNACZANIE SIŁ WEWN

Ę

TRZNYCH I SPORZ

Ą

DZANIE ICH WYKRESÓW

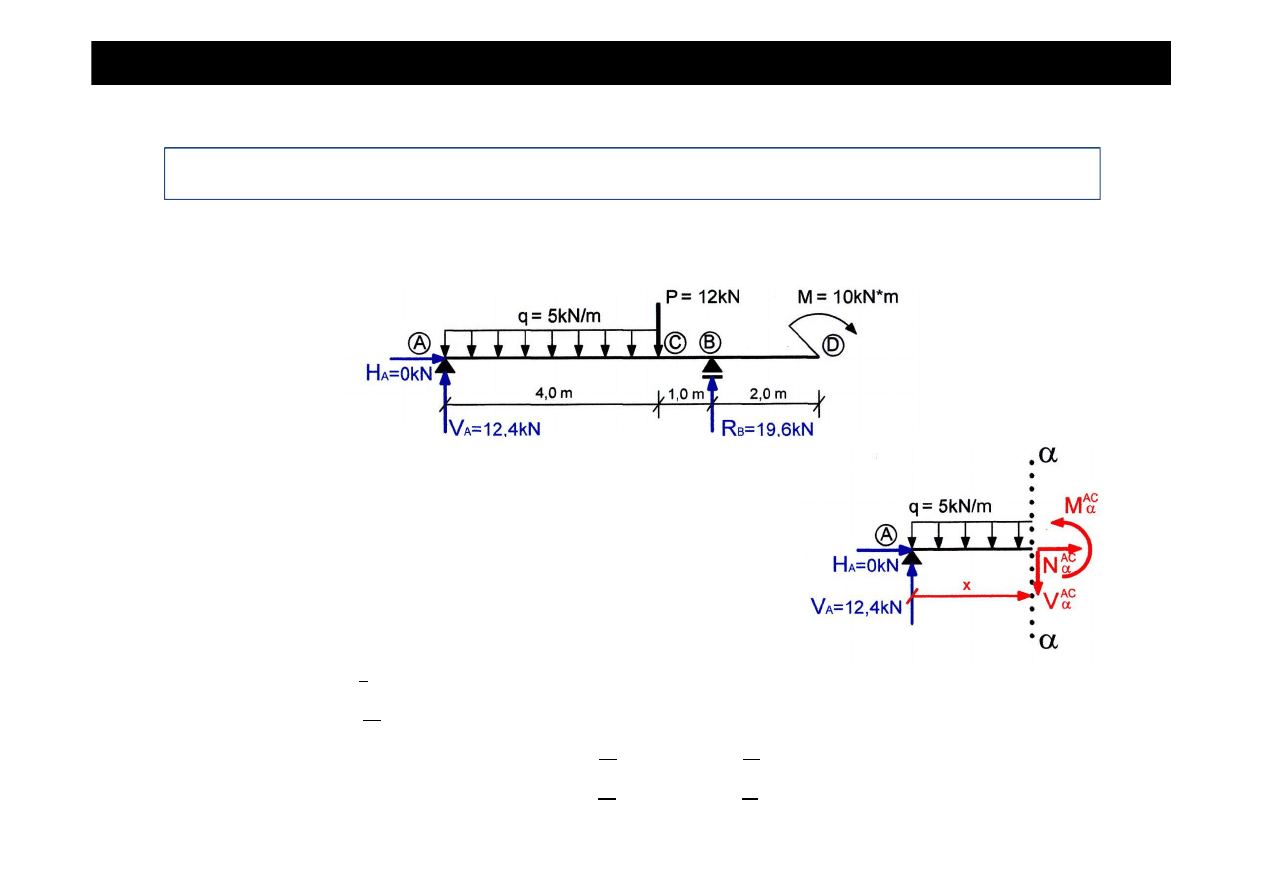
Zadanie cd

•

Wyznaczamy warto

ś

ci sił wewn

ę

trznych (sił podłu

ż

nych, sił poprzecznych i momentów

zginaj

ą

cych) w poszczególnych przedziałach belki.

Przedział AC

, x

∈

(0,4)

siły podłu

ż

ne

;

<

+

= 0

→

;

< = −

= 0 [kN]

siły poprzeczne

−

;

<

+

- q

∙

x = 0

;

<

=

- q

∙

x

dla x=0

;

A

=

- q

∙

x = 12,4 - 5

∙

0 = 0 [kN]

dla x=

4

;

C

=

- q

∙

x = 12,4 - 5

∙

4 = -7,6 [kN]

momenty zginaj

ą

ce

−

;

<

+

∙ x

- q

∙

x

= 0

;

<

=

∙ x

-

F ∙

C

dla x=0

;

A

=

∙ x

-

F ∙

C

= 12,4

∙ 0

- 5

∙

E

C

= 0 [kN

∙

m]

dla x=4

;

C

=

∙ x

-

F ∙

C

= 12,4

∙ 4

- 5

∙

@

C

= 9,6 [kN

∙

m]

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

WYZNACZANIE SIŁ WEWN

Ę

TRZNYCH I SPORZ

Ą

DZANIE ICH WYKRESÓW

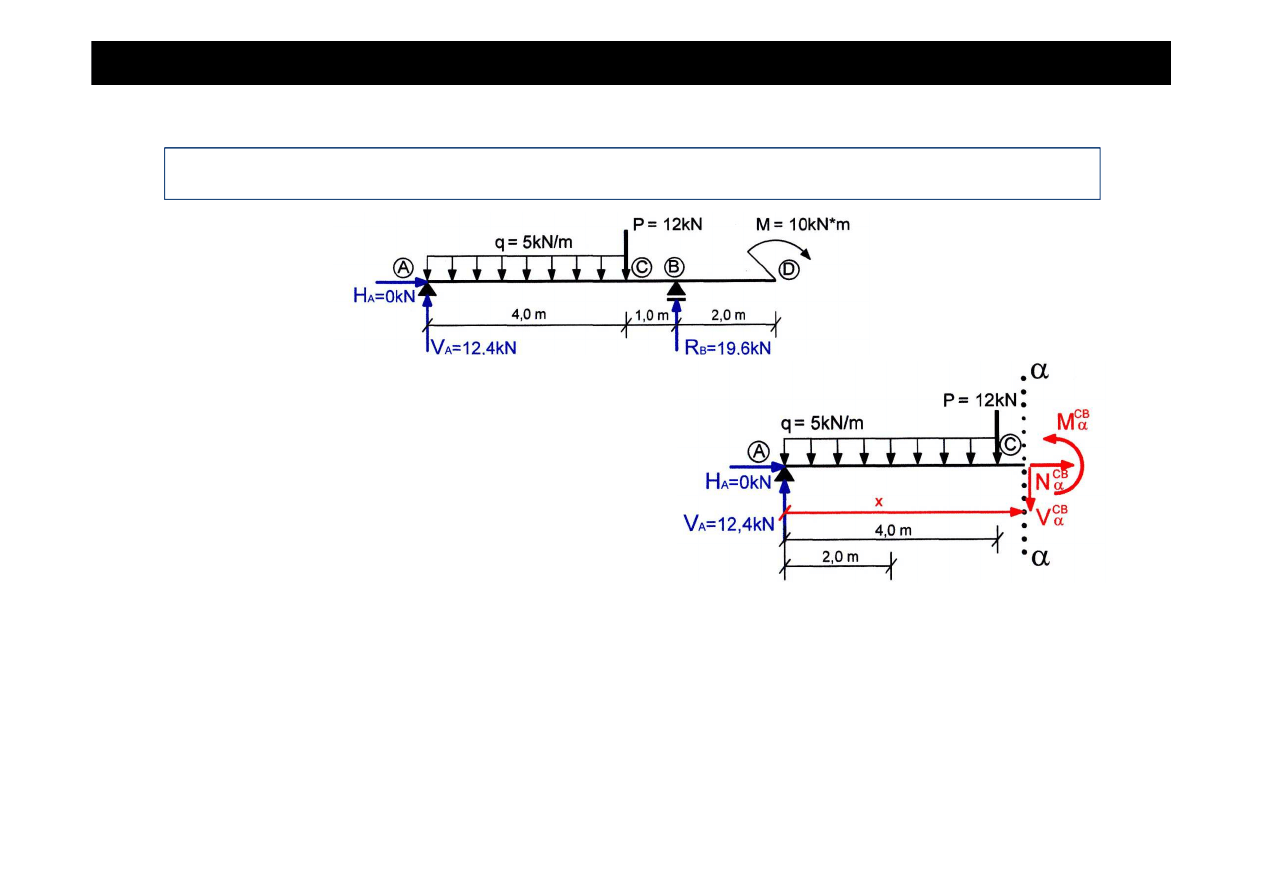
Zadanie cd

Przedział CB

, x

∈

(4,5)

siły podłu

ż

ne

;&

<

+

= 0

→

;&

< = −

= 0 [kN]

siły poprzeczne

−

;&

<

+

- q

∙ 4

- P = 0

;&

<

=

- q

∙ 4

- P

dla x=4

;&

C

=

- q

∙ 4

- P = 12,4 - 5

∙

4 - 12 = -19,6 [kN]

dla x=

5

;&

B

=

- q

∙ 4

- P = 12,4 - 5

∙

4 - 12 = -19,6 [kN]

momenty zginaj

ą

ce

−

;&

<

+

∙ x

- q

∙ 4 ∙

(x-2) - P

∙

(x-4) = 0

;&

<

=

∙ x

- q

∙ 4 ∙

(x-2) - P

∙

(x-4)

dla x=4

;&

C

=

∙ x

-

F ∙

4

∙

(x-2)-P

∙

(x-4) = 12,4

∙

4 - 5

∙

4

∙

(4-2) -12

∙

(4-4) = 9,6 [kN

∙

m]

dla x=5

;&

B

=

∙ x

-

F ∙

4

∙

(x-2)-P

∙

(x-4) = 12,4

∙

5 - 5

∙

4

∙

(5-2) -12

∙

(5-4) = -10 [kN

∙

m]

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

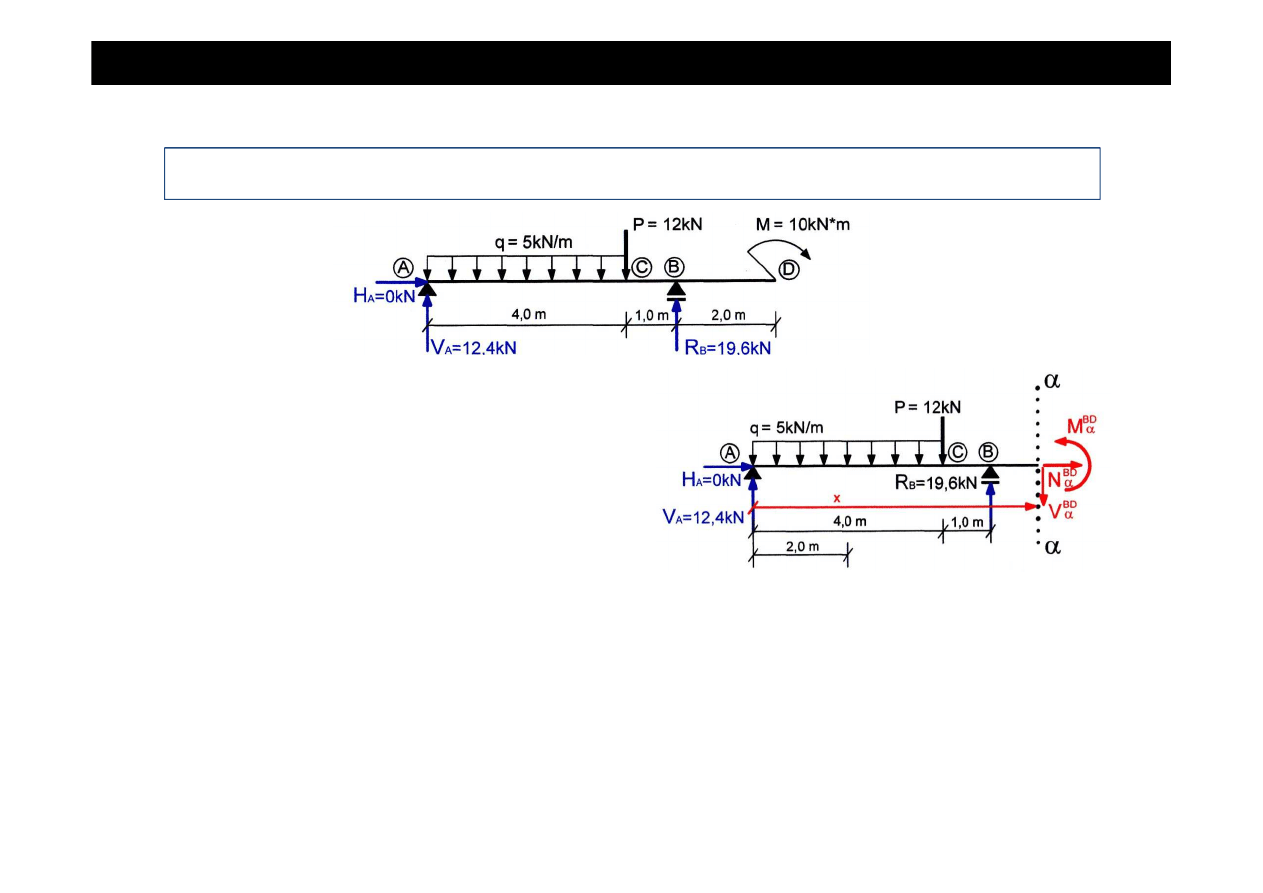
WYZNACZANIE SIŁ WEWN

Ę

TRZNYCH I SPORZ

Ą

DZANIE ICH WYKRESÓW

Zadanie cd

Przedział BD

, x

∈

(5,7)

siły podłu

ż

ne

&Q

<

+

= 0

→

&Q

< = −

= 0 [kN]

siły poprzeczne

−

&Q

<

+

- q

∙ 4

- P +

%

&

= 0

&Q

<

=

- q

∙ 4

- P +

%

&

dla x=5

&Q

B

=

- q

∙ 4

- P = 12,4 - 5

∙

4 - 12 + 19,6 = 0 [kN]

dla x=

7

&Q

D

=

- q

∙ 4

- P = 12,4 - 5

∙

4 - 12 + 19,6 = 0 [kN]

momenty zginaj

ą

ce

−

&Q

<

+

∙ x

- q

∙ 4 ∙

(x-2) - P

∙

(x-4) +

%

&

∙

(x-5) = 0

&Q

<

=

∙ x

- q

∙ 4 ∙

(x-2) - P

∙

(x-4) +

%

&

∙

(x-5)

dla x=5

&Q

B

=

∙ x

-

F ∙

4

∙

(x-2)-P

∙

(x-4) +

%

&

∙

(x-5) = 12,4

∙

5 - 5

∙

4

∙

(5-2) -12

∙

(5-4) +

+ 19,6

∙

(5-5)= -10 [kN

∙

m]

dla x=7

&Q

D

=

∙ x

-

F ∙

4

∙

(x-2)-P

∙

(x-4) +

%

&

∙

(x-5) = 12,4

∙

7 - 5

∙

4

∙

(7-2) -12

∙

(7-4) +

+ 19,6

∙

(7-5)= -10 [kN

∙

m]

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8

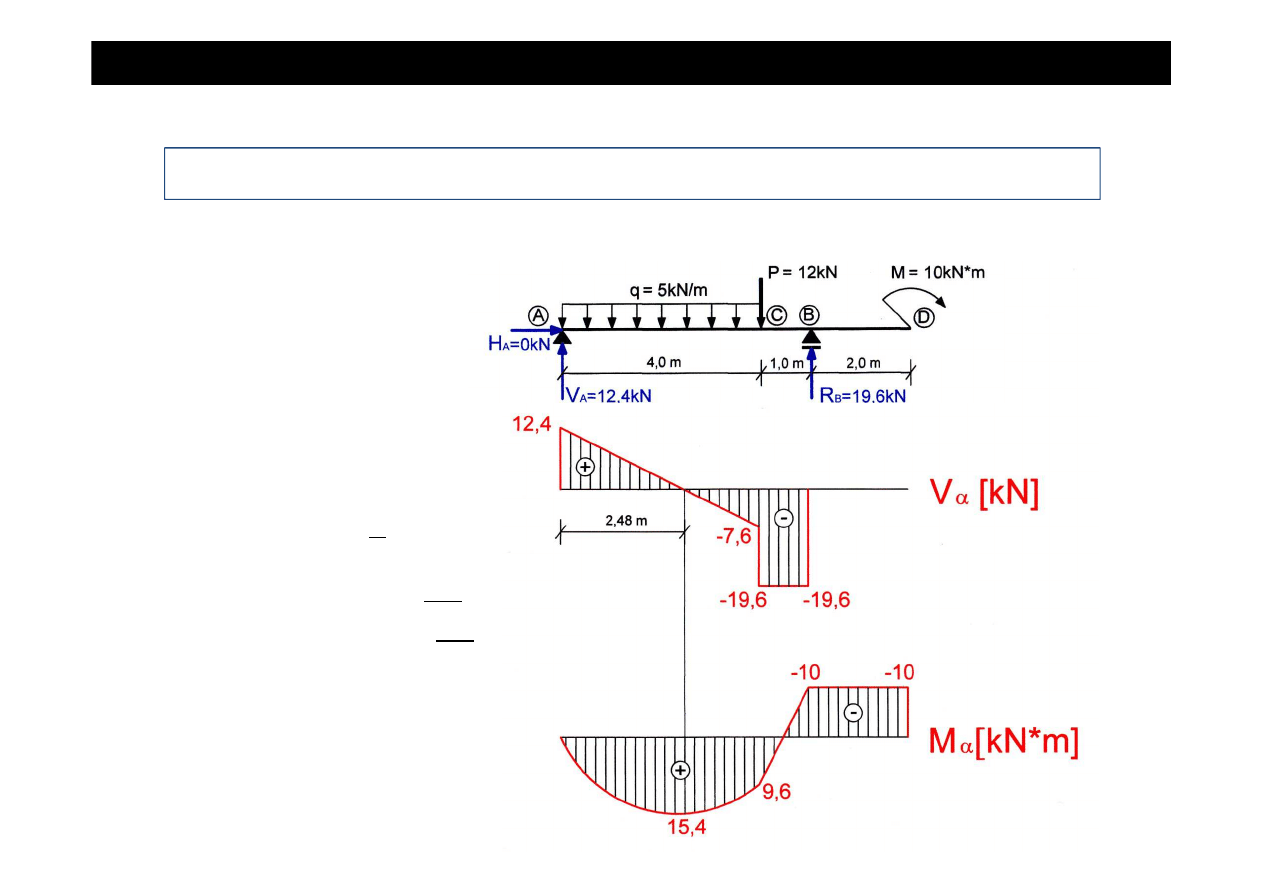
WYZNACZANIE SIŁ WEWN

Ę

TRZNYCH I SPORZ

Ą

DZANIE ICH WYKRESÓW

Zadanie cd

•

sporz

ą

dzamy

wykresy sił wewn

ę

trznych

ekstremum w przedziale AB

;

<

= 0

;

<

=

- q

∙

x

- q

∙

x = 0

q

∙

x =

5

∙

x = 12,4 /:5

x = 2,48m

;

<

=

∙ x

-

F ∙

C

dla x = 2,48m

;

*.G

=

∙ 2,48

-

F ∙

,@J

C

=

= 12,4

∙

2,48 – 5

∙

,@J

C

=

= 15,4 [kN

∙

m]

M e c h a n i k a B u d o w l i i K o n s t r u k c j i Wykład nr7 i 8