Kwadryki (powierzchnie stopnia drugiego)

Powierzchni¹ stopnia drugiego

,

lub kr

ótko

kwadryk¹

, nazywamy zbi

ór punktów

P

(

x,y,z

), kt

órych wspóùrzêdne speùniaj¹ równanie:

0

2

2

2

2

2

2

44

34

24

14

23

13

12

2

33

2

22

2

11























a

z

a

y

a

x

a

yz

a

xz

a

xy

a

z

a

y

a

x

a

gdzie

0

2

33

2

22

2

11







a

a

a

.

W niniejszym rozdziale ograniczymy rozwa

¿ania do wykresów powierzchni

stopnia drugiego maj

¹cych zastosowania w caùkach wielokrotnych.

Ka

¿d¹ powierzchniê stopnia drugiego mo¿na za pomoc¹ translacji i obrotu

sprowadzi

ã do

postaci kanonicznej

,

tzn. takiej gdzie w r

ównaniu nie wystêpuj¹

wyrazy mieszane, a liczba wyraz

ów liniowych jest jak najmniejsza. Wykorzystuj¹c

posta

ã kanoniczn¹ mo¿na zaklasyfikowaã kwadrykê do jednego z piêciu typów.

TYPY KWADRYK

Typ elipsoidalny

pusty

zbiór

punkt

elipsoida
























1

0

1

2

2

2

2

2

2

c

z

b

y

a

x

definicja
kwadryk

id4495734 pdfMachine by Broadgun Software - a great PDF writer! - a great PDF creator! - http://www.pdfmachine.com http://www.broadgun.com

..........................................................................................

PRZYK£AD 1

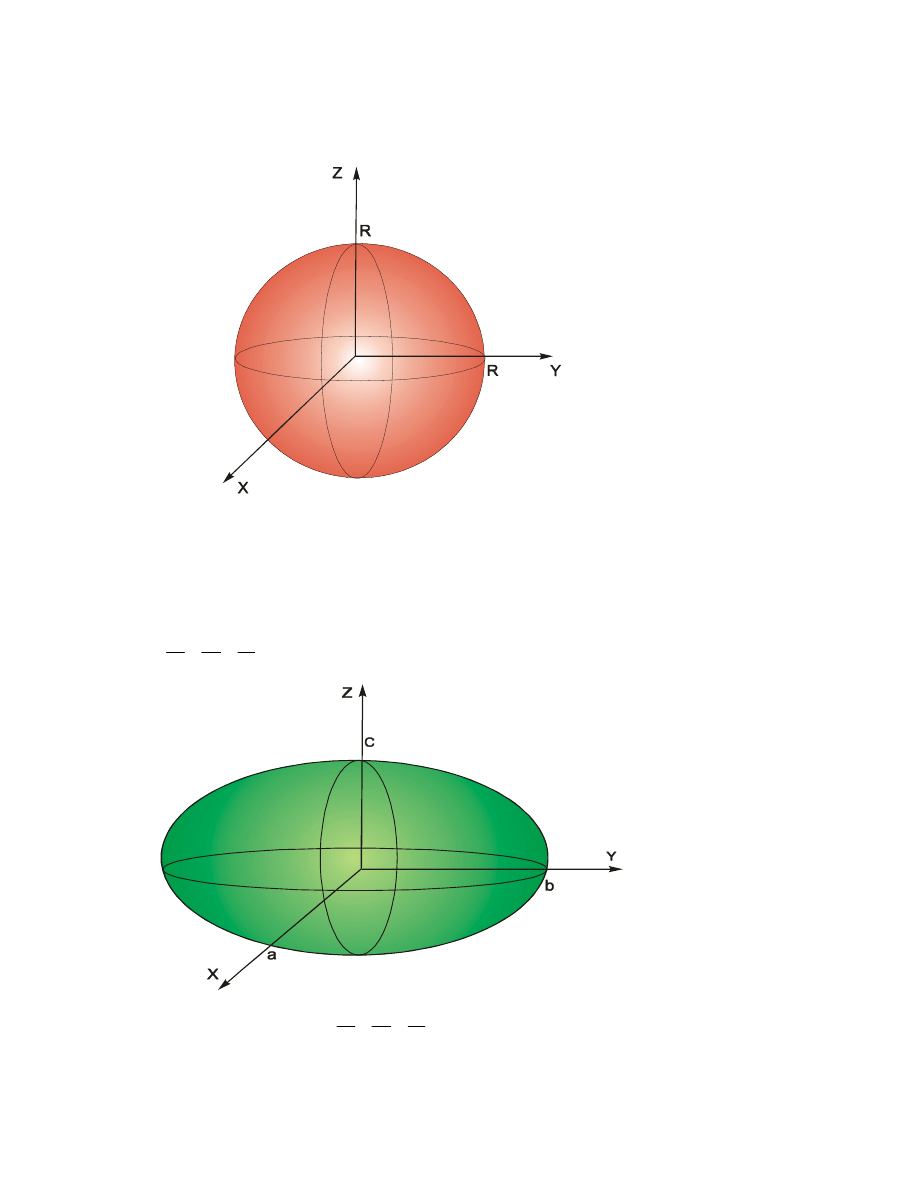
R

ównanie

2

2

2

2

R

z

y

x







(

a

=

b

=

c

=

R

) jest r

ównaniem sfery o œrodku w

pocz

¹tku ukùadu wspóùrzêdnych i promieniu R

(Rysunek 1).

Rysunek 1. Sfera o r

ównaniu

2

2

2

2

R

z

y

x







.

..........................................................................................

PRZYK£AD 2

R

ównanie

1

2

2

2

2

2

2







c

z

b

y

a

x

jest r

ównaniem elipsoidy (Rysunek 2)

Rysunek 2 . Elipsoida o r

ównaniu

1

2

2

2

2

2

2







c

z

b

y

a

x

.

............................................................................................

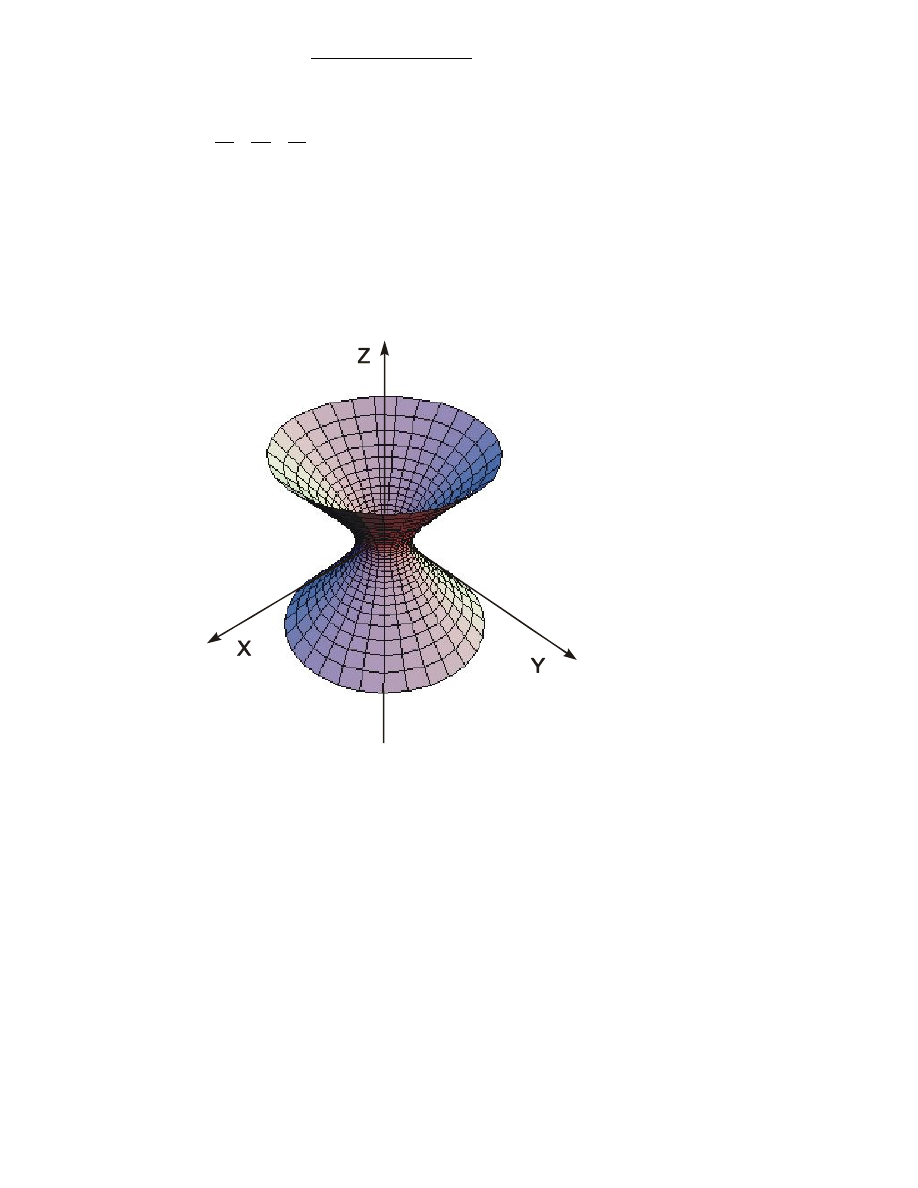
Typ hiperboloidalny


















1

0

1

2

2

2

2

2

2

c

z

b

y

a

x

..........................................................................................

PRZYK£AD 3

R

ównanie

1

2

2

2







z

y

x

przedstawia hiperboloid

ê jednopowùokow¹ (Rysunek 3).

Rysunek 3. Hiperboloida jednopow

ùokowa.

..........................................................................................



hiperboloida jednopow

ùokowa



sto

¿ek



hiperboloida dwupow

ùokowa

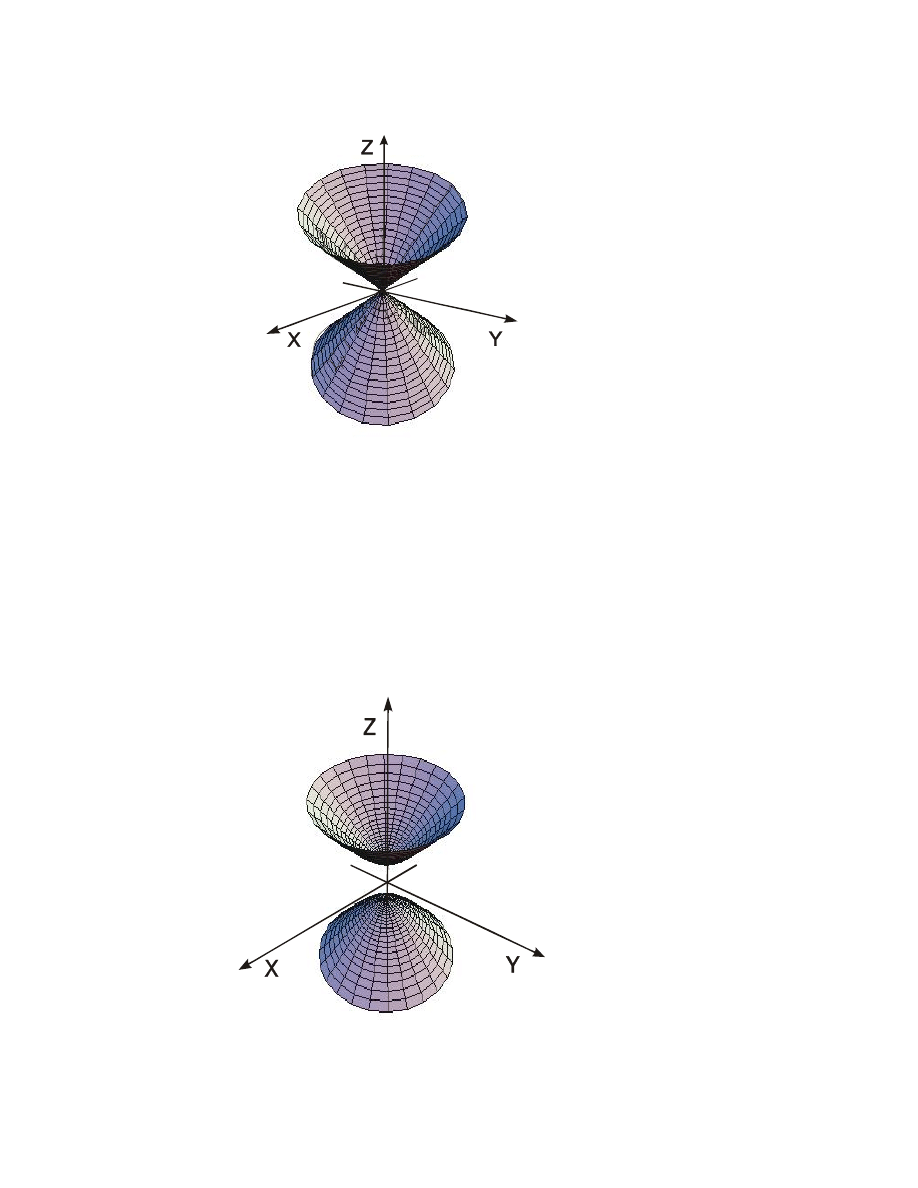
PRZYK£AD 4

R

ównanie

2

2

2

z

y

x





przedstawia sto

¿ek (Rysunek 4).

Rysunek 4. Sto

¿ek.

..........................................................................................

PRZYK£AD 5

R

ównanie

1

2

2

2









z

y

x

jest r

ównaniem

hiperboloidy

dwupowùokowej

(Rysunek 5) .

Rysunek 5. Hiperboloida dwupow

ùokowa.

............................................................................................

Typ paraboloidalny























0

0

0

2

2

2

2

a

p

,

a

a

,

px

y

..........................................................................................

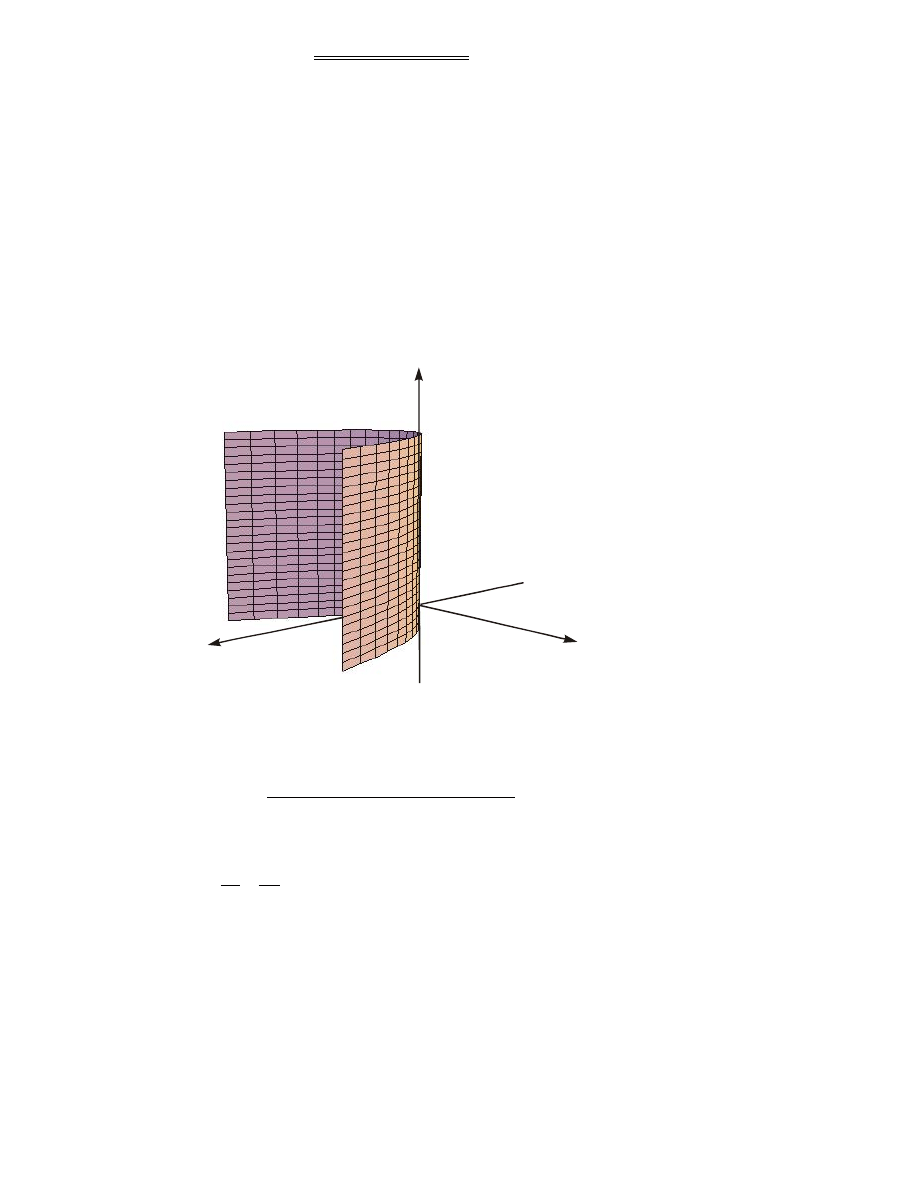
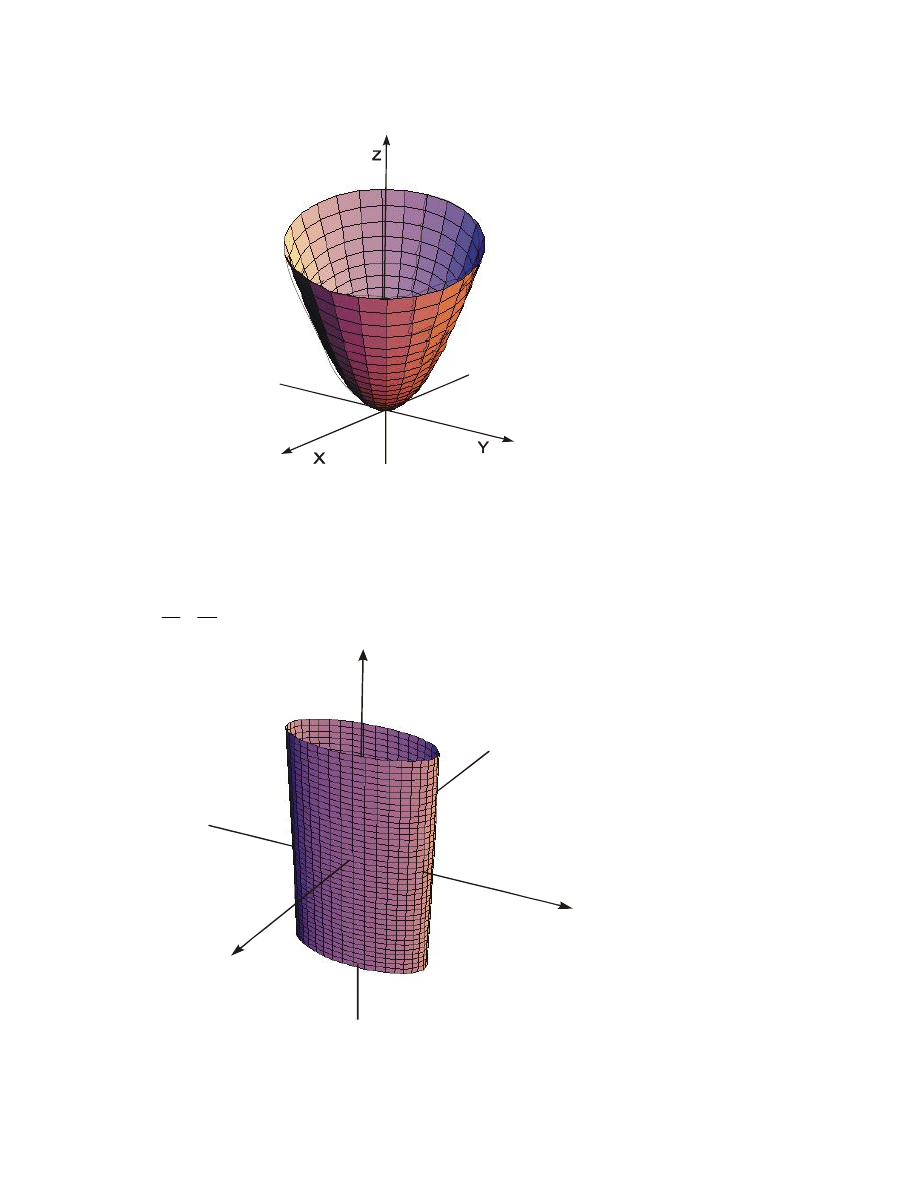
PRZYK£AD 6

R

ównanie

x

,

y

5

0

2



przedstawia walec paraboliczny (Rysunek 6).

Y

X

Z

Rysunek 6. Walec paraboliczny.

...........................................................................................

Typ paraboloidalno- eliptyczny

1

1

2

2

2

2

2






















urojony

eliptyczny

walec

eliptyczny

walec

eliptyczna

a

paraboloid

z

b

y

a

x



walec paraboliczny



p

ùaszczyzny ró¿ne i równolegùe



p

ùaszczyzna podwójna



p

ùaszczyzny urojone ró¿ne i równolegùe

..........................................................................................

PRZYK£AD 7

R

ównanie

z

y

x





2

2

przedstawia paraboloid

ê (Rysunek 7).

Rysunek 7. Paraboloida.

...........................................................................................

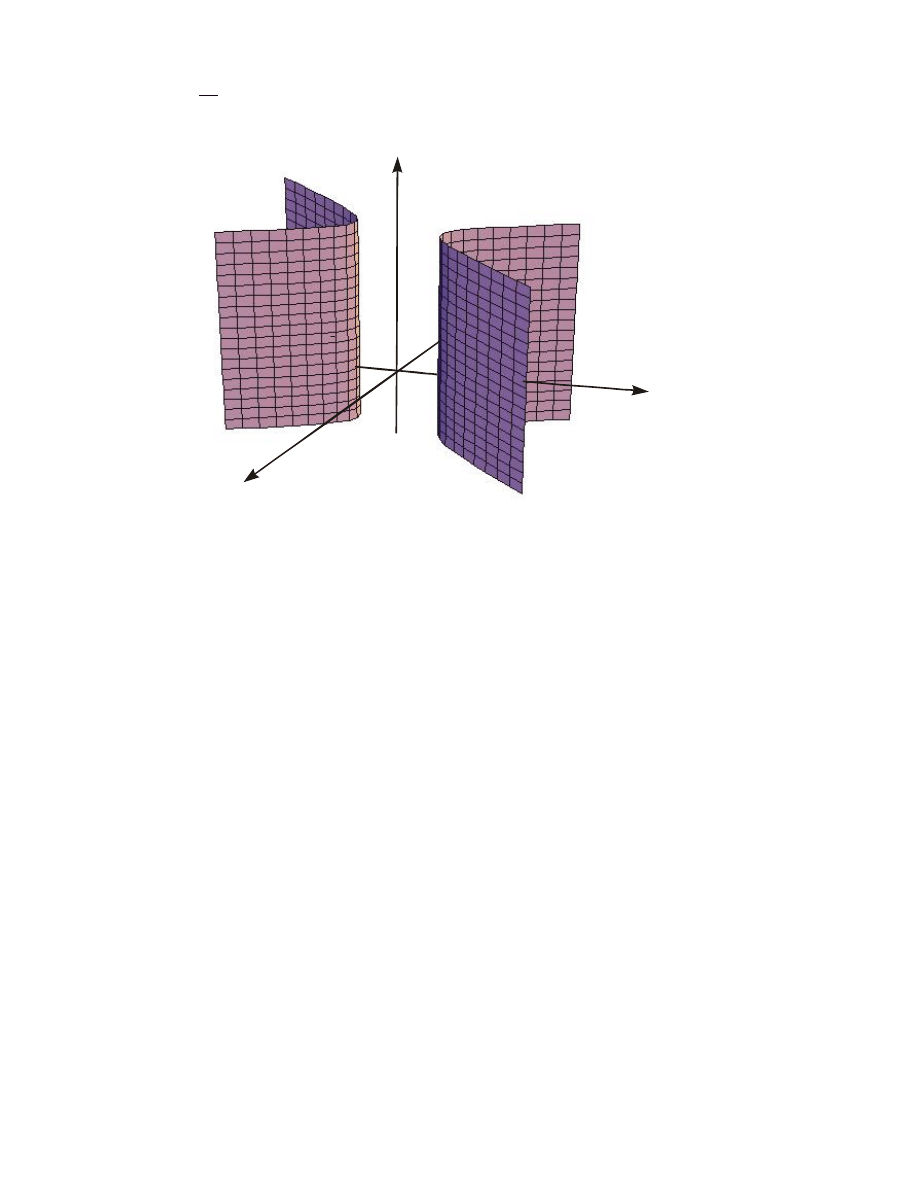
PRZYK£AD 8

R

ównanie

1

9

4

2

2





y

x

przedstawia walec eliptyczny (Rysunek 8).

X

Y

Z

Rysunek 8. Walec eliptyczny.

...........................................................................................

Typ paraboloidalno- hiperboliczny

1

1

2

2

2

2






















y

p

ùùaszczyz

si

ê

ce

przecinaj

¹

zny

hiperbolic

walec

zna

hiperbolic

a

paraboloid

z

b

y

a

x

..........................................................................................

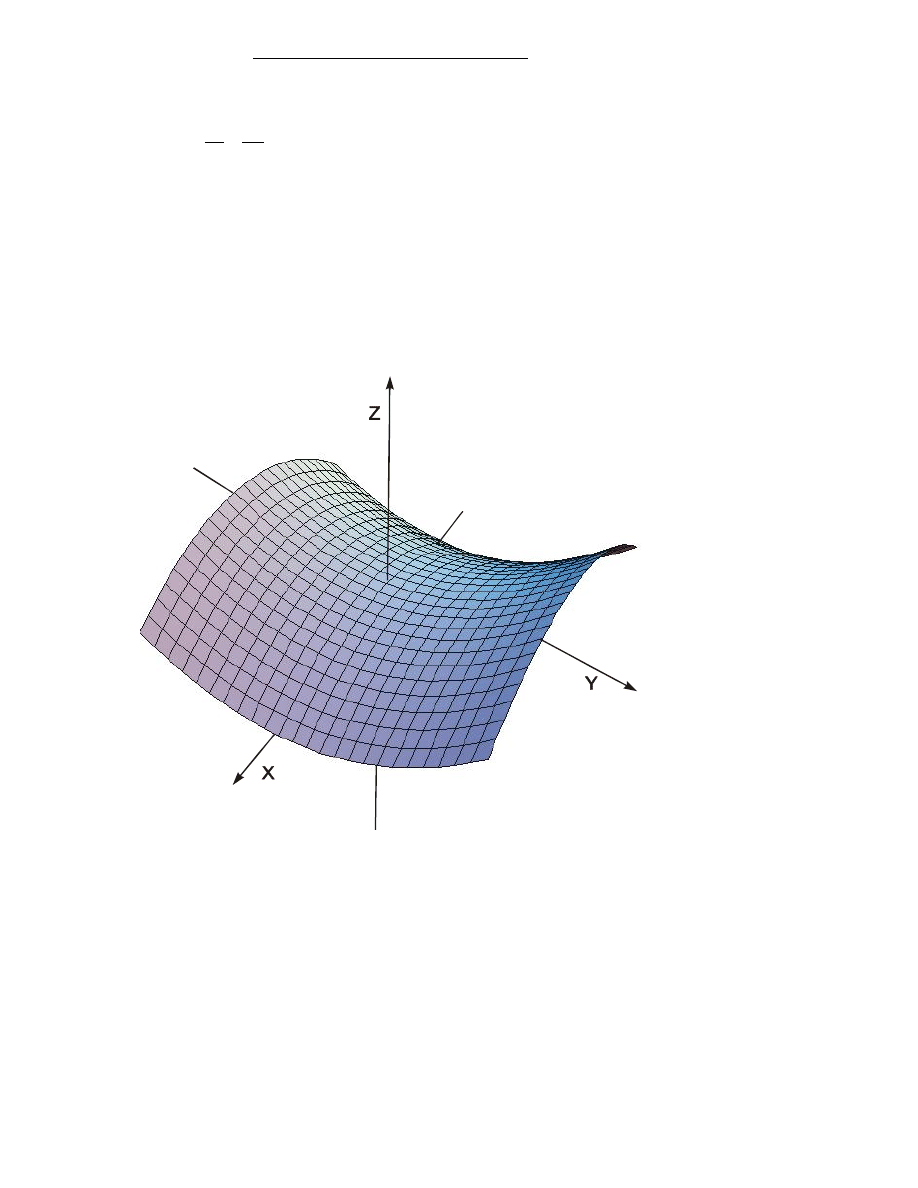
PRZYK£AD 9

R

ównanie

z

y

x





2

2

przedstawia paraboloid

ê hiperboliczn¹ (siodùo) (Rysunek

9).

Rysunek 9. Paraboloida hiperboliczna (siod

ùo).

...........................................................................................

PRZYK£AD 10

R

ównanie

1

4

2

2





x

y

przedstawia walec hiperboliczny (Rysunek 10).

X

Y

Z

1

-1

Rysunek 10. Walec hiperboliczny.

...........................................................................................