
Tę stronę ostatnio zmodyfikowano 21:38, 19 cze 2009.
Tekst udostępniany na
licencji Creative Commons:
uznanie autorstwa, na tych samych warunkach
, z możliwością obowi ązywania dodatkowych ograniczeń. Zobacz
szczegółowe informacje o
warunkach korzystania
.
Zasady ochrony prywatności
O Wikipedii
Informacje prawne
Kwadryka
Kwadryka lub powierzchnia drugiego stopnia – w
dana
drugiego stopnia ze względu na współrzędne
:
gdzie
przy czym nie zachodzi
(przynajmniej jeden z powyższych współczynników musi być różny od zera).
W zależności od wartości współczynników
kwadryka może należeć do jednego z wielu typów, różniących się właściwościami.
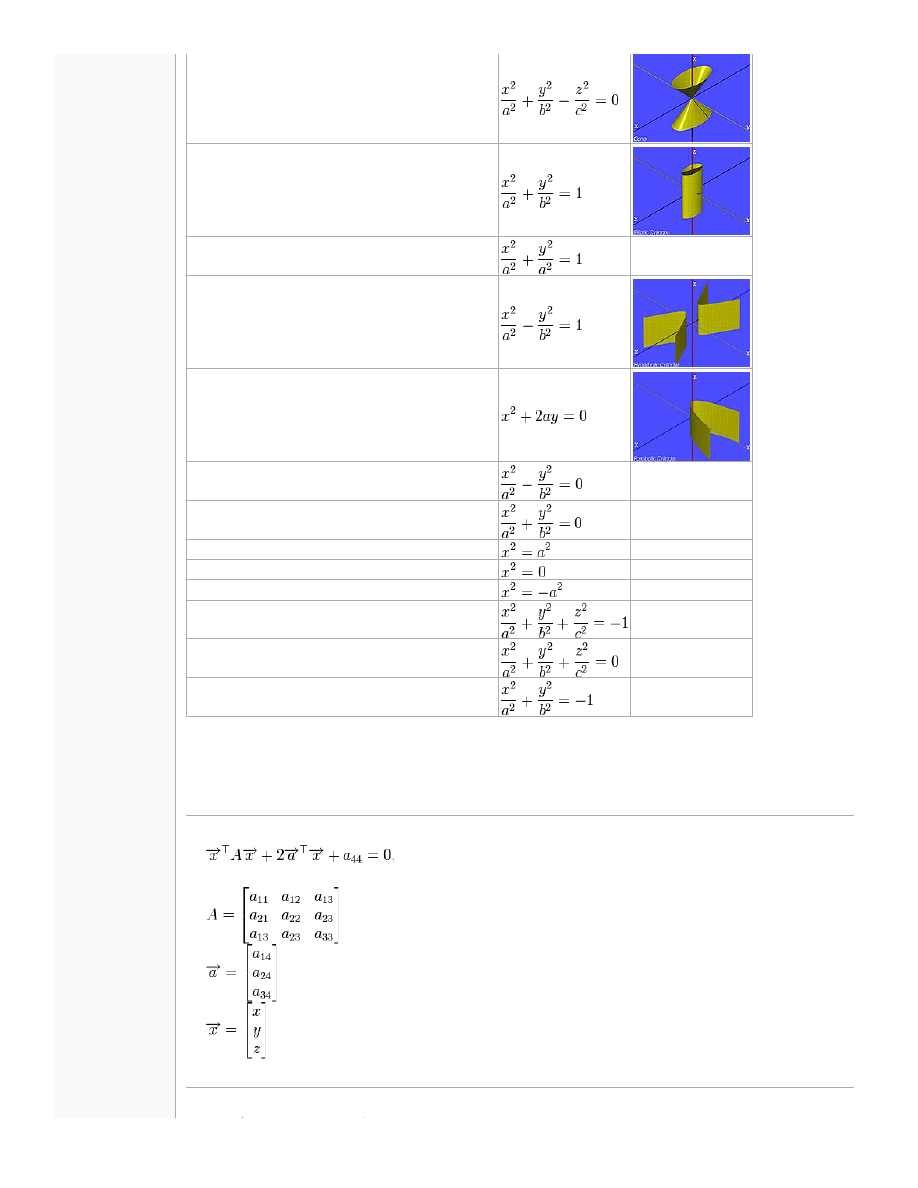
Wykresy i równania kanoniczne
Poprzez odpowiednie przekształcenie układu współrzędnych można równanie kwadryki sprowadzić do postaci kanonicznej, charakterystycznej dla
jednego z wymienionych niżej 17 typów.
W poniższych wzorach
.
Ostatnie kilka przypadków opisuje kwadryki zdegenerowane, w których dla kanonicznego układu współrzędnych znika co najmniej jedna ze
współrzędnych. Niektórzy autorzy nie zaliczają ich do kwadryk. W tym sensie także walce są przypadkami zdegenerowanymi, gdyż można je
przedstawić w postaci zawierającej tylko dwie współrzędne. Ponadto warto zauważyć, że niektóre z tych zdegenerowanych kwadryk nie są
powierzchniami (prosta, punkt, zbiór pusty).
Postać macierzowa równania
Równanie kwadryki można też przedstawić w postaci macierzowej:
gdzie:
Niezmienniki
Poniższe wielkości nie zmieniają się przy zmianie początku układu współrzędnych i rotacji jego osi:
Określenie typu na podstawie współczynników
Korzystając ze znaku niezmienników można określić typ danej powierzchni danej równaniem (1) niezależnie od jej położenia w przestrzeni i
wybranego układu współrzędnych.
tzw. powierzchnie środkowe:
elipsoida
(w szczególnym przypadku
sfera
)
hiperboloida dwupowłokowa
hiperboloida dwupowłokowa
zbiór pusty (tzw. elipsoida urojona)
hiperboloida jednopowłokowa
hiperboloida jednopowłokowa
pojedynczy punkt (tzw. stożek urojony)
powierzchnia stożkowa
powierzchnia stożkowa
paraboloidy
:
paraboloida eliptyczna
(w szczególnym przypadku
paraboloida obrotowa
)
paraboloida hiperboliczna
:
przypadek zdegenerowany (suma dwóch płaszczyzn, jedna płaszczyzna,
prosta
lub zbiór pusty)
w przeciwnym wypadku powierzchnia walcowa oparta na
krzywej stożkowej
:
walec eliptyczny
rzeczywisty lub urojony
walec hiperboliczny
walec paraboliczny
Bibliografia
I.N. Bronsztejn, K.A. Siemiendiajew: Matematyka – Poradnik encyklopedyczny. Wyd. 6. Warszawa: PWN, 1976, ss. 299 301.
Spis treści
1 Wykresy i równania kanoniczne
4 Określenie typu na podstawie współczynników
[
(szczególny przypadek elipsoidy)
(szczególny przypadek elipsoidy obrotowej)
(szczególny przypadek paraboloidy eliptycznej)
powierzchnia stożkowa
walec eliptyczny
powierzchnia boczna zwykłego
walca
o nieskończonej wysokości
(szczególny przypadek walca eliptycznego)
walec hiperboliczny
walec paraboliczny
przecinające się
płaszczyzny
tzw. przecinające się płaszczyzny urojone
prosta
równoległe płaszczyzny
nakładające się płaszczyzny
tzw. równoległe płaszczyzny urojone
zbiór pusty
tzw. elipsoida urojona
zbiór pusty
tzw. stożek urojony
pojedynczy punkt
tzw. urojony walec eliptyczny
zbiór pusty
[
edytuj
]
[
edytuj
]
[
edytuj
]
[
edytuj
]
Kategoria
:
Powierzchnie
dla edytorów
utwórz książkę
narzędzia
szukaj
Przejdź
Szukaj
w innych językach
Tę stronę ostatnio zmodyfikowano 21:38, 19 cze 2009.
Tekst udostępniany na
licencji Creative Commons:
uznanie autorstwa, na tych samych warunkach
, z możliwością obowi ązywania dodatkowych ograniczeń. Zobacz
szczegółowe informacje o
warunkach korzystania
.
Zasady ochrony prywatności
O Wikipedii
Informacje prawne
Kwadryka
Kwadryka lub powierzchnia drugiego stopnia – w
matematyce
powierzchnia
dana
równaniem
drugiego stopnia ze względu na współrzędne
:
gdzie
przy czym nie zachodzi
(przynajmniej jeden z powyższych współczynników musi być różny od zera).
W zależności od wartości współczynników
kwadryka może należeć do jednego z wielu typów, różniących się właściwościami.
Wykresy i równania kanoniczne
Poprzez odpowiednie przekształcenie układu współrzędnych można równanie kwadryki sprowadzić do postaci kanonicznej, charakterystycznej dla
jednego z wymienionych niżej 17 typów.
W poniższych wzorach
.
Ostatnie kilka przypadków opisuje kwadryki zdegenerowane, w których dla kanonicznego układu współrzędnych znika co najmniej jedna ze
współrzędnych. Niektórzy autorzy nie zaliczają ich do kwadryk. W tym sensie także walce są przypadkami zdegenerowanymi, gdyż można je
przedstawić w postaci zawierającej tylko dwie współrzędne. Ponadto warto zauważyć, że niektóre z tych zdegenerowanych kwadryk nie są
powierzchniami (prosta, punkt, zbiór pusty).
Postać macierzowa równania
Równanie kwadryki można też przedstawić w postaci macierzowej:
gdzie:
Niezmienniki
Poniższe wielkości nie zmieniają się przy zmianie początku układu współrzędnych i rotacji jego osi:
Określenie typu na podstawie współczynników
Korzystając ze znaku niezmienników można określić typ danej powierzchni danej równaniem (1) niezależnie od jej położenia w przestrzeni i
wybranego układu współrzędnych.
tzw. powierzchnie środkowe:
elipsoida
(w szczególnym przypadku
sfera
)
hiperboloida dwupowłokowa
hiperboloida dwupowłokowa
zbiór pusty (tzw. elipsoida urojona)
hiperboloida jednopowłokowa
hiperboloida jednopowłokowa
pojedynczy punkt (tzw. stożek urojony)
powierzchnia stożkowa
powierzchnia stożkowa
paraboloidy
:
paraboloida eliptyczna
(w szczególnym przypadku
paraboloida obrotowa
)
paraboloida hiperboliczna
:
przypadek zdegenerowany (suma dwóch płaszczyzn, jedna płaszczyzna,
prosta
lub zbiór pusty)
w przeciwnym wypadku powierzchnia walcowa oparta na
krzywej stożkowej
:
walec eliptyczny
rzeczywisty lub urojony
walec hiperboliczny
walec paraboliczny
Bibliografia
I.N. Bronsztejn, K.A. Siemiendiajew: Matematyka – Poradnik encyklopedyczny. Wyd. 6. Warszawa: PWN, 1976, ss. 299 301.
Spis treści
1 Wykresy i równania kanoniczne
2 Postać macierzowa równania
3 Niezmienniki
4 Określenie typu na podstawie współczynników
5 Bibliografia
[
edytuj
]
elipsoida
elipsoida obrotowa
(szczególny przypadek elipsoidy)
sfera
(szczególny przypadek elipsoidy obrotowej)
paraboloida eliptyczna
paraboloida obrotowa
(szczególny przypadek paraboloidy eliptycznej)
paraboloida hiperboliczna
hiperboloida jednopowłokowa
hiperboloida dwupowłokowa
powierzchnia boczna zwykłego
o nieskończonej wysokości
(szczególny przypadek walca eliptycznego)
przecinające się
tzw. przecinające się płaszczyzny urojone
równoległe płaszczyzny
nakładające się płaszczyzny
tzw. równoległe płaszczyzny urojone
zbiór pusty
tzw. elipsoida urojona
zbiór pusty
tzw. stożek urojony
pojedynczy punkt
tzw. urojony walec eliptyczny
zbiór pusty
[
[
[
edytuj
]
[
edytuj
]
Kategoria
:
Powierzchnie
Strona główna
Kategorie artykułów
Bieżące wydarzenia
Losuj artykuł
Zgłoś błąd
Częste pytania
(FAQ)
Kontakt z Wikipedią
Wspom óż Fundację
dla edytorów
Ostatnie zmiany
Zasady edytowania
Pomoc
Portal wikipedystów
Ogłoszenia
utwórz książkę
Dodaj stron ę do
książki
Książki – pomoc
narzędzia
Linkujące
Zmiany w
dolinkowanych
Strony specjalne
Wersja do druku
Link do tej wersji
Cytowanie tego
artykułu
Wersja PDF
Wypróbuj wersj ę testową
Logowanie i rejestracja
dyskusja
edytuj
historia i autorzy
artykuł
szukaj
Przejdź
Szukaj
w innych językach
ﺍﻟﻌﺮﺑﻴﺔ
Deutsch
English
Espa ñol
Français
Italiano
Nederlands
日本語
Português
Русский
ไทย
中文

Tę stronę ostatnio zmodyfikowano 21:38, 19 cze 2009.
uznanie autorstwa, na tych samych warunkach
, z możliwością obowi ązywania dodatkowych ograniczeń. Zobacz
szczegółowe informacje o
Kwadryka
Kwadryka lub powierzchnia drugiego stopnia – w
matematyce
powierzchnia
dana
równaniem
drugiego stopnia ze względu na współrzędne
:
gdzie
przy czym nie zachodzi
(przynajmniej jeden z powyższych współczynników musi być różny od zera).
W zależności od wartości współczynników
kwadryka może należeć do jednego z wielu typów, różniących się właściwościami.
Wykresy i równania kanoniczne
Poprzez odpowiednie przekształcenie układu współrzędnych można równanie kwadryki sprowadzić do postaci kanonicznej, charakterystycznej dla
jednego z wymienionych niżej 17 typów.
W poniższych wzorach
.
Ostatnie kilka przypadków opisuje kwadryki zdegenerowane, w których dla kanonicznego układu współrzędnych znika co najmniej jedna ze
współrzędnych. Niektórzy autorzy nie zaliczają ich do kwadryk. W tym sensie także walce są przypadkami zdegenerowanymi, gdyż można je
przedstawić w postaci zawierającej tylko dwie współrzędne. Ponadto warto zauważyć, że niektóre z tych zdegenerowanych kwadryk nie są
powierzchniami (prosta, punkt, zbiór pusty).
Postać macierzowa równania
Równanie kwadryki można też przedstawić w postaci macierzowej:
gdzie:
Niezmienniki
Poniższe wielkości nie zmieniają się przy zmianie początku układu współrzędnych i rotacji jego osi:
Określenie typu na podstawie współczynników
Korzystając ze znaku niezmienników można określić typ danej powierzchni danej równaniem (1) niezależnie od jej położenia w przestrzeni i
wybranego układu współrzędnych.
tzw. powierzchnie środkowe:
(w szczególnym przypadku
)
zbiór pusty (tzw. elipsoida urojona)
pojedynczy punkt (tzw. stożek urojony)
(w szczególnym przypadku
)
:
przypadek zdegenerowany (suma dwóch płaszczyzn, jedna płaszczyzna,
lub zbiór pusty)
w przeciwnym wypadku powierzchnia walcowa oparta na
:
Bibliografia
I.N. Bronsztejn, K.A. Siemiendiajew: Matematyka – Poradnik encyklopedyczny. Wyd. 6. Warszawa: PWN, 1976, ss. 299 301.
Spis treści
1 Wykresy i równania kanoniczne
2 Postać macierzowa równania
3 Niezmienniki
4 Określenie typu na podstawie współczynników
5 Bibliografia
[
edytuj
]
elipsoida
elipsoida obrotowa
(szczególny przypadek elipsoidy)
sfera
(szczególny przypadek elipsoidy obrotowej)
paraboloida eliptyczna
paraboloida obrotowa
(szczególny przypadek paraboloidy eliptycznej)
paraboloida hiperboliczna
hiperboloida jednopowłokowa
hiperboloida dwupowłokowa
powierzchnia stożkowa
walec eliptyczny
powierzchnia boczna zwykłego
walca
o nieskończonej wysokości
(szczególny przypadek walca eliptycznego)
walec hiperboliczny
walec paraboliczny
przecinające się
płaszczyzny
tzw. przecinające się płaszczyzny urojone
prosta
równoległe płaszczyzny
nakładające się płaszczyzny
tzw. równoległe płaszczyzny urojone
zbiór pusty
tzw. elipsoida urojona
zbiór pusty
tzw. stożek urojony
pojedynczy punkt
tzw. urojony walec eliptyczny
zbiór pusty
[
edytuj
]
[
edytuj
]
[
[
:
Strona główna
Kategorie artykułów
Bieżące wydarzenia
Losuj artykuł
Zgłoś błąd
Częste pytania
(FAQ)
Kontakt z Wikipedią
Wspom óż Fundację
dla edytorów
Ostatnie zmiany
Zasady edytowania
Pomoc
Portal wikipedystów
Ogłoszenia
utwórz książkę
Dodaj stron ę do
książki
Książki – pomoc
narzędzia
Linkujące
Zmiany w
dolinkowanych
Strony specjalne
Wersja do druku
Link do tej wersji
Cytowanie tego
artykułu
Wersja PDF
Wypróbuj wersj ę testową
Logowanie i rejestracja
dyskusja
edytuj
historia i autorzy
artykuł
szukaj
Przejdź
Szukaj
w innych językach
ﺍﻟﻌﺮﺑﻴﺔ
Deutsch
English
Espa ñol
Français
Italiano
Nederlands
日本語
Português
Русский
ไทย
中文
Wyszukiwarka
Podobne podstrony:
pl wikipedia org wiki Zasady (polityka) rachunkowoś
pl wikipedia org wiki Zasady (polityka) rachunkowoś
http pl wikipedia org wiki Obwód rezonansowy LC
pl wikipedia org wiki Turbo (guma)
http, pl wikipedia org wiki Starożytny Egipt BOGUSLAWA
pl wikibooks org wiki Optymalizacja systemu Windows XP A
pl wikipedia org
pl wikibooks org wiki Analiza matematyczna Szeregi liczbowe d23baveb
org wym spr w pl UVGVZWZMJSSOXSRMX754765OJSJRSAUW35UFIOI
Uczestnictwo w AA, aa.org.pl
TheWork.org.pl-Lista-stanow-emocji-i uczuc
tabela z form org-pr, BUDOWNICTWO PŁ, Semestr I, Ekonomia
Dostepna przestrzeń publiczna firr org pl
TheWork.org.pl-Jedno-przekonanie-na-raz
www opoka org pl
Lean Production PL org prod
http, mandriva org pl instalacja programow repozytoria 75 inst
więcej podobnych podstron