
styczeń 1999
POLSKA NORMA
Numer: PN-B-03264:1999
Tytuł: Konstrukcje betonowe, żelbetowe i sprężone - Obliczenia
statyczne i projektowanie
Grupa ICS: 91.080.40
Deskryptory: 0067918A - konstrukcje betonowe, 0580346 - konstrukcje żelbetowe, 0225651 - beton, 0236904 - beton
zbrojony, 0096800 - beton sprężony, 0833023 - elementy prefabrykowane, 0054900 - stal zbrojeniowa, 0814919 - pręty
zbrojeniowe, 0631027 - projekty budowlane, 0315549 - obliczanie, 0396727 - wymagania
PRZEDMOWA
Niniejsza norma jest nowelizacją PN-84/B-03264 Konstrukcje betonowe, żelbetowe i sprężone - Obliczenia statyczne i
projektowanie, w stosunku do której wprowadzono zmiany obejmujące:
- symbole i definicje,
- klasy wytrzymałości betonu i wartości częściowych współczynników bezpieczeństwa dla betonu,
- wymagania stawiane stalom sprężającym,
- zasady projektowania,
- zasady ogólne sprawdzania nośności elementów żelbetowych na zginanie, ściskanie i rozciąganie
- sprawdzanie elementów żelbetowych na ścinanie i skręcanie,
- obliczanie sztywności elementów żelbetowych,
- obliczanie szerokości rys,
- obliczanie konstrukcji sprężonych,
- obliczanie konstrukcji poddanych obciążeniu wielokrotnie zmiennemu,
- obliczanie konstrukcji zespolonych,
- wymagania i zalecenia dotyczące zbrojenia konstrukcji,
- zbrojenie belek na ścinanie,
- ograniczenie zakresu szkód wywołanych przez oddziaływania wyjątkowe,
- maksymalne odległości między przerwami dylatacyjnymi.
Wprowadzone zmiany mają na celu dostosowanie projektowania konstrukcji z betonu do zasad przyjętych w europejskich
prenormach projektowania konstrukcji:
ENV 1992-1-1:1992 Eurocode 2: Design of Concrete Structures Part 1-1: General Rules and Rules for Buildings,
ENV 1992-1-3:1994 Eurocode 2: Design of Concrete Structures Part 1-3: Precast Concrete Elements and Structures,
ENV 1992-1-6:1994 Eurocode 2: Design of Concrete Structures Part 1-6: Plain or Lightly Reinforced Concrete
Wprowadzono dodatkowo postanowienia dotyczące:
- stropów gęstożebrowych,
- ograniczenia szkód spowodowanych oddziaływaniami wyjątkowymi.
Norma zawiera pięć załączników normatywnych, oznaczonych literami A, B, C, D i E.
SPIS TREŚCI
Strona 1

1.1 Zakres normy
1.2 Normy powołane
1.3 Definicje
1.4 Podstawowe symbole
1.4.1 Duże litery łacińskie
1.4.2 Małe litery łacińskie
1.4.3 Litery greckie
2 Beton
2.1 Klasy betonu i przypisane im wytrzymałości
2.1.1 Stosowane klasy betonu
2.1.2 Wytrzymałość i moduł sprężystości betonu
2.2 Odkształcalność betonu
2.2.1 Związek σ-ε przy sprawdzaniu stanu granicznego nośności
2.2.2 Moduł sprężystości betonu
2.2.3 Pełzanie i skurcz betonu
2.2.4 Współczynnik odkształcenia poprzecznego
2.2.5 Współczynnik liniowej rozszerzalności termicznej
3 Stal
3.1 Stal zwykła
3.1.1 Stosowane klasy stali
3.1.2 Charakterystyczna i obliczeniowa granica plastyczności stali
3.1.3 Odkształcalność stali
3.2 Stal sprężająca
4 Zasady proj
4.1 Wymagania podstawowe
4.1.1 Zapewnienie niezawodności konstrukcji
4.1.2 Sytuacje obliczeniowe
4.2 Wymagania ogólne dotyczące obliczeń konstrukcji
4.2.1 Ogólne zasady obliczeń
4.2.2 Zakres, układ i forma obliczeń statycznych
4.2.3 Jednostki miar
4.2.4 Wartości pośrednie
4.3 Oddziaływania
4.4 Analiza konstrukcji
4.4.1 Modele obliczeniowe
4.4.2 Redystrybucja momentów
4.4.3 Dane geometryczne
4.5 Trwałość konstrukcji
4.6 Sprawdzanie stanów granicznych nośności
4.7 Sprawdzanie stanów granicznych użytkowalności
4.7.1 Zasady ogólne
4.7.2 Sprawdzanie stanu granicznego naprężeń
4.7.3 Sprawdzanie stanu granicznego zarysowania
4.7.4 Sprawdzanie stanu granicznego ugięć
4.8 Minimalny przekrój zbrojenia podłużnego
5 Stany graniczne no
5.1 Zasady obliczania elementów zginanych, ściskanych i rozciąganych
5.1.1 Zasady ogólne
5.1.2 Zasady metody uproszczonej
5.2 Zginanie - metoda uproszczona
5.3 Ściskanie
5.3.1 Długości obliczeniowe
5.3.2 Mimośród początkowy
5.3.3 Nośność elementów ściskanych - metoda uproszczona
5.3.3.1 Elementy betonowe
5.3.3.2 Elementy żelbetowe
5.3.4 Słupy uzwojone
5.3.5 Elementy podlegające dwukierunkowemu ściskaniu mimośrodowemu
5.4 Rozciąganie
5.4.1 Nośność elementów rozciąganych mimośrodowo - metoda uproszczona
5.4.2 Elementy rozciągane osiowo
5.5 Ścinanie elementów żelbetowych
Strona 2

5.5.1 Zasady ogólne
5.5.1.1 Podstawowe założenia
5.5.1.2 Graniczne siły poprzeczne, siła V
5.5.1.3 Wymagania
5.5.2 Nośność odcinków pierwszego rodzaju
5.5.2.1 Siła V
5.5.3 Nośność odcinków drugiego rodzaju
5.5.3.1 Elementy o stałej wysokości przekroju
5.5.3.2 Zbrojenie podłużne na odcinkach drugiego rodzaju
5.5.3.3 Elementy o zmiennej wysokości przekroju
5.5.4 Ścinanie między środnikiem i półkami
5.6 Przebicie
5.6.1 Zasady ogólne
5.6.2 Elementy niezbrojone na przebicie
5.6.3 Elementy zbrojone na przebicie
5.7 Skręcanie
5.7.1 Zasady ogólne
5.7.2 Czyste skręcanie
5.7.3 Skręcanie połączone ze ścinaniem
5.8 Docisk
5.8.1 Zasady ogólne
5.8.2 Elementy niezbrojone na docisk
5.8.3 Elem
6.1 Zasady ogólne
6.2 Minimalne pole przekroju zbrojenia
6.3 Szerokość rys prostopadłych do osi elementu
6.4 Szerokość rys ukośnych
6.5 Ugięcie elementów zginanych
7 Konstruk
7.1 Konstrukcje sprężone
7.1.1 Zasady ogólne
7.1.2 Naprężenia w cięgnach sprężających
7.1.3 Siła sprężająca
7.1.4 Naprężenia normalne
7.1.5 Straty doraźne
7.1.5.1 Straty spowodowane tarciem kabli o ścianki kanału
7.1.5.2 Straty spowodowane poślizgiem cięgien w zakotwieniu
7.1.5.3 Straty spowodowane częściową relaksacją stali
7.1.5.4 Straty spowodowane odkształceniem sprężystym betonu
7.1.6 Straty opóźnione
7.1.7 Sytuacja początkowa konstrukcji sprężonych
7.1.7.1 Ograniczenie naprężeń w betonie
7.1.7.2 Nośność
7.1.7.3 Zarysowanie i ugięcie
7.1.7.4 Strefa zakotwienia w strunobetonie
7.1.7.5 Strefa zakotwienia w kablobetonie
7.1.8 Nośność konstrukcji sprężonych w sytuacji trwałej
7.1.8.1 Elementy zginane
7.1.8.2 Elementy ściskane
7.1.8.3 Elementy rozciągane
7.1.8.4 Ścinanie
7.1.9 Stan graniczny użytkowalności
7.1.9.1 Pojawienie się rys prostopadłych do osi elementu
7.1.9.2 Pojawienie się rys ukośnych
7.1.9.3 Rozwarcie rys prostopadłych do osi elementu
7.1.9.4 Ugięcie elementów sprężonych
7.1.10 Konstrukcje sprężone bez przyczepności
7.2. Konstrukcje poddane działaniu obciążeń wielokrotnie zmiennych
7.2.1 Zasady ogólne
7.2.2 Zmęczenie elementów konstrukcji
Strona 3

7.3 Konstrukcje zespolone
7.3.1 Zasady ogólne
7.3.2 Zabezpieczenie konstrukcji przed rozwarstwieniem w płaszczyźnie zespolenia
7.3.3 Nośność konstrukcji zespolonych
7.3.4 Zarysowanie i ugięcia konstrukcji zespolonych
8 W
agania i zalecenia dotyczące zbroj
8.1 Konstrukcje żelbetowe
8.1.1 Zasady ogólne
8.1.1.1 Rozmieszczenie prętów zbrojenia w przekroju
8.1.1.2 Otulenie prętów zbrojenia
8.1.1.3 Dopuszczalne krzywizny zagięć
8.1.2 Przyczepność zbrojenia do betonu
8.1.2.1 Warunki przyczepności
8.1.2.2 Graniczne naprężenia przyczepności
8.1.2.3 Podstawowa długość zakotwienia
8.1.3 Zakotwienie
8.1.3.1 Zasady ogólne
8.1.3.2 Zakotwienie prętów i siatek
8.1.3.3 Zbrojenie poprzeczne w strefie zakotwienia
8.1.3.4 Wymagana długość zakotwienia prętów
8.1.3.5 Wymagana długość zakotwienia siatek spajanych z prętów żebrowanych
8.1.3.6 Wymagana długość zakotwienia siatek spajanych z prętów gładkich
8.1.3.7 Zakotwienie strzemion i zbrojenia na ścinanie
8.1.4 Połączenia
8.1.4.1 Zasady ogólne
8.1.4.2 Połączenia spajane
8.1.4.3 Połączenia na zakład
8.1.4.4 Połączenia na zakład siatek spajanych
8.1.5 Dodatkowe wymagania dotyczące prętów żebrowanych o średnicy większej niż 32 mm
8.1.5.1 Zasady ogólne
8.1.5.2 Przyczepność
8.1.5.3 Zakotwienia i połączenia
8.1.6 Wiązki prętów żebrowanych
8.1.6.1 Zasady ogólne
8.1.6.2 Zakotwienia i połączenia
8.1.7 Zbrojenie przypowierzchniowe
8.1.8 Zbrojenie elementów o kształcie załamanym lub zakrzywionym
8.1.9 Zbrojenie poprzeczne strefy docisku
8.2 Konstrukcje sprężone
8.2.1 Średnica cięgna
8.2.2 Rozmieszczenie cięgien w przekroju
8.2.3 Kotwienie cięgien
8.2.4 Otulenie cięgien sprężających
8.2.5 Zabezpieczenie cięgien przed korozją w konstrukcjach kablobetonowych
8.2.6 Zbrojenie poprzeczne strefy zakotwienia
8.2.7 Zbrojenie konstrukcyjne elementów sprężonych
9 Proj
9.1 Płyty
9.1.1 Konstrukcja płyt
9.1.1.1 Minimalne grubości płyt
9.1.1.2 Głębokość oparcia płyt na podporze
9.1.1.3 Zbrojenie płyt
9.1.1.4 Zbrojenie na przebicie
9.1.2 Obliczenia statyczne płyt
9.1.2.1 Zasady ogólne
9.1.2.2 Rozpiętość obliczeniowa
9.1.2.3 Obliczanie płyt ciągłych jednokierunkowo zbrojonych
9.1.2.4 Obliczanie prostokątnych płyt dwukierunkowo zbrojonych
9.2 Stropy gęstożebrowe
9.3 Belki
9.3.1 Konstrukcja belek
9.3.1.1 Wymiary belek
9.3.1.2 Głębokość oparcia belek na podporze
Strona 4

9.3.1.3 Połączenie belki z podciągiem
9.3.1.4 Podciągi z wbetonowanymi końcami belek prefabrykowanych
9.3.1.5 Zbrojenie belek
9.3.2 Obliczenia statyczne belek
9.3.2.1 Zasady ogólne
9.3.2.2 Obliczanie belek ciągłych
9.4 Wsporniki krótkie
9.4.1 Konstrukcja wsporników
9.4.2 Zbrojenie wsporników
9.5 Słupy
9.5.1 Konstrukcja słupów
9.5.1.1 Wymiary przekroju poprzecznego słupów
9.5.1.2 Zbrojenie słupów nieuzwojonych
9.5.1.3 Zbrojenie słupów uzwojonych
9.6 Ograniczenie zakresu szkód wywołanych przez oddziaływania wyjątkowe
9.7 Wpływ temperatury i skurczu betonu na odkształcenia konstrukcji. Przerwy dylatacyjne
9.7.1 Odkształcenia konstrukcji od wpływu temperatury i skurczu betonu
9.7.2 Odległości między przerwami dylatacyjnymi
9.7.3 Konstrukcja przerw dylatacyjnych
Zał
Zmiany, Poprawki, Uwagi
UWAGI
Norma obowiązująca w całości od 1 września 2001 r., z wyłączeniem do 31 sierpnia 2002 r. jej zastosowania dla
prefabrykatów betonowych wykonywanych w zakładach prefabrykacji; dla tych prefabrykatów w okresie od 1 września 2001
r. do 31 sierpnia 2002 r. dopuszcza się jej alternatywne stosowanie z PN-84/B-03264
Strona 5
1 Wstęp
1.1 Zakres normy
Niniejszą normą objęto obliczanie i projektowanie konstrukcji betonowych, żelbetowych i sprężonych, wykonywanych z
betonu zwykłego i użytkowanych w zakresie temperatur od -30°C do + 200°C.
1.2 Normy powołane
PN-80/B-01800 Antykorozyjne zabezpieczenia w budownictwie - Konstrukcje betonowe i żelbetowe - Klasyfikacja i określenie
ś
rodowisk
PN-82/B-01801 Antykorozyjne zabezpieczenia w budownictwie - Konstrukcje betonowe i żelbetowe - Podstawowe zasady
projektowania
PN-82/B-02000
Obciążenia budowli - Zasady ustalania wartości
PN-82/B-02001
Obciążenia budowli - Obciążenia stałe
PN-82/B-02003
Obciążenia budowli - Obciążenia zmienne technologiczne - Podstawowe obciążenia technologiczne i
montażowe
PN-82/B-02004
Obciążenia budowli - Obciążenia zmienne technologiczne - Obciążenia pojazdami
PN-86/B-02005
Obciążenia budowli - Obciążenia suwnicami pomostowymi, wciągarkami i wciągnikami
PN-80/B-02010
Obciążenia budowli - Obciążenia w obliczeniach statycznych - Obciążenie śniegiem
PN-77/B-02011
Obciążenia w obliczeniach statycznych - Obciążenie wiatrem
PN-87/B-02013
Obciążenia budowli - Obciążenia zmienne środowiskowe - Obciążenie oblodzeniem
PN-86/B-02015
Obciążenia budowli - Obciążenia zmienne środowiskowe - Obciążenie temperaturą
PN-90/B-03000 Projekty budowlane - Obliczenia statyczne
PN-76/B-03001
Konstrukcje i podłoża budowli - Ogólne zasady obliczeń
PN-81/B-03020
Grunty budowlane - Posadowienie bezpośrednie budowli - Obliczenia statyczne i projektowanie
PN-90/B-03200
Konstrukcje stalowe - Obliczenia statyczne i projektowanie
PN-88/B-06250 Beton zwykły
PN-71/B-06280
Konstrukcje z wielkowymiarowych prefabrykatów żelbetowych - Wymagania w zakresie wykonywania i
badania przy odbiorze
PN-89/H-84023-06 Stal określonego zastosowania - Stal do zbrojenia betonu - Gatunki
PN-82/H-93215 Walcówka i pręty stalowe do zbrojenia betonu
1.3 Definicje
1.3.1 Rodzaje konstrukcji z betonu
1.3.1.1
konstrukcje betonowe
konstrukcje z betonu bez zbrojenia lub ze zbrojeniem mniejszym niż podane w 4.8.
1.3.1.2
konstrukcje żelbetowe
konstrukcje z betonu zbrojone wiotkimi prętami stalowymi w taki sposób, że sztywność i nośność konstrukcji uwarunkowana
jest współpracą betonu i stali
1.3.1.3
konstrukcje sprężone
konstrukcje z betonu zbrojone cięgnami, których wstępny naciąg wywołuje trwałe naprężenie w betonie
1.3.1.4.
konstrukcje strunobetonowe
konstrukcje sprężone (1.3.1.3), w których naciąg cięgien następuje przed zabetonowaniem, a siły naciągu są przekazywane
na beton przez przyczepność
1.3.1.5.
konstrukcje kablobetonowe
konstrukcje sprężone (1.3.1.3), w których naciąg cięgien następuje po osiągnięciu przez beton odpowiedniej wytrzymałości,
a siły naciągu są przekazywane na beton przez zakotwienia mechaniczne
1.3.1.6.
konstrukcje kablobetonowe z przyczepnością
konstrukcje, w których przyczepność betonu i stali zapewniona jest przez iniekcję, stanowiącą zarazem ochronę
antykorozyjną
1.3.1.7.
konstrukcje kablobetonowe bez przyczepności
konstrukcje, w których ochrona antykorozyjna cięgien zapewniona jest za pomocą smarów, wosków lub smół, nie
Część 2 Strona 1

zapewniających współpracy betonu i stali
1.3.1.8.
konstrukcje kablobetonowe o cięgnach zewnętrznych
konstrukcje, w których cięgna sprężające umieszczone są poza przekrojem betonu
1.3.1.9.
betonowe konstrukcje zespolone
konstrukcje powstałe w wyniku zapewnienia współpracy w przekroju poprzecznym jednego lub kilku wcześniej wykonanych
elementów żelbetowych lub sprężonych oraz betonu uzupełniającego, wykonanego w terminie późniejszym
1.3.2 Określenia ogólne
1.3.2.1
oddziaływanie bezpośrednie lub obciążenie
siły przyłożone bezpośrednio do konstrukcji, wywołujące naprężenia w elementach konstrukcji
1.3.2.2
oddziaływanie pośrednie
odkształcenie elementów konstrukcji wymuszone przez więzy łączące je z innymi elementami lub podłożem gruntowym (np.
nierównomierne osiadanie podpór, skurcz i pełzanie betonu, zmiany temperatury)
1.3.2.3
sytuacja obliczeniowa
sytuacja w jakiej znajduje się konstrukcja w okresie, w którym rozkłady i procesy dotyczące wszystkich wielkości związanych
z niezawodnością można uważać za niezmienne
1.3.2.4
sytuacja trwała
sytuacja obliczeniowa (1.3.2.3), występująca w warunkach zwykłego użytkowania konstrukcji
1.3.2.5
sytuacja przejściowa
sytuacja obliczeniowa (1.3.2.3), występująca w warunkach przejściowych, takich jak wznoszenie lub naprawa konstrukcji
1.3.2.6
sytuacja wyjątkowa
sytuacja obliczeniowa (1.3.2.3), występująca w warunkach takich, jak np. w trakcie pożaru, eksplozji lub uderzenia
1.3.3 Beton
1.3.3.1
klasa betonu
określenie jakości betonu odpowiadające wytrzymałości gwarantowanej, oznaczone literą B i liczbą wyrażającą wartość
wytrzymałości gwarantowanej w MPa, np. B20
1.3.3.2
wytrzymałość gwarantowana betonu
wytrzymałość betonu na ściskanie mierzona zgodnie z PN-88/B-06250 na kostkach sześciennych o krawędzi 150 mm,
gwarantowana przez producenta
1.3.3.3
wytrzymałość betonu na ściskanie
maksymalne naprężenie ściskające w jednoosiowym stanie naprężenia
1.3.3.4
wytrzymałość charakterystyczna betonu na ściskanie
5 % kwantyl rozkładu statystycznego wytrzymałości betonu na ściskanie, mierzonej na walcach o średnicy 150 mm i
wysokości 300 mm
1.3.3.5
wytrzymałość charakterystyczna betonu na rozciąganie
5% kwantyl rozkładu statystycznego wytrzymałości betonu na rozciąganie osiowe
1.3.3.6
wytrzymałość obliczeniowa betonu
wytrzymałość przyjmowana przy sprawdzaniu stanów granicznych nośności konstrukcji, otrzymywana w wyniku podzielenia
wytrzymałości charakterystycznej przez częściowy współczynnik bezpieczeństwa dla betonu
1.3.3.7
częściowy współczynnik bezpieczeństwa dla betonu
współczynnik uwzględniający możliwość występowania wytrzymałości betonu niższych od wartości charakterystycznych,
odchyłek wymiarów przekroju elementu (nie większych jednak od dopuszczalnych) i różnic między wytrzymałością betonu
badaną na próbkach i wytrzymałością betonu w konstrukcji; w konstrukcjach niezbrojonych wartość współczynnika
bezpieczeństwa dla betonu uwzględnia możliwość zniszczenia konstrukcji bez ostrzeżenia.
1.3.4 Stal
Część 2 Strona 2

1.3.4.1
pręty zbrojenia
pręty proste lub odcinki walcówki dostarczanej w kręgach oraz druty, przycięte i ukształtowane odpowiednio do wymagań
projektu
1.3.4.2
siatki zbrojeniowe
elementy zbrojenia złożone z prętów podłużnych i poprzecznych, połączonych za pomocą zgrzewania
1.3.4.3
spajanie
łączenie prętów ze sobą lub z innymi elementami stalowymi za pomocą spawania lub zgrzewania
1.3.4.4
cięgna sprężające
druty, sploty, pręty lub ich wiązki ze stali o wysokiej wytrzymałości, przeznaczone do wstępnego naciągu
1.3.4.5
klasa stali
określenie własności mechanicznych stali zbrojeniowych do żelbetu wyrażone literą A i cyfrą 0 lub cyfrą rzymską (w jednym
przypadku uzupełnioną literą N), np. A-III
1.3.4.6
charakterystyczna granica plastyczności stali zbrojeniowej
gwarantowana umowna lub rzeczywista granica plastyczności stali
1.3.4.7
obliczeniowa granica plastyczności stali zbrojeniowej
wartość uzyskana w wyniku podzielenia charakterystycznej granicy plastyczności stali zbrojeniowej (1.3.4.6) przez
częściowy współczynnik bezpieczeństwa dla stali
1.3.4.8
wytrzymałość charakterystyczna stali zbrojeniowej na rozciąganie
0,85 minimalnej wytrzymałości stali na zerwanie
1.3.4.9
charakterystyczna umowna granica plastyczności stali sprężającej
gwarantowana wartość naprężenia odpowiadającego odkształceniu trwałemu stali sprężającej 0,1%
1.3.4.10
wytrzymałość obliczeniowa stali sprężającej
wartość uzyskana w wyniku podzielenia wytrzymałości charakterystycznej stali sprężającej przez częściowy współczynnik
bezpieczeństwa dla stali sprężającej
1.3.4.11
częściowy współczynnik bezpieczeństwa dla stali
współczynnik uwzględniający możliwość występowania niższej granicy plastyczności stali zbrojeniowej niż charakterystyczna
granica plastyczności względnie niższej wytrzymałości stali sprężającej niż wytrzymałość charakterystyczna, a także odchyłki
wymiarów przekroju pręta i elementu konstrukcji (nie większe jednak od dopuszczalnych).
1.4 Podstawowe symbole
1.4.1 Duże litery łacińskie
4
A
-
pole powierzchni
A
c
-
pole przekroju betonu
A
cc,eff
-
pole efektywne strefy ściskanej przekroju betonu o wysokości X
eff
= 0,8 x
A
co
-
pole powierzchni docisku
A
core
-
pole przekroju betonowego rdzenia uzwojonego
A
cs
-
pole powierzchni przekroju sprowadzonego
A
ct
-
pole strefy rozciąganej przekroju betonu
A
ct,eff
-
pole efektywne rozciąganej strefy przekroju
A
c1
-
pole powierzchni rozdziału
A
d
-
wartość obliczeniowa oddziaływania wyjątkowego
A
j
-
pole powierzchni styku w elementach zespolonych
zęść 2 Strona 3

A
k
-
pole powierzchni ograniczone linią środkową przekroju elementu cienkościennego (łącznie z
polem powierzchni wewnętrznej części pustej)
A
p
-
pole przekroju zbrojenia sprężającego
A
p1
-
pole przekroju zbrojenia sprężającego w strefie rozciąganej lub mniej ściskanej
A
p2
-
pole przekroju zbrojenia sprężającego w strefie ściskanej przekroju
A
s
-
pole przekroju zbrojenia
A
sf
-
pole przekroju zbrojenia poprzecznego w półce przekroju teowego
A
sl
-
pole przekroju dodatkowego zbrojenia podłużnego
A
s1
-
pole przekroju zbrojenia rozciąganego, a także bardziej rozciąganego lub mniej ściskanego
(w przypadku zbrojenia złożonego z dwóch grup prętów o polach A
s1
i A
s2
)
A
s2
-
pole przekroju zbrojenia ściskanego, a także bardziej ściskanego lub mniej rozciąganego (w
przypadku zbrojenia złożonego z dwóch grup prętów o polach A
s1
i A
s2
)
A
sw
-
pole przekroju zbrojenia na ścinanie
B
-
sztywność zginanego elementu żelbetowego
E
c
-
moduł styczny sprężystości betonu
E
c,eff
-
efektywny sieczny moduł sprężystości betonu (z uwzględnieniem czasu trwania obciążenia)
E
cd
-
wartość obliczeniowa siecznego modułu sprężystości E
c,nom
E
cm
-
wartość średnia E
c,nom
E
c,nom
-
sieczny moduł sprężystości betonu
E
s
-
moduł sprężystości stali zwykłej
E
p
-
moduł sprężystości stali sprężającej
F
-
siła, oddziaływanie
F
c
-
wypadkowa bryły naprężeń ściskanej strefy przekroju betonu
F
pk
-
siła zrywająca cięgno ze stali sprężającej
F
s
-
siła w prętach zbrojenia
H
-
siła pozioma
I
-
moment bezwładności przekroju
I
cs
-
moment bezwładności przekroju sprowadzonego
M
-
moment zginający
M
cr
-
moment rysujący
M
Rd
-
nośność obliczeniowa przekroju na zginanie
M
Sd
-
moment zginający wywołany obciążeniem obliczeniowym
N
-
osiowa siła podłużna
N
cr
-
osiowa siła podłużna wywołująca rysę
N
crit
-
umowna siła krytyczna
N
p
-
osiowa siła podłużna od sprężenia
N
Rd
-
nośność obliczeniowa z uwagi na siłę podłużną
N
Sd
-
siła podłużna wywołana obciążeniem obliczeniowym
N
Sd,It
-
siła podłużna wywołana działaniem obliczeniowego obciążenia długotrwałego
P
-
siła sprężająca
P
d
-
wartość obliczeniowa siły sprężającej
P
k,inf
-
dolna wartość siły sprężającej w stanie granicznym użytkowalności
Część 2 Strona 4

P
k,sup
-
górna wartość siły sprężającej w stanie granicznym użytkowalności
P
m,o
-
ś
rednia wartość siły sprężającej po uwzględnieniu strat doraźnych
P
m,t
-
ś
rednia wartość siły sprężającej po czasie t
P
m,
∞
-
ś
rednia wartość siły sprężąjącej po uwzględnieniu strat całkowitych
P
o
-
początkowa wartość siły sprężającej (suma naciągu poszczególnych cięgien)
∆P
c
-
strata siły sprężającej spowodowana odkształceniem sprężystym betonu
∆P
sl
-
strata siły sprężającej spowodowana poślizgiem cięgna w zakotwieniu
∆P
t
(t)
-
strata siły sprężającej po czasie t, spowodowana pełzaniem i skurczem betonu oraz
relaksacją stali sprężającej
∆P
µ
(x)
-
strata siły sprężającej spowodowana tarciem kabli o ścianki kanału
R
-
nośność elementu
R
d
-
nośność obliczeniowa elementu
S
-
moment statyczny
S
cc,eff
-
moment statyczny efektywnego pola ściskanej strefy przekroju betonu o wysokości
X
eff
= 0,8 x, obliczony względem środka ciężkości zbrojenia rozciąganego
S
co
-
moment statyczny części przekroju położonej powyżej rozpatrywanego włókna, obliczany
względem środka ciężkości przekroju betonu
T
d
-
obliczeniowa siła rozciągająca w zbrojeniu podłużnym w przekroju sprawdzanym na ścinanie
T
Rd1
-
nośność obliczeniowa na skręcanie z uwagi na maksymalny moment skręcający, który może
być przeniesiony przez ściskane krzyżulce betonowe
T
Rd2
-
nośność obliczeniowa na skręcanie z uwagi na maksymalny moment skręcający, który może
być przeniesiony przez zbrojenie
T
Sd
-
moment skręcający wywołany obciążeniem obliczeniowym
V
-
siła poprzeczna
V
Rd
-
nośność obliczeniowa na ścinanie
V
Rd1
-
graniczna siła poprzeczna ze względu na ukośne rozciąganie, powstające przy ścinaniu w
elemencie nie mającym poprzecznego zbrojenia na ścinanie
V
Rd2
-
graniczna siła poprzeczna ze względu na ukośne ściskanie, powstające przy ścinaniu w
elementach zginanych
V
Rd3
-
graniczna siła poprzeczna ze względu na rozciąganie poprzecznego zbrojenia na ścinanie
V
Sd
-
siła poprzeczna wywołana obciążeniem obliczeniowym
W
c
-
wskaźnik wytrzymałości przekroju betonowego na zginanie, obliczony jak dla materiału
liniowo sprężystego
1.4.2 Małe litery łacińskie
a
-
liniowa wielkość geometryczna, także - ugięcie, obliczeniowa grubość spoiny
a
lim
-
ugięcie graniczne
a
p
-
poślizg cięgien w zakotwieniu
a
s
-
pole przekroju pręta
a
1
-
odległość środka ciężkości zbrojenia A
s1
od krawędzi rozciąganej lub mniej ściskanej
a
2
-
odległość środka ciężkości zbrojenia A
s2
od krawędzi ściskanej lub mniej rozciąganej
b
-
szerokość, także - rozstaw belek
Część 2 Strona 5

b
eff
-
szerokość efektywna półki przekroju teowego
b
j
-
szerokość płaszczyzny zespolenia prefabrykatu z betonem uzupełniającym
b
w
-
szerokość środnika przekroju teowego, także najmniejsza szerokość strefy ścinania
c
-
grubość otuliny prętów zbrojenia
d
-
wysokość użyteczna przekroju
d
c
-
ś
rednica słupa o przekroju kołowym
d
core
-
ś
rednica uzwojenia rdzenia betonowego
d
g
-
maksymalny wymiar ziarna kruszywa
e
-
mimośród
e
a
-
mimośród niezamierzony (przypadkowy)
e
e
-
mimośród konstrukcyjny, otrzymany z obliczeń statycznych
e
o
-
mimośród początkowy (bez uwzględnienia wpływu smukłości) siły podłużnej względem środka
ciężkości przekroju betonowego
e
s1
-
odległość siły N
Rd
od środka ciężkości zbrojenia A
s1
e*
s1
-
odległość siły N
sd
od środka ciężkości zbrojenia A
s1
e
s2
-
odległość siły N
Rd
od środka ciężkości zbrojenia A
s2
e*
s2
-
odległość siły N
sd
od środka ciężkości zbrojenia A
s2
e
tot
-
mimośród całkowity, uwzględniający wpływ smukłości na zwiększenie mimośrodu początkowego
f
bd
-
graniczne obliczeniowe naprężenie przyczepności
f
c
-
wytrzymałość betonu na ściskanie w jednoosiowym stanie naprężenia
f
G
c,cube
-
wytrzymałość gwarantowana betonu
f
cd
-
wytrzymałość obliczeniowa betonu na ściskanie w konstrukcjach żelbetowych i sprężonych
f*
cd
-
wytrzymałość obliczeniowa betonu na ściskanie w konstrukcjach betonowych
f
ck
-
wytrzymałość charakterystyczna betonu na ściskanie
f
cm
-
wytrzymałość średnia betonu w jednoosiowym stanie naprężenia
f
ctd
-
wytrzymałość obliczeniowa betonu na rozciąganie w konstrukcjach żelbetowych i sprężonych
f
ct,eff
-
wytrzymałość średnia betonu na rozciąganie w chwili spodziewanego zarysowania
f
ctk
-
wytrzymałość charakterystyczna betonu na rozciąganie
f
ctm
-
wytrzymałość średnia betonu na rozciąganie
f
cud
-
wytrzymałość obliczeniowa betonu na docisk
f
pd
-
wytrzymałość obliczeniowa stali sprężającej
f
pk
-
wytrzymałość charakterystyczna stali sprężającej
f
p0,1k
-
charakterystyczna umowna granica plastyczności stali sprężającej
f
td
-
wytrzymałość obliczeniowa stali zbrojeniowej na rozciąganie
f
tk
-
wytrzymałość charakterystyczna stali zbrojeniowej na rozciąganie
f
yd
-
obliczeniowa granica plastyczności stali zbrojeniowej
f
y
*
d
-
obliczeniowa granica plastyczności stali uzwojenia
f
yk
-
charakterystyczna granica plastyczności stali zbrojeniowej
f
ywd
-
obliczeniowa granica plastyczności stali zbrojenia poprzecznego przy sprawdzaniu nośności na
ś
cinanie
g
-
obciążenie stałe równomiernie rozłożone
h
-
wysokość przekroju
Część 2 Strona 6

h
f
-
grubość półki w przekroju teowym
h
j
-
wysokość styku betonu uzupełniającego z płytami prefabrykowanymi w elementach zespolonych
i
-
promień bezwładności przekroju betonowego
k
-
współczynnik, a także - niezamierzony kąt falowania trasy cięgna na jednostkę długości
k
lt
-
współczynnik wyrażający wpływ oddziaływania długotrwałego
l
b
-
podstawowa długość zakotwienia
l
b, net
-
wymagana długość zakotwienia
l
bp
-
długość zakotwienia cięgien sprężających, na której następuje pełne przekazanie siły sprężającej
na beton
l
bpd
-
obliczeniowa długość zakotwienia cięgien sprężających
l
p,eff
-
efektywna długość rozkładu, poza którą naprężenia w przekroju poprzecznym zmieniają się liniowo
l
col
-
odległość między punktami podparcia słupa
l
eff
-
rozpętość lub długość efektywna, przyjmowana do obliczeń
l
n
-
rozpiętość w świetle podpór
l
o
-
długość obliczeniowa słupa
m
-
moment zginający na jednostkę długości
n
-
liczba
n
1
-
liczba wszystkich drutów lub splotów w cięgnie
n
2
-
liczba drutów lub splotów dociskanych składową siły naciągu na zakrzywieniu
n
w
-
liczba ramion strzemion
q
-
obciążenie zmienne równomiernie rozłożone
r
-
promień krzywizny
s
-
rozstaw, odstęp
s
f
-
rozstaw prętów zbrojenia poprzecznego w półce przekroju teowego
s
l
-
odstęp między prętami zbrojenia mierzony w świetle
s
n
-
rozstaw siatek zbrojenia poprzecznego w strefie docisku, skok uzwojenia
s
rm
-
ś
redni, końcowy rozstaw rys
t
-
szerokość podpory, a także - czas działania obciążenia
u
-
obwód
u
p
-
ś
rednia arytmetyczna obwodów powierzchni rozkładu sił przy przebiciu
v
-
siła ścinająca na jednostkę długości
v
Sd
-
obliczeniowa siła ścinająca na jednostkę długości
w
-
szerokość rysy
w
k
-
obliczeniowa szerokość rysy
w
lim
-
graniczna szerokość rysy
x
-
wysokość ściskanej strefy przekroju, a także - odległość rozpatrywanego przekroju od przekroju
przyłożenia siłownika naciągowego
x
eff
-
wysokość efektywna ściskanej strefy przekroju
x
eff,lim
-
wartość graniczna x
eff
y
-
odległość rozpatrywanego włókna od środka ciężkości przekroju betonowego
z
-
ramię sił wewnętrznych w przekroju
z
cp
-
odległość siły N
p
od środka ciężkości przekroju sprowadzonego
Część 2 Strona 7

1.4.3 Litery greckie
α
-
kąt, współczynnik redukujący wytrzymałość obliczeniową betonu na ściskanie
α
e
-
stosunek modułu sprężystości stali E
s
do modułu sprężystości betonu E
cm
α
e,t
-
stosunek modułu sprężystości stali E
s
do efektywnego modułu sprężystości betonu E
c,eff
α
k
-
współczynnik zależny od układu obciążeń i warunków podparcia elementu
α
t
-
współczynnik liniowej rozszerzalności termicznej
β
-
współczynnik
β
p
-
współczynnik długości zakotwienia drutów i splotów
γ
-
częściowy współczynnik bezpieczeństwa
γ
c
-
częściowy współczynnik bezpieczeństwa dla betonu
γ
n
-
współczynnik konsekwencji zniszczenia (ustalany indywidualnie)
γ
s
-
częściowy współczynnik bezpieczeństwa dla stali
γ
f
-
częściowy współczynnik bezpieczeństwa dla oddziaływania
γ
p
-
częściowy współczynnik bezpieczeństwa dla siły sprężającej
ε
c
-
odkształcenie betonu
ε
c1
-
odkształcenie betonu odpowiadające wytrzymałości na ściskanie f
c
ε
cs
(t,t
s
)
-
odkształcenie skurczowe betonu, określane w przedziale czasu od t
s
do t
ε
cs
,
∞
-
końcowe odkształcenie skurczowe betonu
ε
cu
-
graniczne odkształcenie betonu
ε
s
-
odkształcenie stali
ε
sm
-
odkształcenie średnie stali
ε
uk
-
odkształcenie charakterystyczne stali odpowiadające maksymalnej sile
ξ
-
stosunek z/d, także - współczynnik
η
-
współczynnik
θ
-
kąt, a także - suma kątów zakrzywienia trasy kabla
κ
p
-
współczynnik wykorzystania zbrojenia sprężającego w ściskanych elementach sprężonych
κ
s
-
współczynnik wykorzystania zbrojenia w ściskanych elementach żelbetowych
µ
-
współczynnik tarcia
ν
-
współczynnik
ν
c
-
współczynnik odkształcenia poprzecznego betonu
ν
cu
-
współczynnik korekcyjny do wytrzymałości obliczeniowej betonu w przypadku działania
obciążeń miejscowych
ρ
-
stopień zbrojenia
ρ
i
-
stopień zbrojenia poprzecznego w złączu, równy stosunkowi A
s
/A
j
ρ
l
-
stopień zbrojenia podłużnego
ρ
p
-
stopień zbrojenia sprężającego
ρ
r
-
stopień zbrojenia odniesiony do efektywnego pola betonu rozciąganego
ρ
w
-
stopień zbrojenia na ścinanie
σ
-
naprężenie normalne
Część 2 Strona 8

σ
c
-
naprężenie normalne w betonie
σ
cg
-
naprężenie w betonie na poziomie środka ciężkości cięgien
σ
cN
-
naprężenie w betonie wywołane zewnętrzną siłą podłużną
σ
cp
-
naprężenie w betonie wywołane siłą sprężającą
σ
cpo
-
początkowe naprężenie w betonie na poziomie środka ciężkości cięgien, wywołane sprężeniem
σ
cR
-
naprężenie graniczne w betonie przy działaniu obciążeń wielokrotnie zmiennych
σ
ctm
-
ś
rednie naprężenie rozciągające w betonie
σ
N
-
naprężenie wywołane przez siłę zewnętrzną prostopadłą do powierzchni styku elementów
zespolonych
σ
o,max
-
maksymalne naprężenie w cięgnach sprężających przy naciągu
σ
p
-
naprężenie w stali sprężającej
σ
pmo
-
naprężenie w cięgnach bezpośrednio po sprężeniu (po zakotwieniu) i po uwzględnieniu strat
doraźnych
σ
pmt
-
naprężenie w cięgnach sprężających po uwzględnieniu strat całkowitych
σ
p2
-
naprężenie w cięgnach sprężających, usytuowanych w strefie ściskanej, określane w stanie
granicznym nośności
∆σ
p,c+s+r
-
strata naprężeń w cięgnach sprężających, spowodowana pełzaniem i skurczem betonu oraz
relaksacją stali
∆σ
pr
-
strata naprężeń w cięgnach sprężających, spowodowana relaksacją stali
σ
s
-
naprężenie w stali zwykłej
∆σ
sR
-
dopuszczalny zakres zmian naprężeń w stali przy działaniu obciążeń wielokrotnie zmiennych
τ
-
naprężenie styczne
τ
Rd
-
wytrzymałość obliczeniowa betonu na ścinanie
τ
Rdj
-
nośność obliczeniowa złącza na ścinanie podłużne, określona na jednostkę powierzchni styku
τ
Sdj
-
podłużne naprężenie styczne w płaszczyźnie styku elementów zespolonych, wywołane
obciążeniem obliczeniowym
ϕ
-
współczynnik wyrażający wpływ mimośrodu i smukłości na nośność betonowych elementów
ś
ciskanych
φ
-
ś
rednica pręta zbrojenia
φ
d
-
ś
rednica kanału w elementach kablobetonowych
φ
r
-
ś
rednica trzpieni rolkowych, stosowanych do wykonywania haków i pętli kotwiących
φ(t,t
o
)
-
współczynnik pełzania betonu, określany w przedziale czasu od t
o
do t
φ
∞,t
o
-
końcowy współczynnik pełzania betonu
Część 2 Strona 9
2 Beton
2.1 Klasy betonu i przypisane im wytrzymałości
2.1.1 Stosowane klasy betonu
Do wykonywania konstrukcji stosować należy beton wg PN-88/B-06250 następujących klas: B15; B20; B25; B30; B37; B45;
B50; B55; B60; B65 i B70.
Najniższe klasy betonu dla poszczególnych rodzajów konstrukcji podano w tablicy 1.
Tablica 1 - Najniższe klasy betonu dla poszczególnych rodzajów konstrukcji
Rodzaj konstrukcji
Najniższa klasa betonu
Konstrukcje betonowe
B15
Konstrukcje żelbetowe
- zbrojone stalą klas A-0, A-I, A-II i A-III
B15
- zbrojone stalą klasy A-IIIN
B20
Konstrukcje sprężone:
- kablobetonowe
B30
- strunobetonowe
B37
Konstrukcje żelbetowe poddane
obciążeniu wielokrotnie zmiennemu
B30
2.1.2 Wytrzymałości i moduł sprężystości betonu
Wytrzymałości charakterystyczne betonu na ściskanie f
ck
i na rozciąganie f
ctk
oraz wytrzymałości średnie betonu na
rozciąganie f
ctm
, wytrzymałości obliczeniowe betonu na ściskanie f
cd
i rozciąganie f
ctd
, w obliczeniowych sytuacjach trwałych i
przejściowych, a także moduły sprężystości E
cm
przyporządkowane poszczególnym klasom betonu - podano w tablicy 2
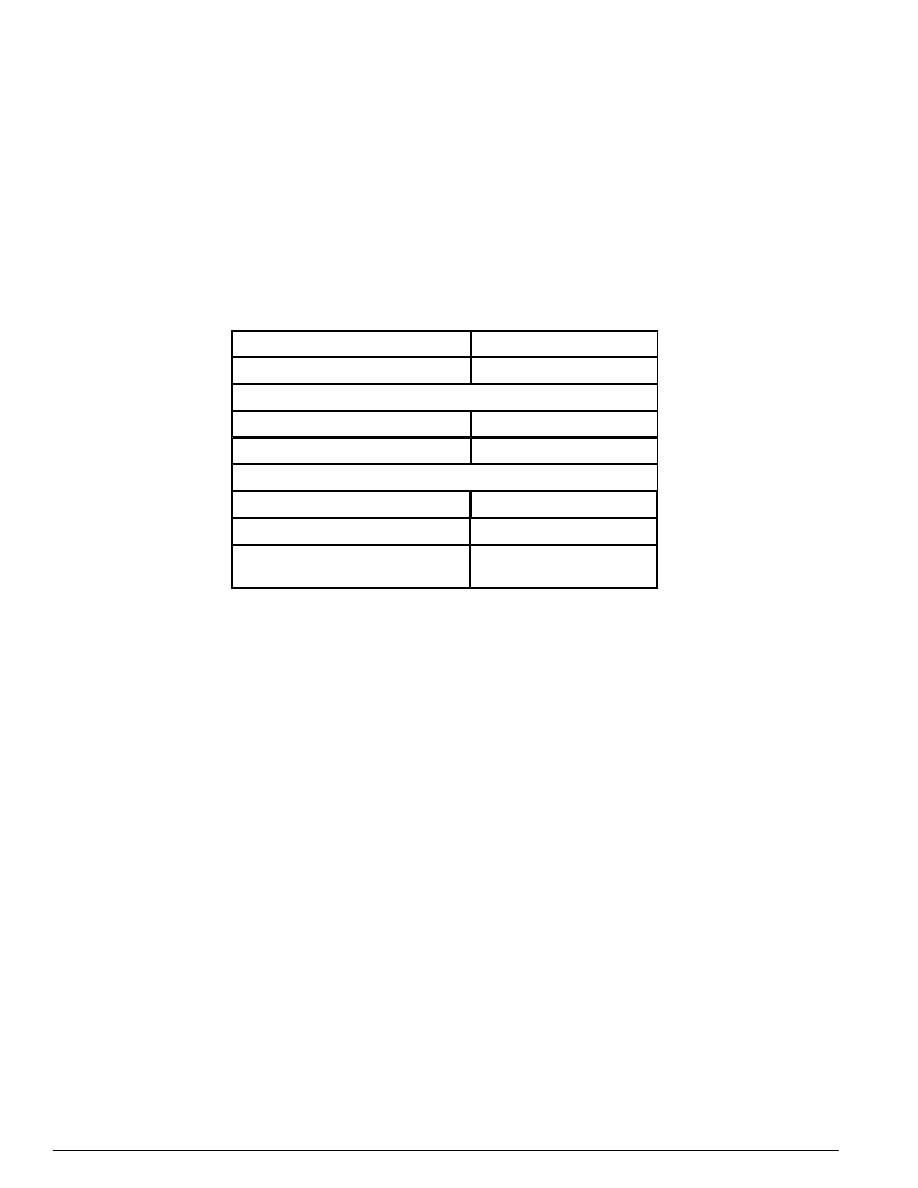
Tablica 2 - Wytrzymałości i moduł sprężystości betonu przyjmowane do obliczeń
Część 3 Strona 1
Klasa betonu
B15
B20
B25
B30
B37
B45
B50
B55
B60
B65
B70
Wytrzymałość gwarantowana
15
20
25
30
37
45
50
55
60
65
70
Wytrzymałość
charakterystyczna,
MPa
na
ś
ciskanie
f
ck
12
16
20
25
30
35
40
45
50
55
60
na
rozciąganie
f
ctk
1,1
1,3
1,5
1,8
2,0
2,2
2,5
2,7
2,9
3,1
*)
3,2
*)
Wytrzymałość średnia na
rozciąganie f
ctm
, MPa
1,6
1,9
2,2
2,6
2,9
3,2
3,5
3,8
4,1
4,4
*)
4,6
*)
Wytrzymałość
obliczeniowa dla
konstrukcji
ż
elbetowych i
sprężonych, MPa
na
ś
ciskanie
f
cd
8,0
10,6
13,3
16,7
20,0
23,3
26,7
30,0
33,3
36,7
40,0
na
rozciąganie
f
ctd
0,73
0,87
1,00
1,20
1,33
1,47
1,67
1,80
1,93
2,06
*)
2,13
*)
Wytrzymałość
obliczeniowa dla
konstrukcji
betonowych, MPa
na
ś
ciskanie
6,7
8,9
11,1
13,9
16,7
19,4
22,2
25,0
27,8
30,6
33,3
Moduł sprężystości
E
cm
.
10
-3
MPa
26
27,5
29
30,5
32
33,5
35
36
37
38
*)
39
*)
*) wartości orientacyjne, należy sprawdzić doświadczalnie
Wytrzymałości obliczeniowe betonu na ściskanie f
cd
i rozciąganie f
ctd
wyznacza się dzieląc wytrzymałości charakterystyczne
betonu - odpowiednio: na ściskanie f
ck
i rozciąganie f
ctk
- przez częściowy współczynnik bezpieczeństwa γ
c
równy
- w sytuacjach trwałych i przejściowych:
γ
c
= 1,5 w konstrukcjach żelbetowych i sprężonych
γ
c
= 1,8 w konstrukcjach betonowych
- w sytuacji wyjątkowej:
γ
c
= 1,3 w konstrukcjach żelbetowych i sprężonych
γ
c
= 1,6 w konstrukcjach betonowych.
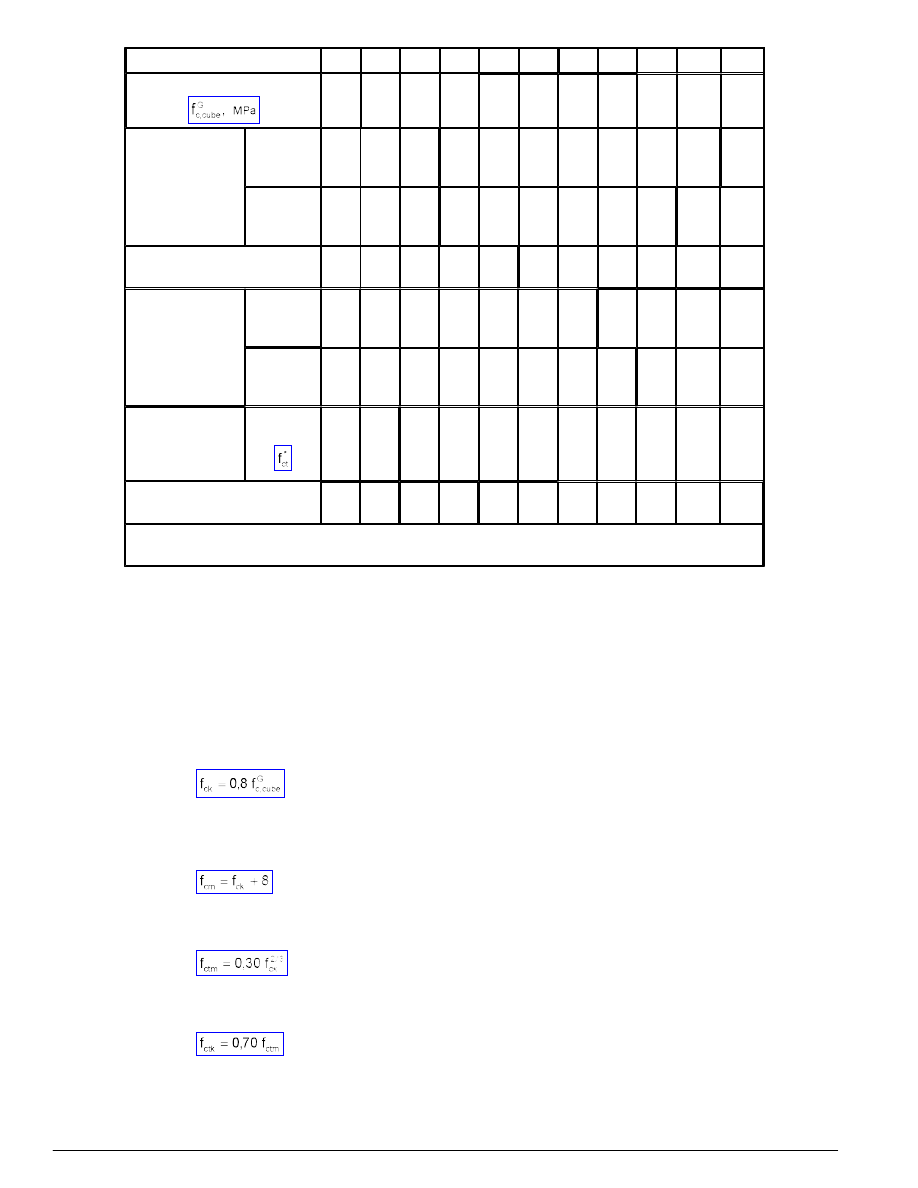
Wytrzymałość charakterystyczną betonu na ściskanie f
ck
obliczać można ze wzoru
(1)
a wytrzymałość średnią betonu na ściskanie f
cm
(MPa)
- przy braku ściślejszych danych - ze wzoru
(2)
Do obliczeń przyjmować można wytrzymałość średnią betonu na rozciąganie f
ctm
określoną ze wzoru
(3)
a wytrzymałość charakterystyczną betonu na rozciąganie f
ctk
- ze wzoru
(4)
Część 3 Strona 2
2.2 Odkształcalność betonu
2.2.1 Związek σ
σ
σ
σ-ε
εε
ε przy sprawdzaniu stanu granicznego nośności
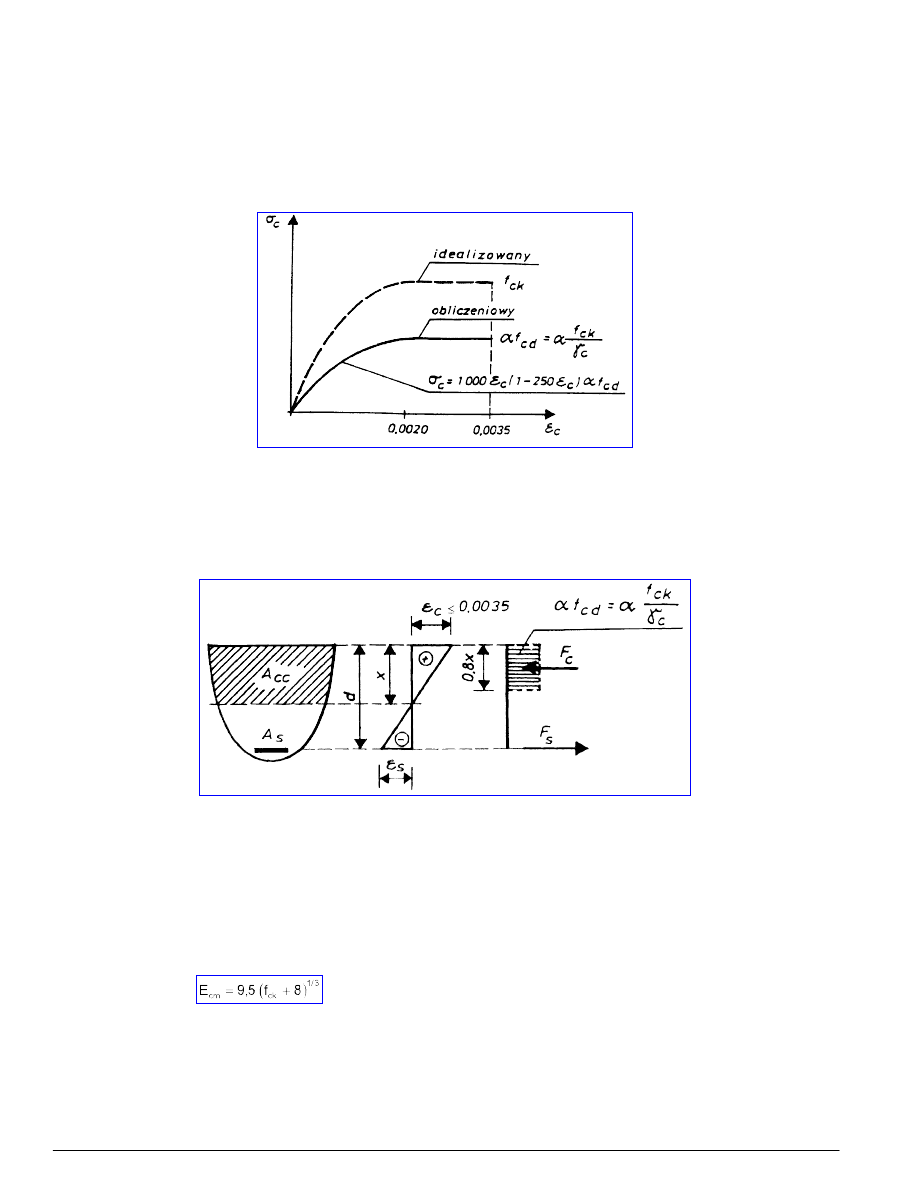
Przy wyznaczaniu rozkładu naprężeń w przekroju można posługiwać się paraboliczno-prostokątnym wykresem naprężeń, jak
na rysunku 1.
Naprężenia ściskające i skrócenia przyjmuje się ze znakiem plus, a naprężenia rozciągające i wydłużenia - ze znakiem
minus.
Rysunek 1 - Paraboliczno-prostokątny wykres σ-ε betonu
Przy wyznaczaniu nośności przekroju zginanego, mimośrodowo ściskanego i mimośrodowo rozciąganego posługiwać się
można wykresem prostokątnym jak na rysunku 2.
Rysunek 2 - Naprężenia i odkształcenia przy prostokątnym wykresie naprężeń
Przy sprawdzaniu stanu granicznego nośności, wytrzymałość obliczeniową f
cd
betonu na ściskanie mnoży się przez
współczynnik α = 0,85, uwzględniający wpływ obciążenia długotrwałego na wytrzymałość betonu i niekorzystny wpływ
sposobu przykładania obciążenia.
2.2.2 Moduł sprężystości betonu
Ś
redni sieczny moduł sprężystości betonu E
cm
obliczać można ze wzoru
(5)
gdzie: E
cm
- 10
3
MPa, f
ck
- MPa
Wartości E
cm
, przyporządkowane poszczególnym klasom betonu - podano w tablicy 2.
Część 3 Strona 3
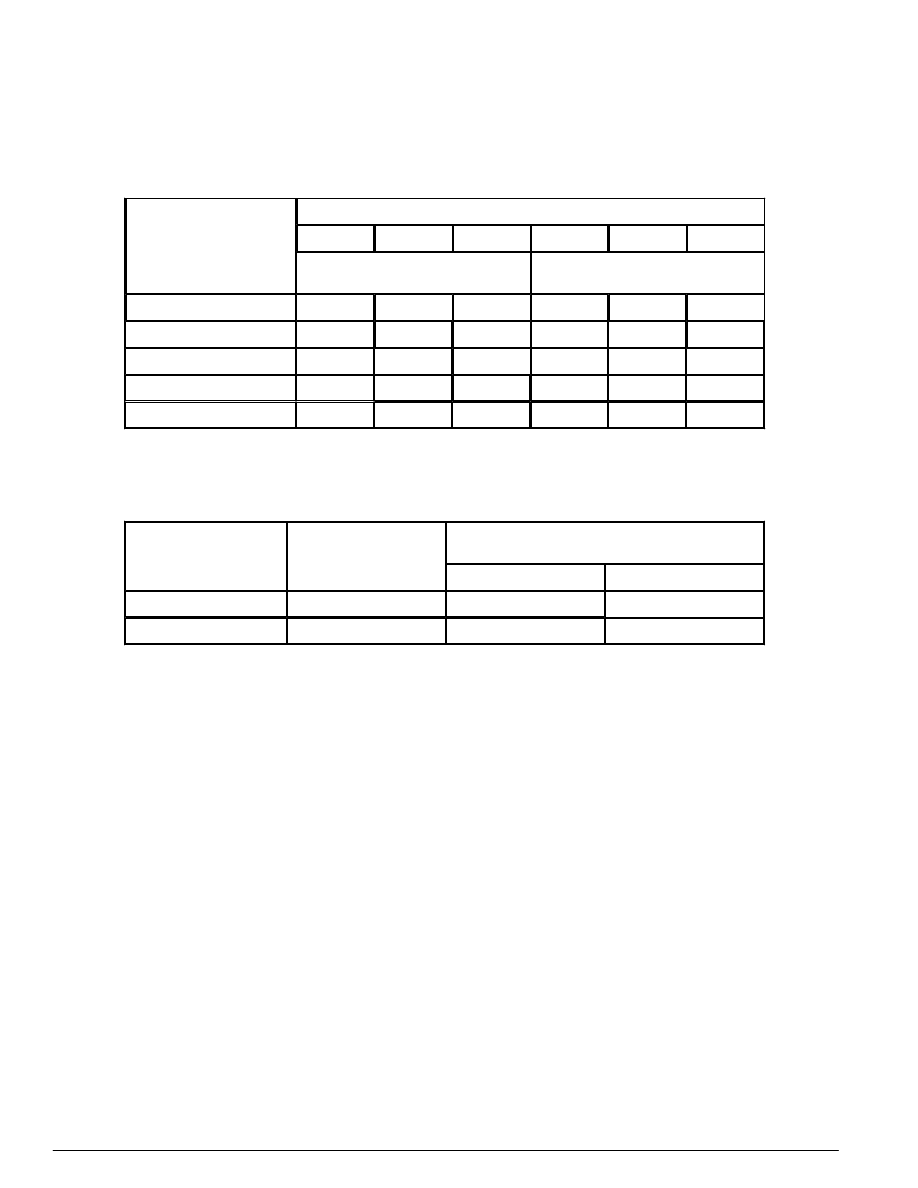
2.2.3 Pełzanie i skurcz betonu
Wartości końcowego współczynnika pełzania betonu φ
∞,t
o
oraz końcowego odkształcenia skurczowego ε
cs ∞
- podano w
tablicach 3 i 4.
Tablica 3 - Końcowy współczynnik pełzania φ
φ
φ
φ
∞,t
o
betonu
Wiek betonu w chwili
obciążenia
t
o
(dni)
Miarodajny wymiar 2A
c
/u (mm)
50
150
600
50
150
600
wilgotność względna (wewnątrz)
RH = 50 %
wilgotność względna (na zewnątrz)
RH = 80 %
1
5,4
4,4
3,6
3,5
3,0
2,6
7
3,9
3,2
2,5
2,5
2,1
1,9
28
3,2
2,5
2,0
1,9
1,7
1,5
90
2,6
2,1
1,6
1,6
1,4
1,2
365
1,6
2,0
1,2
1,2
1,0
1,0
Tablica 4 - Końcowe odkształcenie skurczowe εεεε
cs ∞
(‰)
Miejsce elementu
Wilgotność względna
RH (%)
Miarodajny wymiar 2A
c/
u
(mm)
≤ 150
600
wewnątrz
50
0,60
0,50
na zewnątrz
80
0,33
0,28
W tablicach 3 i 4 - A
c
oznacza pole przekroju elementu, u obwód tego pola. Dla wartości pośrednich dopuszcza się
interpolację liniową.
Wartości współczynnika pełzania betonu φ(t,t
o
) oraz odkształceń skurczowych ε
cs
(t,t
s
) w rozważanej chwili t - określać można
wg załączników A i B.
2.2.4 Współczynnik odkształcenia poprzecznego
Wartość współczynnika odkształcenia poprzecznego betonu ściskanego przyjmować można ν
c
= 0,2.
2.2.5 Współczynnik liniowej rozszerzalności termicznej
Wartość współczynnika liniowej rozszerzalności termicznej betonu przyjmować można α
t
= 1 ⋅ 10
-5
/°C.
Część 3 Strona 4
3 Stal
3.1 Stal zwykła
3.1.1 Stosowane klasy stali
Do zbrojenia konstrukcji żelbetowych stosować należy pręty ze stali klas A-0, A-l, A-ll, A-III i A-IIIN oraz druty o
właściwościach mechanicznych określonych wg PN-82/H-93215
1)
.
3.1.2 Charakterystyczna i obliczeniowa granica plastyczności stali
Obliczeniową granicę plastyczności f
yd
stali wyznacza się dzieląc charakterystyczną granicę plastyczności f
yk
stali przez
częściowy współczynnik bezpieczeństwa γ
s
równy
γ
s
= 1,15 - w sytuacji trwałej i przejściowej,
γ
s
= 1,00 - w sytuacji wyjątkowej
Charakterystyczne granice plastyczności f
yk
i obliczeniowe granice plastyczności f
yd
stali klas od A-0 do A-IIIN - podane są w
tablicy 5.
Dla drutów o średnicy od 3 mm do 5 mm, jeżeli ich właściwości mechaniczne mają znaczenie dla obliczeń konstrukcji,
wartości f
yk
i f
yd
przyjmować należy jak dla stali A-0 z tablicy 5.
Spajanie walcówki i prętów należy wykonać zgodnie z ustaloną technologią.
Spawalność stali jest dobra, jeśli dla:
- prętów z gatunków 20G2Y i 18G2 o średnicy do 20 mm,
- prętów z gatunków 35G2Y i 34GS o średnicy do 12 mm,
- prętów z gatunku 20G2VY-b o średnicy do 28 mm,
- walcówki z gatunku 34GS o średnicy do 12 mm,
- walcówki z gatunku 20G2VY-b o średnicy do 10 mm,
nie są przekroczone wartości równoważnika węgla C
E
podane w PN-89/H-84023-06.
Zgrzewalność stali o wyżej podanych średnicach jest ograniczona.
Przy złączach doczołowych, w celu uzyskania własności wymaganych w budownictwie, konieczne jest stosowanie
specjalnych technologii.
Spajalność stali A-0 i A-I jest dobra.
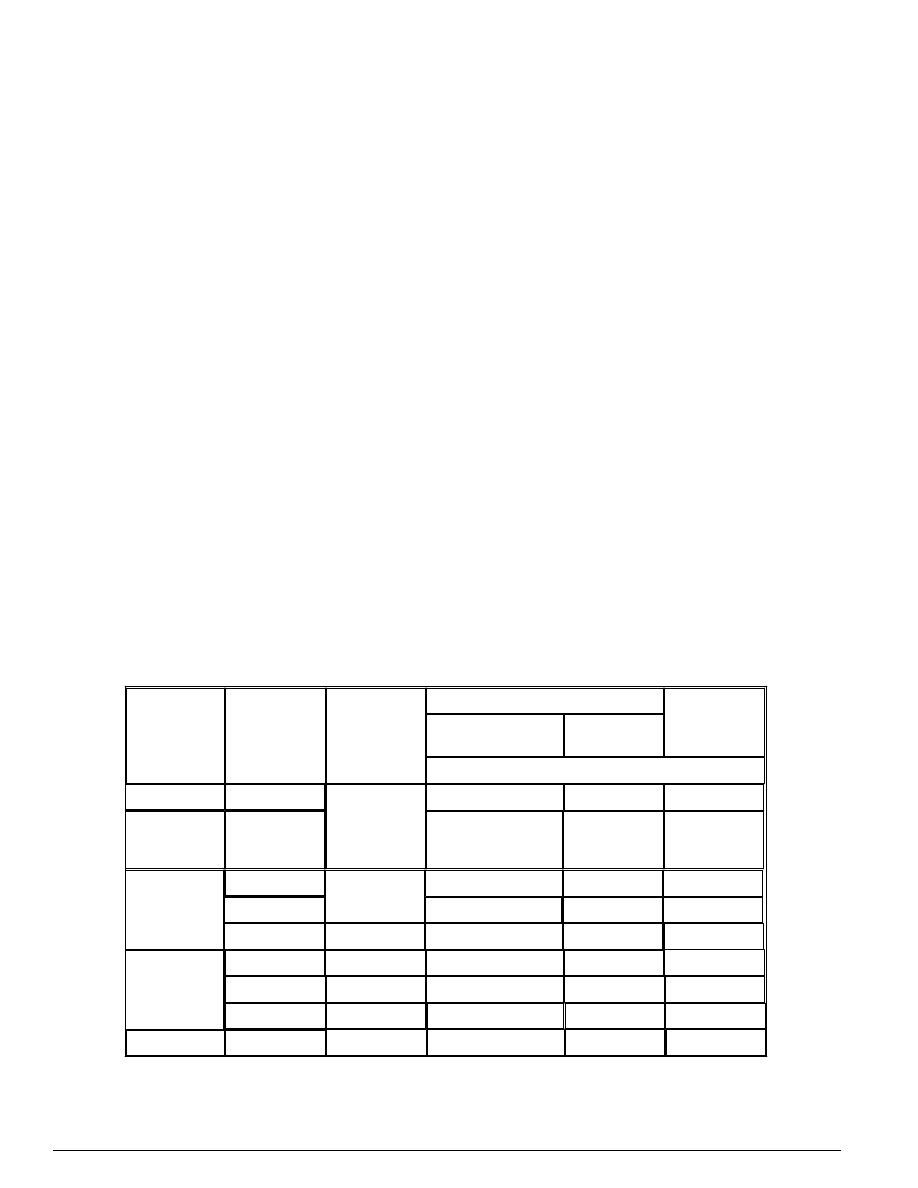
Tablica 5 - Charakterystyczne f
yk
i obliczeniowe f
yd
granice plastyczności oraz wytrzymałości charakterystyczne f
tk
stali zbrojeniowej klas od A-0 do A-IIIN
Klasa stali
Znak gatunku
stali
Nominalna
ś
rednica
prętów
φ
mm
Granice plastyczności stali
f
tk
charakterystyczna
f
yk
obliczeniowa
f
yd
MPa
A-0
StOS-b
5,5 ÷ 40
220
190
260
A-I
St3SX-b
St3SY-b
St3S-b
240
210
310
A-II
St50B
6 ÷ 32
355
310
410
18G2-b
355
310
410
20G2Y-b
6 ÷ 28
355
310
410
A-III
25G2S
6 ÷ 40
395
350
500
35G2Y
6 ÷ 20
410
350
500
34GS
6 ÷ 32
410
350
500
A-IIIN
20G2VY-b
6 ÷ 28
490
420
500
Część 4 Strona 1
3.1.3 Odkształcalność stali
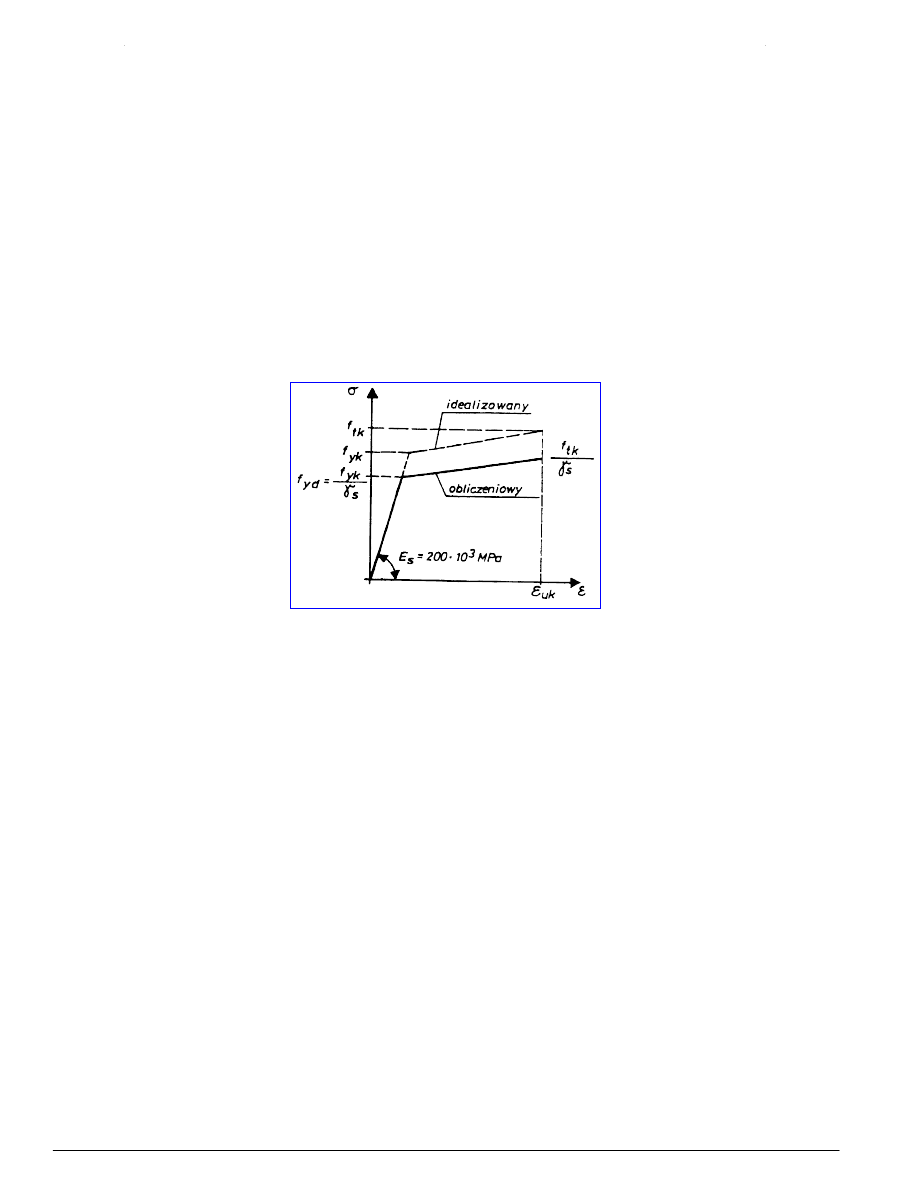
Związek σ-ε stali przyjmować należy zgodnie z wykresem przedstawionym na rysunku 3 (gdzie f
tk
- wytrzymałość
charakterystyczna stali na zerwanie, ε
uk
- wartość charakterystyczna odkształcenia stali odpowiadająca naprężeniu
zrywającemu) lub w postaci uproszczonej z poziomym odcinkiem od f
yd
/E
s
do ε
uk
.
Do obliczeń przyjąć można wykres σ-ε z nachyloną gałęzią górną, jeżeli istnieją odpowiednie dane doświadczalne, niezbędne
dla jej określenia.
Stale klas A-0 do A-III charakteryzują się dużą ciągliwością tj.
ε
uk
> 5% oraz f
tk
/f
yk
> 1,08
natomiast stal klasy A-IIIN - średnią ciągliwością tj.
ε
uk
> 2,5% oraz f
tk
/f
yk
> 1,05
gdzie: f
tk
/f
yk
- stosunek charakterystycznej wytrzymałości stali na rozciąganie f
tk
i charakterystycznej granicy plastyczności f
yk
.
Rysunek 3 - Wykres σ-ε stali zbrojeniowej
Moduł sprężystości stali E
s
w przedziale temperatury od -30 °C do 200 °C przyjmować można E
s
= 200 ⋅ 10
3
MPa.
3.2 Stal sprężająca
Do sprężania konstrukcji żelbetowych stosować należy druty, sploty lub pręty ze stali o wysokiej wytrzymałości.
Druty i sploty sprężające oznacza się podając:
- charakterystyczną wytrzymałość stali f
pk
, charakterystyczną umowną granicę plastyczności f
p0,1k
przy czym f
p0,1k
≥ 0,85 f
pk
,
oraz wydłużenie graniczne ε
uk
≥ 3,5%,
- klasę, wskazującą na charakterystykę relaksacji stali drutów, splotów i prętów w ciągu 1000h,
klasa 1 - wysoka relaksacja drutów i splotów (do 12% przy σ
p
/f
pk
= 0,8)
klasa 2 - niska relaksacja drutów i splotów (do 4,5% przy σ
p
/f
pk
= 0,8)
klasa 3 - niska relaksacja prętów (do 7% przy σ
p
/f
pk
= 0,8)
- średnicę: 4 mm < φ < 10 mm dla drutów
5,2 mm < φ < 16 mm dla splotów złożonych z 3 lub 7 drutów
- wytrzymałość zmęczeniową określaną jako minimalny zakres zmian naprężeń ∆σ przy górnym poziomie naprężenia
σ
p
= 0,7 f
pk
i 2 ⋅10
6
cykli obciążeń:
∆σ ≥ 200 MPa - dla drutów gładkich,
∆σ ≥ 180 MPa - dla drutów nagniatanych,
∆σ ≥ 190 MPa - dla splotów z drutów gładkich,
∆σ ≥ 170 MPa - dla splotów z drutów nagniatanych,
- odporność na korozję naprężeniową, badaną przy naprężeniu 0,8 f
pk
w roztworze rodanku amonowego NH
4
SCN. Miarą
odporności jest czas t do zerwania pojedynczej próbki t > 1,5h oraz t > 4h dla 50% ogólnej liczby próbek poddanych badaniu.
- wrażliwość splotów na złożony stan naprężenia, określaną przez procent obniżenia wytrzymałości f
pk
, przy zrywaniu próbek
odgiętych o 20° od prostej na odpowiednim urządzeniu badawczym.
Pręty sprężające określa się według:
Część 4 Strona 2
- wytrzymałości f
pk
,
- średnicy 15 mm < φ < 50 mm,
- siły zrywającej 190 kN ≤ F
pk
≤ 1500 kN,
- wytrzymałości zmęczeniowej:
∆σ > 200 MPa - dla prętów gładkich,
∆σ > 180 MPa - dla prętów żebrowanych,
- odporności na korozję naprężeniową mierzoną w h do chwili zerwania w roztworze NH
4
SCN.
Wszystkie wymienione właściwości gwarantowane są przez producenta stali.
Dopuszcza się stosowanie drutów i splotów o właściwościach wymienionych w tablicy 6.
Zaleca się stosowanie splotów φ 13 mm do strunobetonu, a splotów φ 16 mm do tworzenia kabli sprężających.
Tablica 6 - Charakterystyczne właściwości drutów i splotów sprężających
Nazwa
Oznaczenie
Ś
rednica
φ
mm
Przekrój
A
p
mm
2
Wytrzymałość f
pk
, MPa
odmiana
Siła zrywająca F
pk
, kN
odmiana
I
II
I
II
Drut
φ 2,5
2,5
4,9
2160
1860
10,6
9,1
φ 5
5,0
19,6
1670
1470
32,7
28,8
φ 7
7,0
38,5
1470
-
56,6
-
Splot
6×2,5+1×2,8
7,8
35,6
1940
1740
69
62
6×5+1×5,5
15,5
141,5
1470
1370
208
194
Y 1860 S7
1)
12,5
93
1860
-
173
-
Y 1860 S7
1)
13,0
100
1860
-
186
-
Y 1770 S7
1)
16,0
150
1770
-
265
-
1)
Wybrane sploty według prEN 10138-3
Wytrzymałość obliczeniową f
pd
stali sprężającej określa się dzieląc wytrzymałość charakterystyczną f
pk
przez częściowy
współczynnik bezpieczeństwa γ
s
= 1,25 oraz mnożąc przez współczynnik 0,9.
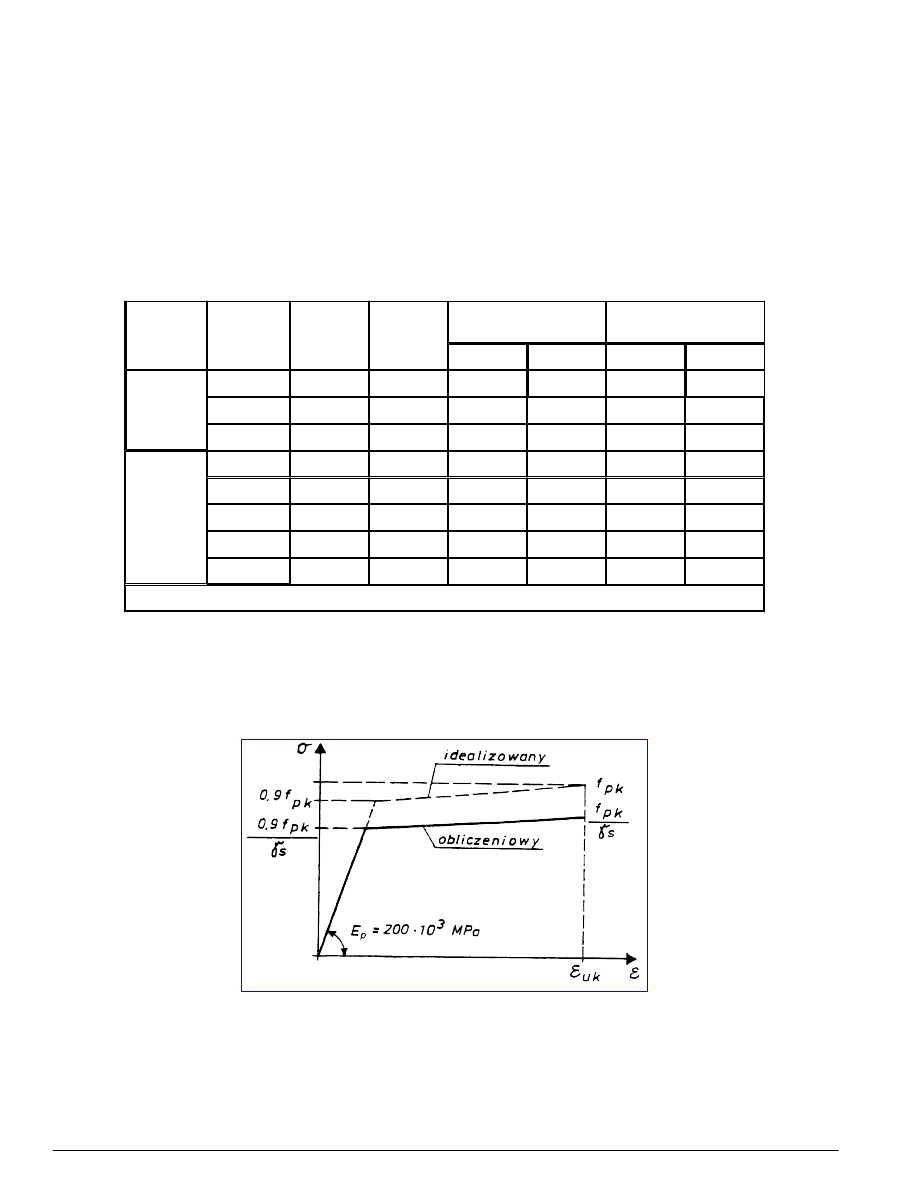
Obliczeniowy wykres zależności naprężenia od odkształcenia dla stali sprężającej przedstawia rysunek 4.
Rysunek 4 - Wykres σ-ε stali sprężającej
Moduł sprężystości stali drutów i prętów można przyjąć E
p
= 200 ⋅ 10
3
MPa, a stali splotów E
p
= 190 ⋅ 10
3
MPa, jeżeli wykres
Część 4 Strona 3
zależności σ-ε dostarczony z partią stali nie określa innych wartości.
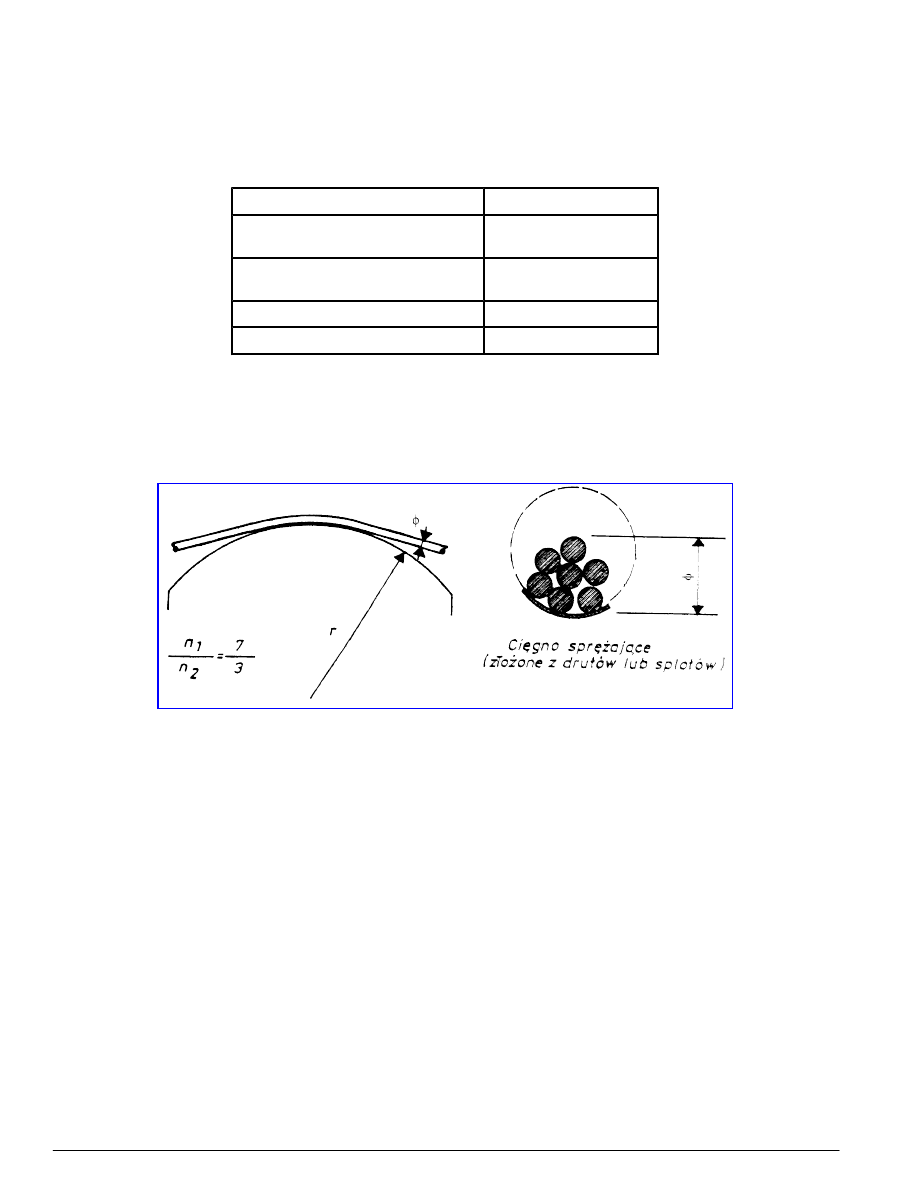
Cięgna sprężające osiągają pełną wytrzymałość na rozciąganie jedynie wtedy, gdy promień krzywizny w cięgnach
zakrzywionych spełnia wymagania podane w tablicy 7 i na rysunku 5.
Tablica 7 - Dopuszczalne promienie krzywizny odgięcia drutów i splotów sprężających
Rodzaj cięgna
Promień zagięcia r
pojedynczy drut lub splot zakrzywiony po
naciągu
15 φ
pojedynczy drut lub splot w gładkiej
osłonce
20 φ
jw. w osłonce falistej
40 φ
cięgno złożone z wielu drutów lub splotów
r ⋅⋅⋅⋅ n
1
/n
2
W tablicy 7 i na rysunku 5 przyjęto oznaczenia:
n
1
- liczba wszystkich drutów lub splotów w cięgnie
n
2
- liczba drutów lub splotów dociskanych składową siły naciągu na zakrzywieniu.
Rysunek 5 - Oznaczenia do tablicy 7
Część 4 Strona 4

4 Zasady projektowania
4.1 Wymagania podstawowe
4.1.1 Zapewnienie niezawodności konstrukcji
Konstrukcję obiektu budowlanego należy tak zaprojektować i wykonać, aby mogła być uznana za niezawodną, to jest aby w
przewidywanym okresie użytkowania, bez nadmiernych kosztów i z należytym prawdopodobieństwem
- nie nastąpiło przekroczenie stanów granicznych nośności, a także użytkowalności,
- oddziaływania wyjątkowe, takie jak pożar lub eksplozje, na skutek których ulega zniszczeniu część konstrukcji, a także
błędy ludzkie przy projektowaniu, wykonywaniu i użytkowaniu obiektu, nie powodowały zniszczenia konstrukcji w zakresie
nieproporcjonalnie dużym w stosunku do przyczyny.
Niezawodność konstrukcji zapewnić należy przez dobór właściwych materiałów i racjonalnego ustroju konstrukcyjnego,
wykazanie w obliczeniach, że stany graniczne nie zostały przekroczone oraz przez dopełnienie wymagań konstrukcyjnych i
należytą kontrolę wykonania konstrukcji zgodnie z projektem.
Konstrukcja powinna być tak zaprojektowana, aby przez cały przewidywany okres użytkowania odpowiadała założonemu
przeznaczeniu przy zadanym poziomie konserwacji.
Niezawodność konstrukcji w warunkach oddziaływań wyjątkowych zapewnia się zwykle spełniając odpowiednie wymagania
konstrukcyjne (p. 9.6). W szczególnych przypadkach (np. oddziaływań górniczych) może zachodzić również potrzeba
obliczeniowego wykazania nieprzekroczenia stanu granicznego nośności w takich warunkach.
4.1.2 Sytuacje obliczeniowe
W obliczeniach konstrukcji rozważyć należy okoliczności, w jakich konstrukcja ma spełniać swoje funkcje i wybrać sytuacje
obliczeniowe, wywołujące maksymalne wytężenie, w których sprawdza się nieprzekroczenie określonych stanów granicznych.
Sytuacje obliczeniowe dzielą się na trwałe, przejściowe i wyjątkowe.
Poza sprawdzeniem konstrukcji w sytuacjach
trwałych, określonych przez przeznaczenie obiektu, zachodzić może również
potrzeba sprawdzenia sytuacji przejściowych, które powstają m.in.:
- w konstrukcjach monolitycznych - podczas kolejnych etapów wznoszenia konstrukcji,
- w konstrukcjach prefabrykowanych - podczas rozformowania, transportu i montażu,
- w konstrukcjach sprężonych - dodatkowo w sytuacji początkowej (sprężenie wstępne zmniejszone o straty doraźne),
- w konstrukcjach zespolonych - w sytuacjach montażowych (bez udziału betonu uzupełniającego).
Wyjątkowe sytuacje obliczeniowe dotyczyć mogą:
- elementów konstrukcji, poddanych oddziaływaniom wyjątkowym lub
- wtórnego ustroju konstrukcyjnego, który utworzył się po zniszczeniu jednego lub kilku elementów konstrukcji na skutek
oddziaływania wyjątkowego.
4.2 Wymagania ogólne dotyczące obliczeń konstrukcji
4.2.1 Ogólne zasady obliczeń
Obliczenia konstrukcji należy wykonywać zgodnie z
PN-76/B-03001
, przyjmując nominalne wymiary elementów z
uwzględnieniem tolerancji wykonania i montażu wg PN-62/B-02356 i
PN-71/B-06280
.
Przy projektowaniu konstrukcji należy uwzględniać wymagania przeciwpożarowe zawarte w odpowiednich przepisach oraz
warunki ochrony antykorozyjnej konstrukcji, podane w PN-82/B-01801.
4.2.2 Zakres, układ i forma obliczeń statycznych
Powinny być zgodne z PN-90/B-03000.
4.2.3 Jednostki miar
W obliczeniach stosować należy legalne jednostki miar.
4.2.4 Wartości pośrednie
W stosunku do podanych w tablicach, wartości pośrednie można interpolować liniowo. Nie dopuszcza się ekstrapolacji.
4.3 Oddziaływania
Wartości charakterystyczne oddziaływań przyjmować należy wg
PN-82/B-02001
,
PN-82/B-02003
,
PN-82/B-02004
,
PN-
86/B-02005
,
PN-80/B-02010
,
PN-77/B-02011
,
PN-87/B-02013
i
PN-81/B-03020
.
Kombinacje oddziaływań przyjmować należy zgodnie z
PN-82/B-02000
.
Wartości częściowych współczynników bezpieczeństwa γ
f
przyjmować należy zgodnie z
PN-82/B-02001
.
Część 5 Strona 1

Obciążenia obliczeniowe budowli, których zniszczenie pociągnęłoby za sobą katastrofalne skutki materialne oraz budowli o
charakterze monumentalnym należy, zgodnie z
PN-76/B-03001
, mnożyć przez współczynnik konsekwencji zniszczenia γ
n
.
Wartość tego współczynnika ustala się indywidualnie.
Zaleca się też w takich przypadkach uwzględniać możliwość wystąpienia innych oddziaływań (poza określonymi w
wymienionych wyżej normach) i sprawdzać zachowanie się konstrukcji w powstałej sytuacji wyjątkowej.
4.4 Analiza konstrukcji
4.4.1 Modele obliczeniowe
Siły wewnętrzne w konstrukcji oblicza się przyjmując modele obliczeniowe, odwzorowujące warunki pracy konstrukcji w
rozpatrywanych stanach granicznych konstrukcji.
Zależnie od szczególnych cech konstrukcji, rozważanych stanów granicznych i specyficznych uwarunkowań projektu i
wykonawstwa stosowane być mogą metody analizy liniowo sprężystej (bez lub z redystrybucją), nieliniowej i plastycznej.
Do analizy stanu granicznego użytkowalności stosuje się z reguły metody analizy liniowo sprężystej.
Jeżeli stosuje się redystrybucję momentów obliczonych metodami analizy liniowo sprężystej, konieczne jest nadanie
przekrojom krytycznym dostatecznej zdolności obrotu, aby mogły przystosować się do przewidzianej redystrybucji.
Analizę plastyczną stosować można tylko do elementów zbrojonych stalą o dużej ciągliwości (p. 9.1.2.3 i 9.3.2.3).
W obliczeniach konstrukcji poddanych działaniom obciążeń wielokrotnie zmiennych należy stosować metody analizy liniowo
sprężystej.
Metody uproszczone stosować można pod warunkiem, że zapewniają one w całym zakresie stosowania stopień
niezawodności nie mniejszy, niż przyjęty w metodach podanych w niniejszej normie.
4.4.2 Redystrybucja momentów
W belkach i w płytach ciągłych, w których stosunek rozpiętości sąsiednich przęseł zawarty jest w przedziale od 0,5 do 2,0, w
ryglach ram nieprzesuwnych i w elementach podlegających głównie zginaniu - momenty wyznaczone z analizy liniowo
sprężystej mogą być redystrybuowane bez sprawdzania zdolności obrotu przekrojów krytycznych, jeżeli są spełnione podane
niżej warunki (a) i (b):
(a) dla betonu klas nie wyższych niż B45
(6)
dla betonu klas wyższych niż B45
(7)
(b) dla stali o dużej ciągliwości: δ ≥ 0,7 (3.1.3) oraz dla stali o średniej ciągliwości δ ≥ 0,85
gdzie:
δ - stosunek momentu po redystrybucji do momentu przed redystrybucją,
x - wysokość strefy ściskanej w stanie granicznym nośności po redystrybucji,
d - wysokość użyteczna przekroju.
Stosowanie metody analizy plastycznej do płyt i układów prętowych bez sprawdzania zdolności obrotu przekrojów jest
możliwe, jeżeli:
- do zbrojenia stosuje się stal o dużej ciągliwości (3.1.3),
- przekrój zbrojenia rozciąganego w żadnym punkcie i kierunku nie przekracza wartości odpowiadającej nośności strefy
ś
ciskanej przy x/d = 0,25,
- w płytach ciągłych stosunek wartości momentów w przęśle i na podporze zawiera się w przedziale od 0,5 do 2,0.
Zaleca się, aby różnica momentów między plastycznym a sprężystym rozkładem momentów nie przekraczała ą 30 %.
W ramach o węzłach przesuwnych nie należy stosować redystrybucji momentów.
4.4.3 Dane geometryczne
Efektywną rozpiętość I
eff
elementu można wyznaczyć następująco
(8)
gdzie:
I
n
- rozpiętość w świetle podpór,
a
1
i a
2
- wartości określane na podstawie odpowiednich wartości a
i
z rysunku 6.
Do obliczeń przyjmować można efektywną szerokość b
eff
półki w przekrojach teowych - stałą na całej długości
rozpatrywanego przęsła, na której występuje moment jednakowego znaku, równą
Część 5 Strona 2
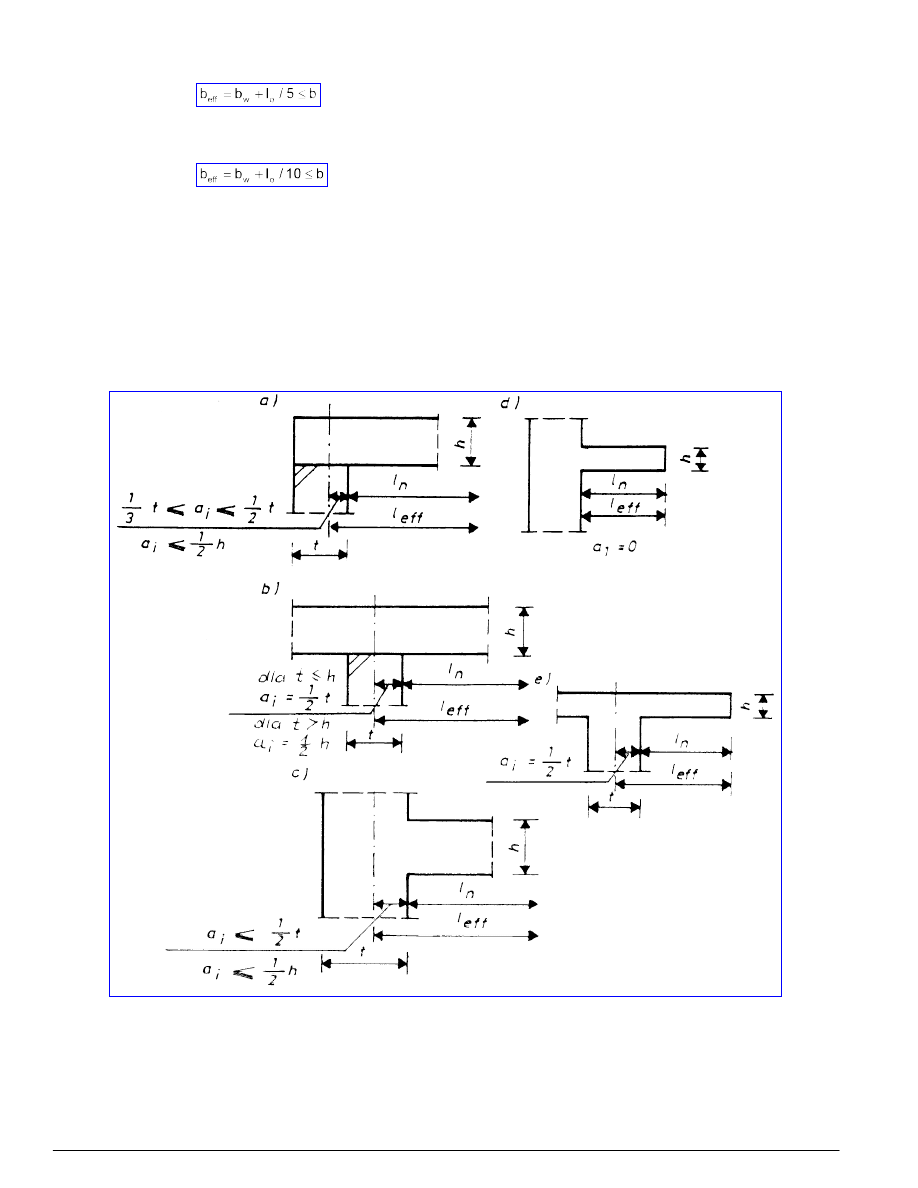
- dla przekrojów symetrycznych
(9)
- dla przekrojów z półką tylko z jednej strony
(10)
Oznaczenia we wzorach (9) i (10) przyjmuje się zgodnie z rysunkami 7 i 8.
Odległości obliczeniowe I
o
pomiędzy zerowymi wartościami momentów zginających można przyjmować według schematu
podanego na rysunku 8, pod warunkiem, że:
- długość wspornika nie jest większa od połowy rozpiętości przyległego przęsła,
- stosunek rozpiętości przyległych przęseł mieści się w przedziale od 1 do 1,5.
Przy sprawdzaniu stanu granicznego nośności należy ponadto przyjmować przy wysięgu dwustronnym b
eff1
lub b
eff2
≤ 6 h
f
, a
przy wysięgu jednostronnym b
eff1
lub b
eff2
≤ 4 h
f
.
W belkach obciążonych siłą skupioną, której wartość jest większa od pozostałego łącznego obciążenia belki, szerokość
wysięgu płyty w przęśle należy zmniejszyć o 20%.
Rysunek 6 - Wyznaczanie rozpiętości efektywnej I
eff
wg wzoru (8) dla różnych warunków na podporze:
(a) podpora skrajna swobodna
(b) podpora wewnętrzna w elemencie ciągłym
(c) podpora skrajna z pełnym zamocowaniem
Część 5 Strona 3
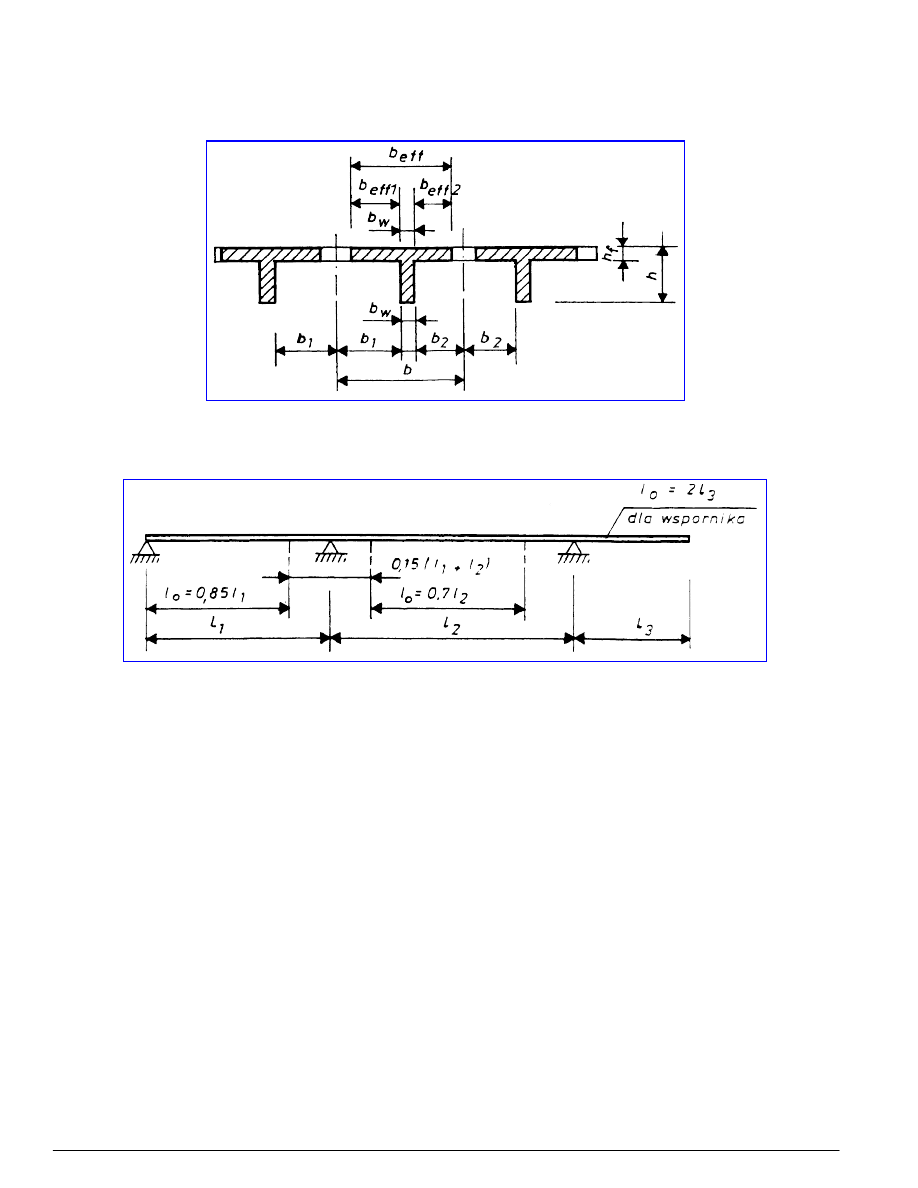
(d) zamocowanie
(e) podpora skrajna przy wsporniku
Rysunek 7 - Oznaczenie wymiarów
Rysunek 8 - Wartości I
o
między punktami zerowych momentów, przyjmowane do wyznaczania efektywnej szerokości półki
przekrojów teowych
4.5 Trwałość konstrukcji
Konstrukcję należy tak zaprojektować, aby przez cały przewidywany okres użytkowania w zadanych warunkach
ś
rodowiskowych i przy zadanej konserwacji - odpowiadała założonemu przeznaczeniu.
W zależności od warunków środowiskowych rozróżnia się pięć klas środowiska, jak podano w tablicy 8.
Tablica 8 - Klasy środowiska zależne od warunków środowiskowych
Część 5 Strona 4
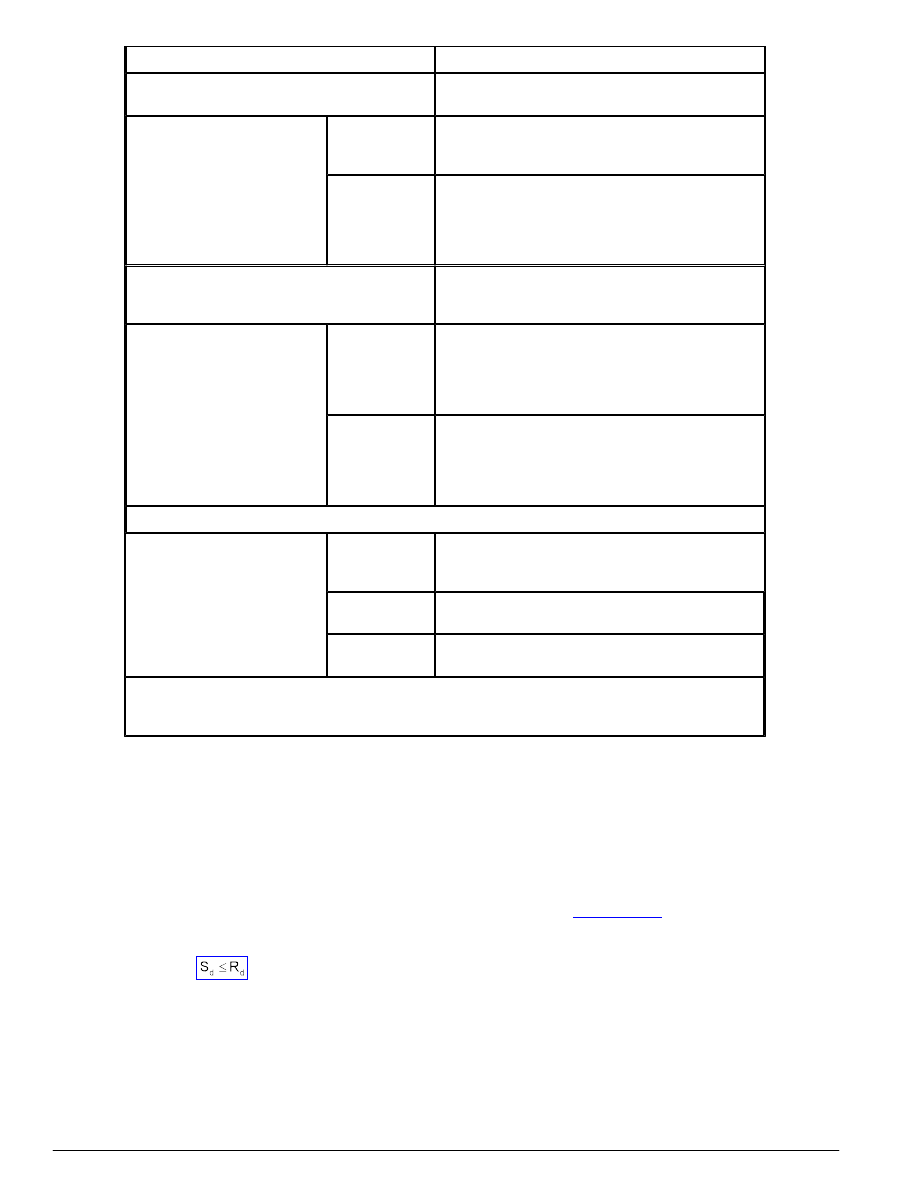
Klasa środowiska
Przykłady warunków środowiskowych
1
ś
rodowisko suche
1)
wnętrza budynków mieszkalnych, biur i hal
przemysłowych
2
ś
rodowisko wilgotne
a
bez mrozu
- wnętrza budynków o wysokiej wilgotności (np. pralnie)
- elementy zewnętrzne
- elementy w nieagresywnym gruncie i/lub wodzie
b
z mrozem
- elementy zewnętrzne narażone na mróz
- elementy w nieagresywnym gruncie i/lub w wodzie
narażone na mróz
- elementy we wnętrzach o wysokiej wilgotności,
narażone na mróz
3
ś
rodowisko wilgotne z mrozem i środkami
odladzającymi
- elementy wewnętrzne i zewnętrzne narażone na mróz i
ś
rodki odladzające
4
ś
rodowisko wody morskiej
a
bez mrozu
- elementy całkowicie lub częściowo zanurzone w
wodzie morskiej lub podlegające rozbryzgom wody
morskiej
- elementy w powietrzu nasyconym solą (strefa
przybrzeżna)
b
z mrozem
- elementy częściowo zanurzone w wodzie morskiej lub
podlegające rozbryzgom wody morskiej narażone na
mróz
- elementy w powietrzu nasyconym solą narażone na
mróz
Następujące klasy mogą występować same albo w kombinacji z klasami podanymi wyżej:
5
ś
rodowiska aresywne
chemicznie
2)
a
- środowisko słabo agresywne chemicznie (gazowe,
ciekłe lub stałe)
- agresywna atmosfera przemysłowa
b
- środowisko umiarkowanie agresywne chemicznie
(gazowe, ciekłe lub stałe)
c
- środowisko silnie agresywne chemicznie (gazowe,
ciekłe lub stałe)
1)
Ta klasa środowiska dotyczy tylko tych przypadków, w których podczas budowy konstrukcja lub niektóre jej
elementy nie są narażone na bardziej surowe warunki przez dłuższy okres.
2)
Środowiska agresywne chemicznie można klasyfikować zgodnie z PN-80/B-01800.
4.6 Sprawdzanie stanów granicznych nośności
Do stanów granicznych nośności, sprawdzanych według zasad podanych w normie, należą:
- wyczerpanie nośności miarodajnych przekrojów lub fragmentów konstrukcji,
- utrata stateczności przez ściskane elementy konstrukcji (sprowadzona w normie do stanu granicznego wyczerpania
nośności miarodajnych przekrojów tych elementów),
- zniszczenie na skutek zmęczenia stali zbrojeniowej, sprężającej lub betonu w elementach konstrukcji, w wyniku działania
obciążeń wielokrotnie zmiennych.
Sprawdzanie stanów granicznych nośności polega na wykazaniu, że w każdym miarodajnym przekroju (elemencie)
konstrukcji, dla każdej z kombinacji oddziaływań obliczeniowych - określonych w
PN-82/B-02000
p. 4.2 - spełniony jest
warunek
(11)
w którym S
d
oznacza siłę wewnętrzną wywołaną tymi oddziaływaniami, a R
d
- odpowiednią nośność obliczoną przy założeniu,
ż
e wytrzymałości materiałów i granica plastyczności stali osiągają wartości obliczeniowe.
Konstrukcje narażone na obciążenia wielokrotnie zmienne, wymagają dodatkowego sprawdzenia wg 7.2.
Poza sprawdzeniem wymienionych stanów granicznych, należy również przeanalizować możliwości wystąpienia w konstrukcji
Część 5 Strona 5
innych wymienionych w
PN-76/B-03001
stanów granicznych nośności i odpowiednio zabezpieczyć konstrukcję przed ich
wystąpieniem.
4.7 Sprawdzanie stanów granicznych użytkowalności
4.7.1 Zasady ogólne
Do stanów granicznych użytkowalności, sprawdzanych według zasad podanych w normie należą:
- stan graniczny naprężeń,
- stan graniczny zarysowania,
- stan graniczny ugięć.
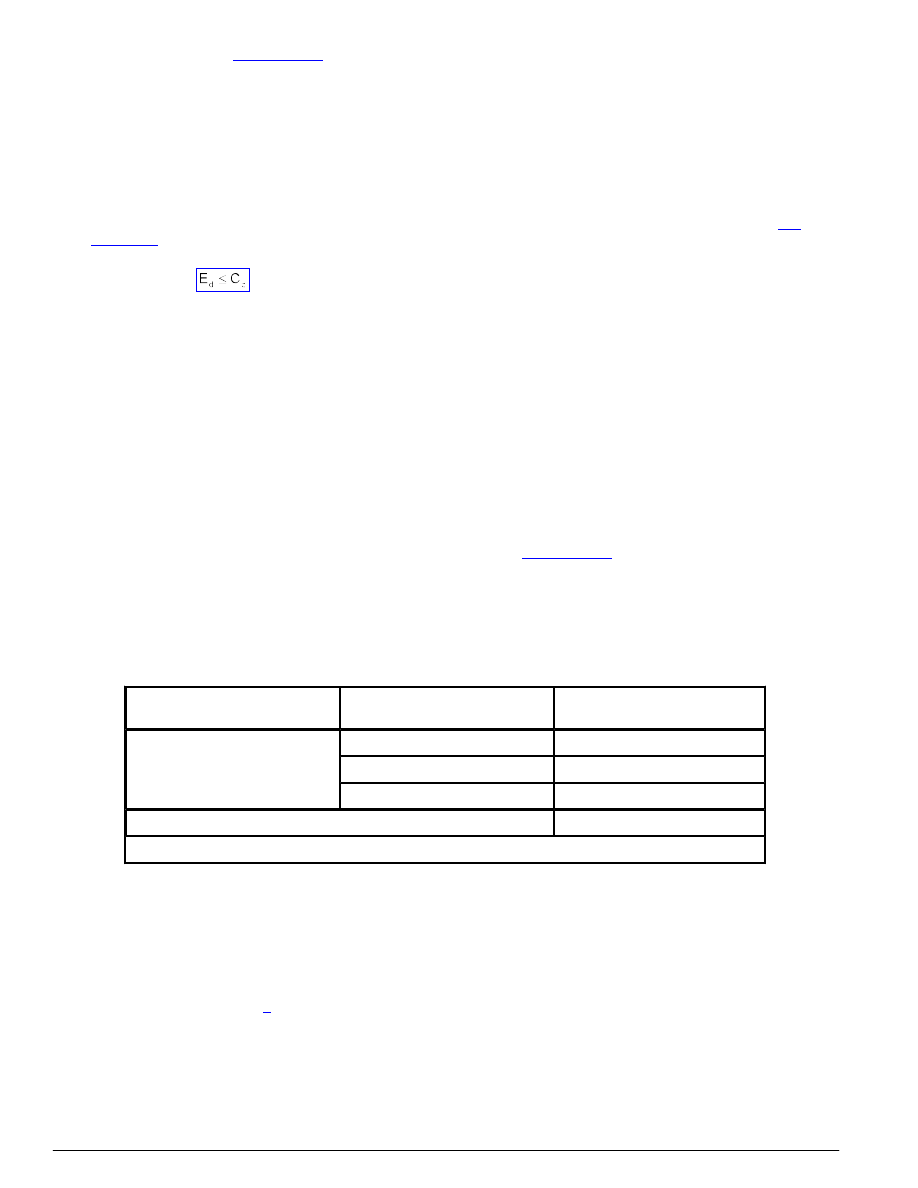
Sprawdzanie stanów granicznych użytkowalności polega na wykazaniu, że dla kombinacji oddziaływań określonych w
PN-
82/B-02000
p. 4.3. spełniony jest warunek
, (12)
w którym E
d
oznacza efekt (naprężenie, szerokość rys, ugięcie) tych oddziaływań, a C
d
jest graniczną wartością tego efektu,
określoną w p. 4.7.2., 4.7.3 i 4.7.4.
Efekty oddziaływań wyznacza się stosując w obliczeniach średnie moduły sprężystości i wytrzymałości materiałów, z
wyjątkiem tych przypadków, w których przepisy rozdziałów 6 i 7 lub uzgodnienia z inwestorem ustalają inaczej.
Poza sprawdzeniem wymienionych wyżej stanów granicznych należy również przeanalizować możliwość wystąpienia w
konstrukcji innych stanów granicznych użytkowalności (np. stanu granicznego drgań) i odpowiednio zabezpieczyć konstrukcję
przed ich wystąpieniem.
4.7.2 Sprawdzenie stanu granicznego naprężeń
Sprawdzenie stanu granicznego naprężeń wykonuje się w sytuacji początkowej konstrukcji sprężonych według zasad
określonych w p. 7.1.7.1 oraz 7.1.2.
4.7.3 Sprawdzenie stanu granicznego zarysowania
Sprawdzenie stanu granicznego zarysowania polega na wykazaniu, że występujące w konstrukcji siły wewnętrzne,
wyznaczone dla kombinacji obciążeń długotrwałych zgodnie z p. 4.3.
PN-82/B-02000
- nie powodują rozwarcia rys
prostopadłych do osi elementu i rys ukośnych większych od szerokości uznanych za graniczne. Graniczne szerokości rys dla
konstrukcji żelbetowych podano w tablicy 9. Wymagania dotyczące konstrukcji sprężonych podano w p. 7.1.1.
Tablica 9 - Graniczne szerokości rys w
lim
Wymagania użytkowe
Klasa
ś
rodowiska
w
lim
mm
Ochrona przed
korozją
5b i 5c
0,1
1)
3 - 5a
0,2
1 i 2
0,3
Zapewnienie szczelności
0,1
1)
1)
Jeżeli przepisy szczegółowe nie stanowią inaczej.
Konstrukcje w środowisku klasy 5b i 5c należy chronić przed korozją zgodnie z wymaganiami PN-80/B-01800.
4.7.4 Sprawdzanie stanu granicznego ugięć
Sprawdzanie stanu granicznego ugięć polega na wykazaniu, że występujące w konstrukcji siły wewnętrzne wyznaczone dla
kombinacji obciążeń długotrwałych, nie powodują ugięć większych od uznanych za graniczne ze względu na przeznaczenie
budowli, możliwość uszkodzenia elementów przylegających do konstrukcji, estetykę oraz poczucie zagrożenia
bezpieczeństwa użytkowników
3)
.
W budownictwie ogólnym, a także w budownictwie przemysłowym i rolniczym, jeżeli warunki użytkowania nie powodują
konieczności specjalnego ograniczenia ugięć, sprawdzanie ugięć konieczne jest jedynie dla elementów dachowych i
stropowych. Ugięcia tych elementów, pod działaniem obciążeń w kombinacji długotrwałej, nie powinny przekraczać wartości
Część 5 Strona 6
podanych w tablicy 10.
Tablica 10 - Graniczne wartości ugięć a
lim
Rodzaj konstrukcji
Rozpiętość
a
lim
Belki oraz płyty stropów
1)
i
stropodachów
I
eff
≤ 6,0 m
6,0 < I
eff
< 7,5 m
I
eff
≥ 7,5 m
I
eff
/200
30 mm
I
eff
/250
Przekrycia dachowe
I
eff
≤ 6,0 m
6,0 < I
eff
< 10 m
I
eff
≥ 10 m
I
eff
/150
40 mm
I
eff
/250
Wsporniki
bez względu na wysięg I
eff
I
eff
/150
1)
W pomieszczeniach inwentarskich budownictwa rolniczego oraz w pomieszczeniach w budownictwie
przemysłowym, kiedy dopuszczalne jest to ze względów użytkowych, a także w drugorzędnych obiektach
budownictwa ogólnego, wartości a
lim
przyjmować można jak dla przekryć dachowych.
W celu kompensacji całego ugięcia lub jego części można nadawać elementowi wstępne ugięcie odwrotne. Zaleca się, aby
odwrotna strzałka ugięcia nie była większa od 1/250 rozpiętości.
Przy obliczaniu ugięć uwzględnić należy wpływ pełzania betonu na sztywność elementu zginanego. Wpływ skurczu betonu na
ugięcie żelbetowych elementów zginanych można z reguły pomijać, z wyjątkiem elementów zespolonych.
4.8 Minimalny przekrój zbrojenia podłużnego
Stopień zbrojenia podłużnego odniesiony do efektywnego pola strefy rozciąganej przekroju elementu nie może być mniejszy
od wymaganego z uwagi na ograniczenie szerokości rys w konstrukcji zgodnie z 6.2.
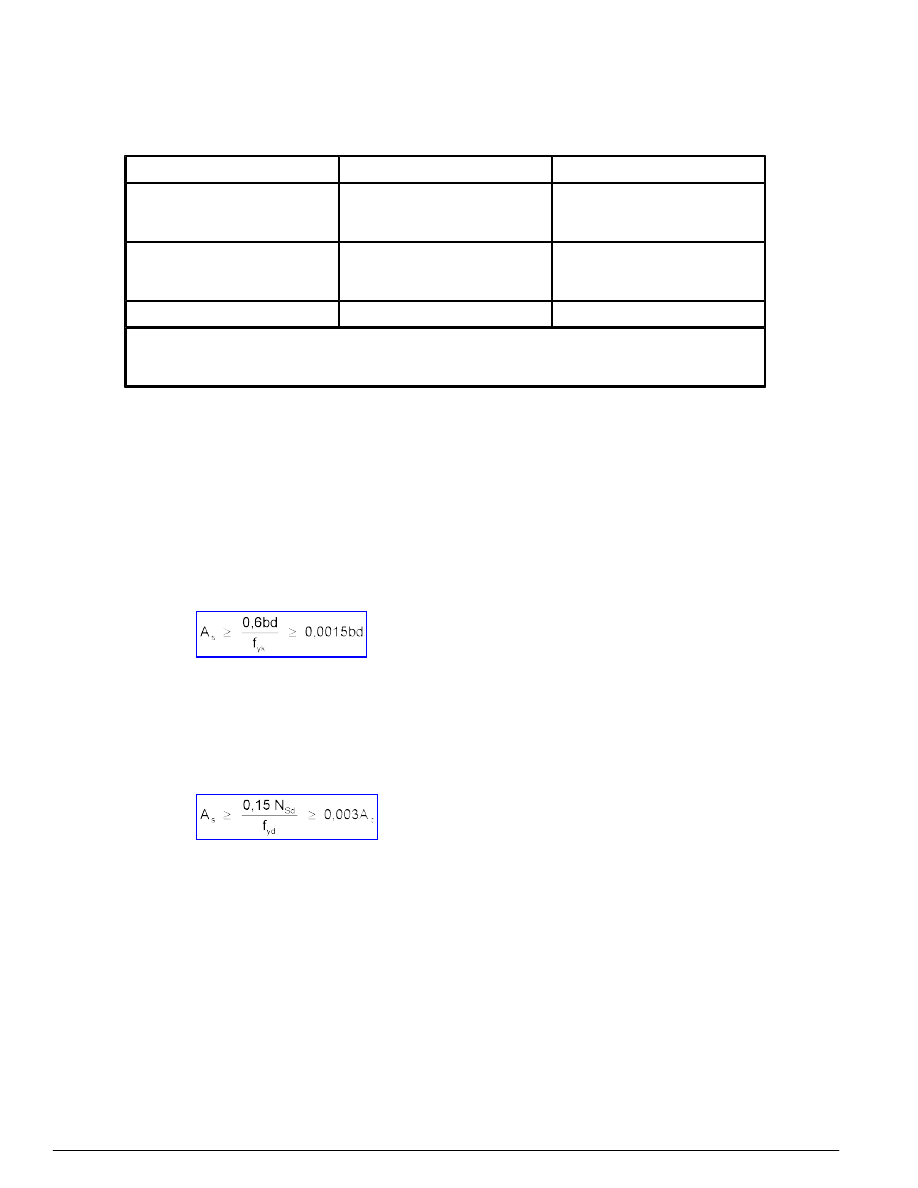
Ponadto minimalne pole przekroju podłużnego zbrojenia rozciąganego nie może być mniejsze niż:
- w elementach zginanych bez udziału siły podłużnej pole przekroju zbrojenia rozciąganego
(13)
gdzie:
A
s
- pole przekroju zbrojenia podłużnego, w metrach kwadratowych,
b - średnia szerokość strefy rozciąganej na poziomie środka ciężkości zbrojenia, w metrach,
d - wysokość użyteczna przekroju, w metrach,
f
yk
- charakterystyczna granica plastyczności stali zbrojeniowej, w MPa.
- w elementach ściskanych sumaryczne pole zbrojenia podłużnego
(14)
gdzie:
N
Sd
- siła podłużna wywołana obciążeniem obliczeniowym,
f
yd
- obliczeniowa granica plastyczności stali zbrojeniowej w MPa,
A
c
- pole przekroju betonu.
W elementach rozciąganych stopień zbrojenia podłużnego odniesiony do użytecznego przekroju elementu, usytuowanego
przy każdej z dwóch przeciwległych stron przekroju, powinien być nie mniejszy niż 0,0020.
W słupach uzwojonych stopień całego zbrojenia podłużnego, odniesiony do przekroju rdzenia, powinien wynosić co najmniej
0,0080.
Część 5 Strona 7
5 Stany graniczne nośności konstrukcji betonowych i żelbetowych
5.1 Zasady obliczania elementów zginanych, ściskanych i rozciąganych
5.1.1 Zasady ogólne
Nośność elementów zginanych, ściskanych i rozciąganych określa się z warunków równowagi sił wewnętrznych w przekroju,
przyjmując następujące założenia:
a) przekroje płaskie przed odkształceniem pozostają płaskimi po odkształceniu,
b) wytrzym
ało
ść
betonu na rozciąganie j
est pom
ij
ana,
c) naprężenia w betonie ściskanym ustala się zgodnie z zasadami podanymi w p. 2.2.1,
d) naprężenia w stali ustala się zgodnie z zasadami podanymi w p. 3.1.3,
e) stan graniczny nośności występuje, gdy jest osiągnięty przynajmniej jeden, z poniższych warunków:
ε
s
= - 0,0100 w zbrojeniu rozciąganym
ε
c
= 0,0035 w skrajnym włóknie betonu
ε
c
= 0,0020 we włóknie betonu odległym o 3/7 h od krawędzi bardziej ściskanej.
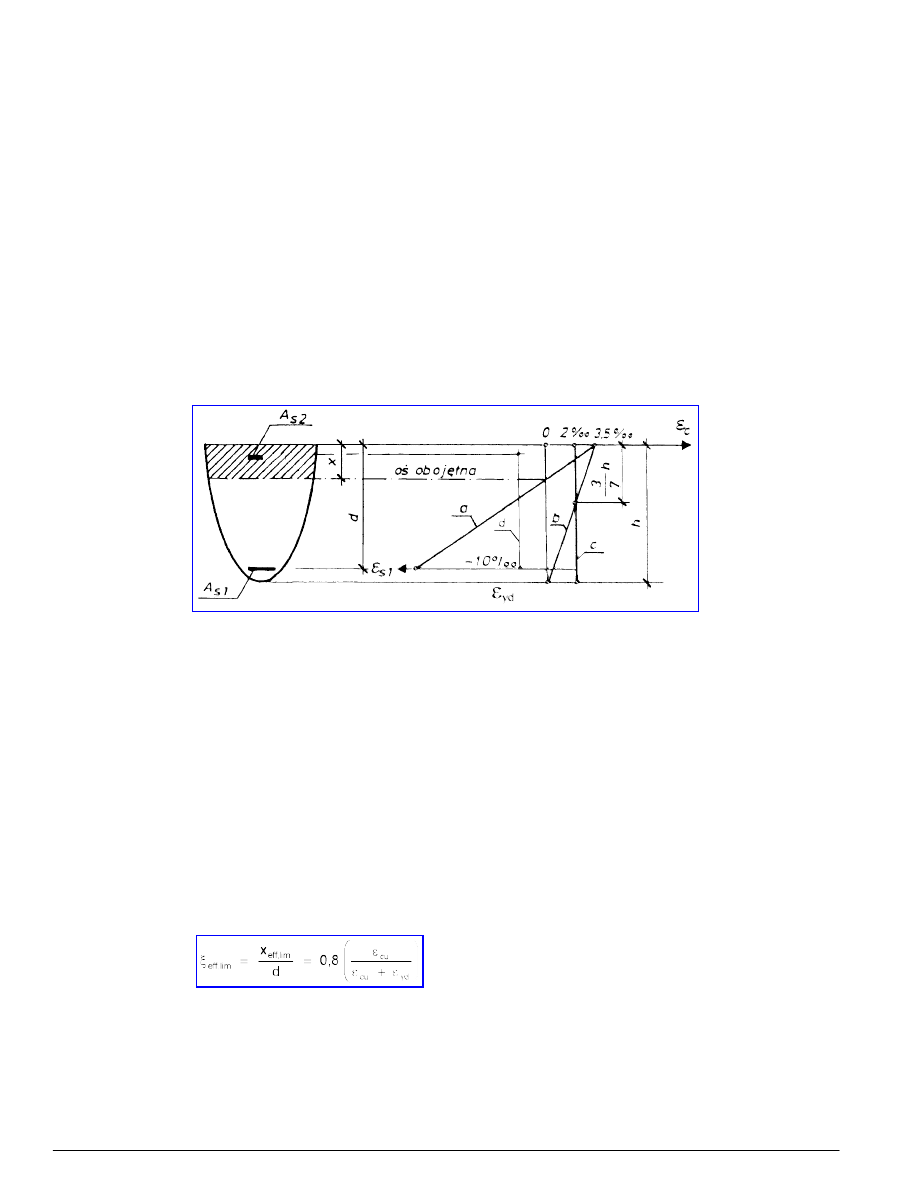
Odkształcenia przekrojów w stanie granicznym nośności podane są na rysunku 9.
Rysunek 9 - Odkształcenia w stanie granicznym nośności (a) w części przekroju występują naprężenia rozciągające, (b) w
przekroju nie występują naprężenia rozciągające, (c) cały przekrój jest równomiernie ściskany, (d) cały przekrój jest
równomiernie rozciągany (
ε
yd
= f
yd
/E
s
)
Do obliczeń nośności przekroju zginanego w dowolnej płaszczyźnie przyjmuje się za wysokość przekroju h rzut na kierunek
prostopadły do osi obojętnej odcinka łączącego najbardziej ściskany lub najmniej rozciągany punkt przekroju z punktem
najbardziej rozciąganym lub najmniej ściskanym.
Wysokość użyteczną d określa się odpowiednio jako rzut odcinka łączącego punkt najbardziej ściskany lub najmniej
rozciągany przekroju z najbardziej rozciąganym lub najmniej ściskanym prętem zbrojenia.
Nośność przekroju można obliczać z pominięciem siły podłużnej, jeżeli średnie naprężenie ściskające wywołane przez tę siłę
nie przekracza 0,08 f
ck
.
5.1.2 Zasady metody uproszczonej
Nośność elementów żelbetowych wykonanych z betonu klasy nie wyższej niż B55, obliczać można w sposób uproszczony z
warunku równowagi sił i założenia prostokątnego wykresu naprężeń w betonie strefy ściskanej posługując się wzorami,
podanymi w 5.2, 5.3.3 i 5.4.
Graniczną wartość względnej wysokości strefy ściskanej przekroju
ξ
eff,lim
wyraża w takim przypadku wzór
(15)
w którym:
ε
cu
= 0,0035
ε
yd
= f
yd
/E
s
Część 6 Strona 1

d - wysokość użyteczna przekroju przyjmowana w metodzie uproszczonej, równa odległości środka ciężkości zbrojenia
rozciąganego od ściskanej krawędzi przekroju; w przypadku zbrojenia ułożonego w kilku warstwach - użyteczna wysokość
przekroju powinna spełniać warunek
(16)
Przybliżone wartości
ξ
eff,lim
podano w tablicy 11.
Tablica 11 - Graniczne wartości
ξ
ξξ
ξ
eff,lim
względnej wysokości strefy ściskanej przekroju
Klasa stali
ξ
eff,lim
A-0
0,63
A-I
0,62
A-II
0,55
A-III
0,53
A-IIIN
0,50
druty i sploty w elementach sprężonych
0,50
5.2 Zginanie - metoda uproszczona
Stan graficzny nośności zginanych elementów żelbetowych o przekroju mającym przynajmniej jedną płaszczyznę symetrii i
zginanym w tej płaszczyźnie (rysunek 10) sprawdza się z warunku
(17)
gdzie:
α = 0,85.
A
s2
- pole przekroju zbrojenia ściskanego,
S
cc,eff
- moment statyczny efektywnego pola betonu strefy ściskanej o wysokości x
eff
= 0,8x, obliczony względem środka
ciężkości zbrojenia rozciąganego.
Położenie x
eff
osi obojętnej wyznacza się z równania
(18)
gdzie:
A
s1
- pole przekroju zbrojenia rozciąganego,
A
cc,eff
- efektywne pole betonu strefy ściskanej o wysokości x
eff
= 0,8x.
Jeżeli wartość x
eff
obliczona ze wzoru (18) jest większa od x
eff,lim
, to do wzoru (17) należy podstawić x
eff
= x
eff,lim
.
Jeżeli w obliczeniu nośności uwzględnia się zbrojenie ściskane, a środek ciężkości tego zbrojenia położony jest dalej od
krawędzi ściskanej przekroju niż środek ciężkości bryły naprężeń ściskających w betonie, nośność przekroju należy
sprawdzać z warunku
(19)
Część 6 Strona 2
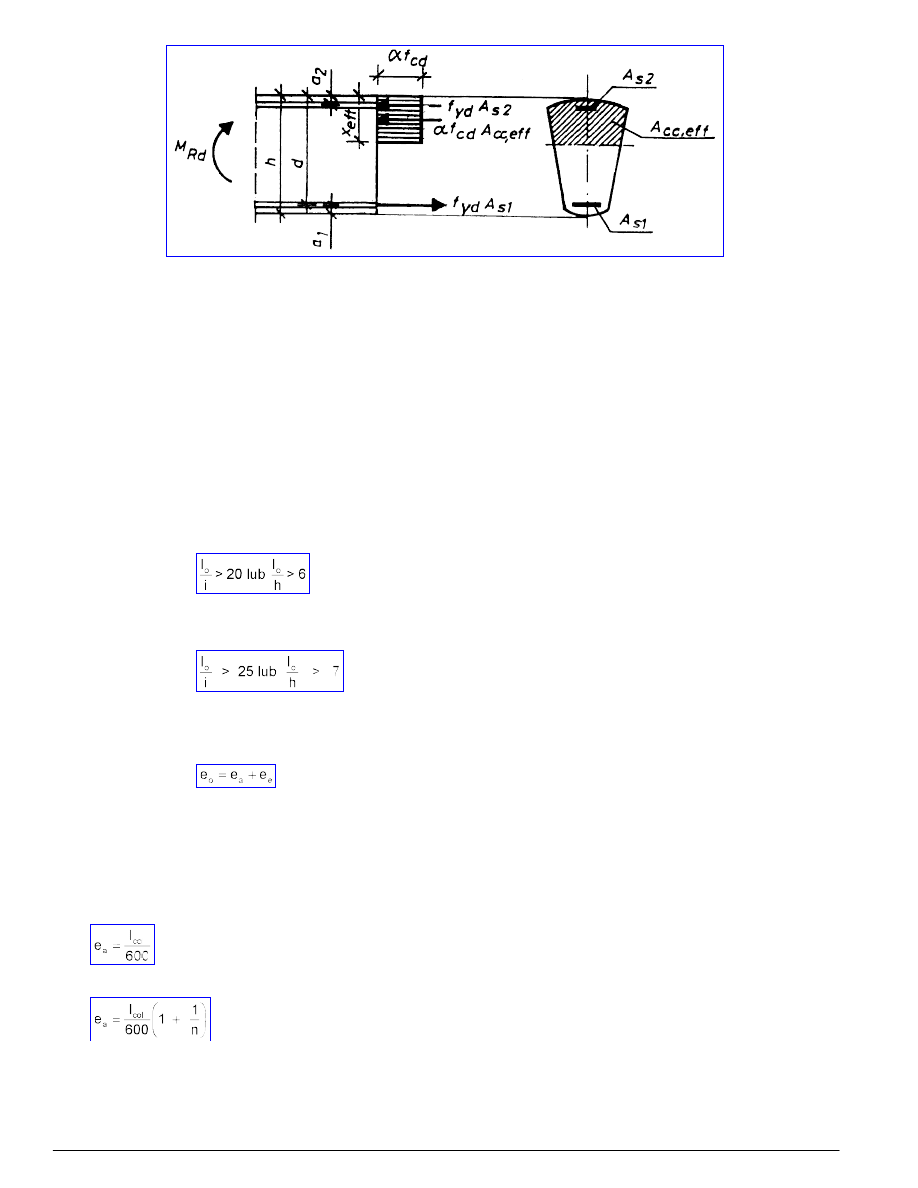
Rysunek 10 - Schemat do obliczania nośności zginanego przekroju żelbetowego
5.3 Ściskanie
5.3.1 Długości obliczeniowe
Długości obliczeniowe l
o
elementów ściskanych wyznaczać można według zasad mechaniki budowli, jak dla elementów z
materiału liniowo sprężystego.
Długości obliczeniowe l
o
słupów wielokondygnacyjnych budynków szkieletowych i jednokondygnacyjnych budynków
halowych, słupów estakad oraz ściskanych elementów dźwigarów kratowych mogą być przyjmowane według tablicy C.1
załącznika C, a długości obliczeniowe słupów występujących w układach ramowych mogą być wyznaczane według wzorów
podanych w tym załączniku.
Nośność elementów ściskanych należy sprawdzać z uwzględnieniem ich smukłości i wpływu obciążeń długotrwałych wg
5.3.3.1 i 5.3.3.2 jeżeli zachodzą warunki
- dla elementów betonowych
- dla elementów żelbetowych i sprężonych
5.3.2 Mimośród początkowy
Mimośród początkowy siły ściskającej w stosunku do środka ciężkości przekroju betonowego należy określać wg wzoru
(20)
w którym:
e
a
- niezamierzony mimośród przypadkowy, spowodowany zróżnicowaniem cech wytrzymałościowych betonu, początkową
krzywizną elementu oraz odchyłkami od założonego usytuowania elementu w konstrukcji itp.,
e
e
- mimośród konstrukcyjny, równy ilorazowi momentu zginającego M
Sd
i siły podłużnej N
Sd
, wywołanych obciążeniem
obliczeniowym.
Wartość niezamierzonego mimośrodu przypadkowego e
a
należy przyjmować równą największej z podanych niżej wartości:
- w ustrojach ścianowych i w ustrojach szkieletowych o węzłach nieprzesuwnych, gdzie I
col
- odległość między
punktami podparcia elementu; dla słupa wspornikowego - długość słupa,
lub
- w ustrojach szkieletowych o węzłach przesuwnych dla elementów n-tej kondygnacji licząc od góry,
Część 6 Strona 3
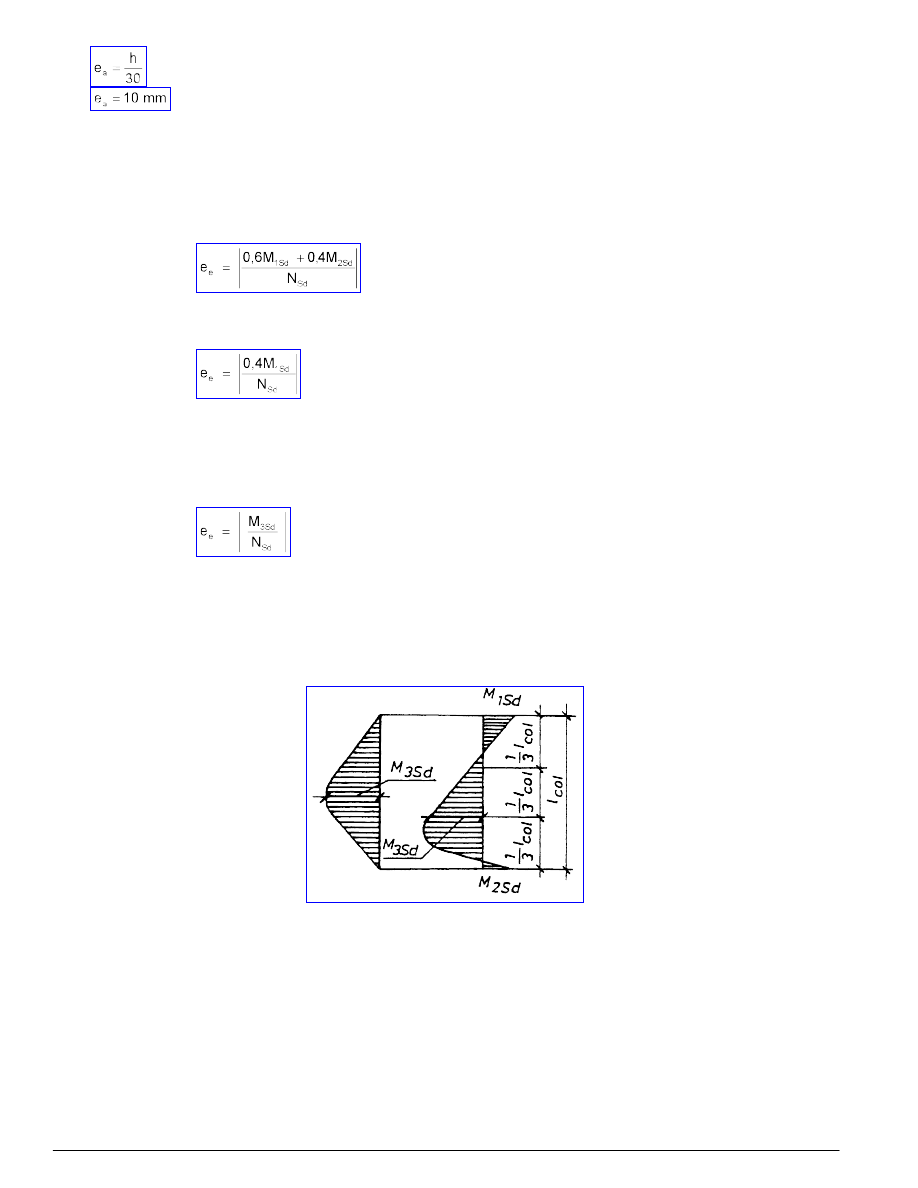
gdzie h - wysokość przekroju w obliczanej płaszczyźnie,
dla konstrukcji monolitycznych, ścian i powłok oraz 20 mm dla konstrukcji prefabrykowanych, z wyjątkiem
ś
cian i powłok.
Wartość mimośrodu konstrukcyjnego e
e
określać należy z uwzględnieniem możliwości przesuwu węzłów w rozpatrywanym
układzie konstrukcyjnym oraz kształtu wykresu momentów zginających na długości elementu ściskanego.
Gdy nośność elementów ściskanych sprawdzana jest z uwzględnieniem wpływu smukłości, do obliczeń przyjmować należy
wartość mimośrodu e
e
wyznaczoną:
a) gdy elementy występują w układach o węzłach nieprzesuwnych:
- przy prostoliniowym wykresie momentów - według wzoru
(21)
lecz nie mniej niż
(22)
w którym:
M
1Sd
, M
2Sd
- momenty zginające wraz z ich znakami występujące na końcach elementów, przy czym |M
1Sd
|
≥ |M
2Sd
|;
- przy krzywoliniowym wykresie momentów według wzoru
(23)
w którym:
M
3Sd
- ekstremalna wartość momentu zginającego, występująca na odcinku środkowym równym 1/3 długości elementu
(rysunek 11).
Rysunek 11 - Położenie przekrojów rozpatrywanych przy sprawdzaniu nośności elementów mimośrodowo ściskanych
mających na obu końcach podparcie nieprzesuwne w kierunku prostopadłym do osi elementu
Nośność przekrojów przypodporowych występujących w układach o węzłach nieprzesuwnych obciążonych momentami M
1Sd
i M
2Sd
należy sprawdzać bez uwzględnienia wpływu smukłości.
b) gdy elementy występują w układach o węzłach przesuwnych - według wzoru
Część 6 Strona 4
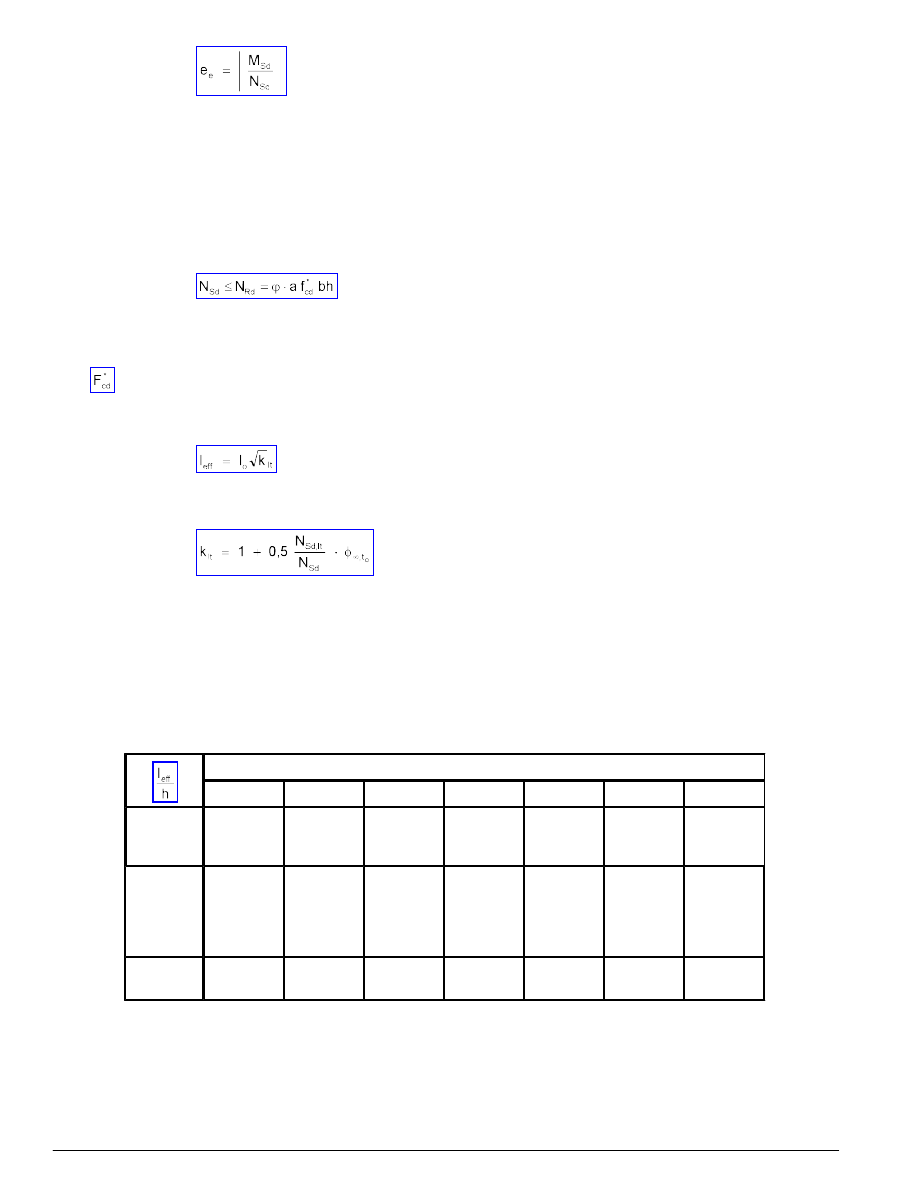
(24)
w którym:
M
Sd
- ekstremalna wartość momentu zginającego występująca na długości elementu.
5.3.3 Nośność elementów ściskanych - metoda uproszczona
5.3.3.1 Elementy betonowe
Nośność ściskanych elementów betonowych N
Rd
o przekroju prostokątnym wykonanych z betonu klas B15 i B20 określać
można z warunku
(25)
w którym:
ϕ - współczynnik, którego wartości podane są w tablicy 12,
α = 0,85
- wytrzymałość obliczeniowa betonu na ściskanie w elementach niezbrojonych.
Zastępczą długość obliczeniową l
eff
występującą w tablicy 12 należy, przy nieuwzględnianiu wpływu smukłości, przyjmować
l
eff
= l
o
, a przy uwzględnianiu wpływu smukłości obliczać wg wzoru
(26)
w którym:
(27)
gdzie:
φ
∞
,
to
- końcowy współczynnik pełzania betonu według tablicy 3; dla konstrukcji w środowisku o wilgotności względnej
RH = (40 ÷ 75)% obciążonych po 28 dniach, przyjmować można
φ
∞
,
to
= 2,0,
N
Sd,It
- siła podłużna wywołana działaniem długotrwałej części obciążenia obliczeniowego.
Tablica 12 - Wartość współczynnika
ϕ
ϕ
ϕ
ϕ
e
o
/h
0,03
0,05
0,10
0,15
0,20
0,25
0,30
0
8
10
0,94
0,92
0,92
0,90
0,88
0,87
0,80
0,78
0,76
0,70
0,67
0,65
0,60
0,56
0,55
0,50
0,46
0,45
0,40
0,36
0,35
12
14
16
18
20
0,91
0,90
0,89
0,87
0,85
0,86
0,85
0,84
0,82
0,79
0,74
0,72
0,70
0,68
0,65
0,63
0,61
0,59
0,56
0,54
0,53
0,51
0,48
0,46
0,43
0,43
0,40
0,38
0,36
0,33
0,33
0,31
0,29
0,27
0,24
22
24
0,82
0,80
0,76
0,74
0,63
0,60
0,51
0,48
0,40
0,37
0,30
0,28
0,22
0,20
Jeżeli nie jest wymagana duża dokładność obliczeń, to w przybliżeniu można przyjąć I
eff
= 1,3 I
o
Część 6 Strona 5
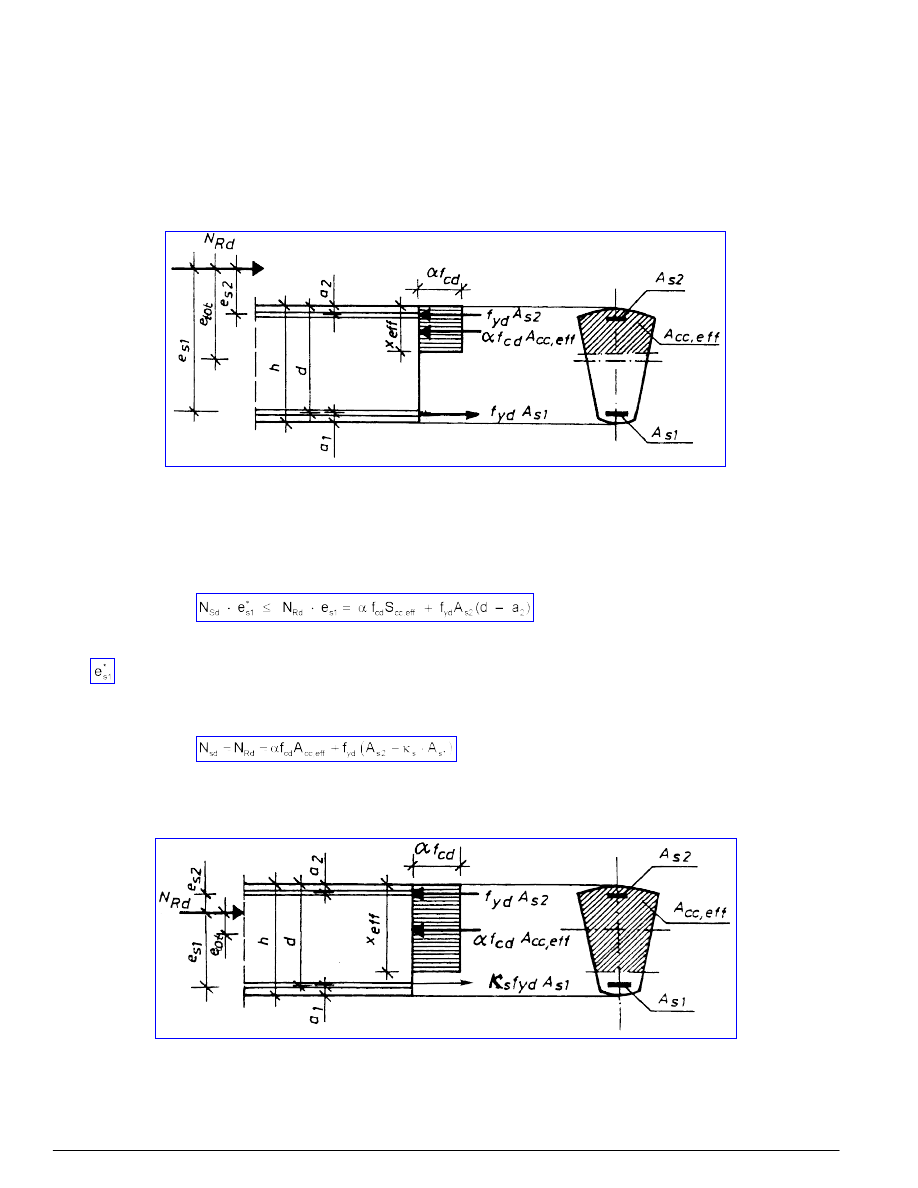
Nośność elementów betonowych o przekroju innym niż prostokątny, a także o przekroju prostokątnym, wykonanych z betonu
klas B25 i wyższych, obliczać można przy założeniu prostokątnego wykresu naprężeń ściskających w betonie według zasad
podanych dla elementów żelbetowych, przyjmując we wzorach (28) lub (29):
f
cd
= f*
cd
i A
s1
= A
s2
= 0. Wpływ smukłości na nośność należy uwzględniać również jak w elementach żelbetowych,
wyznaczając N
crit
według wzoru (33) przy założeniu I
s
= 0.
5.3.3.2 Elementy żelbetowe
Przy obliczaniu żelbetowych przekrojów mimośrodowo ściskanych rozróżnia się dwa przypadki:
- przypadek dużego mimośrodu, kiedy x
eff
/d
≤ ξ
eff,lim
(rysunek 12),
- przypadek małego mimośrodu, kiedy x
eff
/d >
ξ
eff,lim
(rysunek 13).
Rysunek 12 - Schemat do obliczania nośności mimośrodowo ściskanego przekroju żelbetowego w przypadku dużego
mimośrodu
Stan graniczny nośności elementów o przekroju mającym przynajmniej jedną płaszczyznę symetrii, obciążonym siłami
działającymi w tej płaszczyźnie należy sprawdzać z warunku
(28)
w którym:
- odległość siły N
Sd
od środka ciężkości zbrojenia A
s1
,
e
s1
- odległość siły N
Rd
od środka ciężkości zbrojenia A
s1
.
Położenie osi obojętnej wyznacza się z równania
(29)
W
arto
ść
α we wzorach (28) i (29) przyj
m
j
e się równą 0,85.
Rysunek 13 - Schem
at do obliczania no
ś
no
ś
ci m
im
o
ś
rodowo ścisk
anego przek
roj
u żelbetowego w przypadk
u m
ałego
Część 6 Strona 6
mimośrodu
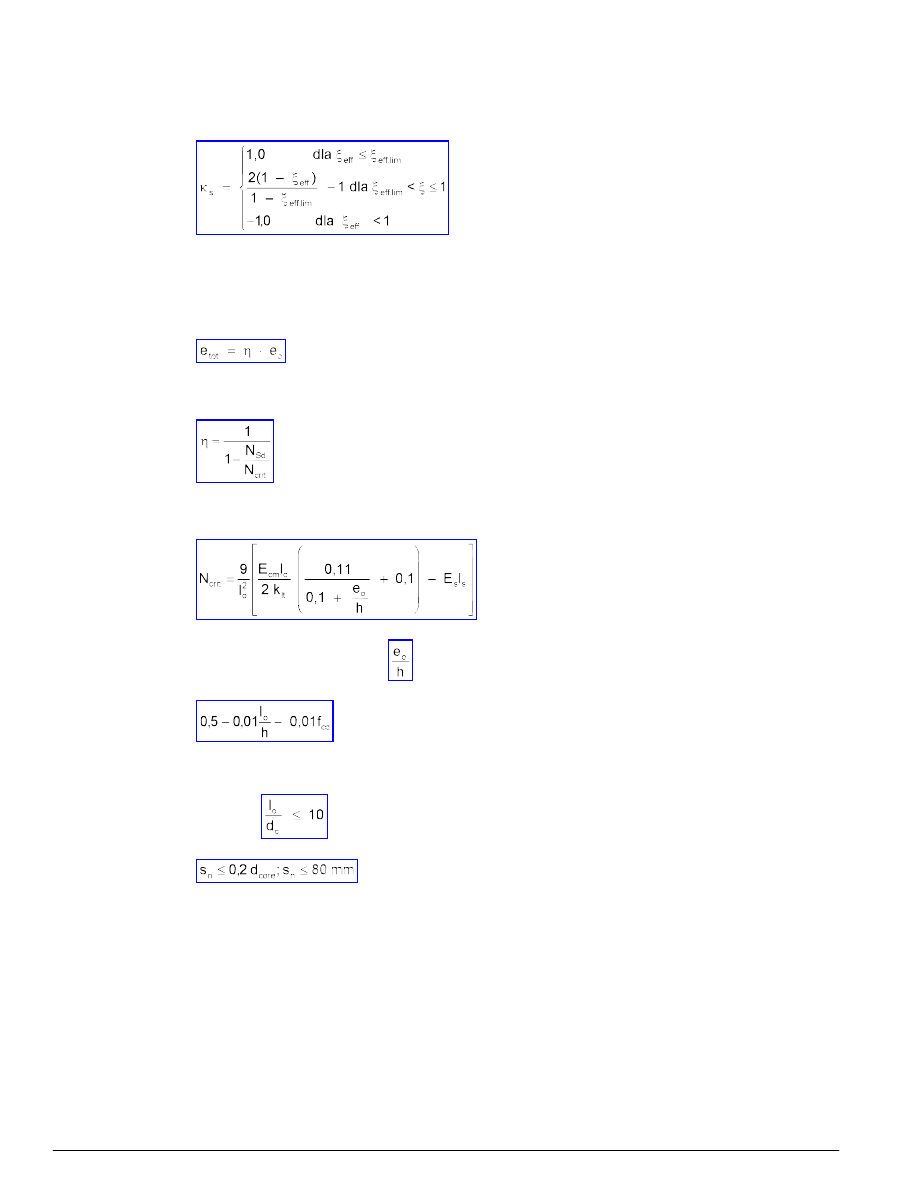
Wartość
κ
s
wyznacza się ze wzoru
(30)
Jeżeli środek ciężkości zbrojenia A
s2
znajduje się dalej od bardziej ściskanej krawędzi przekroju niż środek ciężkości bryły
naprężeń ściskających w betonie, to należy przyjąć, że ramię sił wewnętrznych jest równe d - a
2
.
Wpływ smukłości na nośność elementów żelbetowych uwzględniać należy w obliczeniach przez zwiększenie mimośrodu
początkowego e
o
= e
a
+ e
e
do wartości e
tot
wyznaczanej wg wzoru
(31)
w którym:
(32)
Wartość N
crit
należy obliczać wg wzoru
(33)
przy czym do wzoru (33) należy podstawiać wartość
nie mniejszą niż 0,05 oraz nie mniejszą niż
(34)
5.3.4 Słupy uzwojone
Wpływ uzwojenia na nośność słupów może być uwzględniany w obliczeniach jedynie w przypadku obciążenia osiowego
(e
e
= 0) jeżeli smukłość słupa
oraz jeżeli skok s
n
linii śrubowej uzwojenia spełnia warunki (rysunek 14).
Jeżeli warunki te nie są spełnione, nośność słupów uzwojonych należy sprawdzać bez uwzględnienia wpływu uzwojenia.
Wpływ niezamierzonego mimośrodu e
a
siły podłużnej uwzględniono w podanych niżej wzorach przez obniżenie wytrzymałości
betonu na ściskanie do wartości 0,9
α f
cd
.
Część 6 Strona 7
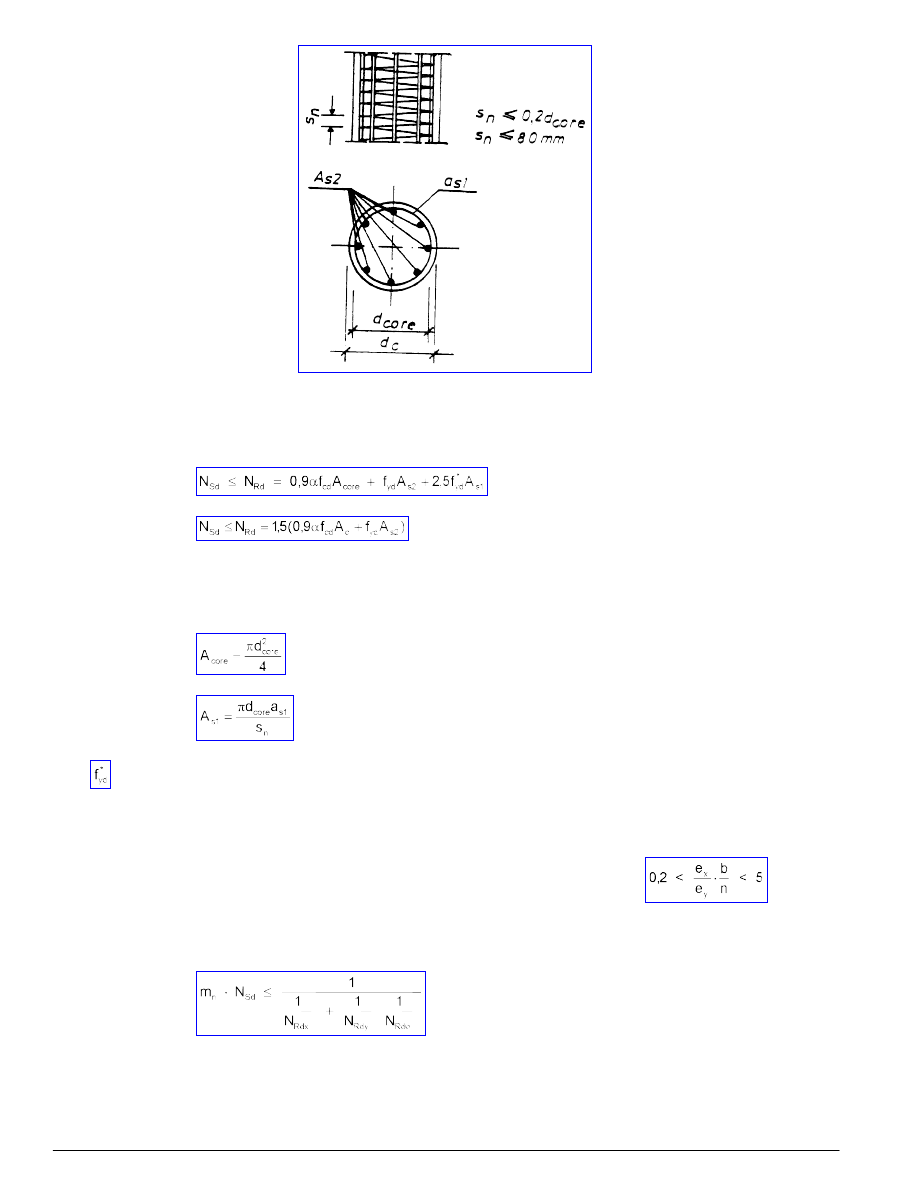
Rysunek 14 - Słup uzwojony
Stan graniczny nośności słupa uzwojonego sprawdzać należy ze wzorów
(35)
(36)
w których:
α = 0,85
- obliczeniowa granica plastyczności stali uzwojenia.
5.3.5 Elementy podlegające dwukierunkowemu ściskaniu mimośrodowemu
Elementy o przekroju symetrycznym względem dwóch osi wzajemnie prostopadłych, podlegające równoczesnemu działaniu
siły podłużnej i momentów zginających działających w płaszczyźnie obu osi symetrii przekroju, należy obliczać jako elementy
podlegające dwukierunkowemu ściskaniu mimośrodowemu, gdy mimośrody spełniają warunek
, przy
czym e
x
, e
y
- mimośrody siły podłużnej, odpowiednio w kierunku osi x i y, względem środka ciężkości przekroju betonowego,
obliczone z uwzględnieniem wpływu smukłości (w odpowiednim kierunku) według 5.3.3.2.
Noścość elementów podlegających dwukierunkowemu ściskaniu mimośrodowemu można sprawdzać z warunku
(37)
Część 6 Strona 8
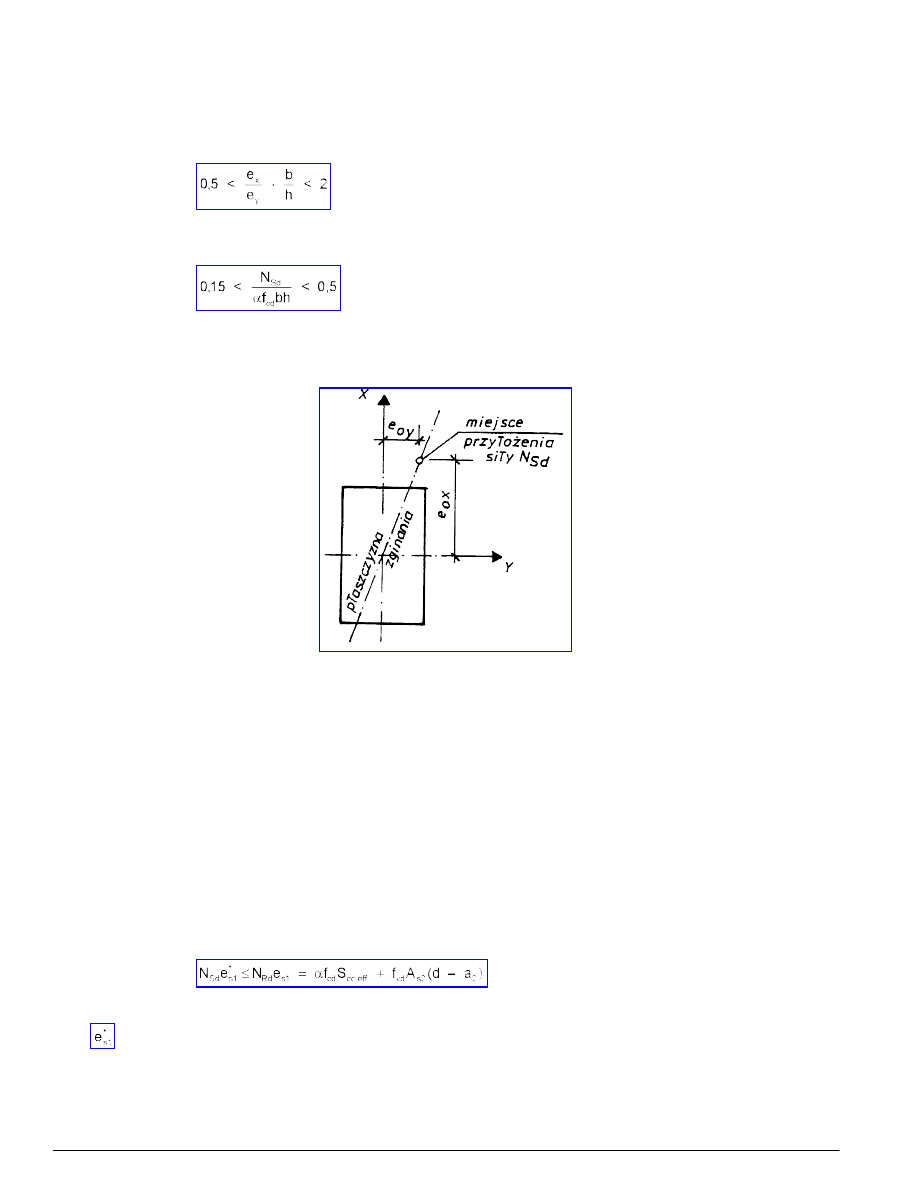
w którym:
N
Rdx,
N
Rdy
- obliczeniowe siły podłużne, jakie mogą być przeniesione przez rozpatrywany przekrój (nośności obliczeniowe)
przy założeniu, że działają one na mimośrodach początkowych e
ox
i e
oy
(rysunek 15); siły te, jeżeli smukłość elementu jest
większa niż podano w 5.3.1. obliczać należy z uwzględnieniem wpływu smukłości,
N
Rdo
- nośność obliczeniowa przekroju obciążonego osiowo, obliczana bez uwzględnienia wpływu smukłości,
m
n
- współczynnik korekcyjny o wartości: m
n
= 1,1 jeżeli liczba prętów w przekroju jest mniejsza niż 8 i jednocześnie
oraz
m
n
= 1,0 w pozostałych przypadkach.
Rysunek 15 - Przekrój podlegający dwukierunkowemu ściskaniu mimośrodowemu
5.4 Rozciąganie
5.4.1 Nośność elementów rozciąganych mimośrodowo - metoda uproszczona
Przy obliczaniu nośności rozciąganych elementów żelbetowych, tzn. obciążonych siłą N
Sd
na mimośrodzie e
o
= e
e
(bez
uwzględnienia niezamierzonego mimośrodu przypadkowego), rozróżnia się dwa przypadki:
- przypadek dużego mimośrodu, gdy wypadkowa sił podłużnych leży na zewnątrz odcinka ograniczonego przez środki
ciężkości zbrojenia A
s1
i A
s2
,
- przypadek małego mimośrodu gdy wypadkowa sił podłużnych leży wewnątrz odcinka ograniczonego przez środki ciężkości
zbrojenia A
s1
i A
s2
.
Nośność mimośrodowo rozciąganych elementów żelbetowych obciążonych z dużym mimośrodem (rysunek 16) określać
można przy założeniu prostokątnego wykresu naprężeń ściskających w betonie przy tych samych założeniach, które
przyjmuje się przy sprawdzaniu elementów zginanych według 5.2.
Zgodnie z takimi założeniami stan graniczny nośności elementów mających przynajmniej jedną płaszczyznę symetrii i
obciążonych siłami działającymi w tej płaszczyźnie sprawdza się z warunku
(38)
w którym:
i e
s1
- jak we wzorze (28).
Część 6 Strona 9
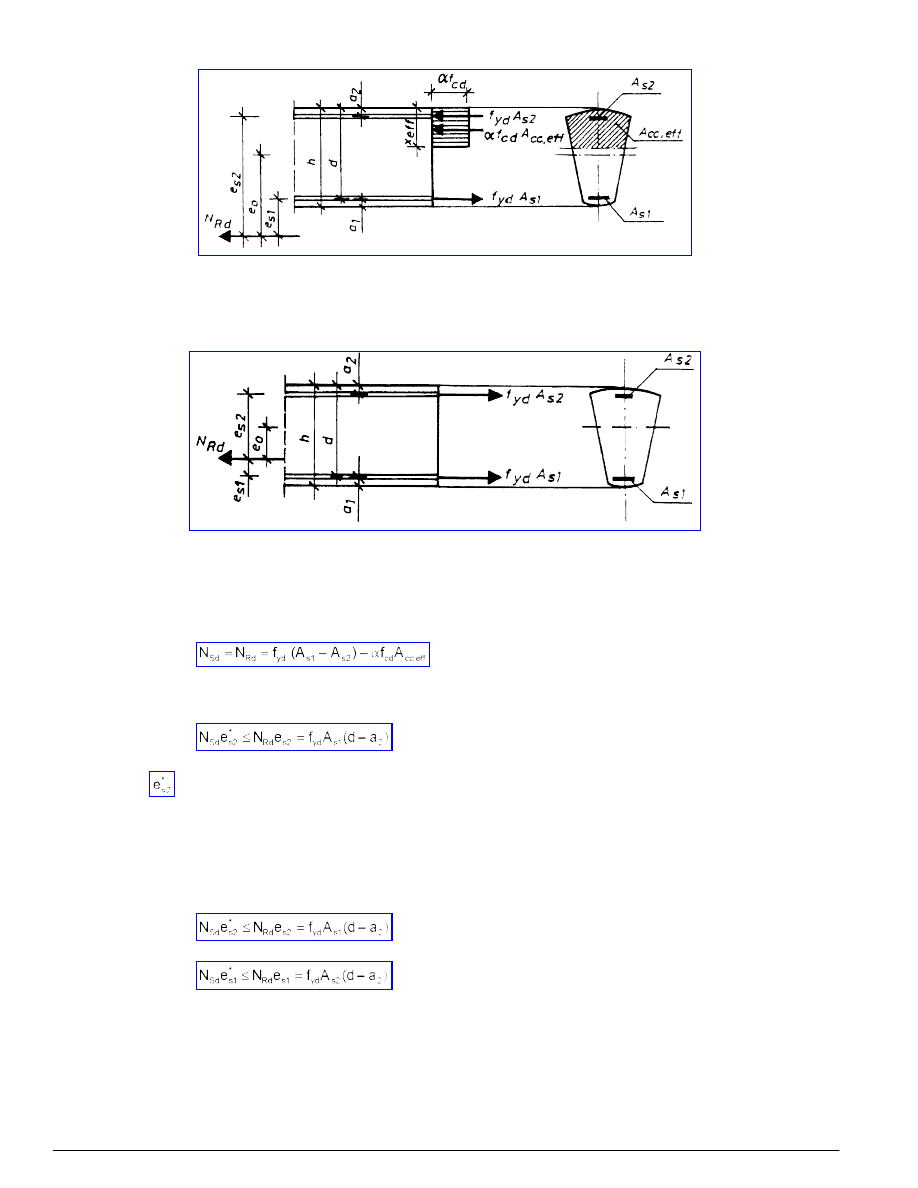
Rysunek 16 - Schemat do obliczania nośności mimośrodowo rozciąganego przekroju żelbetowego w przypadku dużego
mimośrodu
Rysunek 17 - Schemat do obliczania nośności mimośrodowo rozciąganego przekroju żelbetowego w przypadku małego
mimośrodu
Położenie osi obojętnej wyznacza się z równania
(39)
Jeśli x
eff
≤ 2a
2
to nośność przekroju należy sprawdzić z warunku
(40)
w którym:
- odległość siły N
sd
od środka ciężkości zbrojenia A
s2
,
e
s2
- odległość siły N
Rd
od środka ciężkości zbrojenia A
s2
.
Nośność elementów obciążonych z małym mimośrodem (rysunek 17) należy sprawdzać przy założeniu, że:
a) pomija się wytrzymałość betonu na rozciąganie,
b) naprężenia w całym zbrojeniu przekroju równe są najwyżej obliczeniowej granicy plastyczności stali na rozciąganie f
yd
.
Zgodnie z takimi założeniami stan graniczny nośności elementów obciążonych z małym mimośrodem sprawdza się z
warunków
(41)
(42)
5.4.2 Elementy rozciągane osiowo
Stan graniczny nośności elementów rozciąganych osiowo tj. kiedy siła przyłożona jest w środku ciężkości przekroju całego
zbrojenia - sprawdza się z warunku
Część 6 Strona 10
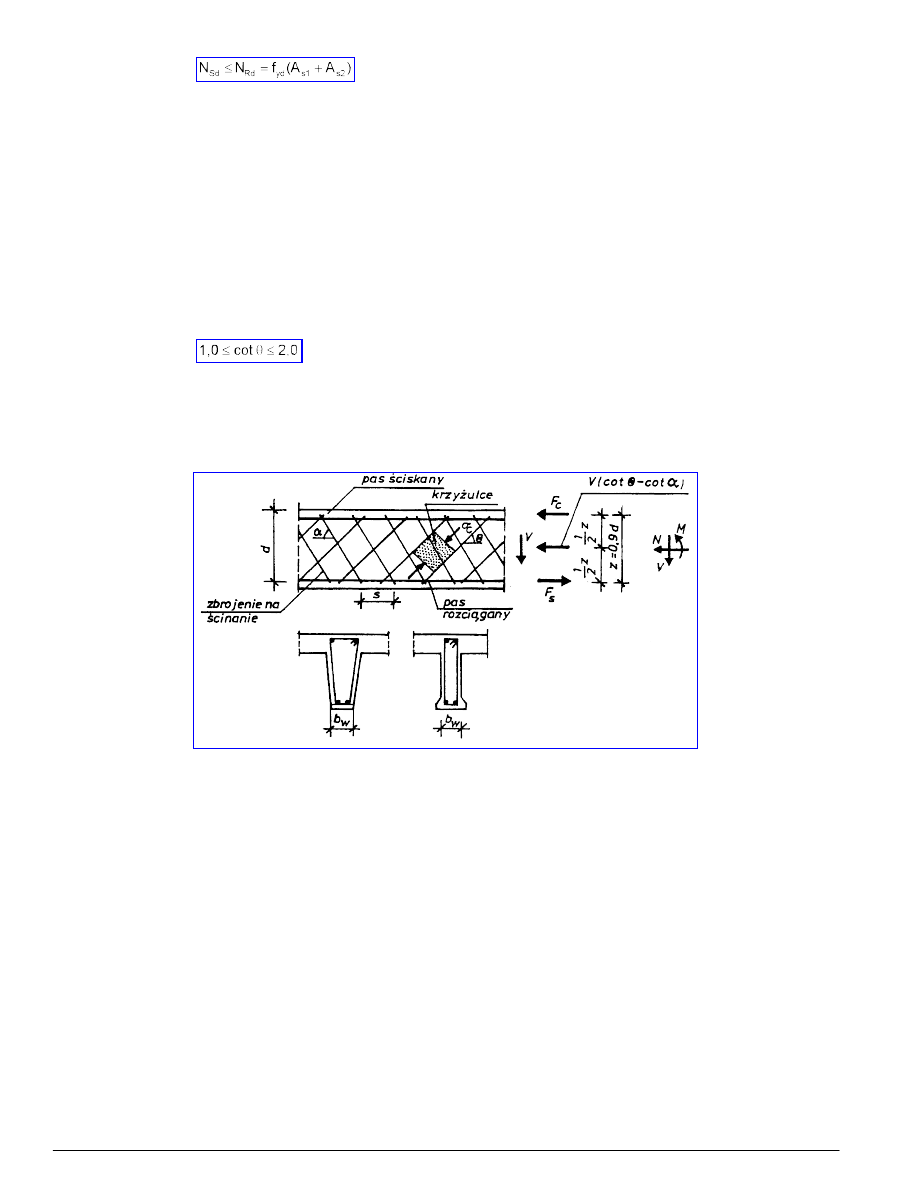
(43)
w którym:
A
s1
+ A
s2
- całkowity przekrój zbrojenia elementu.
5.5 Ścinanie elementów żelbetowych
5.5.1 Zasady ogólne
5.5.1.1 Podstawowe założenia
Zakłada się, że element żelbetowy składa się ze strefy ściskanej, strefy rozciąganej (zbrojenia podłużnego) i strefy ścinania,
położonej pomiędzy wypadkowymi sił F
c
i F
s
w strefach ściskanej i rozciąganej (rysunek 18).
Strefa ścinania składa się ze ściskanych, betonowych krzyżulców nachylonych pod kątem
θ do osi elementu i z rozciąganego
zbrojenia poprzecznego, rozmieszczonego w płaszczyznach o rozstawie s, nachylonego pod kątem
α do tej osi.
Kąt
α zbrojenia poprzecznego uwzględnianego w obliczeniach nie może być mniejszy niż 45°, a kąt θ można dobierać
dowolnie z przedziału określonego nierównością
(44)
Wysokość strefy ścinania jest równa ramieniu sił wewnętrznych z. Można przyjmować, że w elementach zginanych i
rozciąganych z = 0,9d. Jeżeli nie korzysta się z powyższego uproszczenia, to za z należy przyjmować najmniejsze ramię sił
wewnętrznych na rozpatrywanym odcinku, obliczone z pominięciem wpływu ukośnego zbrojenia na ścinanie.
Rysunek 18 - Ścinanie odcinka belki, schemat rozkładu sił i oznaczenia:
α - kąt nachylenia zbrojenia na ścinanie do osi podłużnej elementu,
θ - kąt nachylenia krzyżulców betonowych do osi podłużnej elementu,
F
s
- siła rozciągająca w zbrojeniu podłużnym,
F
c
- siła ściskająca w betonie (w kierunku osi podłużnej elementu),
b
w
- najmniejsza szerokość strefy ścinania,
z - ramię sił wewnętrznych.
Naprężenia
σ
c
w ściskanych krzyżulcach betonowych nie powinny przekraczać
νf
cd
, a naprężenia
σ
s
w zbrojeniu
poprzecznym nie powinny przekraczać obliczeniowej granicy plastyczności tego zbrojenia f
ywd
. Stan graniczny nośności jest
osiągany wtedy, gdy
σ
c
=
νf
cd
lub
σ
s
= f
ywd
.
5.5.1.2 Graniczne siły poprzeczne, siła V
Sd
i rodzaje odcinków
Obliczeniowa nośność na ścinanie V
Rd
jest równa jednej z trzech granicznych sił poprzecznych: V
Rd1
, V
Rd2
albo V
Rd2,red
,
V
Rd3
.
V
Rd1
- jest graniczną siłą poprzeczną ze względu na ukośne rozciąganie, powstające przy ścinaniu w elemencie nie mającym
poprzecznego zbrojenia na ścinanie,
V
Rd2
- jest graniczną siłą poprzeczną ze względu na ukośne ściskanie, powstające przy ścinaniu w elementach zginanych,
V
Rd2,red
- jest graniczną siłą poprzeczną jak V
Rd2
, ale w elementach mimośrodowo ściskanych,
Część 6 Strona 11

V
Rd3
- jest graniczną siłą poprzeczną ze względu na rozciąganie poprzecznego zbrojenia na ścinanie.
Siłę V
Rd2,red
oblicza się ze wzoru
(45)
We wzorze (45)
σ
cp,eff
jest efektywnym, średnim naprężeniem w betonie wywołanym przez siłę podłużną, obliczanym ze
wzoru
(46)
w którym:
N
Sd
- obliczeniowa siła podłużna (dodatnia przy ściskaniu), a w elementach sprężonych suma obliczeniowej siły podłużnej i
siły podłużnej wywołanej sprężeniem według p. 7.1.8.4,
A
S2
- pole przekroju zbrojenia w strefie ściskanej,
σ
s2
- naprężenie równe f
yd
, lecz nie większe niż 400 MPa,
A
c
- pole poprzecznego przekroju betonu.
Warunek stanu granicznego nośności jest spełniony wtedy, gdy na każdym odcinku, który można wydzielić z elementu,
spełniona jest nierówność
(47)
w której V
Sd
i V
Rd
oznaczają odpowiednio wartość bezwzględną obliczeniowej siły poprzecznej i obliczeniową nośność,
przyporządkowane rozpatrywanemu odcinkowi.
Jeżeli zachodzi bezpośrednie przekazywanie obciążenia belki lub płyty na podporę, tzn. jeżeli reakcja podpory działa na
dolną krawędź elementu, a równomiernie rozłożone obciążenie działa na górną krawędź elementu, to przy sprawdzaniu
warunków V
Sd
≤ V
Rd1
i V
Sd
≤ V
Rd3
na odcinku przypodporowym można za V
Sd
przyjąć największą (co do wartości
bezwzględnej) siłę poprzeczną występującą w odległości d od krawędzi podpory. W innych przypadkach za V
Sd
należy
przyjmować największą (co do wartości bezwzględnej) obliczeniową siłę poprzeczną na rozpatrywanym odcinku.
Te odcinki elementu, na których spełniony jest warunek
(48)
nazywa się odcinkami pierwszego rodzaju. Odcinki, na których nierówność (48) nie jest spełniona nazywa się odcinkami
drugiego rodzaju.
5.5.1.3 Wymagania
Zbrojenie poprzeczne powinno spełniać wymagania dotyczące minimum
ρ
w
określone w 9.3.1.5. Wymagania te mogą być
pominięte w elementach takich jak płyty pełne, użebrowane i płyty z kanałami lub wewnętrznymi pustkami, gdy konstrukcja
tych elementów zapewnia poprzeczne przekazywanie sił wewnętrznych, pod warunkiem, że nie występują znaczące podłużne
siły rozciągające.
Gdy obciążenie nie jest przyłożone do górnej części belki lub gdy reakcja podpory nie jest przyłożona do dolnej części belki,
to należy zaprojektować zbrojenie podwieszające, uniemożliwiające zniszczenie przez rozciąganie wywołane takim układem
sił.
Sprawdzanie stanu granicznego nośności na odcinkach pierwszego rodzaju polega na wykazaniu, że siła V
sd
nie jest większa
od mniejszej z sił V
Rd1
i V
Rd2
(przy czystym zginaniu) lub mniejszej z sił V
Rd1
i V
Rd2,red
(przy mimośrodowym ściskaniu).
Obliczanie zbrojenia poprzecznego i szerokości rys ukośnych na tych odcinkach nie jest wymagane.
Sprawdzanie stanu granicznego nośności na odcinkach drugiego rodzaju polega na wykazaniu, że siła V
Sd
nie jest większa
od mniejszej z sił V
Rd3
i V
Rd2
(przy czystym zginaniu) lub V
Rd3
i V
Rd2,red
(przy mimośrodowym ściskaniu).
Ponadto należy wykazać, że szerokość rys ukośnych na tych odcinkach, obliczona zgodnie z 6.3 nie przekracza szerokości
granicznej według 4.7.3. Odcinek drugiego rodzaju można podzielić na krótsze części i wykonać obliczenia każdej części w
zależności od występującej na niej maksymalnej siły V
Sd
. Części nie mogą być krótsze niż z
⋅ cot θ.
5.5.2 Nośność odcinków pierwszego rodzaju
5.5.2.1 Siła V
Rd1
Siłę V
Rd1
oblicza się ze wzoru
Część 6 Strona 12
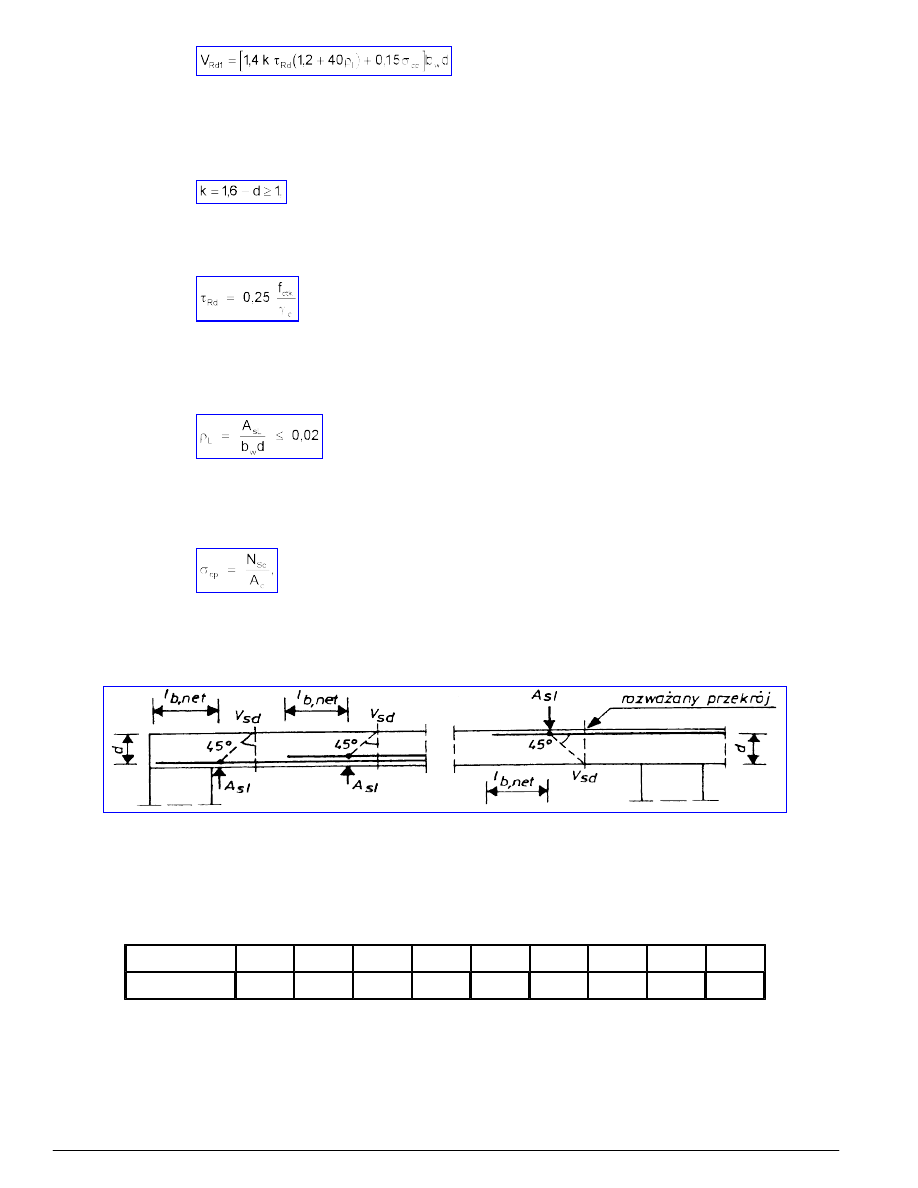
(49)
w którym:
b
w
- najmniejsza szerokość strefy ścinania (rysunek 18),
k - współczynnik równy 1,0, gdy do podpory doprowadzono mniej niż 50% rozciąganego zbrojenia przęsłowego, a w innych
przypadkach wyznaczany ze wzoru
(50)
w którym d oznacza wysokość użyteczną przekroju w metrach,
τ
Rd
- obliczeniowa wytrzymałość betonu na ścinanie wyznaczona dla betonów klasy nie wyższej niż B55 ze wzoru
Wartość
τ
Rd
dla
γc = 1,5 podano w tablicy 13.
ρ
L
- stopień zbrojenia wyznaczany ze wzoru
(51)
A
sL
- pole przekroju głównego zbrojenia rozciąganego, mającego długość nie mniejszą niż d + I
b,net
poza rozpatrywanym
przekrojem elementu (rysunek 19),
σ
cp
- naprężenie wyznaczane ze wzoru
w którym N
Sd
oznacza siłę podłużną wywołaną obciążeniem i sprężeniem (dodatnią przy ściskaniu), a A
c
oznacza pole
przekroju poprzecznego betonu.
Rysunek 19 - Definicja A
sL
we wzorze (51)
Tablica 13 - Wytrzymałość obliczeniowa na ścinanie
ττττ
Rd
(MPa)
Klasa betonu
B15
B20
B25
B30
B37
B45
B50
B55
wyższa
τ
Rd
0,18
0,22
0,26
0,30
0,34
0,37
0,41
0,44
0,48
5.5.2.2 Siła V
Rd1
w płytach żelbetowych
Część 6 Strona 13

Przy sprawdzaniu płyt o szerokości b
≥ 4h i wysokości użytecznej d ≤ 0,25 m siłę graniczną V
Rd1
można obliczać ze wzoru
(52)
5.5.2.3 Siła V
Rd2
Siłę V
Rd2
oblicza się ze wzoru
(53)
w którym:
(54)
5.5.3 Nośność odcinków drugiego rodzaju
5.5.3.1 Elementy o stałej wysokości przekroju
Jeżeli zbrojenie na ścinanie składa się wyłącznie ze strzemion prostopadłych do osi belki (tzn. gdy nie stosuje się prętów
odgiętych lub pomija się wpływ tych prętów), to siły \/
Rd2
i V
Rd3
oblicza się ze wzorów
(55)
(56)
Jeżeli zbrojenie na ścinanie składa się ze strzemion prostopadłych do osi belki oraz z prętów odgiętych lub strzemion
ukośnych, to siły V
Rd2
i V
Rd3
oblicza się ze wzorów
(57)
w którym
(58)
We wzorach (57) i (58):
ν - współczynnik według wzoru (54),
α - kąt nachylenia prętów odgiętych lub ukośnych strzemion,
A
sw1
- pole przekroju poprzecznego prętów tworzących jedno strzemię (np. pole czterech prętów
φ6 w przypadku podwójnych
strzemion
φ6),
f
ywd1
- obliczeniowa granica plastyczności strzemion,
s
1
- rozstaw strzemion prostopadłych do osi elementu,
A
sw2
- pole przekroju poprzecznego ukośnych strzemion lub prętów odgiętych tworzących jedną płaszczyznę odgięć,
s
2
- średni rozstaw płaszczyzn odgięć lub strzemion ukośnych mierzony wzdłuż osi belki,
f
ywd2
- obliczeniowa granica plastyczności zbrojenia A
sw2
.
W belkach pręty odgięte mogą być uwzględniane jako zbrojenie na ścinanie tylko wtedy, gdy strzemiona pionowe przenoszą
co najmniej 50 % siły V
Sd
.
Jeżeli zbrojenie na ścinanie składa się wyłącznie z prętów ukośnych, to siły V
Rd2
i V
Rd3
oblicza się podstawiając do wzorów
Część 6 Strona 14
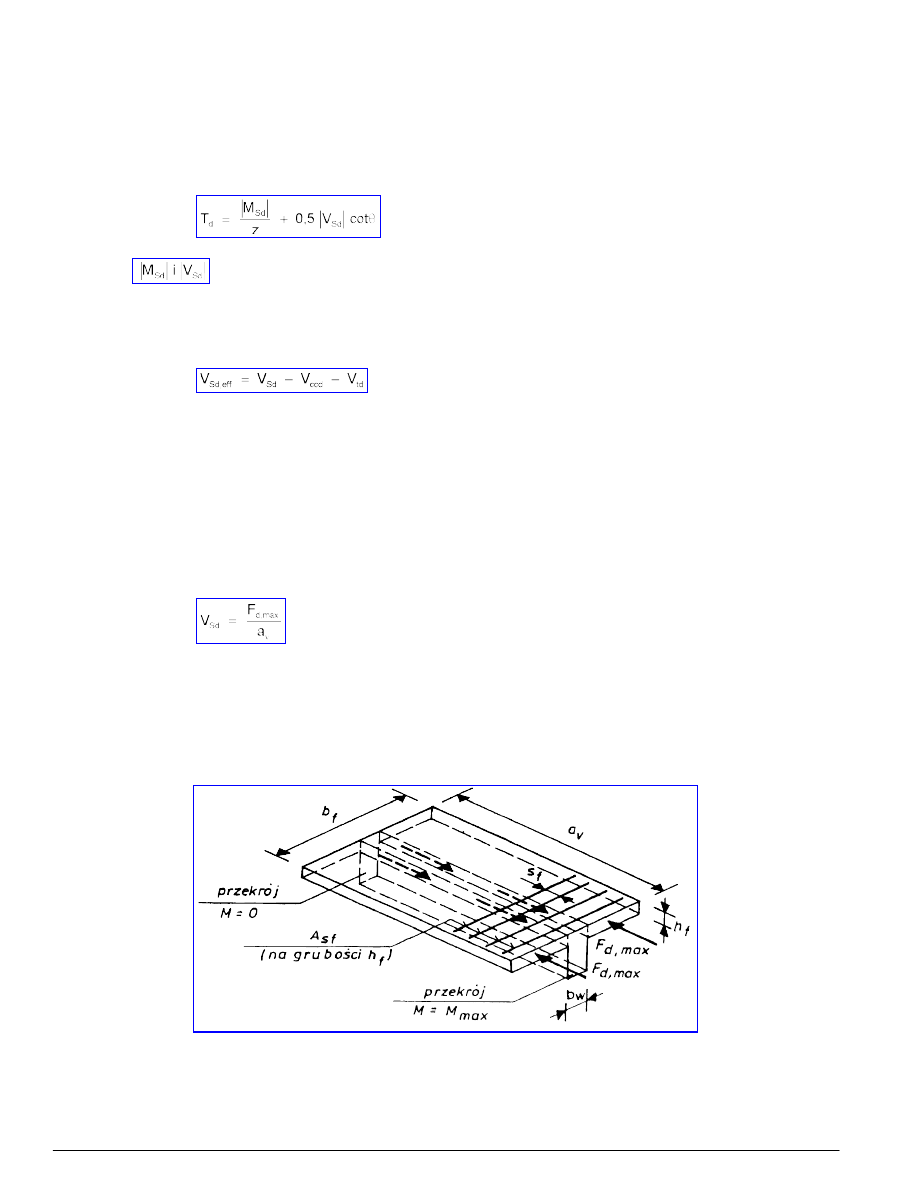
(57) i (58) A
sw1
= 0 i
∆V
Rd
= vf
cd
b
w
z cot
α / (1 + col
2
θ).
5.5.3.2 Zbrojenie podłużne na odcinkach drugiego rodzaju
Przedstawiony w 5.5.1.1 układ sił wewnętrznych może powstać tylko wtedy, gdy główne, podłużne zbrojenie rozciągane jest
należycie zakotwione poza przekrojem, w którym powstaje największa siła V
Sd
. Zbrojenie to należy rozmieszczać kierując się
zasadą, że pomiędzy wykresem przedstawiającym nośność zbrojenia a obwiednią momentów zginających powinien mieścić
się odcinek (odkładany równolegle do osi belki) o długości nie mniejszej niż 0,5 z cot
θ. Przy podporach, na których
występują małe momenty zginające, należy stosować rozciągane zbrojenie dołem (rysunek 19), mogące przenieść siłę T
d
nie mniejszą niż
(59)
gdzie:
- wartości bezwzględne obliczeniowego momentu zginającego i obliczeniowej siły poprzecznej w
rozważanym przekroju.
5.5.3.3 Elementy o zmiennej wysokości przekroju
Elementy o zmiennej wysokości przekroju sprawdzać należy na ścinanie zgodnie z warunkami V
Sd
≤ V
Rd2
i V
Sd
≤ V
Rd3
przyjmując za V
Sd
wartość V
Sd,eff
określoną wzorem
(60)
gdzie:
V
Sd
- siła poprzeczna wywołana obciążeniem obliczeniowym,
V
ccd
- równoległa do V
Sd
składowa wypadkowej siły w strefie ściskanej,
V
td
- równoległa do V
Sd
składowa wypadkowej siły w strefie rozciąganej.
Składowe V
ccd
i V
td
przyjmuje się jako dodatnie, kiedy ich kierunek jest taki sam jak V
Sd
.
5.5.4 Ścinanie między środnikiem i półkami
Nośność na ścinanie półki oblicza się traktując półkę jako zespół ściskanych krzyżulców połączonych cięgnami w postaci
zbrojenia rozciąganego.
Ś
rednią podłużną siłę ścinającą na jednostkę długości określa wzór
(61)
gdzie:
F
d,max
- maksymalna wartość obliczeniowej siły podłużnej w półce, po jednej stronie środnika (ściskającej, przenoszonej
przez beton w przekroju przęsłowym lub rozciągającej, przenoszonej przez zbrojenie podłużne półki w przekroju
podporowym),
a
v
- odległość miejsca momentu zerowego od miejsca momentu maksymalnego (rysunek 20).
Rysunek 20 - Oznaczenia dotyczące połączenia półki ze środnikiem
Część 6 Strona 15
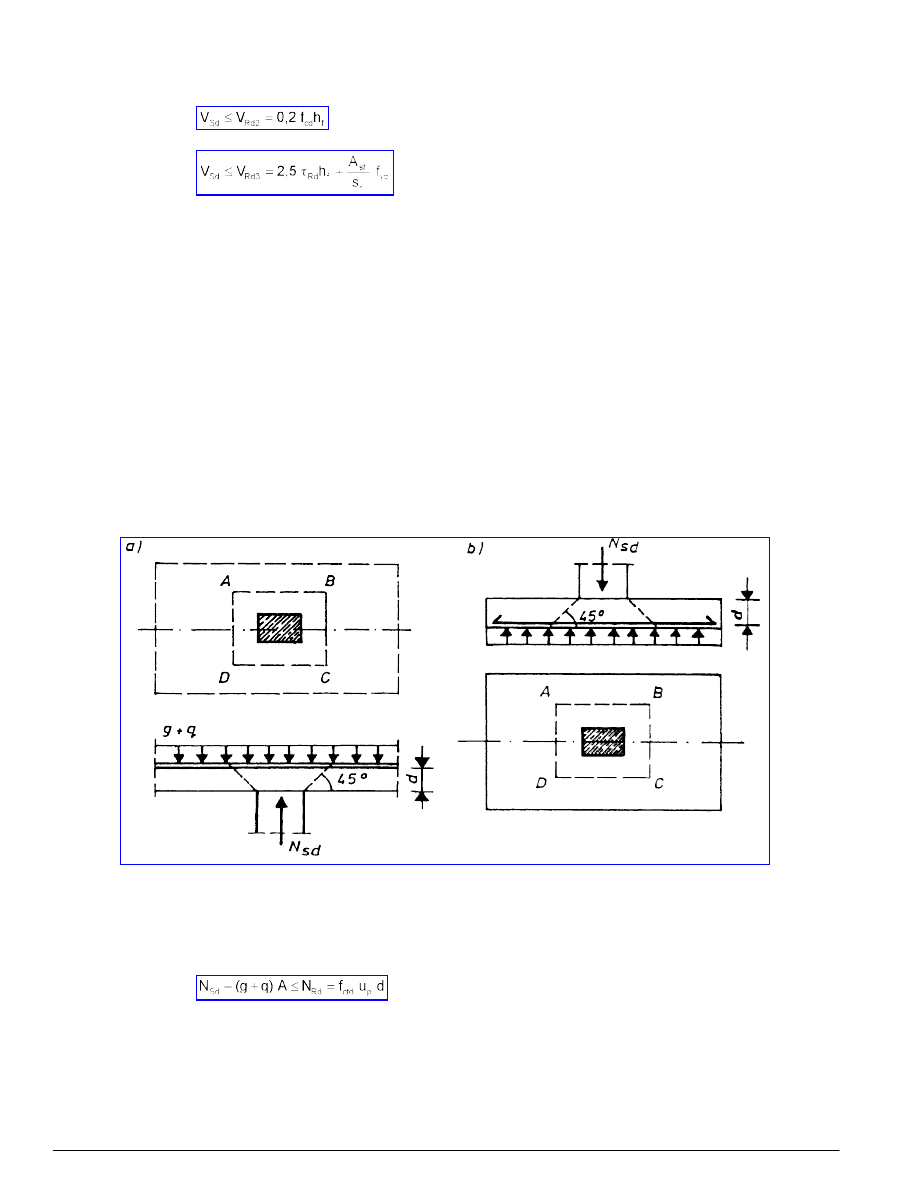
W obliczeniach wykazać należy że:
(62)
(63)
gdzie:
τ
Rd
- wg tablicy 13,
h
f
- grubość półki przekroju teowego,
A
sf
i s
f
- odpowiednio: pole przekroju i rozstaw prętów zbrojenia poprzecznego w półce przekroju teowego.
Jeżeli na odcinku a
v
półka podlega podłużnemu rozciąganiu, to człon 2,5
τ
Rd
h
f
we wzorze (63) należy pominąć.
W przypadku, kiedy ścinanie między półką i środnikiem występuje łącznie ze zginaniem w kierunku poprzecznym, przekrój
zbrojenia powinien odpowiadać większej z dwóch wartości wymaganych ze względu na ścinanie (63) lub zginanie.
5.6 Przebicie
5.6.1 Zasady ogólne
Nośność elementów płytowych i stóp fundamentowych na przebicie należy sprawdzać w przekrojach ukośnych
poprowadzonych pod kątem nie mniejszym niż 45° od krawędzi powierzchni, na którą działa obliczeniowa siła N
Sd
, do
poziomu płaszczyzny zbrojenia (rysunek 21). Kształt powierzchni odciętej przekrojami przebicia w poziomie zbrojenia zależy
od kształtu pola, na które działa siła.
Stopień zbrojenia podłużnego elementów sprawdzanych na przebicie zgodnie z 5.6.2 lub 5.6.3 - nie może być mniejszy niż
0,005 w obu kierunkach.
Rysunek 21 - Powierzchnie przebicia: a) w stropach płaskich, b) w płytowych stopach fundamentowych
5.6.2 Elementy niezbrojone na przebicie
Nośność elementów obciążonych w sposób ciągły, w przybliżeniu symetryczny, można obliczać ze wzoru
(64)
gdzie:
A - pole powierzchni odciętej przekrojami przebicia w poziomie (średnim) zbrojenia na zginanie (prostokąt ABCD na rysunku
Część 6 Strona 16
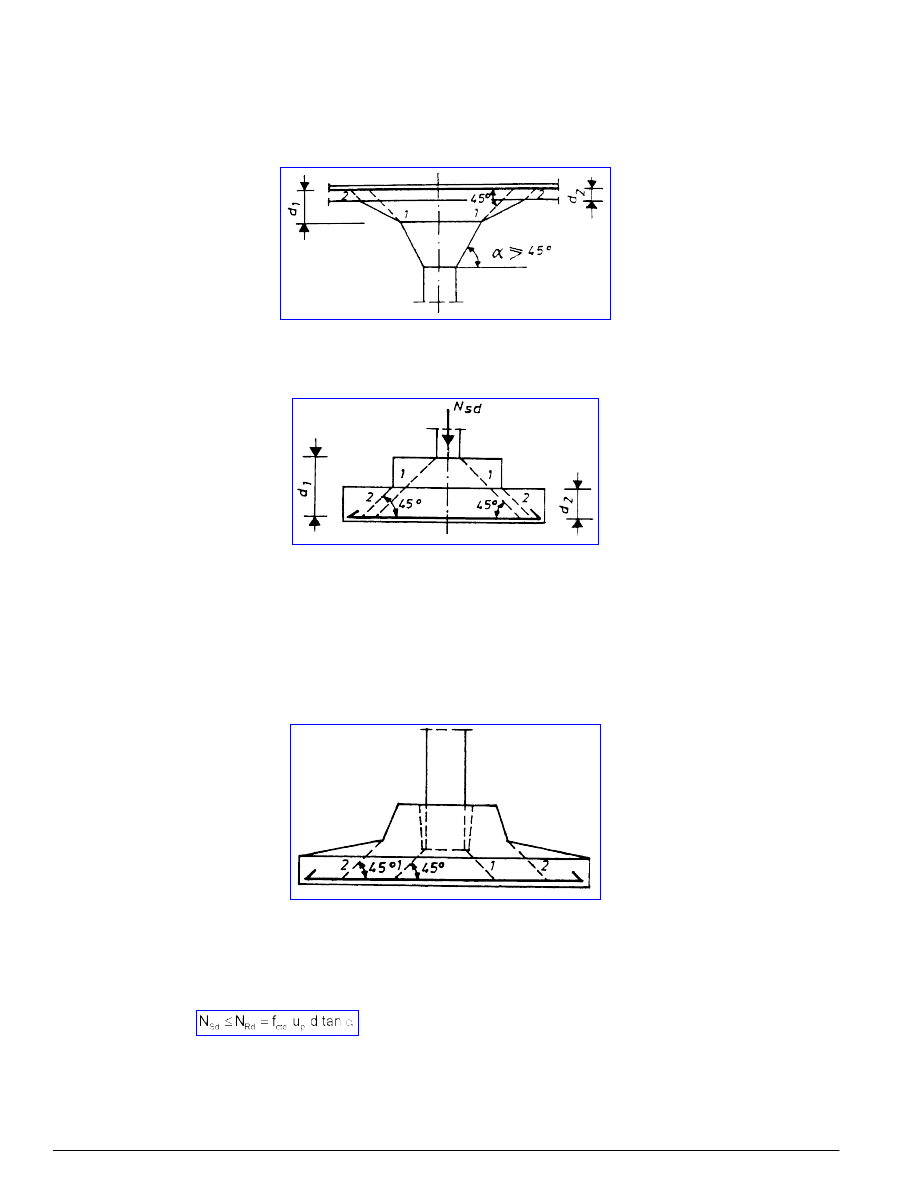
21),
g, q - obciążenia równomierne lub odpór podłoża,
u
p
- średnia arytmetyczna obwodów: powierzchni, na którą działa siła i powierzchni powstającej w poziomie zbrojenia przy
założeniu, że płaszczyzny boczne ostrosłupa pochylone są pod kątem 45°,
d - wysokość użyteczna; jako d należy przyjmować wartość średnią dla kierunków x i y.
Rysunek 22 - Przekroje sprawdzane na przebicie w stropie grzybkowym
Rysunek 23 - Przekroje sprawdzane na przebicie w schodkowych stopach fundamentowych
W przypadku głowic w stropach grzybkowych nośność na przebicie należy sprawdzać we wszystkich przekrojach
wynikających z powyższych zasad (rysunek 22 - przekroje 1 i 2), zaś w schodkowych stopach fundamentowych - poniżej
każdej odsadzki (rysunek 23 - przekroje 1 i 2).
W kielichowych stopach fundamentowych (rysunek 24) nośność na przebicie należy sprawdzać w przekrojach 1 na
obciążenie montażowe i w przekrojach 2 na obciążenie całkowite.
Rysunek 24 - Przekroje sprawdzane na przebicie w stopach kielichowych
W przypadku elementów, w których przebicie może nastąpić tylko w przekrojach nachylonych pod kątem większym niż 45°
(np. płyta fundamentowa oparta na palach - rysunek 25), obliczenie na przebicie można przeprowadzać na podstawie wzoru
(65)
Część 6 Strona 17
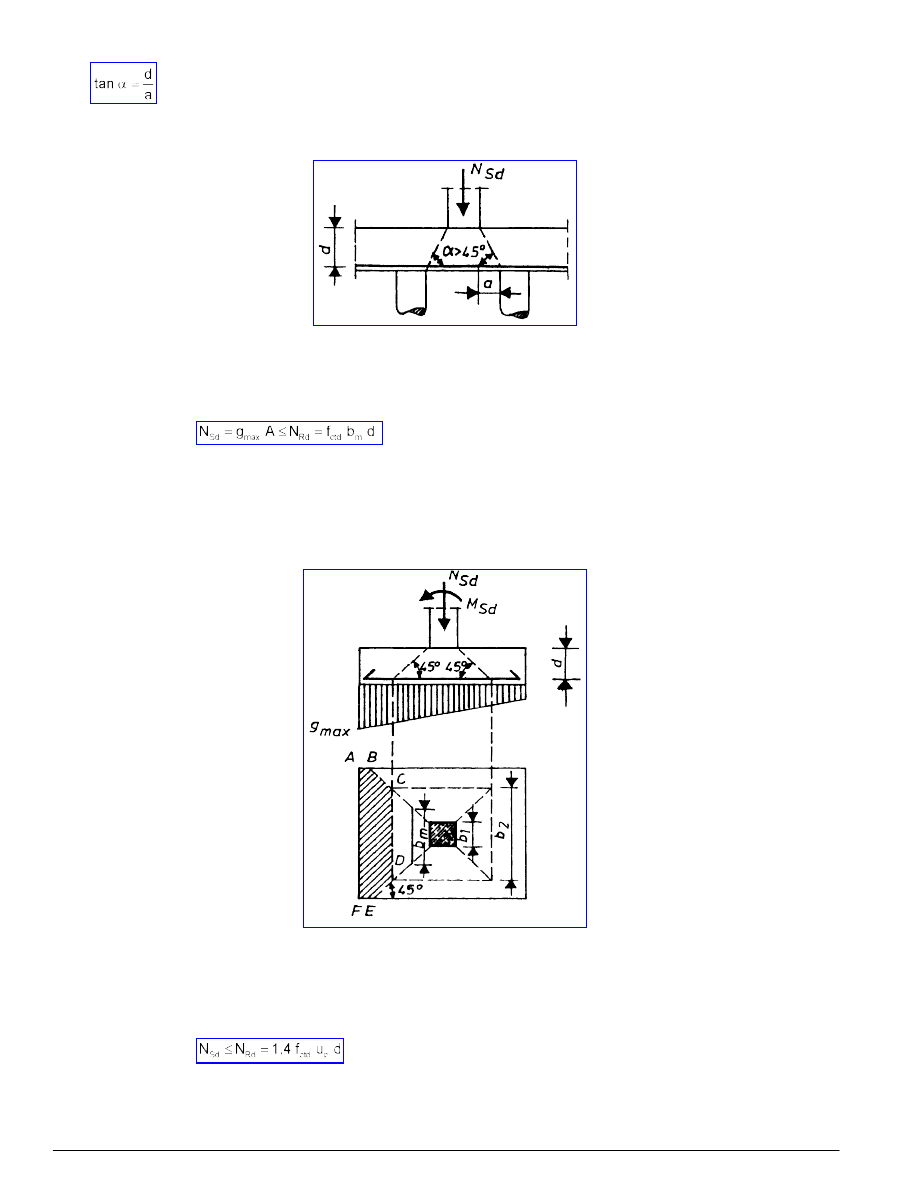
w którym:
lecz nie więcej niż 2,5,
a - długość odcinka, według rysunku 25.
Rysunek 25 - Przypadek przebicia pod kątem większym niż 45° (1 - przekrój przebicia)
W przypadku mimośrodowo obciążonych stóp fundamentowych nośność na przebicie można sprawdzać ze wzoru
(66)
w którym:
g
max
- największy krawędziowy obliczeniowy odpór jednostkowy podłoża (rysunek 26),
A - pole powierzchni wielokąta ABCDEF,
b
m
- średnia arytmetyczna szerokości b
1
i b
2
, gdzie b
1
i b
2
według rysunku 26.
Rysunek 26 - Schemat do obliczania nośności na przebicie stopy fundamentowej obciążonej mimośrodowo
5.6.3 Elementy zbrojone na przebicie
Nośność elementów zbrojonych poprzecznie można obliczać ze wzorów
(67)
Część 6 Strona 18
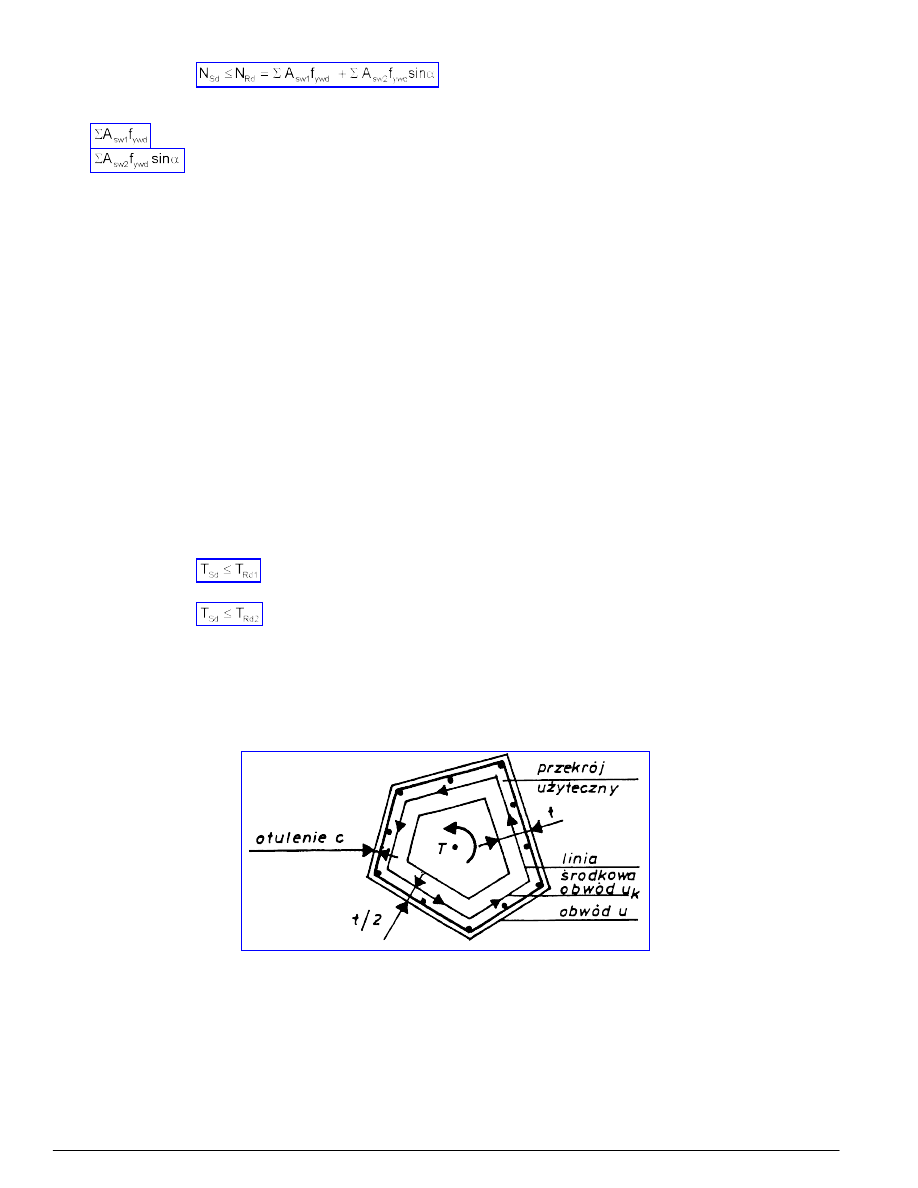
(68)
w których:
- suma sił w strzemionach prostopadłych do płaszczyzny płyty,
- suma rzutów sił w prętach odgiętych i w strzemionach nachylonych na kierunek prostopadły do
płaszczyzny płyty.
Zbrojenie na przebicie powinno spełniać warunki konstrukcyjne podane w 9.1.1.4.
5.7 Skręcanie
5.7.1 Zasady ogólne
Nośność przekrojów na skręcanie oblicza się jak dla cienkościennego przekroju zamkniętego. Przekroje pełne zastępuje się
przez równoważne przekroje cienkościenne. W przekrojach o złożonym kształcie, takich jak przekroje teowe, wydziela się
części, z których każda jest modelowana jako równoważny przekrój cienkościenny, a całkowita nośność na skręcanie jest
wyznaczona jako suma nośności wydzielonych części. Moment skręcający, przenoszony przez elementy zgodnie z teorią
sprężystości wyznaczać należy na podstawie sztywności na skręcanie. Sztywność na skręcanie dla przekroju
nieprostokątnego otrzymuje się dzieląc przekrój na zespół prostokątów i sumując sztywności na skręcanie poszczególnych
prostokątów. Przekrój dzielić należy na prostokąty w ten sposób, aby z obliczeń uzyskać maksymalną sztywność. Zwykle
osiąga się to, przyjmując dla najszerszego prostokąta możliwie największą długość.
Moment skręcający, przenoszony przez każdą z wydzielonych części, nie może zbytnio odbiegać od wielkości wyznaczonej
na podstawie analizy sprężystej bez zarysowania. Dla przekrojów niepełnych równoważna grubość ścianki nie może
przewyższać rzeczywistej grubości ścianki.
Przy obliczaniu przekrojów poddanych łącznemu działaniu ścinania i skręcania strzemiona wymiaruje się oddzielnie na
skręcanie i na ścinanie. Kąt
θ nachylenia krzyżulców betonowych przyjmuje się ten sam dla skręcania i ścinania.
5.7.2 Czyste skręcanie
Obliczeniowy moment skręcający powinien spełniać następujące warunki:
(69)
(70)
gdzie:
T
Rd1
- nośność na skręcanie z uwagi na maksymalny moment skręcający, który może być przeniesiony przez ściskane
krzyżulce betonowe,
T
Rd2
- nośność na skręcanie z uwagi na maksymalny moment skręcający, który może być przeniesiony przez zbrojenie.
Rysunek 27 - Stosowane oznaczenia
Część 6 Strona 19

Rysunek 28 - Przestrzenna kratownica zastępcza, służąca do wyznaczenia sił w strzemionach poprzecznych
Nośność na skręcanie T
Rd1
określa wzór
(71)
w którym:
t
≤ A/u - nie większe od rzeczywistej grubość ścianki. W przypadku przekroju pełnego t oznacza równoważną grubość ścianki
(rysunek 27). Grubość mniejszą niż A/u przyjmować można pod warunkiem, że T
Sd
≤ T
Rd1
, gdzie T
Rd1
określona jest wzorem
(71). Przyjmowanie grubości mniejszej od podwójnego otulenia c prętów podłużnych jest niedopuszczalne,
A - całkowite pole przekroju wewnątrz obwodu zewnętrznego, łącznie z polem przekroju wewnętrznej części pustej,
u - obwód zewnętrzny,
A
k
- pole powierzchni zawartej wewnątrz linii środkowej, łącznie z polem przekroju wewnętrznej części pustej.
ν - współczynnik, którego wartość określa się następująco
(72)
Wartość tę stosuje się w przypadku, kiedy strzemiona znajdują się tylko przy zewnętrznej powierzchni elementu. Jeżeli
przewiduje się strzemiona zamknięte po obu stronach każdej ścianki równoważnego przekroju zamkniętego lub każdej ze
ś
cianek przekroju skrzynkowego, wartość
ν określać można ze wzoru (54).
θ - kąt nachylenia betonowych krzyżulców do osi podłużnej; kąt ten powinien być dobrany, zgodnie z 5.5.1
Nośność na skręcanie T
Rd2
określa wzór
(73)
a pole przekroju dodatkowego zbrojenia podłużnego z uwagi na skręcanie wyznacza się ze wzoru
(74)
w którym:
u
k
- obwód powierzchni A
k
,
s - odstęp strzemion,
f
ywd
- obliczeniowa granica plastyczności strzemion,
f
yld
- obliczeniowa granica plastyczności zbrojenia podłużnego,
A
sw
- pole przekroju jednej gałęzi strzemienia,
Część 6 Strona 20

A
sl
- pole przekroju wymaganego dodatkowo zbrojenia podłużnego z uwagi na skręcanie.
Jeżeli zbrojenie jest dane, wartości
θ i T
Rd2
wyznaczyć można z podanych niżej wzorów
(75)
(76)
Jeżeli obliczona w ten sposób wartość
θ znajduje się poza przedziałem określonym w 5.5.1, za miarodajną przyjąć należy
najbliższą wartość graniczną.
W celu zapewnienia, aby siła ściskająca w krzyżulcach betonowych przekazana była na strzemiona, wymaga się, żeby co
najmniej jeden pręt podłużny znajdował się w każdym narożu przekroju elementu.
W przypadku czystego skręcania obowiązują następujące wymagania:
- minimalny stopień zbrojenia zgodnie z tablicą 33,
- ograniczenie szerokości rys zgodnie z 4.7.3,
- wymagania konstrukcyjne zgodnie z 9.3.1.5.
5.7.3 Skręcanie połączone ze ścinaniem
Obliczeniowy moment skręcający T
Sd
i obliczeniowa siła poprzeczna V
Sd
powinny spełniać warunek
(77)
gdzie:
T
Rd1
- obliczeniowa nośność na skręcanie, określona wzorem (71),
V
Rd2
- obliczeniowa nośność na ścinanie, dotycząca krzyżulców nachylonych pod kątem
θ, zgodnie ze wzorem (55) lub (57).
Strzemiona wymiarować można oddzielnie na skręcanie i na ścinanie, zgodnie 5.5.2 i 5.5.3. Kąt
θ nachylenia krzyżulców
betonowych należy przyjmować ten sam dla skręcania i ścinania.
Dla przekrojów pełnych, w przybliżeniu prostokątnych, zbrojenie na ścinanie i skręcanie nie jest wymagane, poza zbrojeniem
minimalnym określonym w tablicy 33, jeżeli:
(78)
(79)
5.8 Docisk
5.8.1 Zasady ogólne
Nośność przekrojów poddanych działaniu obciążeń miejscowych należy sprawdzać przy założeniu, że wytrzymałość betonu
na docisk f
cud
zależy od stosunku powierzchni docisku, tj. powierzchni, na którą przykładane jest obciążenie miejscowe, do
powierzchni rozdziału, tj. powierzchni współpracującej przy przenoszeniu tego obciążenia.
Wytrzymałość betonu na docisk należy obliczać wg wzorów:
- dla elementu niezbrojonego na docisk
(80)
w którym:
(81)
- dla elementu zbrojonego na docisk
Część 6 Strona 21

(82)
w którym:
(83)
We wzorach (81) i (83):
(84)
lecz nie więcej niż
ω
u
,
max
wg tablicy 14, przy czym:
A
co
- pole powierzchni docisku (rysunek 29),
A
c1
- pole powierzchni rozdziału (rysunek 29),
σ
cum
- średnie naprężenie ściskające na powierzchni rozdziału poza powierzchnią docisku (rysunek 30).
Część 6 Strona 22
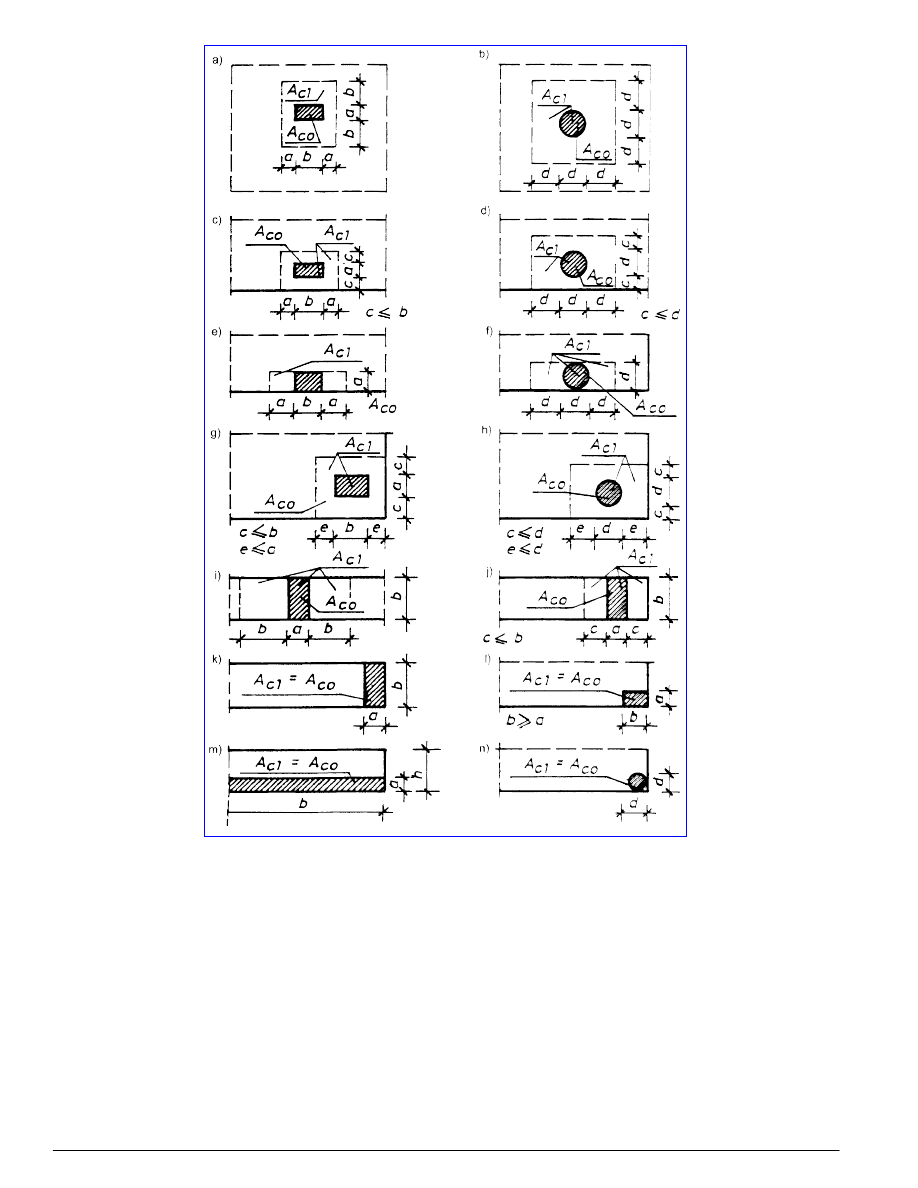
Rysunek 29 - Zasady przyjmowania powierzchni rozdziału A
c1
(przypadki uwzględnione w tablicy 14)
Część 6 Strona 23
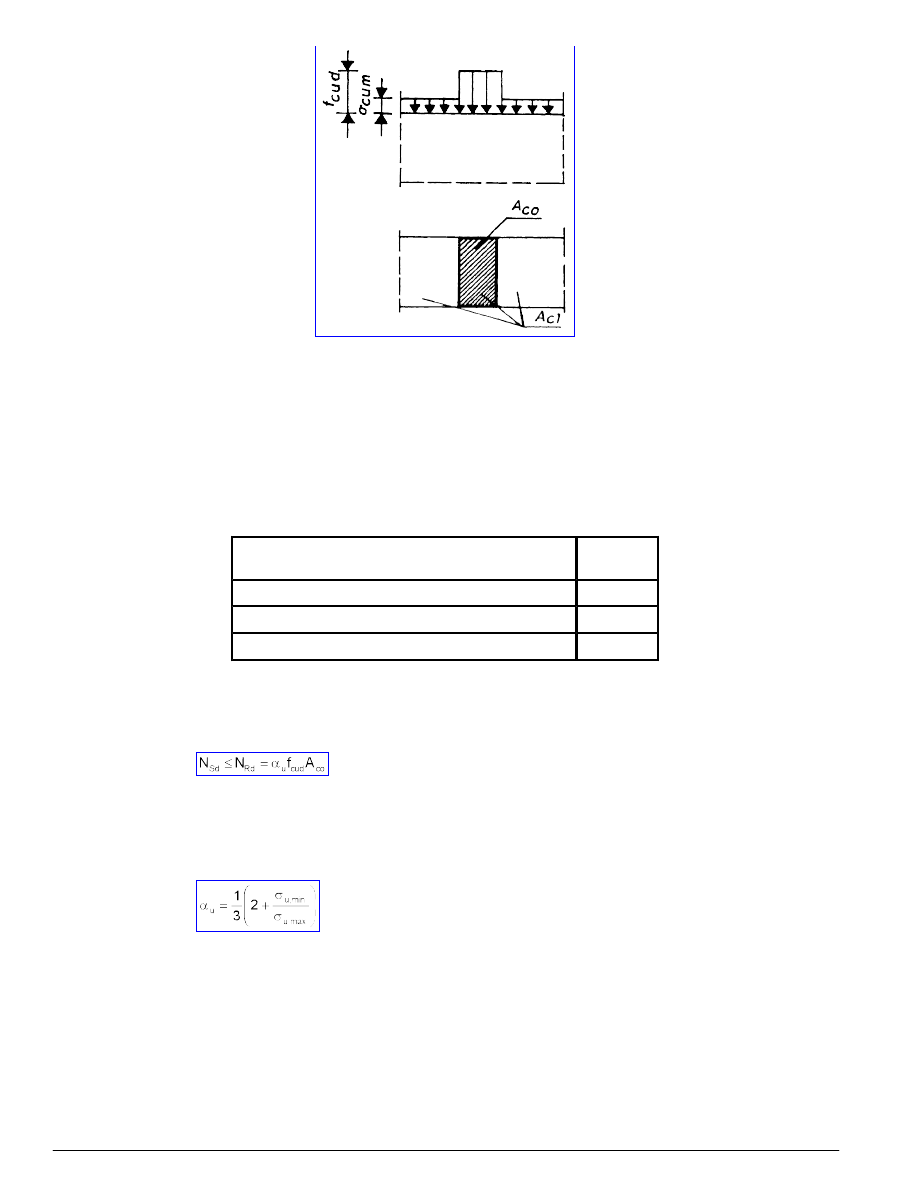
Rysunek 30 - Schemat do określenia wytrzymałości na docisk według wzorów (80) i (82) w przypadku obciążenia
miejscowego i równomiernie rozłożonego na pozostałej części przekroju
Powierzchnie rozdziału należy przyjmować zgodnie z zasadami przedstawionymi na rysunku 29 z tym, że w przekroju, na
który działa więcej niż jedno obciążenie miejscowe, przyjmowane powierzchnie rozdziału nie mogą pokrywać się wzajemnie.
Tablica 14 - Wartości współczynnika
ω
ω
ω
ω
u,max
Schemat przyłożenia obciążenia
miejscowego wg rysunku 29
ω
u,max
Przypadek a), b)
2,5
Przypadek c), d), e), f), g), h), i), j)
2,0
Przypadek k), l, m), n)
1,0
5.8.2 Elementy niezbrojone na docisk
Nośność przekroju poddanego działaniu obciążeń miejscowych określać należy z warunku
(85)
w którym:
N
Sd
- siła działająca prostopadle na powierzchnię docisku A
co
wyznaczona dla miarodajnej kombinacji obciążeń
obliczeniowych,
α
u
- współczynnik zależny od rozkładu obciążenia na powierzchni docisku, określony wzorem
(86)
gdzie:
σ
u,min
i
σ
u,max
- odpowiednio: minimalne i maksymalne naprężenia docisku.
5.8.3 Elementy zbrojone na docisk
Nośność przekroju poddanego działaniu obciążeń miejscowych określać należy z warunku
Część 6 Strona 24
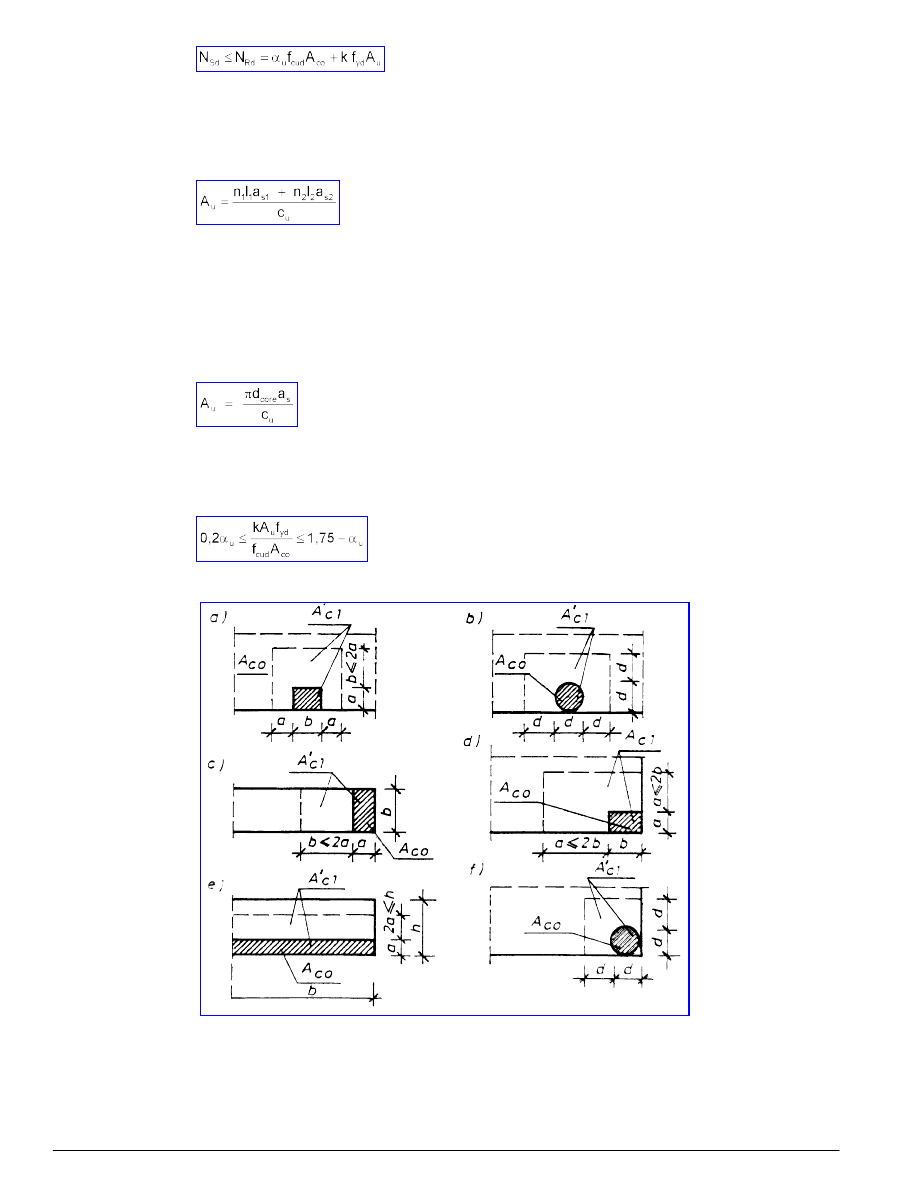
(87)
w którym:
- dla zbrojenia w postaci siatek zgrzewanych lub wyginanych według rysunku 55 przyjmuje się
k = 1,5
(88)
gdzie: n
1
, n
2
, I
1
, I
2
, a
s1
, a
s2
- odpowiednio liczba, długość i pole przekroju pręta siatki w obydwu kierunkach, przy czym jako
miarodajne do ustalenia tych wielkości należy uważać pręty ograniczone powierzchnią rozdziału lub w szczególnych
przypadkach (rysunek 29 e, f, k, l, m, n) zastępczą powierzchnią A
c1
przyjmowaną według rysunku 31,
c
u
- odstęp siatek.
- dla zbrojenia w postaci uzwojenia według rysunku 55 przyjmuje się
k =2,5
(89)
gdzie:
d
core
, c
u
, a
s
- odpowiednio: średnica uzwojenia, skok uzwojenia oraz pole przekroju pręta.
Zbrojenie strefy docisku powinno spełniać warunek
(90)
Rysunek 31 - Zasady przyjmowania zastępczej powierzchni A'
c1
Część 6 Strona 25
Jeżeli siła działająca na powierzchnię docisku nie jest do niej prostopadła wówczas składową styczną tej siły należy
przenieść przy pomocy odpowiedniego zbrojenia.
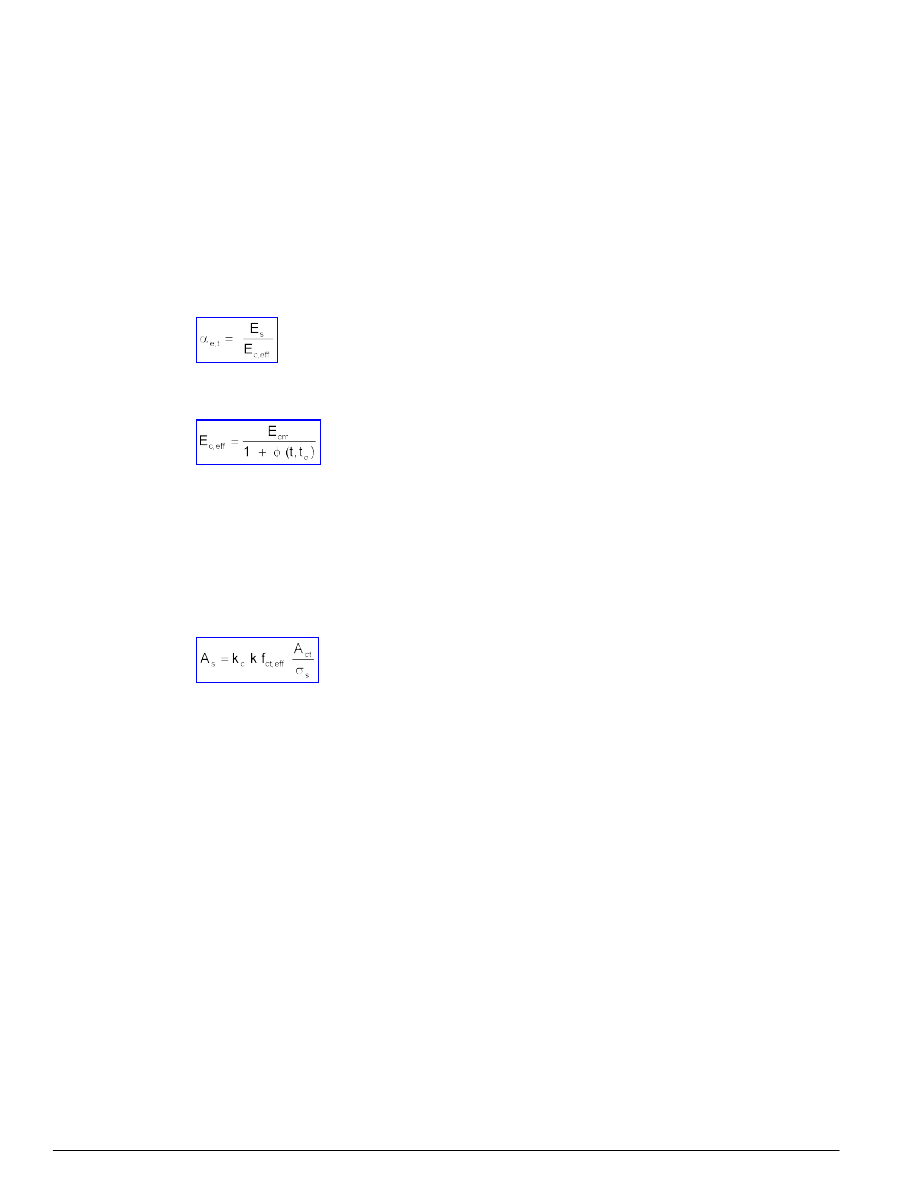
6 Stany graniczne użytkowalności elementów konstrukcji
6.1 Zasady ogólne
Pola przekrojów, momenty statyczne, wskaźniki wytrzymałości, momenty bezwładności, zasięgi stref ściskanej i rozciąganej
oraz naprężenia w betonie i w zbrojeniu, występujące we wzorach stosowanych przy sprawdzaniu stanów granicznych
użytkowalności, oblicza się przyjmując, że przekroje płaskie przed odkształceniem pozostają płaskimi po odkształceniu, a
stal jest materiałem sprężystym o module sprężystości E
s
. Jeżeli rozpatrywane oddziaływania nie wywołują zarysowania
przekroju, to stosuje się teorię opartą na założeniu, że beton jest materiałem sprężystym zarówno przy ściskaniu jak i przy
rozciąganiu (teoria fazy l). Jeżeli oddziaływania mogą wywołać zarysowanie przekroju, to przyjmuje się, że beton nie przenosi
naprężeń rozciągających, a przy ściskaniu zachowuje się jak materiał sprężysty (teoria fazy II).
Przy obciążeniach krótkotrwałych przyjmuje się, że stosunek modułów sprężystości stali i betonu jest równy α
e
= E
s
/E
cm
.
Przy obciążeniach długotrwałych wpływ pełzania betonu uwzględnia się zastępując współczynnik α
e
przez α
e,t
według wzoru
(91)
w którym E
c,eff
jest efektywnym modułem sprężystości betonu, wyznaczanym ze wzoru
Zezwala się na odstępstwa od powyższych zasad w tych przypadkach, w których inne punkty normy określają uproszczone
sposoby wyznaczania charakterystyk przekroju lub naprężeń (np. polegające na stosowaniu charakterystyk przekroju z
pominięciem wpływu zbrojenia).
6.2 Minimalne pole przekroju zbrojenia
Minimalne pole A
s
przekroju zbrojenia rozciąganego, wymagane z uwagi na ograniczenie szerokości rys spowodowanych
naprężeniami wywołanymi przez odkształcenia wymuszone przyczynami wewnętrznymi (skurcz) lub zewnętrznymi (osiadanie
podpór) - można wyznaczać ze wzoru
(92)
w którym:
k
c
- współczynnik uwzględniający rozkład naprężeń w przekroju w chwili poprzedzającej zarysowanie,
k - współczynnik uwzględniający wpływ nierównomiernych naprężeń samorównoważących się w ustroju,
f
ct,eff
- średnia wytrzymałość betonu na rozciąganie w chwili spodziewanego zarysowania,
A
ct
- pole przekroju strefy rozciąganej elementu w chwili poprzedzającej zarysowanie,
σ
s
- naprężenie w zbrojeniu rozciąganym natychmiast po zarysowaniu.
Wartość współczynnika k
c
określa się następująco:
przy rozciąganiu osiowym k
c
= 1,0
przy zginaniu k
c
= 0,4.
Wartość współczynnika k przyjmuje się zależnie od rodzaju przyczyn wymuszenia odkształceń.
Przy naprężeniach wywołanych odkształceniem wymuszonym przyczynami wewnętrznymi przyjmuje się ogólnie k = 0,8.
Dla przekrojów prostokątnych przy
h ≤ 300 mm k = 0,8,
h ≥ 800 mm k = 0,5.
W przypadkach pośrednich, wartości współczynnika k można interpolować liniowo. Przy naprężeniach wywołanych
odkształceniem wymuszonym przyczynami zewnętrznymi przyjmuje się k = 1,0.
Pole A
ct
przekroju strefy rozciąganej prostokątnego elementu żelbetowego przyjmuje się:
A
ct
= bh - przy rozciąganiu osiowym,
A
ct
= 0,5 bh - przy zginaniu.
Wartość f
ct,eff
przyjmować należy odpowiednio do wieku betonu w chwili spodziewanego pojawienia się rys. W przypadku
braku ściślejszych informacji zaleca się przyjmować f
ct,eff
= f
ctm
odpowiednio do projektowanej klasy betonu.
Wartość σ
s
naprężeń w zbrojeniu rozciąganym przyjąć można równą f
yk
z tym, że z uwagi na nieprzekroczenie granicznej
Część 7 Strona 1

szerokości rys - może być potrzebne obniżenie tego naprężenia.
6.3 Szerokość rys prostopadłych do osi elementu
Obliczeniową szerokość w
k
rys prostopadłych do osi elementu wyznacza się ze wzoru
(93)
w którym
β - współczynnik wyrażający stosunek obliczeniowej szerokości rysy do szerokości średniej,
s
rm
- średni, końcowy rozstaw rys,
ε
sm
- średnie odkształcenie zbrojenia rozciąganego.
Wartość współczynnika β, wyrażającego stosunek obliczeniowej szerokości rysy do szerokości średniej - przyjmuje się:
β = 1,7 dla zarysowania wywołanego przez obciążenie i dla zarysowania wywołanego przez opór stawiany odkształceniom
wymuszonym w przekrojach, których najmniejszy wymiar przekracza 800 mm,
β = 1,3 dla zarysowania wywołanego przez opór stawiany odkształceniom wymuszonym w przekrojach, których najmniejszy
wymiar nie przekracza 300 mm.
Dla przekrojów o wymiarach pośrednich, wartości współczynnika β można interpolować liniowo.
Ś
redni rozstaw s
rm
(mm) rys w elementach zginanych lub rozciąganych wyznacza się ze wzoru
(94)
w którym:
φ - średnica pręta w mm; przy stosowaniu prętów o różnych średnicach można przyjmować średnicę zastępczą φ = Σ n
i
φ
i
/Σn
i
,
gdzie n
i
oznacza liczbę prętów o średnicy φ
i
,
k
1
- współczynnik zależny od przyczepności prętów:
k
1
= 0,8 dla prętów żebrowanych,
k
1
= 1,6 dla prętów gładkich,
k
2
- współczynnik zależny od rozkładu odkształceń rozciągających:
k
2
= 0,5 przy zginaniu,
k
2
= 1,0 przy rozciąganiu osiowym,
k
2
= (ε
1
+ ε
2
)/2ε
1
przy rozciąganiu mimośrodowym, gdzie ε
1
i ε
2
oznaczają największe i najmniejsze odkształcenia na
krawędziach przekroju zarysowanego,
ρ
r
- efektywny stopień zbrojenia A
s
/A
ct,eff
; gdzie A
s
jest polem przekroju zbrojenia zawartego wewnątrz efektywnego pola
A
ct,eff
przekroju strefy rozciąganej.
Efektywne pole A
ct,eff
przekroju strefy rozciąganej jest w belkach polem przekroju betonu otaczającego rozciągane zbrojenie,
o szerokości równej 2,5-krotnej odległości od rozciąganej krawędzi przekroju do środka ciężkości zbrojenia (rysunek 32a).
Część 7 Strona 2
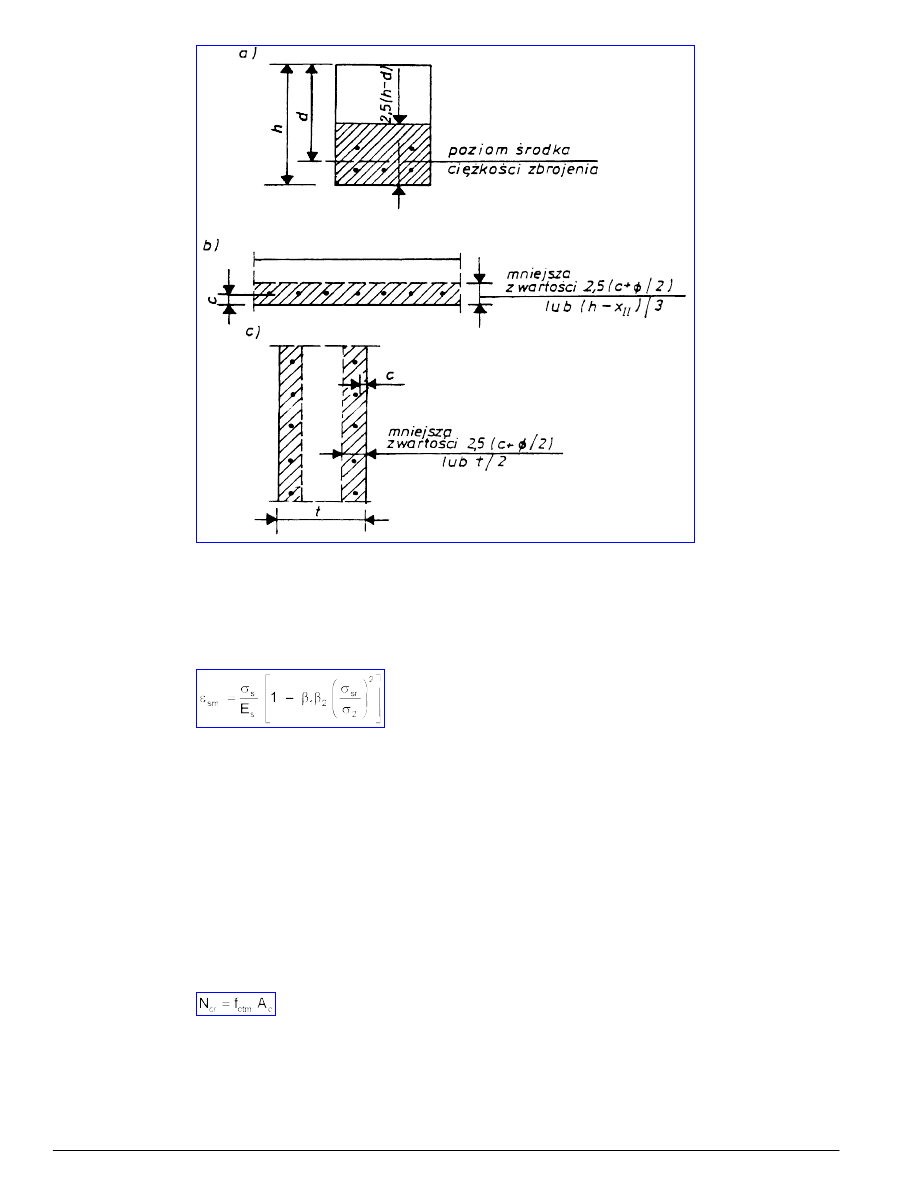
Rysunek 32 - Efektywne pole A
ct,eff
przekroju strefy rozciąganej:
a) belka, b) płyta (x
II
- wysokość strefy ściskanej przekroju zarysowanego),
c) element rozciągany
Wartość ε
sm
średniego odkształcenia zbrojenia rozciąganego - określa się ze wzoru
(95)
w którym:
σ
s
- naprężenie w zbrojeniu rozciąganym, obliczone dla przekroju przez rysę,
σ
sr
- naprężenie w zbrojeniu rozciąganym, obliczone dla przekroju przez rysę, dla obciążenia powodującego zarysowanie,
β
1
- współczynnik zależny od przyczepności prętów:
β
1
= 1,0 dla prętów żebrowanych,
β
2
= 0,5 dla prętów gładkich,
β
2
- współczynnik zależny od czasu działania i powtarzalności obciążenia:
β
2
= 1,0 dla jednokrotnego obciążenia krótkotrwałego,
β
2
= 0,5 dla obciążeń długotrwałych lub wielokrotnie powtarzalnych.
We wzorze (95) zamiast stosunku σ
sr
/σ
s
przyjmować można:
- przy rozciąganiu N
cr
/N
Sd
,
- przy zginaniu M
cr
/M
Sd
.
Siłę rysującą N
cr
i moment rysujący M
cr
wyznaczać można ze wzorów
przy rozciąganiu osiowym
(96)
przy zginaniu
Część 7 Strona 3
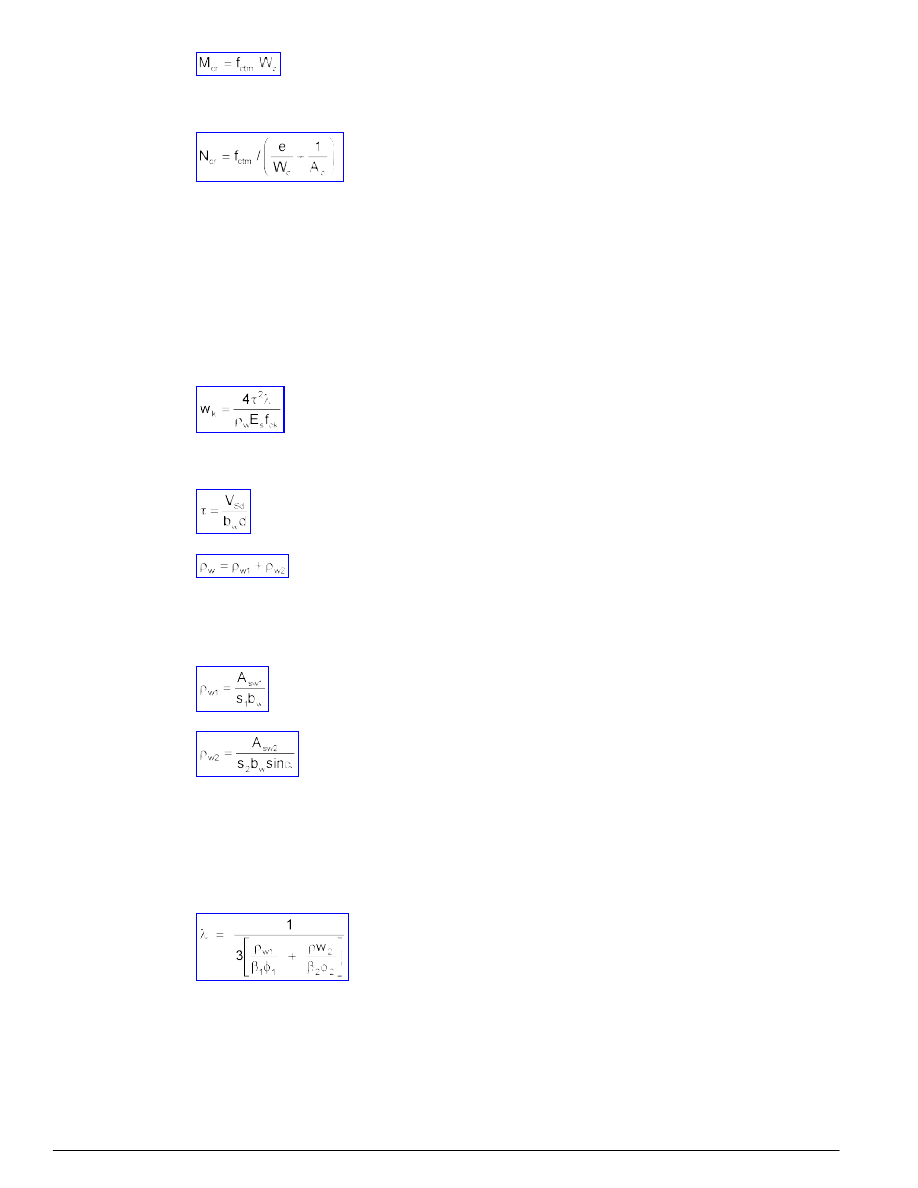
(97)
przy rozciąganiu mimośrodowym
(98)
w których:
f
ctm
- średnia wytrzymałość betonu na rozciąganie,
A
c
i W
c
- odpowiednio: pole i wskaźnik wytrzymałości przekroju betonowego,
e - mimośród siły rozciągającej względem środka ciężkości przekroju betonowego.
Siła rozciągająca N
Sd
i moment zginający M
Sd
wyznaczone są dla kombinacji obciążeń długotrwałych (γ
f
= 1,0).
Dla elementów poddanych tylko działaniu wewnętrznych odkształceń wymuszonych można przyjmować σ
s
= σ
sr
.
Uproszczony sposób sprawdzania warunku w
k
≤ w
lim
dla rys prostopadłych do osi elementu - podano w załączniku D.
6.4 Szerokość rys ukośnych
Szerokość w
k
rys ukośnych w elementach zginanych obliczać można ze wzoru
(99)
w którym:
(100)
(101)
V
Sd
- siła poprzeczna wyznaczona dla kombinacji obciążeń długotrwałych (γ
f
= 1,0),
b
w
- najmniejsza szerokość strefy ścinania.
Stopień zbrojenia strzemionami ρ
w1
i prętami odgiętymi ρ
w2
oblicza się ze wzorów
(102)
(103)
w których:
A
sw1
, A
sw2
- odpowiednio: pole przekroju strzemion i prętów odgiętych,
s
1
- rozstaw strzemion prostopadłych do osi elementu,
s
2
- średni rozstaw płaszczyzn odgięć lub strzemion ukośnych, mierzony wzdłuż osi podłużnej elementu,
α - kąt nachylenia prętów odgiętych lub strzemion ukośnych.
Wartość λ we wzorze (99) oblicza się ze wzoru
(104)
w którym:
φ
1,
φ
2
- odpowiednio: średnica strzemion pionowych i prętów odgiętych,
β
1,
β
2
- współczynniki zależne od przyczepności strzemion (β
1
) i prętów odgiętych (β
2
) równe:
1,0 - dla prętów gładkich,
Część 7 Strona 4

0,7 - dla prętów żebrowanych.
Jeżeli strzemiona pionowe ze stali A-0 o średnicy φ
1
≤ 8 mm zapewniają przy cot Θ ≤ 1,75 wystarczającą nośność na
ś
cinanie według 5.5 (bez uwzględnienia wpływu prętów odgiętych) to przy w
lim
= 0,3 mm sprawdzanie szerokości rys
ukośnych nie jest potrzebne.
6.5 Ugięcie elementów zginanych
Krzywizny i sztywności, służące do obliczania ugięć, należy wyznaczać biorąc pod uwagę wpływ momentu zginającego,
zarysowania i pełzania betonu na sztywność przekrojów elementu. Wpływ skurczu betonu można na ogół pomijać, ale trzeba
go uwzględniać przy obliczaniu elementów zespolonych. Wzory służące do obliczania sztywności przekroju (z pominięciem
wpływu skurczu betonu) podano w załączniku E.
Ugięcia elementów, mających stałe wymiary przekroju poprzecznego, w przypadku, gdy całe obciążenie jest długotrwałe lub
całe obciążenie jest krótkotrwałe, można obliczać stosując wzór
(105)
w którym:
α
k
- współczynnik zależny od rozkładu momentu zginającego, wyznaczony według zasad mechaniki budowli (np. w belce
swobodnie podpartej i równomiernie obciążonej α
k
= 5/48),
M
Sd
- maksymalny moment zginający wywołany rozpatrywanym obciążeniem,
B - sztywność przekroju, w którym osiąga się moment M
Sd
, obliczona według załącznika E.
Przy obliczaniu ugięć, które mają być porównane z wartościami granicznymi a
lim
według tablicy 10, do wzoru (105) za M
Sd
podstawia się moment wywołany kombinacją obciążeń długotrwałych i sztywność B = B∞, wyznaczoną w zależności od stanu
zarysowania elementu. Jeżeli moment zginający od całego obciążenia (długotrwałego i krótkotrwałego) nie przekracza
momentu rysującego M
cr
, to sztywność B∞ wyznacza się ze wzoru (E.1), a w przeciwnym przypadku uwzględnia się wpływ
zarysowania obliczając B∞ ze wzoru (E.3), do którego podstawia się σ
sr
= σ
s
.
Na ogół obciążenie krótkotrwałe działa na element, który ugiął się wcześniej pod wpływem obciążeń długotrwałych. Wartości
graniczne ugięć, wywołanych jednoczesnym działaniem tych dwóch rodzajów obciążeń, nie są określone w tej normie - jeżeli
zachodzi taka potrzeba, to ustala się je stosownie do wymagań w rozpatrywanym przypadku.
Maksymalne ugięcie można obliczyć ze wzoru
w którym:
a
o,k+d
- ugięcie, które powstałoby natychmiast po jednoczesnym przyłożeniu obciążeń krótko- i długotrwałych (do wzoru (105)
podstawia się moment od całego obciążenia i sztywność B
0
),
a
o,d
- ugięcie, które powstałoby natychmiast po przyłożeniu obciążeń długotrwałych (do wzoru (105) podstawia się moment
od obciążeń długotrwałych i sztywność B
0
),
a
∞,d
- ugięcie długotrwałe, wywołane obciążeniami długotrwałymi (do wzoru (105) podstawia się moment od obciążeń
długotrwałych i sztywność B∞).
Ugięcia stropów i stropodachów oraz przekryć dachowych o rozpiętości obliczeniowej I
eff
≤ 6,0 m uważać można za
ograniczone do odpowiednich wartości a
lim
jeśli stosunek rozpiętości I
eff
do wysokości użytecznej d elementów o określonym
stopniu ρ
l
zbrojenia podłużnego - jest nie większy niż podano w tablicy 15.
Wartości I
eff
/d podane w tablicy 15 dla stropów i stropodachów można uważać również za maksymalne ze względu na nie
przekroczenie ugięć dopuszczalnych dla płyt zbrojonych dwukierunkowo, jeżeli:
- dla płyt opartych na całym obwodzie stosunek długości większego boku I
1
do długości mniejszego boku I
2
jest większy niż
2,0,
- dla płyt opartych na trzech krawędziach - stosunek długości jednego z dwóch boków podpartych wzajemnie równoległych, l
a
do długości boku niepodpartego I
b
jest większy niż 1,5.
Jeżeli wartości stosunku
lub
są mniejsze od wartości podanych wyżej, wartości l
eff
/d podane w tablicy 15 można
zwiększyć mnożąc je - dla płyt opartych na całym obwodzie przez
a dla płyt opartych na trzech krawędziach przez
.
Maksymalne wartości stosunku l
eff
/d w tablicy 15 wyznaczono dla wartości naprężeń rozciągających w stali żebrowanej
σ
s
= 250 MPa. Dla innych wartości σ
s
podane w tablicy 15 wartości stosunku l
eff
/d mnożyć należy przez 250/σ
s
.
Dla elementów o rozpiętości l
eff
> 6,0 m maksymalne wartości stosunku l
eff
/d podane w tablicy 15 należy mnożyć przez:
Część 7 Strona 5

- w przypadku stropów i stropodachów,
- w przypadku przekryć dachowych,
przy czym a
lim
jest wartością graniczną ugięcia (w mm) określoną w tablicy 10 dla odpowiedniej rozpiętości I
eff
(w mm).
Jeżeli na każdej podporze występuje częściowe zamocowanie, zapewniające, że pod obciążeniem długotrwałym wystąpi
moment, wynoszący co najmniej 20% momentu wywołanego przez to obciążenie na tej podporze w przypadku całkowitego
zamocowania obu podpór, to odpowiednie wartości dotyczące elementów swobodnie podpartych z tablicy 15 można
zwiększyć o 10 %.
Część 7 Strona 6
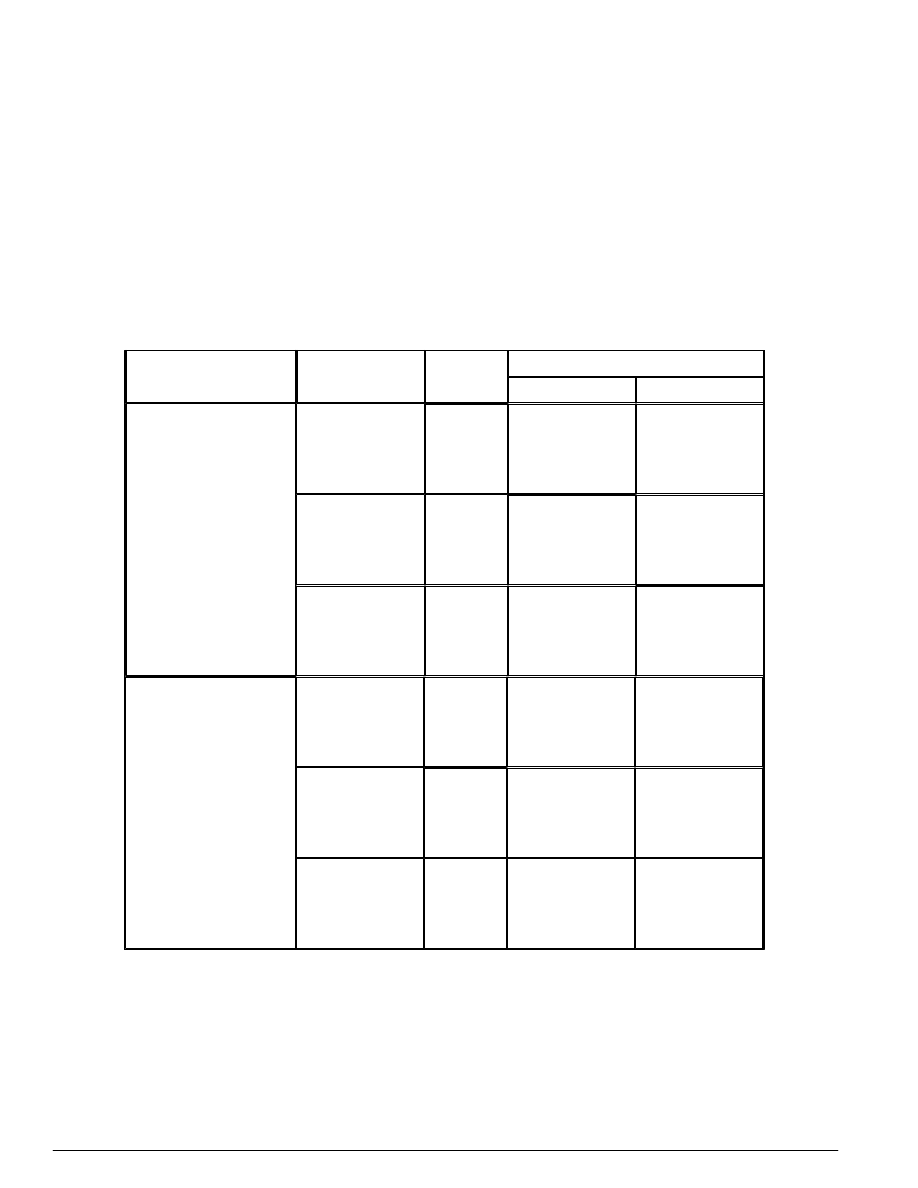
7 Konstrukcje sprężone, konstrukcje poddane działaniu obciążeń wielokrotnie zmiennych i
konstrukcje zespolone
7.1 Konstrukcje sprężone
7.1.1 Zasady ogólne
W odniesieniu do konstrukcji sprężonych obowiązują ogólne wymagania dotyczące materiałów, zasad projektowania i
konstruowania podane w innych rozdziałach niniejszej normy dla wszystkich konstrukcji z betonu.
Tablica 15 - Maksymalne wartości stosunku rozpiętości I
eff
do wysokości użytecznej d, przy której można nie
sprawdzać ugięć
Rodzaj konstrukcji
Schemat statyczny
As/bd
(%)
σ
s
= 250 MPa
B 15
B 25
Belki oraz płyty stropów i
stropodachów przy I
eff
≤ 6,0
m
Belka swobodnie
podparta
0,50
0,75
1,00
1,25
1,50
23
20
18
17
16
24
21
19
18
17
Skrajne przęsło
belki ciągłej
0,50
0,75
1,00
1,25
1,50
27
24
21
20
18
28
25
22
21
19
Wewnętrzne przęsło
belki ciągłej
0,50
0,75
1,00
1,25
1,50
33
29
27
24
23
35
30
28
25
24
Przekrycia dachowe przy
I
eff
≤ 6,0 m
Belka swobodnie
podparta
0,50
0,75
1,00
1,25
1,50
31
27
25
23
21
32
28
26
24
22
Skrajne przęsło
belki ciągłej
0,50
0,75
1,00
1,25
1,50
36
31
29
26
25
38
33
30
28
26
Wewnętrzne przęsło
belki ciągłej
0,50
0,75
1,00
1,25
1,50
44
37
35
32
30
46
41
37
34
32
Stany graniczne konstrukcji sprężonych sprawdzać należy w obliczeniowej sytuacji trwałej, dla t =
∞ i sytuacji początkowej,
dla t = 0 oraz w innych sytuacjach przejściowych, wymagających sprawdzenia.
Przy sprawdzaniu stanów granicznych należy przyjmować odpowiednią dla analizowanej sytuacji wartość siły sprężającej z
uwzględnieniem strat sprężenia.
Część 8 Strona 1
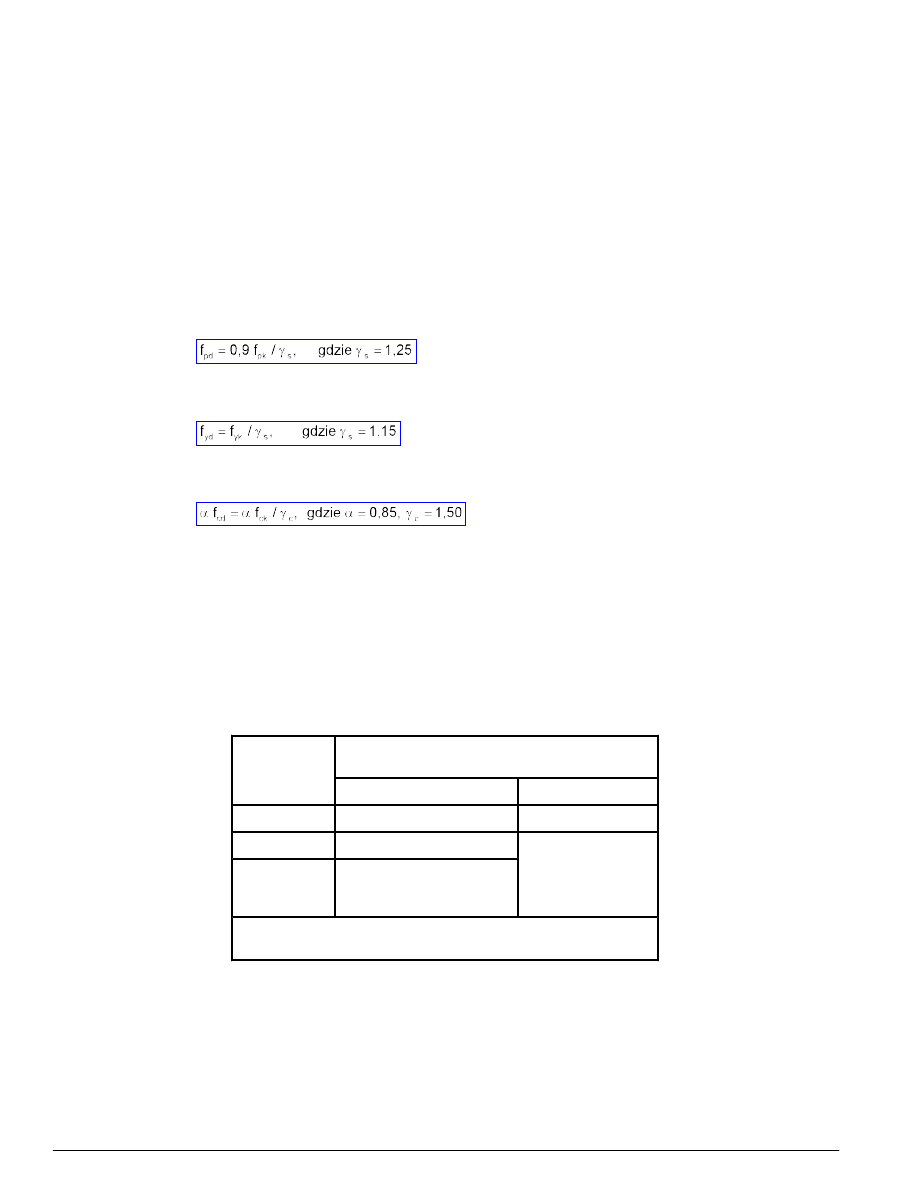
Straty sprężenia należy obliczać w zależności od naprężeń normalnych, wyznaczonych dla sytuacji początkowej i trwałej.
Naprężenia te należy wyznaczać dla obciążenia charakterystycznego i średnich wartości siły sprężającej P
m,o
i P
m,t
. Straty
należy obliczać w kolejności ich występowania tj.:
a) w konstrukcjach strunobetonowych:
- straty doraźne wywołane częściową relaksacją stali oraz odkształceniami sprężystymi betonu,
- straty opóźnione (reologiczne) wywołane skurczem i pełzaniem betonu oraz pozostałą częścią relaksacji stali.
b) w konstrukcjach kablobetonowych:
- straty doraźne, wywołane tarciem cięgien w zakotwieniu i o ścianki kanału, poślizgiem cięgien w zakotwieniu,
odkształceniem sprężystym betonu (w przypadku naciągu kolejnych cięgien).
- straty opóźnione (reologiczne) wywołane relaksacją stali, skurczem i pełzaniem betonu,
c) w konstrukcjach sprężonych bez przyczepności:
- straty doraźne, wywołane tarciem cięgien w zakotwieniu, na dewiatorach i o ścianki kanału, poślizgiem cięgien w
zakotwieniu, odkształceniem sprężystym betonu (w przypadku naciągu kolejnych cięgien).
- straty opóźnione (reologiczne) wywołane relaksacją stali, skurczem i pełzaniem betonu.
Straty w konstrukcjach sprężonych bez przyczepności przenoszą się na całą długość cięgna.
Nośność zginanego przekroju sprężonego wyznacza się przyjmując:
- dla stali sprężającej
(106)
- dla stali zwykłej
(107)
- dla betonu
(108)
Nośność przekroju sprężonego na ścinanie określa się jak w elementach żelbetowych z uwzględnieniem obliczeniowej siły
sprężającej.
Stan graniczny użytkowalności sprawdza się w zakresie:
- ograniczenia naprężeń w betonie, w stali sprężającej i w stali zwykłej,
- ograniczenia szerokości rys zgodnie z tablicą 16,
- ograniczenia ugięć.
Tablica 16 - Wymagania z uwagi na zarysowanie elementów sprężonych
Klasa
ś
rodowiska
Graniczna szerokość rys w
lim
dla podstawowej
kombinacji obciążeń, mm
kablobeton
strunobeton
1
0,2
0,2
2
0,2
brak rozciągania
1)
3 i wyższe
brak rozciągania
1)
lub trwałe
zabezpieczenia cięgien i
w
≤ w
lim
= 0,2
1)
dotyczy warstwy betonu wokół cięgien o grubości nie mniejszej niż
25 mm
Elementy sprężone powinny posiadać we wstępnie sprężonej strefie rozciąganej taką liczbę cięgien, aby zerwanie jednego
lub kilku z nich nie spowodowało zniszczenia konstrukcji.
Minimalną liczbę cięgien podano w tablicy 17.
Część 8 Strona 2
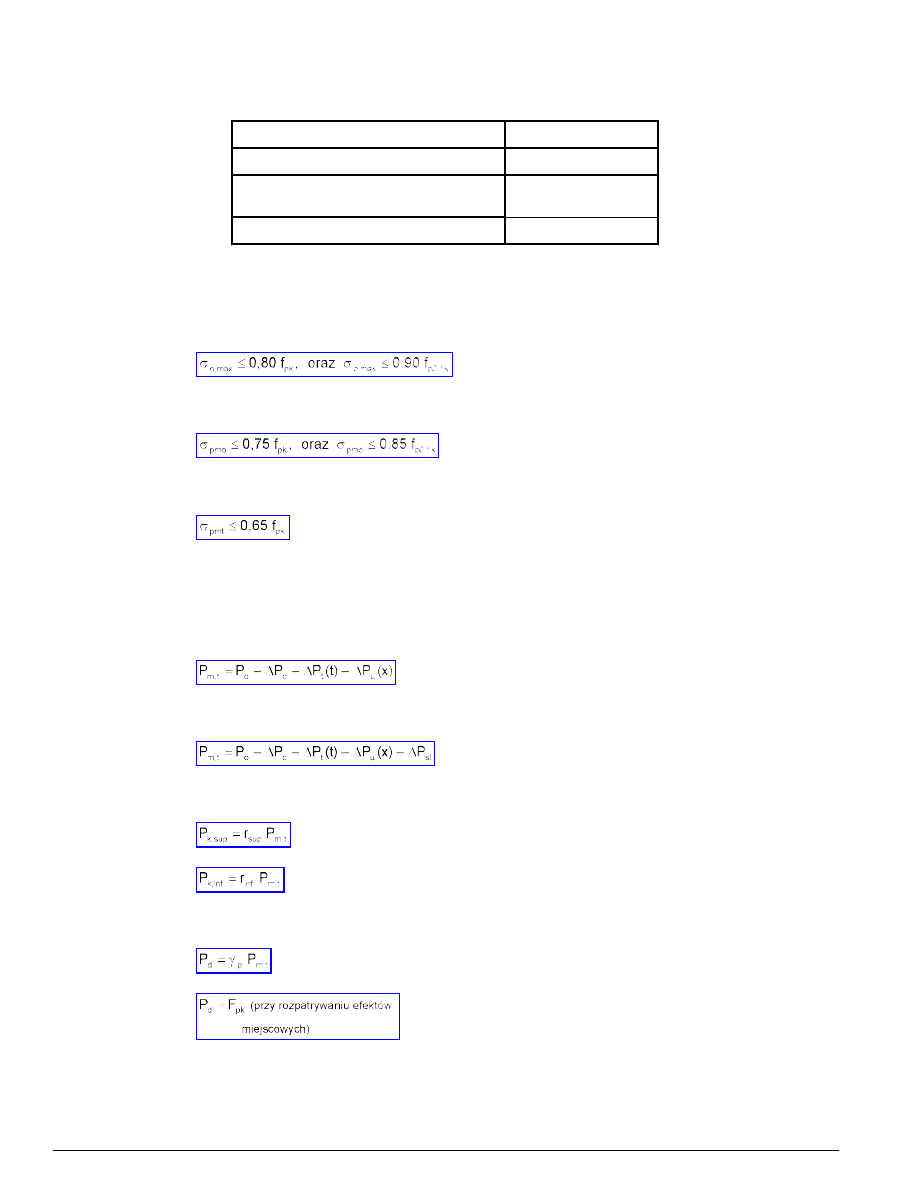
Tablica 17 - Minimalna liczba cięgien w sprężonej strefie poddanej rozciąganiu
Rodzaj cięgna
Minimalna liczba
pojedyncze druty lub pręty
3
splot lub kabel złożony z nie mniej niż 7
drutów
1
sploty o mniejszej liczbie drutów
3
7.1.2 Naprężenia w cięgnach sprężających
Wartości naprężeń w cięgnach sprężających powinny być nie większe niż:
- przy chwilowym przeciążeniu stosowanym w celu zmniejszenia strat spowodowanych tarciem oraz poślizgiem w zakotwieniu
(109)
- po zakotwieniu cięgien i uwzględnieniu strat doraźnych
(110)
- po uwzględnieniu strat całkowitych
(111)
7.1.3 Siła sprężająca
Przy sprawdzaniu stanów granicznych nośności i stanów granicznych użytkowalności należy przyjmować wartości siły
sprężającej, odpowiadające rozpatrywanej sytuacji obliczeniowej konstrukcji (sytuacja początkowa, trwała), obliczone ze
wzorów (112) do (117):
- średnia wartość siły sprężającej w elementach strunobetonowych:
(112)
- średnia wartość siły sprężającej w elementach kablobetonowych
(113)
- charakterystyczne wartości siły sprężającej w stanie granicznym użytkowalności
(114)
(115)
- obliczeniowe wartości siły sprężającej w stanie granicznym nośności
(116)
(117)
Część 8 Strona 3

W powyższych wzorach przyjęto następujące oznaczenia:
P
o
- początkowa wartość siły sprężającej (suma naciągu poszczególnych cięgien),
P
m,t
- średnia wartość siły sprężającej po czasie t; rozróżnia się ponadto P
m,o
i P
m,
∞
jako średnie siły sprężające po stratach
doraźnych i całkowitych.
∆P
c
- strata siły sprężającej spowodowana odkształceniem sprężystym betonu,
∆P
t
(t) - strata siły sprężającej spowodowana pełzaniem i skurczem betonu oraz relaksacją stali po czasie t,
∆P
µ
,(x) - strata siły sprężającej spowodowana tarciem (w strunobetonie jedynie przy cięgnach zagiętych),
∆P
sl
- strata siły sprężającej spowodowana poślizgiem cięgien w zakotwieniu,
r
sup
= 1,1 - współczynnik wyznaczający górną wartość siły sprężającej w stanie granicznym użytkowalności,
r
inf
= 0,9 - współczynnik wyznaczający dolną wartość siły sprężającej w stanie granicznym użytkowalności,
γ
p
- częściowy współczynnik bezpieczeństwa dla siły sprężającej równy:
0,9 lub 1,0 - dla efektów korzystnych,
1,2 lub 1,0 - dla efektów niekorzystnych,
F
pk
- charakterystyczna siła zrywająca cięgno sprężające.
7.1.4 Naprężenia normalne
Naprężenia normalne
σx w betonie należy obliczać jak dla materiału liniowo sprężystego w przekroju niezarysowanym,
przyjmując odpowiednie znaki algebraiczne przy N
Sd
, N
pd
, M
Sd
, e
o
, z
cp
i y, wg wzoru
(118)
w którym:
(119)
(120)
gdzie:
N
Sd
- osiowa siła podłużna od obciążeń zewnętrznych,
M
Sd
- moment zginający od obciążeń zewnętrznych,
N
pd
- osiowa siła podłużna od sprężenia,
A
cs
- pole powierzchni przekroju sprowadzonego,
I
cs
- moment bezwładności przekroju sprowadzonego,
e
o
- mimośród siły N
sd
względem środka ciężkości przekroju,
z
cp
- odległość siły N
pd
od środka ciężkości przekroju sprowadzonego,
y - odległość rozpatrywanego włókna od środka ciężkości przekroju.
Wartość siły N
pd
należy przyjmować:
N
pd
= P
m,t
przy obliczaniu strat
N
pd
= P
k, sup
lub P
k,inf
przy obliczaniu naprężeń w stanach granicznych użytkowalności,
N
pd
= P
d
przy obliczaniu nośności.
Pole przekroju A
cs
i moment bezwładności I
cs
należy wyznaczać odpowiednio do warunków występujących w rozpatrywanej
sytuacji obliczeniowej, przyjmując przekrój betonu osłabiony kanałami i wzmocniony przekrojem zbrojenia zwykłego i
sprężającego w stosunku
α = E
s
/E
cm
jeżeli zapewniona jest przyczepność tego zbrojenia do betonu (np. po zainiektowaniu
kanałów). W konstrukcjach zespolonych należy ponadto uwzględniać różne moduły sprężystości połączonych części
przekroju.
7.1.5 Straty doraźne
7.1.5.1 Straty spowodowane tarciem kabli o ścianki kanału
Straty te należy uwzględniać zarówno dla kabli o trasie prostoliniowej, jak i krzywoliniowej. Zmniejszenie siły sprężającej
należy obliczać ze wzoru
(121)
gdzie:
k - niezamierzony kąt falowania trasy cięgna na jednostkę długości 0,005
≤ k ≤ 0,01, rad/m,
x - odległość rozpatrywanego przekroju od punktu przyłożenia siłownika naciągowego, m,
Część 8 Strona 4
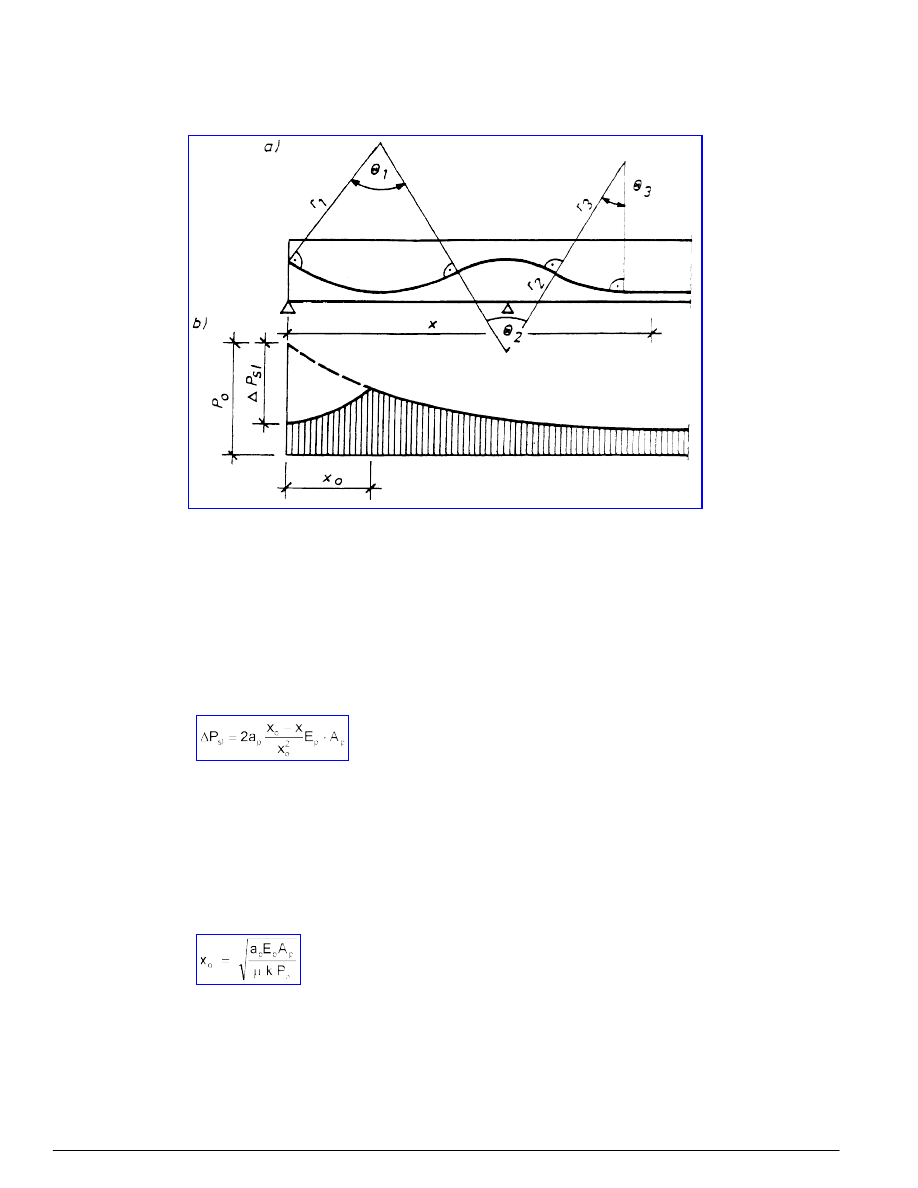
µ - współczynnik tarcia kabla o ściankę kanału,
Θ - suma kątów zakrzywienia trasy kabla od punktu przyłożenia siłownika naciągowego, do rozpatrywanego przekroju w
radianach (rysunek 33a).
Rysunek 33 - Oznaczenia przyjmowane przy obliczaniu strat wywołanych: a) tarciem, b) poślizgiem cięgien w zakotwieniu
Współczynnik k należy określać doświadczalnie. Wartości współczynnika µ można przyjmować:
0,17 - dla tarcia drutów po stali osłonki,
0,19 - dla tarcia splotów po stali osłonki,
0,35 - dla tarcia prętów gładkich po stali,
0,65 - dla tarcia prętów żebrowanych po stali.
7.1.5.2 Straty spowodowane poślizgiem cięgien w zakotwieniu
Straty spowodowane poślizgiem cięgna w zakotwieniu, występujące na odcinku x
o
zasięgu poślizgu (rysunek 33,b), należy
obliczać ze wzoru
(122)
w którym:
a
p
- wartość poślizgu, którą określać należy na podstawie doświadczeń, odpowiednio do rodzaju zakotwienia; dla zakotwienia
stożkowego należy przyjmować a
p
≥ 5 mm,
x - odległość rozpatrywanego przekroju od punktu przyłożenia siłownika naciągowego; w przypadku gdy x
≥ x
o
należy przyjąć
∆P
sl
= 0.
Odległość x
o
należy określać ze wzorów
- dla kabli prostych
(123)
- dla kabli zakrzywionych
Część 8 Strona 5
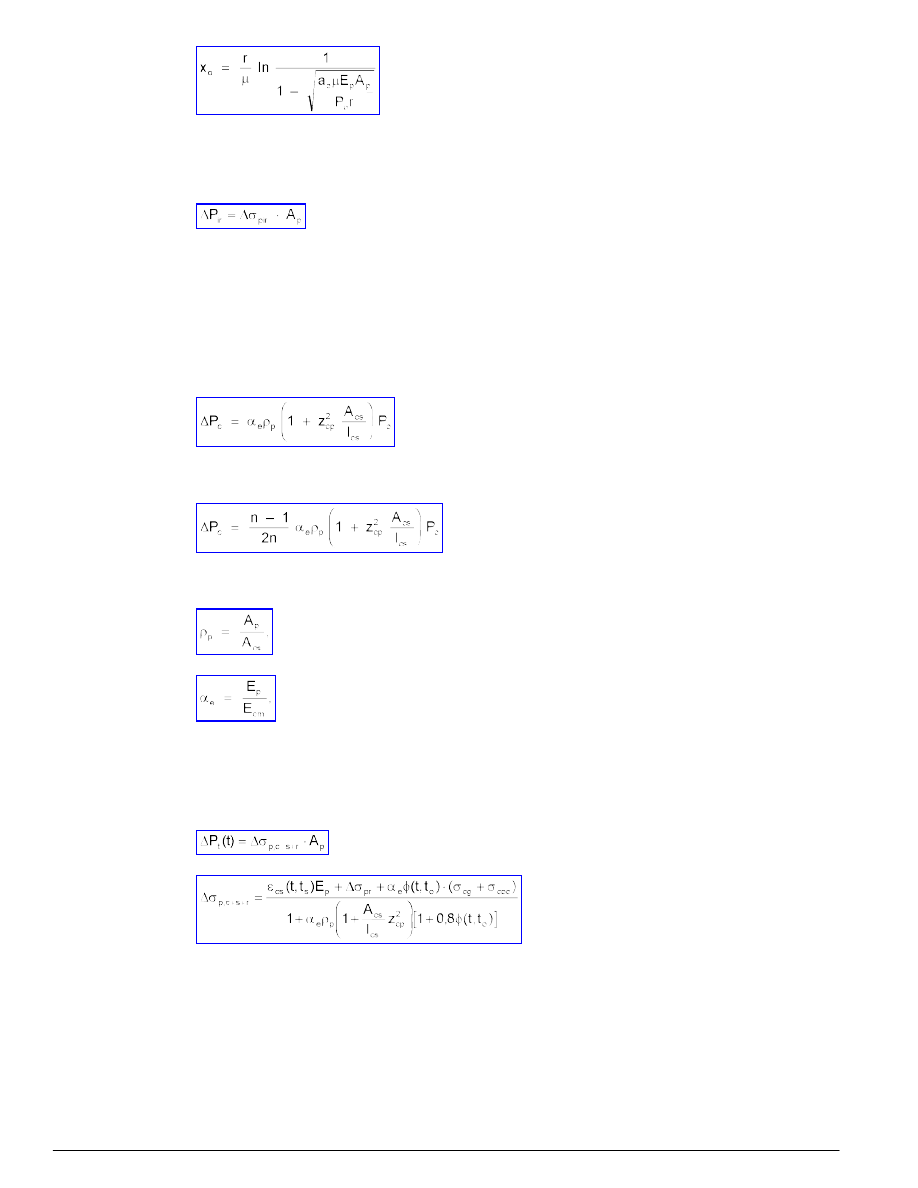
(124)
przyjmując za miarodajną wartość bardziej niekorzystną wg (123) lub (124).
7.1.5.3 Straty spowodowane częściową relaksacją stali
W elementach strunobetonowych straty te oblicza się ze wzoru
(125)
w którym:
∆σ
pir
- strata naprężenia w cięgnach sprężających spowodowana relaksacją stali w czasie od naciągu cięgien do przekazania
siły na beton, określona zgodnie z 7.1.6 dla początkowego poziomu naprężeń
σ
p
=
σ
pmo
.
7.1.5.4 Straty spowodowane odkształceniem sprężystym betonu
Straty te należy uwzględniać w elementach strunobetonowych, a w elementach kablobetonowych tylko w przypadku
kolejnego naciągu kabli.
Straty te można obliczać ze wzorów
w elementach strunobetonowych
(126)
w elementach kablobetonowych
(127)
w których:
(128)
(129)
n - liczba kabli.
7.1.6 Straty opóźnione
Straty opóźnione spowodowane pełzaniem i skurczem betonu oraz relaksacją stali sprężającej - oblicza się ze wzoru
(130)
(131)
w którym:
∆σ
p,c+s+r
- strata naprężenia w cięgnach spowodowana pełzaniem, skurczem i relaksacją w odległości x i w czasie t,
ε
cs
(t,t
s
) - przewidywane odkształcenia skurczowe betonu (według załącznika B),
α
e
- stosunek E
p
/E
cm
,
ρ
p
- stopień zbrojenia sprężającego A
p
/A
cs
,
φ(t,t
o
) - współczynnik pełzania betonu w czasie od t
o
do t (wg załącznika A),
Część 8 Strona 6
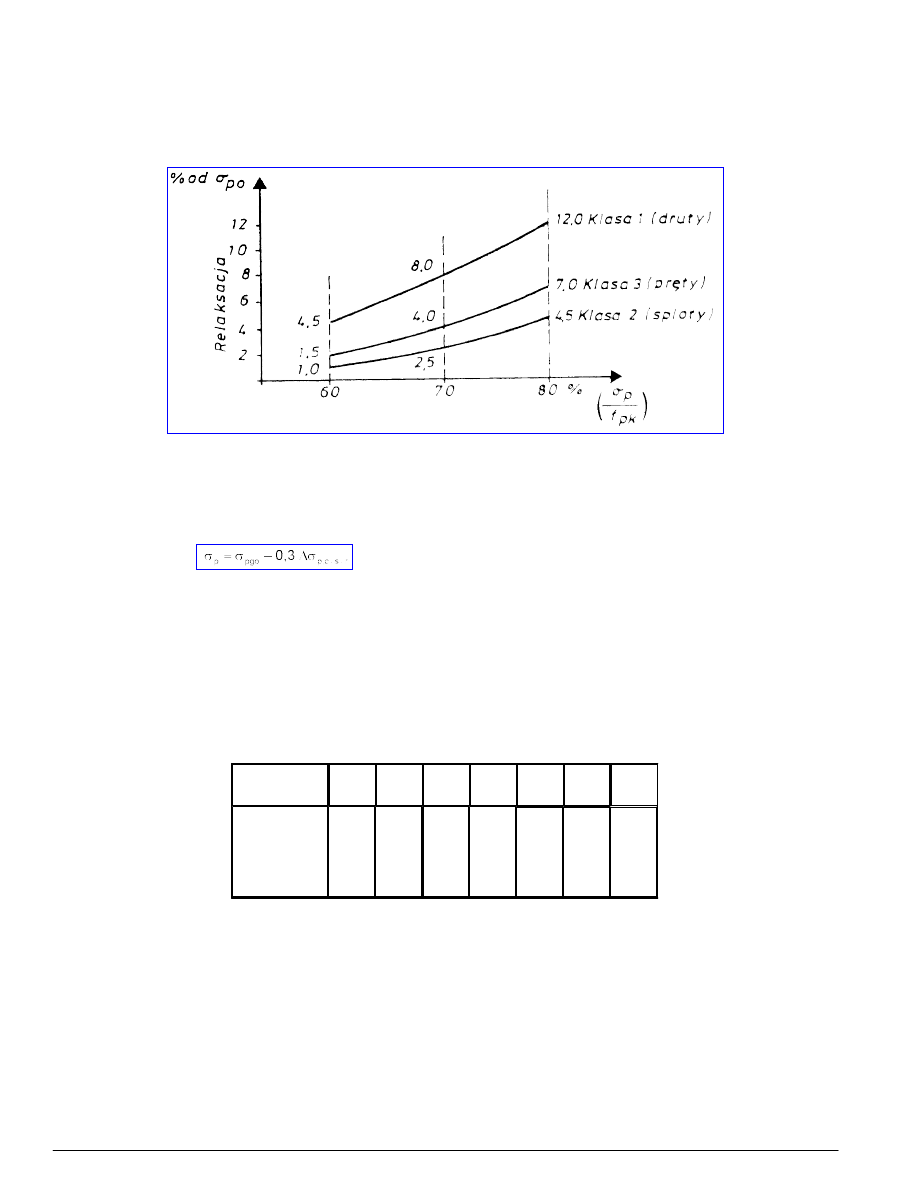
σ
cg
- naprężenie w betonie na poziomie środka ciężkości cięgien od ciężaru własnego i innych obciążeń stałych,
σ
cpo
- początkowe naprężenie w betonie na poziomie środka ciężkości cięgien wywołane sprężeniem,
∆σ
pr
- zmiana naprężenia w cięgnach sprężających spowodowana relaksacją stali,
z
cp
- odległość środka ciężkości cięgien od środka ciężkości przekroju A
cs
.
Wartość
∆σ
pr
można określić na podstawie rysunku 34 w zależności od klasy stali oraz względnego poziomu naprężeń
σ
p
/f
pk
.
Rysunek 34 - Straty spowodowane relaksacją stali po 1 000 h, t = 20°C
Wartość
∆σ
pr
dla t =
∞ można przyjmować 2-krotnie większą od wartości określonej dla t = 1 000 h.
Wartość
σ
p
należy obliczać ze wzoru
(132)
przy czym w budynkach można przyjmować
σ
p
≈ 0,85 σ
pgo
gdzie:
σ
pgo
- początkowe naprężenie w cięgnach wywołane naciągiem i obciążeniami stałymi.
Straty reologiczne należy obliczać w przekrojach najbardziej wytężonych w sytuacji początkowej i trwałej.
Przybliżony przyrost strat na skutek relaksacji w czasie od 0 do 1 000 h podano w tablicy 18.
Tablica 18 - Przybliżony wzrost strat na skutek relaksacji w czasie od 0 do 1 000 h
Czas w
godzinach
1
5
20
100
200
500
1000
Straty na
skutek
relaksacji w %
strat po
1 000 h
15
25
35
55
65
85
100
Przy temperaturze konstrukcji powyżej 60 °C straty spowodowane relaksacją po krótkim okresie czasu mogą być 2 do 3
razy większe niż przy temperaturze 20 °C. Można przyjmować, że krótkotrwała obróbka cieplna nie ma wpływu na relaksację
po długim okresie czasu.
7.1.7 Sytuacja początkowa konstrukcji sprężonych
7.1.7.1 Ograniczenie naprężeń w betonie
Naprężenia ściskające w betonie w sytuacji początkowej obliczone wg wzoru (120) pod działaniem siły N
pd
= P
k,sup
nie
Część 8 Strona 7
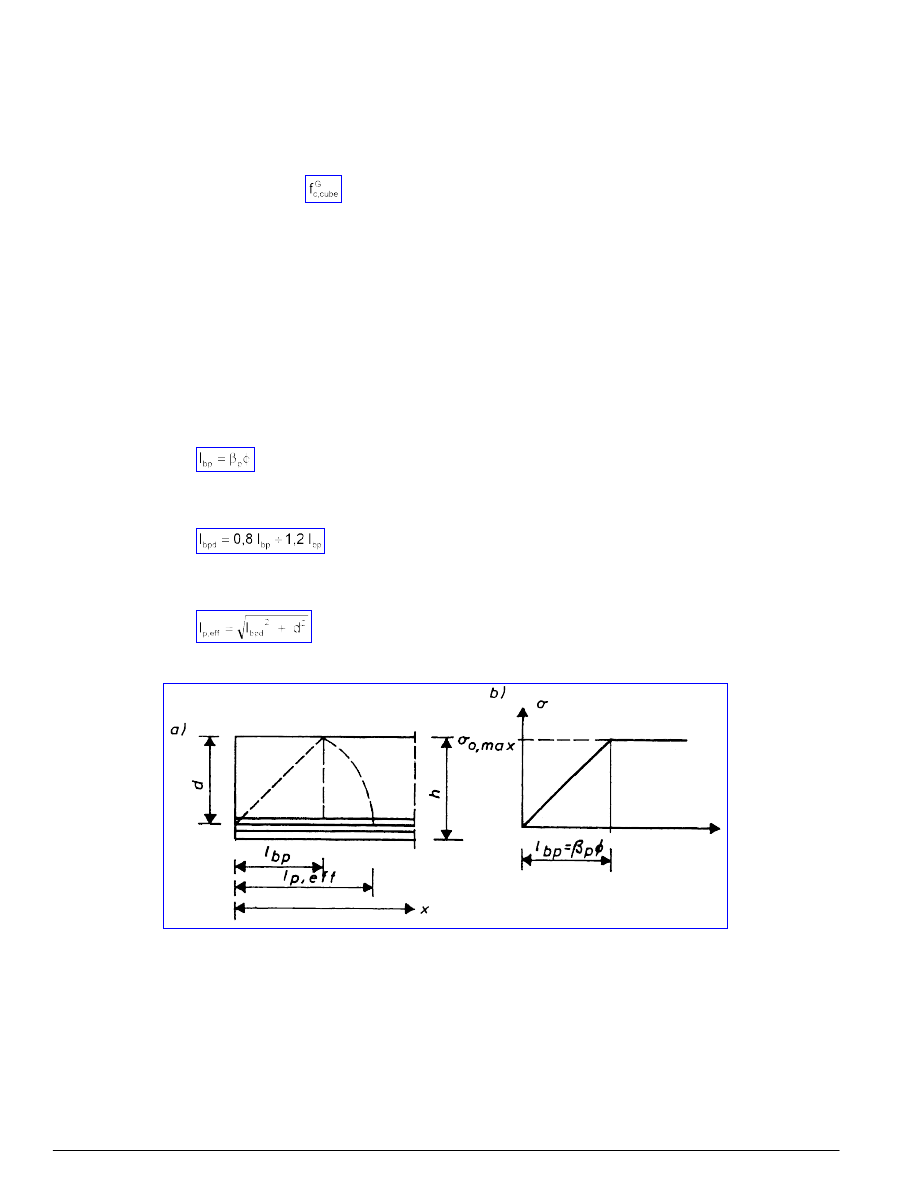
powinny przekraczać podanych niżej wartości
- w elementach strunobetonowych:
przy sprężeniu osiowym - 0,6 f
cm
przy sprężeniu mimośrodowym - 0,7 f
cm
- w elementach kablobetonowych:
przy sprężeniu osiowym - 0,5 f
cm
przy sprężeniu mimośrodowym - 0,6 f
cm
Przy projektowaniu średnią wytrzymałość betonu w chwili sprężania f
cm
można przyjmować równą 0,85 założonej, 28-dniowej
gwarantowanej wytrzymałości betonu
.
7.1.7.2 Nośność
Stan graniczny nośności elementów sprężonych w sytuacji początkowej można sprawdzać pod działaniem obliczeniowej siły
sprężającej według uproszczonych zasad, przyjętych dla ściskania mimośrodowego elementów betonowych lub żelbetowych,
lecz z pominięciem mimośrodów przypadkowych i wpływu smukłości. Zgodnie z tymi zasadami nośność elementów
sprężonych w sytuacji początkowej można sprawdzać wg 5.3.3.2 podstawiając zamiast N
Sd
wartość N
pd
= P
d
oraz
przyjmując
α = 1,0.
Sprawdzenie stanu granicznego nośności w sytuacji początkowej można pominąć, jeżeli naprężenia na krawędzi ściskanej
przekroju nie przekraczają wartości podanych w 7.1.7.1, a naprężenia rozciągające na krawędzi przeciwnej nie przekraczają
wartości f
ctm
.
7.1.7.3 Zarysowanie i ugięcie
Rysy i ugięcia w sytuacji początkowej należy sprawdzać zgodnie z 7.1.9.3 i 7.1.9.4.
7.1.7.4 Strefa zakotwienia w strunobetonie
Zgodnie z rysunkiem 35 należy rozróżniać:
I
bp
- długość zakotwienia, na której następuje pełne przekazanie początkowej siły sprężającej na beton
(133)
I
bpd
- obliczeniową długość zakotwienia
(134)
I
p,eff
- efektywną długość rozkładu, poza którą naprężenia w przekroju poprzecznym zmieniają się w sposób liniowy
(135)
Rysunek 35 - Przekazywanie siły sprężającej w strunobetonie
Tablica 19 - Współczynnik długości zakotwienia
β
β
β
β
p
dla drutów i splotów
Część 8 Strona 8
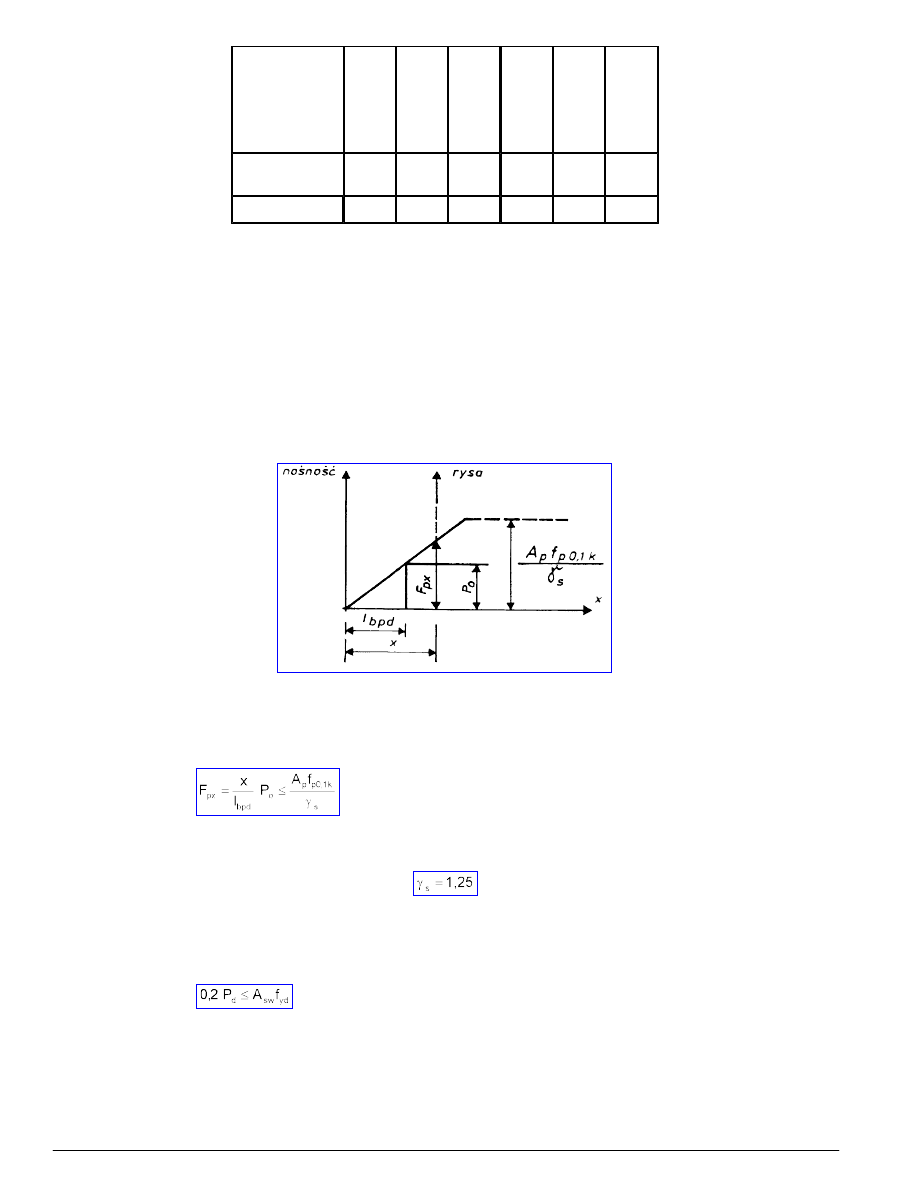
Wytrzymałość
betonu f
ck
w
chwili
przekazywania
siły sprężającej
na beton MPa
25
30
35
40
45
50
sploty i druty
nagniatane
75
70
65
60
55
50
pręty żebrowane
55
50
45
40
35
30
Długość zakotwienia określa się od przekroju, w którym bierze początek przyczepność efektywna, uwzględniając:
- odcinki końcowe cięgien celowo pozbawione przyczepności
- odcinki końcowe cięgien, na których przyczepność została zerwana na skutek nagłego zwolnienia naciągu.
Zakotwienie cięgien sprężających w strunobetonowych elementach zginanych należy sprawdzać biorąc pod uwagę
możliwość zarysowania betonu w strefie zakotwienia. Jeżeli naprężenia rozciągające w betonie od zginania oraz naprężenia
główne określone dla stanu granicznego nośności nie przekraczają f
ctd
to strefę zakotwienia można traktować jako
niezarysowaną a warunki zakotwienia cięgien spełnione bez potrzeby dodatkowych obliczeń. W przeciwnym przypadku
należy wykazać, że podłużna siła rozciągająca T
d
od obciążeń zewnętrznych określona zgodnie ze wzorem (59) nie
przekracza nośności cięgien i zbrojenia zwykłego w rozpatrywanych przekrojach. Obliczeniowy rozkład siły sprężającej w
strefie zakotwienia w strunobetonie należy przyjmować według rysunku 36.
Rysunek 36 - Obliczeniowy rozkład siły sprężającej w strefie zakotwienia w strunobetonie
Nośność cięgien sprężających w określonym przekroju strefy zakotwienia obliczać należy ze wzoru:
(136)
gdzie:
Zbrojenie poprzeczne w strefie zakotwienia cięgien sprężających należy określać stosownie do wartości i rozkładu
poprzecznych naprężeń rozciągających ustalonych na podstawie analizy sprężystej. Jeżeli nie przeprowadza się
dokładniejszych obliczeń to przekrój A
sw
tego zbrojenia należy wyznaczyć z warunku
(137)
Zbrojenie poprzeczne w strefie zakotwienia cięgien należy kształtować zgodnie z 8.2.6.
Część 8 Strona 9
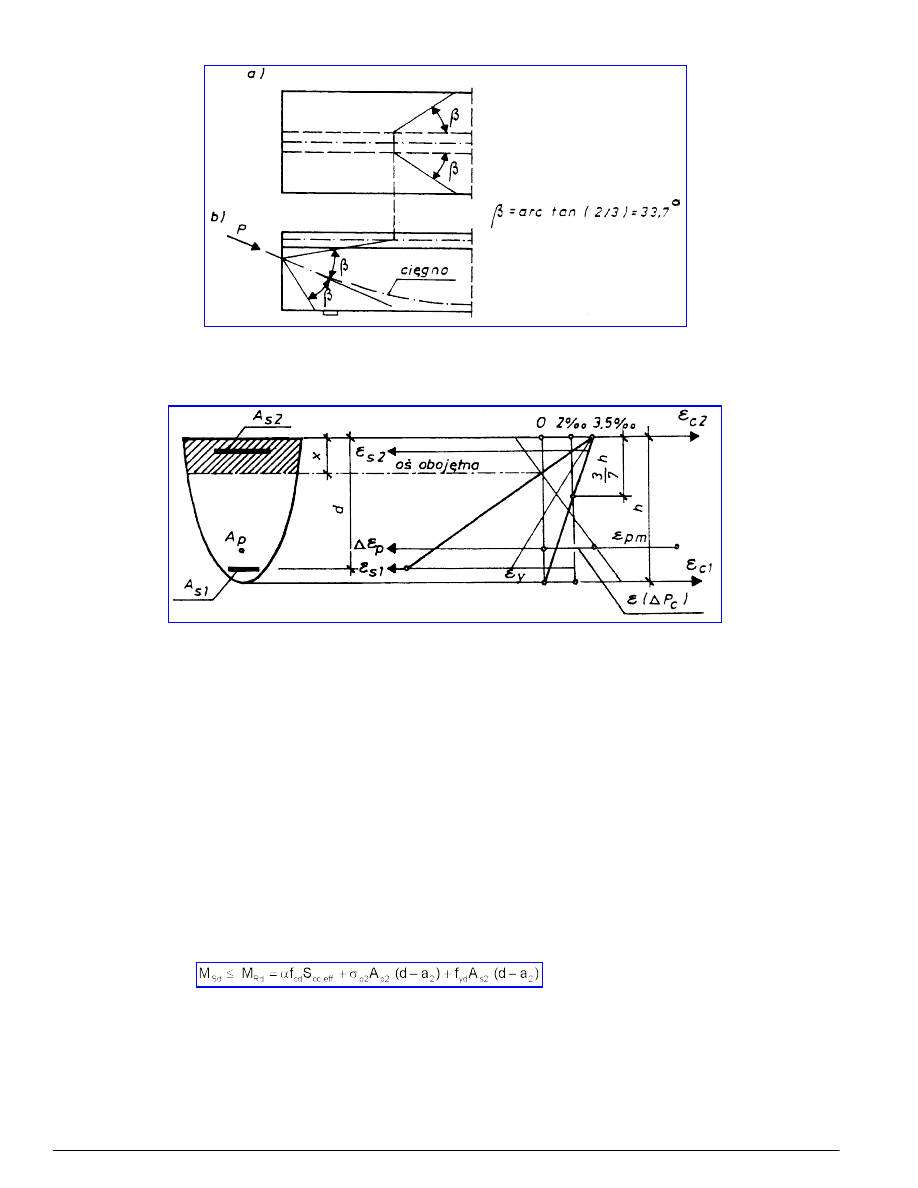
Rysunek 37 - Rozkład siły sprężającej w strefie zakotwienia kabli
Rysunek 38 - Odkształcenia w stanie granicznym nośności
7.1.7.5 Strefa zakotwienia w kablobetonie
Nośność na docisk oraz zbrojenie poprzeczne pod zakotwieniami kabli sprężających należy obliczać zgodnie z 5.7 przy
założeniu, że obliczeniowa siła sprężająca P
d
równa jest sile zrywającej cięgno F
pk
.
Poprzeczne siły rozciągające przyczołowe i wgłębne wynikające z łącznego działania sił skupionych oblicza się na podstawie
analizy sprężystej, przyjmując model kratownicowy lub inną stosowną idealizację rzeczywistego rozkładu sił wewnętrznych.
Rozkład siły sprężającej w strefie zakotwienia kabla można przyjmować jak na rysunku 37.
Poprzeczne siły rozciągające należy przenieść przez zbrojenie obejmujące całą wysokość przekroju. Przekrój tego zbrojenia
powinien być nie mniejszy niż określony z warunku (137).
7.1.8 Nośność konstrukcji sprężonych w sytuacji trwałej
7.1.8.1 Elementy zginane
Nośność elementów sprężonych na zginanie należy określać z warunku równowagi sił wewnętrznych w przekroju, zgodnie z
zasadą liniowego rozkładu odkształceń (rysunek 38) stosując te same założenia, które przyjęto w 5.1 dla elementów
ż
elbetowych.
Nośność elementów sprężonych wykonanych z betonu klasy nie wyższej niż B55 sprawdzać można metodą uproszczoną,
przyjmując prostokątny wykres naprężeń ściskających w betonie (rysunek 39) z warunku
(138)
przy czym położenie osi obojętnej i pole ściskanej strefy betonu określa się z równania
Część 8 Strona 10
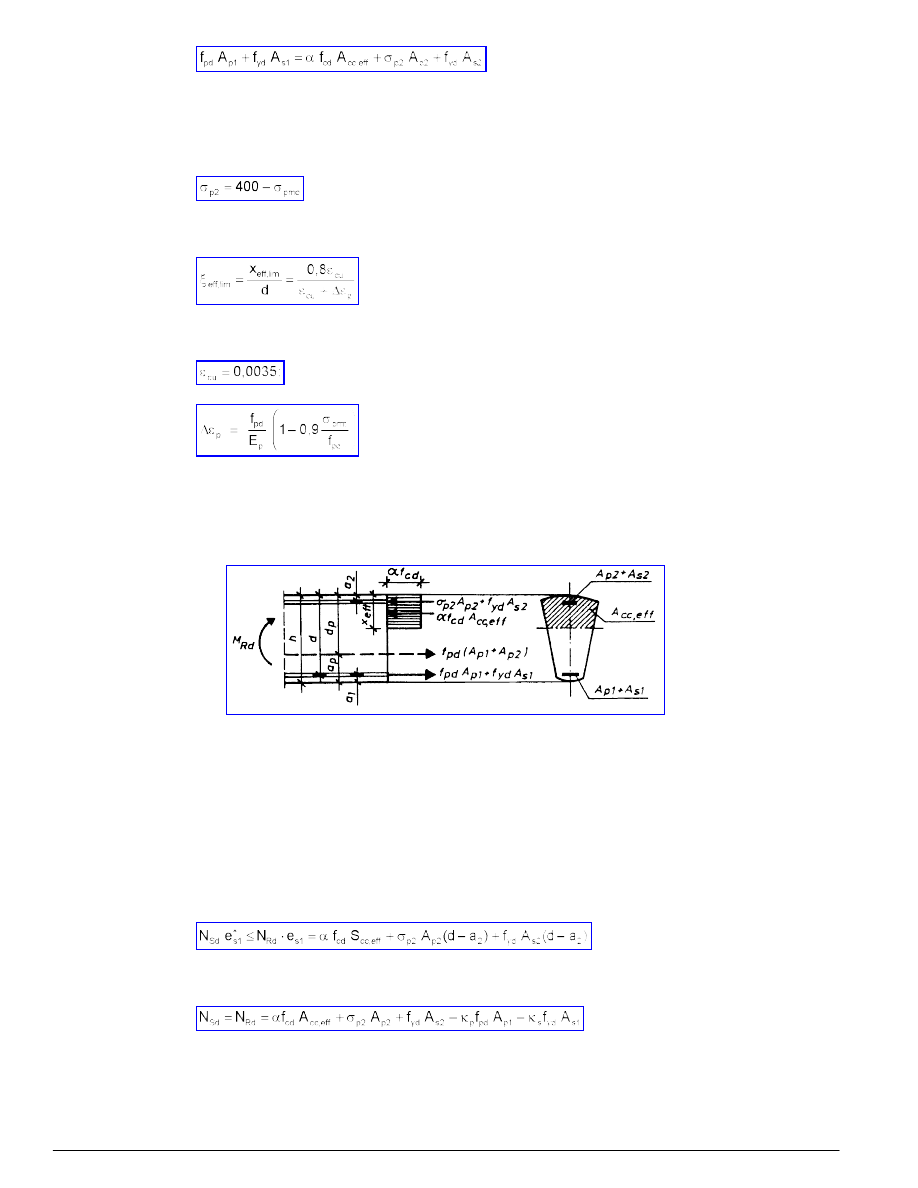
(139)
w którym:
α f
cd
- naprężenia ściskające w betonie według wzoru (108)
f
pd
- naprężenia w stali sprężającej po stronie rozciąganej według wzoru (106)
σ
p2
- naprężenia w stali sprężającej po stronie ściskanej obliczone ze wzoru
(140)
Graniczną wartość względnej wysokości strefy ściskanej określa się ze wzoru
(141)
w którym:
(142)
(143)
d - użyteczna wysokość przekroju sprężonego równa odległości środka ciężkości zbrojenia sprężającego, usytuowanego po
stronie rozciąganej, od krawędzi ściskanej.
Przybliżoną wartość
ξ
eff,lim
dla przeciętnych warunków podano w tablicy 11.
Rysunek 39 - Schemat do obliczania nośności zginanych elementów sprężonych
Nośność elementów sprężonych można sprawdzać sposobem uproszczonym, przyjmując następujące założenia
- przekrój zbrojenia rozciąganego wynosi A
p
= A
p1
+ A
p2
,
- położenie tego zbrojenia w przekroju odpowiada położeniu jego środka ciężkości,
- naprężenia w tym zbrojeniu osiągają wartość f
pd
.
- graniczną wysokość strefy ściskanej ustala się zgodnie ze wzorem (141).
7.1.8.2 Elementy ściskane
Nośność ściskanych elementów sprężonych należy określać podobnie jak w przypadku ściskanych elementów żelbetowych,
z warunku
(144)
wyznaczając położenie osi obojętnej z równania
(145)
Wartość współczynnika
κ
p
należy obliczać ze wzoru:
Część 8 Strona 11
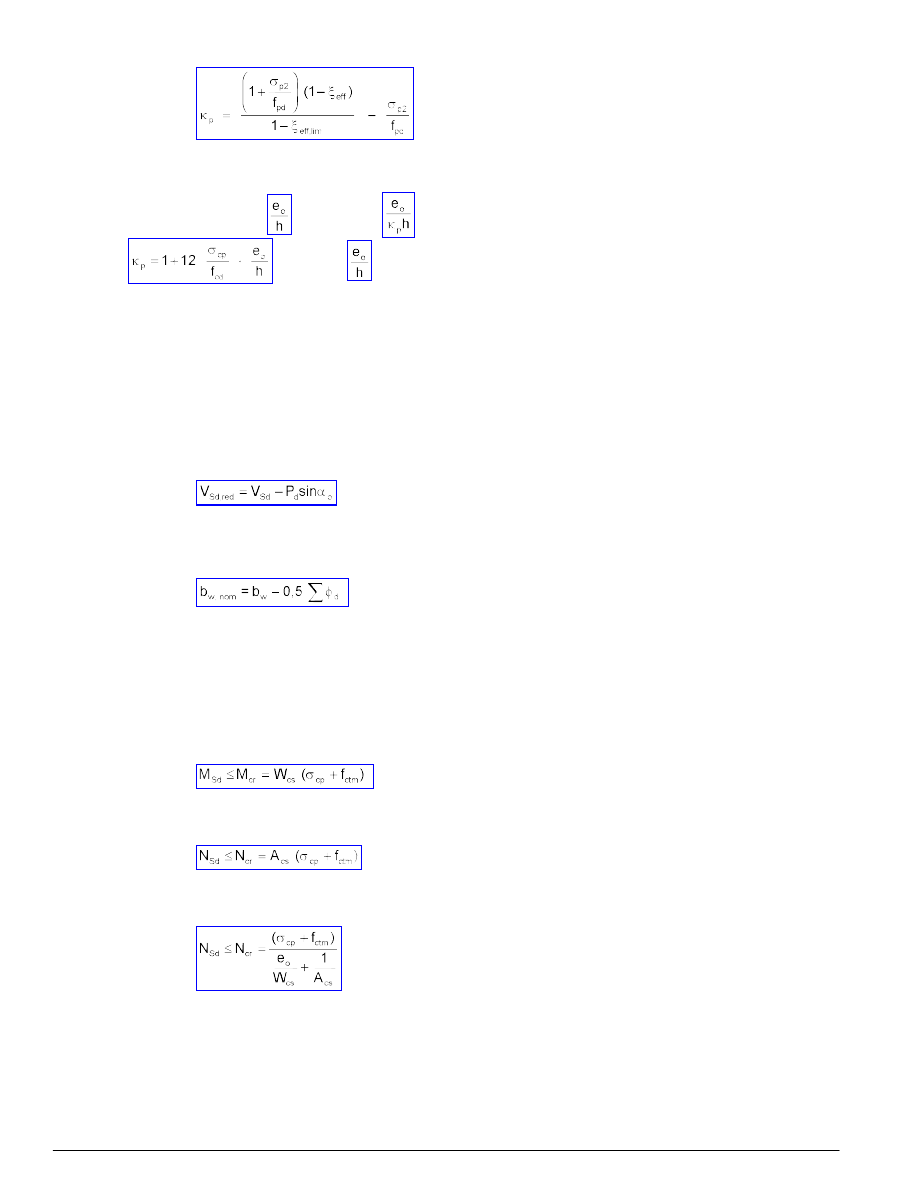
(146)
Wartość współczynnika
κ
s
oblicza się ze wzoru (28). W przypadku dużego mimośrodu gdy
ξ
eff
≤ ξ
eff,lim
,
κ
p
= 1,
κ
s
= 1.
Wpływ smukłości na nośność elementów sprężonych należy uwzględniać wg 5.3.3.2, obliczając wartość siły krytycznej ze
wzoru (33), w którym zamiast
należy przyjąć
. Współczynnik
κ
p
w przypadku osiowego sprężenia oblicza się ze
wzoru
dla wartości
nie większej niż 1,5.
7.1.8.3 Elementy rozciągane
Nośność rozciąganych elementów sprężonych należy określać według tych samych wzorów, które przyjmuje się przy
sprawdzaniu nośności rozciąganych elementów żelbetowych podstawiając dla cięgien sprężających w strefie rozciąganej
zamiast f
yd
wartość f
pd
, natomiast dla cięgien sprężających w strefie ściskanej zamiast f
yd
wartość
σ
p2
obliczoną ze wzoru
(140).
7.1.8.4 Ścinanie
Nośność elementów sprężonych na ścinanie należy określać według 5.5 analogicznie jak dla elementów żelbetowych,
uwzględniając przy obliczaniu nośności V
Rd1
i V
Rd2
wpływ siły podłużnej od sprężenia N
pd
= P
d
określonej ze wzoru (116) dla
niekorzystniejszego przypadku.
W przypadku cięgien odgiętych pod kątem
α
o
do obliczeń należy przyjmować zredukowaną wartość siły poprzecznej V
Sd,red
wyznaczoną ze wzoru
(147)
Jeżeli w środniku znajdują się wypełnione kanały o średnicy
φ
d
> b
w
/8 nośność V
Rd2
należy obliczać przyjmując nominalną
grubość środnika wyznaczoną ze wzoru
(148)
gdzie:
Σφ
d
- suma średnic kanałów kablowych na szerokości środnika w najniekorzystniejszym przekroju.
7.1.9 Stan graniczny użytkowalności
7.1.9.1 Pojawienie się rys prostopadłych do osi elementu
Możliwość pojawienia się rys prostopadłych do osi elementu należy sprawdzać z warunków
- w elementach zginanych
(149)
- w elementach osiowo rozciąganych
(150)
- w elementach mimośrodowo rozciąganych
(151)
gdzie:
W
cs
- wskaźnik wytrzymałości przekroju sprowadzonego.
7.1.9.2 Pojawienie się rys ukośnych
Część 8 Strona 12
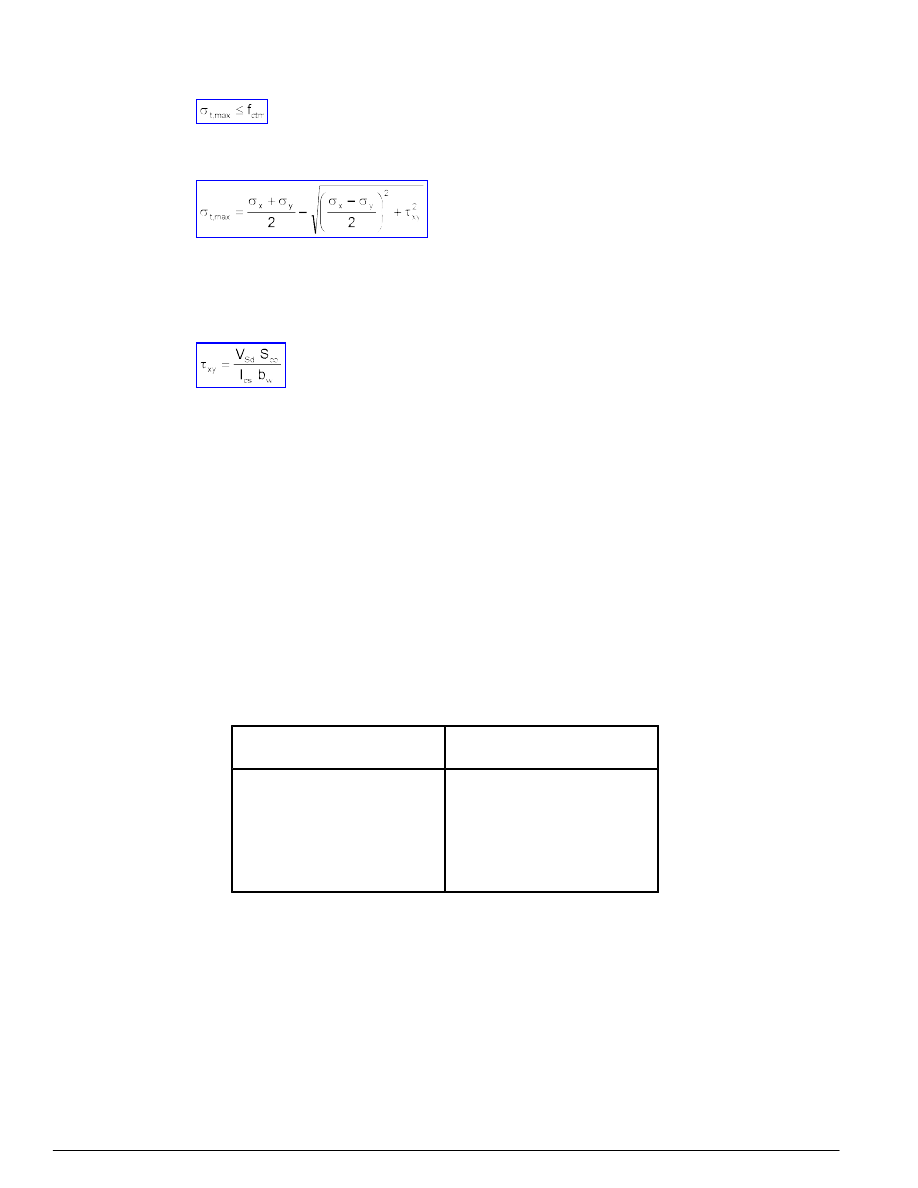
Możliwość pojawienia się rys ukośnych w elementach sprężonych należy sprawdzać w miejscach występowania
maksymalnych wartości głównych naprężeń rozciągających na podstawie warunku
(152)
Wartości głównych naprężeń rozciągających oblicza się ze wzoru
(153)
w którym:
σ
x
- naprężenia normalne od siły sprężającej i obciążeń zewnętrznych w kierunku osi x,
σ
y
- naprężenia normalne w kierunku osi y,
τ
xy
- naprężenia styczne obliczone ze wzoru
(154)
V
sd
- siła poprzeczna, a w przypadku cięgien odgiętych zredukowana siła poprzeczna,
S
co
- moment statyczny części przekroju położonej powyżej rozpatrywanego włókna obliczany względem środka ciężkości
przekroju.
7.1.9.3 Rozwarcie rys prostopadłych do osi elementu
Sprawdzenie szerokości rys prostopadłych do osi elementu nie jest wymagane jeżeli warunek pojawienia się rys wg 7.1.9.1
nie został przekroczony, a w strefie przekroju poddanej działaniu naprężeń rozciągających istnieje zbrojenie o przekroju nie
mniejszym od wartości określonej wzorem (92).
Pole przekroju strefy rozciąganej A
ct
w elemencie sprężonym w chwili poprzedzającej zarysowanie określa się odpowiednio
do rozpatrywanego przypadku obciążenia na podstawie liniowego rozkładu naprężeń.
Wartość
σ
s
we wzorze (92) w odniesieniu do elementów sprężonych oznacza przyrost naprężenia w stali zwykłej i
sprężającej od stanu dekompresji do pojawienia się rysy. Wartość
σ
s
przyjmuje się odpowiednio do średnicy pręta lub cięgna
sprężającego w strefie rozciąganej zgodnie z tablicą 20.
Wartości
σ
s
podane w tablicy 20 zostały tak dobrane, aby szerokość rysy w przypadku jej powstania nie przekraczała
0,2 mm.
Tablica 20 - Maksymalne średnice prętów o dużej przyczepności w elementach sprężonych
Przyrost naprężeń w stali
σ
s
[MPa]
Maksymalna średnica pręta [mm]
160
200
240
280
320
360
400
25
16
12
8
6
5
4
Jeżeli warunek pojawienia się rys został przekroczony, szerokość rys prostopadłych do osi elementu należy obliczać zgodnie
z 6.3 jak dla elementów żelbetowych, traktując wartość
ε
sm
we wzorze (93) jako przyrost odkształceń stali zwykłej i
sprężającej od stanu dekompresji do rozpatrywanego poziomu obciążenia.
Obliczając średni rozstaw rys s
rm
według wzoru (94) należy przyjmować:
k
1
= 0,8 dla prętów, splotów i drutów nagniatanych o dużej przyczepności,
k
1
= 1,6 dla prętów i drutów gładkich,
k
1
= 2,0 dla kabli sprężających.
W przypadku jednoczesnego występowania prętów i cięgien o różnych średnicach i różnej przyczepności wartość k
1
φ można
Część 8 Strona 13

zastąpić przez wartość średnią ważoną
Σ k
1
φ/n.
Efektywne pole przekroju strefy rozciąganej A
ct,eff
w otoczeniu prętów, drutów i splotów określa się jak w elementach
ż
elbetowych (rysunek 32). Przy określaniu A
ct,eff
w otoczeniu kabli sprężających można przyjmować dla każdego kabla pole
kwadratu o boku 300 mm.
7.1.9.4 Ugięcie elementów sprężonych
Ugięcie elementów sprężonych należy obliczać stosując zasadę superpozycji ugięć od obciążeń zewnętrznych i sprężenia,
np. zgodnie ze wzorem
(155)
gdzie:
M
Sd
- moment zginający wyznaczony dla kombinacji obciążeń długotrwałych,
N
pd
= P
k,sup
lub P
k,inf,
α
k
- współczynnik zależny od układu obciążeń,
α
p
- współczynnik zależny od trasy cięgna,
- sztywność elementu określona wg załącznika E.
7.1.10 Konstrukcje sprężone bez przyczepności
Rozróżnia się konstrukcje sprężone bez przyczepności, w których cięgna mogą być usytuowane w przekroju betonowym
(zwykle w osłonkach polietylenowych) lub też poza tym przekrojem (zwykle w osłonach specjalnych). Cięgna te mogą być
jedno- lub wielosplotowe. Oddziaływanie cięgien bez przyczepności należy w obliczeniach traktować jak obciążenie
zewnętrzne reprezentowane przez:
- podłużne siły ściskające przyłożone w strefach zakotwień,
- oddziaływania radialne na trasie cięgien lub na dewiatorach.
Szczegółowe wymagania odnośnie cięgien zewnętrznych oraz zasady ich stosowania zamieszczone są w odpowiednich
przepisach
4)
i nie są objęte niniejszą normą.
Straty siły sprężającej spowodowane tarciem należy określać stosownie do typu cięgna i osłonki na podstawie odpowiednich
przepisów
4)
.
Straty opóźnione określone zgodnie ze wzorem (130) można przyjmować jako stałe na całej długości cięgna.
W stanie granicznym nośności można przyjmować, że siła w cięgnie jest równa obliczeniowej sile sprężającej powiększonej o
przyrost wynikający ze średniego odkształcenia betonu wzdłuż trasy cięgna. Dopuszcza się dla uproszczenia pominięcie tego
przyrostu w cięgnach zewnętrznych.
Można przyjmować, że przyrost naprężeń w cięgnach wewnętrznych bez przyczepności wynosi 100 MPa na odcinku jednego
przęsła. W przypadku większej liczby przęseł wartość tę można zmniejszyć uwzględniając liczbę przęseł.
Przy obliczaniu nośności na siły poprzeczne siła sprężająca powinna być uwzględniona jako siła zewnętrzna, działająca w
ś
rodku ciężkości przekroju ściskanego.
Przy sprawdzaniu stanu granicznego użytkowalności należy przyjmować różnicę temperatury cięgien zewnętrznych i betonu
wynoszącą ą 10° C.
Gdy wszystkie cięgna są zewnętrzne lub wewnętrzne bez przyczepności element należy uważać za żelbetowy z dodatkowo
działającą siłą podłużną.
Minimalne promienie zakrzywienia cięgien wewnętrznych bez przyczepności wynoszą:
dla splotu
φ 13 mm r = 1,7 m,
dla splotu
φ 15 mm r = 2,5 m.
Liczbę cięgien w płytach ciągłych należy dobierać w taki sposób, aby zwolnienie naciągu 2 sąsiednich cięgien nie
spowodowało zniszczenia konstrukcji.
W przypadku zerwania jednego cięgna bez przyczepności redystrybucję sił wewnętrznych powinno zapewniać zbrojenie ze
stali zwykłej.
7.2 Konstrukcje poddane działaniu obciążeń wielokrotnie zmiennych
7.2.1 Zasady ogólne
Wpływ obciążeń wielokrotnie zmiennych, które mogą spowodować zmęczenie konstrukcji należy uwzględniać w obliczeniach,
jeżeli występują one co najmniej 5
⋅ 10
5
-krotnie w przewidywanym okresie użytkowania i stanowią co najmniej 60%
całkowitego obciążenia. Przykładem takich konstrukcji są belki podsuwnicowe.
W przypadku działania obciążeń wielokrotnie zmiennych nie należy stosować konstrukcji betonowych.
Konstrukcje poddane działaniu obciążeń wielokrotnie zmiennych muszą spełniać wymagania stanów granicznych dla
obciążeń statycznych.
Do zbrojenia konstrukcji poddanych działaniu obciążeń wielokrotnie zmiennych zaleca się stosowanie stali klasy A-I i A-II
znaku 18G2 lub innych o podobnych właściwościach. Prętów ze stali klasy A-0 nie należy stosować.
Część 8 Strona 14
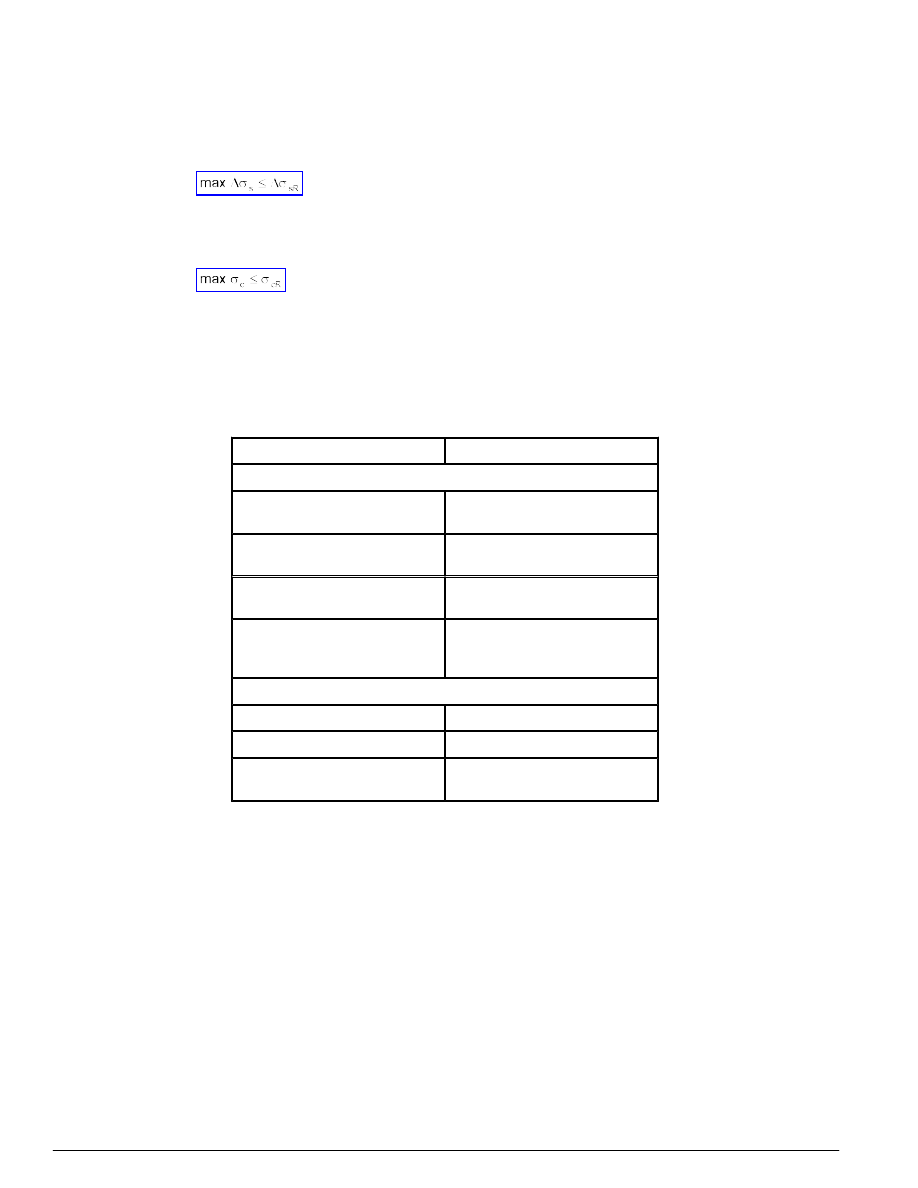
7.2.2 Zmęczenie elementów konstrukcji
Sprawdzenie stanu granicznego nośności wywołanego zmęczeniem materiałów polega na wykazaniu, że uszkodzenia
zmęczeniowe betonu i stali w miarodajnych przekrojach elementu, spowodowane przez charakterystyczne obciążenia
wielokrotnie zmienne, nie przekraczają wielkości dopuszczalnych.
Możliwość zmęczenia materiałów sprawdzać należy z warunków
- maksymalny zakres zmian naprężeń w stali max
∆σ
s
nie jest większy od zakresu dopuszczalnego
∆σ
sR
(156)
maksymalne naprężenie normalne w betonie max
σ
c
, obliczone przy założeniu liniowego rozkładu naprężeń w przekroju i
α
e
=
E
s
/E
cm
- nie jest większe od naprężenia dopuszczalnego
σ
cR
.
(157)
Wartości dopuszczalnego zakresu zmian naprężeń
∆σ
sR
dla liczby cykli obciążeń wielokrotnie zmiennych nie przekraczającej
10
7
- należy przyjmować według tablicy 21.
Tablica 21 - Wartości dopuszczalnego zakresu zmian naprężeń w stali
∆
∆
∆
∆σ
σ
σ
σ
sR
∆σ
sR
[MPa]
Stal zbrojeniowa
Pręty proste i odgięte przy
ś
rednicach odgięć
≥ 15 φ
100
Pręty odgięte przy średnicach
odgięć < 15
φ
60
Pręty w konstrukcjach i elementach
w środowisku klasy 4, 5b i 5c
35
Połączenia prętów zgrzewane
doczołowo i spawane z
dwustronnymi nakładkami
35
Cięgna sprężające
W konstrukcjach strunobetonowych
60
W konstrukcjach innych
45
Zakotwienia i łączniki cięgien
sprężających
35
Wartości dopuszczalne
σ
cR
należy przyjmować według zależności:
σ
cR
= 0,25 f
ck
- ściskanie,
σ
cR
= 0,18 f
ck
- ściskanie - rozciąganie przy maksymalnych naprężeniach rozciągających nie większych od 0,02 max
σ
c
,
σ
cR
= 0,25 f
ctk
rozciąganie.
Dopuszcza się możliwość sprawdzania stanu granicznego nośności wywołanego zmęczeniem materiałów w oparciu o analizę
granicznej liczby cykli obciążenia lub analizę uszkodzeń, pod warunkiem naukowego uzasadnienia przyjętej metody.
7.3 Konstrukcje zespolone
7.3.1 Zasady ogólne
Konstrukcje zespolone należy projektować i wykonywać w taki sposób, aby w sytuacji przejściowej (montażowej) i trwałej
spełnione były wymagania stanów granicznych w stosunku do elementów łączonych oraz ustroju zespolonego. Podstawowy
element prefabrykowany lub wcześniej wykonany - powinien być zdolny do przeniesienia wszystkich obciążeń występujących
Część 8 Strona 15
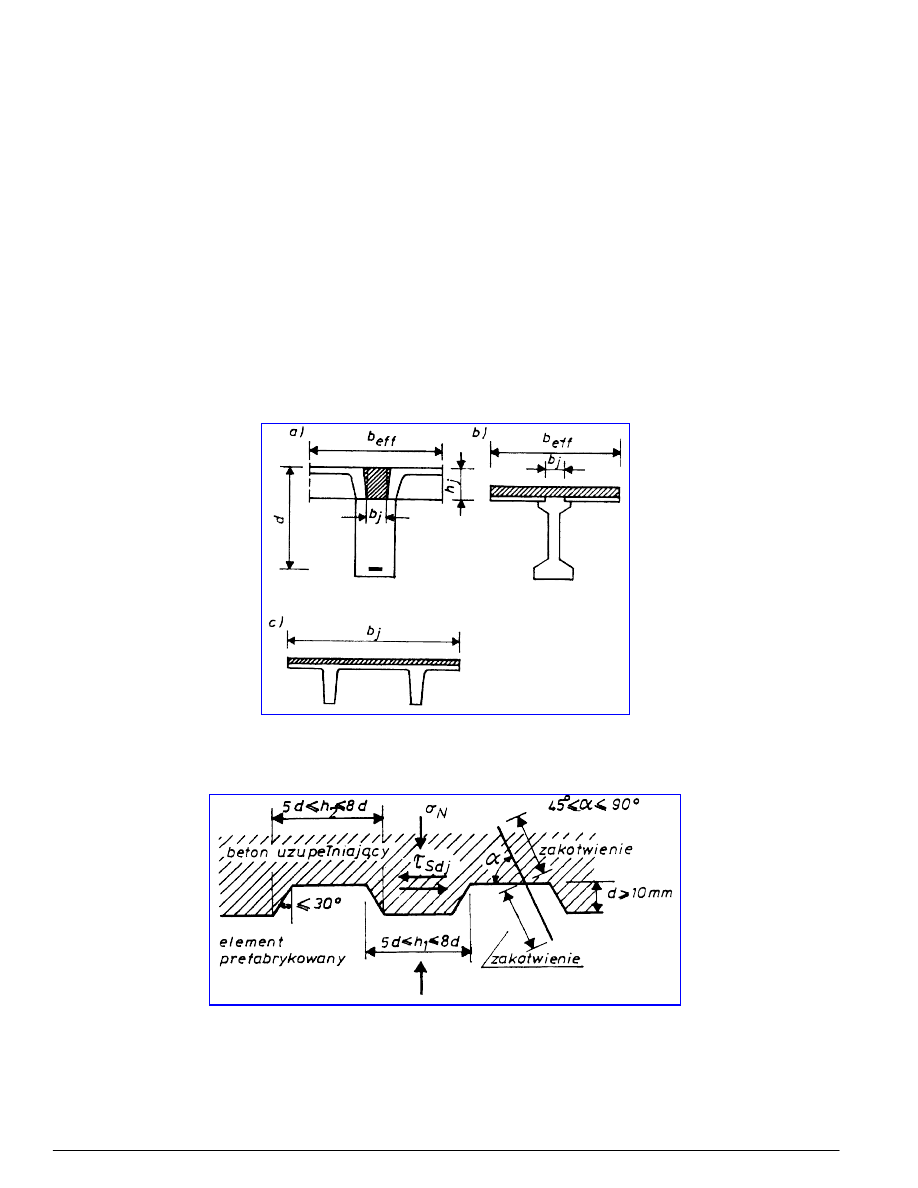
przed osiągnięciem pełnej wytrzymałości przez beton uzupełniający.
Konstrukcję można uznać za zespoloną, jeżeli:
a) zachowana jest nośność na rozwarstwienie połączenia prefabrykatu z betonem uzupełniającym,
b) zachowana jest ciągłość w przekazywaniu sił normalnych przez elementy współpracujące oraz między nimi,
c) klasa betonu uzupełniającego jest nie niższa niż B20,
d) grubość warstwy betonu uzupełniającego jest nie mniejsza niż 40 mm.
Prefabrykowane elementy stropów i stropodachów połączone z elementem podstawowym za pomocą betonu
uzupełniającego i zbrojenia (rysunek 40) mogą być uwzględniane przy sprawdzaniu nośności przekroju zespolonego na
zginanie jedynie wówczas, gdy są usytuowane w strefie ściskanej. Szerokość współpracującą tych elementów należy
określać według 4.4.3. Elementów tych nie należy uwzględniać przy sprawdzaniu nośności przekroju poprzecznego na
ś
cinanie.
Podane zasady obliczeń nie mogą być stosowane w przypadku konstrukcji zespolonych, poddanych działaniu obciążeń
wielokrotnie zmiennych.
Nośność na ścinanie podłużne w płaszczyźnie zespolenia prefabrykatu z betonem uzupełniającym osiąga się poprzez
odpowiednie zbrojenie poprzeczne, przyczepność naturalną oraz tarcie.
Nośność połączenia zależy m.in. od rodzaju powierzchni prefabrykatu, która może być:
bardzo gładka - uzyskiwana w formie stalowej lub w gładkiej formie drewnianej,
gładka - uzyskiwana w formie ślizgowej lub po wibrowaniu bez dodatkowych zabiegów,
szorstka - pozostawiona w stanie szorstkim po zabetonowaniu lub poddana zabiegowi zgrabienia wywołującemu bruzdy o
głębokości nie mniejszej niż 3 mm w rozstawie nie większym niż 40 mm, lub jeżeli zostało odsłonięte kruszywo,
dyblowa - celowo ukształtowana jak na rysunku 41.
Rysunek 40 - Przekroje zespolone
Rysunek 41 - Złącze dyblowe
Część 8 Strona 16

Powierzchnia prefabrykatu przewidziana do zespolenia powinna być szorstka, oczyszczona, bez zacieków mleczka
cementowego, a bezpośrednio przed betonowaniem odpowiednio nawilżona. Dopuszcza się stosowanie środków
zwiększających trwale przyczepność obu betonów. Dla zachowania wymaganej ciągłości konstrukcji, warunków zespolenia i
przeciwdziałania efektom skurczu - zaleca się, aby beton uzupełniający, szczególnie w elementach prętowych, posiadał
odpowiednie zbrojenie podłużne. Konsystencja betonu uzupełniającego powinna umożliwiać odpowiednią urabialność
mieszanki bez segregacji składników oraz jej pełne zagęszczenie w danych warunkach wykonania konstrukcji.
7.3.2 Zabezpieczenie konstrukcji przed rozwarstwieniem w płaszczyźnie zespolenia
Nośność złącza na rozwarstwienie należy sprawdzać na podstawie warunku
(158)
w którym:
τ
Sdj
- podłużne naprężenia ścinające w styku od obciążeń obliczeniowych,
τ
Rdj
- nośność obliczeniowa na ścinanie na jednostkę powierzchni styku.
Naprężenia
τ
Sdj
należy wyznaczać odpowiednio do wartości i rozkładu podłużnej siły ścinającej. Wartość tej siły na
określonym odcinku ścinania równa jest różnicy sił normalnych, działających na końcach tego odcinka w tej części przekroju,
która położona jest ponad rozpatrywaną płaszczyzną zespolenia.
Naprężenia
τ
Sdj
w elementach zginanych, poprzecznie obciążonych można obliczać ze wzoru
(159)
w którym:
β - współczynnik wyrażający stosunek wypadkowej bryły normalnych naprężeń ściskających ponad rozpatrywaną
płaszczyzną zespolenia do wypadkowej całej bryły tych naprężeń w najbardziej wytężonym przekroju zginanym,
V
Sd
- obliczeniowa siła poprzeczna w rozpatrywanym przekroju od całości obciążeń zewnętrznych (montażowych i
uzupełniających),
z - ramię sił wewnętrznych w przekroju zespolonym wyznaczone przy sprawdzaniu nośności na zginanie, nie większe niż:
0,85 d - w konstrukcjach żelbetowych,
0,80 d - w konstrukcjach sprężonych,
b
j
- szerokość płaszczyzny zespolenia prefabrykatu z betonem uzupełniającym.
Naprężenia ścinające w płaszczyźnie zespolenia betonu uzupełniającego z elementami współpracującymi w strefie ściskanej
można obliczać według wzoru (159) podstawiając odpowiednią wartość
β oraz właściwą szerokość rozpatrywanej
płaszczyzny zespolenia b
j
= h
j
.
Naprężenia ścinające w płaszczyźnie zespolenia wynikające z różnic skurczu i pełzania elementów współpracujących mogą
być w obliczeniach pominięte.
Nośność obliczeniową na ścinanie na jednostkę powierzchni styku należy określać ze wzoru
(160)
z warunkiem ograniczającym
(161)
gdzie:
k
T
- współczynnik podany w tablicy 22; jeżeli złącze znajduje się w strefie rozciąganej należy przyjmować:
k
T
= 0 - dla powierzchni gładkich i szorstkich
k
T
= 0,5 - dla powierzchni dyblowych;
τ
Rd
- wytrzymałość obliczeniowa betonu na ścinanie wg tablicy 13, określona dla betonu niższej klasy,
µ - współczynnik tarcia przy ścinaniu wg tablicy 22,
ν = 0,7 - f
ck
/200 (f
ck
w Mpa)
σ
N
- naprężenie wywołane przez zewnętrzną siłę prostopadłą do powierzchni styku: dodatnie dla ściskania, ujemne dla
rozciągania, przy czym
σ
N
≤ 0,6 f
cd
,
ρ
j
= A
s
/A
j
≥ 0,001,
A
s
- pole przekroju zbrojenia poprzecznego w złączu, łącznie ze zwykłym zbrojeniem na ścinanie (jeżeli występuje),
A
j
- pole powierzchni styku,
α - kąt podany na rysunku 41 zawarty w przedziale 45° ≤ α ≤ 90°
Część 8 Strona 17

Tablica 22 - Wartości współczynników k
T
i µ
Rodzaj powierzchni
k
T
µ
monolit
2,5
1,0
dyblowa
1,8
1,0
szorstka
1,4
0,8
gładka
0,9
0,6
bardzo gładka
0,3
0,4
Zbrojenie na ścinanie podłużne w złączu jest obliczeniowo potrzebne, kiedy zachodzi warunek:
(162)
Pole przekroju zbrojenia poprzecznego wyznacza się ze wzoru (160) przy czym rozkładu tego zbrojenia w kierunku
podłużnym należy dokonać stosownie do wyrażenia
(163)
Można przyjmować rozkład schodkowy jak na rysunku 42.
Rysunek 42 - Wykres ilustrujący obliczeniowo potrzebne zbrojenie złącza
Zbrojenie poprzeczne można wykonywać w postaci strzemion, pętli, siatek zgrzewanych ze stali gładkiej lub żebrowanej
klasy nie wyższej niż A-lll. Zbrojenie to powinno być w pełni zakotwione w elementach współpracujących.
Jeżeli zbrojenie poprzeczne wyznaczone ze wzoru (160) sięga na całą wysokość przekroju zespolonego to można je również
uwzględniać przy sprawdzaniu nośności na ścinanie.
7.3.3 Nośność konstrukcji zespolonych
Przy sprawdzaniu nośności konstrukcji zespolonych przyjmuje się następujące założenia.
Nośność elementów zespolonych w przekrojach normalnych i ukośnych oblicza się według tych samych zasad, które
przyjmowane są dla elementów jednorodnych.
Nośność elementów, które w sytuacji montażowej są dodatkowo podpierane w przęśle, sprawdzać należy w sytuacji trwałej
według tych samych zasad co nośność elementów bez dodatkowego podparcia montażowego.
Konstrukcje złożone z elementów o różnej wytrzymałości należy sprowadzać do przekroju jednorodnego odpowiednio do
stosunku obliczeniowych wytrzymałości betonu na ściskanie tych elementów.
Część 8 Strona 18

Siły wewnętrzne wywołane różnicą skurczu i pełzania mogą być w obliczeniach pominięte.
7.3.4 Zarysowanie i ugięcia konstrukcji zespolonych
Przy sprawdzaniu zarysowania i ugięć konstrukcji zespolonych należy postępować jak w przypadku konstrukcji jednorodnych
przyjmując następujące założenia.
Odkształcenie elementu powstałe przed zespoleniem sumuje się z odkształceniem elementu po jego zespoleniu; założenie
to, wyrażające zasadę superpozycji odkształceń, może być przy ocenie odpowiednich stanów granicznych zastąpione przez
zasadę odpowiedniej superpozycji naprężeń i ugięć.
Konstrukcje zespolone, złożone z elementów o różnej odkształcalności, należy sprowadzać do przekroju jednorodnego
odpowiednio do stosunku modułów sprężystości betonu E
cm
tych elementów.
Podparcie elementu podstawowego w sytuacji montażowej można uwzględniać przy sprawdzaniu stanów granicznych
użytkowalności konstrukcji zespolonej pod warunkiem, że podparcie to nie jest usuwane do chwili uzyskania 80%
wytrzymałości betonu uzupełniającego; w obliczeniach uwzględniać należy podatność podpór montażowych.
Naprężenia w konstrukcji zespolonej, wywołane różnicą skurczu i pełzania betonu, znajdują się w stanie równowagi
wewnętrznej, a krzywizny łączonych elementów po odkształceniu są jednakowe. W konstrukcjach zespolonych stropów i
stropodachów (rysunek 40) wpływ skurczu betonu uzupełniającego może być w obliczeniach pominięty dla przekrojów typu
a), natomiast powinien być uwzględniony dla przekrojów typu b) i c).
Część 8 Strona 19
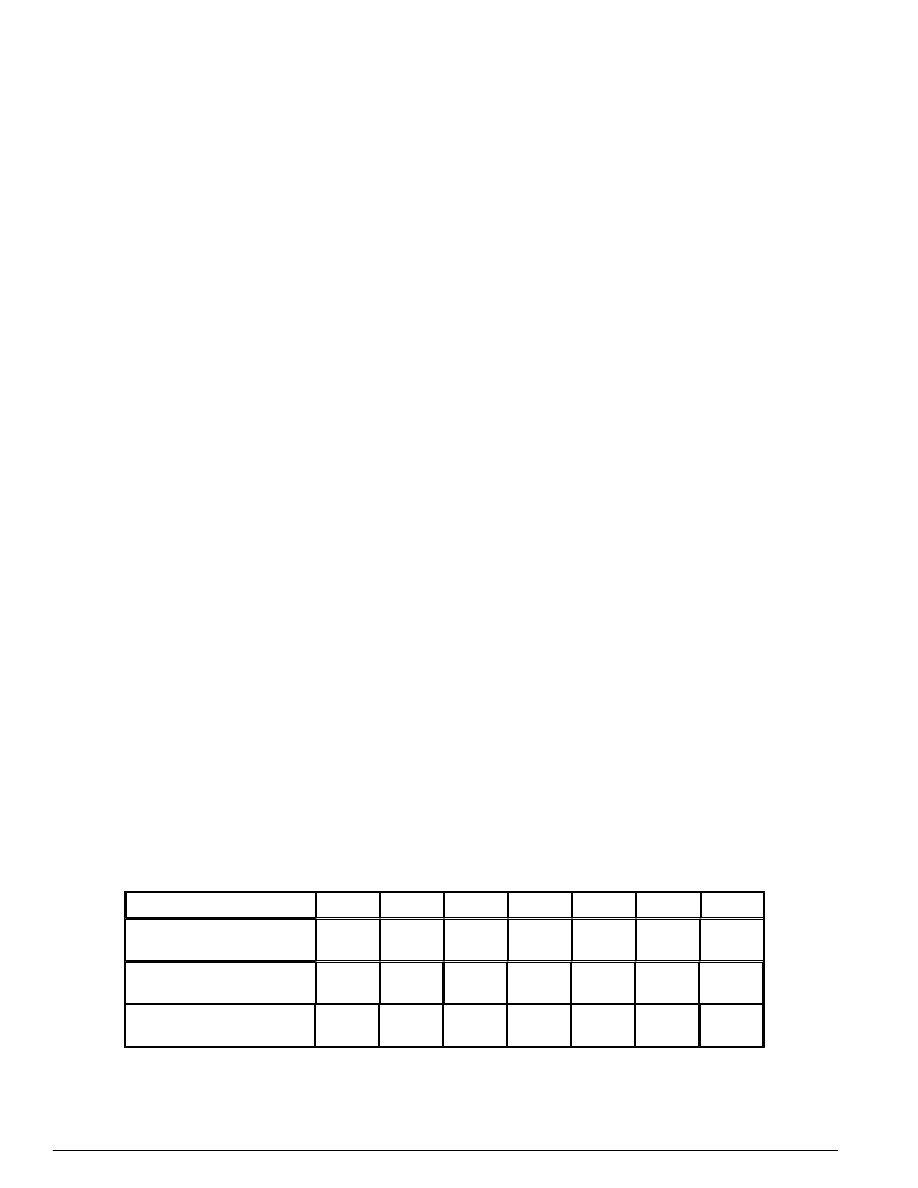
8 Wymagania i zalecenia dotyczące zbrojenia konstrukcji
8.1 Konstrukcje żelbetowe
8.1.1 Zasady ogólne
8.1.1.1 Rozmieszczenie prętów zbrojenia w przekroju
Rozstaw prętów w przekroju powinien umożliwiać należyte ułożenie i zagęszczenie mieszanki betonowej bez segregacji
składników, przy zapewnieniu właściwych warunków przyczepności zbrojenia do betonu.
Odległości poziome i pionowe s
l
mierzone w świetle między poszczególnymi prętami lub warstwami prętów powinny być nie
mniejsze niż:
s
l
≥ φ
s
l
≥ 20 mm
s
l
≥ d
g
+ 5 mm
gdzie:
φ - maksymalna średnica pręta
d
g
- maksymalny wymiar kruszywa
Odległości s
l
między parami prętów powinny być nie mniejsze niż:
s
I
≥ 1,5 φ
s
I
≥ 30 mm
s
I
≥ d
g
+ 5 mm
Na długości zakładu pręty zbrojenia mogą być układane na styk.
Pręty ułożone w kilku warstwach powinny być usytuowane jeden nad drugim, a przestrzeń między prętami powinna mieć
szerokość wystarczającą do wprowadzenia wibratora wgłębnego.
Rozstaw w osiach prętów zbrojenia w przekrojach krytycznych płyt powinien być nie większy niż:
- przy zbrojeniu jednokierunkowym
250 mm i 1,2 h dla h > 100 mm,
120 mm dla h ≤ 100 mm
- przy zbrojeniu dwukierunkowym - 250 mm.
W elementach ściskanych maksymalny rozstaw w osiach prętów powinien być nie większy niż 400 mm.
8.1.1.2 Otulenie prętów zbrojenia
Grubość warstwy betonu między wewnętrzną powierzchnią formy i zbrojeniem należy ustalać odpowiednio do średnicy pręta i
warunków środowiskowych. Przyjęta grubość otulenia powinna zapewniać bezpieczne przekazywanie sił przyczepności,
ochronę stali przed korozją, ochronę przeciwpożarową oraz umożliwiać należyte ułożenie i zagęszczenie betonu.
W celu bezpiecznego przekazania sił przyczepności i należytego zagęszczenia betonu, grubość otulenia zbrojenia w
elementach żelbetowych powinna być nie mniejsza niż:
c ≥ φ lub φ
n
c ≥ d
g
+ 5 mm
gdzie:
φ - średnica pręta,
φ
n
- średnica wiązki prętów,
d
g
- maksymalny wymiar kruszywa.
W celu ochrony stali przed korozją grubość otulenia dla całego zbrojenia, włączając pręty rozdzielcze i strzemiona, powinna
być nie mniejsza od wartości podanych w tablicy 23.
Tablica 23 - Minimalne grubości otulenia prętów i wymagania dotyczące jakości betonu
Klasa środowiska
1
2a
2b
3 i 4
5a
5b
5c
Minimalna grubość otulenia,
mm
15
20
25
40
25
30
40
maksymalny stosunek
w/c
0,65
0,60
0,55
0,50
0,55
0,50
0,45
minimalna zawartość cementu,
kg/m
3
260
280
280
300
280
300
300
Część 9 Strona 1
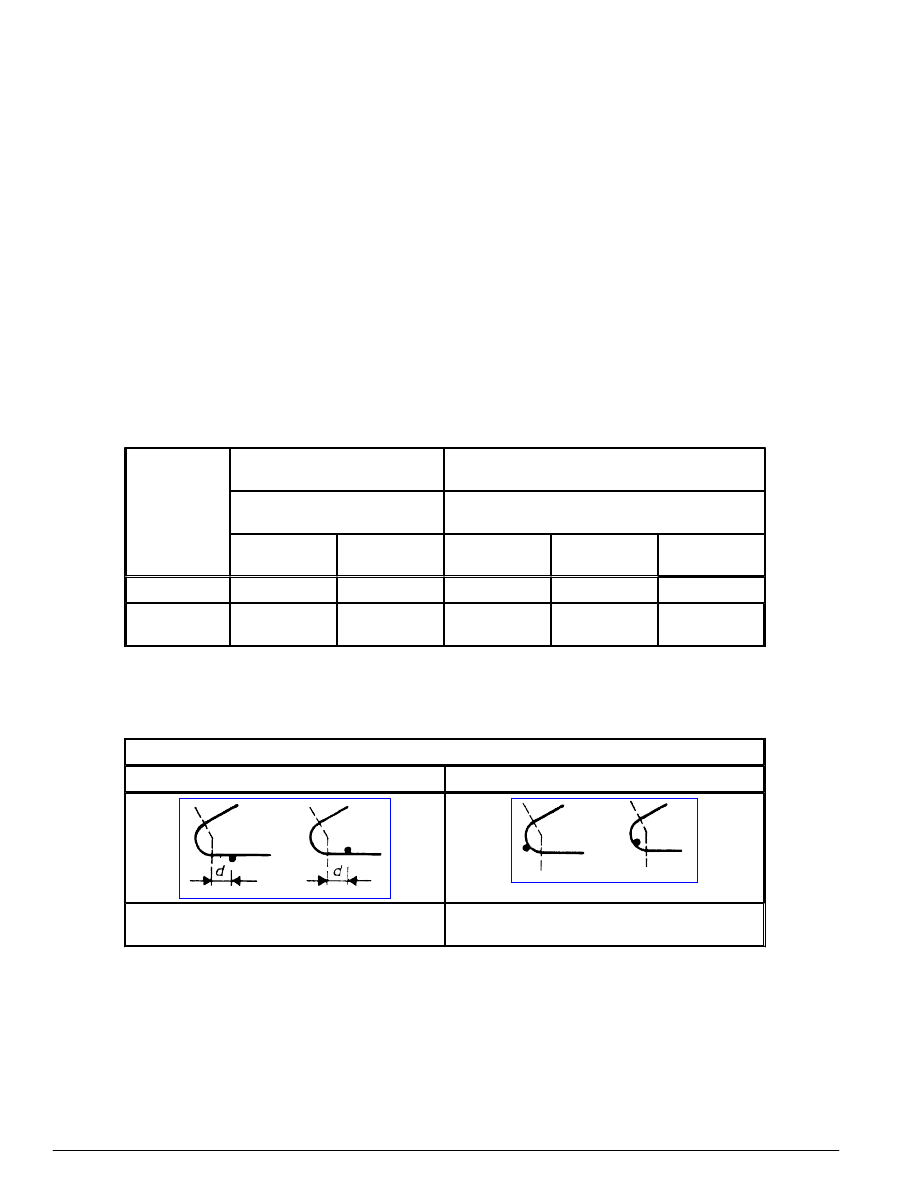
Zachowaniu minimalnej grubości otulenia musi towarzyszyć odpowiednia jakość betonu, określona przez maksymalny
stosunek w/c oraz minimalną zawartość cementu w kg/m
3
. W środowisku klasy 5c stosować należy ochronę powierzchniową
betonu.
Minimalne grubości otulenia podane w tablicy 23 można zmniejszyć o 5 mm w elementach płytowych oraz dodatkowo w
elementach z betonu klasy B50 lub wyższej, lecz do wartości nie niższej niż wymagana dla środowiska klasy 1. Jeżeli beton
układany jest wprost na podłożu gruntowym to grubość otulenia powinna być nie mniejsza niż 75 mm, a jeżeli na podłożu
betonowym - nie mniejsza niż 40 mm.
Przy projektowaniu, minimalną grubość otulenia należy zwiększyć o wartość dopuszczalnej odchyłki ∆h, zależnej od poziomu
wykonawstwa i kontroli jakości:
∆h = 0 ÷ 5 mm - dla elementów prefabrykowanych,
∆h = 5 ÷ 10 mm - dla elementów betonowanych w miejscu wbudowania.
Grubość otulenia wymaganą ze względu na odporność ogniową określa się według oddzielnych przepisów.
8.1.1.3 Dopuszczalne krzywizny zagięć
Minimalna średnica wewnętrzna zagięcia pręta powinna być tak dobrana, aby nie mogło nastąpić miażdżenie lub
rozłupywanie betonu wewnątrz zagięcia, jak również pojawianie się pęknięć w prętach na skutek ich zginania.
Minimalna średnica wewnętrzna zagięcia prętów i drutów powinna być nie mniejsza od podanej w tablicy 24.
Dla prętów spajanych i siatek zbrojeniowych zaginanych po spojeniu - minimalną średnicę wewnętrzną zagięcia podaje
tablica 25.
Tablica 24 - Minimalna średnica wewnętrzna zagięcia
Rodzaj prętów
Haki półokrągłe, haki proste, pętle
(rysunek 44)
Pręty odgięte lub inne pręty zaginane
Ś
rednica prętów
Minimalne otulenie betonem prostopadłe do
płaszczyzny zagięcia
φ < 20 mm
φ ≥ 20 mm
> 100 mm
oraz > 7 φ
> 50 mm
oraz > 3 φ
≤ 50 mm
oraz ≤ 3 φ
Pręty gładkie
2,5 φ
5 φ
10 φ
10 φ
15 φ
Pręty
ż
ebrowane
4 φ
7 φ
10 φ
15 φ
20 φ
Tablica 25 - Minimalna średnica wewnętrzna zagięcia dla zaginanego zbrojenia spajanego
Minimalna średnica wewnętrzna zagięcia
Połączenia spajane poza zagięciem
Połączenia spajane wewnątrz zagięcia
przy d < 4 φ - 20 φ
przy d ≥ 4 φ - jak w tablicy 24
20 φ
8.1.2 Przyczepność zbrojenia do betonu
8.1.2.1 Warunki przyczepności
Przyczepność zbrojenia do betonu zależy od ukształtowania powierzchni pręta, wymiarów elementu oraz od umiejscowienia i
nachylenia zbrojenia w czasie betonowania.
Warunki przyczepności można uważać za dobre:
Część 9 Strona 2
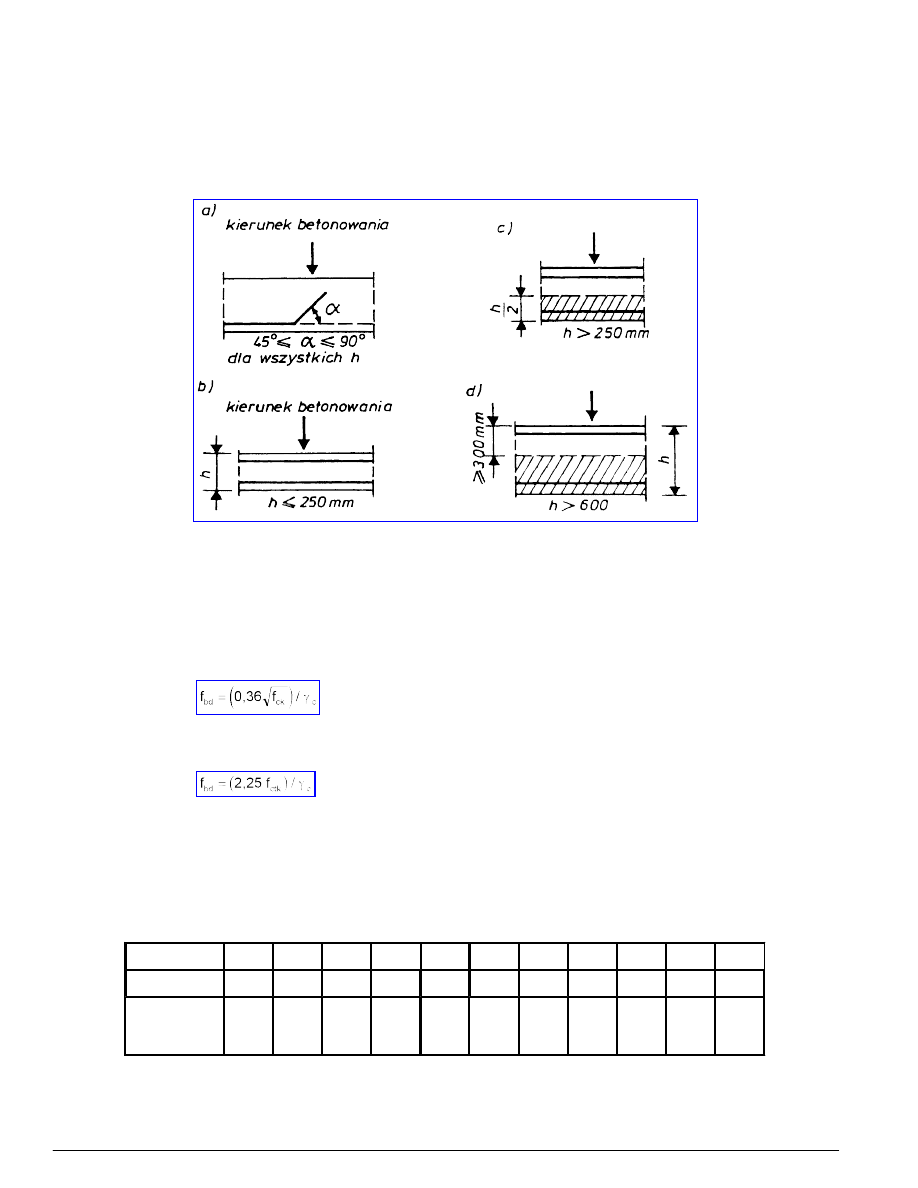
a) dla wszystkich prętów nachylonych podczas betonowania pod kątem 45° do 90° w stosunku do poziomu (rysunek 43, a),
b) dla wszystkich prętów nachylonych podczas betonowania pod kątem 0° do 45° w stosunku do poziomu, które znajdują się:
- w elementach o grubości nie przekraczającej 250 mm (rysunek 43, b),
- w dolnej połowie elementów o grubości większej niż 250 mm (rysunek 43, c)
lub
- co najmniej 300 mm poniżej górnej powierzchni elementu (rysunek 43, d).
Wszystkie inne warunki uważa się za mierne.
Rysunek 43 - Określenie warunków przyczepności: a) i b) - warunki dobre, c) i d) - warunki dobre w części zakreskowanej
8.1.2.2 Graniczne naprężenia przyczepności
Graniczne naprężenia przyczepności należy tak ustalać, aby przy obciążeniu użytkowym nie występował znaczący poślizg
zbrojenia względem betonu i aby zapewniony był dostateczny zapas bezpieczeństwa przed utratą przyczepności.
Graniczne naprężenia obliczeniowe f
bd
oblicza się z następujących wzorów z uwzględnieniem współczynnika γ
c
= 1,5:
- dla prętów gładkich
(164)
- dla prętów żebrowanych
(165)
Graniczne naprężenia obliczeniowe f
bd
dla dobrych warunków przyczepności przyjmować można z tablicy 26. Dla innych
warunków przyczepności wartości te należy mnożyć przez 0,7.
Tablica 26 - Graniczne naprężenia obliczeniowe f
bd
(MPa) dla dobrych warunków przyczepności
Klasa betonu
B15
B20
B25
B30
B37
B45
B50
B55
B60
B65
B70
Pręty gładkie
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
Pręty
ż
ebrowane
φ ≤ 32 mm
1,5
2,0
2,3
2,7
3,0
3,4
3,7
4,0
4,3
4,6
4,8
Część 9 Strona 3
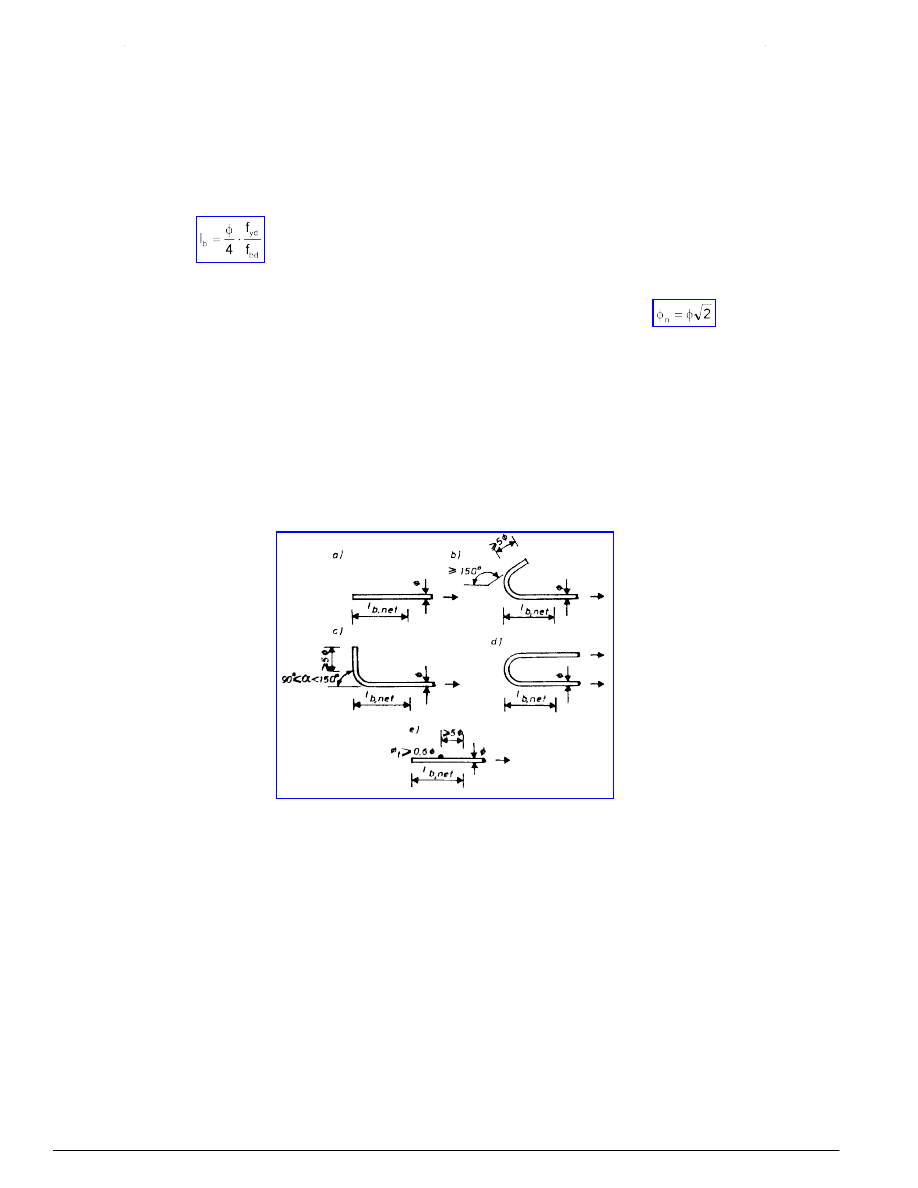
Jeżeli pręty poddane są poprzecznemu naprężeniu ściskającemu σ
cb
(prostopadłemu do możliwej płaszczyzny odłupania) to
wartości podane w tablicy 26 lub wzorami (164) i (165) zwiększyć można mnożąc je przez 1/(1 - 0,04 σ
cb
) ≤ 1,4.
8.1.2.3 Podstawowa długość zakotwienia
Podstawowa długość zakotwienia jest długością prostego odcinka pręta, wymaganą dla przekazania z pręta na beton siły A
s
f
yd
w założeniu, że przyczepność ma stałą wartość na tej długości, równą f
bd
. Przy ustalaniu podstawowej długości
zakotwienia uwzględniać należy rodzaj stali oraz właściwości przyczepnościowe prętów.
Podstawową długość zakotwienia I
b
, wymaganą dla zakotwienia pręta o średnicy φ, określa się ze wzoru
(166)
Wartości f
bd
podano w tablicy 26.
Dla prętów grupowanych parami średnicę φ we wzorze (166) należy zastąpić średnicą równoważną
.
W przypadku konstrukcji poddanych obciążeniom wielokrotnie zmiennym, wartość I
b
należy zwiększyć o 50%.
8.1.3 Zakotwienie
8.1.3.1 Zasady ogólne
Pręty zbrojenia, druty lub siatki zgrzewane kotwić należy w ten sposób, aby siły wewnętrzne, które w nich występują,
przenoszone były na beton z wyłączeniem możliwości pojawienia się rys podłużnych lub wykruszania się betonu. W razie
potrzeby, stosować należy zbrojenie poprzeczne.
Zakotwienia mechaniczne, w przypadku ich stosowania, powinny być sprawdzone doświadczalnie.
8.1.3.2 Zakotwienie prętów i siatek
Sposoby kotwienia prętów przedstawiono na rysunku 44.
Rysunek 44 - Wymagane długości zakotwienia: a) zakotwienia proste, b) hak półokrągły, c) hak prosty, d) pętla, e)
przyspojony pręt poprzeczny
Zakotwienia prostego i haków prostych (rysunek 44,a lub 44,c) nie należy stosować dla kotwienia prętów gładkich o średnicy
większej niż 8 mm.
Nie zaleca się stosowania haków prostych, haków półokrągłych jak również pętli do kotwienia prętów ściskanych. Zalecenie
to nie dotyczy prętów gładkich, w których mogą pojawić się przy pewnych obciążeniach siły rozciągające w strefie
zakotwienia. Średnice zagięcia prętów określa się zgodnie z tablicą 24.
8.1.3.3 Zbrojenie poprzeczne w strefie zakotwienia
Zbrojenie poprzeczne powinno być stosowane:
- przy kotwieniu prętów w strefie rozciąganej, gdy w kierunku poprzecznym nie występuje ściskanie,
- przy kotwieniu prętów w strefie ściskanej.
Pole przekroju wszystkich prętów zbrojenia poprzecznego na długości zakotwienia Σ A
st
powinno być nie mniejsze niż 25%
pola przekroju A
s
jednego pręta kotwionego (rysunek 45).
Część 9 Strona 4

Rysunek 45 - Zbrojenie poprzeczne w strefie zakotwienia prętów: a) belka, b) płyta
Zbrojenie poprzeczne powinno być rozmieszczone równomiernie na długości zakotwienia.
Przynajmniej jeden z prętów poprzecznych powinien być umieszczony przy haku lub pętli kotwionego pręta. Pręty kotwione w
strefie ściskanej powinny być objęte zbrojeniem poprzecznym, skoncentrowanym przy końcu długości zakotwienia, jak na
rysunku 50,b).
8.1.3.4 Wymagana długość zakotwienia prętów
Wymaganą długość zakotwienia prętów l
b,net
(rysunek 44) obliczać można ze wzoru
(168)
w którym:
I
b
- podstawowa długość zakotwienia wyznaczona ze wzoru (166),
A
s,req
, A
s,prov
- odpowiednio: pole przekroju zbrojenia wymaganego zgodnie z obliczeniem i pole przekroju zbrojenia
zastosowanego,
I
b,min
- minimalna długość zakotwienia, określana następująco:
- dla prętów rozciąganych
- dla prętów ściskanych
α
a
- współczynnik efektywności zakotwienia, którego wartość wynosi:
α
a
= 1 dla prętów prostych,
α
a
= 0,7 dla zagiętych prętów rozciąganych, jeżeli w strefie haka lub pętli grubość otulenia betonem w kierunku prostopadłym
do płaszczyzny zagięcia wynosi co najmniej 3 φ.
Pręty należy przedłużać poza przekrój, w którym obliczeniowo przestają być potrzebne, na długość nie mniejszą niż:
0,5 h + l
b,net
- dla prętów rozciąganych,
l
b,net
- dla prętów ściskanych.
Zbrojenie przęsłowe, doprowadzone do podpory, należy przedłużać poza jej krawędź o odcinek nie krótszy niż:
2/3 l
b,net
- przy podparciu bezpośrednim,
I
b,net
- przy podparciu pośrednim.
Jeżeli nie przeprowadza się szczegółowych obliczeń, to długość tego odcinka dla elementów zginanych o stosunku l
eff
/h ≥ 12
można przyjmować:
a) 5 φ w elementach nie wymagających obliczania zbrojenia na siłę poprzeczną,
b) w elementach wymagających obliczenia zbrojenia na siłę poprzeczną:
15 φ - przy doprowadzeniu do podpory 1/3 prętów wymaganych w przęśle,
10 φ - przy doprowadzeniu do podpory co najmniej 2/3 prętów wymaganych w przęśle.
Długość zakotwienia prętów zbrojenia rozciągającego elementów zamocowanych w murze (rysunek 46) powinna być nie
mniejsza niż 0,3 h + l
b,net
.
Część 9 Strona 5
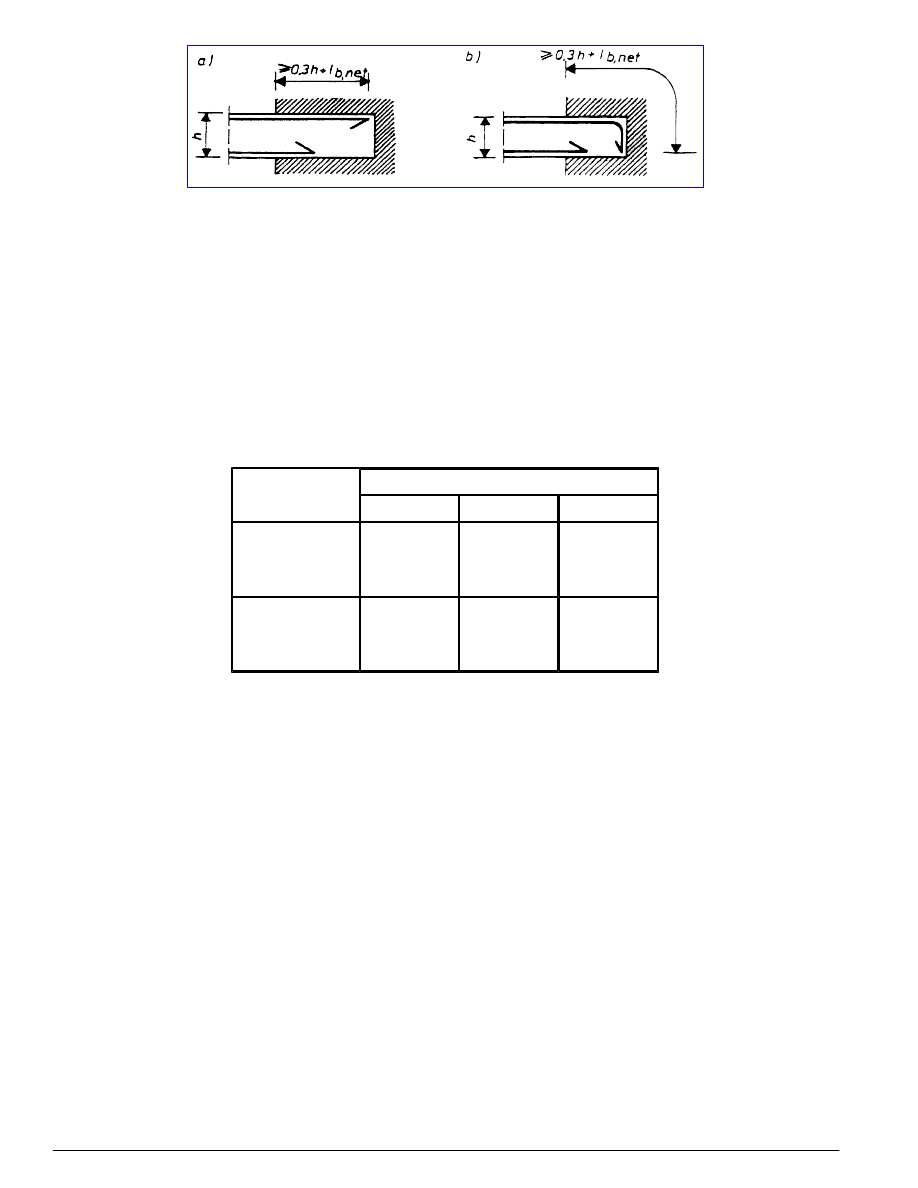
Rysunek 46 - Zakotwienie prętów zbrojenia elementów zamocowanych w murze:
a) prętów prostych, b) prętów zagiętych
8.1.3.5 Wymagana długość zakotwienia siatek spajanych z prętów żebrowanych
Wymaganą długość zakotwienia siatek spajanych z prętów żebrowanych wyznaczać można ze wzoru (168). Jeżeli w strefie
zakotwienia znajduje się przynajmniej jeden spojony pręt poprzeczny, to wartość otrzymaną ze wzoru (168) należy mnożyć
przez 0,7.
8.1.3.6 Wymagana długość zakotwienia siatek spajanych z prętów gładkich
Długość zakotwienia l
b,net
siatek spajanych z prętów gładkich powinna być nie mniejsza niż wartość podstawowej długości
zakotwienia I
b
, podana w tablicy 27 oraz nie mniejsza niż 200 mm.
Tablica 27 - Długość I
b
zakotwienia siatek spajanych z prętów gładkich ze stali klasy A-0 i A-I
Sposób kotwienia
Klasa betonu
B15
B20
≥ B25
Dwa pręty
poprzeczne na
długość I
b,net
rysunek 47 a)
28 φ
25 φ
22 φ
Trzy pręty
poprzeczne na
długość I
b,net
rysunek 47 b)
20 φ
18 φ
15 φ
Nośność spoiny łączącej pręt poprzeczny z prętem podłużnym powinna być nie mniejsza niż 1/3 nośności pręta podłużnego.
Wymaganą długość odcinka, o jaki należy przedłużyć siatki zbrojeniowe poza krawędź podpór elementów zginanych, należy
określać wg 8.1.3.4 z tym, że na długości odcinka przedłużonego poza krawędź podpory powinien być umieszczony
przynajmniej jeden pręt poprzeczny.
8.1.3.7 Zakotwienie strzemion i zbrojenia na ścinanie
Strzemiona i zbrojenie na ścinanie kotwić należy za pomocą haków półokrągłych lub przyspajanego zbrojenia poprzecznego.
Pręty i druty żebrowane kotwić można również za pomocą haków prostych. Wewnątrz haka półokrągłego lub prostego zaleca
się umieszczać pręt poprzeczny.
Dopuszczalne średnice wewnętrzne zagięcia podane są w 8.1.1.3.
Zakotwienie jest właściwe, jeżeli:
- długość odcinka prostego za zagięciem jest nie mniejsza niż
- 5 φ lub 50 mm - dla kąta zagięcia 135° lub większego (rysunek 48, a);
- 10 φ lub 70 mm - dla kąta zagięcia 90° (rysunek 48, b);
- na końcu pręta prostego znajdują się
- dwa przyspojone pręty poprzeczne (rysunek 48, c) lub
- jeden pręt poprzeczny o średnicy nie mniejszej niż 1,4 średnicy przekroju strzemienia (rysunek 48, d).
Część 9 Strona 6
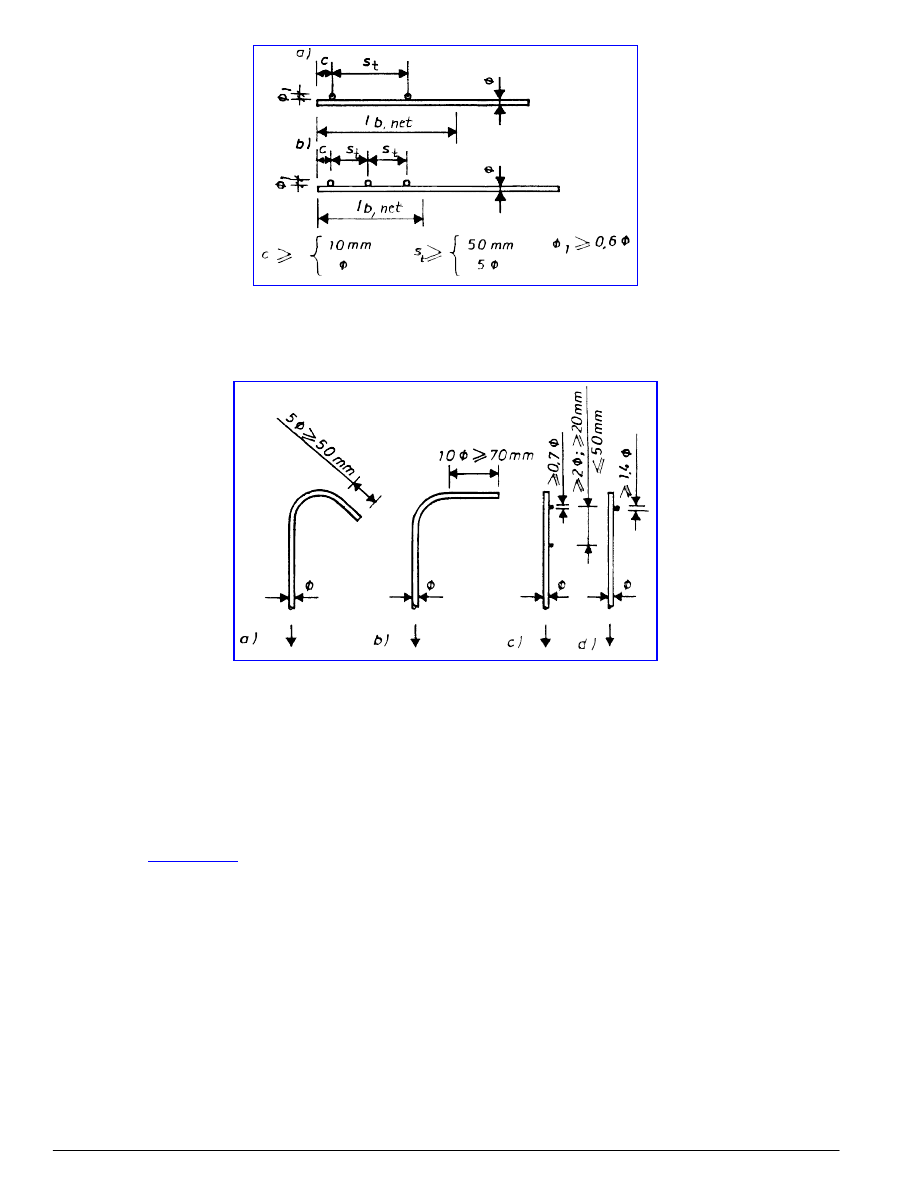
Rysunek 47 - Sposoby kotwienia siatek zbrojeniowych: a) dwa pręty poprzeczne na długości zakotwienia, b) trzy pręty
poprzeczne na długości zakotwienia
Rysunek 48 - Zakotwienie strzemion
8.1.4 Połączenia
8.1.4.1 Zasady ogólne
Zbrojenie powinno składać się, jeżeli jest to możliwe, z prętów nieprzerwanych na długości jednego przęsła tub jednego
elementu konstrukcyjnego. Gdy warunek ten nie może być spełniony, odcinki prętów powinny być w zasadzie łączone za
pomocą spajania lub zacisków mechanicznych. Dopuszcza się łączenie prętów na zakład wg 8.1.4.3.
Zaleca się, aby połączenia prętów znajdowały się w przekrojach, w których nośność prętów nie jest w pełni wykorzystana.
8.1.4.2 Połączenia spajane
Typy połączeń spajanych i sposoby ich wykonywania - podano w tablicy 28. Nośność połączeń spajanych należy obliczać
zgodnie z
PN-90/B-03200
.
Tablica 28 - Sposoby połączeń spajanych
Część 9 Strona 7
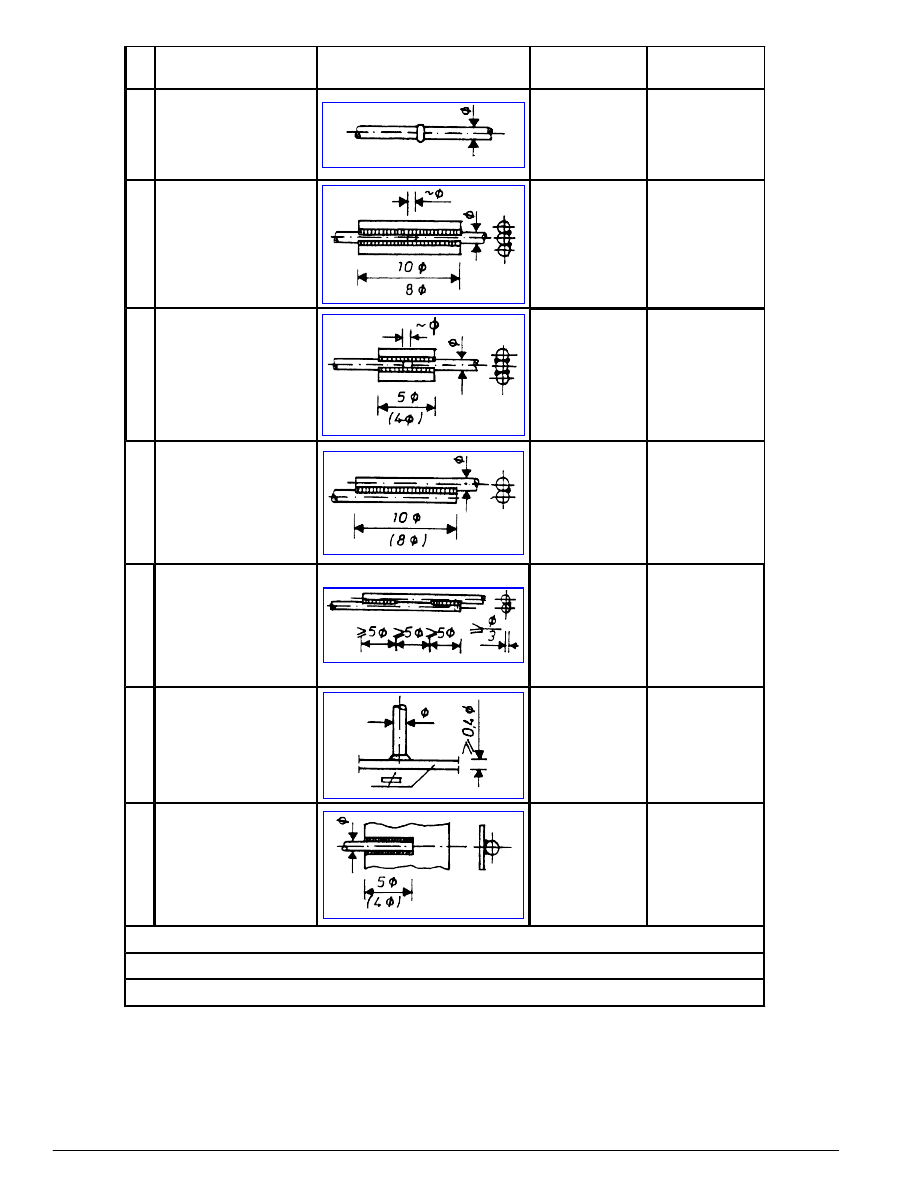
Lp.
Rodzaj spajania i typ
połączenia
Konstrukcja połączenia
Klasa
gatunek stali
Ś
rednica pręta
mm
1
Doczołowe zgrzewanie
iskrowe prętów
zbrojeniowych
A-0
A-I
A-II
A-III
A-IIIN
5,5 ÷ 40
5,5 ÷ 40
6 ÷ 32
6 ÷ 32
6 ÷ 20
2
Połączenia nakładkowe
jednostronne wykonane
łukiem elektrycznym
A-I St3S
A-I St3SX
A-I St3SY
A-II 18G2
A-III
A-IIIN
A-0
5,5 ÷ 40
5,5 ÷ 12
5,5 ÷ 20
6 ÷ 32
6 ÷ 32
6 ÷ 20
6 ÷ 40
3
Połączenia nakładkowe
dwustronne wykonane
łukiem elektrycznym
A-I St3S
A-I St3SX
A-ISt3SY
A-II 18G2
A-III
A-IIIN
A-0
5,5 ÷ 40
5,5 ÷ 12
5,5 ÷ 20
6 ÷ 32
6 ÷ 32
6 ÷ 20
6 ÷ 40
4
Połączenia zakładkowe
jednostronne wykonane
łukiem elektrycznm
A-I St3S
A-I St3SX
A-I St3SY
A-II 18G2
A-III
A-IIIN
A-0
5,5 ÷ 40
5,5 ÷ 12
5,5 ÷ 20
6 ÷ 32
6 ÷ 14
6 ÷ 20
6 ÷ 40
5
Jednostronne połączenie
zakładkowe przerywane
wykonane łukiem
elektrycznym
A-I St3S
A-I St3SX
A-I St3SY
A-II 18G2
A-III 34GS
A-IIIN
A-0
5,5 ÷ 40
5,5 ÷ 12
5,5 ÷ 20
6 ÷ 32
6 ÷ 32
6 ÷ 20
6 ÷ 40
6
Półautomatyczne spajanie
łączników sworzniowych
1
*)
1
*)
7
Spawanie łukiem
elektrycznym prętów
zbrojeniowych z
elementami płaskimi lub
profilowanymi ze stali
walcowanej dwiema
spoinami bocznymi
A-0
A-I St3S
A-I St3SX
A-I St3SY
A-II 18G2
A-III
A-IIIN
8 ÷ 40
8 ÷ 40
8 ÷ 12
8 ÷ 20
8 ÷ 32
8 ÷ 32
8 ÷ 20
Grubość spoiny bez obliczeń można przyjmować a = 0,3 φ.
Wartości podane w nawiasach dotyczą prętów ze stali gładkiej.
1
*)
Parametry łączników oraz technologia spajania - według aktualnej aprobaty technicznej.
8.1.4.3 Połączenia na zakład
Część 9 Strona 8
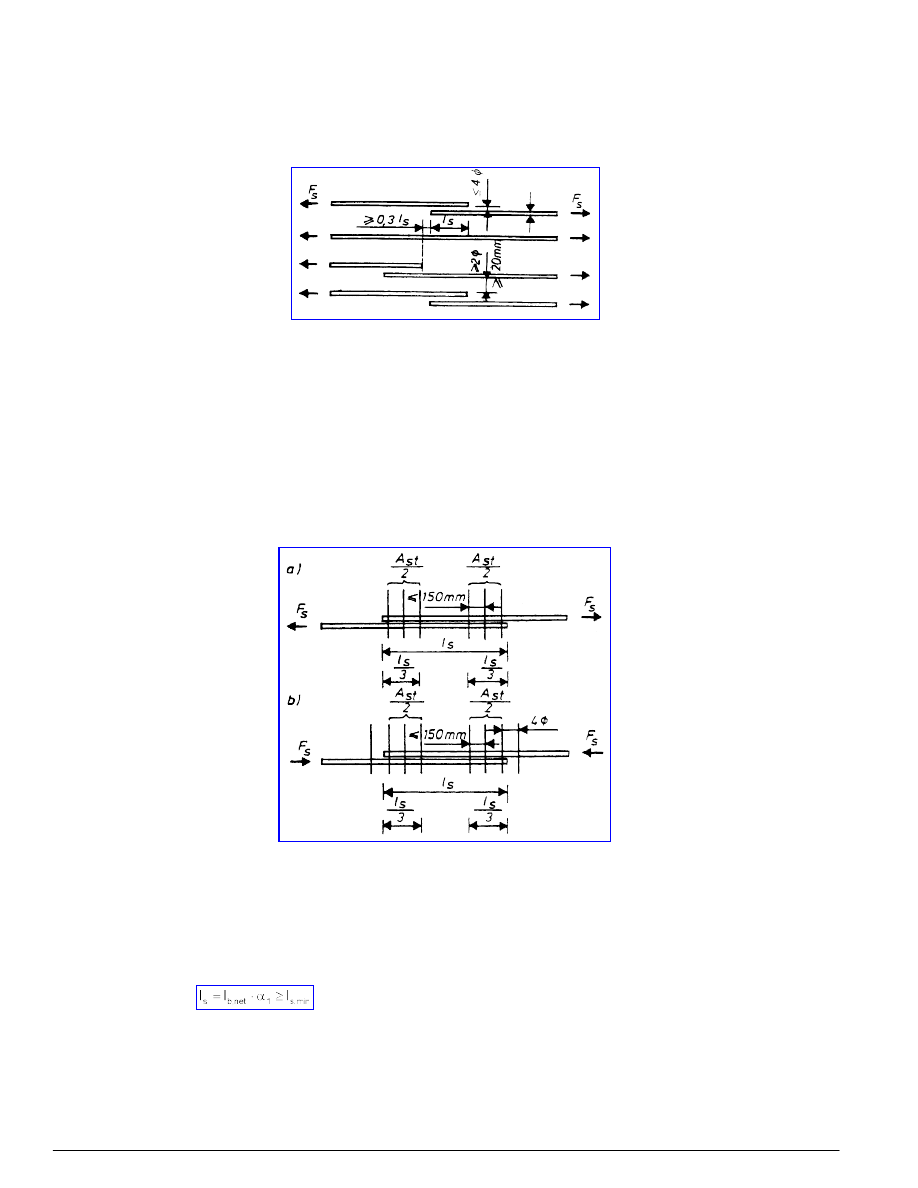
Połączenia prętów na zakład powinny być wzajemnie przesunięte i nie powinny znajdować się w miejscu znacznych
naprężeń.
Zakłady prętów w każdym przekroju powinny być symetryczne i równoległe do powierzchni zewnętrznej elementu.
Pręty łączone na zakład powinny być kotwione zgodnie z p. 8.1.3.2.
Odległości w świetle prętów łączonych na zakład powinny być zgodne z rysunkiem 49.
Rysunek 49 - Odległości prętów łączonych na zakład
Pręty łączone na zakład powinny posiadać na długości połączenia odpowiednie zbrojenie poprzeczne.
Jeżeli średnica φ prętów łączonych na zakład jest mniejsza niż 16 mm lub jeżeli procent łączonych prętów nie jest w żadnym
przekroju większy niż 20 %, to minimalne zbrojenie poprzeczne, zastosowane w elemencie z innych powodów (np. zbrojenie
na ścinanie, pręty rozdzielcze) - uważa się za wystarczające.
Jeżeli średnica prętów łączonych na zakład jest równa lub większa niż 16 mm, to na długości zakładu między łączonym
zbrojeniem podłużnym i powierzchnią betonu należy przewidzieć odpowiednie zbrojenie poprzeczne.
Pole przekroju wszystkich prętów zbrojenia poprzecznego ΣA
st
, w płaszczyźnie równoległej do rozpatrywanej warstwy prętów
podłużnych, powinno być nie mniejsze niż pole przekroju A
s
pojedynczego pręta łączonego w tej warstwie (rysunek 50).
Rysunek 50 - Zbrojenie poprzeczne w miejscu łączenia prętów na zakład: a) rozciąganie, b) ściskanie
Zależnie od kształtu przekroju elementu konstrukcyjnego i rozstawu prętów podłużnych, zbrojenie poprzeczne powinno być
ukształtowane w postaci strzemion lub prętów prostych.
Przy rozmieszczaniu zbrojenia poprzecznego należy również uwzględniać zasady podane w 8.1.3.3.
Wymaganą długość zakładu określa się według wzoru
(169)
w którym:
I
b,net
- wymagana długość zakotwienia według wzoru (168),
Część 9 Strona 9
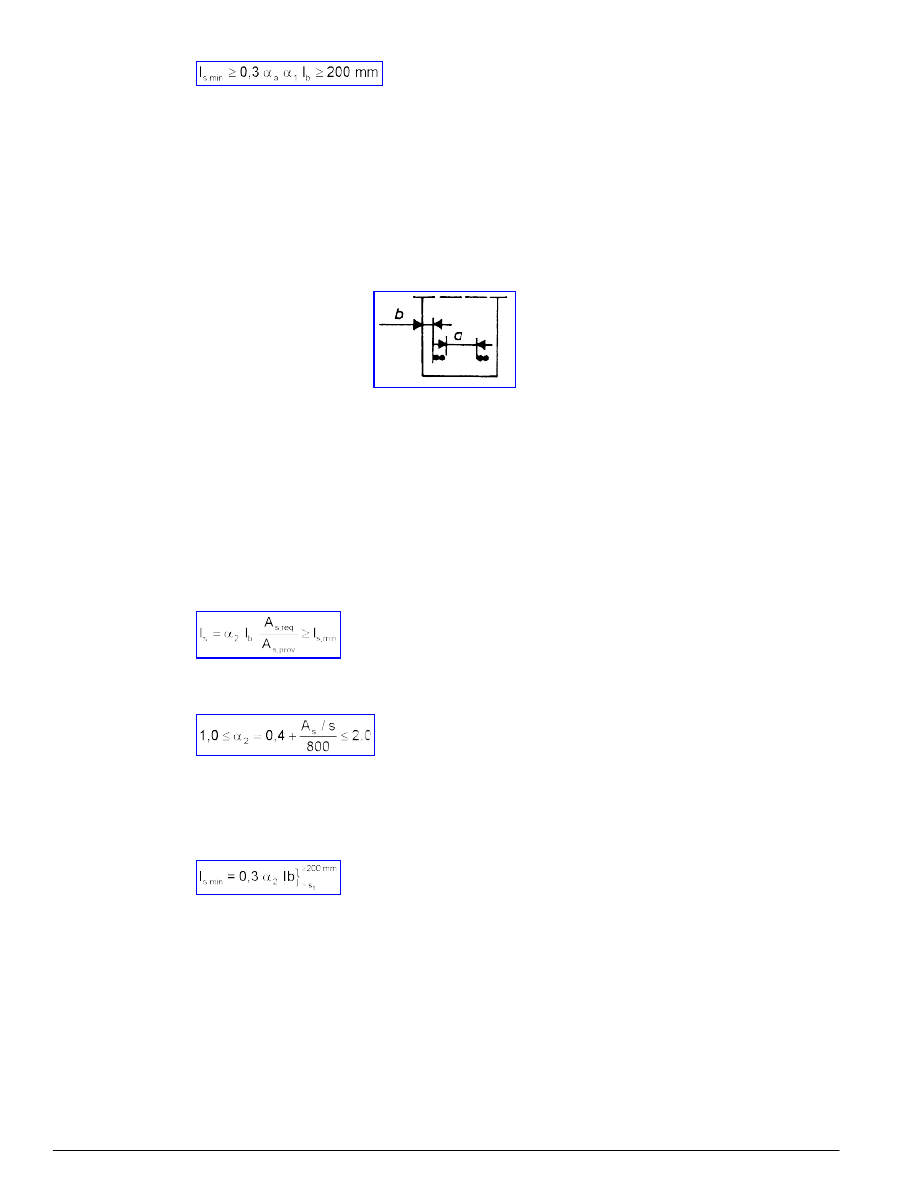
(170)
gdzie:
α
a
- współczynnik efektywności zakotwienia, jak we wzorze (168),
α
1
= 1 - w strefie ściskanej,
α
1
= 1 - w strefie rozciąganej, kiedy w jednym przekroju łączonych jest mniej niż 30% prętów i kiedy (zgodnie z rysunkiem 51)
a ≥ 10 φ i b ≥ 5 φ,
α
1
= 1,4 - w strefie rozciąganej, kiedy w jednym przekroju łączonych jest więcej niż 30% prętów lub kiedy (zgodnie z
rysunkiem 51) a < 10 φ lub b < 5 φ,
α
1
= 2,0 - w strefie rozciąganej, kiedy w jednym przekroju łączonych jest więcej niż 30% prętów i równocześnie a < 10 φ lub b
< 5 φ.
Rysunek 51 - Usytuowanie wzajemne prętów do wyznaczania wartości współczynnika α
1
8.1.4.4 Połączenia na zakład siatek spajanych
Podane postanowienia dotyczą tylko przypadku, kiedy siatki łączone są na zakład.
Dopuszczalny procent zbrojenia głównego łączonego w jednym przekroju, odniesiony do całego pola przekroju zbrojenia,
wynosi:
- 100%, jeżeli sprowadzone pole przekroju prętów siatki, wyrażone przez stosunek A
s
/s wynosi A
s
/s ≤ 1200 mm
2
/,
- 60%, kiedy A
s
/s > 1200 mm
2
/m, a siatka ta jest siatką wewnętrzną (w przypadku zbrojenia w kilku warstwach).
W przypadku kilku warstw siatek połączenia w poszczególnych warstwach powinny być przesunięte względem siebie o 1,3 I
s
,
gdzie I
s
długość zakładu wyznaczona ze wzoru (171).
Długość zakładu I
s
określa się następująco
(171)
gdzie:
(172)
I
b
- podstawowa długość zakotwienia określona według wzoru (166) przy przyjęciu f
bd
jak dla prętów żebrowanych, lub
I
b
= I
b,net
z tablicy 27 dla siatek z prętów gładkich,
A
s,req,
A
s,prov
- jak we wzorze (168),
A
s
/s - w mm
2
/m,
(173)
s
t
- odstęp między prętami poprzecznymi siatki.
Dodatkowe zbrojenie poprzeczne w strefie zakładu nie jest wymagane.
Całe zbrojenie poprzeczne siatek może być łączone w tym samym przekroju.
Minimalne długości zakładu I
s
prętów zbrojenia poprzecznego siatek podane są w tablicy 29.
Na długości zakładu powinny znajdować się przynajmniej dwa pręty poprzeczne (tj. jedno oczko siatki).
Część 9 Strona 10
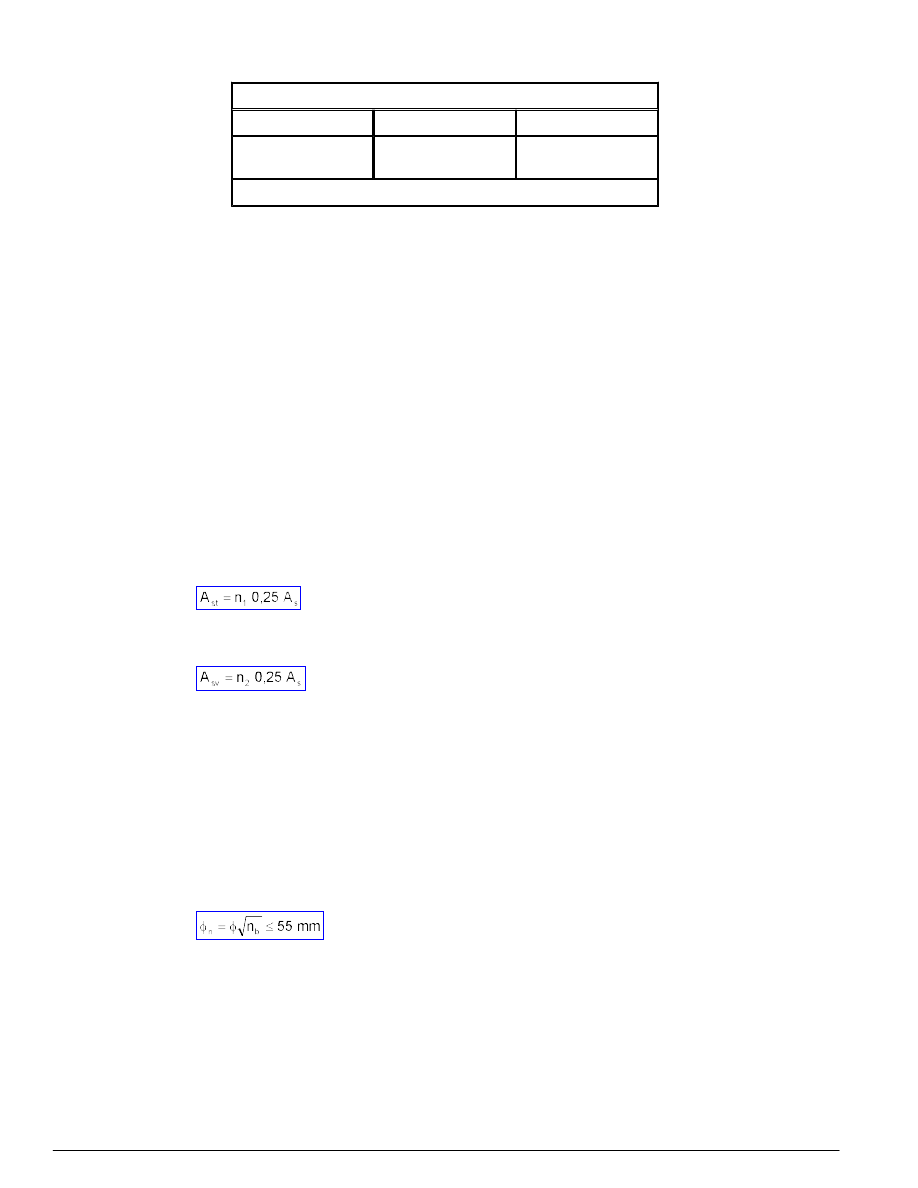
Tablica 29 - Minimalne długości zakładu zbrojenia poprzecznego siatek z prętów żebrowanych
Ś
rednica prętów (mm)
φ ≤ 6
6 < φ ≤ 8,5
8,5 < φ ≤ 1,2
≥ s
l
≥ 150 mm
≥ s
l
≥ 250 mm
≥ s
l
≥ 350 mm
s
l
= odstęp między prętami podłużnymi
8.1.5 Dodatkowe wymagania dotyczące prętów żebrowanych o średnicy większej niż 32 mm
8.1.5.1 Zasady ogólne
Pręty o średnicy φ > 32 mm stosować można tylko w elementach, których wysokość przekroju jest nie mniejsza niż 15 φ.
Jeżeli stosuje się pręty dużej średnicy, należy ograniczyć odpowiednio szerokość rys przez zastosowanie zbrojenia
przypowierzchniowego.
Otulenie betonem powinno wynosić c ≥ φ.
Odległość w świetle (w kierunku poziomym i pionowym) poszczególnych prętów równoległych lub warstw poziomych prętów
równoległych powinna być nie mniejsza niż średnica najgrubszego z prętów lub d
g
+ 5 mm, gdzie d
g
jest nominalnym
maksymalnym wymiarem kruszywa.
8.1.5.2 Przyczepność
Dla prętów o średnicy φ > 32 mm wartości f
bd
podane w tablicy 26 lub obliczone z wzorów (164) lub (165), należy mnożyć
przez współczynnik (132 - φ)/100, przy czym φ przyjmuje się w mm.
8.1.5.3 Zakotwienia i połączenia
Pręty o dużych średnicach kotwić należy jako pręty proste lub za pomocą blach kotwiących. Prętów tych nie wolno kotwić w
strefie rozciąganej.
Nie należy stosować połączeń na zakład ani dla prętów ściskanych ani rozciąganych.
W belkach i płytach, w których w strefie zakotwienia nie występują naprężenia ściskające w kierunku poprzecznym,
potrzebne jest dodatkowe zbrojenie poza zastosowanym zbrojeniem na ścinanie.
W przypadku zakotwienia prostego zbrojenie dodatkowe nie powinno być mniejsze niż:
- w kierunku równoległym do najbliższej powierzchni
(174)
- w kierunku prostopadłym do najbliższej powierzchni
(175)
gdzie:
A
s
- powierzchnia przekroju pręta kotwionego,
n
1
- liczba warstw zbrojenia kotwionego w tym samym przekroju,
n
2
- liczba prętów kotwionych w każdej warstwie.
8.1.6 Wiązki prętów żebrowanych
8.1.6.1 Zasady ogólne
Dla wiązek prętów obowiązują wymagania podane dla prętów pojedynczych. Wiązka zawierać powinna pręty jednakowego
rodzaju, o takiej samej średnicy i wytrzymałości.
Przy wymiarowaniu wiązkę prętów traktuje się jako jeden pręt zastępczy o tej samej powierzchni przekroju i tym samym
położeniu środka ciężkości co wiązka. Zastępczą średnicę φn wiązki prętów określa wzór
(176)
w którym:
n
b
- liczba prętów w wiązce, ograniczona do:
n
b
≤ 4 w przypadku prętów pionowych i w miejscach zakładu prętów,
n
b
≤ 3 we wszystkich innych przypadkach.
Dla wiązek prętów przyjmuje się rozmieszczenia zgodnie z 8.1.1.1 w odniesieniu do średnicy zastępczej φ
n
z tym, że rozstaw
wiązek w świetle mierzy się od rzeczywistego konturu zewnętrznego wiązki. Otulenie betonem, mierzone od rzeczywistego
Część 9 Strona 11
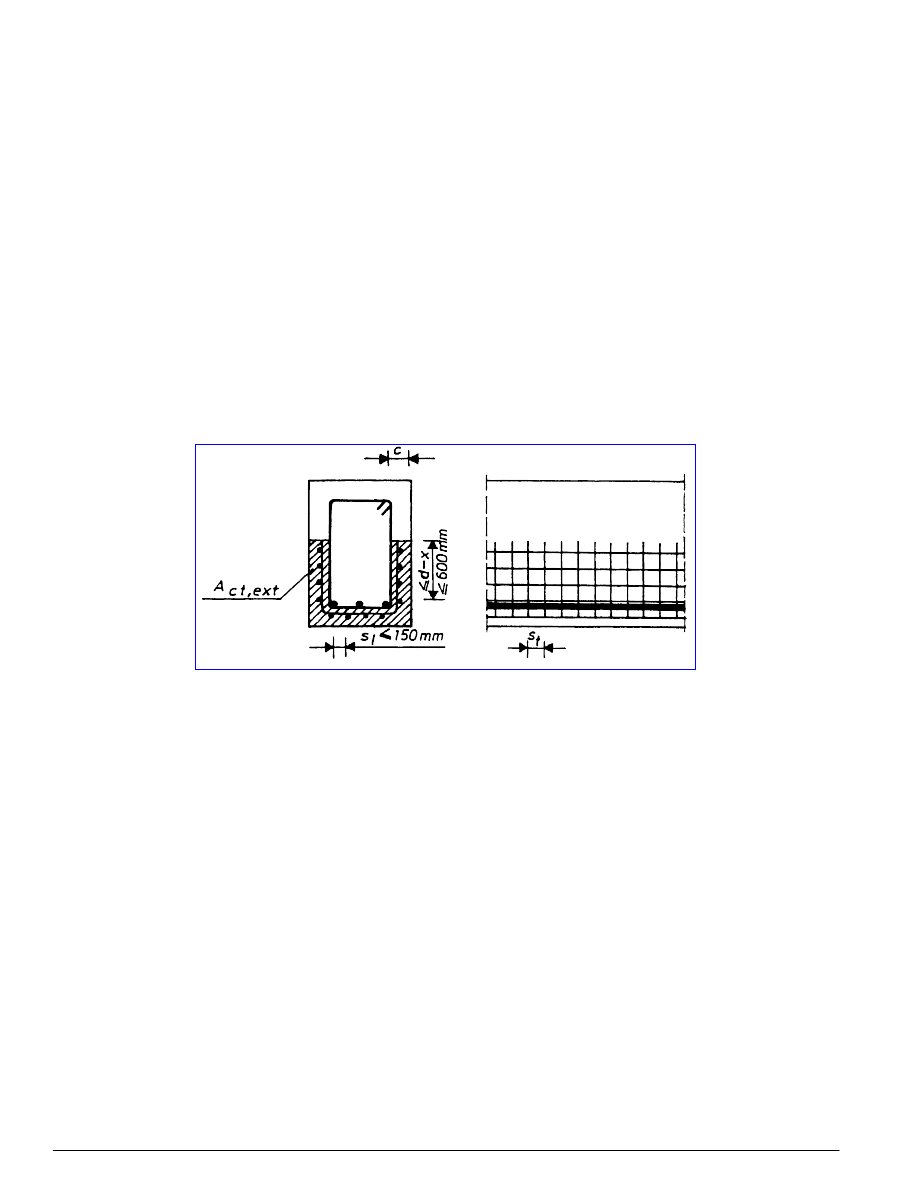
konturu zewnętrznego wiązki, powinno wynosić c ≥ φ
n
.
8.1.6.2 Zakotwienia i połączenia
Zakotwienie lub połączenie na zakład wiązki prętów zapewnić należy przez zakotwienie lub połączenie poszczególnych
prętów wiązki. Dopuszcza się wyłącznie zakotwienie proste, przesunięte wzajemnie dla poszczególnych prętów.
W przypadku wiązek złożonych z 2, 3 lub 4 prętów, odległość połączeń prętów określa się mnożąc ich długości zakotwienia
odpowiednio przez 1,2, 1,3 i 1,4.
Pręty powinny być łączone na zakład pojedynczo. W żadnym przypadku nie powinno być więcej niż 4 pręty w przekroju
wiązki. Połączenia na zakład pojedynczych prętów powinny być przesunięte względem siebie jak podano wyżej.
8.1.7 Zbrojenie przypowierzchniowe
Stosowanie zbrojenia przypowierzchniowego ma na celu ograniczenie szerokości rys lub przeciwdziałanie odłupywaniu się
betonu otuliny.
Zbrojenie przypowierzchniowe mające na celu ograniczenie szerokości rys, powinno być stosowane w belkach o wysokości
większej niż 1 m.
Zbrojenie przypowierzchniowe, przeciwdziałające odłupywaniu się betonu otuliny - stosuje się w belkach zbrojonych wiązkami
prętów lub prętami o średnicy większej niż 25 mm. Zbrojenie takie stanowi zwykle siatka z drutów lub pręty żebrowane o
małej średnicy, umieszczone na zewnątrz strzemion, jak pokazano na rysunku 52.
Pole przekroju zbrojenia przypowierzchniowego A
s,surf
rozmieszczonego w kierunku równoległym do zbrojenia rozciąganego
belki - powinno być nie mniejsze niż 0,01 A
ct,ext
, przy czym A
ct,ext
oznacza pole przekroju betonu rozciąganego poza
strzemionami, pokazane na rysunku 52.
Pręty podłużne zbrojenia przypowierzchniowego można wliczać do zbrojenia podłużnego na zginanie, a pręty poprzeczne -
do zbrojenia na ścinanie, pod warunkiem, że spełniają one wymagania dotyczące rozmieszczenia i zakotwienia.
Rysunek 52 - Zbrojenie przypowierzchniowe
8.1.8 Zbrojenie elementów o kształcie załamanym lub zakrzywionym
Belki o kształcie załamanym, w których pręty rozciągane znajdują się od strony wklęsłej, należy zbroić przez skrzyżowanie
tych prętów w punkcie załamania belki (rysunek 53). Długość zakotwienia od miejsca skrzyżowania należy przyjmować
zgodnie z 8.1.3.4.
Część 9 Strona 12
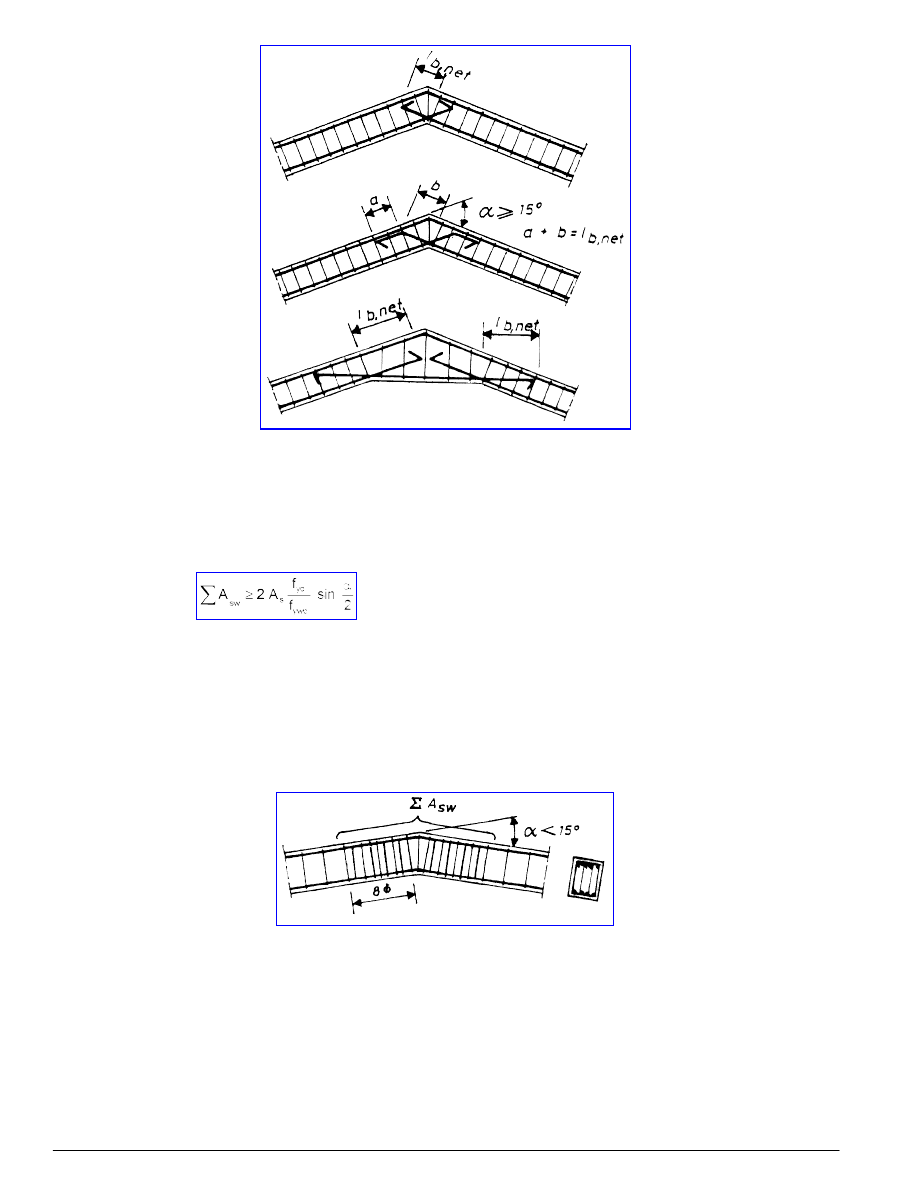
Rysunek 53 - Zbrojenie elementów załamanych przy α ≥ 15°
W przypadku gdy kąt załamania elementu jest mniejszy niż 15°, zbrojenie rozciągane można załamać, pod warunkiem
zabezpieczenia prętów przed wyrwaniem za pomocą dodatkowych strzemion (rysunek 54). Strzemiona te powinny
odpowiadać następującym warunkom:
a) sumaryczne pole przekroju strzemion powinno wynosić
(177)
gdzie:
A
s
- pole przekroju prętów załamanych,
α - kąt załamania elementu,
b) każdy załamany pręt rozciągany musi być uchwycony co najmniej przez jedno ramię strzemion (rysunek 54),
c) przy średnicy prętów załamanych większej niż 20 mm pręty i strzemiona powinny być ze sobą zespawane,
d) strzemiona, których przekrój obliczony jest według wzoru (177), powinny być rozstawione na długości nie większej niż 8
ś
rednic prętów załamanych, licząc w każdą stronę od miejsca załamania.
Rysunek 54 - Zbrojenie elementów załamanych przy α < 15°
W elementach zakrzywionych każdy zakrzywiony pręt rozciągany o średnicy większej niż 12 mm, znajdujący się po wklęsłej
stronie elementu, powinien być uchwycony co najmniej przez jedno ramię strzemienia. Odstęp strzemion nie powinien w tym
przypadku przekraczać 1/4 promienia krzywizny. Najmniejszy promień krzywizny prętów powinien spełniać postanowienia wg
8.1.1.3.
Część 9 Strona 13
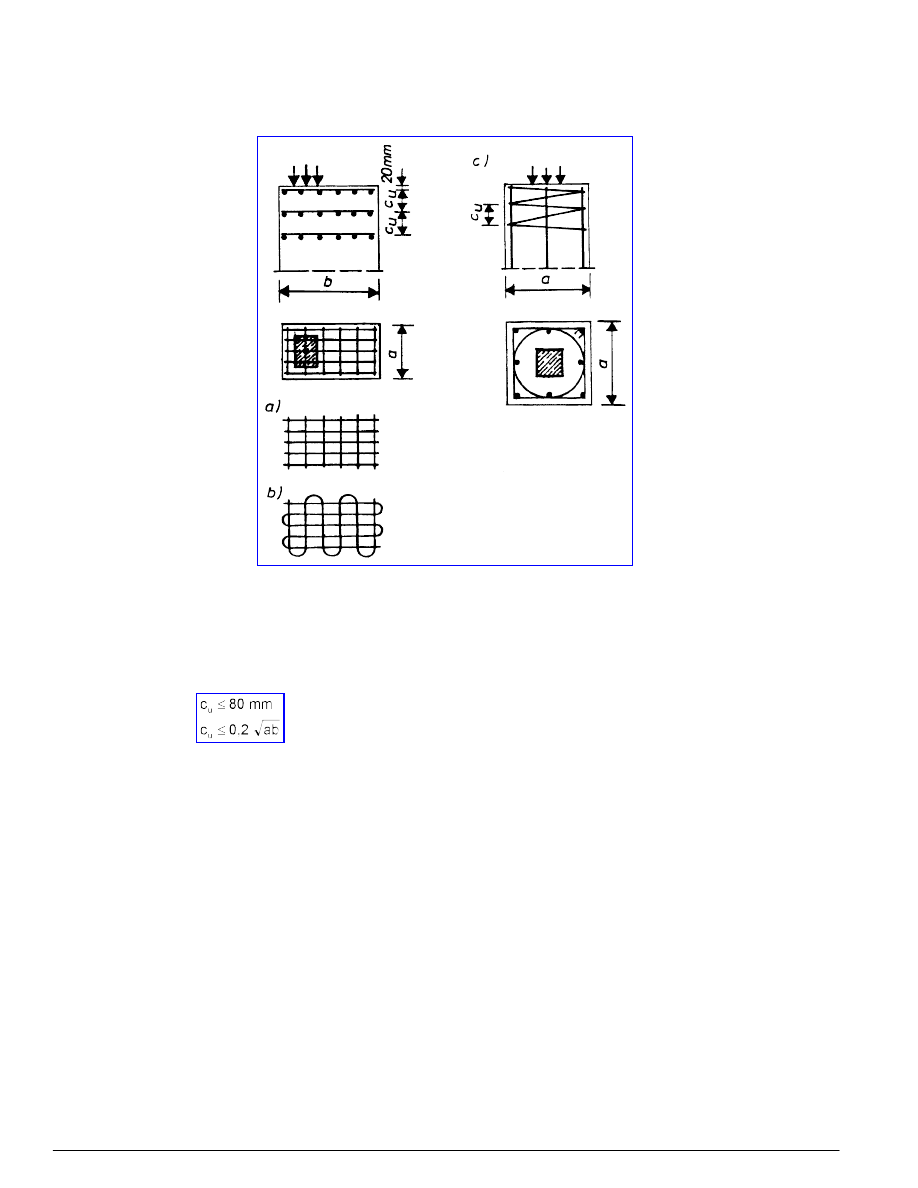
8.1.9 Zbrojenie poprzeczne strefy docisku
Zbrojenie obliczone według 5.8 należy projektować w postaci siatek zgrzewanych, siatek wyginanych lub uzwojenia zgodnie z
rysunkiem 55.
Rysunek 55 - Zbrojenie poprzeczne strefy docisku w postaci: a) siatek zgrzewanych, b) siatek wyginanych, c) uzwojenia
Zbrojenie poprzeczne należy rozmieszczać co najmniej w trzech warstwach lub trzech zwojach, przy czym pierwsza z nich
powinna być usytuowana w odległości 20 mm od czoła elementu, a środek ciężkości całego zbrojenia powinien się mieścić w
przedziale 0,3 a ÷ 0,5 a. Odstęp kolejnych siatek lub skok linii śrubowej uzwojenia powinien odpowiadać warunkom
gdzie:
a, b - wymiary powierzchni rozdziału według rysunku 29.
Siatki powinny być rozmieszczone na powierzchni nie mniejszej niż powierzchnia rozdziału według rysunku 29 lub
powierzchnia zastępcza według rysunku 31. Uzwojenie powinno obejmować strefę współśrodkową względem powierzchni
docisku, nie większą niż powierzchnia rozdziału. Końce uzwojenia powinny być przyspojone do ostatniego zwoju lub zagięte i
prawidłowo zakotwione w betonie rdzenia.
Pręty zbrojenia poprzecznego powinny być należycie zakotwione, a ich średnica powinna odpowiadać warunkom φ ≤ 12 mm
oraz φ ≤ a/30
.
8.2 Konstrukcje sprężone
8.2.1 Średnica cięgna
Za średnicę cięgna φ przyjmuje się w strunobetonie średnicę otworu, jaki powstałby w betonie po wyciągnięciu cięgna, a w
kablobetonie - średnicę kanału kablowego lub osłony.
8.2.2 Rozmieszczenie cięgien w przekroju
Część 9 Strona 14
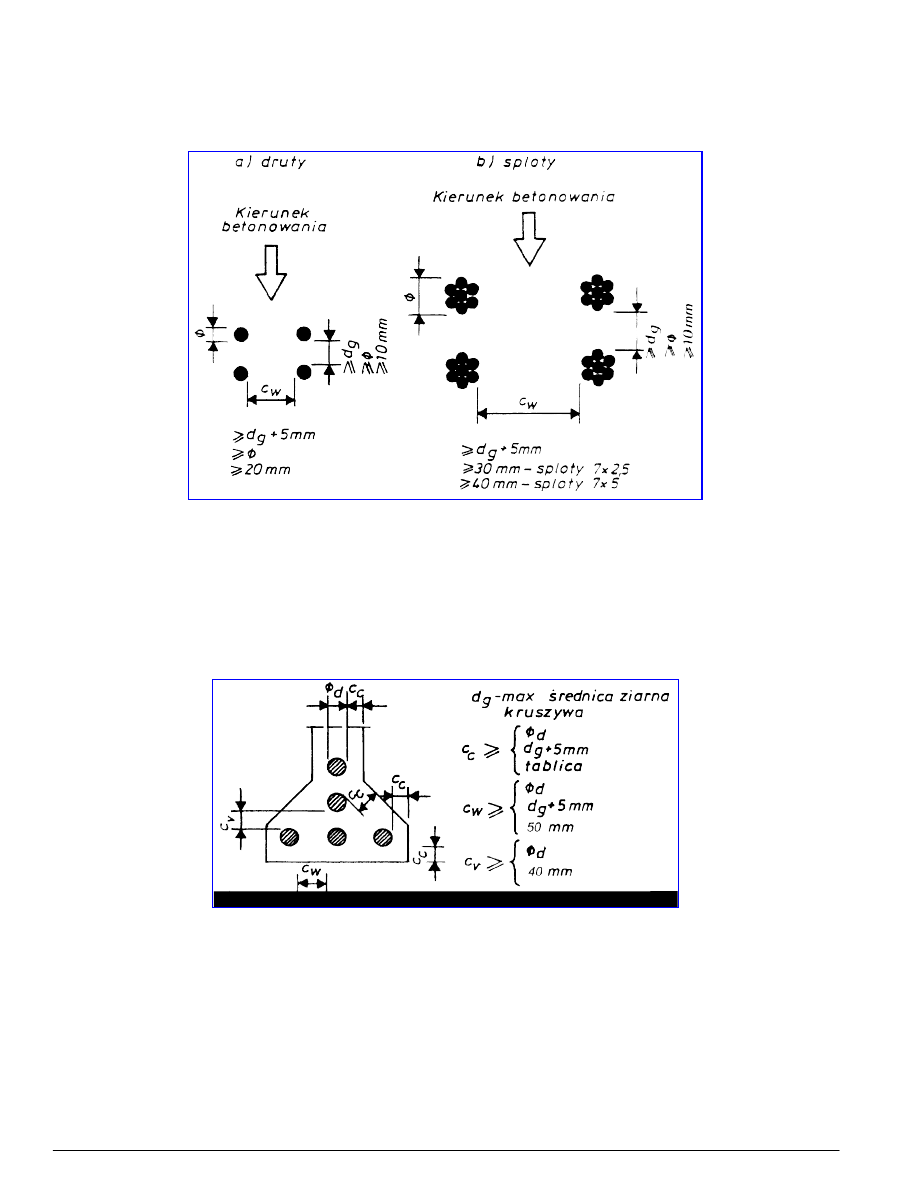
Rozstaw kanałów w elementach kablobetonowych lub cięgien w elementach strunobetonowych powinien być tak dobrany,
aby umożliwiał należyte ułożenie i zagęszczenie betonu oraz zapewniał dobrą przyczepność betonu do cięgien.
W elementach strunobetonowych poszczególne cięgna powinny być rozmieszczone oddzielnie. Warunki określające
minimalne odległości w świetle między poszczególnymi cięgnami w kierunku poziomym i pionowym podano na rysunku 56.
Rysunek 56 - Minimalne odstępy cięgien w przekroju elementu strunobetonowego
W elementach kablobetonowych cięgna uformowane w postaci kabli umieszcza się we wcześniej przygotowanych kanałach.
Zasadniczo nie stosuje się kabli w wiązkach. Dopuszcza się pary kabli umieszczonych pionowo jeden nad drugim przy
zachowaniu odpowiednich środków ostrożności podczas naciągu i iniektowania. Szczególnej uwagi wymagają przy tym
cięgna podwójnie zakrzywione.
Minimalny rozstaw kanałów w świetle osłonek oraz minimalne otulenie podano na rysunku 57.
Rysunek 57 - Minimalne odstępy cięgien w przekroju elementu kablobetonowego
8.2.3 Kotwienie cięgien
Długość zakotwienia cięgien w konstrukcjach strunobetonowych oraz ich nośność w strefie zakotwienia należy określać
zgodnie z 7.1.7.4 pod warunkiem zachowania wymaganych rozstawów cięgien, grubości otuliny i stosowania zbrojenia
poprzecznego. Długość zakotwienia cięgien w płytach bez zbrojenia poprzecznego należy zwiększyć dwukrotnie w stosunku
do wartości nominalnych.
W elementach kablobetonowych zakotwienia powinny zapewniać przeniesienie bez widocznych uszkodzeń siły równej sile
Część 9 Strona 15
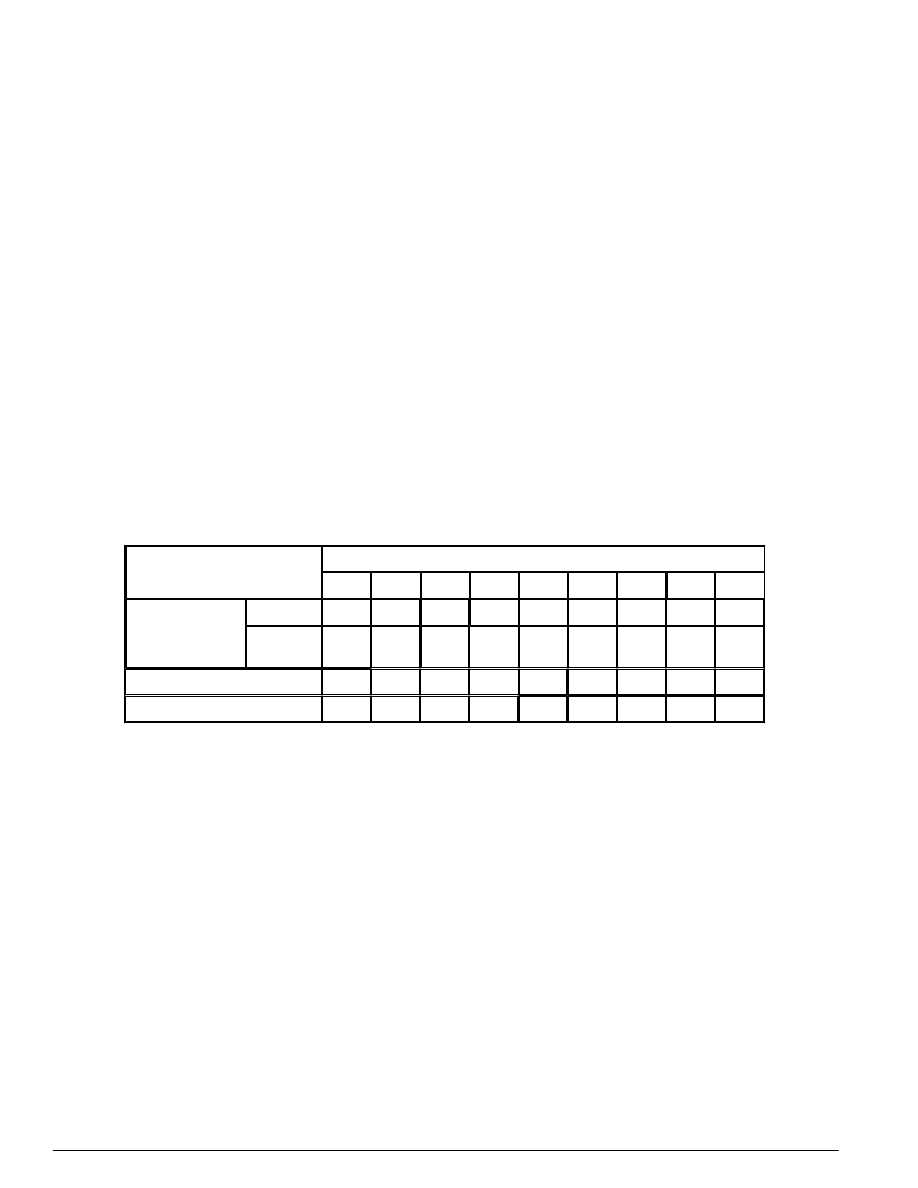
zrywającej cięgno. Zakotwienia powinny posiadać aprobatę techniczną upoważnionej placówki naukowo-badawczej.
8.2.4 Otulenie cięgien sprężających
Grubość warstwy betonu między wewnętrzną powierzchnią formy i cięgnami sprężającymi w elementach strunobetonowych
lub kanałami na cięgna w elementach kablobetonowych, należy ustalać odpowiednio do wymiarów cięgna lub kanału oraz
warunków środowiska.
Przyjęta grubość otulenia betonem powinna zapewniać:
- bezpieczne przekazywanie sił przyczepności,
- należytą ochronę przeciwpożarową,
- ochronę stali przed korozją.
W celu bezpiecznego przekazania sił przyczepności, minimalna grubość otulenia w elementach strunobetonowych powinna
być nie mniejsza niż wielokrotność średnicy cięgna
2 φ - dla drutów i splotów,
3 φ - dla prętów żebrowanych.
W elementach kablobetonowych minimalna grubość otulenia powinna być nie mniejsza niż:
φ
d
- średnica kanału okrągłego,
b
d
lub 0,5 h
d
- szerokość lub połowa wysokości kanału prostokątnego.
W celu umożliwienia należytego ułożenia i zagęszczenia betonu minimalna grubość otulenia powinna być nie mniejsza niż:
d
g
+ 5 mm
gdzie:
d
g
- oznacza maksymalny wymiar kruszywa.
W celu ochrony stali przed korozją, minimalna grubość otulenia dla całego zbrojenia - włączając pręty rozdzielcze i
strzemiona - powinna być nie mniejsza od wartości podanych w tablicy 30.
Zachowaniu minimalnej grubości otulenia musi towarzyszyć odpowiednia jakość betonu, który powinien być szczelny, dobrze
zagęszczony, pielęgnowany i spełniający podstawowe wymagania trwałości związane z oddziaływaniem środowiska.
Tablica 30 - Minimalne grubości otulenia betonem oraz wymagania dotyczące jakości betonu
Klasa środowiska wg tablicy 8
1
2a
2b
3
4a
4b
5a
5b
5c
Min. grubość
otulenia mm
Zbrojenie
15
20
25
40
40
40
25
30
40
Stal
sprężająca
25
30
35
50
50
50
35
40
50
Max. stosunek w/c
0,60
0,60
0,55
0,50
0,55
0,50
0,55
0,50
0,45
Min. zawartość cementu kg/m
3
300
300
300
300
300
300
300
300
300
Minimalne grubości otulenia podane w tablicy 30 należy zwiększyć o wartość dopuszczalnej odchyłki ∆h zależnej od poziomu
wykonawstwa i kontroli jakości:
∆h = 0 ÷ 5 mm dla elementów prefabrykowanych,
∆h = 5 ÷ 10 mm dla elementów betonowanych w miejscu wbudowania.
Minimalne grubości otulenia podane w tablicy 30 można zmniejszyć o 5 mm w elementach płytowych, oraz dodatkowo w
elementach z betonu klasy B50 lub wyższej, lecz do wartości nie niższej, niż wymagana dla środowiska klasy 1.
W środowisku klasy 5c stosować należy ochronę powierzchniową betonu w celu uniemożliwienia bezpośredniego kontaktu z
czynnikami agresywnymi.
Grubość otulenia wymaganą ze względu na odporność ogniową określa się według oddzielnych przepisów.
8.2.5 Zabezpieczenie cięgien przed korozją w konstrukcjach kablobetonowych
Cięgna sprężające, łączniki i zakotwienia należy zabezpieczyć przed korozją w sposób trwały.
Kable prowadzone w kanałach należy zabezpieczyć za pomocą iniekcji zapewniającej ochronę stali przed korozją.
Kable prowadzone na zewnątrz należy zabezpieczyć warstwą ochronną z betonu zbrojonego lub inną równorzędną. Warstwa
ochronna musi być szczelna, spełniać warunek rysoodporności i przyczepności do betonu, a druty kabla w okresie od
naciągu do otulenia muszą być zabezpieczone przed korozją. Okres pozostawienia cięgien po naciągu bez warstwy
ochronnej nie może być dłuższy niż 30 dni.
W przypadku środowisk klas 2-5 wszystkie zakotwienia lub łączniki, które nie są całkowicie obetonowane, muszą być trwale
Część 9 Strona 16

zabezpieczone przed korozją w inny sposób.
W konstrukcjach narażonych na wpływ agresji chemicznej i zwiększonej wilgotności sposób zabezpieczenia antykorozyjengo
kabli i betonu należy każdorazowo opracować odpowiednio do występujących warunków.
8.2.6 Zbrojenie poprzeczne strefy zakotwienia
W strefie zakotwienia cięgien sprężających należy stosować odpowiednie zbrojenie poprzeczne, obliczane ze względu na
docisk oraz rozciąganie przyczołowe. Zbrojenie na docisk stosuje się w strefach oddziaływania znacznych obciążeń
miejscowych, głównie pod zakotwieniami elementów kablobetonowych. Należy je kształtować zgodnie z 8.1.9 w postaci
siatek zgrzewanych lub siatek z prętów zaginanych, równoległych do płaszczyzny docisku oraz w postaci uzwojenia.
W przypadku gdy cięgna sprężające działają mimośrodowo w stosunku do środka ciężkości przekroju lub w dwóch
poziomach w pewnej odległości od siebie, w strefie przyczołowej elementu powstają znaczne siły rozciągające, których
wartość należy określać zgodnie z 7.1.7.4 lub 7.1.7.5. W celu przejęcia tych sił należy stosować zbrojenie poprzeczne
ukształtowane w postaci strzemion zamkniętych lub w pełni zakotwionych pionowych siatek zgrzewanych. Zbrojenie to
powinno być rozmieszczone na długości nie większej niż wysokość przekroju.
8.2.7 Zbrojenie konstrukcyjne elementów sprężonych
Zbrojenie przyjmowane ze względów konstrukcyjnych należy kształtować zgodnie z wymaganiami podanymi w 8.1 dla
elementów żelbetowych.
Część 9 Strona 17
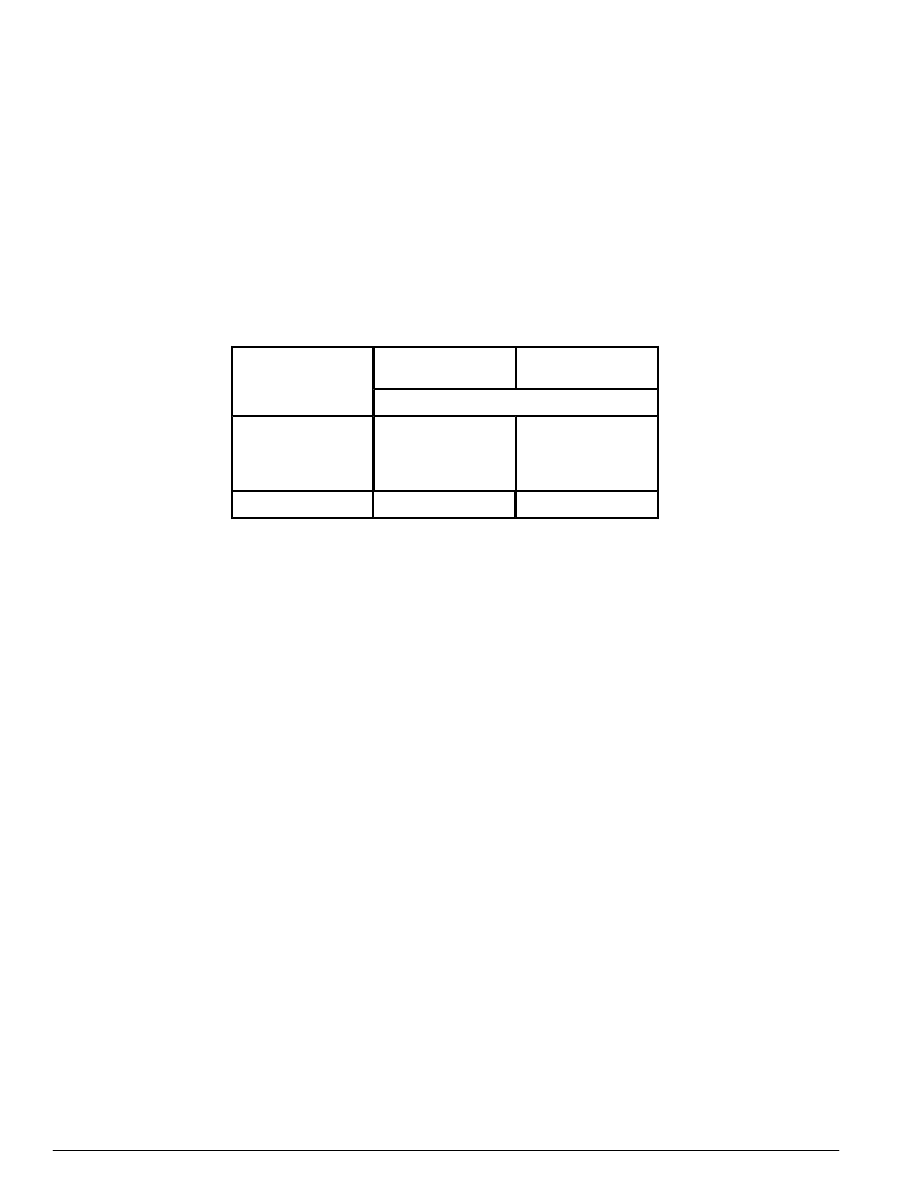
9 Projektowanie konstrukcji
9.1 Płyty
9.1.1 Konstrukcja płyt
9.1.1.1 Minimalne grubości płyt
Minimalne grubości płyt ze względu na ich przeznaczenie podane są w tablicy 31.
W płytach prefabrykowanych, usztywnionych żebrami wzdłuż obwodu, grubości podane w tablicy 31 mogą być zmniejszone o
10 mm.
Tablica 31 - Minimalne grubości płyt
Przeznaczenie płyty
Płyty prefabrykowane
Płyty betonowane na
miejscu budowy
mm
Płyty stropowe w
obiektach
budownictwa
powszechnego
40
60
Płyty pod przejazdami
100
120
Ponadto stosunek rozpiętości l
eff
płyty do wysokości użytecznej przekroju d nie powinien być większy niż:
40 - w przypadku płyt wolno podpartych jednokierunkowo zbrojonych,
50 - w przypadku płyt zamocowanych i ciągłych jednokierunkowo zbrojonych oraz krzyżowo zbrojonych.
Płyty obciążone jedynie ciężarem własnym mogą mieć grubości mniejsze niż podane wyżej.
W każdym przypadku grubość płyty nie może być jednak mniejsza niż wynika to z warunku nie przekroczenia granicznych
wartości ugięć wg 4.7.4, prawidłowego otulenia wg 8.1.1.2 i przepisów przeciwpożarowych.
Płyty wymagające zbrojenia na przebicie powinny mieć grubość nie mniejszą niż 200 mm.
9.1.1.2 Głębokość oparcia płyt na podporze
Powinna zapewniać możliwość prawidłowego zakotwienia prętów zbrojenia wg 8.1.3 i być nie mniejsza niż:
80 mm - przy oparciu na murze lub ścianie z betonu lekkiego względnie zwykłego klasy B15,
60 mm - przy oparciu na ścianie z betonu zwykłego klas wyższych niż B15,
40 mm - przy oparciu na belkach stalowych.
Głębokość oparcia prefabrykowanych płyt dwukierunkowo zbrojonych powinna być nie mniejsza niż 40 mm.
W przypadku płyt ze zbrojeniem górnym na podporze, przewidzianym do zabetonowania w wieńcu żelbetowym, głębokość
oparcia płyty może być zmniejszona o 20 mm, lecz nie może wynosić mniej niż 40 mm.
Głębokość oparcia płyt o rozpiętości nie większej niż 1,20 m i wykonanych z odchyłką nie większą niż ą 10 mm może być
zmniejszona do 30 mm pod warunkiem, że obliczeniowe obciążenie płyty ponad ciężar własny nie przekracza 2,0 kN/m
2
9.1.1.3 Zbrojenie płyt
Ś
rednica prętów stosowanych do zbrojenia płyt powinna być nie mniejsza niż 4,5 mm.
W przypadku siatek zgrzewanych dopuszcza się stosowanie drutów o średnicy 3 mm.
Do podpory należy doprowadzić bez odgięć nie mniej niż 1/3 dolnych prętów potrzebnych w przęśle i nie mniej niż 3 pręty na
1 m szerokości przekroju.
Jeżeli na podporze nie występują warunki zapewniające swobodę obrotu przekroju, należy zastosować odpowiednie
zbrojenie górne.
Pręty rozdzielcze powinny mieć rozstaw nie większy niż 300 mm oraz łączną nośność nie mniejszą niż:
- 1/10 nośności zbrojenia głównego przy obciążeniu równomiernie rozłożonym,
- 1/4 nośności zbrojenia głównego przy obciążeniu równomiernie rozłożonym i obciążeniu siłami skupionymi w przypadku, gdy
momenty zginające wywołane obciążeniami skupionymi są nie większe niż 50% momentów całkowitych. W przeciwnym
przypadku zbrojenie prostopadłe do zbrojenia głównego należy odpowiednio obliczyć.
W przypadku otworów występujących w polu płyty, obrzeża otworów powinny być dodatkowo zbrojone. Jeżeli wymiary otworu
nie przekraczają 1/4 obliczeniowej rozpiętości płyty, zaś obliczeniowe obciążenie płyty ponad ciężar własny jest nie większe
Część 10 Strona 1
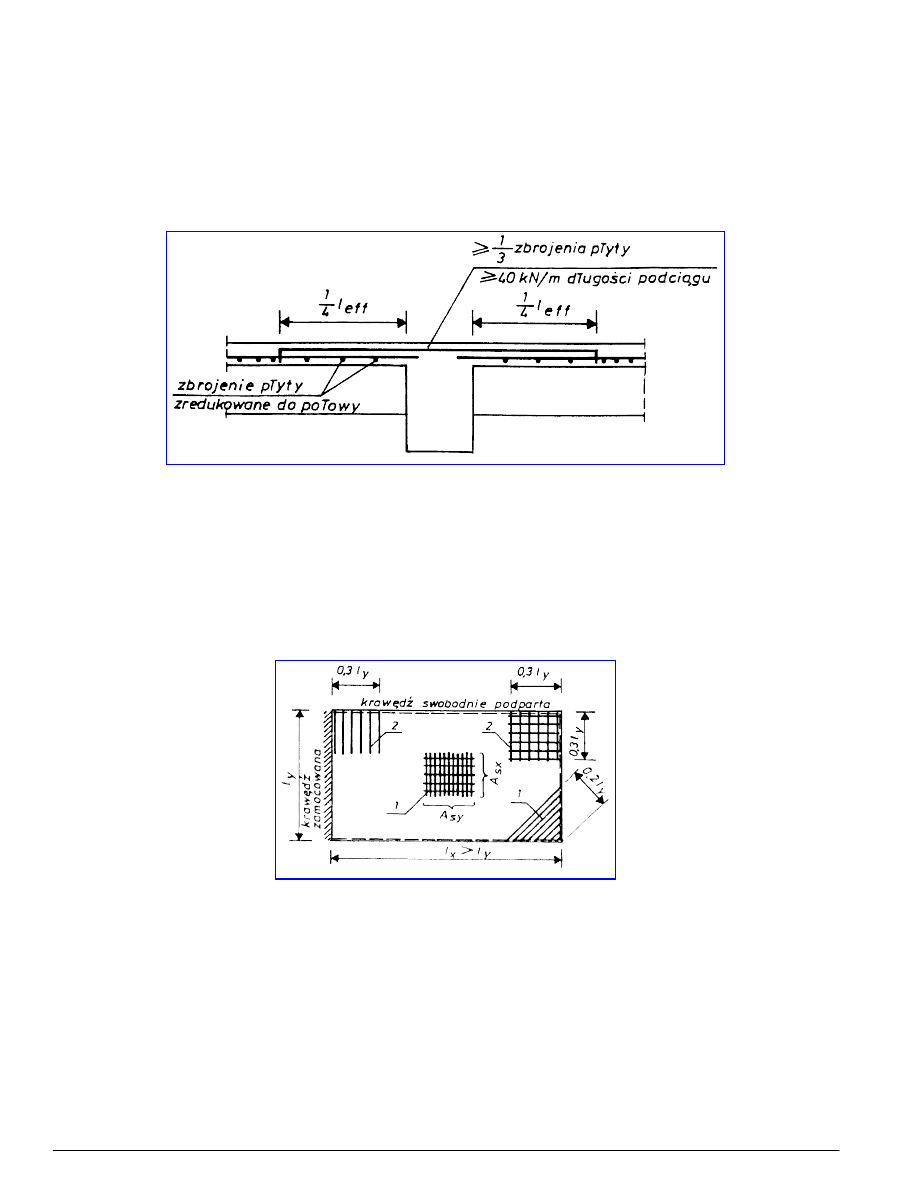
niż 10 kN/m
2
, przekrój zbrojenia obrzeżnego powinien być nie mniejszy niż przekrój zbrojenia przypadającego na szerokość
otworu. W przeciwnym przypadku wzmocnienie płyty przy otworze należy zaprojektować w postaci wymianów. Przy przyjęciu
wymianów jako belek ukrytych w grubości płyty, ich szerokość nie może przekraczać 4 grubości płyty.
W płycie ze zbrojeniem głównym ułożonym równolegle do podpory, którą stanowi belka lub ściana, należy zastosować
dodatkowe zbrojenie górne, prostopadłe do tej podpory, o nośności nie mniejszej niż 1/3 nośności zbrojenia głównego w tej
płycie, o przekroju zdolnym przenieść siłę rozciągającą nie mniejszą niż 40 kN/m długości podciągu. Zbrojenie to powinno
być wpuszczone w płytę na długość nie mniejszą niż 1/4 obliczeniowej rozpiętości płyty po każdej stronie podpory, licząc od
jej krawędzi (rysunek 58). Jednocześnie zbrojenie główne płyty w paśmie o szerokości równej 1/4 obliczeniowej rozpiętości
płyty, przylegającym do tej podpory, można zredukować do połowy.
Rysunek 58 - Połączenie płyty z podciągiem
Zbrojenie płyt dwukierunkowo zbrojonych należy konstruować zgodnie z założeniami metody obliczania momentów
zginających.
W jednoprzęsłowych płytach podpartych na 4 krawędziach (rysunek 59), obliczanych według analizy liniowo sprężystej,
zbrojenie każdego z dwóch kierunków wyznaczone dla środkowej części płyty powinno być układane w paśmie środkowym o
szerokości równej 3/5 szerokości płyty. W pasmach skrajnych, obejmujących po 1/5 szerokości płyty, przekrój zbrojenia
może być zmniejszony do połowy.
Rysunek 59 - Zbrojenie płyt krzyżowo zbrojonych: 1 - zbrojenie dolne, 2 - zbrojenie górne
W narożach wolno podpartych należy umieszczać dwukierunkowe zbrojenie górne, równoległe do krawędzi, na szerokości
równej 0,3 mniejszej rozpiętości (rysunek 59). Przekrój tego zbrojenia na jednostkę szerokości przekroju płyty powinien
wynosić w każdym kierunku co najmniej połowę przekroju większego zbrojenia, znajdującego się w środku płyty. W
narożach, w których zbiega się krawędź swobodnie podparta z krawędzią zamocowaną, postanowienie to rozciąga się
jedynie na zbrojenie naroża równoległe do krawędzi zamocowanej, natomiast przekrój zbrojenia prostopadłego do krawędzi
zamocowanej wynika z obliczeń.
W narożach wolno podpartych należy również umieszczać dodatkowe zbrojenie dolne, układane prostopadle do dwusiecznej
i rozmieszczone na szerokości równej 0,2 mniejszej rozpiętości płyty. Przekrój tego zbrojenia na 1 m szerokości przekroju
Część 10 Strona 2
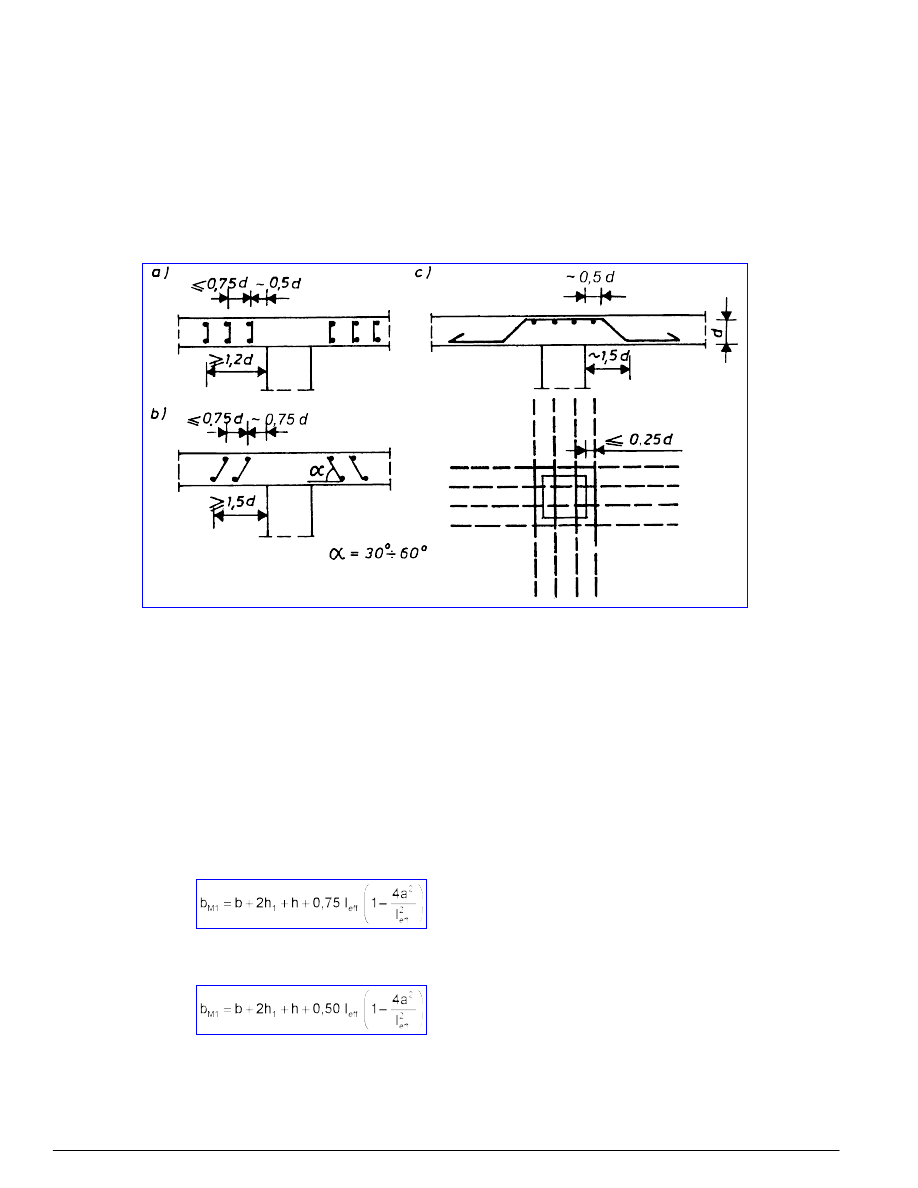
powinien być co najmniej równy przekrojowi większego zbrojenia w środku płyty.
W płytach obliczanych metodą równowagi granicznej przy założeniu stałej nośności w każdym przekroju równoległym do obu
prostopadłych do siebie krawędzi, pręty zbrojenia w przęśle powinny mieć stały rozstaw w obu kierunkach. Dotyczy to
również zbrojenia podporowego płyt zamocowanych i ciągłych. Zbrojenie naroży płyt swobodnie podpartych należy obliczać i
konstruować w zależności od przyjętego schematu pracy naroża (swobodnego albo ograniczonego odkształcenia ku górze).
W stropach ustrojów płytowo-słupowych, stopień zbrojenia płyty nad podporą powinien być nie mniejszy niż 0,005 w obu
kierunkach na szerokości nie mniejszej niż 0,25 krótszej rozpiętości w każdą stronę.
9.1.1.4 Zbrojenie na przebicie
Powinno składać się ze strzemion pionowych lub ukośnych, zamkniętych lub inaczej dobrze zakotwionych przy obydwu
powierzchniach płyty (rysunek 60a,b), lub z prętów odgiętych (rysunek 60c). Łączny przekrój zbrojenia w sprawdzanym
przekroju płyty powinien odpowiadać przekrojowi wymaganemu ze wzoru (68).
Rysunek 60 - Zbrojenie płyt na przebicie: a) strzemionami pionowymi, b) strzemionami nachylonymi, c) prętami odgiętymi
9.1.2 Obliczenia statyczne płyt
9.1.2.1 Zasady ogólne
Płyty ciągłe, sztywno połączone na podporach z belkami, można obliczać jako przegubowo podparte. Przy obliczaniu
momentu przęsłowego w przęśle skrajnym utwierdzenie na podporze skrajnej można uwzględniać jedynie w tym przypadku,
w którym wystąpienie tego momentu utwierdzenia można uzasadnić obliczeniowo.
Przyjmowane do obliczeń wartości przęsłowych momentów zginających w środkowych przęsłach płyt ciągłych nie powinny
być mniejsze od momentów wyznaczonych przy założeniu obustronnego utwierdzenia przęsła (w przęsłach skrajnych -
jednostronnego utwierdzenia przęsła).
Jeżeli na płytę działa obciążenie skupione, to szerokość współpracującą płyty, przejmującą działanie tego obciążenia, można
określać według podanych niżej wzorów (rysunek 61).
a) Przy obliczaniu wpływu momentu zginającego:
- w jednoprzęsłowych płytach swobodnie podpartych
(177)
- w jednoprzęsłowych płytach obustronnie utwierdzonych oraz środkowych przęsłach płyt ciągłych
(178)
Część 10 Strona 3
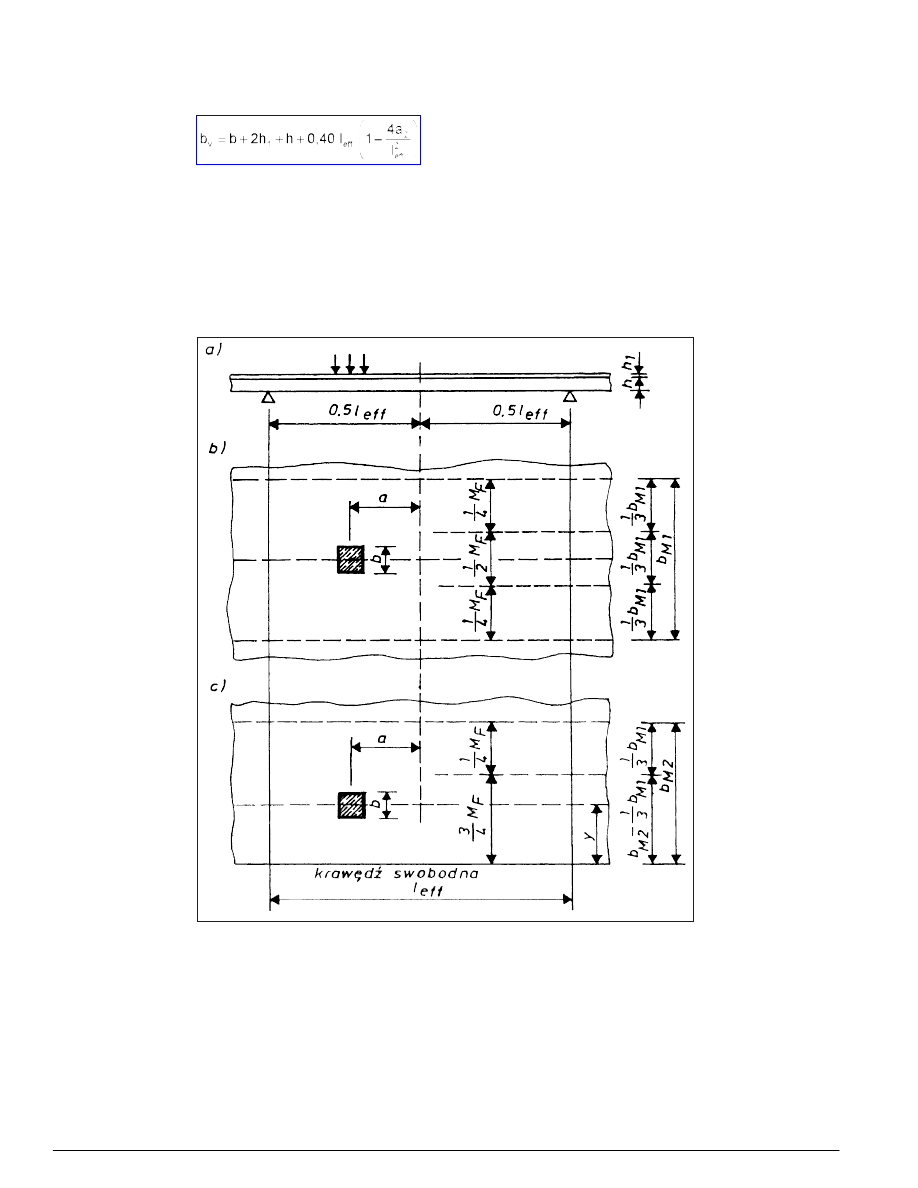
W jednoprzęsłowych płytach utwierdzonych na jednej podporze i swobodnie podpartych na drugiej oraz w przęsłach
skrajnych płyt ciągłych, b
M1
przyjmuje się jako średnią wartość obliczoną według wzorów (177) i (178).
b) Przy obliczaniu wpływu siły poprzecznej bez względu na schemat statyczny płyty
(179)
We wzorach (177) ÷ (179) przyjęto oznaczenia:
b - szerokość powierzchni, na którą działa obciążenie skupione,
h
1
- grubość posadzki,
a - odległość środka ciężkości powierzchni obciążonej od osi symetrii przęsła płyty.
Szerokość współpracującą płyt wspornikowych należy obliczać odpowiednio według wzoru (177) lub (179), podstawiając
zamiast l
eff
podwojoną rozpiętość obliczeniową płyty wspornikowej, zaś jako a - odległość środka ciężkości powierzchni
obciążonej od swobodnej krawędzi płyty.
Rysunek 61 - Szerokość współpracująca płyty przy obciążeniu skupionym:
a) schemat płyty, b) przypadek dowolnego usytuowania siły skupionej, c) usytuowanie siły przy krawędzi swobodnej
Jeżeli obciążenie skupione usytuowane jest w ten sposób, że odległość środka ciężkości powierzchni obciążonej od krawędzi
swobodnej y, jest mniejsza od połowy obliczonej szerokości b
M1
(rysunek 61,c), to szerokość współpracującą b
M2
należy
określać według wzoru
Część 10 Strona 4
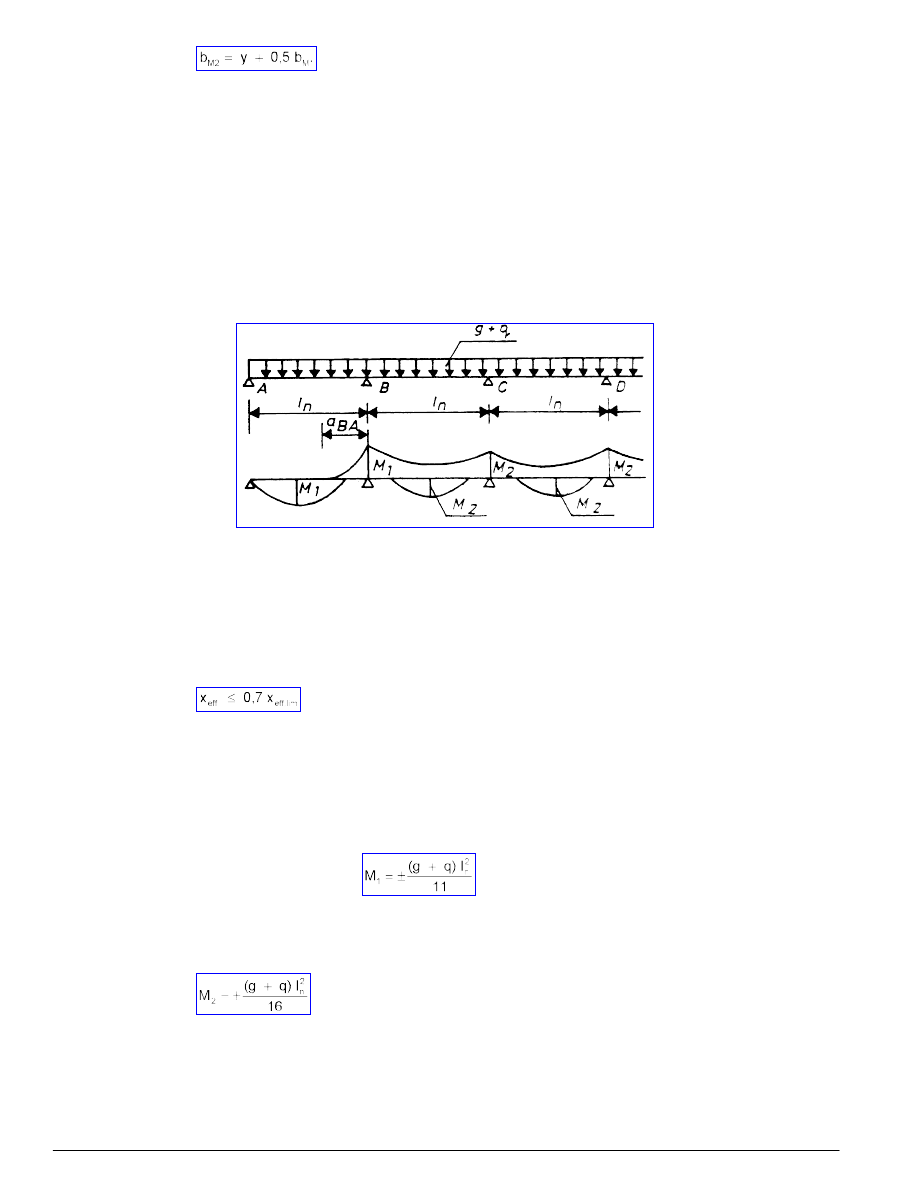
(180)
Moment zginający M
F
wywołany obciążeniem skupionym należy podzielić na szerokości współpracującej w ten sposób, aby
0,5 M
F
przypadała na środkowe pasmo o szerokości 1/3 b
M1
, zaś po 0,25 M
F
- na pasma skrajne (rysunek 61,b). W
przypadku obciążenia skupionego usytuowanego blisko krawędzi swobodnej, moment M
F
należy podzielić na szerokości b
M2
w ten sposób, aby 0,25 M
F
przypadało na wewnętrzne pasmo o szerokości 1/3 b
M1
, zaś 0,75 M
F
- na pasmo skrajne o
szerokości b
M2
- 1/3 b
M1
(rysunek 61,c).
9.1.2.2 Rozpiętość obliczeniowa
W elementach prefabrykowanych położenie teoretycznych punktów podparcia można przyjmować w połowie głębokości
oparcia elementu z tym, że wielkość ta powinna być wyznaczona z uwzględnieniem tolerancji produkcji i montażu oraz
docisku.
W przypadku obliczania płyt ciągłych metodą plastycznego wyrównania momentów zgodnie z 9.1.2.3, za rozpiętość
obliczeniową przyjmuje się rozpiętość l
eff
w świetle żeber lub wieńców z wyjątkiem płyt opartych swobodnie na murze, w
których do rozpiętości w świetle należy dodać 0,5 grubości płyty.
Rysunek 62 - Schemat statyczny płyty ciągłej
9.1.2.3 Obliczanie płyt ciągłych jednokierunkowo zbrojonych
Przeprowadzać można stosując metody analizy liniowo-sprężystej lub plastycznej zgodnie z 4.4.
Płyty ciągłe mogą być obliczane metodą analizy plastycznej, jeżeli spełnione są jednocześnie warunki:
a) zbrojenie elementów stanowią pręty klasy A-0 do A-III,
b) wymiary przekroju betonowego dobrane są w ten sposób, że:
(181)
gdzie: x
eff,lim
wg 5.1.2.
c) płyty połączone są monolitycznie z belkami, spełniającymi rolę podpór.
Przy równych lub nie różniących się więcej niż o 20 % rozpiętościach przęseł, momenty zginające w przypadku obciążenia
rozłożonego równomiernie można wyznaczać według wzorów (rysunek 62)
- moment w przęśle skrajnym oraz moment na podporze przyskrajnej (środkowej w przypadku płyty dwuprzęsłowej)
(182)
- momenty w przęsłach pośrednich oraz momenty na podporach pośrednich
(183)
w których: g i q - obliczeniowe obciążenie stałe i zmienne.
W przypadku nierównych przęseł (w granicach podanych wyżej) momenty podporowe należy obliczać wprowadzając do
Część 10 Strona 5
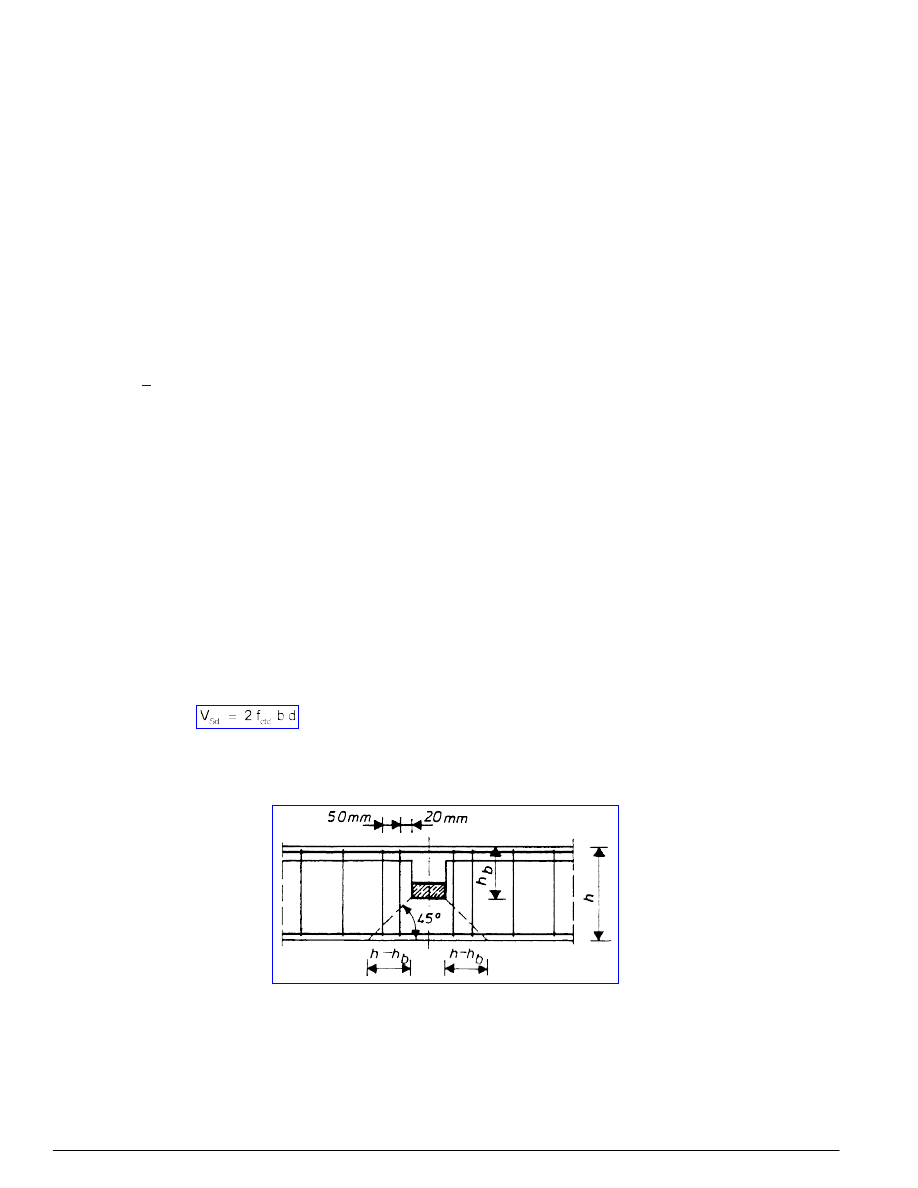
powyższych wzorów większą z rozpiętości dwóch przyległych przęseł.
9.1.2.4 Obliczanie prostokątnych płyt dwukierunkowo zbrojonych
Płyty dwukierunkowo zbrojone można obliczać na podstawie metody analizy sprężystej. Obliczenie płyt o rozpiętości
mniejszej od 6,0 m można również przeprowadzać na podstawie analizy sił wewnętrznych dla warunków równowagi
granicznej.
W płytach ciągłych dwukierunkowo zbrojonych podpartych na 4 krawędziach na belkach żelbetowych, monolitycznie
połączonych z płytą, obliczone wartości momentów można zmniejszyć o:
- 20 % w przekrojach przęseł i podpór środkowych,
- 10 % w przekrojach przęseł skrajnych i na podporze przyskrajnej.
9.2 Stropy gęstożebrowe
Stropy gęstożebrowe z wypełnieniem sztywnym i trwałym, z żebrami rozdzielczymi w rozstawie nie większym niż 4,0 m i płytą
górną grubości co najmniej 30 mm - uważać można w obliczeniach sił wewnętrznych za płyty pełne.
Zbrojenie żeber rozdzielczych stanowić powinny co najmniej dwa pręty, górny i dolny, zdolne do przeniesienia siły nie
mniejszej niż I
i
⋅ 40 kN (I
i
- rozstaw żeber rozdzielczych w metrach).
Kiedy stropy gęstożebrowe projektowane są jako wolno podparte, a na podporze nie zapewniono im pełnej swobody obrotu
przekroju, posiadać powinny na podporze pręty zakotwione w zbrojeniu łączącym ze zbrojeniem górnym o polu przekroju nie
mniejszym niż 0,20 pola przekroju zbrojenia dolnego w przęśle i zdolne przenieść siłę rozciągającą nie mniejszą niż 40 kN/m
szerokości stropu.
9.3 Belki
5)
9.3.1 Konstrukcja belek
9.3.1.1 Wymiary belek
W celu ujednolicenia wymiarów przekrojów zaleca się przestrzegać następującego stopniowania wymiarów belek (z
wyłączeniem elementów prefabrykowanych):
a) szerokość belek prostokątnych i żeber belek teowych - 150, 180, 200, 250 mm i dalej co 50 mm,
b) wysokość belek prostokątnych i teowych - 250, 300 mm i dalej co 50 mm do 800 mm, a powyżej 800 mm co 100 mm.
Grubość ścianek w belkach o przekroju złożonym, wykonywanych na budowie, powinna wynosić co najmniej 60 mm. W
belkach prefabrykowanych żelbetowych i sprężonych grubość środników, stopek, ścianek przekrojów skrzynkowych itp.
powinna być nie mniejsza niż 30 mm z tym, że równocześnie powinny być zachowane wymagania w zakresie prawidłowego
otulenia zbrojenia betonem (8.1.1.2) oraz przepisów przeciwpożarowych.
9.3.1.2 Głębokość oparcia belek na podporze
Powinna zapewniać możliwość prawidłowego zakotwienia prętów zbrojenia wg 8.1.3.
9.3.1.3 Połączenie belki z podciągiem
W przypadku przekazywania reakcji belki przez podwieszenie lub zaczepienie do podciągu w obrębie jego wysokości,
połączenie belki z podciągiem powinno być zabezpieczone dodatkowym zbrojeniem nie uwzględnionym w obliczeniu
podciągu na siły poprzeczne.
Jeżeli obliczeniowa siła poprzeczna w podciągu w miejscu połączenia z belką nie przekracza wartości
(184)
należy zastosować co najmniej 4 strzemiona jak na rysunku 63.
Rysunek 63 - Długość odcinka, na którym należy umieścić dodatkowe zbrojenie poprzeczne przenoszące reakcję belki na
podciąg
Część 10 Strona 6
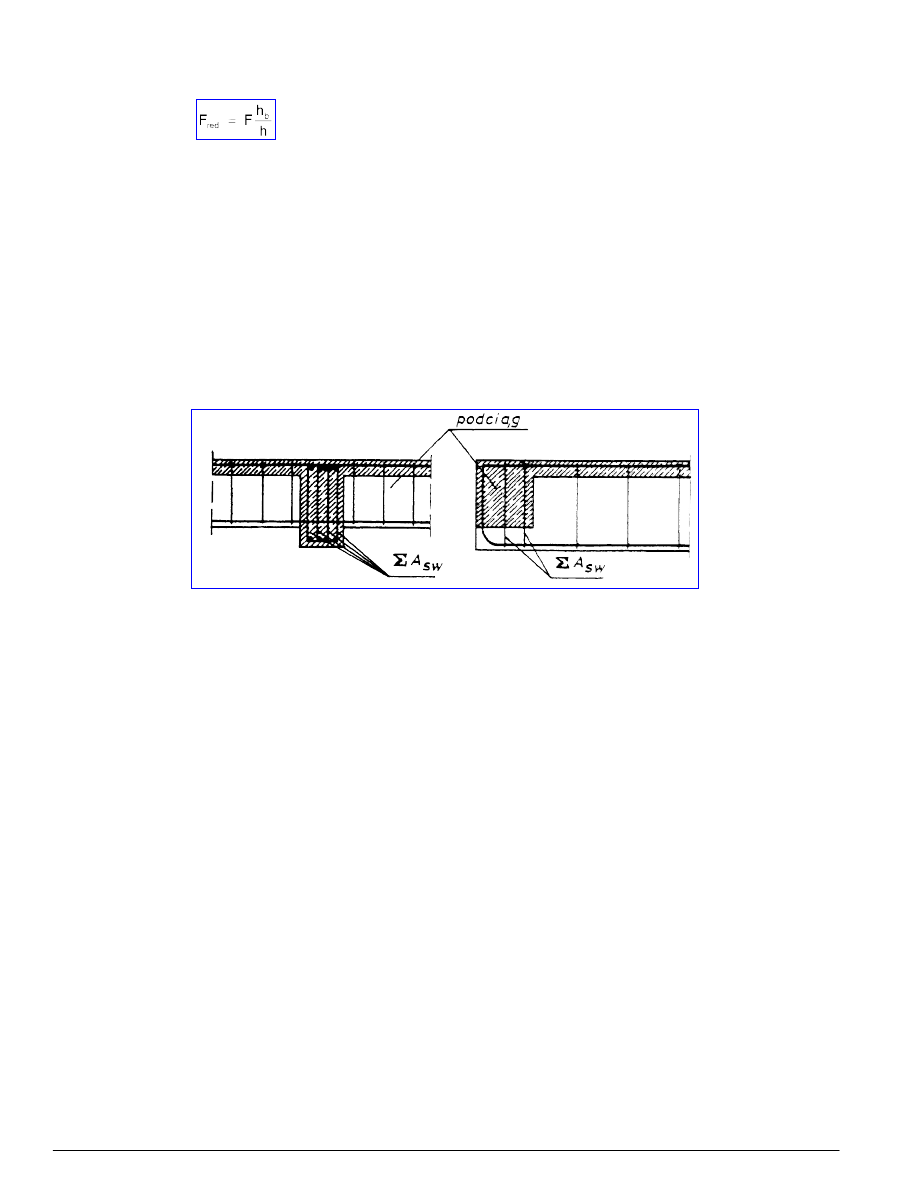
Przy większej sile poprzecznej przekrój strzemion lub prętów odgiętych należy obliczać z warunku przeniesienia przez to
zbrojenie zredukowanej reakcji F
red
belki na podciąg według wzoru
(185)
w którym:
F - reakcja belki,
h
b
, h - wysokość belki i podciągu.
Jeżeli zbrojenie rozciągane belki znajduje się poniżej dolnej krawędzi podciągu (rysunek 64), reakcję podporową belki należy
przejąć w całości przez strzemiona o przekroju ΣA
sw
obejmujące pręty dolnego zbrojenia belki lub przyspojone do tych
prętów. Do ΣA
sw
można wliczyć przekrój odgiętego zbrojenia głównego belki (rysunek 64) pod warunkiem spełnienia
wymagań w zakresie zagięcia prętów (8.1.1.3) i zakotwienia (8.1.3).
9.3.1.4 Podciągi z wbetonowanymi końcami belek prefabrykowanych
Mogą być obliczane jak elementy o pełnej szerokości przekroju tylko wówczas, jeżeli górne pręty zbrojenia podłużnego
(głównego lub montażowego) biegną nieprzerwanie na całej długości podciągu i połączone są ze zbrojeniem dolnym za
pomocą strzemion (rysunek 65 a i b). Odległość w świetle pomiędzy belkami prefabrykowanymi wzdłuż podciągów powinna
być nie mniejsza niż 3 głębokości oparcia belek. W przypadku przedstawionym na rysunku 65,c) należy przyjmować, że
przekrojem pracującym jest jedynie przekrój dolnej części podciągu o wymiarach bh.
Rysunek 64 - Zbrojenie belki podwieszonej do podciągu
Część 10 Strona 7
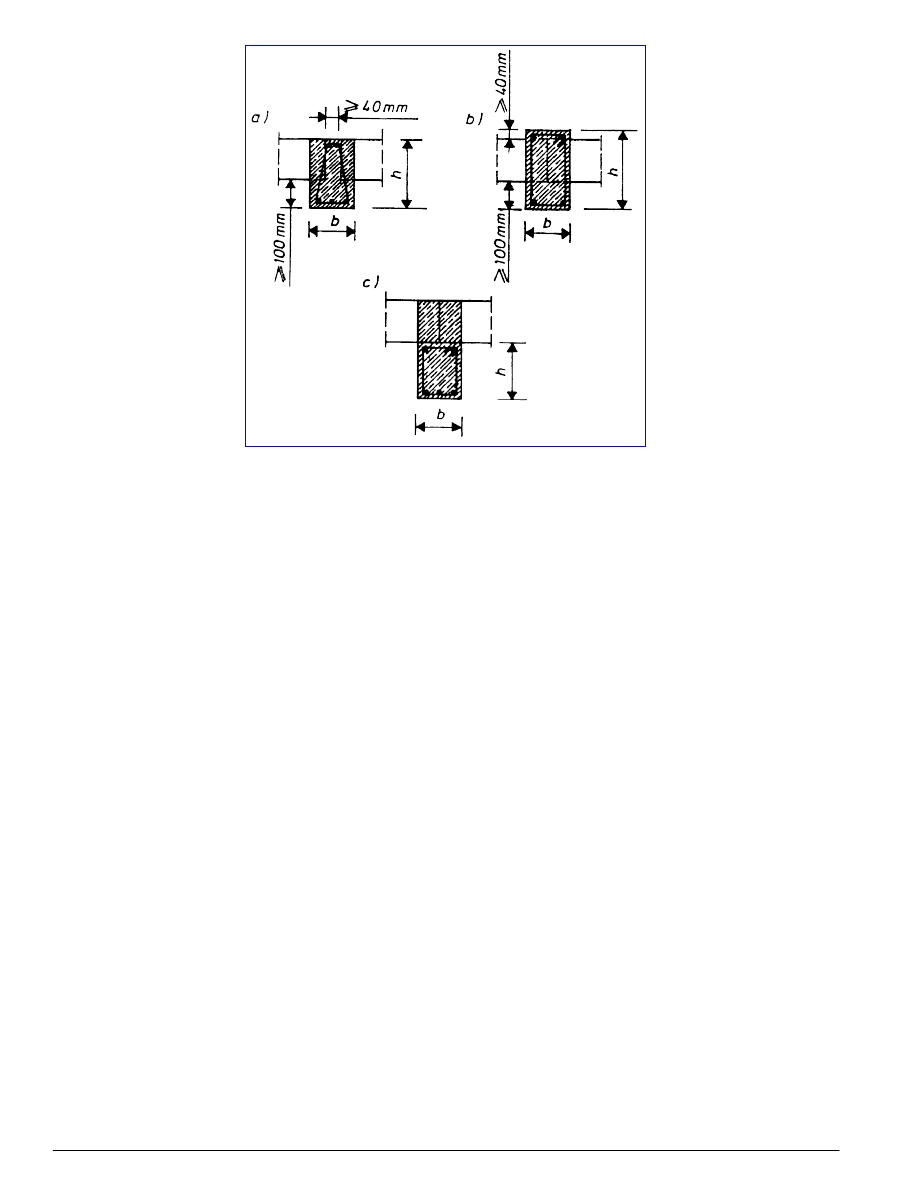
Rysunek 65 - Przyjmowane do obliczeń przekroje podciągów z wbetonowanymi końcami belek: a) i b) przekroje o pełnej
wysokości, c) przekrój ograniczony do dolnej części podciągu
Przy sprawdzaniu stanu granicznego nośności w przypadkach przedstawionych na rysunku 65 a i b) w obliczeniach należy
przyjmować całą szerokość pracującego przekroju podciągu b z tym, że należy zaprojektować wzmocnienie podciągu wg
9.3.1.3.
Przy sprawdzaniu stanu granicznego zarysowania uwzględnia się całą szerokość podciągu b, jeżeli spełnione są wyżej
podane zalecenia.
W przypadku występowania obciążeń wielokrotnie zmiennych za przekrój pracujący należy przyjąć:
- jeżeli odległość pomiędzy wbetonowanymi końcami belek (rysunek 65,a) jest mniejsza niż 100 mm, jedynie przekrój dolnej
części podciągu (rysunek 65,c),
- jeżeli odległość pomiędzy wbetonowanymi końcami belek jest nie mniejsza niż 100 mm, przekrój podciągu o pełnej
wysokości przy szerokości górnej części przekroju równej odległości pomiędzy końcami belek.
Zbrojenie podciągu z wbetonowanymi końcami belek prefabrykowanych powinno spełniać warunki podane w 9.3.1.3.
9.3.1.5 Zbrojenie belek
Ś
rednica podłużnych prętów rozciąganych nie powinna być mniejsza niż:
8 mm - w belkach wykonywanych na miejscu budowy,
5,5 mm - w belkach prefabrykowanych.
Ś
rednica podłużnych prętów ściskanych nie powinna być mniejsza niż:
12 mm - w belkach wykonywanych na miejscu budowy,
10 mm - w belkach prefabrykowanych.
W belkach żelbetowych co najmniej 1/3 prętów zbrojenia dolnego potrzebnych w przęśle i nie mniej niż 2 pręty powinny być
doprowadzone bez odgięć do podpory.
W belkach żelbetowych i sprężonych, w których dopuszcza się zarysowanie, jeżeli wysokość przekroju belki jest większa niż
700 mm, przy powierzchniach bocznych należy umieszczać podłużne pręty konstrukcyjne o średnicy nie mniejszej niż 8 mm
w rozstawie nie większym niż 250 mm.
Belki o wysokości przekroju większej niż 1000 mm, jak również belki zbrojone prętami o średnicy większej niż 25 mm -
powinny posiadać zbrojenie przypowierzchniowe, określone zgodnie z 8.1.7.
Ś
rednica strzemion powinna być nie mniejsza niż:
4,5 mm - w belkach wykonywanych na miejscu budowy,
3,0 mm - w belkach prefabrykowanych.
Ponadto średnica strzemion powinna być nie mniejsza niż 0,2 średnicy zbrojenia podłużnego.
Stopień zbrojenia strzemionami na ścinanie ρ
w
nie może być mniejszy od wartości podanych w tablicy 32.
Część 10 Strona 8
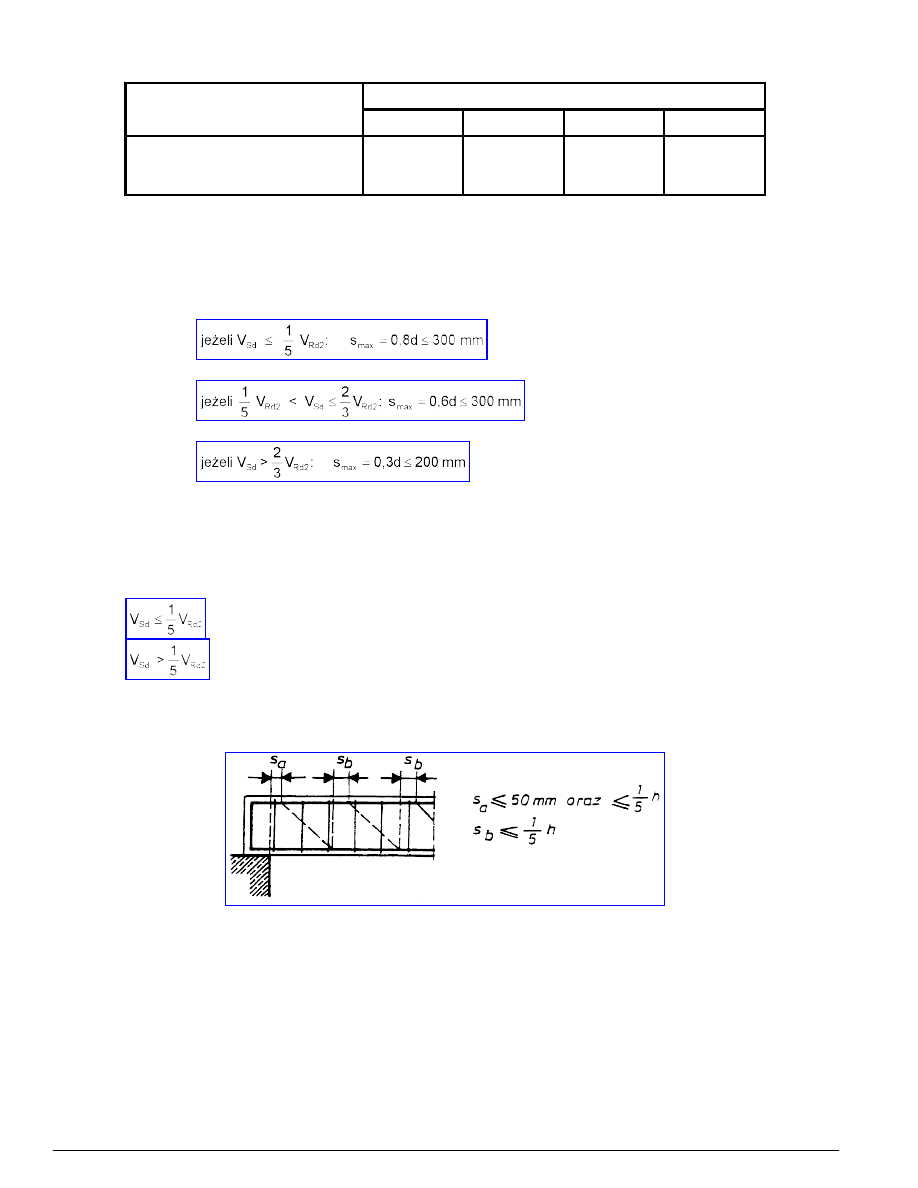
Tablica 32 - Minimalne wartości ρ
ρ
ρ
ρ
w
Klasy wytrzymałości betonu
Klasa stali
A-0
A-I
A-II
A-III
B15 do B25
B30 do B45
B50 do B70
0,0014
0,0020
0,0026
0,0013
0,0018
0,0024
0,0009
0,0012
0,0016
0,0008
0,0011
0,0014
Ś
rednica strzemion wykonanych z prętów gładkich nie powinna być większa niż 12 mm.
Strzemiona powinny być należycie zakotwione. Połączenie na zakład przy powierzchni bocznej środnika dopuszcza się tylko
dla prętów żebrowanych.
Maksymalny odstęp ramion strzemion s
max
w kierunku podłużnym określają następujące warunki:
(186)
(187)
(188)
gdzie:
V
Sd
- siła poprzeczna, wywołana obciążeniem obliczeniowym,
V
Rd2
- nośność obliczeniowa na ścinanie z uwagi na zmiażdżenie ściskanych krzyżulców betonowych, określona zgodnie z
5.5,
d - wysokość użyteczna przekroju.
Maksymalny odstęp ramion strzemion s
max
w kierunku poprzecznym nie powinien przekraczać:
- przy
- mniejszej z dwóch wartości: s
max
= d lub 800 mm
- przy
- obowiązują warunki (187) i (188).
Pręty odgięte, uwzględniane w obliczeniach, powinny być rozmieszczane w strefie przypodporowej tak, aby odległości s
a
i s
b
były nie większe od wartości podanych na rysunku 66.
Rysunek 66 - Rozstaw prętów odgiętych w strefie przypodporowej
Jeżeli w belce zastosowano pręty ściskane, potrzebne ze względów obliczeniowych, rozstaw strzemion zamkniętych powinien
być nie większy niż 15 średnic tego zbrojenia.
W belkach prostokątnych nie połączonych z płytami, należy stosować strzemiona zamknięte. W belkach o szerokości
większej niż 350 mm zbrojonych w strefie rozciąganej więcej niż 3 prętami, należy stosować strzemiona czteroramienne
(rysunek 67).
Część 10 Strona 9
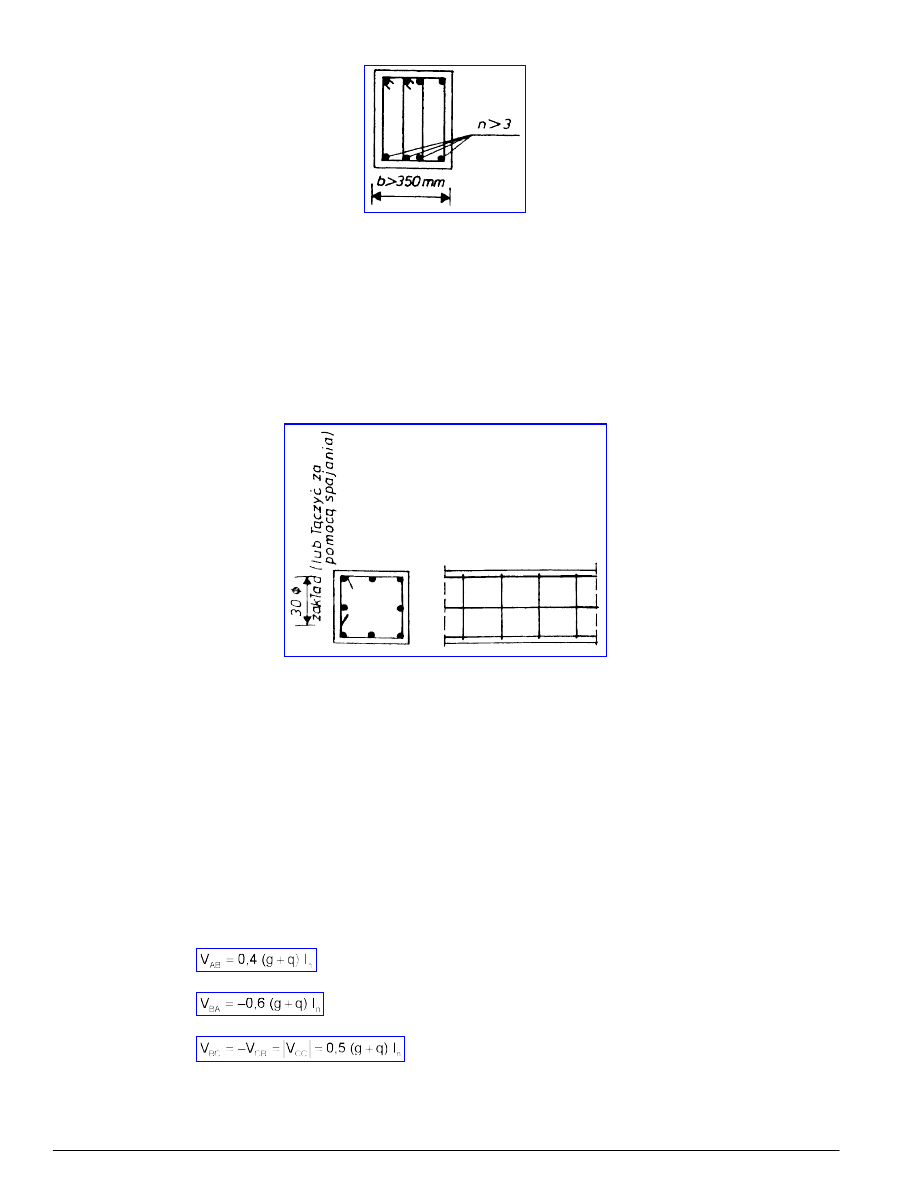
Rysunek 67 - Strzemiona czteroramienne w belkach
Zbrojenie elementów skręcanych lub jednocześnie skręcanych i zginanych powinno składać się z dwuramiennych strzemion i
dodatkowych - w stosunku do zbrojenia ze względu na moment zginający - prętów podłużnych rozmieszczonych
równomiernie na obwodzie rdzenia belki. Zbrojenie elementów skręcanych, jeżeli znak momentu skręcającego nie ulega
zmianie, można projektować w postaci uzwojenia o kierunku zgodnym z kierunkiem skręcania. Rozstaw prętów uzwojenia
powinien być nie większy niż mniejszy bok przekroju prostokątnego.
W elementach skręcanych należy stosować strzemiona zamknięte, łączone na zakład o długości równej co najmniej 30
ś
rednic strzemienia, lub łączone za pomocą spajania (rysunek 68).
Rysunek 68 - Zbrojenie na skręcanie w postaci dodatkowych prętów podłużnych i strzemion
Odstęp strzemion powinien spełniać podane wyżej warunki dla elementów zginanych.
9.3.2 Obliczenia statyczne belek
9.3.2.1 Zasady ogólne
Belki ciągłe sztywno połączone na podporach z belkami lub słupami można obliczać jako belki ciągłe podparte przegubowo.
Przyjmowane do obliczeń wartości przęsłowych momentów zginających w środkowych przęsłach belek ciągłych nie powinny
być mniejsze niż momenty wyznaczone przy założeniu obustronnego utwierdzenia przęsła (w przęsłach skrajnych -
jednostronnego utwierdzenia).
9.3.2.2 Obliczanie belek ciągłych
Przeprowadzać można stosując metodę analizy liniowo-sprężystej lub plastycznej (4.4).
Drugorzędne belki ciągłe mogą być również obliczane metodą analizy plastycznej wg 9.1.2.3., jeżeli spełnione są wymagania
a) i b) podane w tym punkcie, oraz jeżeli belki połączone są monolitycznie z podciągami lub słupami, spełniającymi rolę
podpór. Wartości sił poprzecznych w licu podpory należy w tym przypadku obliczać według wzorów (rysunek 62).
(189)
(190)
(191)
Część 10 Strona 10
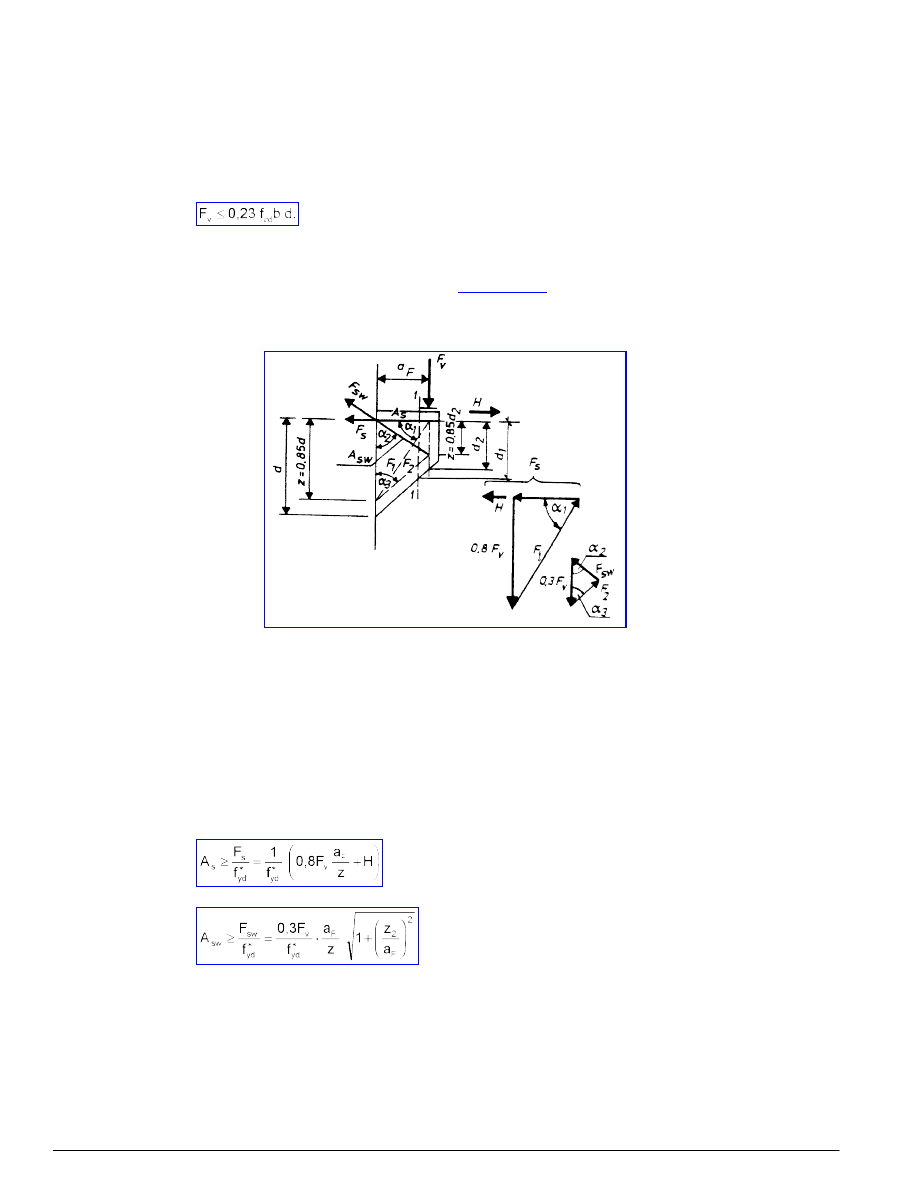
przyjmując przy równych lub nie różniących się więcej niż o 20% rozpiętościach przęseł, rozpiętość rozpatrywanego przęsła
(w świetle).
9.4 Wsporniki krótkie
9.4.1 Konstrukcja wsporników
Wymiary przekroju wsporników krótkich, dla których a
F
≤ d (rysunek 69) należy sprawdzać z warunku
(192)
w którym:
F
v
- obliczeniowa siła pionowa działająca na wspornik; w przypadku belek podsuwnicowych obliczeniowa reakcja belki,
wyznaczona z uwzględnieniem współczynnika dynamicznego wg
PN-86/B-02005
,
b, d
1
- szerokość i wysokość użyteczna przekroju 1-1 (rysunek 69).
Rysunek 69 - Schemat rozkładu sił we wsporniku przy przyłożeniu siły F
v
na górnej jego krawędzi
Wysokość przekroju wspornika w strefie przyłożenia obciążenia powinna być nie mniejsza niż połowa wysokości przekroju
podporowego. Kąt nachylenia dolnej krawędzi wspornika do poziomu powinien być nie większy niż 45°.
9.4.2 Zbrojenie wsporników
Główne zbrojenie wsporników krótkich należy wymiarować w zależności od sposobu ich obciążenia, przyjmując za
obliczeniową granicę plastyczności stali wartości f*
yd
podane w tablicy 33.
Jeżeli siła F
v
jest przyłożona na górnej krawędzi wspornika, przekroje głównego zbrojenia poziomego A
s
i ukośnego A
sw
należy obliczać zgodnie z rozkładem sił podanym na rysunku 69, korzystając z warunków
(193)
(194)
Jeżeli siła F
v
jest przyłożona poniżej górnej krawędzi wspornika, przekroje głównego zbrojenia poziomego A
s
i ukośnego A
sw
należy obliczać zgodnie z rozkładem sił podanym na rysunku 70, korzystając z warunków
Część 10 Strona 11
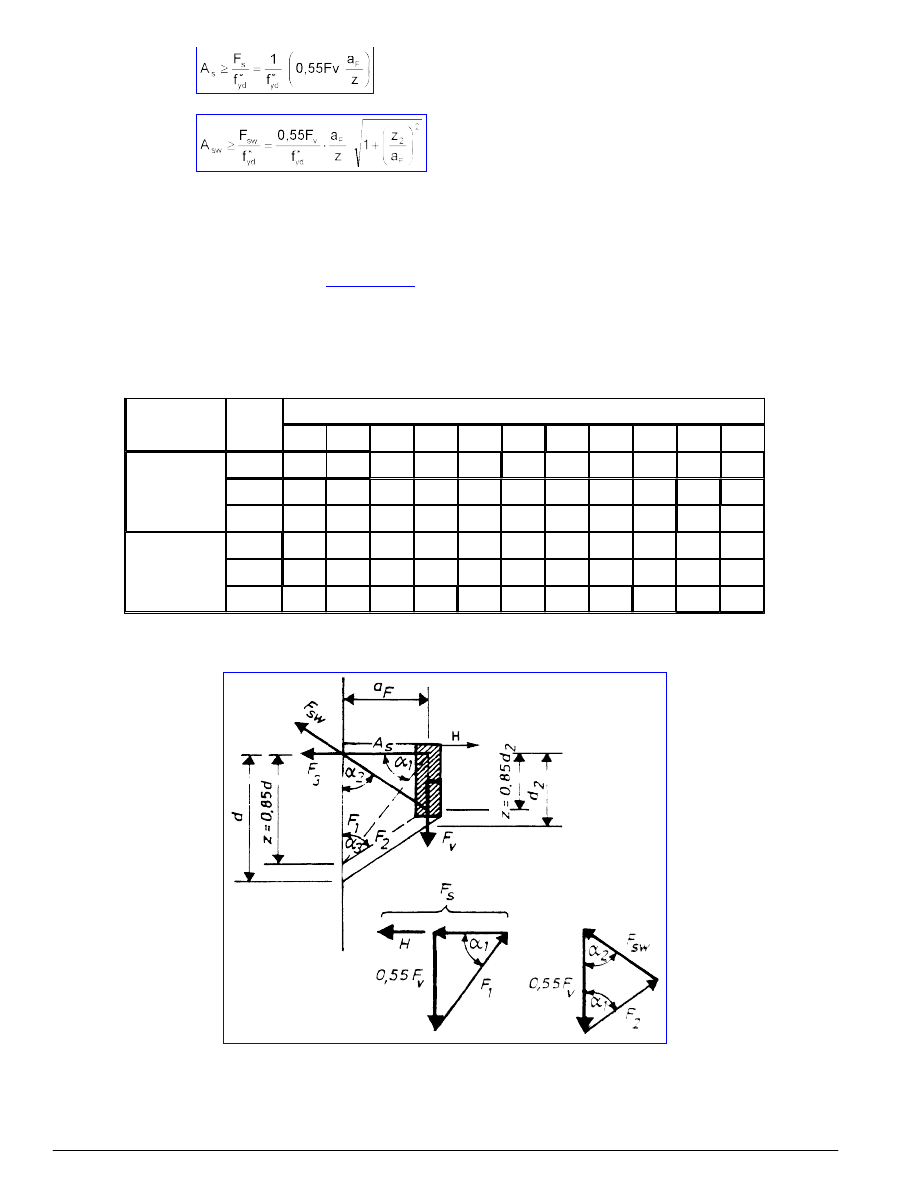
(195)
(196)
W powyższych wzorach należy przyjmować:
z = 0,85d, gdzie d - wysokość użyteczna przekroju podporowego wspornika,
z
2
= 0,85d
2
, gdzie d
2
- wysokość użyteczna przekroju wspornika w miejscu przyłożenia wypadkowej obciążenia pionowego;
dla wsporników prostokątnych z
2
= z = 0,85d,
H - obliczeniowa siła pozioma, prostopadła do przekroju podporowego wspornika; w przypadku obciążenia wspornika belką
podsuwnicową przyjmowana zgodnie z
PN-86/B-02005
, a w przypadku gdy wywołana jest skurczem lub temperaturą -
zgodnie z obliczeniami, lecz nie mniej niż 0,2F
v
.
Tablica 33 - Wartości f*
yd
(w MPa) przyjmowane do obliczania głównego zbrojenia wsporników
Rodzaj prętów
w
lim
mm
Ś
rednica prętów, mm
6
8
10
12
14
16
18
20
22
24
25
Gładkie
0,3
f
yd
f
yd
f
yd
f
yd
f
yd
190
180
160
145
135
-
0,2
f
yd
f
yd
f
yd
180
150
130
120
110
100
90
-
0,1
180
135
110
90
75
65
60
55
50
45
-
Ż
ebrowane
0,3
f
yd
f
yd
f
yd
310
310
285
255
225
210
-
18
0,2
f
yd
310
300
250
220
190
170
150
140
-
12
0,1
255
190
150
125
110
95
85
75
70
-
6
Rysunek 70 - Schemat rozkładu sił we wsporniku przy przyłożeniu siły F
v
w połowie wysokości jego przekroju
Część 10 Strona 12

Zbrojenie główne wsporników należy rozmieszczać zgodnie z przebiegiem sił rozciągających F
s
i F
sw
wynikającym z
obliczeniowego rozkładu sił wewnętrznych, przy czym kąt nachylenia zbrojenia ukośnego do poziomu powinien być nie
mniejszy niż 30° i nie większy niż 60°. Osie prętów zbrojenia poziomego i ukośnego powinny przecinać się w przekroju
podporowym wspornika. Sumaryczna powierzchnia przekroju prętów zbrojenia głównego (poziomego i ukośnego) powinna
być nie mniejsza niż 0,004 bd. Średnica prętów zbrojenia głównego powinna być nie większa niż 25 mm. Zbrojenie to należy
prawidłowo zakotwić zarówno poza przekrojem podporowym, jak i na końcu wspornika poza linią działania siły F
v
.
Zaleca się wykonywanie głównego zbrojenia w postaci pętli przy zachowaniu średnic zagięcia prętów zgodnie z 8.1.1.3.
Odległość między zewnętrzną krawędzią elementu przekazującego obciążenie na wspornik, a początkiem łuku zagięcia
prętów powinna być nie mniejsza niż średnica tych prętów (rysunek 71). Jeżeli główne zbrojenie poziome wykonane jest w
postaci pętli poziomych, należy stosować zbrojenie montażowe wzdłuż czołowej i dolnej krawędzi wspornika.
W przypadkach gdy górna krawędź wspornika przedłużona jest poza przekrój podporowy, należy stosować dodatkowe
zbrojenie o przekroju 0,5 A
sw
równolegle do zbrojenia ukośnego, jak pokazano na rysunku 71, a.
Poza zbrojeniem głównym należy stosować strzemiona poziome, (rysunek 71).
Sumaryczny przekrój strzemion powinien spełniać warunki
(197)
(198)
Odstęp strzemion powinien być nie większy niż 150 mm i nie większy niż 0,25 d oraz nie powinien przekraczać 12 φ zbrojenia
głównego. Zbrojenie pionowe słupa usytuowane przy przekroju podporowym wspornika powinno mieć przekrój równy co
najmniej przekrojowi A
s
, obliczonemu według wzoru (193) lub (195). Ewentualne dodatkowe pręty zbrojenia w słupie (A
s1
)
powinny być zakotwione powyżej i poniżej osi głównego, poziomego zbrojenia wspornika na długości równej co najmniej 30 φ
i nie mniejszej niż odległość siły F
v
od krawędzi słupa (rysunek 71, b).
Część 10 Strona 13
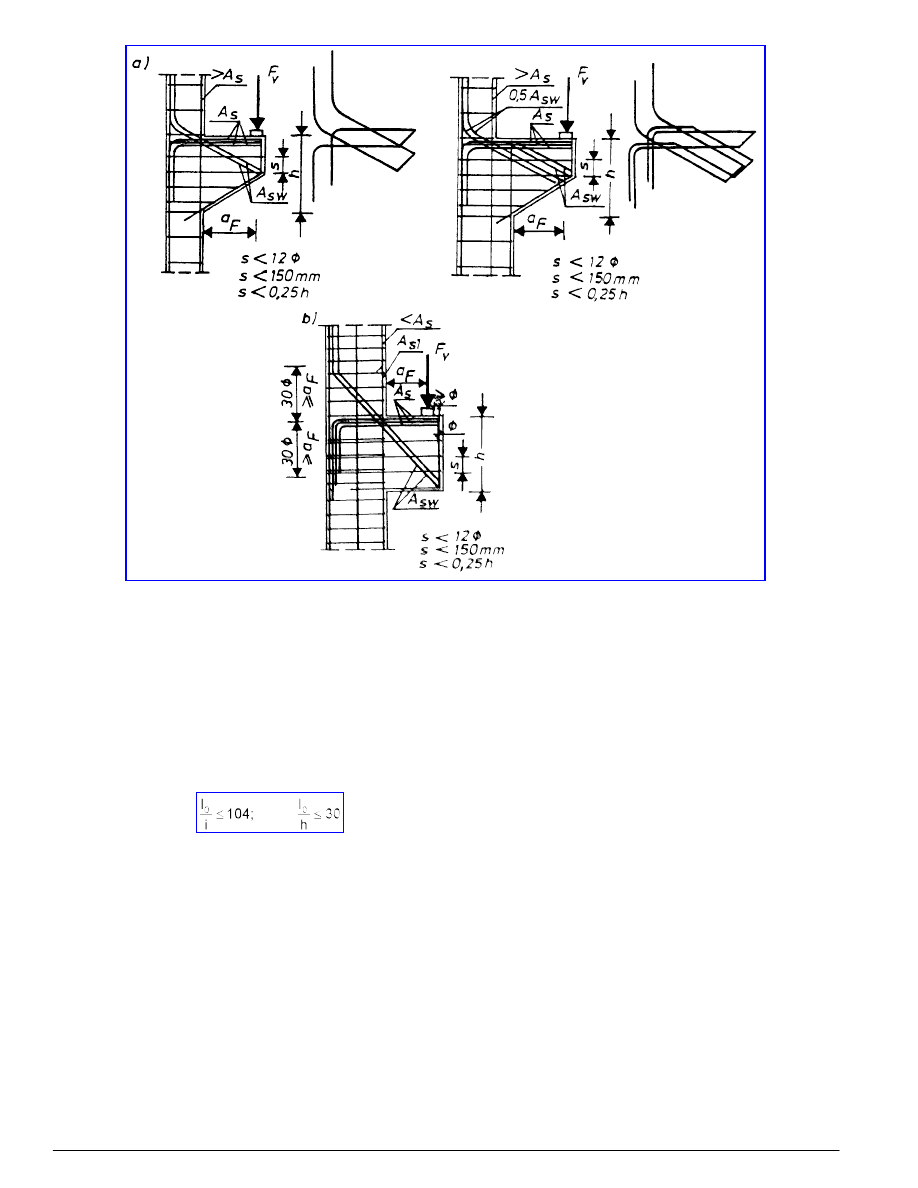
Rysunek 71 - Zbrojenie krótkich wsporników: a) wspornik trapezowy ze strzemionami poziomymi i ukośnymi, b) wspornik
prostokątny ze strzemionami poziomymi
9.5 Słupy
9.5.1 Konstrukcja słupów
9.5.1.1 Wymiary przekroju poprzecznego słupów
Podane wymagania konstrukcyjne dotyczą słupów, w których stosunek boków przekroju poprzecznego jest nie większy niż
cztery.
Zaleca się, aby smukłość słupów była nie większa niż
(199)
Grubość ścianek prefabrykowanych elementów ściskanych o przekroju teowym, dwuteowym, skrzynkowym, rurowym itp.
powinna być nie mniejsza niż 40 mm z tym, że równocześnie powinny być zachowane wymagania w zakresie prawidłowego
otulenia zbrojenia betonem oraz wymagania w zakresie przepisów przeciwpożarowych.
Wymiary przekroju poprzecznego słupów, z wyjątkiem słupów prefabrykowanych, należy przyjmować: przy wymiarze boku
do 600 mm - z zaokrągleniem do 50 mm, powyżej 600 mm - z zaokrągleniem do 100 mm.
9.5.1.2 Zbrojenie słupów nieuzwojonych
Zbrojenie podłużne słupów powinno składać się co najmniej z takiej liczby prętów, aby w każdym narożu znajdował się jeden
pręt, resztę prętów należy rozmieszczać na obwodzie, w odstępie nie przekraczającym 400 mm. W przekroju okrągłym
liczba prętów powinna wynosić co najmniej 6 sztuk.
Całkowity przekrój zbrojenia podłużnego powinien być nie większy niż 6% użytecznej powierzchni przekroju słupa.
Do zbrojenia podłużnego słupów należy stosować pręty o średnicy od 12 do 40 mm. W słupach prefabrykowanych można
stosować pręty o średnicy 10 mm.
Ś
rednica strzemion powinna być nie mniejsza niż 0,2 średnicy zbrojenia podłużnego i wynosić nie mniej niż 4,5 mm.
Część 10 Strona 14
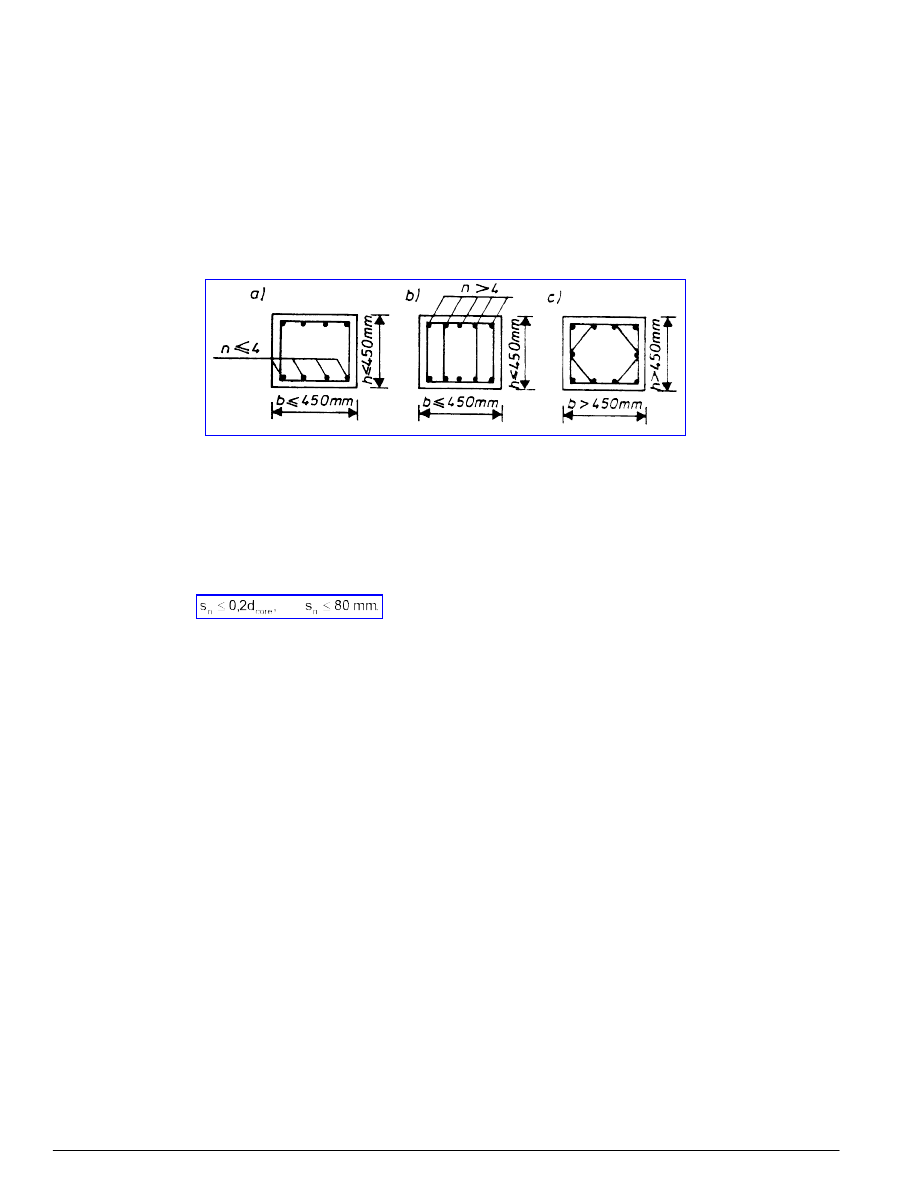
Rozstaw strzemion powinien być nie większy niż:
- 15 φ zbrojenia podłużnego, gdy sumaryczny stopień zbrojenia słupa jest nie większy niż 3 %,
- 10 φ zbrojenia podłużnego, gdy sumaryczny stopień zbrojenia słupa jest większy niż 3 %,
- najmniejszy wymiar poprzeczny słupa lub jego średnica i powinien być nie większy niż 400 mm.
W miejscu łączenia prętów zbrojenia podłużnego (dotyczy to także miejsca zmiany przekroju słupa) rozstaw ten powinien być
zmniejszony do połowy, a na końcach słupów prefabrykowanych, na odcinku równym większemu wymiarowi przekroju
poprzecznego słupa - do 1/3.
Stosowanie strzemion pojedynczych dozwolone jest tylko w tych przypadkach, w których wymiary boków słupa są nie
większe niż 450 mm przy liczbie prętów zbrojenia podłużnego z każdej strony nie większej niż cztery (rysunek 72,a). W
innych przypadkach stosować należy strzemiona podwójne (rysunek 72,b i c).
Jeżeli stopień zbrojenia słupa jest większy niż 3 %, strzemiona podwójne należy stosować bez względu na wymiary przekroju
poprzecznego słupa.
Rysunek 72 - Stosowanie strzemion podwójnych w słupach: a) strzemiona podwójne nie wymagane, b) i c) wymagane
9.5.1.3 Zbrojenie słupów uzwojonych
Zbrojenie podłużne powinno składać się z co najmniej z 6 prętów o średnicy od 12 do 32 mm. Średnica pręta uzwajającego
powinna być co najmniej równa 4,5 mm. Uzwojenie należy przeprowadzać przez całą wysokość belki opierającej się na
słupie.
Skok linii śrubowej uzwojenia powinien spełniać warunki (rysunek 14):
Sumaryczny przekrój zbrojenia podłużnego powinien być nie większy niż 8 % powierzchni przekroju betonowego rdzenia
uzwojonego słupa.
9.6 Ograniczenie zakresu szkód wywołanych przez oddziaływania wyjątkowe
W celu ograniczenia zakresu szkód wywołanych przez oddziaływania wyjątkowe przewidzieć należy zbrojenie łączące:
- zapobiegające lokalnemu uszkodzeniu spowodowanemu np. przez silne uderzenie lub wybuch i
- umożliwiające powstanie wtórnego ustroju nośnego po pojawieniu się lokalnego uszkodzenia.
Na zbrojenie łączące składa się (rysunek 73):
- zbrojenie łączące ściany względnie słupy w poziomie stropu (zbrojenie wieńcowe) oraz
- zbrojenie łączące stropy nad podporą (w kierunku rozpiętości stropu oraz w kierunku prostopadłym do rozpiętości stropu),
a w przypadkach szczególnych - również zbrojenie łączące w kierunku pionowym.
Zbrojenie łączące wykonuje się ze stali o dużej ciągliwości ε
uk
> 5 % oraz f
tk
/f
yk
> 1,08, do których zalicza się stale A-0 do A-
III.
Zbrojenie zaprojektowane z uwagi na inne wymagania uważać można za część lub całość zbrojenia łączącego.
Przy sprawdzaniu stanu granicznego nośności w sytuacji wyjątkowej, za kryterium wyczerpania nośności zbrojenia
przyjmować można ε
s
≤ ε
uk
.
Potrzebny przekrój zbrojenia wyznacza się przyjmując charakterystyczną granicę plastyczności stali jak dla sytuacji
wyjątkowej (3.1.2).
Część 10 Strona 15
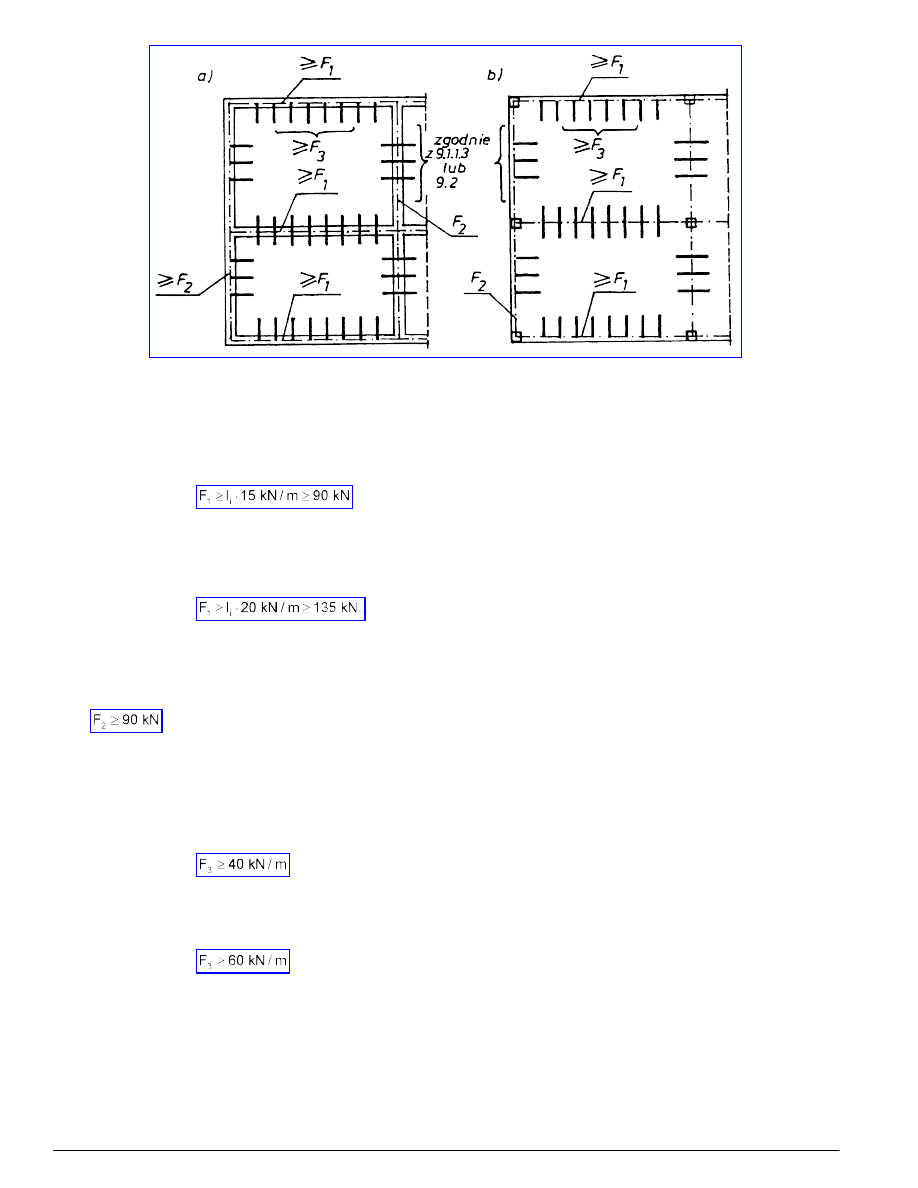
Rysunek 73 - Zbrojenie łączące w stropach: a) w budynkach ścianowych, b) w budynkach szkieletowych
Zbrojenie wieńcowe ścian, na których oparte są stropy, a także zbrojenie łączące ze słupami podciągi w konstrukcji
szkieletowej, na których oparte są stropy - powinno być zdolne do przeniesienia siły rozciągającej F
1
(rysunek 73) nie
mniejszej niż
(200)
gdzie: l
i
- odległość podpór.
W przypadku zbrojenia stalą A-III wymaganie to odpowiada nie mniej niż 3 φ 10. W budynkach o wysokości większej niż 8
kondygnacji ze stropami wielkopłytowymi zbrojonymi jednokierunkowo wymaga się aby
(201)
co odpowiada 3 φ 12 ze stali A-III.
Zbrojenie wieńcowe ścian, na których nie są oparte stropy, oraz zbrojenie łączące ze słupami podciągi, na których nie są
oparte stropy, powinno być zdolne do przeniesienia siły F
2
nie mniejszej niż
(202)
Zbrojenie łączące stropy nad podporą w kierunku rozpiętości stropów powinno być zdolne do przeniesienia siły rozciągającej
F
3
nie mniejszej niż:
- w przypadku stropów ze zbrojeniem nad ścianą lub belką - w kierunku równoległym do zbrojenia nie mniejszym niż
wymagane, kiedy wzdłuż zbrojenia głównego płyty znajduje się belka lub ściana stanowiąca podporę dla płyty, lub kiedy w
stropie występują żebra rozdzielcze,
(203)
- w przypadku stropów wielkopłytowych bez zbrojenia w kierunku prostopadłym do zbrojenia głównego, łączącego strop z
przyległą belką lub ścianą - nie mniejszej niż
(204)
Na zewnętrznych ścianach nośnych oraz na wewnętrznych ścianach i na podciągach, na których strop opiera się tylko z
jednej strony, zbrojenie łączące strop nad podporą zakotwić należy w leżącym na ścianie wieńcu żelbetowym lub w podciągu.
Połączenie słupów w kierunku pionowym w budynkach wielokondygnacyjnych powinno być zdolne do przeniesienia siły
rozciągającej równej co najmniej obciążeniu obliczeniowemu, przypadającemu na strop z jednej kondygnacji.
Część 10 Strona 16
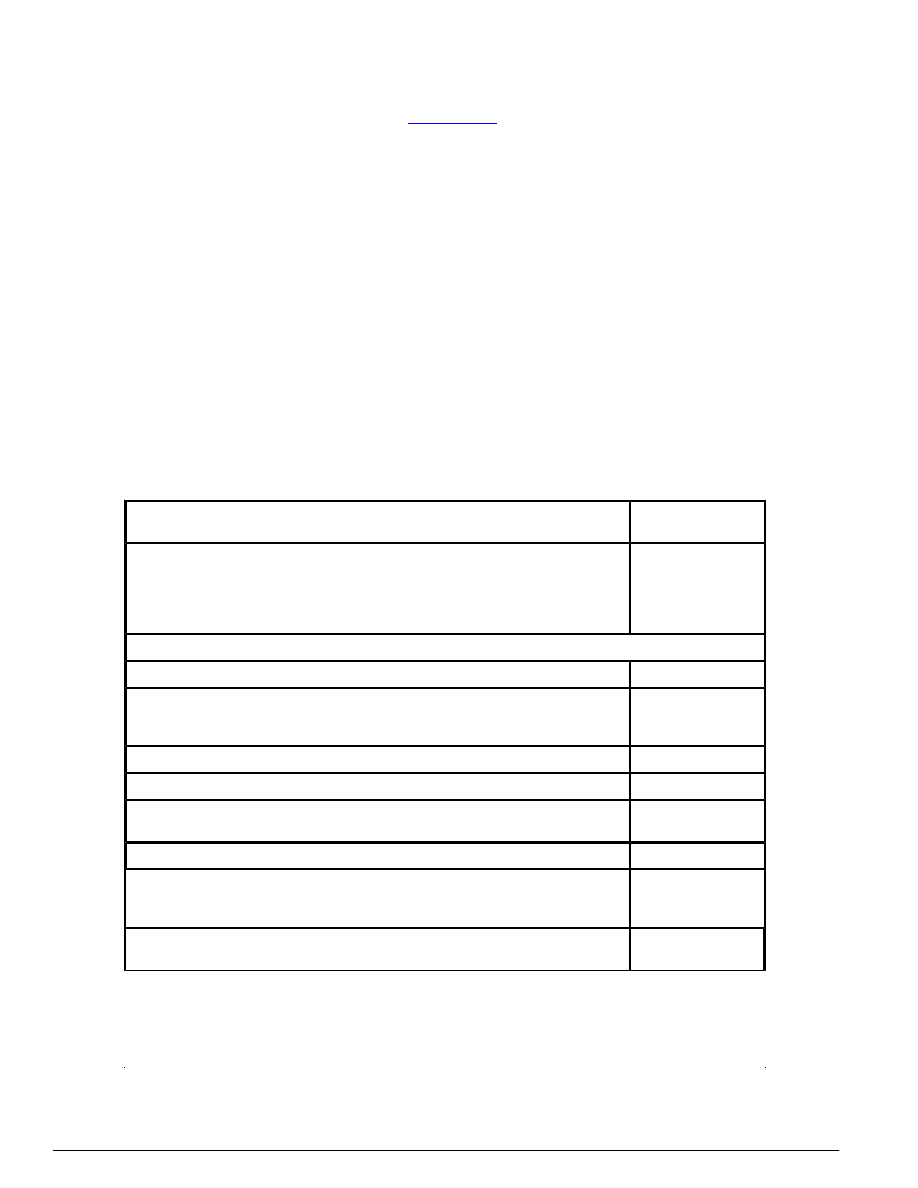
9.7 Wpływ temperatury i skurczu betonu na odkształcenia konstrukcji. Przerwy dylatacyjne
9.7.1 Odkształcenia konstrukcji od wpływu temperatury i skurczu betonu
Granice zmian temperatury należy przyjmować zgodnie
PN-86/B-02015
.
W częściach budowli, w których najmniejszy wymiar przekroju betonu wynosi 700 mm albo które są chronione nadsypką,
obliczeniowe różnice temperatur mogą, być obniżone o 5 °C.
Wpływ skurczu w konstrukcjach żelbetowych można przyjmować za równoważny z obniżeniem się temperatury o 15 °C.
9.7.2 Odległości między przerwami dylatacyjnymi
Rozmieszczenie przerw dylatacyjnych powinno być ustalane na podstawie analizy pracy konstrukcji poddanej działaniu
skurczu betonu i różnicy temperatur. Dla konstrukcji betonowych oraz konstrukcji żelbetowych i częściowo sprężonych -
można nie wykonywać obliczeń, jeżeli odległość między przerwami dylatacyjnymi jest nie większa niż wartości podane w
tablicy 34.
Odległości między przerwami dylatacyjnymi podane w tablicy 34 nie dotyczą obiektów wznoszonych na terenach eksploatacji
górniczej, a także przypadków, kiedy wprowadzanie dylatacji jest konieczne z innych względów niż wpływy termiczno-
skurczowe.
9.7.3 Konstrukcja przerw dylatacyjnych
Przerwy dylatacyjne w budynkach ze ścianami betonowymi powinny być wykonane przez przecięcie w jednym przekroju
wszystkich elementów konstrukcyjnych od wierzchu fundamentu do dachu. Masywne konstrukcje inżynierskie, np. mury
oporowe, powinny być przecięte na całej wysokości.
Tablica 34 - Maksymalne odległości między przerwami dylatacyjnymi
Rodzaj konstrukcji
Odleglość między
dylatacjami, [m]
Konstrukcje poddane wahaniom temperatury zewnętrznej:
a) ściany nie zbrojone
b) ściany zbrojone
c) żelbetowe konstrukcje szkieletowe
d) dachy nieocieplane, gzymsy
5
20
30
20
Ogrzewane budynki wielokondygnacyjne
a) wewnętrzne ściany i stropy monolityczne betonowane w jednym ciągu
30
b) jak wyżej - betonowane odcinkami nie większymi niż 15 m, z pozostawieniem przerw
do późniejszego betonowania
jak w przypadku
wewnętrzych ścian
prefabryk.
c) wewnętrzne ściany prefabrykowane z zewnętrznymi ścianami wielowarstwowymi
50
d) jak wyżej - ze ścianami zewnętrznymi z betonu komórkowego
40
e) jak wyżej - z lekkimi ścianami zewnętrznymi, podłużna ściana usztywniająca w
części środkowej budynku
70
f) jak wyżej - ze ścianami usztywniającymi w częściach skrajnych budynku
50
g) prefabrykowane konstrukcje szkieletowe i konstrukcje monolityczne z usztywnieniem
w części środkowej budynku
jak w przypadku
wewnętrznych ścian
prefabryk.
h) monolityczne konstrukcje szkieletowe ze ścianami usztywniającymi w częściach
skrajnych budynku - odpowiednio
jak dla a) lub b)
Część 10 Strona 17

Ogrzewane jednokondygnacyjne hale żelbetowe bez ścian usztywniających lub tylko w
części środkowej z zewnętrznymi ścianami o małej sztywności - w zależności od
wysokości konstrukcji h
a) h ≤ 5 m
b) 5 < h < 8 m
c) h ≥ 8 m
60
10 + 10h
90
W ścianach monolitycznych niezbędne jest zbrojenie przeciwskurczowe zgodnie z p. 6.2, ze zwróceniem szczególnej uwagi
na zbrojenie nadproży i wokół otworów.
Część 10 Strona 18

Załącznik A
(normatywny)
PEŁZANIE BETONU
Współczynnik φ(t,t
o
) pełzania betonu obliczać można z następującego wzoru
(A.1)
t - wiek betonu w rozważanej chwili (w dniach),
t
o
- wiek betonu w chwili obciążenia (w dniach),
φ
o
- podstawowy współczynnik pełzania,
β
c
(t - t
o
) - współczynnik określający postęp pełzania po przyłożeniu obciążenia.
Podstawowy współczynnik pełzania φ
o
określony jest wzorem
(A.2)
w którym:
(A.3)
(A.4)
(A.5)
We wzorach (A.3) i (A.4) przyjęto następujące oznaczenia:
RH - względna wilgotność powietrza w (procentach),
h
o
- sprowadzony wymiar przekroju elementu (w milimetrach), wyznaczony ze wzoru
(A.6)
w którym:
A
c
- oznacza pole przekroju elementu, a u - obwód przekroju poddany działaniu powietrza,
f
cm
- średnia wytrzymałość betonu po 28 dniach (w MPa).
Współczynnik β
c
(t - t
o
), określający postęp pełzania betonu po przyłożeniu obciążenia wyznaczyć można ze wzoru
(A.7)
w którym:
t-t
o
- czas trwania obciążenia (w dniach),
β
H
- współczynnik zależny od wilgotności względnej powietrza RH w procentach oraz sprowadzonego wymiaru przekroju
elementu h
o
w milimetrach, określony wzorem
(A.8)
Wpływ rodzaju cementu na współczynnik pełzania betonu uwzględnić można przyjmując we wzorze (A.5) wartość t
o
obliczoną z następującego wzoru
Część 11 Strona 1
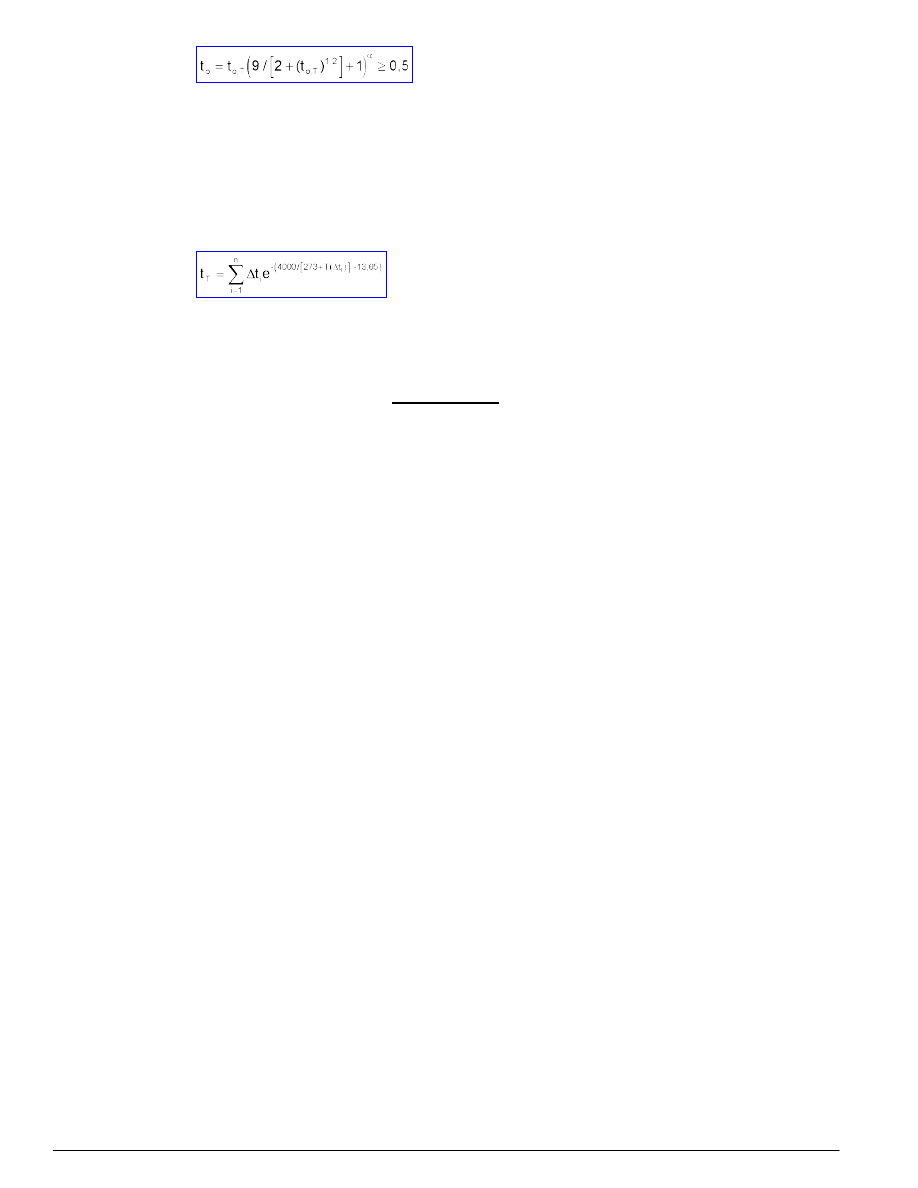
(A.9)
w którym:
t
o,T
- wiek betonu w chwili obciążenia, skorygowany z uwagi na temperaturę zgodnie ze wzorem (A.10),
α - wykładnik potęgowy, zależny od rodzaju cementu; przyjmuje się:
α = -1 - dla cementów wolnotwardniejących,
α = 0 - dla cementów zwykłych i szybkotwardniejących,
α = 1 - dla szybkotwardniejących cementów wysokiej wytrzymałości.
Wpływ temperatury w przedziale od 0°C do 80°C na twardnienie betonu uwzględnić można określając wiek betonu t według
następującego wzoru
(A.10)
w którym:
t
T
- wiek betonu określony z uwzględnieniem temperatury, zastępujący wartość t w odpowiednich wzorach,
∆t
i
- liczba dni z temperaturą T,
T(∆t
i
) - temperatura (w °C), występująca w przedziale czasu ∆t
i
.
Część 11 Strona 2

Załącznik B
(normatywny)
SKURCZ BETONU
Odkształcenie skurczowe ε
cs
(t,t
s
) betonu obliczać można z następującego wzoru
(B.1)
w którym:
t - wiek betonu w rozważanej chwili (w dniach),
t
s
- wiek betonu na początku skurczu (w dniach),
ε
cso
- podstawowy współczynnik skurczu,
β
s
(t-t
s
) - współczynnik określający postęp skurczu.
Podstawowy współczynnik skurczu określony jest wzorem
(B.2)
w którym:
ε
s
(f
cm
) - współczynnik uwzględniający wpływ średniej wytrzymałości f
cm
betonu po 28 dniach (w MPa) na odkształcenie
skurczowe, wyrażony wzorem
(B.3)
β
RH
- współczynnik zależny od wilgotności względnej powietrza RH (w procentach); wartość tego współczynnika dla
40% ≤ RH ≤ 99% wyznacza się ze wzoru
(B.4)
Współczynnik β
sc
we wzorze (B.3) zależy od rodzaju cementu; przyjmuje się:
β
sc
= 4 - dla cementów wolnotwardniejących,
β
sc
= 5 - dla cementów zwykłych i szybkotwardniejących,
β
sc
= 8 - dla szybkotwardniejących cementów wysokiej wytrzymałości.
Współczynnik β
s
(t - t
s
) określający postęp skurczu w czasie obliczyć można z następującego wzoru
(B.5)
w którym:
t - t
s
- czas trwania skurczu (w dniach),
h
o
- sprowadzony wymiar przekroju elementu (w milimetrach), określony ze wzoru (A.6) w załączniku A.
Część 12 Strona 1
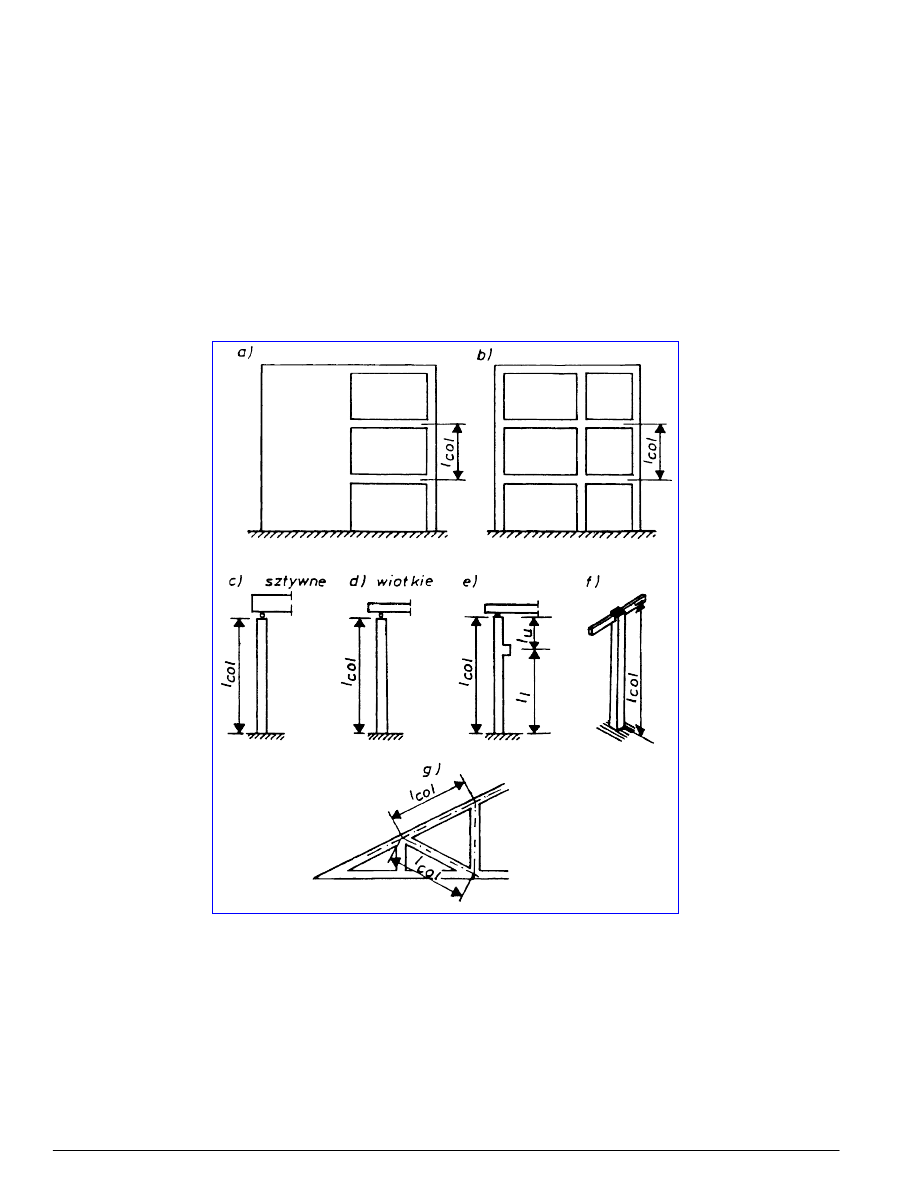
Załącznik C
(normatywny)
Ś
CISKANIE
Długości obliczeniowe l
0
słupów wielokondygnacyjnych budynków szkieletowych i jednokondygnacyjnych budynków
halowych, słupów estakad oraz ściskanych elementów dźwigarów kratowych mogą być przyjmowane według tablicy C.1
(rysunek C.1).Wartości zamieszczone w kolumnie 3 należy przyjmować przy sprawdzaniu elementów w płaszczyźnie
rozpatrywanego układu konstrukcyjnego lub w płaszczyźnie konstrukcji nośnej przekrycia, a dla słupów estakad - w
płaszczyźnie prostopadłej do osi estakady, wartości zamieszczone w kolumnie 4 - przy sprawdzaniu elementów w
płaszczyźnie prostopadłej do płaszczyzny układu (konstrukcji nośnej przekrycia) i w płaszczyźnie równoległej do osi
estakady.
Rysunek C.1 - Długości słupów przyjmowane przy wyznaczaniu wartości I
0
Tablica C.1 - Długości obliczeniowe I
0
Część 13 Strona 1
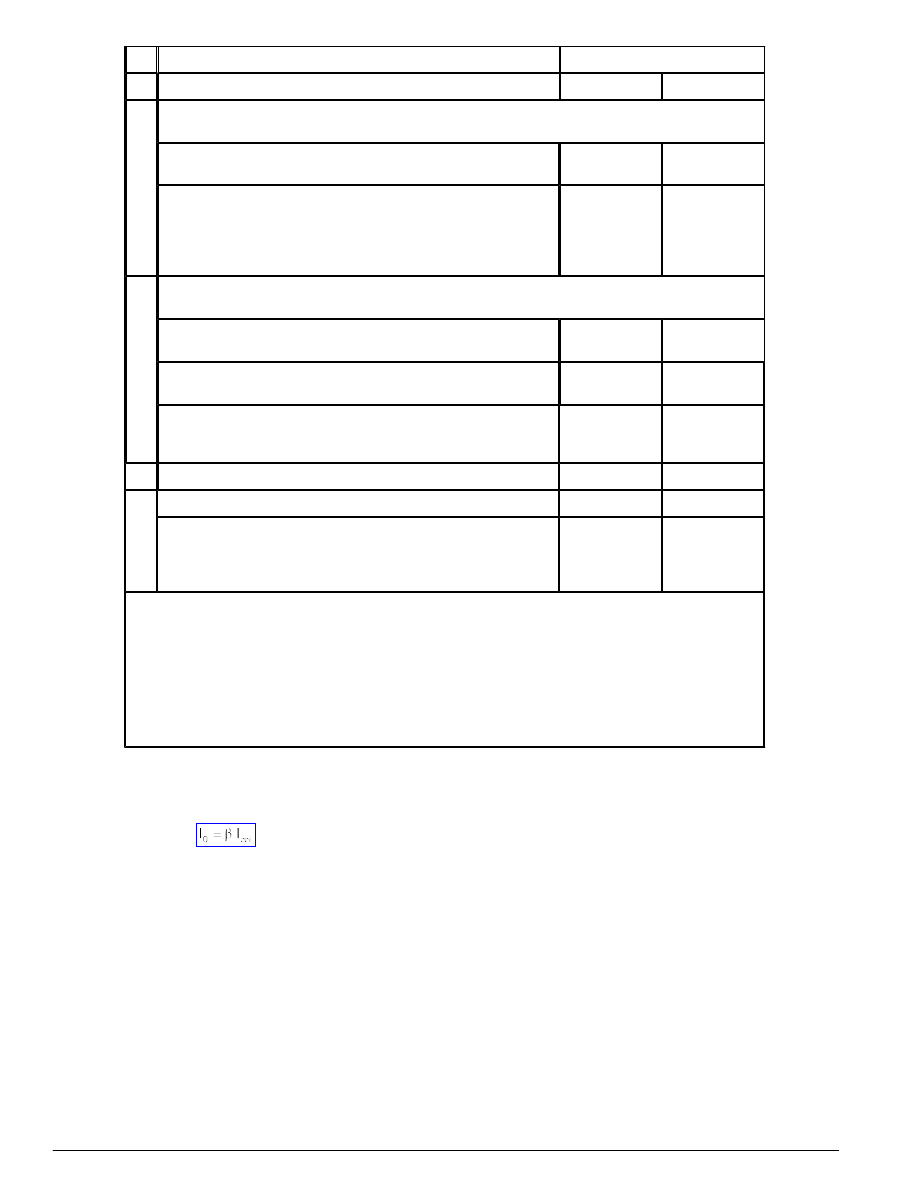
Lp.
Rodzaj elementu
I
0
1
2
3
4
1
Słupy w wielokondynacyjnych budynkach szkieletowych ze stropami o konstrukcji monolitycznej lub ze
zmonolityzowanych elementów prefabrykowanych:
a) budynki, w których siły poziome przenoszone są przez ustroje
usztywniające w postaci ścian, trzonów itp. (rysunek C.1a)
0,7 I
col
0,7 I
col
b) budynki, w których siły poziome przenoszone są przez szkielet o
węzłach sztywnych z tym, że szerokość budynku jest nie mniejsza
niż 1/3 jego wysokości, liczba naw jest nie mniejsza od dwóch, a
sztywność rygli (w obydwu kierunkach) jest nie mniejsza niż
sztywność słupów (rysunek C. 1b)
1,0 I
col
1,0 I
col
2
Słupy w jednokondygnacyjnych budynkach halowych, utwierdzone w stopach fundamentowych i
połączone z konstrukcją dachu w sposób przegubowy
1)
a) budynki bez suwnic, przekryte dachami o konstrukcji sztywnej, np.
z prefabrykowanych płyt żelbetowych (rysunek C.1c)
1,6 I
col
1,6 I
col
b) budynki bez suwnic, przykryte dachami z elementów wiotkich
(rysunek C. 1d)
2,0 I
col
2,0 I
col
c) budynki z suwnicami
2), 4)
(rysunek C.1e)
- dolny odcinek słupa
- górny odcinek słupa
1,6 I
l
2,5 l
u
1,2 I
l
2,0 I
u
3
Słupy estakad
3)
(rysunek C.1f)
2,0 I
col
1,8 I
col
4
Ś
ciskane elementy dźwigarów kratowych (rysunek C.1g)
- pas górny
- krzyżulce i słupki
I
col
- odległość między środkami węzłów,
I
n
- odległość między stężeniami poprzecznymi dźwigarów
1,0 I
col
0,8 I
col
1,0 I
n
1,0 I
col
1)
Wartości podane w kolumnie 4 odpowiadają założeniu, że w płaszczyźnie prostopadłej do konstrukcji nośnej
przekrycia - górne końce słupów połączone są elementami sztywnymi.
2)
Poza sprawdzeniem nośności dolnego i górnego odcinka słupa, przy przyjęciu długości obliczeniowych
podanych w kolumnie 3 i przy uwzględnieniu maksymalnego obciążenia suwnicami - należy także sprawdzać
nośność całego słupa, nie uwzględniając obciążenia suwnicami i przyjmując długości obliczeniowe jak dla
budynków bez belek podsuwnicowych, wg 2a) lub 2b).
3)
W przypadku zastosowania elementów ograniczających przemieszczenie słupów w płaszczyźnie estakady,
wartości podane w kolumnie 4 mogą być odpowiednio zmniejszone, lecz do wartości nie mniejszej niż 1,0 I
col
.
4)
Dotyczy słupów obciążonych belkami podsuwnicowymi, prostopadłymi do płaszczyzny wsporników.
Długości obliczeniowe l
0
słupów występujących w żelbetowych układach ramowych mogą być wyznaczane według wzoru
(C.1)
Wartości współczynnika β należy obliczać według wzorów podanych w tablicy C.2.
Tablica C.2 - Wartości współczynnika β
β
β
β
Część 13 Strona 2
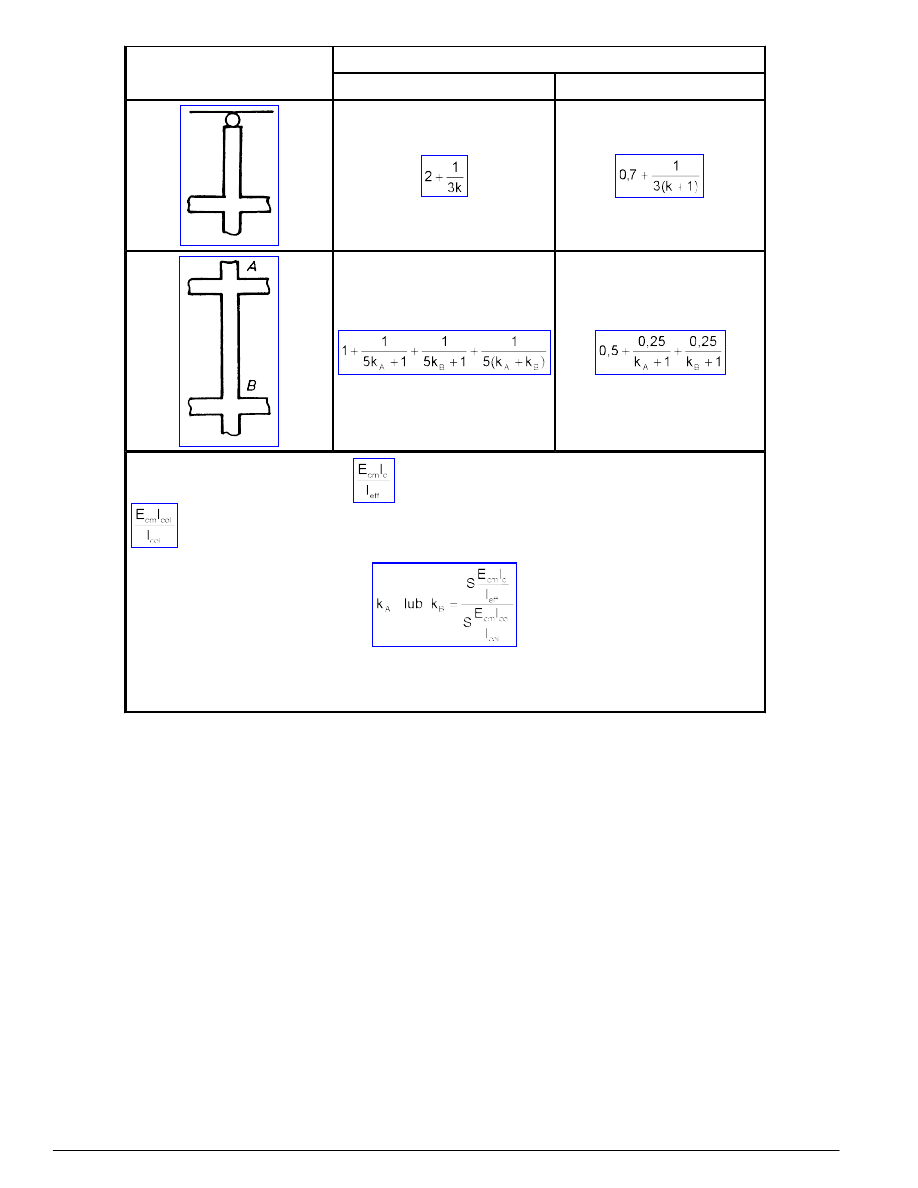
Sposób podparcia końców słupa
Układy o węzłach
przesuwnych
nieprzesuwnych
k - stosunek sumy sztywności giętnych
elementów poziomych (rygli) do sumy sztywności giętnych
słupów zamocowanych w rozpatrywanym węźle ramy
k
A
- dla węzła górnego, k
B
- dla węzła dolnego.
W przypadku zamocowania słupa w stopie k = ∞.
Część 13 Strona 3
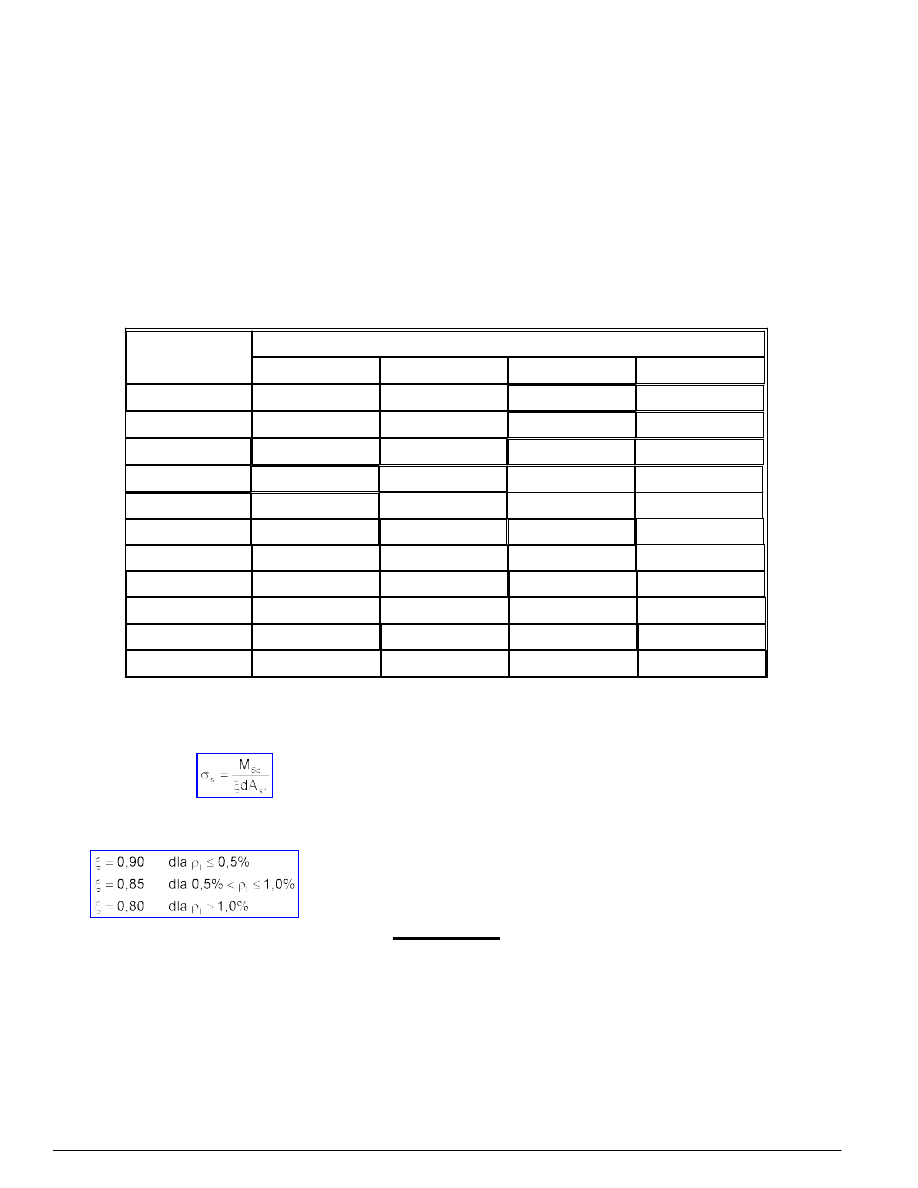
Załącznik D
(normatywny)
SZEROKOŚĆ RYS PROSTOPADŁYCH
Szerokość rys prostopadłych w elementach zginanych o przekroju prostokątnym, zbrojonych stalą żebrowaną, przy wartości
stosunku d/h = 0,85 ÷ 0,95 - uważać można za ograniczoną do wartości w
lim
= 0,3 mm, jeśli maksymalna średnica prętów
zbrojenia jest nie większa niż podano w tablicy D.1.
Tablica D.1- Maksymalna średnica prętów zbrojenia (w milimetrach)
σ
s
MPa
ρ
l
= A
s1
/bd(%)
0,25
0,50
0,75
1,00
150
32
32
32
32
175
25
32
32
32
200
18
25
32
32
225
16
22
32
32
250
12
18
28
32
275
10
16
22
32
300
8
14
20
28
325
6
12
18
24
350
5,5
10
16
20
375
5
9
14
18
400
4,5
8
12
16
Naprężenia σ
s
w zbrojeniu rozciąganym obliczać można ze wzoru:
(D.1)
gdzie:
M
Sd
- moment wyznaczony dla kombinacji obciążeń długotrwałych (γ
f
= 1,0)
Część 14 Strona 1
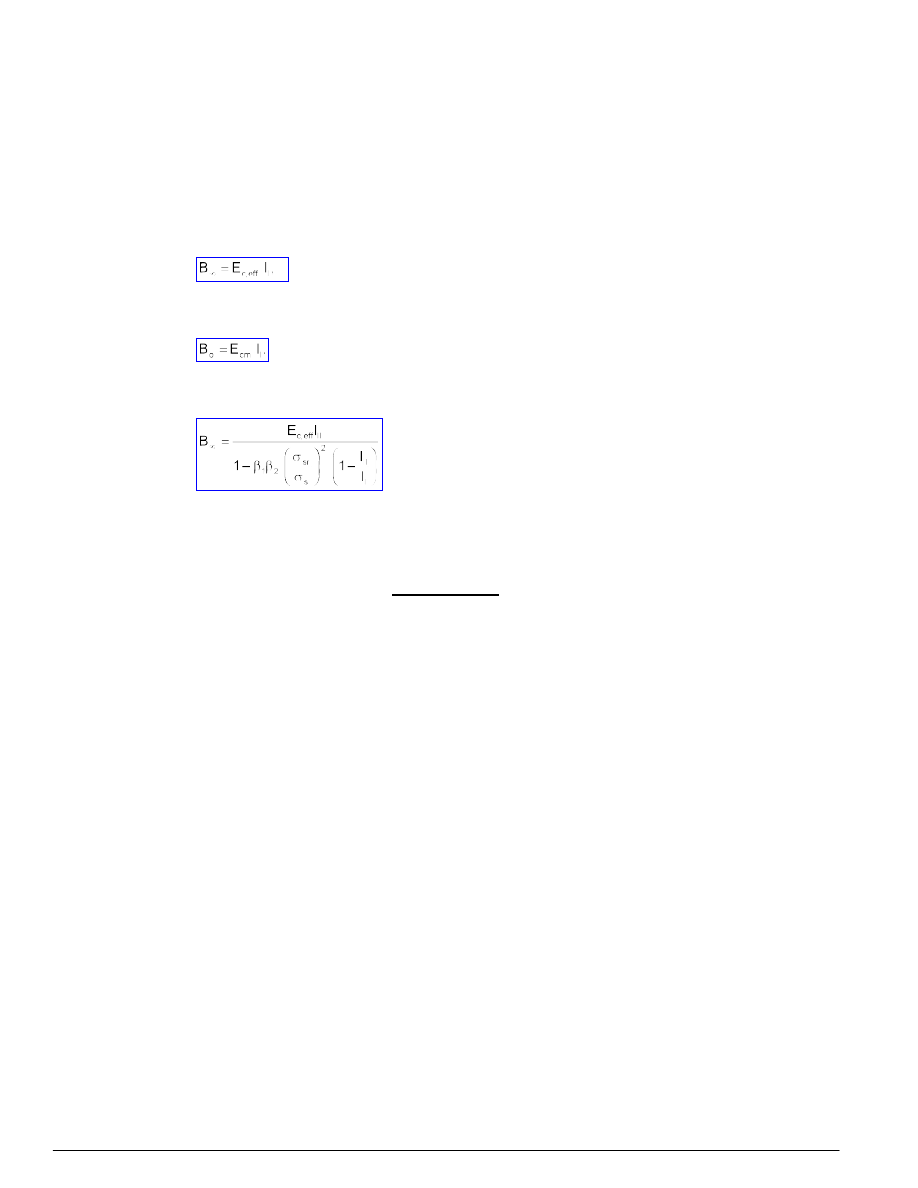
Załącznik E
(normatywny)
SZTYWNOŚĆ ELEMENTÓW ZGINANYCH
Efektywny moduł sprężystości betonu E
c,eff
oraz sprowadzone momenty bezwładności w fazie l (I
l
) i w fazie II (I
ll
) wyznacza
się zgodnie z zasadami określonymi w p. 6.1.
Sztywność elementów niezarysowanych przy obciążeniu długotrwałym wyznacza się ze wzoru
(E.1)
a przy obciążeniu krótkotrwałym ze wzoru
(E.2)
Sztywność elementów zarysowanych przy obciążeniu długotrwałym można wyznaczać ze wzoru
(E.3)
w którym: β
1
, β
2
, σ
s
i σ
sr
są zmiennymi określonymi w objaśnieniach do wzoru (95).
Sztywność B
o
elementów zarysowanych przy obciążeniu krótkotrwałym wyznacza się zastępując we wzorze (E.3) E
c,eff
przez
E
cm
i nadając zmiennym β
2
, σ
s,
I
l
i I
ll
wartości odpowiednie przy obciążeniu krótkotrwałym.
We wzorze (E.3) stosunek σ
sr
/σ
s
można zastąpić stosunkiem M
cr
/M
Sd
.
Część 15 Strona 1
Document Outline
- Polska norma PN-B-03264:1999
- Spis treŚci
- 1. Wstęp
- 2. Beton
- 3. Stal
- 4. Zasady projektowania
- 5. Stany graniczne nosnosci konstrukcji betonowych i żelbetowych
- 6. Stany graniczne użytkowalnosci elementów konstrukcji
- 7. Konstrukcje sprężone, konstrukcje poddane działaniu obciążeń wielokrotnie zmiennych i konstrukcje zespolone
- 8. Wymagania i zalecenia dotyczące zbrojenia konstrukcji
- 9. Projektowanie konstrukcji
- 9.1 Płyty
- 9.1.1.1 Minimalne gruboŚci płyt
- 9.1.1.2 GłębokoŚć oparcia płyt na podporze
- 9.1.1.3 Zbrojenie płyt
- 9.1.1.4 Zbrojenie na przebicie
- 9.1.2 Obliczenia statyczne
- 9.1.2.1 Zasady ogólne
- 9.1.2.2 RozpiętoŚć obliczeniowa
- 9.1.2.3 Obliczanie płyt ciągłych jednokierunkowo zbrojonych
- 9.1.2.4 Obliczanie prostokątnych płyt dwukierunkowo zbrojonych
- 9.2 Stropy gęstożebrowe
- 9.3 Belki
- 9.3.1 Konstrukcja belek
- 9.3.1.1 Wymairy belek
- 9.3.1.2 GłębokoŚć oparcia belek na podporze
- 9.3.1.3 Połączenie belki z podciągiem
- 9.3.1.4 Podciągi z wbetonowanymi końcami belek prefabrykowanych
- 9.3.1.5 Zbrojenie belek
- 9.3.2 Obliczenia statyczne belek
- 9.3.2.1 Zasady ogółne
- 9.3.2.2 Obliczanie belek ciągłych
- 9.4 Wsporniki krótkie
- 9.5 Słupy
- 9.6 Ograniczenie zakresu szkód wywołanych przez oddziaływania wyjątkowe
- 9.7 Wpływ temp i skurczu betonu na odkształcenia konstrukcji.Przerwy dylatacyjne
- 9.1 Płyty
- Załącznik A - Pełzanie betonu
- Załącznik B - Skurcz betonu
- Załącznik C - Ściskanie
- Załącznik D - SzerokoŚć rys prostopadłych
- Załącznik E - SztywnoŚć elementów zginanych
Wyszukiwarka
Podobne podstrony:
PN B 03264 2002 Konstrukcje betonowe zelbetowe i sprezone Obliczenia statyczne i projektowanie c2
Norma Pn B 03264 2002 Konstrukcje Betonowe, zelbetowe I Sprobne Obliczenia Statyczne I Projektowanie
PN B 03264 2002 Konstrukcje betonowe zelbetowe i sprezone Obliczenia statyczne i projektowanie c3
PN B 03264 2002 Konstrukcje betonowe zelbetowe i sprezone Obliczenia statyczne i projektowanie cz
PN B 03264 2002 Konstrukcje betonowe zelbetowe i sprezone Obliczenia statyczne i projektowanie c5
PN B 03264 2002 Konstrukcje betonowe zelbetowe i sprezone Obliczenia statyczne i projektowanie c4
PN B 03264 2002 Konstrukcje betonowe zelbetowe i sprezone Obliczenia statyczne i projektowanie c2
Norma Pn B 03264 2002 Konstrukcje Betonowe, zelbetowe I Sprobne Obliczenia Statyczne I Projektowanie
PN B 03002 1999 Konstrukcje murowe niezbrojone Projektowanie i obliczanie
PN B 03340 1999 Konstrukcje murowe zbrojone Projektowanie i obliczanie
Pn B 03002 1999 Konstrukcje Murowe Niezbrojone Projektowanie
więcej podobnych podstron