AKADEMIA GÓRNICZO – HUTNICZA

im. Stanisława Staszica w Krakowie

Wydział Inżynierii Mechanicznej i Robotyki

Systemy Wizyjne

Sprawozdanie z laboratorium nr 4 MatLab

Damian Bubak

grupa 23, rok III, Mechatronika (IMiR)

Data wykonania ćw: 31.03.14r.

Godzina 10:30

Katedra Robotyki i Mechatroniki

Systemy wizyjne.

Matlab_Cw_3_4

Temat:

Analiza obrazu w programie Matlab

Cel ćwiczenia : Nabycie umiejętności w implementacji zaawansowanych procedur analizy obrazu.

Metody wstępnego przetwarzania i analizy obrazów , cechy obrazu , współczynniki kształtu

,

funkcje

Matlab'a

Prowadzący: dr inż. Piotr KOHUT

Grupa:

Imię i nazwisko:

Data:

Uwagi:

1.

Dla obrazów z Ćw1 w oparciu o techniki segmentacji obszarowej wyznaczyć zadane
współczynniki kształtu (współczynnik Malinowskiej, Feret’a, Haralick’a) oraz pola
powierzchni, środki ciężkości i orientację analizowanych obrazów.

Uwaga: cały kod znajduje się w dodatkowym m-pliku.

Poniżej zamieszczono obraz który został poddany dalszej analizie:

Poniżej znajduje sie obraz na którym zaznaczono środki m.in. środki ciężkości oraz orientacje
obiektów:

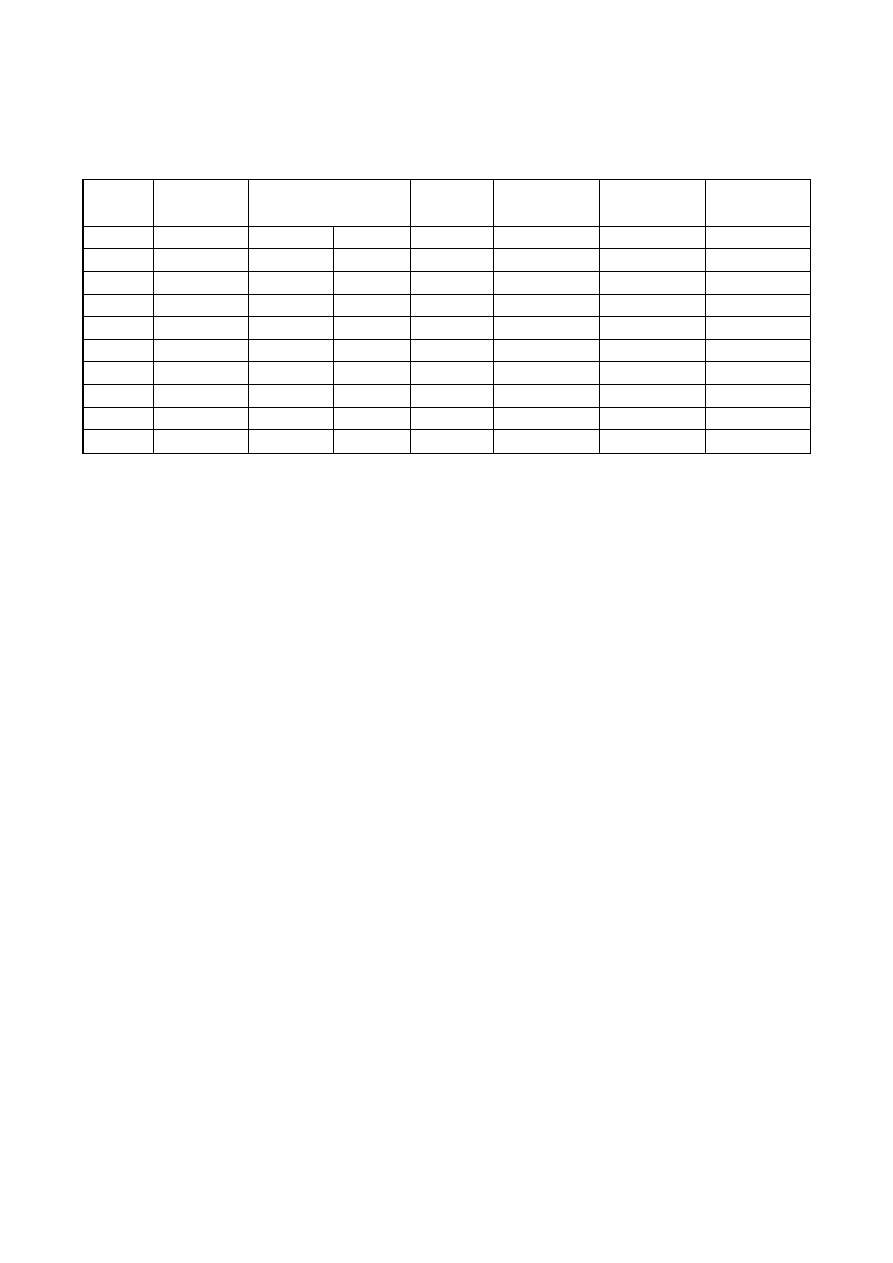
Zestawienie obliczonych współczynników oraz pozostałych cech obiektów w postaci tabeli:

Pole
powierzchni

Środek ciężkości

Orientacja

Współczynnik

Malinowskiej

Współczynnik

Fereta

Współczynnik

Haralicka

1

8424.0000

139.5000

78.5000

0.0000

0.3032

3.1154

0.9300

2 22702.0000

204.5000 300.0043

0.0000

0.1500

2.0504

0.9324

3 17891.0000

197.0302 524.0332

73.1233

0.0480

1.0000

0.9936

4 17950.0000

471.9364 202.8036

-29.6612

0.1947

1.0000

0.9909

5 14539.0000

504.8058 440.7033

-18.6189

0.4553

1.8211

0.9185

6 13689.0000

713.0000 305.0000

0.0000

0.1187

1.0000

0.9967

7 26617.0000

777.7446 106.9645

-29.1862

0.0768

1.2695

0.9982

8 13533.0000

865.4423 508.1669

2.7378

0.1541

1.1298

0.9959

9 10113.0000

953.5085 348.9995

0.0876

0.6030

1.6396

0.9981

10 13345.0000 1038.1128 200.8029

9.1389

0.2576

2.2941

0.9988

Z danych przedstawionych powyżej można wywnioskować że współczynnik malinowskiej
pozwala rozpoznać koło dla którego przyjmuje wartości bliskie zeru (tutaj 0.04). Ma to swoje
uzasadnienie w teorii gdyż właśnie współczynnik ten jest nazywany współczynnikiem krągłości.
Widzimy również że niską wartość (0.15) ma rónież elipsa ale już np. prostokąt ma znacznie
wyższą równą (0.30).
Współczynnik Fereta który jest stosunkiem największych średnic obiektu w poziomie i pionie
osiąga wartości (1.00) dla koła, kwadratu oraz około (1.00) dla innych niesmukłych figur. Zatem
współczynnik ten może sugerować że mamy do czynienia z kwadratem lub kołem lecz nie daje
pewności. Aby osiągnąć precyzyjną informacje o obiekcie należy obserwować większą liczbę
współczynników.
Współczynnik Haralicka jest bardzo dokładnym współczynnikiem lecz czas jego obliczania jest
o wiele dłuższy niż pozostałych 2 wpółczynników z racji skomplikowanego algorytmu jego
obiczania. Np. wartość około (0.93) tego współczynnika może wskazywać że obiektem jest
prostokąt lub trójkąt prostokątny.

2.

Dokonać obrotu obiektów obrazu o zadane kąty (45, 90 deg) a następnie ponownie
wyznaczyć zadane cechy obrazu.

Poniżej znajdują się obrazy obróconych obiektów o zadane kąty:

Obrót o 45 deg:

Obrót o 90 deg:

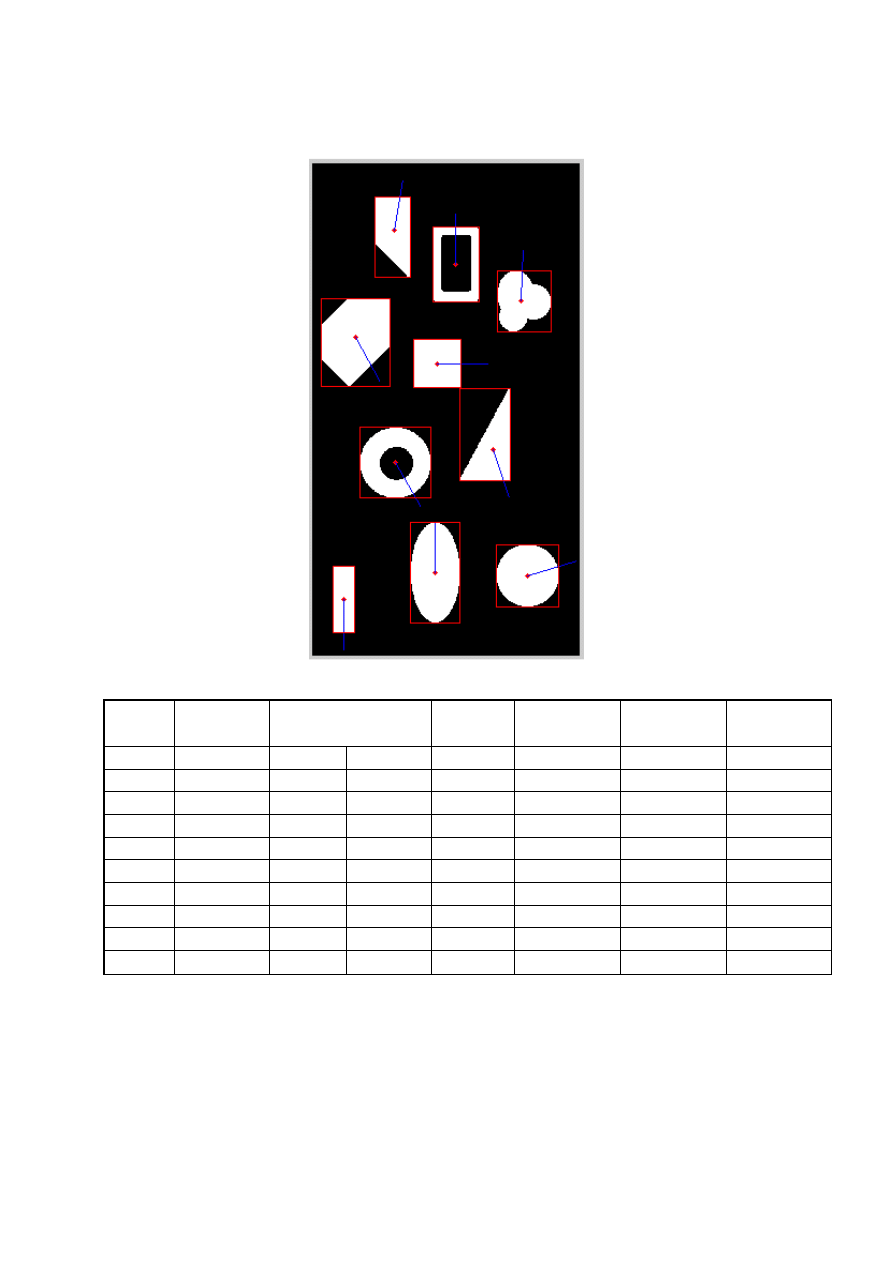
Zestawienie obliczonych współczynników oraz pozostałych cech obiektów w postaci tabeli:
Tabela dla obrotu o 45 deg:

Pole
powierzchni

Środek ciężkości

Orientacja

Współczynnik

Malinowskiej

Współczynnik

Fereta

Współczynnik

Haralicka

1

8473.0000 154.2489

806.2489

45.0000

0.3020

1.0000

0.9981

2 22708.0000 356.9919

917.0078

44.9973

0.1771

1.0000

0.9949

3 17899.0000 510.0984 1080.6946

-29.9389

0.1078

1.0000

0.9979

4 17946.0000 477.3054

659.1677

17.8505

0.2729

1.0000

0.9812

5 14602.0000 669.1398

804.1069

26.3759

0.4984

1.5123

0.9280

6 13613.0000 720.0000

561.0000

0.0000

0.1215

1.0000

0.9800

7 26613.0000 625.6400

375.1839

15.9172

0.1315

1.4167

0.9799

8 13533.0000 971.5335

596.8214

47.6861

0.2141

1.0000

0.9959

9 10114.0000 921.4896

422.4566

45.0534

0.6111

1.0000

0.9962

10 13324.0000 876.3338

257.5311

54.1064

0.2645

0.7208

0.9972

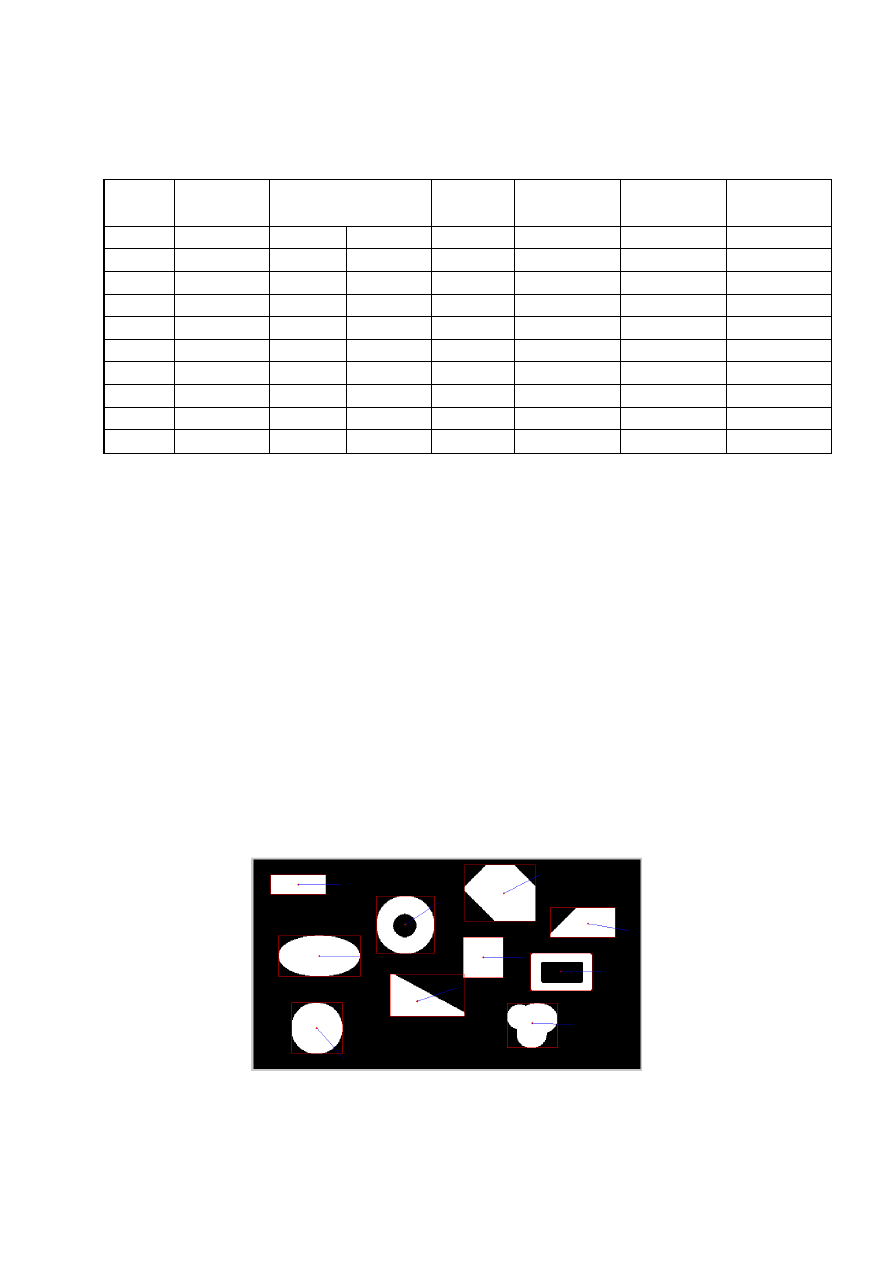
Tabela dla obrotu o 90 deg:

Pole
powierzchni

Środek ciężkości

Orientacja

Współczynnik

Malinowskiej

Współczynnik

Fereta

Współczynnik

Haralicka

1

8424.0000

78.5000 1061.5000

90.0000

0.3032

0.3210

0.9995

2 22702.0000 300.0043

996.5000

-90.0000

0.1500

0.4877

0.9980

3 17891.0000 524.0332 1003.9698

-16.8767

0.0480

1.0000

0.9970

4 17950.0000 202.8036

729.0636

60.3388

0.1947

1.0000

0.9976

5 14539.0000 440.7033

696.1942

71.3811

0.4553

0.5491

0.9815

6 13689.0000 305.0000

488.0000

0.0000

0.1187

1.0000

0.9842

7 26617.0000 106.9645

423.2554

60.8138

0.0768

0.7877

0.9860

8 13533.0000 508.1669

335.5577

-87.2622

0.1541

0.8851

0.9826

9 10113.0000 348.9995

247.4915

-89.9124

0.6030

0.6099

0.9495

10 13345.0000 200.8029

162.8872

-80.8611

0.2576

0.4359

0.9222

Po przeprowadzeniu analizy można powiedzieć że współczynnik Malinowskiej jest nie wrażliwy
na zmianę orientacji obiektu gdyż w większości przypadków różnice w wartościach są
pomijalnie małe co widac w tabelach.

Współczynnik Fereta natomiast w ogólnym przypadku jest wrażliwy na zmianę orientacji
obiektów co doskonale widac na przykładzie prostokąta nr. 1. Na początku miał wartość (3.11)
po obrocie o 45 deg (1.00) a po obrocie o 90 deg (0.32). Warto tutaj jednak zauważyć że dla
niektórych wyjątkowych figur takich jak koło czy kwadrat jego wartość jest stała.

Współczynnik Haralicka jest niewrażliwy na zmianę kształtu. W większości przypadków różnice
są bardzo niewielkie.

3.

Dokonać zmiany wielkości obiektów obrazu o zadaną wartość (0.5x, 2.0x) a następnie
ponownie wyznaczyć zadane cechy obrazu.

Poniżej znajdują się obrazy przeskalowanych obiektów:



Skalowanie 0.5x:

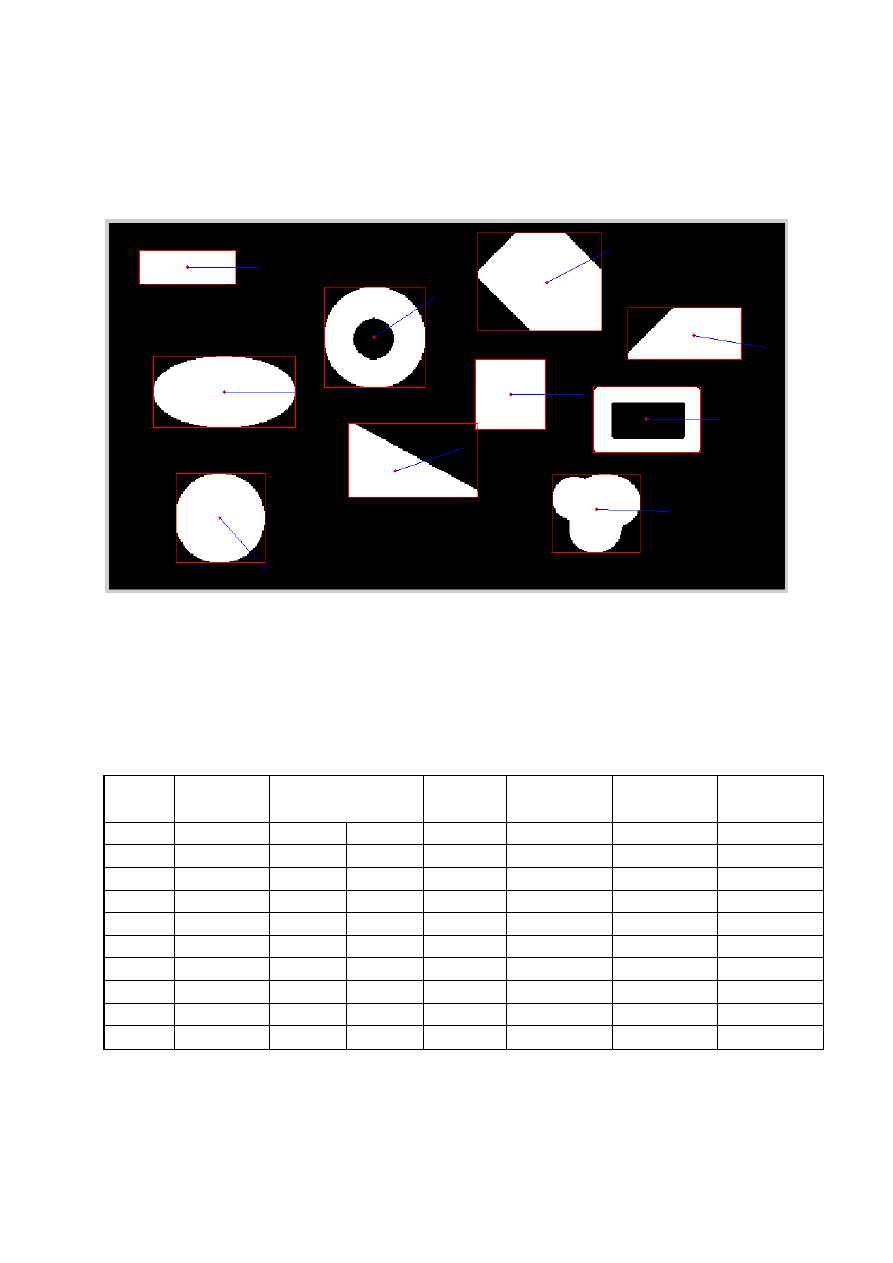
Skalowanie 2.0x:

Zestawienie obliczonych współczynników oraz pozostałych cech obiektów w postaci tabeli:
Tabela dla skalowania 0.5x:

Pole
powierzchni

Środek ciężkości

Orientacja

Współczynnik

Malinowskiej

Współczynnik

Fereta

Współczynnik

Haralicka

1

2550.0000

70.0000

39.5000

0.0000

0.2625

2.8333

0.9247

2

6328.0000 102.5000 150.2276

0.0000

0.2352

2.0000

0.9284

3

5013.0000

98.7796 262.2340

48.5276

0.0400

1.0000

0.9929

4

5372.0000 236.1385 101.7759

-33.3846

0.1883

1.0000

0.9899

5

4264.0000 254.0886 220.6986

-18.6276

0.4486

1.7692

0.9171

6

3844.0000 356.5000 152.5000

0.0000

0.1102

1.0000

0.9963

7

7353.0000 388.6812

53.5683

-27.7011

0.1072

1.2644

0.9980

8

3895.0000 432.9271 254.3859

2.0194

0.1160

1.1159

0.9954

9

3448.0000 477.3802 174.4313

0.0939

0.4323

1.6102

0.9980

10

3826.0000 518.9300 100.5361

9.3064

0.2157

2.1957

0.9987

Tabela dla skalowania 2.0x:

Pole
powierzchni

Środek ciężkości

Orientacja

Współczynnik

Malinowskiej

Współczynnik

Fereta

Współczynnik

Haralicka

1

36300.0000

278.5000

156.5000

0.0000

0.2970

3.0000

0.9273

2

95200.0000

408.5000

599.5080

0.0000

0.2473

2.0246

0.9291

3

75224.0000

393.5588 1047.5651

72.7201

0.1570

1.0000

0.9932

4

77872.0000

943.2320

405.3390

-29.5331

0.2934

1.0000

0.9904

5

62356.0000 1011.2811

880.7567

-18.6179

0.5138

1.8016

0.9234

6

57600.0000 1425.5000

609.5000

0.0000

0.1237

1.0000

0.9965

7 111052.0000 1554.4096

213.3134

-28.6645

0.1892

1.2647

0.9980

8

57608.0000 1730.2920 1015.9370

2.1458

0.2572

1.1269

0.9956

9

46500.0000 1907.2494

697.8653

0.0635

0.5456

1.6228

0.9981

10

56776.0000 2074.3611

401.3336

9.1864

0.3011

2.2500

0.9988

Po dokonaniu analizy powyższych danych można powiedzieć że wszystkie z badanych
współczynników kształtu są niewrażliwe na zmiane rozmiaru obiektów.

4.

Wnioski końcowe dla przejżystości zostaną sformułowane w postaci tabeli:

Czy:

Współczynnik

Malinowskiej

Współczynnik

Fereta

Współczynnik

Haralicka

nadaje się do

rozpoznawania

obrazów

TAK

NIE

TAK

jest wrażliwy

na obroty

obiektów

NIE

TAK

NIE

jest wrażliwy

na zmiane

rozmiarów

obiektów

NIE

NIE

NIE

Tabela ta została przygotowana na podstawie obserwacji współczynników przy operacjach
skalowania i obracania obiektów. Szczegółowe wnioski znajdują się po każdym punkcie
ć

wiczenia. Warto w tym miejscu dodać że współczynnik Fereta nie nadaje się do rozpoznawania

obrazów gdyż jego wartości mogą zmieniać się znacząco przy zmianie orientacji obiektu. Bardzo
dobrym przykładem jest prostokąt dla którego po obrocie o 45 deg wartość wsp. Fereta wynosiła
(1) która może wskazyważe jest to koło lub kwadrat. W związku z tym że pozostałe 2
współczynniki nie są wrażliwe na zmianę orientacji ani na zmianę wielkości obiektów mogą być
one wykorzystane do rozpoznawania obrazów.