AKADEMIA GÓRNICZO – HUTNICZA

im. Stanisława Staszica w Krakowie

Systemy Wizyjne

Sprawozdanie z laboratorium nr 2 MatLab

Damian Bubak

grupa 23, rok III, Mechatronika (IMiR)

Data wykonania ćw: 17.03.14r.

Godzina 10:30

1.Etapy algorytmu segmentacji i analizy obrazu
a) pierwszym krokiem była konwersja obrazu kolorowego do obrazu w skali szarości.
b) kolejnym krokiem było wykonanie histogramu i na jego podstawie określenie progów
binaryzacji
c) następnie wykonano binaryzacje oraz filtracje w celu usunięcia szumów, nierówności itp.
d) przeprowadzenie segmentacji obrazu i wyodrębnienie poszczególnych obiektów
e) ostatnim krokiem było wydobycie cech (np. orientacji, położenia) obiektów znajdujących się
na obrazie.

Ad a) Wczytanie obrazu do przestrzeni roboczej MatLaba oraz wyświetlenie go. Polecenia:

img = imread(

'photo1.jpg'

);

figure(1), imshow(img);

Konwersja obrazu do skali szarości. Polecenie:

gray = rgb2gray(img);

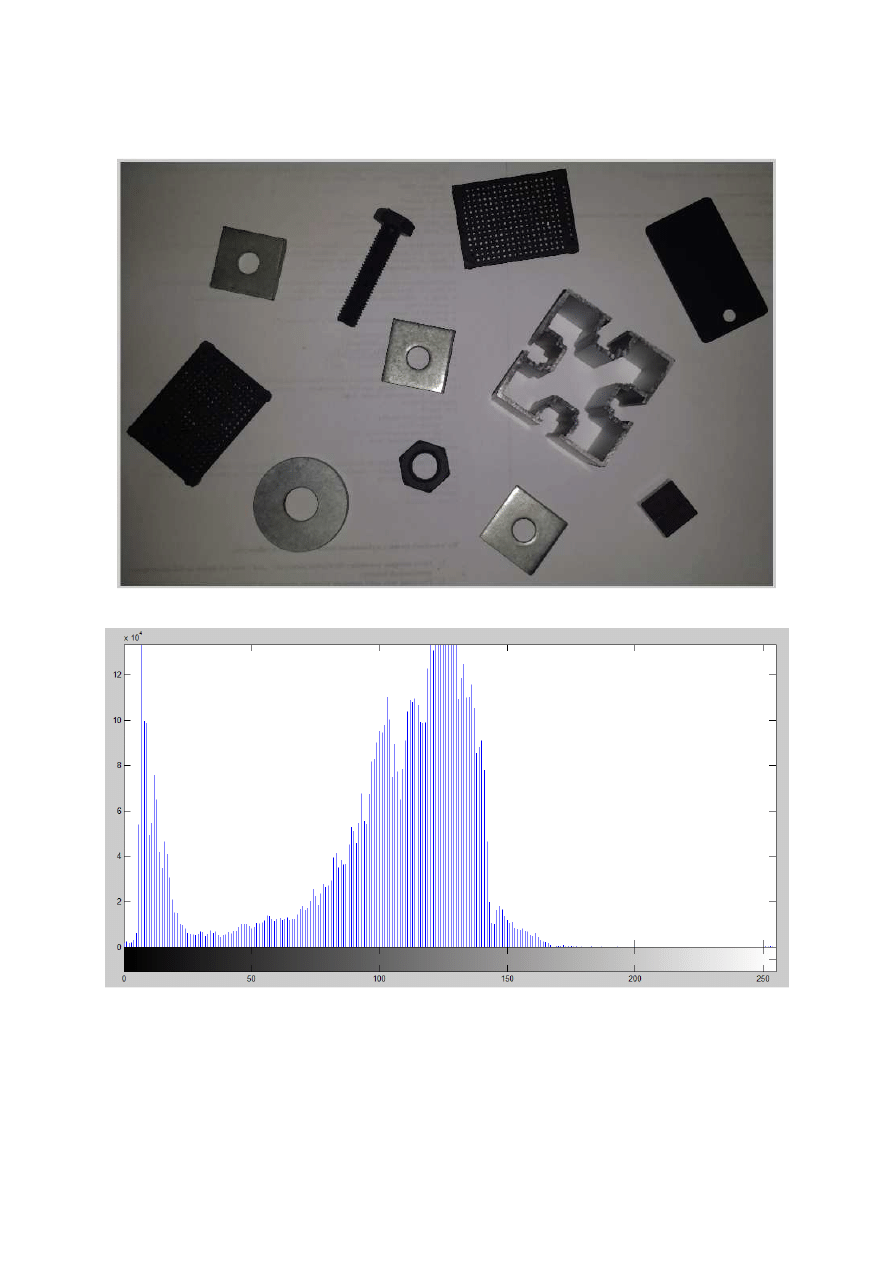
Ad b) Wykonanie histogramu dla obrazu w skali szarości. Polecenie:

imhist(gray);

Ad c) Z racji tego że bardzo trudne było wyodrębnienie wszystkich obiektów na obrazie naraz
stosowano różne progi binaryzacji dla różnych elementów a następnie tak zbinaryzowane obrazy
poddawano filtracji. Poniżej przedstawiono sposób wyodrębniania jednego z elementów
(zaznaczony na czerwono), pozostałe wydobywano analogicznie z tą różnicą że ustalano inne
progi binaryzacji i filtrowano tak aby wydobyty obiekt jak najlepiej odzwierciedlał rzeczywisty.

Binaryzacja:

bw = (gray>=0 & gray<=90);

imshow(bw);

Po zbinaryzowaniu przeprowadzono filtracje. W tym przypadku bardzo dobre rezultaty
przyniosło zastosowanie filtrów erozji i dylatacji morfologicznej z elementem strukturalnym w
kształcie dysku. Polecenia umożliwiające przeprowadzenie tej filtracji oraz wyświetlenie
rezultatu filtracji:

se = strel(

'disk'

,5);

bw1 = imdilate(bw,se);

bw1 = imerode(bw1,se);

imshow(bw1);

Ad d) Po przeprowadzeniu filtracji wykonano segmentacje obrazu.

Nadanie etykiet

poszczególnym obiektom - czarne tło przyjmuje wartość zero, zaś każdy kolejny obiekt
(skupisko białych pikseli) kolejne, naturalne wartości dodatnie. Wykorzystano do tego polecenie:

[L1, num1] = bwlabel(bw1,8);

Argumentami jest tutaj obraz który poddawany jest segmentacji oraz określenie sąsiedztwa tutaj
mamy sąsiedztwo ośmiospójne. Aby zobaczyć jaką etykietę ma dany obiekt można posłużyć się
funkcją:

imtool(L1)

Jak widać na poniższym screenie wystarczy najechać na obiekt a w lewym dolnym rogu okiena
wyświatla się nr jego etykiety. W naszym przypadku jest to nr 10.

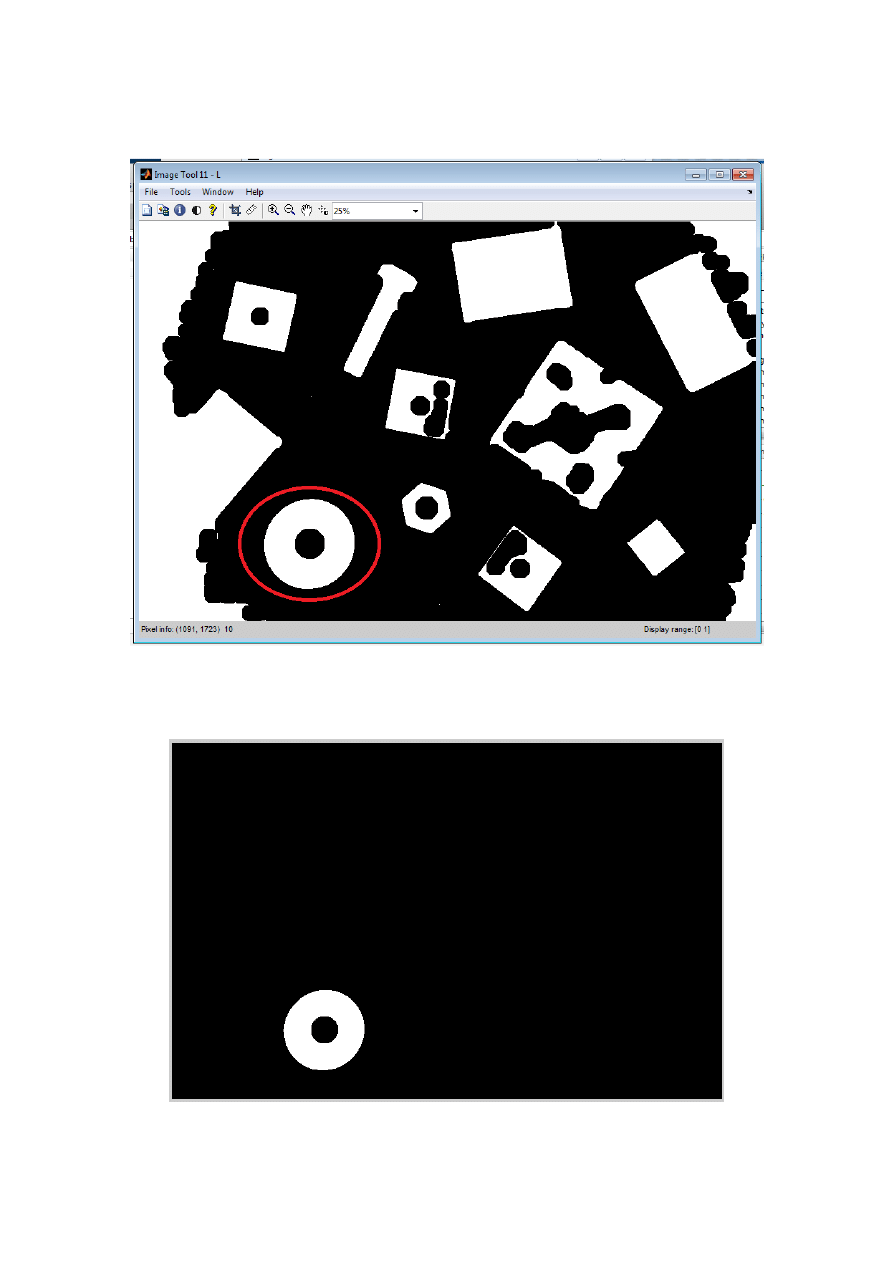
Znając etykiete obiektu który nas interesuje nic już nie stoi na przeszkodze aby go wyodrębnić z
obrazu i wyświetlić. Dokonać tego można za pomocą poleceń:

bw1_1 = ismember(L,10);

imshow(bw1_1)

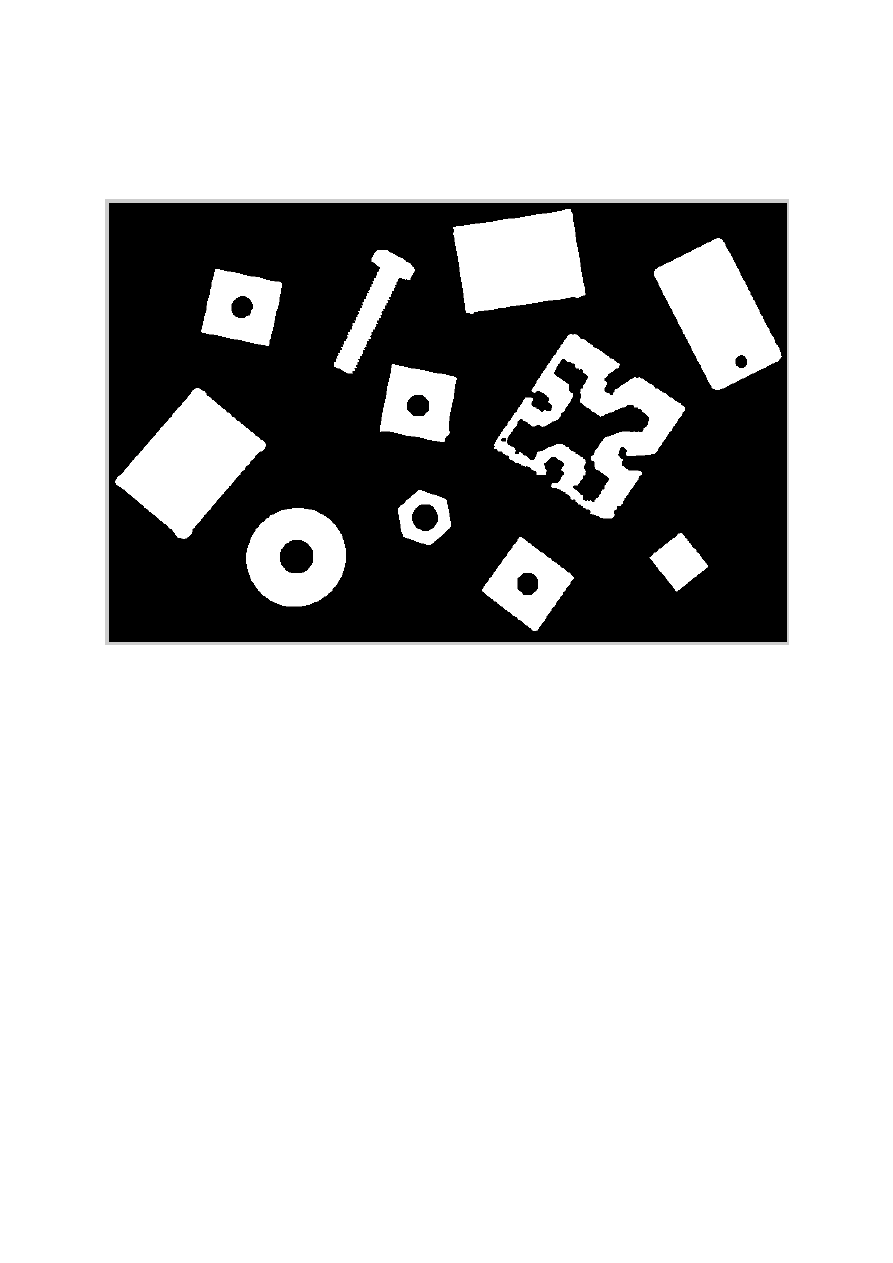
W podobny sposób wyodrębniono pozostałe objekty. Na koniec zsumowano je wszystkie. W
wyniku czego otrzymano:

2. Instrukcja regionprops
Instrukcjaa REGIONPROPS umożliwia wybór i pomiar charakterystyk elementów
obrazu. Składnia funkcji: FEATS = REGIONPROPS(CC,PROPERTIES) gdzie:
CC- macierz etykiet, lub obraz; PROPERTIES- wybrana cecha do pomiaru.

Dostępne parametry z krótkim opisem:

•

All - pomiar wszystkich parametrów

•

Basic - pomiar podstawowych parametrów(Area, Centroid, Bounding Box)

•

Area - zwraca liczbę pikseli z których składa się obiekt

•

BoundingBox - przedstawia najmniejszy prostokąt w jakim mieści się dany
obiekt (zwrot współrzędnych lewego górnego rogu oraz wymiarów prostokąta)

•

Centroid - środek ciężkości obiektu

•

MajorAxisLength – zwraca długość (w pikselach) głównej osi elipsy, która ma
ten sam drugi moment centralny taki sam jak region. Tylko dla macierzy 2-D

•

MinorAxisLength – j.w. lecz w odniesieniu do małej osi elipsy. Tylko dla
macierzy 2-D

•

Eccentricity – zwraca wartość między 0 a 1. Stosunek odległości między
ogniskiem elipsy i długością jej osi wielkiej. Tylko dla macierzy 2-D

•

Orientation – zwraca kąt (w stopniach) między osią x a główną osią elipsy,
która ma ten sam drugi moment centralny co region. Tylko macierze 2-D

•

Image - zwraca obcięty obraz obiektu wielkości BoundingBox danego obiektu

•

FilledImage - zwraca obraz jw. wraz z wypełnionymi lukami wewnątrz obiektu

•

Filled Area - zwraca liczbę pikseli FilledImage

•

ConvexHull – zwrot współrzędnych wierzchołków najmniejszego wielokąta
wypukłego, zawierającego obiekt. Dla macierzy 2-D

•

ConvexImage – zwraca obraz obiektu z wyeliminowanymi wklęśnięciami,
rozmiarze bounding box

•

ConvexArea - zwraca liczbę pikseli ConvexImage

•

EulerNumber – równy liczbie obiektów w regionie minus liczba dziur w nim.
Tylko dla 2-D

•

Extrema – macierz 8x2, współrzędne punktów charakterystycznych. Macierze
2-D

•

EquivDiameter – średnica koła o tym samym polu co region . Tylko 2-D

•

Solidity – Stosunek między Area, a ConvexArea. Macierz 2-D

•

Extent – Stosunek między Area, a BoundingBox Area . Macierze 2-D

•

PixelIdxList – indeksy pikseli danego obiektu

•

PixelList – macierz współrzędnych pikseli danego obiektu

•

Perimeter - zwraca wartość skalarną określającą długość krawędzi obiektu

3. Przedstawienie uzyskanych wyników

Poniżej zamieszczono kod z MatLaba. W wyniku jego działania wyświetlone zostają Środki
ciężkości, orientacje i najmniejsze prostokąty obejmujące obiekty:

[L,num] = bwlabel(bw_ost,8);

feats = regionprops(L,

'All'

);

%%%%%%%%%% Po?o?enie

figure(1)

hold

on

h1 = imshow(L)

r1 = 50;

r2 = 300;

for

i=1:size(feats)

h1 =
line(feats(i).Centroid(1),feats(i).Centroid(2),

'Marker'

,

'.'

,

'MarkerEdgeColor'

,

'r'

)

end

hold

off

%%%%%%%%%% Orientacja

figure(2)

hold

on

h2 = imshow(L)

for

i=1:size(feats)

h1 =
line([feats(i).Centroid(1),feats(i).Centroid(1)+r2*cos(feats(i).Orientation*(
pi/180))

],[feats(i).Centroid(2),feats(i).Centroid(2)+r2*sin(feats(i).Orientation*(pi/
180))]);

end

hold

off

%%%%%%%%%% Prostok

ą

t opisany na obiekcie

figure(3)

hold

on

h3 = imshow(L)

for

i=1:size(feats)

h3 =
rectangle(

'position'

,[feats(i).BoundingBox(1),feats(i).BoundingBox(2),feats(i

).BoundingBox(3),feats(i).BoundingBox(4)],

'EdgeColor'

,

'r'

);

end

hold

off

W wyniku otrzymano:

•

Ś

rodek ciężkości (Centroid):

•

Orientacja (Orientation)

•

Prostokąt opisany na obiekcie (BoundingBox)

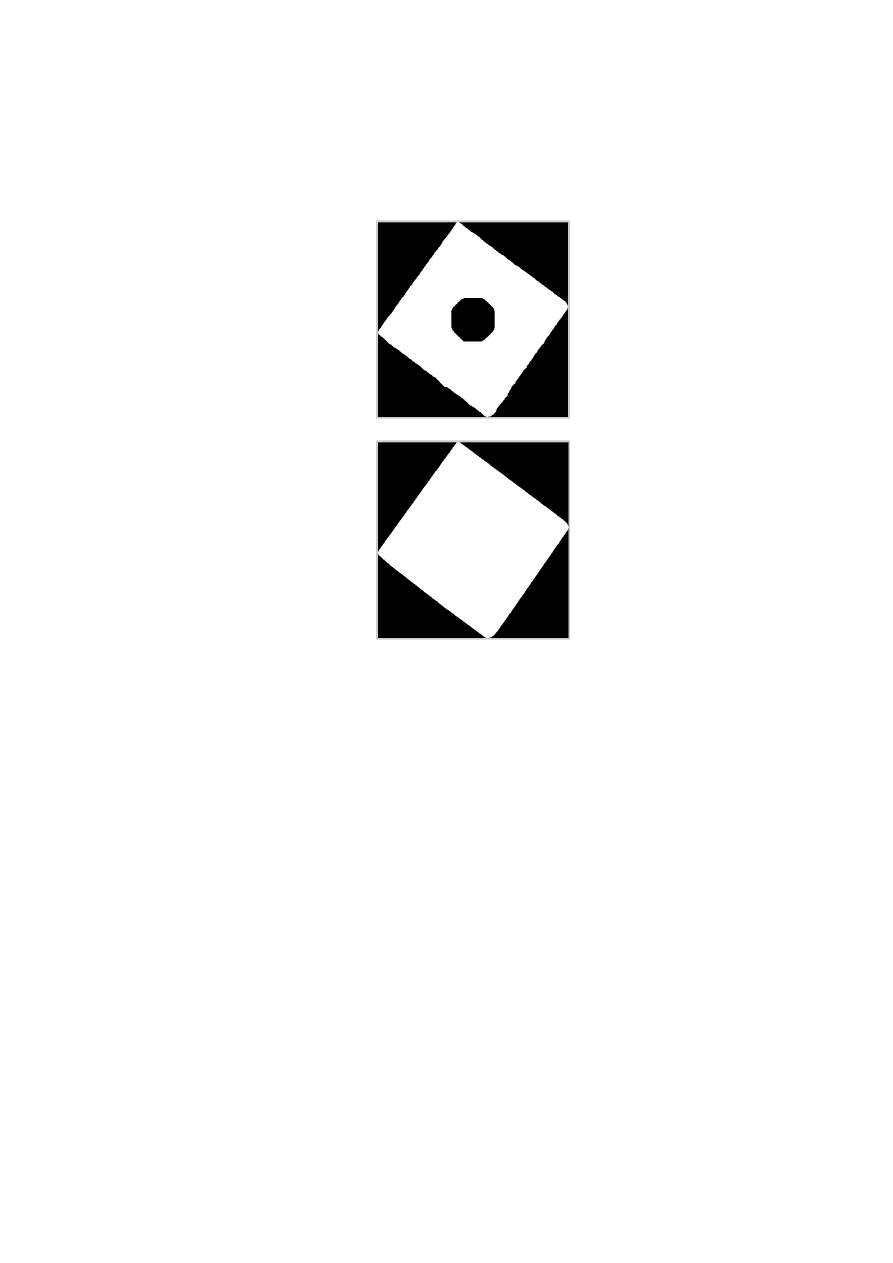
Poniżej przedstawiono dodatkowo działanie Image oraz ConvexImage:

•

Image

•

ConvexImage

4. Implementacja współczynników kształtu
Poniżej zamieszczono fragment kodu który pozwala wyznaczyć odpowiednie współczynniki.
Dla wygody wyniki zostają automatycznie wprowadzone do macierzy.

%%%%%%%%%% Wyliczenie charakterystyk

CHAR = zeros(size(feats),5);

for

i=1:size(feats)

%%form_factor

CHAR(i,1) = 4*pi*feats(i).Area / feats(i).Perimeter^2;

%%roundness

CHAR(i,2) = 4*feats(i).Area / (pi*feats(i).MajorAxisLength^2);

%%acpect_ratio

CHAR(i,3) = feats(i).MajorAxisLength / feats(i).MinorAxisLength;

%%solidity

CHAR(i,4) = feats(i).Solidity;

%%compactness

CHAR(i,5) = sqrt(4*feats(i).Area/pi) / feats(i).MajorAxisLength;

end

Legenda:

Tabela z wynikami:

Nr obj.\Cecha

Form Factor

Roundness

Aspect Ratio

Solidity

Compactness

1

0.7119

0.6783

1.4027

0.9568

0.8236

2

0.6528

0.7621

1.0652

0.9042

0.8730

3

0.7965

0.7670

1.0359

0.8823

0.8758

4

0.2246

0.1639

4.8430

0.7116

0.4048

5

0.6345

0.7982

1.0108

0.8726

0.8934

6

0.6304

0.5803

1.0163

0.7395

0.7618

7

0.6969

0.6910

1.3791

0.9702

0.8313

8

0.6702

0.7843

1.0332

0.9037

0.8856

9

0.2016

0.4800

1.0424

0.5987

0.6928

10

0.7344

0.8843

1.0804

0.9852

0.9404

11

0.6390

0.5416

1.7478

0.9718

0.7359

Powyższe charakterystyki umożliwiają identyfikacje kształtu obiektu. Współczynniki te nie są
wrażliwe na powiększenie obiektu, sa natomiast wrazliwe na zmiane orientacji. Jak widać w
powyższej tabeli śrubę możemy zidentyfikować poprzez współczynnik Aspect Ratio ponieważ
osiąga on znacznie większą wartość (tutaj ponad 3 krotnie). Obiekt nr 9 można rozpoznać na
podstawie niskich wartościach współczynników Form Factor oraz Roundness przy

współczynniku Aspect Ratio równym około 1. Z kolei podkładkę 3 możemy zidentyfikowac po
stosunkowo wysokich współczynnikach Form Factor oraz Roundness. Nakrętke można
zidentyfikować po dość niskim współczynniku Roundness oraz dość wysokim współczynniku
Compactness.

Generalnie parametr Aspect Ratio pozwala wykryć obiekty symetryczne np. odróżnić prostokąt
od kwadratu czy elipse od koła.

Obiekt o smukłym kształcie ma mały współczynnik Compactness, natomiast np. koło i kwadrat
mają ten współczynnik ok. 1 lub większy.

Współczynnik Solidity dobrze charakteryzuje elementy drążone. Czym większe wydrążenie tym
wartość tego współczynnika jest mniejsza. Jeśli obiekt nie jest drążony to współczynnik ten
przyjmuje wartość 1.