3

Natężenie deszczu miarodajnego



Dla rowu 2 – 1
- długość rowu L

2-1

=220,0 [m]

- przyjęta prędkość przepływu





s

m

V

/

04

,

1



- prędkość dopuszczalna przepływu V

d

=1,8 [m/s]- przyjęto dla rodzaju umocnienia:

darnina w płotkach wiklinowych

wg.tab. 3.6. poz.1[2]

t

d,2-1

= t

p,2-1

=

min

53

,

3

54

,

211

04

,

1

220

1

2









s

V

L



Dla rowu 3 – 1
- długość rowu L

3-1

=240,0 [m]

- przyjęta prędkość przepływu





s

m

V

/

04

,

1



- prędkość dopuszczalna przepływu V

d

=1,8 [m/s]- przyjęto dla rodzaju umocnienia:

darnina w płotkach wiklinowych

wg.tab. 3.6. poz.1[2]

t

d,3-1

= t

p,3-1

=

min

85

,

3

77

,

230

04

,

1

240

1

3









s

V

L

Natężenie deszczu miarodajnego zależy od czasu jego trwania i prawdopodobieństwa jego
pojawienia się:

=

,

[

∗ ℎ

]

t - czas trwania deszczu [min]
A - współczynnik zależny od prawdopodobieństwa pojawienia się deszczu oraz średniej
rocznej wysokości opadu przyjmowane z Tab. 3.2. [1].

Wymiary urządzeń odwadniających drogę, ustala się zgodnie z Rozporządzeniem Ministra
Transportu i Gospodarki Morskiej z dnia 2.03.1999 r., na podstawie deszczu miarodajnego,
określonego przy założeniu prawdopodobieństwa p, pojawienia się opadów w zależności od
klasy drogi.

Dla drogi klasy G – droga główna  p = 50% (c = 2 lata)
Średnia roczna wysokość opadu wynosi do 1000 mm. Na podstawie powyższych danych
przyjęto wartość współczynnika A = 720.



Zlewnia A

=

720

3,53

,

= 310,43

∗ ℎ



Zlewnia B

=

720

3,85

,

= 292,97

∗ ℎ

4

Obliczenie współczynnika opóźnienia odpływu

=

1

√

F - powierzchnia zlewni [ha],
n - współczynnik zależny od spadku i formy terenu, przyjęto 8(dla spadków większych
i zlewni wydłużonych)



Zlewnia A

=

1

√7,987

= 0,77



Zlewnia B

=

1

7,254

= 0,78

Obliczenie spływu wód opadowych

=

= 0,77 ∗ 0,127 ∗ 310,43 ∗ 7,987 = 242,46

= 0,242

= 0,78 ∗ 0,150 ∗ 292,97 ∗ 7,254 = 248,65

= 0,249

3. Obliczenie przekroju rowów odwadniających
3.1.

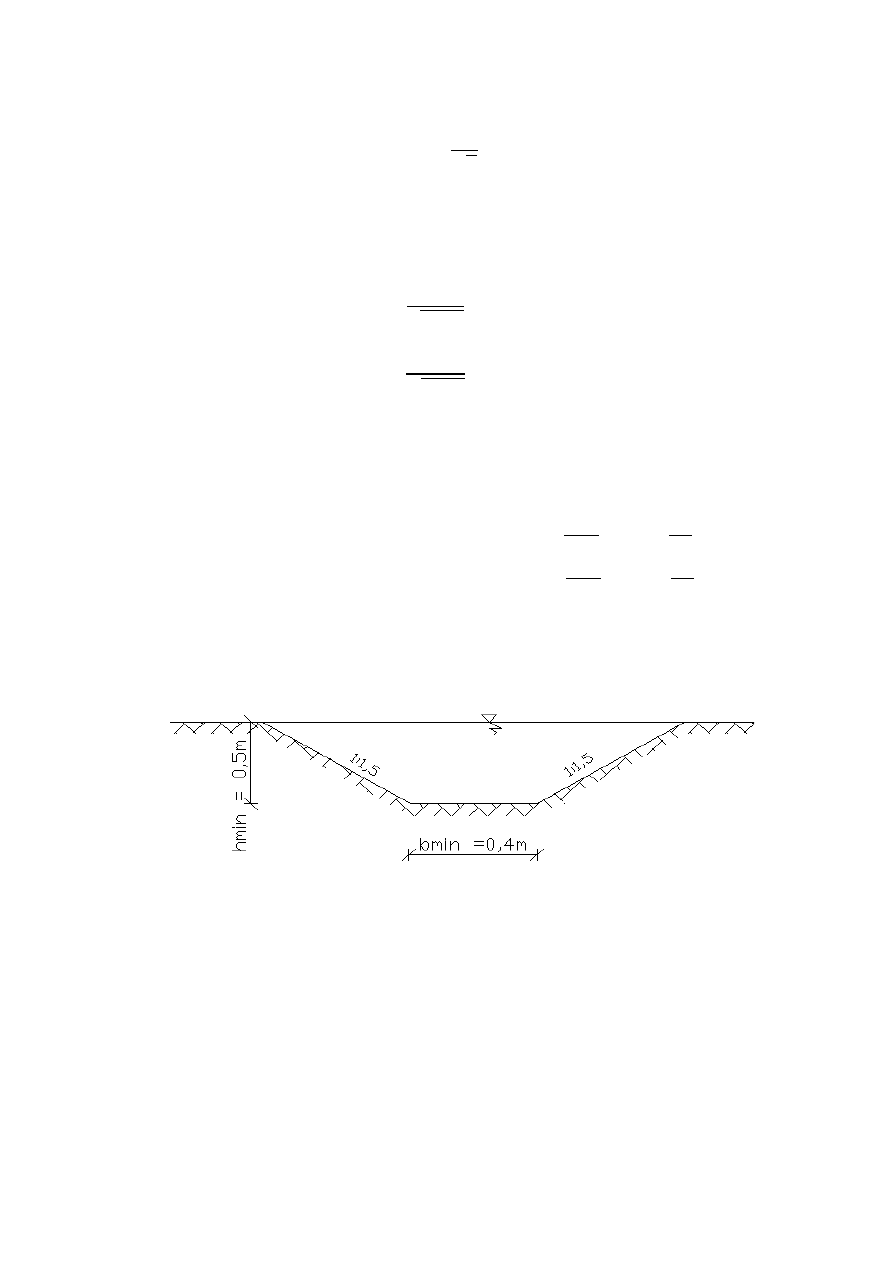
Rów trapezowy

Parametry rowu:
h = 0,5 m
b = 0,4 m
Q

m

= Q

3-1

= 0,249 m

3

/s

v

d

= 1,8 m/s

I

E

= 0,6 % - spadek podłużny rowu

n = 1,5
k

st

= 40 m

3

/s – ciek naturalny (Tab. 5.1 [1])

Pole powierzchni czynnego rowu

= ℎ( + ℎ) = 0,5 ∗ (0,4 + 1,5 ∗ 0,5) = 0,575

5

Obwód zwilżony

=

+ 2ℎ 1 +

= 0,4 + 2 ∗ 0,5 ∗ 1 + 1,5 = 2,21

Promień hydrauliczny

=

=

0,575

2,21

= 0,26

Prędkość przepływu

=

∗

∗

= 40 ∗ 0,26 ∗ 0,006 = 1,26

Sprawdzenie warunku na nieprzekroczenie prędkości dopuszczalnej cieku w rowie

<

= 1,26

<

= 1,80

= 1,80 - darniowanie w płotkach wiklinowych(Tab. 3.6 [2])

Warunek spełniony

Wyznaczenie przepływu w rowie

=

= 0,575 ∗ 1,26 = 0,72

Sprawdzenie warunku nieprzekroczenia przepływu miarodajnego w rowie

>

= 0,72

>

= 0,249

Warunek spełniony

3.2.

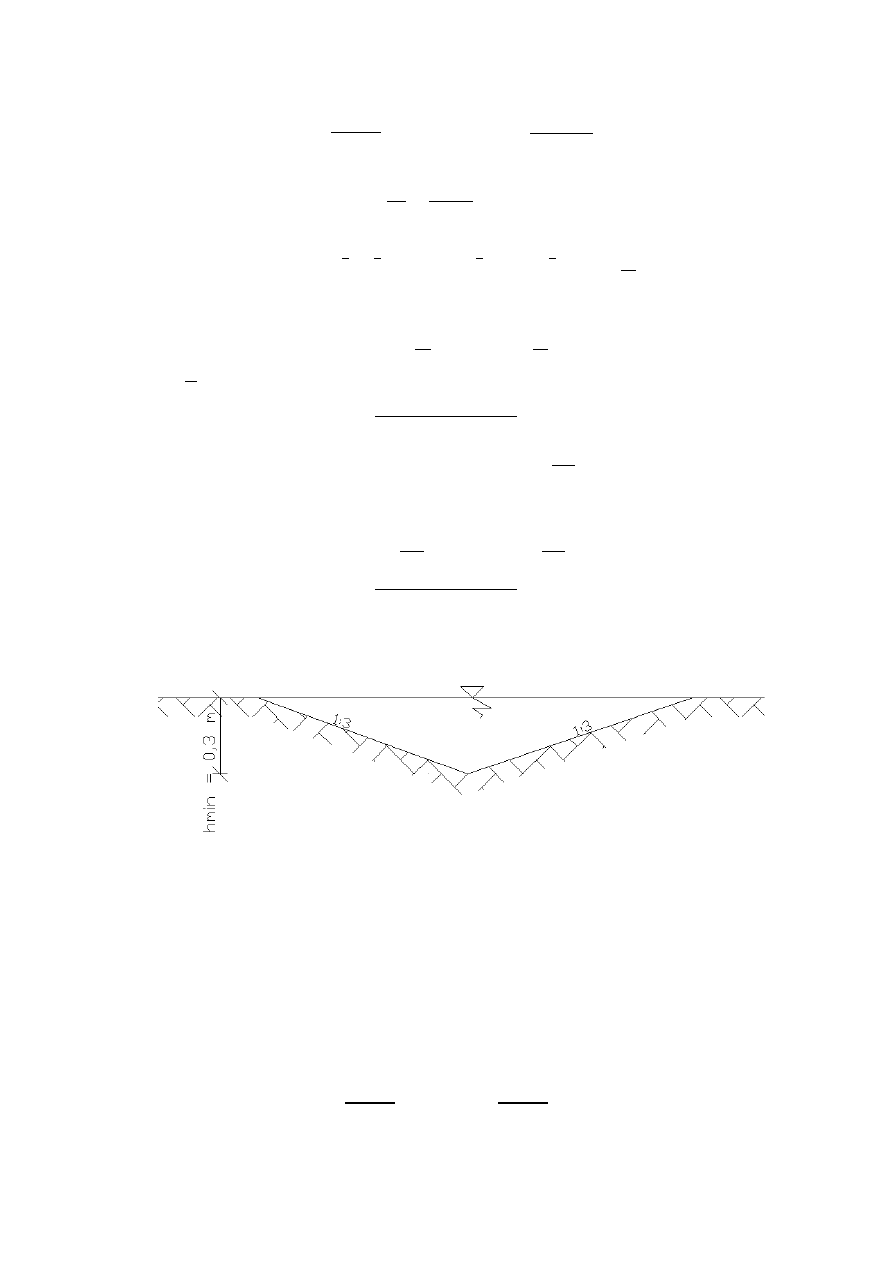
Obliczenie rowu trójkątnego

Parametry rowu:
h = 0,4 m
Q

m

= Q

3-1

= 0,249 m

3

/s

v

d

= 1,8 m/s

I

E

= 0,6 % - spadek podłużny rowu

n = 3
k

st

= 40 m

3

/s – ciek naturalny (Tab. 5.1 [1])

Pole powierzchni czynnego rowu

= ℎ = 3 ∗ 0,4 = 0,48

Obwód zwilżony

= 2ℎ 1 +

= 2 ∗ 0,4 ∗ 1 + 3 = 2,53

6

Promień hydrauliczny

=

=

0,48
2,53

= 0,19

Prędkość przepływu

=

∗

∗

= 40 ∗ 0,19 ∗ 0,006 = 1,02

Sprawdzenie warunku na nieprzekroczenie prędkości dopuszczalnej cieku w rowie

<

= 1,02

<

= 1,80

= 1,80 - darniowanie w płotkach wiklinowych(Tab. 3.6 [2])

Warunek spełniony

Wyznaczenie przepływu w rowie

=

= 0,48 ∗ 1,02 = 0,49

Sprawdzenie warunku nieprzekroczenia przepływu miarodajnego w rowie

>

= 0,49

>

= 0,249

Warunek spełniony

Wniosek: Przyjęte parametry rowu spełniają warunek przepływu.
Przyjęte wymiary rowu trapezowego jak i trójkątnego w podobnym stopniu
spełniają warunki przepływu. Do odwodnienia zlewni zastosowane zostaną rowy
trapezowe.

3.3.

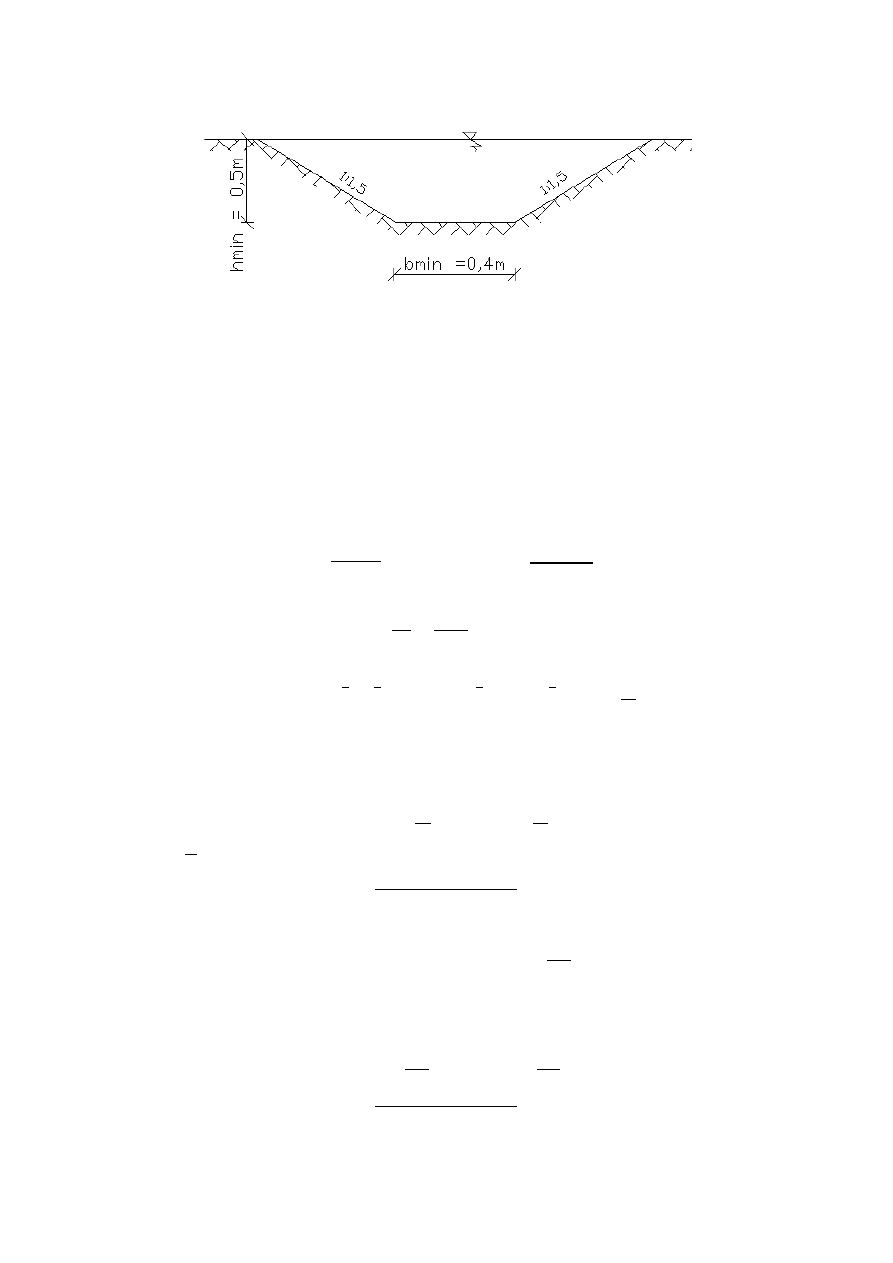
Obliczenie rowu trapezowego doprowadzającego wodę do przepustu

= 5 ÷ 8

,

+

,

= 5 ÷ 8 (0,242 + 0,249) = 2,45 ÷ 3,92

= 3,18

Q

m

7

Parametry rowu:
h = 1, 6 m
b = 0, 7m
Q

m

= 3, 18 m

3

/s

v

d

= 1, 8 m/s

I

E

= 0, 7 % - spadek podłużny rowu

n = 1,5
k

st

= 30 m

3

/s – mulda – kształtki betonowe (Tab. 5.1 [1])

Pole powierzchni czynnego rowu

= ℎ( + ℎ) = 1,6 ∗ (0,7 + 1,5 ∗ 1) = 3,52

Obwód zwilżony

=

+ 2ℎ 1 +

= 0,7 + 2 ∗ 1,6 ∗ 1 + 1,5 = 6,47

Promień hydrauliczny

=

=

3,52
6,47

= 0,54

Prędkość przepływu

=

∗

∗

= 30 ∗ 0,54 ∗ 0,007 = 1,66

Sprawdzenie warunku na nieprzekroczenie prędkości dopuszczalnej cieku w rowie

<

= 1,66

<

= 1,80

= 1,80 - darniowanie w płotkach wiklinowych(Tab. 3.6 [2])

Warunek spełniony

Wyznaczenie przepływu w rowie

=

= 3,52 ∗ 1,66 = 5,84

Sprawdzenie warunku nieprzekroczenia przepływu miarodajnego w rowie

>

= 5,84

>

= 3,18

Warunek spełniony

Wniosek: Przyjęte parametry rowu są prawidłowe.

8

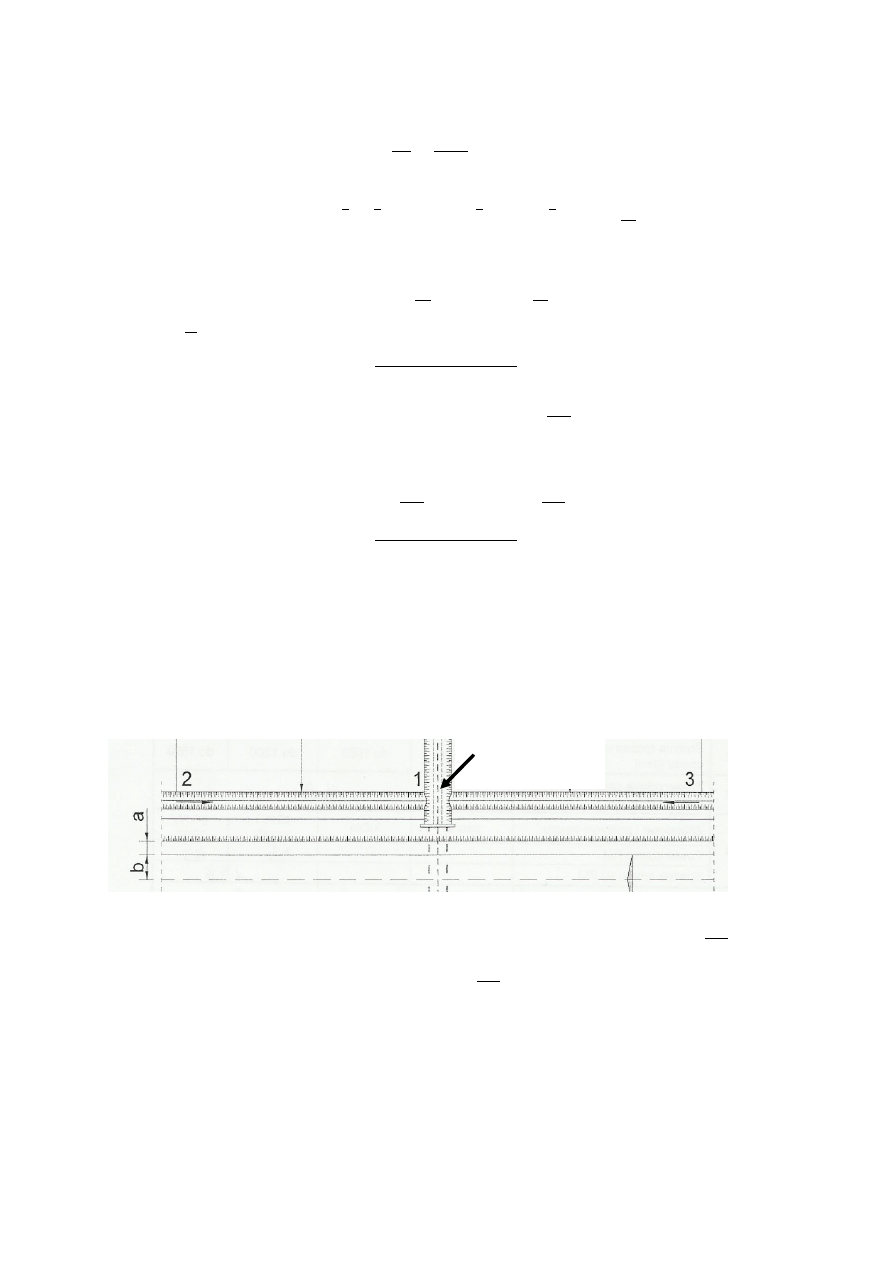
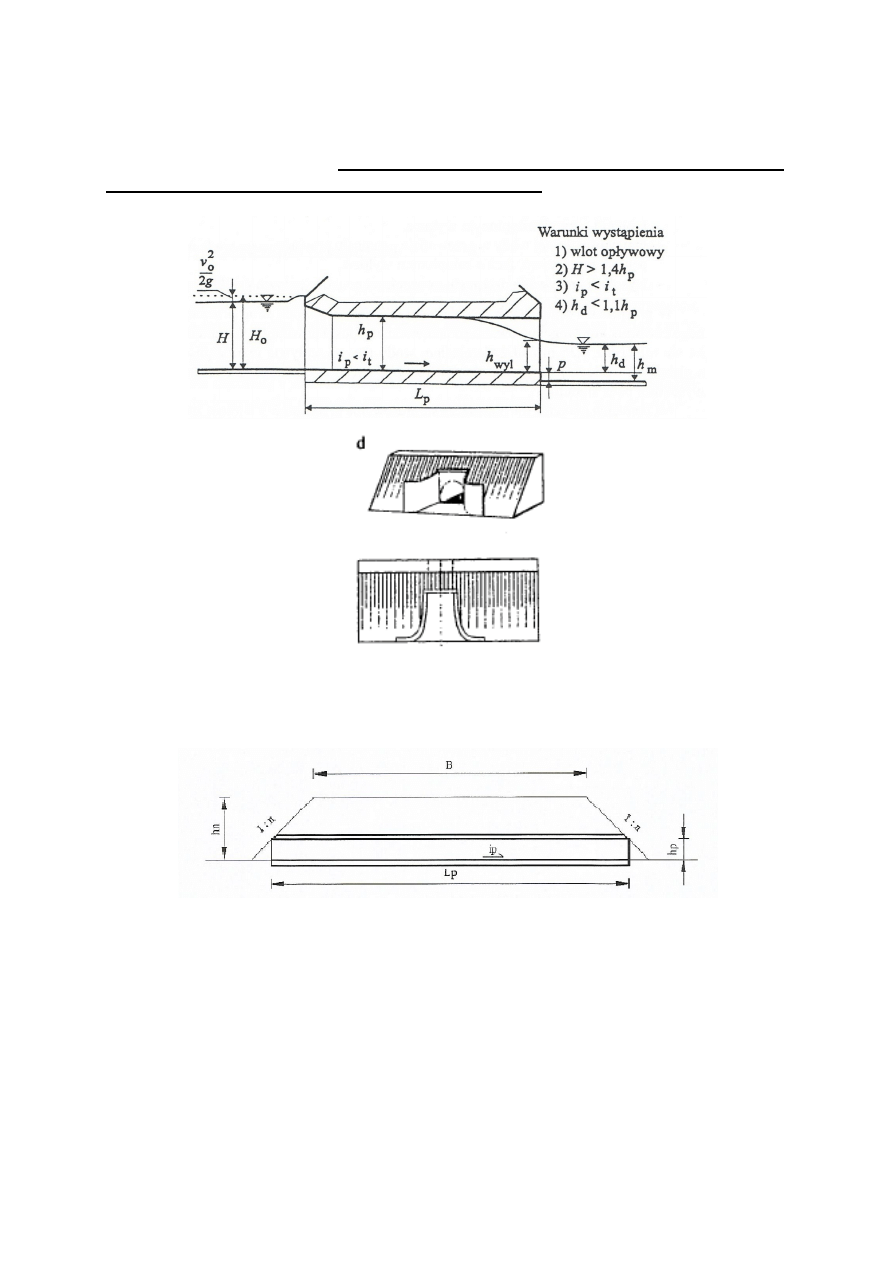
4. Obliczenie wymiarów przepustu

Przyjęty schemat obliczeniowy: zatopiony wlot i niezatopiony wylot, całkowicie wypełniony
o przekroju poprzecznym kołowym, wlocie korytarzowym.

Wlot korytarzowy ze skrzydłami krzywoliniowymi

4.1 Obliczenie przepustu.

Dane przyjęte do obliczeń:
D= h

p

= 1,1 m – wysokość przepustu

v

max

= 3,5 m – dla przepustów o wysokości do 1,5m

h

n

= 2,30 m – wysokość nasypu liczona do dna przepustu

=90° - kąt zawarty między osią drogi i osią przepustu

n = 1,0 – nachylenie skarpy korony drogi
Q

m

=3,18 m

3

/s – ilość wody doprowadzona do przepustu

B = 2*(3,5+2,0)= 11 m – szerokość korony nasypu drogi
v =1,60 m/s – prędkość przepływu w przewodzie przepustu

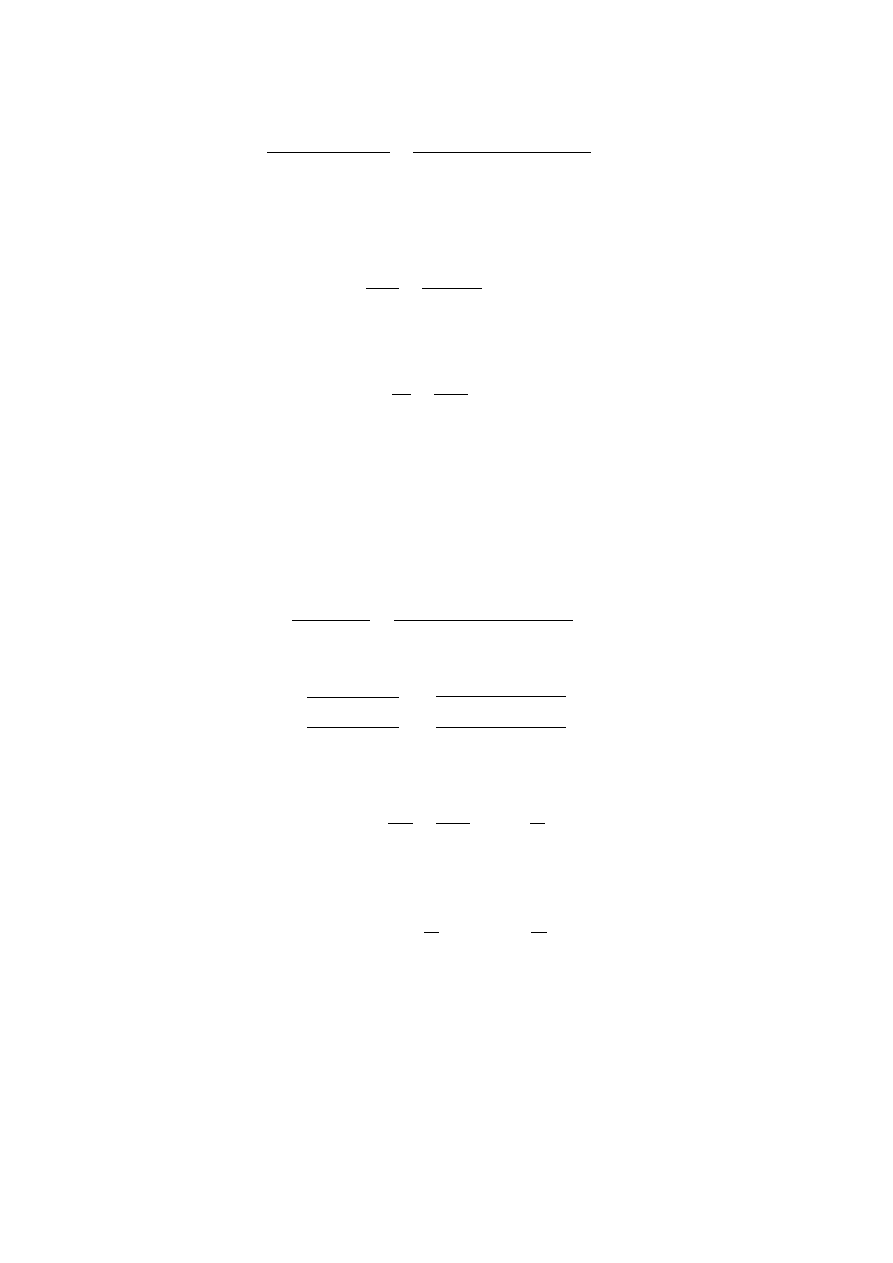
9

Długość przepustu

=

+ 2 (ℎ − )

sin

=

11 + 2 ∗ 1 ∗ (2,3 − 1,1)

sin 90

= 13,4

= 13,4

< 20ℎ = 20 ∗ 1,1

= 22

Przepust krótki – nie uwzględnia się strat energii

Pole przekroju czynnego

=

4

=

∗ 1,1

4

= 0,95

Obwód zwilżony

=

=

∗ 1,1 = 3,45

Promień hydrauliczny

=

=

0,95
3,45

= 0,28

Długość obliczeniowa przepustu

=

− 3,6 ∗ ℎ = 13,4 − 3,6 ∗ 1,1 = 9,44

Współczynnik strat na długości przewodu

= 0,011- współczynnik szorstkości przewodu przepustu – przewód o powierzchni

betonowej, Tab. 3-1. [2].

=

2

0,157

/

=

2 ∗ 9,81 ∗ 0,011 ∗ 9,44

0,157 ∗ 1,1

/

= 0,133

Współczynnik wydatku

= 0,33 – współczynnik strat na wlocie dla wlotów opływowych

=

1

1 +

+

=

1

1 + 0,33 + 0,133

= 0,827

Prędkość przepływu wody w przepuście

=

=

3,18
0,95

= 3,35

Sprawdzenie warunku nieprzekroczenia prędkość dopuszczalnej przepływu

= 3,35

<

= 3,5

Warunek spełniony

Spadek dna przekroju przepustu

Przyjęto spadek

= 2%.

10

Wysokość linii energii spiętrzonego strumienia przy przepływie miarodajnym

= ℎ +

2

−

= 0,79 – współczynnik zależny od rodzaju przekroju poprzecznego o rodzaju wlotu

przepustu (Tab. 3-10. [2], wlot kołnierzowy).

= 0,79 ∗ 1,1 +

3,18

2 ∗ 9,81 ∗ 0,95 ∗ 0,827

− 0,01 ∗ 13,4 = 1,68

Głębokość wody górnej

=

−

2

= 1,68 −

1,60

2 ∗ 9,81

= 1,55

Sprawdzenie warunku na zatopienie wlotu

= 1,55

> 1,4ℎ = 1,4 ∗ 1,1 = 1,54

= 1,60

>

= 1,55

Warunek jest spełniony

Obliczenia stanowiska dolnego

Obliczenia głębokości i prędkości wody na wylocie z przepustu



Głębokość wody wypływającej z przepustu, tab. 3.4. [R]

m

h

h

p

wyl

88

,

0

1

,

1

8

,

0

8

,

0













Prędkość wody w przekroju wylotowym

= 0,6736

= 0,82





s

m

F

Q

V

wyl

m

wyl

/

88

,

3

82

,

0

18

,

3









Sprawdzenie czy wypad wymaga umocnienia

gdy V

wyl

>1,2V

nr

– wypad wymaga umocnienia

Przyjęto na stanowisku dolnym grunt rodzimy, jako gliny zwięzłe





s

m

V

nr

/

2

,

1



- przy głębokości strumienia 1m

z tabl. 2.3. [R]





s

m

V

nr

/

27

,

1

88

,

0

2

,

1

2

,

1









s

m

V

s

m

V

nr

wyl

/

27

,

1

/

88

,

3







- wypad wymaga umocnienia

Ocena warunków hydraulicznych poniżej wylotu

m

h

m

h

kr

wyl

95

,

0

88

,

0







Jeżeli h

wyl

<h

kr

to w obrębie stanowiska dolnego wystąpi odskok

hydrauliczny i wymagane jest umocnienie dna odpowiednie dla
prędkości.

m

d

g

Q

h

m

kr

95

,

0

1

,

1

81

,

9

18

,

3

3

2

2

3

2

2











11

Wymiarowanie wypadu

Obliczenie energii

spokojny

ruch

-

23

,

1

81

,

9

2

60

,

1

1

,

1

2

2

2













g

V

h

E

d

a) Kąt β, dla ruchu spokojnego z wykresu Serenkova, rys.3.3[R]

Obliczenie liczby Froude’a na wylocie:

74

,

1

88

,

0

81

,

9

88

,

3

2

2











wyl

wyl

wyl

h

g

V

Fr

Obliczenie liczny Froude’a w przekroju koryta odpływowego na wypadzie

24

,

0

1

,

1

81

,

9

60

,

1

2

2











d

d

h

g

V

Fr

Z wykresu odczytano kąt β=35

b) Długość wypadu L

w

, na którym wystąpi całkowite rozszerzenie się strumienia



tg

h

B

L

wyl

w

w

2





m

h

wyl

88

,

0







m

h

B

wyl

w

52

,

3

88

,

0

4

5

3













m

L

w

89

,

1

700

,

0

2

88

,

0

52

,

3









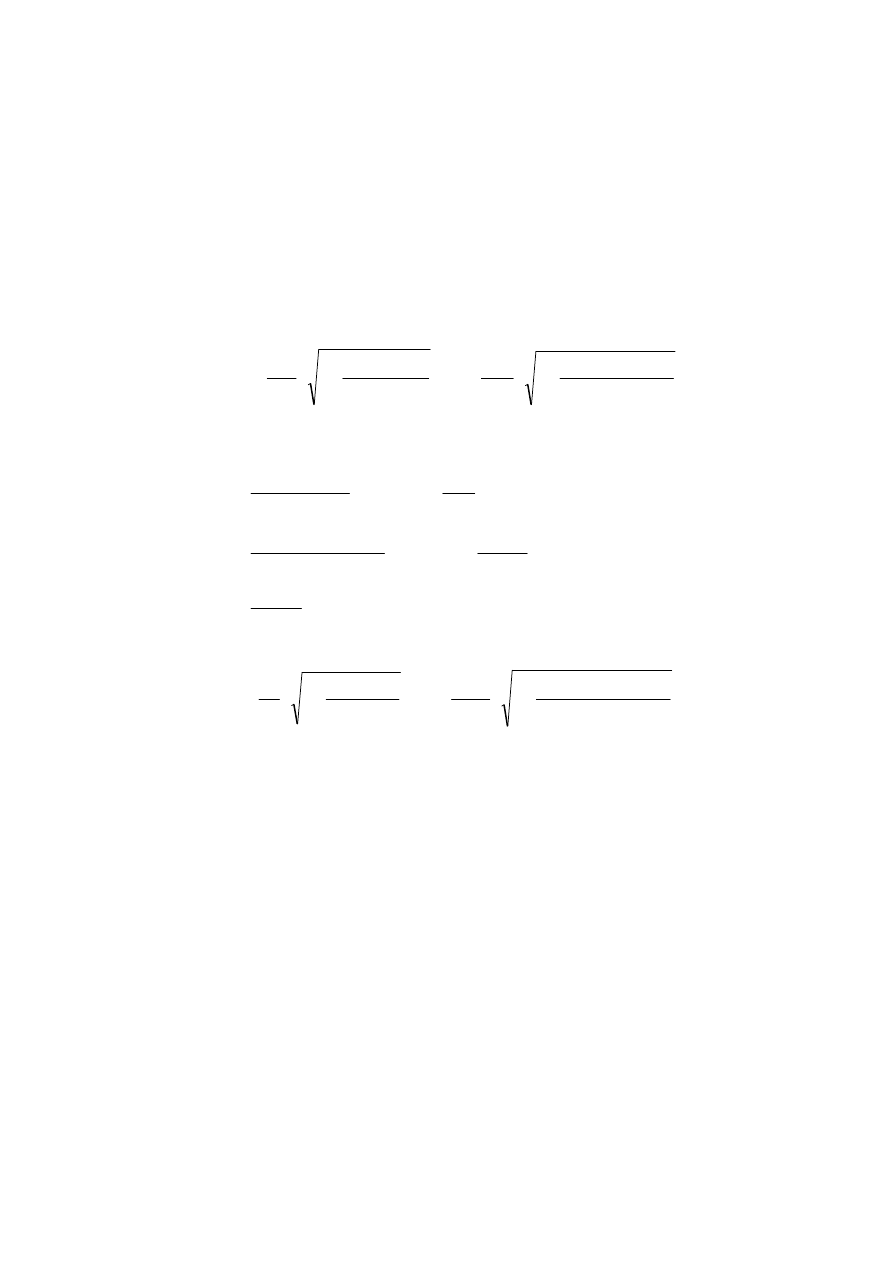
12

c) Długość umocnienia stanowiska dolnego L

U

d)

m

L

L

w

U

89

,

1









m

D

L

U

3

,

3

1

,

1

3

3

2













Jako długość umocnienia przyjęto wartość maksymalną z powyższych równań:
L

U

=3,3m.

Ponieważ nastąpi odskok hydrauliczny należy obliczyć głębokość sprzężoną z
głębokością na wylocie

m

h

b

g

Q

h

h

wyl

wyl

m

wyl

wyl

39

,

1

1

88

,

0

1

,

1

81

,

9

18

,

3

8

1

2

88

,

0

1

8

1

2

3

2

2

3

2

2

2



























































Głębokość strumienia w ruchu rwącym, w przekroju poprzecznym na końcu
rozszerzenia wypadu

81

,

9

2

88

,

3

88

,

0

0

52

,

3

81

,

9

2

18

,

3

1

,

1

2

2

1

,

1

2

2

2

2

2

2

2

2





































w

w

wyl

wyl

w

w

m

w

h

h

g

V

h

p

B

h

g

Q

h

 

m

h

h

h

w

w

w

633

,

1

65

,

1

0458

,

0

2









Głębokość strumienia sprzężoną z głębokością h

w

 

m

h

B

g

Q

h

h

w

w

m

w

w

06

,

0

1

633

,

1

52

,

3

81

,

9

18

,

3

8

1

2

633

,

1

1

8

1

2

3

2

2

3

2

2

2





























































Przyjęto, że głębokość wody w kanale odpływowym jest równa głębokości
wody przed przepustem

m

h

p

h

d

m

1

,

1

1

,

1

0











Po porównaniu obliczonych wartości głębokości zakwalifikowano
rozpatrywaną sytuację do przypadku b), strona 3926 [3]

m

h

m

h

m

h

w

m

wyl

06

,

0

1

,

1

39

,

1

2

2











Oznacza to, że odskok hydrauliczny nastąpi w rozszerzającej się części wypadu
lub przed jej końcem.

13

Obliczenie głębokości rozmycia za przepustem

Głębokość rozmycia za przepustem dla przypadku b oblicza się ze wzoru

m

h

h

h

d

w

r

989

,

0

1

,

1

06

,

0

85

,

1

85

,

1

2



















Ponieważ ∆h

r

jest wartością ujemną, można przyjąć, że rozmycie nie nastąpi.

W związku z tym jako umocnienie dna wypadu dla prędkości V

wyl

=3,88m/s,

zgodnie z tab.2.4 [3] przyjęto bruk pojedynczy z kamienia łamanego którego
V

d

=3,5÷4m/s.

Dla podanych wartości zaprojektowany przepust spełnia warunki dla tego typu
przepustów o zatopionym wlocie i niezatopionym wylocie całkowicie wypełnionym.