Kryterium Nyquista

Kryterium Nyquista pozwala na badanie stabilności jednowymiarowego układu zamkniętego

na podstawie przebiegu wykresu funkcji

)

(

ω

j

G

o

układu otwartego na płaszczyźnie zmiennej

zespolonej.
Sformułowane przez Nyquista kryterium stabilności przedstawia się następująco:

1.

Układ zamknięty jest stabilny asymptotycznie, przy założeniu, że równanie
charakterystyczne układu otwartego ma k pierwiastków w prawej półpłaszczyźnie i
n-k pierwiastków w lewej półpłaszczyźnie, wtedy i tylko wtedy, gdy
charakterystyka amplitudowo-fazowa układu otwartego przy zmianie pulsacji ω od
-∞ do ∞ obejmuje w kierunku dodatnim k razy punkt (-1,j0)

2.

Układ zamknięty jest stabilny asymptotycznie, przy założeniu, że równanie
charakterystyczne układu otwartego nie ma pierwiastków w prawej półpłaszczyźnie
zmiennej zespolonej, wtedy i tylko wtedy, gdy charakterystyka amplitudowo-
fazowa układu otwartego przy zmianie pulsacji ω od -∞ do ∞ nie obejmuje punktu
(-1,j0).

3.

Na płaszczyźnie zmiennej zespolonej punkt (-1,j0) nazywamy punktem Nyquista.

W pewnych przypadkach wygodniej jest posługiwać tzw. regułą lewej strony, która mówi, że
układ zamknięty jest stabilny, jeżeli przy wzroście

ω

od 0 do

∞

, punkt (-1,j0) znajduje się w

obszarze po lewej stronie wykresu G

o

(jw).

W praktycznych zastosowaniach kryterium Nyquista jest szczególnie przydatne w przypadku,

gdy układ otwarty jest stabilny. Można wtedy korzystać z przebiegu charakterystyki

)

(

ω

j

G

o

układu otwartego zdjętej doświadczalnie, co pozwala na badanie stabilności także układu,
którego opis matematyczny nie jest znany.

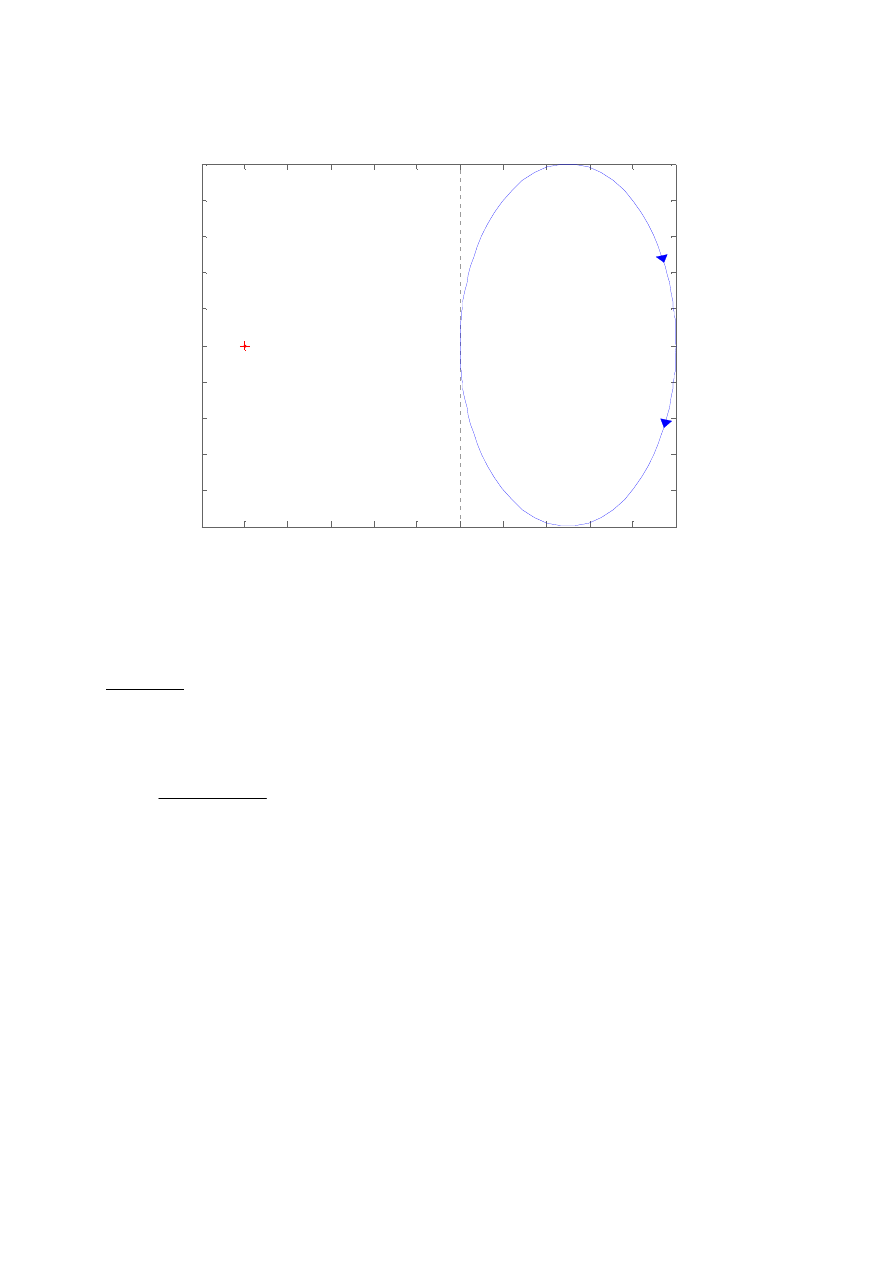
Przykład 1

Pokażemy obszar płaszczyzny zmiennej zespolonej zakreślany przez charakterystykę
amplitudowo fazową stabilnego modelu.

1

1

)

(

+

=

s

s

T

, zmiana pulsacji ω od -∞ do ∞

Punkt Nyquista nie należy do obszaru zakreślonego przez charakterystykę czyli nie jest przez
nią obejmowany. W związku z tym po zamknięciu pętlą sprzężenia zwrotnego powstały układ
nadal będzie stabilny, co wynika z tw. Nyquista.
Transmitancja układu zamkniętego :

2

1

)

(

1

)

(

)

(

+

=

+

=

s

s

T

s

T

s

Tz

<- układ jest nadal stabilny, s=-2

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

-0.5

-0.4

-0.3

-0.2

-0.1

0

0.1

0.2

0.3

0.4

0.5

Nyquist Diagram

Real Axis

Im

a

g

in

a

ry

A

x

is

Komendy w Matlabie:

Ts=tf([1],[1 1]);

nyquist(Ts);

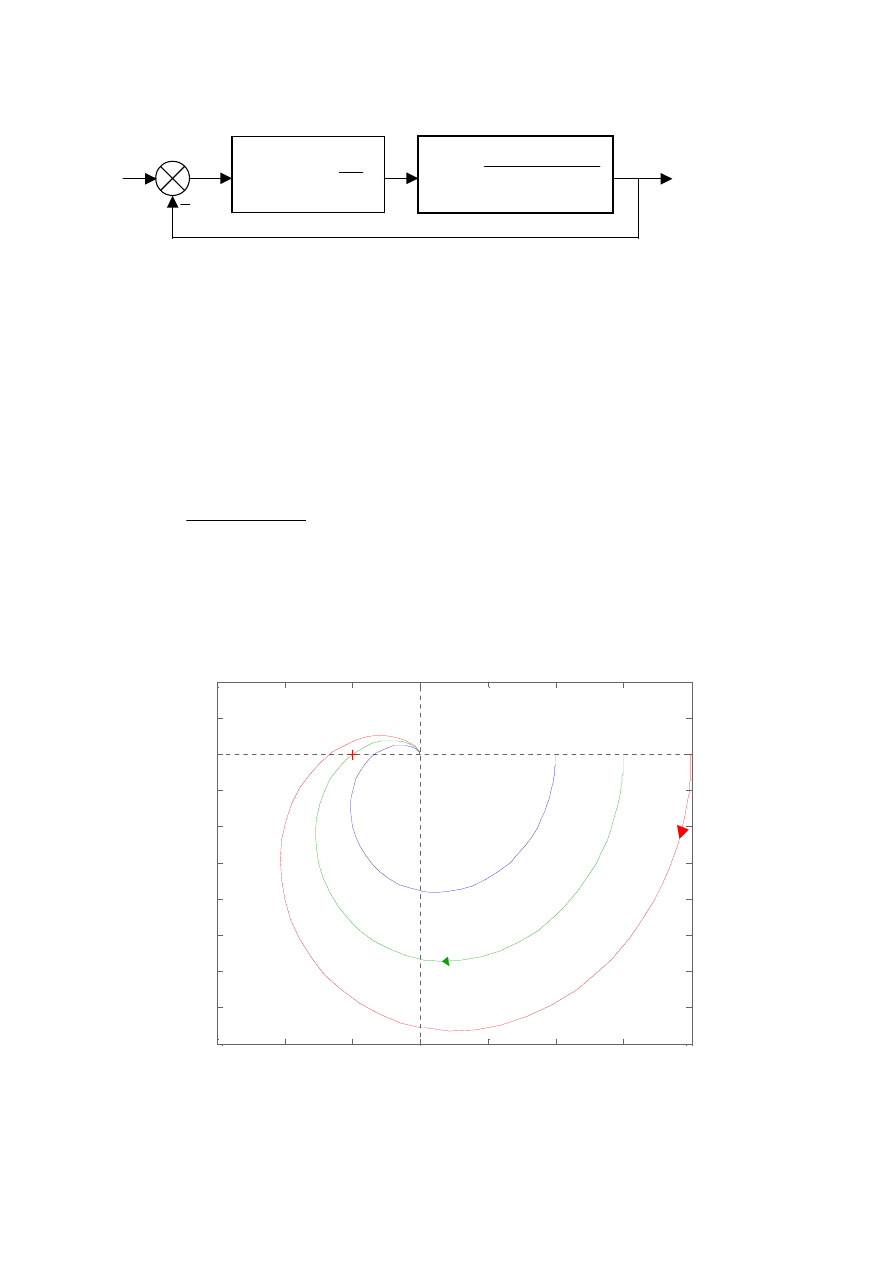
Przykład 2

Rozważmy układ niestabilny. Zbadamy możliwość ustabilizowania modelu układu o
transmitancji :

5

.

0

5

.

0

1

1

.

0

)

(

2

−

+

+

=

s

s

s

s

T

Pierwiastki równania charakterystycznego tego modelu to :

s

1

=-1 , s

2

=0.5

Wynika stąd, że model jest niestabilny. W celu ustabilizowania układu opisanego
transmitancją T(s) zastosujemy sprzężenie zwrotne. Przed zamknięciem pętli sprzężenia
zwrotnego należy sprawdzić, wykorzystując twierdzenie Nyquista, czy ten zabieg może
spowodować ustabilizowanie układu.

Z wykonanej charakterystyki widać, że punkt Nyquista jest nią obejmowany jednokrotnie
podczas zmiany pulsacji od -∞ do ∞. Ponieważ badany układ ma jeden pierwiastek w prawej
półpłaszczyźnie zmiennej zespolonej, wiec na mocy tw. Nyquista wiadomo, że po zamknięciu
pętli sprzężenia zwrotnego układ ten stanie się stabilny. Po zamknięciu pętli sprzężenia
zwrotnego uzyskujemy układ o transmitancji :

5

.

0

6

.

0

1

1

.

0

)

(

2

+

+

+

=

s

s

s

s

Tz

, którego pierwiastki leżą w lewej półpłaszczyźnie zmiennej

zespolonej s

1

=-0.3+j0,6403 oraz s

2

=-0.3-j0,6403 oraz

-2

-1.5

-1

-0.5

0

0.5

-0.5

-0.4

-0.3

-0.2

-0.1

0

0.1

0.2

0.3

0.4

0.5

Nyquist Diagram

Real Axis

Im

a

g

in

a

ry

A

x

is

Komendy w Matlabie:

Ts=tf([0.1 1],[1 0.5 -0.5]);

nyquist(Ts);
Tsz=feedback(Ts);
P=roots([1 0.6 0.5]);

Przykład 3

Obiekt o transmitancji

1

2

2

)

(

2

3

+

+

+

=

s

s

s

k

s

G

pracuje w układzie zamkniętym z regulatorem proporcjonalno-całkującym o transmitancji













+

=

s

T

k

G

i

p

r

1

1













+

=

s

T

k

G

i

p

r

1

1

1

2

2

)

(

2

3

+

+

+

=

s

s

s

k

s

G

Rys.

Błąd! Nie zdefiniowano zakładki. Schemat układu zamkniętego z obiektem

statycznym trzeciego rzędu i regulatorem PJ

Transmitancja układu otwartego

)

(

)

(

)

(

s

G

s

G

s

G

r

o

=

Rozpatrzymy dwa przypadki regulacji: z regulatorem nastawionym na działanie wyłącznie
proporcjonalne i drugi – z regulatorem proporcjonalno-całkującym.

a) Przyjmiemy wzmocnienie obiektu k = 1 oraz wyłączamy działanie całkujące

regulatora przez nastawienie czasu izodromu

∞

→

i

T

.

Stąd mamy

1

2

2

)

(

2

3

+

+

+

=

s

s

s

k

s

G

p

o

Za pomocą polecenia

nyquist z pakietu MATLAB-a, wykonamy wykresy charakterystyk

amplitudowo-fazowych układu otwartego Go(jw) dla trzech wartości wzmocnienia regulatora
k

p

=2, 3 i 4.

-3

-2

-1

0

1

2

3

4

-4

-3.5

-3

-2.5

-2

-1.5

-1

-0.5

0

0.5

1

W ykres Nyquista Go(jw)

P (w)

Q

(w

)

k p= 2

k p= 3

k p= 4

w

Rys.

Błąd! Nie zdefiniowano zakładki. Charakterystyki amplitudowo-fazowe układu

otwartego Go(jw) dla k

p

= 2, 3, 4

Wykresy Nyquista układu otwartego Go(jw) obejmują trzy charakterystyczne przypadki
regulacji. W pierwszym z nich dla k

p

= 2 charakterystyka Go(jw) przy zwiększaniu

częstotliwości

∞

do

od 0

ω

nie obejmuje punktu (-1,j0) – układ zamknięty jest wtedy

stabilny. W drugim przypadku dla k

p

= 3 charakterystyka G(jw) przechodzi przez punkt (-

1,j0) – układ jest na granicy stabilności. Wreszcie dla k

p

= 4 charakterystyka Go(jw) przy

wzroście

∞

do

od 0

ω

obejmuje punkt (-1,j0) – układ po zamknięciu sprzężenia zwrotnego

będzie niestabilny.
Potwierdzenie tego znajdujemy przez stwierdzenie położenia biegunów transmitancji układu
zamkniętego na płaszczyźnie zmiennej zespolonej.
Wyznaczamy transmitancję układu zamkniętego

1

2

2

)

(

1

)

(

)

(

2

3

+

+

+

+

=

+

=

p

p

o

o

z

k

s

s

s

k

s

G

s

G

s

G

A stąd równanie charakterystyczne układu

0

1

2

2

)

(

2

3

=

+

+

+

+

=

p

z

k

s

s

s

s

M

Wyznaczamy pierwiastki równania charakterystycznego za pomocą polecenia

roots z pakietu

MATLAB-a,

dla k

p

= 2 mamy

s

1

= -1.8105

s

2

= -0.0947 + 1.2837j

s

3

= -0.0947 - 1.2837j

Jak widać wszystkie pierwiastki mają części rzeczywiste ujemne, czyli istotnie układ
zamknięty spełnia warunek konieczny i dostateczny stabilności.
Obliczamy z kolei pierwiastki dla k

p

=3

s

1

= - 2.0000

s

2

= 0.0000 + 1.4142j

s

3

= 0.0000 - 1.4142j

W tym przypadku występują pierwiastki urojone sprzężone, zatem układ zamknięty jest na
granicy stabilności.
W końcu dla k

p

= 4, mamy pierwiastki

s

1

= -2.1509

s

2

= 0.0755 + 1.5228j

s

3

= 0.0755 - 1.5228j

Tym razem występują pierwiastki zespolone sprzężone, których części rzeczywiste są
dodatnie, wobec tego układ zamknięty jest dla tego przypadku niestabilny.
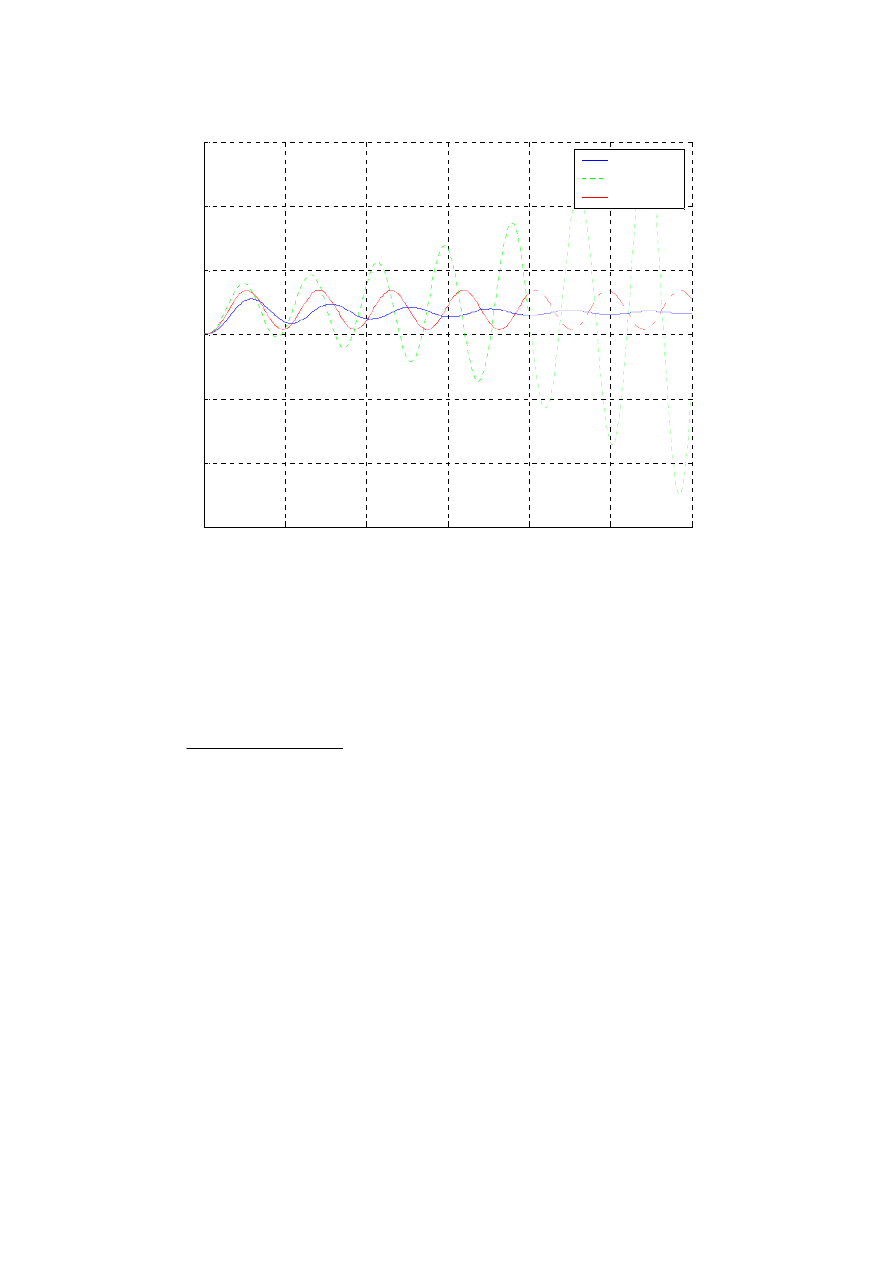
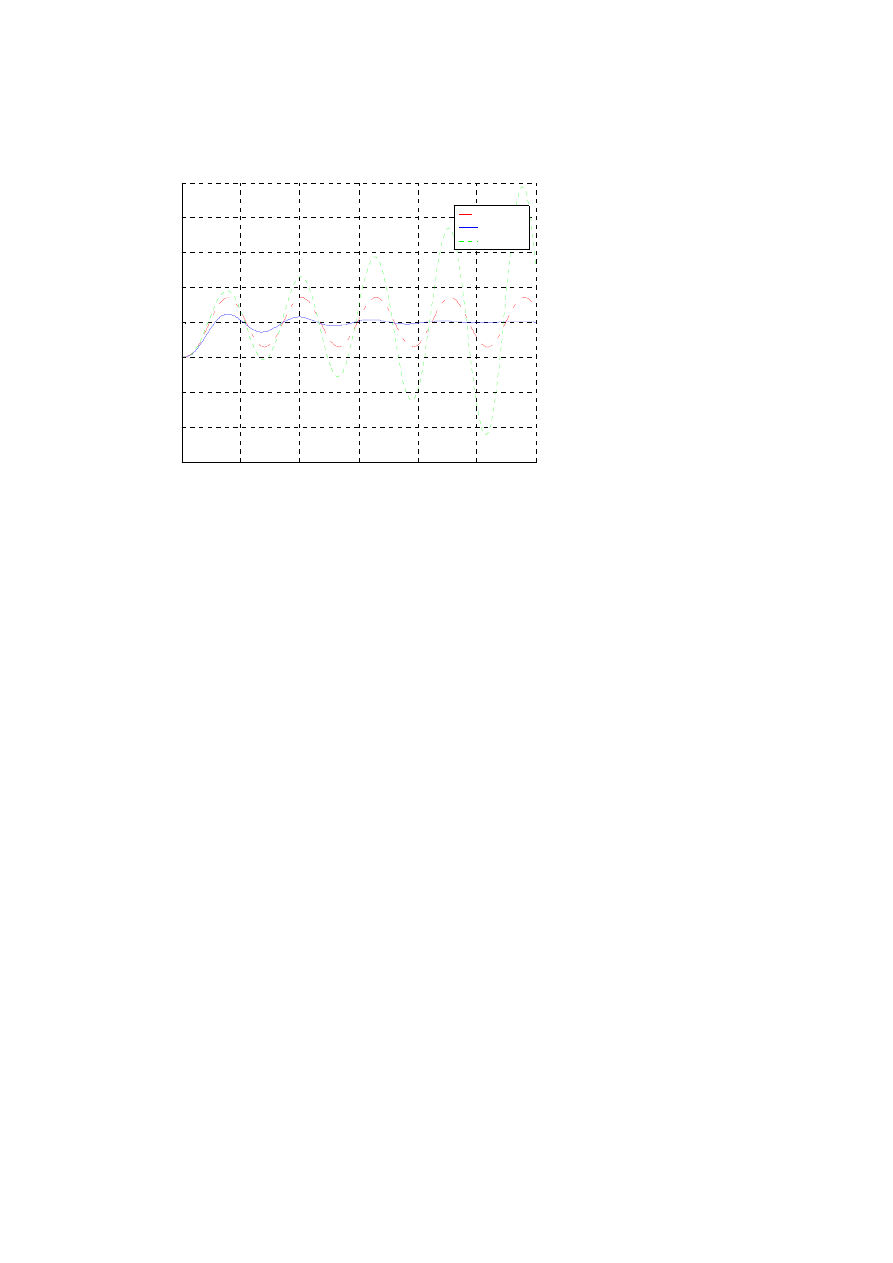
Innym sposobem jak najbardziej wizualnym, zaprezentowania reakcji układu zamkniętego na
zakłócenie w postaci skoku jednostkowego przyłożonego do jego wejścia, jest przedstawienie
przebiegów charakterystyk skokowych.

0

5

10

15

20

25

30

-6

-4

-2

0

2

4

6

Cz as [s ek]

W

y

js

c

ie

Reakcja układu zamkni

ę

tego na skok jednostkowy

dla k p= 2
dla k p= 4
dla k p= 3

Rys.

Błąd! Nie zdefiniowano zakładki. Odpowiedzi układu zamkniętego z regulatorem

proporcjonalnym na zakłócenie na wejściu w postaci skoku jednostkowego

b) Zbadamy teraz stabilność układu zamkniętego z regulatorem proporcjonalno-

całkującym dla stałego wzmocnienia regulatora kp = 1 i różnych wartości czasu izodromu.

Wykonujemy charakterystyki amplitudowo-fazowe układu otwartego

)

1

2

2

(

)

1

(

)

(

2

3

+

+

+

+

=

s

s

s

s

T

s

T

kk

s

G

i

i

p

o

-2

-1.8

-1.6

-1.4

-1.2

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

-5

-4.5

-4

-3.5

-3

-2.5

-2

-1.5

-1

-0.5

0

0.5

W ykres Nyquista Go(jw)

P (w)

Q

(w

)

w

Ti = 0,8

Ti = 1

Ti = 2

Rys. 4 Charakterystyki amplitudowo-fazowe układu otwartego Go(jw) z regulatorem

proporcjonalno-całkującym przy k

p

= 1 dla czasu izodromu T

i

= 0,8, 1 i 2

Układ otwarty jest w tym przypadku astatyczny ze względu na akcję całkującą regulatora.
Charakterystyka Nyquista biegnie po ujemnych wartościach od minus nieskończoności do
zera przy zwiększaniu częstotliwości od zera do nieskończoności.

Jeżeli wykres G

o

(jw) przechodzi przez punkt (-1,j0), to układ zamknięty jest na granicy

stabilności, a na jego wyjściu występują drgania o ustalonej amplitudzie, jak na wykresie dla
T

i

= 1 na rys. 5.

Transmitancja układu zamkniętego z regulatorem PI przyjmuje postać:

p

p

i

i

i

i

i

p

z

kk

kk

s

T

s

T

s

T

s

T

s

T

kk

s

G

+

+

+

+

+

+

=

)

1

(

2

2

)

1

(

)

(

2

3

4

Stąd dla przyjętych wartości parametrów układu otrzymujemy przebiegi charakterystyk
skokowych jak na rys. 5.

0

5

10

15

20

25

30

-3

-2

-1

0

1

2

3

4

5

Cz as [sek ]

O

d

p

o

w

ie

d

z

C harakterystyka skokowa

Ti = 1
Ti = 2
Ti = 0,8

Rys. 5 Reakcja układu zamkniętego z regulatorem proporcjonalno-całkującym na

zakłócenie na jego wejściu w postaci skoku jednostkowego

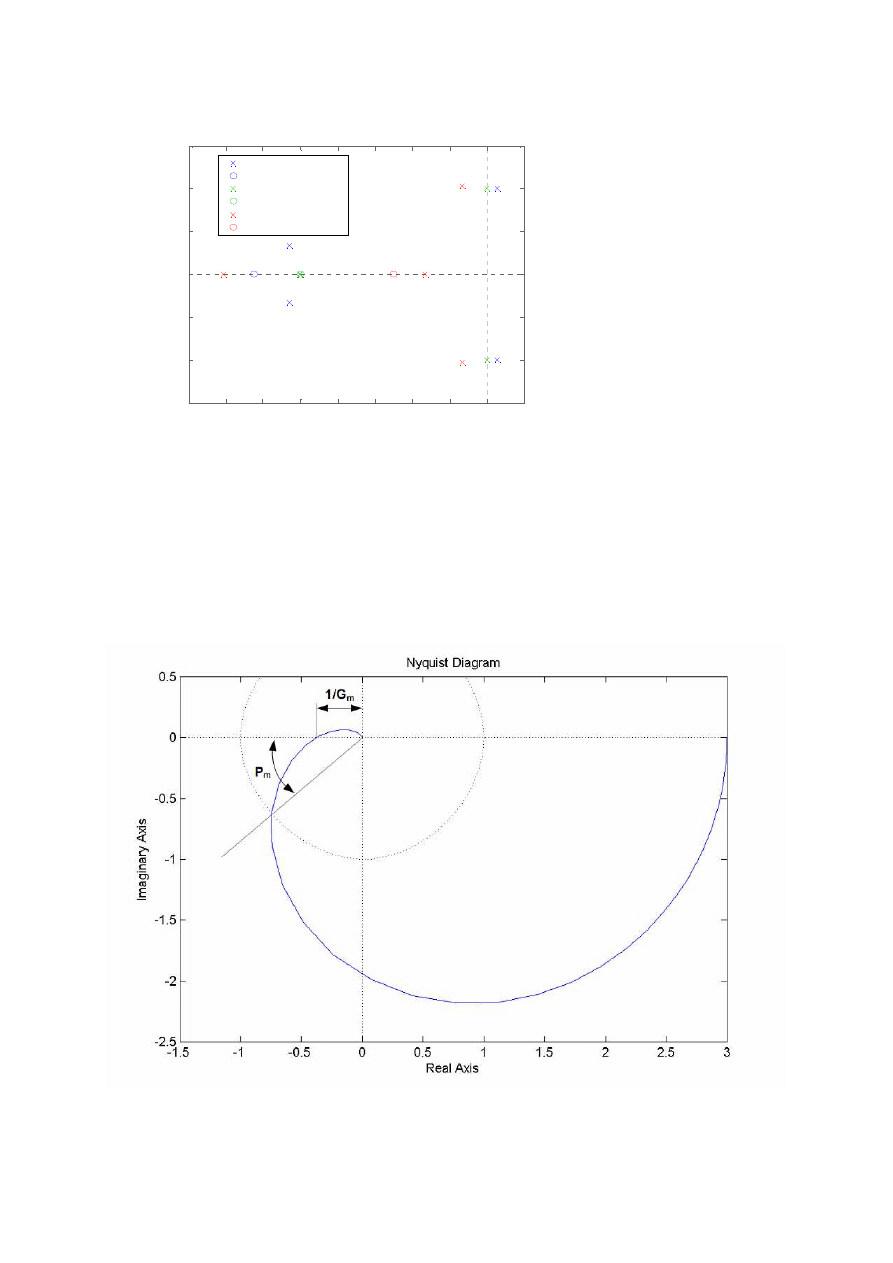
Zbadamy teraz położenie biegunów transmitancji układu zamkniętego z regulatorem
proporcjonalno-całkującym. Posłużymy się tym razem poleceniem

pzmap MATLAB-a, które

tworzy wykres na płaszczyźnie zmiennej zespolonej z zaznaczonymi biegunami i zerami
transmitancji układu zamkniętego. Jak widać na rys. 6 dla Ti = 0,8 dwa bieguny transmitancji
mają części rzeczywiste dodatnie, więc układ zamknięty jest dla tej wartości czasu izodromu
– niestabilny. Dla Ti = 1 układ ma dwa bieguny położone na osi urojonej, zatem jest na
granicy stabilności. I wreszcie dla Ti = 2 wszystkie bieguny leżą w lewej półpłaszczyźnie,
czyli układ jest w tym przypadku stabilny.

-1.6

-1.4

-1.2

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

-1.5

-1

-0.5

0

0.5

1

1.5

B ieguny dla Ti = 0,8
Zero dla Ti = 0,8
Ti = 1
Ti = 1
Ti = 2
Ti = 2

Mapa zer i biegunów

Real A xis

Im

a

g

in

a

ry

A

x

is

Rys.

Błąd! Nie zdefiniowano zakładki. Rozkład biegunów i zer transmitancji układu

zamkniętego

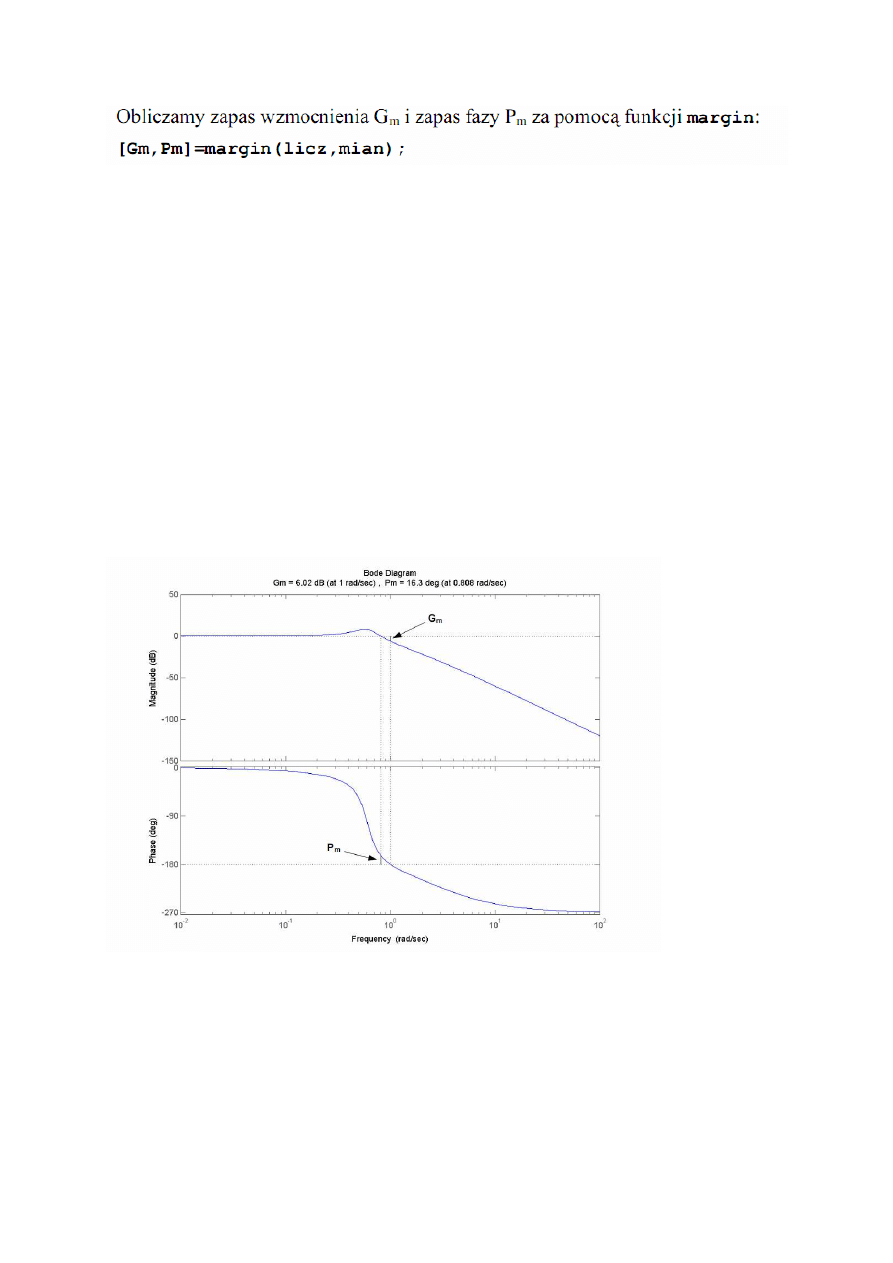
Zapas stabilności – Nyguist

Zapas wzmocnienia Gm – odwrotność długości odcinka wyznaczonego przez początek
układu współrzędnych oraz punkt przecięcia wykresu Nyquista z ujemną półosią Re(G(jω)).

Zapas fazy Pm – kąt między półprostą wychodzącą z początku układu współrzędnych i
przechodzącą przez punkt przecięcia wykresu Nyquista z kołem jednostkowym.

Wyznaczenie zapasu wzmocnienia i zapasu fazy na podstawie wykresów Bodego

Zapas wzmocnienia Gm (ang. gain margin) – wartość wzmocnienia, dla którego faza osiąga -
180°. Jego wartość oznacza o ile można zwiększyć wzmocnienie zanim stracimy stabilność.

Zapas fazy Pm (ang. phase margin) – wartość fazy dla częstotliwości, przy której zmocnienie
wynosi 1 (0 dB). Jego wartość oznacza o ile można zmniejszyć przesunięcie fazowe zanim
stracimy stabilność.
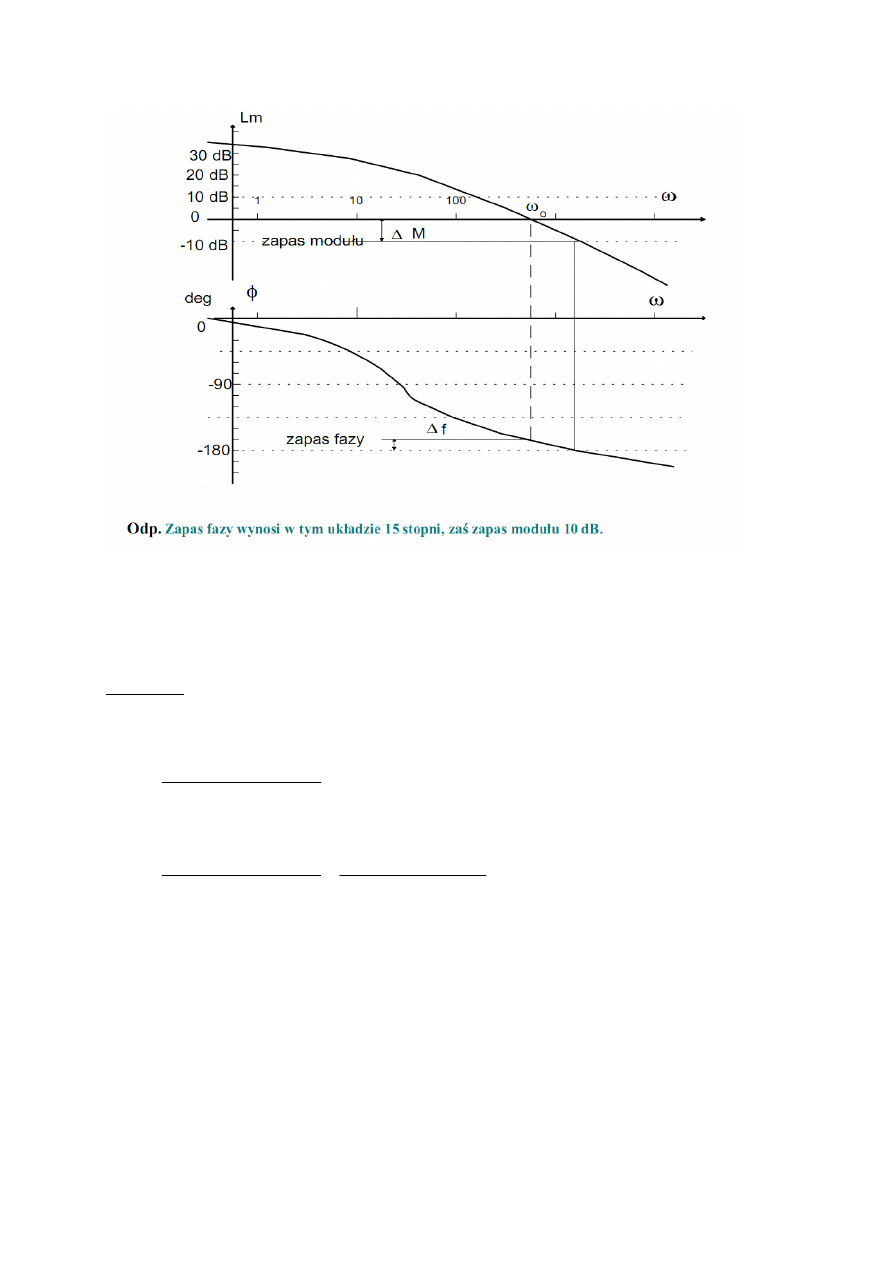
W celu wyznaczenia zapasu fazy należy wyznaczyć tzw. pulsację odcięcia, tj. pulsacje ,która
spełnia warunek 20lg M(ωo)=0 a następnie określić fazę Φ(ωo). Zapasem fazy określa się
sumę ∆f= 180 - Φ(ωo) [deg] Jeśli jest ona dodatnia układ jest stabilny z zapasem fazy ∆f,
który mówi o tym, o ile można zwiększyć fazę układu otwartego bez zmiany jego
wzmocnienia, aby układ pozozstawał jeszcze stabilnym . Zapas modułu można wyznaczyć
określając ω dla której Φ(ω -Π) = -180 deg a następnie pomierzyć dla tej samej pulsacji
moduł Lm(ω -Π) . Jest on równy zapasowi modułu, gdyż właśnie o tyle można zwiększyć
moduł w układzie, aby przy niezmiennej fazie pozostawał on stabilny. Aby wyznaczyć, o ile
można zwiększyć wzmocnienie układu otwartego, należy skorzystać z zależności: Lm=20lgK
.

Przykład 4

Model o transmitancji :

)

3

.

0

7

.

0

1

.

0

(

5

.

0

)

(

2

3

+

+

+

=

s

s

s

s

s

K

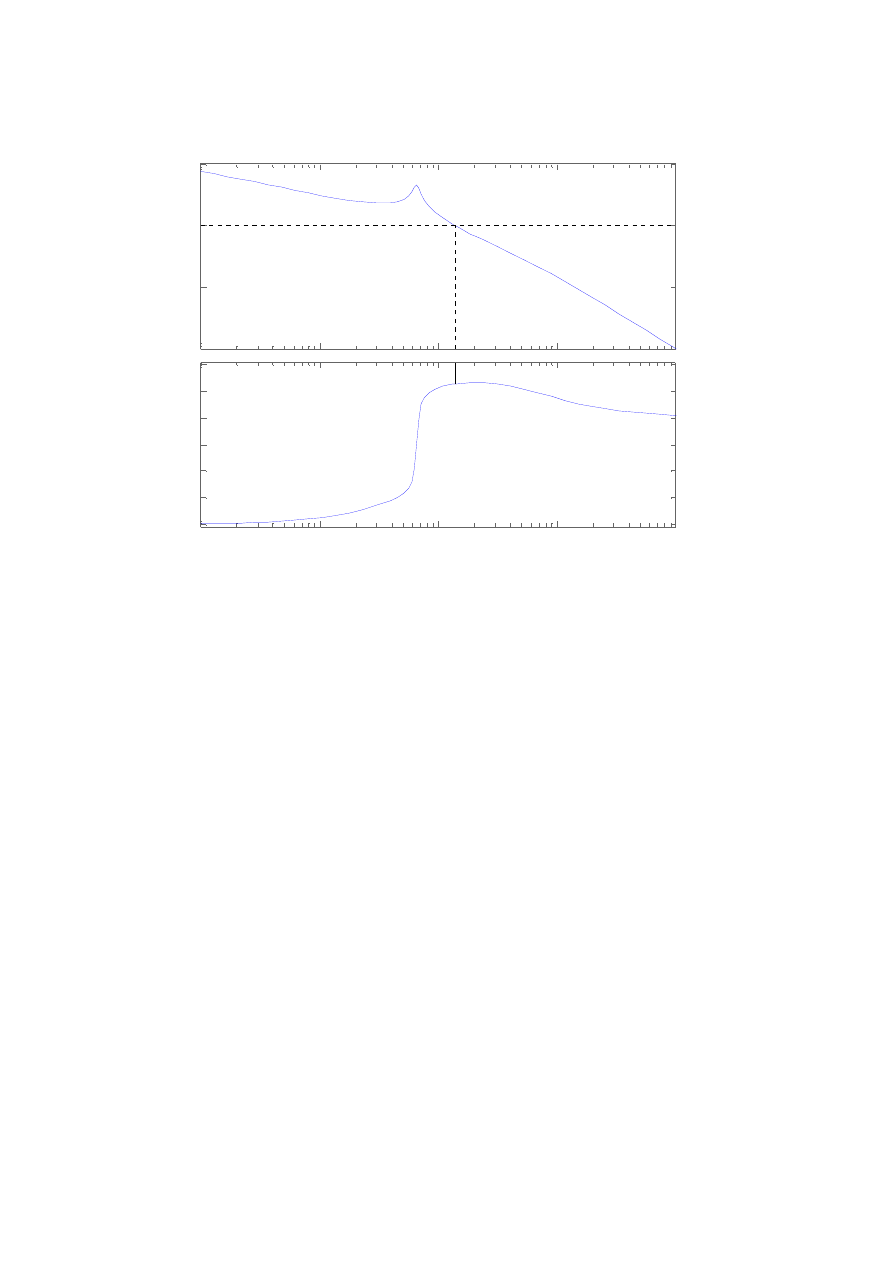
Wyznaczyć zapas amplitudy i fazy na charakterystyce Bodego.

s

s

s

s

s

s

s

s

s

K

3

.

0

7

.

0

1

.

0

5

.

0

)

3

.

0

7

.

0

1

.

0

(

5

.

0

)

(

3

4

2

3

+

+

+

=

+

+

+

=

Komendy w Matlabie:

Ks=tf([1 0.5],[0.1 0.7 0 0.3 0])

Figure(1),margin(Ks);
k=roots([0.1 0.7 0 0.3 0])
figure(2),nyquist(Ks);

-100

-50

0

50

M

a

g

n

itu

d

e

(

d

B

)

10

-2

10

-1

10

0

10

1

10

2

-450

-405

-360

-315

-270

-225

-180

P

h

a

s

e

(

d

e

g

)

Bode Diagram

Gm = Inf , Pm = -34.2 deg (at 1.38 rad/sec)

Frequency (rad/sec)

Biegunami modelu są liczby s

1

=0, s

2

=-7.0602 , s

3

=0.0301+j0.6512 , s

4

=0.0301-j0.6512

Model ten jest niestabilny, co rozpoznajemy po wartościach biegunów modelu. Dwa z nich
(s3,s4) znajdują się w prawej półpłaszczyźnie zmiennej zespolonej. Według tw. Nyquista
zamknięcie pętli sprzężenia zwrotnego ustabilizuje model tylko wtedy, gdy charakterystyka
modelu dwukrotnie obejmuje punkt Nyquista przy zmianie pulsacji od -∞ do ∞. Ponieważ
charakterystyka fazowa znajduje się poniżej linii odpowiadającej przesunięciu fazowemu –π
to punkt Nyquista nie jest obejmowany przez nią ani razu. Objęcie danego modelu pętlą
sprzężenia zwrotnego nie ustabilizuje go. Charakterystykę pokazano poniżej.

-10

-5

0

5

10

15

20

25

30

35

40

-60

-40

-20

0

20

40

60

Nyquist Diagram

Real Axis

Im

a

g

in

a

ry

A

x

is

Kryterium stabilności Michałowa

Układ jest stabilny asymptotycznie, jeżeli charakterystyka amplitudowo-fazowa mianownika
transmitancji przebiega kolejno, w lewo przez tyle ćwiartek płaszczyzny zespolonej s ile
wynosi stopień tego mianownika., tzn charakterystyki układów stabilnych przebiegają
kolejno, w lewo przez tyle ćwiartek płaszczyzny ile wynosi ich rząd, gdy pulsacja dąży do
nieskończoności.