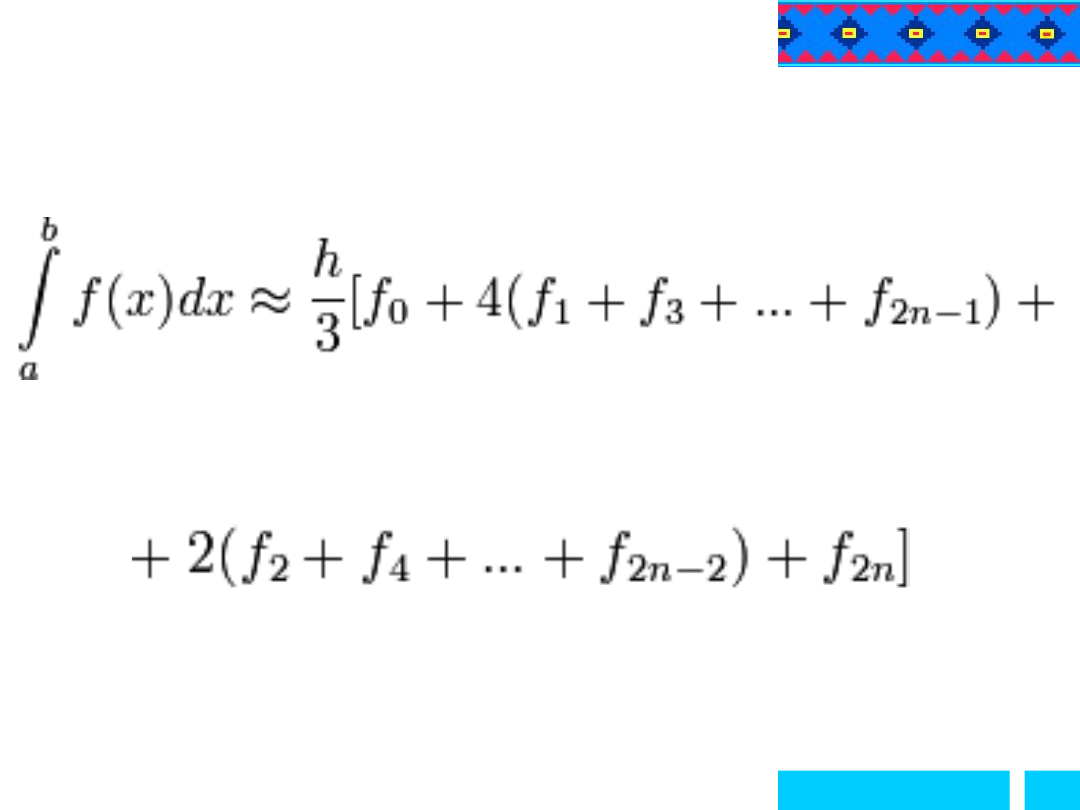Jadwiga Chudzicka 1

Jadwiga Chudzicka 2

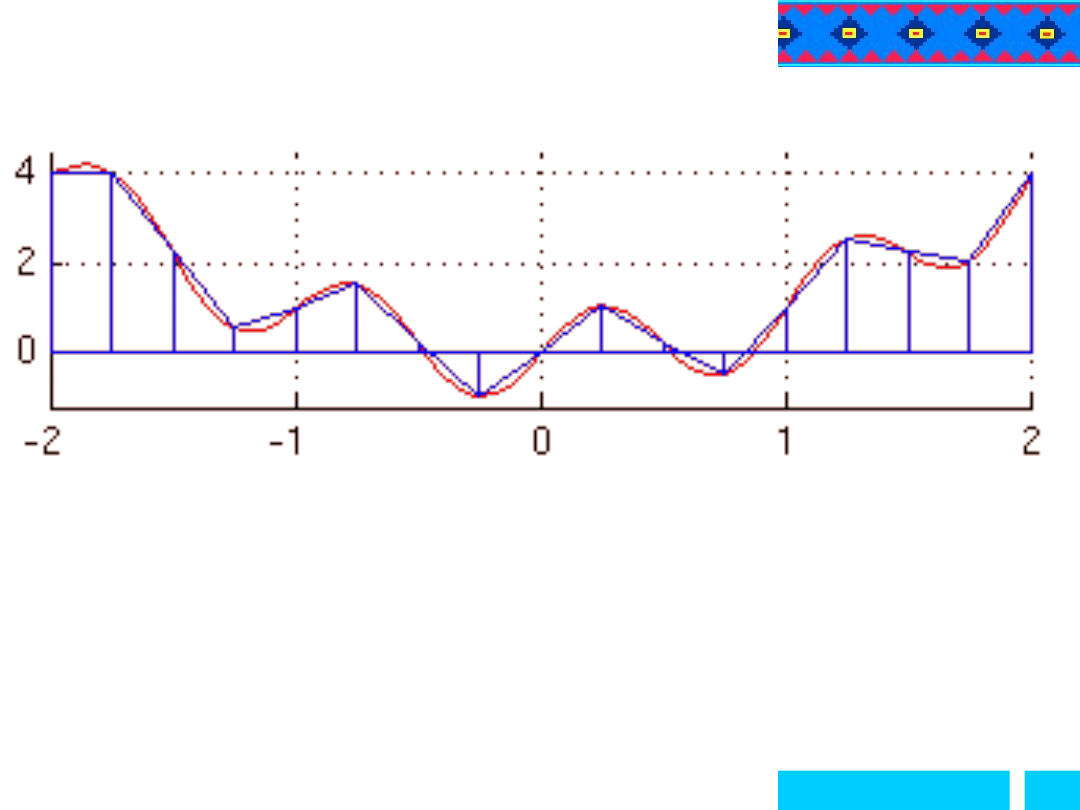
Metoda trapezów

Metoda trapezów polega na tym, że figurę ABCD 
zastępujemy figurą złożoną z trapezów wpisanych, tzn. 
krzywą aproksymujemy linią łamaną w nią wpisaną. 

. 

Przedział całkowania (a,b) dzielimy przy tym na n równych 
części o długościach: h= (b – a) / n

Jadwiga Chudzicka 3

Punktami podziału (końcami części) są wówczas:

Wówczas pole figury złożonej z trapezów wynosi

Gdzie y

i

: = f(x

i

) – wartości funkcji w punktach podziału. 

Jadwiga Chudzicka 4

Stąd otrzymujemy wzór przybliżony w metodzie trapezów:

Oszacowanie błędu tej metody wynosi

gdzie

PROGRAM

Jadwiga Chudzicka 5

Przedstawiony dalej program w Delphi 7 

służy do całkowania funkcji f(x) w 
przedziale [a, b] dla zadanej liczby 
podprzedziałów m z wykorzystaniem 4 
rodzajów złożonych kwadratur:

1) wzoru trapezów,

2) wzoru parabol,

3) wzoru Gaussa z dwoma węzłami,

4) wzoru Gaussa z trzema węzłami.

Jadwiga Chudzicka 6

W programie przyjęto m = 10 i obliczono 3 całki o wartościach:

099

056

389

,

6

1

2

2

0

≈

−

=

∫

e

dx

e

x

181

147

693

.

0

2

ln

1

1

0

≈

=

+

∫

x

dx

474

717

398

.

1

3

1

3

2

1

1

0

≈

−

=

+

∫

dx

x

Wg wzoru trapezów:
0,693 7…
Wg wzoru Simpsona:
0,693 15…

SIMPSON

PODSUMOWANIE

Jadwiga Chudzicka 7

unit Unit1;

interface

uses

  Windows, Messages, SysUtils, Variants, Classes, 
Graphics, 

  Controls, Forms,   Dialogs, StdCtrls, ExtCtrls;

Program w Delphi 7

type

  TForm1 = class(TForm)

    Label5: TLabel; Button1: TButton; Button2: TButton;

    Button3: TButton; GroupBox1: TGroupBox;

Jadwiga Chudzicka 8

SaveDialog1: TSaveDialog; LabeledEdit1: TLabeledEdit;
LabeledEdit2: TLabeledEdit; LabeledEdit3: TLabeledEdit;
RadioButton1: TRadioButton; RadioButton2: TRadioButton;
RadioButton3: TRadioButton; LabeledEdit4: TLabeledEdit;
LabeledEdit5: TLabeledEdit; LabeledEdit6: TLabeledEdit;
LabeledEdit7: TLabeledEdit;
procedure FormShow(Sender: TObject);
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure Button3Click(Sender: TObject);
private
    { Private declarations }
public
    { Public declarations }
    function ZapiszWyniki:Boolean;
end;   

Jadwiga Chudzicka 9

var

  Form1: TForm1;

implementation

{$R  *.dfm}

function TForm1.ZapiszWyniki:Boolean;

var

  plik:TextFile;

begin

  if SaveDialog1.Execute then

    begin

      AssignFile(plik,SaveDialog1.FileName);

      Rewrite(plik);

Jadwiga Chudzicka 10

      Writeln(plik,'Program 5.1.');
      Writeln(plik,'Obliczanie całki oznaczonej.');
      Writeln(plik,'Funkcja podcałkowa: ');
      if RadioButton1.Checked = True then
         Writeln(plik,'f = Exp(x).');
      if RadioButton2.Checked = True then
         Writeln(plik,'f = 1/(1+x).');
      if RadioButton3.Checked = True then
         Writeln(plik,'f = Sqrt(1+2*x).');
      Writeln(plik,' ');
      Writeln(plik,'Granice całkowania:');
      Writeln(plik,'   a = ',StrToFloat(LabeledEdit1.Text));
      Writeln(plik,'   b = ',StrToFloat(LabeledEdit2.Text));

        

Writeln(plik,'Liczba podprzedziałów - m = ', 

      StrToInt(LabeledEdit3.Text));
      Writeln(plik,' ');

3 różne 
funkcje 
podcałkowe

Jadwiga Chudzicka 11

 Writeln(plik,'Obliczone wartości całki:');

      Writeln(plik,'1) wzór trapezów     - I = 
',StrToFloat(LabeledEdit4.Text));

      Writeln(plik,'1) wzór parabol      - I = 
',StrToFloat(LabeledEdit5.Text));

      Writeln(plik,'1) wzór Gaussa (n=2) - I = 
',StrToFloat(LabeledEdit6.Text));

      Writeln(plik,'1) wzór Gaussa (n=3) - I = 
',StrToFloat(LabeledEdit7.Text));

      CloseFile(plik);
      Result:=True;
    end

  else Result:=False;

end;

Koniec funkcji TForm1

Jadwiga Chudzicka 12

procedure TForm1.Button1Click(Sender: TObject);

var

    m: Integer;    a,b: Real;

label powt;

function f(x: Real): Real;

begin

  if RadioButton1.Checked = True then  f:=Exp(x);

  if RadioButton2.Checked = True then  f:=1/(1+x);

  if RadioButton3.Checked = True then  f:=Sqrt(1+2*x);

end;

Jadwiga Chudzicka 13

function Calka1(a,b: Real; m: Integer): Real;
{złożony wzór trapezów}
var

    i: Integer;   h,s,x: Real;

begin

    h:=(b-a)/m;

    s:=(f(a)+f(b))/2;

    for i:=1 to m-1 do begin

        x:=a+i*h;

        s:=s+f(x);

    end;

    Calka1:=s*h;

end;

m – liczba 
podprzedziałów

Jadwiga Chudzicka 14

function Calka2(a,b: Real; m: Integer): Real;
{złożony wzór parabol}
var
    k,q: Integer; h,s1,s2,x1,x2: Real;
begin
    h:=(b-a)/m;   q:=m div 2;    s1:=0;    s2:=0;

    for k:=1 to q do begin

        x1:=a+(2*k -1)*h;   s1:=s1+f(x1);

    end;

    for k:=1 to q -1 do begin
       x2:=a+2*k*h;    s2:=s2+f(x2);
    end;
    Calka2:=h*(f(a)+f(b)+4*s1+2*s2)/3;
end;

m – liczba 
podprzedziałów

s1 – suma w 
punktach 
nieparzystych

s2 – suma 
w punktach 
parzystych

Jadwiga Chudzicka 15

function Calka3(a,b: Real; m: Integer): Real;
{złożony wzór Gaussa z dwoma węzłami}
var
     i: Integer;     h,s,t0,t1,x0,x1,xp: Real;

begin

     s:=0;

     h:=(b-a)/m;

     t0:=-1/Sqrt(3);

     t1:=1/Sqrt(3);

     for i:=1 to m do begin

         xp:=a+(i-1)*h+h/2;

         x0:=xp+h*t0/2;

         x1:=xp+h*t1/2;

         s:=s+(f(x0)+f(x1));

     end;

     Calka3:=s*h/2;

end;

Jadwiga Chudzicka 16

function Calka4(a,b: Real; m: Integer): Real;
{złożony wzór Gaussa z trzema węzłami}
var
     i: Integer;    h,s,t0,t1,t2,x0,x1,x2,xp: Real;
begin
     s:=0;   h:=(b-a)/m;

     t0:=-Sqrt(3/5);     t1:=0;

     t2:=Sqrt(3/5);

     for i:=1 to m do begin

         xp:=a+(i-1)*h+h/2;

         x0:=xp+h*t0/2;

         x1:=xp+h*t1/2;

       x2:=xp+h*t2/2;

         s:=s+(5*f(x0)+8*f(x1)+5*f(x2));

     end;

     Calka4:=s*h/18;

end;

Jadwiga Chudzicka 17

begin

    a:=StrToFloat(LabeledEdit1.Text);

    b:=StrToFloat(LabeledEdit2.Text);

    m:=StrToInt(LabeledEdit3.Text);

    if (m div 2)*2<>m then begin

       m:=m+1;

       end;

    LabeledEdit4.Text:=FloatToStrF(Calka1(a,b,m),ffExponent,12,12);

    LabeledEdit5.Text:=FloatToStrF(Calka2(a,b,m),ffExponent,12,12);

    LabeledEdit6.Text:=FloatToStrF(Calka3(a,b,m),ffExponent,12,12);

    LabeledEdit7.Text:=FloatToStrF(Calka4(a,b,m),ffExponent,12,12);

end;

Jadwiga Chudzicka 18

procedure TForm1.Button2Click(Sender: TObject);
begin
  ZapiszWyniki;
end;

procedure TForm1.Button3Click(Sender: TObject);
begin
  Close;
end;

procedure TForm1.FormShow(Sender: TObject);
begin
  RadioButton1.Checked:=True;
  LabeledEdit1.Text:='0';
  LabeledEdit2.Text:='2';
  LabeledEdit3.Text:='10';
  SaveDialog1.InitialDir:=ExtractFilePath(Application.ExeName);
end;

end. 

Koniec programu

Jadwiga Chudzicka 19

Metoda parabol (Simpsona)

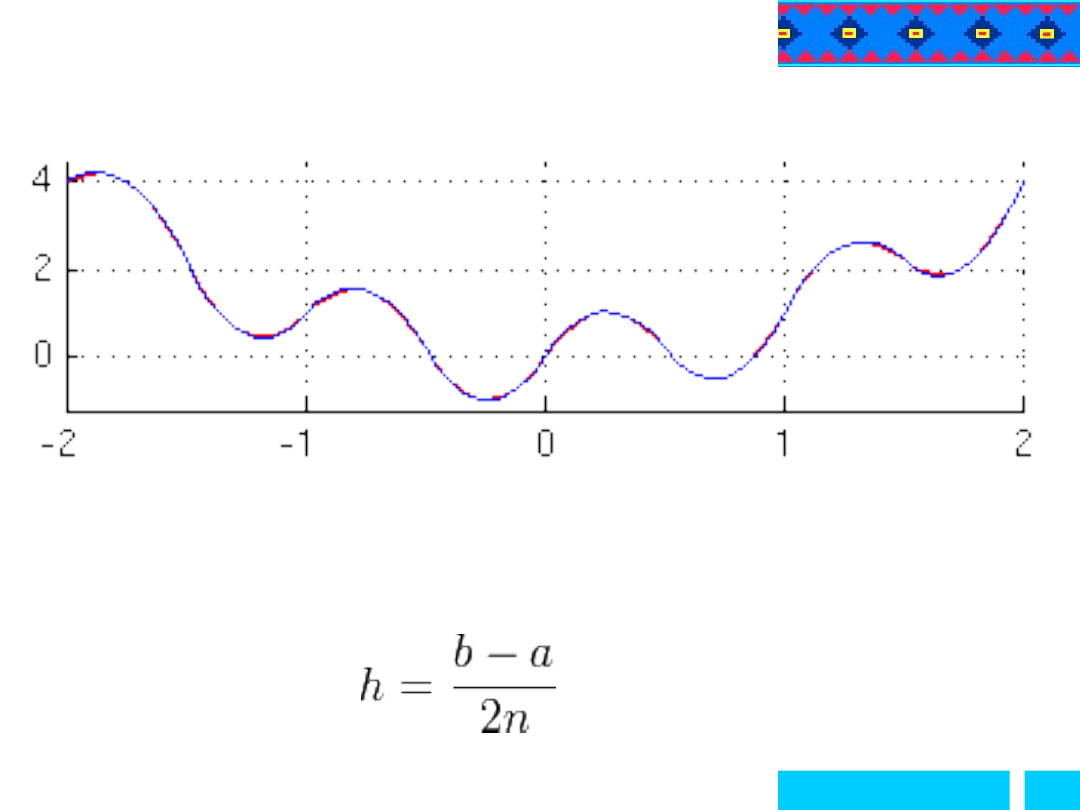
Wymaga podzielenia przedziału całkowania na parzystą liczbę 
podprzedziałów, tzn.

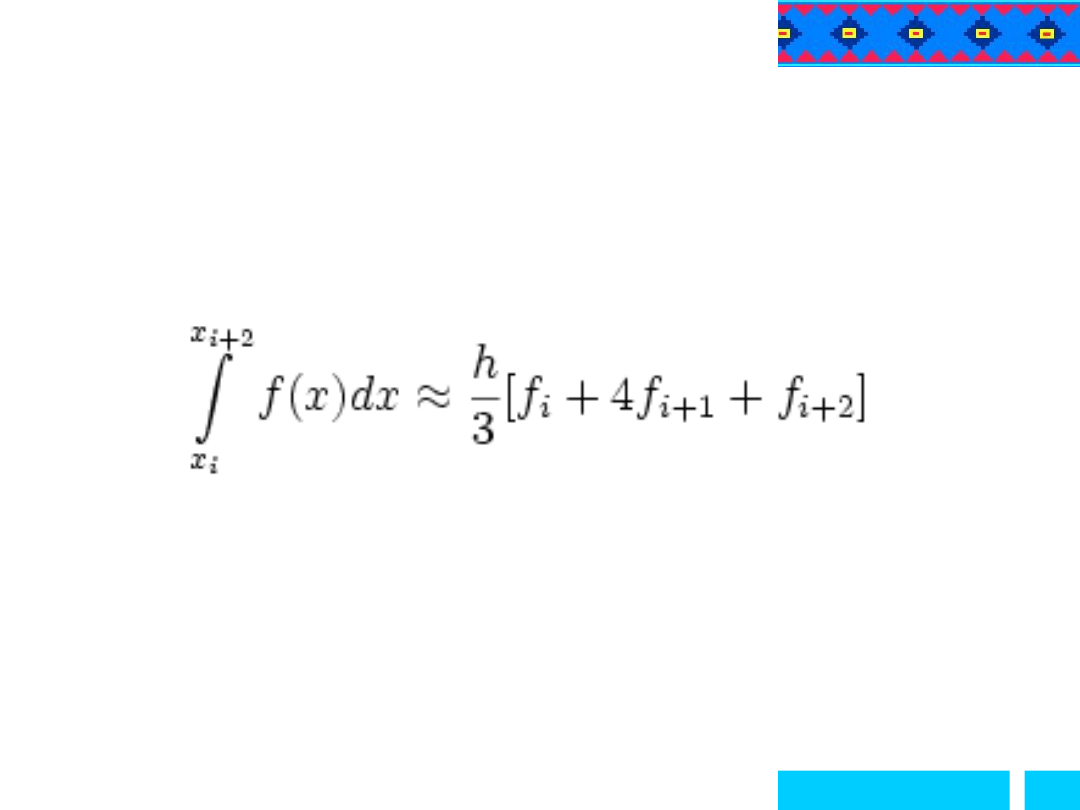
Jadwiga Chudzicka 20

Wykonując całkowanie wielomianu interpolacyjnego Lagrange'a 
z 3 kolejnych punktów otrzymujemy wzór Simpsona:

dla uproszczenia oznaczamy: x

i

 = a + ih    oraz f

i

 = f(x

i

) 

Zamiast trapezami zastępujemy f. podcałkową na danym 
odcinku parabolą opartą na 3 p-ktach: w wierzchołku i na 
końcach odcinka. Stąd 2 podprzedziały na każdym odcinku.

Jadwiga Chudzicka 21

Dla całego przedziału (a,b) otrzymujemy:

PROGRAM

Jadwiga Chudzicka 22

Złożony wzór trapezów i złożony wzór parabol 
są szczególnymi przypadkami złożonych 
kwadratur Newtona-Cotesa. Są to kwadratury 
otrzymane przez całkowanie wielomianów 
interpolacyjnych opartych na równoodległych 
węzłach: 
x

0

 = a,   x

1

 = a + h, …,  x

n

 = a + nh = b.

Kwadratury Newtona-Cotesa mają więc ustalone 
węzły. Natomiast w kwadraturach Gaussa 
dobierane są współczynniki i węzły x

i 

w taki sposób, 

aby kwadratura była dokładna dla możliwie 
najwyższego stopnia wielomianu.