127

 
 
 
 

 
 
W

OJCIECH 

Z

EŃCZAK

1

 

 

 

MODEL MATEMATYCZNY OGNIWA PALIWOWEGO W STANACH 

USTALONYCH 

 

Streszczenie 

 

W oparciu o podstawowe równania opisujące właściwości termodynamiczne 
i 

elektrochemiczne zbudowano prosty model matematyczny ogniwa paliwowego 

wodorowo tlenowego zaimplementowany w środowisku programu Mathcad. Za pomocą 
programu można uzyskać przebiegi charakterystyki prądowo-napięciowej, a także 
krzywej sprawności ogniwa. Możliwe jest także badanie wpływu ciśnienia i temperatury 
substratów i produktów biorących udział w reakcji zachodzącej w ogniwie a także 
koncentracji tlenu w powietrzu na wartość siły elektromotorycznej ogniwa. W referacie 
przedstawiono również przykład obliczeniowy. 

 

 

1. WPROWADZENIE 

Zainteresowanie ogniwami paliwowymi do różnych zastosowań, w tym także 

w okrętowych systemach energetycznych, rośnie w miarę wyczerpywania się zasobów paliw 
kopalnych i wzrostu ich cen. Stosowanie nowych technologii energetycznych, do których zalicza 
się ogniwa paliwowe, wymuszane jest także coraz bardziej przez przepisy ochrony środowiska 
np. zawarte w aneksie VI do konwencji MARPOL 73/78 obowiązujące na całym świecie, czy też 
przepisy regionalne obowiązujące w krajach Unii Europejskiej, Japonii czy USA [1]. Warto 
wspomnieć także o wielu zaletach ogniw paliwowych w stosunku do silników cieplnych jak np. 
osiąganie większych sprawności, pomijalnie niska emisja związków toksycznych, niskie koszty 
eksploatacji, cicha praca i brak zanieczyszczeń ropopochodnych, które także są przyczyną dużego 
nimi zainteresowania. Upowszechnieniu ogniw w okrętownictwie szczególnie sprzyja także 
rozwijana i upowszechniana koncepcja statku w pełni zelektryfikowanego (all electric ships). 
Możliwe zastosowania ogniw paliwowych w okrętownictwie przedstawiono m. in. w [2]. Tam też 
zaprezentowano wybrane wyniki badań eksperymentalnych ogniw paliwowych w aspekcie 
zastosowań morskich, które przeprowadzono w laboratorium Fachhochschule Stralsund w 
Niemczech. Do badań eksperymentalnych jednak niezbędne są posiadanie ogniwa i dostęp do 
odpowiedniej infrastruktury laboratoryjnej. Stąd też wiele badań ogniw paliwowych wykonuje się 
przy użyciu modeli matematycznych i programów komputerowych. Programy do badania ogniw 
paliwowych są dostępne także w Polsce jednakże są one bardzo drogie i niewiele ośrodków 
badawczych w Polsce stać na ich zakup. Dla wielu analiz, w tym także dla celów dydaktycznych, 
wystarczą jednak znacznie mniej złożone modele, które w zadawalający sposób pozwalają na 
przedstawienie istotnych charakterystyk ogniw paliwowych. Stąd też podjęto próbę opracowania 
modelu matematycznego zerowymiarowego „0D” ogniwa paliwowego wodorowo tlenowego, 
który w połączeniu ze środowiskiem programu Mathcad tworzy narzędzie umożliwiające 
                                                 

1

 Dr inż., Politechnika Szczecińska 

 

128

uzyskanie typowych dla ogniw charakterystyk jak: napięciowo –prądowa, krzywa sprawności, 
czy przebiegu siły elektromotorycznej w zależności od parametrów substratów oraz produktów 
biorących udział w reakcji zachodzącej w ogniwie.  

 

2. SIŁA ELEKTROMOTORYCZNA I SPRAWNOŚĆ IDEALNEGO OGNIWA 

WODOROWO TLENOWEGO  

W ogniwie paliwowym zachodzi bezpośrednia zamiana energii chemicznej paliwa w 

energię elektryczną. Ponieważ  są różne rodzaje elektrolitów w ogniwach to także różne są 
procesy elektrochemiczne na elektrodach. W rozważanym modelu wzięto pod uwagę ogniwo 
wodorowo tlenowe. W celu wyznaczenia energii elektrycznej możliwej do uzyskania z 
ogniwa określa się energię chemiczną produktów wejściowych (tlen i wodór) i wyjściowych 
(woda) dla reakcji zachodzącej w ogniwie, identycznej z reakcją spalania wodoru tj.

  

H

2

 + 1/2 O

2

 

→

 H

2

O.   

 

 

 

     (1) 

Wykorzystuje się w tym celu pojęcie entalpii swobodnej, zwanej też potencjałem 
termodynamicznym, którą można zapisać [3] 

Ts

h

g

−

=

   

 

 

 

 

(2) 

gdzie: h – entalpia , T – temperatura, s – entropia. 
Zmiana entalpii swobodnej dla rozważanej reakcji jest różnicą entalpii swobodnej produktów 
(wody) i substratów (wodoru i tlenu) reakcji. Dla jednego mola powstałej wody jest więc:  

( )

( )

( )

2

2

2

O

H

O

H

g

2

1

g

g

g

−

−

=

Δ

   

 

 

          (3) 

W przypadku układów odwracalnych (bez strat) praca prądu elektrycznego jest równa 

zmianie entalpii swobodnej Δg czyli  

(

)

FE

2

V

V

F

2

s

T

h

g

A

K

−

=

−

−

=

Δ

−

Δ

=

Δ

.  

 

           (4) 

gdzie:  F – stała Faraday’a, V

A

 i V

K 

– potencjał anody i katody, E – siła elektromotoryczna [4]. 

Z równania tego wyznacza się w opisywanym modelu siłę elektromotoryczną (SEM) E

0

 

idealnego ogniwa wodorowo tlenowego w stanie jałowym dla dowolnej temperatury przy 
ciśnieniu standardowym (0,1 MPa).  

⎟

⎠

⎞

⎜

⎝

⎛

Δ

−

Δ

−

=

F

2

s

T

h

E

0

 

 

 

 

 

(5) 

W modelu obliczana jest także sprawność  η  jaką może osiągnąć ogniwo wodorowo tlenowe 
przy braku strat. Zamiast pracy prądu elektrycznego, zgodnie z zależnością 4, odnosi się 
równoważną jej zmianę entalpii swobodnej Δg do entalpii tworzenia czyli wartości opałowej 
wodoru tj. 

h

g

ideal

Δ

Δ

=

η

. 

     

 

 

 

 

(6) 

 

3. WPŁYW CIŚNIENIA NA SIŁĘ ELEKTROMOTORYCZNĄ IDEALNEGO 

OGNIWA WODOROWO TLENOWEGO  

Ogniwo paliwowe może pracować przy różnych ciśnieniach począwszy od ciśnienia 

atmosferycznego do ok. 0,8 MPa, w przypadku ogniw polimerowych (PEMFC), do nawet ok. 
1,5 MPa w przypadku ogniw ze stałymi tlenkami metali (SOFC). Generalnie wzrost ciśnienia 

 

129

substratów wpływa na zwiększenie SEM ogniwa [5]. Zależność SEM ogniwa (zwanej też 
idealnym potencjałem Nernsta) od ciśnienia ujmuje równanie Nernsta [4,5,6], które ma 
następująca postać: 

⎟

⎟

⎟

⎠

⎞

⎜

⎜

⎜

⎝

⎛

⋅

+

=

O

H

2

1

O

H

0

2

2

2

p

p

p

ln

F

2

RT

E

E

   

 

 

 

(7) 

gdzie: E

0

 – SEM ogniwa przy ciśnieniu standardowym według równania 5. 

Ciśnienia w nawiasie we wzorze 7 są ciśnieniami cząstkowymi poszczególnych składników. 
A więc jeśli np. ogniwo będzie zasilane z reformera to wodór będzie w mieszaninie 
z dwutlenkiem węgla i parą wodną. Podobnie tlen najczęściej dostarczany jest do ogniwa w 
powietrzu, którego jest składnikiem. Ciśnienie cząstkowe danego gazu jest proporcjonalne do 
jego udziału w mieszaninie. Widać więc z równania 7, że zastąpienie czystego tlenu 
powietrzem powodować będzie spadek siły elektromotorycznej ogniwa.  

 

4. SPADEK SEM W OGNIWIE PALIWOWYM 

 

Obciążenie ogniwa przez podłączenie do układu z odbiornikiem prądu oraz 

nieodwracalność procesów są źródłem spadku różnicy potencjałów i w efekcie zmniejszenia 
siły elektromotorycznej co też w literaturze nazywa się stratą potencjału ogniwa [4,5,7]. Aby 
uniknąć nieporozumień wynikających z różnic w nazewnictwie, trzeba nadmienić,  że w 
elektrotechnice teoretycznej pojęcie strat napięcia dotyczy jedynie prądu przemiennego. W 
teorii ogniw paliwowych natomiast za starty powszechnie uważa się spadki napięcia 
wywołujące zmniejszenie SEM ogniwa podczas przepływu prądu stałego. Wyróżnia się trzy 
grupy strat: straty biegu jałowego

 

V

0

, straty związane ze spadkiem napięcia wywołane 

rezystancją V

Ω

 

oraz straty elektrokinetyczne V

E

. SEM ogniwa będzie więc równa: 

 

E

o

V

V

V

E

E

−

−

−

=

Ω

0

. 

     

 

 

(8) 

Dla różnych rodzajów ogniw udział poszczególnych rodzajów strat jest zróżnicowany. 

Straty biegu jałowego są spowodowane przez nieprecyzyjne wykonanie elektrod, 
zanieczyszczenia paliwa oraz występowanie reakcji odwrotnej do głównych procesów 
zachodzących w ogniwie [7]. Straty biegu jałowego są niezależne od natężenia prądu i dla 
typowych ogniw wodorowo-tlenowych ich wielkość jest równa 0,15–0,25V. 

Spadek napięcia wywołany rezystancją przewodzenia wyznacza się na podstawie 

prawa Ohma: 

 

r

i

V

⋅

=

Ω

 

 

 

 

 

 

     (9) 

gdzie: i

 

– gęstość prądu przepływającego przez ogniwo, r – całkowita powierzchniowa rezy-

stancja właściwa ogniwa. 
Na rezystancję ogniwa składają się rezystancja elektrolitu R

EL

 oraz rezystancja  elektrod R

E

. 

Decydujący wpływ na wartość spadku napięcia mają straty wywołane rezystancją elektrolitu. 
Dlatego też w modelu przyjęto stałą wartość rezystancji elektrod, której wielkość zależna jest 
od rodzaju zastosowanego materiału. W wielu przypadkach jak np. dla elektrod grafitowych 
jej wartość się pomija [5]. Rezystancję elektrolitu opisuje natomiast zależność: 

q

S

l

R

EL

⋅

=

 

 

 

 

 

     (10) 

 

130

gdzie:  l  – odległość między elektrodami , S  – powierzchnia elektrody, q  – konduktancja 
właściwa elektrolitu. 
Ponieważ w teorii ogniw powszechnie stosuje się gęstość prądu i to wówczas rezystancje R

EL

 

oraz  R

E

 należy odnieść do jednostki powierzchni ogniwa i dla odróżnienia oznaczane są w 

modelu jako r

EL

 i r

E

 .  

Do grupy strat elektrokinetycznych zalicza się straty powstałe wskutek procesów 

elektrodowych takich jak: adsorpcja– desorpcja substratów i produktów, straty przejścia 
ładunku i polaryzacja.  

V

E

=ΔV

p

+ΔV

D

  

 

 

 

          (11) 

gdzie: ΔV

p

 – spadek napięcia wskutek strat aktywacji,  ΔV

D

 – spadek napięcia wskutek start 

masowych transportu lub koncentracji  
Na granicy pomiędzy elektrodą i elektrolitem powstaje warstwa elektryczna o podwójnym 
ładunku, który jest ujemny na powierzchni elektrody i dodatni od strony elektrolitu. W celu 
pokonania tego progu przez ładunek elektryczny potrzebna jest odpowiednia energia 
aktywacji. Stąd też często mówi się o stracie aktywacji. Najbardziej charakterystycznymi 
etapami procesów elektrodowych są: dyfuzja, przejścia ładunków oraz reakcja chemiczna na 
powierzchni elektrody lub w warstwie elektrolitu graniczącej bezpośrednio z nią. Przejście 
ładunku oznacza wymianę elektronów między cząsteczkami znajdującymi się w elektrolicie, a 
elektrodą i tworzenie jonów lub ich neutralizację. Etap przejścia  ładunku jest hamowany 
przez polaryzację przejścia. 
Zależność pomiędzy polaryzacją przejścia a gęstością prądu opisuje wzór Tafela [4,5]: 

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅

=

Δ

0

P

i

i

ln

A

V

 

 

 

 

           (12) 

gdzie: A – współczynnik Tafela,  i – gęstość prądu,  i

0 

– gęstość prądu wymiany.  

Wzór 12 obowiązuje jedynie, gdy zachodzi zależność  i > i

0

 , natomiast współczynnik Tafela 

określa się z równania 

 

F

2

RT

A

α

=

 

 

 

 

 

(13) 

gdzie: 

α – współczynnik transferu ładunku [4].   

Straty masowe transportu lub koncentracji powstają w wyniku transportu reagentów 

przy wyższych prądach gdzie decydującym czynnikiem jest przepływ gazu przez porowate 
elektrody do katalizatora i elektrolitu. Straty koncentracji pojawiają się gdy gaz w kontakcie z 
katalizatorem i elektrodą zużywa się szybciej niż może do niej dotrzeć. Straty te oblicza się ze 
wzoru: 

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

−

=

Δ

l

D

i

i

1

ln

B

V

   

 

 

 

(14) 

gdzie: B – współczynnik zależny od rodzaju ogniwa i reagenta, i

l 

– graniczna gęstość prądu, 

która jest miarą maksymalnej szybkości reakcji jaka może być uzyskiwana na elektrodzie.  
Współczynnik  B dla wodoru jest równy 

F

2

RT

 natomiast dla tlenu 

F

4

RT

. Po uwzględnieniu 

wszystkich strat SEM ogniwa będzie równa: 

(

)

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

⋅

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⋅

−

+

⋅

−

−

=

l

0

E

EL

0

0

i

i

1

ln

B

i

i

ln

A

r

r

i

V

E

E

  . 

 

(15)

 

 

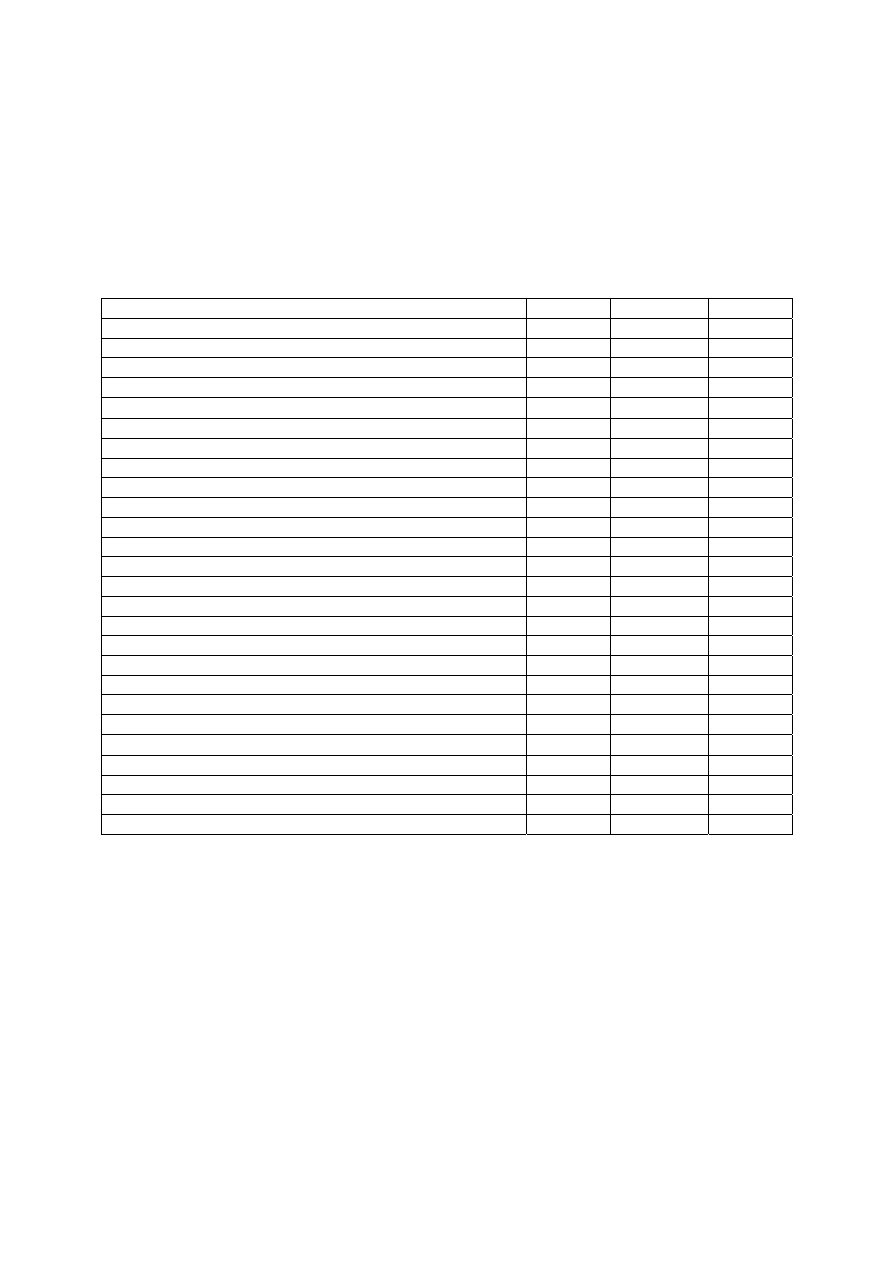
131

4. PRZYKŁAD OBLICZENIOWY 

Po wprowadzeniu poszczególnych wzorów do programu Mathcad przeprowadzono 

przykładowe obliczenia ogniwa wodorowo tlenowego jak również określono jego 
charakterystyki. Jako punkt odniesienia do obliczeń entalpii i entropii przyjęto warunki 
standardowe dla ogniw tj. 298,15K oraz 0,1MPa. W tabeli 1 zebrano najważniejsze dane 
wejściowe i wyniki obliczeń ogniwa w temperaturze pracy 80

º

C.   

 

Tabela 1. Dane wejściowe i wyniki obliczeń ogniwa paliwowego wodorowo tlenowego 

 

Parametr Symbol 

Jednostka 

Wartość 

Temperatura pracy ogniwa   

T

2

 

K 353 

Ciśnienie wodoru   

p

1

 

MPa 0,1 

Ciśnienie tlenu   

p

2

 

MPa 0,1 

Ciśnienie wody   

p

3

 

MPa 0,1 

Udział tlenu w przypadku zasilania ogniwa powietrzem 

σ 

 

– 0,21 

Gęstość prądu   

i 

mA/cm

2

 100 

Odległość między elektrodami   

l 

cm 0,2 

Powierzchnia elektrody   

S 

cm

2

 10 

Konduktancja właściwa elektrolitu   

q 

Ω

-1

 cm

-1

 0,55 

Entropia wody w temperaturze  T

2

 

s

H2O

 

kJ/(mol K) 

0,0756 

Entropia wodoru w temperaturze  T

2

 

s

H2

 

kJ/(mol K) 

0,1354 

Entropia tlenu w temperaturze  T

2

 

s

O2

 

kJ/(mol K) 

0,2103 

Różnica entropii produktów i substratów  

Δs 

kJ/(mol K) 

-0,1650 

Entalpia tworzenia wody w temperaturze  T

2      

 

Δh 

kJ/mol -286,45 

Potencjał termodynamiczny ogniwa w temperaturze  T

2      

 

Δg 

kJ/mol -228,19 

SEM idealnego ogniwa w stanie jałowym w temp T

2 .

 

E

0

 

V 1,183 

Sprawność idealnego ogniwa temp T

2 

    

η

ideal

 

- 79,66 

SEM ogniwa przy zastąpieniu tlenu powietrzem  

E 

V 1,171 

Straty biegu jałowego   

V

0

 

V 0,25 

Powierzchniowa rezystancja właściwa elektrod    

r

E

 

Ω cm

2

 0,02 

Powierzchniowa rezystancja właściwa elektrolitu    

r

EL

 

Ω cm

2

 0,36 

Straty oporu przewodzenia   

V

Ω

 

  

V 0,038 

Straty aktywacji  

ΔV

p

 

V 0,137 

Starty masowe transportu lub koncentracji  

ΔV

D

 

V 0,0016 

Rzeczywista SEM ogniwa zasilanego tlenem  

E 

V 0,756 

Rzeczywista SEM ogniwa zasilanego powietrzem 

E 

V 0,744 

 

Zastosowanie programu Mathcad pozwala na zmianę dowolnej wartości w dowolnym 

miejscu. Można zatem szybko sprawdzić jaki efekt daje zmiana na końcowy wynik. W 
środowisku Mathcad wzory wprowadzone jako funkcje jednej lub wielu zmiennych można 
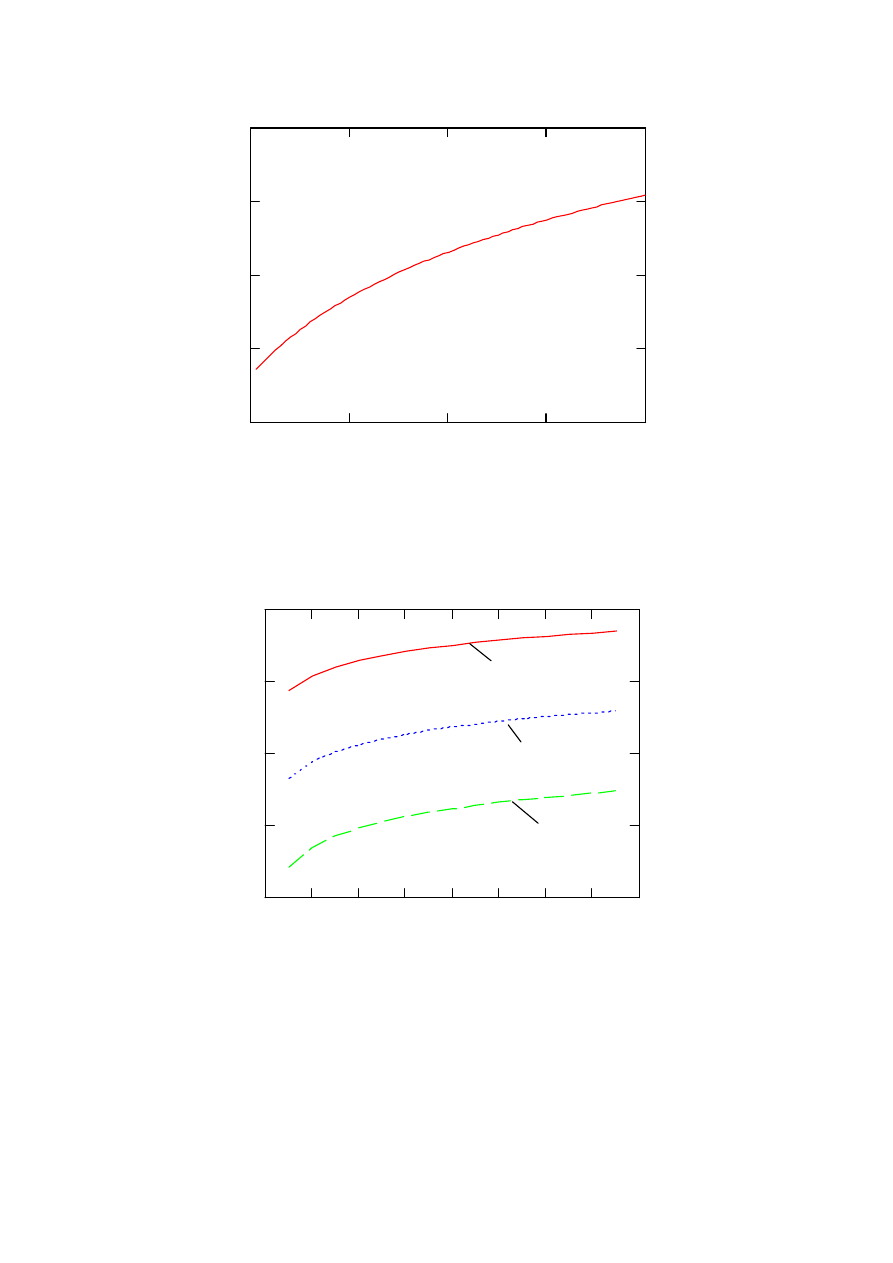
przedstawić na wykresie. Przykładowo równanie 15 stanowi charakterystykę napięciowo 
prądową ogniwa, która może być przedstawiona jako funkcja temperatury, ciśnienia, gęstości 
prądu i stężenia tlenu. Przebieg tej charakterystyki dla temperatur 353, 403 i 453 K, pokazano 
na rys. 1. Jej przebieg odpowiada przebiegom przedstawianym w literaturze [5]. Na rysunku 2 
przedstawiono natomiast przebieg sprawności idealnego ogniwa w funkcji temperatury 
uzyskany na podstawie zależności 6 także zgodny z teorią.   

 

132

0

200

400

600

800

1000

0

0.2

0.4

0.6

0.8

1

)

 

 

 

 

 

 

i [mA/cm

2

] 

 

Rys.1. Charakterystyka napięciowo prądowa ogniwa dla różnych temperatur 

 

260

280

300

320

340

360

380

400

420

440

74

76

78

80

82

84

86

 

 

 

 

 

 

 

 

 

 

T

2

 [K]  

 

Rys.2. Sprawność ogniwa idealnego w funkcji temperatury 

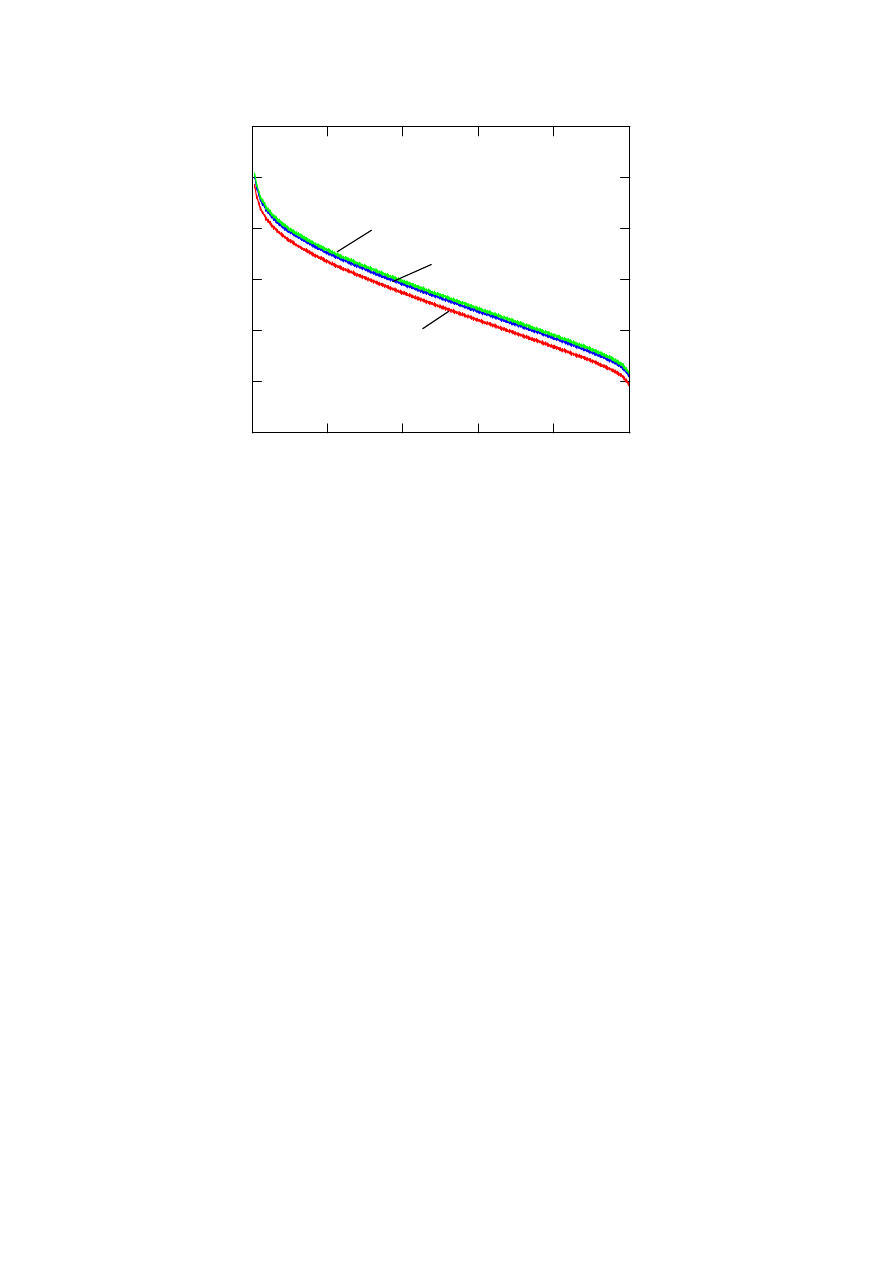
Na rysunku 3 przedstawiono natomiast zależność SEM ogniwa paliwowego od stężenia tlenu 
σ w mieszaninie gazów począwszy od 0,21 tj. wartości odpowiadającej stężeniu tlenu w 
powietrzu do wartości 1, kiedy ogniwo zasilane jest czystym tlenem.   
 

353 K 

403K 

453K 

E [V] 

η 

453K 

 

133

0.2

0.4

0.6

0.8

0.74

0.745

0.75

0.755

0.76

)

 

 

 

 

 

 

 

 

σ  

Rys. 3. Zależność siły elektromotorycznej ogniwa od stężenia tlenu w mieszaninie gazów 

 

Rysunek 4 przedstawia zależność SEM ogniwa od ciśnienia wodoru dla temperatur  353, 403 
i 453 K przy stałej gęstości prądu równej 100 mA/cm

2 

zaś na rysunku 5 pokazano wpływ 

ciśnienia wodoru na charakterystykę napięciowo prądową w temperaturze 353K.    

 

0

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

0.6

0.65

0.7

0.75

0.8

)

 

 

 

 

 

 

p [MPa] 

 

Rys.4. Zależność siły elektromotorycznej ogniwa od ciśnienia wodoru 

 
 

E [V] 

E [V] 

353 K 

403K 

453K 

 

134

0

200

400

600

800

1000

0

0.2

0.4

0.6

0.8

1

1.2

 

 

 

 

 

 

i [mA/cm

2

] 

 

Rys. 5. Wpływ ciśnienia wodoru na charakterystykę napięciowo prądową ogniwa  

 
 

5. PODSUMOWANIE 

Przedstawiony model obliczeniowy ogniwa paliwowego oparty na podstawowych 

zależnościach termodynamicznych i elektrochemicznych zrealizowany w środowisku 
Mathcad pozwala na bardzo szybkie analizy wpływu istotnych parametrów pracy ogniwa na 
jego charakterystyki. Łatwa zmiana danych wejściowych, bądź dowolnych stałych 
stosowanych do obliczeń pozwala na szybkie uzyskanie wyników w postaci liczbowej lub w 
formie graficznej. Model ten może być przydatny w badaniach eksperymentalnych do 
wstępnej weryfikacji wyników a także jako proste narzędzie projektowe. Duża przydatność 
modelu potwierdza się także na polu dydaktycznym.  
 
 

LITERATURA 

 

[1] Zeńczak W.: Koncepcja rozwiązania systemu energetycznego statku typu rzeka-morze z 

ogniwem paliwowym, VIII Konferencja Okrętownictwo i Oceanotechnika, Perspektywy 
rozwoju systemów transportowych, Międzyzdroje, czerwiec 2006.  

[2] Zeńczak W.: Rozwój okrętowych systemów energetycznych opartych na ogniwach 

paliwowych, Zeszyty Naukowe AMW, XXVI Sympozjum Siłowni Okrętowych SYMSO 
2005, Gdynia 2005 

[3] Bielski 

S., 

Zeńczak W.: Selected Technical Problems Connected with Perspective 

Applications of fuel Cells in Marine Power Plants, WSM Zeszyty Naukowe nr 71, XXIV  
Międzynarodowe Sympozjum  Siłowni Okrętowych, Świnoujście 2003 

[4] 

Larminie J., Dicks A.: Fuel Cell Systems Explained, John Wiley & Sons LTD, 2003 

[5] 

Barbir F.: PEM Fuel Cells: Theory and Practice, ELSEVIER Academic Press, London 2005 

[6] 

 Massardo A.F., Lubelli F.: Internal Reforming Solid Oxide Fuel Cell –Gas Turbine Combined 
Cycles: Part A- Cell Modell and Cycle thermodynamic Analysis, Journal of Engineering for 
Gas Turbines and Power, ASME January 2000 vol.122/7 

[7] 

Chmielniak T.J.: Technologie energetyczne, Wydawnictwo Politechniki Śląskiej, Gliwice 
2004 

E [V] 

2 MPa 

1 MPa 

0.1 MPa 

T=353K