MODEL MATEMATYCZNY ZBIORNIKA

RETENCYJNO-INFILTRACYJNEGO

Maciej MROWIEC

Instytut Inżynierii Środowiska, ul. Brzeźnicka 60a,

42-200 Częstochowa

STRESZCZENIE

W artykule zaprezentowano konstrukcję rurowego zbiornika retencyjno-infiltracyjnego,
działającego w układzie szeregowym. Koncepcja wykonania zbiorników retencyjnych jako
odcinków rur o dużych średnicach umożliwia znaczące uproszczenie procesów
projektowania i wykonawstwa inwestycji. W stosunku do standardowych konstrukcji
zbiorników budowanych w układzie szeregowym, proponowana konstrukcja charakteryzuje
się tym, że główna komora jest ułożona w spadku odwrotnym do kierunku przepływu
cieczy zaś komora wlotowa ma perforowane dno, umożliwiające infiltrację wód
deszczowych do gruntu. Przedstawione zostały wszystkie charakterystyczne fazy działania
zbiornika wraz z warunkami brzegowymi ich występowania. Dla zdefiniowanych faz
działania został opracowany model matematyczny zbiornika, którego efektem jest
możliwość prowadzenia badań symulacyjnych dla zmiennych danych wejściowych.

SŁOWA KLUCZOWE: zbiorniki retencyjne, kanalizacja, infiltracja

WPROWADZENIE

Budowa, rozbudowa i modernizacja układów i systemów kanalizacyjnych jest

aktualnym i ważnym problemem z uwagi na głęboki aspekt ekonomiczny wynikający z
zakresu koniecznych inwestycji związanych dostosowaniem Polski do wymagań UE w
zakresie gospodarki wodno-ściekowej. Zbiorniki retencyjnej w sieciach kanalizacyjnych są
standardowymi urządzeniami stosowanymi w rozwiniętych krajach UE, stanowiąc ważny
element w procesie optymalnego projektowania sieci kanalizacji rozdzielczej i
ogólnospławnej (Mays, 2000). Zbiorniki retencyjne, wykonane z odcinków rur o dużych
średnicach stanowią doskonałe rozwiązanie z uwagi na uproszczenie procesów projektowania
jak i wykonawstwa (Mrowiec, 2002). Dotychczas opisane konstrukcje zbiorników rurowych
charakteryzowały się zwiększona efektywnością hydrauliczną, umożliwiając redukcje
wymaganej pojemności retencyjnej nawet o kilkadziesiąt procent (Mrowiec, 2002, 2003).
Przedstawiony w niniejszym artykule zbiornik stanowi autorskie rozwinięcie wcześniejszych
konstrukcji, które przy zachowaniu równie wysokiej efektywności hydraulicznej umożliwia
ograniczenie konieczności nadmiernego zagłębiania kanału odpływowego.

BUDOWA ZBIORNIKA RETENCYJNO-INFILTRACYJNEGO

Proponowany zbiornik retencyjny (rys. 1) składa się z trzech komór: wlotowej,

wylotowej oraz retencyjnej, wykonanej z odcinka rury o dużej średnicy. Doprowadzenie
ścieków do komory wlotowej realizowane jest poprzez kanał dopływowy, natomiast odpływ
jest możliwy tylko kanałem tranzytowym, którego wlot znajduje się w części przydennej
przegrody rozdzielającej komorę retencyjną od wlotowej. Przegroda ta jest zakończona
krawędzią przelewową, przez którą nadmiar ścieków deszczowych odprowadzany jest do
komory retencyjnej. Aby umożliwić opróżnienie komory retencyjnej przegroda wyposażona
jest w jednokierunkowy zawór klapowy, działający samoczynnie pod wpływem różnicy
ciśnień hydrostatycznych analogicznie jak w zbiorniku typu Contract (Dziopak 2002). Cechą

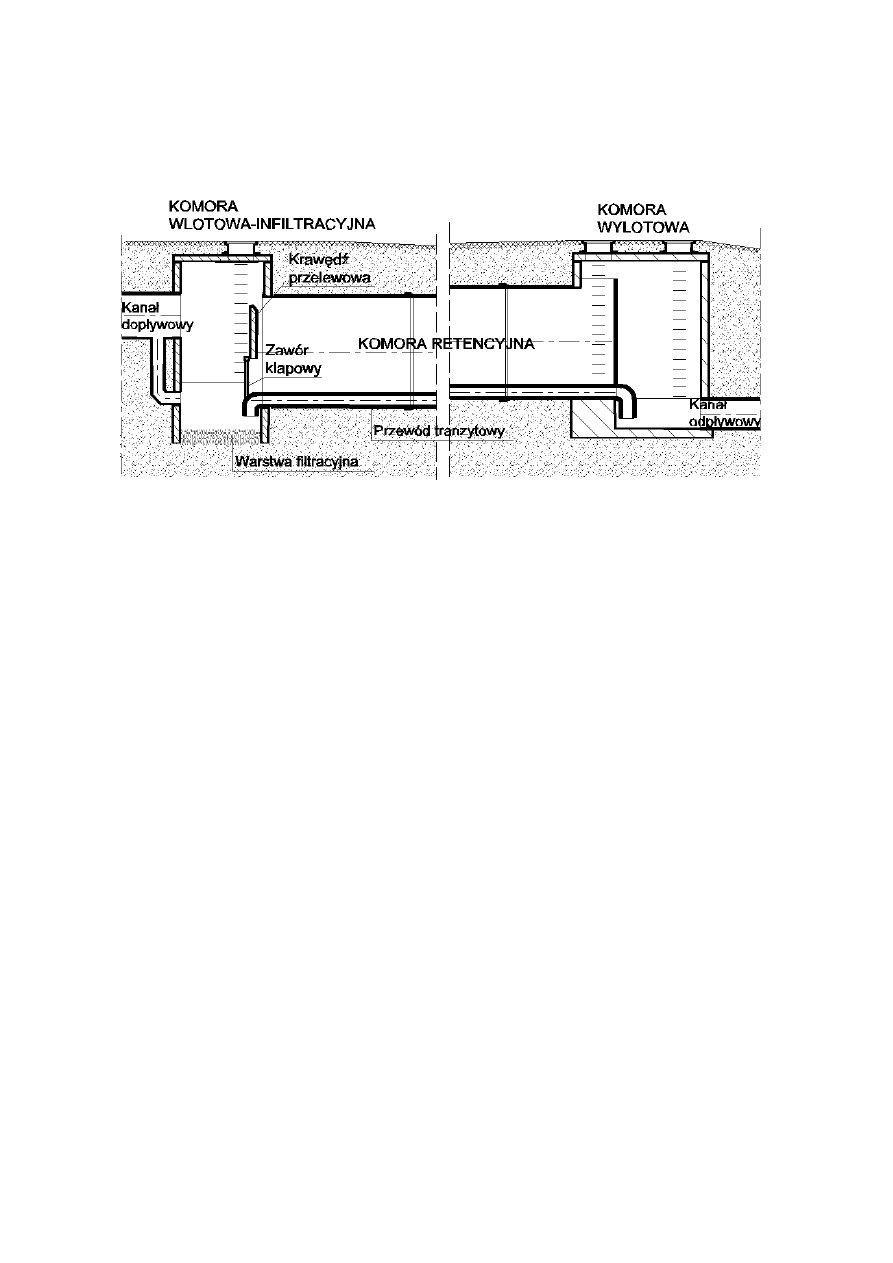
charakterystyczną tego zbiornika jest to, że w przeciwieństwie do poprzednio prezentowanych
rozwiązań, jego komora retencyjna ułożona jest w spadku przeciwnym do przyjętego dla
kierunku przepływu tranzytowego wód deszczowych.

Rys.1. Rurowy zbiornik infiltracyjno- retencyjny (Proximus).

Transportowane do zbiornika zanieczyszczenia, głównie zawiesina, mogą powodować

szybką kolmatację złoża filtracyjnego i z tego względu dopływające wody deszczowe
powinny być wstępnie oczyszczane. Wartość spadku, w jakim ułożona będzie komora
retencyjna będzie zależny od lokalnych warunków topograficznych i infrastrukturalnych.
Ułożenie zbiornika w przeciwspadku daje możliwość ograniczenia zagłębienia kanału
odpływowego co bezpośrednio rzutuje na koszty wykonania dalszych odcinków sieci. Jest to
szczególnie istotne na obszarach topograficznie płaskich, gdzie nawet minimalny spadek
powoduje stopniowe zagłębianie kolejnych odcinków kanalizacyjnych. Zwiększanie
przeciwspadku będzie mieć oczywiście swoje naturalne ograniczenia, wynikające z
minimalnego przykrycia przewodów oraz zapewnienia odpowiedniej różnicy rzędnych
zwierciadeł w komorze wlotowej i wylotowej, decydujących o natężeniu odpływu. Ponadto
przy większych wartościach spadku ułożenia zbiornika zwiększa się udział objętości
retencyjnej, która odprowadzenie będzie możliwe wyłącznie poprzez infiltrację. W efekcie
może zaistnieć konieczność znaczącego powiększenia powierzchni komory wlotowej aby
zapobiec nadmiernie długiemu procesowi opróżniania zbiornika.

PODSTAWOWE RÓWNANIA MODELU MATEMATYCZNEGO

Podstawą sformułowania równań modelowych charakteryzujących proces akumulacji

wód deszczowych w zbiorniku retencyjnym jest zasada zachowania masy, którą można
zapisać w najogólniejszej postaci jako równanie bilansu (Kisiel i Dziopak 1999, Becker i in.
2001). Dla komory wlotowej równanie to będzie miało postać

0

0

(h )

0

dop(t)

Ti

IN

dV

F

dh

Q

dt Q dt Q dt

=

⋅

=

−

−

(1)

gdzie: Q

dop(t)

– natężenie dopływu [m

3

/s], Q

Ti

– natężenie odpływu przez przewód tranzytowy

[m

3

/s], Q

IN

– natężenie odpływu przez dno komory wlotowej [m

3

/s], F

WL

– pole

powierzchni zwierciadła wody [m

2

].

Zmienna wartość natężenie dopływu w czasie Q

dop(t)

jest wielkością ściśle uzależnioną

od przyjętej metody wymiarowania sieci kanalizacji deszczowej. W przypadku zbiorników
retencyjnych najczęściej przyjmowany jest hydrogram dopływu w kształcie trapezu stąd
natężenie dopływu w czasie będzie w tym przypadku ciągiem 3 funkcji liniowych (rosnącej,
stałej i malejącej) z określonymi punktami brzegowymi. Istnieje oczywiście możliwość
przyjęcia jako funkcji dopływu hydrogrmu historycznego, wymaga to jednak jego uprzedniej
transformacji na ciąg funkcji (niekoniecznie liniowych) ze zdefiniowanymi wartościami
brzegowymi. Na etapie sprawdzenia poprawności działania zbiornika modelu często
stosowany jest hydrogram o stałym natężeniu (Q

dop(t)

=const).

Natężenie odpływu Q

Ti

przez przewód tranzytowy można z dużą dokładnością

obliczyć przy zastosowaniu wzoru:

(

)

T

T

2
T

T

L

d

d

2g H

Q

4

1

π

∆

=

λ + ζ +

(2)

gdzie:

∆H – różnica położenia rzędnych zwierciadeł cieczy w komorze wlotowej i wylotowej

[m], L

T

– długość przewodu tranzytowego [m], d

T

– średnica przewodu tranzytowego

[m],

ζ – współczynnik strat na wlocie do przewodu [-], λ – współczynnik oporów

liniowych (zależny od liczby Reynoldsa i chropowatości względnej) [-].

Teoretyczna wartość natężenia przepływu infiltrującego przez dno komory wlotowej

Q

IN

zgodnie z prawem Darcy jest równa:

IN

WL

Q

k F

=

(3)

gdzie: k - współczynnik filtracji gruntu k [m/s], F

WL

- powierzchni wsiąkania (powierzchnia

dna komory wlotowej).

Formuła (3) jest słuszna tylko w sytuacji, gdy wszystkie pory gruntu są wypełnione woda
(strefa saturacji). W praktyce warunek ten nie będzie spełniony w początkowej fazie
wypełniania komory wlotowej, co oznacza, że rzeczywista wartość Q

IN

będzie nieco

mniejsza. Ponieważ w proponowanej konstrukcji zbiornika infiltracja nie odgrywa wiodącej
roli (nabiera znaczenia dopiero w końcowej fazie opróżniania zbiornika) to w
przedstawionym modelu zdecydowano się na stosowanie wzoru (3) w każdej fazie jego
działania. Ten element modelu będzie przedmiotem badań weryfikacyjnych w warunkach
laboratoryjnych, a w dalszej perspektywie także w pełnej skali technicznej.

W przypadku gdy napełnienie komory wlotowej będzie większe niż położenie

krawędzi przelewowej (H

0p

),w modelu matematycznym należy uwzględnić dwa odrębne

równania bilansu:

- dla komory wlotowej

0

dop(t)

0i

IN

R

0

(h )

Q

dt Q dt Q dt Q dt

dh

F

−

−

−

=

(4)

gdzie:

Q

R

–natężenie przepływu przez krawędź przelewową [m

3

/s], pozostałe

oznaczenia jak wyżej.

- dla komory retencyjnej:

R

Ri

R

(h )

Q dt

dh

F

=

(5)

gdzie:

F

(hR)

– pole powierzchni zwierciadła cieczy w komorze retencyjnej [m

2

],

pozostałe oznaczenia jak wyżej.

Natężenie przepływu wody przez przelew należy obliczać przy zastosowaniu wzoru dla
przelewów o kształtach praktycznych (Erb, 1999):

3/ 2

R

P

P

P

Q

2g

B (h )

=

µ

(6)

gdzie:

µ

p

– współczynnik wydatku przelewu [-], B

p

– długość korony przelewu [m], h

p

– wysokość

warstwy ścieków na przelewie [m].

We wzorze (6) założono że przelew działa jako niezatopiony, nie posiada kontrakcji bocznej
oraz że nie jest uwzględniana wysokość prędkości dopływającego strumienia wody.

Jeśli spadek podłużny komory retencyjnej jest uwzględniany w modelu, to zwierciadło

ścieków będzie mieć kształt wycinka elipsy, a postać wzoru zmienia się będzie w określonych
zakresach napełnień komór (Mrowiec 2003). Obliczenia powierzchni F

(h0)

można jednak

uprościć, pomijając spadek komory, co w praktyce nie generuje znaczących błędów
obliczeniowych. Powierzchnia swobodna ścieków ma w takim przypadku prostokątny kształt
i można ją obliczyć stosując jeden wzór:

R (h)

R

R

hR

F

L D sin

=

⋅

⋅

β (4)

gdzie: L

R

– długość komory retencyjnej [m], D

R

– średnica komory retencyjnej [m],

β

hR

–

połowa kata środkowego w komorze retencyjnej przy napełnieniu h

R

[rad].

Przyjęte w modelu dodatkowe uproszczenia dotyczyły przede wszystkim przyjęcia

stałych wartości współczynników wydatku (przelewu, otworów), strat liniowych itp.,
niezmiennego charakteru przebiegu zjawiska wypływu cieczy przez otwór spustowy oraz
krawędź przelewową (bez kontrakcji, kształty praktyczne) przy dowolnym napełnieniu komór
zbiorników. Założenia tego typu nie maja znaczącego wpływu na uzyskiwane wyniki, co
zostało dowiedzione w badaniach laboratoryjnych prowadzonych na modelach fizycznych
zbiorników innego typu (Mrowiec 2002, 2003).

FAZY DZIAŁANIA ZBIORNIKA RETENCYJNO-INFILTRACYJNEGO

Określenie warunków brzegowych dla poszczególnych faz działania oraz stanów

chwilowych stanowi podstawę do opracowania modelu matematyczno-symulacyjnego
zbiornika. Na rysunkach 2 do 9 przedstawiono kolejne fazy działania zbiornika wraz
z przedziałami podstawowych parametrów hydraulicznych: napełnień poszczególnych komór
oraz charakterystycznych natężeń przepływu.

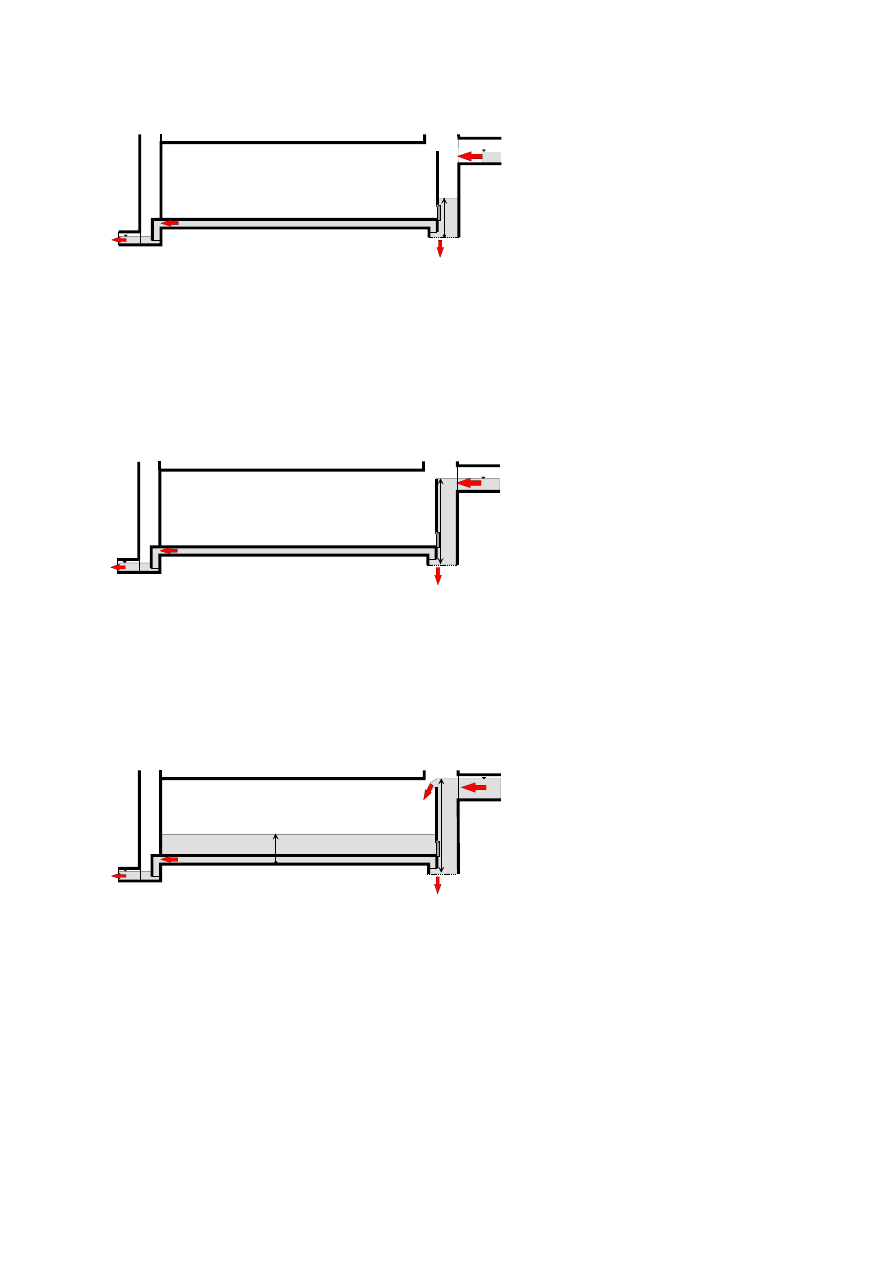
Podczas trwania przepływów o natężeniu mniejszym niż przepustowość infiltracyjna

dna komory wlotowej całość dopływających wód opadowych będzie wsiąkać przez dno
komory wlotowej, nie powodując odpływu przez przewód tranzytowy. Jeśli Q

dop(t)

>Q

IN

to

nastąpi stopniowe wypełnianie komory wlotowej (rys. 2)

Q

dop(t)

Q

0i

Q

Ti

h

0

Q

IN

IN

dop(t)

M

Q

Q

Q

<

<

0

0

0 h

H

p

<

<

R

h

0

=

0i

0

0 Q

Q

<

<

dop(t)

0i

Q

Q

>

0i

Ti

Q

Q

=

Rys. 2. Faza napełniania komory wlotowej.

Przepływ ścieków przez przewód tranzytowy, działający w układzie lewarowym możliwy jest
od momentu, w którym poziom napełnienia komory wlotowej przewyższy rzędna dna komory
retencyjnej w przekroju wylotowym, na tyle by umożliwić zadziałanie przewodu. Dalsze
wypełnianie komory wlotowej powodować będzie zwiększanie wartości natężenia odpływu
zgodnie ze wzorem (2).

Q

dop(t)

H

0p

Q

0i

Q

Ti

Q

IN

IN

dop(t)

M

Q

Q

Q

<

<

p

0

0

H

h

=

R

h

0

=

Tp

p

0

i

0

Q

Q

Q

=

=

i

0

)

t

(

dop

Q

Q

>

Rys. 3. Komora wlotowa wypełniona do poziomu krawędzi przelewowej (stan chwilowy).

Wypełnienie komory do poziomu H

0p

(rys. 3) oznacza jednocześnie osiągnięcie maksymalnej

wartości przepływu tranzytowego przez zbiornik retencyjny. Do tego momentu komora
retencyjna pozostaje pusta. Przepływ Q

dop(t)

dla deszczów eksploatacyjnych nie powoduje

zanieczyszczania jej dna, ponieważ stanowi maksymalną wartość przepływu tranzytowego
Q

dop(t)

=Q

0p.

Q

dop(t)

H

0

Q

0

Q

T

Q

Ri

h

R

Q

IN

IN

dop(t)

M

Q

Q

Q

<

≤

0p

0

0

H

h

H

<

≤

R

0 h D

< <

0

i

0

Q

Q

=

i

0

)

t

(

dop

Ri

Q

Q

Q

−

=

Rys. 4. Faza napełniania komory retencyjnej.

Faza napełniania komory retencyjnej (rys.4) w sposób zasadniczy decyduje o przebiegu
procesu akumulacji oraz obliczeniowej objętości zbiornika. Rozpoczyna się w momencie
zadziałania przelewu szczytowego (h

0

>H

0p

), gdy natężenie dopływających do zbiornika

ścieków jest większe od maksymalnej wartości odpływu zredukowanego (Q

0

). Gdy dopływ

ścieków do zbiornika osiągnie maksymalną wartość Q

M

, następuje ustalony przebieg procesu

wypełniania zbiornika. Wysokość warstwy ścieków na przelewie wynosi h

p

, natomiast

wartość natężenia odpływu ścieków przewodem tranzytowym osiąga wartość maksymalną
Q

T

=Q

0

, podobnie jak przepływ retencjonowany Q

R

=Q

M

-Q

0

. W trakcie wypełniania komory

retencyjnej zawór klapowy pozostaje zamknięty, ponieważ napełnienie komory wlotowej jest
większe od napełnienia komory retencyjnej. Wypełnianie komory retencyjnej powyżej

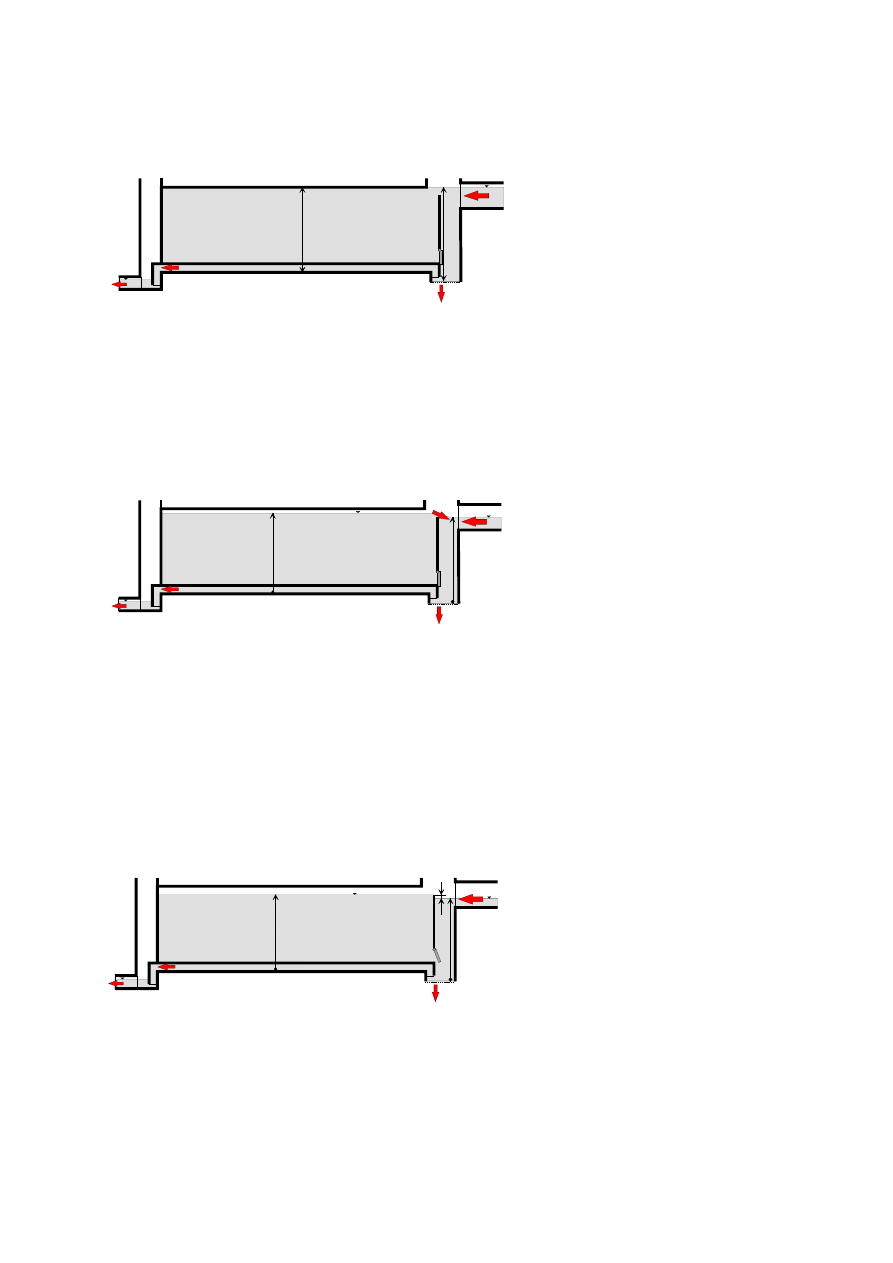
poziomu krawędzi przelewowej będzie identyczne jak dla zbiornika jednokomorowego tzn. z
pominięciem działania przelewu zatopionego.

Q

dop(t)

H

0

Q

0

Q

T

h

R

=D

R

Q

IN

IN

dop(t)

M

Q

Q

Q

<

<

0

0

h

H

=

,

R

h D

=

T

0

i

0

Q

Q

Q

=

=

0

)

t

(

dop

Q

Q

=

0

Q

Ri

=

Rys. 5. Całkowite wypełnienie zbiornika ściekami (stan chwilowy).

Wypełnienie całego zbiornika ściekami (rys. 5) następuje w momencie, gdy zmniejszająca się
stopniowo wartość dopływu ścieków do zbiornika będzie równa maksymalnej wartości
odpływu ścieków ze zbiornika Q

0

. W sytuacji, gdy poziomy zwierciadeł w komorach

wlotowej i retencyjnej znajdują się na tym samym poziomie, zawór klapowy traci szczelność,
pozostając w takim samym położeniu, jak przy pustym zbiorniku.

Q

dop(t)

Q

0i

Q

Ti

Q

Pi

h

0

h

R

Q

IN

dop(t)

M

0 Q

Q

<

<

0

0P

0

0 h

H , h

h

R

<

<

<

,

Rp

R

R

H

h

D

<

<

0i

Ti

Q

Q

=

Ti

dop(t)

Pi

Q

Q

Q

≥

+

i

0

)

t

(

dop

Q

Q

<

Rys. 6. Faza opróżniania komory retencyjnej przez przelew.

Stopniowe zmniejszanie wartości dopływu ścieków do zbiornika, przy jego całkowitym
wypełnieniu oznacza rozpoczęcie fazy opróżniania zbiornika (rys. 6). Ciągły odpływ ścieków
przewodem tranzytowym powodować będzie obniżanie się stanu napełnienia w komorze
wlotowej. W konsekwencji tego, ścieki z komory retencyjnej, poprzez koronę przelewu
przepływać będą do komory wlotowej. W czasie trwania tej fazy zakłada się, że zawór
klapowy pozostaje jeszcze zamknięty, jednak w rzeczywistości, wskutek występowania
różnicy ciśnień hydrostatycznych będzie następować niewielki przepływ otworem klapowym.

Q

dop(t)

Q

0i

Q

Ti

∆h

h

0

h

R

Q

IN

dop(t)

M

0 Q

Q

<

<

0

0P

0 h

H

<

<

,

R

R

h

H

=

p

R

0

h h

h

∆ =

−

Ti

i

0

Q

Q

=

i

0

)

t

(

dop

Q

Q

<

0

Q

pi

=

Rys. 7. Komora retencyjna wypełniona do poziomu krawędzi przelewowej (stan chwilowy).

Przepływ przez przelew ustaje w chwili obniżenia się poziomu zwierciadła ścieków w
komorze retencyjnej do poziomu krawędzi przelewowej. W trakcie fazy opróżniania
zbiornika istotna kwestią jest osiągnięcie odpowiedniej różnicy poziomów ścieków między
komorami wlotową i retencyjną, zapewniającej otwarcie zaworu klapowego.

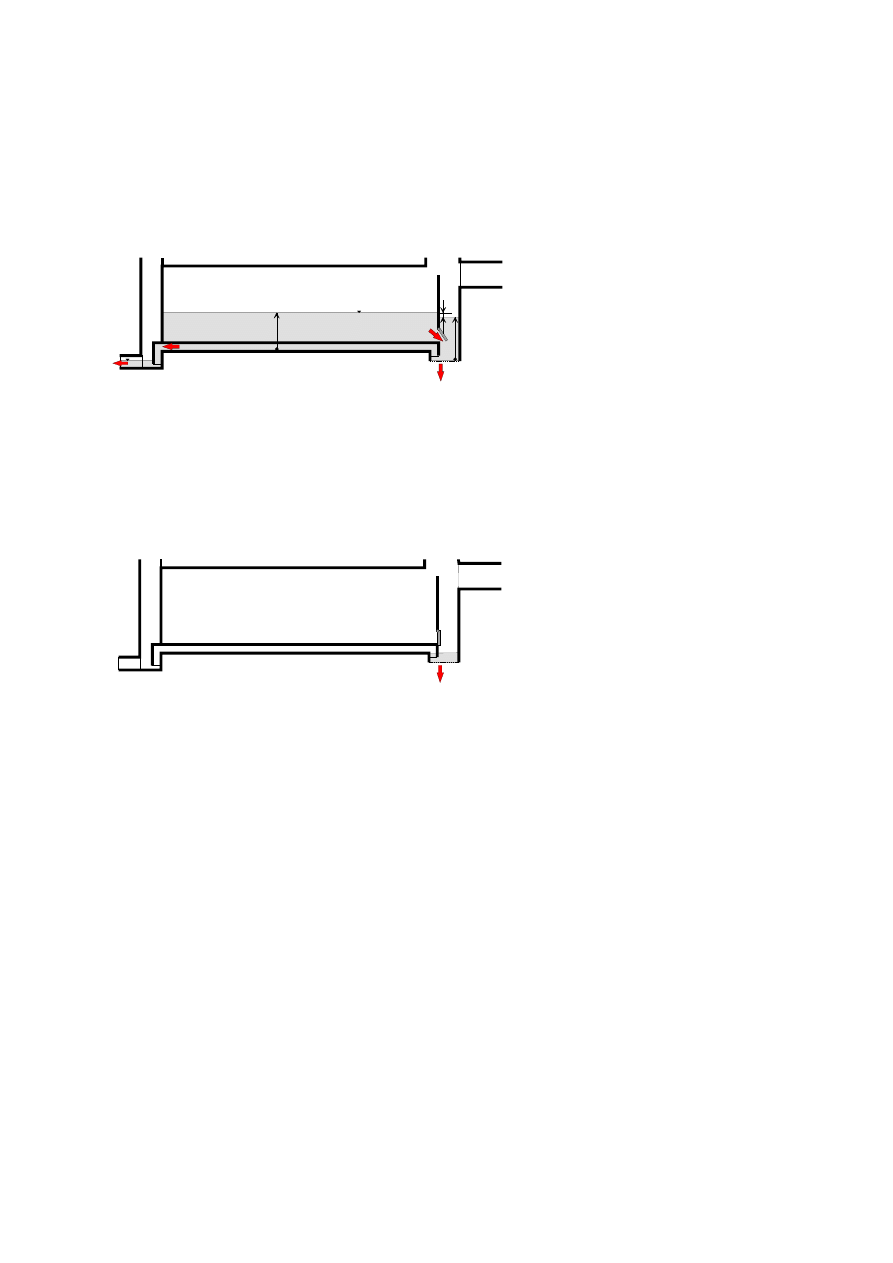
W rzeczywistości tę różnice wysokości napełnień zbiornik może osiągnąć w różnych fazach
jego opróżniania i ma na to wpływ wiele czynników trudnych do matematycznego określenia.
Otwarty różnicą ciśnień hydrostatycznych zawór klapowy umożliwia przepływ cieczy z
komory retencyjnej do komory wlotowej, skąd przewodem tranzytowym zasila ona komorę
wylotową (rys. 8). Proces opróżniania zbiornika można uznać za zakończony w chwili, gdy w
komorze retencyjnej nie będzie już wody.

h

0

Q

0i

Q

Ti

∆h

Q

Zi

h

R

Q

IN

dop(t )

IN

Q

0, Q

0

=

>

0

0P

0 h

H

<

<

R

R

0 h

H

P

<

<

R

0

h h

h

∆ =

−

0i

Ti

Q

Q

=

Rys. 8. Faza opróżniania komory retencyjnej przez otwór spustowy.

Ostatnią fazą działania zbiornika jest opróżnienie tej objętości zbiornika, która nie może być
odprowadzona przewodem tranzytowym i podlega stopniowemu wsiąkaniu poprzez dno
komory wlotowej (rys. 9). W zależności od przepuszczalności gruntu i ilości infiltrującej
wody faza ta może trwać od kilku do kilkunastu godzin.

h

0

Q

IN

IN

dop(t)

Q

0, Q

>

= 0

p

0

0

0 h

H

<

<

R

h

0

=

0i

Ti

Q

Q

0

=

=

Rys. 9. Faza opróżniania komory wlotowej wyłącznie poprzez infiltrację.


PRZYKŁAD SYMULACJI DZIAŁANIA ZBIORNIKA DLA ZAPROPONOWANEGO
MODELU MATEMATYCZNEGO

Ponieważ w najbliższym czasie planowane jest podjęcie serii badań weryfikacyjnych

na modelu fizycznym zbiornika w skali laboratoryjnej to poniższy przykład symulacji
działania zbiornika został opracowany w oparciu o planowany model.
Podstawowe wymiary geometryczne modelu zbiornika:

- średnica komory retencyjnej D

R

=0,29 m

- długość komory retencyjnej L

R

= 2,08 m

- średnica przewodu tranzytowego d

T

=0,032 m

- wymiary komory wlotowej: 0,125

×0,367 m

- spadek komory retencyjnej i=1,0 %
- wysokość położenia krawędzi przelewowej H

0p

=0,282 m (licząc od dna komory

retencyjnej w przekroju wlotowym).

Dla tak zdefiniowanej geometrii zbiornika złożono następujące dane hydrauliczne:

- maksymalne

natężenie dopływu Q

M

=0,001 [m

3

/s]

- maksymalne

natężenie odpływu Q

0

=0,0006 [m

3

/s]

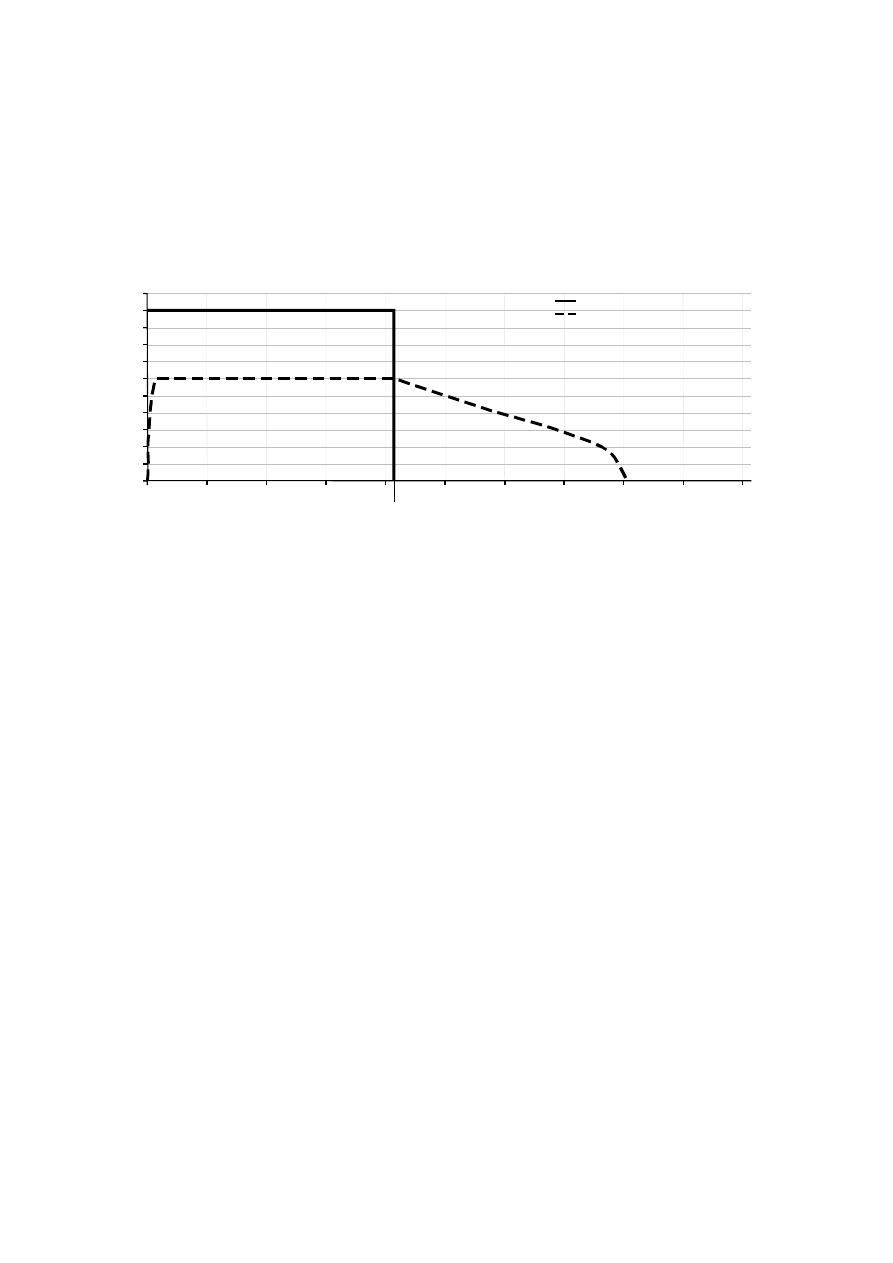
Wynikiem symulacji jest wykres zaprezentowany na rysunku 10, który obrazuje

przebieg zmienności natężenia odpływu ze zbiornika dla zadanego hydrogramu dopływu (w
tym przypadku o stałej wartości w czasie Q

dop(t)

=const). Czas całkowitego napełnienia

zbiornika wodą wyniósł w tym przypadku 415 sekund. Warto zauważyć, że kształt krzywej
odpływu w fazie napełniania jest identyczny jak dla wcześniej przedstawianych zbiorników
wielokomorowych. Oznacza to, zbiornik typu Proximus także będzie się charakteryzował
wysoką efektywnością hydrauliczną.

Q

M

=0,0010

100

200

300

400

500

600

700

800

900

1000

0,0001

0,0002

0,0003

0,0004

0,0005

0,0006

0,0007

0,0008

0,0009

Czas, [s]

Przepływ, [m

3

/s]

0,0010

T

k

=415

Q

0

=0,0006

0,0011

0,0

0

hydrogram dopływu
hydrogram odpływu

Rys. 10. Przebieg hydrogramu odpływu ze zbiornika typu Proximus dla hydrogramu dopływu o
stałym natężeniu.

Ponieważ założono, że w momencie całkowitego wypełnienia zbiornika następuje

zanik dopływu, to po czasie T

k

(koniec fazy napełniania) rozpoczyna się faza opróżniania

zbiornika. Jak widać na wykresie po 810 sekundach następuje zakończenie fazy opróżniania
przez przewód tranzytowy co jednak nie oznacza że zbiornik jest pusty. Pozostała woda (w
sumie blisko 15 dm

3

) odprowadzana jest poprzez dno komory wlotowej o powierzchni 0,046

m

2

do gruntu. Dla założonego współczynnika filtracji k=10

-4

[m/s] czas opróżnienia tej

objętości będzie wynosić ok. 3200s. Widać zatem, że czas trwania fazy opróżniania poprzez
infiltrację będzie wielokrotnie dłuższy niż czas opróżniania poprzez przewód tranzytowy (w
danym przykładzie ośmiokrotnie). Dlatego też przy projektowaniu tego typu zbiornika należy
ograniczyć objętość, która będzie opróżniana wyłącznie przez infiltrację (V

IN

) bądź też

obliczeniową pojemność retencyjną zbiornika powiększyć o V

IN

. Znaczący wpływ na kwestie

wymiarowania powierzchni infiltracji będzie mieć też współczynnik redukcji przepływu
(definiowany jako stosunek maksymalnego natężenia odpływu ze zbiornika do
maksymalnego natężenia dopływu), który ma istotny wpływ na czasy trwania faz napełniania
jak i opróżniania zbiorników retencyjnych.

PODSUMOWANIE

Korzystne oddziaływanie zbiorników retencyjnych na działanie sieci kanalizacyjnej,

oczyszczalni ścieków a także ochronę wód odbiorników stanowią silną motywację do
poszukiwania nowych, bardziej efektywnych rozwiązań konstrukcyjnych. Zaproponowany w
artykule retencyjno-infiltracyjny zbiornik rurowy poszerza zakres praktycznie uzasadnionych
zastosowań systemów retencyjnych do regulowania natężenia przepływu wód opadowych w
istniejących jak i nowoprojektowanych systemach kanalizacji deszczowej. Przedstawiony
model matematyczny tego zbiornika został oparty na szeregu założeń upraszczających, z
których część musi zostać poddana weryfikacji dla warunków rzeczywistych - dotyczy to
przede wszystkim części infiltracyjnej zbiornika. Zalety prezentowanej konstrukcji to przede
wszystkim: efektywność hydrauliczna na poziomie innych zbiorników wielokomorowych

oraz możliwość ograniczania zagłębienia kanału odpływowego. Pewnym ograniczeniem w
stosowaniu tej konstrukcji będzie niewątpliwie konieczność zapewnienia odpowiedniej
przepuszczalności gruntu w miejscu budowy zbiornika (współczynnik filtracji minimum
k=10

-5

m/s).

BIBLIOGRAFIA

Becker M., Prinz R., Liebig T. (2001), Effectiveness of a stormwater tank with overflow with a downstream

stormwater holding, KA - Wasserwirtschaft, Abwasser, Abfall 1/2001, 16-24.

Dziopak J. (2002), Zbiorniki retencyjne stosowane w kanalizacji, Rynek Instalacyjny, nr 9, 86-91.
Erb H. (1999) Technika pomiarów przepływu wody i ścieków, Wydawnictwo Seidel-Przywecki, Bydgoszcz.
Kisiel A., Dziopak J. (1999), Oddziaływanie zbiorników retencyjnych na funkcjonowanie systemów

kanalizacyjnych, Gaz, Woda i Technika Sanitarna, nr 3, 75-80.

Mays L. (2000), Stormwater Collection Systems Design Handbook, McGraw-Hill Professional Publishing, New

York.

Mrowiec M. (2002), Możliwości stosowania rurowych zbiorników retencyjnych o zwiększonej efektywności

hydraulicznej w systemach kanalizacyjnych, IV Konferencja naukowo - techniczna "Nowe technologie w
sieciach i instalacjach wodociągowych i kanalizacyjnych", Ustroń, 373-382.

Mrowiec M. (2003), Teoretyczno-eksperymentalna analiza hydraulicznego działania rurowych zbiorników

retencyjnych w kanalizacji deszczowej, rozprawa doktorska, Politechnika Częstochowska.

SUMMARY
This paper presents an innovative design of an in-line retention tank. The
detention tanks made of large diameter pipes offer a number of advantages
on both stages: design and construction. In comparison to the other in-line
detention tanks the proposed one is characterized by opposite slope of main
detention chamber. Moreover the inlet chamber has an perforated bottom
that allows to infiltration into the ground. The paper have shown all the
characteristic phases of the operation of the tank along with boundary
conditions. For such defined phases, the mathematical model of the tank has
been proposed. The model allows to conduct the simulation research for
wide range of input parameters (geometry of the tank, flow rates etc.).