PKM – Ćwiczenia nr 2 – Połączenia śrubowe luźne

1

Ćwiczenia 2 – Połączenia śrubowe luźne

1) Stan naprężenia połączeń śrubowych

a) Rozciąganie

r

r

c

r

c

r

k

d

Q

A

Q

≤

⋅

⋅

=

=

2

4

π

σ

(1)

gdzie:

σ

r

– naprężenia normalne w śrubie, [MPa]

A

r

– pole przekroju poprzecznego śruby, [mm

2

]

d

r

– średnica rdzenia śruby, [mm]

k

r

– naprężenia kryterialne w przypadku rozciągania, [MPa]

Q

c

– siła osiowa, [N]

s

k

p

w

c

c

c

Q

Q

Q

+

⋅

+

=

1

1

(2)

gdzie:
Q

w

– napięcie wstępne, [N]

Q

p

– obciążenie robocze, [N]

c

k

– sztywność elementów ściskanych, [N/m]

c

s

– sztywność śruby, [N/m]

a.1) Wyznaczenie sztywności elementów ściskanych i śruby

Wyznaczenie sztywności elementów złącza jest jednym z etapów konstruowania połączenia. Zależność (3)
przedstawia ogólny wzór na sztywność.

L

EA

c

=

(3)

gdzie:
E – moduł Young’a, [MPa]
A – pole przekroju poprzecznego, [mm

2

]

L – długość elementu (wymiar elementu wzdłuż działania siły), [mm]

W przypadku złącza śrubowego wyznacza się sztywności poszczególnych jego elementów (bierzemy pod uwagę
te elementu na które działa obciążenie robocze – tzn. rozciągana cześć śruby i ściskana część blach). W
przypadku śruby dzieli się ją na dwie części – gwintowaną i niegwintowaną. Dla każdej części śruby wyznacza
się oddzielnie sztywność. W kolejnym kroku wyznacza się sztywności zastępcze. Sztywność zastępczą można
wyznaczyć na podstawie podatności zastępczej opisanej wzorem (4).

∑

∑

=

=

⋅

=

=

N

i

i

i

i

N

i

i

A

E

L

c

c

1

1

1

1

(4)

Stąd podatność zastępczą śruby można wyznaczyć (patrz rys.1a):

2

2

1

1

1

A

E

L

A

E

L

c

s

s

s

⋅

+

⋅

=

(5)

gdzie:

4

2

1

r

d

A

⋅

=

π

oraz

4

2

2

d

A

⋅

=

π

d

r

– średnica rdzenia śruby, [mm]

d – średnica śruby w części niegwintowanej, [mm]
E

s

– moduł Younga tworzywa śruby, [MPa]

L

1

, L

2

– długości odpowiednio odcinka gwintowanego i niegwintowanego rozciąganej części śruby (Rys.1a)

PKM – Ćwiczenia nr 2 – Połączenia śrubowe luźne

2

W przypadku elementów ściskanych sytuacja jest bardziej złożona. Wszystkie łączone elementy rozpatruje się
jako pakiet elementów ściskanych. Nie ma tu problemu na ile „części” należy podzielić ten pakiet – jest to liczba
blach (każda blacha ma inną sztywność w zależności od grubości i tworzywa). Problem pojawia się przy
określaniu niezbędnych do wyznaczenia sztywności wymiarów geometrycznych blach. Z uwagi na to, że
połączenie śrubowe ma charakter zbliżony do punktowego, na stan odkształcenia/naprężenia złącza wpływ ma
tylko część blachy w jego najbliższym otoczeniu. Rzeczywisty wpływ siły ściskającej blachy na ich stan
odkształcenia nie jest znany. W związku z tym w obliczeniach inżynierski zakłada się przybliżony kształt strefy
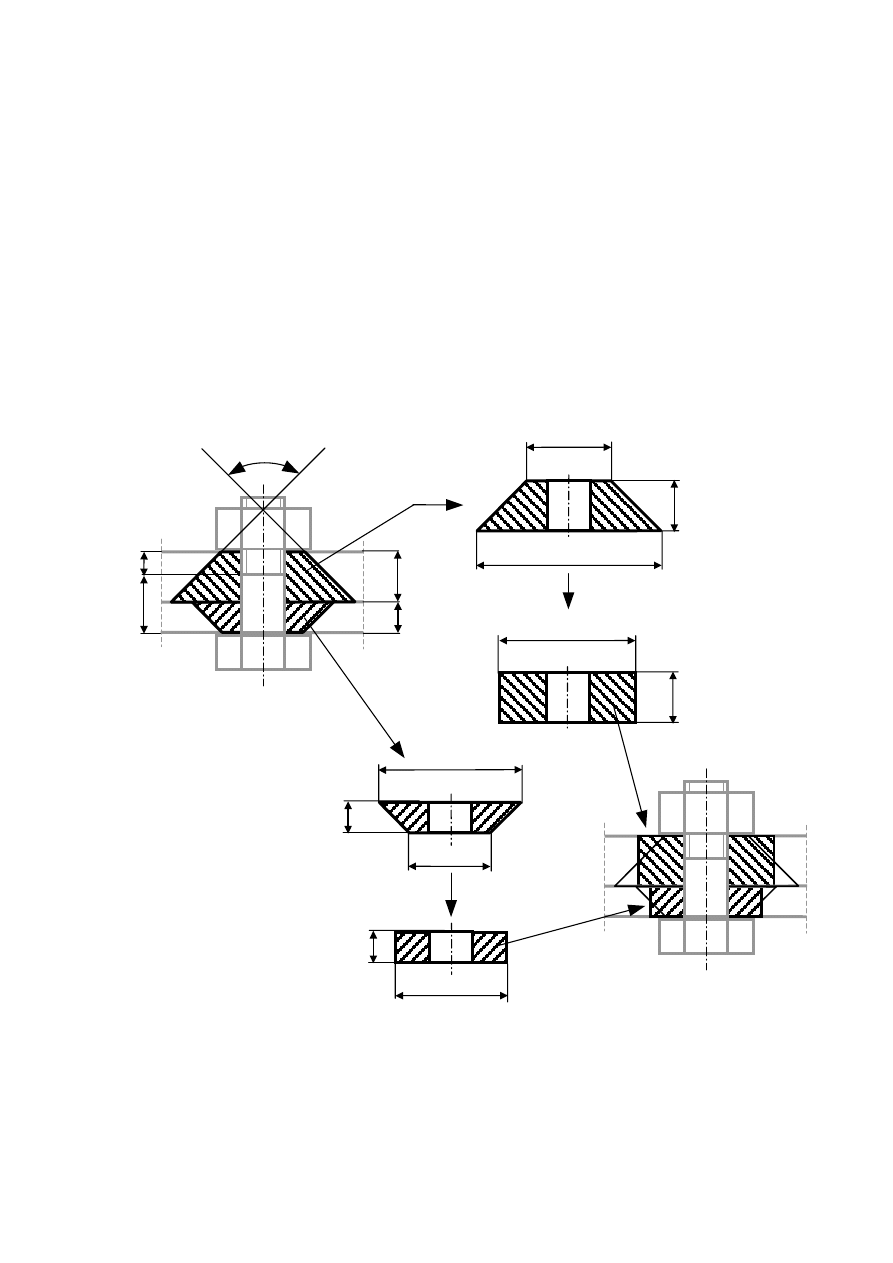
naprężeń ściskających w elementach łączonych. Na rysunku 1a przedstawiono przybliżony kształt przyjmowany
w obliczeniach. Strefę naprężeń ściskających stanowią dwa ścięte stożki złączone większymi podstawami. Kąt
wierzchołkowy przyjmowany jest około 90º, wysokość każdego stożka jest równa grubości blachy a mniejsza
średnica jest równa średnicy oporowej łba śruby lub nakrętki (średnica powierzchni oporowej jest jedną z
wielkości podawanych w normach). Średnica otworu osiowego w stożku jest równa średnicy otworu pod śruby
d

0

. W celu ułatwienia dalszych obliczeń stożki te są zamieniane na walce drążone, których średnica wewnętrzna

pozostaje bez zmian, zaś średnica zewnętrzna jest średnią średnic podstaw stożka (górna blacha – rys. 1 b, c ,
dolna blacha rys. 1 d, e). Rysunek 1f przedstawia model strefy ściskania blach w postaci otrzymanych dwóch
drążonych walców.

L

1

L

2

L

3

L

4

90

°

L

3

D

D

D+2L

4

D+2L

3

L

4

L

3

D+L

4

D+L

3

L

4

a)

b)

d)

c)

e)

f)

Rysunek 1. Modelowanie wpływu połączenia śrubowego na łączone elementy.

PKM – Ćwiczenia nr 2 – Połączenia śrubowe luźne

3

Sztywność elementów łączonych wyznaczamy przez wyznaczenie sztywności poszczególnych walców drążony
a następnie wyznaczenie sztywności zastępczej analogicznie jak dla śruby. Na podstawie zależności (4) można
wyrazić podatność zastępczą elementów łączonych:

2

2

4

1

1

3

1

w

w

k

A

E

L

A

E

L

c

⋅

+

⋅

=

(6)

gdzie:

(

)

4

2

0

3

1

d

L

D

A

w

−

+

⋅

=

π

oraz

(

)

4

2

0

4

1

d

L

D

A

w

−

+

⋅

=

π

E

1

, E

2

– moduły Younga tworzyw poszczególnych elementów ściskanych,

A

w1

, A

w2

– pole powierzchni walców drążonych

UWAGA:
Należy zwrócić uwagę studentom, że w przypadku łączenia większej liczby blach liczba składników w
zależności (6) jest zawsze równa liczbie blach (dla każdej blachy rozpatrujemy jeden walec drążony).

b) Rozciąganie i skręcanie

r

s

s

c

r

r

z

k

k

k

≤













⋅

+

=

2

,

2

τ

σ

σ

(7)

gdzie:

σ

z

– naprężenia zredukowane, [MPa]

τ

s

– naprężenia styczne, [MPa]

k

r,c

– naprężenie kryterialne w przypadku rozciągania lub ściskania (dla stali k

r

= k

c

), [MPa]

k

s

– naprężenia kryterialne w przypadku skręcania, [MPa]

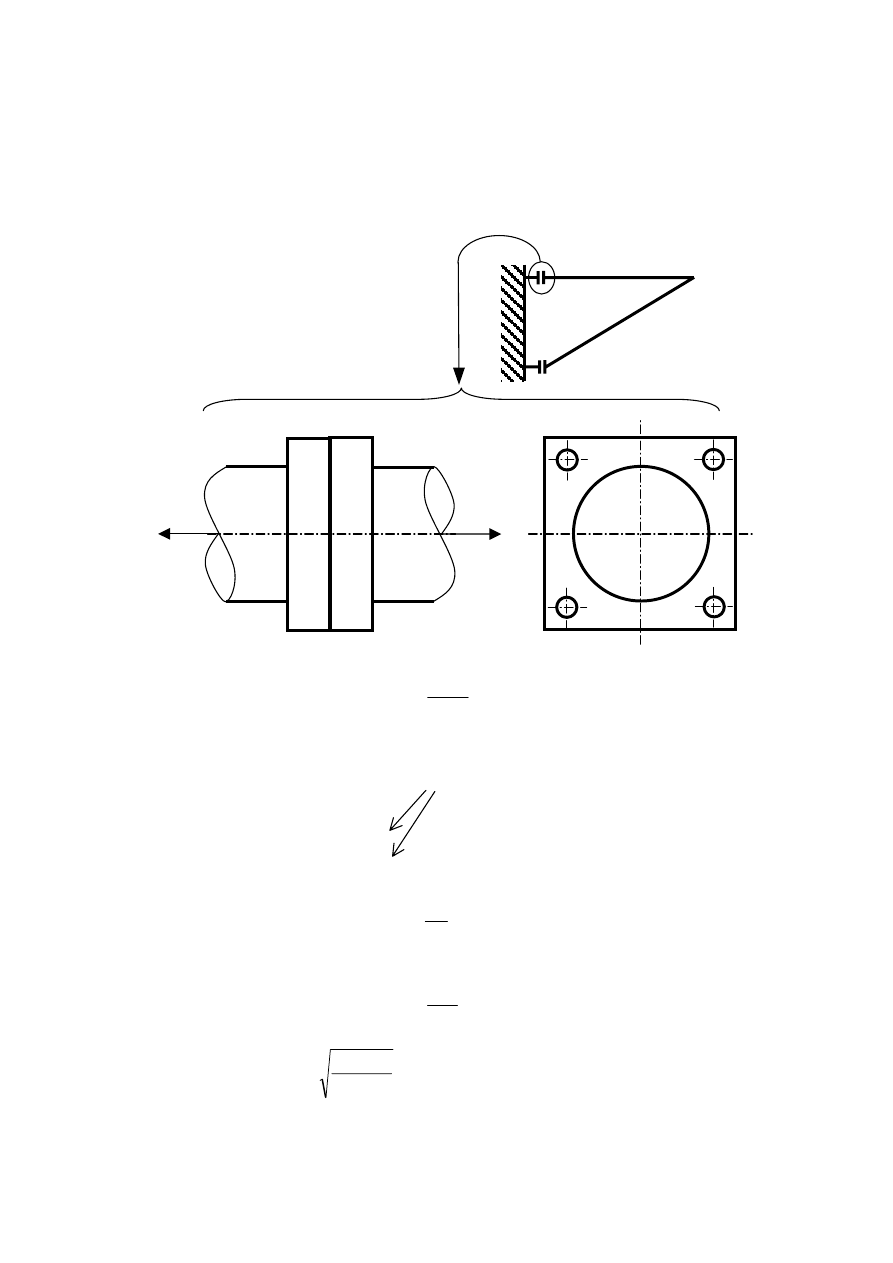
c) Obciążenie poprzeczne

µ

π

µ

⋅

⋅

=

⋅

=

≤

P

d

r

4

Q

T

Q

2

w

T

(8)

gdzie:
Q

T

– siła poprzeczna, [N]

T – siła tarcia, [N]

µ – liczba tarcia
P – naciski powierzchniowe, [MPa]

PKM – Ćwiczenia nr 2 – Połączenia śrubowe luźne

4

2) Przykłady zadań

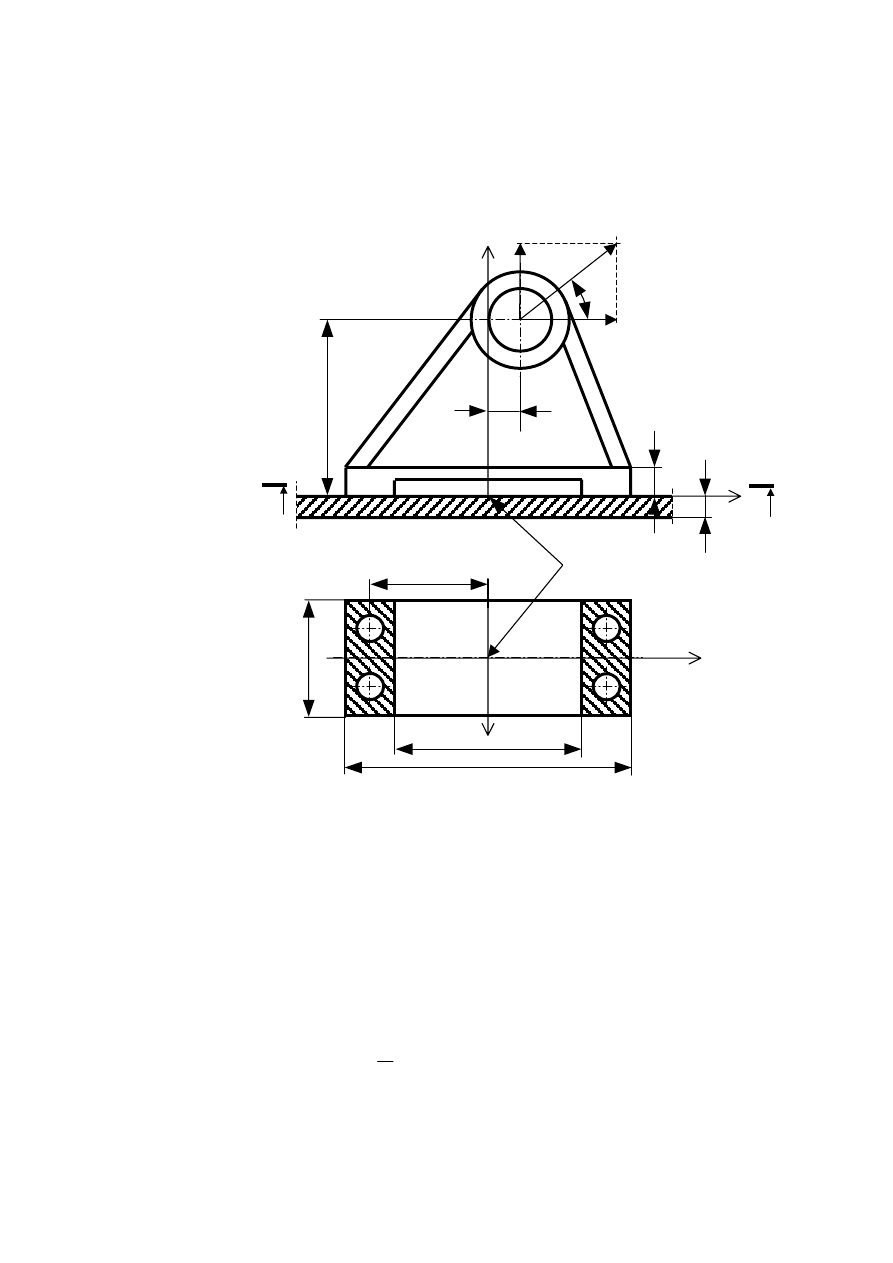
Zad.1.

Dwa pręty wysięgnika promieniowego połączono za pomocą złącza śrubowego ze śrubami luźnymi jak na
rysunku. Obliczyć i dobrać wymagane wymiary śrub wiedząc, że:
Siła wynosi Q=2,5

⋅10

4

N

Liczba śrub wynosi n = 4
Liczba bezpieczeństwa wynosi δ = 2,5























Stan naprężenia śruby:

r

r

r

k

A

n

Q ≤

⋅

=

σ

(1.1)

W celu określenia własności wytrzymałościowych tworzywa śrub podaje się tzw. klasę własności
mechanicznych śruby. W każdej normie dotyczącej śrub jest wymieniona lista zalecanych klas własności
mechanicznych dla każdej grupy śrub. Zakładamy, że śruby będą klasy 5.6.
Na podstawie klasy własności mechanicznych śruby 5.6 wiadomo, że tworzywo śruby ma następujące własności
wytrzymałościowe:

MPa

MPa

R

m

500

100

5

=

⋅

=

(1.2)

MPa

R

R

m

e

300

6

.

0

=

⋅

=

(1.3)

stąd:

MPa

R

k

e

r

120

=

=

δ

(1.4)

a pole przekroju poprzecznego rdzenia śruby można wyrazić:

4

2

r

r

d

A

π

=

(1.5)

wówczas:

r

r

k

n

Q

d

⋅

⋅

⋅

≥

π

4

stąd

mm

d

r

143

,

8

≥

(1.6)

Dobrano śrubę M10, dla której średnica rdzenia wynosi d

r

= 8,160 mm

Q

Q

PKM – Ćwiczenia nr 2 – Połączenia śrubowe luźne

5

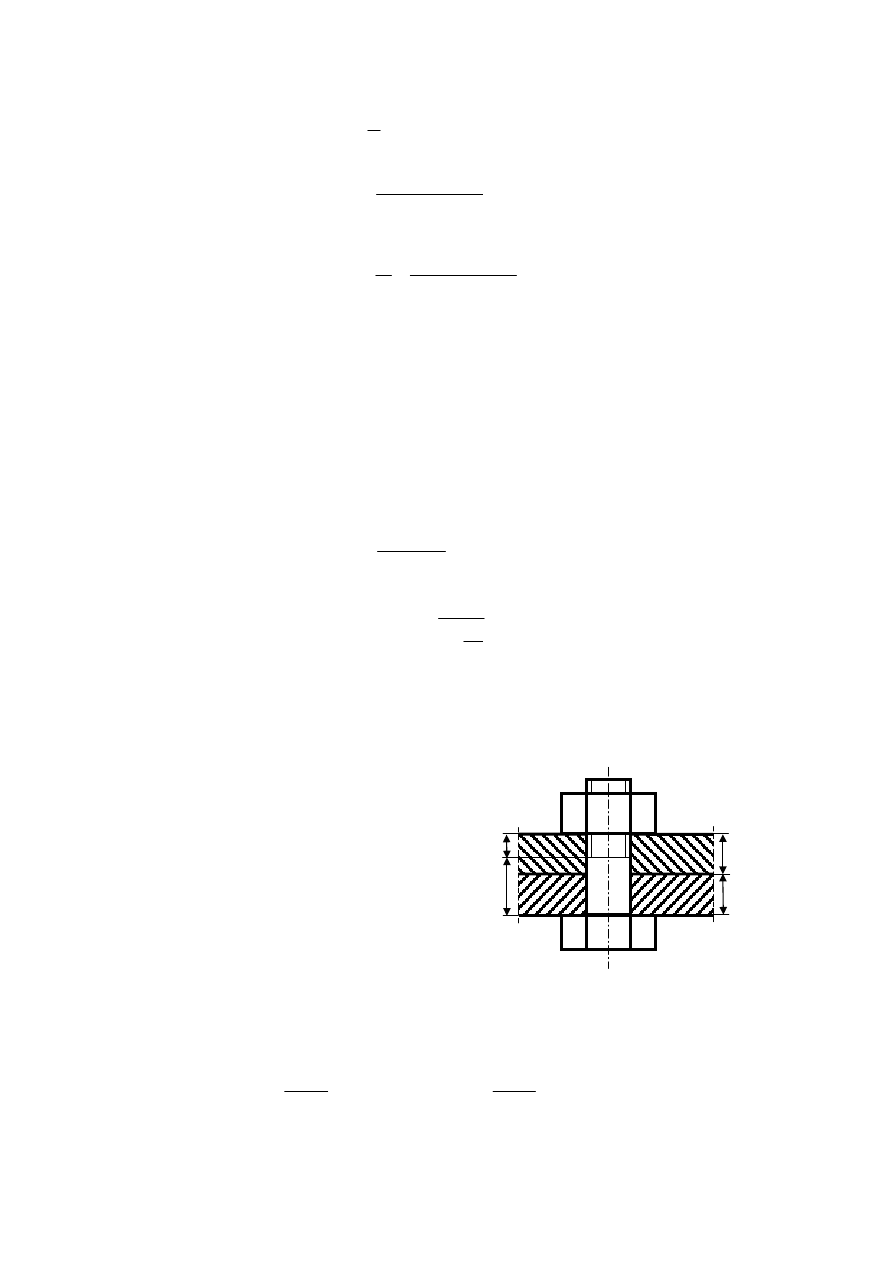
Zad.2.

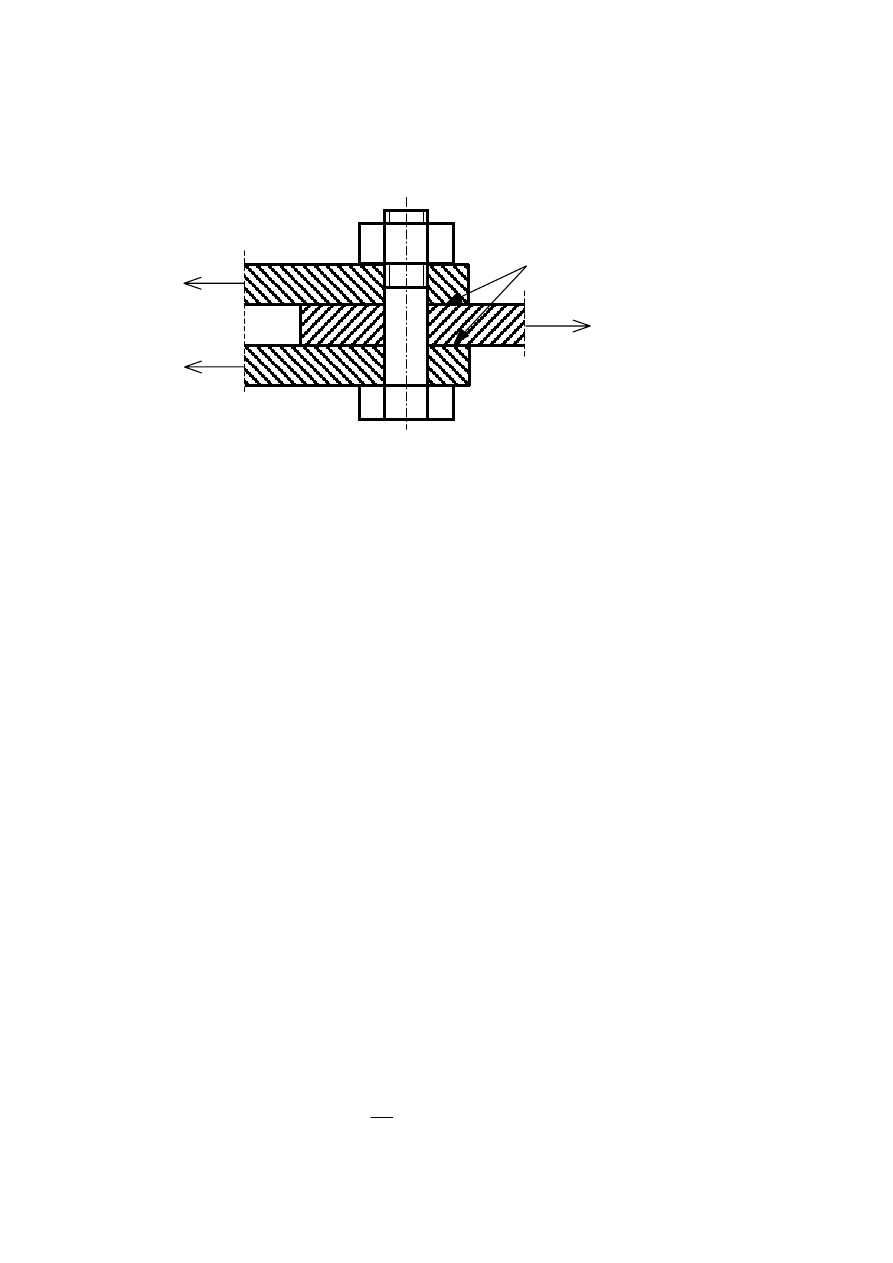
Korpus łożyska ślizgowego przymocowany jest do podstawy stalowej 4 śrubami. Skonstruować połączenie
śrubowe łączące korpus z podstawą, jeżeli obciążenie przenoszone przez łożysko jest równe R = 5000 N.
Tworzywo korpusu Zl300, tworzywo podstawy 45. Zadanie rozwiązać przy założeniach, że:

- między płaszczyznami styku korpusu łożyska i podstawy nie powstanie szczelina podczas

obciążenia zewnętrznego

- płaszczyzny styku nie mogą przemieszczać się względem siebie
- liczba

bezpieczeństwa δ = 1,5

Dane:
a = 30 mm
b = 60 mm
c = 80 mm
h = 100 mm
H = 150 mm
α = 30º
l = 55 mm
µ = 0,3
g

k

= 25 mm

g

p

= 20 mm

Rozkład obciążenia R na składowe N i S:







=

=

=

=

N

R

S

N

R

N

4330

cos

2500

sin

α

α

(2.1)

gdzie:
N – siła odrywająca korpus
S – siła przesuwająca korpus po powierzchni podstawy

Obciążenie robocze:

S

N

p

Q

Q

Q

+

=

(2.2)

gdzie:
Q

N

– siła rozciągająca śrubę wywołana działaniem siły N

n

N

Q

N

=

(2.3)

Q

S

– siła rozciągająca śrubę wywołana działaniem siły S. (Należy zwrócić studentom uwagę na fakt, że chociaż

siła S działa prostopadle do osi śrub to w śrubach po lewej stronie powoduje ona zwiększenie a w śrubach po
prawej zmniejszenie siły rozciągającej, co wynika z równania momentów względem środka ciężkości śrub 4.4)

b

l

c

H

środek ciężkości śrub
(początek układu wsp.)

y

x

z

S

N

R

h

a

g

k

g

p

α

A

A

A - A

x

PKM – Ćwiczenia nr 2 – Połączenia śrubowe luźne

6

a

N

h

S

l

n

Q

S

⋅

−

⋅

=

⋅

⋅

2

(2.4)

stąd:

(

)

l

n

a

N

h

S

Q

S

⋅

⋅

−

⋅

=

2

(2.5)

Wstawiając (4.3) i (4.5) do (4.2) otrzymujemy:

(

)

N

l

n

a

N

h

S

n

N

Q

p

3880

2

=

⋅

⋅

−

⋅

+

=

(2.6)

Zgodnie z założeniami zadania, aby nie powstała szczelina między powierzchniami styku musi być spełniony
następujący warunek (jest to warunek dla połączeń, od których nie wymaga się szczelności):

w

z

Q

Q

6

,

0

2

,

0

÷

≥

(2.7)

gdzie:
Q

w

– napięcie wstępne śruby

Q

z

– zacisk resztkowy (w rozpatrywanym przypadku przyjęto

w

z

Q

Q

⋅

= 2

,

0

)

Wyrażenie (4.8) określa warunek, jaki musi być spełniony, aby nie następowało wzajemne przemieszczenie
obydwu elementów (założenie drugie):

S

n

Q

z

≥

⋅

⋅

µ

(2.8)

wówczas na podstawie (4.7) i (4.8) można określić napięcie wstępne śruby:

N

n

S

Q

w

18042

2

,

0

=

⋅

⋅

=

µ

(2.9)

Na podstawie (4.6) i (4.9) można określić całkowite obciążenie śruby:

s

k

p

w

c

c

c

Q

Q

Q

+

⋅

+

=

1

1

(2.10)

W celu wyznaczenia obciążenia całkowitego śruby należy określić pozostałe wymiary geometryczne złącza
śrubowego (konieczność wyznaczenia sztywności elementów ściskanych i śrub), a następnie poddać założenia
weryfikacji

W związku z tym zakładamy śrubę: M20 x 1,5 x 80 – 6.8 – B o długości części gwintowanej wynoszącej 46 mm.

Dane dodatkowe:
d

0

= 21 mm

– średnica otworu

d

r

= 18,16 mm

– średnica rdzenia śruby

D = 27,7 mm

– średnica pow. oporowej

L

dr

= 11 mm

– długość rozciąganego odcinka

gwintowanego

śruby

L

d

= 34 mm

– długość niegwintowanego odcinka

śruby

E

s

= E

45

= 2,1·10

5

MPa – moduł Younga materiałów śruby

i

korpusu

E

Zl300

= 1,1·10

5

MPa

– moduł Younga materiału podstawy

Na podstawie powyższych danych można określić sztywności elementów złącza śrubowego:

Podatność śruby:

2

2

1

259

4

mm

d

A

r

=

⋅

=

π

oraz

2

2

2

16

,

314

4

mm

d

A

=

⋅

=

π

L

dr

L

d

g

k

g

p

PKM – Ćwiczenia nr 2 – Połączenia śrubowe luźne

7

N

mm

A

E

L

A

E

L

c

s

d

s

dr

s

7

2

1

10

18

,

7

1

−

⋅

=

⋅

+

⋅

=

(2.11)

Podatność elementów ściskanych:

(

)

2

2

0

560

4

mm

d

g

D

A

p

p

=

−

+

⋅

=

π

(

)

2

2

0

2

,

789

4

mm

d

g

D

A

k

k

=

−

+

⋅

=

π

gdzie:
A

p

, A

k

– pola powierzchni przekrojów walców drążonych (patrz zalezność 6 i 7 w rozdz. 1)

N

mm

A

E

g

A

E

g

c

k

Zl

k

p

p

k

7

300

45

10

58

,

4

1

−

⋅

=

⋅

+

⋅

=

(2.12)

Na podstawie (4.11) i (4.12) można zapisać:

57

,

1

=

s

k

c

c

(2.13)

Na podstawie (4.10) i (4.13) otrzymujemy:

N

Q

c

19551

=

(2.14)

Naprężenia kryterialne:

Na podstawie klasy wytrzymałości śrubu i liczby bezpieczeństwa wyznaczamy wartość naprężeń kryterialnych:

klasa śruby – 6.8
stąd

R

m

= 600 MPa

R

e

= 480 MPa

wówczas:

MPa

R

k

e

r

192

=

=

δ

(2.15)

Stan naprężenia:

r

r

c

r

k

MPa

mm

N

d

Q

≤

=

⋅

⋅

=

⋅

⋅

=

48

,

75

)

16

,

18

(

14

,

3

19551

4

4

2

2

π

σ

(2.16)

Nośność śrub jest wystarczająca.

PKM – Ćwiczenia nr 2 – Połączenia śrubowe luźne

8

Zad.3.

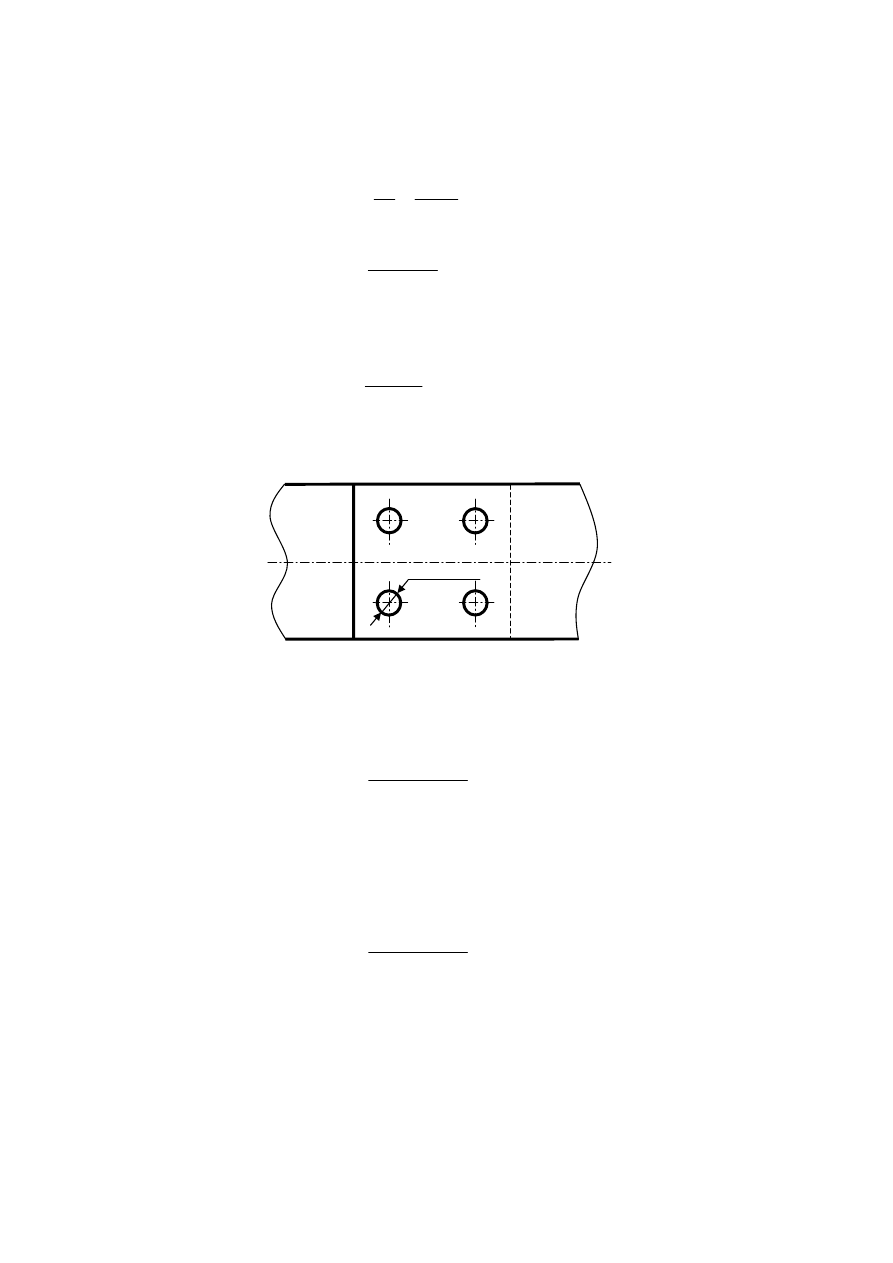
Płaskowniki o wymiarach przekroju poprzecznego 10 x 100mm połączono śrubami luźno pasowanymi (jak na
rysunku) i obciążono siłą P = 10 000 N. Kierunek działania siły jest prostopadły do osi śrub. Skonstruować
połączenie wiedząc, że płaskowniki wykonane są ze stali 30. Wielkość zakładki wynosi 100 mm. Liczba
bezpieczeństwa wynosi δ=2.

Projektowane połączenie śrubowe powinno wytworzyć taką siłę tarcia między płaskownikami, aby po
obciążeniu złącza siłą P płaskowniki nie przesunęły się:

P

T

≥

(3.1)

Siłę tarcia można wyznaczyć następująco:

µ

⋅

⋅

⋅

=

n

z

Q

T

(3.2)

gdzie:
Q – siła rozciągająca jedną śrubę (zsumowane siły ze wszystkich śrub stanowią siłę ściskającą płaskowniki)
z – liczba powierchni styku łączonych elementów (w rozpatrywanym przypadku z=2)
n – liczba śrub w połączeniu

µ - liczba tarcia (stal po stali µ = 0,15)

Dobór cech geometrycznych tego połączenia można przeprowadzić dwoma sposobami:

wariant A:
Zakładamy liczbę śrub n, a następnie na jej podstawie wyliczamy średnicę rdzenia śruby d

r

co umozliwi dobór

średnicy śruby M.... (Tok rozumowania został już przedstawiony w zadaniu 1 !!!)

wariant B:
Zakładamy średnicę śruby M ..... a na jej podstawie wyznaczamy liczbę śrub n.

Dalsze postępowanie przebiegać będzie wg wariantu B.

Zakładamy śruby M10 klasy 4.8.
d

r

= 8,466 mm

Na podstawie klasy wytrzymałości śruby i liczby bezpieczeństwa wyznaczamy wartość naprężeń kryterialnych
dla śruby:

klasa śruby – 4.8
stąd

R

m

= 400 MPa

R

e

= 320 MPa

wówczas:

MPa

R

k

e

r

160

=

=

δ

(3.3)

P

0,5P

Powierzchnia styku (z=2)

0,5P

PKM – Ćwiczenia nr 2 – Połączenia śrubowe luźne

9

Stan naprężenia jednej śruby:

r

r

r

r

k

d

Q

A

Q

≤

⋅

⋅

=

=

2

4

π

σ

(3.4)

stąd:

N

k

d

Q

r

r

3

2

10

9

4

⋅

=

⋅

⋅

≤

π

(3.5)

Q = 9000 N – maksymalna siła obciążająca jedną śrubę

Na podstawie zależności (2.1) i (2.2) można zapisać:

7

,

3

=

⋅

⋅

≥

µ

z

Q

P

n

(3.6)

Stąd n = 4

Projektowane złącze przedstawia poniższy rysunek:













Oprócz wyznaczenia niezbędnej liczby śrub należy sprawdzić, nie zostaną przekroczone dopuszczalne
naprężenia rozciągające płaskowniki. Należy zwrócić uwagę, że naprężenia te są wyznaczane w przekroju
płaskownika osłabionym otworami. Dla płaskowników 1 i 3 stan naprężenia opisuje zależność 3.7.

r

k

MPa

g

d

b

P

≤

=

⋅

⋅

−

⋅

=

4

,

6

)

2

(

5

,

0

0

σ

(3.7)

gdzie:
b – szerokość płaskowników = 100 mm
g – grubość płaskownika = 10 mm
k

r

– dopuszczalne naprężenia rozciągające płaskowniki – k

r

= 160 MPa

Dla płaskownika 2 stan naprężenia opisuje zależność 3.8

r

k

MPa

g

d

b

P

≤

=

⋅

⋅

−

=

8

,

12

)

2

(

0

σ

(3.8)

Połączenie zostało skonstruowane poprawnie.

d

0

= 17 mm

PKM – Ćwiczenia nr 2 – Połączenia śrubowe luźne

10

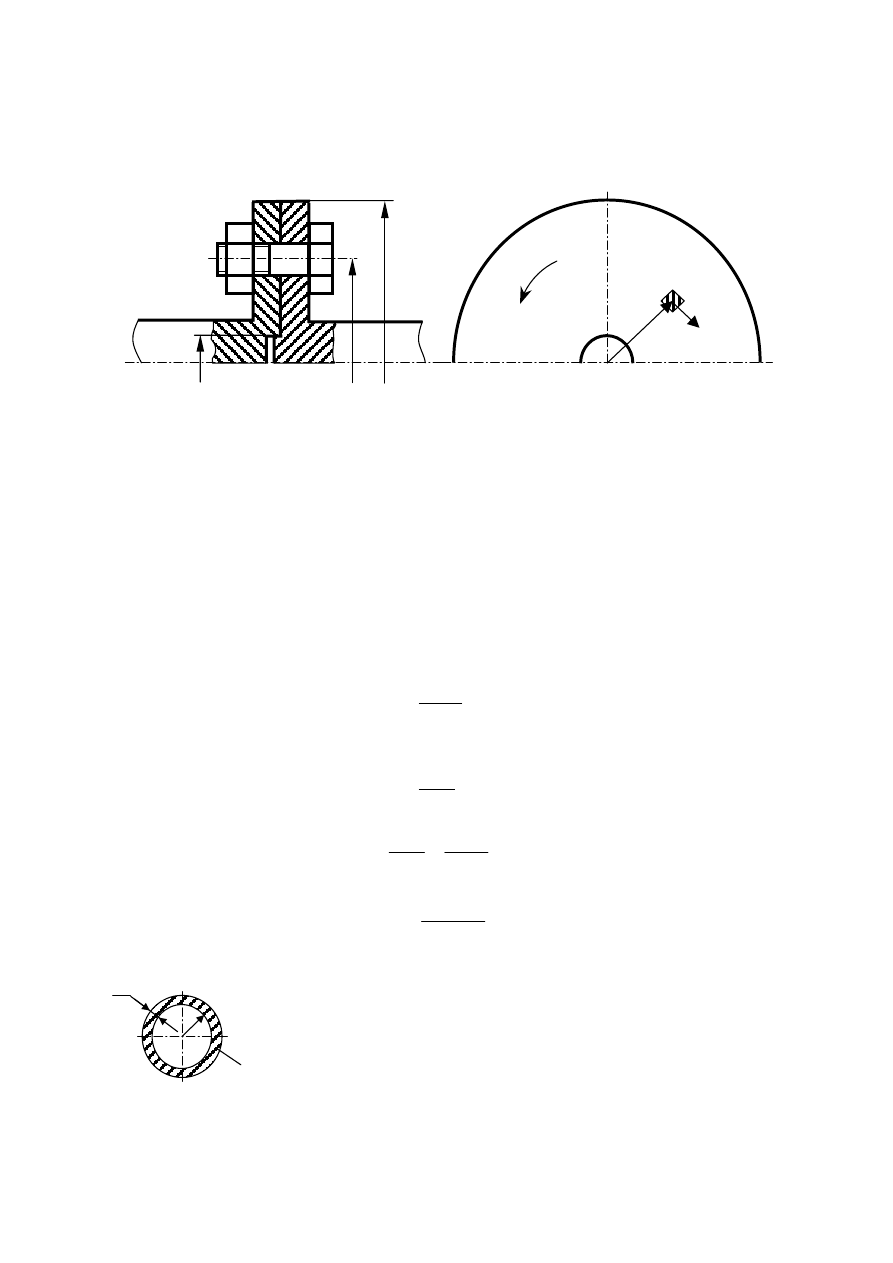
Zad. 4.

Obliczyć śruby łączące dwa wały obciążone momentem skręcającym M

s

=600 Nm. Sześć śrub założonych z

luzem założono tak, że moment M

s

przenoszony jest przez moment tarcia miedzy powierzchniami tarcz

ukształtowanych na wale. Liczba tarcia

µ = 0,15. Liczba bezpieczeństwa wynosi δ = 2.6

D

w

= 110 mm

D

0

= 115 mm

D

z

= 200 mm

n = 6









Wariant A – równomierny nacisk na powierzchni styku:

Przy luźnych śrubach przenoszony moment M

s

równoważony jest sumą momentów jednostkowych sił tarcia τ

względem środka ciężkości powierzchni styku. Zakładamy, że łączone części są sztywne i nacisk p na
powierzchni styku jest równomierny – siły tarcia we wszystkich punktach powierzchni styku są jednakowe.

µ

τ

⋅

= p

(4.1)

0

1

1

1

1

1

1

S

p

dA

r

p

dA

r

p

dA

r

M

A

A

A

s

⋅

⋅

=

⋅

⋅

⋅

=

⋅

⋅

⋅

=

⋅

⋅

=

∫

∫

∫

µ

µ

µ

τ

(4.2)

gdzie:
S

0

– biegunowy moment statyczny powierzchni względem jej środka ciężkości

Stąd wymagany nacisk:

0

S

M

p

s

⋅

=

µ

(4.3)

Nacisk ten wywołany jest przez napięcie wstępne śrub:

A

n

Q

p

⋅

=

(4.4)

Na podstawie (3.3) i (3.4):

0

S

M

A

n

Q

s

⋅

=

⋅

µ

(4.5)

stąd:

0

S

n

A

M

Q

s

⋅

⋅

⋅

=

µ

(4.6)

Wyznaczenie S

0

:

∫

⋅

⋅

⋅

=

z

w

r

r

dr

r

dA

π

2

2

(4.7)

UWAGA: należy zaznaczyć studentom, że dA

1

i dA

2

stanowią powierzchnie elementarne tego samego pola A.

Całkowanie po dA

1

zostało zastosowane do określenia siły tarcia.

Całkowanie po dA

2

zostało zastosowane do wyznaczenia momentu bezwładności S

0

.

dA

2

r

dr

D

W

D

0

D

Z

r

dA

1

τ

M

s

PKM – Ćwiczenia nr 2 – Połączenia śrubowe luźne

11

(

)

3

3

3

2

2

0

3

2

3

2

2

2

w

z

r

r

r

r

A

r

r

r

dr

r

dA

r

S

z

w

z

w

−

⋅

⋅

=

⋅

⋅

=

⋅

⋅

⋅

=

⋅

=

∫

∫

π

π

π

(4.8)

Pole powierzchni wówczas wynosi:

(

) (

)

2

2

2

2

4

w

z

w

z

D

D

r

r

A

−

=

−

⋅

=

π

π

(4.9)

wstawiając (3.8) i (3.9) do (3.6) otrzymujemy:

(

)

(

)

( ) ( )

[

]

N

D

D

n

D

D

M

Q

w

z

w

z

s

8367

55

100

3

2

15

0

6

110

200

4

600000

2

2

3

2

4

3

3

2

2

3

3

2

2

=

−

⋅

⋅

⋅

−

⋅

=





























−













⋅

⋅

⋅

⋅

−

⋅

⋅

=

π

π

π

µ

π

,

(4.10)

Stan naprężenia śruby:
Zakładamy śruby klasy 6.8 (R

m

= 600MPa, R

e

= 480MPa)

r

r

r

Z

d

Q ≤

⋅

⋅

=

2

4

π

σ

(4.11)

gdzie:
Z

r

– naprężenia kryterialne

MPa

R

k

e

r

185

6

,

2

480 =

=

=

δ

(4.12)

stąd:

mm

k

Q

d

r

r

59

,

7

4

=

⋅

⋅

≥

π

(4.13)

Przyjęto śrubę M10 x 1, dla której d

r

= 8,466 mm

Wariant B – nierównomierny nacisk na powierzchni styku

Jeżeli nacisk jest nierównomierny to między momentem napędowym i momentem tarcia zachodzi zależność:

t

s

M

M

≤

(4.14)

2

m

t

D

T

M

⋅

=

(4.15)

gdzie D

m

jest średnicą tarczy, na której działa siła T równą:

mm

D

D

D

z

w

m

155

2

=

+

=

(4.16)

stąd:

2

m

t

D

n

Q

M

⋅

⋅

⋅

=

µ

(4.17)

wówczas:

r

r

r

r

r

k

d

Q

k

d

Q

⋅

⋅

≤

⇒

≤

⋅

⋅

=

4

4

2

2

π

π

σ

(4.18)

s

m

r

r

t

M

D

n

k

d

M

≥

⋅

⋅

⋅

⋅

⋅

=

2

4

2

µ

π

(4.19)

mm

D

n

Z

M

d

m

r

s

r

69

,

7

155

6

15

,

0

185

600000

8

8

=

⋅

⋅

⋅

⋅

⋅

=

⋅

⋅

⋅

⋅

⋅

≥

π

µ

π

(4.20)

Przyjęto śrubę M10 x 1, dla której d

r

= 8,466 mm

PKM – Ćwiczenia nr 2 – Połączenia śrubowe luźne

12

Lteratura

[1] Dietrich M. et al., Podstawy konstrukcji maszyn. Tom 2, WNT, Warszawa 1995
[2] Garncarz G., Markusik S., Pomoce projektowe w budowie maszyn, Skrypt Pol. Śl. nr

1817, Gliwice 1995

[3] Jaskóła Z. et al., Podstawy konstrukcji maszyn. Zasada optymalnego doboru

obciążenia, połączenia śrubowe, łożyska toczne, sprzęgło jakośrodek optymalizacji
obciążenia,

Skrypt Pol. Śl. nr 1267, Gliwice 1987

[4] Niezgodziński M.E., Niezgodziński T., Wzory, wykresy i tablice wytrzymałościowe,

WNT, Warszawa 1996

[5] Podstawy konstrukcji maszyn. Część II. Ditrych J. (red.), Korewa W. (red.), Zygmunt

K. (red.), WNT, Warszawa 1965

[6] Szewczyk K., PKM. Połączenia gwintowe, PWN, Warszawa 1991