Ćwiczenie 1

Egzemplarz dla prowadzącego

Pomiary statyczne

1.

Cel i zakres ćwiczenia

Jest to ćwiczenie wprowadzające w tematykę pomiarowo-interpretacyjną. Ma ono za

zadanie przygotować i oswoić studenta z techniką pomiarową, i pozwolić mu na swobodne
poruszanie się po laboratorium oraz rozpoznawanie przyrządów i oprogramowania służącego
do pomiaru sygnału, jego obróbki numerycznej i interpretacji oraz przypomnienie
teoretycznych podstaw z mechaniki budowli i wytrzymałości materiałów, związanych z
badaniem odkształceń, przemieszczeń i naprężeń w konstrukcji.

Dodatkowo należy uprzedzić studentów o przestrzeganiu przepisów BHP w pracowni.

2.

Opis stanowiska dla badania odkształceń i przemieszczeń konstrukcji.

Stanowisko składa się ze swobodnie podpartej belki z przewieszeniami o długości

a

1

+a

2

+a

3

między podporami i przewieszeniach L, znajdującej się na standzie. Belka ma

przekrój prostokątny b

x

h. Do belki na przewieszeniach umocowano dwa wyskalowane

dynamometry – służące do pomiaru wielkości sił poprzecznych obciążających belkę.
Dodatkowo w przekrojach A i B umieszczono zegarowe czujniki drogi, pozwalające na
pomiar przemieszczeń w tych przekrojach. Przy pomocy przymiaru i suwmiarki mierzymy
charakterystyczne wymiary belki. Do przeprowadzenia ćwiczenia potrzebna jest rejestracja
cyfrowa (lub odczyt) sygnału w postaci zbioru czterech elementów: sił P

L1

, P

P1

oraz

przemieszczeń y

A1

, y

B1

. Dokonujemy tego przy pomocy odpowiedniego mostka, karty

przetworników a/c i komputera rejestrującego, lub odczytów napięcia bezpośrednio z mostka
lub oscyloskopu. Sygnał (P

L1

, P

P1

, y

A1

,

y

B1

) może być wykorzystany w wywołanym w

programie Mathcad z dowolnego stanowiska komputerowego zbiorze cwiczenie 1.mcd.

3.

Wykonanie ćwiczenia.

Do przeprowadzenia ćwiczenia potrzebne jest obciążenie przygotowanej konstrukcji

siłami P

L

i P

P

zrealizowanymi przy pomocy śrub rzymskich i zarejestrowanie w stanie

równowagi trwałej sygnału (P

L1

, P

P1

, y

A1

,

y

B1

). Ponieważ interesują nas zależności

wynikające ze statyki, konieczne jest takie dobranie obciążeń, aby spowodować stan prostego
zginania. Wtedy wykorzystamy wzory potrzebne na:

•

odczyt sił P

L1

, P

P1

– pozwala on na obliczenie przemieszczeń y

A

i y

B

(całkowanie

graficzne) oraz porównanie do wyniku teoretycznego (wstępnie znane siły i
momenty, oraz EI)

•

odczyt przemieszczeń y

A1

,

y

B1

(całkowanie graficzne) oraz porównanie do wyniku

teoretycznego P

L,

P

P

(wstępnie znane przemieszczenia, oraz EI),

4.

Opracowanie wyników badań i obliczenie błędów.

Student mając do dyspozycji program Mathcad oraz dane pomiarowe, zarówno

dotyczące właściwego eksperymentu (P

L1

, P

P1

, y

A1

,

y

B1

), jak i stałe materiałowe oraz dane

przekrojowe i belki – każdorazowo pomierzone i uśrednione powinien:

•

opisać stanowisko badawcze i podstawy teoretyczne.

•

wprowadzić prawidłowo dane do komputera,

•

obliczyć numerycznie błędy pomiaru i wypełnić załączoną tabelkę.

5.

Zaliczenie projektu

Student powinien na zakończenie ćwiczenia umieć

•

opisać stanowisko badawcze, z zaznaczeniem nowych elementów występujących
w ćwiczeniu czujniki, mostek, karta przetworników, rejestracja sygnału,

•

znać podstawy teoretyczne: zginanie, metoda sił, związki odkształcenia-
naprężenia,

•

wykonywać najprostsze czynności w Mathcadzie.

Ćwiczenie 2

Egzemplarz dla prowadzącego

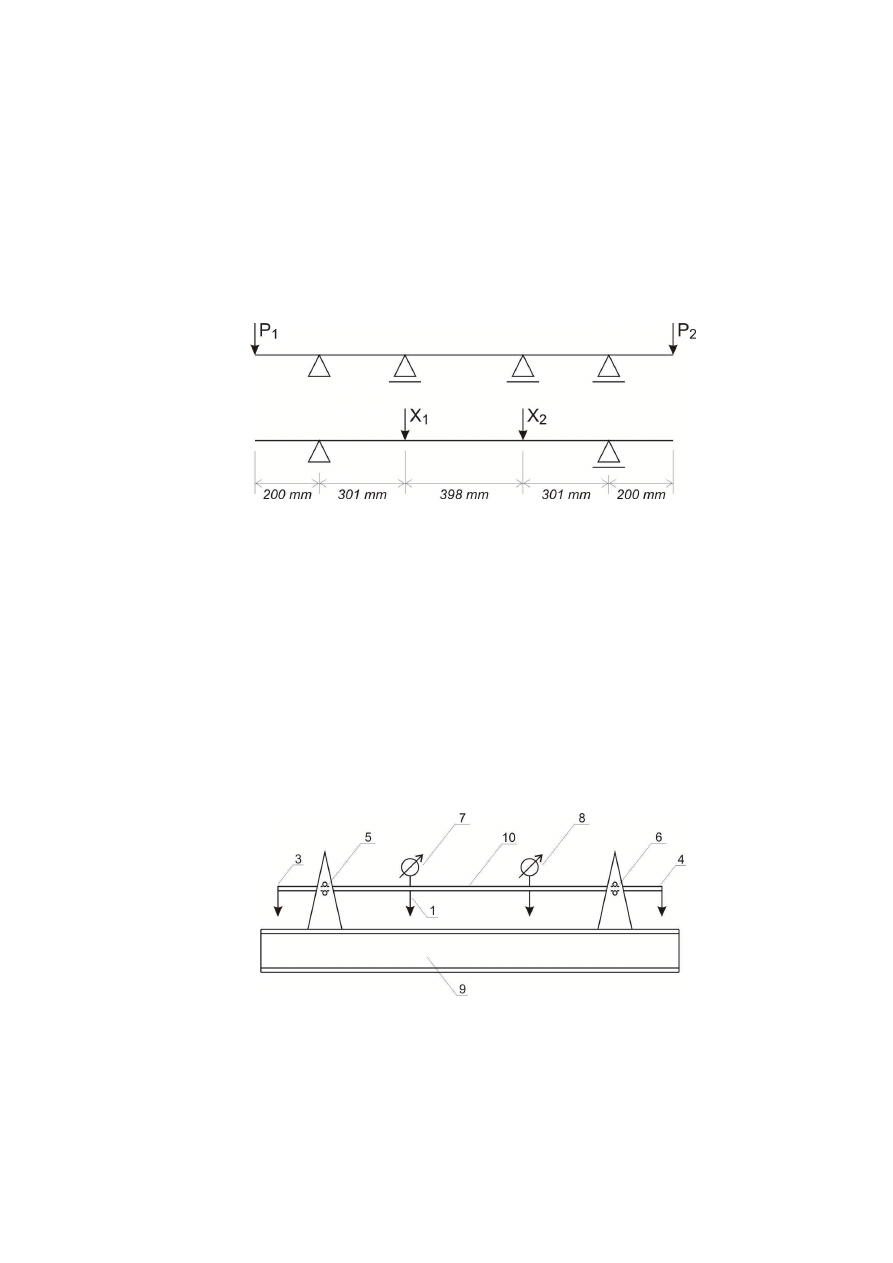
Doświadczalne wyznaczanie reakcji belki

trójprzęsłowej

Cel ćwiczenia

Celem ćwiczenia jest pokazanie sensu fizycznego współczynników układu równań
kanonicznych metody sił oraz sensu fizycznego poszczególnych równań jak i całego
układu; jest też celem pokazanie zasady wzajemności przemieszczeń.

Reakcje podpór 1 i 2 dla belki jak na rysunku można wyznaczyć w dwojaki sposób:

1.

Wyznaczając teoretycznie współczynniki układu równań wg zasad Metody Sił:

δ

11

,

δ

12

,

δ

21

,

δ

22

,

∆

1P

,

∆

2P

, przy przyjęciu za niewiadome hiperstatyczne poszukiwanych

reakcj. Siły X

1

i X

2

wyznacza się z układu równań:

δ

11

X

1

+

δ

12

X

2

+

∆

1P

=0

δ

21

X

1

+

δ

22

X

2

+

∆

2P

=0

2.

Wyznaczając eksperymentalnie współczynniki układu równań kanonicznych. Siły X

1

i

X

2

wyznacza się z układu równań, jak wyżej.

3.

Wyznaczając wprost reakcje X

1

i X

2

z warunku, że przemieszczenia punktów 1 i 2 dla

układu zastępczego mają być równe zero.

Krótki opis stanowiska

1-, 2-, 3-, 4-, punkty realizacji obciążeń (dynamometry)

5-, 6-, podpory

7- czujnik przemieszczeń dla punktu 1

8-

czujnik przemieszczeń dla punktu 2

9-

stend

10-

belka

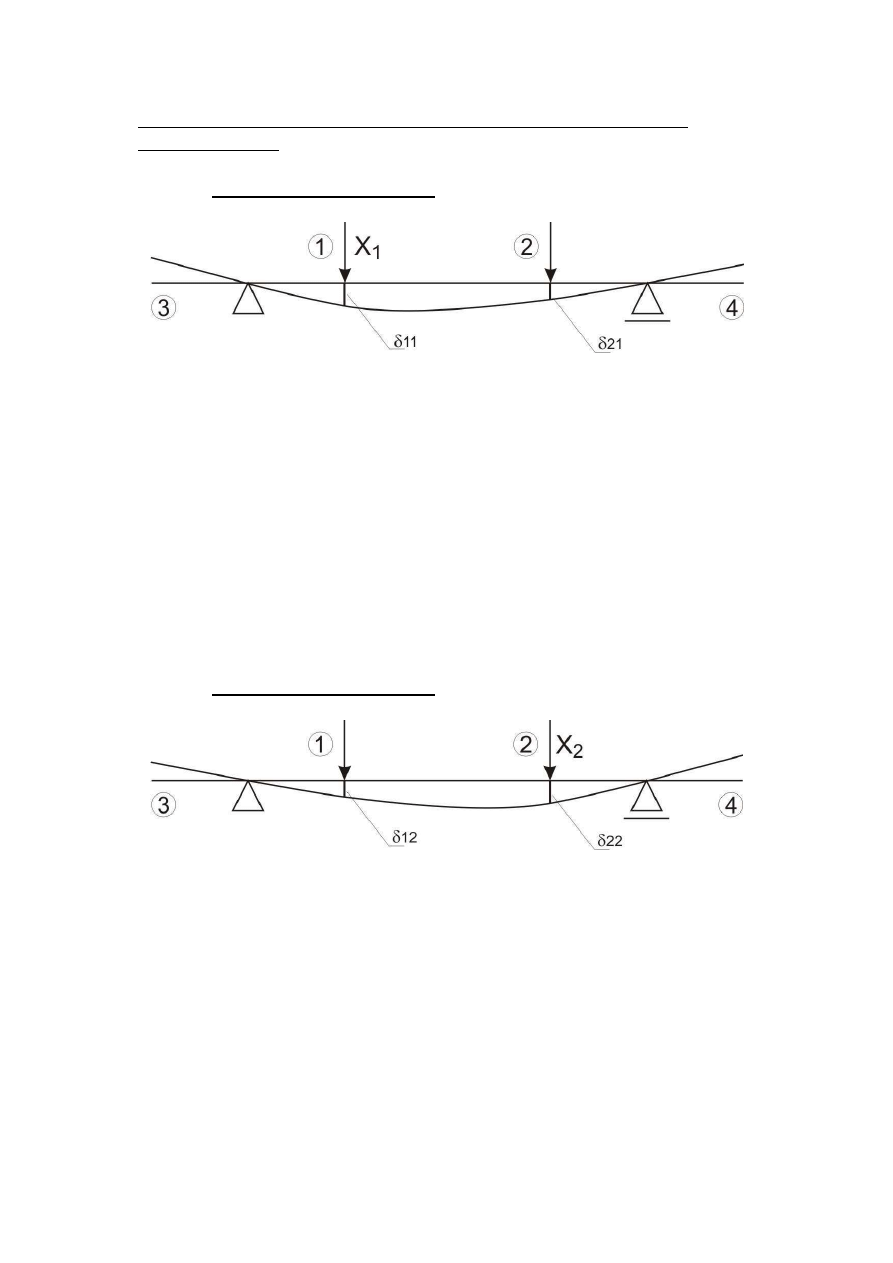
Doświadczalne wyznaczanie współczynników

δ

11

,

δ

21

układu równań

kanonicznych MS

Wyznaczanie

δδδδ

11

oraz

δδδδ

21

-

ustawiamy czujniki w punktach 1 i 2 w pozycji 0.00

-

w punkcie 1 przykładamy obciążenie za pomocą dynamometru (pozostałe
dynamometry są „zwolnione”)

-

odczytujemy wskazanie napięcia w Voltach na tensometrze (V

1

) oraz

przemieszczenia w punktach 1 i 2 (a

11

oraz a

21

) w milimetrach

-

obliczamy

δ

11

oraz

δ

21

jako iloraz odczytanej wartości przemieszczenia (w

metrach, a zatem po podzieleniu przez 1000) przez wartość siły obciążającej
odpowiadającej odczytanemu napięciu na tensometrze

Wyznaczanie

δδδδ

12

oraz

δδδδ

22

-

ustawiamy czujniki w punktach 1 i 2 w pozycji 0.00

-

w punkcie 2 przykładamy obciążenie za pomocą dynamometru (pozostałe
dynamometry są „zwolnione”)

-

odczytujemy wskazanie napięcia w Voltach na tensometrze (V

2

) oraz

przemieszczenia w punktach 1 i 2 (a

12

oraz a

22

) w milimetrach

-

obliczamy

δ

12

oraz

δ

22

jako iloraz odczytanej wartości przemieszczenia ( w

metrach, a zatem po podzieleniu przez 1000) przez wartość siły obciążającej
odpowiadającej odczytanemu napięciu na tensometrze

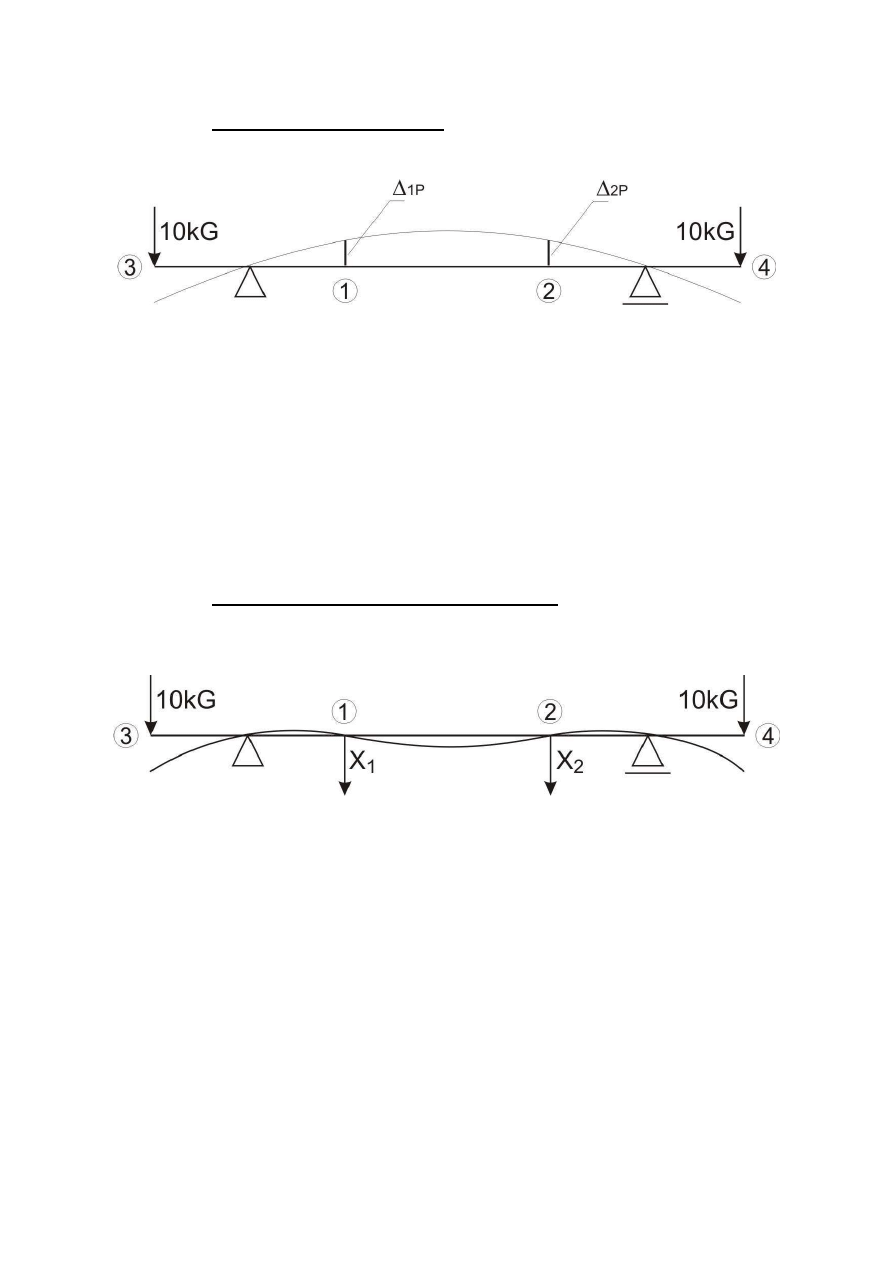
Wyznaczanie

∆∆∆∆

1P

oraz

∆∆∆∆

2P

-

ustawiamy czujniki w punktach 1 i 2 w pozycji 0.00

-

w punktach 1 oraz 4 przykładamy obciążenie 98.1 N (10 kG) za pomocą
dynamometrów (pozostałe dynamometry są „zwolnione”)

-

odczytujemy przemieszczenia w punktach 1 i 2 (A

1P

oraz A

2P

) w milimetrach

-

obliczamy

∆

1P oraz

∆

2P dzieląc odczytane wartości przez 1000

(sprowadzając do jednostek w układzie SI)

Doświadczalne wyznaczanie X1 oraz X2

-

ustawiamy czujniki w punktach 1 i 2 w pozycji 0.00

-

w punktach 1 oraz 4 przykładamy obciążenie 98.1 N (10 kG) za pomocą
dynamometrów (pozostałe dynamometry są „zwolnione”)

-

przykładamy obciążenie w punktach 1 i 2 za pomocą dynamometrów (które
dotąd były „zwolnione”) tak, aby przemieszczenie w punktach 1 i 2 osiągnęło
wartość

0.00

-

odczytujemy wartości napięcia na dynamometrach w punktach 1 i 2 w Voltach

-

obliczamy siły w powyższych punktach korzystając z charakterystyk
dynamometrów

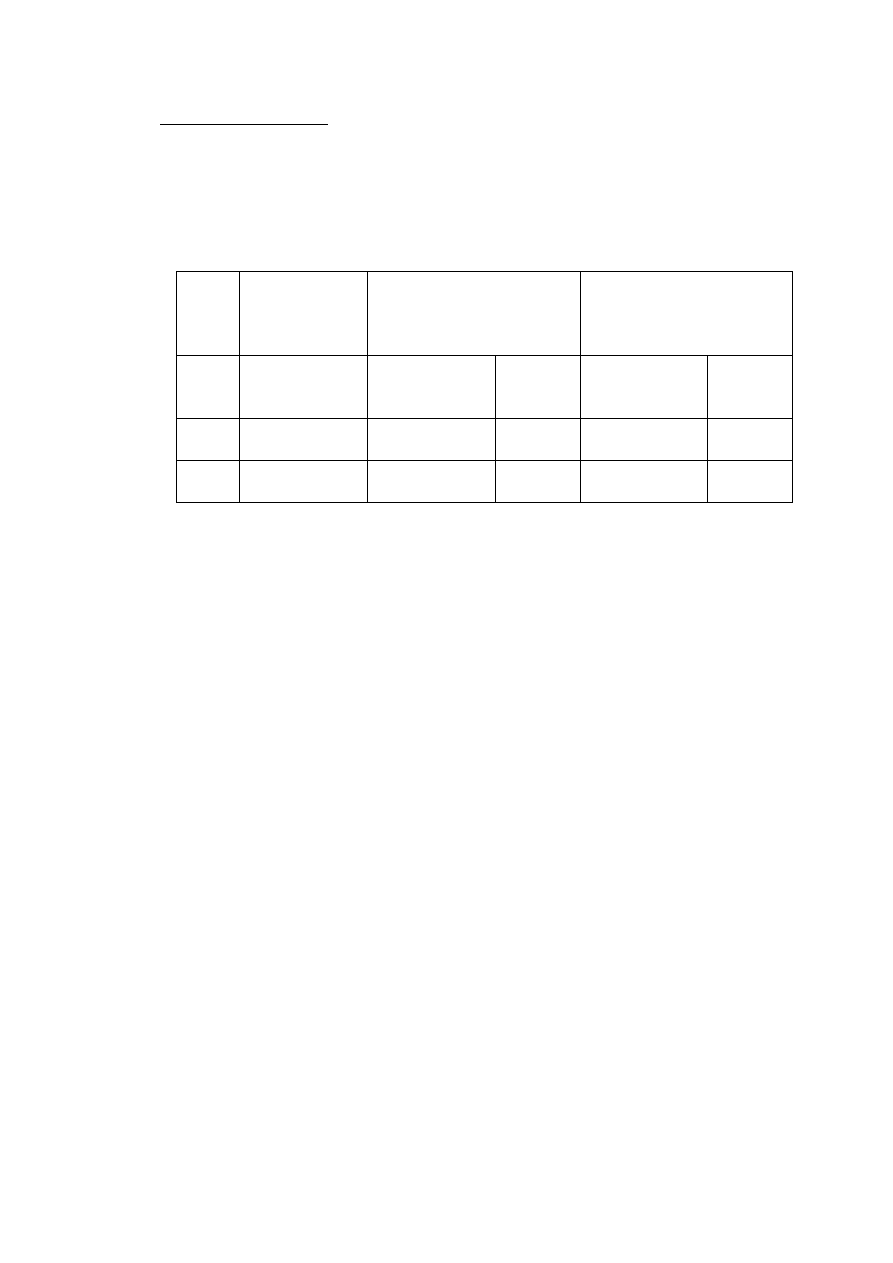
Zakończenie ćwiczenia

Po obliczeniu reakcji w belce trójprzęsłowej trzema sposobami student oblicza
względny błąd (w odniesieniu do reakcji wyznaczonych teoretycznie- metodą sił), jaki
został popełniony w trakcie przeprowadzania eksperymentu:

Wyznaczone
teoretycznie

Wyznaczone na podstawie
pomierzonych
współczynników układu
równań kanonicznych

Pomierzone w czasie
eksperymentu

wartość

wartość

błąd
względny
[%]

wartość

błąd
względny
[%]

X

1

X

2

Ćwiczenie 4

Egzemplarz dla prowadzącego

Drgania własne układów prętowych

1.

Cel i zakres:

Celem

przedstawianych

doświadczeń

jest

określenie

właściwości

dynamicznych

(częstotliwości drgań własnych i logarytmicznego dekrementu tłumienia) wybranych
układów:

•

belki dwuprzęsłowej

•

ramy symetrycznej.

Wyznaczone doświadczalnie wartości częstotliwości drgań własnych belki dwuprzęsłowej
porównuje się z wartościami uzyskanymi z obliczeń analitycznych.

2.

Opis stanowisk i torów pomiarowych

a.

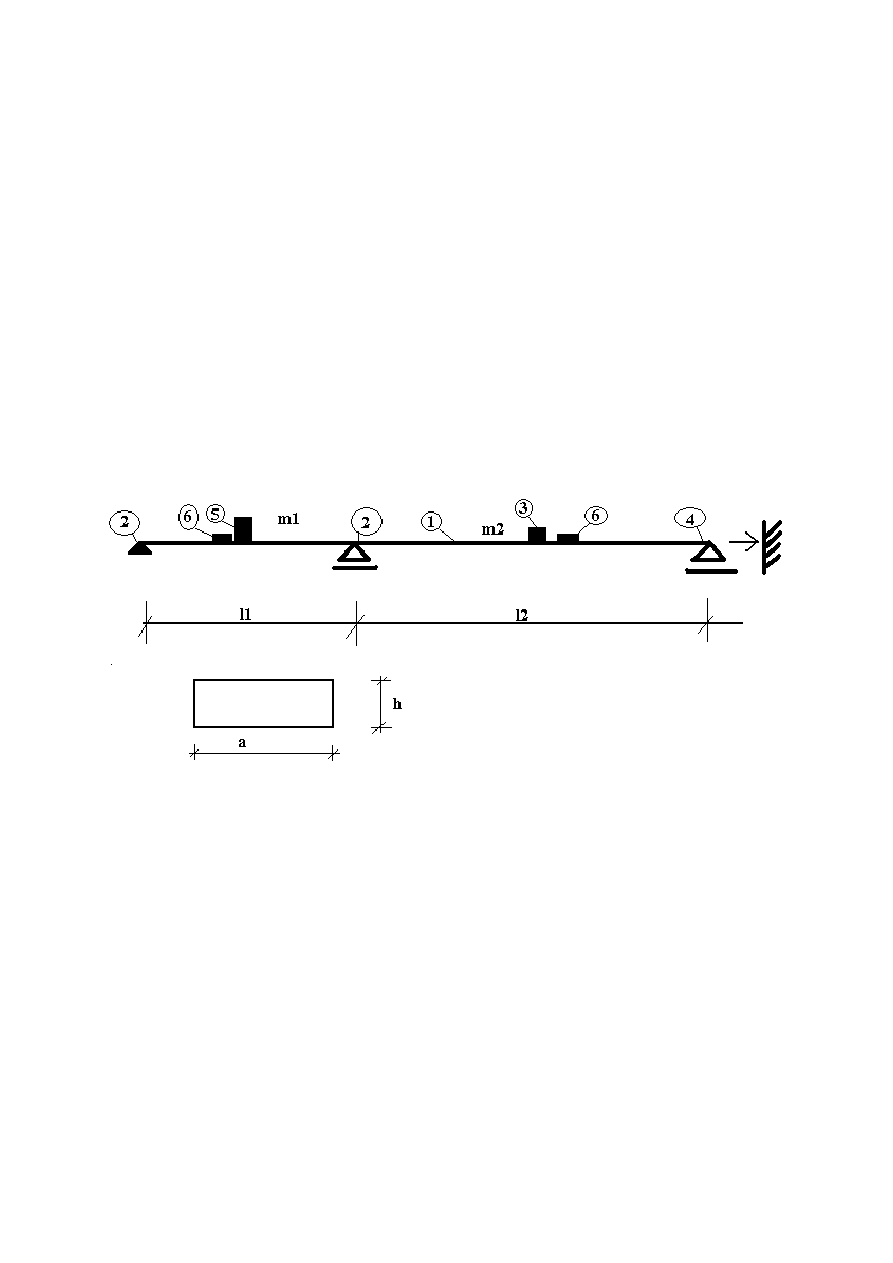
belka dwuprzęsłowa

① - pręt aluminiowy
② - podpora przegubowa
③ - wirująca tarcza z masą mimośrodową sprzęgnięta z silnikiem
④ - podpora zamienna (przegub ➙ utwierdzenie)
⑤ - akcelerometr
⑥ - tensometr elektrooporowy

Dane charakteryzujące belkę:
E = 7*10

4

MPa

l

1

=0.56m

m

1

= 0.488kg

a = 3*10

-2

m

l

2

= 0.92m

m

2

= 0.518kg

h = 0.8*10

-2

m

g = 0.026*10

4

N/m

3

Ix = 0.12810

-4

m

2

EIx = 89.6N m

2

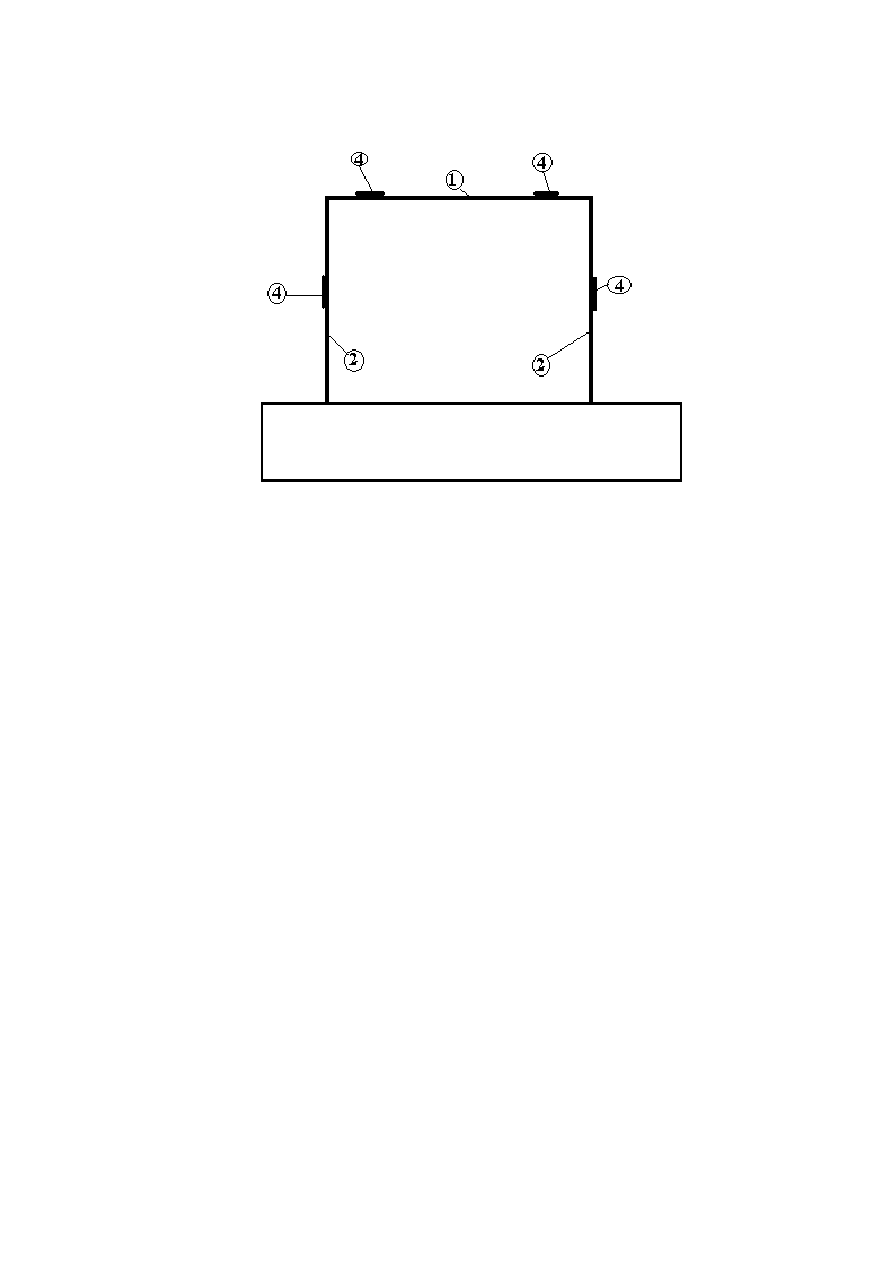
b.

rama symetryczna

① - rygiel ramy
② - słupy ramy
③- tensometry

Czujniki pomiarowe (akcelerometr i tensometr/y) połączone są poprzez wzmacniacz do
urządzenia rejestrującego (cyfrującego) przebieg drgań.

3.

Doświadczalne wyznaczenie częstotliwości drgań własnych i logarytmicznego
dekrementu tłumienia

Drgania badanych układów z częstotliwościami

własnymi wzbudza się za pomocą:

•

silnika z płynnie regulowaną liczbą obrotów,

•

impulsów (uderzeń) w rygiel ramy.

W momencie przechodzenia przez strefy rezonansu (kolejne czestotliwości drgań własnych
badanego układu pokrywają się z częstotliwościami obrotów silnika) następuje widoczny
wzrost amplitud drgań.

Podczas eksperymentów, w belce dwuprzesłowej zmienia się skrajną podporę przegubową na
utwierdzenie. W ten sposób zmienia się sztywność układu, co uwidacznia się podczas badań
zmianą wartości częstotliwości drgań własnych.

Drgania własne ramy symetrycznej wzbudza się poprzez uderzenia w rygiel ramy, równolegle
do osi rygla (drgania antysymetryczne) i prostopadle do osi rygla w środku jego rozpietości
(drgania symetryczne).

Wartości częstotliwości drgań własnych badanych układów wyznacza się wykorzystując
zapisane i scyfrowane przebiegi przyspieszeń drgań lub odkształceń. Zbiory tych danych
wprowadza się do programu MCAD i wykorzystuje gotową procedurę FFT.
Dane zapisywane są w następujących zbiorach:

•

belka dwuprzęsłowa, przegubowo podparta

-

przebiegi odkształceń: t1_t2f1p.dat – odpowiadające f

1

-

przebiegi odkształceń: t1_t2f2p.dat – odpowiadające f

2

•

belka dwuprzęsłowa, przegubowo podparta z utwierdzeniem na prawym końcu

-

przebiegi odkształceń: t1_t2f1u.dat – odpowiadające f

1

-

przebiegi odkształceń: t1_t2f2u.dat – odpowiadające f

2

Ponadto zbiory acc_f1pu.dat i accf2pu.dat zawierają wartości przyspieszeń odpowiadających
odpowiednio f

1

i f

2

. Pierwsza kolumna w tych zbiorach odpowiada belce z wszystkimi

podporami przegubowymi, a kolumna druga odpowiada przypadkowi z utwierdzeniem belki
na prawej podporze.

•

rama

-

przebiegi odkształceń opowiadające antysymetrycznej postaci drgań (boczne uderzenie
w poziomie rygla) - t1_t4rb.dat (tensometry T1 i T4), t2_t3rb.dat (tensometry T2 i T3)

-

przebiegi odkształceń opowiadające symetrycznej postaci drgań (uderzenie od góry w
ś

rodku rozpiętości rygla) - t1_t4rg.dat (tensometry T1 i T4), t2_t3rb.dat (tensometry

T2 i T3)

•

Wartości logarytmicznego dekrementu tłumienia (

d) drgań wyznacza się wykorzystując

wzór:

d

d

d

d = (1/n) * ln(A

1

/A

1+n

)

gdzie:
n – liczba okresów drgań,
A

1

, A

1+n

– odpowiednio amplitudy początkowa i końcowa przebiegu drgań.

4.

Analityczne wyznaczenie częstotliwości drgań własnych belki dwuprzesłowej

Belkę modeluje się układe4m po dwóch stopniach dynamicznej swobody. W przypadku
wszystkich podpór przegubowych belka jest układem 1-krotnie statycznie niewyznaczalnym.
Gdy analizujemy belkę z utwierdzoną skrajną prawą podporą wówczas układ jest 2-krotnie
statycznie niewyznaczalny. Do analitycznego wyznaczenia częstotliwości drgań własnych f

1

i

f

2

[Hz] wykorzystujemy wzór:

f

1,2

= 1/2

p

p

p

p * sqrt {[m

1

d

d

d

d

11

+ m

2

d

d

d

d

22

m

m

m

m

sqrt ((m

1

d

d

d

d

11

+ m

2

d

d

d

d

22

)

2

- 4 m

1

m

2

(

d

d

d

d

11

d

d

d

d

22

-

d

d

d

d

12

2

))]/2m

1

m

2

(

d

d

d

d

11

d

d

d

d

22

-

d

d

d

d

12

2

)}

gdzie:

d

11,

d

22,

d

12

– elementy macierzy podatności analizowanego układu.

©

©

©

©

Dla układu z podporami przegubowymi:

d

11

= 2.878*10

-3

/ EIx

d

22

= 10.55*10

-3

/ EIx

d

12

= -2.105*10

-3

/ Eix

f

1

= 19.51Hz

A11 = 1

A21 = -3.961

f

2

= 44.51Hz

A12 = 1

A22 = 0.238

©

©

©

©

Dla układu z utwierdzeniem:

d

11

= 2.718*10

-3

/ EIx

d

22

= 5.45*10

-3

/ EIx

d

12

= -1.235*10

-3

/ Eix

f

1

= 27.28Hz

A11 = 1

A21 = -2.69

f

2

= 45.37Hz

A12 = 1

A22 = 0.35

5.

Tabelaryczne zestawienie wyników

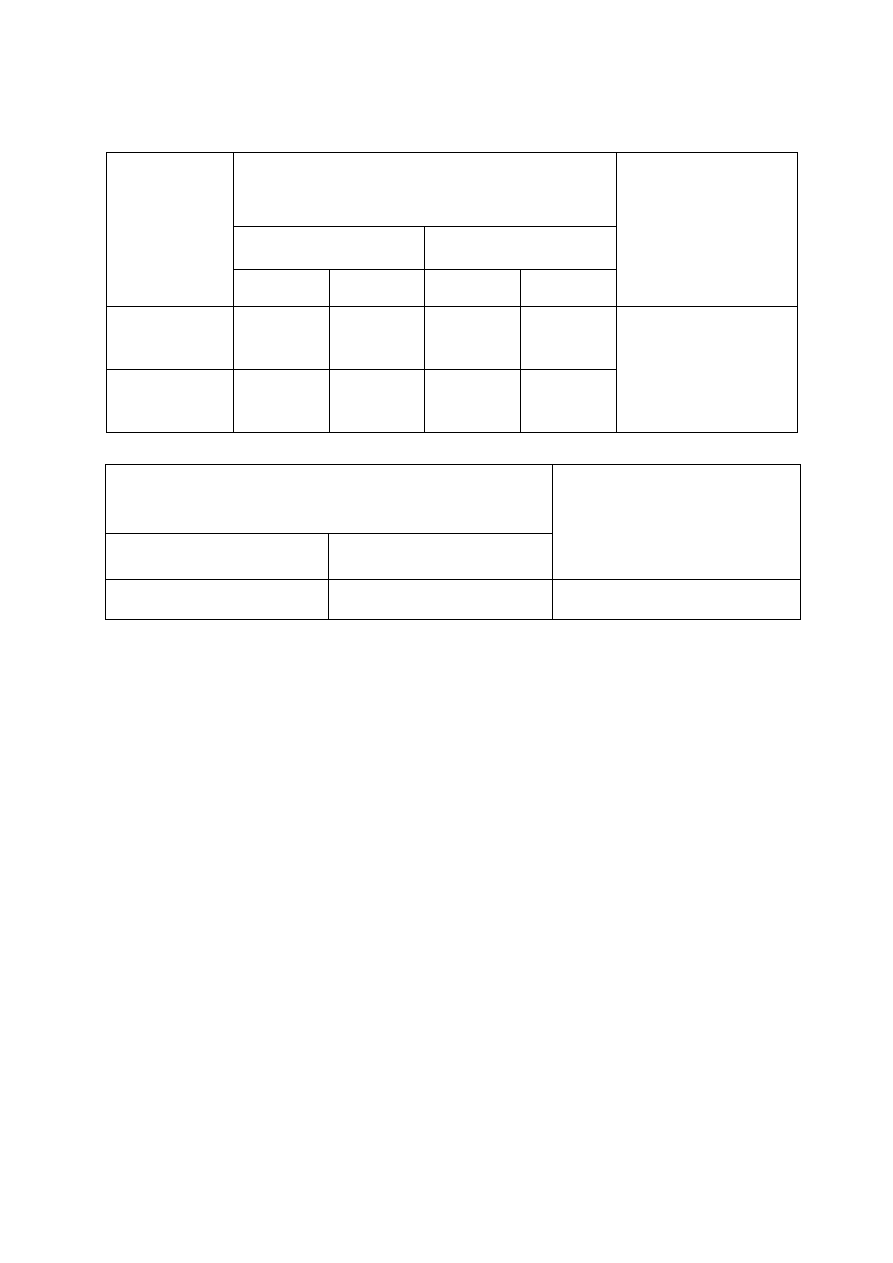
Dane do obliczeń

Belka

dwuprzęsłowa

Wartości częstotliwości drgań własnych

[Hz]

Wartość

logarytmicznego

dekrementu

tłumienia

d

d

d

d [-]

f1

f2

z obliczeń z pomiaru z obliczeń z pomiaru

z podporami

przegubowymi

19.51

21.05

44.51

44.25

d

ś

r.

= 0.132

z

utwierdzeniem

27.28

28.5

45.37

46.5

Pomierzone częstotliwości drgań własnych ramy
[Hz]

Wartość logarytmicznego

dekrementu tłumienia

d

d

d

d [-]

f

1

f

2

20.5

60.8 - 61.6

d

ś

r.

= 0.021

Dane do obliczenia logarytmicznego dekrementu tłumienia drgań ramy:

-

uderzenie z góry w środek rygla

n = 100

Tensometry:

T1 - A

1

= 0.466663, A

101

= 0.059558, T2 - A

1

= 1.462364, A

101

= 0.258751

T3 - A

1

= 1.89602, A

101

= 0.30178,

T4 - A

1

= 0.27428, A

101

= 0.04448

-

uderzenie boczne w poziomie rygla

n = 100

Tensometry:

T1 - A

1

= 0.432055, A

101

= 0.044787

T2 - A

1

= 1.943908, A

101

= 0.190368

T3 - A

1

= 2.19178, A

101

= 0.22309

T4 - A

1

= 0.36081, A

101

= 0.03092

Dane do obliczenia logarytmicznego dekrementu tłumienia drgań belki dwuprzęsłowej:

-

belka podparta przegubowo

n = 14

Tensometry:

T1 - A

1

= 0.904, A

15

= 0.176,

T2 - A

1

= 2.343, A

15

= 0.229

-

belka z utwierdzeniem

n = 15

Tensometr T2: A

1

= 1.185, A

16

= 0.2209

Ćwiczenie 5

Egzemplarz dla prowadzącego

DRGANIA WYMUSZONE

BELKI STATYCZNIE NIEWYZNACZALNEJ

1.

Cel laboratorium

•

Pokazanie możliwości wyznaczenia sił dynamicznych i momentów zginających

w belce statycznie niewyznaczalnej, wywołanych obciążeniem dynamicznym
harmonicznie

zmiennym

(dwie

metody

wyznaczania:

siły

z

przyspieszeń

zarejestrowanych akcelerometrem i momenty zginające wyznaczone w oparciu o odczyty
z tensometrów). Porównanie uzyskanych wyników z rozwiązaniem teoretycznym.

•

Pokazanie wpływu tłumienia konstrukcji na ograniczenie wielkości amplitud drgań

przęseł belki pracującej w rezonansie.

2.

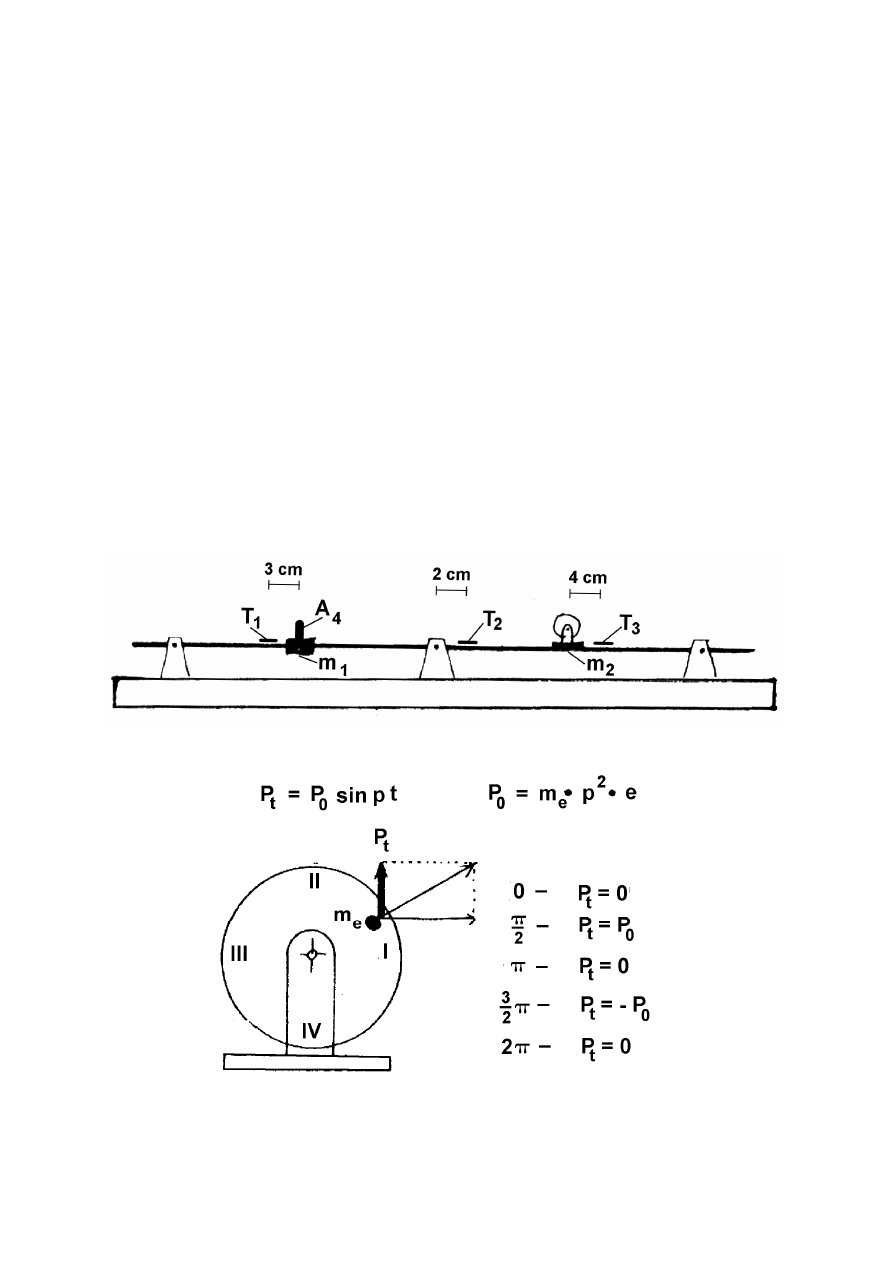
Opis modelu belki (rys. 1)

•

Przypomnienie konstrukcji belki i poszczególnych jej elementów z ćwiczenia nr 4

•

Krótki opis toru pomiarowego (tensometry, akcelerometr, rejestrator)

•

Siły działające na belkę w trakcie drgań (siła wymuszająca od wirującego mimośrodu,
siły ciężkości od mas skupionych, siły bezwładności)

•

Opis poszczególnych faz działania siły wymuszającej m

e

= 7,36g, e = 1,675cm (rys. 2)

Rys. 1.

Rys. 2.

3.

Krótki wstęp teoretyczny

•

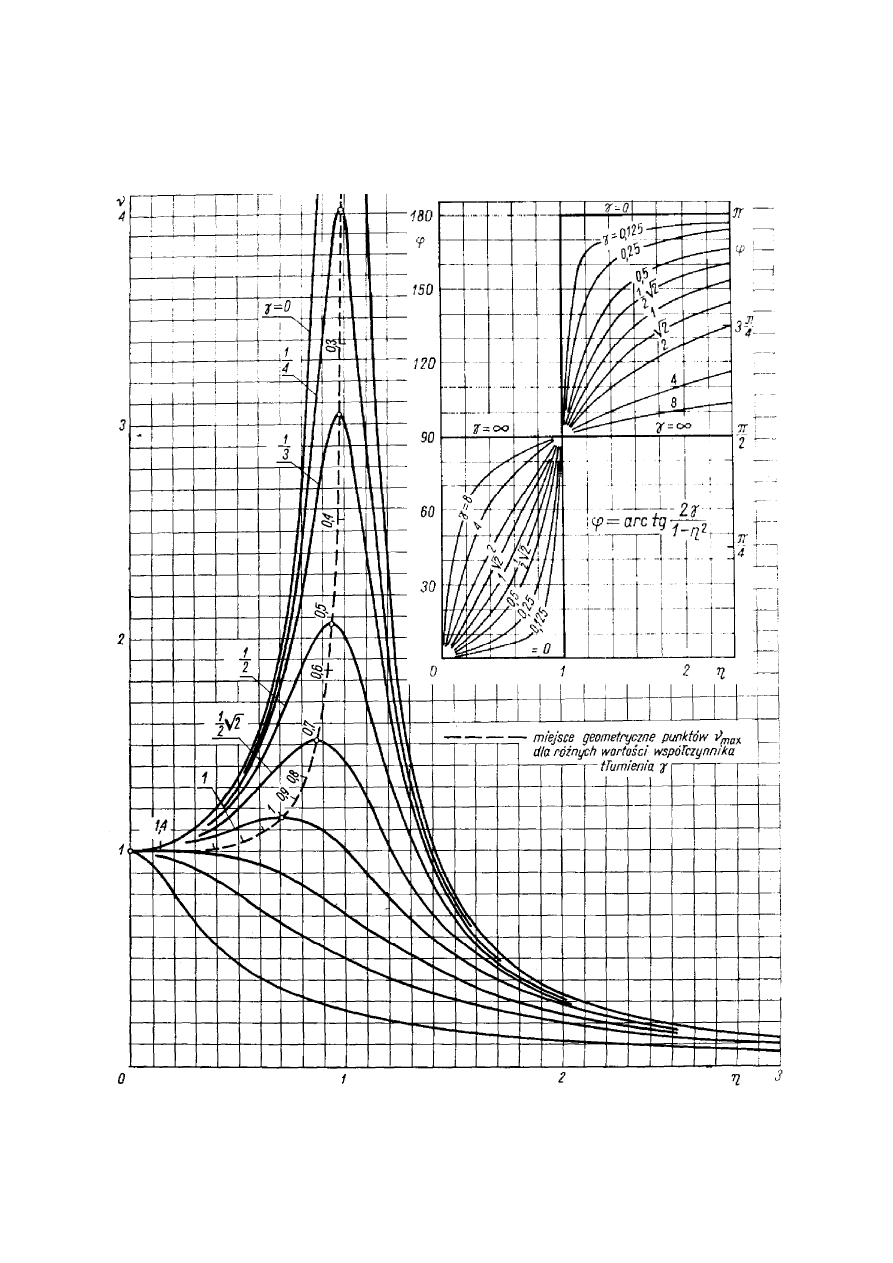
Opis pracy konstrukcji w zależności od częstotliwości wymuszających – krzywa

rezonansowa (rys. 3) – amplifikacja wartości amplitud, zmiana fazy, ograniczenie
wielkości amplitud przez tłumienie.

Rys. 3.

•

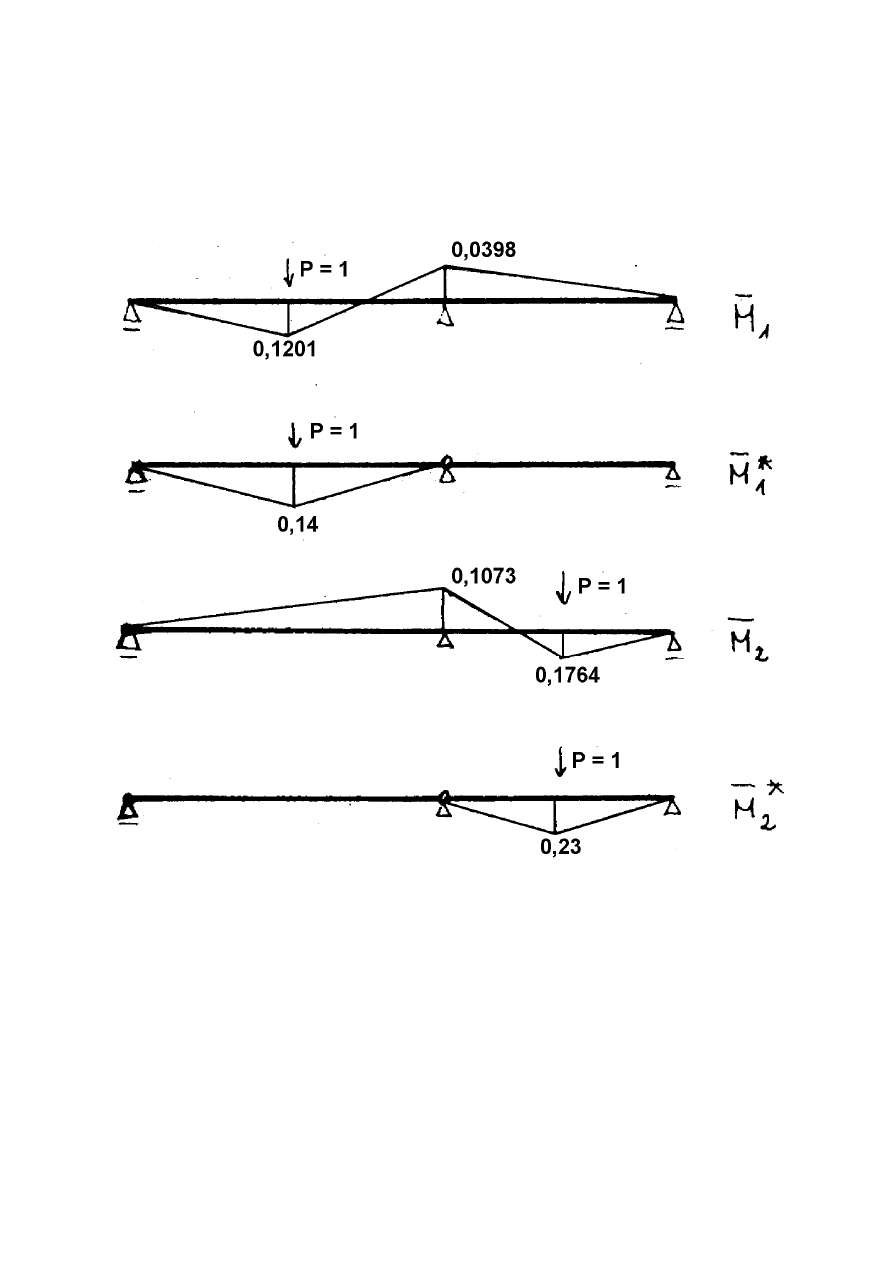
Przypomnienie rozwiązania teoretycznego (obliczenie delt dynamicznych – rys. 4,

obliczenie delt modyfikowanych, obliczenie delt od stanu P, rozwiązanie układu równań i
wyznaczenie sił bezwładności X

1

i X

2

dla dodatniej i ujemnej wartości siły P

0

,

narysowanie obwiedni momentów zginających z uwzględnieniem sił ciężkości, siły
wymuszającej i sił bezwładności)

Rys. 4.

•

Uzasadnienie wprowadzenia współczynników korekcyjnych dla tensometrów

(k

1

= 1,12, k

2

= 1,05, k

3

= 1,09), wynikających z nieosiowego umieszczenia tensometrów

na punktach charakterystycznych belki (rys.1)

•

Podanie formuł na obliczenie wartości sił i momentów zginających z danych

pomiarowych

1

)

(

m

a

F

⋅

±

−

=

±

W

E

M

i

i

⋅

⋅

⋅

±

=

±

−

6

10

ε

4.

Przeprowadzenie wymuszenia drgań belki i ich rejestracja

•

Drgania z częstotliwością rezonansową f

1

= 21,7 Hz

•

Drgania z częstotliwością rezonansową f

2

= 45,0 Hz (różnica o 2 Hz w stosunku do

rozwiązania teoretycznego)

•

Drgania z częstotliwością wybraną np. f = 16.6 Hz

5.

Kopiowanie danych z serwera na poszczególne stanowiska (dla każdego stanowiska
zbiory z częstotliwościami rezonansowymi i jedną wybraną częstotliwość z pośród 8
zarejestrowanych uprzednio wymuszeń):

Częstotliwość:

Zbiór:

13.5 Hz

cz13_5.dat

16.6 Hz

cz16_6.dat

24.1 Hz

cz24_1.dat

29.8 Hz

cz29_8.dat

34.0 Hz

cz34.dat

51.2 Hz

cz51_2.dat

55.6 Hz

cz55_6.dat

59.0 Hz

cz 59.dat

I rez 27.1 Hz

cz27_1Ir.dat

II rez 45.0 Hz

cz 45IIr.dat

6.

Samodzielne opracowanie wyników pomiarów przez studentów w oparciu o program
komputerowy (Mathcad) – pola niebieskie to wzory, pola żółte to wyniki obliczeń, pola
zielone to miejsce gdzie student wprowadza dane i odczytuje do sprawozdania
(a)

Zadana częstotliwość wymuszająca

•

Wprowadzenie

do

obliczeń

teoretycznych

analizowanej

częstotliwości

wymuszenia (wybranej przez prowadzącego z pośród ośmiu)

•

Wprowadzenie nazwy zbioru pomiarowego (*.dat) odpowiadającego wybranej
częstotliwości

•

W razie potrzeby wprowadzenie filtracji dolnoprzepustowej dla porównania jej
wpływu na zmianę wyników

•

Odczyt maksymalnych wartości momentów zginających i sił bezwładności

•

Odczyt błędu

(b)

Pierwsza częstotliwość rezonansowa

•

Wprowadzenie do obliczeń teoretycznych pierwszej częstotliwości rezonansowej

•

Wprowadzenie nazwy zbioru pomiarowego (*.dat) odpowiadającego wybranej
częstotliwości

•

W razie potrzeby wprowadzenie filtracji dolnoprzepustowej dla porównania jej
wpływu na zmianę wyników

•

Odczyt maksymalnych wartości momentów zginających i sił bezwładności z
pomiaru

(c)

Druga częstotliwość rezonansowa

•

Wprowadzenie do obliczeń teoretycznych drugiej częstotliwości rezonansowej

•

Wprowadzenie nazwy zbioru pomiarowego (*.dat) odpowiadającego wybranej
częstotliwości

•

W razie potrzeby wprowadzenie filtracji dolnoprzepustowej dla porównania jej
wpływu na zmianę wyników

•

Odczyt maksymalnych wartości momentów zginających i sił bezwładności z
pomiaru

7.

Wykonanie sprawozdania i zaliczenie ćwiczenia