UNIWERSYTET KAZIMIERZA WIELKIEGO

Instytut Mechaniki Środowiska

i Informatyki Stosowanej

PRACOWNIA SPECJALISTYCZNA

INSTRUKCJA DO ĆWICZEŃ

Nr ćwiczenia

TEMAT: Wyznaczanie przepuszczalności ziarnistych

materiałów porowatych metodą zmiennego

ciśnienia

Celem ćwiczenia jest zapoznanie się z podstawowym prawem (prawem Darcy)

rządzącym przepływem płynu przez porowate materiały oraz metodami

eksperymentalnego wyznaczania współczynnika ich przepuszczalności.

WYPOSAŻENIE STANOWISKA:

1. Układ do pomiaru przepuszczalności metodą zmiennego ciśnienia.
2. Układ zalewowy.
3. Granulat szklany.
4. Woda destylowana.
5. Stoper.
6. Instrukcja.

LITERATURA:

1. A.Wieczysty: Hydrogeologia inżynierska, W-wa, PWN 1982.

2. E.Myślińska, Laboratoryjne badanie gruntów, W-wa, PWN

3. G.Castany, Poszukiwanie i eksploatacja wód podziemnych, W-wa, PWN 1972.

1. PODSTAWY TEORETYCZNE

Przepływ płynów przez porowate materiały przepuszczalne.

Wiele materiałów naturalnych i technicznych spośród rodziny ciał stałych

charakteryzuje się tym, że posiada przepuszczalną strukturę porowatą. Są to ciała,

które zawierają dużą liczbę porów (pustych przestrzeni) o bardzo różnorodnym

kształcie, a ich charakterystyczne wymiary są małe w porównaniu z wymiarem

charakterystycznym samego ciała. Szczególną i fizycznie bardzo ważną cechą ciał

porowatych jest ich przepuszczalność. Jest to zdolność takich materiałów do

wchłaniania cieczy i gazów a także ich transportu wewnętrznymi kanałami

utworzonymi przez wzajemnie połączone pory.

Przepuszczalne materiały porowate występują powszechnie w przyrodzie

jako gleby, roponośne i gazonośne skały, podziemne zbiorniki wodne, a także jako

biologiczne materiały porowate np.: tkanka kostna i płuca. Ważną rolę odgrywają

techniczne materiały porowaye np.: spieki metalifiltry, katalizatory. Ich znaczenie

wynikaz faktu, że jednoczą w sobie dwie przeciwstawne cechy, sztywność struktury

zapewnioną przez szkielet i możliwośćtransportu różnych substancji ważnych np.

dla życia organizmu.

1.1. Zasada zachowania energii cieczy.

Ciecze doskonałe pozostające w ustalonym ruchu w polu sił ciężkości

zachowują swą energię. Wyraża to zasada zachowania energii cieczy doskonałej

sformułowanej w 1738 r. przez D. Bernoulliego:

•

suma energii kinetycznej, potencjalnej i energii ciśnienia cząstki cieczy

doskonałej w ustalonym ruchu w polu sił ciężkości pozostaje stała.

2

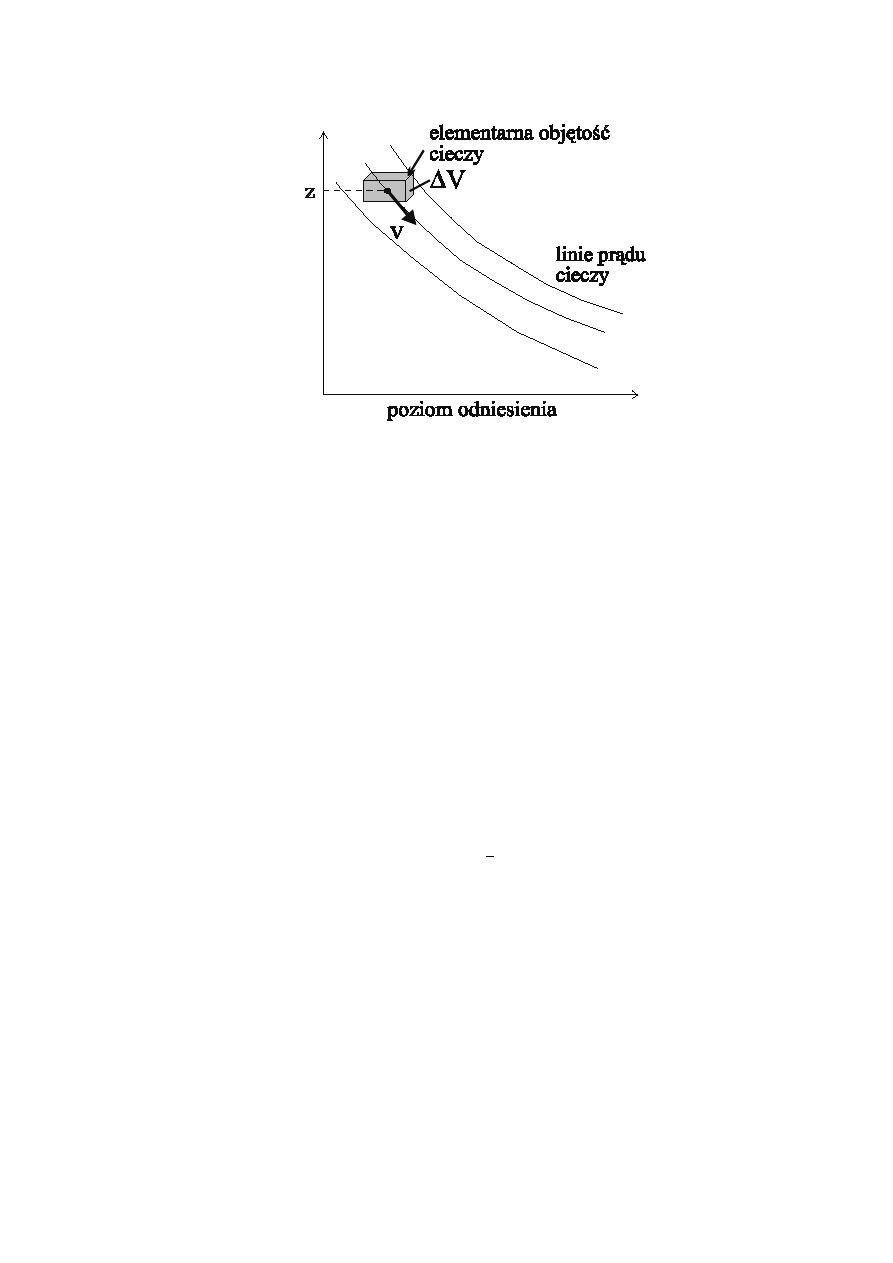
Rys. 1.

Aby przedstawić tę zasadę w postaci formuły matematycznej rozważmy dowolny,

ustalony przepływ cieczy o gęstości

ρ

(Rys. 1.).

Założenie że przepływ jest ustalony oznacza że wielkości opisujące ruch

cieczy: prędkość v i ciśnienie p nie zależą od czasu. Wielkości te natomiast mogą

przyjmować różne wartości w różnych punktach przestrzeni w której ruch ten ma

miejsce.

Biorąc pod uwagę elementarną objętość

∆

V cieczy poruszającej się z

prędkością V jej energia kinetyczna dana jest wzorem

(1)

2

2

1

K

v

m

E

∆

=

∆

gdzie

(2)

V

=

m

∆

∆

ρ

jest masą cieczą zawartej w objętości

∆

V.

Z kolei wybierając pewien poziom odniesienia dla energii potencjalnej w polu

grawitacyjnym, energię tę dla elementu cieczy o masie

∆

m znajdującego się na

wysokości z od poziomu odniesienia możemy przedstawić w postaci

3

(3)

z

g

m

E

P

∆

=

∆

gdzie g jest przyspieszeniem ziemskim.

Ostatnią formą energii wymagającą uwzględnienia przy ruchu płynu jest energia

ciśnienia cieczy. Można ją przedstawić w postaci

(4)

V

p

=

E

C

∆

∆

Dysponując wyrażeniami (1), (3) i (4) dla poszczególnych form energii zasadę

Bernoulliego możemy przedstawić za pomocą równania

(5)

K

E

∆

+

P

E

∆

+

C

E

∆

=

E

∆

=

const

.

Oznacza to, że energia całkowita cząstki cieczy doskonałej w ruchu ustalonym w

polu sił ciężkości pozostaje stała.

Podstawiając (1), (3) i (4) do (5) otrzymujemy

(6)

2

2

1

v

m

∆

+

z

g

m

∆

+

V

p

∆

=

const

.

Po podzieleniu obu stron równania (6) przez

∆

mg przyjmuje ono postać

(7)

const

=

z

g

p

2g

V

2

+

+

ρ

)

g

m

const

(

∆

=

gdzie wykorzystano definicję gęstości (2) oraz wprowadzono nową stałą po prawej

stronie równania.

Równanie (7) znajduje szerokie zastosowanie przy analizie różnych

zagadnień związanych z ustalonym przepływem cieczy doskonałej.

Przykładowo umożliwia określenie prędkości wypływu cieczy ze zbiornika

wywołanego naporem słupa cieczy o wysokości h (Rys. 2.).

4

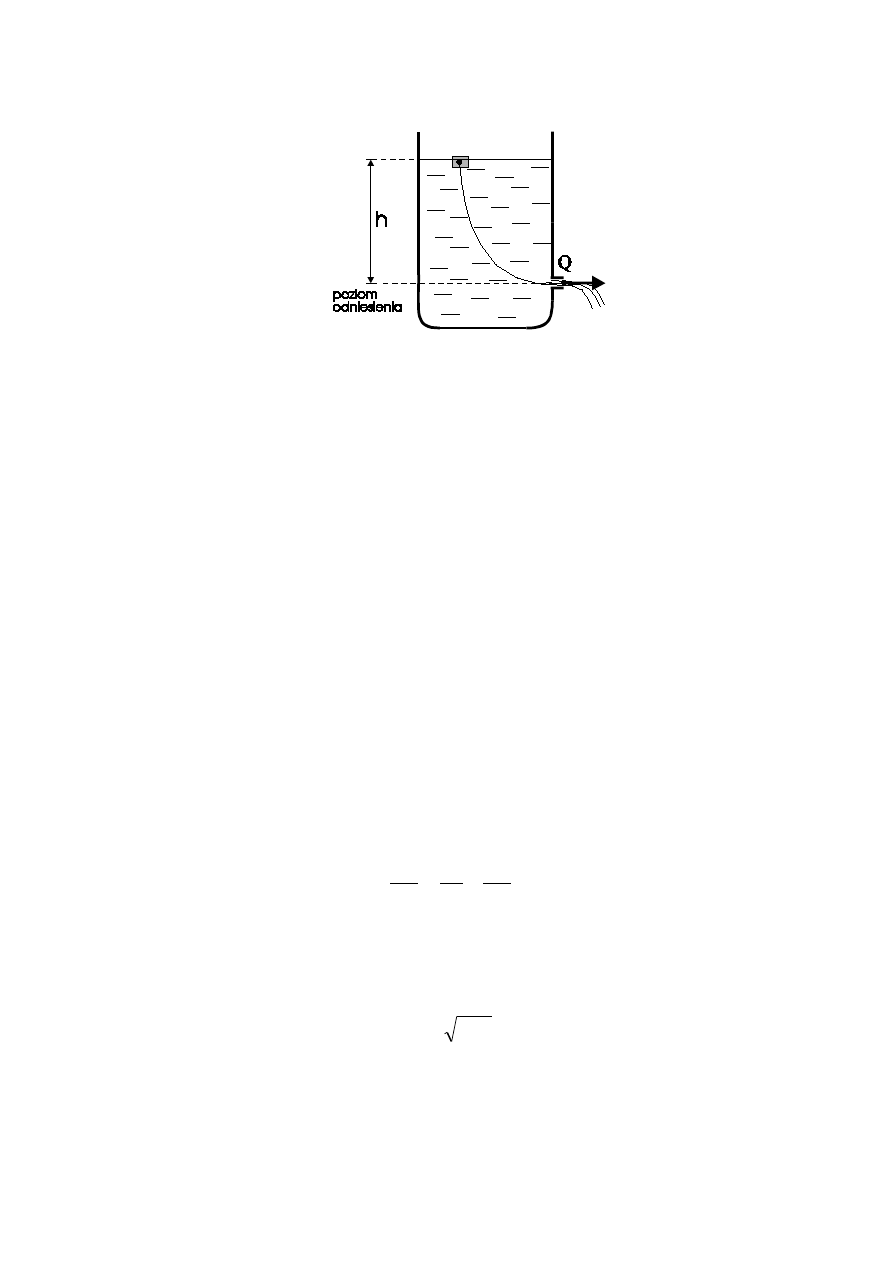
Rys. 2.

Stan cząstki płynu w punkcie P określony jest parametrami

p = p

o

,

v = 0,

z = h,

natomiast w punkcie Q tej samej linii prądu przyjmują one wartości

p = p

o

,

v = v

o

,

z = 0,

Wykorzystując równanie Bernoulliego (7) otrzymamy

Q

P

E

E

∆

=

∆

czyli

g

p

g

2

v

g

p

o

2
o

o

ρ

ρ

+

=

.

Stąd mamy

h

g

2

v

o

=

.

5

p

o

v

o

p

o

P

1.2. Wysokość hydrauliczna, wysokość piezometryczna.

W zagadnieniach związanych z hydrauliką i hydrologią wód podziemnych suma

trzech członów występujących w równaniu (7) i oznaczana jest przez H nazywana

jest wysokością hydrauliczną, wysokością naporu hydraulicznego lub wprost

naporem. Mamy tu jak w (7)

(8)

z

g

p

g

2

v

=

H

2

+

+

ρ

.

Każda z wielkości występujących w tej sumie ma wymiar wysokości (długości).

Dlatego z - jest nazywana wysokością położenia,

g

p

ρ

-

wysokością ciśnienia, a

g

2

v

2

-

wysokością prędkości.

Wysokość ciśnienia

g

p

ρ

jest wysokością słupa cieczy o ciężarze właściwym

γ

=

ρ

g,

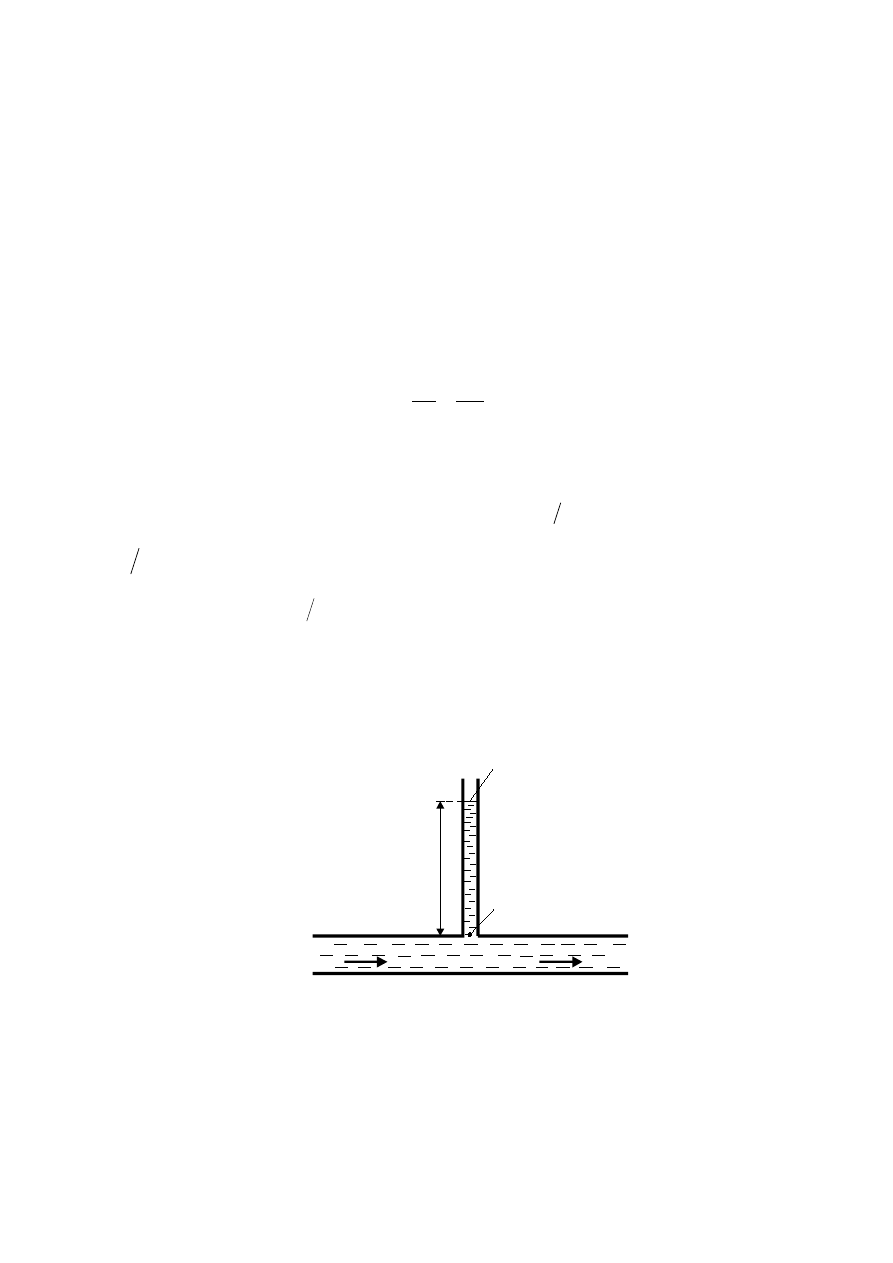
nad punktem cieczy w którym panuje ciśnienie p (Rys. 3.)

Rys. 3.

6

v

p

p = 0

o

p/ g

ρ

Wysokość położenia z jest to wysokość wzniesienia rozważanego punktu nad

dowolnie przyjętym poziomem odniesienia.

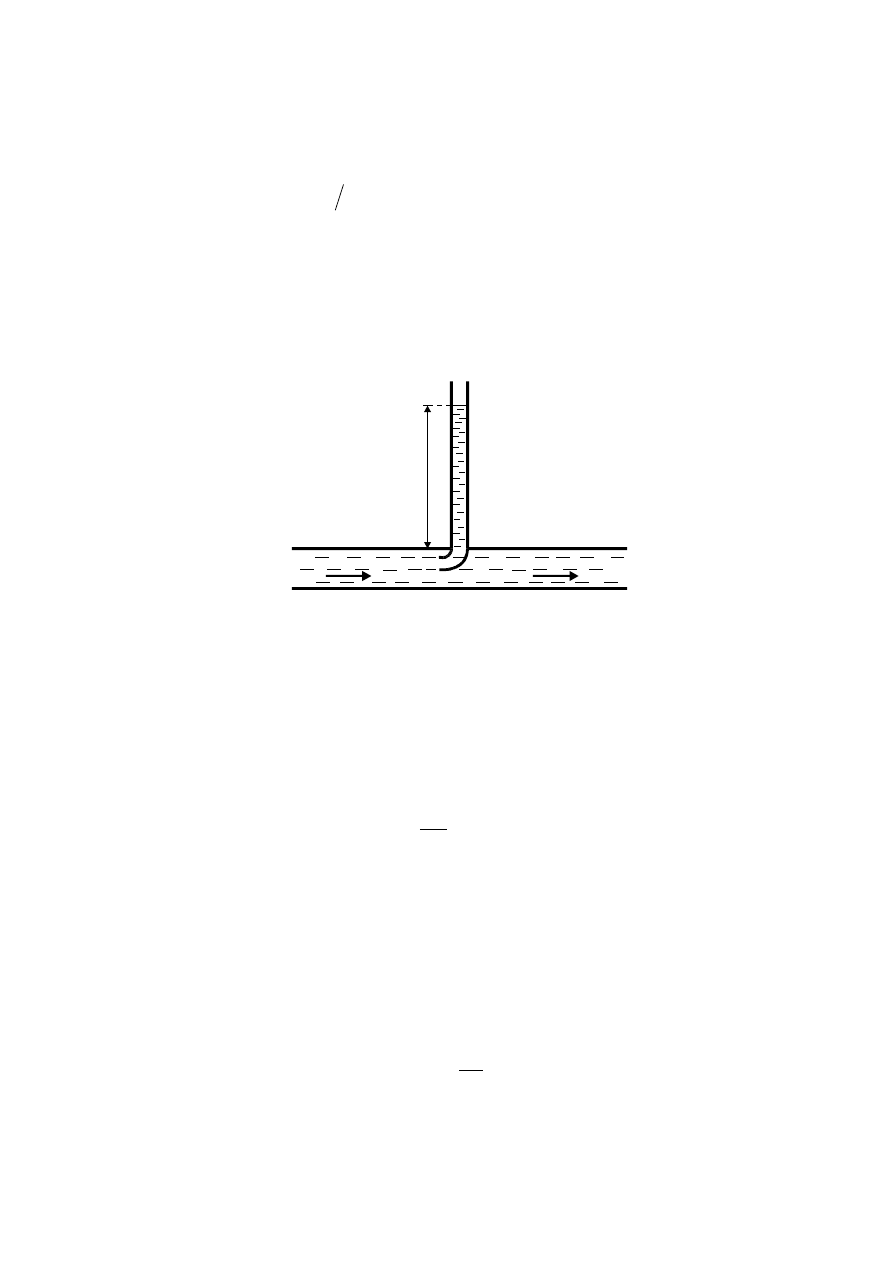
Wysokość prędkości

g

2

v

2

jest miarą ciśnienia dynamicznego jakie wywiera

ciecz płynąca z prędkością v. Odpowiada ona wysokości na jaką wzniesie się ciecz

w pionowej rurce jeśli na drugi koniec rurki napływa ciecz z prędkością v. (Rys. 4.)

Rys. 4.

Te trzy wysokości stanowią miarę trzech rodzajów energii mechanicznej tj.

energii ciśnienia, energii położenia i energii kinetycznej cząstek cieczy. Suma

wysokości ciśnienia i wysokości położenia

(9)

z

g

p

H

S

+

=

ρ

jest nazywana wysokością piezometryczną, i stanowi część statyczną całkowitej

energii cząstek płynu. Wysokość prędkości stanowi część dynamiczną tej energii.

Uwzględniając (9), wzór (8) możemy przedstawić w postaci

(10)

g

2

v

H

=

H

2

S

+

7

v /2g

2

v

p

p

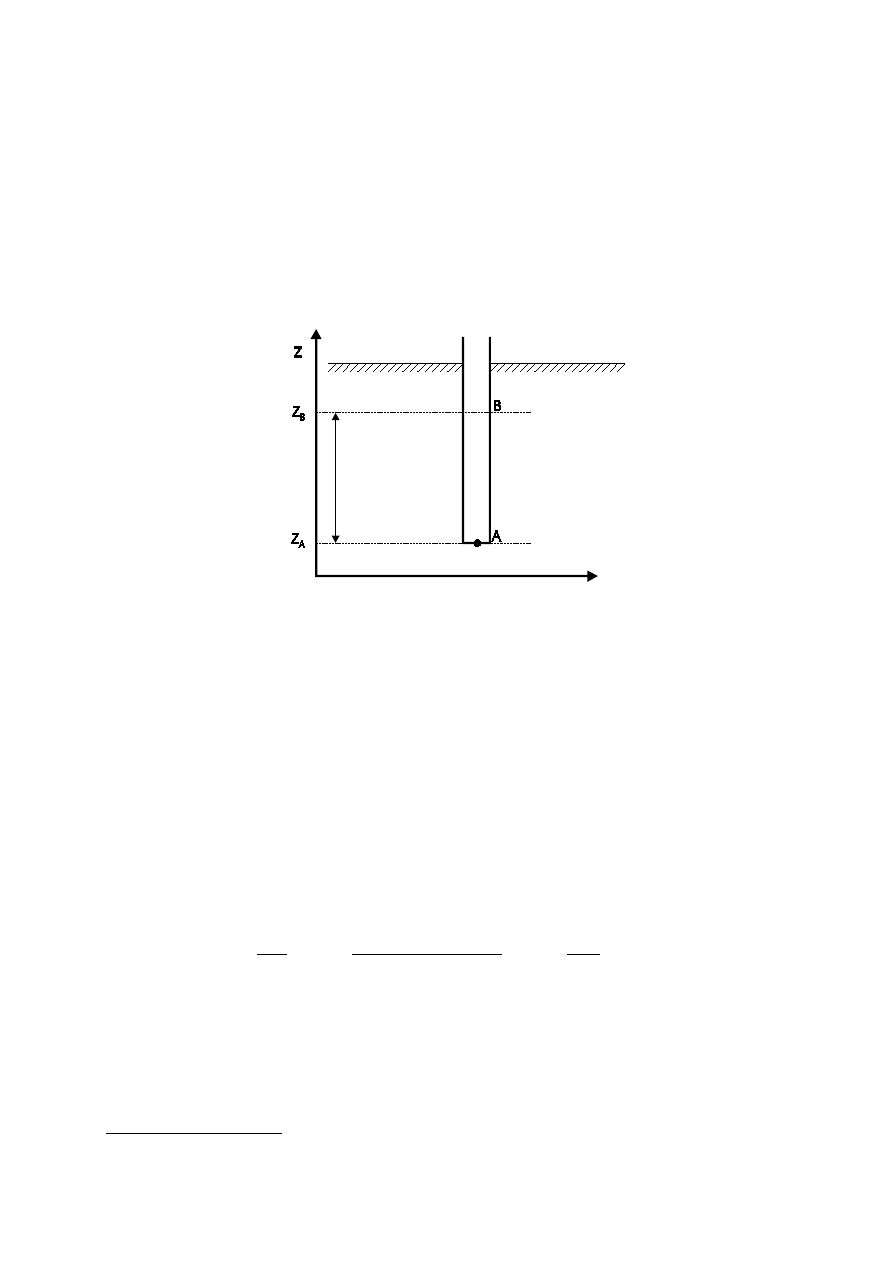
Aby wyznaczyć (zmierzyć) wysokość piezometryczną (hydrauliczną) w

nasyconym cieczą (wodą) porowatym gruncie w punkcie A położonym na pewnej

głębokości pod powierzchnią ziemi (Rys. 5.) należy wywiercić otwór aż do punktu

A i wpuścić rurkę

1)

. Po ustaleniu się położenia powierzchni swobodnej wody w

rurce, wyznaczenie

Rys. 5.

wysokości położenia z

B

umożliwia wyznaczenie wysokości hydraulicznej H

A

w

punkcie A gdyż w nieruchomej cieczy (a taka jest w rurce) wysokości hydrauliczne

w każdym punkcie rurki są jednakowe. Biorąc pod uwagę, że

p

A

=

ρ

g ( z

B

- z

A

)

otrzymujemy:

B

B

B

A

A

B

B

A

A

A

H

z

g

p

z

g

)

z

z

(

g

p

=

z

g

p

H

=

+

=

+

−

+

+

=

ρ

ρ

ρ

ρ

.

Dla cieczy doskonałej energia cząstek (elementarnej objętości) cieczy w trakcie

ich ustalonego ruchu (wzdłuż strugi cieczy) pozostaje stała

(11)

H = const.

1

Urządzenie tego typu nazywa się piezometrem.

8

powierzchnia
swobodna cieczy

poziom
odniesienia

p / g

A

ρ

p = p

B

A

W zagadnieniach związanych z przepływem cieczy rzeczywistej np. przez

ośrodki porowate ze względu na dysypację energii powodowaną lepkością płynu,

wysokość hydrauliczna H nie jest wielkością stałą wzdłuż strugi cieczy. W takim

przypadku prędkość przepływu cieczy przyjmuje małe wartości a wysokość

prędkości

v

2

/ 2g

jest znacznie mniejsza od wysokości piezometrycznej H

s

i

dlatego może być pominięta. Wówczas wysokość hydrauliczną H możemy

utożsamiać z wysokością piezometryczną H

s

(12)

z

g

p

H

=

H

S

+

=

ρ

.

1.3. Prawo Darcy

Henry Darcy badając przepływy wody przez materiały porowate utworzone z

piasku eksperymentalnie stwierdził, że objętość wody jaka przepływa w jednostce

czasu przez warstwę przepuszczalnego piasku o grubości L jest wprost

proporcjonalna do różnicy wysokości hydraulicznych

∆

H = H

A

- H

B

po obu

stronach porowatej warstwy (Rys. 6.) oraz do wielkości pola A jej przekroju

poprzecznego przez którą przepływa woda, natomiast jest odwrotnie

proporcjonalna do grubości tej warstwy. Mamy

(13)

L

H

A

K

=

Q

∆

gdzie K jest współczynnikiem proporcjonalności. Zależy on od własności

porowatego materiału a także od lepkości cieczy (wody).

Współczynnik ten w hydrologii nazywany jest przewodnością hydrauliczną.

9

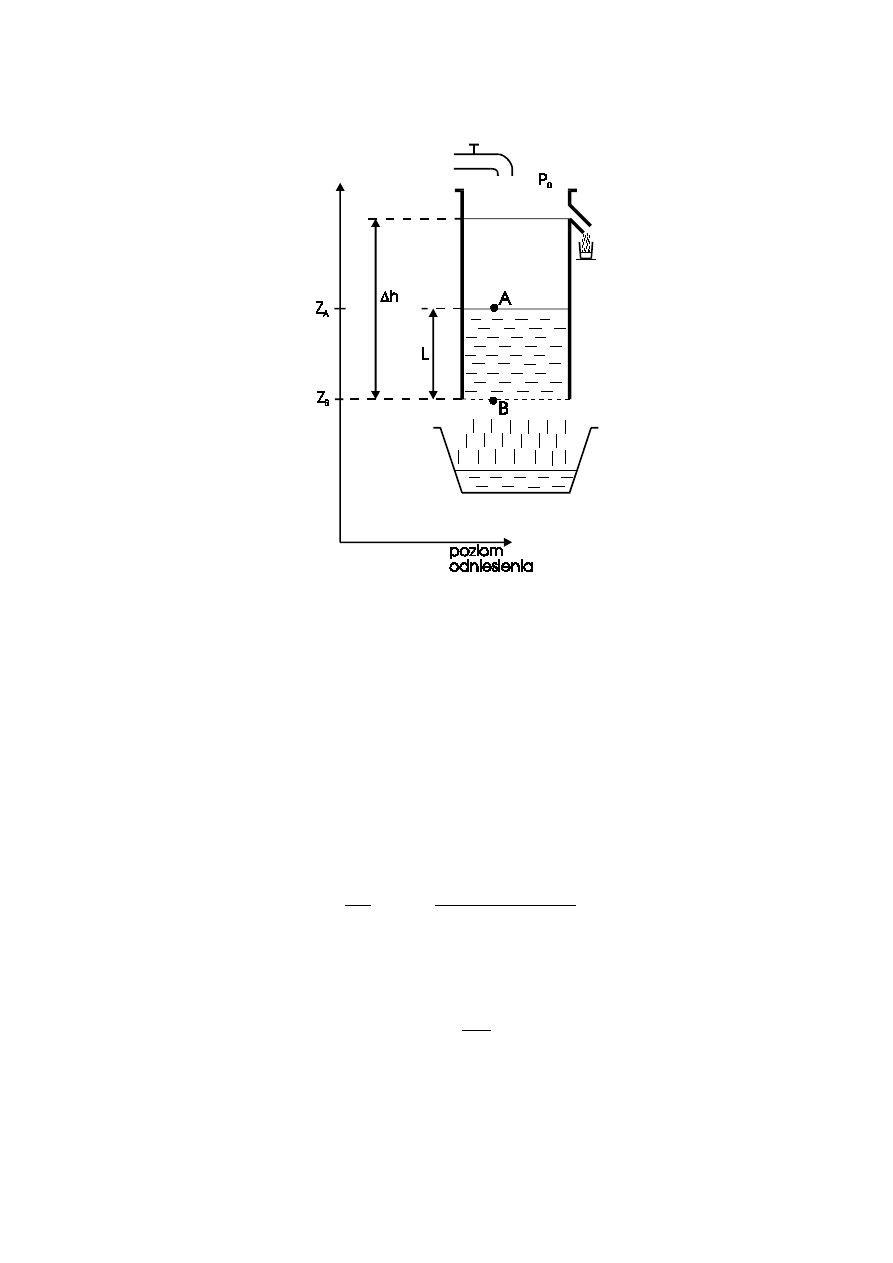
Wielkość Q nazywana jest wydatkiem przepływu cieczy.

Rys. 6.

Biorąc pod uwagę, że

)

(

A

o

A

A

A

z

g

L

-

h

g

p

z

g

p

+

∆

+

=

+

=

Η

ρ

ρ

ρ

natomiast

B

o

B

z

g

p

+

=

Η

ρ

10

dla przyrostu

∆

H wysokości hydraulicznych otrzymamy

(14)

)

(

h

Δ

z

g

p

z

g

L

-

h

Δ

g

p

Η

Η

=

Η

Δ

B

o

A

o

B

A

=

−

−

+

+

=

−

ρ

ρ

ρ

uwzględniając (14) w równaniu (13) otrzymamy

(15)

L

h

Δ

A

K

Q

=

Równanie Darcy (13) możemy także zapisać w postaci

(16)

U = K i

gdzie wielkość

(17)

A

Q

=

U

jest nazywana prędkością filtracyjną, natomiast wielkość

(18)

L

L

=

i

∆Η

=

∆Η

jest nazywana gradientem hydraulicznym.

Równanie (16) jest najprostszą postacią prawa Darcy.

Inną postać prawa Darcy otrzymamy rozważając poziomy przepływu dowolnej

cieczy przez porowatą warstwę (Rys. 7.)

11

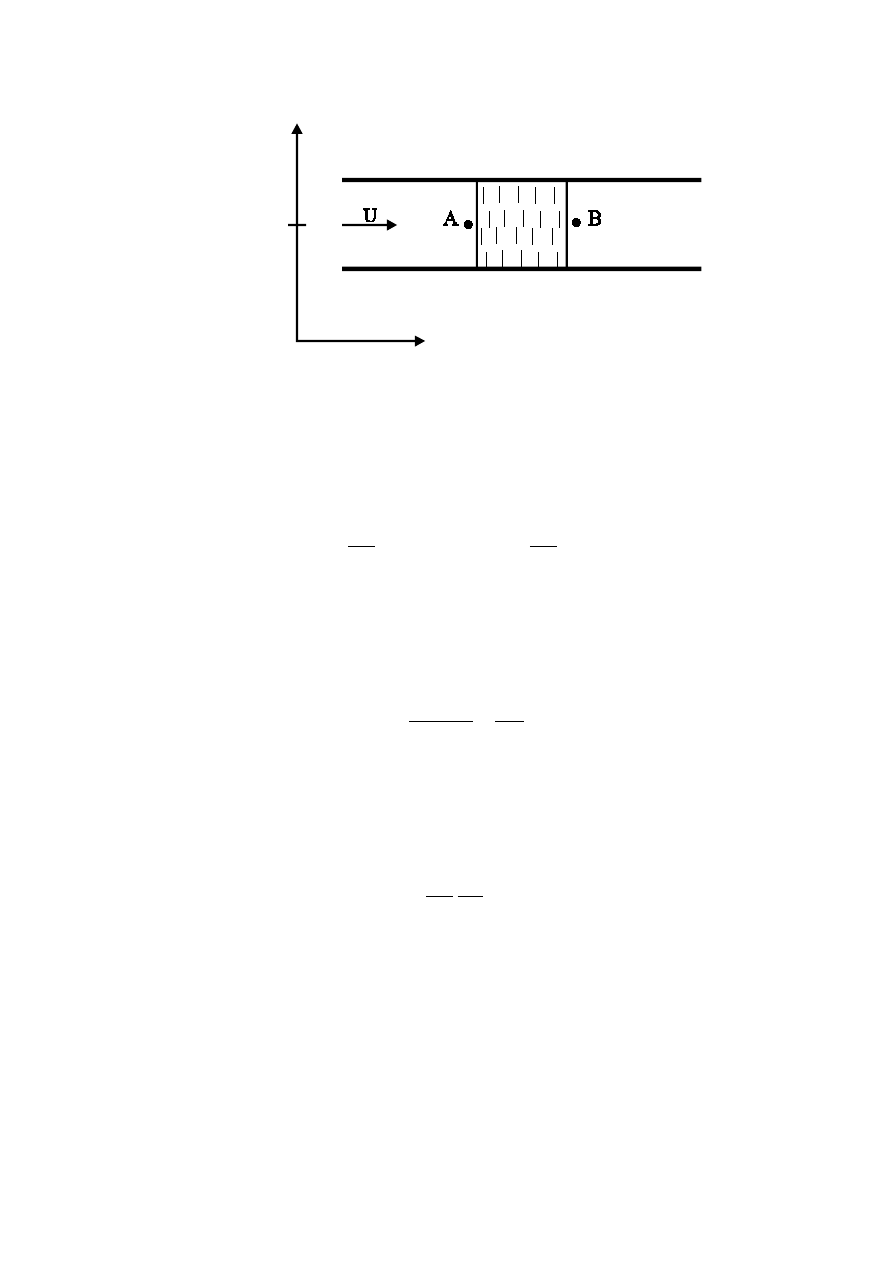
Rys. 7.

W takim przypadku

A

A

A

z

g

p

H

+

=

ρ

,

B

B

B

z

g

p

+

=

Η

ρ

.

Ponieważ z

A

= z

A

mamy

(19)

g

g

ρ

ρ

p

p

p

B

A

∆

=

−

=

∆Η

.

Podstawiając wyrażenie (19) do (18) równanie (16) przyjmie postać

(20)

L

p

g

=

U

∆

Κ

ρ

.

Stosunek

∆

p / L spadku ciśnienia

∆

p do długości L na którym on występuje

nazywany jest gradientem ciśnienia.

12

z = z

A

B

poziom

odniesienia

Doświadczalnie i teoretycznie wykazano, że współczynnik K /

ρ

g jest

odwrotnie proporcjonalny do lepkości cieczy

µ

(21)

µ

ρ

k

g

Κ

=

.

Wówczas z (20) mamy

L

p

Δ

k

=

U

µ

.

Współczynnik k nazywany jest przepuszczalnością porowatego ośrodka. Wielkość

ta dla umiarkowanej prędkości przepływu płynów nie zależy od własności płynu i

jest parametrem charakteryzującym wyłącznie strukturę porów porowatego

materiału.

2. PODSTAWOWE METODY WYZNACZANIA PRZEPUSZCZALNOŚCI

MATERIAŁÓW POROWATYCH

Przepuszczalność materiału porowatego charakteryzuje jego zdolność do

przepuszczania płynu pod działaniem różnicy ciśnień (gradientu ciśnienia, gradientu

hydraulicznego). Określa ją współczynnik przewodności hydraulicznej K (patrz

wzór (16)) lub współczynnik przepuszczalności k (patrz wzór (21)) . Wartość

współczynnika K jest zdeterminowana przez strukturę porowatego materiału i

własności płynu, natomiast parametr k jedynie przez strukturę.

Przepuszczalność materiału porowatego może być mierzona przy pomocy

cieczy lub gazu, przy czym zastosowanie cieczy jest korzystniejsze ze względu na

konieczność pomiary mniejszej liczby parametrów.

Przepuszczalność i przewodnośc wyznacza się bądź przez badanie próbek w

laboratorium, bądź w warunkach badań terenowych.

13

Do najważniejszych metod laboratoryjnych poniaru przepuszczalności

materiałów porowatych należą:

•

metoda ze stałym ciśnieniem cieczy,

•

metoda ze zmiennym ciśnieniemcieczy.

2.1. Metoda ze stałym ciśnieniem cieczy.

Metoda ze stałym ciśnieniem cieczy polega na tym, że przez próbkę

materiałui porowatego przepuszczana jest ciecz przy stałej różnicy ciśnień po obu

stronach próbki. Do tego wykorzystuje się urządzenie zwane

przepuszczalnomierzem (Rys. 6). Urządzenie to zbudowane jest z komory

pomiarowej i zbiornika utrzymującego stałe ciśnienie. Do zbiornika w sposób ciągły

doprowadzana jest ciecz. Zbiornik wyposażony jest w przelew, dzięki któremu

można utrzymać stały poziom cieczy w zbiorniku. W komorze pomiarowej

zamocowana jest próbka materiału porowatego, przez którą przepływa ciecz.

Nadmiar cieczy usuwany jest z komory za pomocą przelewu.

Podczas wykonywania pomiarów tą metodą mierzymy objętość wody V

jaka przepływa przez próbkę o grubości L i powierzchni poprzecznego przekroju

A w czasie t . Wysokość

∆

h oraz pole przekroju A są wielkościami znanymi.

Współczynnik K wyznacza się z prawa Darcy danego wzorem (15). Biorąc pod

uwagę, że V = Q

⋅

t ze wzoru (15) otrzymujemy

h

At

VL

K

∆

=

.

2.2 Metoda ze zmiennym ciśnieniem cieczy

14

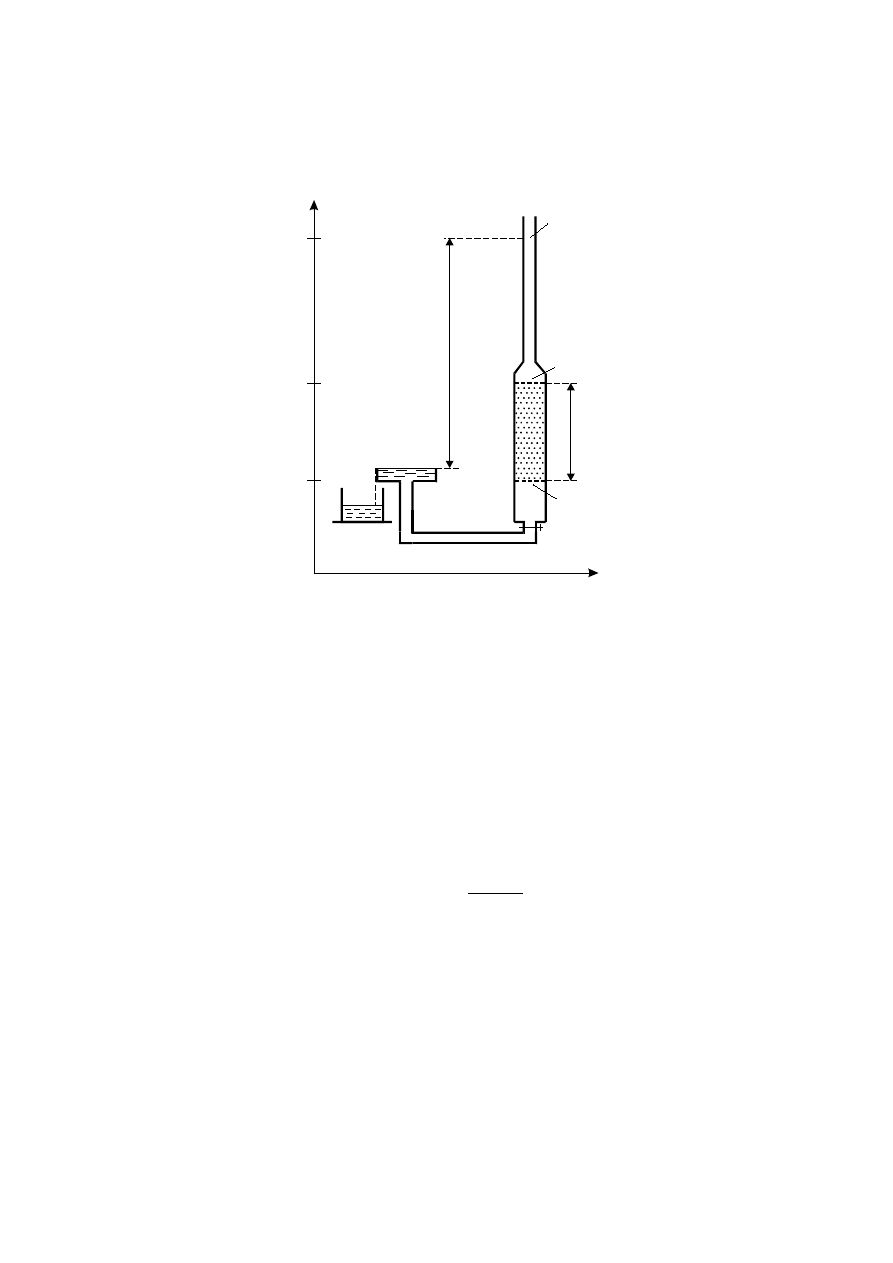
Schemat stanowiska do pomiaru metodą zmiennego ciśnienia przedstawia Rys.8.

Rys.8.

Cechą charakterystyczną tej metody jest to, że w trakcie pomiaru różnica

wysokości hydraulicznych

∆Η

(t) = H

A

(t) – H

B

, wymuszające przepływ płynu przez

warstwę porowatego materiału ulega zmianie. W rezultacie zmienia się również

wydatek Q(t) przepływającej cieczy.

Równanie (13) przepływu Darcy w takim przypadku przyjmuje postać

(22)

L

(t)

H

A

K

(t)

Q

Δ

=

gdzie

∆Η

(t) = H

A

(t) - H

B

Biorąc pod uwagę, że wysokość hydrauliczna H

A

nad warstwą porowatego

materiału określana jest wzorem

15

z

A

z

B

z

X

p

A

p

o

p

o

p

B

A

B

h

L

(

)

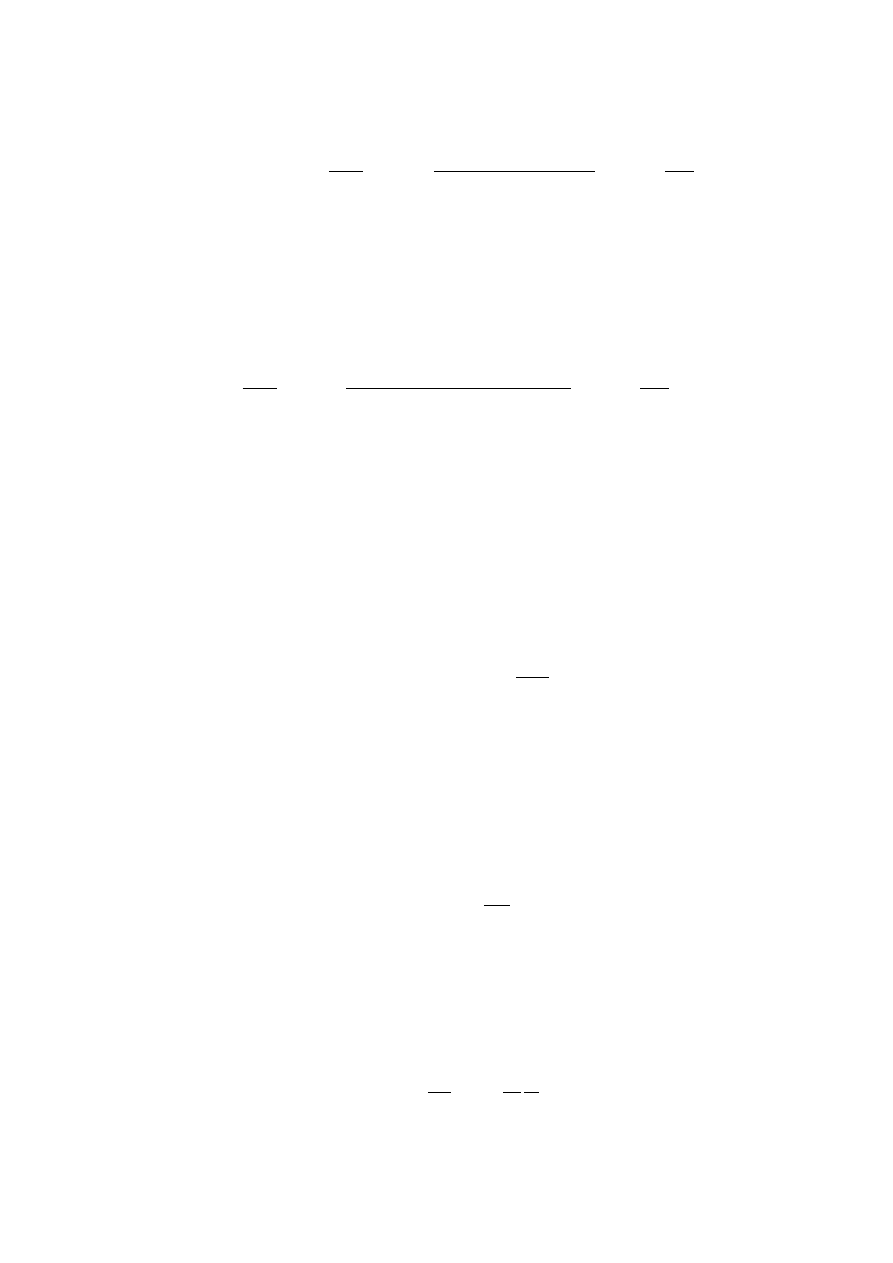
X

o

A

A

X

o

A

A

Z

g

p

Z

g

Z

Z

g

p

Z

g

p

+

=

+

−

+

=

+

=

ρ

ρ

ρ

ρ

Α

Η

,

natomiast wysokość hydrauliczna H

B

pod warstwą wynosi

(

)

h(t)

Z

g

p

Z

g

)

Z

h(t)

(

Z

g

p

Z

g

p

Η

X

o

B

B

X

o

B

B

B

−

+

=

+

+

−

+

=

+

=

ρ

ρ

ρ

ρ

,

dla różnicy

∆Η

(t) otrzymamy

(23)

∆Η

(t) = h (t) .

Podstawiając (23) do (22) mamy

(24)

( )

( )

L

t

h

KA

t

Q

=

.

Z drugiej strony o wydatku przepływu cieczy przez porowatą warstwę decyduje

szybkość ruchu powierzchni cieczy w rurce pomiarowej. Przyjmując, że pole

przekroju tej rurki wynosi a , wydatek cieczy będzie określony wzorem

(25)

t

d

h

d

a

-

Q

=

.

Uwzględniając wyrażenie (25) z prawa Darcy (24) otrzymamy wyrażenie

(26)

L

h

a

A

K

dt

dh

−

=

16

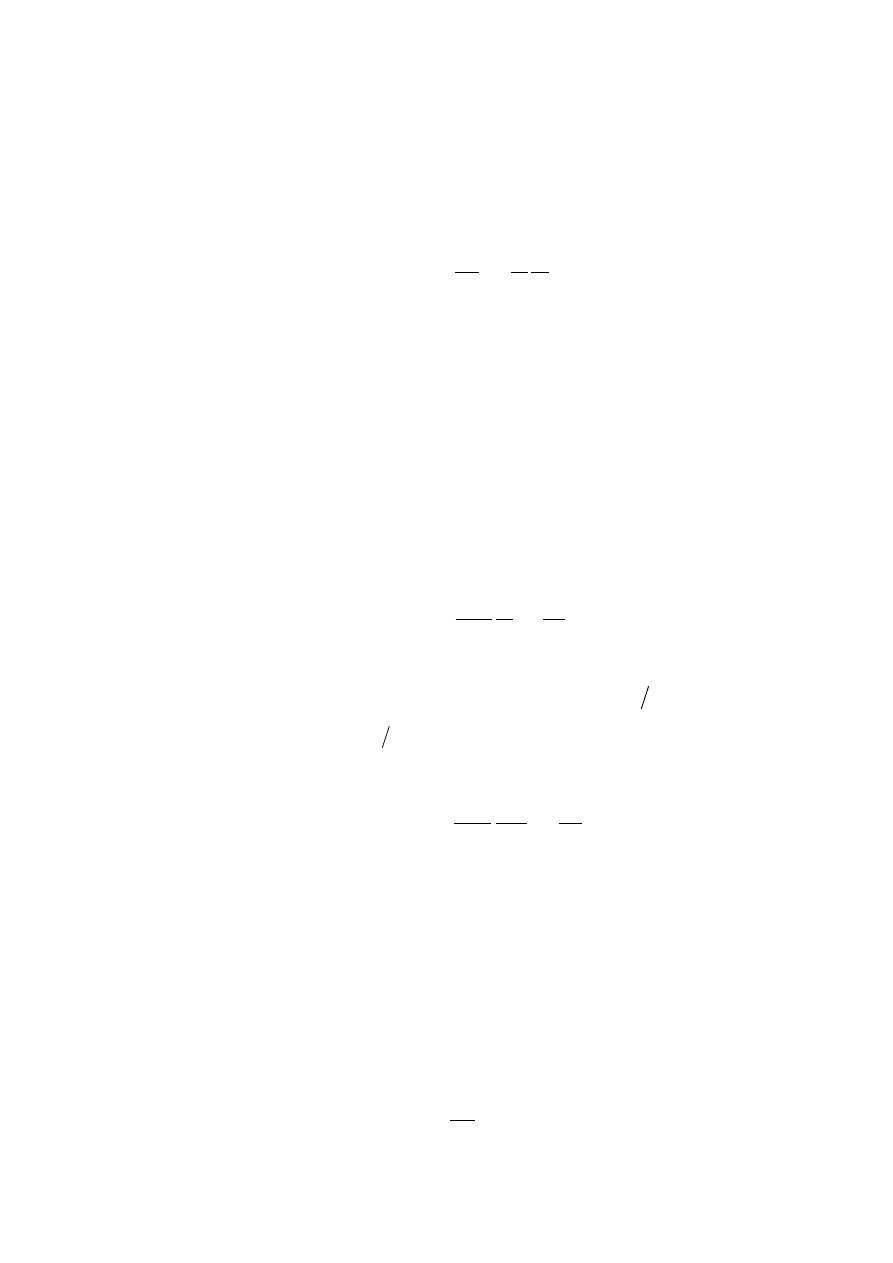
opisując ruch powierzchni wody w rurce pomiarowej.

Rozwiązaniem równania (26) jest wyrażenie

(27)

(

)

o

o

t

-

t

L

K

a

A

h

h

ln

=













gdzie h

o

jest wartością początkową wysokości h, którą zajmuje powierzchnia wody

w rurce w chwili t = t

o

.

Pomiar czasu

o

t

t

−

, w którym powierzchnia wody przemieści się z

wysokości

h

o

na wysokość h oraz zależność (27) umożliwiają wyznaczenie

przewodności hydraulicznej K . Przekształcając zależność (27) otrzymujemy

(28)

,

ln













−

=

h

h

A

a

t

t

L

K

o

o

a po wprowadzeniu średnicy rurki pomiarowej d (

a

d

= π

2

4

) oraz średnicy

komory pomiarowej D (

A

D

= π

2

4

) wyrażenie (29) przyjmuje postać

(29)

.

ln













−

=

h

h

2

d

t

t

L

K

o

o

2

D

Jeśli wielkości L ,

h

o

, h , d , D wyrazimy w centymetrach [cm], a czas w

sekundach [s], wówczas przewodność hydrauliczna określona będzie w jednostkach

[cm/s].

Wykorzystując zależność (21) możemy określić wartość przepuszczalności k.

Wielkość ta dana będzie wzorem

(30)

K

g

k

ρ

µ

=

.

17

W układzie SI jednostką podstawową przepuszczalności jest m2. Jednak dla ciał

porowatych jest to jednostka zbyt duża i dlatego stosuje się inną jednostkę zwaną

darcy [Da]. Za przepuszczalność równą 1 Da uważa się przepuszczalność takiego

ośrodka porowatego, przez którego próbkę o powierzchni przekroju 1 cm2 = 10-4

m2, ciecz o lepkości 10-3 Pa s , pod wpływem gradientu ciśnienia 9.8 10-4 Pa/m

przepływa z natężeniem 10-3 m3/s . Jednostka przepuszczlności 1 Da jest w

przybliżeniu 1012 razy mniejsza od jednostki przepuszczalności 1 m2. Np.

przepuszczalność 1 Da ma kapilara o promieniu r = 2.8 10-6 m , a

przepuszczalność skał roponośnych i gazonośnych leży zazwyczaj w granicach 10-
15 - 10-12 , a więc od kilku milidarcy do kilku darcy.

Zależność pomiędzy przepuszczalnością k i przewodnością hydrauliczną K

dana wzorem (30) w przypadku wody (

µ

= 10-3 Pa s ,

ρ

= 103 kg/m3 , g = 9.81

m/s2) przyjmuje postać

k

≈

10-7 K .

3. STANOWISKO

DO

POMIARU

PRZEPUSZCZALNOŚCI

ZIARNISTYCH MATERIAŁÓW POROWATYCH METODĄ

ZMIENNEGO CIŚNIENIA

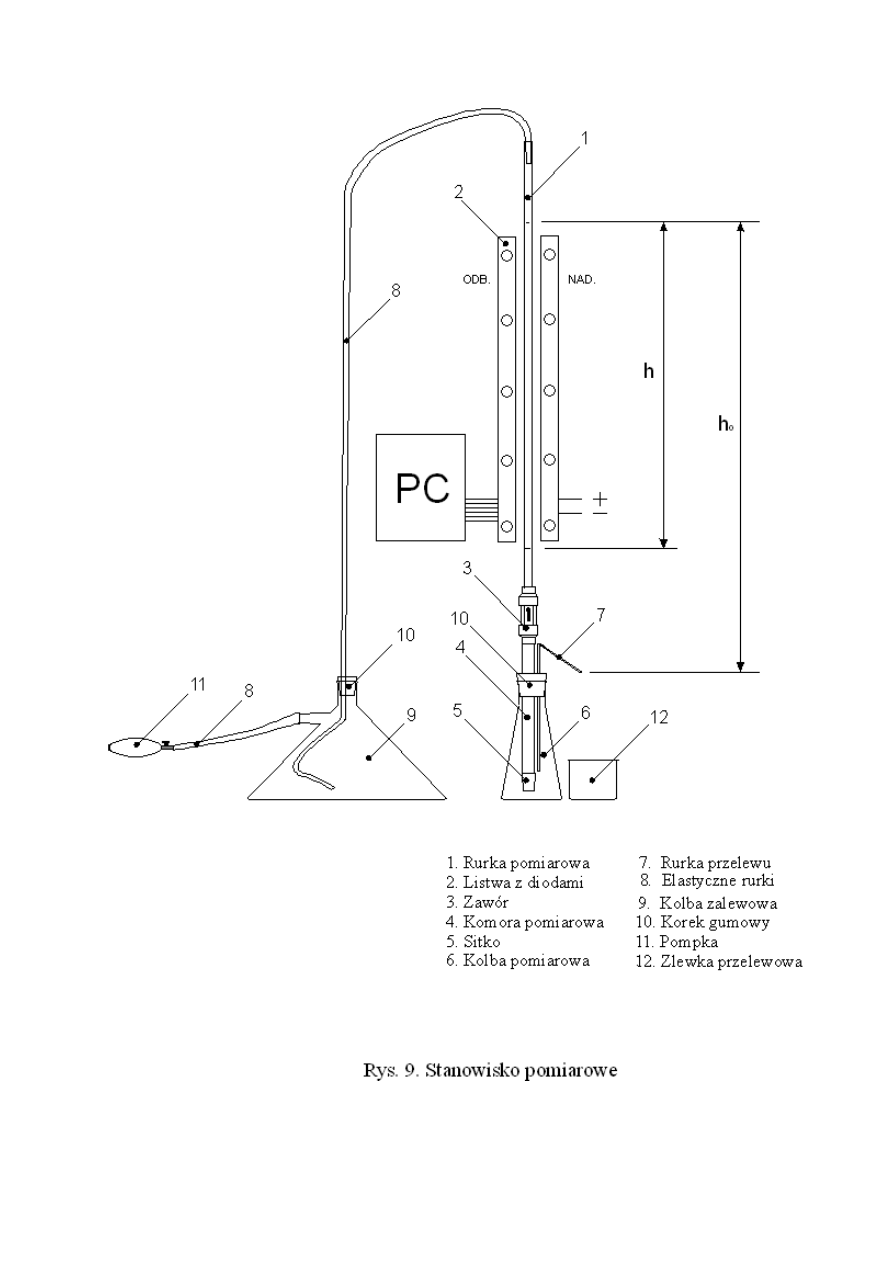
Schemat stanowiska do wyznaczania przepuszczalności ziarnistych

materiałów porowatych przedstawia się na rys. 9. Zasadniczą część stanowią: dwie

szklane rurki o różnych średnicach, zawór kulkowy oraz dwie kolby wraz z

zestawem elastycznych rurek i ręczną pneumatyczną pompką. Zawór kulkowy,

którego zadaniem jest blokowanie strumienia spływającej grawitacyjnie cieczy,

pełni również rolę łącznika pomiędzy cieńszą rurką pomiarową umieszczoną

powyżej zaworu, a grubszą rurką tworzącą komorę pomiarową umieszczoną

poniżej zaworu. W rurce znajdują się szklane kulki tworzące warstwę materiału

18

porowatego. Dolny koniec komory rurki umieszczony jest w szczelnie zamkniętej

kolbie wypełnionej badaną cieczą. W kolbie tej umieszczono także rurkę

przelewową. Ten koniec rurki zamknięty jest drucianą siateczką o otworach

mniejszych niż średnica kulek utrzymującą je we wnętrzu komory. Cienka rurka

pomiarowa spełnia rolę pola do odczytu szybkości opadania poziomu badanej

cieczy, znajdującej się w jej wnętrzu. Kolba druga pełni rolę przyrządu

zalewowego. Dzięki niej można w prosty i szybki sposób napełnić rurkę pomiarową

badaną cieczą. Wykorzystuje się w tym celu nadciśnienie wytwarzane przez

pompkę pneumatyczną.

19

20

4.

PRZEBIEG ĆWICZENIA

Przygotowanie stanowiska pomiarowego

Pierwszym etapem przygotowania układu pomiarowego do badań jest

napełnienie komory pomiarowej (grubsza rurka) wypełnionej nasyconym wodą

materiałem ziarnistym. Aby zapewnić całkowite nasycenie porowatego materiału

napełniamy najpierw kolbę pomiarową wodą. Czynność tę należy przeprowadzać w

taki sposób, aby po zamknięciu kolby korkiem z umocowaną w nim komorą

pomiarową, wewnątrz kolby nie było powietrza. Następnie do komory pomiarowej

wsypujemy materiał ziarnisty tak, aby utworzona warstwa materiału porowatego

miała założoną grubość.

Taka kolejność postępowania zapewnia, że pomiędzy ziarnami utworzonej

warstwy materiału porowatego nie zostaną uwięzione pęcherzyki powietrza, które

zaburzałyby prowadzone pomiary.

Kolbę wraz z osadzoną w niej komorą pomiarową łączymy z rurką

pomiarową umocowaną w statywie.

Kolbę urządzenia zalewowego napełniamy do połowy wodą i zamykamy

korkiem z którego wyprowadzony jest plastikowy wężyk. Drugi koniec wężyka

wkładamy do górnego końca rurki pomiarowej.

Opis procedury pomiarowej

Podstawową wielkością mierzoną przy wyznaczaniu przepuszczalności

materiałów porowatych metodą zmiennego ciśnienia jest czas opadania lustra wody

w rurce pomiarowej pomiędzy górnym i dolnym punktem pomiarowym.

Aby przeprowadzić pomiar czasu opadania lustra wody zamykamy zawór i

napełniamy rurkę pomiarową powyżej początkowego (górnego) punktu

pomiarowego. Następnie otwieramy zawór i w momencie gdy lustro wody

21

przekroczy początkowy punkt pomiarowy, włączamy stoper. Stoper zatrzymujemy

w momencie gdy lustro wody osiągnie końcowy (dolny) punkt pomiarowy. Po

przekroczeniu tego punktu zawór zamykamy. Zmierzony czas zapisujemy w tabeli

pomiarowej. Czynności pomiarowe powtarzamy trzykrotnie dla każdej granulacji

materiału ziarnistego.

W ramach ćwiczenia przewiduje się przeprowadzenie pomiarów przepuszczalności

dla trzech-czterech różnych granulacji materiału ziarnistego.

Wyznaczanie przepuszczalności

Przewodność hydrauliczną K materiału porowatego przy pomiarze metodą

zmiennego ciśnienia wyznaczamy na podstawie wzoru (29), który ma postać

.

ln













−

=

h

h

2

d

t

t

L

K

o

o

2

D

Podstawowe parametry stanowiska pomiarowego:

•

średnica rurki pomiarowej

d = 9 mm

•

średnica rurki komory pomiarowej

D = 16 mm

•

grubość warstwy granulatu szklanego

L = 100 mm

22

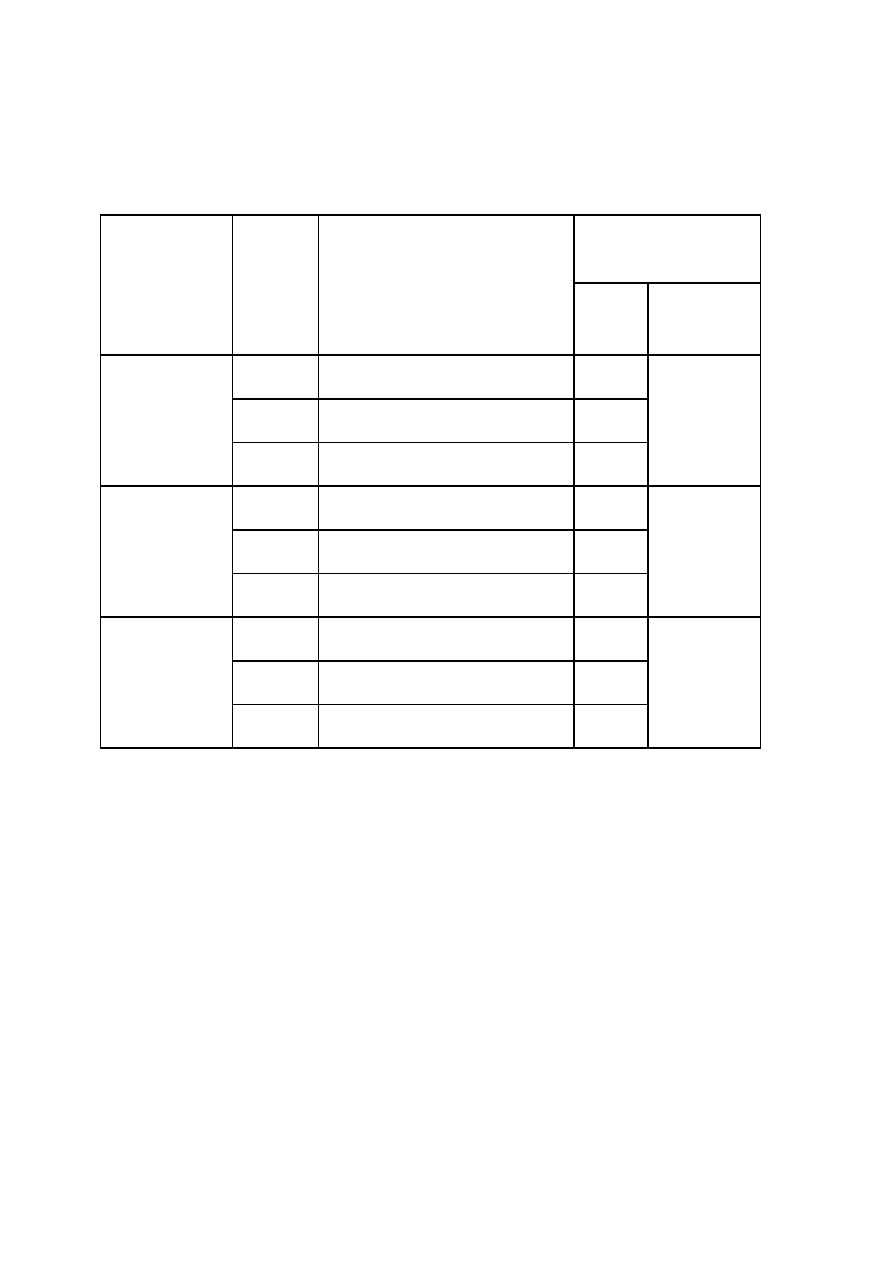
Tabela wyników pomiarów i obliczeń

Rodzaj

Przewodność

hydrauliczna

granulatu

Nr

pomiaru

Czas

K

[cm/s]

Kśr

[cm/s]

Próbka I

Próbka II

Próbka III

Wykres zależności przewodności hydraulicznej K od średnicy kulek szklanych.

TREŚĆ SPRAWOZDANIA

1. Krótki opis stanowiska laboratoryjnego oraz metody pomiaru.

2. Zestawienie wyników - tabela i wykres.

3. Uwagi i wnioski.

23