POLITECHNIKA WARSZAWSKA 

 

INSTYTUT TECHNIK WYTWARZANIA 

 
 
 
 
 

   

 

 
 
 

   

 

 

 

 

 

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 

 
 

Opracował: dr inż. Leszek Moszczyński 

 

Warszawa 

 

2007 

 
 
 
 
 
 
 

 

LABORATORIUM 

   
 
PODSTAW  
 
 
  TEORII  
   

 

 

 
S Y G N A Ł U 

 

For i = start: skok: koniec 
 

... polecenie Matlaba 

 

end 

if <warunek> 
 

... polecenie Matlaba 

 

end 

while <wyrazenie> 
 

... polecenie Matlaba 

 

end 

 
 
 
 
 

 

Ćwiczenie lab -2 

 

Sygnał jako wektor 

 

 

Różne sposoby konstrukcji sygnałów, proste zależności i przekształcenia 

 
Objaśnienie 

 

Funkcje do konstruowania wektorów i macierzy 

 

Nazwa 

Opis funkcji 

linspace 
ones 
zeros 
rand 
randn 
sort 
length 

wektor o wartościach równomiernie rozłożonych 
macierz o elementach równych 1 
macierz o zerowych elementach 
macierz losowa o rozkładzie równomiernym 
macierz o rozkładzie normalnym 
sortowanie elementów według narastających wartości 
zwraca wymiar wektora lub macierzy dłuższy z jej wymiarów 

 
Tworzenie wektorów: 
 

 

j:k   

definiuje wektor [j, j+1, ..., k] 

 

j:i:k  

zapisuje wektor [j, j+i, j+2i, ..., k] 

 
Wybór żądanych wierszy, kolumn i elementów macierzy lub wektora 
 
 

 

a(:,j)  

wypisanie j-tej kolumny macierzy a 

 

 

a(:, j:k) 

wypisanie kolumn a(j), a(j+1), ..., a(k) 

 

 

a=[ ]  

definiuje pusty wektor lub macierz 

 

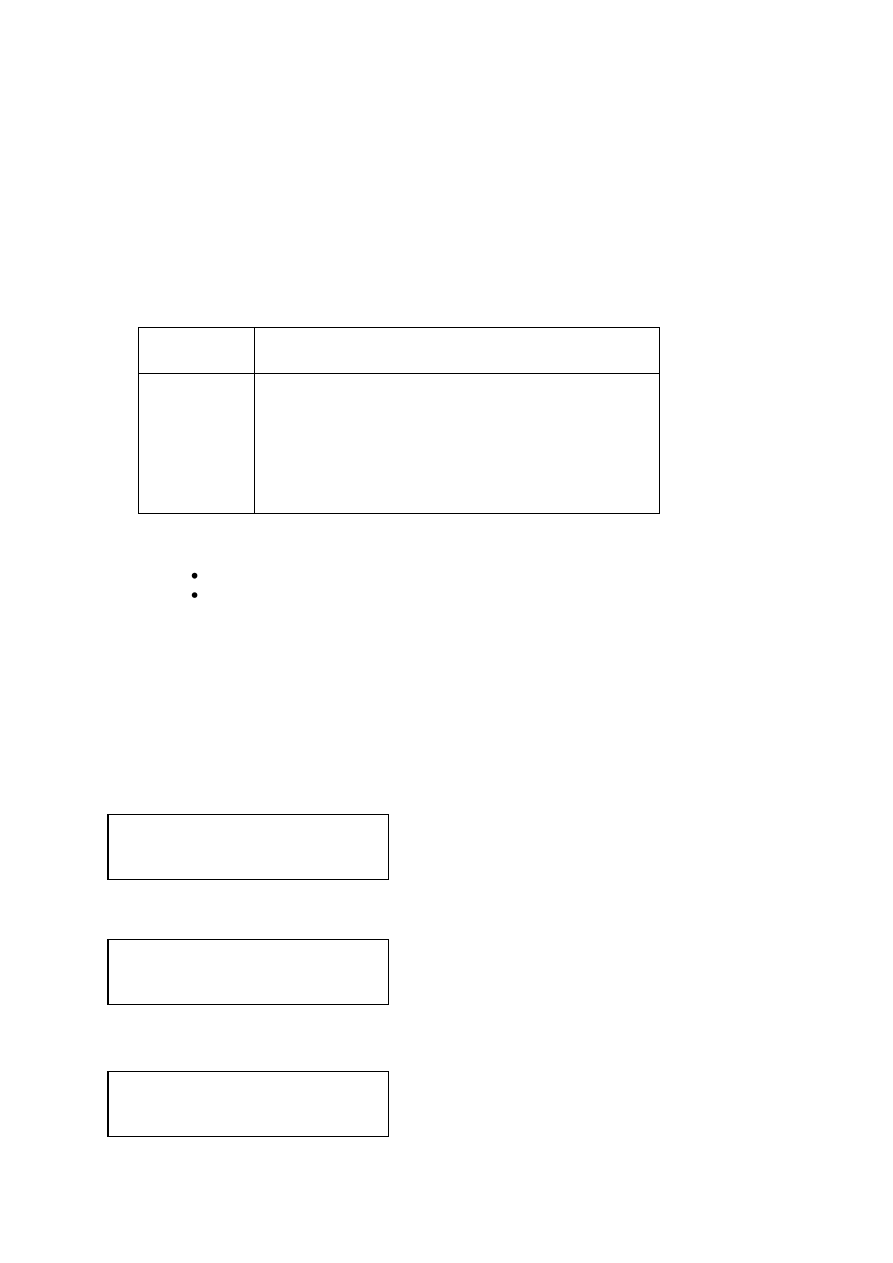
Organizacja pętli 

 
 
Struktura pętli for 

 
Podprogram wykonawczy zawarty pomiędzy for i end 
wykonywany jest i powtarzany dla każdego elementu 
określonego zmienną i. 
 

 
Struktura pętli if 

 
Wykonywanie instrukcji if polega na wykonaniu poleceń 
związanych z wyrażeniem warunkowym. Jeśli nie zachodzi 
warunek następuje wyjście poza pętlę. 
 

 
 
Struktura pętli while 

 
Wykonywanie sekwencji poleceń jest powtarzane tak długo jak 
wyrażenie po while przyjmuje wartość różną od zera 
(TRUE). 
 

 

 
 
 
 
Objaśnienie 

 

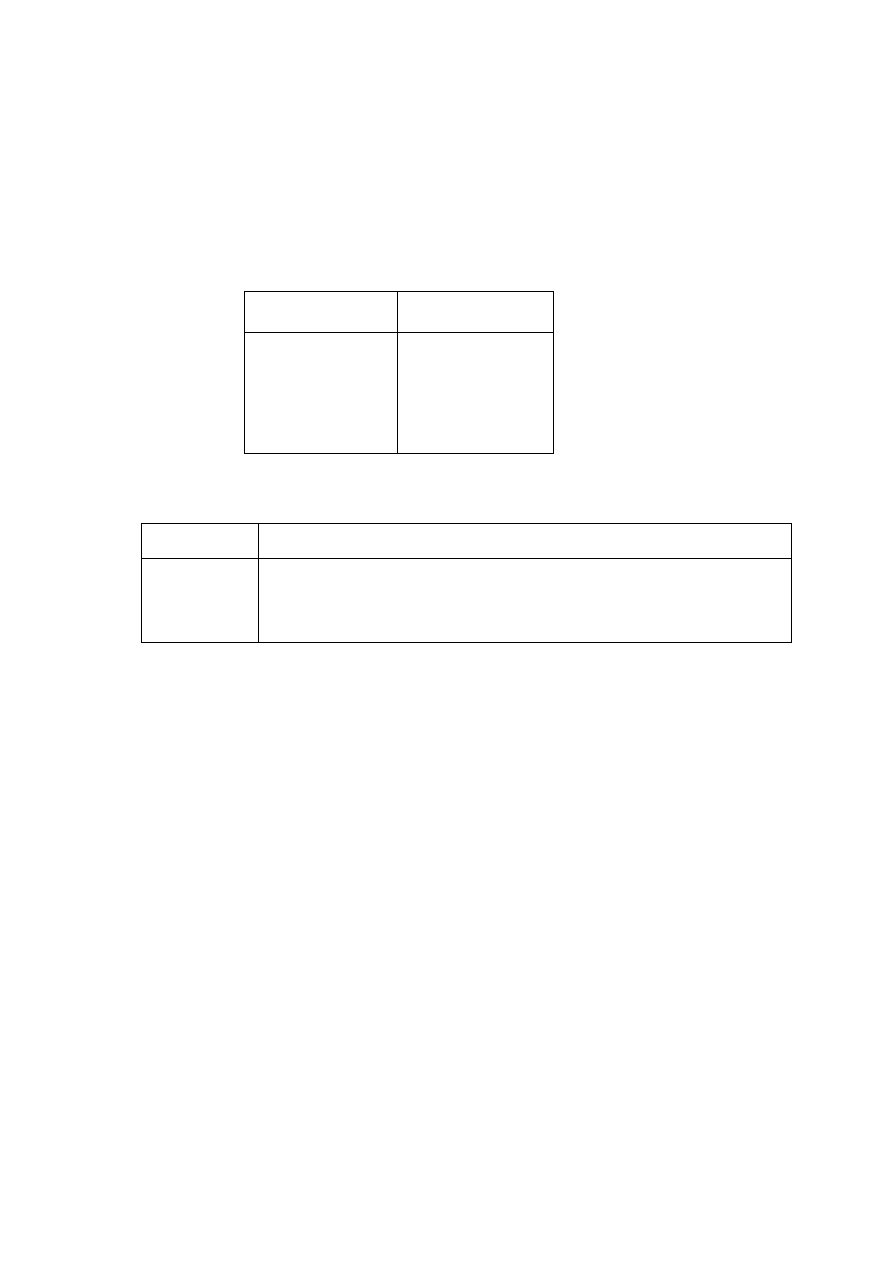
Relacje i wyrażenia logiczne 

 

Fałsz – odpowiada macierzy lub wektorowi pustemu zawierającemu co najmniej jedno zero. 
Logiczna prawda – odpowiada macierzy lub wektorowi o elementach niezerowych. 
 
Operatory porównania 
 

Wyrażenie 

Relacja 

a = = b 
a ~ = b 
a < b 
a > b 
a < = b 
a > = b 
 

a równe b 
a różne od b 
a mniejsze od b 
a większe od b 
a mniejsze równe b 
a większe równe b 

 

Funkcje logiczne 

Operatory 

 

Operator 

Opis działania operacji 

a | b 
a & b 
xor(a, b) 
~ a 

alternatywa: 1 wówczas jeśli co najmniej jeden z operatorów różny od zera 
koniunkcja: 1 wówczas jeśli oba operatory niezerowe 
różnice symetryczne: 1 tam gdzie jeden z operatorów jest niezerowy ale nie oba naraz 
negacja : 1 wówczas jeśli a = = 0, 0 tam gdzie a ~ = 0 

 
 
 
 

ZADANIA 

 
Zadanie 1 
 
Utworzyć wektor t składający się z dziesięciu elementów równo rozmieszczonych w zakresie <0, 1>. 
Sprawdź wynik wykonania polecenia: format short i format long. 
W jaki sposób przekonać się, że polecenie format short oraz format long steruje jedynie formatem 
prezentacji wyniku, nie wpływając na wartości zmiennych? 
 
 
Zadanie 2 
Dany jest wektor a. Jak wykorzystując własności indeksowania zmienić kolejność zapisu jego elementów? 
 
Zadanie 3 
Utworzyć sygnał losowy o rozkładzie równomiernym (funkcja rand) złożony z 10 elementów. Wybrać z 
sygnału wektor składający się z czterech największych wartości i zapisać w postaci uporządkowanego wektora o 
malejących wartościach.   
 
Zadanie 4 
Utworzyć sygnał x, którego wektor zbudowany jest z pięciu elementów o wartości zero, sześciu jedynek i 
czterech zer. Jak zmienić ten sygnał by jego amplituda była pięć racy większa? 
 
 
 

 Zadanie 5 
Dana jest macierz zapisana w postaci: 
 
A=[0 1 2 3 ; 4 5 6 7]; 
Co oznacza zapis: 
a)  A(:,4) =[ ] 
b)  A(:,2 : 3)=[ ] ? 
 
 
Zadanie 6 
Podaj wynik relacji: 
 
a)  3 < 2; 
b)  x = 6; 

x^2 > 4 * x; 

c)  ~ (2 > -4); 
d)  x =2; z =6; y =-4;  (x^2 + y^2) > z^2/2 |(z * y <x) 
e)x = 6;  y = 12;  z =-4; 

xor(z, x-2*y) 

 
Zadanie 7 
 
Jaki wynik uzyskamy realizując zapis: 
 
a)  
while (i < 3) & (x < 35) 
 

 

x = -x * (i +1) 

end 
 
b)  
i = 1; x = -3; 
while(xor(i < 3 , x < 35)) 
 

 

x = -x*(i + 1) 

 

 
Zadanie 8 
 
Dany jest sygnał x = [0 1 –3 4 –5 5 6  3]. 
Jakie liczby uzyskamy realizując zapis? 
n = find( x >2); 
 
 
Zadanie 9 
 
Dany jest sygnał x = [-4 1 2 –3 5 –5 3 4]. 
Jak zapisać procedurę sumowania elementów x mniejszych od dwóch? 
 
Zadanie 10 
 
W Matlabie zapisano polecenie: 
 
for k = 1 : 2 : 5; 
 

x(k) = 2 

end 
 
Zapisz wartości uzyskanego wektora x. 
 
Zadanie 11 
 
Wyjaśnij działanie instrukcji: 
 
n = 7; 
x = []; 
for i = 1 : n 
x = [x sqrt(i)]; 
end 
Z jakich liczb zbudowany jest wektor x ? 

 
Zadanie 12 
 
Dane są dwa sygnały x = [5 3 2 1 7] i y = [0 2 4 5 6 ]. 
Co realizuje polecenie z = x(x < y)? 
 
Zadanie 13 
 
Dla danych Zadania 12 podaj wynik działania polecenia z = find(x < y). 
 
Zadanie 14 
 
Dla danych z zadań 12 i 13 podaj wynik działania polecenia l = length (z). 
 
Zadanie 15 
 
Dany jest sygnał x = 0.1 : 0.1 : 1. Wiedząc, że funkcja rem podaje resztę z dzielenia przeanalizuj 
następujący algorytm: 
 
k=0; 
n = length(x); 
for i = 2 : 1 : n 
 

if(rem(i,2) == 0) 

 

 

k = k +1; 

wynik(k)= x(i); 
 

end 

end 
 wynik 
Jakie liczby tworzą wynik? 
 
Zadanie 16 
 
Niech wektor x= -1: 0.2:1;    W jaki sposób należy uzupełnić algorytm z zadania 15, aby w  wyniku 
uzyskać sygnał  x złożony z elementów dodatnich o parzystych indeksach? 
 
Zadanie 17 
 
Czy wektor t = -pi : pi/10 : 0 ma taką sama długość jak wektor sygnału  
x = linspace (1, 10, 11). 
 
Zadanie 18 
 
Wskaż błąd w zapisie sygnału względem zmiennej dyskretnej t 
t = 0 : 1 : 10; 
x = linspace (1, 2, 10); 
plot (t, x). 
 
Zadanie 19 
 
Wyjaśnij dlaczego pętla: 
 
x = 1 
while x ~= 0 
 

x = x-0.2 

 

end 

działa nieprawidłowo? 
 
Zadanie 20 
 
Dany jest sygnał zapisany jako: x=[ -23 1 -12  3 -4  2]; 
Napisz polecenie zastępujące wartości ujemne  sygnału zerami. 
 
 
 

 
Zadanie 21 
 
Dany jest sygnał jak w zadaniu 20. 
Napisz polecenie zastępujące wartości ujemne zawarte sygnale wartościami  jeden. 
 
Zadanie 22 
 
Dany jest sygnał  A=[1 2 3 4; 5 6 7 8]. Co realizuje zapis A(:)  ? 
Uzasadnij odpowiedź. 
Zadanie 23 
 
Zapisz w postaci zależności analitycznej (wzoru) poniższy sygnał: 
  
n1= -2; 
n2= 2; 
n = [n1: n2] 
x = 2 *(.5).^n; 
% .^ operator mnożenia  elementu przez element 
 
Zadanie 24 
 
Dany jest dowolny sygnał ciągły x. W Matlabie  dokonano obliczeń zapisanych w postaci poleceń:  
 
x_min = min(x) 

 

 

 

% oblicza wartość minimalną 

x_max = max(x) 

 

 

 

% oblicza wartość maksymalną 

 
x_przed = x_max - x_min; 

 

%  

Nbit = 6 

 

 

 

 

% Liczba bitów 

Lbit = 2 ^ Nbit 

 

 

 

%  

dx = x_przed/(Lbit + 1) ; 

 

% 

 
Wstaw brakujące komentarze. Co oblicza ostatnia linia programu (zmienna dx )? 
 
Zadanie 25 
 
Dany jest zapis: 
 
n = [ -6 : 6 ]; 

 

 

x = [ 0 0 x 0 0 ]; 
 
Z ilu elementów składa się wektor x?