N
IWELACJA
T
RYGONOMETRYCZNA
1
N
IWELACJA
T
RYGONOMETRYCZNA
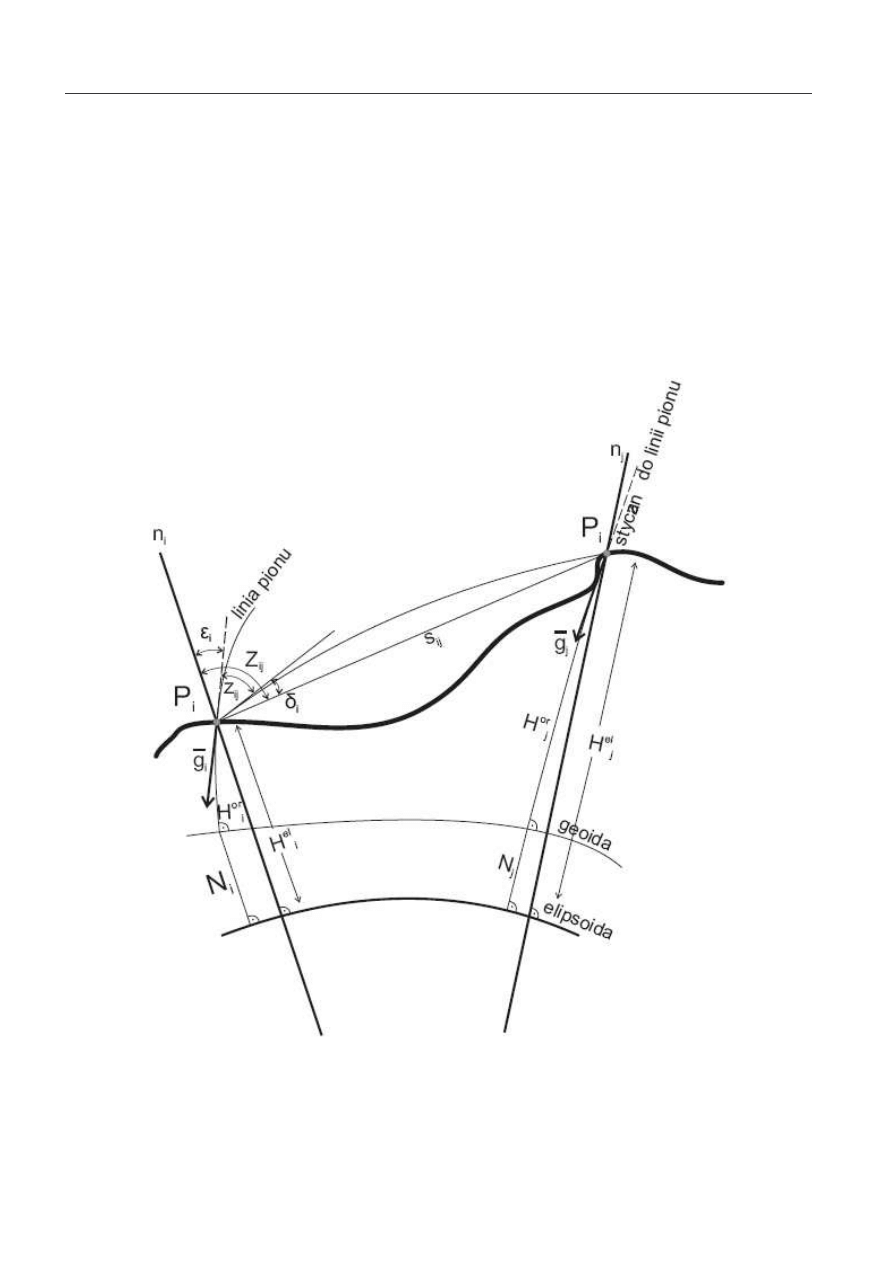
polega na
wyznaczeniu ró nicy wysoko ci pomi dzy dwoma
punktami na fizycznej powierzchni Ziemi na
podstawie
pomiarów
k towych
(odległo
zenitalna) i liniowych (odległo mi dzy punktami).
szukane:
H
el
ij
= H
el
j
- H
el
i
,
powierzchnia odniesienia: elipsoida
N
IWELACJA
T
RYGONOMETRYCZNA
2
Pomiar Z
ij
niemo liwy bo:
wpływ ziemskiego pola siły ci ko ci – odległo
zenitalna z
ij
mierzona jest od normalnej do
powierzchni
ekwipotencjalnej
(stycznej
do
rzeczywistej linii pionu w punkcie P
i
– wektor g
i
),
wpływ atmosfery ziemskiej – pionowa refrakcja
atmosferyczna.
i
i
ij
ij
z
Z
ε
δ
+
+
=
gdzie:
•
Z
ij
– odległo zenitaln Z
ij
odniesion do normalnej
do elipsoidy n
i
oraz do niezniekształconej wpływem
atmosfery celowej P
i
– P
j
,
•
z
ij
– obserwowana odległo zenitalna,
•
δ
i
– k t refrakcji pionowej w punkcie P
i
dla celowej
P
i
– P
j
,
•
ε
i
– odchylenie pionu w azymucie linii P
i
– P
j
,
P
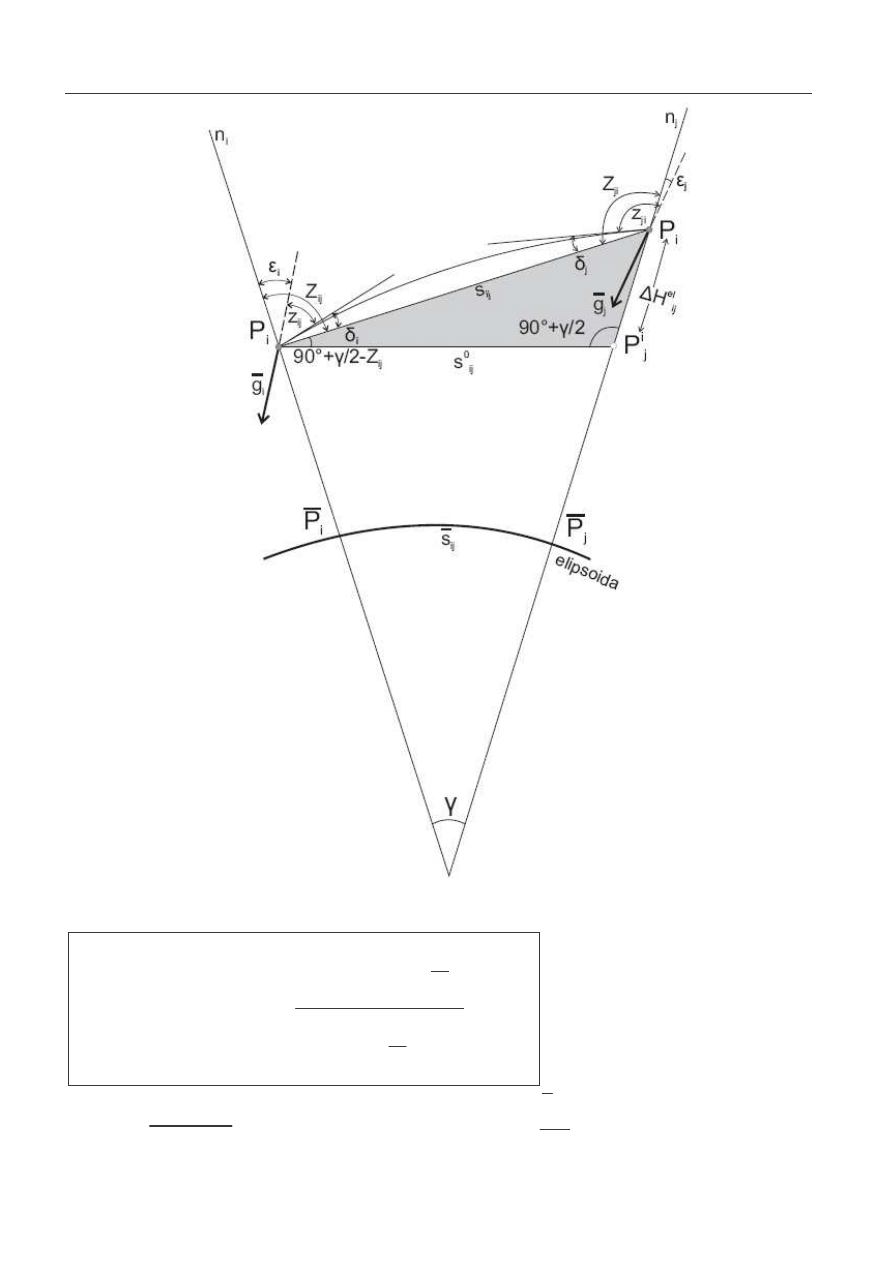
RZEWY SZENIE
J
EDNOSTRONNE
przyjmujemy e łuk elipsoidy
j
i
P
P
−
jest łukiem kołowym
o promieniu równym redniemu promieniowi krzywizn
przekrojów normalnych w punktach P
i
, P
j
w azymucie
celowej (uproszczenie to dla odległo ci mi dzy punktami
s=30km powoduje bł d wysoko ci 1mm i dla odległo ci
wi kszych nie powinno by stosowane);
pomijamy wpływ wichrowato ci normalnych do elipsoidy
w punktach P
i
i P
j
– ró nica wysoko ci obliczana jest w
płaszczy nie przekroju normalnego punktu celowania - P
i
(maksymalny wpływ tego uproszczenia na
H nie
przekroczy 0.014 mm dla s=100km, H=10km).
N
IWELACJA
T
RYGONOMETRYCZNA
3
c
i
Z
s
H
H
H
ij
ij
el
i
el
j
el
ij
−
+
−
=
−
=
∆
2
cos
2
cos
γ
γ
ij
e
j
ij
Z
H
R
s
sin
sin
+
=
γ
lub
R
s
ij
=
γ
N
IWELACJA
T
RYGONOMETRYCZNA
4
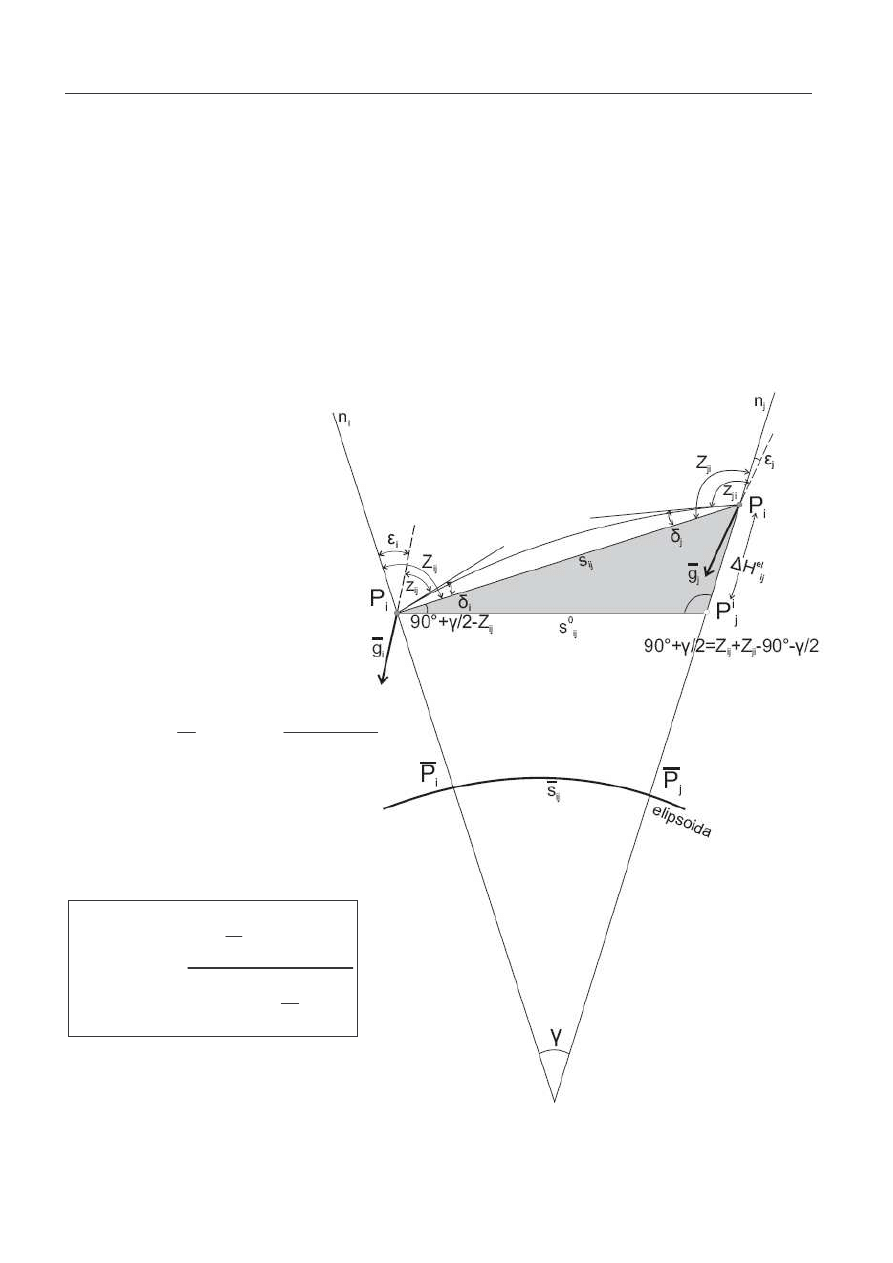
N
IWELACJA
T
RYGONOMETRYCZNA
D
WUSTRONNA
wykonywane s wzajemne obserwacje odległo ci
zenitalnej z dwóch ko ców celowej P
i
– P
j
,
odległo ci zenitalne z
ij
, z
ji
w punktach P
i
, P
j
, oraz
długo ci sko ne s
ij
i s
ji
,
pozwala na uproszczenie problemu poprzez
eliminacj niektórych czynników …
−
=
−
°
−
+
=
2
sin
2
cos
180
ij
ji
ij
ji
ij
Z
Z
Z
Z
Z
γ
γ
(
)
2
cos
2
1
sin
γ
ij
ji
ij
el
ij
Z
Z
s
H
−
=
∆
- rednia z pomiarów wzajemnych
gdzie:
i
i
ij
ij
z
Z
ε
δ
+
+
=
,
j
j
ji
ji
z
Z
ε
δ
−
+
=
N
IWELACJA
T
RYGONOMETRYCZNA
5
Atmosfera ziemska, która jest o rodkiem dla obserwacji
w niwelacji trygonometrycznej, charakteryzuje si
zmiennym współczynnikiem załamania, co powoduje
zakrzywienie promienia wietlnego i zmienn pr dko
fali pomiarowej. Zgodnie z zasad Fermata tor
promienia wietlnego jest taki, aby czas przebiegu fali T
wzdłu toru był minimalny.
zakrzywienie promienia wietlnego -
δ
, k
zmienna pr dko fali pomiarowej – n rzeczywiste
Opisuj c wpływ atmosfery na pomiar odległo ci
zenitalnej wprowadzamy redni współczynnik refrakcji:
r
R
k
=
gdzie: R – promie łuku elipsoidy
r – promie łuku celowej przyjmowanej za łuk
okr gu, (np. dla fal optycznych przyjmowany
cz sto jako r=8R k 0.13).
K t refrakcji wynosi:
R
ks
r
s
2
2
=
=
δ
Najwi kszy wpływ na k t refrakcyjny maj :
warunki meteorologiczne w pobli u stanowiska,
przede wszystkim pionowy gradient temperatury.
Zakrzywienie toru nie ma praktycznego wpływu na
pomierzon odległo sko n (np. ró nica mi dzy
ci ciw a strzałk dla 10km i k=0.13 wynosi
∆
S=0.01
mm).
N
IWELACJA
T
RYGONOMETRYCZNA
6
N
IWELACJA
T
RYGONOMETRYCZNA O
K
RÓTKICH
B
OKACH
Wyznaczaj c przewy szenie mi dzy dwoma reperami
dzielimy to przewy szenie na kilka stanowisk
instrumentu – analogicznie do podziały odcinka na
stanowiska niwelatora – i sumujemy jednostkowe
ró nice wysoko ci.
Rozwijaj c w szereg Taylora wzór jednostronnej
niwelacji
trygonometrycznej
(pomijaj c
wyrazy
wy szych rz dów i przyjmuj c cos(
γ
/2)=1 – bł d 0.1mm
dla s=2km) otrzymamy:
−
+
−
=
∆
2
sin
cos
γ
δ
ε
i
i
ij
ij
ij
ij
el
ij
z
s
z
s
H
Przyjmuj c:
sin
2
ij
i
i
ij
s
k
z
R
δ
=
sin
ij
ij
s
z
R
γ
=
otrzymamy:
(
)
(
)
i
ij
ij
ij
ij
i
ij
ij
el
ij
k
R
z
s
z
s
z
s
H
−
+
−
=
∆
1
2
sin
sin
cos
2
ε
N
IWELACJA
T
RYGONOMETRYCZNA
7
Obliczaj c analogicznie przewy szenie
∆
H
el
ji
i
obliczaj c
redni otrzymamy wzór ko cowy na
dwustronn wzajemn niwelacj trygonometryczn :
(
) (
) ( )
(
)
j
i
ij
ij
j
i
ij
ij
ji
ij
ij
el
ij
z
s
k
k
R
z
s
z
z
s
H
ε
ε
+
−
−
−
−
=
∆
sin
2
1
4
sin
cos
cos
2
1
2
Stosuj c:
odpowiedni dobór punktów,
jednoczesny moment pomiaru – obserwacje
synchroniczne,
identyczny przebieg obustronnych celowych –
obserwacje wzajemne
krótkie celowe
mo emy zało y , e k
i
= k
j
, wówczas:
(
)
(
)
j
i
ij
ij
ji
ij
ij
el
ij
z
s
z
z
s
H
ε
ε
+
−
−
=
∆
sin
2
1
cos
cos
2
1
Pierwszy wyraz – elementarna ró nica wysoko ci
wyznaczona na podstawie pomiaru z
ij
, z
ji
i s
ij
;
Drugi wyraz - opisuje wpływ ziemskiego pola siły
ci ko ci i ł czy wyniki niwelacji trygonometrycznej z
przewy szeniem elipsoidalnym.
N
IWELACJA
T
RYGONOMETRYCZNA
8
Je eli znamy odchylenia pionu w punktach
pocz tkowym i ko cowym w wyniku niwelacji
trygonometrycznej otrzymamy elipsoidaln ró nic
wysoko ci.
Jednak nawet nieznajomo odchyle pionu nie
eliminuje tej metody wyznaczania przewy sze . W
pewnych szczególnych przypadkach wyniki niwelacji
trygonometrycznej bez uwzgl dnienia wpływu pola siły
ci ko ci równowa ne s przewy szeniom otrzymanym
z niwelacji geometrycznej.
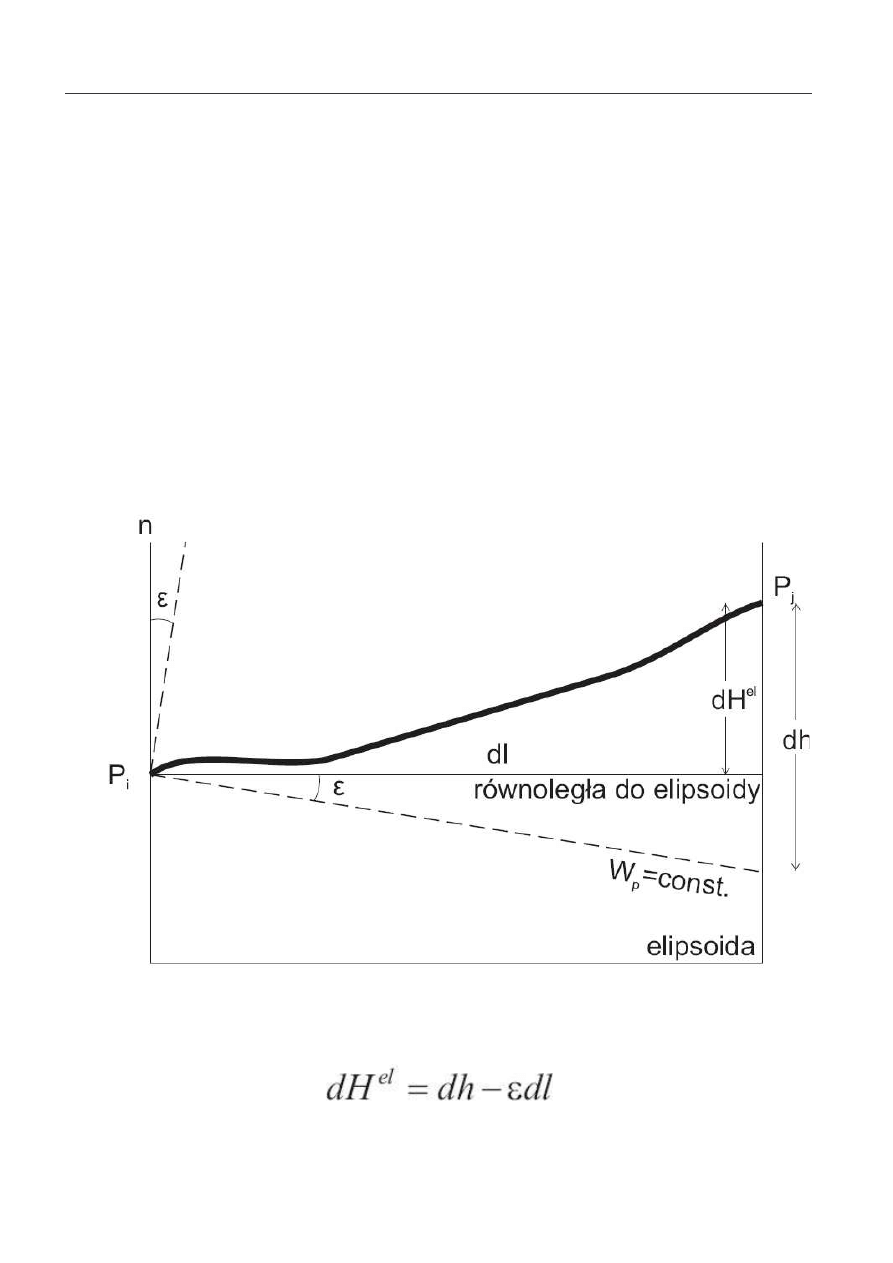
Ró nica przewy szenia na stanowisku niwelacji
geometrycznej, a elipsoidalna ró nica przewy szenia:
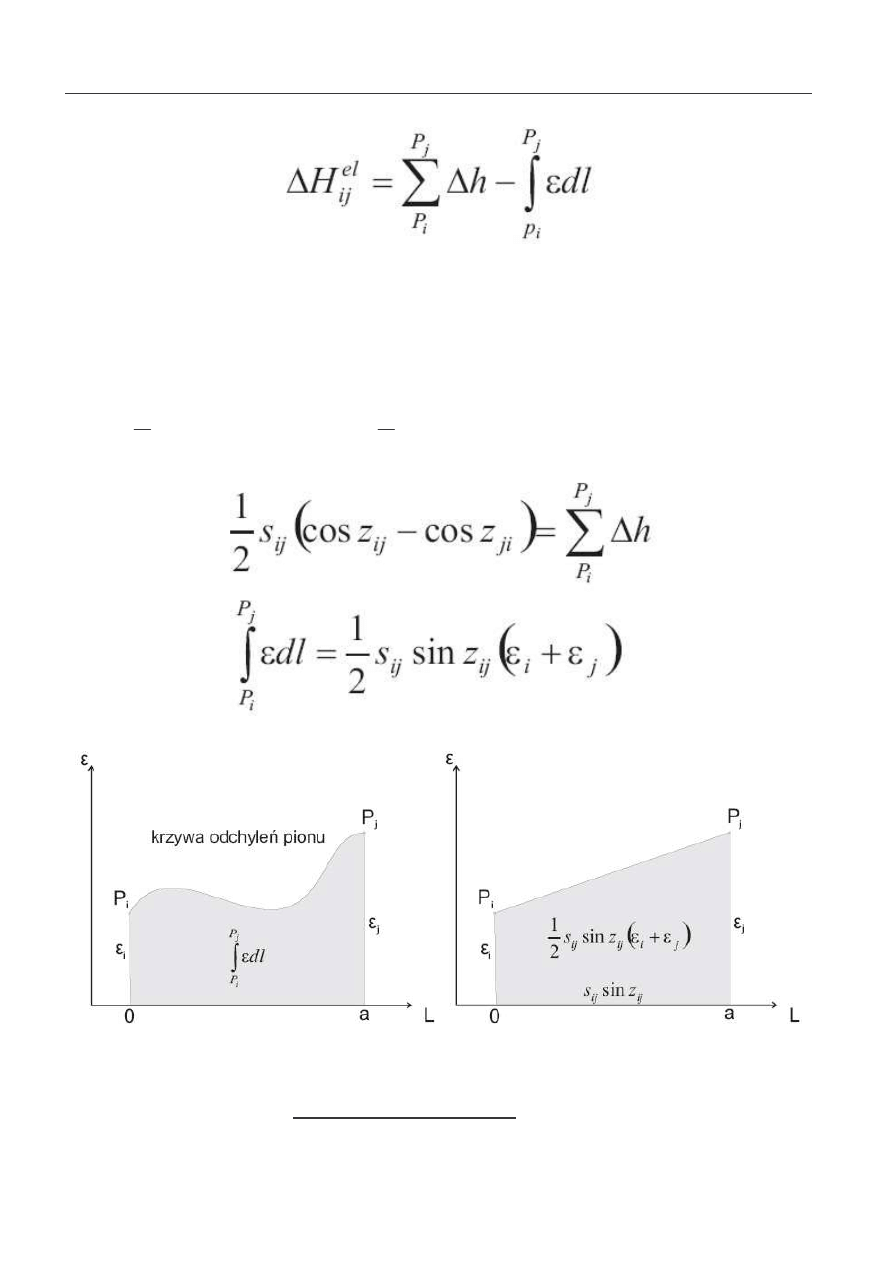
N
IWELACJA
T
RYGONOMETRYCZNA
9
dla całego odcinka P
i
– P
j
:
Aby zachodziła równo mi dzy sum elementarnych
przewy sze uzyskanych z niwelacji geometrycznej i
przewy szeniem otrzymanych z niwelacji trygonometrycznej
musi zachodzi równo :
(
)
(
)
−
∆
=
+
−
−
j
i
j
i
P
P
P
P
j
i
ij
ij
ji
ij
ij
dl
h
z
s
z
z
s
ε
ε
ε
sin
2
1
cos
cos
2
1
Aby ten warunek był spełniony – zmiana odchyle
pionu musi mie charakter liniowy – celowe do 500m.
N
IWELACJA
T
RYGONOMETRYCZNA
10
Gdy celowe do 500 m:
„surowe wyniki” niwelacji geometrycznej i
trygonometrycznej s równe;
przewy szenie wyznaczone jest w „systemie
naturalnym” zwi zanym z lini pionu i powierzchni
ekwipotencjaln ;
po
wprowadzeniu
poprawek
systemowych
otrzymamy
przewy szenie
normalne,
ortometryczne;
wzór roboczy na przewy szenie elementarne:
(
)
ji
ij
ij
ij
z
z
s
h
cos
cos
2
1
−
=
∆
Jak dokładnie nale y mierzy z,s ?
(
)
2
2
2
cos
2
sin
s
z
H
m
z
m
z
s
m
⋅
+
=
∆
Aby wpływy poszczególnych bł dów obserwacji nie
przekraczały warto 1mm dla przewy szenia:
[ ]
mm
z
m
S
cos
1
<
z [g]
95
90
80
70
60
50
ms [mm] 12,7 6,4 3,2 2,2 1,7 1,4
N
IWELACJA
T
RYGONOMETRYCZNA
11
z
s
m
z
sin
2
<
dla s=400 m :
z [g]
95
90
80
70
60
50
mz [cc]
2,3 2,3 2,4 2,5 2,8 3,2
Bł d przewy szenia składaj cego si z n jednakowych
prz seł:
H
H
m
n
M
∆
∆
⋅
=
dla boku 1 km:
∆
s [m]/z [g]
100 90 60 50
50
0,76 1,03 2,67 3,22
100
1,04 1,14 2,06 2,34
200
1,50 1,52 1,79 1,90
300
1,73 1,73 1,73 1,73
500
2,35 2,33 2,07 1,93
Dowi zanie instrumentu do łaty:
α
tan
⋅
−
=
d
O
i
N
IWELACJA
T
RYGONOMETRYCZNA
12
Wnioski – technologia pomiaru:
pomiar odległo ci z dokładno ci milimetrow
(tereny górskie),
u redniony pomiar z dwóch stanowisk,
konieczno uwzgl dnienia poprawki
atmosferycznej,
pomiar temperatury i ci nienia na obu
stanowiskach – odczyty z dokładno ci 0.2
o
C,
0,5mmHg,
wilgotno powietrza na jednym ze stanowisk,
stała dodawania zastawu dalmierz-lustro,
k ty zenitalne mierzone synchronicznie – radio,
sekundowa dokładno pomiaru k tów,
pomiar w trzech seriach, ró nice mi dzy seriami <
10
cc
,
cel – obiektyw lunety lub specjalne tarcze –
obserwacje wzajemne,
krótsze prz sła w terenach o mało zró nicowanej
rze bie, dłu sze w terenach górskich;
dowi zanie do reperów – pomiar do łat przy „prawie
poziomej celowej”,
odległo instrumentu od łaty do 8m,
pomiar odległo ci do łaty z dokładno ci ~10 cm.