1

Mechanizm wentylacji płuc

Ruch powietrza do płuc i z płuc wywoływany jest różnicą ciśnień pomiędzy

powietrzem atmosferycznym a powietrzem w płucach. Pęcherzyki płucne oplecione
są sprężystymi włókienkami białkowymi (kolagenowymi), które nadają tkance wła-
sności sprężyste.
W otwartej klatce piersiowej płuca są skurczone (zapadnięte). W zamkniętej klat-
ce płuca wypełniają ją całkowicie, gdyż ciśnienie w pęcherzykach,

ciśnienie śród-

pęcherzykowe p

p

,

jest większe od

ciśnienia wewnątrzopłucnowego p

op

(panują-

cego w przestrzeni opłucnowej). Ta różnica ciśnień:

p = p

p

- p

op

rozciąga płuca

wywołując naprężenia sprężyste tkanki

. Sytuacja jest podobna do

tej zilustrowanej na poniższym rysunku z balonikiem. Wynikiem działania sił sprę-
żystych tkanki jest ciśnienie sprężyste tkanki. W warunkach równowagi:

p

sp

=

p

p

- p

op

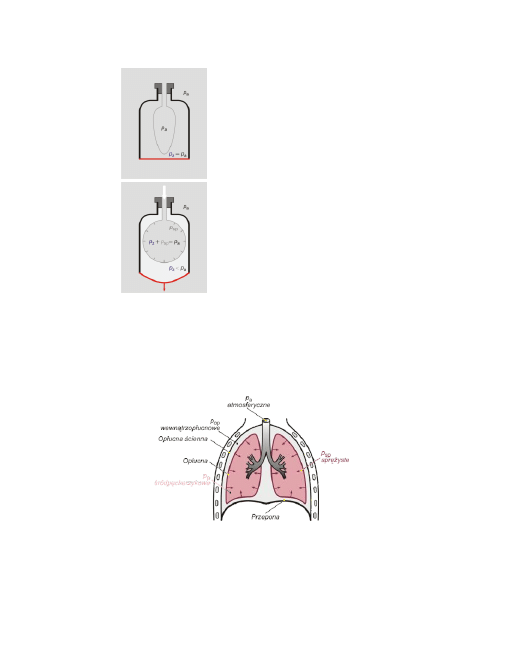
Poniższy rysunek ilustruje mechanizm napełniania pęcherzyków płucnych.

2

Naczynie z gumowym dnem symuluje klatkę
piersiową: naczynie to żebra, gumowe dno to
przepona. Balon pełni role pęcherzyków płuc-
nych.

Początkowo ciśnienie powietrza w naczyniu
(ciśnienie wewnątrzopłucnowe) jest równe
ciśnieniu zewnętrznemu.

Przesunięcie „przepony” w dół powoduje wzrost
objętości wewnatrzopłucnowej.

Pociąga to za sobą zassanie powietrza przez
pęcherzyk-balon, który zwiększa swoją obję-
tość tak długa, póki ciśnienie sprężyste (od-
kształconego balonu) i ciśnienie wewnatrzop-
łucnowe nie zrównoważą ciśnienia atmosfe-
rycznego.

Ciśnienia panujące w płucach.

Ciśnienie sprężyste tkanki płucnej równoważny różnicę ciśnień śródpęcherzykowego
i wewnątrzopłucnowego.

p

op

+

p

sp

=

p

p

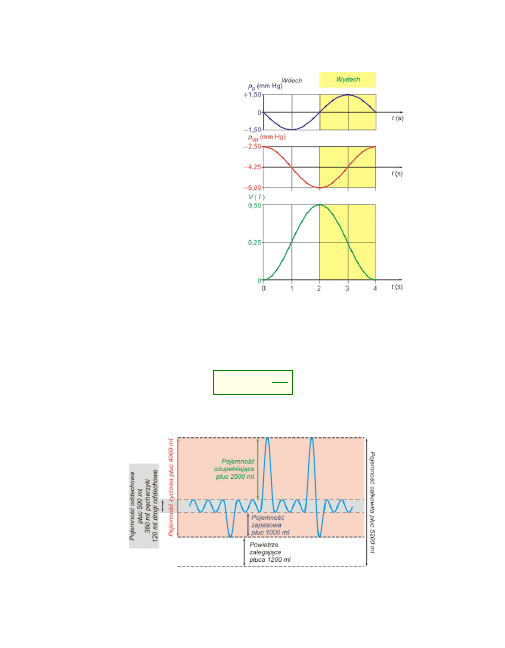
3

Ciśnienie wewnątrzopłucnowe zmie-
nia się w czasie oddychania w grani-
cach od:

-2,5 mm Hg do -6 mm Hg

względem ciśnienia atmosferycznego.

Pociąga to za sobą zmiany ciśnienia
śródpęcherzykowego w granicach od:

-1,5 mm Hg do +1,5 mmHg

odpowiednio przy wdechu i wydechu.

Rysunek pokazuje też, jak zmienia się
jednocześnie objętość płuc.

Δ

Wentylacja

Δ

T

V

t



Podczas wdechu zostaje wprowadzona do płuc objętość powietrza,

objętość

oddechowa V

T

.

Objętość powietrza wdychana w ciągu jednej minuty zwana jest

wentylacją minutową:

przy spokojnym oddychaniu (15 oddechów/1 min.) wentylacja płuc wynosi około:

Wentylacja = 8 l/min

Przy intensywnym wysiłku wentylacja może wzrosnąć 20-krotnie, w wyniku wzrostu
objętości oddechowej i częstotliwości oddechów.

Zmiany objętości płuc mierzone spirometrem.

4

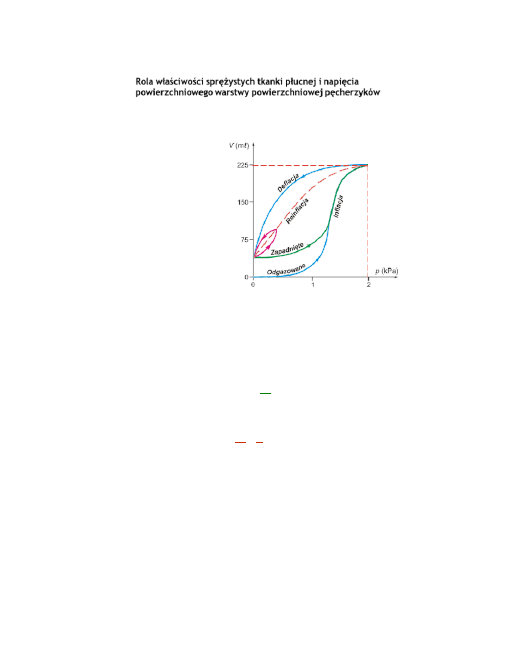
Rola właściwości sprężystych tkanki płucnej i napięcia
powierzchniowego warstwy powierzchniowej pęcherzyków

Właściwości mechaniczne tkanki płucnej bada się na płucu wyizolowanym.

Płuca

nadmuchuje

się powietrzem

(inflacja)

, mierząc ciśnienie i odpowiadającą mu

objętość płuc. Taki sam pomiar wykonuje się przy

opróżnianiu płuc - deflacji

. Poniż-

szy rysunek ilustruje wyniki takich pomiarów otrzymane dla płuca kota.

Histereza

objętościowo-ciśnie-

niowa podczas inflacji i deflacji
izolowanego płuca kota.
Mała pętla odpowiada procesowi
spokojnego oddychania.

ΔV

σ

K

V

 



Δ

1

V

σ

V

K

k

 

Naprężenie wewnętrzne

σ

powstaje w wyniku odkształcenia mechanicznego

ΔV/V

i zależy od wartości

modułu sprężystości

objętościowej

K

:

Odwrotność modułu sprężystości

k - współczynnik sprężystości

objętościowej (współ-

czynnik ściśliwości, podatność sprężysta) określa wielkość odkształcenia powstają-
cego w wyniku przyłożenia naprężenia

σ

:

Histereza objętościowo-ciśnieniowa związana jest z właściwościami sprężystymi tkan-
ki płucnej oraz napięciem powierzchniowym warstwy powierzchniowej pęcherzyków
płucnych.
Zwiększenie powierzchni swobodnej cieczy o

dS

wymaga wykonania pracy

dW

,

która

zwiększającej energię powierzchniową cieczy. Przy czym:

dW = σ

p

·dS,

gdzie

σ

p

oznacza napięcie powierzchniowe cieczy.

Stany powierzchniowe cieczy powodują, że pod zakrzywioną powierzchnią panuje in-
ne ciśnienie niż pod płaską.

Nadwyżka ciśnienia skierowana jest w kierunku środ-

ka powierzchni krzywizny cieczy.

5

Rozważmy powierzchnię kulistą. Zwiększenie promienia krzywizny kuli z

r

do

r+dr

związane jest ze zwiększeniem powierzchni o:

S = 4·π·r

2

 dS = 8·π·r·dr

Zatem energia powierzchniowa wzrośnie o:

dW = σ

p

·8·π·r·dr

Praca związana ze wzrostem objętości kuli:

dV = 4·π·r

2

·dr  dW = p·dV = p· 4·π·r

2

·dr

Dodatkowe ciśnienie związane z zakrzywieniem swobodnej powierzchni cieczy wy-
raża wzór Laplace'a:

Jest ono skierowane w stronę środka promienia krzywizny (wyjaśnia poziom cieczy
w kapilarach w zależności od kształtu menisku).

Dla powierzchni cieczy o różnych promieniach krzywizny wzór Laplace'a przyj-
muje postać:

R

1

i R

2

oznaczają promienie krzywizny przekrojów głównych powierzchni cieczy.

3

4

3

V

π r



 

2

p

σ

p

r





1

2

1

1

p

p

σ

R

R



























Przekroje główne danej powierzchni, to przekroje o ekstremalnych (naj-

mniejszych lub największych) promieniach krzywizny. Przekroje te leżą we wza-
jemnie prostopadłych płaszczyznach.

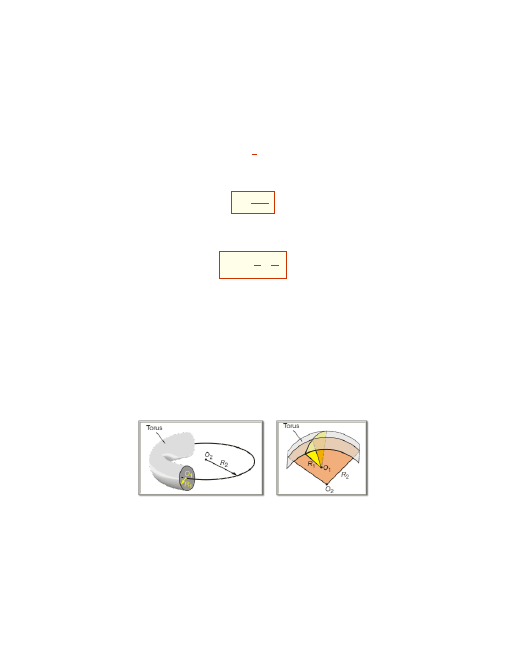
Powierzchnia mająca dwa różne promienie krzywizny to np. torus (rysunek).

O

1

i O

2

środki promieni krzywizny przekrojów głównych. R

1

i R

2

oznaczają odpowie-

dnie promienie krzywizny przekrojów głównych zaznaczonych powierzchni.

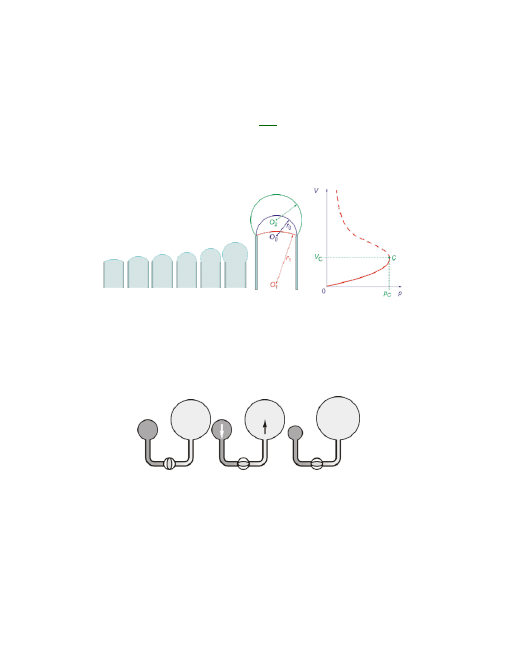
Dla łatwiejszego zrozumienia roli napięcia powierzchniowego warstwy powierzchnio-
wej pęcherzyków płucnych porównajmy rozprężanie pęcherzyka z wydmuchiwaniem
bańki mydlanej.

6

Podczas wydmuchiwania bańki mydlanej jej promień krzywizny:



wpierw maleje od r

1

do r

0

, gdzie r

0

promień rurki,



po czym rośnie od r

0

do r

2

.

Ciśnienie powietrza w bańce jest sumą ciśnienia atmosferycznego p

a

oraz ciśnienia

Laplace’a:

Wraz ze wzrostem objętości bańki ciśnienie w bańce stopniowo narasta, aż osiągnie
maksimum przy minimalnej wartości promienia krzywizny r

0

po czym maleje pod-

czas dalszego wzrostu objętości bańki, tak jak to pokazuje rysunek ilustrujący

zależ-

ność objętości bańki od ciśnienia podczas jej wydmuchiwania.
Po osiągnięciu maksymalnego ciśnienia p

C

bańka staje się niestabilna.

4

p

a

σ

p

p

r







Na powyższym rysunku pokazano dwie bańki mydlane. Na podstawie prawa
Laplace’a można zauważyć, że w większej bańce panuje mniejsze ciśnienie
powietrza. Wobec tego, po otwarciu zaworu, powietrze przepływa z bańki
mniejszej do większej pod wpływem istniejącego w mniejszej bańce wyższe-
go ciśnienia powietrza.
Napełnianie mniejszej bańki wymaga większego „wysiłku” niż większej.

Zawór

7

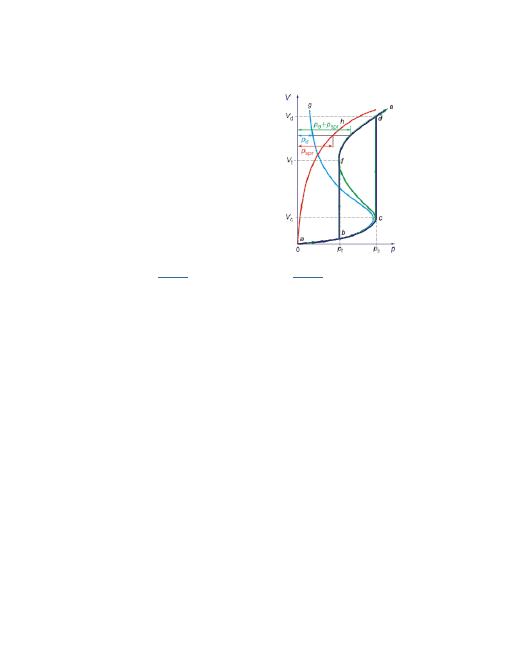
Krzywa

abcg

wyraża zależność objętości od ciś-

nienia napięcia powierzchniowego powłok pęche-
rzyków płucnych

p

σ

.

Krzywa

ah

odpowiada zależności objętości od ciś-

nienia sił sprężystości ścian pęcherzyków

p

sp

.

Krzywa

abcfde

wyraża zależności objętości od ciś-

nienia sumarycznego:

p

σ

+

p

sp

. Wzrostowi objęto-

ści ponad

V

d

sprzeciwiają się wyłącznie siły sprę-

żystości.

Gdyby pęcherzyki płucne zachowywały się jak połą-
czone bańki mydlane, płuca stanowiłyby

układ

niestabilny.

Podczas inflacji wypełniałyby się je-

dynie większe pęcherzyki. Objętość wzrastałaby
do wartości

V

C

,

której odpowiada maksymalne

ciśnienie po czym skokowo przyjęłaby objętość

V

d

,

przy której siły napięcia powierzchniowego

zastąpione zostają przez siły sprężystości.

Zatem przy takich założeniach podczas inflacji objętość płuc zmieniałaby się po dro-
dze

abc

potem skokowo do de i podczas deflacji

edf

i skokowo zapadałyby się do

ba.

Zapewnienie ciągłej zmiany objętości związane musi być z jakimś dodatko-

wym czynnikiem. Czynnikiem tym jest

zmieniająca się wartość napięcia powierz-

chniowego warstwy powierzchniowej pęcherzyków płucnych.

Ściany pęcherzyków pokryte są substancją powierzchniowo czynną -

surfaktantem

,

którego napięcie powierzchniowe zależy od grubości warstwy.

Grubsze

ich warstwy

mają małe napięcie powierzchniowe w granicach od

0,5÷1,0·10

-

2

N/m

, natomiast

cienkie

(prawie monomolekularne) większe o wartości około

5,0·10

-

2

N/m.

Takie właściwości surfaktantów powodują, że ze wzrostem promienia krzywizny ciś-
nienie Laplace'a, mimo wzrostu promienia krzywizny, także rośnie wspomagając ciś-
nienie sprężyste. Zapewnia to utrzymanie równowagi pomiędzy ciśnieniem napły-
wającego do płuc powietrza a ciśnieniem Laplace'a i ciśnieniem sprężystym.

Umożliwia to ciągłe zmiany objętości płuc, eliminuje opisane wyżej skokowe zmia-
ny ich objetości.

Przy wydechu zmniejsza się napięcie powierzchniowe warstwy powierzchniowej pęche-
rzyków płucnych co zapewnia płynne zmniejszanie objętości pęcherzyków płucnych.

8

Można teraz jeszcze raz wrócić do wykresu histerezy objętościowo – ciśnie-

niowej płuca izolowanego. W pierwszej fazie

inflacji

płuca są

mało podatne

na od-

kształcenie. Następnie objętość płuc rośnie wraz ze wzrostem ciśnienia najpierw wol-
no a potem coraz gwałtowniej. Najpierw napełniają się mało liczne pęcherzyki

więk-

sze

(co nie prowadzi do wzrostu objętości), gdy zaczną napełniać się znacznie licz-

niejsze

mniejsze

pęcherzyki — objętość wzrasta gwałtownie. Pojawienie się

sił sprę-

żystych

ogranicza dalszy wzrost objętości — płuca ponownie stają się

mało podatne

na odkształcenie.

Wzrost napięcia powierzchniowego przy rozciąganiu pęcherzyków

sprzyja ciągłym zmianom objętości płuc.
Przy

deflacji

ciśnienie spada gwałtownie przy małej zmianie objętości (płuca są ma-

ło podatne) — maleją siły naprężeń sprężystych. W drugie fazie deflacji, objętość
maleje gwałtownie przy małej zmianie ciśnienia, ale płuca nie zapadają się, gdyż
maleje napięcie powierzchniowe surfaktantów.

Warto zwrócić uwagę na dwa zjawiska:



jeśli inflację płuc izolowanych wykonywać przy pomocy cieczy (eliminacja na-
pięcia powierzchniowego), to objętość płuc wzrasta wraz ze wzrostem ciśnienia
jak krzywa ah (rolę odgrywa jedynie napięcie sprężyste tkanki płucnej),



gdy brak surfaktantów (np. u wcześniaków) wtedy obserwuje się skokowe zmiany
objętości przy inflacji i deflacji abcdfb.

Praca wykonywana przez układ oddechowy. Moc oddechowa

Praca wykonywana przez układ oddechowy wiąże się z wprowadzaniem w ruch:



klatki piersiowej,



przepony,



narządów śródpiersia i jamy brzusznej,



płuc,



powietrza.

Trudno obliczyć 3 pierwsze składniki pracy wykonywanej przez układ oddechowy.
Praca związana z uruchomieniem płuc i powierza związana jest ze zwiększeniem
objętości płuc o

dV

przy różnicy ciśnienia

p

panującego pomiędzy pęcherzykami a

opłucną

dW = p·dV

. Zatem pracę wykonaną na zwiększenie objętości płuc o obję-

tość oddechową

V

T

można obliczyć ze wzoru:

Obliczenie tej całki wymaga znajomości zależności ciśnienia od objętości. Na ciśnie-
nie p składa się:

• ciśnienie

p

sp

pokonujące opory

sprężyste

tkanki płucnej,

• ciśnienie

p

pow

pokonujące

opory ruchu powietrza

,

• ciśnienie

p

l

pokonujące opory

lepkościowe

tkanki płucnej,

• ciśnienie

p

m

pokonujące opory

bezwładności

mas wprowadzanych w ruch.

T

0

d

V

W

p V







9



sp

pow

m

np

pomijamy

l

p

p

p

p

p

p











T

T

sp

np

0

0

d

d

V

V

W

p

V

p

V













Zatem:

Jeśli pominąć pracę związaną z pokonaniem oporów bezwładnościowych powietrza
z uwagi na małą masę wdychanego powietrza, to można założyć, że ciśnienie składa
się z dwóch składników: ciśnienia pokonującego opory sprężyste i opory niespręży-
ste (tarcie). Stąd:

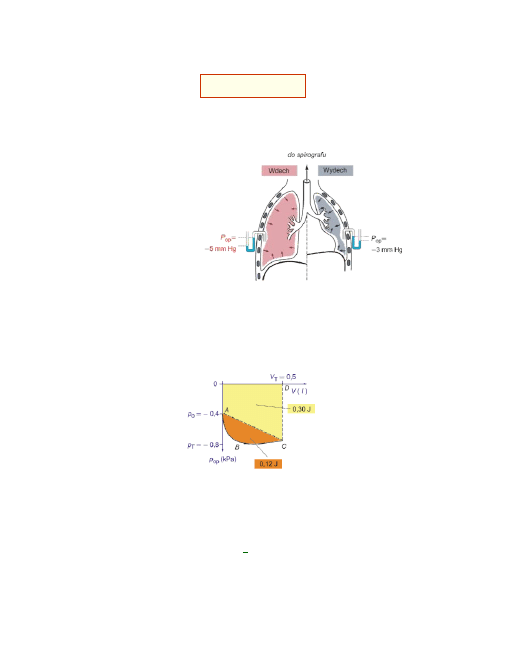
Pomiar dynamicznej histerezy ciśnieniowo – objętościowej.

Rejestrując w czasie oddy-
chania ciśnienie wewnątrz-
opłucnowe (patrz rysunek)
oraz odpowiadającą danej
wartości ciśnienia objętość
wdychanego do płuc po-
wietrza (spirometrem) mo-
żna wykreślić zależność
ciśnienia wewnątrzopłuc-
nowego od objętości wdy-
chanego powietrza.

Przykładowe wyniki takiego eksperymentu przy spokojnym wdechu ilustruje poniż-
szy rysunek.

Przy spokojnym oddychaniu ciśnienie wewnątrzopłucnowe p

op

zmienia się wraz z ob-

jętością V wdychanego powietrza „wzdłuż” linii ABC.
Gdyby występowały tylko opory sprężyste, to ciśnienie zmieniałoby się w funkcji ob-
jętości wzdłuż linii AC (siły sprężyste podlegają prawu Hooke'a).
Pole OACD oznacza zatem pracę przeciwko oporom sprężystym.
Obliczenie pracy przeciwko siłom sprężystym przy wdechu nie sprawia problemów:

T

sp

sp

0

T

T

0

1

(

)

0,30 J

2

V

W

p

dV

p

p

V





 









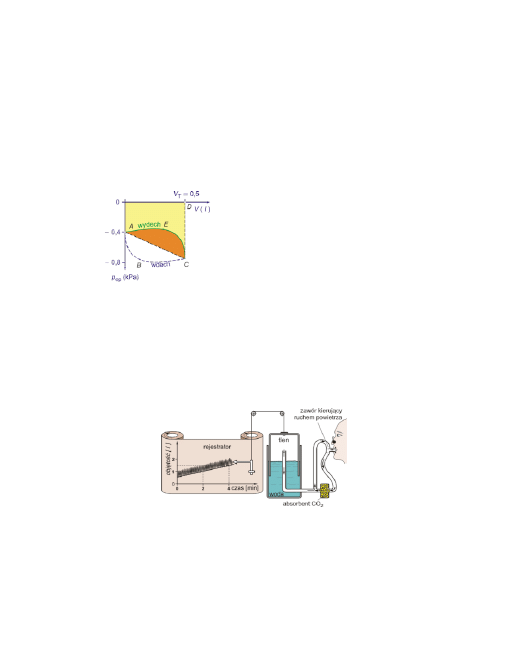
Pole ABCA oznacza pracę na pokonanie oporów niesprężystych przy wdechu.

10

Całkowita praca podczas wdechu wynosi zatem około

0,42 J,

z czego około

70 % zostaje zgromadzona w postaci energii potencjalnej sprężystości odkształconych
elementach sprężystych płuc.
Praca na pokonanie oporów niesprężystych (pole

ABCA

) - stanowi 30 % pracy przy wde-

chu, wynosi

około 0,12 J

z czego 25 % pracy całkowitej idzie na pokonanie oporów

powietrza a 5 % na pozostałe opory lepkościowe. Kosztem tej pracy wydziela się cie-
pło (około 0,12 J).
Podczas wydechu praca wykonywana jest przy rozluźnionych mięśniach oddechowych,
kosztem energii potencjalnej sprężystości nagromadzonej podczas wdechu.
Pole ACEA - ilustruje pracę na pokonanie oporów niesprężystych przy wydechu.

W jednym cyklu oddechowym wykonywana jest praca:

Przy wentylacji 8 l/min i objętości oddechowej 0,5 l,
jeden cykl oddechowy trwa około 3,75 s, to moc od-

dechowa wynosi około 0,54 J/3,45 s = 0,14 W.

Nie jest to oczywiście cała praca zużyta na proces od-
dychania - nie uwzględnialiśmy w rachunkach ruchów
klatki piersiowej i narządów w niej umieszczonych.



sp wdech

np wdech

np wydech

jeden cykl

0,3 J

0,12 J

0,12 J

0,54 J

W

W

W

W













Całkowitą pracę (względnie moc) zużytą przez mięśnie oddechowe można

obliczyć na postawie wydatku energetycznego przeznaczonego na ten cel - oblicza
się tak zwany

koszt tlenowy oddychania.

Mierzy się w tym celu, metodą respiracyj-

ną, nadwyżkę zużytego tlenu, ponad poziom spoczynkowy, przy oddychaniu wysiłko-
wym.

Schemat budowy spirografu. W czasie pomiaru zmniejsza się objętość tlenu w naczy-
niu, które zanurza się w wodzie. Rejestruje się zmiany położenia naczynia w funk-
cji czasu. Głębokość zanurzenia zbiornika jest proporcjonalna do objętości zużyte-
go tlenu.

11

Z takich pomiarów, poprzez ekstrapolację, można wyznaczyć zużycie tlenu

przy spokojnym oddychaniu. Przy wentylacji 8 l/min zużycie tlenu na oddychanie
wynosi około 4·10

-

2

l/min. Wartość energetyczna tlenu wynosi około 20 kJ/lO

2

. Za-

tem na oddychanie zużywana jest moc około 1,33 W z 80 W przemiany spoczynko-
wej.
Z powyższych danych wynika, że wydajność energetyczna mięśni oddechowych wyno-
si:

Podczas wysiłku fizycznego moc zużywana na oddychanie może wzrosnąć aż do 40 W.

pokonanie oporów sprężystych i niesprężystych tkanki płucnej i powietrza

układu oddechowego

zużuta na oddychanie

0,14 W

10 %

1,33 W

P

η

P







Wymiana gazowa

Jaki jest mechanizm przenikania tlenu do krwi i dwutlenku węgla do powie-

trza zawartego w pęcherzykach płucnych? Pęcherzyki płucne są oplecione gęstą sie-
cią naczyń włosowatych. Wymiana gazów pomiędzy powietrzem a krwią zachodzi
na drodze

dyfuzji.

Ważną rolę odgrywa rozpuszczalność gazów w krwi. Rozpuszczanie gazów w cieczy
podlega prawu Henry’ego:

gdzie:

c - oznacza

stężenie

rozpuszczonego gazu w cieczy i wyrażone jest stosunkiem ob-

jętości jaką zajmowałby rozpuszczony gaz V

g

w warunkach normalnych do ob-

jętości cieczy V

cieczy

,

p - ciśnienie cząstkowe gazu na cieczą,
α - współczynnik rozpuszczalności gazu zależny od rodzaju gazu i cieczy, w której

gaz jest rozpuszczany, temperatury (maleje ze wzrostem temperatury) oraz
od całkowitego ciśnienia.

g

cieczy

V

c

a p

V



 

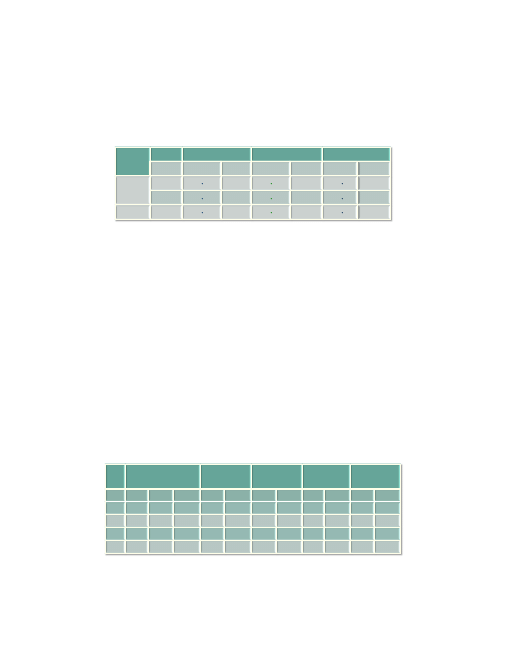
12

Tabela wartości współczynników rozpuszczalności

α

gazów oddechowych w wodzie

i osoczu.

W jednym litrze wody w temperaturze 20ºC rozpuszcza się:

V

g

=

3,06·10

-

7

Pa

-

1

·21000 Pa·1 l = 0,0064 l O

2

V

g

=

1,62·10

-

7

Pa

-

1

·79400 Pa·1 l = 0,0128 l N

2

Ciecz

T

O

2

N

2

CO

2

ºC

Pa

-1

atm

-1

Pa

-1

atm

-1

Pa

-1

atm

-1

Woda

20

3,06 10

-7

0,0310

1,62 10

-7

0,0164

86,6 10

-7

0,878

30

2,59 10

-7

0,0262

1,36 10

-7

0,0138

65,6 10

-7

0,665

Osocze

30

2,17 10

-7

0,0220

1,09 10

-7

0,0110

5,0 10

-7

0,511

Podczas wdechu do płuc dostaje się 0,5 l powietrza - z czego 0,12 l pozo-

staje w przestrzeni martwej (drogach oddechowych: tchawicy, oskrzelach, oskrze-
likach), pozostałe 0,38 l miesza się z powietrzem zawartym w przestrzeni czynno-
ściowej płuc. Zatem skład powietrza w pęcherzykach różni się od składu powietrza
atmosferycznego (więcej CO

2

mniej O

2

). Podobnie powietrze wydychane zmienia

skład w stosunku do pęcherzykowego (więcej O

2

mniej CO

2

).

W tabeli podano ciśnienia cząstkowe gazów w powietrzu atmosferycznym, pęche-
rzykowym, wydechowym oraz we krwi tętniczej i żylnej.

Gaz

Powietrze

atmosferyczne

Pęcherzyki

płucne

Gaz

wydychany

Krew
żylna

Krew

tętnicza

%

kPa

mm Hg

kPa

mm Hg

kPa

mm Hg kPa mm Hg

kPa

mm Hg

O

2

20,7

21,0

158

13,3

100

15,4

116

5,3

40

13,3

100

CO

2

0,04

0,04

0,3

5,3

40

4,3

32

6,1

46

5,3

40

N

2

78,4

79,4

596

76,4

573

75,3

565 76,4

573

76,4

573

H

2

O

0,75

0,76

5,7

6,3

47

6,3

47

6,3

47

6,3

47

13

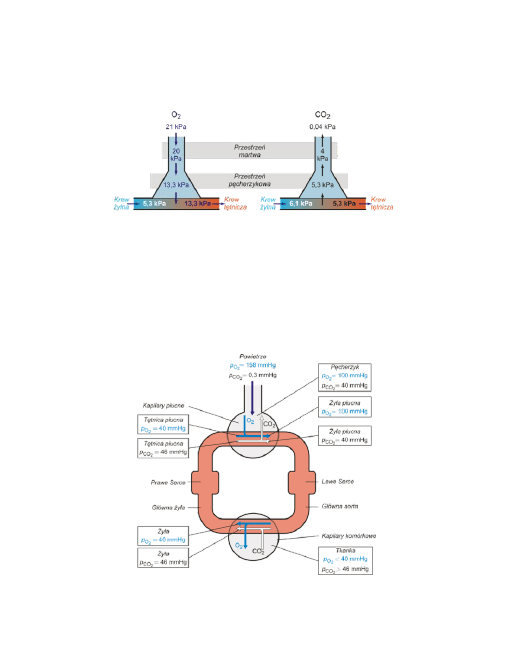
Porównanie ciśnień cząstkowych określa kierunek dyfuzji gazów oddecho-

wych. Kierunek wymiany gazowej zilustrowano schematycznie na poniższym rysun-
ku.

Schemat mechanizmu wymiany gazowej w pęcherzykach płucnych. Podano warto-
ści ciśnień cząstkowych tlenu i dwutlenku węgla w różnych miejscach dróg oddecho-
wych. Rysunek z lewej strony ilustruje wymianę tlenu, z prawej dwutlenku węgla.

Utrzymywanie dużej różnicy ciśnień cząsteczkowych tlenu w pęcherzykach

i krwi zapewnia ciągły przepływ krwi przez naczynia włosowate oraz obecność hemo-
globiny we krwi. Krew bez hemoglobiny musiałby przepływać strumieniem 75 razy
większym, aby zapewnić odpowiedni transport tlenu.

14

Z prawa dyfuzji przez błonę:

gdzie stężenia wyrażone są stosunkiem objętości gazu jaką zajmowałby w warun-
kach normalnych do objętości cieczy. Wtedy na podstawie prawa Henry'ego można
napisać:

gdzie

D

m

oznacza

zdolność dyfuzyjną

płuc.

Zdolność dyfuzyjna zależy od wielu czynników:

• właściwości błon,
• powierzchni,
• rozpuszczalności gazu.

Zdolność dyfuzyjna tlenu wynosi w warunkach spoczynkowych:

(2,5 ÷ 5,4)·10

-

3

cm

3

·Pa

-

1

·s

-

1

Przy wysiłku zdolność dyfuzyjna tlenu rośnie do:

(4,6 ÷ 7,0)·10

-

3

cm

3

·Pa

-

1

·s

-

1

Dla dwutlenku węgla zdolność dyfuzyjna jest 20 ÷ 30 większa (większa jest bowiem
rozpuszczalność dwutlenku w osoczu).

d

(

)

d

p

k

V

P S c

c

t

  



d

(

)

d

p

k

m

V

P S α p

p

t

D

   



