
Wykład 4
Weryfikacja modelu, cz. I

2
Procedura weryfikacji:
•
Dobro
ć
dopasowania do danych empirycznych
•
Istotno
ść
parametrów strukturalnych
•
Normalno
ść
, homoskedastyczno
ść
, brak autokorelacji
składników losowych
•
Dobór zmiennych obja
ś
niaj
ą
cych
•
Posta
ć
funkcyjna

3
Dopasowanie do danych empirycznych
Niech
t
0
1
t1
K
tK
t
Y
X
X
= β + β
+
+ β
+ ξ
= β + β
+
+ β
+ ξ
= β + β
+
+ β
+ ξ
= β + β
+
+ β
+ ξ
…
…
…
…
Załó
ż
my,
ż
e
i
b jest estymatorem
i
ββββ
(i
1,2,
,K
====
…
…
…
…
) uzyskanym MNK.
Wówczas
t
0
1
t1
K
tK
t
Y
b
b X
b X
u
=
+
+
+
+
=
+
+
+
+
=
+
+
+
+
=
+
+
+
+
…
…
…
…
,
t
u
– reszta
Dekompozycja ł
ą
cznej sumy kwadratów odchyle
ń
zm. obja
ś
nianej
od jej
ś
redniej
T
T
T
T
T
2
2
2
2
t
t
t
t
t
t
t
t 1
t 1
t 1
t 1
t 1
ˆ
ˆ
(Y Y)
(Y u
Y)
(Y Y)
u
2
(Y Y)u
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
−
=
+ −
=
−
+
+
−
−
=
+ −
=
−
+
+
−
−
=
+ −
=
−
+
+
−
−
=
+ −
=
−
+
+
−
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
Własno
ś
ci numeryczne estymatora MNK
T
t
t 1
u
0
====
====
∑
∑
∑
∑
,
T
tj
t
t 1
X u
0
(j 1,2,
,K)
====
=
=
=
=
=
=
=
=
∑
∑
∑
∑
…
…
…
…
4
Konsekwencje:
T
T
T
2
2
2
t
t
t
t 1
t 1
t 1
ˆ
(Y Y)
(Y Y)
u
=
=
=
=
=
=
=
=
=
=
=
=
−
=
−
+
−
=
−
+
−
=
−
+
−
=
−
+
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
TSS = ESS + RSS
(ł
ą
czna, wyja
ś
niona oraz resztowa suma kwa-
dratów)
Dziel
ą
c obustronnie przez TSS uzyskuje si
ę
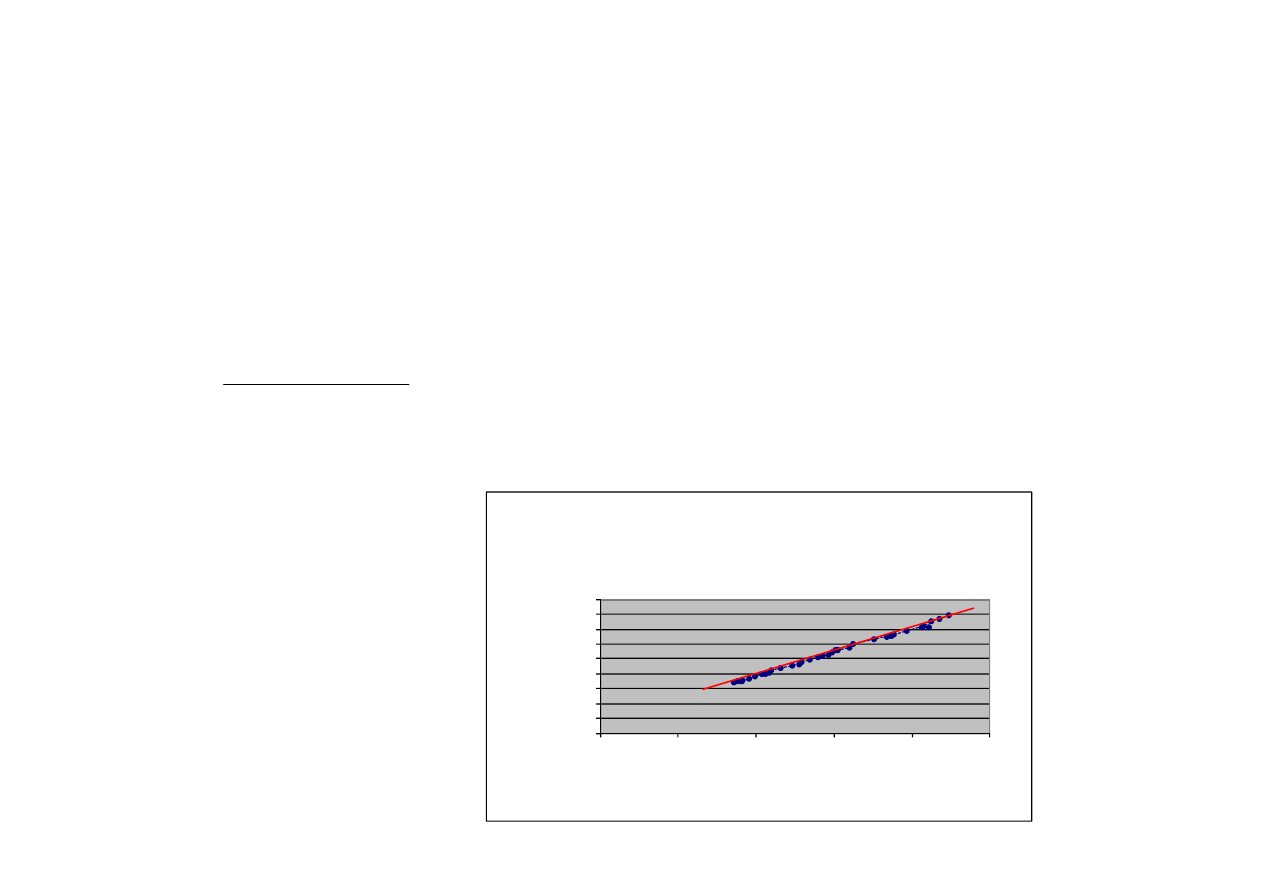
ESS
RSS
1
TSS
TSS
=
+
=
+
=
+
=
+
Wspołczynnik determinacji
2
ESS
R
TSS
====
Im wi
ę
kszy
2
R , tym lepsze dopasowanie
2
R
[0,1]
∈
∈
∈
∈
pod warunkiem,
ż
e w modelu wyst
ę
puje wyraz wolny
5
Obliczenia dla makroekonomicznej funkcji konsumpcji dla Wlk.
Brytanii
TSS=7228800000000
ESS=7210000000000
RSS=18800000
2
7210000000000
R
0,9973993
7228800000000
=
=
=
=
=
=
=
=
(interpretacja?)
(prawie doskonałe dopasowanie)
0
10000
20000
30000
40000
50000
60000
70000
80000
90000
0
20000
40000
60000
80000
100000
k
o
n
s
u
m
p
c
j
a
dochód
Dochód i konsumpcja w Wlk. Brytanii,
1948-1985 (mln Ł)
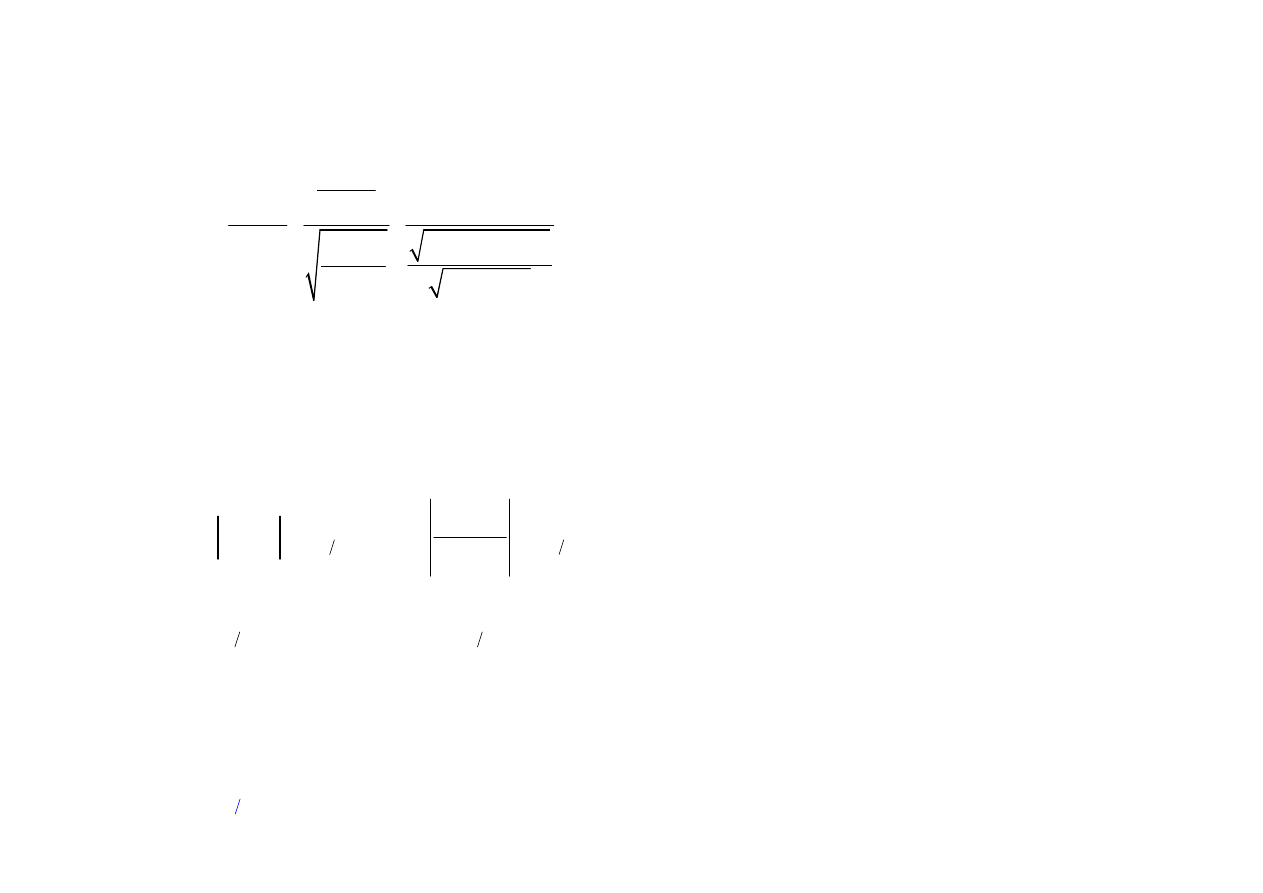
6
Istotno
ść
parametrów strukturalnych
(((( ))))
j
j
j
j
j
j
2
2
j
j
2
j
b
b
(b )
N 0,1
t(b )
~t[T (K 1)]
(j 0,1,2,
,K)
S(b )
S (b )
[T (K 1)]
(b )
T (K 1)
−β
−β
−β
−β
−β
σ
−β
σ
−β
σ
−β
σ
=
=
=
− +
=
=
=
=
− +
=
=
=
=
− +
=
=
=
=
− +
=
χ
− +
χ
− +
χ
− +
χ
− +
σσσσ
− +
− +
− +
− +
…
…
…
…
rozkład t-Studenta z T-(K+1) stopniami swobody
(1
) 100
− α ×
− α ×
− α ×
− α ×
% przedział ufno
ś
ci dla
j
ββββ
(((( ))))
j
j
j
2
2
j
b
Pr t b
t
Pr
t
1
S(b )
α
α
α
α
α
α
α
α
− β
− β
− β
− β
≤
=
≤
= − α
≤
=
≤
= − α
≤
=
≤
= − α
≤
=
≤
= − α
j
2
j
j
j
2
j
b
t
S(b )
b
t
S(b )
α
α
α
α
α
α
α
α
−
×
≤ β ≤
+
×
−
×
≤ β ≤
+
×
−
×
≤ β ≤
+
×
−
×
≤ β ≤
+
×
Interpretacja przedziału ufno
ś
ci?
j
b i
j
S(b ) s
ą
zmiennymi losowymi zanim próba zostanie wylosowana, zatem
j
2
j
b
t
S(b )
α
αα
α
±
×
±
×
±
×
±
×
– granice (losowe) przedziału ufno
ś
ci

7
Obliczenia dla makroekonomicznej funkcji konsumpcji dla Wlk. Brytanii
0
b
6969,3
====
0
S(b )
420,64
====
1
b
0,79251
====
1
S(b )
0,00675
====
T
(K
1)
38
2
36
−
+ =
− =
−
+ =
− =
−
+ =
− =
−
+ =
− =
0,05
α =
α =
α =
α =
0,025
t
(36)
2,03
====
0
6969,3
2,03 420,64
6969,3
2,03 420,64
−
×
≤ β ≤
+
×
−
×
≤ β ≤
+
×
−
×
≤ β ≤
+
×
−
×
≤ β ≤
+
×
0
6115, 4
7823,2
≤ β ≤
≤ β ≤
≤ β ≤
≤ β ≤
(interpretacja?)
1
0,79251 2,03 0,00675
0,79251 2,03 0,00675
−
×
≤ β ≤
+
×
−
×
≤ β ≤
+
×
−
×
≤ β ≤
+
×
−
×
≤ β ≤
+
×
1
0,77882
0,80621
≤ β ≤
≤ β ≤
≤ β ≤
≤ β ≤
(interpretacja?)
Załó
ż
my,
ż
e przypuszczasz, i
ż
0
6800
β =
β =
β =
β =
i
1
0,82
β =
β =
β =
β =
. Czy Twoje przypuszcze-
nie jest prawidłowe w
ś
wietle wyznaczonych przedziałów ufno
ś
ci dla parame-
trów strukturalnych?
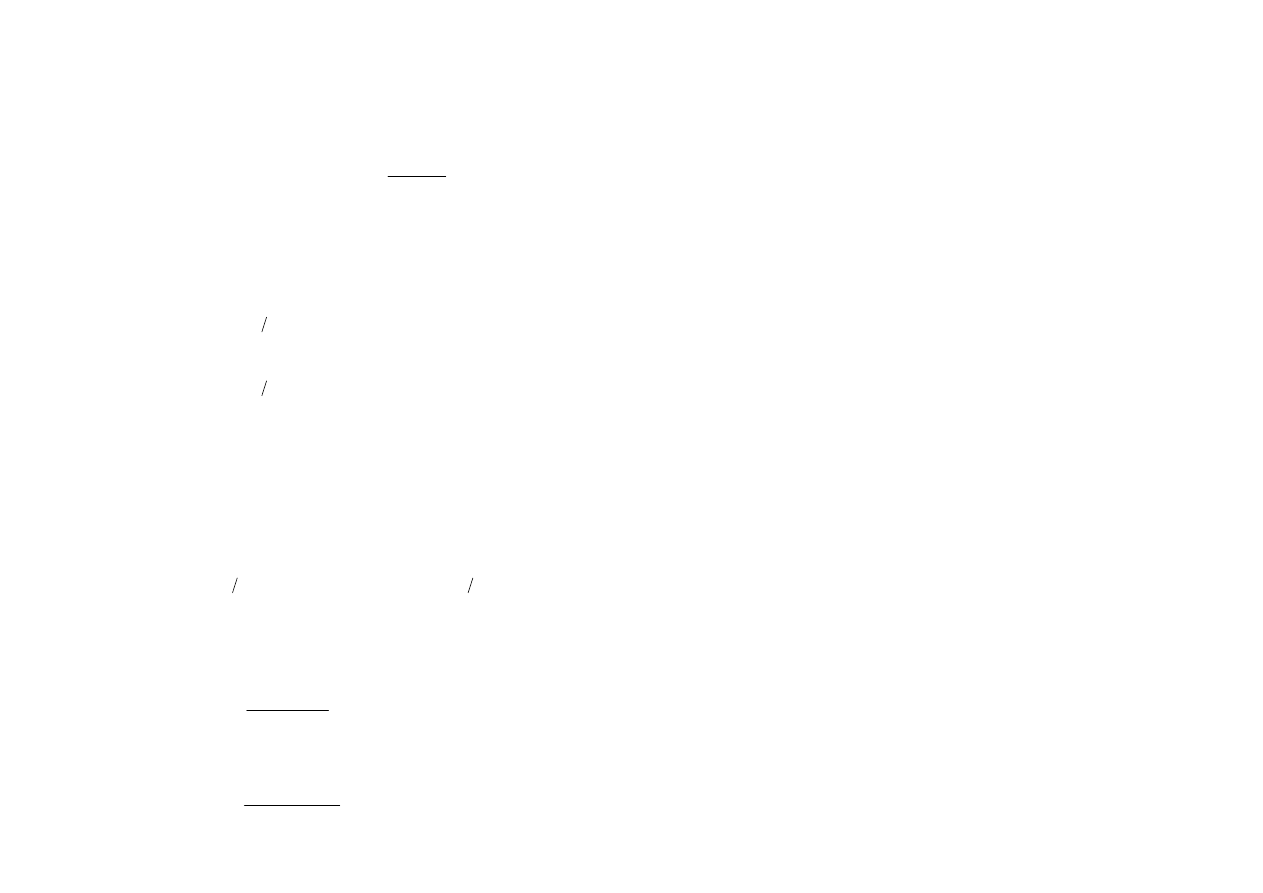
8
Testowanie hipotez
j
0
j
j
j
b
H :
0
t(b )
~ t[T
(K
1)]
S(b )
β =
β =
β =
β =
⇒
⇒
⇒
⇒
=
−
+
=
−
+
=
−
+
=
−
+
Reguła decyzyjna:
j
2
0
j
t(b )
t
[T
(K
1)]
H :
0
α
αα
α
≤
−
+
≤
−
+
≤
−
+
≤
−
+
⇒
⇒
⇒
⇒
β =
β =
β =
β =
,
j
2
A
j
t(b )
t
[T
(K
1)]
H :
0
α
αα
α
>
−
+
>
−
+
>
−
+
>
−
+
⇒
⇒
⇒
⇒
β ≠
β ≠
β ≠
β ≠
Naszkicuj obszar krytyczny i niekrytyczny; jaka jest ró
ż
nica pomi
ę
dzy obsza-
rem krytycznym/niekrytycznym a obszarem przyj
ę
cia/odrzucenia H
0
?
Wskazówka: niech
0
j
j
H :
β = β
β = β
β = β
β = β
ɶ
ɶɶ
ɶ
jest prawdziwa, zwró
ć
uwag
ę
na
j
2
j
j
j
2
j
t
S(b )
b
t
S(b )
α
α
α
α
α
α
α
α
β −
×
≤
≤ β +
×
β −
×
≤
≤ β +
×
β −
×
≤
≤ β +
×
β −
×
≤
≤ β +
×
ɶ
ɶ
ɶ
ɶ
ɶ
ɶ
ɶ
ɶ
Obliczenia, c.d.
0
A
6993,2
t(b )
16,568
2,03
H
420,64
=
=
>
=
=
>
=
=
>
=
=
>
⇒
⇒
⇒
⇒
1
A
0,79251
t(b )
117,491 2,03
H
0,00675
=
=
>
=
=
>
=
=
>
=
=
>
⇒
⇒
⇒
⇒
9
Testowanie hipotez, c.d.
Niech
t
0
1
t1
K
tK
t
Y
X
X
= β + β
+
+ β
+ ξ
= β + β
+
+ β
+ ξ
= β + β
+
+ β
+ ξ
= β + β
+
+ β
+ ξ
…
…
…
…
Jeste
ś
zainteresowany weryfikacj
ą
0
1
2
K
H :
β = β =
= β
β = β =
= β
β = β =
= β
β = β =
= β
…
…
…
…
wobec
A
j
H : przynajmniej jeden
0
β ≠
β ≠
β ≠
β ≠
Zwró
ć
uwag
ę
na
T
T
T
2
2
2
t
t
t
t 1
t 1
t 1
ˆ
u
(Y
Y)
(Y
Y)
=
=
=
=
=
=
=
=
=
=
=
=
=
−
−
−
=
−
−
−
=
−
−
−
=
−
−
−
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
oraz
T
T
2
2
t
t
t 1
t 1
u
(Y
Y)
=
=
=
=
=
=
=
=
=
−
=
−
=
−
=
−
∑
∑
∑
∑
∑
∑
∑
∑
pod warunkiem,
ż
e
0
H
jest prawdziwa
T
T
T
2
2
2
t
t
t
t 1
t 1
t 1
2
T
T
2
2
2
t
t
t 1
t 1
ˆ
(Y
Y)
(Y
Y)
u
T (K 1) R
K
K
F
~ F[K,T (K 1)]
K
1 R
u
u
T (K 1)
T (K 1)
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
−
−
−
−
−
−
−
−
−
−
−
−
− +
− +
− +
− +
=
=
=
− +
=
=
=
− +
=
=
=
− +
=
=
=
− +
−−−−
− +
− +
− +
− +
− +
− +
− +
− +
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
∑
Iloraz wariancji jest niski (wysoki) w wypadku, gdy
0
H jest prawdziwa (fał-
szywa)

10
Pr{F
F [K,T
(K
1)]}
α
αα
α
≥
−
+
= α
≥
−
+
= α
≥
−
+
= α
≥
−
+
= α
(narszkicuj)
Reguła decyzyjna
A
F
F [K,T
(K
1)]
H
α
αα
α
≥
−
+
≥
−
+
≥
−
+
≥
−
+
⇒
⇒
⇒
⇒
0
F
F [K,T
(K
1)]
H
α
αα
α
<
−
+
<
−
+
<
−
+
<
−
+
⇒
⇒
⇒
⇒
Alternatywne statystyki testowe:
Test LM (mno
ż
nka Lagrange’a) dla dodawanych zmiennych
t
0
1
t1
K
tK
t
Y
X
X
(R)
= β + β
+ + β
+ ξ
= β + β
+ + β
+ ξ
= β + β
+ + β
+ ξ
= β + β
+ + β
+ ξ
…
…
…
…
t
0
1
t1
K
tK
K 1
tK 1
K m
tK m
t
Y
X
X
X
X
(U)
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
= β + β
+
+ β
+ β
+
+ β
+ ξ
= β + β
+
+ β
+ β
+
+ β
+ ξ
= β + β
+
+ β
+ β
+
+ β
+ ξ
= β + β
+
+ β
+ β
+
+ β
+ ξ
…
…
…
…
…
…
…
…
0
K 1
K m
H :
0
+
+
+
+
+
+
+
+
β
=
= β
=
β
=
= β
=
β
=
= β
=
β
=
= β
=
…
…
…
…
,
A
K l
H : przynajmniej jeden
0
++++
β
≠
β
≠
β
≠
β
≠
(l
1,2,
,m
====
…
…
…
…
)
2
2
TR ~
(K)
χχχχ
(w du
ż
ych próbach)
Obliczenia dla makroekonomicznej funkcji konsumpcji
0,05
A
38
2 0,9973993
F
13806, 426
4,11 F
(1,36)
H
1
1 0,9973993
−−−−
=
=
>
=
=
=
>
=
=
=
>
=
=
=
>
=
⇒
⇒
⇒
⇒
−−−−
2
2
0,05
A
TR
38 0,9973993
37,901
3,84
(1)
H
=
×
=
>
= χ
=
×
=
>
= χ
=
×
=
>
= χ
=
×
=
>
= χ
⇒
⇒
⇒
⇒

11
Test Walda
t
0
1
t1
m
tm
t
Y
X
X
(R)
= β + β
+ + β
+ ξ
= β + β
+ + β
+ ξ
= β + β
+ + β
+ ξ
= β + β
+ + β
+ ξ
…
…
…
…
t
0
1
t1
m
tm
m 1
tm 1
K
tK
t
Y
X
X
X
X
(U)
+
+
+
+
+
+
+
+
= β + β
+ + β
+ β
+ + β
+ ξ
= β + β
+ + β
+ β
+ + β
+ ξ
= β + β
+ + β
+ β
+ + β
+ ξ
= β + β
+ + β
+ β
+ + β
+ ξ
…
…
…
…
…
…
…
…
0
m 1
K
H :
0
++++
β
=
= β =
β
=
= β =
β
=
= β =
β
=
= β =
…
…
…
…
,
A
m l
H : przynajmniej jeden z
0
++++
β
≠
β
≠
β
≠
β
≠
(l
1,2,
,m
====
…
…
…
…
)
2
2
R
U
R
U
R
U
U
R
2
U
U
U
U
(RSS
RSS ) /(df df )
(RSS
RSS ) /(K m)
(R
R ) /(K m)
F
~ F[K m,T (K 1)]
RSS / df
RSS /[T (K 1)]
(1 R ) /(T (K 1)]
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
=
=
=
−
− +
=
=
=
−
− +
=
=
=
−
− +
=
=
=
−
− +
− +
−
− +
− +
−
− +
− +
−
− +
− +
−
− +
12
Wydruk z Microfita – wyniki estymacji i weryfikacji modelu
Ordinary Least Squares Estimation
*******************************************************************************
Dependent variable is C
38 observations used for estimation from 1948 to 1985
*******************************************************************************
Regressor Coefficient Standard Error T-Ratio[Prob]
ST 6969.3 420.4459 16.5760[.000]
Y .79251 .0067438 117.5173[.000]
*******************************************************************************
R-Squared .99740 R-Bar-Squared .99733
S.E. of Regression 722.3114 F-stat. F( 1, 36) 13810.3[.000]
Mean of Dependent Variable 54421.4 S.D. of Dependent Variable 13973.0
Residual Sum of Squares 1.88E+07 Equation Log-likelihood -303.0257
Akaike Info. Criterion -305.0257 Schwarz Bayesian Criterion -306.6633
DW-statistic .71210
*******************************************************************************

13
Prosz
ę
wykona
ć
odpowiednie obliczenia dla modelu cen domów jednorodzinnych w mia-
steczku uniwersyteckim San Diego oraz modelu wydatków na ochron
ę
zdrowia w USA!
Wyszukiwarka
Podobne podstrony:
ekonometria W4
Metody analiz?ektywności ekonomicznej W4
ekonomika w4
Ekonomia Drdrozdrowski, w4
W4, Naika, stomatologia, Zarządzanie i ekonomika
W4 E, Ekonometria
Ekonomia Drdrozdrowski w4
EKONOMIKA MIAST I REGIONÓW W4
W4 Proces wytwórczy oprogramowania
W4 2010
Statystyka SUM w4
w4 3
Spoleczno ekonomiczne uwarunkowania somatyczne stanu zdrowia ludnosci Polski
Ekonomia konspekt1
EKONOMIKA TRANSPORTU IX
Ekonomia II ZACHOWANIA PROEKOLOGICZNE
więcej podobnych podstron