
GRUNTY BUDOWLANE
Grunt budowlany (w skrócie „grunt”) – część skorupy ziemskiej:
• współpracująca z obiektem budowlanym,
• stanowiąca jego element,
• służąca jako tworzywo do wykonania z niego budowli ziemnych.
Grunt składa się z trzech faz:
• stałej – tzw. szkieletu gruntowego – oddzielnych ziaren i cząstek,
tworzących porowaty układ,
• ciekłej – wody wypełniającej pory:
o
całkowicie – w strefie poniżej poziomu wód gruntowych (w tzw.
strefie saturacji)
o
częściowo – woda zawieszona lub wilgotność występująca powyżej
poziomu wód gruntowych (w tzw. strefie aeracji),
• gazowej – powietrza wypełniającego pory w strefie aeracji.
Grunt naturalny – grunt, którego szkielet powstał w wyniku procesów
geologicznych – np. wietrzenia, erozji i sedymentacji w wyniku procesów eolicznych
(działanie wiatru) i fluwialnych (działanie płynącej wody).
Rozróżniamy trzy rodzaje gruntów naturalnych:
• skaliste – zbudowane z litych lub spękanych bloków o minimalnych
wymiarach > niż 10 cm,
• nieskaliste mineralne – zawartość części organicznych (roślinnych i
zwierzęcych) < niż 2 %
• nieskaliste organiczne - zawartość części organicznych > niż 2 %
Grunt antropogeniczny – grunt nasypowy powstały z produktów gospodarczej i
przemysłowej działalności człowieka (np. odpadów komunalnych, gruzu
budowlanego, pyłów dymnicowych, odpadów poflotacyjnych, odpadów z przerobu
surowców mineralnych itp.) występujący w wysypiskach, zwałowiskach (hałdach),
osadnikach oraz niektórych budowlach ziemnych.
Szkielet gruntowy składa się ziaren i cząstek różnego kształtu i wielkości, które
charakteryzuje tzw. średnica zastępcza:
• ziarna
mają średnicę zastępczą d > 0,05 mm
• cząstki mają średnicę zastępczą d ≤ 0,05 mm
Ziarna i cząstki gruntu dzielimy według wielkości na grupy zwane frakcjami.
Nazwa frakcji
Symbol
Zakres średnic zastępczych d
(mm)
Kamienista
f
k
d > 40
Żwirowa
f
ż
40 ≥ d > 2
Piaskowa
f
p
2 ≥ d > 0,05
Pyłowa
f
π
0,05 ≥ d > 0,002
Iłowa
f
i
0,002 ≥ d
Do oznaczenia uziarnienia gruntu stosuje się metody:
• sitową – stosowaną dla gruntów piaszczystych i żwirowych,
• areometryczną, dla gruntów zawierających dużą ilość cząstek mniejszych
o d < 0,07 mm.
W metodzie sitowej średnicą zastępczą ziarna jest średnica oczka sita przez które
przechodzi dana cząstka. Metoda ta polega na:
• przesiewaniu próbki gruntu przez zestaw sit o różnych wymiarach oczek,
• oznaczeniu
ciężaru cząstek zatrzymanych na poszczególnych sitach,
• określeniu ich procentowego udziału w wadze całej próbki,
• sporządzeniu krzywej uziarnienia gruntu
Z krzywej przesiewu można określić:
• średnicę przeciętną (miarodajną) d
50
– średnica charakterystyczna, która
wraz z ziarnami większymi stanowi wagowo 50 % próbki;
• zawartość poszczególnych frakcji;
• wskaźnik uziarnienia
10
60
d
d
u
=
.
Gdy u ≤ 5 grunt jest równomiernie uziarniony.
Średnice d
60
i d
10
są ziarnami, które wraz z większymi stanowią odpowiednio
60% i 10% wagi próbki.
Klasyfikacja gruntów
Rodzaj gruntu określa się na podstawie procentowej zawartości poszczególnych
frakcji oraz dodatkowych kryteriów:
• wielkości średnic charakterystycznych d
50
(d
90
)
• wskaźnika plastyczności gruntu I
p
Wskaźnik plastyczności I
p
pokazuje, jaką ilość wody (w procentach)
wchłania grunt przy przejściu ze stanu półzwartego w płynny.
Na podstawie tego wskaźnika grunty dzielimy na:
• niespoiste (sypkie) – gdy I
p
≤ 1 %
• spoiste – gdy I
p
> 1 %
Przy ustalaniu rodzaj gruntu wykorzystuje się:
• zestawienia
tabelaryczne
• wykres w postaci tzw. trójkąta Fereta
Trójkąt Fereta pozwala na określenie rodzaju gruntu, w którym frakcja żwirowa
stanowi f
ż
< 10 %.
Cechy fizyczne gruntów
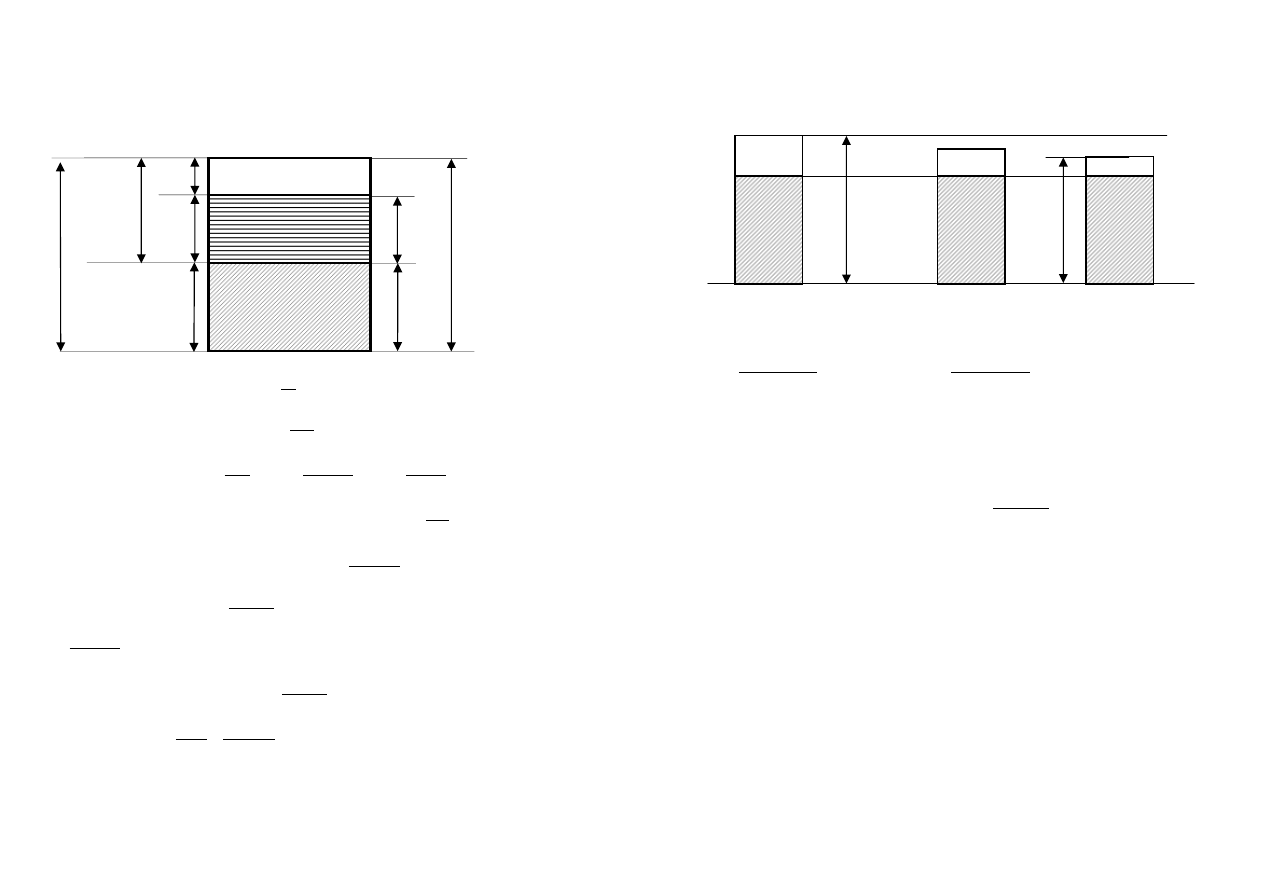
Zależności objętościowe i wagowe poszczególnych faz gruntu
Objętość (cm
3
)
Masa (g)
V
p
powietrze
V
porów
V
w
woda
M
w
V
M
V
s
szkielet gruntowy
M
s
Gęstość objętościowa (g/cm
3
)
V
M
=
ρ
Gęstość właściwa (g/cm
3
)
s
s
s
V
M
=
ρ
Wilgotność gruntu (%)
100
100
M
M
M
100
M
M
w
s
s
s
s
s
w
×
ρ
ρ
−
ρ
=
×
−
=
×
=
Gęstość objętościowa szkieletu gruntowego (g/cm
3
)
V
M
s
d
=
ρ
lub
po
wprowadzeniu odpowiednich zależności
100
w
100
d
×
+
ρ
=
ρ
Porowatość gruntu (-)
V
V
n
porów
=
lub po wprowadzeniu odpowiednich zależności
s
d
s
n
ρ
ρ
−
ρ
=
Wskaźnik porowatości (-)
s
porów
V
V
e
=
lub po wprowadzeniu odpowiednich
zależności
d
d
s
n
1
n
e
ρ
ρ
−
ρ
=
−
=
Stopień zagęszczenia gruntów piaszczystych I
D
(-) – jest to stosunek zagęszczenia
istniejącego w naturze do największego możliwego zagęszczenia danego gruntu.
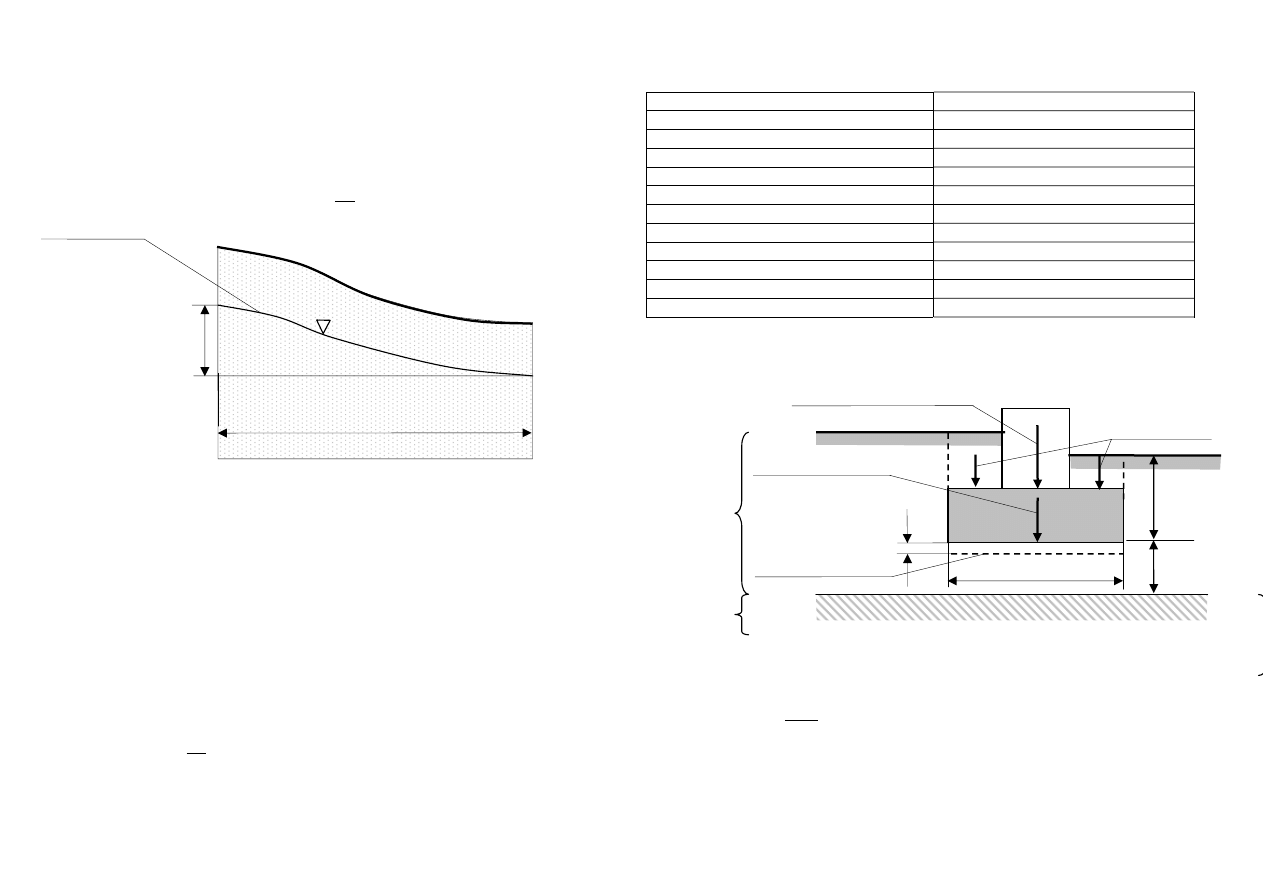
a)
b)
c)
V
porów
V
s
V
max
V
V
min
a) objętość próbki piasku najbardziej luźnego
b) objętość próbki piasku w naturze
c) objętość próbki piasku najbardziej zagęszczonego
min
max
max
D
V
V
V
V
I
−
−
=
lub
min
max
max
D
e
e
e
e
I
−
−
=
Zależnie od stopnia zagęszczenia grunty sypkie mogą być w stanie:
• I
d
≤ 0,33 – luźnym
• 0,33 < I
d
≤ 0,67 – średnio zagęszczonym
• 0,67 < I
d
≤ 1,0 – zagęszczonym
Stopień plastyczności gruntów spoistych I
L
(-):
p
L
p
L
w
w
w
w
I
−
−
=
gdzie:
w – wilgotność naturalna (%)
w
p
– wilgotność na granicy plastyczności (%)
w
L
– wilgotność na granicy płynności (%)
W zależności od stopnia plastyczności grunty spoiste mogą być w stanie:
• I
L
< 0 – zwartym lub półzwartym
• 0 < I
L
≤ 0,25 – twardoplastycznym
• 0,25 < I
d
≤ 0,50 – plastycznym
• 0,50 < I
d
≤ 1,0 – miękkoplastycznym
• I
L
> 1,0 – płynnym
Współczynnik filtracji k (cm/s, m/dobę) – jest miarą wodoprzepuszczalności
gruntu:
J
k
V
⋅
=
gdzie:
V – prędkość filtracji (przepływu wody w gruncie) (cm/s, m/dobę),
k – współczynnik filtracji (cm/s, m/dobę)
J – spadek hydrauliczny (-)
L
h
J
Δ
=
poziom wody
gruntowej
Δh
L
Wartość wsp. filtracji
k określa się na podstawie:
• badań terenowych lub laboratoryjnych,
• wzorów
empirycznych,
• orientacyjne
wartości – z tabel.
Przykładowe wzory empiryczne:
2
•
(
d
50
d
357
,
0
k
⋅
=
50
w mm,
k w cm/s)
•
(cm/s)
2
10
1
d
C
k
⋅
=
dla średnicy charakterystycznej
d
10
= 0,1 ÷ 3,0 mm i gruntów
równomiernie uziarnionych:
C
1
= 1,39 dla
u = 1
C
1
= 0,925 dla
u = 1 ÷ 4
C
1
= 0,463 dla
u = 4 ÷ 5
•
6
2
10
45
n
d
150
k
⎟
⎠
⎞
⎜
⎝
⎛
⋅
=
(
d
10
w mm,
k w m/dobę)
n – porowatość gruntu (%)
Orientacyjne wartości współczynników filtracji k
Rodzaj gruntu
k (cm/s)
Żwir
10 – 10
-1
Piasek gruby i średni 10
-1
– 10
-2
Piasek drobny
10
-2
– 10
-3
Piasek pylasty
10
-3
– 10
-4
Pył 10
-4
– 10
-6
Glina 10
-6
– 10
-8
Glina zwięzła 10
-7
– 10
-9
Ił 10
-9
– 10
-10
Torf słabo rozłożony 5·10
-3
– 10
-4
Torf średnio rozłożony 5·10
-4
– 10
-5
Torf silnie rozłożony 2·10
-4
– 10
-6
Wytrzymałość gruntów
Obciążenie od konstrukcji
Q
k
Ciężar gruntu
Ciężar fundamentu
Q
1
Q
2
h
D
Grunt 1
Osiadanie
s
Q
f
Poziom
fundamentu
B
h
i
po osiadaniu
Grunt 2
Wytrzymałość gruntów charakteryzuje:
• moduł ściśliwości M
o
(kPa) – wyraża podatność gruntu na osiadanie pod
wpływem obciążenia:
dop
o
i
s
M
h
s
≤
⋅
σ
=
gdzie:
s – osiadanie budowli, (cm),
s
dop
= 5 ÷ 15 cm – osiadanie dopuszczalne zależne od rodzaju
konstrukcji,
h
i
– grubość warstwy gruntu (cm),
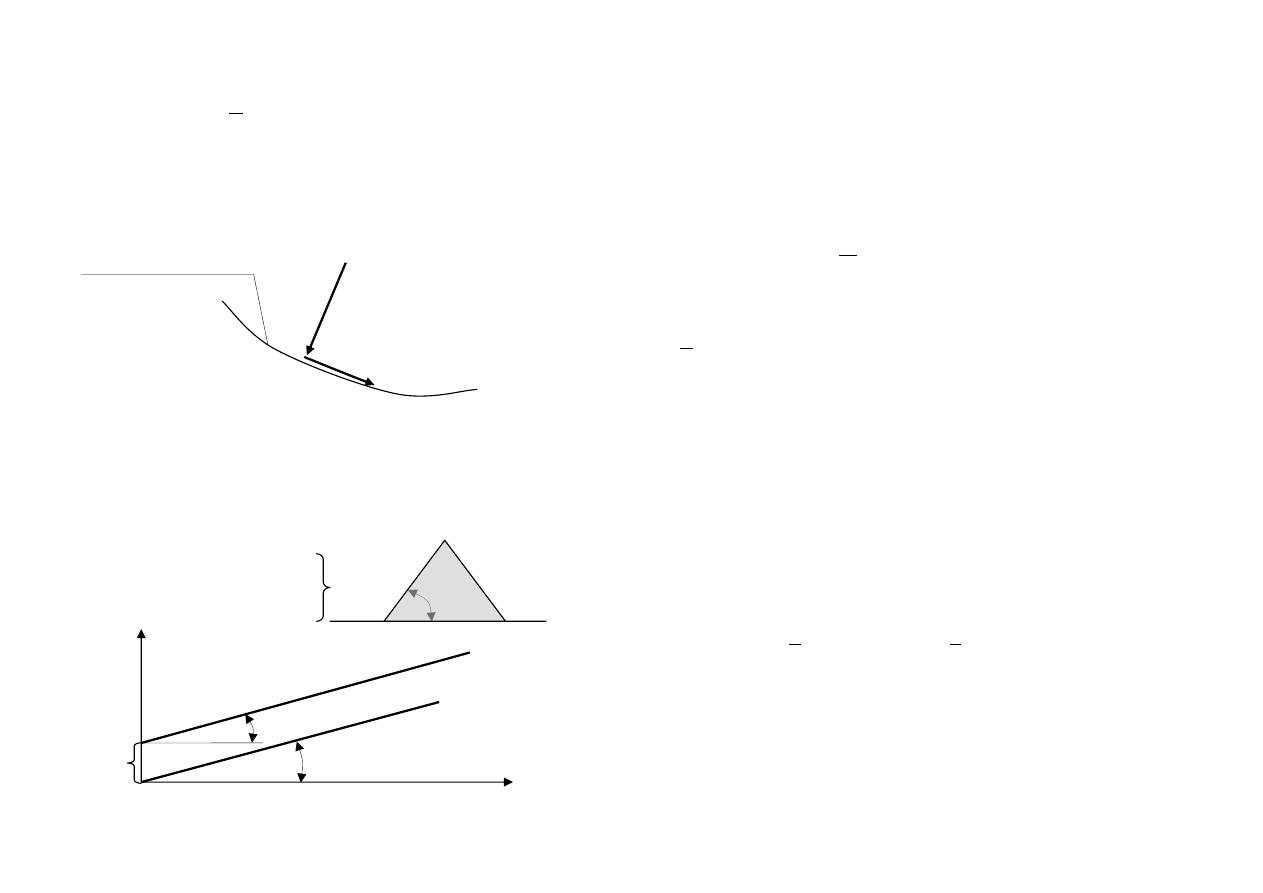
σ – naprężenie (kPa) w gruncie na poziomie posadowienia:
A
Q
=
σ
Q – Nacisk pionowy fundamentu (kN):
Q = Q
k
+ Q
f
+ Q
1
+ Q
2
A = B L – powierzchnia fundamentu (m
2
),
B – szerokość, L – długość fundamentu.
• Naprężenie styczne τ – powstające na płaszczyźnie poślizgu:
Płaszczyzna poślizgu
σ
τ
Naprężenie styczne τ (kPa):
c
tg
+
ϕ
⋅
σ
=
τ
gdzie:
σ – składowa normalna naprężenia, (kPa) – prostopadła do płaszczyzny poślizgu,
tgφ – tangens kąta tarcia wewnętrznego gruntu, (-),
c – spójność gruntu (kohezja), (kPa) – charakteryzuje siłę wzajemnego
przyciągania się cząstek gruntu.
Kąt tarcia wewnętrznego dla gruntów nie-
spoistych jest równy kątowi stoku natura-
lnego
φ
n
– kąt pod jakim utrzymuje się
φ = φ
n
skarpa luźno usypanej pryzmy gruntu.
τ (kPa)
grunt
spoisty
c
tg
+
ϕ
⋅
σ
=
τ
φ
grunt niespoisty
ϕ
⋅
σ
=
τ
tg
c
φ
σ (kPa)
Wartości
φ i c zależą od:
• rodzaju gruntu – (spoisty, niespoisty),
• pochodzenia geologicznego – dotyczy gruntów spoistych (np. gliny
morenowe, iły trzeciorzędowe),
• stopnia
zagęszczenia gruntu niespoistego
I
D
,
• stopnia
plastyczności gruntu spoistego
I
L
,
Warunki graniczne na poziomie posadowienia – takie warunki przy których nie
nastąpi wyparcie gruntu spod fundamentu – brak poślizgu fundamentu:
F
q
f
≤
σ
gdzie:
σ – naprężenie (kPa) w poziomie posadowienia od sił działających na fundament
i ciężaru fundamentu
A
Q
=
σ
Q – Nacisk pionowy fundamentu (kN), Q = Q
k
+ Q
f
+ Q
1
+ Q
2
A = B · L – powierzchnia fundamentu (m
2
),
B – szerokość, L – długość fundamentu.
q
f
– obciążenie graniczne gruntu pod fundamentem, (kPa),
F = 2÷3 – współczynnik pewności (bezpieczeństwa).
Obciążenie graniczne
q
f
(kPa) dla gruntu jednorodnego pod fundamentem
obliczamy ze wzoru:
γ
⋅
⋅
γ
⋅
+
⋅
⋅
γ
+
⋅
⋅
=
N
B
a
N
h
N
c
a
q
2
q
D
c
1
f
gdzie:
c – spójność gruntu, (kPa),
N
c
, N
q
, N
γ
– współczynniki wytrzymałości gruntu zależne od kąta tarcia
wewnętrznego
φ
g
⋅
ρ
=
γ
- ciężar objętościowy gruntu (kN/m
3
), ρ – gęstość objętościowa (t/m
3
),
g =
9,81 m/s
2
,
a
1
, a
2
– współczynniki zależne od wymiarów fundamentu:
⎟
⎠
⎞
⎜
⎝
⎛ +
=
L
B
3
,
0
1
a
1
⎟
⎠
⎞
⎜
⎝
⎛ −
=
L
B
2
,
0
1
a
2
B – szerokość, L – długość fundamentu

Zakres i zadania przedmiotu „mechanika górotworu”. Górotwór jako ośrodek materialny w
polu grawitacyjnym ziemskim (2);
Górotwór jako ośrodek 1-fazowy stały. Modele górotworu. Pierwotny stan naprężenia i
odkształcenia górotworu. Pierwotne naprężenie pionowe i poziome (boczne). Współczynnik
rozporu bocznego. Zależność składowych pierwotnego stanu naprężenia i odkształcenia
górotworu od głębokości (2);
Klasyfikacja struktur górotworu. Stosowanie zasady de Saint Venanta w mechanice
górotworu. Założenie pierwotnego stanu naprężenia górotworu przez wykonanie wyrobiska.
Wnioski ogólne (2);
Stan naprężenia górotworu w otoczeniu nieobudowanych wyrobisk korytarzowych.
Rozwiązanie Kirscha dla wyrobiska o przekroju kołowym (2);
Rozkład naprężeń w otoczeniu wyrobiska korytarzowego o przekroju kołowym. Zależność
od głębokości. Naprężenia i przemieszczenia przy ciśnieniu wewnętrznym na konturze
przekroju wyrobiska (4);
Wyrobisko korytarzowe o przekroju prostokątnym. Rozwiązanie Sawina i Morgajewskiego.
Wyrobisko korytarzowe o przekroju eliptycznym (tunelowym) (2);
Teoria sklepienia ciśnień. Rozwiązanie Sałustowicza. Sklepienie ciśnień. Strzałka sklepienia.
Strefa spękań (odprężona) (2);
Obciążenie statystyczne obudowy wyrobisk korytarzowych. Teoria Sałustowicza. Teoria
Protodiakonowa. Teoria Cymbariewicza. Teoria Bierbaumera (4);
Obciążenie deformacyjne obudowy wyrobisk korytarzowych. Współczynniki współdziałania
obudowy z otaczającym górotworem (statyczny, dynamiczny. Obciążenie deformacyjne w
górotworze typu „Maxwell” oraz „standard”. Opóźnienie obudowy. Przebudowa wyrobiska
(4);
Obciążenie obudowy szybów i innych wyrobisk pionowych w górotworze uwarstwionym.
Głębokość krytyczna (2);
Stan przemieszczenia i naprężenia górotworu w otoczeniu wyrobisk niestacjonarnym ociosie
(eksploatacyjnych). Teoria fali ciśnień. Ciśnienie eksploatacyjne (2);
Wstrząsy górotworu i tąpnięcia. Hipocentrum i epicentrum. Energia sejsmiczna wstrząsu.
Przyspieszenie gruntu (2);
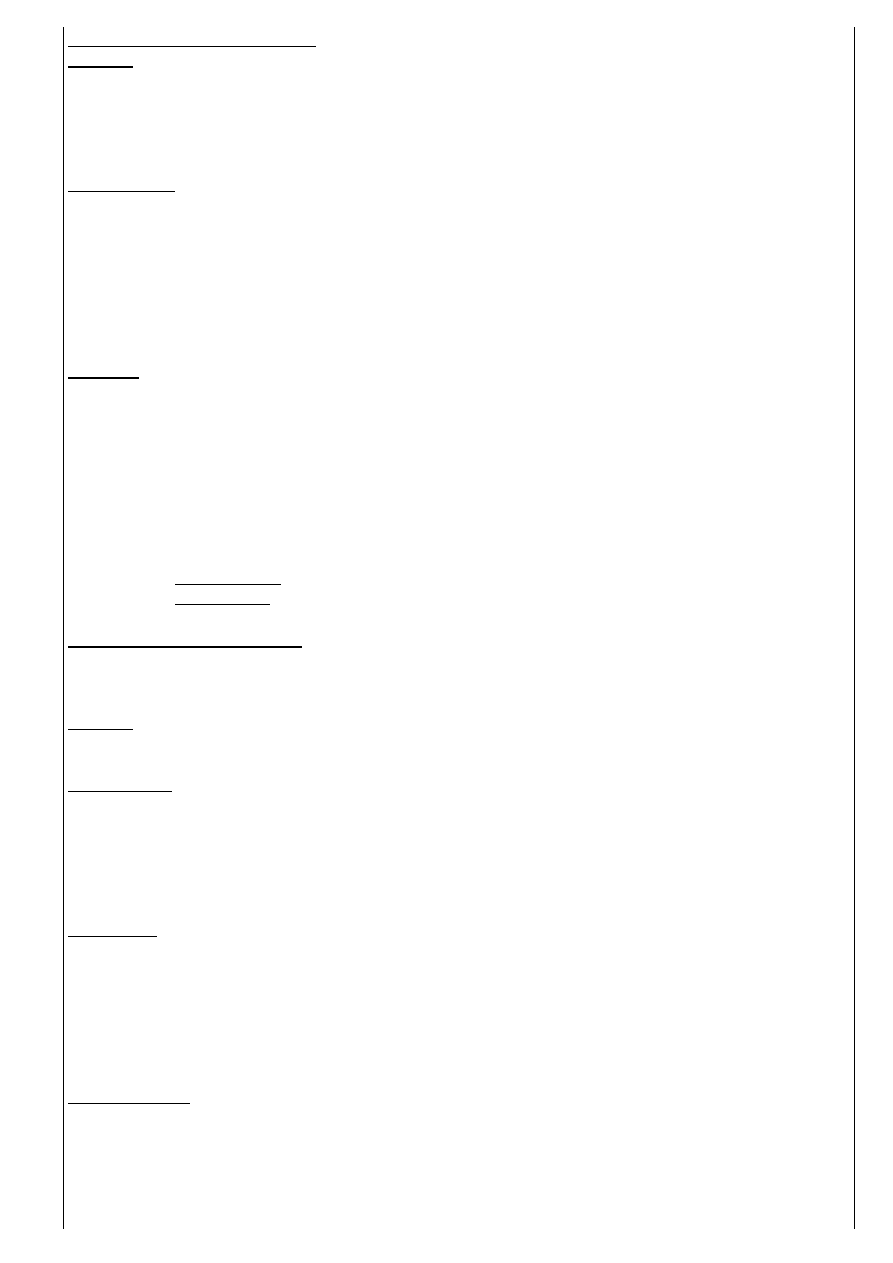
4.Cechy strukturalne górotworu
Ciągłość
Środowisko materialne będzie środowiskiem ciągłym, jeżeli dla dwóch bliskich jego punktów (cząstek)
różnica własności fizycznych tego środowiska będzie dowolnie mała. Najczęściej pojęcie ciągłości odnosi
się do rozmieszczenia masy wewnątrz obszaru zajmowanego przez dane środowisko. Ciało spełniające w
dużym stopniu postulat ciągłości masy me musi jednocześnie spełniać postulatu ciągłości innych własności
fizycznych, np. własności wytrzymałościowych
Jednorodność
Ciało materialne jest jednorodnym, jeżeli w każdym punkcie jego własności będą takie same. W
odniesieniu do ośrodka skalnego oprócz pojęcia jednorodności stosuje się również pojęcie tzw. statystycznej
jednorodności.
Środowisko materialne jest statystycznie jednorodne, jeżeli jego każda podstawowa objętość — o
rozmiarach wynikających z przyjętej skali rozważań — posiada jednakowe własności fizyczne
Ziarno mineralne posiadające strukturę krystaliczną może być uznane za ciało prawie doskonale
statystycznie jednorodne, jeżeli za podstawową objętość przyjmie się układ cząstek wielokrotnie
powtarzający się w sieci krystalicznej.
Izotropia
Ciało materialne jest izotropowe, gdy we wszystkich kierunkach badania wykazuje jednakowe wartości
własności fizycznych. Gdy ośrodek wykazuje różne wartości własności fizycznych w różnych kierunkach,
wtedy jest anizotropowy
Dla oceny stopnia anizotropii wprowadza się pojecie współczynnika anizotropii. Współczynnik ten jest
stosunkiem wartości największej do wartości najmniejszej danej wielkości fizycznej. Dla ciał izotropowych
wartość współczynnika anizotropii wynosi 1, a dla anizotropowych jest większa od 1. Izotropowe są gazy,
ciecze Jednorodne substancje bezpostaciowe (szkło wulkaniczne, opal), a anizotropowe są kryształy —
dzięki uporządkowanej sieci krystalicznej. Skały posiadają na ogół własności anizotropowe, przy czym
wyróżnia się:
- anizotropie syngenetyczną — związaną z warunkami powstawania złóż skalnych;
- anizotropie epigenetyczną — powstała w późniejszych okresach w wyniku
działania sił tektonicznych lub zjawisk metamorficznych
Cechy strukturalne górotworu
Rozpatrując rzeczywista. budowę wewnętrzną skal należy oprócz wymienionych cech strukturalnych
określić również cechy teksturalne związane ze stopniem wypełnienia przestrzeni zajmowanej przez skałę.
Do cech tekstury zalicza się lupność(cios, kliważ), uwarstwienie, porowatość szczelinowatość
Lupność
Lupność jest zdolnością skał do łatwiejszego pękania wzdłuż określonego układu płaszczyzn, w których
występuje osłabiona spójność między ziarnami. Lupność jest jedną z najistotniejszych cech skat osadowych
Uwarstwienie skał uwarunkowane jest kolejnością, powstawania nakładających się utworów skalnych o
różnym składzie chemicznym i mineralnym, różnej ziarnistości i różnej orientacji ziarn.,
Ukształtowanie powierzchni osłabionej spójności skały, przede wszystkim zaś wzajemne ich odległości, są
na ogól różne dla różnych skał. Na podstawie przeprowadzonych pomiarów i obserwacji można stwierdzić,
ze przeciętna grubość warstw skał karbońskich ("średnia warstwowa podzielność skał") wzrasta kolejno dla
skał ilastych, mutowców i piaskowców, a odpowiednie wartości przedstawiają się następująco: 20,7 cm,
28,7 cm, 40,1 cm
Porowatosć
Porowatość jest wynikiem występowania w skalach pustek i szczelin oraz istnienia miedzy ziarnami
mineralnymi drobnych kanalików i wolnych przestrzeni, czyli porów nawet w przypadku występowania
materiału cementującego te ziarna.
Jeżeli wolne przestrzenie istniejące w skalach łączą się ze sobą i z zewnętrzną powierzchnią skały to skala
ma porowatosc otwartą
Przy porowatości zamkniętej pory nie są połączone ze sobą. Porowatość tzw. ogólną określa się stosunkiem
objętości wszystkich wolnych przestrzeni w skale do jej objętości.
Szczelinowatość — jest wynikiem procesów tektonicznych i fizyczno-che-micznych zachodzących w
ośrodku skalnym. Pod pojęciem szczelinowatości skały rozumie się istnienie w jej budowie nieciągłości i
powierzchni osłabienia o zasiegu przewyższającym wymiary ziam minerałów tworzących masyw skalny
Spośród powierzchni szczelin przecinających górotwór wydzielić można szczeliny pierwotne i wtórne.
Szczelinowatość pierwotna wystepuje w skalach o nienaruszonej strukturze, to znaczy w obszarach gdzie
nie zaznaczyl się jeszcze wpływ dziatalnosci górniczej lub budowlanej. Szczeliny wtorne wiaza sie z
dzialalnoscią gornicza, a powstaja przede wszystkim w stropach wyrobisk gómiczych. Ilościowo

szczelinowatosc okresia sie rozmiarami szczelin, gęstoscia. ich wystepowania oraz wzajemnym ich
usytuowaniem
5. Skały jako ośrodki 3- fazowe
Cieczą zawartą w określonych ilościach w każdej prawie skale jest woda. Ze względu na rodzaj więzi
laczacej cząstki wody z faza. stałą wyroznia się w skatach:
— wodę chemicznie zwiazana,;
— wodę fizycznie związana;
— wodę swobodną (wolna).
Woda chemicznie związana jest cześcią sieci krystalicznej ziarn mineralnych, gdzie czasteczki wystepują
razem z innymi molekulami i jonam usuniecie tej wody prowadzi do rozkładu danego materiału i do
przekształcenia go w inny odrębny
związek chemiczny.
Woda fizycznie związana
przylega ścisle do powierzchni ziarn mineralnych, przytrzymywana miedzyczasteczkowymi silami
przyciagania. Otacza ona ziarna cienką blonka, zwana jest więc wodą blonkową
Woda swobodna — wypełnia wolne przestrzenie porow i szczelin w skale. Na wodę swobodną sklada sie
tzw.woda kapilarna,— mogąca utrzymywać się w stosunkowo nieduzych porach pod dzialaniem sil
kapilamych oraz woda grawitacyjna wypelniająca duze pory, szczeliny lub kawemy w skalach, a mogąca się
przemieszczac pod dziataniem przyłożonego cisnienia. Przestrzenie porow i szczelin w skalach mogą.byc
wypełnione częsciowo lub calkowicie gazami np.: powietrzem, parą wodna, dwutlenkiem węgia, metanem.
Gazy te moga.znajdowac się pod roznym cisnieniem
Gazy w skalach mogą występowac w trzech postaciach:
-gazu absorbowanego, tzn. pochloniętego przez substance skały;
- gazu adsorbowanego na powierzchni scianek porow;
-gazu wolnego, wypełniającego szczeliny i pory w skalach
6.Klasyfikacja własności fizycznych skał
Pod pojęciem własności fizycznych skały rozumie się te cechy charakterystyczne skały związane z jej
budowa, które:
- pozwalaja.na odroznienie lub porownanie danej skaty z innymi;
- stwarzaja. mozliwosci przewidywania przebiegów i skutków interesujących nas procesów fizycznych;
- pojawiają się przy oddziaływaniu na skałą okreslonych p61 fizycznych lub ciał.
Liczbowo każda własność fizyczna skały określona jest jednym lub kilkoma parametrami (wskaznikami)
bedącymi ilosciowymi miarami własności
Fizyczne wlasnosci skal na ogol dzielimy ze względu na rodzaj wywołujacych je pól zewnętrznych, przy
czym pod pojęciem "pól zewnętrznych" rozumiemy ten rodzaj energii lub materii, pod dzialaniem ktorej w
danej chwili znajduje się skala. Uwzgledniając powyzsze wyróżniamy pole mechaniczne (cisnienie) i
odpowiadające mu mechaniczne wlasnosci skał,pole cieplne (temperatura) i odpowiadające mu termiczne
wlasnosci skal, pole elektryczne, magnetyczne, promieniotwórcze i odpowiadające im wlasnosci skal
Prócz tego istnieją jeszcze pola materialne (substancjalne) i odpowiadające im wlasnosci
hydrogazomechaniczne okreslające przeplyw cieczy i gazow przez skaly pod dzialaniem roznicy naporów.
Ze wzgledu na istote fizykalną. wszystkie parametry dzielimy na 3 grupy:
Do pierwszej grupy zaiiczamy parametry charakteryzujace odwracalne zmiany ilosci energii lub materii
wewnatrz skaly Do nich zaiiczamy: modul sprezystosci objetosciowej K ,dielektryczna przenikalność
wlasciwą pojemnosc cieplną Cw,wilgotnoscią W
D
O
drugiej grupy zaliczamy parametry okreslajace nieodwracalne przemiany danego rodzaju energii w
skalach w inny rodzaj energii, a prowadzące do istotnej zmiany stanu skały. Do nich zaliczamy:
wspolczynnik plastycznosci Jp, granice wytrzymalosci na sciskanie Rc i rozciaganie Rr, wspolczynnik
cieplnej rozszerzalnosci liniowej
β i objętościowej
ϖ
itd.
Do trzeciej grupy naleza. parametry opisujace procesy przekazywania energii, a takze przepływu cieczy i
gazu w skalach. Do nich zaliczamy: wspolczynnik przewodnictwa cieplnego, i wspolczynnik filtracji kf,
itd.Znanych jest przeszlo sto parametrow fizycznych skal. Pomiar takiej ilosci parametrow dla wszystkich
rodzajów skal jest zadaniem praktycznie niewykonalnym. W praktyce laboratoryjnej pojawila sie
koniecznosc wyroznienia pewnej grupy parametrow fizycznych skal bedacej liczbowo minimalną, ale
wystarczajacą dla pełnej charakterystyki skaly, jako ciala fizykalnego i geologicznego. Wyroznione w ten
sposób parametry noszą nazwę podst. parametrów skał( 12:Gęstość, porowatść, liczba P,moduł Yonga,
wytrzymałość na ściskanie, rozciąganie, przew. Cieplnego, cieplna pojemność rozszerzalność cieplna,
elektryczny opór, przenikalność elektr., przenikalność magnetyczna).
7.Podzial gruntow budowlanych
Przez grunt budowlany zgodnie z norma, PN-86/B-02480 rozumie się wierzchnią, czesc skorupy ziemskiej
wspolpracujaca. z obiektem budowlanym lub tez stanowiacą jego element, wzglednie shizącą jako
tworzywo do wykonania z niego budowli ziemnych
W mysl tej definicji gmnt budowlany jest zawsze skala.w ogolnym pojęciu , przy czym skala nie zawsze
bedzie spelniala wymagania stawiane gruntom budowlanym.
Ze wzgledu na pochodzenie grunty dzieli sie na antropogeniczne i naturalne.
Grunty antropogeniczne to grunty nasypowe utworzone z produktow gospodarczej lub przemyslowej
dzialalnosci cztowieka z odpadow komunalnych, pylow dymnicowych, odpadow poflotacyjnych, itp.
Grunty naturalne to grunty, ktorych szkielet powstat w wyniku procesow geologicznych, ktore ze
wzglqdu na pochodzenie dzieli sie na grunty rodzime i grunty nasypowe.
Grunty rodzime powstały w miejscu zalegania w wyniku procesow geologicznych takich jak wietrzenie,
sedymentacja, metamorfizm, itp.
Grunty nasypowe powstały w wyniku działalnosci człowieka z gruntu naturalnego lub antropogenicznego
np. w
wysypiskach, zwałowiskach, zbiomikach osadowych, budowlach ziemnych, nasypach budowlanych, itp.
Ze wzgledu na zawartosc substancji organicznej grunty rodzime dzieli sie na grunty mineralne i grunty
organiczne.
Grunty mineralne są to grunty rodzime zawierajace mniej niz 2 % substancji organicznej. Przyjmuje sie, ze
w gruntach organicznych zawartosc czesci organicznych jest wieksza niz 2 %
J
Ze wzgledu na odkształcenie podłoza, czyli wytrzymatosc grunty mineralne i organiczne dzieli sie na
skaliste i nieskaliste
Grunty skaliste mineralne to grunty lite lub spekane o nie przesunietych blokach(przy czym najmniejszy
wymiar bloku jest wiekszy od 10 cm), ktorych probki nie wykazują zmian objetosci, ani nie rozpadają sie
pod dzialaniem wody destylowanej, a ich wytrzymatosc na sciskanie Rc > 0,2 MPa.( wytrzymałość:skaliste
miekkie i twarde :spękania: skała lita, mało, średnio, bardzo spękana)Grunty nieskalite to takie, ktore nie
spełniają. warunkow gruntu skalistego (grunt rozdrobniony, bez silnych wiazan krystalicznych), a zawartosc
w nich czesci organicznych wynosi 2 % lub jest mniejszaj
Biorac pod uwage uziamienie gruntow rodzimych nieskalistych mineralnych wyroznia sie:
- grunty kamieniste o zawartosci ziarn o srednicach wiekszych od 40 mm stanowiacej wiecej niz 50 % {dso
> 40 mm);
-grunty gruboziamiste o zawartosci ziam o srednicach mniejszych od 40 mm stanowiacej wiecej niz 50 %
oraz o zawartosci ziam o srednicach wiekszych od 2 mm stanowiacej wiecej niz 90 %
- grunty drobnoziarniste o zawartosci ziam o srednicach mniejszych od 2 mm stanowiacej wiecej niz 90 %
Frakcja gruntu to zbior ziarn lub cząstek gruntu o srednicach zastepczych, zawartych w okreslonym
przedziale. Srednica zastępcza dz dla ziam jest to srednica oczka sita, przez ktore ziamojuz nie przechodzi,
zas dia cząstek jest to srednica kulki o identycznej gestosci wlasciwej, co dana cząstka opadajaca w wodzie
z taka. sama. predkoscia.jak dana czastka gruntu( frakcje-kamienista,pyłowa, piaskowa,iłowa,żwirowa)
Kryteria podziału gruntów budowlanych
Przedstawiona klasyfikacja gruntow budowlanych wg normy PN-86/B-02480 oparta jest na kilku
kryteriach podział na uwzgledniajacych:
- pochodzenie;
- uziamienie;
- zawartosc czesci organicznych;
- sposob formowania;
- wskażnik osiadania zapadowego
Analiza granulometryczna Wykonuje sie ja. w celu wyznaczenia procentowejzawartosciwystepujących w
gruncie frakcji. Pozwala to w koncowym efekcie na wykreślenie krzywej uziamienia oraz ustalenie rodzaju
i nazwy badanego gruntu. Skład granulometryczny gruntu dla celow budowlanych najczesciej okresla się
metodq sitową — gdy ziama w gruncie mają wymiary ponad 0,063 mm i metodq areometryczną— gdy
czastki gruntu maja wymiary mniejsze od 0,063 mm")
W przypadku, gdy grunt sklada sie z ziam o wymiarach d > 0,063 mm, jak i czastek o wymia-rach d <
0,063 mm stosuje sie kombinacje obydwu metod Metoda analizy sitowej polega na przesianiu wysuszonej
w temperaturze 105° - 110° C probki gruntu niespoistego przez odpowiedni komplet sit o roznych
wymiarach oczek i obliczeniu w procentach masy ziarn.
Zawartosc wagową ziarn gruntu pozostatych na kazdym sicie oblicza sie ze wzoru:
Zi=(m
si
/m
s
)*100%
gdzie:
msi — masa suchych ziarn pozostatych na sicie, g;
ms — masa calej suchej probki wziętej do analizy, g.
Krzywe te nanosi sie na siatke połlogarytmiczna, gdzie na osi odcietych podano w skali logarytmicznej
srednice ziam i czastek, a na osi rzednych w skali dziesietnej ich procentowe zawartości
Z wykresow uziamienia mozna.wyznaczyć:
- procentowe zawartosci poszczegolnych frakcji (niezbedne do okreslenia rodzaju gruntu);
-srednice d10, d30 i d60 (niezbedne do okreslenia wskaznikow uziamienia), gdzie d60 — srednica cząstek,
ponizej ktorej jest 60 % czastek w danym gruncie, d10 — srednica czastek, ponizej ktorej jest 10 % czastek
w danym gruncie.
Uziamienie gruntu charakteryzują dwa wskazniki:
- wskaznik roznoziamistosc U=d60/d10 -wskaznik krzywizny uziamienia C=d
2
30
/d
10
*d
60
W zaieznosci od wskaznika roznoziamistosci wyrozniamy grunty:
- rownoziamiste 1 < U<. 5;
-roznoziamiste 5 < U < 15;
- bardzo roznoziamiste U> 15.
Za pomoca. analizy sitowej okresia sie sklad granulometryczny gmntow syp-kich (kamienistych,
gmboziamistych, drobnoziamistych niespoistych z wyjatkiem piasku pylastego) i okresia ich nazwe
Melody sedymentacyjne. polegajace na podziale gruntu na frakcje w zawiesinie wodnej, są oparte na
prawie Stokesa, ktore mowi, ze prędkosc swobodnego opadania czastek kulistych jest wprost
proporcjonalna do ich srednicy i gestosci wlasciwej i zależy ponadto od gestosci wlasciwej i lepkosci cieczy
w ktorej opadają cząstki oraz od przyspieszenia ziemskiego:
v-prędkość opadania
di—srednica zastepcza cząstki, cm
Mając obliczone wartosci J, i Z, sporzadza sie wykres uziamienia Po wykresleniu krzywej uziamienia
gruntu odczytuje sie zawartosc poszczegolnych frakcji] piaskowej, pytowej i ilowej. Suma tych frakcji must
wynosic 100 %.Majac te dane i postugujac się trojkatem Fereta określa się nazwę gruntu. Trójkąt Fereta jest
trojkatem rownobocznym, ktorego boki podzielone są na 10 równych czesci. Kazdy z bokow reprezentuje
zawartosc od 0 do 100 % jednej frakcji. Pole trojkata podzielone jest na czesci, z ktorych lazda w zaieznosci
odjej polozenia w stosunku do bokow trojkata reprezentuje określoną nazwę gruntu.
Sposób formowania gruntow Grunty budowlane powstate w wyniku dzialalnosci cztowieka to grunty
nasy-powe. W zaieznosci od sposobu ich formowania (pochodzenia) nasypy dzieli się na:
- nasypy budowlane — powstale w wyniku kontrolowanego procesu tech-nologicznego (budowie ziemne);
- nasypy niebudowlane — formowane w sposob przypadkowy, np. wysypiska, zwałowiska
Wskaźnik osiadania zapadowego
Grunty o strukturze nietrwalej ulegajacej zmianie pod wptywem zawilgoeenia bez zmiany dzialajacego
obcia^zenia nazywa si? gnmtami zapadowymi
Ilosciowo takie grunty charakteryzowane są przez wskaznik osiadania zapadowego i
mp
=(h’-h’’)/h
o
h
o
-wysokosc probki w stanie naturalnym;
Badania makroskopowe gruntow budowlanych
Badania makroskopowe polegaja na przyblizonym okresleniu nazwy i rodza-ju gruntu oraz niektorychjego
cech fizycznych bez pomocy przyrzadow. Najcze-sciej prowadzi siejew terenie lubjako badania wstepne w
laboratorium. Podczas badan makroskopowych okresia sie nastepujace cechy gruntow:
-rodzaj i nazwe gruntu;
- stan gruntu;
- barw
- wilgotnosc naturalna;
- zawartosc weglanu wapnia CaC03.
Probki do badan makroskopowych pobiera sie z kazdej warstwy gruntu rozniacej sie rodzaj em lub stanem
lecz nie rzadziej niz co 1 m gtebokosci [28]. Wyroznia sie trzy rodzaje pobieranych probek gruntow:
-probki o naturalnym uziamieniu;
- probki o naturalnej wilgotnosci;
- probki o naturalnej strukturze.
Rodzaje gruntu
Oznaczenia gruntów skalistych i ich podział dokonuje sie makroskopowo przez ogledziny i proste proby
wytrzymalosciowe jak: uderzenie mtotkiem, ryso-wanie, scieranie-y
W obrebie gruntow kamienistych dokonuje sie wydzieleń poprzez pomiar naj-wiekszych ziarn i orientacyjne
okreslenie ich stosunku do ziam pozostatego gruntu oraz stwierdzenie ich stopnia obtoczenia. W skali
obtoczenia wyroznia się ziama ostro krawędziste, kanciaste, słabo obtoczone, obtoczone i dobrze obtoczone.
Przy oznaczaniu nazwy gruntow gruboziamistych i drobnoziamistych nalezy wstepnie oddzielic grunty
spoiste od niespoistych.
D
O
gruntow spoistych zalicza sie wszystkie grunty, ktore po wyschnieciu tworza. zwarte bryty. Grunty
niespoiste (sypkie) po wyschnieciu nie tworza bryl czy grudek lecz sa, sypkie
Jeżeli trzeba okreslic, czy grunt jest spoisty czy niespoisty, gdy probka jest wilgetna, z gruntu tego probuje
sie uformowac w dioni kuike o srednicy 7-8 mm. Jesli kulka da sie uformowac — grunt mozna zaiiczyc do
spoistych, w przeciwnym przypadku—do sypkich.
Majac okreslona. spoistosc gruntu ustala się w sposob szacunkowy zawartosć w gruncie frakcji piaskowej
poprzez rozcieranie probki gruntu miedzy dwoma palcami zanurzonymi w wodzie. \
P
O
okresleniu zawartosci frakcji piaskowej, kwalifikujemy grunt dojednej ztrzechgrup: I. grunty piaszczyste
(fp > 50 %, /„ < 30 %);
II. grunty posrednie (fp > 30 %, /„ > 30 %);
III. grunty pylaste (fp < 50 %, /„ > 50 %).
W przypadkach watpliwych sprawdza sie probe waleczkowania proba rozmakania. W tym celu grudke
wysuszonego gruntu umieszcza sie w siatce o oczkach kwadratowych (5x5 mm) i zanurza w wodzie.Rodzaj
gruntow niespoistych (sypkich) okresia sie na podstawie wzrokowej oceny wielkosci ziam i ich
procentowej zawartosci w poszczegolnych frakcjach. Wielkosc ziam mozna okreslic za pomoca lupy z
podzialką mikrometryczną przy badaniach makroskopowych okreslenie rodzaju gruntu uzupełnia się opisem
przewarstwień, domieszek zanieczyszczen, a przede wszystkim —jesli jest znana geneza gruntu.
Stan gruntów
Stan gruntow spoistych okresia sie na podstawie liczby wykonanych wałecz-kowan. Proba waleczkowania
polega na uformowaniu z gruntu kuleczki o sredni-cy 7 mm, z ktorej wykonuje się wałeczek o srednicy 3
mm.W przypadku badania gruntow malo spoistych czesto juz pierwszy waleczek rozsypuje sie, co
uniemozliwia okresleniejego stanu. Przyjmuje sie, ze grunty wystepują w stanie:
- zwartym, jesli nie mozna uformowac kuiki — grunt zbyt twardy;
- polzwartym, jesli z gruntu mozna uformowac kuike, a waleczek peka pod-czas pierwszego
waleczkowania (ze wzgledu na male zawilgocenie);
- płynnym, jesli z uwagi na nawodnienie gruntu nie da się uformowac kulek — grunt oblepia dionie.
Barwa i rodzaj gruntówBarwe gruntu okresia sie na probce o wilgotnosci naturalnej. Na ogół barwę idaje
sie za pomoca. dwoch wyrazow. Barwę podstawowa. przedstawia drugi wyraz, odcienie i intensywnosc
barwy wyraz pierwszy np. grunt snoszaro-zolty.
Wilgotnosc naturalna gruntow w czasie badan makroskopowych okresia sie następująco; grunt jest:
-
suchy, jesli brylka gruntu spoistego przy zgniataniu p?ka, a po rozdrobnie-niu daje suchy proszek
- malo wilgotny, jesli brylka gruntu spoistego przy zgniataniu odkszłca się plastycznie, a reka przyłozona
do gruntu nie staje sie wilgotna;
-wilgotny, jesli reka przylozona do gruntu staje się wilgotna;
-mokry ,jeżeli przy ściskaniu gruntu w dłoni, grunt odsącza wodę
-nawodniony, jeżeli grunt odsącza wodę grawitacyjnie
8Strukturalne wlasnosci skał i gruntow
Dla oceny stopnia niejednorodnosci skat i umozliwienia ogolnego rozroznienia skal pod względem ich
wewnętrznej budowy wprowadza się szereg pojęc ulatwiających to zadanie. Do podstawowych pojęc
charakteryzujących własnosci strukturalne skal zaliczamy gestosc objętosciową(pozoma) i gestosc wlasciwą
(rzeczywista). W praktyce geotechnicznej przy wyznaczaniu napręzen w gorotworze poshigujemy się
najczęsciej cięzarem objętosciowym i cięzarem wlasciwym. Ze względu na rodzaj wiezow występujacych
między poszczegolnymi ziarnami wyroznia się trzy podstawowe grupy skah
-skaty okruchowe — będące prosta. mieszaniną roznych mineralow albo zbiorem ziamjednego mineralu bez
zadnych wzajemnych więzi przeciw-dzialających rozdzielaniu się ziam, np.: piasek, zwir;
- skaty spoiste (argilitowe) — ktorych ziama mineralne posiadają otoczki wodno-
koloidalne spajające ziama wjedna^catosc np.: gliny, ify, boksyty;
-skaty zwięzte — (mocne, lite) — w ktorych istnieja. trwate, sztywne lub spręzyste więzi między
poszczegolnymi ziamami np.: granity, gnejsy, piaskowce, wapienie.
-Gestosc skał rzeczywistych w ogolnym przypadku jest okreslana przez stosunek sumy masy fazy stalej m
1
,
cieklej m
2
i gazowej m
3
do sumy objetosci tych fazfz.
3
2
1
3
2
1
V
V
V
m
m
m
r
+
+
+
+
=
ρ
Objętość i masę dowolnego elementu wycietego z warstwy skalnej mozna przedstawic nastepujaco:
V=V1+V2+V3
Gdzie:
V1,m1-obj, masa cząstek stałych
V2,m2-obj,masa wody zaw. w porach
V3- obj pow zaw w porach
Gęstosc objętosciowa
ρ
—jest to stosunek masy probki skalnej m do jej objętosci V. p=m/V
Gęstosc własciwa po —jest to stosunek masy czastek stalych probki skalnej mi do ich objetosci Vi.
po=m1/V1
Ciężar objętościowy- jest to stosunek ciężru fazy stałej G wraz z zawartymi w niej porami do jej obj.V
N/m
3
V
G /
=
γ
Ciężar właściwy —jest to stosunek ciezaru fazy stalej w stanie sproszko-wanym i wysuszonym G do jej
objetosci V
1
/
1 V
G
=
γ
1
Między cięzarem objętosciowym a gęstościa. objętościową istnieje nastę-pujaca zaieznosc
g
ρ
γ
=
y -— cięzar objętosciowy, N/m
3
;
p — gęstosc objętosciowa, kg/m
3
;
g— przyspieszenie ziemskie, m/s
2
. Podobna zaieznosc istnieje miedzy ciężarem
właściwym a gęstością
właściwa
g
0
0
ρ
γ
=
yo-ciężar wł po- gęst wł
Gęstosc objętosciowa szkieletu gruntowego pd—jest to stosunek masy ziarn i czastek statych szkieletu
gruntowego do objetosci całej probki (przed wysuszeniem):pd=m1/V
W przypadku gdy znana jest wartosc wilgotnosci, czyli procentowy stosunek wody m2 zawartej w porach
do masy szkieletu gruntowego m1 W=(m2/m1)*100 a pd=(p/100+W)*100
Cieżar objetosciowy szkieletu gruntowego Jest to stosunek ciezaru wysuszonej probki G
s
do jej objetosci
przed wysuszeniem V
V
G
s
d
/
=
γ
PorowatoscP—jest to stosunek objetosci porow w probce skały Vp do objętosci calej probki V:
%
100
*
V
Vp
P
=
Wskaźnik porowatości e- jest to stosunek objętości porów Vp do obj. materiału skalnego zawartego w
próbce Vs :
Vs
e
=
Vp
Współczynnik szczelnosci ks —jest to stosunek ciezaru objetosciowego
γ do ciezaru wlasciwego γ
0
γ
=
s
k
0
γ
Współczynnik rozluzowania kr — jest to stosunek objetosci rozluzowanej skafy V do jej objetosci w stanie
nienaruszonym (w masywie) V.:
V
Vr
k
r
=
Gęstosc nasypowa
ρ
n
—jest to stosunek gestosci objętosciowej p skały w masywie do wspolczynnika
rozluzowania:
ρ
n
k
ρ =
r
Stopień zagęszczenia Jd —jest to stosunek zageszczenia istniejącego w naturze do najwiekszego
mozliwego zageszczenia danego gruntu.
min
max
max
e
e
e
e
J
d
−
−
=
e
max
— wskaznik porowatosci maksymalnej, ktorą otrzymuje sie przez najbardziej luzne usypanie piasku;
e
min
— wskaznik porowatosci minimalnej, przy mozliwie największym zagęszczeniu piasku uzyskanym
przez wibracją
e—wskaznik porowatosci naturalnej,
W zaieznosci od stopnia zagęszczenia wyrozniamy tzw.stany gruntow sypkich:
Jd <0,33 — grunt jest luzny;
0,33 < Jd < 0,67 — grunt śr. zagęszczony
0,67 < Jd <1,00 — grunt jest zageszczony
9.Hydrogazomechaniczne wł skał i gruntów
Wlasnosci hydrogazomechaniczne charakteryzują zdolnosc skal do przepuszczania, pochlaniania i
zatrzymywania roznych cieczy i gazow oraz sklonnosc skal do zmiany swego stanu mechanicznego podczas
oddzialywania cieczami wzglednie gazami. Podstawowym parametrem wlasnosci hydrogazomechanicznych
skal i gruntow jest więc wilgotnosc
Wilgotność skaty W—jest to procentowy stosunek masy wody M
w
porach skały do masy suchej probki M.d
(masy szkieletu skafy):W=(M
w
/M
d
)*100%
Wilgotność naturalna Wn — odpowiada naturalnej zawartosci wody w skale, niezaleznie od tej ilosci jaka.
moze skata w ogole wchłonac.
W celu okreslenia stanu zawilgocenia skafy i sprawdzenia, wjakim stopniujej pory s£[ wypehiione woda,
nalezy wyznaczyc wilgotnosc całkowitą i stopień wilgotności . .
Wilgotność całkowita Wsr — jest to najwieksza wzgledna ilosci wody, gdy pory skafy sa, calkowicie
wypehiione wodą.:
%
100
⋅
⋅
=
γ
γ
w
sr
e
W
gdzie:
e — wskaznik porowatosci, -;
p — cięzar wlasciwy szkieletu skalnego, kN/m
3
; :
γ
w — ciezar wlasciwy wody = 9,81 kN/m
3
;
Stopien wilgotnosci Sr—jest to stosunek objętosci wody znajdujacej sie w porach i pustkach skaly Vw, do
ich objetosci calkowitej Vp:
w
s
n
r
e
W
S
γ
γ
⋅
⋅
⋅
=
100
W
n
— wilgotnosc naturalna probki.
W zaieznosci od wartosci stopnia wilgotnosci wyrozniamy nastepujace stany zawilgocenia gruntow
sypkich:
Sr=0-gr suchy
0,0<Sr<0,4-gr małowilgotny
0,4 < Sr < 0,8 — grunt wilgotny;
0,8 < Sr<1,0— grunt mokry
Obecnosc wody wpływa rowniez na ksztattowanie sie wlasnosci gruntow spoistych, zwłaszcza na tzw.
konsystencje. Rozróżnia się następujące konsystencje gruntow spoistych:
- płynną — grunt zachowuje się jak ciecz i nie ma prawie zadnej wytrzymalosci na scinanie
- plastyczną — grunt o tej konsystencji poddany pewnemu naciskowi odksztatca się, nie ulega przy tym
spekaniom i zachowuje nadany mu kształt
-zwartą — grunt o tej konsystencji odksztatea sie dopiero przy duzych
naciskach, a odksztalceniom towarzyszą spekania. Poszczególne konsystencje są odgraniczone od siebie e
sposób bardzo umowny gr-mi konststencji
Granica ptynnosci
WL
,
jest to wilgotność w procentach jaką ma masa gruntowa umieszczona w miseczce
aparatu Casagrande'a, gdy wykonana w niej bruzda zlewa sie przy dwudziestym piatym uderzeniu miseczki
o podstawe aparatu.
Granica plastyczności W
p
– jest to wilgotność w % jaką ma grunt gdy przy kolejnym wałeczkowaniu
bryłki gruntu wałeczek pęka po osiągnięciu śr 3mm
Granica skurczalności W
s
- jest to wilgotność w % jaką ma grunt gdy przy suszeniu bryłka gruntu przestaje
zmniejszać swą objętość.
Plastyczne wlasnosci gruntow charakteryzuje stopien plastycznosci i wska-znik plastycznosci.
Stopien plastycznosci J
L
. — jest to stosunek roznicy wilgotnosci naturalnej danego gruntu i granicy
plastycznosci do roznicy granicy plynnosci i granicy plastycznosci:
p
L
p
n
L
W
W
W
W
J
−
−
=
gdzie:
Wn — wilgotnosc naturalna, %;
Wp — granica plastycznosci, %;
WL
— granica pfynnosci, %.
W zaieznosci od stopnia plastycznosci i wilgotnosci naturalnej wyrozniamy nastepujaące stany gruntow
spoistych(grunty:zwarty,połzwarty,twardoplastyczny,plastyczny miękkoplastyczny, płynny)
Wskaznik plastycznosci Jp jest to roznica pomiedzy granicaą plynnosci
WL
i granica plastycznosci Wp:
J
p
= W
L
-W
p
%
Zdolność skał porowatych do przepuszczania cieczy lub gazu siecią kanalików, utworzonych z ich porów
pod działaniem naporu hydraulicznego naz. się przepuszczalnością
Wspolczynnik przepuszczalnosci kprz okreslony jest objetoscią cieczy lub gazu Q o lepkosci
η
; przez
jednostke przekroju poprzecznego skaly Sw jenostce czasu
τ
przy gradiencie cisnienia gradp rownym
jednostce:
η
τ
⋅
⋅
⋅
=
gradp
S
Q
k
prz
m
2
Q — ilosc cieczy lub gazu przechodzacego przez probke, m ;
S — powierzchnia przekroju poprzecznego probki, m
2
;
T
—czas przeptywu, s;
η
— lepkosc dynamiczna w temperaturze doswiadczenia, Pa-s;
grad p — spadek cisnienia na drodze L, tzn. gradp =(p/ -po)/L, Pa/m.
Fizyczny sens takiego wymiaru polega na tym, ze charakteryzuje on wielkosc powierzchni przekroju
poprzecznego porow i kanalikow skały, przez ktora odbywa sie przeplyw praktyczną jednostką
przepuszczalnosci jest 1 darcy (1 D),
1 D = 1,02*10'
12
m
2
Powolne przesączanie się cieczy lub gazu poprzez splatany system porow i kanalikow pod wpływem
ciśnienia nazywa sie filtracją.
Wspoiczynnik filtracji kf— przy danej temperaturze okreslany jest stosunkiem objetosci przeplywającej
cieczy Q do pola przekroju probki prostopadlego do kierunku przeplywu S oraz czasu przeplywu
τ
i spadku
hydraulicznego:
)
*
*
/(
i
S
Q
k
f
τ
=
m/s
W zależnosci od wartosci wspołczynnika filtracji, skaly dzielimy na:
-dobrze przepuszczalne—kf> 1000 m/dobe
-srednio przepuszczalne — 10 m/dobe <kf <1000 m/dobe;
- slabo przepuszczalne — 0,1 m/dobe < kf< 10 m/dobe;
-nieprzepuszczalne—kf< 0,1 m/dobe.
Zwiazek miedzy wspolczynnikiem filtracji i współczynnikiem przepuszczalnosci wyrazony jest nastepujacą
zaleznoscia;
gdzie:
kprz — wspolczynnik przepuszczalnosci, m
2
;
o
γ
— ciezar wlasciwy cieczy lub gazu, N/m
3
;
η
— lepkosc dynamiczna cieczy lub gazu,
Pa*s =N*s/m
2
.
Zdolnosc skal do zwiekszania swej objetosci przy nasyceniu wodą nazywa się pęcznieniem.
Wspolczynnik pęcznienia Pv — okreslony jest stosunkiem przyrostu objetosci specznialej skaly do jej
objetosci pierwotnej lub stosunkiem przyrostu wysokosci specznialej skaly do jej wysokosci pierwotnej
%
100
0
0
⋅
−
=
V
V
V
Pv
k
%
100
0
0
⋅
−
=
h
h
h
Ph
k
Gdzie:
Pv-wspołczynnik pecznienia okreslany w warunkach nieograniczonego pecznienia probki, %;
Ph — wspolczynnik pecznienia okreslany w warunkach ograniczonego pęcznienia probki, %;
V
k
, h
k
- objętość, wysokość próbki po spęcznieniu
V
0
, h
0
- objętość, wysokość początkowa próbki
10. Mechaniczne wlasnosci skal Mechaniczne wtasnosci skat charakteryzują zachowanie się skat pod
wplywem oddzialywania mechanicznych obciazen. W zaieznosci od typu, kierunku, wartosci i czasu
dziatania obciązenia powstaja. roznorodne zwiazki między napręzeniami i odkształceniami w skatach.
Na podstawie charakteru tych związkow wyrozniamy:
-wtasnosci spręzyste skał — charakteryzujące zaleznosc między napręzeniami i odkształceniami
spręzystymi (odwracalnymi);
-wlasnosci wytrzymatosciowe skat — charakteryzujace zaieznosc miedzy napręzeniami i odksztalceniami
niszczącymi (nieodwracalnymi);
-wlasnosci plastyczne skał — charakteryzujace zaieznosc miedzy napreze-niami i odkształceniami
nieodwracalnymi zachodzacymi bez naruszenia ciaglosci skaly;
-wlasnosci reologiczne skał— charakteryzujace zmiane podanych wyzej wtasnosci przy długotrwałym
oddziatywaniu obciazen.
Sprężyste własnosci skał

Wlasnosci spręzyste skał ilosciowo okreslone są modulami spręzystosci czyli
wspotczynnikami proporcjonalnosci między okreslonymi napręzeniami i odpowiadającymi im
odksztatceniami spręzystymi. Wyrozniamy następujące moduły spręzystosci:
-modul spręzystosci podłiznej, E
-liczby Poissona, v
-modul sprezystosci postaciowej, G;
-modul sprezystosci objetosciowej, K;
-modul jednostronnego sciskania, M.
Modul sprezystosci podluznej (modul Younga) E — jest to wspolczynnik proporcjonalnosci miedzy
wielkoscia. naprezen nonnalnych (sciskajacych lub rozciagajacych) a, a odksztalceniem wzglednym e
występującym wzdhiz osi probki
ε
σ
*
E
=
:Modul spręzystosci podłuznej jest jednym z podstawowych parametrow spręzystych skat. Nie ma on
wartosci statej, bowiem wartoscjego zmienia się w zaleznosci od obciazenia
Liczba Poissona v –jest to współ. Proporcjonalności między względnymi odkształceniami poprzecznymi,
oraz względnymo odkształceniami wzdłużnymi:
l
d
Δ
Δ
l
d
=
ν
Modul spręzystosci postaciowej (modul Kirchhoffa), G — jest to wspolczynnik proporcjonalnosci
między wielkoscią napręzen stycznych
τ
(scinajacych) i odpowiadajacym im odksztalceniom postaciowym
γ
charakteryzujacym zmianę kształtu ciała:
γ
τ
*
G
=
Modul spręzystosci objętosciowej, K—jest to wspolczynnik proporcjonalnosci miedzy naprezeniami
sciskajacymi
σ
i wzgledna. zmiana. objetosci
Δ
V/V.
V
V
K
Δ
=
*
σ
Wytrzymałościowe wlasności skal
WIasnosci wytrzymalosciowe okreslane są doraznymi wytrzymalosciami skał występujacymi przy
okreslonych napręzeniach.
Wyrozniamy dorazną wytrzymalosc skal na: sciskanie Rc, rozciąganie Rr, ścinanie Rt, zginanie Rg, itd.
Wytrzymalosc dorazna na sciskanie Rc jest to stosunek największej krytycznej sily sciskajacej F,
niszczacej probkę do pola powierzchni jej poczatkowego przekroju poprzecznego:
S
F
=
Rc
N/m
2
Dla okreslenia wartosci Re uzywa si^ probek skalnych o ksztattach kostek szesciennych lub walcow o
okreslonej smuklosci hid = 1, d == 40 — 50 mm
Wytrzymalość doraźna na scinanie Rt —Przy czystym scinaniu wytrzymalosc dorazna na scinanie Rt
definiowana jest jako stosunek krytycznej sity F do pola powierzchni sciecia S. Rt=F/S. Na ogol
wytrzymalosc na scinanie przedstawiona jest za pomoca. dwoch parametrow spojnosci i kąta tarcia
wewnetrznego
Wytrzymałość dorażna na rozciąganie Rr –jest to stosunek najw, siły rozciągającej F, przy której próbka
ulega zniszczeniu do pola powieerzchni jej poczatkowego przekroju poprzecznego: Rr=F/S
N/m
2
Wytrzymalosc dorazna na zginanie Rg —jest to krytyczna wartosc naprezenia, przy ktorym probka
skalna poddana obciazeniu zgmającemu ulega zniszczeniu. Dia probki w ksztalcie beleczki o przekroju
prostokatnym swobodnie podpartej na koncach, a obciazonej jedna. silą skupiona. w srodku długosci
probki, dorazna wytrzymalosc na zginanie oblicza sie za pomocą wzoru:
2
*
2 h
b
W
*
3 l
F
x
Mg
Rg
=
=
N/m
2
gdzie:
F—sila lamiaąca beleczkę, N;
l— odstęp podpor beleczki, m;
b — szerokosc przekroju poprzecznegobeleczki, m;
h —wysokosc tego przekroju, m;
Mg — moment zginajacy odpowiadajacy sile niszczacej, N-m;
Wx — wskaznik wytrzymalosci przekroju na zginanie, m
3
.
Orientacyjne zaieznosci miedzy wytrzymaloscią na sciskanie a innymi są nastepujace:
Rc>Rt>Rg>Rr i zawarte w granicach:
Rc
Rr
80
1
20
1 ÷
=
Rc
Rt
15
1
5
1 ÷
=
Rc
Rg
15
1
5
1 ÷
=
Właściwości mechaniczne ośrodka gruntowego – ściśliwość i wytrzymałość na ścinanie
Scisliwosc gruntow
Scisliwosc gruntu jest to zdolnosc gruntu do zmniejszania swej objetosci pod wpfywem obciazenia. Miara.
scisliwosci są moduły scisliwosci.Edometryczny modul scisliwosci pierwotnej Mo —jest to stosunek

przyrostu efektywnego naprezenia normalnego
σ
Δ
do przyrostu calkowitego odksztalcenia wzglednego
ε
Δ
mierzonego w kierunku dzialania sily obciazającej w jednoosiowym (edometrycznym) stanie odksztalcen w
warunkach umownej konsolidacji gruntu:
ε
σ
Δ
Δ
=
Mo
σ
Δ
— przyrost naprezenia normalnego probki gruntu (cr; -
CT
,
_ i), N/m
2
;
ε
Δ
— odksztalcenie wzgle^dne probki gruntu ;hi — wysokosc probki po zwiekszeniu obciazenia, m;
hi-1 — wysokosc probki w edometrze przed zwiekszeniem obciazenia, m
i — numer zakresu obciazenia;
Edometryczny modul scisliwosci wtornej M — jest to stosunek przyrostu efektywnego naprezenia
normalnego
σ
Δ
do przyrostu sprezystego (odwracalnego) odksztalcenia wzglednego
ε
mierzonego w kierunku działania siły obciazajacej w jednoosiowym (edometrycznym) stanie odksztatcen
Edometryczny modul odprezenia M jest to stosunek zmniejszenia efektywnego naprezenia normalnego
σ
do jednostkowego przyrostu wysokosci próbki
Δ
Moduł ten odczytuje sie z tej czesci krzywej scisliwosci, ktora odpowiada odciazeniu próbki.
Aby sporządzic wykres e = f(a) nalezy przeliczyc wysokosc probki hi na wskaznik porowatosci wg wzoru:
)
1
(
0
o
o
i
o
i
e
h
h
h
e
e
+
−
−
=
Gdzie:
ei -— wskaznik porowatosci gruntu przy wysokosci probki hi pod obciazeniem
σ
eo — wskaznik porowatosci gruntu przed obciazaniem;
ho — poczatkowa wysokosc probki, mm;
hii — wysokosc probki skonsolidowanej pod obciqzeniem
σ
mm.
Wytrzymałość gruntów na scinanie
Wytrzymałością gruntów na ścinanie nazywamy opór jaki stawia grunt naprężeniom ścinającym, po
pokonaniu którego następuje poślizg pewnej części ośrodka w stosunku do pozostałej. Dla skał spoistych
oraz sypkich zawilgoconych zależność między wytrzymałością na ścinanie, tarciem wewnętrznym i
spójnością określa równanie Coulomba:
τ=σ
n
tgφ + c
τ – naprężenie ścinające w płaszczyźnie ścinania, Pa
σ
n
- naprężenie normalne, Pa
tg φ - współczynnik tarcia wewnętrznego;
φ - kat tarcia wewnetrznego.
c – spójność, Pa dla skał sypkich wysuszonych c = 0
W gruntach sypkich siłom scinajacym przeciwdziała opór tarcia wewnetrznego, który powstaje w czasie
przesuwu ziam gruntu wzgledem siebie w płaszczyźnie poślizgu oraz na skutek obrotu ziarn gruntu
względem ziarn sąsiednich. W gruntach spoistych naprężeniom ścinającym przeciwdziała opór tarcia
wewnętrznego, spójność rzeczywista zwana kohezją.
Spojnosc, czyli kohezja, jest to opor gruntu stawiany sitom zewnetrznym, a wywołany wzajemnym
przyciąganiem cząstek składowych gruntu. Spowodowana jest ona ścisłym wzajemnym przyleganiem ziarn
i czastek gruntu, czesciowym ich zlepieniem przez czastki koloidalne oraz napieciem blonek wody
otaczajacej ziama mineralne
Oznaczanie wartosci φ i c w warunkach laboratoryjnych należy przeprowadzić zgodnie z przewidywanym
sposobem obciazania podloza gruntowego pod projektowaną budowle
Dla budowli, dla których obciążenie użytkowe wynosić będzie:
- ponad 70 % obciążenia całkowitego
- 30 - 70 % obciążenia całkowitego — ścinanie próbek należy wykonać po y konsolidacji ale bez odpływu
wody z porów ; mniej niż 30% obciążenia całkowitego
Mechanizm zniszczenia skaly kruchej
|l — Stadium nieliniowego odksztalcania sie skaly.
W stadium tym pod wplywem dzialania naprezenia (01 - 03) nastepuje zamykanie sie mikroszczelin i
mikroporow czyli wzrost gestosci skaly, a wiec jej kompakcja. Objetosc probki maleje, a odksztalceniejest
tyiko czesciowo odwracalne. Krzywa odksztalcen podluznych wygietajest zwykle w kierunku
L
osi e. Przy
czym im skalajest bardziej zbita, tym krzywizna tajest mniejsza. | Odksztalcenia poprzeczne stopniowo
wzrastaja, a wartosci modulu sprezy-tstosci i wspolczynnika Poissona zwiekszaja^ sie. W warunkach

dzialania Snienia hydrostatycznego a\ = a-i = 03 o wartosci kilkudziesieciu igapaskali, stadium I nie
wystepuje, a krzywe naprezenie — odksztalcenie Eyjmuja. od samego poczatku postac prostych.
Stadium liniowego odksztalcania sie skaly odpowiadajace sprezystemu 3dksztalcaniu sie mineramego
szkieletu.
Przyrosty odksztalcen sa. proporcjonalne do przyrostow naprezen. Stosunek poprzecznego i podhiznego
odksztalcenia jest staly. Moduly sprezystosci iwartosci stale. Skala zachowuje siejak cialo sprezyste zgodnie
z liniowa. znoscia. naprezenie-odksztalcenie.
Stadium liniowosci odksztalcen podhiznych Cz oraz nieliniowosci tsztalcen poprzecznych Exy i
objetosciowych £»,.
-idium tym zostaje zapoczatkowany proces niszczenia skaly. Rozpoczyna ae propagacja mikroszczelin
pierwotnych, istniejacych w skale. Towarzyszy Najwygodniejsza, metody badania Rr jest metoda
poprzecznego sciskania Metoda ta polega na obciazaniu probki skalnej w kszwzdhiz tworzacej walea lub
wzdhiz podhiznej kraw^dzi prostopadloscianu.;——.-wartosc pd mozna obliczyc poshiguja^c sie
gestQScia. obje^tosciowa150+230)K ze skały ustępuje woda wolna tj. kalama i grawitacyjna; przy dalszym
ogrzewaniu od (150 + 230')° K do (400+230) K odparowuje woda mocno zwiazana przez wolne jony w
miejscach uszkodzeń siatki krystalicznej oraz u wierzcholkow i bokow krysztalow czastek skalnych.
Dopiero przy temperaturze
11. Akustyczne własności skał
Ze względu na częstotliwość fale sprężyste dzieli się na: — fale infradźwiękowe (poddźwiękowe) o
częstotliwości do 16 Hz; — fale dźwiękowe (akustyczne) o częstotliwości od 16 Hz do 20 kHz; — fale
ultradźwiękowe (naddźwiękowe) o częstotliwości od 20 kHz do
l GHz;
— fale hiperdźwiękowe (hiperakustyczne) o częstotliwości ponad l GHz
W zależności od sposobu rozchodzenia się fal sprężystych wyróżnia się falę podłużną, poprzeczną i
powierzchniową.
Fala podłużna—występuje wtedy, gdy cząstki ośrodka drgają równolegle do kierunku rozchodzenia się fali.
Fala poprzeczna— występuje wtedy, gdy cząstki ośrodka drgają prostopadle do kierunku rozchodzenia się
fali.
Fala powierzchniowa Gdy ośrodek stały zostanie ograniczony powierzchnią swobodną, wówczas wzdłuż
tej powierzchni rozchodzi się fala, w której cząsteczki ośrodka wykonują ruch po elipsoidalnej trajektorii, a
więc zarówno wzdłuż i w poprzek kierunku rozchodzenia się fali. Dwa najprostsze typy fal
powierzchniowych to: — fale Rayleigha — w czasie przebiegu których cząsteczki ośrodka poruszają się po
elipsach położonych w płaszczyźnie pionowej, równoległej do kierunku ruchu); — fale Love'a, w czasie
propagacji których cząsteczki drgająw płaszczyźnie poziomej, prostopadłej do kierunku rozchodzenia się
fali
Warunki rozchodzenia się fal sprężystych w skałach charakteryzuj ą parametry akustyczne skał, do
których zaliczamy: prędkość rozchodzenia się fali, akustyczną oporność falową, współczynniki odbicia,
załamania, współczynnik tłumienia
Prędkość fal sprężystych — jest to szybkość rozchodzenia się zmiennych (znakowo) naprężeń lub
odkształceń w skałach.
Prędkość rozchodzenia się fal sprężystych w nieograniczonym, absolutnie sprężystym, izotropowym
ośrodku można określić ze wzorów uzyskanych z teorii sprężystości i ruchu falowego w ośrodku ciągłym.
Prędkość rozchodzenia się fali sprężystej zależy od gęstości ośrodka/o, modułu sprężystości podłużnej E
oraz liczby Poissona v lub innych parametrów sprężystych. Prędkość rozchodzenia się fali podłużnej ^p
wynosi:
(
)
(
)(
)
ν
ν
ρ
ν
ϑ
2
1
1
1
−
+
−
=
E
p
gdzie:
E — moduł sprężystości podłużnej, Pa;
P — gęstość objętościowa ośrodka, kg/m3;
v — liczba Poissona.
Prędko ć rozchodzenia się fali poprzecznej
s
ϑ
wynosi:
ś
(
)
ν
ρ
ϑ
+
=
1
2
E
s

Prędkość rozchodzenia się fali powierzchniowej
R
wynosi:
ϑ
(
)
ν
ρ
ν
ν
ϑ
+
⋅
+
+
=
1
2
1
12
,
1
87
,
0
E
R
Znając wartości prędkości fal podłużnych i poprzecznych można określić stałe sprężyste badanego ośrodka.
Moduł sprężystości podłużnej:
(
)(
)
ν
ν
ν
ϑ
ρ
−
−
+
⋅
⋅⋅
=
1
2
1
1
2
p
E
Moduł sprężystości postaciowej:
(
)
ν
+
=
1
2
E
G
Modu sprężystości objętościowej:
ł
(
)
ν
2
1
3
−
=
E
K
Moduł jednostronnego ściskania:
(
)
(
)(
)
ν
ν
ν
2
1
1
1
−
+
−
=
E
M
Wyznaczone w ten sposób wartości — wykorzystujące prędkości fal sprężystych — noszą nazwę
modułów dynamicznych w odróżnieniu od parametrów sprężystych statycznych wyznaczonych metodami
laboratoryjnymi na próbkach skalnych poprzez statyczne obciążanie.
Współczynnik anizotropii prędkości, który jest określony następującym wzorem:
⊥
=
p
pII
k
ϑ
ϑ
ϑ
⊥
p
pII
ϑ
ϑ
,
- prędkość rozchodzenia się fali podłużnej w kierunku równoległym i prostopadłym do uwarstwienia.
Akustyczna oporność falowa z — charakteryzuje opór skały przy rozchodzeniu się fali sprężystej.
Liczbowo równa jest iloczynowi gęstości skały p i prędkości fali podłużnej
p
ϑ
(
)
]
/
[
,
2
s
m
kg
z
p
⋅
⋅
=
ϑ
ρ
Współczynnik odbicia K
o
— jest to stosunek energii fali odbitej W
o
do energii fali padającej W
p
. Przy
normalnym (prostopadłym) padaniu fali na powierzchnię graniczną, współczynnik odbicia wyraża się
wzorem:
2
2
1
2
1
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
=
=
z
z
z
z
W
W
K
p
o
o
z
1
— oporność falowa ośrodka od którego fala się odbija;
z
2
— oporność falowa ośrodka w którym rozchodzi się fala padająca i fala odbita od powierzchni
granicznej.
Współczynnik załamania n — jest to współczynnik charakteryzujący zmianę kierunku fali sprężystej przy
przejściu z jednego ośrodka do drugiego, ilościowo równy stosunkowi sinusa kąta padania do sinusa kąta
załam nia:
a
2
1
1
2
z
z
z
n
+
=
Współczynnik tłumienia
α
—jest to współczynnik charakteryzujący stopień zmniejszenia amplitudy drgań
sprężystych na jednostkę długości drogi:
]
[
,
ln
1
−
=
m
x
U
U
o
α
Maksymalne tłumienie fal sprężystych obserwuje się w gazach, mniejsze w cieczach, a minimalne w
ciałach stałych. Ośrodek skalny będąc mało sprężystym, niejednorodnym, porowatym tłumi fale silniej niż
ciecz. Dlatego współczynnik tłumienia fali w skałach porowatych w miarę nasycenia ich wodą zmniejsza
się.
12. Termiczne własności skał
Procesy fizyczne związane z przewodzeniem i pochłanianiem ciepła oraz jego oddziaływaniem na ośrodek
skalny charakteryzowane są, własnościami termicznymi skał.
Ogólnie przepływ energii cieplnej w ośrodku skalnym odbywa się na drodze:
- kondukcji (przewodnictwa cieplnego;
- konwekcji (unoszenia);
- radiacji (promieniowania).
Przewodność cieplna skał
Przekazywanie ciepła w ciałach jednorodnych odbywa się na drodze zmiany energii kinetycznej przy
zderzeniach elektronów lub stopniowego przekazywania drgań siatki krystalicznej od jednej części do
drugiej.
Pierwszy typ przewodności nosi nazwę elektronowej i jest charakterystyczny dla metali i
półprzewodników.
Drugi typ można identyfikować zasadniczo z drganiami części siatki krystalicznej. Fonony to kwanty pola

drgań siatki krystalicznej. Każdy fonon podobny jest do fotonu, posiada więc energię równą h
.
f, gdzie:
h — stała Plancka (h = 6,62607
.
10
-34
J
.
s),
f— częstotliwość drgań cieplnych, Hz.
W skałach występuje więc przewodność fononowa.
Współczynnik przewodzenia ciepła
λ
równy jest ilości ciepła Q, przechodzącego w jednostce czasu
τ
przez jednostkę przekroju poprzecznego S, przy gradiencie temperatur równym jednostce w przypadku
stacjonarnego strumienia ciepła (dT/d
τ = O):
(
)
⎥⎦
⎤
⎢⎣
⎡
⋅
−
⋅
⋅
=
K
m
W
T
T
S
L
Q
2
1
τ
λ
Q — ilość ciepła przechodzącego przez próbkę, J;
L — droga przepływu ciepła (długość próbki), m;
T
1
, T
2
— temperatury na skrajnych powierzchniach próbki. K;
τ — czas przepływu ciepła, s;
S — powierzchnia przekroju poprzecznego próbki, m
2
.
Odwrotnością współczynnika przewodzenia ciepła jest cieplna oporność właściwa
ξ
,:
λ
ξ 1
=
Stosunek cieplnej oporności właściwej mierzonej prostopadle do uwarstwienia
ξ
⊥
i do oporności
mierzonej równolegle do uwarstwienia
ξ
II
, charakteryzuje zjawisko anizotropii cieplnej. Współczynnik
anizotropii cieplnej określa się zależnością:
1
>
=
⊥
ii
k
ξ
ξ
ξ
Pojemność cieplna skał
Cieplna pojemność właściwa C
w
równa jest ilości ciepła Q potrzebnego do podwyższenia temperatury
jednostki masy skały o jeden stopień:
⎥
⎦
⎤
⎢
⎣
⎡
⋅
Δ
⋅
=
K
kg
J
T
m
Q
C
w
,
Pojemność cieplna objętościowa C
v
jest liczbowo równa ilości ciepła Q koniecznego do zmiany
temperatury jednostki objętości skały o jeden, stopień.
⎥⎦
⎤
⎢⎣
⎡
⋅
Δ
⋅
=
K
m
J
T
V
Q
C
v
3
,
Między pojemnością cieplną objętościową C
v
i właściwą C
w
istnieje następująca zależność:
C
v
= C
w
.
ρ
gdzie:
p — gęstość objętościowa skały, kg/m
3
.
Przewodność temperaturowa skał
Współczynnik przewodzenia temperatury a — charakteryzuje prędkość rozchodzenia się temperatury w
skale i równy jest stosunkowi przewodzenia ciepła
λ do iloczynu właściwej pojemności cieplnej C
w
i
gęstości obję ściowej skaty
ρ :
to
⎥
⎦
⎤
⎢
⎣
⎡
=
⋅
=
s
m
C
C
a
v
w
2
,
λ
ρ
λ
Rozszerzalność cieplna skał
Związek między przyrostem temperatury próbki skalnej, a zmianą jej wymiarów początkowych charaktery
żuj ą współczynniki cieplnej rozszerzalności liniowej i objętościowej.
Współczynnik cieplnej rozszerzalności liniowej
β
— charakteryzuje zdolność skały do zmiany swoich
wymiarów liniowych podczas przyrostu temperatury:
⎥⎦
⎤
⎢⎣
⎡
Δ
⋅
Δ
=
K
T
L
L
1
'
β
L —początkowa długość nieobciążonej próbki skalnej, mm;
ΔL — przyrost wymiarów liniowych próbki skalnej, mm;
ΔT— przyrost temperatury w wybranym zakresie temperatur, K.
Współczynnik cieplnej rozszerzalności objętościowej
ω
— charakteryzuje zdolność skały do zmiany swej
objętości podczas przyrostu temperatury:
⎥⎦
⎤
⎢⎣
⎡
Δ
⋅
Δ
=
K
T
V
V
1
,
ϖ
Naprężenia termiczne
σ
T
są to naprężenia pojawiające się w skale w wyniku nierównomiernego ogrzewania
poszczególnych ziaren mineralnych skały.
T
L
L
T
Δ
⋅
=
=
Δ
β
ε
Przy uwzględnieniu tylko rozszerzalności liniowej:
[
]
2
/
,
m
N
T
E
Δ
⋅
⋅
=
β
σ
T
Przy uwzględnieniu rozszerzalności objętościowej:
[
]
2
/
,
2
1
m
N
T
E
T
K
T
ν
β
ω
σ
−
Δ
⋅
⋅
=
Δ
⋅
⋅
=
K— moduł sprężystości objętościowej, Pa;
v — liczba Poissona.
Zmiany temperatury z głębokością zalegania skał
Stopień geotermiczny S
g
- jest to liczba metrów przy której temperatura wzrasta o 1°C względnie l
K.
⎥⎦
⎢⎣
Δ
K
T
g
⎤
⎡
Δ
=
m
H
S
,
Δ
H— przyrost głębokości, m;
ΔT— przyrost temperatury o 1°.
Wartość stopnia geotermicznego waha się lokalnie między 5 i 100 m. Dla Europy zachodniej i środkowej,
przeciętny stopień geotermiczny wynosi 33 m.
Gradient geotermiczny G
g
—jest to liczba stopni o jaką temperatura wzrasta na l m głębokości:
⎥⎦
⎤
⎢⎣
⎡
Δ
Δ
=
m
K
H
T
G
g
,
Temperaturę panującą na danej głębokości określa się według wzoru:
T = T
o
+ G
g
(H-H
o
)
gdzie:
T— temperatura panująca na głębokości H;
T
o
— temperatura warstwy neutralnej na H
o
= 20 m, równa średniej rocznej temperaturze powierzchni
Ziemi;
H— rozpatrywana głębokość;
H
o
— głębokość warstwy neutralnej.
Dla skał niejednorodnych przebieg zmiany temperatury z głębokością nie ma jednak charakteru
prostoliniowego, dlatego można go wyrazić za pomocą zależności:
T = T
o
+ a(H-H
o
)
b
gdzie:
a, b -parametry zależne od zmiany gradientu z głębokością.
Fizyka skał to nauko o fizyko technicznych własnościach skał i procesach fizycznych przebiegających w skałach
wywołanych działalnością budowlaną, górniczą, wiertniczą; współzaleznościach miedzy tymi własciwościami i
zasadach ich wykorzystania przy rozwiazywaniu zadań w takich dziedzinach jak górnictwo, bud komunikacyjne
wodne i inne.
Zasdania stawiane przed fiz skał to:
1)
badanie fizycznych wł skał
2)
określenie ich parametrów
3) ustalenie zmian wł fizycznych w warunkach zewnętrznego oddziaływania na skały pozwalajacych zmienić ich
właściwości fiz (podczas ogrzewania, ochładzania, nasycania cieczami, oddziaływań prądów elektrycznych itp.)
4) stworzenie systemów kontroli skladu budowy i zachowania się skał w procesach związanych z
oddziaływaniem pól fiz na osirodek skalny.
5)
Metody badania fizyki skał bliskie sa metoda stosowanym we współczesnej fizyce ciała stałego. W fiz
skał stosuje się szeroko zasady teorri prawdopodobieństwa, statystyki mtematycznej wykorzystując zalezności
uzyskane eksperymentalnie, a zjawisko fizyczne w skałach opisuje się w oparciu o doświadczenie.
FIZYCZNA STRUKTURA GÓROTWORU
GÓR- zewnetrzne warstwy skorupy Ziemskiej, które sa domena działalności górn (szeroko pojetej).
Materie bud górotwór oceniac można w nastepujących, wyraźnie różniących się skalach sormiarów
1)
Skala ultramikroskopowa- skala atomu lub drobiny pierwiastka, o rozmiarze 10^-10 m
2)
Skala mikroskopowa- pojedyńczego ziarna mineralnego o rozmiarze od 10^-6 do 10^-1 m
3)
Skala mezoskopowa- skala próbki skalnej
- labolatoryjnej o rozmiarze od 10^-2 do 10^-1 m
- naturalnej o rozmiarze od 10^-1 do 10m
4)
Skala makroskopowa- skala złoza akalnego o rozm od 10 do 10^2 m
5)
Skala megaskopowa- skala masywu skalnego o rozmiarze 10^2 do 10^4 m
W każdej skali wozmiarów wyrózniony został tzw charakterystyczny element strukturakny górotworu, do
których zaliczamy:
- Atom pierwiastka
- Ziarno mineralne
- Próbka skalna
- Złoze skalne
- Masyw skalny
Wymienione elementy wystepują w war naturalnych w stanie nienaruszonym, wzglednie jako skały rozluzowane
w wyniku urabiania
ELEMENTY STRUKTURALNE GÓROWORU
4 elementy strukturalne, tz: atom pierwiastka, ziarno mineralne, złoze skalne, masyw skalny wyodrebniają się z
górotworu w sposób naturalny. Jedynie próbka skalna to element struktóry wyodrebnionej z górtworu w sposób
sztuczny.
ATOM -zbiór at posiadających te same wł chem nazywamy pierwiastkiem chcem
-ilosciowy udział pierwiastków w bud górotworu nie jest równomierny, jak również ich udziała w składzie
poszczególnych minerałów i skał
- najbardziej rozpowszechnionych jest 8 pierwiastków: tlen 44,06%, krzem 27,72% glin 8,13% żelazo 5% wapń
3,63% sód 2,83% magnez 2,09% potas 2,59% Nastepne pierwiastki wchodza w skład w litosfery w ilości <1%
Ziarno mineralne- Minerały to okreslone zw chcem stanowiące składniki skorupy ziemskiej
- w war naturalnych wystepuje ok. 3000 róznych minerałów, w których 40-50 to tzw minerały skałotwórcze
(główne). Maja one określone właściwości fiz, chem uwarunkowane ich struktórą krystaliczną/
- minerał odpowiada 3 warunka: 1) powstaje w sposób naturalny, czyli samorzutny w skorupie ziemsjiej
- 2) posiada sciśle określony skład chcem 3) wykazuje ściśle określona strukture wewnetrzna
- Pod pojeciem struktóry krysztalicznej rozumie się określony pożądek rozmieszczenia cząstem materi. W
ciałach stałych, atomy, jony lub molekuły rozmieszczone sa w określonym uporządkowanym układzie
powtarzającym się we wszystkich kierunkach. Zbiur jednakowych kom elemntarnych złozonych względem siebie
równolegle i ściśle wypełniajacych przestrzeń stanowi sieć przestrzenna minerału.
- Naturalne, luźne lub lite zespoły materiałów powstałe w wyniku określonego procecu mineralnego nazywane sa
skałami.
ZŁOZE SKALNE – to nagromadzenie kopaliny urzytecznej powstałej w skorupie ziemskiej w wyniku
różnorodnyh procesów geologicznych Wyrózniamy złoza monomineralne i polimineralne
Ze względu na geneze wyróżniamy:
1)
złoza egzogeniczne- powstałe pod wpływem procesów zachodzących na powieszchni ziemi, gł wietrzenia,
sedymentacji.
2)
Złoża endogeniczne podstałe w wyniku krystalizacji magmy i jej resztek ciekłych i gazowych oraz
oddziaływania na srodowisko skalne.
3)
Złoza metamorficzne – powstałe z przeobrazenia powyższych
MASYW SKALNY- zespół różnych złóz skalnych, czyli okreslony obszar górotworu o objetości od kilkuset do
kilkudziesieciu tyś m3, w którym to obszarze zachodzą zjawiska fiz związane z działalnoscią górnicza,
budowlaną.
- przewaznie masyw skalny uległ deformacja siągłym w postaci fałdów (antyklin, synklin) oraz deformacja nie
siagłym w postaci uskoków, zrembów, rowów tektonicznych.
PRÓBKA SKALNA- próba z istoty swej ma charakter subiektywny wynikajacy z zamierzen wynikajacy z
zamierzeń osoby pobierajacej próbki z górotworu. Pobrane do badań labo,atoryjnych próbki nie uwzgledniaja
wpływu spekań jawnych, gdyz sa najcześciej wycinane z partji calizny miedzy istniejacymi szczelinami. Próbka
skalna badana w naturze (in situ) jest kilkadziesiat lub kilkaset razy wieksza od próbki laboratoryjnej;
prawdopodobieństwo napotkabia spekań, szczelin czy defektów strukturalnych jest wieksze w większej objetości,
lecz nawet największe spotykane próbki naturalne nie mogą pbjąć (3x3x3m) wszystkich zmian i defektów w skali
całego masywu skalnego. Ten losowy rozkład własności mechanicznych wystepujacych wyraźnie nawet w
jednym kawałku skały jest przycznyną takzwanego efektu skali.
Próbki o dużych wymiarach mają nizsze wartosci parametrów wytrzymałosciowych niż wykonane z tego samego
materiały próbki o małym wymiarze.
- badajac próbke skalną należy brać pod uwagę z jednej str stosunek rozmiarów próbki, do rozmiaru ziaren
mineralnych, natomiast z drugiej stos rozmiarów próbki, do rozmiarów złoza skalnego, którego własności mają
być oceniane na podstawie wynieków badań próbki skalnej.
CECHY STRUKTURALNE GÓROTWORU
STRUKTURA- te właściwości budowy skały, które uwarunkowane sa rozmiarami, kształtem i charakterem
powieszchni ziarn mineralnych oraz stopniem wykrystalizowania poszczególnych składników mineralnych.
- cechy strukturalne to te własności, które z określonym przybliżeniem wpływają na matematyczny opis
górotworu. Do cech strukturalnych zaliczamy: ciągłośc jednorodność, izotropię.
CIĄGŁOŚC- środowisko materialne jest ciągłym jeżemi dla 2 bliskich jego pkt różnica własności fiz tego
środowiska będzie dowolnie mała; pojecie ciągłosci najcześciej wiazane jest z rozmieszczeniem masy wewnątrz
obszaru zajmowanego przez dane srodowisko.
- Zakładając ciągłoścosrodka skalnego przyjmuje się, że dany obszar przestrzeni wypełniony jest masa bez
możliwości pozostawiania najmniejszych pustek. Gestość masy w danym obszarze jest funkcja ciągłą połozenia.
JEDNORODNOŚĆ – ciało materialne jest jednorodnym jeżeli w każdym pkt jego własności fiz będą takie same
- w odniesienui do osrodka skalnego stosuje się takie pojecie statystycznej jednorodności – środowisko
materialne jest statystycznie jednorodne, jeżeli jego każda podstawowa objetość o rozmiarach wynikających z
przyjetej skali rozważań posiada jednakowe wł fiz.
IZOTROPIA – ciało materialne jest izotropowe gdzy we wszystkich kierunkach badania wykazyją jednakowe
wartości własności fizycznych; gdy ciało wykazuje rózne wartości własności fiz w różnych kierunkach, wtedy
mówimy ze jest anizotropowe
- dla oceny stopnia anizotropii wykożystuje się współczynnik anizotropii, będący stosunkien wartości
najwiekszej do wart najmniejszje danej wł fiz.
- Izotropowe sa gazy, ciesze, jednorodne substancje bezpostaciowe. Anizotropowe sa kryształy, dzieki
upozadkowanej sieci krystalicznej

ELEMENTY I CECHY STRUKTURALNE GÓROTWORU
1)
Skala analizy: ultramikroskopowa, Elementy struktury: nazwa- atom pierwiastka, rozmiar: 10^-10 m,
Cechy strukturalne: ciagłość – nieciągłu, jednorodność - -, izotropia:-
2)
Sa: mikroskopowa, Es: n- ziarno mineralne, r- od10^-6 do 10^-1 Cs: c- ciągłe, defekty sieci krystalicznej,
j- statystycznie jednorodne, i- anizotropowe.
3)
Sa: mezoskopowa, Es: n- próbka skalna, Laboratoryjna: r- od 10^-2 do 10^-1 Cs: C- ciągła,
mikroszczeliny, miktospękania, j– niejednorodna, i- izotropowa. Naturalna: r- 10^-1 do 10 Cs: c- ciągła, spekania,
pory szczeliny, j- statystycznie jednorodna, i- anizotropowa
4)
Sa: Makroskopowa, Es: n- złoże skalne r- 10 do 10^2m, Cs: c- ciągłe, makrospękania, makroszczeliny, j-
niejednorodny, i- anizotropowy
CECHY TEKSTURALNE GÓROTWORU:
TERSTURA- te własciwości , które uwarunkowane sa sposobem przestrzennego ułożenia ziarn miner w osrodku
skalnym.Do cech teksturalnych zaliczamy: łupliwość, uwarstwienie, porowatość, szczelinowość
ŁUPNWOŚĆ- zdolność skał do łatwego pękania wzdłuż określonego układu płaszczyzn w których występuje
osłabiona spójność miedzy ziarnami
- takie skały jak piaskowce mają bardzo rzadką sieć łupnośc, co utrudnia ich załamywanie, w przeciwieństwoe do
skał łupkowych mających gestą sieć łupności
- utrzymanie wyrobiska korytarzowego w łupkach wymaga wzmocnionej obudowy.
UWARSTWIENIE: skał uwarunkowane jest kolejnością powstawania nakładających się utworów skalnych, o
róznym składzie chemicznym i mineralnym, różnej ziarnistości różnej orientacji ziarn.
- płaszczyzny rozdzielajacoe poszczególne warstwy, czytli płaszczyzny uwarstwienia są również płaszczyznami
osłabionej spójnosciskał. Płaszczyzny te w różnych skalach występują w różnych wzajemnych odległościach.
- średnia podzielność warstwowa dla skał ilastych wynosi 20,7 cm dla mułowców 28,7 cm, a dla piaskowców
40,1 cm
POROWATOŚĆ- występowanie w skałach pustek i szczelin oraz istnienie miedzy ziarnami mineralnymi
drobnych kanalików i wolnych przestrzeni, nawet w przypadku występowania materiału cementującego.
- porowatość określa się stosunkiem objetości wszystkich wolnych przestrzeni w skale do jej objętości, jest to
porowatośc ogólna
- pory które kontaktują się ze sobą decydują o porowatości efektywnej określane stosunkiem objętości porów
otwartych do całkowitej objętości skały
SZCZELINOWOŚĆ – istnienie w bud skały nieciągłości i powierzchni osłabienia o zasiegu przewyższającym
wymiary ziarn minerałów tworzących masyw skalny.
- skala w której występuje zespół szczelin nazywana jest skala szczelinową, natomiast gdy występuje sieć
pęknięć skałą spękaną.
- Ilosciowa szczelinowość określa się rozmiarem szczelin gęstością ich występowania oraz wzajemnym ich
usytuowaniem
SKAŁY JAKO OŚRODKI TRÓJFAZOWE
SKAŁY- naturalne zespoły jedno lub wieloskładnikowych minerałów występujących w postaci ziaren
krystalicznych lub cząstek bezpostaciowych, które mogą być spojone w bezpośrednim kontakcie lub przez różne
substancje cementujące
- skała składająca się z ziaren 1 minerału nosi nazwę skały monomineralnej (dolomit, wapień, sól kamienna)
Skała składająca się z z różnych minerałów nazywana jest skałą polimineralną (granity, piaskowce)
- Zarówno pory jak i szczeliny w skałach mogą być wypełnione cieczami lub gazami lub cześciowo cieczami i
gazami.
- Skały sa wiec ośrodkiem trójfazowym (f stała, ciekła, gazowa) Ze względu na rodzaj wiezi łączącej cząstki
wody z fazą stałąw skałach wyróznia się: wode chem związana, wodę fiz zwiazana, wodę wolną (swobodną)
WODA CHEM ZWIĄZANA jest czescią sieci krystalicznej ziarn mineralnych, usunięcie tej wody prowadzi do
rozkładu danego materiału, przekształcenia go w inny, odwodniony związek chem
W FIZYCZNIE ZW przylega ściśle do powierzchni ziarn mineralnych, przytrzymywana międzycząsteczkowymi
siłami przyciągania, otacza ona ziarna cienką błonką, nazywana jest więc woda błonkowa
W SWOBODNA – pypełnia wodne przestrzenie porów i szczelin w skale, a składa się z wody kapilarnej oraz
wody grawitacyjnej.
- woda kapilarna utrzymuje się w małych wąskich porach działaniem sił kapilarnych
- woda grawitacyjna wypełnia drobne pory, szczeliny i może się przemieszczać pod działaniem przyłożonego
cisnienia.

- Przy ogrzewaniu do 150C ze skały ustępuje woda wolna, luźnie związana z ośrodkiem skalnym. Przy dalszym
ogrzewaniu 150-400C odparowuje woda mocno związana przez wolne jony w miejscach uszkodzeń siatki
krystalicznej oraz u wierzchołków i boków kryształów cząstek skał. Przy temp ponad 400C zaczynają ustępować
jony wodorotlenkowe, które sa wewnątrz kryształów minerałów jako wody chemicznie związane
Przestrzenie porów i szczelin mogą być być wypełnione częściowo lub całkowicie gazami np.: powoetrzem, CO2,
metanem, para wodną. Gary w skalach wystepuja w 3 postaciach:
1-
gazu absorbowanego tzn pochłoniętego przez substancje skały
2-
g. Adsorbowanego na powieszchni ścianek porów
3-
g wolnego wypełniajacego szczeliny, pory, kanaliki w skałach.
PODZIAŁ SKAŁ ZE WZG NA GENEZĘ I WIĘZI MIĘDZY ZIARNAMI MINERALNYMI:
Ze wzg na warunki powstawania wyróżniamy skały:
-magmowe
- osadowe
- przeobrażone
SKAŁY MAGMOWE powstały w wyniku stygnięcia rozżarzonego stopu mineralnego pochodzącego z głębi
Ziemi, czyli magmy. Ze wzg na miejsce stygnięcia magmy, wyróżniamy skały:
A)
głębinowe- które krystalizują na dużych głębokościach, a wiec powoli np. sjenit, dioryt gabro
B)
subwulkaniczne- krystalizują bliżej powierzchni ziemi, w warunkach szybko obniżającej się temp i
ciśnienia, zaliczamy do nich pegmatyty i aplity
C)
wylewne- powstały dzieki szybkiemu stygnieciu lawy na powieszchni ziemi lub na dnie oceanów np.
porfiry, bazalty, diabazyt
S OSADOWE- powstały w procesie sedymentacji produktów mechanicznego i chem wietrzenia dawniej
powstałych skał magmowych, osadowych, przeobrażonych. Wyróżniamy skały:
- okruchowe,
- chemiczne, powstały przez wytracenie albo krystalizacje substancji rozpuszczalnych w wodzie (boksyty,
dolomity)
- organogeniczne powstały ze zczatków organizmów żywych (wegle, wapienie)
Wśrud skał okruchowych wyrózniamy:
- przefity- gruboziarniste, śr ziarn 22mm (żwir, gruz, otoczaki)
- psamity- śr ziarn 0,05 do 0,2 mm (piaski)
- pelity- śr ziarn < 0,05mm
S PRZEOBRAŻONE powstały w wyniku przemiany skał magmowych lub osadowych poprzez działanie np.
temp, ciśnienia oraz działanie gorącej wody i gazów, które to działania spowodowały rekrystalizacje skał
pierwotnych (ortognejsy, ortołupki, kwarcyty)
Ze względu na rodzaj więzów między ziarnami mineralnymi wyróżniamy:
- okruchowe
- spoiste
- zwięzłe
S OKRUCHOWE- prosta mieszanina różnych ziaren mineralnych bez żadnych wzajemnych wiązań
przeciwdziałających rozdzielaniu się ziarn (piasek, żwir)
S SPOISTE ziarna mineralne tych skał posiadają otoczki koloidalne spajające ziarna w jedną całość (iły, gliny)
S ZWIĘZŁE (lite,) występują w nich trwałe, sztywne lub spręzyste więzi miedzy ziarnami mineralnymi, czyli
skały typu granity, grejsy, piaskowce, wapienie.
KLASYFIKACJA WŁ FIZYCZNYCH SKAŁ
Pod pojeciem wł fiz rozumie się te cechy charakterystyczne skał związane z jej budową, które pozwalają na
odróżnienie lub porównanie danej skały z innymi oraz stwarzają mozliwośc przewidywania przebiegu i skutków
interesujących nas prcesów fiz ciał. Liczbowo kazda własność fizyczna skały określana jest jednym lub kilkoma
parametrami będącymi ilościowymi miarami własności.
- Wyróżnione parametry fiz dzielimy ze względu na rodzaj wywołujących je pól fiz, określony zespól
parametrów charakteryzuje daną gr wł fiz. Pod pojęciem pól zewnętrznych rozumiemy ten rodzaj energii materi
pod działaniem której w danej chwili znajduje się skała. Wyróżniamy więc:
a)
pole mechaniczne i odpowiadające mu mech wł skał
b)
pole cieplne (termiczne wł skał)
c)
p elektryczne
d)
p magnetyczne
e)
p promieniotwórcze (c-d i odpowiadające im wł skał)
Ponadto wyróżniamy
f) pola malenarne tzw substencjalne i opowiadające im hydrogazomechaniczne wł skał.
Ze wzg na istotę fizyczna parametry fiz dzielimy na 3 gr:
1)
parametry charakteryzujące odwracalne zmiany ilości E lub materii wewnątrz skały (np. moduł
spręzystości objętościowej, wilgotność, względna pojemnośc cieplna)
2)
Parametry określające nieodwracalne zmiany danego rodzaju E w skałach w inny rodzaj E, a prowadzace
do istotnej zmiany stanu skały (np. wytrzymałość dorażna na sciskanie, wsp plastycznośći)
3)
Parametry opisujące procesy przekazywania E a także przepływu cieczy i gazu w skałach ( np. wsp
przepuszczalności, filtracji0
- znanych jest ponad 100 parametrów fiz skał, pomiar takiej ilości parametrów dla wszystkich rodzajów skał jest
zadaniem praktycznie niewykonalnym. W praktyce labolatoryjnej wyróżnia się pewną ograniczoną liczbe
parametrów fiz skał bedoącą czasowo min, ale wystarczającą dla pełnej charakterystyki skały jako ciała fiz,
geologicznego. Wyrożnoine paramerty noszą nazwe podst parametrów skał. Zaliczamy do nich 12
elementarnych, wyjściowych i niezależnych parametrów fiz pozwalających określić max ilość innych parametrów
Do parametrów podst zaliczamy:
1)
grstośc obj
2)
porowatośc
3)
wytrzymałośc doraźną na ściskanie
4)
-//- rozciąganie
5)
moduł spr podłuznej
6)
wsp Poissona
7)
wsp przewodzenia ciapła
8)
cieplna pojemność właściwa
9)
wsp cieplnej rozszeżalności liniowej
10)
elektryczny opór własciwy
11)
przenikalność elektryczna względna
12)
przenikalność magnetyczna wzgl
SKAŁY A GRUNTY BUD
Wyróżnione gr skał ze wzgledo na rodzaj wiezów miedzy ziarnami mineralnymi obejmują 3 gr skał
1)
skały okruchowe (np. zwir, piasek)
2)
s spoiste (np. less, ił)
3)
s zwięzłe (piaskowce, granity)
- Pierwsze 2 gr skał okreslamy nazwa grunty. Skały i grunty to z technicznego pnk widzenia 2 rózne ośrodki.
Grunty reprezentują ośrodek rozdrobniony, skały ośrodek nieciągły w strefie przypowierzchniowej lub osrodek
ciagły na duzych głęgokościach.
- Grunty sa produktem wtórnym powstałym ze skał. Przeprowadzenie ścisłej granicy między skałami a gruntami
jest niekiedy trudne, przykładem mogą być iły które pozbawione wilgoci przybierają wł skał zwięzłych,
natomiast zawilgocone stają się typowym gruntem spoistym
- Róznica miedzy gruntami okruchowymi a spoistymi polega na tym, że w gruntach sypkich jedyną zięź miedzy
ziarnami miner stanowia siły tarcia. Natomiast w gruntach spoistych miedzy cząsteczkami występują pewne siły
spójności określone jako więzi wodno-koloidalne. Róznica między skałami a gruntami polega na tym, ze skały
posiadają charakter ośrodka stałego litego, a grunty ośrodka rozdrobnionego
PODZIAŁ GRUNTÓW BUD
Przez grunt bud rozumie się część skorupy ziemskiej z obiektem bud stanowiącym jego część, wzg słuzacą jako
twozywo do wykonywania z niego bud ziemnych.
Grunty bud dzielimy:
Ze względu na pochodzenie
a)
antropogeniczne
b)
naturalne
g antropogeniczne- nasypowe, utworzone z produktów gospodarczej lub przemysłowej działalności człowieka,
odpadów komunalnych, po flotacyjnych, pyłów
g naturalne- których szkielet powstał w wyniku procesów geologicznych, a które ze wzgledo na pochodzenie
dzieli się na: -rodzime – nasypowe
G naturalne rodzime- są to grunty powstałe w miejscu zaleganie w wyniku procesów geologicznych takich jak:
witrzenie, sedymentacja, metamorfizm
G naturalne nasypowe- sa to g powstałe w wyniku działalności człowieka z g naturalnego lub antropogenicznego
np. w zwałowiskach, wysypiskach, bud ziemnych, nasypach bud itp.
NASYP BUD grunto powstały w skutek kontrolowanego procesu technicznego np. w bud ziemnych

NASYP NIE BUD- grunt powstały w sposób nie kontrolowany, w zwałowiskacj, wysypiskach
G RODZIME ze wzgledo na zawartośc substancji organicznej dzielimy na:
-gr mineralne
-gr organiczne
Gr mineralne – gr rodzime zawierające < 2% substancji organicznej. W gruntach organicznych zawartość
substancji organicznej >2%
ZE wzg na odkształcanie podłoża, czyli wytrzymałość, gr mineralne i organiczne dziela się na gr skaliste i nie
skaliste
GR MIN SKALISTE gr lite lub spekane o nieprzesuniętych blokach, których próbki nie wykazuja zmian
objetości ani nie rozpadaja się pod działaniem wody destylowajej, a ich wytrzymałośc na sciskanie jest wiekszan
0,2 Mpa najmniejszy wymiar bloku jest wiekszy od 10 cm
PODZIAŁ GR SKALISTYCH ZE WZGL NA WYTRZYMALOŚĆ
Nazwa gr: Skalisty twardy, skalisty miękki, Symbol: ST, SM, wytrzymałość na ściskanie: Rc>5Mpa, Rc<=5Mpa
PODZIAŁ GR SKALISTYCH ZE WZGL NA SPĘKANIA
1) Nazwa gruntu: Skała lita, Symbol: Li, Okreslenie spekań: brak widocznych spękań ( szczeliny oszerokości
<=0,1mm)
2) Ng: skała mało spękana, S: Ms, Os: szczeliny występują nie gęściej niż co 1m i mają szerokość nie większą niż
1mm
4)
NG: skała średnio spekana, S: Ss, Os: szczeliny występują geściej niż co 1m i mają szerokość nie wiekszą
niż 1mm, lub szczeliny występują nie gęściej niż co 1m, lecz mają szerokość wiekszą niż 1mm
GR MIN NIESKALISTE- nie spełniają war gruntu skalistego, grunt rozdrobniony, bez silnych wiązań.
ZE WZG NA UZIARNIENIE GR TE DZIELIMY NA:
Nazwa (symbol)- uziarnienie
Kamienisty (K)- d50>40mm
Gruboziarnisty (wg 3,8)- d50<=40mm, d90>2mm
Drobnoziarnisty (wg 3.10.3.13)- d90<= 2mm
GRUNTY KAMIENISTE- zawartość ziarn o srednicach >40mm sdtanowi >50%
GR GRUBOZIARNISTE- zawartość ziarn o srednicach <40mm sdtanowi >50% oraz o zawartośći ziarn
większych od 2mm stanowi >90%
GR DROBNOZIARNISTE- zawartość ziarn o srednicach <2mm sdtanowi >90%
Podana klasyfikacja gr nieskalistych mineralnych wprowadza podział okruchów skalnych na frakcje
FRAKCJA GR- zbior ziarn lub cząstek gruntu o srednicach zastępczych zawartych w określonym przedziale
SREDNICA ZASTĘPCZA dla ziarn mineralnych to średnica oczka sita przez które ziarno już nie przechodzi, zać
dla cząstek jest to średnica kulki o identycznej gęstości właściwej, opadająca w wodzie z taka camą predkościa
jak dana cząstka gruntu.
Wśród gr niestalistych wyróżniamy następujące frakcje:
Nazwa frakcji- symbol % zawartość frakcji- zakres srednic zastępczych d[mm]
Kamienista-fk-d>40
Żwirowa- fż-40=>d>2
Piaskowa- fp-2>=d>0,05
Pyłowa- f(pi)-o,o5>=d>0,002
Iłowa-fi- 0,002>=d
GR KAMIENISTE NIE SKALISTE ze względu na genezę i uziarnienie dzielimy na:
Nazwa- charakterystyka
Zwietrzelina, zwietrzelina gliniasta- grunt występuje w miejscu wietrzenia skały w stanie nienaruszonym
Rumosz, rumosz gliniasty- grunt występuje poza miejscem wietrzenia skały pierwotnej, lecz nie podlegał procesa
transportu i osadzania w wodzie.
Otoczaki –grunt osadzony w wodzie
GR GRUBO ZIARNISTE NIESKALISTE MINERALNE w zal od uziarnienia dzielimy na:
Nazwa- symbol-uziarnienie
Żwir, żwir gliniasty – Ż, Żg- fi’<=2%, fi’>2% fk+fż>50%
Pospółka, pospółka gliniasta- Po, Pog- fi’<=2%, fi’>2%, 50%>=fk+fż>10%
GRUNTY DROBNOZIARNISTE ze względu na UZIARNIENIE dzielimy na
Nazwa gr- symbol- uziarnienie
Piasek gruby-Pr- zawartośc ziarn o srednicy >0,5mm wynosi więcej niż 50% (d50>0,5mm)
Piasek sredni –Pś- zawartość ziarno o srednicy >0,5mm wynosi nie wiecej niż 50%, lecz zawartość ziarn o
średnicy wiekszej niż 0,25mm wynosi więcej niż 50% (0,5mm>=d50>0,25mm)
Piasek drobny- Pd- zawartość ziarn o średnicy <nizo,25mm wynosi więcej niż 50% (d50<=0,25mm)
Piasek pylasty- Ppi- fp’=68 do 90%, fpi’=10 do 30%, fi’=0 do 2%
Wyżej wymieniony podział dotyczy gr drobnoziarnistych niespoistych. W śród gr nie skalistych mineralnych
drobnoziarnistych wyrózniamy także gr spoiste tzn takie gdzie wartośc wskaźnika plastyczności jest >1%.
Poprzednoi wymienione gr drobnoziarniste, niespoiste charakteryzują się wartością wskaźnika plastyczności <1%
GR MINERALNE DROBNOZIARNISTE SPOISTE ze wzg na uziarnienie dzielimy na
a) piasek gliniasty,
b) pył piaszczysty,
c) pył
d) glina piaszczysta
e) glina
f) glina pylasta
g)
glina piaszczysta zwięzła
h)
glina zwiezła
i) glina pylasta zwięzła
j) ił piaszczysty
k)
ił
l) ił pylasty
Wśród gruntów rodzimych oprócz gr mineralnych wyrówna się również gr organiczne, które dzielą się na skaliste
i nie skaliste.
GR ORGANICZNE SPOISTE- dzielą się się ze względu na stopień ich uwęglenia, wyrózniamy: -wegiel
brunatny, -wegiel kamienny
GRUNTY ORGANICZNE NIESKALISTE- gr rodzime w których zawartość cząstek organicznych >2%. W sród
nich wyróżniamy:
-grunt próchniczy, gdzie zawartość czastek organicznych jest w granicach 2-5%
-namuł- zawartuśc cząstek organicznych 5-30%
-torf- zaw cz org >30%
.......GRUNTY BUD......
KRYTERIA PODZIAŁU GR BUD
W podziale gr bud zastosowano następujące kryteria:
a)
pochodzenie
b)
uziarnienie
c)
zawartość cześci organicznych
d)
sposób formowania
e)
wskaźnik opadania zapadowego
UZIARNIENIE- analiza granulometryczna. Analize tą wykonuje się w celu wyznaczenia % zawartości
występujących w gruncie frakcji. Wyrózniamy:
- Metode analizy sitodej d>0,063mm
- Metodę areometryczną d<0,063mm
ANALIZA SITOWA- polega na przesianiu wysuszonej w temp 105-110C próbki gruntu nie spoistego przez
odpowiedni komplet sit, o różnych wymiarach oczek i obliczeniu w % masy ziarn pozostałych na sitach w
stosunku do sałkowitej masy badanej próbki gruntu. Komplet sit składa się z 9 sit o wymiarach oczek
kwadratowej siatki: 40; 25; 10; 2; 1; 0,5; 0,25; 0,1; 0,071 lub 0,063 mm. Czas przesiewania próbki na wstrząsarce
wynosi ok. 5 min, przesiewanie uznaje się za zakończone jeżeli próbka kontrolna nie wykazuje przechodzenia
ziarn przez sita. Zawartość wagową ziarn gruntu pozostałych na każdym sicie okresla się zależnościa
Zi=msi/ms *100%
Msi- masa suchych ziarn pozostałych na sicie
Ms- masa całej suchej próbki wzietej do analizy
Mając wyznaczone wartości Zi, czyli % zawartośći ziarn na poszczególnych sitach oblicza się następnie ich sumu
rozpoczynając os sita najgrubszego, a nas5ępnie sporządza się wykres uziarnienia. Wykresy te nanosi się na
siatkę półlogarytmiczna, gdzie na osi odciętych podano średnice ziarn i cząstek, a na osi rzędnych w skali
dziesiętnej ich % zawartości. Z wykresu uziarnienia można wyznaczyć
1)
poszczególne zawartości poszczególnych frakcji niezbedne do określenia rodzaju gruntu
2)
średnicę dla d10, d30, d60 niezbędne do określenia wskaźników uziarnienia
d60-średnica czastek ponizej której jest 60 % cząstek w danym gruncie.
UZIARNIENIE charakteryzowane jest przez 2 wskaźniki
1)
wskaźnik kóżnoziarnistości

U=d60/d10
2)
wskaźnik krzywizny uziarnienia C= (d30)^2/(d10*d60)
Ze wzgl na wartość wskaźnika róznoziarnistości wyróżniamy grunty:
1)
równo ziarniste 1=<U=<5
2)
różnoziarniste 5<U<=15
3)
b różnoziarniste U>15
ANALIZA AREOMETRYCZNA należy do metod sedymentacyjnych. Badania polegające na rozfrakcjonowaniu
gruntu w zawiesinie wodnej zaliczane są do metod sedymentacyjnych; oparte sa ona na prawie Stocesa, które
określa, że predkość swobodnego opadania cząstek kulistych jest wprost proporcjonalna do ich srednicy i gęstości
właściwej. V= [2(ro s- ro w)*g]/9ń *[d*v^2]/4
v- predkośc opadania cząstek
d- srednica cząstek (zwana srednica zastępczą)
ro s – gęstość wł szkieletu gruntowego
ro w- gestość wł wody
g- przyspieszanie ziemskie
ń- wsp lepkości
Prawo stoklesa dotyczy opadania cząstek kulistych, a cząstki gruntowe maja kształty nieregularne. Ponieważ cz o
jednakowych wymiarach opadaja ze stała predkościa gęstośc zawiesiny ulegała będziezmianie na róznych
głębokościach w zależności od poziomu cieczy w naczyniu, a wielkość zmian gęstości zależeć będzie od czasu.
średnice zastępczą która przyjmuje się w badaniu określa się jako srednicę cząstki kulistej opadającej w wodzie z
taką sama prędkością co rzeczywiste cząstki gruntu.
W laboratorium do tych celów wykonuje się tz analizę granulometryczna, w której zadajemy pytanie jaka jest
średnica cząstki która przebywa drogę w czasie t. Wzór określający średnice cząstki ma postać:
Hr-droga czastki
t- czas opadania cząstki, czas pomiaru
Procentowa zawartość cząstek o srednicach zawartych w badanej próbne można zapisać wykozystujac zapis
skrócony.
Wskażnik odczytu oblicza się z zalezności Ri= (r-1)*10^3
r- odczyt pełna na ereometrze
W celu uproszczenia obiczeń odczyty wstaźnika skróconego Ri wykorzystuje się do określenia, średnic
wzorcowych Dwzi, które odczytywane sa z tabel.
Srednice cząstek można określić z zależności: di= Dwzi*K- wsp.
Procentową zawartość cząstek o średnicach zastępczych <=di wyznacza się z zależności
W wyniku analizy areometrycznej uzyskaliśmy średnice zastępcze, zawartość % poszczególnych frakcji. Mając
obliczone wartości Zi di spoządza się wykres uziarnienia, po wykreśleniu krzywej uziarnienia, odczytuje się z
niej zawartośc frakcji piaskowej, pyłowej i iłowej; zuma tych frakcji musi wynosić 1005. Mjac te dane i
posługując się trójkątem Fereta określa się nazwe gruntu.
TRÓJKAT FERETA to trójkąt równoboczny, którego boki podzielone sa na 10 równych części, z pkt podziału
boków trójkata przeprowadza się linie równoległe do pozostał uch boków. Każdy z boków reprtezentuje
zawartość od 0 do 100% jednej frakcji. Pole trójkata podzielone jest na cześci z których kazda reprezentuje
określona nazwe gruntu. Odkładając uzyskaną zawartość frakcji na boku trójkata prowadzi się linię równoległą
do lini zerowej dla danej frakcji w kierunku środka trójkąta. Pkt przeciecia 3 lini znajdujących się w określonej
części pola trójkata wyznacza rodzaj i nazwe badanego gruntu.
ZAWARTOŚC CZĘŚCI ORGANICZNYCH grunty zawierające ponad 2% cześci organicznych sa okreslane
jako grunty rodzime, nie skaliste, organiczne. W sród nich wyróżniamy:
- gr pruchniczy o zawartości cz organicznych 2-5 %
- namuł -//- 5-30%
- torf -//- >30%
Zawartość cz organicznych można określić 2 metodami:
1)
utleniania
2)
prazenia
Iom=(mst-mu)/(mst-mt) *100
Iom=(mst-mp)/(mst-mt) *100 + (z1+z2)

Z1- poprawka % zależna od zawartości w gruncie CaO zmienia się od 0 do 1%
Z2- poprawka w % uwzgledniająca utraty wodu w czasie prażenia 1-1,5%
Mp- masa tygla lub zlewki z próbka gruntu po wyprażeniu do stałej masy.
Mst- masa tygla lub zletki z próbka gruntu po wysuszeniu do stałej masy
Mu- masa zlewki z próbka gruntu po utlenieniu wody.
Mt- masa tygla lub zlewki
Jako podstawowa metode do kreślania zawartości cząstek org przyjmuje się utlenienie zawartości cząstek org
30% roztworem wody utlenionej. Metody tej nie można stosować, gdy badany grunt zawiera widoczne części
drewna, rośli, czyli ma niweątpliwie ponad 10% częsci organicznych. Wówczas tej metody nie należy stosowac,
zaleca się metode prażenia, która polego na spalaniu substancji organicznej w piecu i obl ilości tej substancji ze
straty masy.
SPOSÓB FORMOWANIA GRUNTU gr bud powstałe w wyniku działalnosci człowieka, to grunty nasypowe, w
zalezności od sposobu ich formowania, czyli pochodzenia wyrózniamy nasypy:
- budowlane- powstałe w wyniku kontrolowanego prcesu technologicznego np. budowle ziemne
- niebudowlane- formowane w sposób przypadkowy np. wysypiska
WSKAŹNIK OSIADANIA ZAPADOWEGO grunty o strókturze nietrwałej, ulegającej zmianie pod wpływem
zawilgocenia bez zmiany działajacego obciążenia nazywa się pkt zapadowymi. Ilościowo takie grunty
charakteryzowane sa przez wskaźnik osiadanie zapadowego. Imp=(h’-h’’)/ho
Ho- wysokość próbki w stanie naturalnym
H’- wysokośc próbki skonsolidowanej pod wpływem naprężenia całkowitego bez nasycenia woda
H’’- wysokośc próbki skonsolidowanej pod wpływem naprężenia całkowitego po uprzednim nasyceniu wodą.
Do próbek zapadowych zalicza się takie dla których imp>0,02
BADANIA MAKROSKOPOWE GR BUD polegaja na przybliżonym określeniu nazwy i rodzaju gruntu oraz
niektórych jego cech fizycznych bez pomocy przyzadów. W ramach badań makroskopowych określa się;
- rodaj i nazwe gruntu
- stan gr
- barwe
- wilgotność naturalną
- zawartośc CaCO3
Próbki do badań makroskopowych pobiera się z każdej warstwy gruntu rózniącej się rodzajem lub stanem
rzadziej niż co 1m głębokości.
Wyróżniamy 3 rodzaje próbek:
- o naturalnym uziarnieniu
- o naturalnej wilgotności
- o naturalnej strukturze
RODZAJ oznaczenie gruntów skalistych makroskopowo dokonuje się poprzez oględziny i proste próby
wytrzymałościowe. W obrebie gruntów kamienistych oznaczen dokonuje się przez pomiar najwiekszych ziaren i
podanie ich stosunku do reszty gruntu. Określamy w ten sposób stopień ich obtoczenia np.: słabo obtoczone, ostro
krawedziste, kanciaste.
Grunty drobnoziarniste wstępnie wydziela się gr spoiste od nie spoistych. Do nie spoistych, czyli sypkich zalicza
się takie, które po wyschnięciu nie tworzą brył, grudek, lecz sa sypkie. Do gr spoistych zalicza się takie które po
wyschniciu tworza zwarta bryłę. Dla rozróznienia zy grunt jest spoisty, czy nie spisty, a próbka jest wilgotna z
gruntu próbuje się uformować kulkę o średnicy 7-8 mm gdy kulka da się uformowac grunt zalicza się do
spoistych. Mając określona spoistość ustala się w sposób szacunkowy zawartośc w gruncie frakcji piaskowej,
przez rozcieranie próbki gruntu miedzy dwoma palcami zanurzonymi w wodzie. Po określeniu frakcji piaskowej
kwalifikujemy grunto do jednej z 3 grup:
- grunty piaszczyste fp>50%, fpi <30%
- grunty pośrednie fp>30%, fpi> 30%
- grunty pylaste fp<30%, fpi>
W przypadkach wątpliwych przeprowadza się próbę rozmakania, w tym celu grudke gruntu umieszcza się na
sitce o oczkach kwadratowych 5x5 mm i zanuza się w wodzie. W zależności od czasu rozpadania okręla się
spoistość gruntu. Gdu grudka rozmaka natychmiast albo do 5 min grunt jest mało spoisty. Gdy grudka rozpada się
w <1 godz grunt średnio spoisty, t<24h zwięzłospoisty, t>24h bardzospoiste. Rodzaj gruntów niespoistych
okresla się w zal od iwlkości ziarn i ich % zawartości w poszczególnych frakcjach: wyróżniamu
żwir, gdy ziarno >2mm,
pospółka(d>2 mm10-50%, d>0,5mm >50%),
piasek gruby (d>2mm, <10%, d>0,5mm >50%),
piasek średni (d>2mm <10%, d>0,5 mm >50%, d>0,25 mm >50%)
piasek drobny (d>2mm <10%, d>0,5 mm >50%, d>0,25 mm <50%)
piasek pylasty 9d>0,0mm >50%, d>0,25 mm <50%)
Przy badaniach makroskopowych określenie rodzaju gruntu uzupełnia się opisem przewarstwień, domieszek,
zanieczyszczeń, geneza rguntu.
STAN gruntów spoistych określa się na podstawie liczby wykonanych wałeczkowań. Próba wałeczkowania
polega na uformowaniu z gruntu kuleczki o srednicy 7 mm, z której wykonuje się wałeczek o srednicy 3 mm. Na
podst rodzaju spekań oraz wyglądu wałeczka określa się spoistość gruntu.
- Kulka rozpłaszcza się lub rozsypuje grunt nie daje się wałeczkowa – pył, pył piaszczysty, piasek gliniasty –
mało spoiste.
- Wleczek rozwarstwia się podłużnie- pył, pył piaszczysty, proszek gliniasty – mało spoiste
- Od początku do końca wałeczkowania powieszchnia wałeczka bez połysku, wałeczek pęka poprzecznie –glina
pylasta, glina, glina piaszczysta- średnio spoisty
- Wałeczek początkowo bezpołysku, przy końcu wałeczkowania z połyskiem- glina pylasta zwięzła, glina
zwiezła, glina piaszczysta zwiezła- zwięzło spoisty
- Kulka i wałeczek od poczatku z połyskiem, ił, ił pylasty, ił piaszczysty – b spoisty
Przyjmuje się ze grunty występuja w następujących stanach:
- zwartym jeśli nie można uformować kulki
- półzwartym, jeżeli z gruntu można uformowac kulkę, a wałeczek peka podczas 1 wałeczkowania
- płynnym, jeśli z uwagi na rozwodnienie gruntu nie da się uformować kulki
BARWA I WILGOTNOŚĆ barwę określa się na próbce o wilgotności naturalnej. Barwe podstawowa podaje się
jako ostatnią, odcienie i intensywnośc barwy na miejscu pierwszym np. jasno-szaro zółta.
Wilgotność naturalna ustala się nastęmujaco:
- grunt jest suchy gdy bryłka gruntu spoistego przy zgniataniu peka, a po rozdrobnieniu daje suchy proszek lub
jeśli grunt stanowi od razu suchy proszek;
- grunt mało wilg. Jeśli bryłka gruntu spoistego odkształca się plastycznie przy zgniataniu, a ręka nie staje się
- wilgotna; grunt mokry jeśli przy sciskaniu gruntu w dłoni grunt odsącza wode
- grunt nawodniony jeśli grunt odsacza wode grawitasyhnie.
ZAWARTOŚĆ WĘGLANU WAPNIA zawartośc CaCO3 określa się na podst reakcji gruntu po pokropieniu go
20% roztworem HCl.
-Gdy grunt buży się intensywnie i długo (ponad 20s) mówimy że zawartośc CaCO3 >5%.
-Grunt burzy się intensywnie, ale krótko, zawartośc CaCO3 od 3 – 5 %
- grunt burzy si e słabo i krótko 1%<CaCO3<3%
- gdy występują tylko ślady reakcji lub jej brak to CaCO3<1%
STRUKTURALNE WŁ SKAŁ I GR
Składniku gruntów i sakał
1-
cz mineralne, 2-woda
2-
powietrze, 3-woda błonkowa
GĘSTOŚĆ jest podstawowym parametrem charakteryzującym własności strukturalne; wyróżniamy gęstość
pozorna (objętościową) oraz gestość własciwą (żaczywistą)
W ogólnym przypadku gestośc okreslanan jest stosunkiem sumy masy fazy stałej, masy fazy ciekłej i masy fazy
gazowej do sumy objetości tych faz: ro r=(m1+m2+m3)/(v1+v2+v3)
W warunkach laboratoryjnych objetość i mase dowolnego elementu wycietego z warstwy skanej określa się
nastepujaco: V= V1+v2+v3, m=m1+m2+m3
GESTOŚŚĆ OBJ jest to stosujek masy próbki skalnej do jej objetości ro= m/v [kg/m3]
GESTOŚĆ WŁ to stosunek masy cząstek stałych do ich objętości ro o= m1/v1, [kg/m3]
Miernikami gestości sa ciężar objętościowy i ciężar właściwy.
CIĘŻAR OBJ stosunek ciężatu fazy stałej G wraz z zawartmi w niej porami do jej objetości v. Gama =G/v
[N/m3]
CIĘŻAR WŁ stosunek ciezaru fazy stałej w stanie sproszkowanym i wysuszonym G1 do jej objetości v1. Gama 0
=g1/v1, [N/m3]
Pomiędzy wyżej wymienionymi zależnościami występują zależności:
Gama= g*ro, gama 0=g*ro 0
GESTOŚĆ OBJ szkieletu gruntowego- stosunek masy ziarn i cząstek stałych szkieletu gruntowego do objętości
całej próbki przed wysuszeniem. Ro d =m1/v
Gdy znana jest wilgotność określona jako stosunek masy wody do masy szkieletu W=mw/ms *100% wówczas:
ro= m/v= (m1+m2)/v =[m1+(W*m1/100%)]/v= ro d +(W/100%)*ro d
ro d = ro/(100+W) *100
CIĘŻAR OBJ szkieletu gruntowego – stosunek ciężaru wysuszonej próbki Gs do jej objetości przed jej
wysuszeniem v. Gama d =Gs/v
Gama d =ro d * g, gama d = gama/ (100+W) *100
GESTOŚC OBJ próbek skalnych najczęściej określa się następujacymi metodami:
1)
W pierścieniu, w cylindrze
Perścień lub cylinder należy wcisnąć równomiernie w grunt następnie oczyścić górną i dolną płaszczyznę i
zważyć, oraz wykozystać zależność: ro= (mmt-mt)/Vp, [g/cm3 lub kg/m3]
Mmt- masa pierścienia lub cylindra z gruntem
Mt- masa pierścienia lub cylindra
Vp- objetość pierścienia lub cylindra
Grunt spoisty- pierścień
Gr sypki - cylinder
2)
W wodzie
Próbke o określonej masie zanuza się w roztopionej parafinie w celu uzyskania powłoki dla zamknięcia porów
następnie próbkę oparafinowana wazy się w powietrzu oraz w wodzie, poprzez ważenie tzw hydrostatyczne. ro
=mm/v =
mm- masa próbki gruntu
v- objętość próbki gruntu
mp- masa próbki oparafinowanej
mpw- masa próbki oparafinowanej i znużonej w wodzie
ro w- gestośc właściwa wody
ro p- gestość wł parafiny
3)
W rtęci
Próbke waży się, a następnie zanurza w specjalnym naczyniu całkowicie wypełnionym rtęcią. Wypartą przez
próbkę rteć, wazy się a następnie określa się gęstość obj. Ro= mm/v/(mm*ro n)/mr
Ro n- gęstość właściwa rtęci
Mr- masa rtęci wypartej przez próbkę.
GESTOŚĆ WŁ szkieletu gruntowego- stosunek masy szkieletu gruntowego do jego objetości ro d= m1/v1
[kg/m3 lub g/cm3]
METODY POMIARU
1)
metoda piktometru
2)
kolba Le Chateliera
Najczęściej wykozystjujemy piktometrem
mt-masa miktometru
mg- masa piktometru z gruntem
mwt- masa piktometru napełnionego do kreski woda destylowaną
mwg- masa piktometru z gruntem i woda wypełniającą piktometr do kreski na szyjce
POROWATOŚĆ jest to stos objetości porów w próbce skały do objetości całej próbki P=Vp/V *100%
Dla wyznaczenia porowatości wykorzystujemy zależności wynikające z rysunku (5)
M1=Vs*ro 0
Ro d = m1/V= Vs*ro 0/ V=Vs*ro 0 =(1-P)* ro 0
Gama d= (1-P)* gama 0
P= (ro 0 – ro d)/ro 0= (gama 0-gama d)/gama 0
P=(1-gama/gama 0)*100%
Gama= gama 0(1- 0,01P)
Stosunek ciężaru objętościowego nosi nazwę wsp szczelności: ks=gama/gama 0
Dla scharakteryzowania porowatości wykozystuje się także wskaźnik porowatości, czyli stosunek objetości
porów Vp do objętości materiału skalnego Vs zawartego w próbce e=Vp/Vs [%]
Pomiędzy w/w występuje zależność P=e/(1+e) *100%
E=Vp/Vs=P/(1-P)= (ro 0 –ro d)/ro d= (gama 0 – gama d)/gama d
W odniesieniu do skały urobionej lub rozdrobnionej wykorzystuje się pojęcia:

1)
wsp rozluzowania- stosunek objetości rozluzowanej skały do jej objetości w stanie nienaruszonym
kr=Vr/V
2)
gestośc nasypowa- stos gęstości objętościowej skały w masywie do współczynnika rozluzowania. Ro n=
ro/kr
STOPIEŃ ZAGĘSZCZENIA- stos zagęszczenia istniejącego w naturze do największego możliwego
zagęszczenia danego gruntu
a)Obj piasku najbardziej luźnego]
b) objętość w naturze
c) objetość piasku najbardziej zagęszczonego
Ze względu na wartość Id wyróżniamy:
- grunt luźny id<=0,33
- grunt średnio zagęszczony 0,33<Id<=0,67
- grunt zagęszczony 0,67<Id<=1
HYDROGAZODYNAMICZNE WŁ SKAŁ charakteryzuja zdolność skał do przepuszczania, pochłaniania i
zatrzymywania różnych cieczy i gazów oraz skłonności skał do zmiany swego stanu mechanicznego podczas
oddziaływania cieczami lub gazami
WILGOTNOŚĆ skały to % stosunek masy wody w porach skały do masy suchej próbki czyli masy czkieletu
mineralnego. W= Mw/Md *100%
Praktycznie wilgotność określa się z zależności: W= (mmt-mst)/(mst-mt) *100%
Mst- masa parowniczki z próbka wilgotna
Mst- -//- suchą
Mt – masa parowniczki
Składniki gruntu ....
Mw= P*V*ro w, Md= Vs* ro s=(1-P)*V*ro s
Dla scharakteryzowania dziełania cieczy na ośrodek gruntowy wykorzystuje się pojęcia:
1)
WILG CAŁKOWITEJ- największa wzgledna ilośc wody, gdy pory skały sa całkowicie wypełnione woda:
Wsr= mw/md 100= [P*V*ro w]/[(1-P)V*ro s] 100= (e*ro w)/ro s *100
Wsr= (e*gama w)/gama s *100
2)
STOPIEŃ WILG: stosunek objętości wody znajdującej się w porach i pustkach skały do ich objetości
całkowitej: Sr=Vw/Vp
Sr=Vw/Vp=(Vw*ro w)/(Vp*ro w)= Mw/[Wsr/100 *Md]= [Mw/Md *100]/Wsr= Wn/Wsr= [Wn*ro s]/[100*e*ro
w]
Wn – wilg naturalna
Sr=(Wn* gama s)/(100*e*gama w)
W zalezności od stopnia wilgotności wyróżniamy:
-Sr=0 grunt suchy
-0<Sr<=0,4 gr mało wilgotny
-0,4<Sr<=0,8 grunt wilgotny
-0,8<Sr<=1 gr mokry
Powyższa klasyfikacja to stany zawilgocenia gruntów sypkich
Rozróżnia się konsystencje gr spoistych:
- płynna- jak ciecz bez wytrzymałości na ścinanie
- plastyczna- pewna wytrzymałość i odkształcalność, krak spekań
- zwartś- nuże naciski, spękania
Poszczególne konsystencje oddzielone są GRANICAMI, wyróżniamy:
1) GRANICA PŁYNNOŚCI Wl jest to wilgotnośc w % jaką ma masa gruntowa umieszczona w miseczce
aparatu Casagrande’a, gdy wykonana w niej bruzda zlewa się przy 25 uderzeniach miseczki o podstawę aparatu.
2) GRANICA PLASTYCZNOŚCI Wp jest to wilgotności w % jaka ma grunt, gdy przy kolejnym
wałeczkowaniu próbki gruntu pęka po osiągnięciu średnicy 8 mm

3) GRANICA SKURCZALNOŚCI Ws jest to wilg w % jaką ma grunt, gdy przy suszeniu bryłka gruntu
przestaje zmniejszać swa objetość. Można ja wyznaczyć z zależności: Ws= ro w (1/go d – 1/ro s)*100%
Ro d-gestośc obj szkieletu gruntowego
Ro s- gestość właściwa gruntu
WŁASNOŚCI PLASTYCZNE GRUNTÓW plastycznych charakteryzujemy:
a)
STOPIEŃ PLASTYCZNOŚCI stosunek różnicy wilgotności naturalnej danego gruntu i granicy
plastychności do różnicy granicy płynności i granicy plastyczności: Il= (Wn-Wp)/(Wl-Wp)
W zależności od wartości stopnia plastyczności i wilgotności naturalnej wyrózniamy następujące stany gruntów
spoistych:
- gr zwarty Wn<=Ws, Il<0
- gr półzwarty Ws<Wn<=Ws, Il<0
- gr twardoplastyczny 0<Il<=0,25
- gr plastyczny 0,25<Il<=0,5
- gr miękkoplastyczny 0,5<Il<=1
- gr płynny Wn>Wl, Il>1
B) WSKAŹNIK PLASTYCZNOŚCI róznica pomiędzy granicą płynności i granicą plastyczności Ip=Wl-Wp
C) STOPIEŃ KONSYSTENCJI: Ik=1-Il= (Wl-Wn)/(Wl-Wp)= (Wl-Wp)/Ip
Zdolność skał porowatych do przepuszczania cieczy i gazów siecią kanalików utworzonych z ich porów nazywa
się przepuszczalnością. Miara przepuszczalności jest wsp przepuszczalności określony z prawa Darcy’ego
WSP PRZEPUSZCZALNOŚCI: kpn=[Q/s*ł*grad p] *ń
Q- ilość cieczy lub gazu przechodząca przez próbkę [m2]
s- powieszchnia przekroju poprzecznego próbki
ł- czas przepływu
ń- lepkość dynamiczna [Pa*s]
grad p- różnica cisnień na pewnej drodze [Pa]
Sens takiego pomiaru wsp przepuszczalności polega na tym, że charakteryzuje on wielkość powieszchni
przekroju porów skały przez którą odbywa się przepływ. Czasem spotykamy się, że kpn [D], 1D=1,02*10^-12
m2
Powolne przesączenie się cieczy lub gazów przez system porów i kanalików pod wpływem cisnienia nazywa się
FILTRACJĄ. Chrakterystyczną cechą filtracji jest laminarny, czyli warstwowy ruch cieczy lub gazu. Miara
filtracjie jest WSP FILTRACJI: kf=Q/(s*ł*i) [m/s]
i- spadek hydrauliczny, róznica poziomów cieczy do drogi przepływu
określa predkość przepływu.
Pomiedzy tymi parametrami istnieje zalezność: kf=kpn*(gama 0/ń)
Gama0- ciężar cieczy, gazu
Ń- lepkośc dynamiczna
W zalezność od wsp filtracji skały dzielimy na:
- dobrze przepuszczalne kf>1000m/dobę
- średnio przepuszczalne 10m/dobe<=kf<=1000m/dobe
- słabo przpuszczalne 0,1m/dobe<=kf<10m/dobę
- nie przepuszczalne kf,0,1 m/dobe
Zdolnośc skał do zwiększania swej objętości przy nasycaniu wodą nazywa się PĘCZNIENIEM.
Miarą ilościową tego zjawiska jest WSP PĘCZNIENIA- określony jest stosunkiem przyrostu objetości
spęczniałej skały do jej objetości pierwotnej, lub stos przyrostu wysokości speczniałej skały do jeje wysokości
pierwotnej. Pv=(Vk-Vo)/Vo, Ph= (hk-ho)/ho
Oddziaływanie cieczy na ośrodek skalny charakteryzowane jest 3 pojęciami
1)
ROZMYWALNOŚĆ- charakteryzuje rozpadanie się skał pod wpływem mechanicznego i chemicznego
działania poruszającej się cieczy
2)
ROZMAKALNOŚC- charakteryzuje zdolnośc skał do utraty spójności i przeobrażania się w pulchna
masę, z częściowym lub pełnym zanikiem nośności pod wpływem wody stojącej.
Dal określenia rozmakalności wykorzystuje się tzw test 3 dobowy. Polegajacy na tym, że próbke umieszcza się w
naczyniu z woda na jedną dobę, następnie próbke wyjmuje się z naczynia i umieszcza się w warunkach
powietrzno-suchych na kolejną dobę. Na 3 dobę próbke wkłada się powtórnie do naczynia z wodą. Stan sróbki
oceniady jest według następującej skali:
TABELA
3)
ROZMIĘKALNOŚĆ- określa utratę wytrzymałości próbki pod wpływem wilgoci. Wyraza się ją poprzez
stosunek doraźnej wytrzymałości próbki na ściskanie w stanie suchym i po nasyceniu woda.

MECHANICZNE WŁ SKAŁ- charakteryzują zachowanie się skał przy oddziaływaniu na nie mechanicznych
obciążeń. W zależności od wielkości, kierunku, czasu działania powstają różnorodne związki między
naprężeniami i odkształceniami skał. Ze względu na charaktery tych zależności wyróżniamy:
-WŁ SPRĘŻYSTE- charakteryzują związki między napręzeniami i odkształceniami sprężystymi
- WŁ WYTRZYMAŁOŚCIOWE- charakteryzują związki między napręzeniami i odkształceniami niszczącymi
- WŁ PLASTYCZNE- charakteryzują związki między napręzeniami i odkształceniami nieodwracalnymi, ale
zachodząsymi bez naruszania struktury skał
- WŁ REOLOGICZNE- charakteryzują zmianę podanych własności przy długotrwałym działaniu odciążeń.
SPRĘŻYSTE WŁ SKAŁ- wł te określane są modułami sprężystości, czyli współczynnikani proporcjonalności
miedzy naprężenia i odpowiadającymi im odkształceniami.
1)
MOD SPRĘŻYSTOŚCI PODŁUŻNEJ E- wsp proporcjonalności między wielkością naprężeń
normalnych (ściskanie, rozciąganie) a odkształceniem względnym występującym wzdłuż osi próbki.
Wartość modułu zmienia się zależnie od obciążenia. W pkt Awykresu napreżenie- odkształcenie wartość jego
określana jest pochodną funkcji naprężenia do odkształcenia. EA=d Napr.A/d EA
W pewnym przedziałe naprężeń warość... określa się za pomocą tg kąta nachylenia cięciwy łączącej 2 pkt
krzywej. EBC=tg alfa=(napr C- napr B)/(EC-EB)
Praktycznie moduł okresla się z zależności: E=(^F*h)/(s*^h) [Pa]
^F- różnica obciążenia ^F=Fk-Fw, Fk=65%RC*s, Fw=(10-15%) Rc*s
s- pole przekroju początkowego
^h- zmniejszenie wysokości próbki przy obciążeniu od Fw do Fk
Na wartość mod sprężyst podł duzy wpływ wywiera porowatość skały, lub ściślej wzajemny stosunek
powieszchni fazy stałej do powieszchni porów Sp w rozpatrywanej płaszczyźnie próbki skalnej
2) LICZBA POISSONA- jest to współczynnik proporcjonalności między wzglednym poprzecznym ^d/d oraz
wsg oddkształceniem podłuznym ^l/l
^d/d=v* ^l/l
Odwrotność l. Poissona zmienia się zaleznie od głebokości zalegania skał.
Dla danego piaskowca przy małym obciązeniu m-12. Ze wzrostem wartości m maleje asymptotycznie do gramicy
m=2, co odpowiada nieściśliwości materiału. Materiał Nieściśliwy – zachowuje swoją objętość ptzy ściskaniu i
rozciąganiu
Wprowadzamy oznaczenia: v/(1-v)~=
λr – wsp rozporu bocznego
-Dla górotwotworu ziarkisto sypkiego:
λr=(1-sinϕ)/(1+sinϕ)=tg^2(45-ϕ/2)
ϕ- kąt tarcia wewnetrznego
- dal górotworu odpowiadającemu prawu Hooke’a
λr=!/(m-1)
3)
MOD SPRĘŻYSTOŚCI POSTACIOWEJ G- wsp proporcjonalności miedzy wielkością naprężeń
stycznych i odpwiadajacym im odkształcenią postaciowym, charakteryzującym zmiane kształtu ciała:
τ=σ*γ
4) MODUŁ SPRĘŻYSTŚOCI OBJĘTOŚCIOWEJ K- współczynnik proporcjonalności między naprężeniami
sciskającymi i wzbledna zmianą objętości^V/V: σ=K* ^V/V
4)
MODUŁ JEDNOSTRONNEGO ŚCISKANIA M:edometryczny moduł sprężystości- współczynnik
poopor. Między napreżeniami podłużnymi i odpowiadającymi im odkształceniami względnymi podczas ściskania
próbki skalnej w nieodkształcalnym cylindrze: σ=M *^l/l Różni się od mod Younga sposobem wykonania, bo
stosuje się bo do skał zwiezłych. Mod Mjest wielkością charakterystyczna dla skał sypkich i spoistych – gruntów.
Moduł spr podłużnej określa się w jednoosiowym stanie naprężenia i w trójosiowym stanie odkształcenia, a
moduł edometryczny określa się w jednoosiowym stanie odkształcenia i trójosiowym stanie naprezenia.
WYTRZYMAŁOŚCIOWE WŁ SKAŁ
Każde działanie sił zewnetrznych powoduje w skale przyrost naprężeń. Z chwila przekraczania wartości sił
miedzycząstechkowych następuje zmiana pierwotnego kształtu skały czyli odkształcenie właściwe określane są
doraźnymi wytrzymałościami skał występującymi przy określonych naprężeniach.
WTYRZYM DORAŹNA NA ŚCISKANIE-Rc: stosunek największej siły ściskającej, niszczącej próbkę do pola
powierzchni początkowego przekroju poprzecznego: Rc=F/S [N/m2]

WYTRZYM DORAŹNA NA ROZCIĄGABIE- Rr stosunek największej siły rozciągającej przy której próbka
ulega zniszczeniu do pola powierzchni początkowego. Rr=F/S [N/m2]
Najwygodniejsza metoda badania, jest metoda poprzecznego ściskania. Polega na obciążaniu próbki skalnej w
kształcie walca lub prostopadłościanu siłą ściskajacą równomiernie rozłożoną wzdłuż tworzącej walca lub wzdłuż
podłużnej krawędzi prostopadłościanu.
- dla próbek walcowych Rr=0,637F/dh [N/m2]
- dla próbek prostopadłościennych Rr= 0,734 F/bh [N/m2]
d- średnica próbki, h- wysokość próbki
F- siła krytyczna
b- przekątna podstawy prostopadłościanu
WYTRZM DORAŹNA NA ŚCINANIE Rt- przy czystym scinaniu Rt to stosunek rkytycznej siły F do pola
powierzchni ścięcia. Na ogół wytrzymałość na ścinanie przedstawiana jest za pomocą 2 parametrów: φ, c
Rt=F/s, ł=σ*tg φ+c, φ- kąt tarcia wewnetrznego
WYTRZYM DORAŹNA NA ZGINANIE Rg- dla próbki w kształcie beleczki o przekroju prostokątnym,
swobodnie podpartej, a obciążonej jedną siła skupioną w środku długości próbki wytrzymałośc na zginanie:
Rg=Mg/Wx=(3*F*l)/(2*b*h^2) [N/m2]
b-szerokośc belek
h- wysokośc przekroju
l- długość beleczki, odległość między podporami
Orientacyjne zależności między wytrzymałościami:
Rc>Rt>Rg>Rr, Rr=1/20 do 1/80 Rc, Rt=1/5 do 1/15 Rc, Rg=1/5 do 1/15 Rc
Mechanizm niszczenia skał kruchych:
Na wyidealizowanej charakterystyce odkształcającej się skały kruchej przy ściskaniu wyróżnić można kilka
odcinków reprezentujących poszczególne stadia zniszczenia skały:
I- stadium nieliniowego odkształcania się skały- pod wpływem napreżenia zamykanie mikro szczelin,
zmniejszenie objętości, krzywa odkształceń podłużnych wygięta jest zwykle w kierunku osi ε przy tym im skała
bardzie zbita, tym
II- stadium liniowego odkształcania się skały- przyrosty odkształceń- proporcjonalne do przyrostów naprężeń.
Stosunek poprzecznego poprzecznego do podłużnego odkształcenia skały.
III- stadium liniowości odkształceń podłużnych i nieliniowości odkształceń poprzecznych σxy i objętościowych
εv. Zapoczątkowany jest proces zniszczenia. Względny wzrost objętości skały. Moduł spręzystości podłużnej jest
stał, l poissona rośnie
IV-stadium nie liniowego odkształcania się skały- wzrost odkształceń poprzecznych, moduł maleje, l piossona
rośnie
V- stadium odkształceń i bezwzględnego wzrostu objetości.- dylatancja dochodzi do niekontrolowanej propagacji
makrospekań. Stadium kończy się osiągnięciem granicy wytrzymałości.
Z chwila skonstruowania tzw sztywnych maszyn wytrzymałościowych uzyskano wykresy na których
wyróżniamy 2 obszary:
1)
część wznoszaca,
2)
częśc opadająca, mimo rozpoczęcia procesu zniszczenia próbka w miarę wzrostu odkształceń posiada
pewna nośność.
Dysponując maszyną sztywną wytrzymałościową
- miduł E
- moduł spadu okreslany jako tg kata machylenia opadającej cześci krzywej do osi odciętych
Największe naprezenia w części pozniszczeniowej i utrzymuje się w części resztkowej, przyjmuje się za tzw
część rezydualną.

WŁ MECHANICZNE OŚR GRUNTOWEGO
Odkszrałcanie ośrodka gr pod działaniem obciążenia polega na zminiejszeniu objętości próbki w wyniku
sciskania i wyciskania gazów oraz wody wypełniającej pory gruntowe. W trakcie odkształcania następuje
przemieszczanie się ziaren i cząstek stałych względem siebie, zgniotami niektórych z nich i również stręzyste
odkształcenia wody błonkowej w pkt kontaktowych i samych cząstek wody. Właściwości mechaniczne oś
gruntowego charakteryzowane sa przez ściśliwość i wytrzymałość na scinanie.
SCIŚLIWOŚĆ GR- zdolnośc do zmniejszania swojej objętości pod wpływem obciążenia. Miara ściśliwości to
moduły ściśliwości.
- edometryczny mod ściśliwości pierwotnej Mo
- -//- wtórnej M
- -//- odprężenia M (z kreską u góry)
Mo- stosunek przyrostu efektywnego naprężenia normalnego do przyrostu całkowitego odkształcenie względnego
mierzonego w kierunku działania siły obciązającej, w jednoosiowym stanie odkształcenia w warunkach umownej
konsolidacji grunti Mo=Δσ/ε= (σi – σ
i-1
)/[( h
i-1
–hi)/ h
i-1
], (σi – σ
i-1
)- przyrost naprężenia jednostkowego.
M- jest to stos przyrostu efektywnego np. normalnego do przyrostu odksz względnego mierzonego w kier
działania siły obciążającej przy czym wartość h
i-1
,hi odczytuje się z tej krzywej ściśliwości, która odpowiada
wtórnemu odkształceniu próbki.
M (z kreską)- stos zmniejszania efektywnego naprężenia normalnego do jednostkowego przyrostu wysokości
próbki. Wzór jak Mo z tym że wartości h
i-1
,hi odczytuje się z tej części krzywej ściśliwości, która odpowiada
obciążenia próbki.
Wyniki pomiarów zmiany wysokości zmiany próbki nanosi się na wykres który przedstawia krzywką sciśliwości.
Może być wykonany jako funkcja zmiany wysokości od obciążenia, lub e od obciążenia. Wtedy wskaźnik
porowatości: ei= eo- (ho-hi)/ho *(1+eo)
wzrost obciążenia próbki powoduje jej konsolidację i zmianę wskaźnika porowatości e według linii ab na krzywej
sciśliwości. Przy odciążaniu próbki – jej odprężenie bc. W gruncie częściowo trwałe i sprężyste odkształcenie.
Ponowne obciążenie daje cd wykazującą pewne opóźnienie i wyraźne załamanie w pkt d
Wykorzystując krzywą ściśliwości można wykreślić krzywe konsolidacji gruntu. Wykres ten sporządza się dla
określonych stopni obciążenia nanosząc na osi odciętych czas liczony od chwili przyłożenia danego obciążenia a
na osi rzędnych poszczególne wysokości próbki obliczone na podstawie jej odkształceń zanotowanych dla
czasów t.
WYTRZYMAŁOŚĆ RGUNTU NA ŚCINANIE- jest to opór jaki stawia grunt naprężenia ścinający, po
pokonaniu którego następuje poślizg w pewnej części w stosunku do pozostałej.
W gruntach sypkich siłą ścinającym przeciwdziała opór tarcia wewnętrznego który powstake w czasie przesuwu
ziarn względem siebie w płaszczyźnie poślizgu- opór tarcia posuwistego. Oraz na skutek obrotu ziarn gruntu
względem ziarn- potoczyste tarcie
W gruntach sypkich hipoteza Culomba ł=σn*tgφ im grubsze sią ziarna tym szersza jest strefa objeta tarciem
wewnętrznym ziarn. Ponad to im ziarna są bardziej hropowate tym większy jest opór tarcia i przy przesuwie i
przy obrocie. W gruntach spoistych naprężenia ścinającym przeciwdziała opór tarcia wewnętrznego, i spójność
zwana kohezją. ł = σn*tgφ + c
KOHEZJA c- to opór stawiany siłą zewnętrznym a wywołany wzajemnym przyciąganiem cząstek składowych
siłami molekularnego przyciągania.
Z badania w aparacie 3-osiowego ściskania naprężenia ścinające i normalne działające w płaszczyźnie ścięcia i
kat tarcia wewnętrznego i spójność wyznacza się graficznie wykorzystując krytyczne wytrzymałości Culomba.
σ=(σ1+σ2)/2+(σ1-σ3)/2 cos 2α= p+q cos 2α
ł= (σ1-σ3)/2 sin2α= q sin 2α
W celu ułatwienia analizy stanu naprężeń analizy w gruncie, często zamiast kół Mohra rysuje się tzw pkt
naprężeń których współrzędne są odpowiednie. Łącząc pkt naprężenia otrzymuje się ścieżkę naprężenia a łącząc
pkt graniczne naprężenia otrzymuje się tzn zmodyfikowane obwiednie kół naprężeń.
FALOWE WŁAŚCIWOŚCI SKAŁ właściwości te charakteryzują zdolność skał do przepuszczania,
pochłaniania, załamywania i odbijania drgań sprężystych wywoływanych ruchem falowym. Ze względu na
częstotliwość fale sprężyste dzielimy na:
-fale infradźwiękowe o częstotliwości do 16 Hz
- f. Dźwiekowe o czestotliwości od 16- 20 kHz- akustyczne
- f ultradźwiekowe -//- 20kHz- 1GHz
- f hiperdźwiekowe ponad 1GHz
Naturalne:
- tzresienia ziemi
- tąpania
- wybuchy
- generatory drgań
W zależności od sposobu rozchodzenia się fal sprężystych wyróżniamy:
1)
F PODŁUZNA- wtedy gdy czestotkiwośc ośrodka drgaką II do kiedunku rozchodzenia się fali. Fale w
ośrodkach ciekłych, stałych, gazowych, występują wtedy odkształsenia objętościowe
2)
FALA POPRZECZNA- wtedy gdy cząsteczki ośrodka drgają prostopadle do kierunku rizchodzenia się
fali, rozchodzą się tylko w ciałach stałych. Tylko odkształcenie postaciowe
3)
FALE POWIESZCHNIOWA występuje na zakłóconej powierzchni cieczy lub powierzchni ciała stałego
graniczącego z próżnia lub gazem. Gdy osrodek stały zostanie ograniczony powierzchnią stałą wówczas wzdłuż
tej powierzchni rozchodzi się fala w której ośrodek wykonuje ruchy po elipsoidalnej trajektorii. Wzdłuż jak i
poprzek rozchodzenia się fali
Warunki rozchodzenia się fal spręż charakteryzują:
- prędkość rozchodzenia się fali
- akustyczna oporność falowa
- współczynnik odbicia, załamania, tłumienia
Prędkość rozchodzenia się fal sprężystych- w nie ograniczonym absolutnie sprężystym ośrodku, prędkość fal
sprężystych można określić ze wzorów uzyskanych z teorii sprężystości i ruchu falowego w ośrodku ciągłym
Vp=√[(E(1-v))/(ro*(1+v)(1-2v))]
Vs=√[E/[2 ro (1+v)]
VR=(0,87+0,12V)/(1+v) *√[E/[2 ro (1+v)]
v- l Poissona
ro- gęstość objętościowa
E- mod odkształcalności podł.
Relacja miedzy wymienionymi prędkościami jest następująca: Wp>Vs>VR
Stosunek prędkości fal podłużnych do poprzecznych zależy talko od l poissona:
Vp/Vs=√[2 (1-v)/(1-2v)] => v= [vp^2- 2Vs^2]/2(Vp^2-Vs^2)
Znając prędkośc fal podłużnych oraz poprzecznych można okteślić moduły sprężystości badanego ośrodka
skalnego.
E=ro Vp^2 *{(1+v)(1-2V)/(1-V)}, M= E(1-v)/(1+v)(1-2V)
G=E/2(1+v), K=E/3(1-2v), E=9KG/(3K+G),
E= 3K(1-2v), E=2G(1+v)
Wyznaczone w ten sposób wartości noszą nazwę dynamicznych modułów sprężystości od parametrów modułów
statecznych wyznaczonych metoda laboratoryjna na próbkach skalnych poprzez obciążanie.
WSP ANIZOTROPI PRĘDKOSCI- stosunek predkości fali w kierinku prostopadłym i II uwarstwienia
charakteryzuję tzw anizotropię K=vp rown/vp prostop.
AKUSTYCZNA OPORNOŚC FALOWA- opór skały przy rozchodzeniu się fali sprężystej charakteryzuje
akustyczna oporność falowa z= ro *vp
WSP ODBICIA- w ośrodku uwarstwionym może nastąpić odbicie. Stosunek E fali odbitej do E fali padającej
Ko=Wo/Wp=[(z1-z2)/(z1+z2)]^2
WSPÓŁCZYNNIK ZAŁAMANIA- charakteryzują zmianę kierunku fali sprężystej przy przejściu z jednego
ośrodka do drugiego ilościowo równy jest stosunkowi sin kąta padania do sin kata odbicia. Może nastąpić
wytłumienie.
W osrodku jednorodnym tłumienie fal spręzystych odbywa się zgodnie z zaleznością A=Ao* e
–αx
A-
amplituda fali w odl x od żródła
α- wsp tłumienia
Ao- amplituda początkowa fali
WSP TŁUMIENIA- max tłumienia fal sprężystych obserwuje się w gazach , mniejsze w cieczach, a minimalne w
ciałach stałych.
Górotwór będący ośrodkiem małosprężystym, niejednorodnym, porowatym, tłumi fale silniej niż ciecz. Dla tego
wsp tłumienia fal w skalach porowatych w miarę nasycenia maleje.
TERMICZNE WŁ SKAŁ WŁ termiczne charakteryzuje proces rozchodzenie się i pochłaniania ciepła w
skałach. Przepływ E cieplnej w ośrodku skalnym odbywa się na drodze:
- KONDUKCJI (w fazie stałej skały)
- KONWEKCJI (w fazie ciekłej gazowej, gazowej)
- RADJACJI (w fazie stałej, ciekłej i gazowej)
W ciałach jednorodnych przekazywanie ciepła odbywa się na drodze zmiany E kinetycznej przy zderzeniach
elektronów. Typ ten nosi nazwę elektronowej. Charakterystycznej dla metali i półprzewodników. W skałach
przekazywanie ciepła identyfikuje się z drganiami siatki krystalicznej. Ten typ przewodności nosi nazwe
przewodność fonowanej.
FONONY- to kwanty pola drgań siatki krystalicznej. Każdy fanon ma określona częstotliwość drgań.
WŁ TERMICZNE sa charakteryzowane następującymi parametrami:
WSP PRZEWODZENIA CIEPŁA- charakteryzuje prędkość rozchodzenia się ciepła w skale:
λ=Q/F*grad T*ł= (Q*L)/(F*(T1-T2)*ł) [W/mK]
Q- ilość ciepła przechodzącego przez próbkę [J]
L- droga przepływu ciepła [m]
F- powierzchnia przekroju poprzecznego próbki [m2]
Ł- czas przepływu ciepła [s]
T1, T2- temp na skrajnych powierzchniach próbki [K]
CIEPLNA OPORNOŚĆ WŁAŚCIWA- odwrotność współczynnika przewodzenia ciepła ξ=1/λ
Stosunek cieplnej oporności właściwej mierzonej prostopadle do uwarstwienia, do cieplnej oporności właściwej
mierzonej równolegle do uwarstwienia charakteryzuje zjawisko anizotropii cieplnej. kξ=ξprost/ξrówn >1
CIEPLNA POJEMNOŚC WŁ- parametr charakteryzujący pochłanianie ciepła przez skałę:
C= Q/(m*^T), Cv=Q/(V*^T) [J/m2*K]
Q- ilość ciepła potrzebna do podwyższenia temperatury jednostki m lub V o jeden stopień.
Pomiędzy ci Cv istnieje następująca zależność: Cv=C* ro
Ro- gęstość objętościowa skały
WSP PRZEWODZENIA TEMP- charakteryzuje prędkość rozchodzenia się temp w skale , charakteryzowany jest
przez wsp przewodzenia temp. a=λ/(C*ro)= λ/cv [m2/s]
W wyniku oddziaływania strumienia cieplnego na skałę, ciepło pochłonięta przez skałę zużywane na jej ogrzanie
oraz prace wewnętrzna związana głownie z rozszerzalnością. Zmianę wymiarów początkowych próbki podczas
jej podgrzewania charakteryzują współczynniki cieplnej rozszerzalności objętościowej i liniowej: β=^L/(L*^T)
[1/K], w= ^V/(V*^T) [1/K]
L- początek długości nie obciążonej próbki
^L- zmiana wymiarów liniowych podczas wzrostu temp, ^T- przyrost temp
Dla skał izotropowych współczynnik w=3β. Skały charakteryzują się anizotropowością, rozszerzalności
termicznej.
NAPRĘŻENIA TERMICZNE: są to naprężenia pojawiające się w skale w wyniku nierównomiernego
rozgrzewania skały lub nierównomiernego rozszerzania się poszczególnych ziarn mineralnych. Przy
uwzględnieniu tylko rozszerzalności liniowej: σr=E*β*^T, σT= K*w*^T= (E*w*^T)/3(1-2v)=(E*β*^T)/(1-2v)
K- mod sprężystości objętościowej
Zmiany temp wraz z głegokością opisane są przez 2 parametry:
STOPIEŃ GEOTERMICZNY: liczma metrów przy której temp wzrasta o 1 stopień C (K)

Sg=^h/^T [m/K] wartości Sg dla Europy wsch-śr przyjmuje się jako 33m, (waha się lokalnie między 5-100 m)
GRADIENT GEOMETRYCZNY- jest to liczba stopni o jaka temp wzrasta na 1 m głębokości. Gg=^T/^H
Temperaturę panującą na danej głębokości można określić w obniesieniu do tzw warstwy neutralnej
T=To+Gg(H-Ho)
- T- tem panująca na gł H
- To- temp warstwy neutralnej, na głębokości Ho=20m= śr roczna temp
- H- rozpatrywana głębokość
Dla skał niejednorodnych zmiany temp z głębokością nie ma charakteru prostoliniowego T=To+a(H-Ho)
b
a,b- parametry związane z charakterem zmiany gradientu z głębokością. Dla Polski a<1, b>1 lub b<1
Zmiany temp skał wraz z głębokością zalegania obserwuje się nie tylko w zakresie temp dodatnich ale też
ujemnych. Po dłuższym oddziaływaniu temp ujemnej na ośrodek gruntowy w war naturalnych obserwuje się
przesuwanie granicy przemarzania. Tworzące się soczewki lodowe zwiększają swoja objetość w skutek
przyciąganie molekuł wodnych od dołu ze swojego najbliższego otoczenie. Wzrost objetości gruntu objawia się
powstałym tzw wysadzin tj podnoszenia się powierzchni terenu, czy nawierzchni drogowej w miejscach gdzie
grunty są szczególnie wrażliwe na przemarzanie. Odmrażanie gruntu pod nawierzchnia drogowa jest powodem
tworzenia się tzw przełomów to znaczy pod nawierzchnia grunt odmarza szybciej niż pod poboczami, co
powoduje powstanie pod jezdnia niecki z której woda nie może ujść. Nawierzchnia się łamie pod obciążeniem.
GŁEBOKOŚCI PRZEMARZANIA- tern Polski pod względem głębokości przemarzania podzielony jest na 4
strefy hz: 0,8 1,0 1,2 1,4 m. Wartości t przyjmuje się przy projektowaniu fundamentu budowy dla przewodów
kanalizacji o 1/3 zwiększamy hz
UKŁAD FIZYCZNY I PARAMETRY UKŁADU znajomość właściwości fizycznych skał może być użyteczna
tylko wtedy, gdy wartości parametrów wykorzystywane sa w praktycznych obliczeniach na podstawie wzorów
wyprowadzonych z ogólnych praw fizyki do opisu procesów przebiegającym w trójwymiarowym układzie
odniesienia. Nie można stosować zależności uzyskanych na próbkach, a odnoszących się do procesów
jednowymiarowych nie zmieniających się w czasie.
Pojęciem podstawowym opisu fizycznego jest układ fizyczny
UKŁAD FIZYCZNY- to wyodrebniona do badań ograniczona cześć przestrzeni materii która może reagować w
określony sposób na jakieś zewnętrzne oddziaływania.
Zewnętrzną w stosunku do ukłdu fizycznego część przestrzeni materialnej nazywa się otoczeniem. Pomiędzy
układem a otoczenie znajduje się osłona posiadająca różne właściwości fiz. Jeżeli osłona doskonale osłania układ
od otoczenia, to układ jest izolowany.
Z układem fiz związane są wielkości zwane parametrami układu:
-EKSTENSYWNE- wielkości związane z wymiarami przestrzennymi układu fizycznego. Pomiar obejmuje cału
układ np. objętość, masa, energia... Są addytywne, dodajemy je gdy łączymy układy.
-INTENSYWNE- mają charakter lokalny, można je mierzyć w określonym miejscu danego układu. Przykład:
gęstość masy, potencjał elektryczny. Przy połączeniu 2 układów wyrównują się.
Wielkości fiz które stanowią iloraz z wielkości ekstensywnych są wielkościami intensywnymi, np.; ro M=M/V, ro
E=E/V
Twierdzenie odwrotnie nie jest słuszne.
PROCES FIZ: jest to zjawisko zmiany parametrów układu fizycznego lub występowania ich przepływów. Proces
fizyczny polega na przepływie wielkości ekstensywnych i wyrównywaniu się wielkości intensywnych. Bywaja
procesy w których dominuje przepływ jednej charakterystycznej wielkości ekstensywnej. Ona okresla rodzaj
procesu.
Ze względu na fizyczny charakter nośnika energii w danym procesie wyróżnia się następujące rodzaje
oddziaływań fizycznych:
Rodzaj oddziaływań- wielkości ekstensywne- charakter wielkości ekstensywnych- charakter wiel intensywnych-
zmiana energii
1)
mechaniczne, objętościowe- energia, objetość- V- P ciśnienie- (-P*^V)
2)
substancji chem- energia masa- M- potencjał chem ń- ń*^M
3)
elektrostatyczny- energia ładunek elektryczny- Qe- potencjał elektrostatyczny φ- φ*^Qe
4)
termiczne- energia entropia- s- temp T- T*^s

5)
mechaniczne reologiczne- energia pęd- Mv- prędkość v- v*^(Mv)
RÓWNANIA BILANSU WIELK EKSTENSYWNYCH
Rozważamy otwarty 0kład fiz będący cześcią przestrzeni materialnej ograniczony powierzchnia oporu Σ i
posiadający objętość V z układem związana jest wielkość fizyczna, ekstensywna Xi, będąca skalarem. Szybkość
zmiany wielkości Xi w danym układzie określa zależność: d^Xi/dt= Qi-Ii
Qi- natezenie źródła wielkości ekstensywnej Xi (ilość tworzącej się wielkości Xi w jednostce czasu)
Ii- natęzenie stłumienia przepływu wielkości Xi (ilośc przepływającej przez powierzchnię Σ wielkości Xi w
jednostce czasu)
Równanie wyraza bilans wielkości Xi dla całej objętości V. Jest to całkowe równanie bilansu dla opisu procesów
fizycznych potrzeba równania odnoszącego się do nieskończenie małej objętości obszaru. Jest to różniczkowe
równanie bilansu. W tym celu wprowadzamy do rozważań następujące oznaczenia:
1)
całkowita wielkość Xi w układzie:
Xi=....
ξi- gęstość objetościowa wielkości Xi (ilośc Xi zawarta w jednostce objętości np. gdy Xi jest masa w kg, to ξi
występuje w jednostkach kg/m3
2)
natężenie źródła:
Qi=...
qi-gęstość objętościowa natężenia źródła( ilość Xi tworzącej się w jednostce objętości na jednostek czasu) np.
gdy Xi jest masą w kg to qi jest w kg/(s*m3)
3)
natezenie strumienia przepływu:
Ii=...
ji-gestośc powierzchniowa natężenia strumienia Xi (ilość Xi przepływająca w jednostce czasu przez jednostkę
pola powierzchni prostopadłej do kierunku przepływu)
Pod całką powierzchniową występuje iloczyn skalarny wektora ji i normalnego wektora n do elementu
powierzchni dΣ.
Stosując wzór Goussa – Ostrobramskiego można całkę powierzchniową wyrazić przez całkę objętościową:
Ii=...
Podstawiając wyżej wymienione zależności otrzymujemy: dxi/dt= Qi-Ii
d/dt...
Operator różniczkowania względem czasu można wprowadzić pod znak całki przy jednoczesnej zmianie
pochodnej zwyczajnej na cząstkową. Granice dla wszystkich całek są wspólne. Stąd poszczególne wyrazy
równania można sprowadzić pod wspólna całkę:
...
Całka może mieć wartość 0 gdy wyrażenie podcałkowe jest równe 0:
...
Jest to różniczkowe równanie bilansu dla skalarnej wielkości ekstensywnej zwanej również równaniem ciągłości.
Gdy wielkością ekstensywną jest masa, to wzór wyraża prawo zachowania masy, gdy xi-energia to prawo
zachowania energi. W równaniu występują 2 gęstości objętościowe ξi i qi, oraz gęstość powierzchniowa Ii
poddana operacji różniczkowania względem współrzędnych, która oznaczona jest symbolem div ji- dywergencja.
Div ji= ...
Operator różniczkowy div przypisuje wektorowi j wartość skalarną, która wyraża gęstość objętościowa
strumienia przepływu. Równanie ciągłości jest wymiarowo jednorodne, stąd wniosek że div przelicza natężenie
przepływu wielkości ekstensywnej z jednostki powierzchni na jednostkę objętości.
RÓWNANIE TRANSPORTU SKALARNEJ WIEKLOŚĆ EKSTENSYWNEJ łącząc różniczkowe równania
bilansu wielkości ekstensywnych z prawem dynamiki przepływów otrzymuje się równanie opisujące transport

przepływającej wielkości ekstensywnej, np. objętości, masy ładunku elektrycznego, energii, entropii, czyli
wielkości skalarnych, względnie pędu czyli wielkości wektorowych.
Do rozważań wprowadzamy równanie bilansu, prawo przepływu wiążące gęstość powierzchniowa całkowitego
strumienia przepływu ji z charakterystyczna wielkością intensywną która jest siłą powodującą przepływ
Li grad xi- gęstość powierzchniowa strumienia kondukcyjnego
ξi*V- gęstość powierzchni strumienia konwekcyjnego
Li- współczynnik proporcjonalności charakteryzuje własności ośrodka.
„-„ oznacza że przepływ odbywa się w kierunku największego spadku wielkości intensywnej Yi
ξi- gęstość objętościowa wielkości Xi
v- prąd przepływu makroskopowego
Otrzymujemy ostatecznie:
Jest to równanie transportu skalarnej wielkości ekstensywnej. Służy do opisu zjawisk gdzie występują przepływy
objętości, masy, ładunku elektrycznego energii cieplnej, czyli skalarnych wielkości ekstensywnych.
OGÓLNE RÓWNANIE PRZEPŁYWU CIECZY:
Dal ilościowego opisu procesu przepływu cieczy przez środowisko przepuszczalne stosuje się równanie
transportu skalarnej wielkości ekstensywnej:
Poszczególne wielkości otrzymują następującą interpretację:
1)
ξi=n*ro
ξi- ilość masy cieczy w jednostce objętości skały
ro- gestośc objetościowa cieczy
n- porowatość
2)
grad Yi=0 W opisie przepływu filtracyjnego nie uwzględnia się kondukcyjnego składnika przepływu gdyż
pomija się efekt dyfuzji.
3)
V=-k/ńp *grad (p+ro*g*z) Prędkość przepływu konwekcyjnego (predkośc filtracji) v może być okreslana
z prawa Darciego. Wielkośc pod gradientem to potencjał przepływu filtracyjnego = p+ro*g*z=...
v- proces filtracki
k- współczynnik przepuszczalności skały
ńp- lepkość dynamiczna cieczy
p- ciśnienie cieczy
ro- gęstość cieczyg0 przyspieszenie ziemskie
z- wysokość niwelacyjna rozważanego pkt
qi=0 W środowisku skalnym nie ma objętości źródeł cieczy
Uwzględniając powyższe zależności otrzymujemy:
W opisie procesu fizycznego poza równaniem transportu należy uwzględnić równanie stanu które dla cieczy
nieściśliwej ro= const zakładając ponadto że porowatość nie zmienia się w czasie otrzymuje się równanie
przepływu filtracyjnego cieczy nieściśliwej:
div(n*ro*(k/ńp)*grad...)=0
Przyjmując ze ośrodek skalny jest jednorodny, izotropowy. Wówczas porowatości wsp rzepuszczalnosci są
liczkami stałymi a równanie upraszcza się do postaci: div grd ....=0 Jest to równanie różniczkowe cząstkowe II
rzedu zwane ogólnym równaniem przepływu cieczy
OGÓLNE RÓWNANIE PRZEPŁYWU CIECZY
...+div(Li
gradYi+ξ*v)=qi- równanie transportu
a)
ξi=n*ro
b)
grad yi=0
c)
v=-k/ńp grad (p+ro*g*z), p+ro*g*z=...
d)
qi=0
div(n*ro*(k/ńp)*grad...)=0, div grad ... =0- ogólne równanie
Obliczamy wydatek cieczy dopływającej do wyrobiska

DOPŁYW WODY DO TUNELU
...- potencjał
L- zakres zmiany potencjału
Rozpatrzymy, długie prostoliniowe wyrobiska tunelowe przebiegające w poziomej warstwie skalnej nasyconej
cieczą, a ograniczonej od stropu i spągu warstwami nieprzepuszczalnymi. W odległości L istnieje obszar zasilania
o granicy równoległej do osi wyrobiska. Można więc przyjąć że potencjał przepływu zależy od 1 współrzędnej
....=p(x) Rozpatrujemy wiec jednowymiarowy przepływ prostoliniowy. W takim przypadku operatory
różniczkowania grad i div sprowadzaja się do pochodnych zwyczajnych, a równanie ogólne przepływu cieczy
sprowadza się do postaci:
d/dx(dp/dx)=0
Całka ogólna równania wyrazana jest wzorem p=C1x+C2, gdzie C1, C2- stałe całkowania
Dla wyznaczenie stałych całkowania wykorzystuje się warunki brzegowe:
Dla x=0, p=p1=> p1=C2
Dla x=L, p=p2 => p2=C1L+C2
Zatem: C2=p1, p2=C1*L+C2 => C1=(p2-p1)* 1/L
Po podstawieniu otrzymujemy
p(x)=(p2-p1)* x/L +p1
LINIOWY SPADEK POTENCJAŁU PRZEPŁYWU
Z tego wynika ze rozkład ciśnienia ma charakter prostoliniowy. Występuje liniowy spadek potencjału przepływu.
Znając rozkład potencjału przepływu z prawa Darcj’ego można obliczyć prędkość przepływu filtracyjnego: V= -
k/ńp * dp/dx= -k(p2-p1)/(ńpL)
k- wsp przepuszczalności, ń- lepkość cieczy
w rozważanym przypadku prędkość przepływu jest stała w całym obszarze przepływu. Wydatek dopływu cieczy
do tunelu, vzyli naterzenie strumienia dopływu wynosi: Q=mw*l*v
mw*l- powierzchnia przekroju wyrobiska (tunelu)
v- predkość
l- długość wyrobiska
mw- wysokość wyrobiska
Q=[mw*l*k*(p2-p1)]/(ńp*L)
DOPŁYW CIECZY DO OTWORU WIERTNICZEGO
Rozważamy sytuacje w której pionowy otwór wiertniczy wykonany z powierzchni ziemi. Przechodzi przez
pozioma warstwę nasycona cieczą. Granice zasilania tej warstwy sa ze wszystkich stron otworu wiertniczego
mniej więcej w jednakowej odległości. Potencjał przepływu zależy wiec od odległości od środka wyrobiska r.
O=p(r)
Przepływ cieczy w tym przypadku ma charakter osiowo symetryczny. Przyjmujemy wiec biegunowy układ
współrzędnych, r, o, w. W tym układzie operatory różniczkowania div oraz grad przyjmują postać: grad
a(r)=da/dr, div c(r)=dc/dr +1/r*c
W przypadku przepływu osiowosymetrycznego ogólne równanie przepływu ma postac:
d^2p/dt^2 +1/r * dp/dr =0
Całka ogólna równania jest zależność p=C1 ln r+C2
Dala wyznaczenia stałych wartości brzegowych dla: r=R1, p=p1 i r=R2, p=p2
p1=C1 ln R1 +C2, p2=C1 ln R2 + C2
p2-p1=C1 ln (R2/R1)=> C1=[p2-p1]/[ln (R2/R1)]
C2=p1-c1*ln R1 => C2=p1-[p2-p1]/ln(R2/R1) *lnR1
Podstawiając do całki ogólnej otrzymujemy:
p=(p2-p1)* [ln(r/R1)/ln(R2/R1)]+p1

Rozkład potencjału przepływu (ciśnienia) ma kształt logarytmiczny. Zgodnie z prawem Darsjego predkośc
przepływu filtracyjnego wynosi:
v=-k/ńp * dp/dr =-k/ńp * (p2-p1)/ln (R2/R1) * 1/r
w przypadku przepływu osiowo symetrycznego płaskiego przepływu cieczy prędkość nie jest wielkościa stała
lecz maleje ze wzrostem odległości od osi wyrobiska. Max prędkość występuje na ścianie wyrobiska dla r=R1
v1=k/ńp * (p2-p1)/ln (R2/R1) * 1/R1
Wydatek dopływu cieczy do otworu wiertniczego równa jest iloczynowi pola dopływu i prędkości dopływu:
Q=F*v= 2Л R1*mp*v1
Q=(2Л*k*mp*(p2-p1))/[ńp*ln(R2/R1)]
PRZEPŁYW GAZU W GÓROTWORZE
Dla ilościowego opisu przepływu gazu przez ośrodek przepuszczalny wykorzystuje się rózniczkowe równaie
transportu skalarnej wielkości ekstremalnej
Poszczególne wyrazy w równaniu otrzymują interpretację fizykalną:
a)
...=p W przepływie filtracyjnym gazu w wyrażeniu na potencjał przepływu można pominąc 2 składnik
uwzględniający wpływ ciężaru płynu na wielkość potencjału, gdyż składnik ten w porównaniu z ciśnieniem gazu
w złożu jest bardzo mały
b)
przy przepływie gazów przez ośrodek skalny należy uwzględnić procesu utleniania lub innych przemian
chemicznych które sa źródłem gazu swobodnego. W przypadku więc przepływu gazu nie można przyjąć (jak w
cieczach) że przepływ ma charakter bezźródłowy. Uwzględniając powyższe uwagi oraz podobieństwa do
przepływu cieczy, otrzymuje się równanie transportu
Gęstość gazu jest zależna zarówno od ciśnienia jak i temperatury: ro =f(p,T).
Przyjmując ze proces przepływu gazu ma proces izotermiczny czyli (T=const) równanie stanu upraszcza się:
p/ro=const=β
Zakładając ponadto izotropię i jednorodność ośrodka skalnego równanie transportu przekształca się do postaci:
Równaie:
Jest to ogólne równanie opisujące przepływ gazu przez ośrodek skalny, porowaty
Przyjmując, że przepływ jest ustalony w czasie oraz pomijając wewnętrzne źródła gazu ogólne równanie
upraszcza się do postaci: div(grad p^2)=0
USTALONY PRZEPŁYW GAZU DO TUNELU:
Rozwazamy długie prostoliniowe wyrobisko tunelowe wykonane w gazonośnej warstwie skalnej ograniczonej od
stropu i spągu warstwami nieprzepuszczalnymi w odległość L od wyrobiska istnieje granica zasilania. Mamy
więc do czynienia z jednowymiarowym, prostoliniowym przepływem filtracyjnym gazu: o=p(x)
W tym przypadku równanie div grad p^2=0 sprowadza się do postaci: d/dx [dp^2/dx]=0
Całke ogólna p^2=C1*x+C2
Wartości brzegowe: dla x=0, p=p1, dla x=L, p=p2
Po wykonaniu odpowiednich przeliczeń wzór opisujący ciśnienie gazu w pokładzie od odległości danego pkt od
wyrobiska ma postać; p^2(x)=(p2^2-p1^2)*x/L+p1^2
W przypadku przepływu gazu linia spadku potencjału przepływu ma kształt paraboliczny. Prędkość przepływu
wynosi: v=-k/ńp * dp/dx=-k/ńp *(p2^2-p1^2)/[2p(x)*L]
Najwieksza predkośc występuje na scianie tunelu i równa jest:
V1= k/ńp *(p2^2-p1^2)/[2pi*L]
Gestość wypływającego gazy jest równa: ro1= p1/β
Wydatek masowy wypływającego gazu ze ściany tunelu o długości l wynosi:
Q=ro1*v1*mw*l=[k*mw*L*(p2^2-p1^2)]/[2β*ńp*L]

DOPŁYW GAZU DO OTWORU WERTNICZEGO
Rozważamy przypadek, gdy pionowy otwór wiertniczy przebija warstwę wypełnioną gazem. Przepływ gazy
zależy więc tylko os odległości od środka wyrobiska, czyli potencjał przepływu: o=p(r)
Przepływ ma charakter osiowo symetryczny. Wprowadzamy biegunowy układ współrzędnych w którym
operatory różniczkowania grad i dif definiowane są następująco: grad a(r)=da/dr, div c(r)=dc/dr+1/r *c
Równania ogólne przyjmują postać:
d^2p^2/dr^2+1/r *dp^2/dr=0
Całką ogólną równania jest wyrażenie: p^2=C1 ln r+C2
Z warunków brzegowych:
Dla r=R1, p=p1, dla r=R2 p=p2.
Korzystając z rozwiązania dotyczącego cieczy otrzymujemy:
p^2=(p2^2-p1^2)* [ln(r/R1)/ln (R2/R1)]+p1^2
Prędkość dopływu gazy określa się z prawa Darsy’ego: V= -k/ńp *dp/dr= -k/ńp (p2^2-p1^2)/[2p(r)ln(R2/R1)]
*1/r
Największa prędkość występuje na ściance otworu: dla r=R1
V1=-k/ńp (p2^2-p1^2)/[2p1*ln(R2/R1)] *1/R1
Uwzględniamy gęstość gazu: ro1=p1/β
Wydatek masowy gazu dopływającego ze wszystkich stron do otworu wiertniczego określa zależność:
Q=ro1*v1*2Л*R1*mw= [Л*k*mw*(p2^2-p1^2)]/[ńp*β*ln (R2/R1)]
Wyprowadzone zależności mogą być zastosowane przy założeniu przepływu ustalonego w czasie oraz
pominięciu efektu desorpcji.
PRZEPŁYW CIEPŁA W GÓROTWORZE:
Dla ilościowego opisu procesów termicznych w ośrodku skalnym można wykorzystać różniczkowe równanie
transportu skalarnej wielkości ekstensywnej:
.../...+div(-Li grad Y1+ξi*v)=qi
Wszystkie wyrazy otrzymują wartości fizykalne:
a)
gęstością objętościową przepływającej wielkości ekstensywnej jest gęstość objętościowa energii
wewnetrznej, którą jest entropia ξi=e
b)
charakterystyczną wielkością ekstensywną procesu termicznego jest temperatura Yi=T
c)
w procesach termicznych współczynnik przewodności wielkości ekstensywnej nosi nazwę współczynnika
przewodzenia ciepła Li=λc
d)
gęstość objętościowa źródeł energii cieplnej w górotworze może być związana z procesami utleniania
substancji organicznych lub też egzotermicznymi procesami zmiany stanów skupienia.
Po uwzglednieniu powyższych uwag otyrzymujemy:
.../...+div(-λc gradT+e*v)=q
Równanie stanu wyraża zależność miedzy energią wewnętrzną, temperaturą, gęstością masy; e=f(T,ro)
Pochodna cząstkowa gęstości energii względem czasu może być określona następująco
Gestość jest niezmienna w czasie:
.../...=0, ..../....=Cv*ro
Ponadto pochodna gęstości enargii względem temperatury jest iloczynem ciepła właściwego danej skały(Cv) i jej
gęstości (ro).
Po podstawieniu otrzymujemy:
..../....=Cv*ro*...../.....
Podstawiając do równania transportu otrzymujemy:
Cv*ro *..../.....*div(-λc* grad T+e*v)=q /: Cv ro
.../... +div[-λc/(Cv ro) *grad T+e/(Cv ro) *v]=q/[Cv ro]

jest to ogólne różniczkowe równanie transportu energii cieplnej. Uwzględnia zarówno przewodzenie, jaki i
unoszenie energii cieplnej. Iloraz 3 wielkości charakteryzujących właściwości cieplne ośrodka nosi nazwę
współczynnika przewodzenia temp. a=λc/(Cv*ro) [m^2/s]
Pomijając przepływ konwekcyjny (e/(Cv*ro) *v) oraz wewnętrzne źródła ciepła otrzymujemy równanie:
..../....-div(a grad T)=0- równanie Fouriera
Przyjmujemy że przepływ odbywa się w ośrodku jednorodnym, izotropowym, a współczynnik przewodzenia
temp jest stały, upraszczamy wzór do postaci:
.../.... – a*div*gradT=0
Przyjecie przepływu stacjonarnego pozwala nam uprościć równanie: div grad T=0
ZALEŻNOŚĆ PIERWOTNEJ TEMP OD GŁEBOKOŚCI:
div grad T=0
Zakładamy że w nienaruszonym jednorodnym górotworze temp pierwotna skał zależy tylko od głębokości.
Wówczas równanie przewodnictwa przyjmuje postać:
d/dx(dT/dx)=0
Całką ogólną równania jest: T=C1*x+C2, Stąd: dT/dx=C1
Temperatura wzrasta liniowo z głębokością. Dla wyznaczenia stałych całkowania korzystamy z warunku:
Dla x=0, T=To.
Gęstość strumienia dopływu energii cieplnej: jc=λc* dT/dx => dT/dx=jc/λc.
C1= jc/λc, C2=To, T= jc/λc *x+To, T=To+Gg(h-ho)
Gg- gradient geeotermiczny
Zmiany temp z głębokościa charakteryzowane sa przez stopięń geotermiczny który jest odwrotnością gradientu
temp:
Sg=1/Gg=1/(dT/dx)=1/( jc/λc)= λc/jc
Iloraz współczynnika przewodzenia i gęstości strumienia energii cieplnej płynącej z głębi ziemi na powierzchnię.
Jeżeli dla 2 różnych głębokości znane są wartości temp czyli: dla x=x1, T=T1, dla x=x2, T=T2
Wyznaczamy stałe całkowania:
T1=C1*x1+C2, T2=C1*x2+C2
T2-T1=C1(x2-x1) => C1=(T2-T1)/(x2-x1)
T1= (T2-T1)/(x2-x1) *x1+C2;
C2=T1-(T2-T1)/(x2-x1) *x1
T==(T2-T1)/(x2-x1) *(x-x1)+T1
Otrzymujemy zależność temp od głębokości:
Gg=dT/dx=(T2-T1)/(x2-x1), Sg=1/Gg=(x2-x1)/(T2-T1)
Znając wartość współczynnika przewodzenia ciepła skał można obliczyć gęstość strumienia energii cieplnej
przepływającej z głębi ziemi ku powierzchni.
Jc=λc (dT/dx)= λc/Sg=λc=(T2-T1)/(x2-x1)
Wzory te odnoszą się do górotworu izotropowego, jednorodnego, nie uwzględniają ewentualnych wewnętrznych
źródeł energii cieplnej

Podstawowe zagadnienia metodyki badań fizycznych własności skał. Określenie górotworu.
Procesy fizyczne w górotworze (2);
Elementy i cechy strukturalne górotworu. Skale rozmiarów elementów strukturalnych. Wpływ
efektu skali na ocenę własności fizycznych skał (2);
Skały jako ośrodki trójfazowe. Cechy strukturalne ośrodka skalnego. Cechy teksturalne
masywu skalnego (2);
Klasyfikacja własności fizycznych skał i ich podstawowych parametrów. Określenie
własności technologicznych skał (2);
Ogólna charakterystyka skał i gruntów oraz ich własności. Podział gruntów budowlanych (2);
Strukturalne własności skał i gruntów. Struktura przestrzeni porowej, gęstość ściśliwość,
zagęszczenie, rozluzowanie (2);
Hydrogazogeomechaniczne własności skał i gruntów, wilgotność i stopień wilgotności,
konsystencje gruntów spoistych, stopień plastyczności, przepuszczalność i filtracja skał oraz
pęcznienie. Nasycenie skał cieczami i gazami (2);
Mechaniczne własności skał, Charakterystyka naprężeniowo-odkształceniowa. Sprężyste
własności skał (4);
Własności wytrzymałościowe skał. Pełna charakterystyka naprężeniowo-odkształceniowa
skały (4);
Falowe własności skał. Rozchodzenie się fal sprężystych w skałach. Dynamiczne moduły
sprężystości (2);
Termiczne własności skał. Przewodzenie ciepła, pojemność cieplna i rozszerzalność cieplna
skał. Naprężenie termiczne (2);
Zmiany temperatury z głębokością. Wpływ pola cieplnego na własności mechaniczne skał
(2);
Własności elektryczne i magnetyczne skał. Przewodność elektryczna, podatność magnetyczna
skał. Propagacja fal elektromagnetycznych w skałach (2);
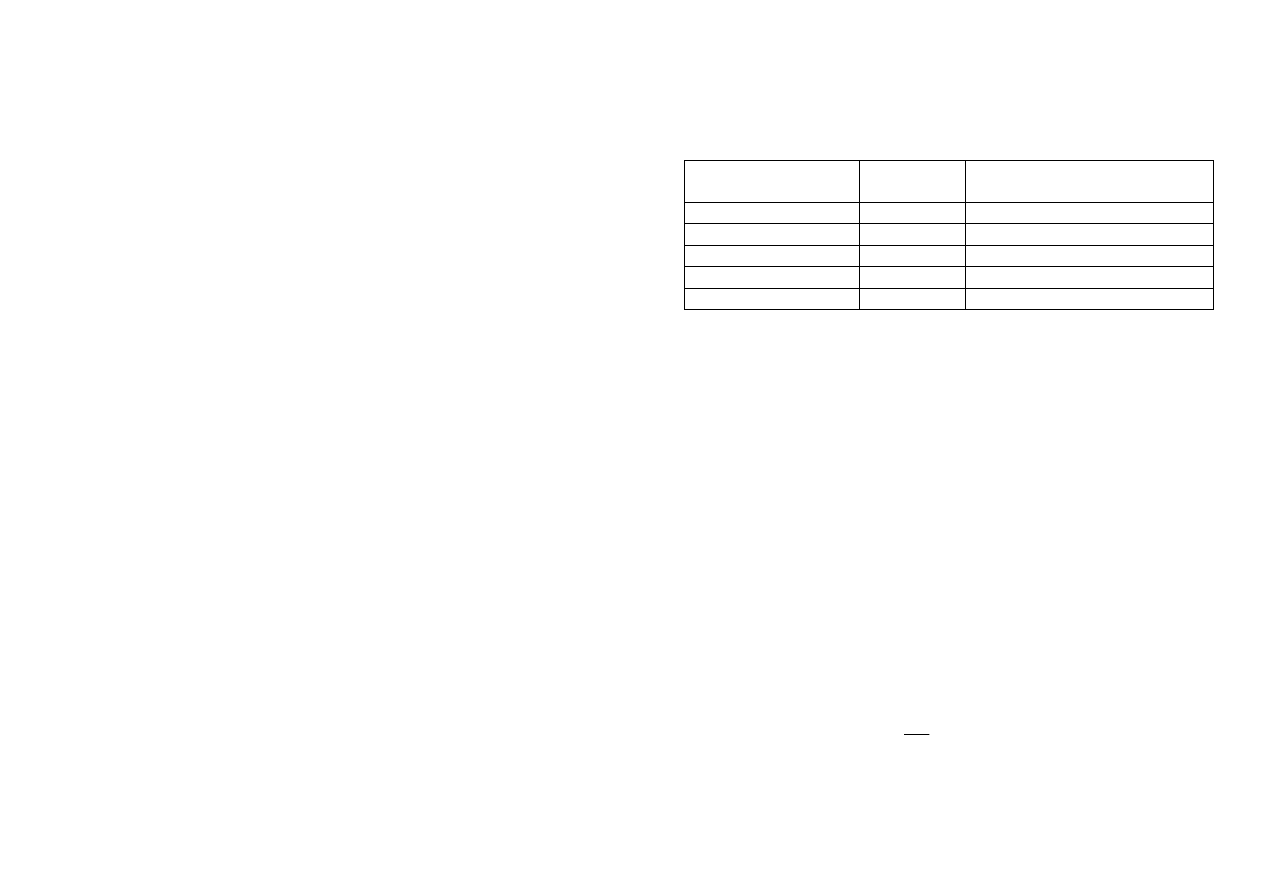
GRUNTY BUDOWLANE
Grunt budowlany (w skrócie „grunt”) – część skorupy ziemskiej:
• współpracująca z obiektem budowlanym,
• stanowiąca jego element,
• służąca jako tworzywo do wykonania z niego budowli
ziemnych.
Grunt składa się z trzech faz:
• stałej – tzw. szkieletu gruntowego – oddzielnych ziaren i
cząstek, tworzących porowaty układ,
• ciekłej – wody wypełniającej pory:
o
całkowicie – w strefie poniżej poziomu wód gruntowych
(w tzw. strefie saturacji)
o
częściowo – woda zawieszona lub wilgotność
występująca powyżej poziomu wód gruntowych (w tzw.
strefie aeracji),
• gazowej – powietrza wypełniającego pory w strefie aeracji.
Grunt naturalny – grunt, którego szkielet powstał w wyniku
procesów geologicznych – np. wietrzenia, erozji i sedymentacji w
wyniku procesów eolicznych (działanie wiatru) i fluwialnych (działanie
płynącej wody).
Rozróżniamy trzy rodzaje gruntów naturalnych:
• skaliste – zbudowane z litych lub spękanych bloków o
minimalnych wymiarach > niż 10 cm,
• nieskaliste mineralne – zawartość części organicznych
(roślinnych i zwierzęcych) < niż 2 %
• nieskaliste organiczne - zawartość części organicznych > niż 2
%
Grunt antropogeniczny – grunt nasypowy powstały z produktów
gospodarczej i przemysłowej działalności człowieka (np. odpadów
komunalnych, gruzu budowlanego, pyłów dymnicowych, odpadów
poflotacyjnych, odpadów z przerobu surowców mineralnych itp.)
występujący w wysypiskach, zwałowiskach (hałdach), osadnikach
oraz niektórych budowlach ziemnych.
Szkielet gruntowy składa się ziaren i cząstek różnego kształtu i
wielkości, które charakteryzuje tzw. średnica zastępcza:
• ziarna
mają średnicę zastępczą d > 0,05 mm
• cząstki mają średnicę zastępczą d ≤ 0,05 mm
Ziarna i cząstki gruntu dzielimy według wielkości na grupy zwane
frakcjami.
Nazwa frakcji
Symbol
Zakres średnic zastępczych d
(mm)
Kamienista
f
k
d > 40
Żwirowa
f
ż
40 ≥ d > 2
Piaskowa
f
p
2 ≥ d > 0,05
Pyłowa
f
π
0,05 ≥ d > 0,002
Iłowa
f
i
0,002 ≥ d
Do oznaczenia uziarnienia gruntu stosuje się metody:
• sitową – stosowaną dla gruntów piaszczystych i żwirowych,
• areometryczną, dla gruntów zawierających dużą ilość cząstek
mniejszych o d < 0,07 mm.
W metodzie sitowej średnicą zastępczą ziarna jest średnica oczka
sita przez które przechodzi dana cząstka. Metoda ta polega na:
• przesiewaniu próbki gruntu przez zestaw sit o różnych
wymiarach oczek,
• oznaczeniu
ciężaru cząstek zatrzymanych na
poszczególnych sitach,
• określeniu ich procentowego udziału w wadze całej próbki,
• sporządzeniu krzywej uziarnienia gruntu
Z krzywej przesiewu można określić:
• średnicę przeciętną (miarodajną) d
50
– średnica
charakterystyczna, która wraz z ziarnami większymi stanowi
wagowo 50 % próbki;
• zawartość poszczególnych frakcji;
• wskaźnik uziarnienia
10
60
d
d
u
=
.
Gdy u ≤ 5 grunt jest równomiernie uziarniony.
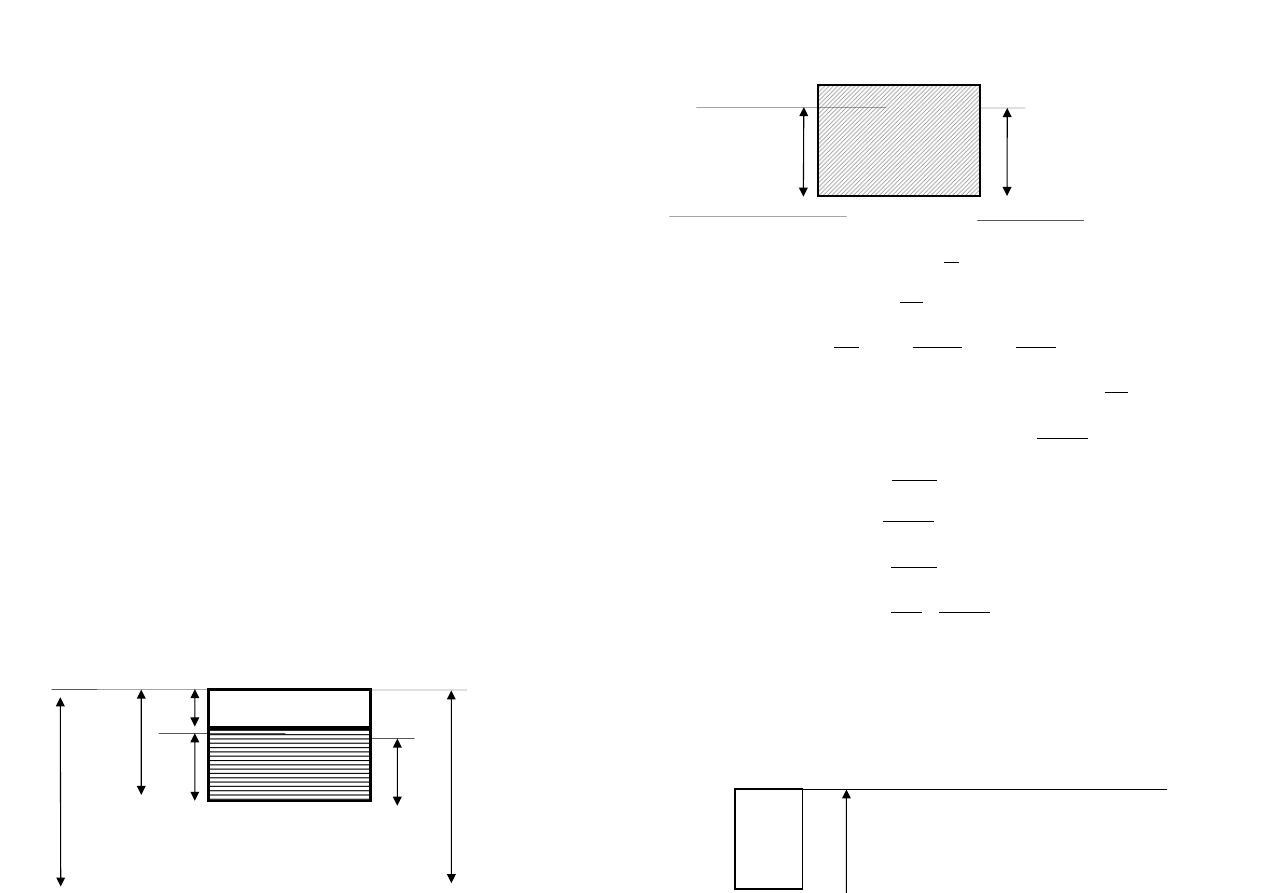
Średnice d
60
i d
10
są ziarnami, które wraz z większymi stanowią
odpowiednio 60% i 10% wagi próbki.
Klasyfikacja gruntów
Rodzaj gruntu określa się na podstawie procentowej zawartości poszczególnych
frakcji oraz dodatkowych kryteriów:
• wielkości średnic charakterystycznych d
50
(d
90
)
• wskaźnika plastyczności gruntu I
p
Wskaźnik plastyczności I
p
pokazuje, jaką ilość wody (w
procentach) wchłania grunt przy przejściu ze stanu
półzwartego w płynny.
Na podstawie tego wskaźnika grunty dzielimy na:
• niespoiste (sypkie) – gdy I
p
≤ 1 %
• spoiste – gdy I
p
> 1 %
Przy ustalaniu rodzaj gruntu wykorzystuje się:
• zestawienia
tabelaryczne
• wykres w postaci tzw. trójkąta Fereta
Trójkąt Fereta pozwala na określenie rodzaju gruntu, w którym
frakcja żwirowa stanowi f
ż
< 10 %.
Cechy fizyczne gruntów
Zależności objętościowe i wagowe poszczególnych faz gruntu
Objętość (cm
3
)
Masa (g)
V
p
powietrze
V
porów
V
w
woda
M
w
V
M
V
s
szkielet gruntowy
M
s
Gęstość objętościowa (g/cm
3
)
V
M
=
ρ
Gęstość właściwa (g/cm
3
)
s
s
s
V
M
=
ρ
Wilgotność gruntu (%)
100
100
M
M
M
100
M
M
w
s
s
s
s
s
w
×
ρ
ρ
−
ρ
=
×
−
=
×
=
Gęstość objętościowa szkieletu gruntowego (g/cm
3
)
V
M
s
d
=
ρ
lub
po wprowadzeniu odpowiednich zależności
100
w
100
d
×
+
ρ
=
ρ
Porowatość gruntu (-)
V
V
n
porów
=
lub po wprowadzeniu
odpowiednich zależności
s
d
s
n
ρ
ρ
−
ρ
=
Wskaźnik porowatości (-)
s
porów
V
V
e
=
lub po wprowadzeniu
odpowiednich zależności
d
d
s
n
1
n
e
ρ
ρ
−
ρ
=
−
=
Stopień zagęszczenia gruntów piaszczystych I
D
(-) – jest to stosunek
zagęszczenia istniejącego w naturze do największego możliwego
zagęszczenia danego gruntu.
a)
b)
c)
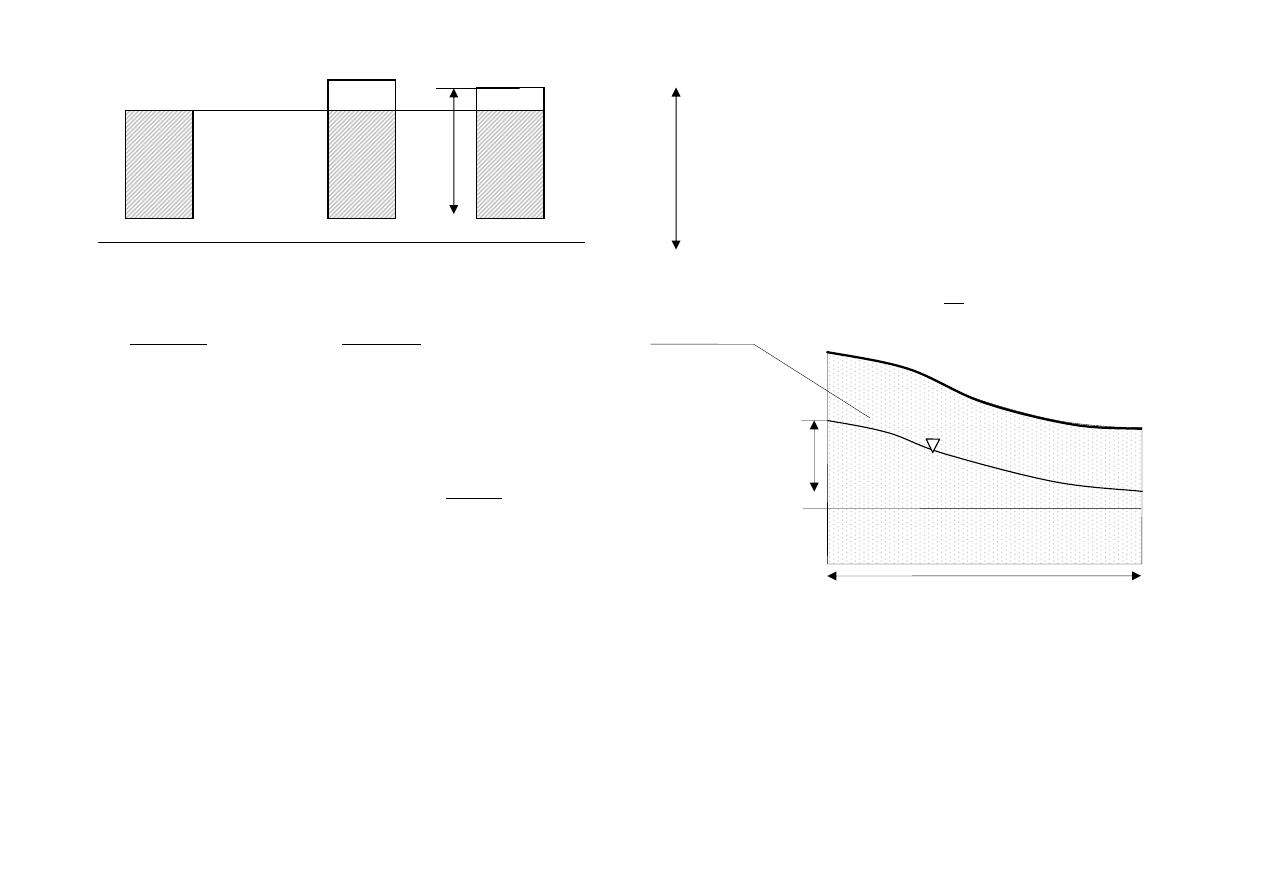
V
porów
V
s
V
max
V
V
min
a) objętość próbki piasku najbardziej luźnego
b) objętość próbki piasku w naturze
c) objętość próbki piasku najbardziej zagęszczonego
min
max
max
D
V
V
V
V
I
−
−
=
lub
min
max
max
D
e
e
e
e
I
−
−
=
Zależnie od stopnia zagęszczenia grunty sypkie mogą być w stanie:
• I
d
≤ 0,33 – luźnym
• 0,33 < I
d
≤ 0,67 – średnio zagęszczonym
• 0,67 < I
d
≤ 1,0 – zagęszczonym
Stopień plastyczności gruntów spoistych I
L
(-):
p
L
p
L
w
w
w
w
I
−
−
=
gdzie:
w – wilgotność naturalna (%)
w
p
– wilgotność na granicy plastyczności (%)
w
L
– wilgotność na granicy płynności (%)
W zależności od stopnia plastyczności grunty spoiste mogą być w
stanie:
• I
L
< 0 – zwartym lub półzwartym
• 0 < I
L
≤ 0,25 – twardoplastycznym
• 0,25 < I
d
≤ 0,50 – plastycznym
• 0,50 < I
d
≤ 1,0 – miękkoplastycznym
• I
L
> 1,0 – płynnym
Współczynnik filtracji k (cm/s, m/dobę) – jest miarą
wodoprzepuszczalności gruntu:
J
k
V
⋅
=
gdzie:
V – prędkość filtracji (przepływu wody w gruncie) (cm/s,
m/dobę),
k – współczynnik filtracji (cm/s, m/dobę)
J – spadek hydrauliczny (-)
L
h
J
Δ
=
poziom wody
gruntowej
Δh
L
Wartość wsp. filtracji k określa się na podstawie:
• badań terenowych lub laboratoryjnych,
• wzorów
empirycznych,
• orientacyjne
wartości – z tabel.
Przykładowe wzory empiryczne:
2
•
(d
50
d
357
,
0
k
⋅
=
50
w mm, k w cm/s)
•
(cm/s)
2
10
1
d
C
k
⋅
=
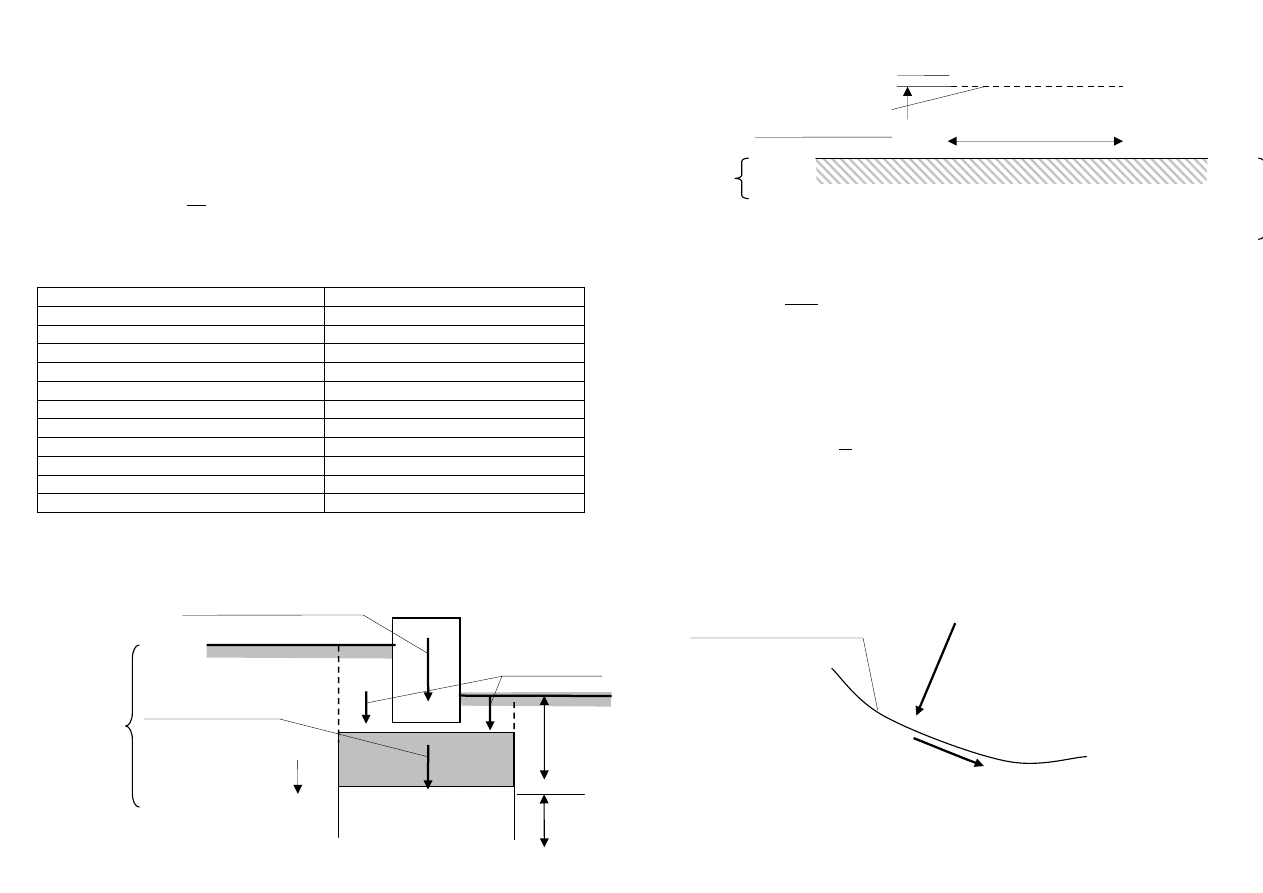
dla średnicy charakterystycznej d
10
= 0,1 ÷ 3,0 mm i gruntów
równomiernie uziarnionych:
C
1
= 1,39 dla u = 1
C
1
= 0,925 dla u = 1 ÷ 4
C
1
= 0,463 dla u = 4 ÷ 5
•
6
2
10
45
n
d
150
k
⎟
⎠
⎞
⎜
⎝
⎛
⋅
=
(d
10
w mm, k w m/dobę)
n – porowatość gruntu (%)
Orientacyjne wartości współczynników filtracji k
Rodzaj gruntu
k (cm/s)
Żwir
10 – 10
-1
Piasek gruby i średni 10
-1
– 10
-2
Piasek drobny
10
-2
– 10
-3
Piasek pylasty
10
-3
– 10
-4
Pył 10
-4
– 10
-6
Glina 10
-6
– 10
-8
Glina zwięzła 10
-7
– 10
-9
Ił 10
-9
– 10
-10
Torf słabo rozłożony 5·10
-3
– 10
-4
Torf średnio rozłożony 5·10
-4
– 10
-5
Torf silnie rozłożony 2·10
-4
– 10
-6
Wytrzymałość gruntów
Obciążenie od konstrukcji
Q
k
Ciężar
gruntu
Ciężar fundamentu
Q
1
Q
2
h
D
Grunt 1
Osiadanie s
Q
f
Poziom
fundamentu
B
h
i
po osiadaniu
Grunt 2
Wytrzymałość gruntów charakteryzuje:
• moduł ściśliwości M
o
(kPa) – wyraża podatność gruntu na
osiadanie pod wpływem obciążenia:
dop
o
i
s
M
h
s
≤
⋅
σ
=
gdzie:
s – osiadanie budowli, (cm),
s
dop
= 5 ÷ 15 cm – osiadanie dopuszczalne zależne od
rodzaju konstrukcji,
h
i
– grubość warstwy gruntu (cm),
σ – naprężenie (kPa) w gruncie na poziomie posadowienia:
A
Q
=
σ
Q – Nacisk pionowy fundamentu (kN):
Q = Q
k
+ Q
f
+ Q
1
+ Q
2
A = B L – powierzchnia fundamentu (m
2
),
B – szerokość, L – długość fundamentu.
• Naprężenie styczne τ – powstające na płaszczyźnie poślizgu:
Płaszczyzna poślizgu
σ
τ
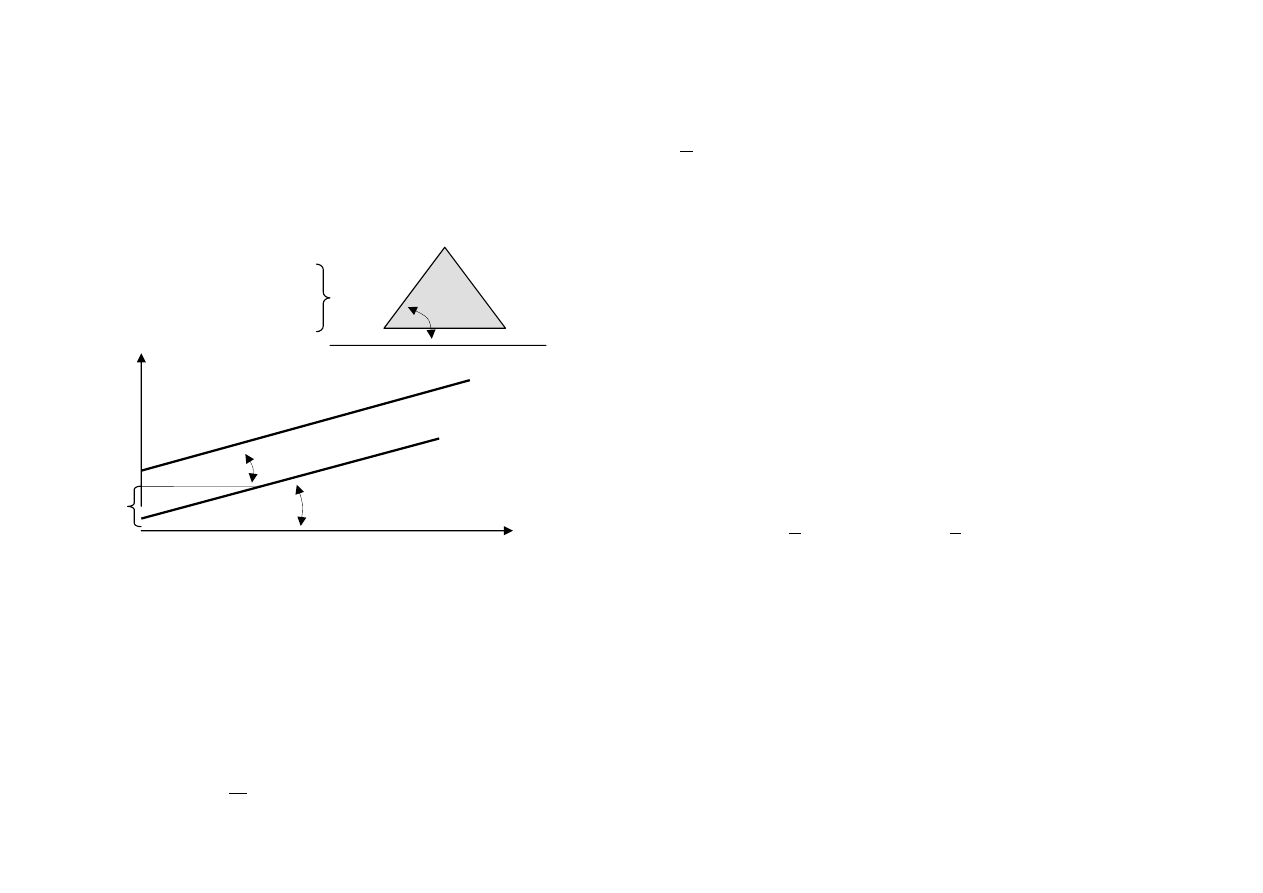
Naprężenie styczne τ (kPa):
c
tg
+
ϕ
⋅
σ
=
τ
gdzie:
σ – składowa normalna naprężenia, (kPa) – prostopadła do
płaszczyzny poślizgu,
tgφ – tangens kąta tarcia wewnętrznego gruntu, (-),
c – spójność gruntu (kohezja), (kPa) – charakteryzuje siłę
wzajemnego przyciągania się cząstek gruntu.
Kąt tarcia wewnętrznego dla gruntów nie-
spoistych jest równy kątowi stoku natura-
lnego φ
n
– kąt pod jakim utrzymuje się φ = φ
n
skarpa luźno usypanej pryzmy gruntu.
τ (kPa)
grunt
spoisty
c
tg
+
ϕ
⋅
σ
=
τ
φ
grunt niespoisty
ϕ
⋅
σ
=
τ
tg
c
φ
σ (kPa)
Wartości φ i c zależą od:
• rodzaju gruntu – (spoisty, niespoisty),
• pochodzenia geologicznego – dotyczy gruntów spoistych (np.
gliny morenowe, iły trzeciorzędowe),
• stopnia
zagęszczenia gruntu niespoistego I
D
,
• stopnia
plastyczności gruntu spoistego I
L
,
Warunki graniczne na poziomie posadowienia – takie warunki przy
których nie nastąpi wyparcie gruntu spod fundamentu – brak poślizgu
fundamentu:
F
q
f
≤
σ
gdzie:
σ – naprężenie (kPa) w poziomie posadowienia od sił działających na fundament
i ciężaru fundamentu
A
Q
=
σ
Q – Nacisk pionowy fundamentu (kN), Q = Q
k
+ Q
f
+
Q
1
+ Q
2
A = B · L – powierzchnia fundamentu (m
2
), B – szerokość, L –
długość fundamentu.
q
f
– obciążenie graniczne gruntu pod fundamentem, (kPa),
F = 2÷3 – współczynnik pewności (bezpieczeństwa).
Obciążenie graniczne q
f
(kPa) dla gruntu jednorodnego pod
fundamentem obliczamy ze wzoru:
γ
⋅
⋅
γ
⋅
+
⋅
⋅
γ
+
⋅
⋅
=
N
B
a
N
h
N
c
a
q
2
q
D
c
1
f
gdzie:
c – spójność gruntu, (kPa),
N
c
, N
q
, N
γ
– współczynniki wytrzymałości gruntu zależne od kąta
tarcia wewnętrznego φ
g
⋅
ρ
=
γ
- ciężar objętościowy gruntu (kN/m
3
), ρ – gęstość
objętościowa (t/m
3
), g = 9,81 m/s
2
,
a
1
, a
2
– współczynniki zależne od wymiarów fundamentu:
⎟
⎠
⎞
⎜
⎝
⎛ +
=
L
B
3
,
0
1
a
1
⎟
⎠
⎞
⎜
⎝
⎛ −
=
L
B
2
,
0
1
a
2
B – szerokość, L – długość fundamentu
Document Outline
- Grunty_budowlane.doc
- MECHANIKA GOROTWORU - PROGRAM.doc
- EGAZMIN FIZYKA SKA+ü I GRUNT+ôW.doc
- fizyka ska+é i grunt+-w egzamin wyk+éady.doc
- FIZYCZNA STRUKTURA GÓROTWORU
- ELEMENTY STRUKTURALNE GÓROWORU
- CECHY STRUKTURALNE GÓROTWORU
- ELEMENTY I CECHY STRUKTURALNE GÓROTWORU
- SKAŁY JAKO OŚRODKI TRÓJFAZOWE
- KLASYFIKACJA WŁ FIZYCZNYCH SKAŁ
- SKAŁY A GRUNTY BUD
- PODZIAŁ GRUNTÓW BUD
- PODZIAŁ GR SKALISTYCH ZE WZGL NA WYTRZYMALOŚĆ
- PODZIAŁ GR SKALISTYCH ZE WZGL NA SPĘKANIA
- KRYTERIA PODZIAŁU GR BUD
- STRUKTURALNE WŁ SKAŁ I GR
- METODY POMIARU
- HYDROGAZODYNAMICZNE WŁ SKAŁ charakteryzuja zdolność skał do przepuszczania, pochłaniania i zatrzymywania różnych cieczy i gazów oraz skłonności skał do zmiany swego stanu mechanicznego podczas oddziaływania cieczami lub gazami
- MECHANICZNE WŁ SKAŁ- charakteryzują zachowanie się skał przy oddziaływaniu na nie mechanicznych obciążeń. W zależności od wielkości, kierunku, czasu działania powstają różnorodne związki między naprężeniami i odkształceniami skał. Ze względu na charaktery tych zależności wyróżniamy:
- WYTRZYMAŁOŚCIOWE WŁ SKAŁ
- WŁ MECHANICZNE OŚR GRUNTOWEGO
- FALOWE WŁAŚCIWOŚCI SKAŁ właściwości te charakteryzują zdolność skał do przepuszczania, pochłaniania, załamywania i odbijania drgań sprężystych wywoływanych ruchem falowym. Ze względu na częstotliwość fale sprężyste dzielimy na:
- -fale infradźwiękowe o częstotliwości do 16 Hz
- TERMICZNE WŁ SKAŁ WŁ termiczne charakteryzuje proces rozchodzenie się i pochłaniania ciepła w skałach. Przepływ E cieplnej w ośrodku skalnym odbywa się na drodze:
- OGÓLNE RÓWNANIE PRZEPŁYWU CIECZY
- DOPŁYW WODY DO TUNELU
- DOPŁYW CIECZY DO OTWORU WIERTNICZEGO
- PRZEPŁYW GAZU W GÓROTWORZE
- DOPŁYW GAZU DO OTWORU WERTNICZEGO
- FIZYKA SKA+ü I GRUNT+ôW PROGRAM.doc
- grunty budowlane -fizyka ska+é i grunt+-w egzamin.doc
Wyszukiwarka
Podobne podstrony:
Fiz.Mech.2.3, kolosy pollub i pwsz chełm
fiz mech 9
woda plus oplaty
5 3 FIZJOLOGIA W FIZ
Fiz kwantowa
KOTŁY OKRĘTOWE ZALICZENIE II MECH
mat fiz 2008 10 06
9, dokumentacja pracy fiz, diagnostyka fizj, problemy i ich rozwiazywane zwiazane z plananem
00090100101 medium plus, 00090100101 solution
frakcje gramulometryczne -sklad mech, gleboznawstwo
Gram plus, Ratownicto Medyczne, MIKROBIOLOGIA
Zestaw Fiz.wsp, AGH, ROK I, fizyka, Fizyka
PŁYNY, Studia, Mech. płynów
więcej podobnych podstron