1
2. Opisy przestrzenne i przekształcenia układów współrzędnych
Wyznaczając trajektorię ruchu końcówki technologicznej manipulatora jesteśmy
zainteresowani usytuowaniem obiektów w jego (trójwymiarowej) przestrzeni roboczej.
Obiektami tymi są człony manipulatora, narzędzia którymi robot operuje, przedmioty
znajdujące się w jego otoczeniu. Obiekty te opisane są przez dwa atrybuty: pozycję i
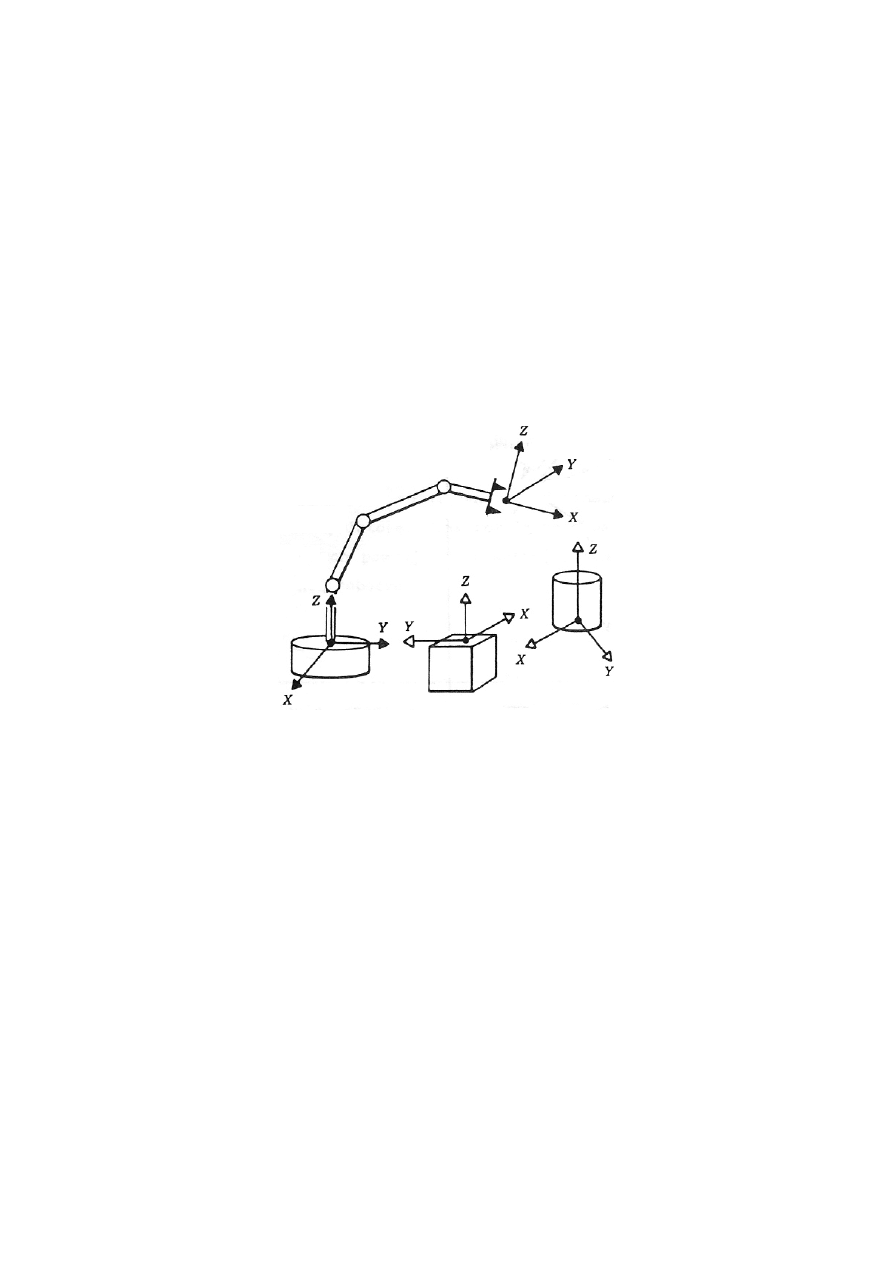
orientację. W celu matematycznego opisu tych atrybutów do każdego z obiektów (rys. 1)
przypisujemy układ współrzędnych. Układy współrzędnych przypisane do obiektów są
najczęściej prawoskrętnymi kartezjańskimi układami współrzędnych prostokątnych.
Rys 1. Przypisanie układów współrzędnych do obiektów
Przyjmijmy, że gdzieś w przestrzeni umieszczony jest nieruchomy globalny układ
współrzędnych. Globalny układ współrzędnych jest najczęściej związany z podstawą
manipulatora. Pozycje i orientacje obiektów można opisać względem globalnego
(podstawowego) układu współrzędnych lub względem innych kartezjańskich układów
współrzędnych.
2.1. Opis pozycji
Położenie dowolnego punktu w przestrzeni można określić za pomocą
wektora pozycji (3x1). Ze względu na to, że obok globalnego układu współrzędnych
będziemy często wprowadzać dodatkowe inne układy współrzędnych, wektory pozycji muszą
zawierać informację identyfikującą układ współrzędnych, w których zostały określone.
2
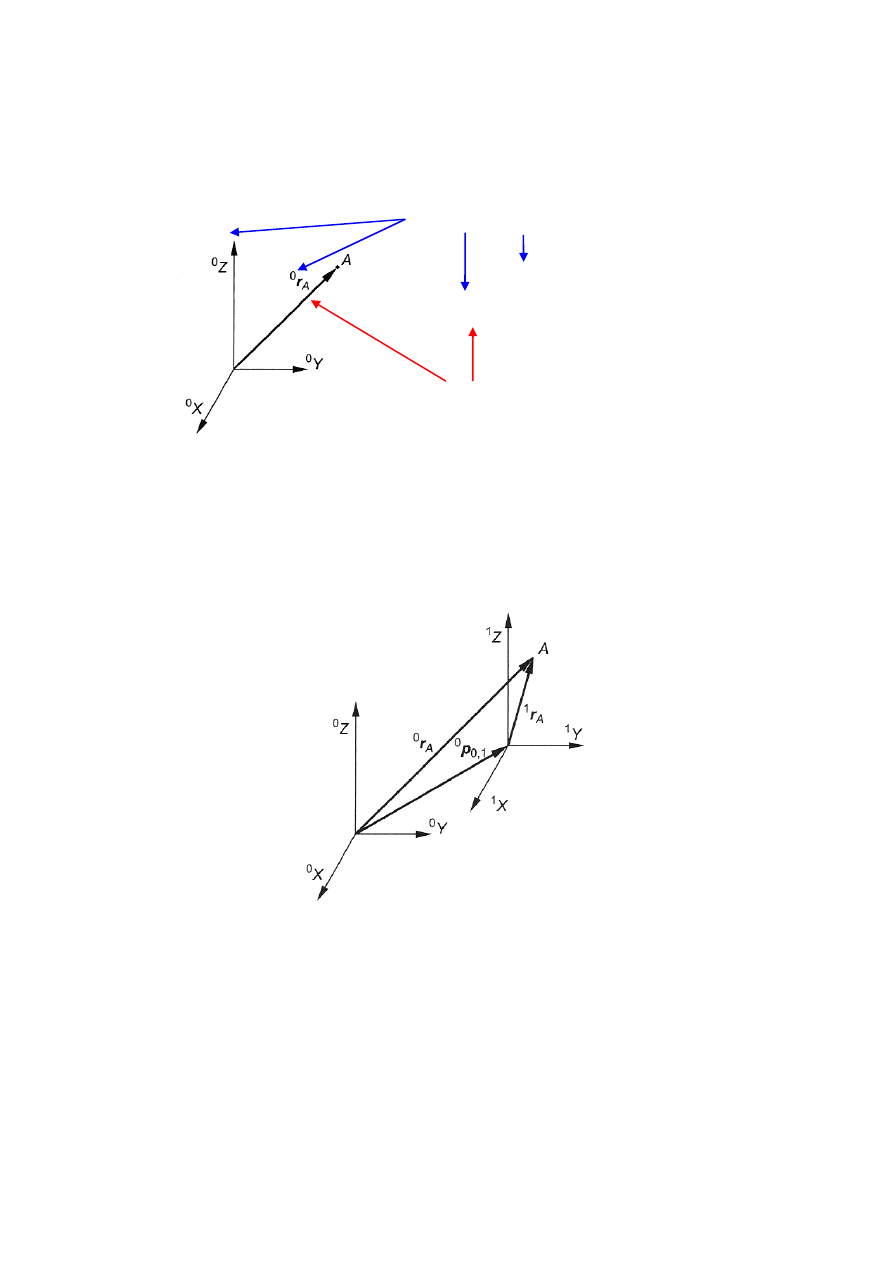
Położenie dowolnie wybranego punktu A opisanego w układzie {0} jest określone za pomocą
wektora pozycji
A
r
0
(rys. 2).
Rys. 2. Wektor pozycji w układzie współrzędnych {0}
2.2. Przesunięcia układów współrzędnych
Opis dowolnie wybranego punktu A w dwóch układach współrzędnych kartezjańskich
{0} i {1}, których osie są wzajemnie równoległe, przedstawiono na rys. 3.
Rys. 3. Przesunięcie równoległe układów
Układ {1} otrzymano przez przesunięcie układu {0} o wektor
1
,
0
0
p
. Położenie punktu A w
układzie {0} jest opisane za pomocą wektora
A
r
0
, a w układzie {1} za pomocą wektora
A
r
1
.
Wektory te połączone są następującą zależnością
=
zA
yA
xA
A
r
r
r
0
0
0
0
r
nazwa układu współrzędnych
Wektor pozycji wyrażony układzie współrzędnych {0}
opisujący położenie punktu A
{0}
3
+
=
zA
yA
xA
z
y
x
zA
yA
xA
r
r
r
p
p
p
r
r
r
1
1
1
1
,
0
0
1
,
0
0
1
,
0
0
0
0
0
.
Dalej równość ta będzie zapisywana w zwartej postaci
A
A
r
p
r
1
1
,
0
0
0
+
=
.
2.3. Opis orientacji (obroty układów współrzędnych)
W celu opisu orientacji ciała wiążemy z nim układ współrzędnych, a następnie
opisujemy orientacje tego układu współrzędnych względem układu odniesienia.
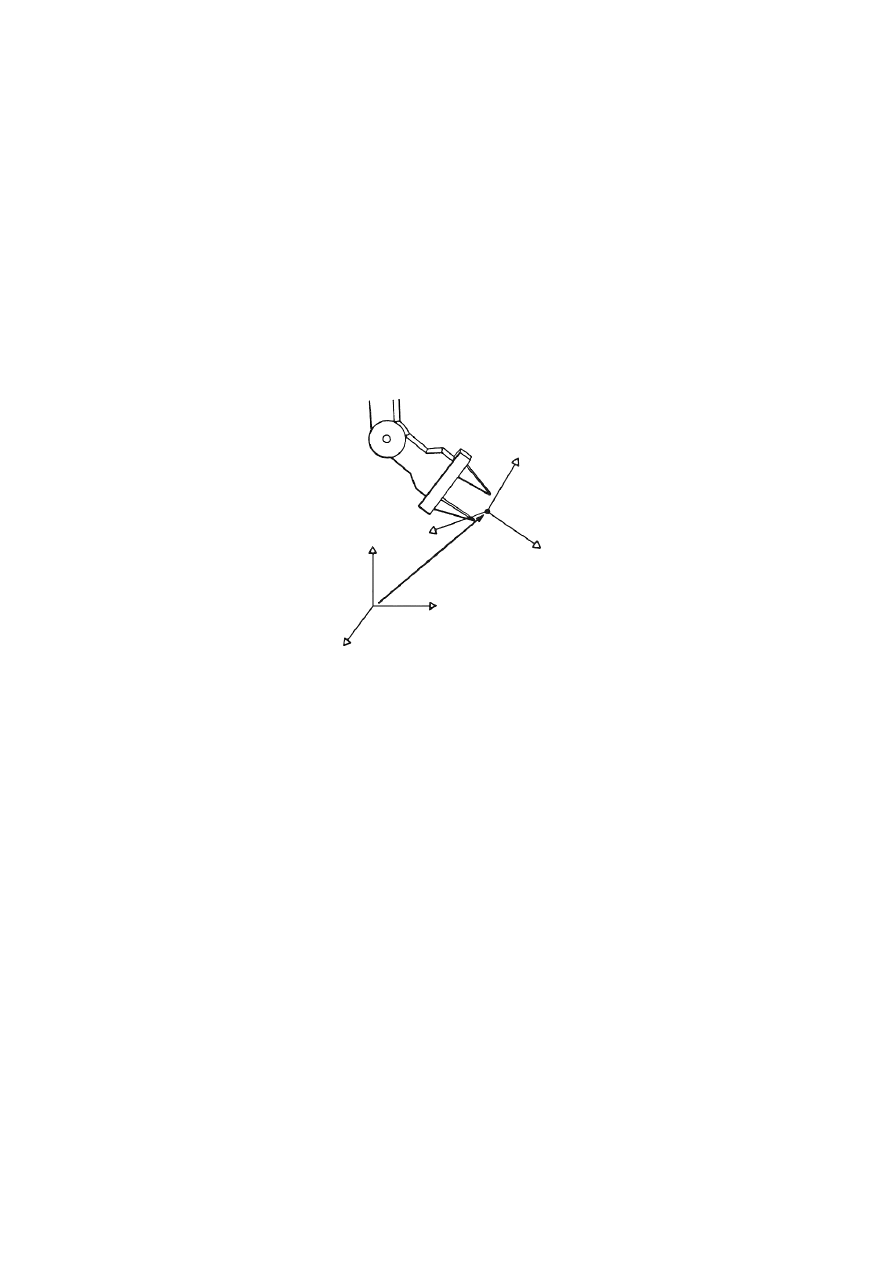
Rys. 4. Usytuowanie obiektu co do pozycji i orientacji
Układ współrzędnych {1}, związany z ciałem (rys. 4) jest przesunięty i obrócony
względem układu {0}. W celu znalezienia orientacji układu {1} względem układu {0} należy
początki układów umieścić w tym samym punkcie.
2.3.1. Obroty podstawowe
Jeżeli układ współrzędnych {1} otrzymano przez obrót układu podstawowego {0}
wokół jednej z jego osi, to taki obrót nazywany jest podstawowym, a odpowiadające mu
przekształcenie obrotem podstawowym.
W przestrzeni R
3
występują trzy możliwości takich obrotów. Pierwszy z nich, obrót
wokół osi X, przedstawiono na rys. 5. Punkt A może być opisany za pomocą wektora
0
r
A
lub
1
r
A
odpowiednio w układzie {0} lub {1}. Zależności pomiędzy tymi wektorami są zapisane
następującym związkiem macierzowym:
{1}
{0}
1
,
0
0
p
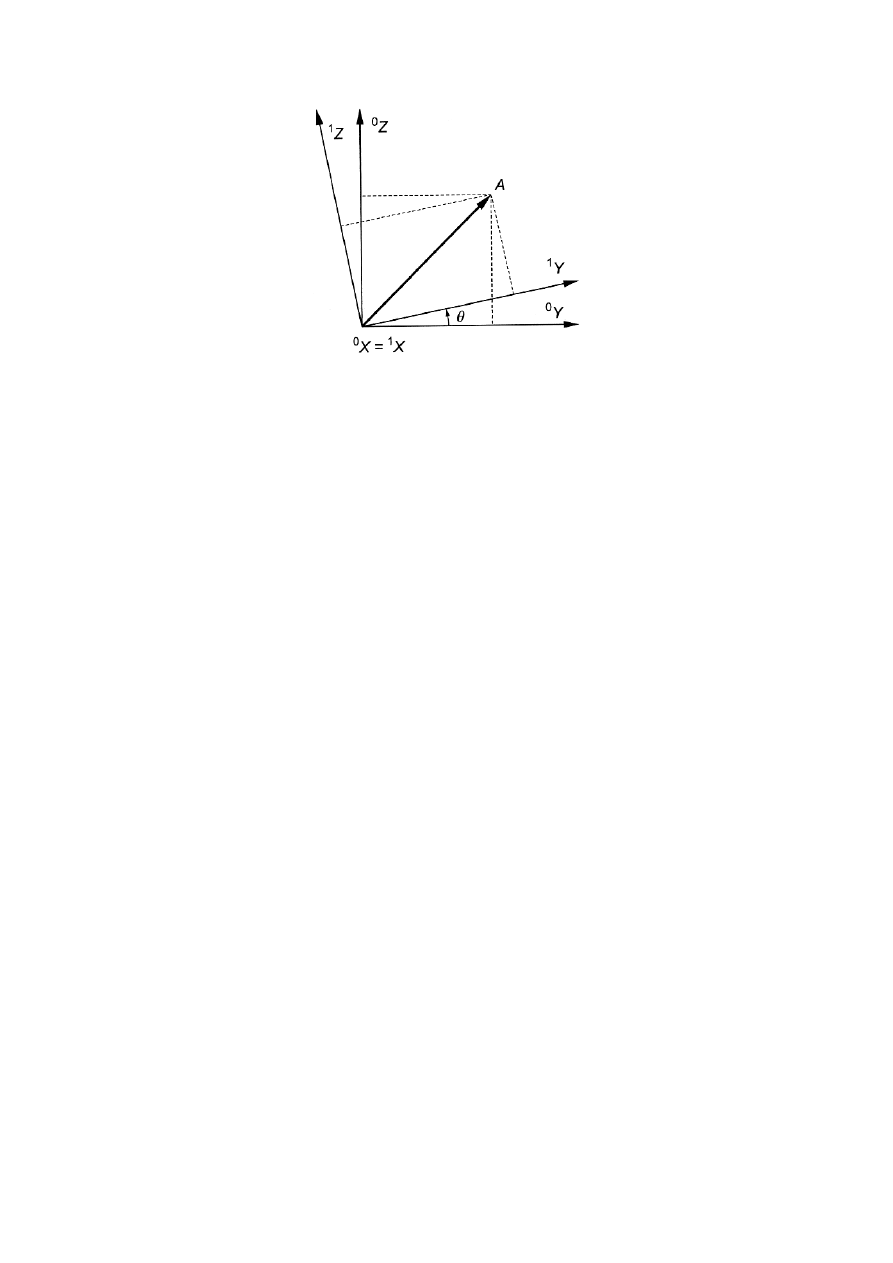
4
Rys. 5. Obrót układu {0} wokół osi
0
X o kąt
θ
−
=
zA
yA
xA
zA
yA
xA
r
r
r
r
r
r
1
1
1
0
0
0
cos
sin
0
sin
cos
0
0
0
1
θ
θ
θ
θ
lub w zwartej postaci
A
A
X
r
R
r
1
0
)
,
(
θ
=
, gdzie
−
=
θ
θ
θ
θ
θ
cos
sin
0
sin
cos
0
0
0
1
)
,
( X
R
jest podstawową macierzą obrotu wokół osi X.
Pozostałe dwie podstawowe macierze obrotu odpowiednio wokół osi Y i Z mają postać
−
=
θ
θ
θ
θ
θ
cos
0
sin
0
1
0
sin
0
cos
)
,
(Y
R
,
−
=
1
0
0
0
cos
sin
0
sin
cos
)
,
(
θ
θ
θ
θ
θ
Z
R
.
Z każdym podstawowym obrotem układu {0} można związać transformację obrotu
A
A
r
R
r
1
1
0
0
=
.
Macierz obrotu jest macierzą ortogonalną, a zatem
T
0
1
1
0
1
1
0
R
R
R
=
=
−
.
5
2.3.2. Obroty złożone
Obrót złożony powstaje w wyniku wykonania sekwencji obrotów podstawowych.
Macierz obrotu złożonego jest iloczynem kolejno mnożonych przez siebie podstawowych
macierzy obrotu.
Przykład:
Układ {1} powstał z układu {0} przez pewien obrót podstawowy, a następnie układ {2} przez
pewien obrót podstawowy układu {1}. Niech wektory opisują położenie punktu A w tych
trzech układach. Wówczas zachodzą następujące związki
A
A
r
R
r
1
1
0
0
=
,
A
A
r
R
r
2
2
1
1
=
. Zatem
obrót złożony jest opisany relacją
A
A
A
r
R
r
R
R
r
2
2
0
2
2
1
1
0
0
=
=
.
Ponieważ mnożenie macierzy nie jest przemienne (AB≠BA), przy składaniu obrotów należy
zwrócić uwagę na kolejność ich wykonywania. Macierz obrotu złożonego, będąca
iloczynem macierzy podstawowych, jest macierzą ortogonalną.
Dowolne obroty złożone, układu współrzędnych w przestrzeni R
3
, względem innego
układu współrzędnych można opisać według dwóch konwencji:
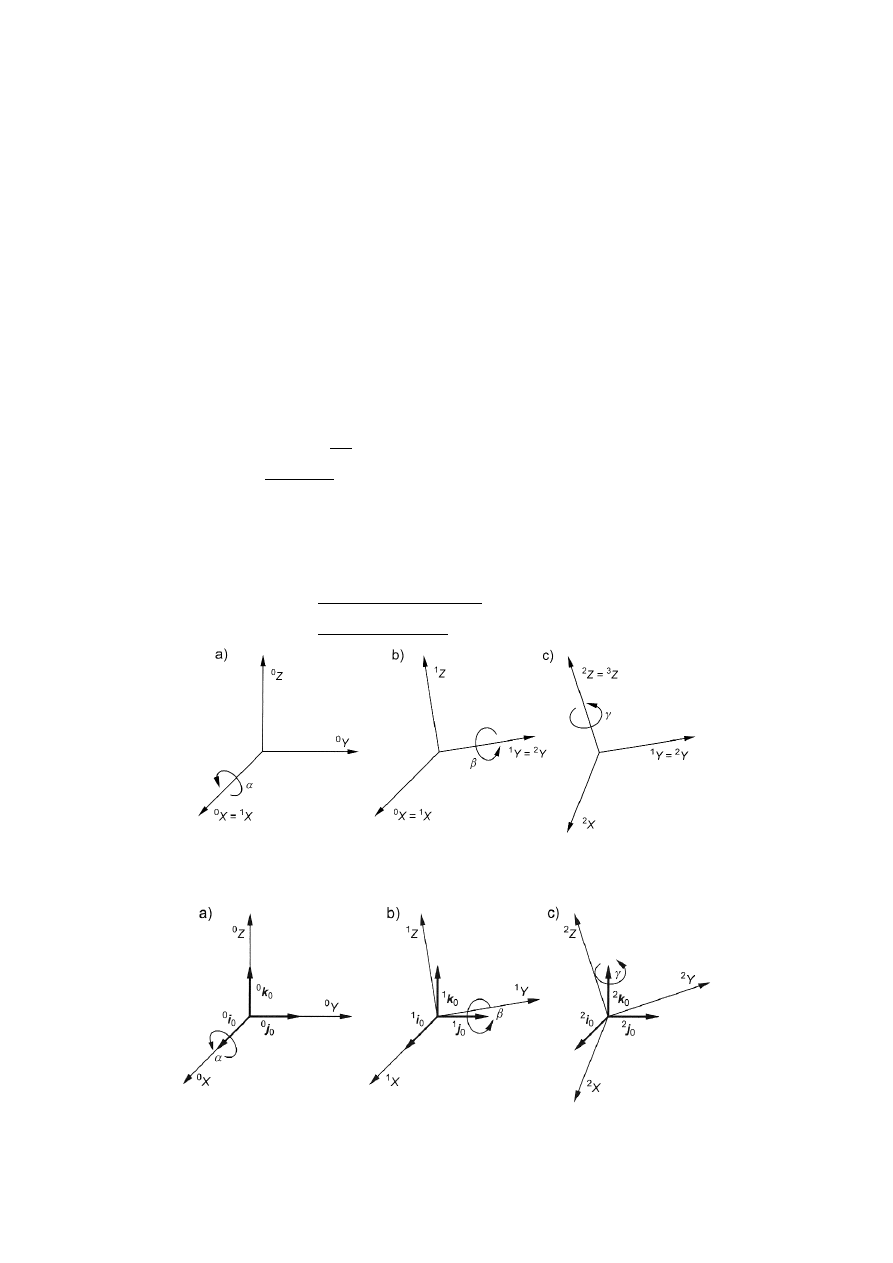
- obroty wykonywane wokół osi układów bieżących (rys. 6)
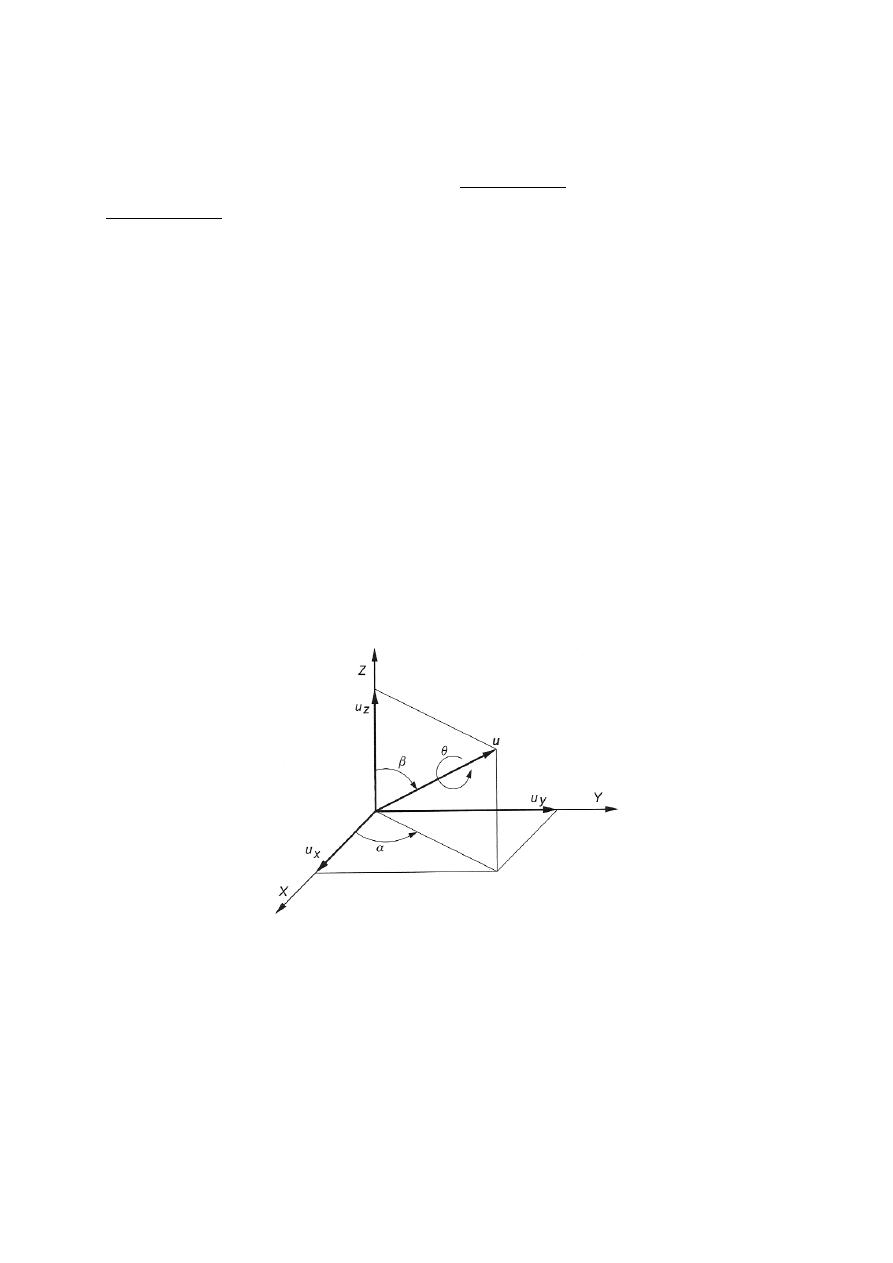
- obroty wykonywane wokół osi układu stałego (rys. 7)
Rys. 6. Kolejne obroty X-Y-Z wokół bieżących osi
Rys. 7. Kolejne obroty wokół stałych osi
6
Dowolny obrót układu współrzędnych jest złożeniem trzech kolejnych obrotów wokół
osi
bieżących.
Przy
ich
określeniu
należy
podać
trzy
kolejne
nazwy
osi
i kąty obrotu wokół nich. Kąty te nazwano kątami Eulera a odpowiadające im obroty
obrotami Eulera. Możliwych jest 12 obrotów Eulera:
Wszystkie układy obrotów są równoważne, jednak najbardziej naturalnym jest układ o
kolejności X-Y-Z (rys. 6). Odpowiadająca mu macierz obrotu ma postać:
+
+
+
+
=
=
−
−
β
α
γ
α
γ
β
α
γ
α
γ
β
α
β
α
γ
α
γ
β
α
γ
α
γ
β
α
β
γ
β
γ
β
γ
β
α
γ
β
α
c
c
c
s
s
s
c
s
s
c
s
c
-
c
s
-
c
c
s
s
s
-
s
c
c
s
s
s
s
c
-
c
c
)
,
(
)
,
(
)
,
(
)
,
,
(
Z
Y
X
Z
Y
X
R
R
R
R
.
2.3.3. Obrót wokół dowolnej osi
Rozważmy
obrót
wokół
dowolnie
wybranego
wektora
jednostkowego
[
]
T
z
y
x
u
u
u
=
u
o zadany kąt
θ
(rys. 8).
Rys. 8. Obrót wokół dowolnej osi
Obrót taki można otrzymać przez złożenie pięciu kolejnych podstawowych obrotów:
1) obrót o kąt
α
wokół osi Z,
2) obrót o kąt
β
wokół bieżącej osi Y (po tych obrotach oś Z pokrywa się z kierunkiem
wektora u),
3) obrót o kąt
θ
wokół bieżącej osi Z,
1) X-Y-Z
2) X-Z-Y
3) Y-X-Z
4) Y-Z-X
5) Z-X-Y
6) Z-Y-X
7) X-Y-X
8) X-Z-X
9) Y-X-Y
10) Y-Z-Y
11) Z-X-Z
12) Z-Y-Z

7
4) obrót o kąt -
β
wokół osi Y,
5) obrót o kąt -
α
wokół bieżącej osi Z
Rozpatrywany obrót złożony ma postać:
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
)
,
(
α
β
θ
β
α
θ
−
−
=
Z
Y
Z
Y
Z
R
R
R
R
R
u
R
.
Podstawiając do poprzedniego wzoru macierze obrotów podstawowych oraz korzystając z
relacji pomiędzy składowymi wektora
u a funkcjami trygonometrycznymi kątów
α
i
β
:
2
2
2
2
sin
,
cos
y
x
y
y
x
x
u
u
u
u
u
u
+
=
+
=
α
α
,
2
2
sin
,
cos
y
x
z
u
u
u
+
=
=
β
β
po obliczeniach otrzymuje się:
=
+
−
+
−
−
−
−
−
+
−
+
−
+
−
−
−
+
−
=
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
c
)
c
1
(
s
)
c
1
(
s
)
c
1
(
s
)
c
1
(
c
)
c
1
(
s
)
c
1
(
s
)
c
1
(
s
)
c
1
(
c
)
c
1
(
)
,
(
z
z
x
y
z
y
x
z
x
z
y
y
y
z
x
y
y
z
x
z
y
x
x
x
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
u
R
(
)
−
−
−
+
−
=
θ
θ
θ
θ
θ
θ
θ
θ
θ
θ
cos
sin
sin
sin
cos
sin
sin
sin
cos
cos
1
x
y
x
z
y
z
T
u
u
u
u
u
u
uu
(1)
Macierz obrotu złożonego wokół dowolnego wektora jednostkowego o kąt
θ
jest macierzą
ortogonalną oraz prawdziwe są następujące zależności:
)
,
(
)
,
(
)
,
(
1
θ
θ
θ
u
R
u
R
u
R
T
=
=
−
−
)
,
(
)
,
(
θ
θ
u
R
u
R
=
−
−
2.3.4. Reprezentacja oś kąt
Dla dowolnej macierzy o postaci
=
33
32
31
23
22
21
13
12
11
r
r
r
r
r
r
r
r
r
R
,
spełniającej warunki:
1
)
det(
i
3
3
=
=
×
R
1
RR
T
można znaleźć wektor u i kąt
θ
, jeśli
zauważy się że ślad macierzy R(u,
θ
) po skorzystaniu ze związku
1
2
2
2
2
=
=
+
+
u
z
y
x
u
u
u
ma
postać
.
cos
2
1
))
,
(
Tr(
θ
θ
+
=
u
R
Stąd kąt
θ
dla dowolnej macierzy obrotu R można wyznaczyć
z zależności:
.
2
1
arccos
2
1
)
Tr(
arccos
33
22
11
−
+
+
=
−
=
r
r
r
R
θ
Porównując wyrazy macierzy R(u,
θ
) położone symetrycznie względem głównej przekątnej

8
θ
θ
θ
sin
2
,
sin
2
,
sin
2
12
21
31
13
23
32
z
y
x
u
r
r
u
r
r
u
r
r
=
−
=
−
=
−
można otrzymać wektor
u z równania
−
−
−
=
12
21
31
13
23
32
sin
2
1
r
r
r
r
r
r
θ
u
.
2.3.5. Obroty złożone wykonywane wokół osi układu stałego
Podobnie jak w przypadku kątów Eulera, możliwych jest 12 złożeń obrotów wokół
tych osi układu stałego. Podstawowym złożeniem obrotów (wokół stałych osi) są trzy kolejne
obroty wykonane wokół osi
0
X,
0
Y,
0
Z, odpowiednio o kąty
α
,
β
,
γ
(rys. 7). Konwencja zapisu
obrotu w tej postaci utożsamiana jest z kiścią manipulatora, gdzie aby odpowiednio
zorientować narzędzie wykonywane są obroty wokół jej osi. Kąty te zwyczajowo nazywa się:
- yaw (odchylenie) – wokół stałej osi X,
- pitch (pochylenie) – wokół stałej osi Y,
- roll (obrót) – wokół stałej osi Z.
Wypadkowa macierz obrotu wokół wersorów układu podstawowego {0} w kolejności jak na
rys. 7, odpowiednio kąty
α
,
β
,
γ
ma postać:
)
,
(
)
,
(
)
,
(
)
,
,
(
0
2
0
1
0
0
γ
β
α
γ
β
α
k
R
j
R
i
R
R
=
XYZ
Wersory jednostkowe
0
0
0
0
0
0
,
,
k
j
i
są trzema kolejnymi kolumnami macierzy jednostkowej:
=
=
=
1
0
0
,
0
1
0
,
0
0
1
0
0
0
0
0
0
k
j
i
.
Układ współrzędnych {1} powstał w wyniku obrotu układu {0} wokół osi
X
0
czyli wokół
wersora
0
0
i . Zależność pomiędzy opisem dowolnie wybranego wektora
A
r
w obu tych
układach współrzędnych wyraża równanie
A
A
A
A
X
r
R
r
i
R
r
R
r
1
1
0
0
1
1
0
0
)
,
(
)
,
(
α
α
=
=
=
Opis wersorów układu {0} wyrażonych w układzie {1} można znaleźć przeprowadzając
następujące działania
0
1
0
0
0
1
0
0
0
1
0
0
)
,
(
,
)
,
(
,
)
,
(
k
R
k
j
R
j
i
R
i
α
α
α
X
X
X
=
=
=
[
]
[
]
0
1
0
1
0
1
0
0
0
0
0
0
)
,
(
k
j
i
R
k
j
i
α
X
=
[
]
)
,
(
)
,
(
1
0
1
0
1
0
1
α
α
X
X
T
R
R
k
j
i
=
=
−
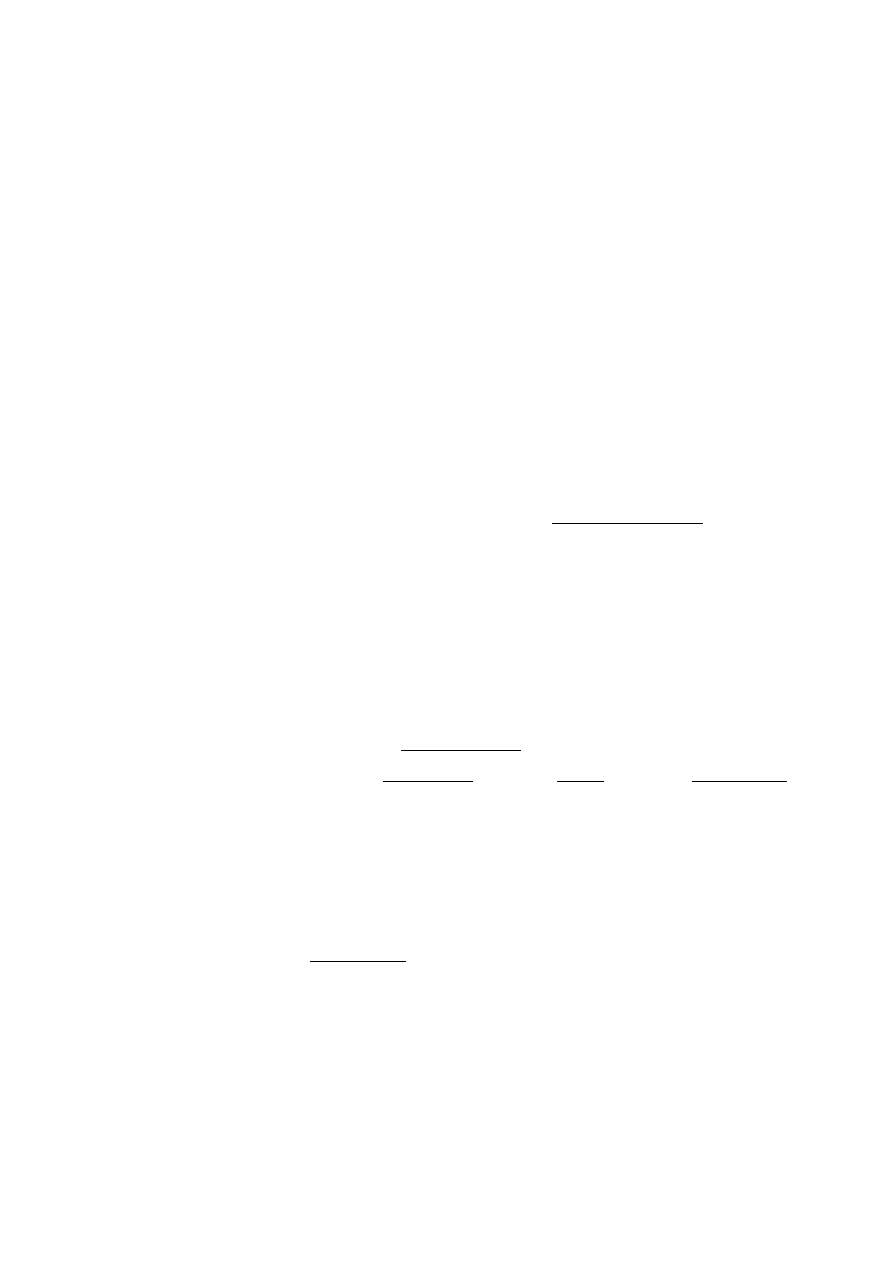
9
Drugi obrót wykonywany jest wokół wektora
[
]
T
α
α
sin
cos
0
0
1
−
=
j
o kąt
β
. Macierz
obrotu znajdujemy ze wzoru (1)
[
]
(
)
+
−
=
β
β
α
β
β
α
β
α
β
α
β
β
α
α
α
α
β
c
0
s
-
0
c
s
s
-
s
c
s
s
c
c
1
s
-
c
0
s
-
c
0
)
,
(
0
1
c
j
R
Wykonując iloczyn
)
,
(
)
,
(
0
1
β
α
j
R
R X
otrzymuje się:
=
=
β
α
β
α
β
α
α
β
α
β
α
β
β
α
β
α
c
c
c
s
s
-
s
-
c
0
s
c
s
s
c
)
,
(
)
,
(
)
,
(
0
1
j
R
R
R
X
XY
Jak można zauważyć, otrzymana macierz obrotu złożonego równa jest iloczynowi dwóch
obrotów podstawowych, to jest
)
,
(
)
,
(
α
β
X
Y
R
R
. Złożona macierz obrotów wykonanych
wokół stałych osi, najpierw o kąt
α
wokół osi
0
X, następnie o kąt
β
wokół osi
0
Y, jest równa
iloczynowi macierzy obrotów podstawowych wykonanych w odwrotnej kolejności
)
,
(
)
,
(
)
,
(
α
β
β
α
X
Y
XY
R
R
R
=
Zasada ta jest słuszna dla dowolnych obrotów wokół stałych osi. Dla rozważanego przypadku
otrzymuje się
)
,
(
)
,
(
)
,
(
)
,
,
(
α
β
γ
γ
β
α
X
Y
Z
XYZ
R
R
R
R
=
2.4.
Przekształcenia jednorodne
Najbardziej ogólny przypadek przemieszczenia układu współrzędnych może być
wyrażony przez kombinację czystego przesunięcia i czystego obrotu, co określa
ruch sztywny
(rys. 9). W wyniku przesunięciu układu {0} o wektor
1
,
0
0
p
powstaje układ {
’}. Układ {1}
otrzymano przez obrót układu {
’} zgodnie z macierzą obrotu
1
0
R .
Związek pomiędzy dowolnie wybranym punktem
A w układach {0} i {1} ma postać
A
A
r
R
p
r
1
1
0
1
,
0
0
0
+
=
Przekształcenie to definiuje ruch sztywny.
Zapis definiujący ruch sztywny jest bardziej złożony, niż zapis samych przesunięć lub samych
obrotów. Aby go uprościć zapisuje się go w postaci zwartej jako
=
1
1
1
1
1
,
0
0
1
0
0
A
A
r
p
R
r
0
lub jeszcze prościej
A
A
r
H
r
ˆ
ˆ
1
1
0
0
=
,
gdzie:
[
]
0
0
0
=
0
.

10
Rys. 9. Przesunięcie równoległe i obrót układu współrzędnych
Macierz
1
0
H nazwana jest macierzą jednorodną przekształcenia.
Wektor
A
rˆ
0
nazwany jest reprezentacją jednorodną wektora
A
r
0
.
Macierz odwrotna do macierzy przekształcenia jednorodnego (przekształcenie odwrotne)
przybiera postać
−
=
−
1
1
0
p
R
R
H
T
T
.
Szczególnym przypadkiem macierzy jednorodnych przekształceń H jest:
jednorodna macierz obrotu
=
1
)
,
(
)
,
(
0
0
θ
θ
u
R
u
Rot
oraz jednorodna macierz przesunięcia
=
1
)
(
0
1
p
p
Trans
.
Literatura:
[1] Craig J. J.: Wprowadzenie do robotyki. Mechanika i sterowanie, Wydawnictwa
Naukowo-Techniczne, 1995
[2] Jezierski E.: Dynamika robotów, Wydawnictwa Naukowo-Techniczne, 2006
[3] Spong M. W., Vidyasagar M.: Dynamika i sterowanie robotów, Wydawnictwa
Naukowo-Techniczne, 1997
Informacja o prawach autorskich
O ile nie zaznaczono inaczej, rysunki i teksty pochodzą z pozycji podanych w literaturze.
Niniejsze opracowanie stanowi pomoc do wykładu „Podstawy Robotyki”.
Wyszukiwarka
Podobne podstrony:
opisy przestrzenne
7 Zasady przywiązywania układów współrzędnych
,algebra liniowa z geometrią analityczną, PRZESTRZENIE I PRZEKSZTAŁCENIA LINIOWE zadania
Algebra 1 04 przestrzenie i przekształcenia liniowe
,algebra liniowa z geometrią analityczną, PRZESTRZENIE I PRZEKSZTAŁCENIA LINIOWE zadania
opisy przestrzenne
3 Statyka układów przestrzennych
Przestrzenna transformacja współrzędnych
Przestrzenna transformacja współrzędnych
materialy Przekształcenie rzutowe przestrzeni, materiały
zagadnienia, punkt 21, XXI Przekształcenia liniowe przestrzeni skończenie wymiarowych
więcej podobnych podstron