Z. Kąkol-Notatki do Wykładu z Fizyki

25-1

Wykład 25

25. Równania Maxwella

25.1 Podstawowe równania elektromagnetyzmu

Poszukiwaliśmy zawsze podstawowego (najmniejszego) zestawu równań pozwalające-
go na pełne opisanie przedmiotu zainteresowań.
W mechanice - trzy zasady dynamiki
W termodynamice - trzy zasady termodynamiki
Teraz chcemy zrobić to samo dla elektromagnetyzmu.
Zacznijmy od poznanych już równań.

Nazwa

Równanie

1

2

3

4

prawo Gaussa dla elektryczności

prawo Gaussa dla magnetyzmu

prawo indukcji Faradaya

prawo Ampera

∫

=

0

/

d

ε

q

S

E

∫

=

0

dS

B

∫

−

=

=

t

B

d

d

d

φ

ε

l

E

∫

=

I

0

d

µ

l

B

r

Te równania jak się okaże są niekompletne Konieczne jest wprowadzenie jeszcze jed-
nego dodatkowego wyrazu do równania 4.
Pozwala on w szczególności na udowodnienie, że prędkość światła w próżni c, jest
związana z czysto elektrycznymi i magnetycznymi wielkościami.

Prześledźmy powyższą tabelę z punktu widzenia symetrii.
Zwróćmy uwagę, że w tych rozważaniach stałe

µ

0

i

ε

0

nie są istotne bo możemy wybrać

układ jednostek, w którym będą te stałe równe 1. Wtedy zauważamy pełną symetrię le-
wych stron równań. Prawe strony NIE są symetryczne.
Przyczynę niesymetrii dla równań 1 i 2 znamy. Wiemy, że

istnieją izolowane centra ła-

dunku

(np. elektron, proton) ale

nie istnieją izolowane centra magnetyczne

(pojedyncze

bieguny magnetyczne - monopole). Dlatego w równaniu 1 pojawia się q, a w 2 zero.
Z tego powodu mamy w równaniu 4 prąd I = dq/dt, a nie mamy prądu monopoli (ładun-
ków magnetycznych) w równaniu 3.
Drugi rodzaj asymetrii wiąże się z wyrazem – d

φ

B

/dt w równaniu 3. Sens tego prawa jest

następujący:

zmieniające się pole magnetyczne wytwarza pole elektryczne

.

Korzystając z zasad symetrii można przypuszczać, że obowiązuje zależność odwrotna:

zmieniając pole elektryczne (d

φ

E

/dt) wytwarzamy pole magnetyczne

∫

)

d

(

l

B

.

25.2 Indukowane pole magnetyczne

Oczywiście doświadczenie daje przykłady: w kondensatorze (cylindrycznym) pole

elektryczne wzrasta (kondensator ładuje się) z prędkością dE/dt co oznacza, że do okła-
dek dopływa ładunek.

Z. Kąkol-Notatki do Wykładu z Fizyki

25-2

Doświadczenie pokazuje, że

powstaje tam pole magnetyczne wytworzone przez zmienia-

jące się pole elektryczne

.

Trzeba to uwzględnić w naszych równaniach. Jeszcze raz rozpatrzmy cylindryczny kon-
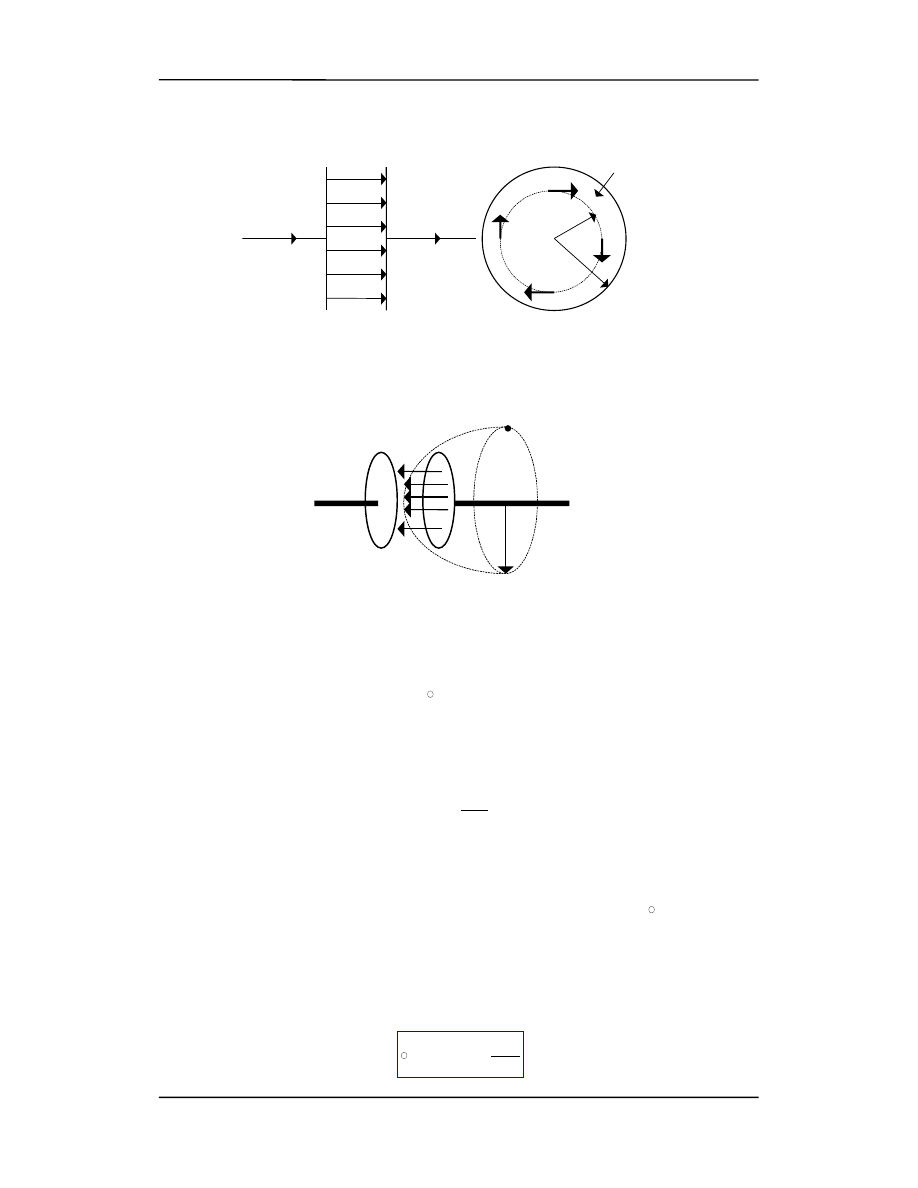
densator i obliczmy z prawa Ampera pole magnetyczne w punkcie P (rysunek poniżej).

Wybieramy kontur obejmujący płaską powierzchnię S, która zawiera prąd I oraz prze-

chodzi przez punkt P (w odległości r) (

∫

=

S

I

S

jd

). Z prawa Ampera otrzymujemy

∫

=

S

kontur

I

0

d

µ

l

B

Stąd

B2

πr=µ

0

I

czyli

r

I

B

π

µ
2

0

=

Prawo Ampera obowiązuje dla dowolnego konturu. Wybieramy więc kontur kołowy na
którym rozpięta jest zakrzywiona powierzchnia S

'

. Żaden prąd nie przechodzi przez tę

powierzchnię więc tym razem kontur nie obejmuje prądu i mamy

∫

=

0

dl

B

co jest

sprzeczne z poprzednim wynikiem. Wynika to z nieciągłości prądu, który nie płynie
pomiędzy okładkami kondensatora. Żeby usunąć tę niespójność Maxwell zaproponował
dodanie nowego członu do prawa Ampera.
Przez analogię do prawa indukcji Faradaya możemy napisać

∫

=

t

E

d

d

d

0

0

φ

ε

µ

l

B

(25.1)

S

S'

E

i

i

r

P

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

x

i

i

E

E

R

r

B

B

B

B

Z. Kąkol-Notatki do Wykładu z Fizyki

25-3

Tak więc prawo Ampera po modyfikacji ma postać

∫

+

=

I

t

E

0

0

0

d

d

d

µ

φ

ε

µ

l

B

(25.2)

Tak więc

pole magnetyczne jest wytwarzane przez przepływ prądu ale też przez

zmieniające się pole elektryczne.

Sprawdźmy czy stosując tę modyfikację uzyskamy teraz poprawny wynik na pole B w
punkcie P (przykład powyżej). W części powierzchni krzywoliniowej S' pomiędzy
okładkami kondensatora z prawa Gaussa wynika, że

φ

E

= ES

C

= q/

ε

0

gdzie S

C

jest powierzchnią okładek kondensatora. Różniczkując po dt mamy

0

0

d

d

1

d

d

ε

ε

φ

I

t

q

t

E

=

=

Przypomnijmy, że

∫

=

I

0

d

µ

l

B

Podstawiając za I otrzymujemy

∫

=

t

E

d

d

d

0

0

φ

ε

µ

l

B

czyli dodany wyraz do prawa Ampera.

25.3 Prąd przesunięcia

Z poprzedniego równania widać, że wyraz

ε

0

d

φ

E

/dt ma wymiar prądu. Mimo, że

nie mamy tu do czynienia z ruchem ładunków, to wyraz ten nazywamy

prądem przesu-

nięcia

. Mówimy, że pole B może być wytworzone przez prąd przewodzenia I lub przez

prąd przesunięcia I

P

.

∫

+

=

)

(

d

0

I

I

P

µ

l

B

(25.3)

Koncepcja prądu przesunięcia pozwala na zachowanie

ciągłości prądu

w przestrzeni

gdzie nie jest przenoszony ładunek (np. między okładkami kondensatora).

Przykład 1

Obliczyć indukowane pole magnetyczne w ładowanym kondensatorze cylindrycznym
w odległości r od osi (rysunek na stronie 2).
Z równania

∫

=

t

E

d

d

d

0

0

φ

ε

µ

l

B

otrzymujemy

Z. Kąkol-Notatki do Wykładu z Fizyki

25-4

t

E

r

t

r

E

r

B

d

d

d

)

(

d

2

2

0

0

2

0

0

π

ε

µ

π

ε

µ

π

=

=

Stąd

R

r

t

E

r

B

<

=

dla

,

d

d

2

1

0

0

ε

µ

dla r = R = 5cm oraz dE/dt = 10

12

V/ms otrzymujemy B = 0.0028 Gs czyli o dwa rzędy

mniej niż pole ziemskie.
Natomiast prąd przesunięcia

t

E

R

t

I

E

P

d

d

d

d

2

0

0

π

ε

φ

ε

=

=

ma całkiem sporą wartość I

P

= 70 mA. Powodem, że B jest tak małe jest to, że ten prąd

(umowny) jest rozłożony na bardzo dużej powierzchni okładki kondensatora podczas
gdy prąd przewodzenia jest "skupiony" w przewodniku.

25.4 Równania Maxwella

Prawo

Równanie

Czego dotyczy

Doświadczenie

1

Gaussa dla

elektryczności

∫

=

0

/

d

ε

q

S

E

ładunek i pole

elektryczne

Przyciąganie, odpychanie

ładunków (1/r

2

).

Ładunki gromadzą się na

powierzchni metalu

2

Gaussa dla

magnetyzmu

∫

=

0

dS

B

pole magnetyczne

nie stwierdzono istnienia mo-

nopola magnetycznego

3

indukcji Fara-

daya

∫

−

=

t

B

d

d

d

φ

l

E

efekt elektryczny

zmieniającego się

pola magnetycz-

nego

indukowanie SEM w obwo-

dzie przez przesuwany ma-

gnes

4

Ampera (roz-

szerzone przez

Maxwella)

∫

=

t

E

d

d

d

0

0

φ

ε

µ

l

B

I

0

µ

+

0

0

1

µ

ε

=

c

efekt magnetycz-

ny zmieniającego

się pola elek-

trycznego

prąd w przewodniku wytwa-

rza wokół pole magnetyczne

prędkość światła można wyli-

czyć z pomiarów EM