Algorytmy i struktury danych

Przykładowe zadania egzaminacyjne

1. Dla poniższych funkcji podaj asymptotyczne ograniczenia górne:

•

f

1



n=2log n4nn

2

,

•

f

2



n =nn

2



2

n

.

2. Niech G=V , E będzie grafem skierowanym, gdzie V ={x

1,

x

2,

x

3,

x

4,

x

5

} oraz

E={ x

1,

x

2



,  x

2,

x

3



, x

3,

x5 , x

5,

x

1



, x

3,

x

2



,  x

4,

x

1



, x

5,

x

1

} .

•

Podaj macierz sąsiedztwa dla grafu G.

•

Narysuj graf G.

•

Czy graf G jest grafem prostym?

•

Czy istnieje co najmniej jeden cykl w grafie G?

3. Narysuj dowolne drzewo z korzeniem zawierające siedem węzłów.

4. Zdefiniuj funkcje w języku C/C++ dla poniższych relacji rekurencyjnych:

a

n

=

{

1

if n=0

2a

n−1

if n0

}

b

n

=

{

1

if n=0

2

if n=1

2b

n−1

−

b

n−2

if n1

}

5. Przedstaw kolejne kroki działania zachłannego algorytmu wydawania reszty dla następujących danych:

○

reszta do wydania: 134,

○

dostępne nominały: 50, 20, 10, 5, 2, 1.

6. Przedstaw kolejne kroki działania algorytmu wyszukiwania liniowego dla następujących danych:

○

szukany element: 8,

○

przeszukiwana tablica: 23 12 3 5 8 -10 10.

7. Przedstaw kolejne kroki działania algorytmu wyszukiwania binarnego dla następujących danych:

○

szukany element: 8,

○

przeszukiwana tablica: 23 12 3 5 8 -10 10.

8. Przedstaw kolejne kroki działania algorytmu sortowania przez wstawianie dla następujące tablicy:

23 12 8 -10 10.

9. Przedstaw kolejne kroki działania algorytmu sortowania bąbelkowego dla następujące tablicy:

23 12 8 -10 10.

10. Przedstaw kolejne kroki działania algorytmu sortowania przez selekcję dla następujące tablicy:

23 12 8 -10 10.

11. Przedstaw kolejne kroki działania algorytmu prostego przeszukiwania tekstu dla następujących danych:

○

wyszukiwany wzorzec: AAB,

○

przeszukiwany tekst: ABAAAB.

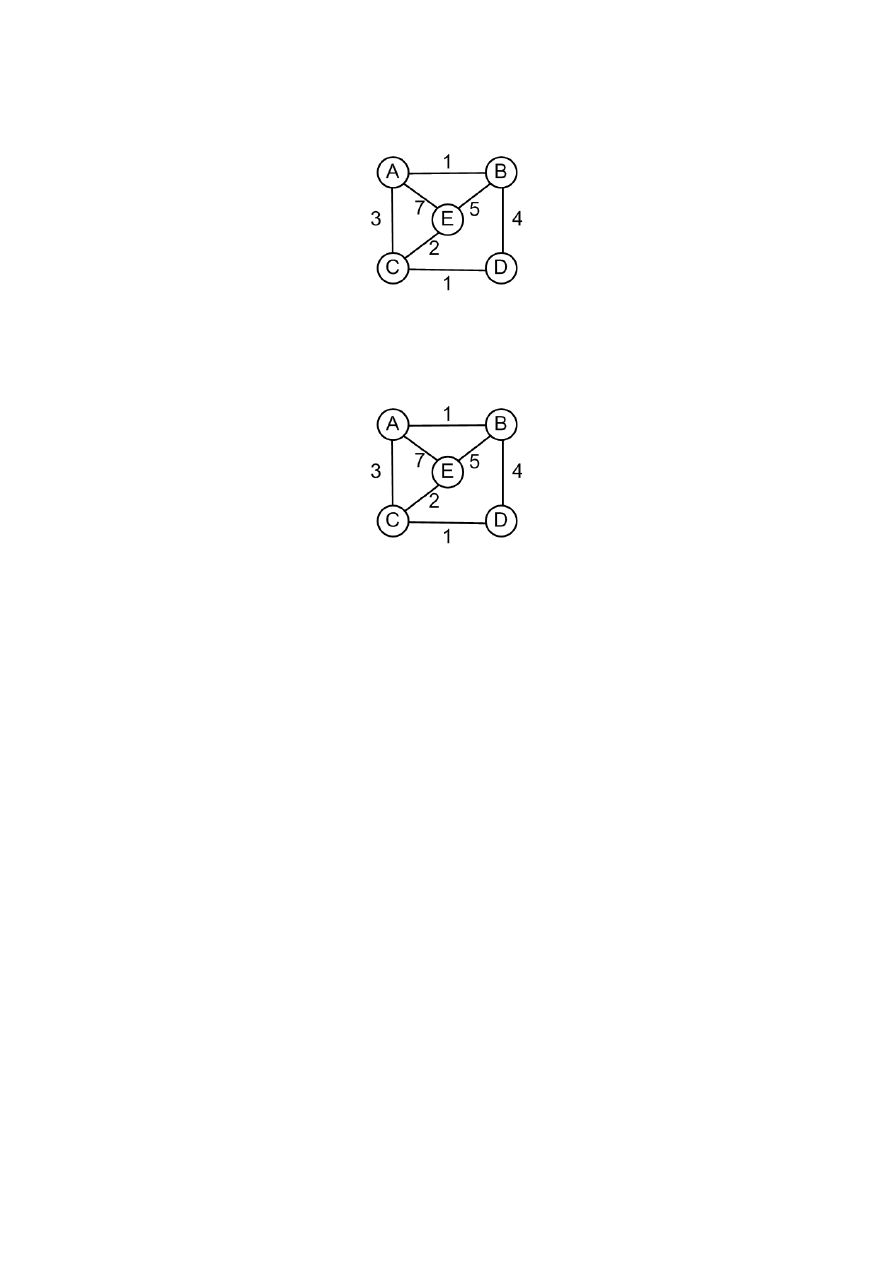
12. Przedstaw kolejne kroki działania algorytmu Prima znajdowania minimalnego drzewa rozpinającego dla

następującego grafu:

13. Przedstaw kolejne kroki działania algorytmu Kruskala znajdowania minimalnego drzewa rozpinającego

dla następującego grafu: