Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 01
Strona 1
f(x)
x
4
0,8
0,6
0
c/x
2
MITE Zadania domowe i testowe seria1
Zadanie 1 (Autor J. Oderfeld)
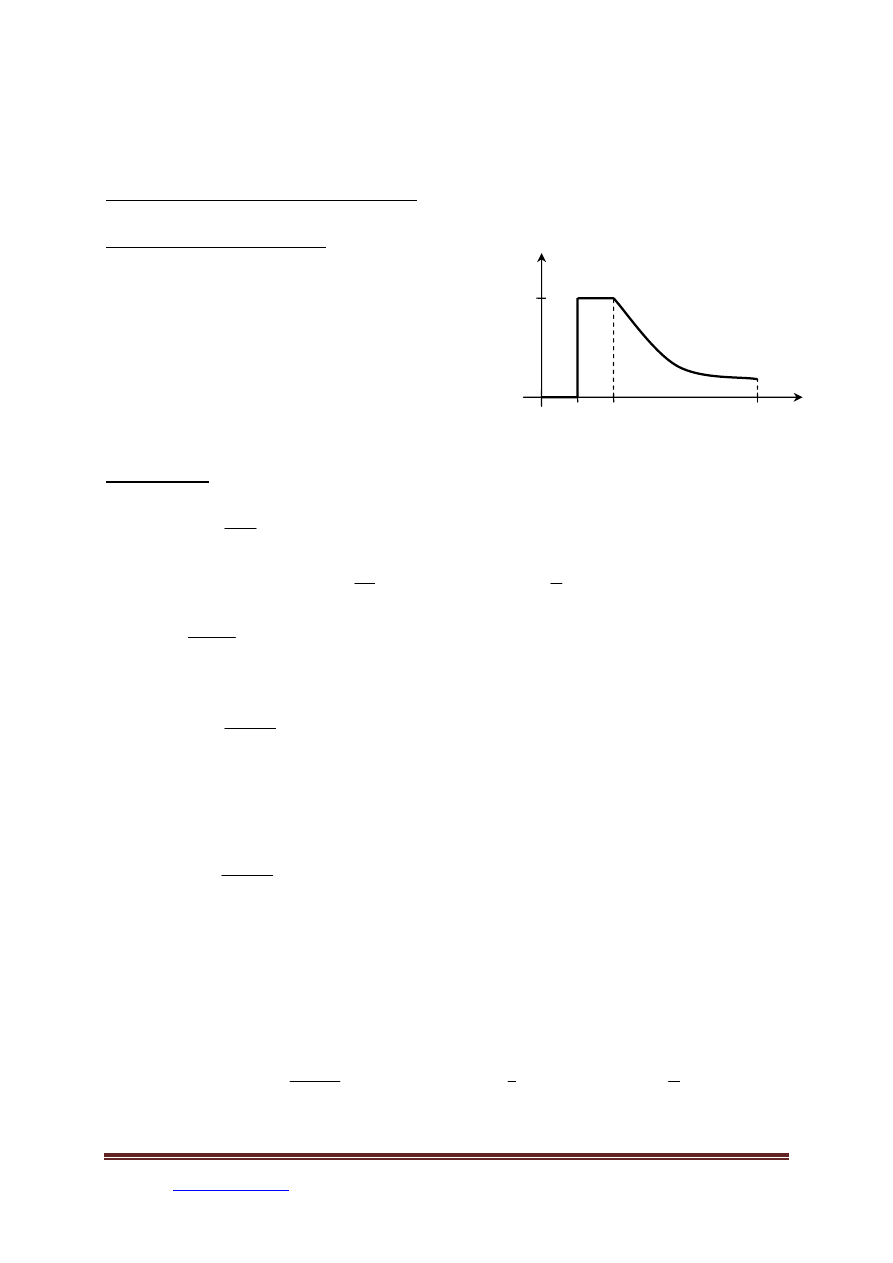
Na rysunku pokazano wykres funkcji gęstości
zmiennej losowej X typu ciągłego.
Należy:
1. Wyznaczyć stałą c,
2. Wyznaczyć funkcję gęstości,
3. Wyznaczyć dystrybuantę,
4. Obliczyć wartość oczekiwaną,
5. Znaleźć medianę x
1/2
.
Rozwiązanie:
Ad. 1
( )
c
c
f
⋅
=
=
5625
,
1
8
,
0
8
,
0
2
(
)
(
)
c
c
c
x
c
c
dx
x
c
c
3125
,
1
25
,
0
25
,
1
3125
,
0
1
2
,
0
5625
,
1
6
,
0
8
,
0
5625
,
1
1
4
8
,
0
4
8
,
0
2
=
−
+
=
⎥⎦
⎤
⎢⎣
⎡−
+
⋅
⋅
=
+
−
⋅
⋅
=
∫
7619
,
0
3125
,
1
1
=
=
c
Ad. 2
( )
1905
,
1
8
,
0
7619
,
0
8
,
0
2
=
=
f
Zapis funkcji gęstości:
( )
⎪
⎪
⎪
⎩
⎪⎪
⎪
⎨
⎧
<
≤
<
≤
<
=
tym
poza
x
dla
x
x
dla
x
dla
x
f
0
4
8
,
0
7619
,
0
8
,
0
6
,
0
1905
,
1
0
0
2
Ad. 3
Dla
8
,
0
6
,
0
<
≤ x
(
)
(
)
6
,
0
1905
,
1
8
,
0
6
,
0
−
=
<
<
x
x
F
;
2381
.
0
2
.
0
1905
.
1
)
8
.
0
(
=
⋅
=
F
Dla 4
8
,
0
<
≤ x
( )
x
t
dt
t
x
F
x
x
1
7619
,
0
1905
,
1
1
7619
,
0
2381
,
0
7619
,
0
2381
,
0
8
,
0
8
,
0
2
−
=
⎥⎦
⎤
⎢⎣
⎡−
+
=
+
=
∫

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 01
Strona 2
( )
(
)
⎪
⎪
⎪
⎩
⎪⎪
⎪
⎨
⎧
≥
<
≤
−
<
≤
−
<
=
4
1
4
8
,
0
1
7619
,
0
1905
,
1
8
,
0
6
,
0
6
,
0
1905
,
1
0
0
x
dla
x
dla
x
x
dla
x
x
dla
x
F
Możemy sprawdzić dla pewności, że
1
4
/
7619
.
0
1905
.
1
)
1
(
=
−
=
F
Ad. 4. Wartość oczekiwana:
( )
( )
(
)
[ ]
(
)
3929
.
1
2262
,
1
1667
.
0
2231
,
0
3863
,
1
7619
,
0
1667
,
0
ln
7619
,
0
6
,
0
8
,
0
5
,
0
1905
,
1
7619
,
0
1905
,
1
E
4
8
,
0
2
2
4
8
,
0
2
8
,
0
6
,
0
1
=
+
=
+
+
=
+
+
−
⋅
⋅
=
+
=
=
=
=
∫
∫
∫
x
dx
x
x
xdx
dx
x
xf
m
X
R
μ
Ad. 5
Ponieważ F(0,8)=0,2381 i F(4) = 1 zatem mediana wypada między x = 0,8 a x = 4.
5
,
0
1
7619
,
0
1905
,
1
2
1
=
−
x
więc
1034
,
1
2
1
=
x
Czyli
( )
X
x
E
79
,
0
2
1
≅
Zadanie 2
Wyznaczyć medianę, kwantyle i wartość oczekiwaną zmiennej losowej typu ciągłego, której
gęstość prawdopodobieństwa wyraża się wzorem:
( )
(
)
2
1
1
x
x
f
+
=
π
(jest to zmienna losowa o rozkładzie Cauchy'ego)
Rozwiązanie:
( )
( )
[
]
2
1
arctan
1
arctan
1
1
2
+
=
=
+
=
∞
−
∞
−
∫
x
x
t
dt
x
F
x
x
π
π
π
(
)
⎟
⎠
⎞
⎜
⎝
⎛
−
=
⇒
=
+
1
2
2
tan
arctan
1
2
1
p
x
p
x
p
p
π
π
Rozkład Cauchy'ego nie ma wartości oczekiwanej bo:
(
)
[
]
)]
1
ln(
)
1
[ln(
2
1
)
1
ln(
2
1
1
2
2
2
2
a
b
x
x
xdx
b
a
b
a
+
−
+
=
+
=
+
∫
π
π
π
( )
(
)
∫
∞
∞
−
+
=
2
1
E
x
xdx
X
π
Wartość oczekiwana nie istnieje bo nie istnieje żadna z powyższych granic.

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 01
Strona 3
Zadanie 3
(Autor J.Oderfeld)
Wśród 10 świec samochodowych 4 są złe, reszta dobre. Należy wybrać z nich jedną dobrą.
„Na oko” nie można poznać, które świece są dobre, próbuje się więc kolejno, aż trafi się po
raz pierwszy na świecę dobrą. Niech X oznacza liczbę prób potrzebnych do tego celu. Jest to
zmienna losowa. Należy:
1. Podać zbiór wartości, które przyjmuje X,
2. Znaleźć rozkład X i sprawdzić, czy prawdopodobieństwa sumują się do jedności,
3. Znaleźć wartość oczekiwaną.
Założenia:
W każdej ustalonej próbie każda konkretna świeca, wszystko jedno czy dobra, czy zła ma
jednakową szanse, że będzie wybrana do próby. Wybory w kolejnych próbach są zdarzeniami
niezależnymi.
Wskazówki:
Aby na przykład X=4 potrzeba i wystarcza, żeby wynik prób był:
zła, zła, zła, dobra
Ze wzrostem liczby kolejnych prób prawdopodobieństwo trafienia na złą świecę maleje,
a trafienia na dobrą rośne.
Rozwiązanie:
1. Oznaczamy wskaźnikiem i kolejny numer próby. Z tematu wynika, że i = 1,2,3,4,5 bo
jeśli cztery kolejne wyniki prób były zła, zła, zła, zła to pozostały same dobre świece.
Zatem w piątej próbie na pewno trafi się po raz pierwszy na dobrą świecę.
2. Dla i=1 zachodzi równość:
(
)
6
,
0
10
6
1
=
=
=
X
P
Dla i>1 układamy tabelkę:
1. 2.
3.
4.
i
Prawdopodobieństwo
zdarzenia, że do próby i-1
włącznie znajdowano
tylko złe świece
Prawdopodobieństwo
zdarzenia, że w próbie i
znaleziono dobrą świece
P(X=i)= 2. *3.
2
10
4
9
6
26667
,
0
5040
1344 =
3
9
3
10
4 ⋅
8
6
1
,
0
5040
504 =
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 01
Strona 4
y
x
2
1
1
D
4
8
2
9
3
10
4
⋅
⋅
7
6
02857
,
0
5040
144 =
5
7
1
8
2
9
3
10
4
⋅
⋅
⋅
1
6
6 =
00476
,
0
5040
24 =
(
)
∑
=
=
+
=
+
+
+
+
=
=
5
1
1
4
,
0
6
,
0
00476
,
0
02857
,
0
1
,
0
26667
,
0
6
,
0
P
i
i
X
3.
( )
57
,
1
5040
5
24
4
144
3
504
2
1344
1
6
,
0
E
=
⋅
+
⋅
+
⋅
+
⋅
+
⋅
=
X
Zadanie 4
Dana jest funkcja:
( )
( )
⎩
⎨
⎧
∈
=
poza
D
y
x
dla
cy
y
x
f
0
,
,
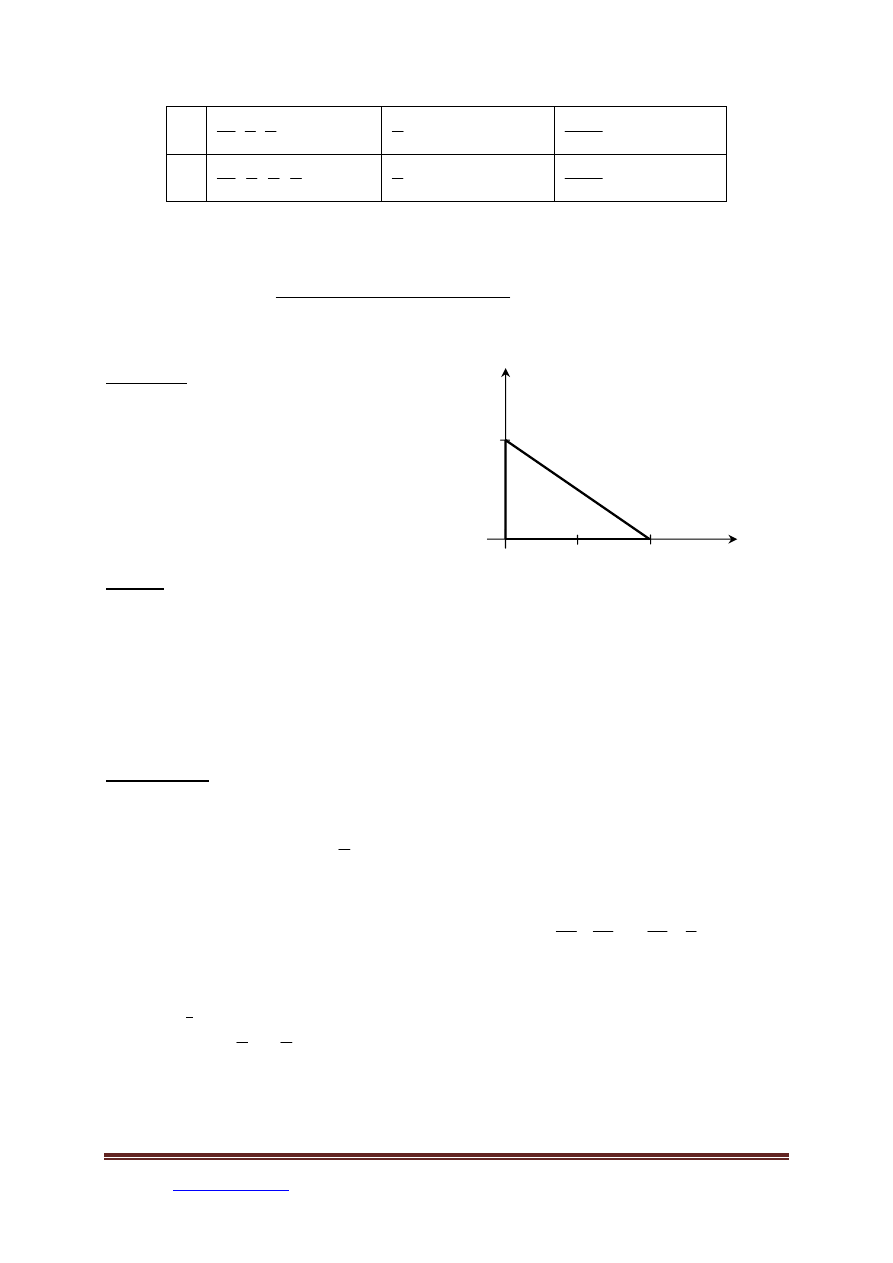
Gdzie obszar D pokazano na rysunku.
Należy:
1. Dobrać stałą c tak, by funkcja f była gęstością pewnego wektora losowego (X, Y)
2. Obliczyć gęstość rozkładów brzegowych
3. Narysować wykresy gęstości brzegowych
4. Obliczyć wartości oczekiwane E(X) i E(Y)
5. Obliczyć kowariancję zmiennych losowych
6. Obliczyć odchylenie standardowe zmiennych o rozkładach brzegowych
7. Obliczyć współczynnik korelacji ρ
X,Y
. Czy istnieje zależność liniowa pomiędzy X a Y ?
Rozwiązanie:
Ad. 1
( )
⎭
⎬
⎫
⎩
⎨
⎧
−
≤
≤
≤
≤
2
1
0
2
0
:
,
:
x
y
i
x
y
x
D
( )
(
)
{
}
y
x
i
y
y
x
D
−
≤
≤
≤
≤
1
2
0
1
0
:
,
:
(
)
(
)
(
)
3
1
3
6
2
3
2
2
2
1
2
1
0
1
2
0
1
0
1
0
1
0
3
2
2
=
⇒
=
=
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
−
=
−
=
=
∫∫
∫ ∫
∫
∫
−
c
c
c
y
y
c
dy
y
y
c
dy
y
y
c
dxdy
y
c
cydv
D
y
Ad. 2
( )
2
2
1
0
2
1
2
3
3
⎟
⎠
⎞
⎜
⎝
⎛ −
=
=
∫
−
x
ydy
x
f
x
X
( )
( )
(
)
(
)
y
y
y
y
ydx
y
f
x
Y
−
=
−
=
=
∫
−
1
6
6
3
2
1
2
0
Ad. 3

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 01
Strona 5
Ad. 4
( )
( )
2
1
1
3
8
2
2
3
16
3
2
2
3
4
2
3
4
1
2
3
2
1
2
3
2
0
4
3
2
2
0
3
2
2
0
2
2
0
2
2
0
10
=
⎥⎦
⎤
⎢⎣
⎡
+
−
=
⎥
⎦
⎤
⎢
⎣
⎡
+
−
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
=
⎟
⎠
⎞
⎜
⎝
⎛ −
=
=
=
∫
∫
∫
∫
x
x
x
dx
x
x
x
dx
x
x
x
dx
x
x
dx
x
xf
m
X
E
X
( )
( )
(
)
2
1
12
1
6
4
3
6
1
6
1
0
4
3
1
0
2
1
0
01
=
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
−
=
=
=
∫
∫
y
y
dy
y
y
dy
y
yf
m
Y
E
Y
Ad. 5
( )
(
)
(
)
(
)
(
)
5
1
5
6
3
2
5
1
2
1
3
1
6
5
4
2
3
6
2
1
6
2
1
4
3
2
3
3
1
0
5
4
3
1
0
2
2
1
0
2
2
1
0
1
2
0
1
0
1
2
0
2
2
2
11
=
+
−
=
⎥⎦
⎤
⎢⎣
⎡
+
−
=
⎥
⎦
⎤
⎢
⎣
⎡
+
−
=
+
−
=
=
−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
=
=
∫
∫
∫∫
∫ ∫
∫
−
−
y
y
y
dy
y
y
y
dy
y
y
dy
y
x
dxdy
xy
xycydv
XY
E
m
D
y
y
(
)
20
1
2
1
2
1
5
1
,
01
10
11
−
=
⋅
−
=
⋅
−
=
m
m
m
Y
X
COV
Ad. 6
( )
( )
5
2
60
96
240
160
2
3
20
32
4
3
8
2
3
20
4
3
2
3
4
2
3
4
1
2
3
2
1
2
3
2
0
5
4
3
2
0
4
3
2
2
0
2
2
2
0
2
2
2
0
2
20
2
=
+
−
⋅
=
⎥⎦
⎤
⎢⎣
⎡
+
−
=
⎥
⎦
⎤
⎢
⎣
⎡
+
−
=
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
=
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
+
−
=
⎟
⎠
⎞
⎜
⎝
⎛ −
=
=
=
∫
∫
∫
∫
x
x
x
dx
x
x
x
dx
x
x
x
dx
x
x
dx
x
f
x
m
X
E
X
( )
( )
(
)
10
3
20
6
5
4
6
1
6
1
0
5
4
1
0
3
1
0
2
02
2
=
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
−
=
=
=
∫
∫
y
y
dy
y
y
dy
y
f
y
m
Y
E
Y
20
3
4
1
5
2
2
10
20
2
=
−
=
−
=
m
m
X
σ
20
1
4
1
10
3
2
01
02
2
=
−
=
−
=
m
m
Y
σ
Ad. 7
(
)
577
,
0
3
1
3
400
20
1
400
3
20
1
20
1
20
3
20
1
,
2
2
−
≅
−
=
⋅
−
=
−
=
⋅
−
=
⋅
=
Y
X
XY
Y
X
COV
σ
σ
ρ
x
2
y
1
f
Y
(y)
f
X
(x)
1,5
1,5
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 01
Strona 6
y
x
1
1
D
Nie istnieje zależność liniowa z prawdopodobieństwem równym 1.
Zadanie 5
Dana jest funkcja:
( )
( )
⎩
⎨
⎧
∈
=
poza
D
y
x
dla
cxy
y
x
f
0
,
,
2
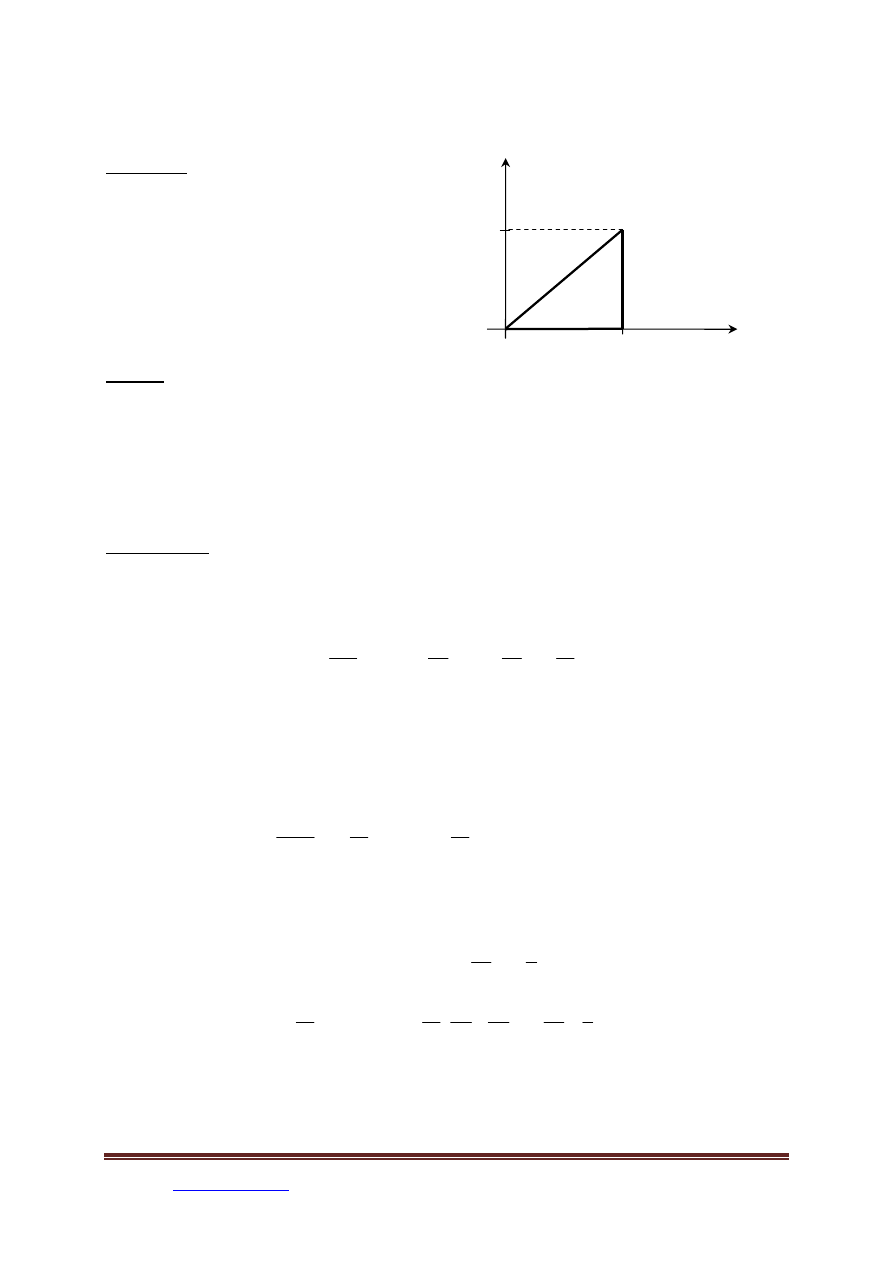
Gdzie obszar D pokazano na rysunku.
Należy:
6. Dobrać stałą c tak, by funkcja f była gęstością pewnego wektora losowego (X, Y)
7. Obliczyć gęstość rozkładów brzegowych
8. Obliczyć wartości oczekiwane E(X) i E(Y)
9. Obliczyć kowariancję zmiennych losowych
10. Obliczyć odchylenie standardowe zmiennych o rozkładach brzegowych
11. Obliczyć współczynnik korelacji ρ
X,Y
. Czy są zależne liniowo, czy nie ?
Rozwiązanie:
Ad. 1
( )
{
}
x
y
i
x
y
x
D
≤
≤
≤
≤
0
1
0
:
,
:
( )
{
}
1
1
0
:
,
:
≤
≤
≤
≤
x
y
i
y
y
x
D
15
1
15
15
3
3
1
0 0
1
0
1
0
1
0
5
4
0
3
2
2
=
⇒
=
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
∫∫
∫∫
∫
∫
c
c
x
c
dx
x
c
dx
xy
c
dydx
xy
c
dv
cxy
D
x
x
Ad. 2
( )
4
1
0
2
5
15
x
dy
xy
x
f
X
=
=
∫
( )
(
)
(
)
2
2
4
2
1
2
2
1
2
1
2
15
2
15
2
15
15
y
y
y
y
y
x
dx
xy
y
f
y
y
Y
−
=
−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
∫
Ad. 3
( )
( )
6
5
6
5
5
5
1
0
6
1
0
5
1
0
4
1
0
10
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
⋅
=
=
=
∫
∫
∫
x
dx
x
dx
x
x
dx
x
xf
m
X
E
X
( )
( )
(
)
8
5
24
15
6
4
2
15
2
15
1
0
6
4
1
0
5
3
1
0
01
=
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
−
=
=
=
∫
∫
y
y
dy
y
y
dy
y
yf
m
Y
E
Y
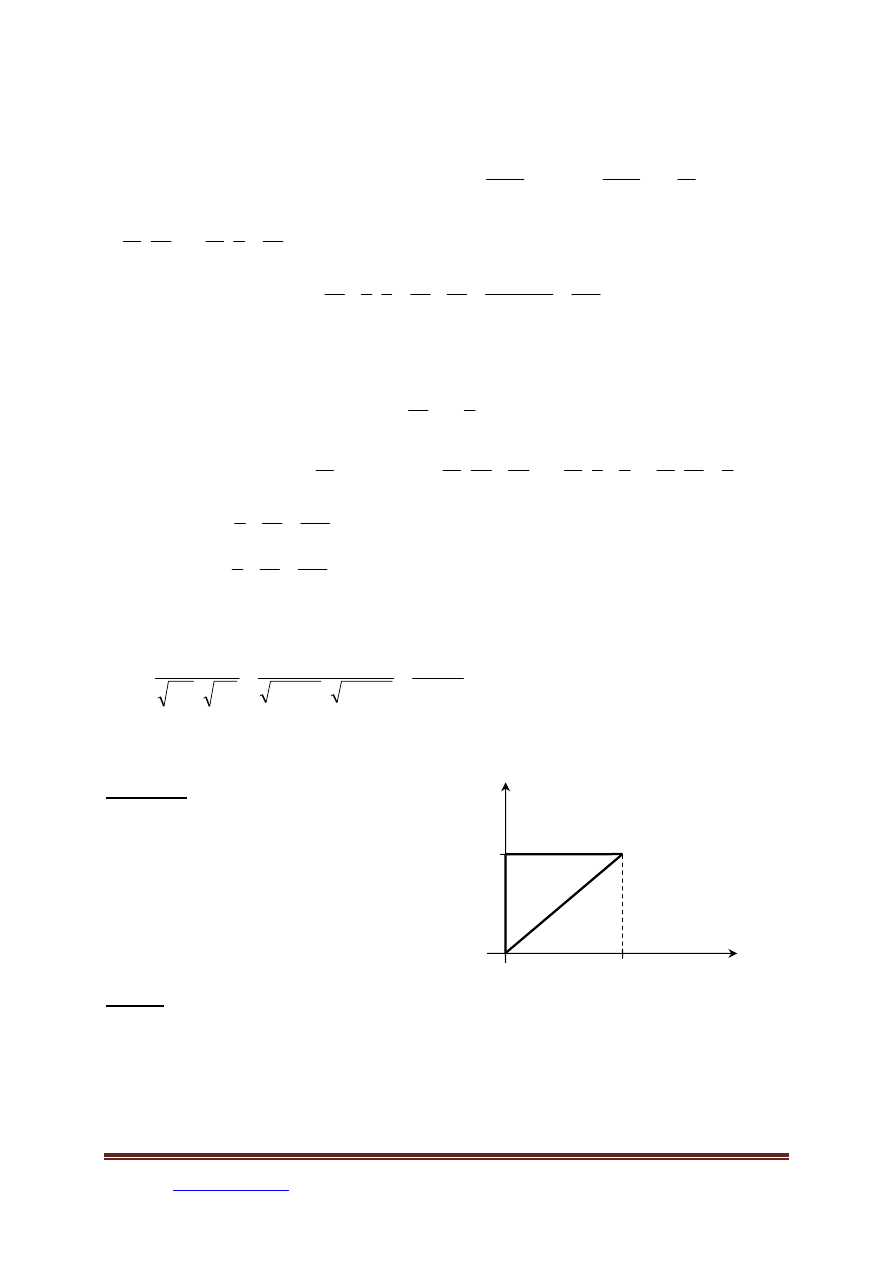
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 01
Strona 7
y
x
1
1
D
Ad. 4
( )
28
15
7
1
4
15
7
4
15
4
15
4
15
4
15
15
15
1
0
7
1
0
6
1
0
4
2
1
0
0
4
2
1
0 0
3
2
2
11
=
⋅
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
=
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
=
=
∫
∫
∫
∫∫
∫∫
x
dx
x
dx
x
x
dx
y
x
dydx
y
x
dv
xyxy
XY
E
m
x
D
x
(
)
0149
,
0
336
5
336
175
180
48
25
28
15
8
5
6
5
28
15
,
01
10
11
≅
=
−
=
−
=
⋅
−
=
⋅
−
=
m
m
m
Y
X
COV
Ad. 5
( )
( )
7
5
7
5
5
1
0
7
1
0
6
1
0
2
20
2
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
=
=
∫
∫
x
dx
x
dx
x
f
x
m
X
E
X
( )
( )
(
)
7
3
35
2
2
15
7
1
5
1
2
15
7
5
2
15
2
15
1
0
7
5
1
0
6
4
1
0
2
02
2
=
⋅
=
⎥⎦
⎤
⎢⎣
⎡ −
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
−
=
=
=
∫
∫
y
y
dy
y
y
dy
y
f
y
m
Y
E
Y
0198
,
0
252
5
36
25
7
5
2
10
20
2
≅
=
−
=
−
=
m
m
X
σ
0379
,
0
448
17
64
25
7
3
2
01
02
2
≅
=
−
=
−
=
m
m
Y
σ
Ad. 6
(
)
544
,
0
0273
,
0
0149
,
0
0379
,
0
0198
,
0
0149
,
0
,
2
2
=
=
⋅
≅
⋅
=
Y
X
XY
Y
X
COV
σ
σ
ρ
Zmienne X i Y nie są zależne.
Zadanie 6
Dana jest funkcja:
( )
( )
⎩
⎨
⎧
∈
=
poza
D
y
x
dla
cxy
y
x
f
0
,
,
3
Gdzie obszar D pokazano na rysunku.
Należy:
1. Zapisać analitycznie obszar D
2. Dobrać stałą c tak, by funkcja f była gęstością pewnego wektora losowego (X, Y)
3. Obliczyć gęstość rozkładów brzegowych
4. Obliczyć momenty zwykłe rzędu (0,1) i (1,0)
5. Obliczyć kowariancję zmiennych losowych
6. Obliczyć odchylenie standardowe zmiennych o rozkładach brzegowych
7. Obliczyć współczynnik korelacji ρ
X,Y
. Czy zmienne losowe X i Y są niezależne?
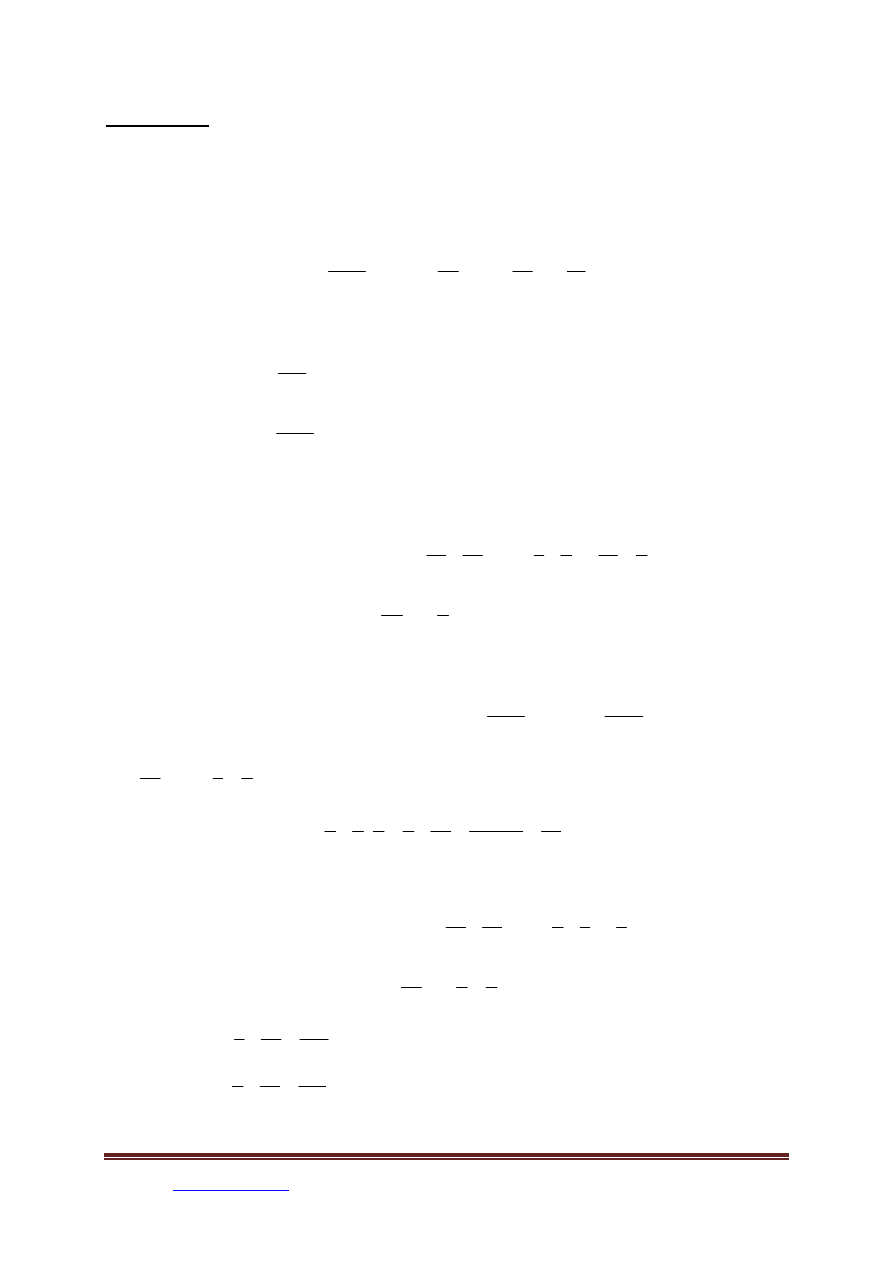
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 01
Strona 8
Rozwiązanie:
Ad. 1
( )
{
}
1
1
0
:
,
:
≤
≤
≤
≤
y
x
i
x
y
x
D
( )
{
}
y
x
i
y
y
x
D
≤
≤
≤
≤
0
1
0
:
,
:
Ad. 2
12
1
12
12
2
2
1
0 0
1
0
1
0
1
0
6
5
0
3
2
3
3
=
⇒
=
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
∫∫
∫∫
∫
∫
c
c
x
c
dy
y
c
dy
y
x
c
dxdy
xy
c
dv
cxy
D
y
y
Ad. 3
( )
(
)
5
1
4
1
3
3
4
12
12
x
x
xy
dy
xy
x
f
x
x
X
−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
∫
( )
5
0
3
2
0
3
6
2
12
12
y
y
x
dx
xy
y
f
y
y
Y
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
∫
Ad. 4
( )
( )
(
)
7
4
21
12
7
1
3
1
3
7
3
3
3
1
0
7
3
1
0
6
2
1
0
10
=
=
⎟
⎠
⎞
⎜
⎝
⎛ −
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
−
=
=
=
∫
∫
x
x
dx
x
x
dx
x
xf
m
X
E
X
( )
( )
7
6
7
6
6
1
0
7
1
0
6
1
0
01
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
=
=
∫
∫
y
dy
y
dy
y
yf
m
Y
E
Y
Ad. 5
( )
2
1
8
1
4
8
4
4
3
12
3
12
12
12
1
0
8
1
0
7
1
0
4
3
1
0
0
4
3
1
0 0
4
2
3
11
=
⋅
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
=
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
=
=
∫
∫
∫
∫∫
∫∫
y
dy
y
dy
y
y
dy
y
x
dxdy
y
x
dv
xyxy
XY
E
m
y
D
y
(
)
0102
,
0
98
1
98
48
49
49
24
2
1
7
6
7
4
2
1
,
01
10
11
≅
=
−
=
−
=
⋅
−
=
⋅
−
=
m
m
m
Y
X
COV
Ad. 6
( )
( )
(
)
8
3
8
1
4
1
3
8
4
3
3
1
0
8
4
1
0
7
3
1
0
2
20
2
=
⎥⎦
⎤
⎢⎣
⎡ −
=
⎥
⎦
⎤
⎢
⎣
⎡
−
=
−
=
=
=
∫
∫
x
x
dx
x
x
dx
x
f
x
m
X
E
X
( )
( )
4
3
8
6
8
6
6
1
0
8
1
0
7
1
0
2
02
2
=
=
⎥
⎦
⎤
⎢
⎣
⎡
=
=
=
=
∫
∫
y
dy
y
dy
y
f
y
m
Y
E
Y
0485
,
0
392
19
49
16
8
3
2
10
20
2
≅
=
−
=
−
=
m
m
X
σ
0153
,
0
196
3
49
36
4
3
2
01
02
2
≅
=
−
=
−
=
m
m
Y
σ
Ad. 7
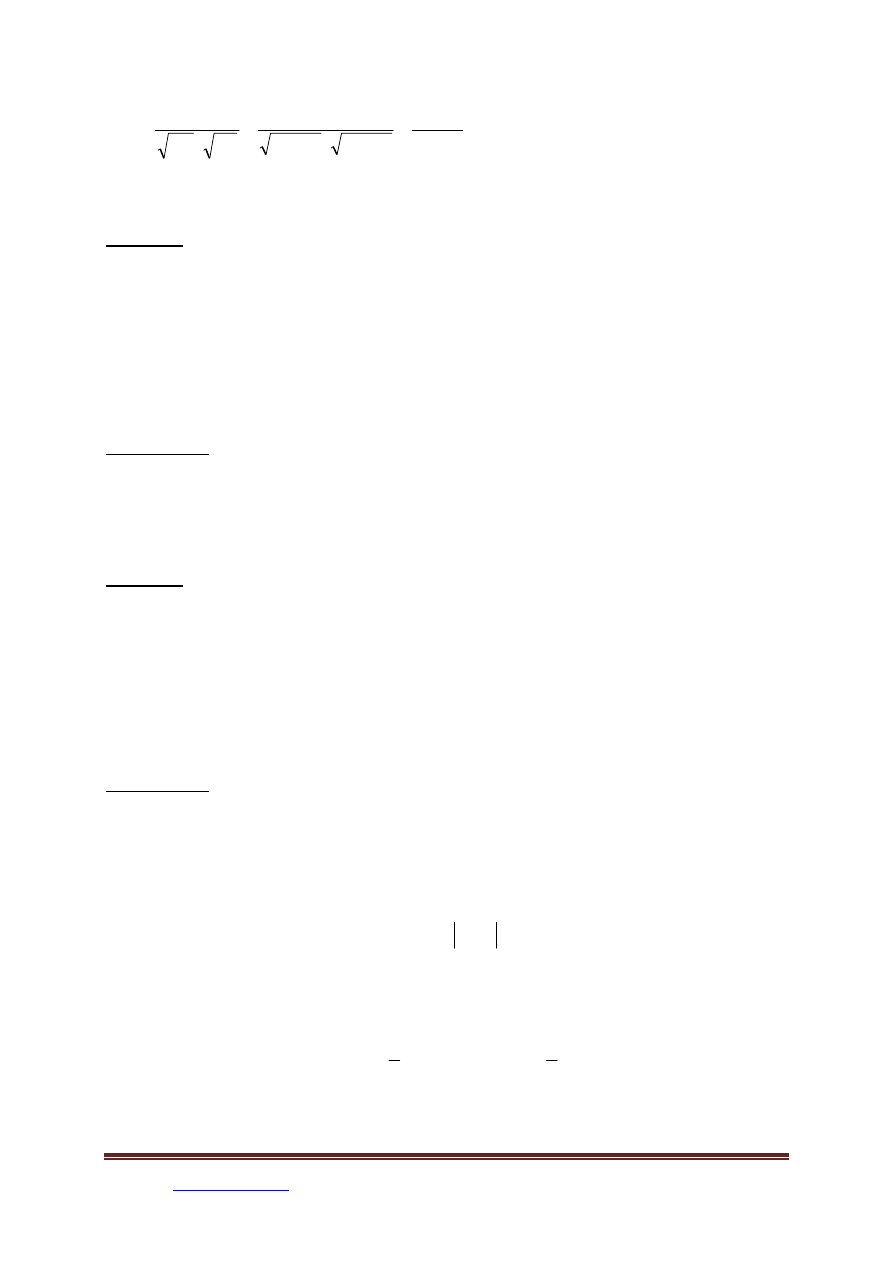
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 01
Strona 9
(
)
37
,
0
0272
,
0
0102
,
0
0153
,
0
0485
,
0
0102
,
0
,
2
2
=
=
⋅
≅
⋅
=
Y
X
XY
Y
X
COV
σ
σ
ρ
Zmienne X i Y nie są zależne.
Zadanie 7
Podano twierdzenie:
COV(X,Y)=0
⇔ zmienne losowe X i Y są niezależne.
Czy twierdzenie jest prawdziwe ?
Odpowiedź uzasadnij.
Rozwiązanie:
Twierdzenie w jedną stronę
⇐ jest prawdziwe (uzasadniono na wykładzie). Natomiast
w drugą stronę
⇒ nie jest prawdziwe. Podano kontrprzykład na wykładzie.
Zadanie 8
Zmienna losowa ma rozkład wykładniczy:
( )
⎩
⎨
⎧
0
>
<
≥
−
=
λ
λ
λ
,
0
0
0
)
exp(
x
dla
x
dla
x
x
f
Oblicz medianę oraz kwantyl rzędu ¼
4
/
1
x .
Rozwiązanie:
Zmienna jest typu ciągłego więc kwantyle i medianę wyznaczymy z równania (podanego na
wykładzie):
p
x
F
p
=
)
(
Wyznaczymy dystrybuantę:
x
x
x
t
t
e
e
dt
e
x
F
λ
λ
λ
λ
−
−
−
−
=
−
=
=
∫
1
)
(
0
0
Wobec tego:
p
e
x
F
p
x
p
=
−
=
−
λ
1
)
(
Np. dla mediany:
2
1
1
2
/
1
=
−
− x
e
λ
czyli
λ
/
)
2
1
ln(
2
/
1
−
=
x
Wyszukiwarka
Podobne podstrony:
MiTE Zadania seria 2 wersja 04 Nieznany
MiTE Zadania seria 2 wersja 04 Nieznany
MiTE Zadania seria 1 wersja 01
MiTE Zadania seria 2 wersja 03
MiTE Zadania seria 2 wersja 06
MiTE Zadania seria 2 wersja 03
MiTE Zadania seria 2 wersja 06
MiTE Zadania seria 2 wersja 04
MiTE Zadania seria 2 wersja 03
MiTE Zadania seria 2 wersja 06
MiTE wykL,ad 7 8 wersja 01 id 3 Nieznany
MiTE wykL,ad 7 8 wersja 01 id 3 Nieznany
MiTE Zadania domowe seria 1 Nieznany
MITE Zadania domowe seria 3 id Nieznany
MITE Zadania domowe seria 2
MITE Zadania domowe seria 2
więcej podobnych podstron