
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 02. Modyfikowana ostatni raz 7.06.09
Strona 1
MITE Zadania domowe i testowe seria 2
Zadanie 1
Czy twierdzenie Moivre’a - Laplace’a jest szczególnym przypadkiem twierdzenia
Lindeberga-Fellera ?. Uzasadnij szczegółowo.
Rozwiązanie:
Omawiano na wykładzie. Zobacz tekst wykładu.
Zadanie 2
Ogniwa krótkie pewnego łańcucha rolkowego mają wymiar
05
.
0
04
.
0
05
.
20
+
−
=
k
, ogniwa o średniej
długości mają wymiar
03
.
0
03
.
0
05
.
25
+
−
=
s
a ogniwa długie wymiar
03
.
0
03
.
0
05
.
27
+
−
=
d
. Montujemy łańcuch z
20 ogniw krótkich, 25 ogniw średnich i 25 długich.
Obliczyć prawdopodobieństwo, że otrzymamy długość całego łańcucha
1
.
0
1
.
0
1703.6
+
−
=
L
mm
(przewidzianą normą).
Wskazówka: Oszacować nieznane parametry rozkładów wymiarów poszczególnych ogniw na
podstawie znajomości pola tolerancji korzystając z prawa
σ
3
a następnie wykorzystać CTG
LF (centralne twierdzenie graniczne Lindeberga-Fellera).
Rozwiązanie:
Wartości średnie i odchylenia standardowe (w mm):
055
.
20
2
04
.
0
05
.
20
05
.
0
05
.
20
1
=
−
+
+
=
μ
,
015
.
0
6
04
.
0
05
.
0
1
=
+
=
σ
05
.
25
2
03
.
0
05
.
25
03
.
0
05
.
25
2
=
−
+
+
=
μ
,
01
.
0
6
03
.
0
03
.
0
2
=
+
=
σ
05
.
27
2
03
.
0
05
.
27
03
.
0
05
.
27
3
=
−
+
+
=
μ
,
01
.
0
6
03
.
0
03
.
0
3
=
+
=
σ
Wartości do standaryzacji zmiennej:
6
.
1703
05
.
27
25
05
.
25
25
055
.
20
20
=
⋅
+
⋅
+
⋅
=
μ
,
0975
.
0
01
.
0
25
01
.
0
25
015
.
0
20
2
2
2
=
⋅
+
⋅
+
⋅
=
σ
oraz
=
−
<
<
−
=
<
<
∑
∑
)
0975
.
0
6
.
1703
7
.
1703
0975
.
0
6
.
1703
5
.
1703
(
)
7
.
1703
5
.
1703
(
i
i
X
P
X
P
70
.
0
1
848
.
0
2
1
)
03
.
1
(
2
)
03
.
1
03
.
1
(
=
−
⋅
=
−
Φ
⋅
=
<
<
−
=
Y
P
Dokonano odczytu z tablic rozkładu normalnego.
Uwaga: Sprawdzić powyższe obliczenia !.
Zadanie 3 (podobne do tego wykładu)
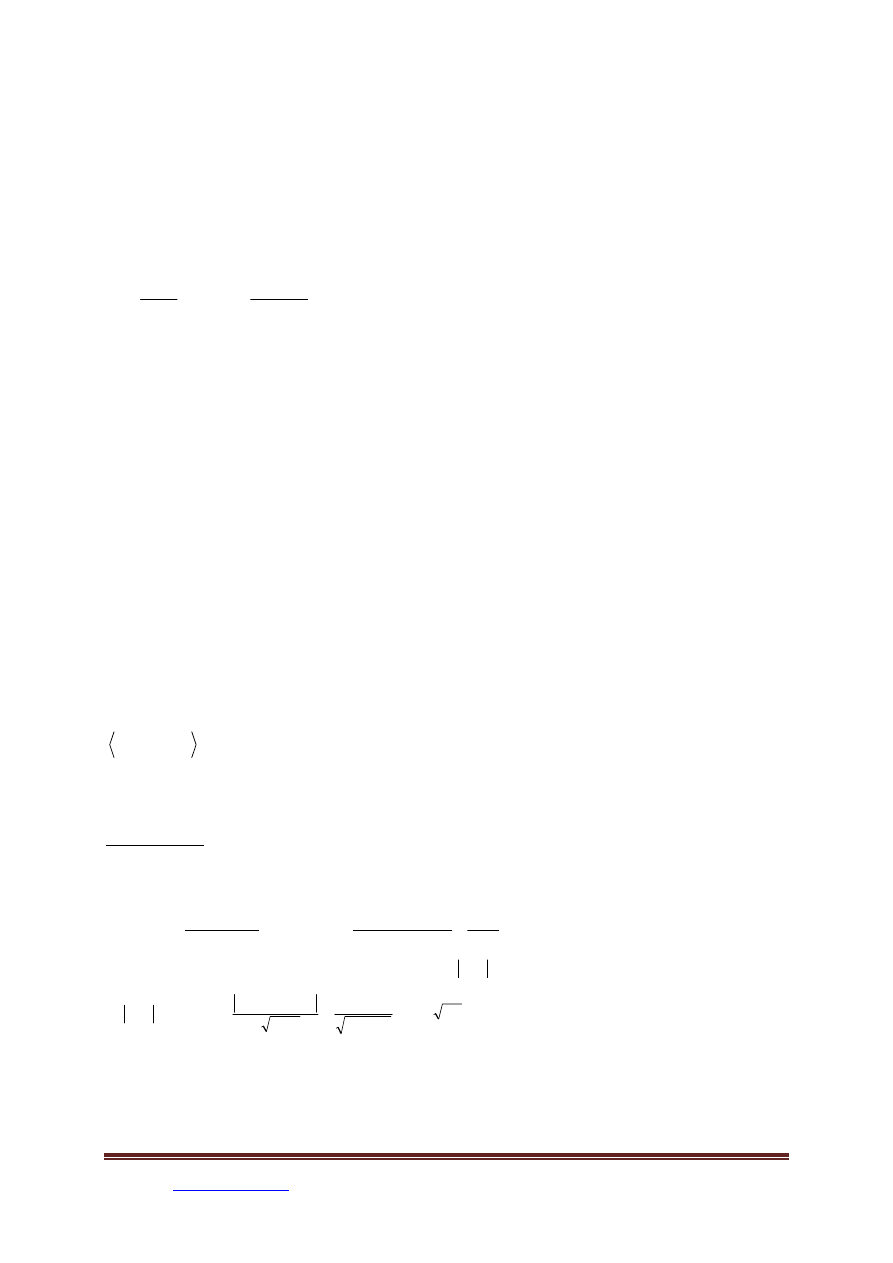
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 02. Modyfikowana ostatni raz 7.06.09
Strona 2
Lina spleciona jest z 20 drutów grubych i 70 cienkich. Wytrzymałość drutu grubego ma
rozkład równomierny w przedziale <3.2,4.8> kN. Wytrzymałość drutu cienkiego ma rozkład
równomierny w przedziale <0.8,1.2>. Przyjmując, że wszystkie te zmienne losowe są
niezależne, i że wytrzymałość liny jest sumą wytrzymałości wszystkich drutów, znaleźć
prawdopodobieństwo, że wytrzymałość liny Q jest większa od 145 kN i mniejsza niż 153 kN.
Uwaga: Wartość średnią oraz wariancję dla rozkładu równomiernego na przedziale <a,b>
oblicza się odpowiednio ze wzorów:
2
b
a
+
=
μ
,
12
)
(
2
2
a
b
−
=
σ
Zadanie 4
Przestudiuj zadanie numer 2.19, str. 58 ze skryptu Jana Oderfelda (zobacz piśmiennictwo w
wykładzie 1)
Zadanie 5
Odczytać wartość kwantyla rzędu 0.90 z tablic rozkładu Studenta dla liczby stopni swobody
r=100 i wartość tego kwantyla z tablic rozkładu N(0.1). Obliczyć względną różnicę
procentową.
Wskazówka: Z tablic rozkładu Studenta odczytuje się wartości krytyczne. Jakiego rzędu
kwantylem jest wartość krytyczna ?
Zadanie 6
Błąd zaokrąglenia przy dodawaniu na kalkulatorze ma rozkład jednostajny w przedziale
8
8
10
,
10
−
−
. Oszacować prawdopodobieństwo, że przy dodawaniu 1001 liczb błąd
bezwzględny nie przekroczy
7
10
−
.
Wskazówka: Wykorzystać CTG LL
Rozwiązanie:
Dodając 1001 liczb wykonamy 1000 działań dodawania. Niech
i
X
oznacza błąd (zmienna losowa) przy
wykonywaniu i-tego dodawania. Zmienna ta rozkład jednostajny więc:
0
2
10
10
)
(
E
8
8
=
+
−
=
=
−
i
X
μ
,
0
3
10
2
))
10
(
10
(
)
(
D
2
16
2
8
8
2
>
=
=
−
−
=
−
−
σ
i
X
Błąd całościowy to
∑
=
=
1000
1
1000
i
i
X
S
. Chcemy oszacować
)
10
(
7
1000
−
≤
S
P
. Z CTG LL otrzymujemy przybliżenie:
418
.
0
1
7088
.
0
2
1
)
55
.
0
(
2
1
)
3
.
0
(
2
3
/
10
0
10
1000
1000
(
)
10
(
13
7
1000
7
1000
=
−
⋅
=
−
Φ
≈
−
Φ
≈
−
≤
−
=
≤
−
−
−
σ
μ
S
P
S
P
Wykorzystaliśmy tablice rozkładu normalnego.

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 02. Modyfikowana ostatni raz 7.06.09
Strona 3
Zadanie 7
Należy oszacować czas bezawaryjnej pracy wyprodukowanej partii dysków twardych.
Wiadomo, że czas pracy ma rozkład normalny z odchyleniem standardowym
σ, które nie jest
znane
. Wylosowana niezależnie z tej partii próba n = 11 dysków dała wyniki pomiarów czasu
ich bezawaryjnej pracy (w tys. godzin): 2630, 2820, 2900, 2810, 2770, 2840, 2700, 2950,
2690, 2720, 2800. Przyjmując poziom ufności 1-
α = 0.98 oszacować metodą przedziałową
średni czas bezawaryjnej pracy tej partii oraz szerokość przedziału ufności.
Uwaga: Proszę przed obliczeniami koniecznie napisać wzór ogólny.
Rozwiązanie:
Średnia z 11 realizacji (jednostki pomijam):
55
.
2784
11
11
1
=
=
∑
=
i
i
x
x
,
Estymator
59
.
90
)
(
11
1
2
=
−
=
∑
=
n
x
x
s
i
i
oraz
65
.
28
10
/
59
.
90
1
=
=
−
n
s
Odczyt z tablic studenta t(0.02,10)=2.76 czyli
05
.
79
65
.
28
76
.
2
1
=
⋅
=
−
⋅
n
s
t
Czyli przedział ufności:
60
,
2863
;
50
,
2705
05
,
79
55
,
2784
;
05
,
79
55
,
2784
=
+
−
Szerokość przedziału
10
,
158
05
,
79
2
=
⋅
=
L
Zadanie 8
Za pomocą metody największej wiarygodności wyznaczyć estymator parametru p rozkładu
populacji ogólnej o rozkładzie dwumianowym:
m
x
p
p
x
m
p
x
P
x
m
x
,...,
2
,
1
,
)
1
(
)
,
(
=
−
⎟⎟
⎠
⎞
⎜⎜
⎝
⎛
=
−
Wyznaczyć, na podstawie n niezależnych pomiarów x
1
,x
2
,...,x
n
, estymator największej
wiarygodności dla p.
Rozwiązanie:
Było na wykładzie. W domu należy sprawdzić, że znalezione rozwiązanie przynosi maksimum funkcji
wiarygodności.
Zadanie 9
Czas pracy elementu jest zmienną losową X o gęstości

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 02. Modyfikowana ostatni raz 7.06.09
Strona 4
⎩
⎨
⎧
≤
>
−
=
−
0
,
0
0
),
(
)
(
1
x
gdy
x
gdy
x
exp
x
x
f
a
β
αβ
α
gdzie
α
jest znanym dodatnim parametrem,
β
zaś jest nieznaną dodatnią stałą (jest to gęstość
rozkładu Weibulla). Wyznaczyć, na podstawie niezależnych pomiarów x
1
,x
2
,...,x
n
czasu pracy
elementu, estymator największej wiarygodności dla
β
.
Zadanie 10
Na podstawie n-elementowej próby prostej pobranej z populacji, w której badana cecha X ma
rozkład Poissona:
⎪⎩
⎪
⎨
⎧
>
=
=
=
−
poza
c
i
e
i
c
i
X
P
c
i
0
0
,...
2
,
1
,
0
!
)
(
należy:
1. Skonstruować estymator parametru c metodą analogii.
2. Skonstruować estymator parametru c metodą największej wiarygodności
3. Wykazać, że estymator według punktu 2 jest nieobciążony.
Zadanie 11
Zmienna losowa określająca populację ma rozkład określony funkcją gęstości
)
0
(
>
λ
:
⎩
⎨
⎧
>
=
−
poza
x
dla
xe
c
x
f
x
0
0
)
(
2
λ
λ
Należy:
1. Wyznaczyć stałą c.
2. Napisać funkcję dystrybuanty.
3. Wyznaczyć estymator parametru
λ metodą największej wiarygodności.
Zadanie 12
Należy oszacować żywotność (w godzinach świecenia) wyprodukowanej partii świetlówek.
Wiadomo, że czas świecenia świetlówek ma rozkład normalny z odchyleniem standardowym
σ. Wylosowana niezależnie z tej partii próba n = 11 świetlówek dała wyniki pomiarów czasu
ich świecenia (w godzinach): 2630, 2820, 2900, 2810, 2770, 2840, 2700, 2950, 2690, 2720,
2800. Przyjmując poziom ufności 1-
α = 0.98 oszacować metodą przedziałową średni czas
świecenia świetlówek tej partii oraz szerokość przedziału ufności.
Rozważyć trzy przypadki:
a) Odchylenie standardowe jest znane i wynosi
σ=100 godzin.

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 02. Modyfikowana ostatni raz 7.06.09
Strona 5
b) Odchylenie standardowe nie jest znane.
c) Jak zmieniłyby się brzegi przedziału ufności w przypadku 2 gdyby oszacowanie
pierwiastka z wariancji było równe wartości odchylenia z przypadku 1 (tzn.
s=
σ=100) ? Przeliczyć.
Uwaga: W zadaniu proszę przed obliczeniami napisać wzór ogólny.
Rozwiązanie:
a)
Średnia z 11 realizacji (jednostki pomijam):
5
.
2784
11
11
1
=
=
∑
=
i
i
x
x
Jeśli odchylenie standardowe jest znane to:
131
.
70
11
100
326
.
2
99
.
0
=
⋅
=
n
x
σ
gdzie
99
.
0
x
jest kwantylem rzędu
2
1
α
−
rozkładu normalnego tzn. kwantylem rzędu 0.99, który odczytujemy z
tablic i
326
.
2
99
.
0
=
x
w takim razie przedział ufności wynosi: <2784.5-70.131;2784.5+70.131>=<2714.4 ; 2854.7>
Szerokość przedziału ufności wynosi 140.3
b)
Estymator
59
.
90
)
(
11
1
2
=
−
=
∑
=
n
x
x
s
i
i
Jeśli odchylenie standardowe nie jest znane to:
181
.
79
1
11
59
.
90
764
.
2
)
10
,
02
.
0
(
=
−
⋅
=
⋅
r
s
t
gdzie
)
10
,
02
.
0
(
t
jest wartościa krytyczną (kwantylem rzędu
2
1
α
−
) rozkładu Studenta, którą odczytujemy z
tablic i
764
.
2
)
10
,
02
.
0
(
=
t
w takim razie przedział ufności wynosi: <2784.5-79.181;2784.5+79.181>=<2705.4 ; 2863.7>
Szerokość przedziału ufności wynosi 158.36
c) Powtarzamy obliczenia z punktu b ale zamiast s wstawiamy wartość 100.
Otrzymujemy przedział ufności <2697.1 ; 2871.9> i szerokość przedziału
równą 174.81 a zatem znacznie więcej niż w punkcie a).
Zadanie 13
Zmienna losowa określająca populację ma rozkład Rayleigha określony funkcją
gęstości
)
0
(
>
λ
:
⎩
⎨
⎧
>
=
−
poza
x
dla
xe
x
f
x
0
0
2
)
(
2
λ
λ

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 02. Modyfikowana ostatni raz 7.06.09
Strona 6
Wyznaczyć estymator parametru
λ metodą największej wiarygodności.
Rozwiązanie:
Funkcja wiarygodności:
i
n
i
x
n
x
i
n
i
x
e
e
x
L
n
i
i
i
Π
Π
=
−
−
=
∑
=
=
=
1
1
1
2
2
)
2
(
)
2
(
λ
λ
λ
λ
Czyli:
)
ln(
]
ln
)
2
[ln(
)
ln(
]
ln[
]
)
2
ln[(
))
2
(
ln(
)
ln(
1
1
2
1
1
1
2
2
i
n
i
n
i
i
i
n
i
x
n
x
i
n
i
x
x
n
x
e
e
x
L
n
i
i
i
Π
Π
Π
=
=
=
−
−
=
+
∑
−
+
=
=
+
∑
+
=
=
=
λ
λ
λ
λ
λ
λ
Obliczamy pochodną lewej strony względem parametru
λ
:
0
))
ln(
)
2
ln(
(
)
ln(
1
2
1
1
2
=
∑
−
=
=
+
∑
−
=
=
=
=
Π
n
i
i
i
n
i
n
i
i
x
n
d
x
x
n
d
d
L
d
λ
λ
λ
λ
λ
Zatem:
∑
=
=
n
i
i
x
n
1
2
ˆ
λ
Nie wiemy jeszcze czy to jest maksimum zatem obliczymy druga pochodną:
2
2
2
)
ln(
λ
λ
n
d
L
d
−
=
Ma ona zawsze znak ujemny bez wględu na to jakie
λ
postawimy.
Zatem estymatorem parametru
λ
otrzymanym MNW jest:
∑
=
Λ
=
n
i
i
X
n
1
2
Zadanie 14
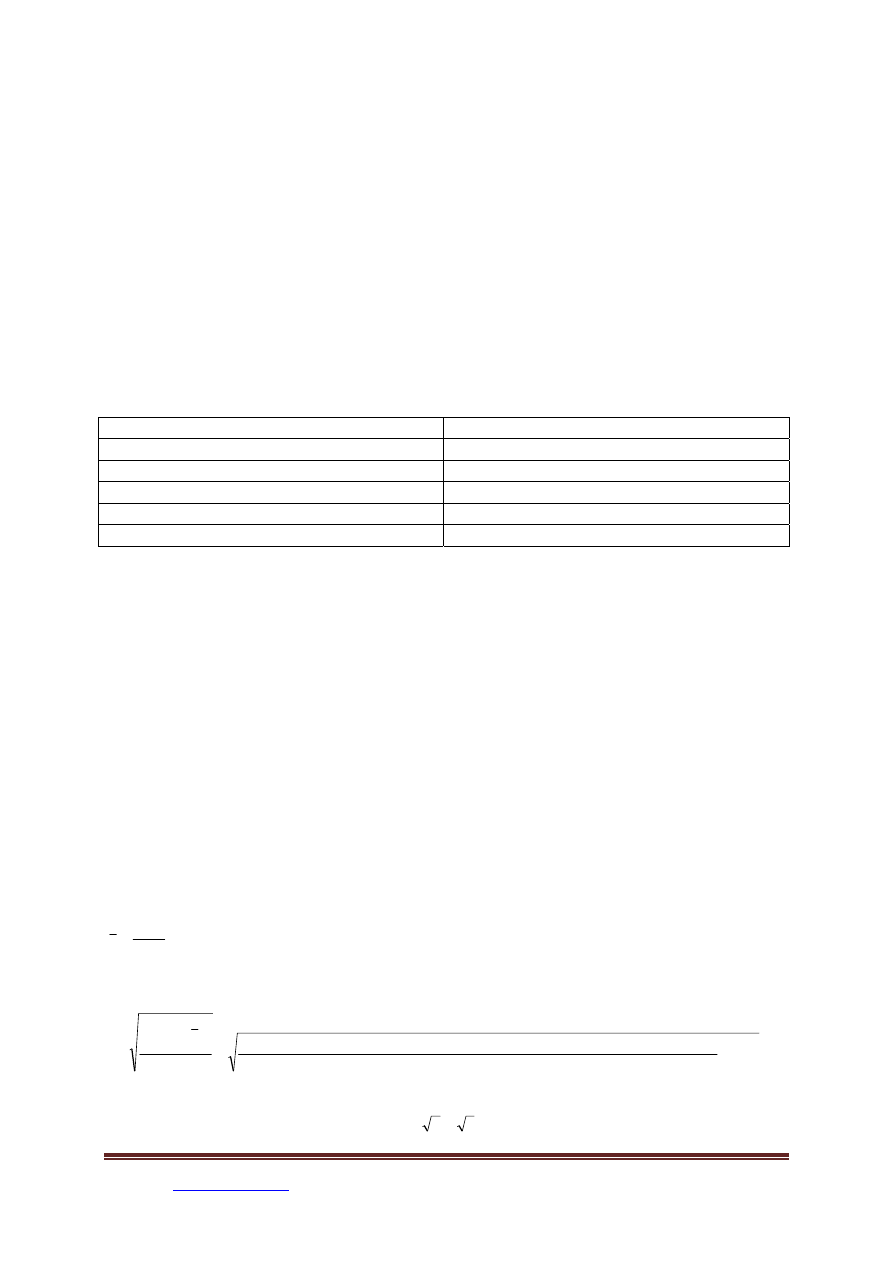
Zmierzono wytrzymałość 10 losowo wybranych gotowych elementów walcowanych i
otrzymano następujące wyniki: 383, 284, 339, 340, 305, 386, 387, 335, 344, 346 [Pa]. Przy
założeniu, że wytrzymałość tych elementów jest zmienną losową
)
,
(
σ
μ
N
o nieznanych
μ
i
σ
, wyznaczyć na podstawie tej próbki 95 % (tzn. przyjąć
α
= 0.05) realizację przedziału
ufności dla
μ
.
Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 02. Modyfikowana ostatni raz 7.06.09
Strona 7
Zadanie 15
Zakłada się następujący sposób zdawania egzaminów poprawkowych:
Prawdopodobieństwo niezadania egzaminu poprawkowego (parametr
θ
) jest stałe dla
określonego przedmiotu i jednakowe dla wszystkich studentów w określonej grupie. Ze
względu na sens fizyczny musi być: 0 <
θ
< 1 (parametr
θ
nie zależy od tego po raz który
zdaje się egzamin poprawkowy).
Niech
X oznacza zmienną losową, która jest zdefiniowana jako liczba egzaminów
poprawkowych ustalonego studenta aż do zdania włącznie. W założonym modelu
X ma
rozkład geometryczny:
)
1
(
)
(
1
θ
θ
−
=
=
−
k
k
X
P
(k=1,2,...)
W pewnej grupie o liczności n=40 studentów zarejestrowano wynik przedstawiony w tablicy:
Krotność zdawania
k:
Liczba studentów o krotności
k:
1 22
2 8
3 5
4 5
>4 0
Oszacować metoda największej wiarygodności parametr
θ
.
Zadanie 16
Dokonano serii 5 pomiarów rezystancji metodą mostkową. Otrzymano następujące wyniki:
53.2, 53.6, 53.1, 54.9, 53.7 Ω. Obliczyć niepewność standardową typu A u
A
oraz
niepewność rozszerzoną U
A
dla poziomu ufności 0.95.
Rozwiązanie:
Przypominam fragment wykładu, że niepewność standardową obliczamy jako odchylenie standardowe lub
estymatę tego odchylenia.Obliczamy kolejno:
Średnia arytmetyczna serii pomiarów (jednostki pomijam):
7
.
53
5
5
1
=
=
∑
=
i
i
x
x
Jako estymator odchylenia standardowego pojedynczego pomiaru przyjmujemy (zobacz fragment wykładu
dotyczący estymowania wariancji w metodzie analogii):
72
.
0
1
5
)
7
.
53
7
.
53
(
)
7
.
53
9
.
54
(
)
7
.
53
1
.
53
(
)
7
.
53
6
.
53
(
)
7
.
53
3
.
52
(
1
)
(
2
2
2
2
2
5
1
2
=
−
−
+
−
+
−
+
−
+
−
=
−
−
=
∑
=
n
x
x
s
i
i
Powyższe jest estymatorem odchylenia standardowego dla pojedynczego pomiaru. Natomiast wiadomo, że
odchylenie standardowe średniej arytmetycznej jest
5
=
n

Prawa zastrzeżone © J.Frączek, Materiał na prawach rękopisu. Kopiowanie bez zgody autora zabronione. W razie wykrycia błędów proszę
o informację.
fraczek@meil.pw.edu.pl
. Wersja 02. Modyfikowana ostatni raz 7.06.09
Strona 8
32
.
0
5
72
.
0
=
=
=
n
s
s
x
A zatem tą wartość przyjmujemy jako niepewność standardową pomiaru to znaczy u
A
=0.32
Ω.
Niepewność rozszerzona jest połową szerokości przedziału ufności dla wartości oczekiwanej na poziomie
ufności 0.95 przy założeniu, że odchylenie standardowe nie jest znane (nie podano w zadaniu).
Oblicza się ja następująco (porównaj rozwiązanie zadania 12b):
32
.
0
776
.
2
)
4
,
05
.
0
(
⋅
=
⋅
=
x
A
s
t
U
=0.89
Ω
gdzie
)
4
,
05
.
0
(
t
jest wartością krytyczną rozkładu studenta o r=4 stopniach swobody, albo jak kto woli
kwantylem rzędu 1-0.05/2. W ocenie niepewności rozszerzonej kwantyl t rozkładu studenta nosi nazwę
współczynnika rozszerzenia i oznacza jako k.
Zadanie 17.
Weźmy pod uwagę zadanie 12 punkt b). Postawimy hipotezę H
0
:
2790
=
μ
przeciwko
hipotezie H
1
:
2790
<
μ
(ta hipoteza jest uzasadniona bo z obliczeń otrzymaliśmy wartość
estymatora wartości oczekiwanej <2790).
Należy zweryfikować hipotezę H
0
na poziomie istotności
05
.
0
=
α
.
Rozwiązanie:
Tworzymy statystykę (odchylenie standardowe nie jest znane):
1
0
−
−
n
S
X
μ
i obliczamy jej realizację dla zadanych danych:
192
.
0
10
59
.
90
2790
5
.
2784
1
0
−
=
−
=
−
−
n
s
x
μ
Tworzymy obszar krytyczny lewostronny dla poziomu istotności
05
.
0
=
α
:
)
,
(
05
.
0
t
U
od
−∞
=
Gdzie t
0.05
jest kwantylem rzędu 0.05 rozkładu Studenta dla 10 stopni swobody. Jest on zatem równy:
)
10
,
1
.
0
(
05
.
0
t
t
−
=
gdzie t(0.1,10) jest wartością krytyczna rozkładu studenta. Z tablic wartości krytycznych
odczytujemy t(0.1,10)=1.81. Stąd:
)
81
.
1
,
(
−
−∞
=
od
U
. Zatem
od
U
∉
− 192
.
0
a zatem brak jest podstaw do odrzucenia hipotezy zerowej
(stosujemy orzekanie dwuorzeczeniowe).
Uwaga:
Analizując rozwiązania wszystkich zadań należy zawsze sprawdzać obliczenia
i wzory!
Wyszukiwarka
Podobne podstrony:
MiTE Zadania seria 2 wersja 03
MiTE Zadania seria 2 wersja 03
MiTE Zadania seria 2 wersja 06
MiTE Zadania seria 2 wersja 04 Nieznany
MiTE Zadania seria 1 wersja 01 Nieznany
MiTE Zadania seria 2 wersja 06
MiTE Zadania seria 2 wersja 04 Nieznany
MiTE Zadania seria 2 wersja 04
MiTE Zadania seria 2 wersja 06
MiTE Zadania seria 1 wersja 01
MITE Zadania domowe seria 2
MITE Zadania domowe seria 2
MiTE Zadania domowe seria 1 Nieznany
MITE Zadania domowe seria 3 id Nieznany
MiTE wykL,ad 7 8 wersja 01 id 3 Nieznany
CEIDG 1 wersja 1 03 1
więcej podobnych podstron