1

1

Wykład nr 6

Wykład nr 6

Obliczanie sił wewnętrznych w

Obliczanie sił wewnętrznych w

układach prętowych.

układach prętowych.

Kratownice.

Kratownice.

2

2





Układ prętów prostoliniowych:

Układ prętów prostoliniowych:

–

–

połączenia przegubowe w węzłach;

połączenia przegubowe w węzłach;

–

–

obciążenia w postaci sił skupionych

obciążenia w postaci sił skupionych

przyłożonych w węzłach.

przyłożonych w węzłach.

3m

3

m

10kN

3,5m

20kN

3m

3

m

10kN

3,5m

20kN

3

3





Węzeł doznaje przesuwu (dwie

Węzeł doznaje przesuwu (dwie

składowe), obrót jest nieistotny;

składowe), obrót jest nieistotny;





W prętach dwustronnie przegubowych,

W prętach dwustronnie przegubowych,

nieobciążonych poprzecznie występuje

nieobciążonych poprzecznie występuje

jedynie siła osiowa (normalna).

jedynie siła osiowa (normalna).

4

4





Pas dolny (D)

Pas dolny (D)





Pas górny (G)

Pas górny (G)





Krzyżulce (K)

Krzyżulce (K)





Słupki (S)

Słupki (S)

G

1

G

2

D

1

D

2

S

1

S

2

S

3

K

1

K

2

5

5





Najprostsza kratownica złożona z trzech

Najprostsza kratownica złożona z trzech

prętów połączonych przegubowo jest

prętów połączonych przegubowo jest

statycznie wyznaczalna.

statycznie wyznaczalna.





Każda kratownica budowana przez

Każda kratownica budowana przez

dostawianie pól zamkniętych

dostawianie pól zamkniętych

tworzonych za pomocą kolejnych dwóch

tworzonych za pomocą kolejnych dwóch

prętów jest statycznie wyznaczalna.

prętów jest statycznie wyznaczalna.

6

6





Statyczna wyznaczalność:

Statyczna wyznaczalność:

–

–

zewnętrzna

zewnętrzna

–

–

możliwość policzenia reakcji:

możliwość policzenia reakcji:

–

–

wewnętrzna

wewnętrzna

–

–

możliwość policzenia sił w

możliwość policzenia sił w

prętach:

prętach:

–

–

całkowita:

całkowita:

3

z

n

r

 

2

3

n

p

w

   

2

w

n

p

w

  

7

7

(1)

(1)





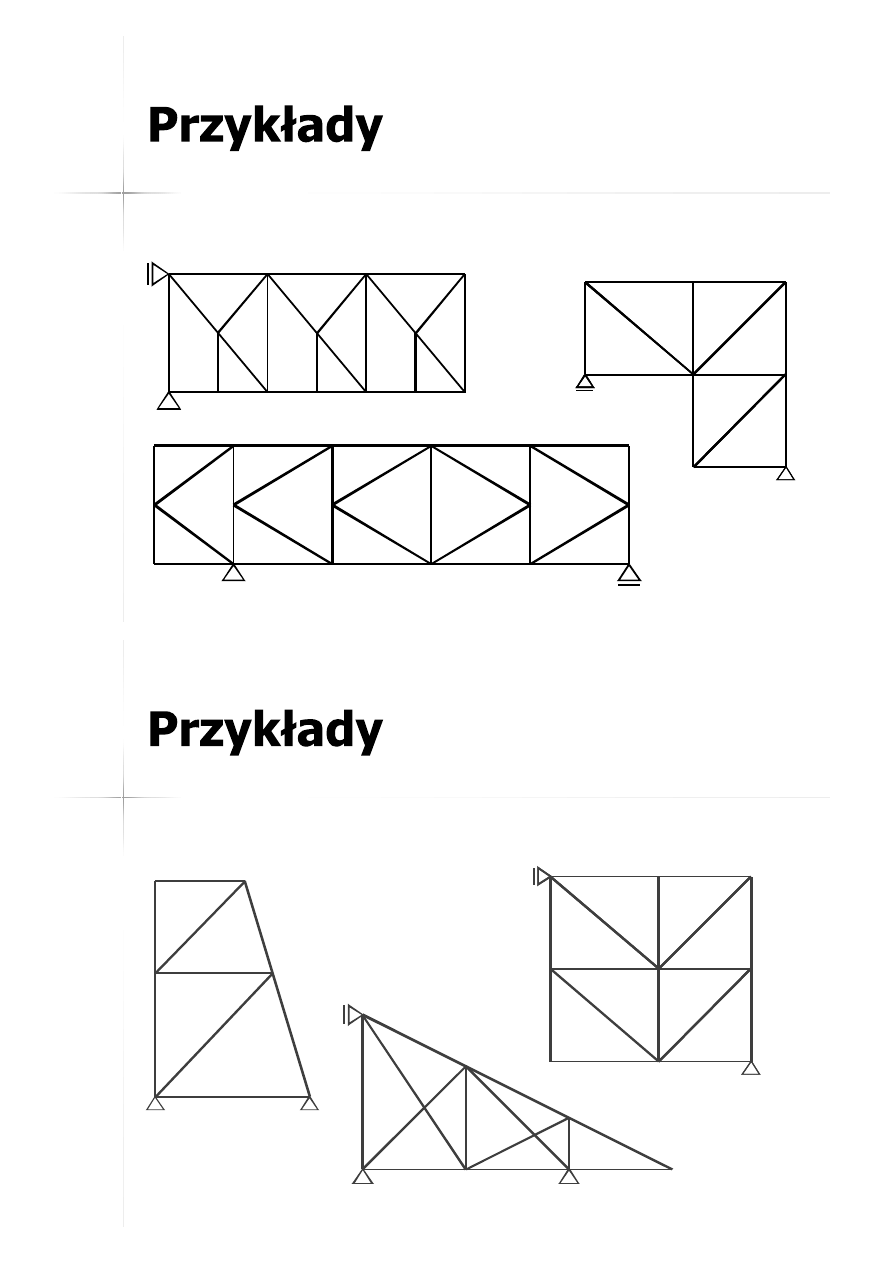
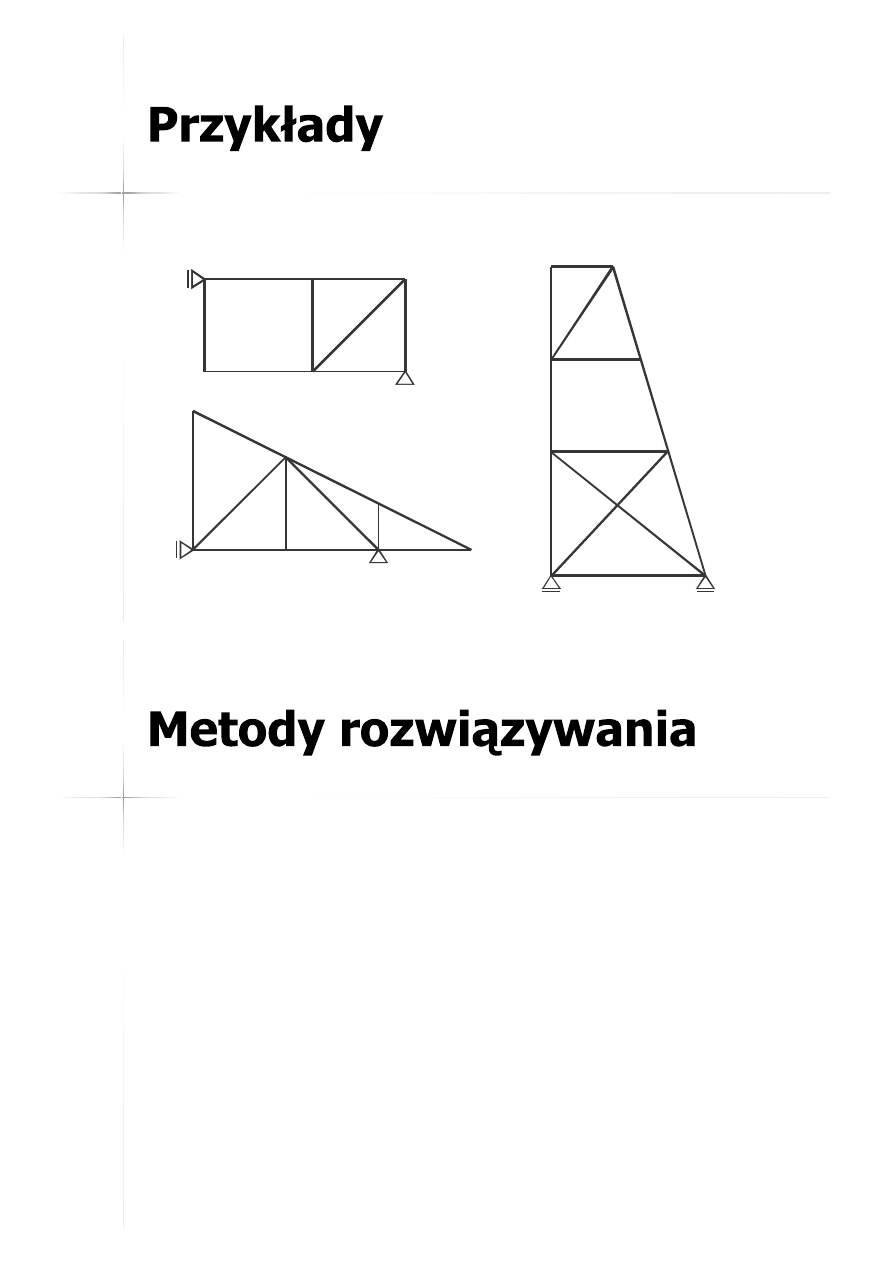
Kratownice statycznie wyznaczalne

Kratownice statycznie wyznaczalne

8

8

(2)

(2)





Kratownice statycznie niewyznaczalne

Kratownice statycznie niewyznaczalne

9

9

(3)

(3)





Kratownice geometrycznie zmienne

Kratownice geometrycznie zmienne

10

10





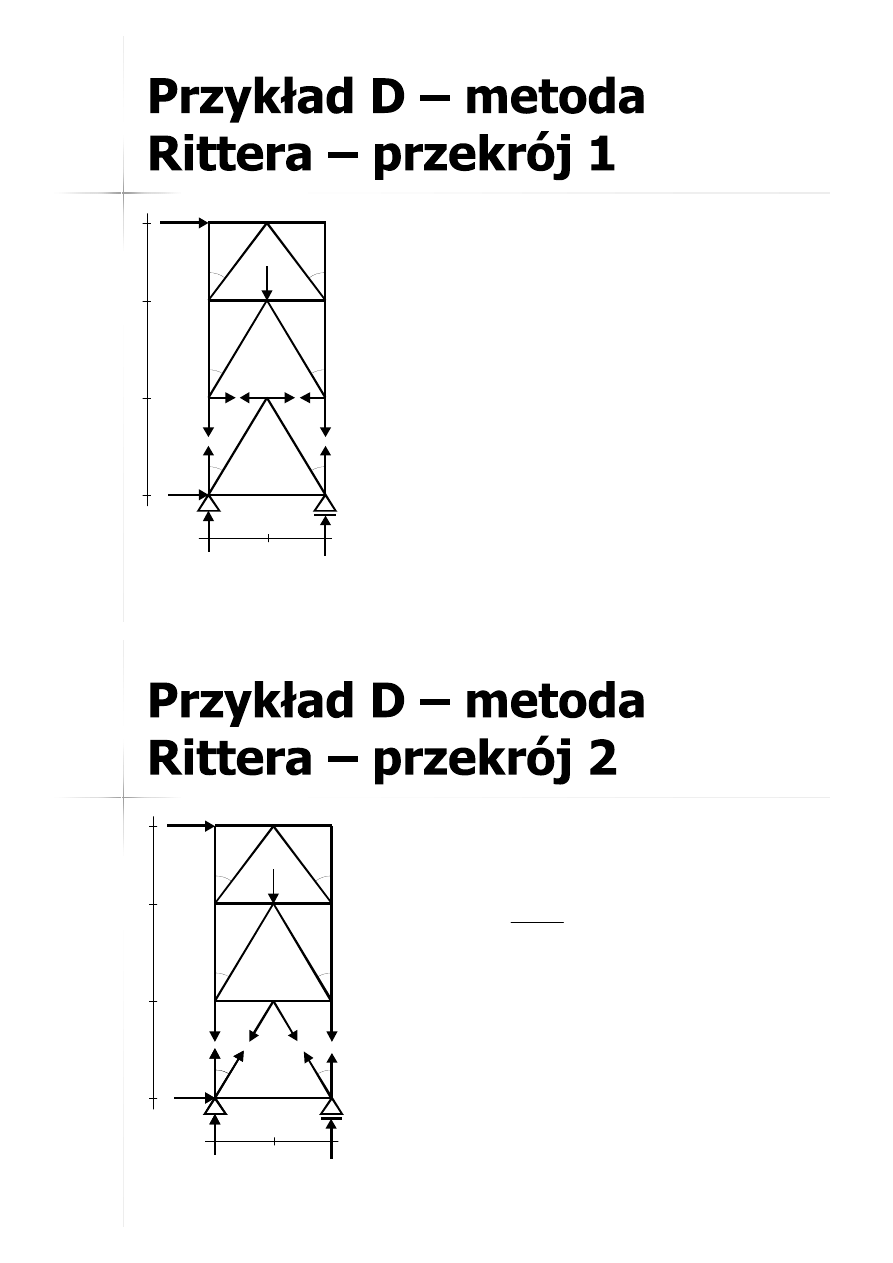
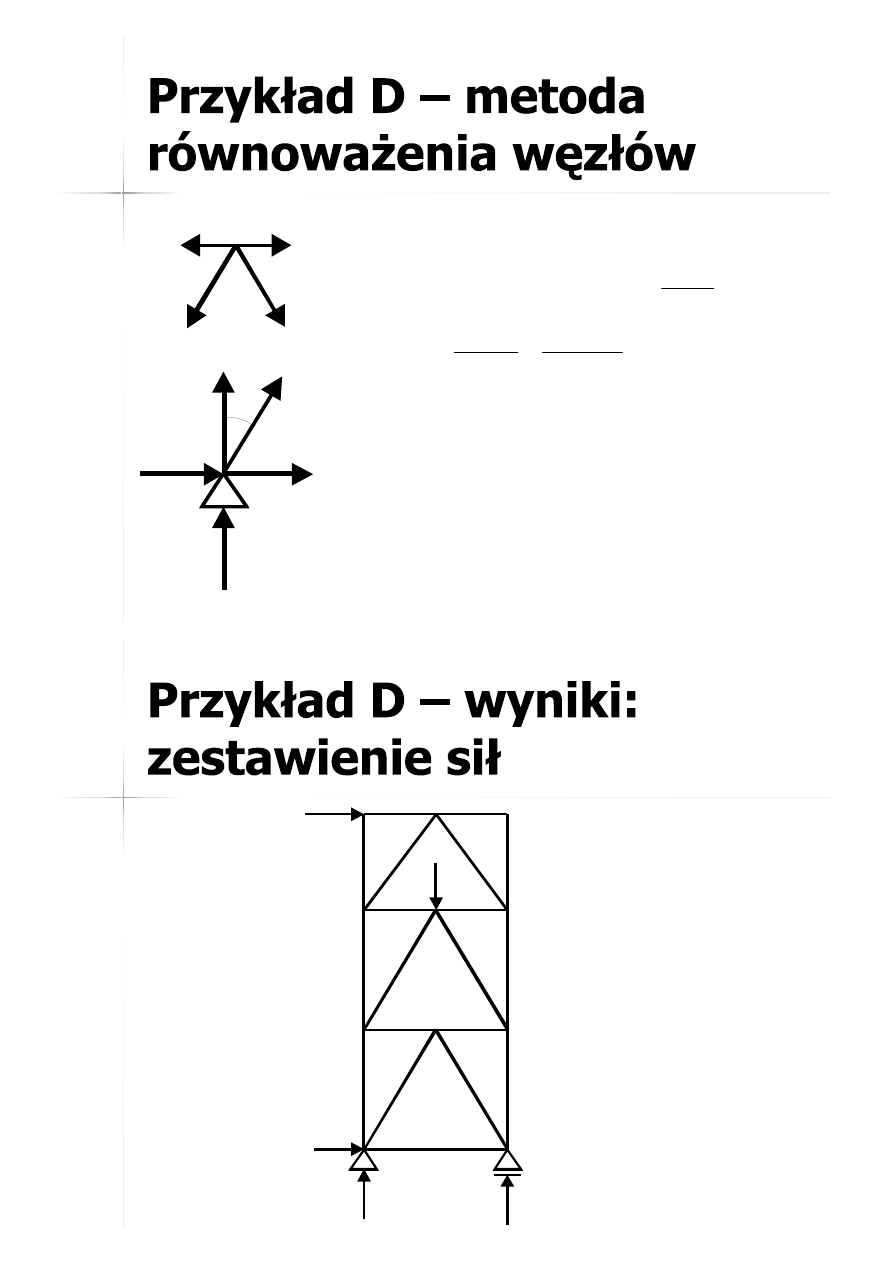
Metoda równoważenia węzłów.

Metoda równoważenia węzłów.





Metoda

Metoda

Rittera

Rittera

.

.





Inne:

Inne:

–

–

wykreślna metoda

wykreślna metoda

Cremony

Cremony

;

;

–

–

metoda

metoda

Culmana

Culmana

;

;

–

–

metoda

metoda

Hanneberga

Hanneberga

(wymiany prętów).

(wymiany prętów).

11

11





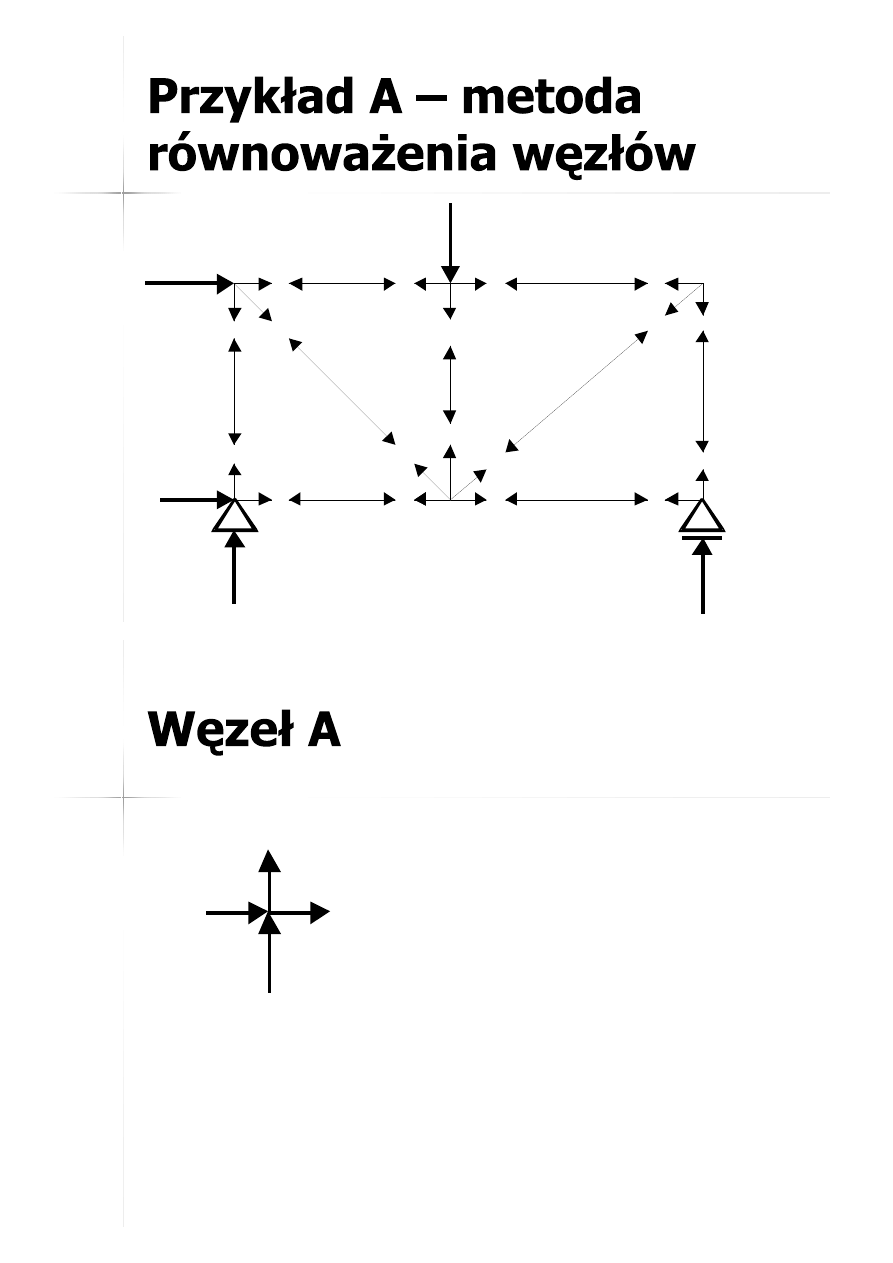
Każdy z węzłów oddzielony zostaje od

Każdy z węzłów oddzielony zostaje od

prętów za pomocą przekroju

prętów za pomocą przekroju

przywęzłowego.

przywęzłowego.





W węzłach otrzymuje się układy sił

W węzłach otrzymuje się układy sił

zbieżnych, w których można zapisać

zbieżnych, w których można zapisać

dwa równania równowagi

dwa równania równowagi

–

–

sumy

sumy

rzutów sił na dwie osie.

rzutów sił na dwie osie.

12

12





Zalety:

Zalety:

–

–

łatwość zapisania równań

łatwość zapisania równań

–

–

sumy rzutów

sumy rzutów

sił;

sił;

–

–

kontrola wyników: ostatnie trzy równania

kontrola wyników: ostatnie trzy równania

są sprawdzeniami;

są sprawdzeniami;





Wady:

Wady:

–

–

propagacja błędu;

propagacja błędu;

–

–

duży nakład pracy wymagany do

duży nakład pracy wymagany do

policzenia siły w wybranym pręcie.

policzenia siły w wybranym pręcie.

13

13





Kratownicę należy przeciąć przekrojem

Kratownicę należy przeciąć przekrojem

takim, aby można było zapisać

takim, aby można było zapisać

równanie, w którym jedyną niewiadomą

równanie, w którym jedyną niewiadomą

będzie szukana siła w pręcie.

będzie szukana siła w pręcie.





Otrzymany układ sił jest

Otrzymany układ sił jest

niezbieżny

niezbieżny

.

.

Równanie równowagi to zazwyczaj

Równanie równowagi to zazwyczaj

suma momentów (czasem suma rzutów

suma momentów (czasem suma rzutów

sił).

sił).

14

14





Zalety:

Zalety:

–

–

szukana siła może zostać wyznaczona za

szukana siła może zostać wyznaczona za

pomocą tylko jednego równania;

pomocą tylko jednego równania;

–

–

brak propagacji błędu;

brak propagacji błędu;





Wady:

Wady:

–

–

konieczność zapisania równań sum

konieczność zapisania równań sum

momentów;

momentów;

–

–

brak kontroli błędów (możliwa

brak kontroli błędów (możliwa

np

np

. za

. za

pomocą metody równoważenia węzłów).

pomocą metody równoważenia węzłów).

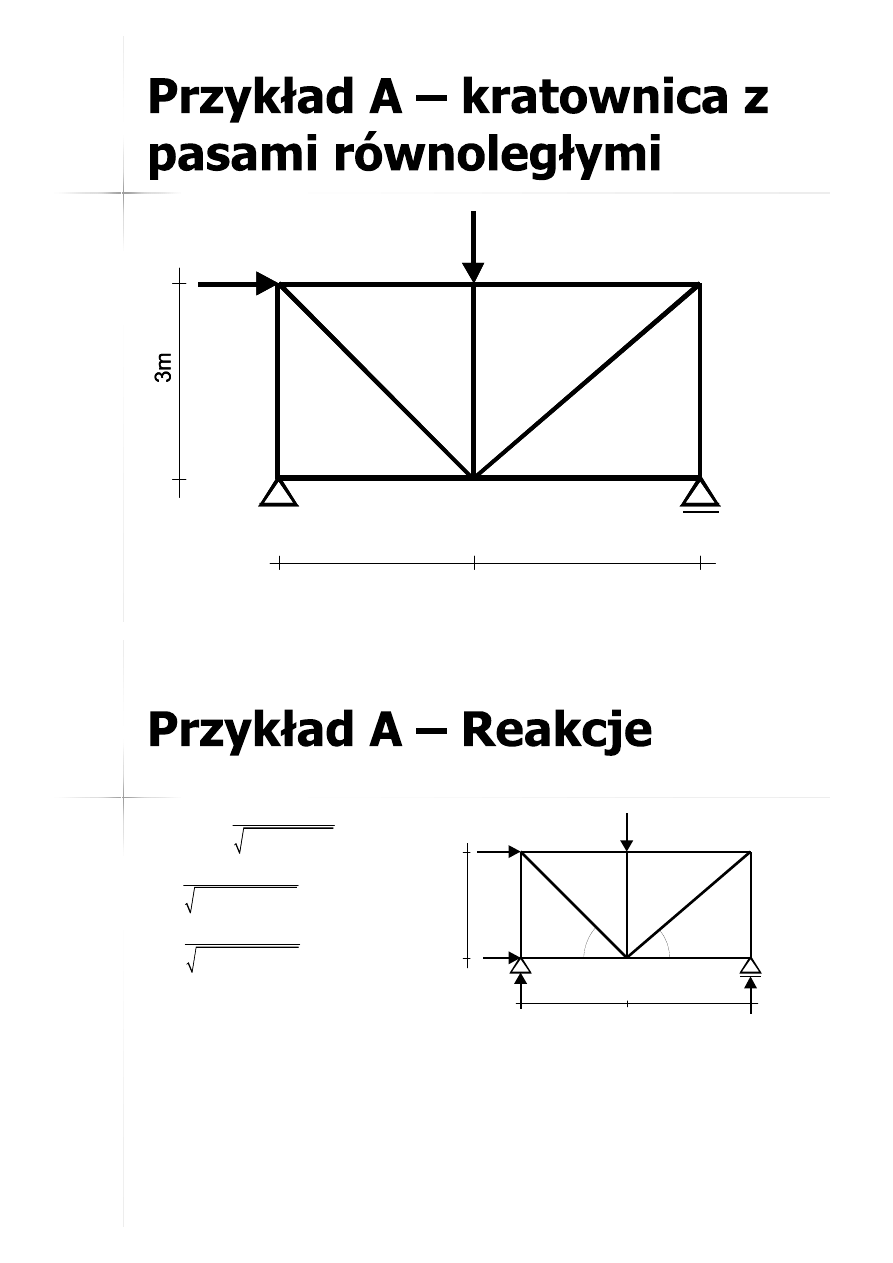
15

15

3m

10kN

3,5m

20kN

3m

10kN

3,5m

20kN

16

16

3m

3

m

10kN

3,5m

20kN

R

B

V

A

H

A





A

B

1

2

3

4

:

10

0

A

X H

kN







:

20

0

A

B

Y V

R

kN









:

6, 5

10

3

20

3

0

A

B

M

R

m

kN

m

kN

m















   

2

2

3

sin

cos

0, 707

3

3

m

m

m













  



2

2

3

sin

0, 651

3

3, 5

m

m

m









  



2

2

3, 5

cos

0, 759

3

3, 5

m

m

m









10

A

H

kN

 

6,154

A

V

kN



13,846

B

R

kN



17

17

10kN

20kN

R

B

V

A

H

A

B

1

2

3

4

A

N

A-2

N

A-1

N

A-1

N

A-2

N

1-A

N

1-A

N

1-B

N

1-4

N

1-4

N

1-3

N

1-2

N

2-A

N

2-A

N

2-3

N

2-3

N

3-2

N

3-2

N

3-4

N

3-4

N

4-3

N

4-3

N

4-B

N

4-1

N

4-1

N

1-3

N

3-1

N

3-1

N

1-2

N

2-1

N

2-1

N

4-B

N

B-4

N

1-B

N

B-1

N

B-1

N

B-4

18

18

V

A

H

A

A

N

A-2

N

A-1

1

:

0

A

A

X H

N









2

:

0

A

A

Y V

N









1

10

A

A

N

H

kN



 



2

6,154

A

A

N

V

kN



 

 

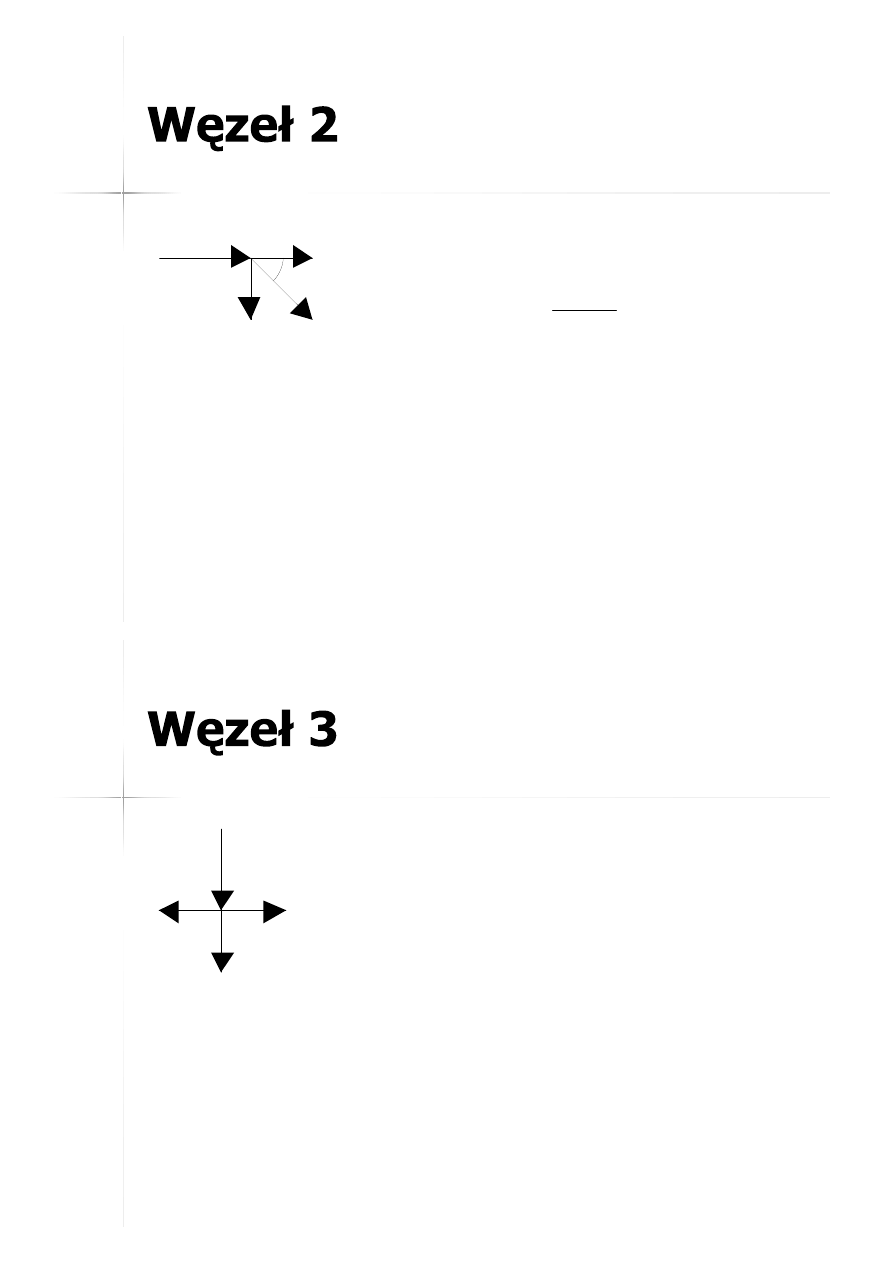
19

19

10kN

2

N

2-A

N

2-3

N

2-1



2 3

2 1

:

cos

10

0

X N

N

kN

















2

2 1

:

sin

0

A

Y N

N















2

2 1

8, 704

0, 707

A

N

N

kN





 



2 3

10

8, 704

0, 707

16,154

N

kN

kN

kN



 





 

20

20

20kN

3

N

3-2

N

3-4

N

3-1

3 2

3 4

:

0

X N

N











3 1

:

20

0

Y N

kN









3 1

20

N

kN



 

3 4

3 2

16,154

N

N

kN







 

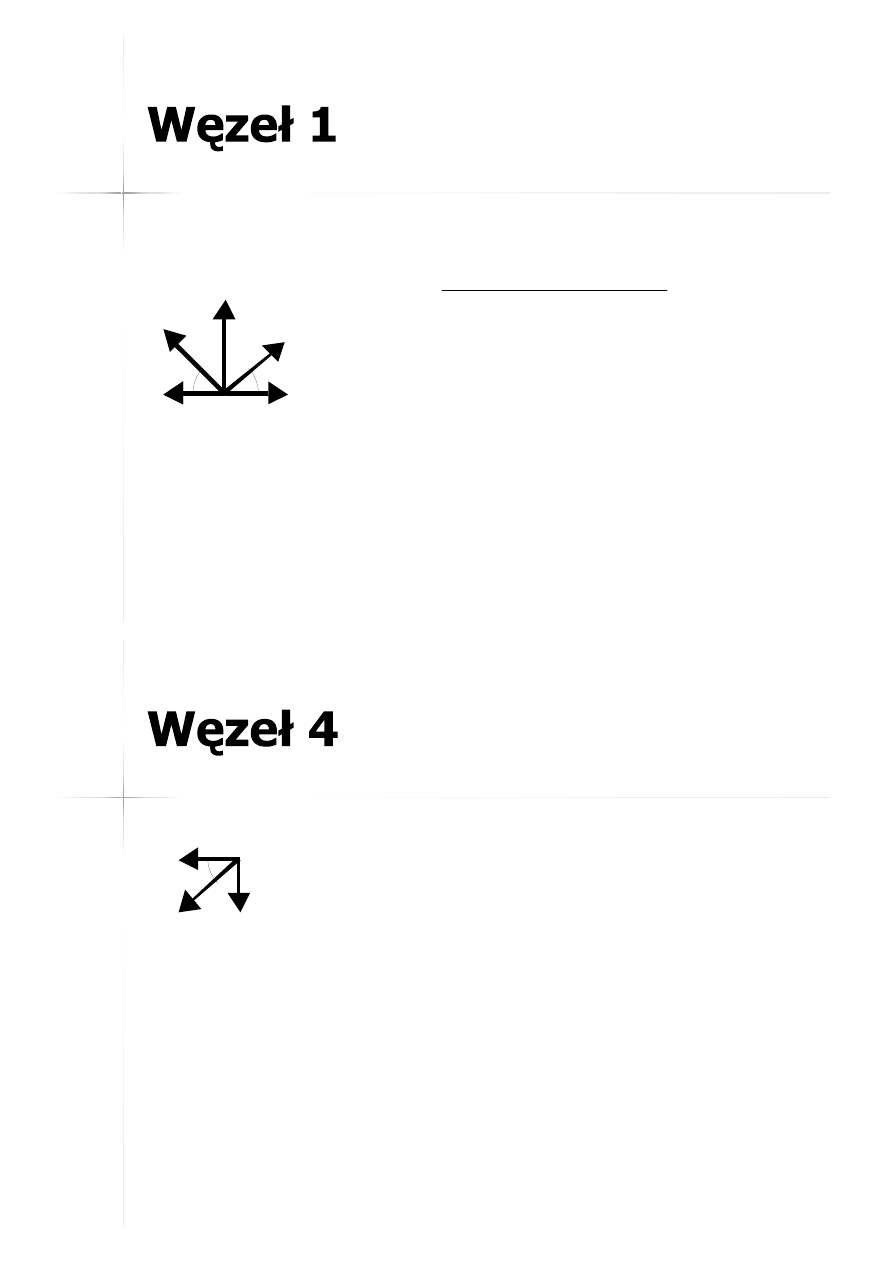
21

21

1

N

1-A

N

1-B

N

1-4

N

1-3

N

1-2





1

1 2

1 4

1

:

cos

cos

0

A

B

X

N

N

N

N





























1 2

1 3

1 4

:

sin

sin

0

Y N

N

N























1 4

8, 704

0, 707 20

21, 269

0, 651

kN

kN

N

kN







 



1

10

8, 704

0, 707 21, 269

0, 759

0, 011

B

N

kN

kN

kN

kN















22

22

4

N

4-3

N

4-B

N

4-1



4 3

4 1

:

cos

0

X N

N















4

4 1

:

sin

0

B

Y N

N















4 3

4 1

0, 759

16,154

21, 269

0, 759

0, 011

0

N

N

kN

kN

kN









 





 



4

21, 269

0, 651

13,846

B

N

kN

kN



 



 

Sprawdzenie:

Sprawdzenie:

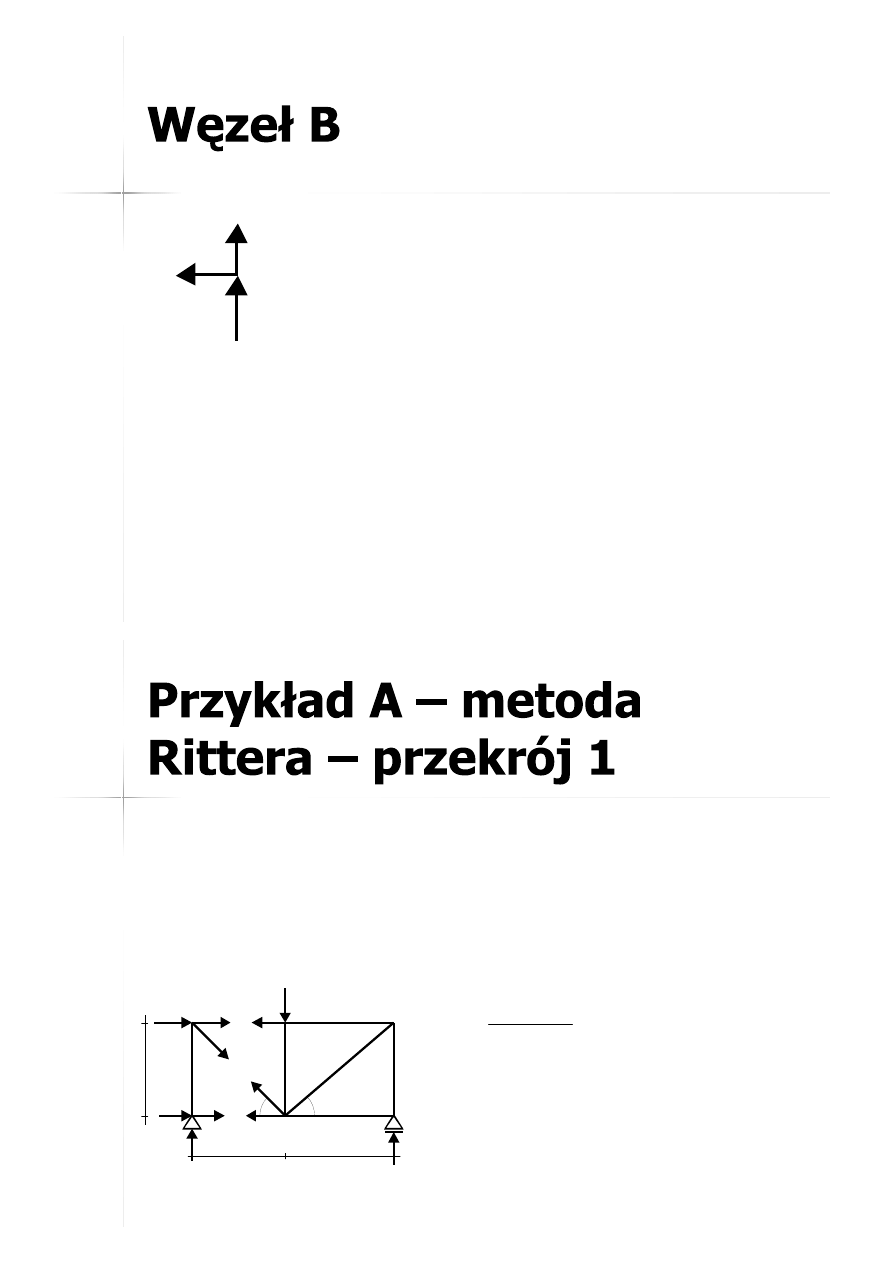
23

23

R

B

B

N

B-4

N

B-1

Sprawdzenie:

Sprawdzenie:

1

:

0

B

X N







4

:

0

B

B

Y N

R









1

0, 011

0

B

N

kN







4

13,864 13,864

0

B

B

N

R





 





Sprawdzenie:

Sprawdzenie:

24

24

(z lewej)

(z lewej)

3m

3

m

10kN

3,5m

20kN

R

B

V

A

H

A





A

B

1

2

3

4

N

A-1

N

1-A

N

2-1

N

1-2

N

2-3

N

3-2

2 1

:

sin

0

l

A

Y

V

N













1

2 3

:

3

10

3

3

0

l

A

M

V

m

kN

m

N

m

















2 1

6,154

8, 704

0, 707

kN

N

kN







2 3

6,154

10

16,154

N

kN

kN

kN



 



 

2

1

:

3

3

0

l

A

A

M

H

m

N

m













1

10

A

N

kN





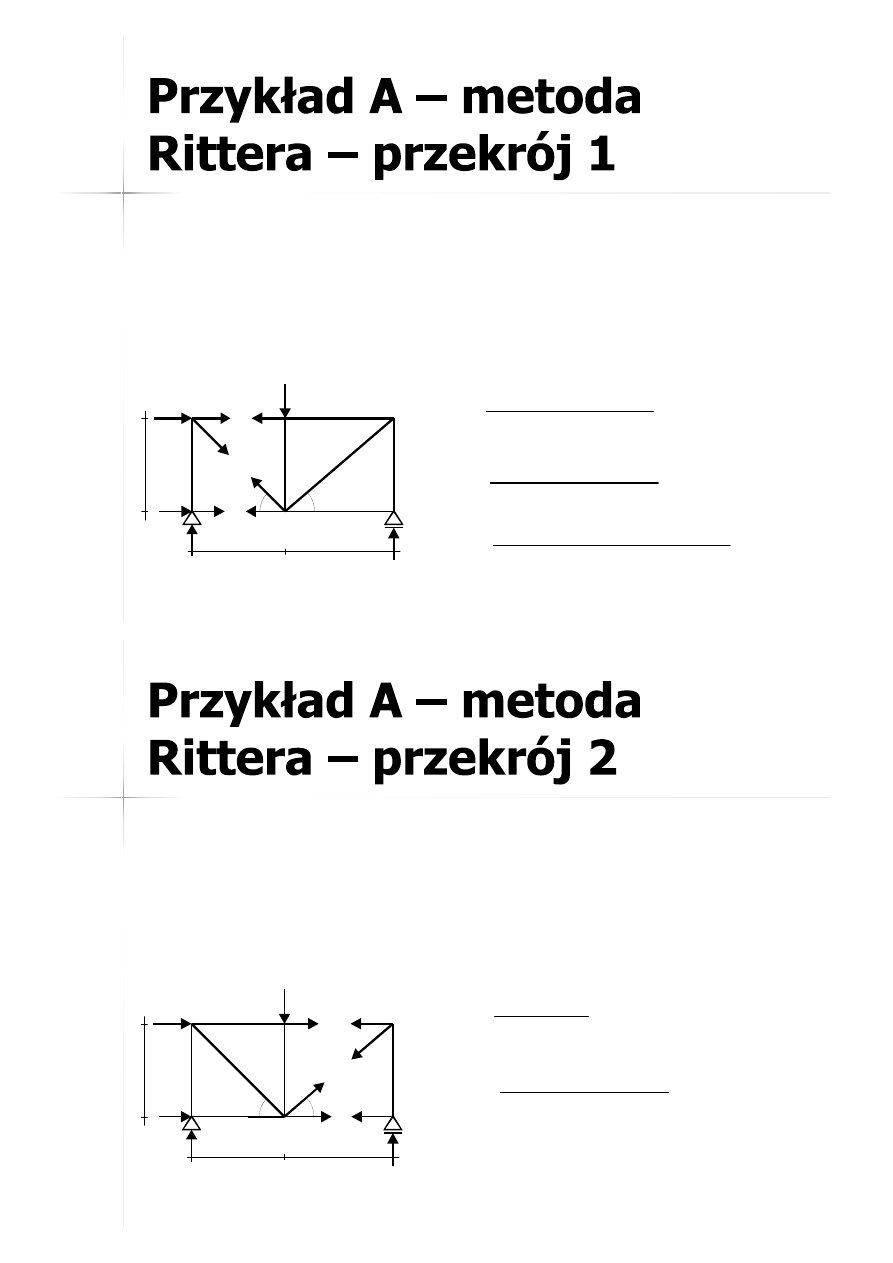
25

25

(z prawej)

(z prawej)

3m

3

m

10kN

3,5m

20kN

R

B

V

A

H

A





A

B

1

2

3

4

N

A-1

N

1-A

N

2-1

N

1-2

N

2-3

N

3-2

1 2

:

sin

20

0

p

B

Y

R

N

kN















1

3 2

:

3, 5

3

0

p

B

M

R

m

N

m













1 2

20

13,846

8, 704

0, 707

kN

kN

N

kN









3 2

13,846

3, 5

16,154

3

kN

m

N

kN

m









 

2

1

:

6, 5

3

20

3

0

p

B

A

M

R

m

N

m

kN

m

















1

13,846 6, 5

20

3

10

3

A

m

kN

m

N

kN

m













26

26

3m

3

m

10kN

3,5m

20kN

R

B

V

A

H

A





A

B

1

2

3

4

N

3-4

N

4-3

N

4-1

N

1-4

N

1-B

N

B-1

4 1

:

sin

0

p

B

Y

R

N













1

4 3

:

3, 5

3

0

p

B

M

R

m

N

m













4 1

13,846

21, 269

0, 651

kN

N

kN







4 3

13,846

3, 5

16,154

3

kN

m

N

kN

m









 

4

1

:

3

0

p

B

M

N

m









1

0

B

N





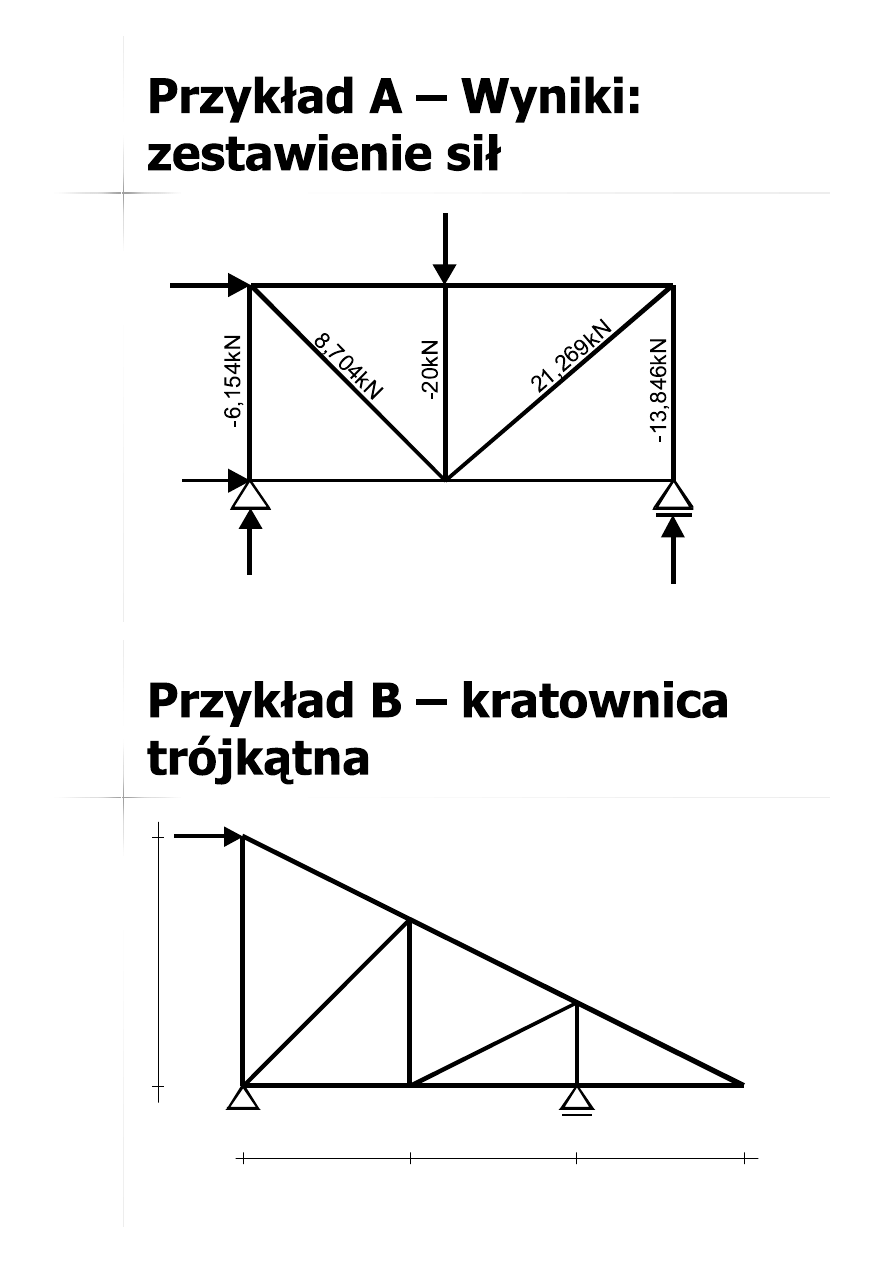
27

27

10kN

20kN

13,846kN

6,154kN

-10kN

0

-16,154kN

10kN

-16,154kN

28

28

3m

4

,5

m

20kN

3m

3m

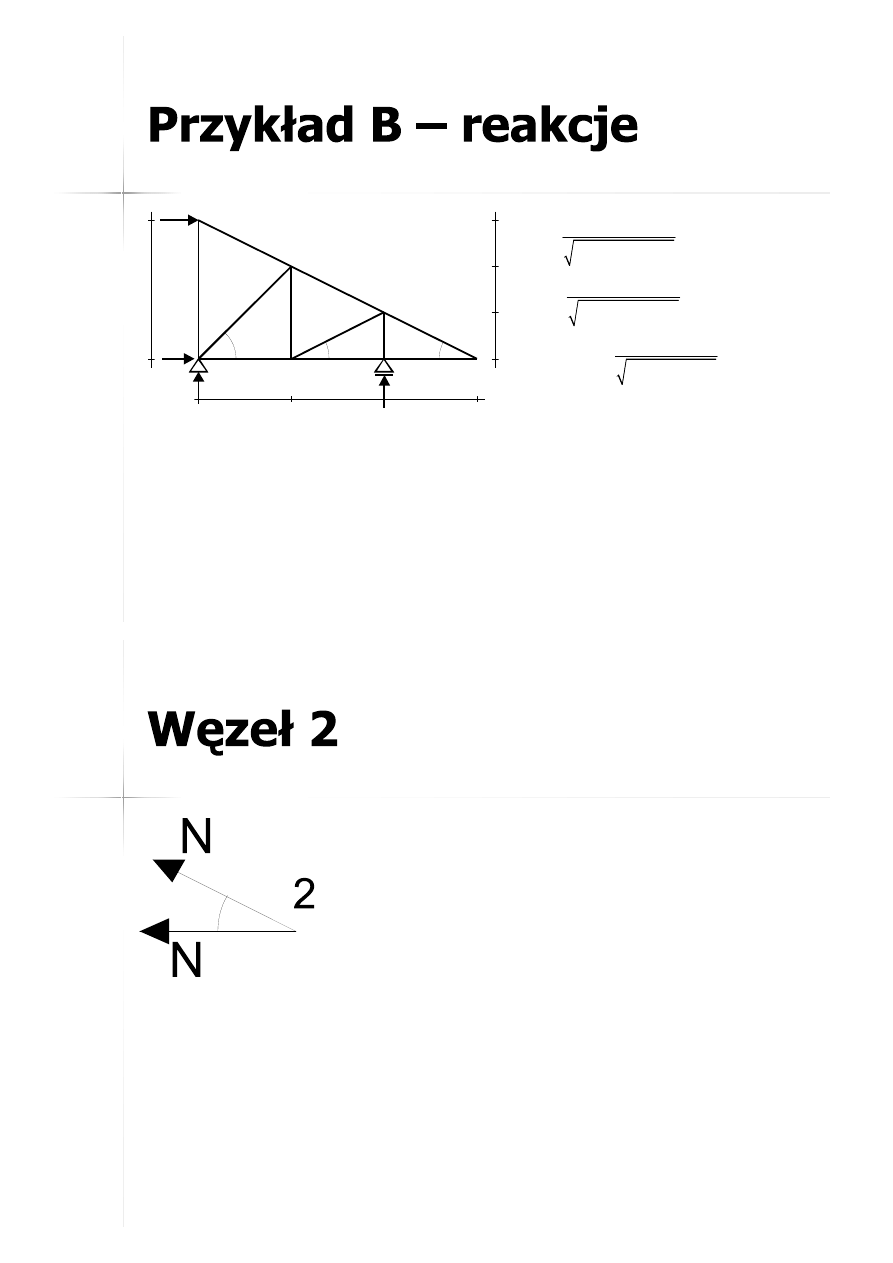
29

29

R

B

V

A

H

A

3m

4

,5

m

20kN

3m

3m







1

,5

m

1

,5

m

1

,5

m

A

B

1

2

3

4

5

:

20

0

A

X H

kN







:

0

A

B

Y V

R







:

6

20

4, 5

0

A

B

M

R

m

kN

m













  

2

2

1, 5

sin

0, 447

1,5

3

m

m

m









   

2

2

3

sin

cos

0, 707

3

3

m

m

m













20

A

H

kN

 

15

A

V

kN

 

15

B

R

kN





  

2

2

3

cos

0,894

1,5

3

m

m

m









30

30



2-B

2-3

2

2 3

:

cos

0

B

X N

N















2 3

:

sin

0

Y N











2 3

0

N





2

0

B

N





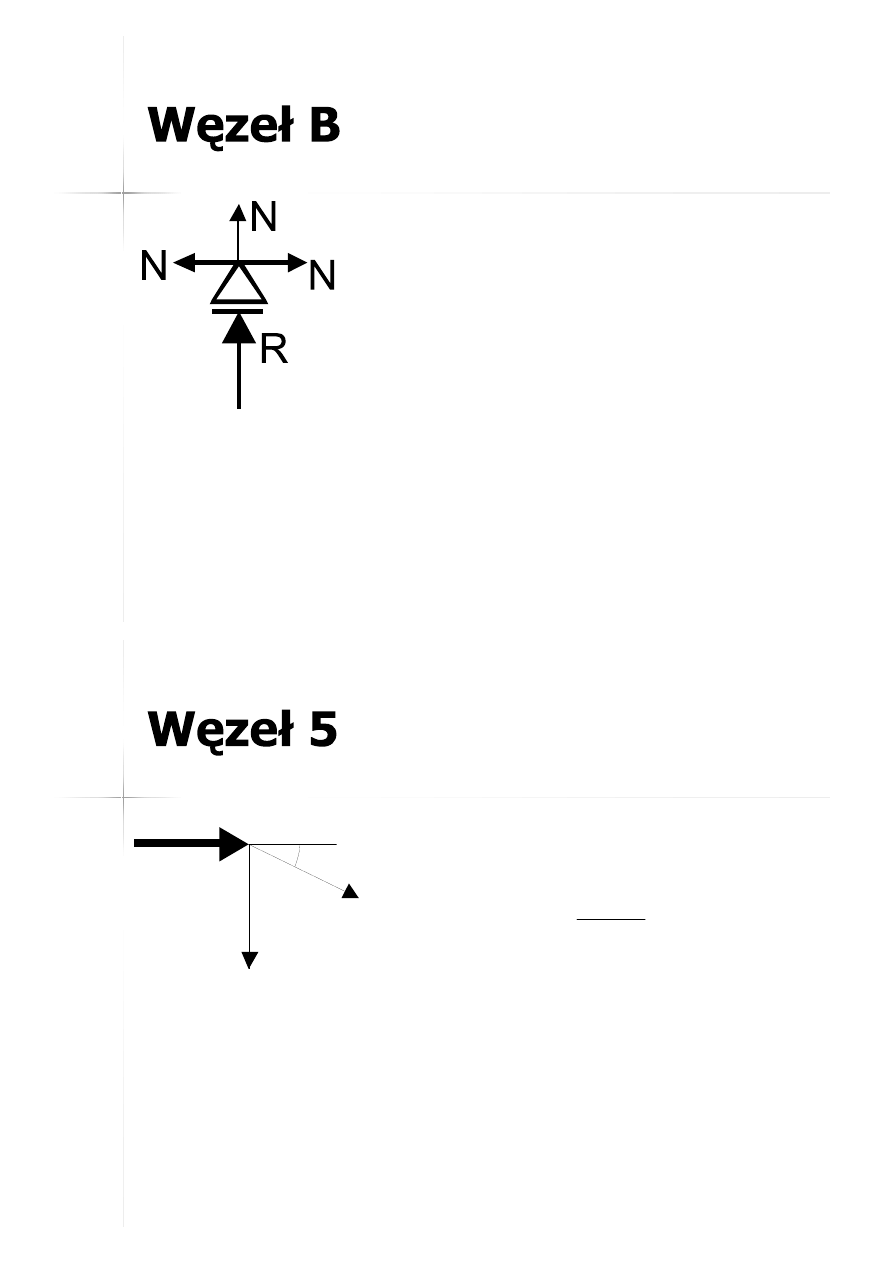
31

31

B

B

B-1

B-3

B-2

2

1

:

0

B

B

X N

N











3

:

0

B

B

Y R

N









1

0

B

N





3

15

B

N

kN



 

32

32

20kN

5

N

5-A

N

5-4



5 4

: 20

cos

0

X

kN

N













5

5 4

:

sin

0

A

Y N

N















5 4

20

22, 371

0,894

kN

N

kN







 

5

22, 371

0, 447

10

A

N

kN

kN









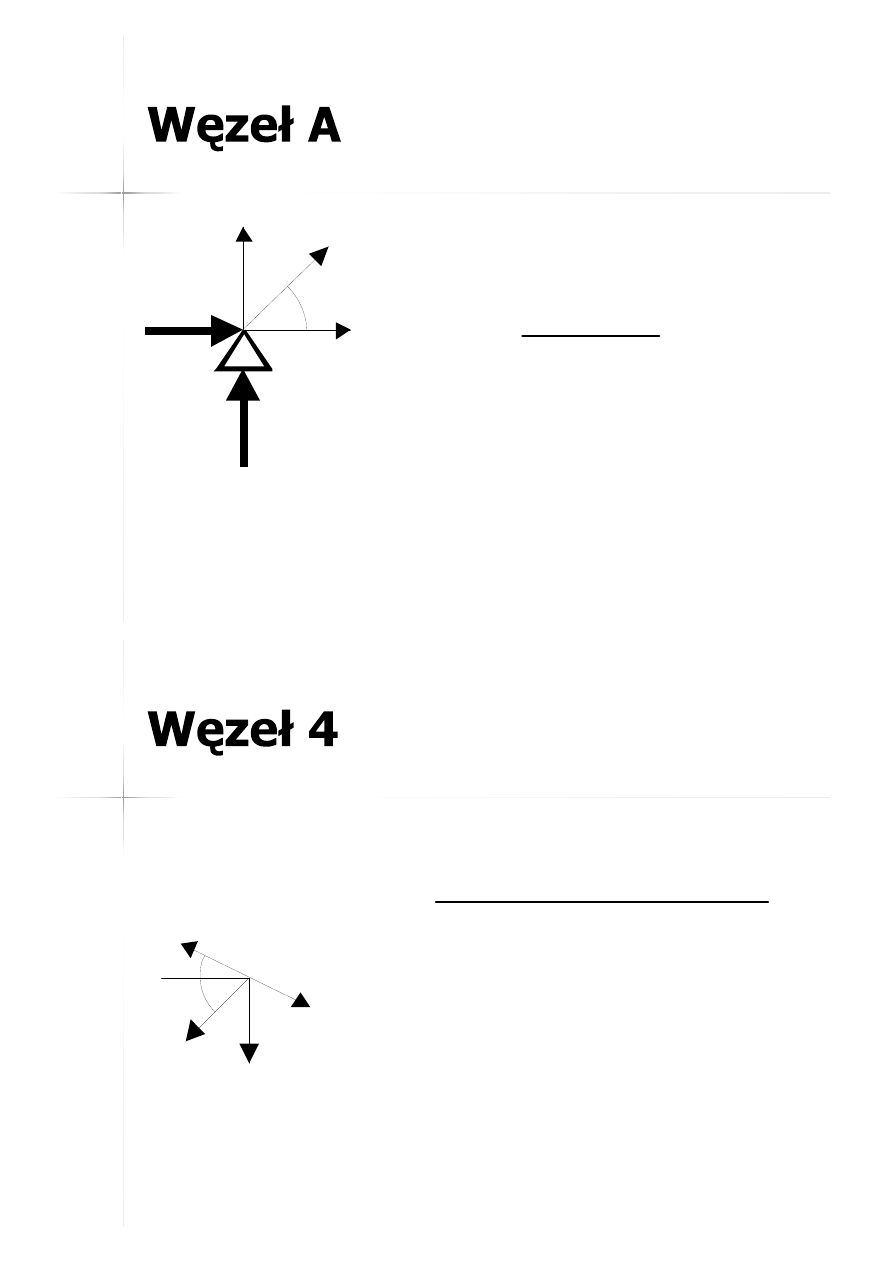
33

33

V

A

H

A



N

A-5

N

A-4

N

A-1

1

4

:

cos

0

A

A

A

X N

N

H

















5

4

:

sin

0

A

A

A

Y N

N

V

















1

20

7, 072

0, 707

15

A

N

kN

kN

kN











4

10

15

7, 072

0, 707

A

kN

kN

N

kN











34

34

4

N

4-5

N

4-3

N

4-1

N

4-A





4 3

4

4 5

:

cos

cos

cos

0

A

X N

N

N



























4 5

4

4 1

4 3

:

sin

sin

sin

0

A

Y N

N

N

N

































4 3

7, 072

0, 707 22, 371

0,894

0,894

16, 778

kN

kN

N

kN













 

4 1

22, 371

0, 447 7, 072

0, 707 16, 778

0, 447

7, 5

N

kN

kN

kN

kN



 











 

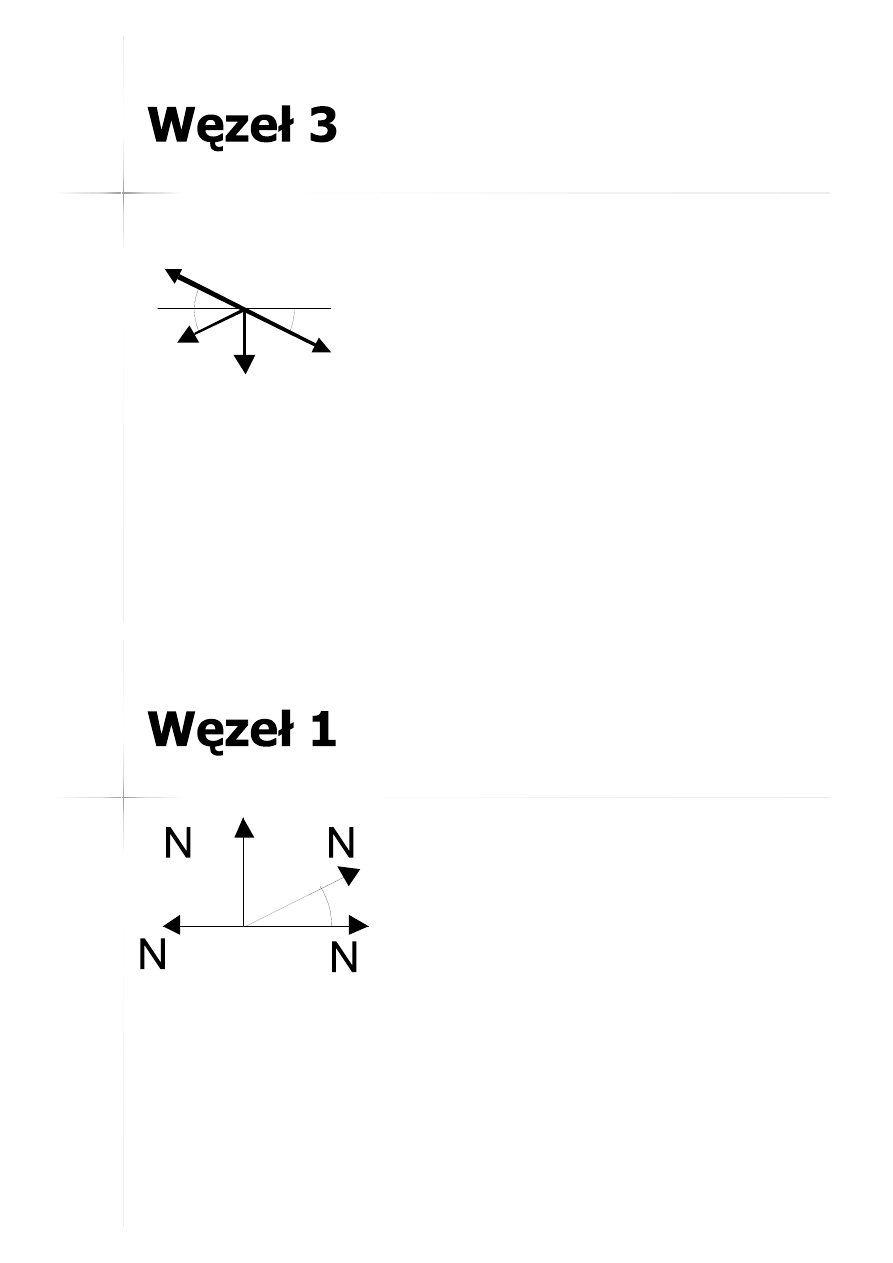
35

35

3

N

4-3







N

3-1

N

3-2

N

3-B

3 2

3 1

3 1

:

cos

cos

cos

0

X N

N

N



























4 3

3

3 1

3 2

:

sin

sin

sin

16, 778

0, 447 16, 778

0, 447 15

0

B

Y N

N

N

N

kN

kN

kN





























 













3 1

16, 778

N

kN





Sprawdzenie:

Sprawdzenie:

36

36



1

1-A

1-4

1-3

1-B

1 3

1

1

:

cos

16, 778

0,894 15

0

B

A

X N

N

N

kN

kN



























1 4

1 3

:

sin

7, 5

16, 778

0, 447

0

Y N

N

kN

kN











 









Sprawdzenie:

Sprawdzenie:

Sprawdzenie:

Sprawdzenie:

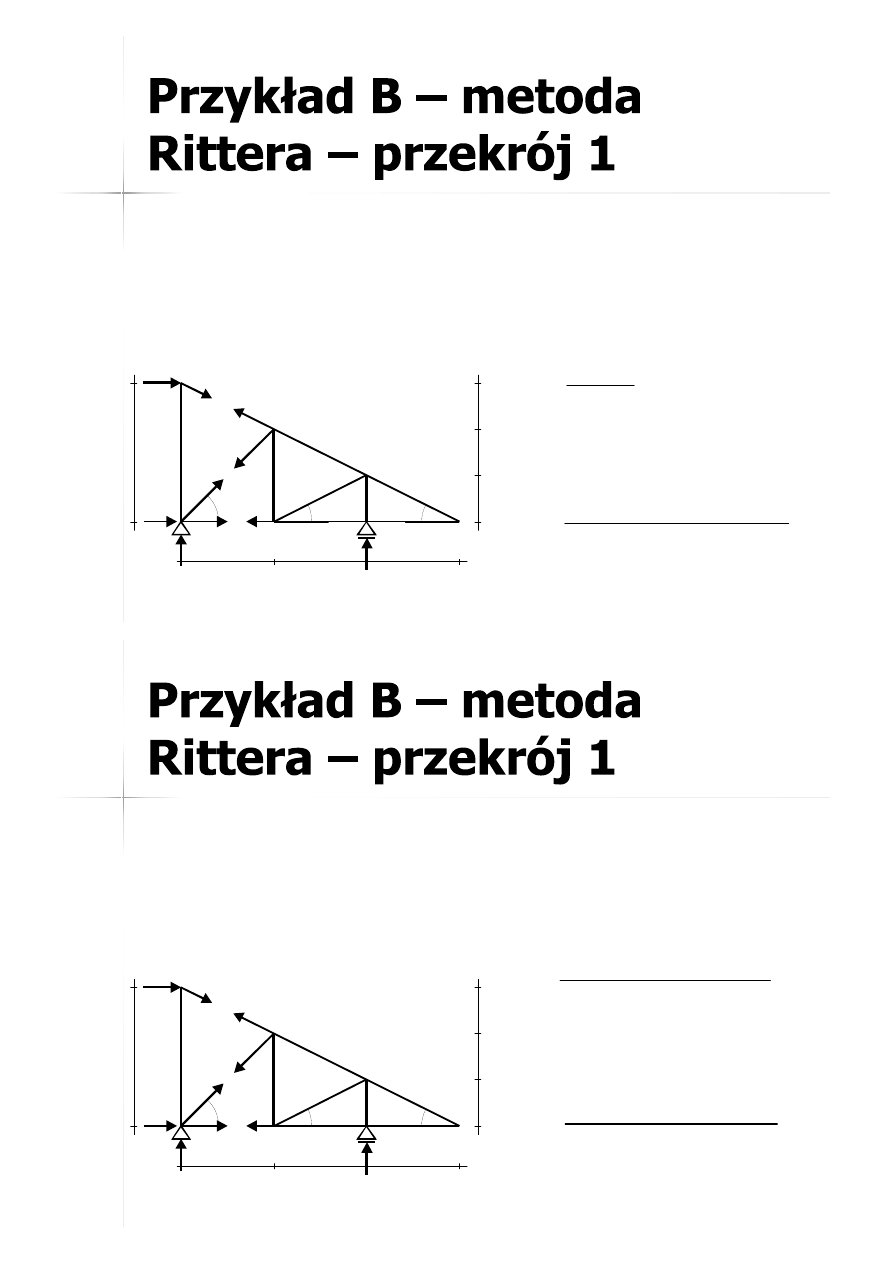
37

37

(z lewej)

(z lewej)

R

B

V

A

H

A

3m

4

,5

m

20kN

3m

3m







1

,5

m

1

,5

m

1

,5

m

A

B

1

2

3

4

5

N

5-4

N

4-5

N

A-4

N

4-A

N

A-1

N

1-A

5 4

:

cos

4, 5

20

4, 5

0

l

A

M

N

m

kN

m

















4

1

:

3

3

20

1, 5

3

0

l

A

A

A

M

V

m

H

m

kN

m

N

m





















2

4

:

9

20

4, 5

sin

9

0

l

A

A

M

V

m

kN

m

N

m





















5 4

20

22, 371

0,894

kN

N

kN







 

1

15

20

10

15

A

N

kN

kN

kN

kN



 









4

15

9

20

4, 5

0, 707 9

7, 072

A

kN

m

kN

m

N

m

kN

















38

38

(z prawej)

(z prawej)

R

B

V

A

H

A

3m

4

,5

m

20kN

3m

3m







1

,5

m

1

,5

m

1

,5

m

A

B

1

2

3

4

5

N

5-4

N

4-5

N

A-4

N

4-A

N

A-1

N

1-A

4 5

4 5

:

cos

3

sin

3

6

0

p

A

B

M

N

m

N

m

R

m



























4

1

:

3

3

0

p

B

A

M

R

m

N

m













2

4

4

:

3

sin

6

cos

3

0

p

B

A

A

M

R

m

N

m

N

m



























4 5

15

6

0,894 3

0, 447 3

22, 371

kN

m

N

m

m

kN















 

1

15

A

N

kN





4

15

3

0, 707 6

0, 707 3

7, 072

A

kN

m

N

m

m

kN

















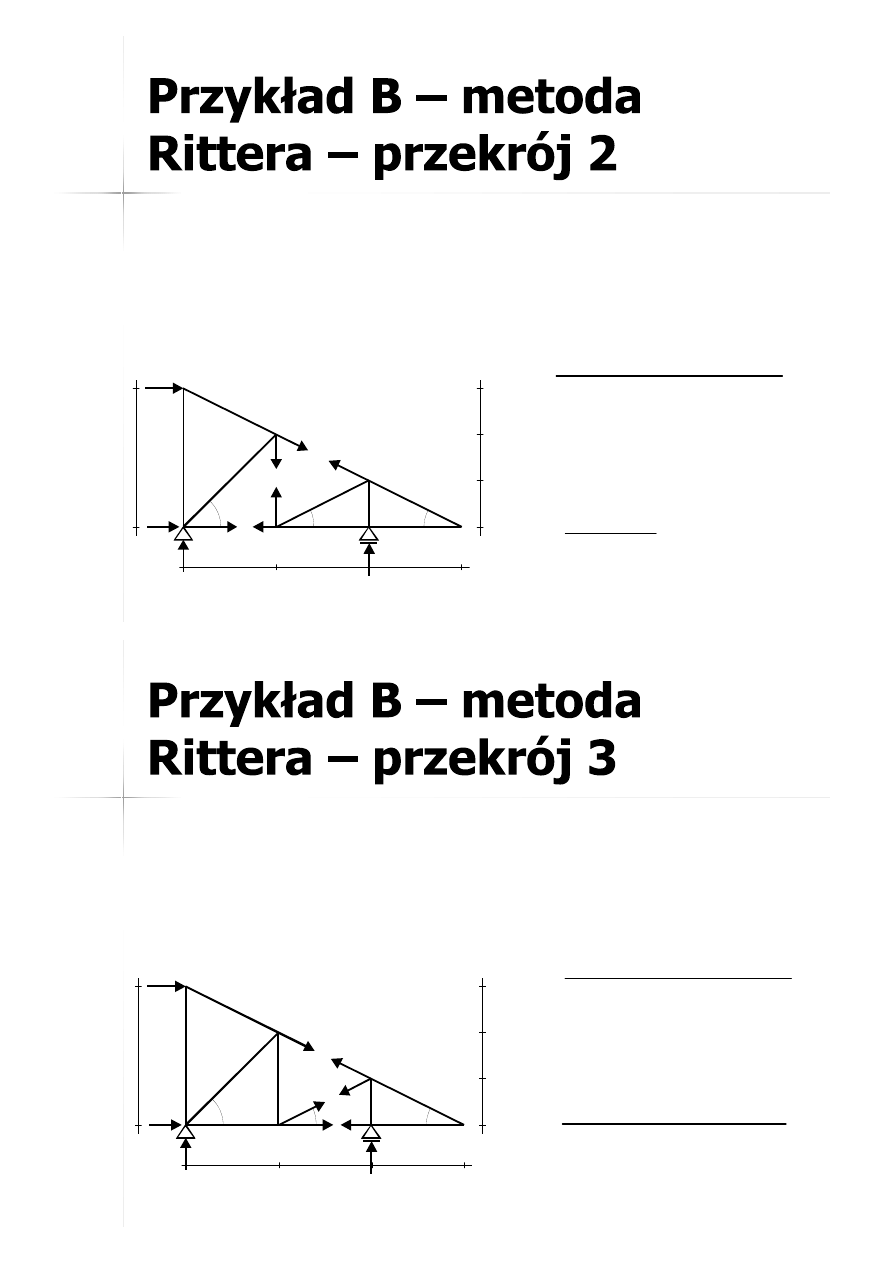
39

39

R

B

V

A

H

A

3m

4

,5

m

20kN

3m

3m







1

,5

m

1

,5

m

1

,5

m

A

B

1

2

3

4

5

N

4-3

N

4-3

N

4-1

N

1-4

N

A-1

N

1-A

1

4 3

4 3

:

cos

1, 5

sin

3

3

0

p

B

M

N

m

N

m

R

m



























4

1

:

3

3

0

p

B

A

M

R

m

N

m













2

1 4

:

3

6

0

p

B

M

R

m

N

m













4 3

15

3

0,894 1, 5

0, 447 3

16, 779

kN

m

N

m

m

kN















 

1

15

A

N

kN





1 4

15

3

7,5

6

kN

m

N

kN

m









40

40

R

B

V

A

H

A

3m

4

,5

m

20kN

3m

3m







1

,5

m

1

,5

m

1

,5

m

A

B

1

2

3

4

5

N

4-3

N

4-3

N

1-3

N

3-1

N

1-B

N

B-1

1

4 3

4 3

:

cos

1, 5

sin

3

3

0

p

B

M

N

m

N

m

R

m



























3

5 1

:

1, 5

0

p

M

N

m









2

1 3

:

9

20

4, 5

sin

6

0

l

A

M

V

m

kN

m

N

m





















4 3

15

3

0,894 1, 5

0, 447 3

16, 779

kN

m

N

m

m

kN















 

5 1

0

N





1 3

15

9

20

4, 5

0, 447 6

16, 779

kN

m

kN

m

N

m

kN

















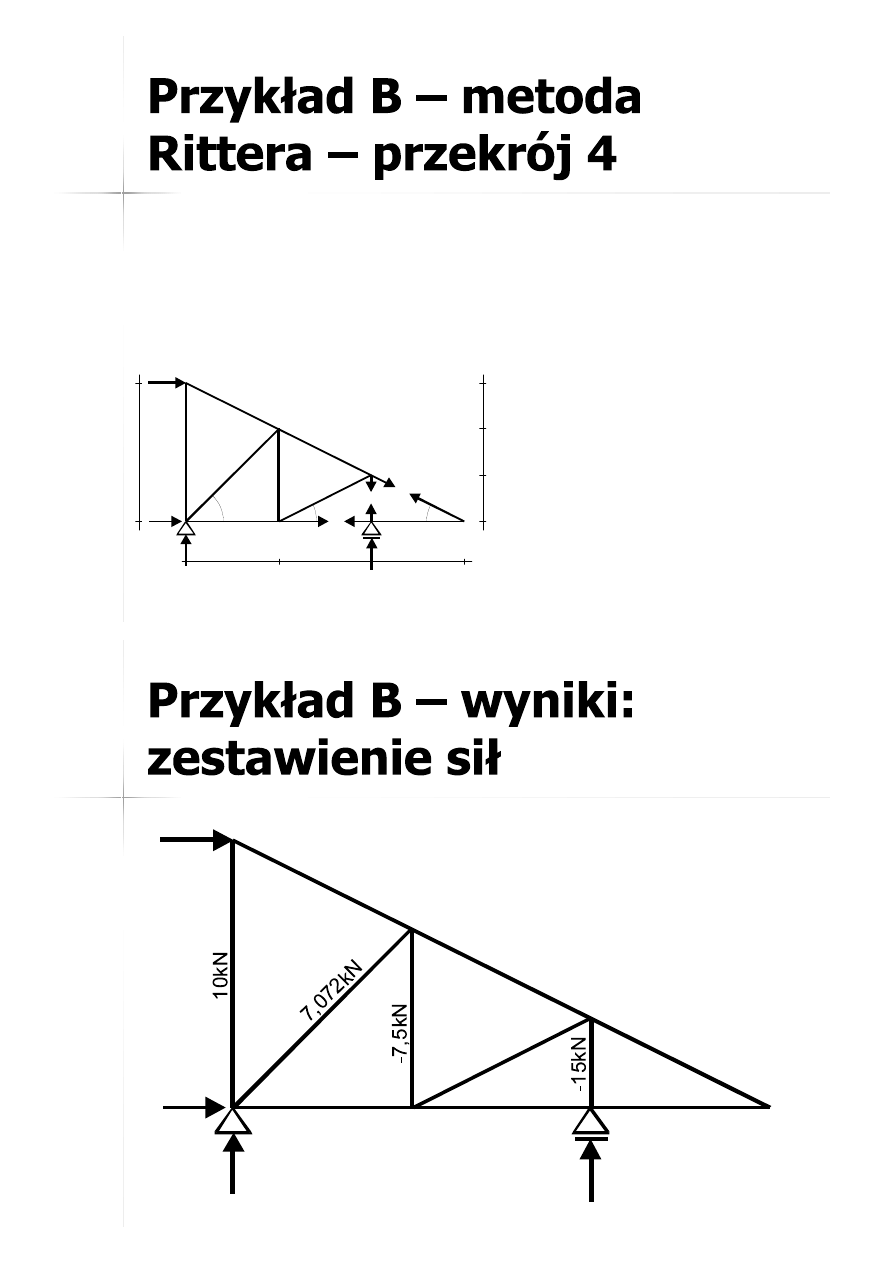
41

41

R

B

V

A

H

A

3m

4

,5

m

20kN

3m

3m







1

,5

m

1

,5

m

1

,5

m

A

B

1

2

3

4

5

N

3-2

N

2-3

N

3-B

N

B-3

N

B-1

N

1-B

3

1

:

1,5

0

p

B

M

N

m









2 3

:

sin

3

0

p

B

M

N

m













2

3

:

3

3

0

p

B

B

M

R

m

N

m













1

0

B

N





2 3

0

N





3

15

B

N

kN



 

42

42

20kN

-20kN

-15kN

-22

,371

kN

-16

,778

kN

0

15kN

0

16

,77

8k

N

15kN

0

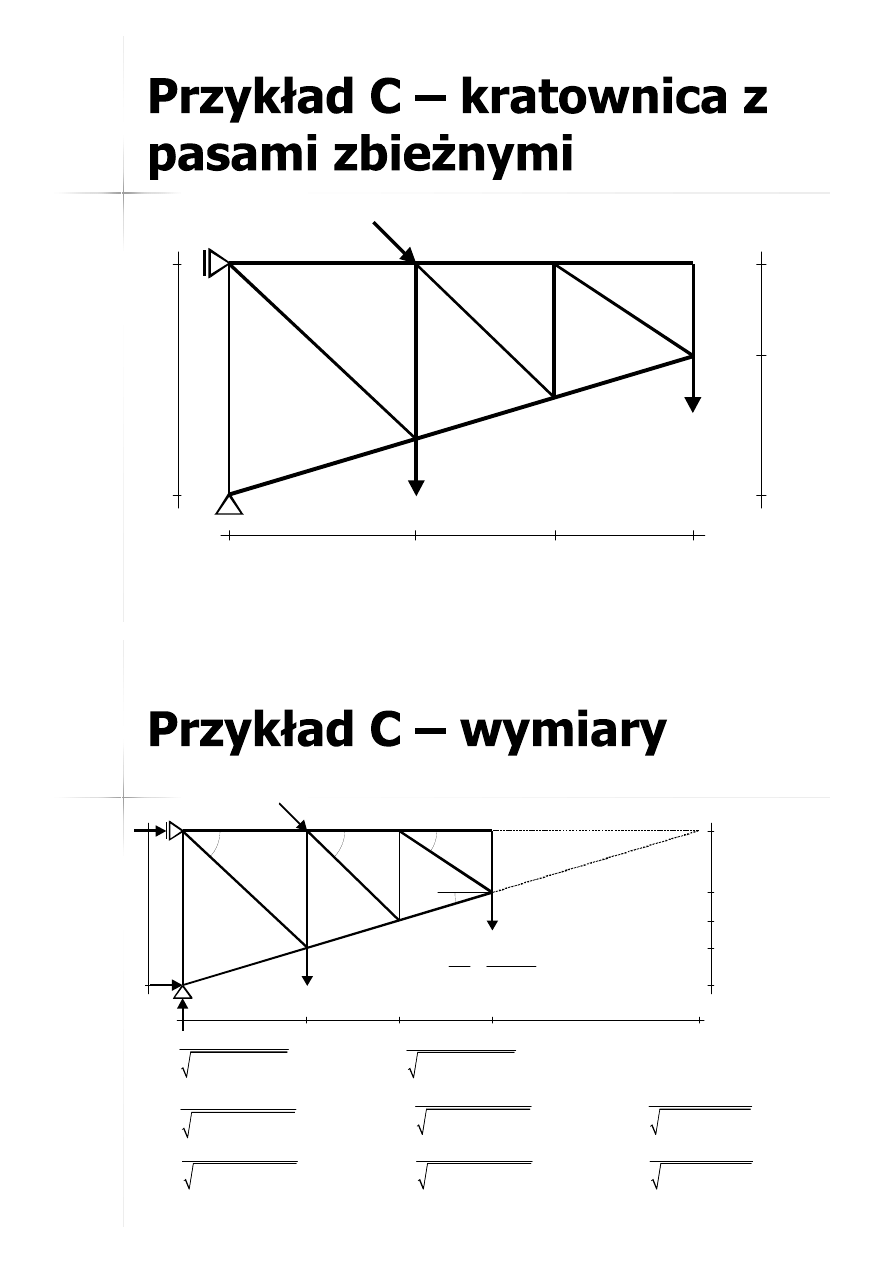
43

43

4m

5

m

10kN

3m

3m

20kN

15kN

2

m

3

m

44

44



  

2

2

3

sin

0, 287

10

3

m

m

m









10

2

5

x

m

x

m

m





6, 667

x

m





  

2

2

10

cos

0, 958

10

3

m

m

m











  

2

2

3,8

sin

0, 689

3,8

4

m

m

m











  

2

2

4

cos

0, 725

3,8

4

m

m

m











  

2

2

2, 9

sin

0, 695

2,9

3

m

m

m











  

2

2

3

cos

0, 719

2, 9

3

m

m

m









   

2

2

2

sin

0, 555

2

3

m

m

m









   

2

2

3

cos

0,832

2

3

m

m

m









4m

5

m

10kN

3m

3m

20kN

15kN

V

A

H

A

R

B

B

1

A

2

3

4

5

6

0

,9

m

2

m

0

,9

m

1,

2

m

x









C

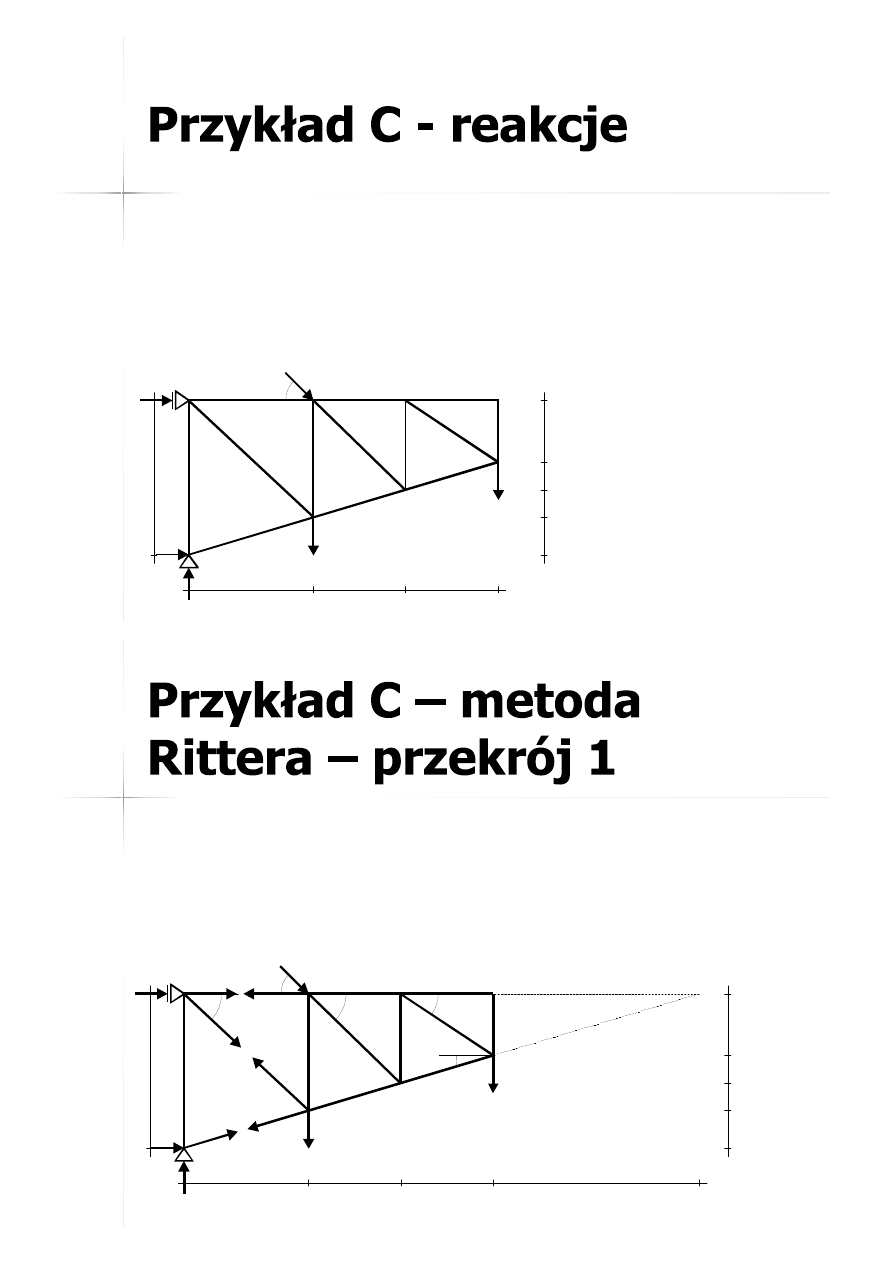
45

45

:

15

cos

0

A

B

X H

R

kN













:

20

10

15

sin

0

A

Y V

kN

kN

kN















:

5

20

4

10

10

15

sin

4

15

cos

5

0

A

B

M

R

m

kN

m

kN

m

kN

m

kN

m

































44, 340

A

H

kN



40, 425

A

V

kN



55,125

B

R

kN

 

4m

5

m

10kN

3m

3m

20kN

15kN

V

A

H

A

R

B

B

1

A

2

3

4

5

6

0

,9

m

2

m

0

,9

m

1,

2

m



46

46

1

4

:

3,8

15

cos

3,8

10

6

0

p

B

M

N

m

kN

m

kN

m





















1

:

cos

5

5

0

l

B

A

A

M

N

m

H

m

















1

:

16, 667

5

sin

16, 667

0

l

C

A

A

B

M

V

m

H

m

N

m





















4

26, 574

B

N

kN





4m

5

m

10kN

3m

3m

20kN

15kN

V

A

H

A

R

B

B

1

A

2

3

4

5

6

0

,9

m

2

m

0

,9

m

1,

2

m

N

4-3

N

B-4

N

4-B

N

B-1

N

1-B

N

1-A

N

A-1









C

6,667m



1

46, 284

A

N

kN



 

4

39, 366

B

N

kN





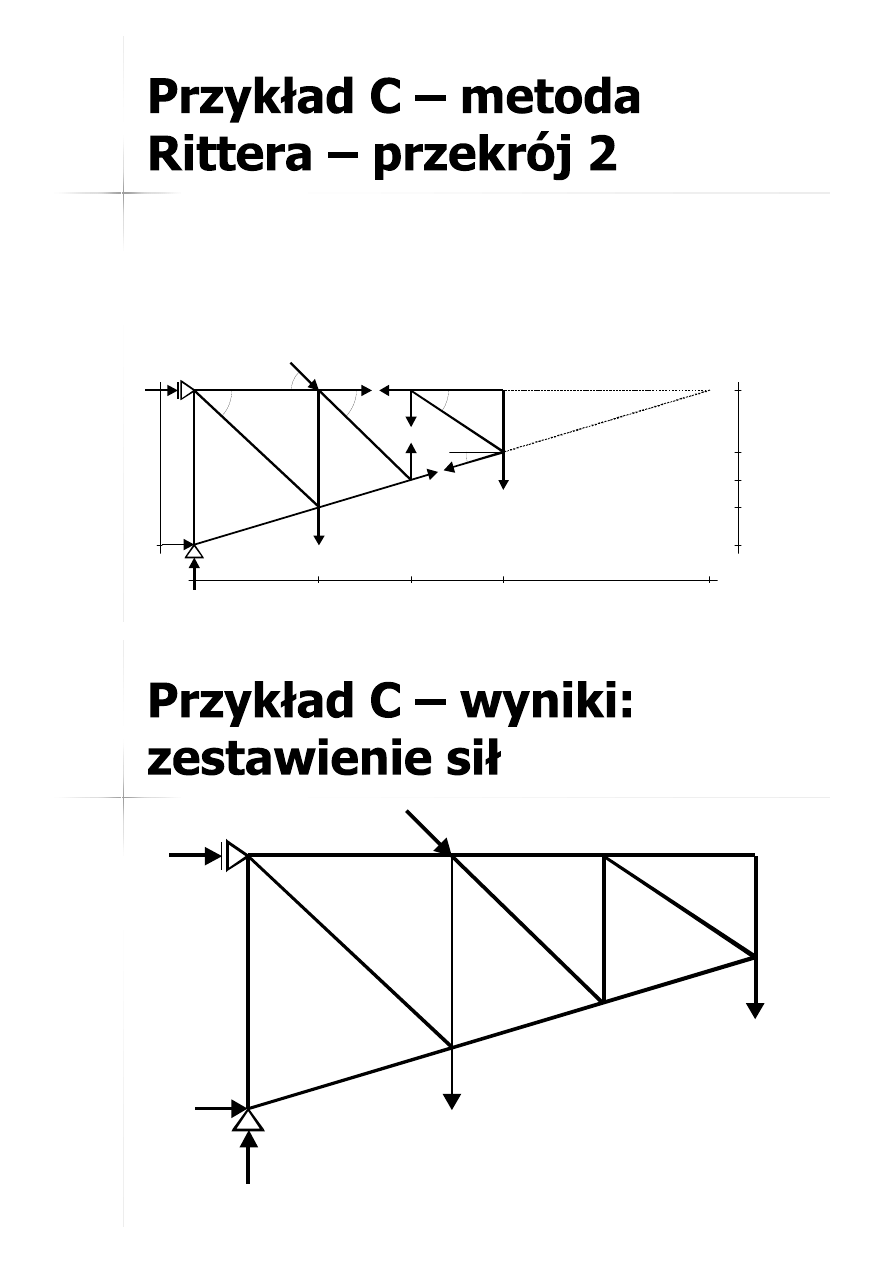
47

47

2

5 4

:

2, 9

10

3

0

p

M

N

m

kN

m













5

3 2

3 2

:

cos

2, 9

sin

3

10

3

0

p

M

N

m

N

m

kN

m



























5 2

:

9, 667

10

6, 667

0

p

C

M

N

m

kN

m













5 4

10, 345

N

kN





2 3

10,803

N

kN



 

5 2

6,897

N

kN



 

4m

5

m

10kN

3m

3m

20kN

15kN

V

A

H

A

R

B

B

1

A

2

3

4

5

6

N

2-3

N

3-2

N

5-2

N

2-5

N

5-4

N

4-5









C

6,667m



0

,9

m

2

m

0

,9

m

1,

2

m

48

48

10kN

20kN

15kN

40,425kN

44,340kN

-55,125kN

26,574kN

10,345kN

0

-46,2

84k

N

-16,

485

kN

-10

,80

3kN

-2

7

,1

2

3

kN

-1

5

,6

8

9

k

N

-6

,8

9

7

k

N

0

39

,3

66

kN

7,5

73

kN

12,4

33

kN

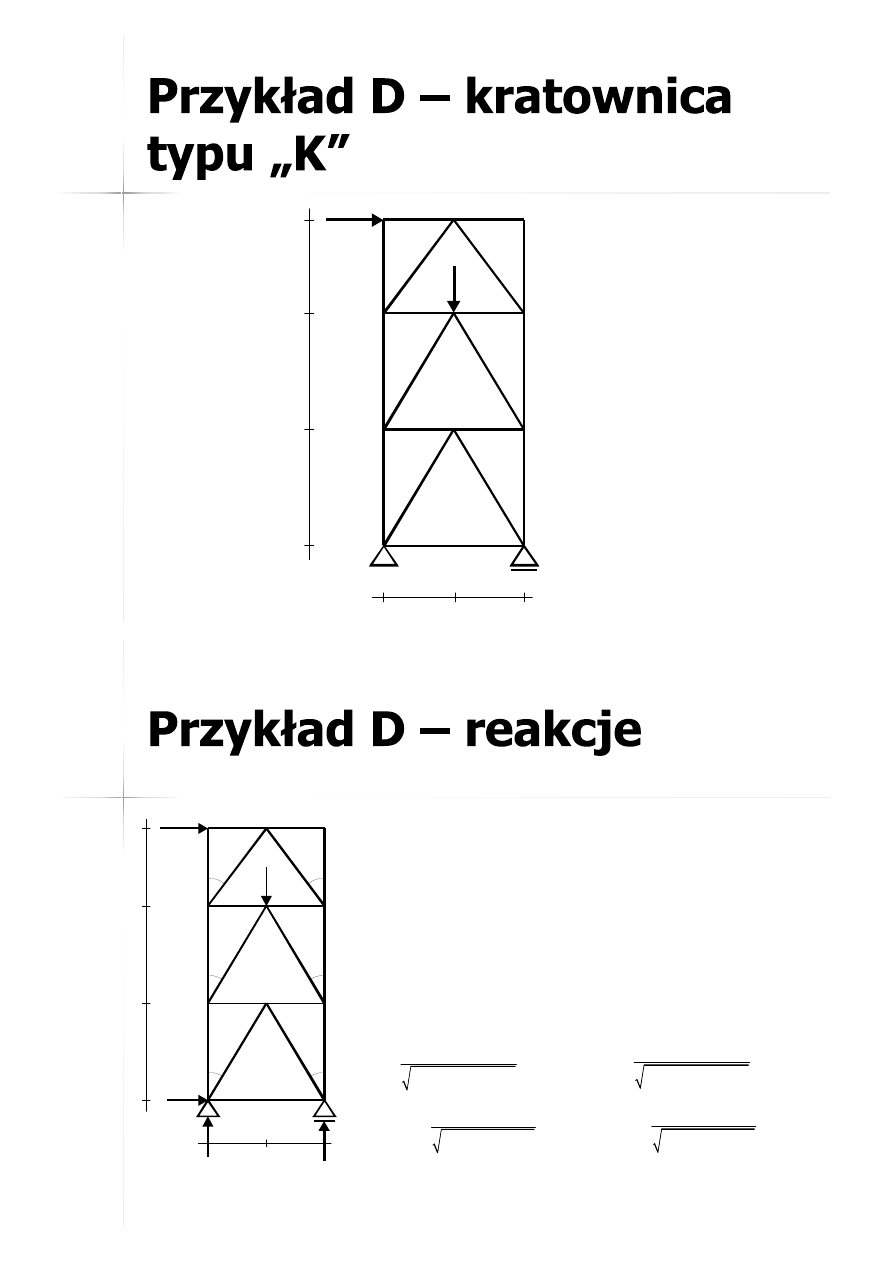
49

49

15kN

1,5m

10kN

2

,5

m

2

,5

m

2

m

1,5m

50

50

:

10

0

A

X H

kN







:

15

0

A

B

Y V

R

kN









:

3

15

1, 5

10

7

0

A

B

M

R

m

kN

m

kN

m















20

A

H

kN

 

15,833

A

V

kN

 

30,833

B

R

kN



15kN

10kN

2

,5

m

2

,5

m

2

m

V

A

H

A

R

B

A

B

1

3

5

4

6

7

9

8

2













1,5m

1,5m



 



2

2

1, 5

sin

0,514

1, 5

2, 5

m

m

m

 







 



2

2

2,5

cos

0,857

1, 5

2,5

m

m

m

 







  

2

2

1, 5

sin

0, 6

1,5

2

m

m

m

 







  

2

2

2

cos

0,8

1,5

2

m

m

m

 





51

51

15kN

10kN

2

,5

m

2

,5

m

2

m

V

A

H

A

R

B

A

B

1

3

5

4

6

7

9

8

2

N

1-A

N

A-1

N

1-2

N

2-1

N

2-3

N

3-2

N

B-3

N

3-B













1,5m

1,5m

1

3

:

3

15

1, 5

10

4, 5

0

g

B

M

N

m

kN

m

kN

m

















3

22, 500

B

N

kN



 

3

1

:

3

15

1, 5

10

4, 5

0

g

A

M

N

m

kN

m

kN

m

















3

7, 500

B

N

kN





52

52

15kN

10kN

2

,5

m

2

,5

m

2

m

H

A

R

B

A

B

1

3

5

4

6

7

9

8

2

N

2-A

N

2-B

N

A-2

N

B-2













N

1-A

N

3-B

N

A-1

N

B-3

V

A

H

A

A

N

A-2



N

A-1

1,5m

1,5m

2

2

:

sin

sin

10

0

g

A

B

X

N

N

kN





















2

2

10

sin

A

B

kN

N

N











53

53

2

N

2-1

N

2-3

N

2-A

N

2-B

V

A

H

A

A

N

A-2



N

A-1

N

A-1

2

2

:

cos

cos

0

A

B

Y N

N



















2

2

B

A

N

N





 

2

10

2

sin

A

kN

N







2

10

10

9, 728

2 sin

2 0, 514

A

kN

kN

N

kN













2

1

:

sin

0

A

A

A

X N

N

H

















1

10

9, 728

0, 514

5

A

N

kN

kN

kN











2

9, 728

B

N

kN



 

54

54

15kN

10kN

-15,833kN

-10kN

30,833kN

-10kN

0

0

0

6

,6

6

7

kN

-6

,6

6

7

k

N

-2

2

,5

k

N

7

,5

k

N

-0,5kN

9,5kN

26,574kN

-5kN

5kN

9

,7

2

8k

N

-9

,7

28

kN

0

,9

7

2

kN

-1

8

,4

65

kN

8,

33

3k

N

-8

,3

3

3

kN