MO
Z3/1. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
ZADANIE 1
1
Z3/1. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH
PŁASKICH - ZADANIE 1
Z3/1.1. Zadanie 1
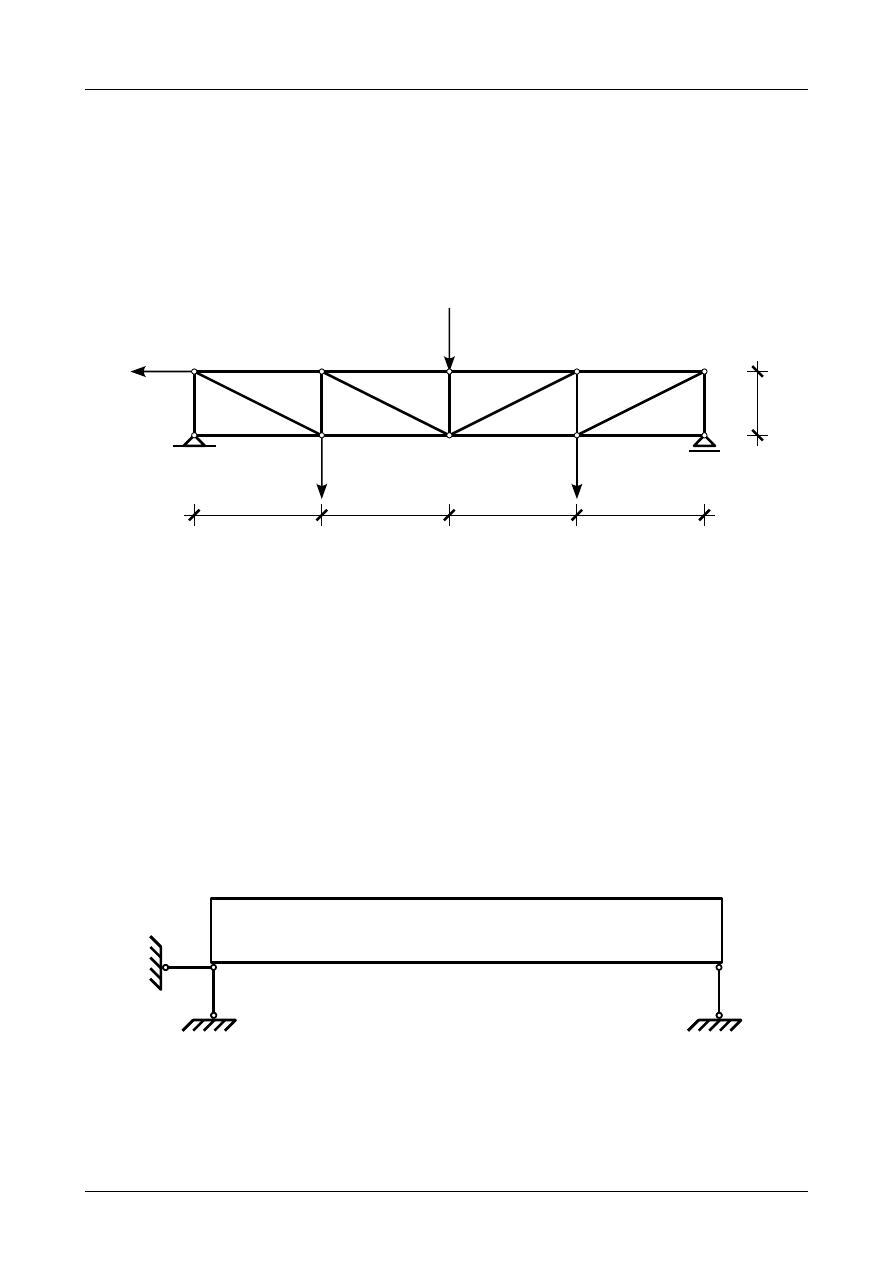
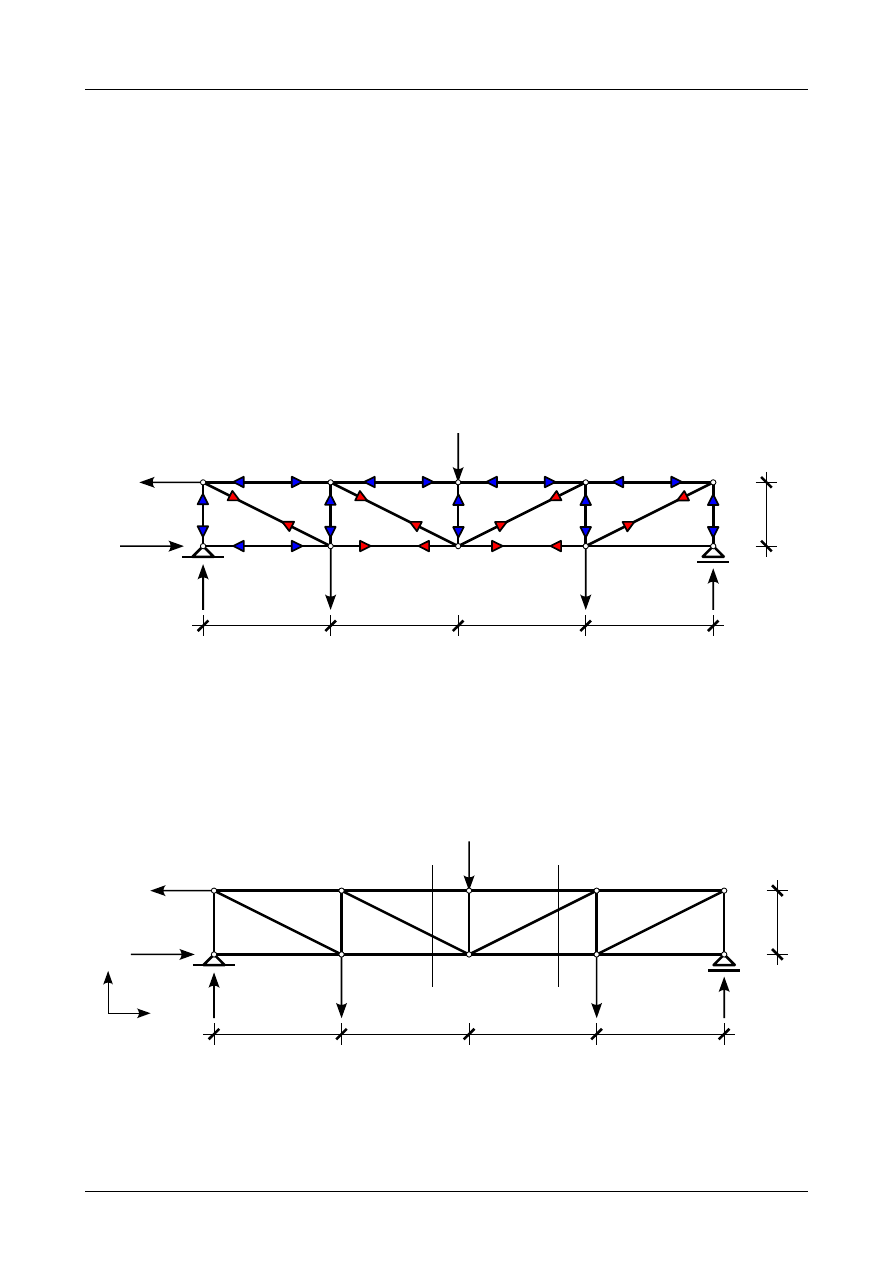
Wyznaczyć siły normalne w prętach kratownicy przedstawionej na rysunku Z3/1.1 metodą
zrównoważenia węzłów. Następnie siły normalne w prętach numer 3, 6 i 15 wyznaczyć metodą Rittera.
Wszystkie wymiary kratownicy płaskiej podane są w metrach.
29,0 kN
25,0 kN
30,0 kN
20,0 kN
6,0
6,0
6,0
6,0
3,
0
[m]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1
2
4
6
8
10
3
5
7
9
Rys. Z3/1.1. Kratownica płaska wraz z siłami czynnymi
Z3/1.2. Analiza kinematyczna kratownicy płaskiej
Kratownica płaska przedstawiona na rysunku Z3/1.1 składa się z 10 węzłów, 17 prętów kratownicy.
Podpory odbierają ponadto trzy stopnie swobody. Warunek konieczny geometrycznej niezmienności będzie
miał więc postać
2
⋅
10
=
17
3
.
(Z3/1.1)
Jak więc widać kratownica płaska na rysunku Z3/1.1 spełnia warunek konieczny geometrycznej
niezmienności. Może ona być układem geometrycznie niezmiennym i statycznie wyznaczalnym.
Kratownica na rysunku Z3/1.1 zbudowana jest z trójkątów, może więc stanowić tarczę sztywną.
Rysunek Z3/1.2 przedstawia tą tarczę sztywną wraz z prętami podporowymi.
I
1
2
3
Rys. Z3/1.2. Zastępcza tarcza sztywna
Tarcza sztywna numer I jest podparta trzema prętami podporowymi 1, 2 i 3. Posiada ona trzy stopnie
swobody, które odbierają jej trzy pręty podporowe. Został więc spełniony warunek konieczny geometrycznej
niezmienności.
Dr inż. Janusz Dębiński
Zaoczni
MO
Z3/1. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
ZADANIE 1
2
Kierunki prętów podporowych numer 1, 2 i 3 nie przecinają się w jednym punkcie. Został tym samym
spełniony warunek dostateczny geometrycznej niezmienności. Tarcza sztywna numer I jest więc
geometrycznie niezmienna i statycznie wyznaczalna. Także więc i kratownica płaska będzie układem
geometrycznie niezmiennym i statycznie wyznaczalnym.
Z3/1.3. Wyznaczenie reakcji podporowych
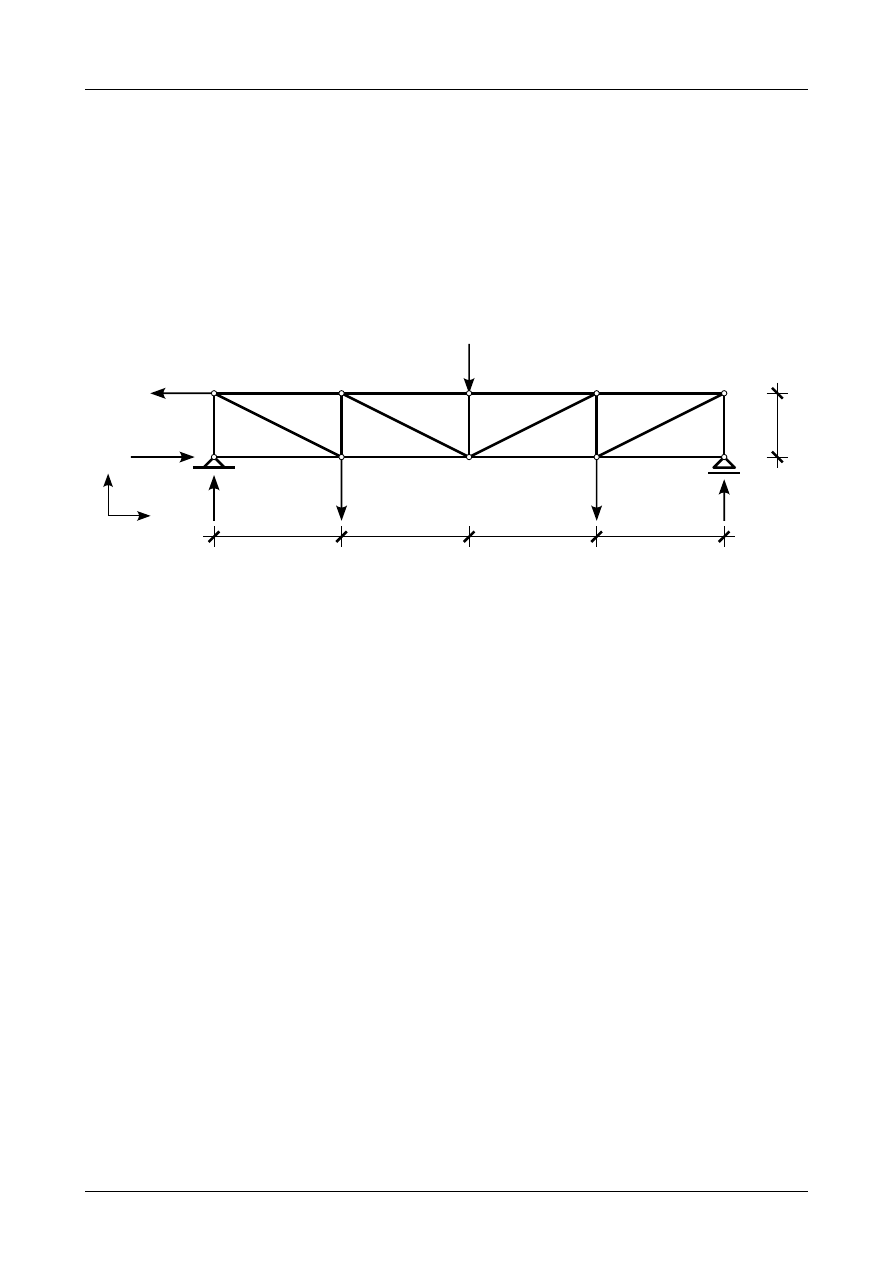
Rysunek Z3/1.3 przedstawia założone zwroty reakcji podporowych na podporze przegubowo-
nieprzesuwnej i przegubowo-przesuwnej.
29,0 kN
25,0 kN
30,0 kN
20,0 kN
6,0
6,0
6,0
6,0
3,
0
[m]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1
2
4
6
8
10
3
5
7
9
H
1
V
1
V
9
X
Y
Rys. Z3/1.3. Założone zwroty reakcji podporowych
Reakcję poziomą H
1
wyznaczymy z równania sumy rzutów wszystkich sił działających na kratownicę
płaską na oś poziomą X. Wynosi ona
X
=
H
1
−
20,0
=
0
H
1
=
20,0 kN
.
(Z3/1.2)
Reakcja ma więc zwrot zgodny z założonym.
Reakcję pionową V
1
wyznaczymy z równania sumy momentów wszystkich sił działających na
kratownicę płaską względem punktu 9. Wynosi ona
M
9
=V
1
⋅4⋅6,0−25,0⋅3⋅6,0−29,0⋅2⋅6,0−30,0⋅6,0−20,0⋅3,0=0
V
1
=43,25 kN
.
(Z3/1.3)
Reakcja ma więc zwrot zgodny z założonym.
Reakcję pionową V
9
wyznaczymy z równania sumy momentów wszystkich sił działających na
kratownicę płaską względem punktu 1. Wynosi ona
M
1
=−V
9
⋅4⋅6,025,0⋅6,029,0⋅2⋅6,030,0⋅3⋅6,0−20,0⋅3,0=0
V
9
=40,75 kN
.
(Z3/1.4)
Reakcja ma więc zwrot zgodny z założonym.
Dr inż. Janusz Dębiński
Zaoczni
MO
Z3/1. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
ZADANIE 1
3
W celu sprawdzenia obliczeń zastosujemy równanie sumy rzutów wszystkich sił działających na
kratownicę płaską na oś pionową Y. Wynosi ona
Y =V
1
V
9
−25,0−29,0−30,0=43,2540,75−25,0−29,0−30,0=0
.
(Z3/1.5)
Pionowe reakcje V
1
oraz V
9
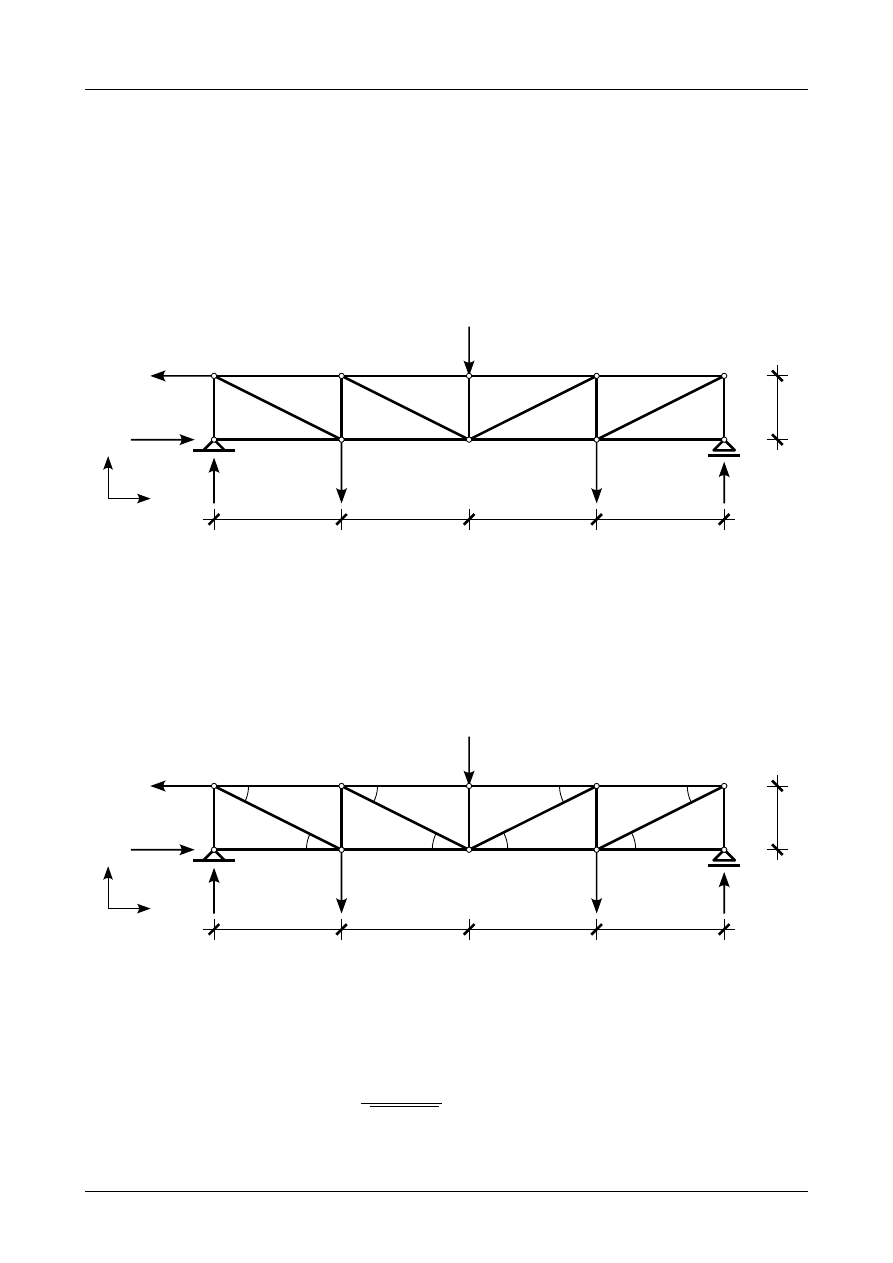
zostały więc wyznaczone poprawnie. Rysunek Z3/1.4 przedstawia prawidłowe
wartości i zwroty reakcji podporowych.
29,0 kN
25,0 kN
30,0 kN
20,0 kN
6,0
6,0
6,0
6,0
3,
0
[m]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1
2
4
6
8
10
3
5
7
9
X
Y
20,0 kN
43,25 kN
40,75 kN
Rys. Z3/1.4. Kratownica płaska w równowadze
Z3/1.4. Wyznaczenie sił normalnych w prętach kratownicy płaskiej metodą zrównoważenia
węzłów
Rysunek Z3/1.5 przedstawia kratownicę płaską z działającymi na nią siłami czynnymi i reakcjami
będącymi w równowadze.
29,0 kN
25,0 kN
30,0 kN
20,0 kN
6,0
6,0
6,0
6,0
3,
0
[m]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1
2
4
6
8
10
3
5
7
9
X
Y
20,0 kN
43,25 kN
40,75 kN
α
α
α
α
α
α
α
α
Rys. Z3/1.5. Kratownica płaska w równowadze
Wartości funkcji sinus i kosinus kąta nachylenia krzyżulców do poziomu, zgodnie z wymiarami
kratownicy płaskiej wynoszą
sin
=
3,0
3,0
2
6,0
2
=
0,4472
,
(Z3/1.6)
Dr inż. Janusz Dębiński
Zaoczni
MO
Z3/1. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
ZADANIE 1
4
cos
=
6,0
3,0
2
6,0
2
=0,8944
.
(Z3/1.7)
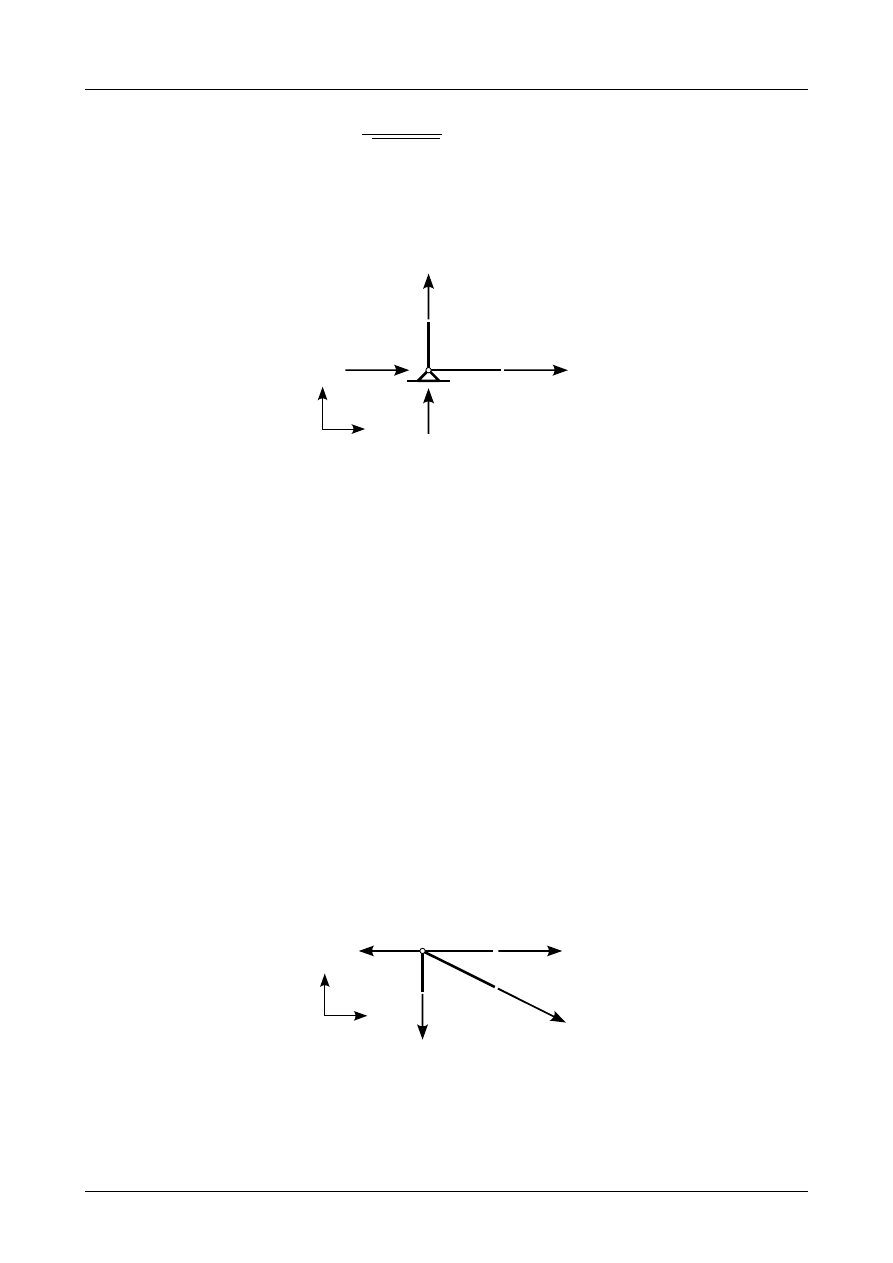
Wyznaczanie sił normalnych metodą zrównoważenia węzłów rozpoczniemy od węzła numer 1.
Rysunek Z3/1.6 przedstawia siły działające w tym węźle.
1
9
1
X
Y
20,0 kN
43,25 kN
N
1
N
9
Rys. Z3/1.6. Siły działające w węźle numer 1
Równania równowagi w tym węźle mają postać
X
=
N
1
20,0
=
0
,
(Z3/1.8)
Y =N
9
43,25=0
.
(Z3/1.9)
Z równań (Z3/1.8) i (Z3/1.9) możemy wyznaczyć siły normalne w prętach numer 1 i 9. Siły te mają
wartości
N
1
=−
20,0 kN
,
(Z3/1.10)
N
9
=−43,25 kN
.
(Z3/1.11)
Oba pręty są więc ściskane.
20,0 kN
5
9
14
2
X
Y
N
9
N
5
N
14
Rys. Z3/1.7. Siły działające w węźle numer 2
Rysunek Z3/1.7 przedstawia siły działające w węźle numer 2. Równania równowagi w tym węźle
mają postać
Dr inż. Janusz Dębiński
Zaoczni

MO
Z3/1. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
ZADANIE 1
5
X
=
N
5
N
14
⋅
cos
−
20,0
=
0
,
(Z3/1.12)
Y =−N
9
−N
14
⋅sin
=0
.
(Z3/1.13)
Z równań (Z3/1.12) i (Z3/1.13) możemy wyznaczyć siły normalne w prętach numer 14 i 5. Siły te
mają wartości
N
14
=
−
N
9
sin
=
−
−
43,25
0,4472
=
96,71 kN
,
(Z3/1.14)
N
5
=−N
14
⋅cos
20,0=−96,71⋅0,894420,0=−66,50 kN
.
(Z3/1.15)
Pręt numer 14 jest rozciągany natomiast pręt numer 5 ściskany.
25,0 kN
1
2
10
14
3
X
Y
N
1
N
2
N
10
N
14
α
Rys. Z3/1.8. Siły działające w węźle numer 3
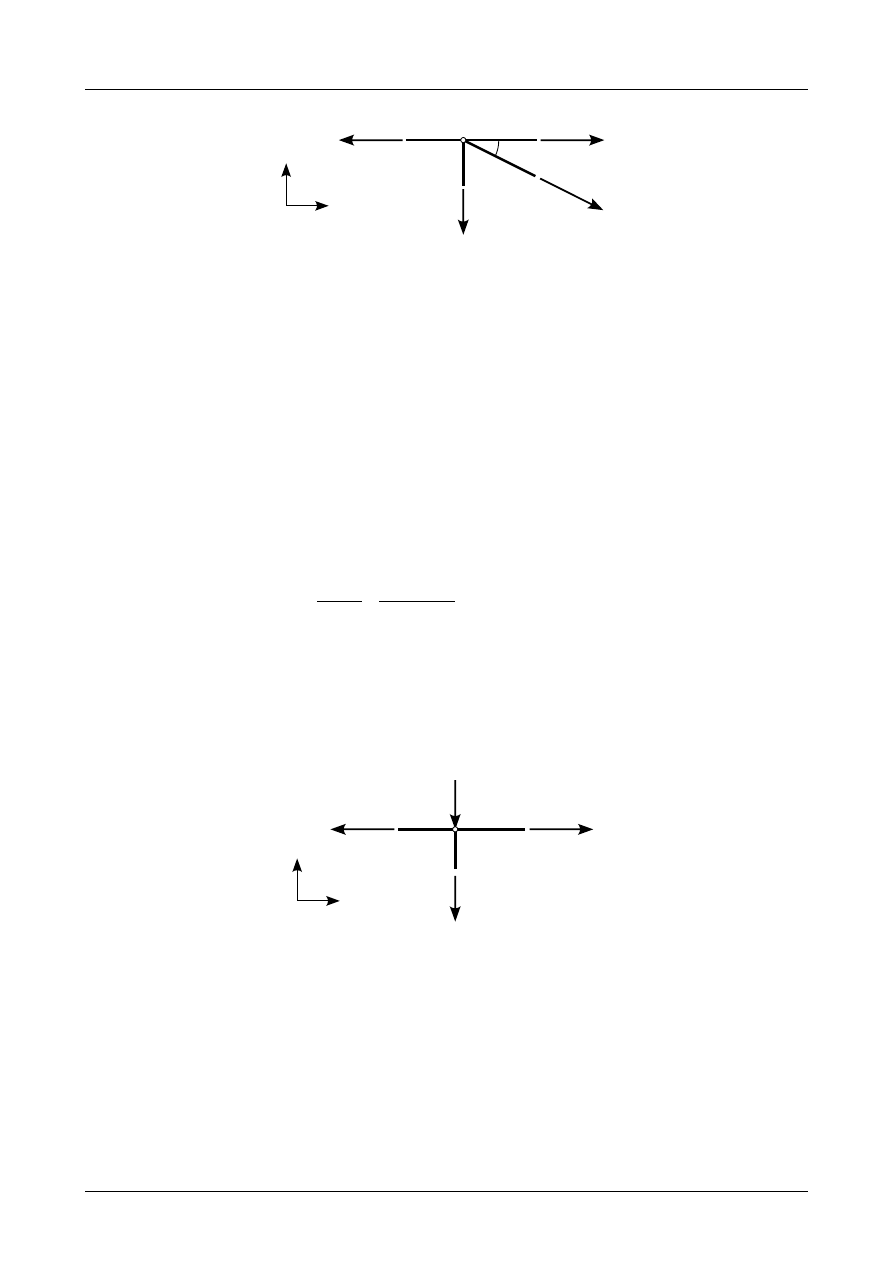
Rysunek Z3/1.8 przedstawia siły działające w węźle numer 3. Równania równowagi w tym węźle
mają postać
X =−N
1
−N
14
⋅cos
N
2
=0
,
(Z3/1.16)
Y =N
10
N
14
⋅sin
−25,0=0
.
(Z3/1.17)
Z równań (Z3/1.16) i (Z3/1.17) możemy wyznaczyć siły normalne w prętach numer 2 i 10. Siły te
mają wartości
N
2
=N
1
N
14
⋅cos
=−20,096,71⋅0,8944=66,50 kN
,
(Z3/1.18)
N
10
=25,0−N
14
⋅sin
=25,0−96,71⋅0,4472=−18,25 kN
.
(Z3/1.19)
Pręt numer 2 jest rozciągany natomiast pręt numer 10 ściskany.
Dr inż. Janusz Dębiński
Zaoczni
MO
Z3/1. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
ZADANIE 1
6
5
6
10
15
4
X
Y
N
5
N
6
N
10
N
15
α
Rys. Z3/1.9. Siły działające w węźle numer 4
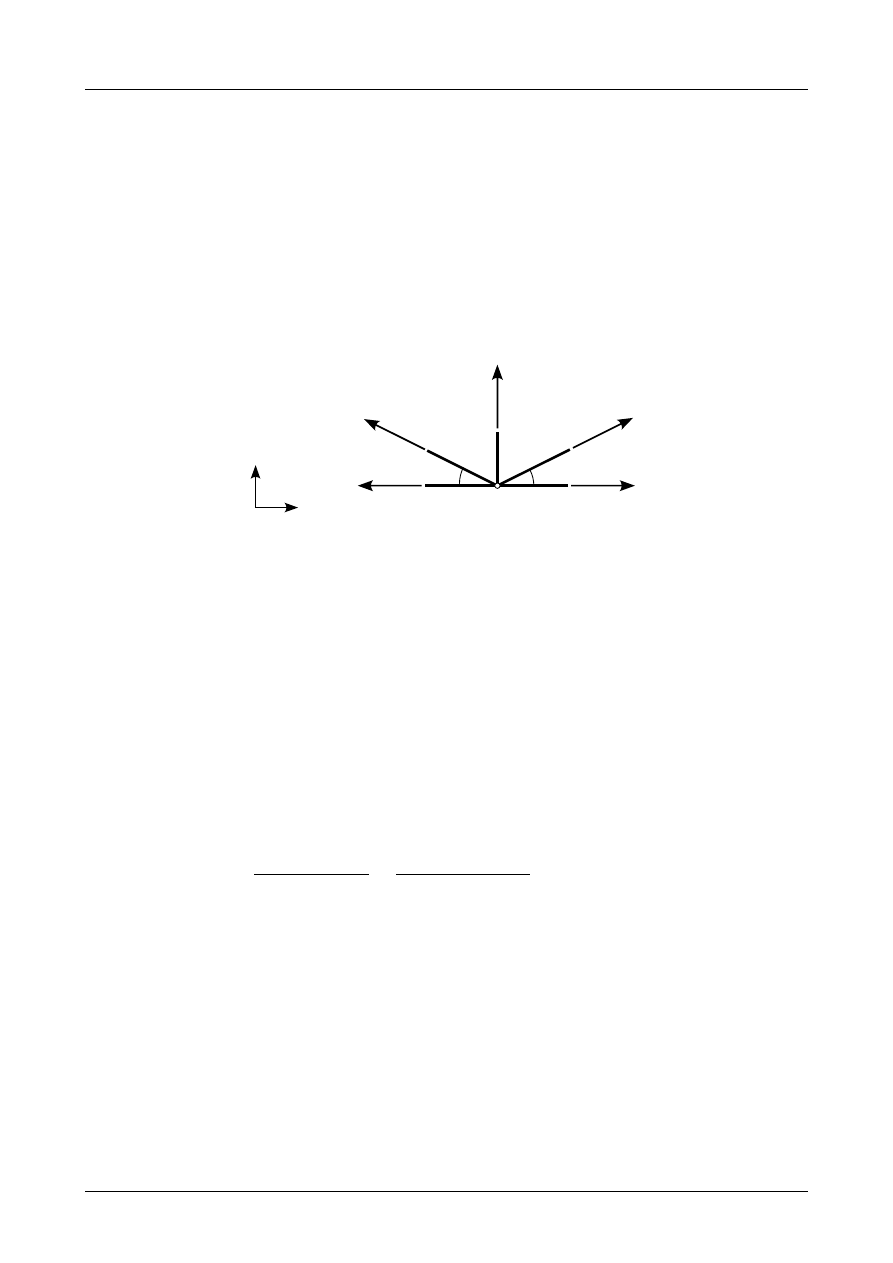
Rysunek Z3/1.9 przedstawia siły działające w węźle numer 4. Równania równowagi w tym węźle
mają postać
X =−N
5
N
15
⋅cos
N
6
=0
,
(Z3/1.20)
Y =−N
10
−N
15
⋅sin
=0
.
(Z3/1.21)
Z równań (Z3/1.20) i (Z3/1.21) możemy wyznaczyć siły normalne w prętach numer 6 i 15. Siły te
mają wartości
N
15
=
−
N
10
sin
=
−
−
18,25
0,4472
=
40,81 kN
,
(Z3/1.22)
N
6
=N
5
−N
15
⋅cos
=−66,50−40,81⋅0,8944=−103,0 kN
.
(Z3/1.23)
Pręt numer 15 jest rozciągany natomiast pręt numer 6 ściskany.
29,0 kN
6
7
11
6
X
Y
N
6
N
7
N
11
Rys. Z3/1.10. Siły działające w węźle numer 6
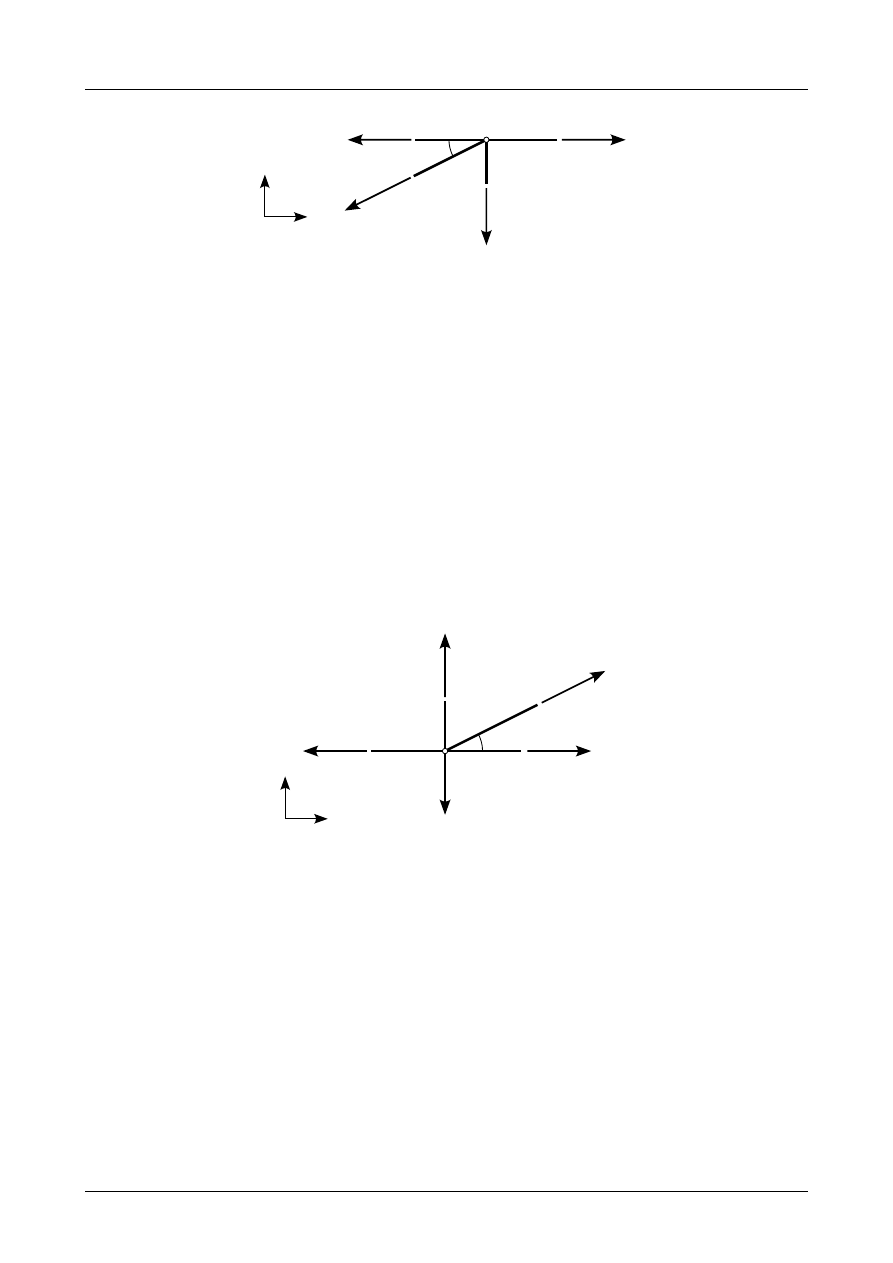
Rysunek Z3/1.10 przedstawia siły działające w węźle numer 6. Równania równowagi w tym węźle
mają postać
X =−N
6
N
7
=0
,
(Z3/1.24)
Y =−N
11
−29,0=0
.
(Z3/1.25)
Dr inż. Janusz Dębiński
Zaoczni
MO
Z3/1. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
ZADANIE 1
7
Z równań (Z3/1.24) i (Z3/1.25) możemy wyznaczyć siły normalne w prętach numer 7 i 11. Siły te
mają wartości
N
7
=
N
6
=−
103,0 kN
,
(Z3/1.26)
N
11
=−
29,0 kN
.
(Z3/1.27)
Oba pręty są ściskane.
2
3
11
15
16
5
X
Y
N
2
N
3
N
11
N
15
N
16
α
α
Rys. Z3/1.11. Siły działające w węźle numer 5
Rysunek Z3/1.11 przedstawia siły działające w węźle numer 5. Równania równowagi w tym węźle
mają postać
X =−N
2
−N
15
⋅cos
N
16
⋅cos
N
3
=0
,
(Z3/1.28)
Y =N
15
⋅sin
N
11
N
16
⋅sin
=0
.
(Z3/1.29)
Z równań (Z3/1.28) i (Z3/1.29) możemy wyznaczyć siły normalne w prętach numer 16 i 3. Siły te
mają wartości
N
16
=−
N
15
⋅sin
N
11
sin
=−
40,81
⋅0,4472−29,0
0,4472
=24,04 kN
,
(Z3/1.30)
N
3
=N
2
N
15
⋅cos
−N
16
⋅cos
=66,5040,81⋅0,8944−24,04⋅0,8944=81,50 kN
.
(Z3/1.31)
Oba pręty są rozciągane.
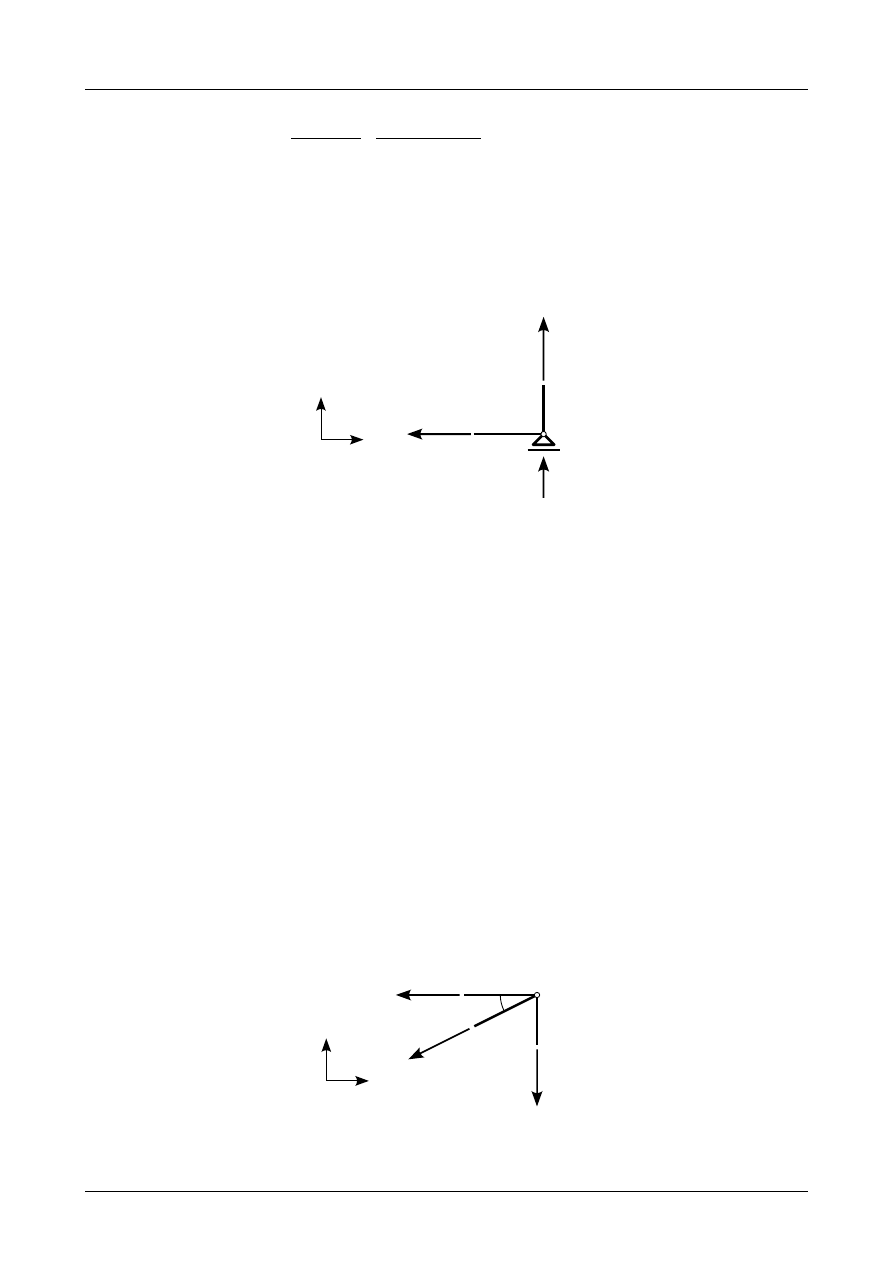
Rysunek Z3/1.12 przedstawia siły działające w węźle numer 8. Równania równowagi w tym węźle
mają postać
X =−N
7
−N
16
⋅cos
N
8
=0
,
(Z3/1.32)
Dr inż. Janusz Dębiński
Zaoczni
MO
Z3/1. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
ZADANIE 1
8
7
8
12
16
8
X
Y
N
7
N
8
N
12
N
16
α
Rys. Z3/1.12. Siły działające w węźle numer 8
Y =−N
16
⋅sin
−N
12
=0
.
(Z3/1.33)
Z równań (Z3/1.32) i (Z3/1.33) możemy wyznaczyć siły normalne w prętach numer 8 i 12. Siły te
mają wartości
N
8
=N
7
N
16
⋅cos
=−103,024,04⋅0,8944=−81,50 kN
,
(Z3/1.34)
N
12
=−
N
16
⋅
sin
=−
24,04
⋅
0,4472
=−
10,75 kN
.
(Z3/1.35)
Oba pręty są ściskane.
30,0 kN
3
4
12
17
7
X
Y
N
3
N
4
N
12
N
17
α
Rys. Z3/1.13. Siły działające w węźle numer 7
Rysunek Z3/1.13 przedstawia siły działające w węźle numer 7. Równania równowagi w tym węźle
mają postać
X =−N
3
N
17
⋅cos
N
4
=0
,
(Z3/1.36)
Y =N
12
N
17
⋅sin
−30,0=0
.
(Z3/1.37)
Z równań (Z3/1.36) i (Z3/1.37) możemy wyznaczyć siły normalne w prętach numer 17 i 4. Siły te
mają wartości
Dr inż. Janusz Dębiński
Zaoczni
MO
Z3/1. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
ZADANIE 1
9
N
17
=
30,0
− N
12
sin
=
30,0
−
−10,75
0,4472
=91,12 kN
,
(Z3/1.38)
N
4
=N
3
−N
17
⋅cos
=81,50−91,12⋅0,8944=0,00227≈0
.
(Z3/1.39)
Pręt numer 17 jest rozciągany natomiast pręt numer 4 jest prętem zerowym.
4
13
9
40,75 kN
X
Y
N
4
N
13
Rys. Z3/1.14. Siły działające w węźle numer 9
Rysunek Z3/1.14 przedstawia siły działające w węźle numer 9. Równania równowagi w tym węźle
mają postać
X =−N
4
=0
,
(Z3/1.40)
Y =N
13
40,75=0
.
(Z3/1.41)
Równanie (Z3/1.40) posłuży nam do sprawdzenia obliczenia siły normalnej w pręcie numer 4. Jak
widać jest to pręt zerowy (Z3/1.39). Z równania (Z3/1.41) możemy wyznaczyć wartośc siły normalnej w
pręcie numer 13. Wynosi ona
N
13
=−40,75 kN
.
(Z3/1.42)
Pręt ten jest więc ściskany.
8
13
17
10
X
Y
N
8
N
13
N
17
α
Rys. Z3/1.15. Siły działające w węźle numer 10
Dr inż. Janusz Dębiński
Zaoczni
MO
Z3/1. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
ZADANIE 1
10
Rysunek Z3/1.15 przedstawia siły działające w węźle numer 10. Równania równowagi w tym węźle
posłużą nam do sprawdzenia obliczeń. Mają postać
X =−N
8
−N
17
⋅cos
=−
−81,50
−91,12⋅0,8944=0,00227≈0
,
(Z3/1.43)
Y =−N
13
−N
17
⋅sin
=−
−40,75
−91,12⋅0,4472=0,00114≈0
.
(Z3/1.44)
Oba równania równowagi zostały spełnione. Obliczenia sił normalnych w prętach kratownicy płaskiej
przeprowadziliśmy poprawnie.
Rysunek Z3/1.16 przedstawia kratownicę płaską wraz z siłami czynnymi i reakcjami działającymi na
nią oraz siłami normalnymi w prętach.
29,0 kN
25,0 kN
30,0 kN
20,0 kN
6,0
6,0
6,0
6,0
3,
0
[m]
20,0
66,50
81,50
0
66,50
103,0
103,0
81,50
43
,2
5
96,7
1
40,81
24,
04
91,1
2
20,0 kN
43,25 kN
40,75 kN
18
,2
5
29
,0
10
,7
5
40
,7
5
Rys. Z3/1.16. Kratownica płaska z siłami czynnymi, reakcjami oraz siłami normalnymi w prętach
Z3/1.5. Wyznaczenie sił normalnych metodą Rittera
Aby wyznaczyć siły normalne w prętach numer 6 i 15 należy wykonać przekrój A-A przedstawiony na
rysunku Z3/1.17. Natomiast aby wyznaczyć siłę normalną w pręcie numer 3 należy wykonać przekrój B-B
tak przedstawiony na rysunku Z3/1.17.
29,0 kN
25,0 kN
30,0 kN
20,0 kN
6,0
6,0
6,0
6,0
3,
0
[m]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1
2
4
6
8
10
3
5
7
9
X
Y
20,0 kN
43,25 kN
40,75 kN
A
A
B
B
Rys. Z3/1.17. Przekroje A-A i B-B
Aby wyznaczyć siły normalne w prętach numer 6 i 15 będziemy rozpatrywali równowagę lewej części
kratownicy płaskiej. Siły działające na tę część kratownicy płaskiej przedstawia rysunek Z3/1.18.
Dr inż. Janusz Dębiński
Zaoczni
MO
Z3/1. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
ZADANIE 1
11
25,0 kN
20,0 kN
6,0
6,0
3,
0
[m]
1
2
5
6
9
10
14
15
1
2
4
3
5
X
Y
20,0 kN
43,25 kN
N
2
N
6
N
15
α
Rys. Z3/1.18. Siły działające na lewą część kratownicy płaskiej w przekroju A-A
Punktem Rittera dla pręta numer 6 jest węzeł numer 5. Siłę normalną w tym pręcie wyznaczymy z
równania sumy momentów wszystkich sił działających na lewą część kratownicy płaskiej względem tego
punktu. Równanie to ma postać
M
5
=
N
6
⋅
3,0
−
25,0
⋅
6,0
43,25
⋅
2
⋅
6,0
−
20,0
⋅
3,0
=
0
.
(Z3/1.45)
Siła normalna w pręcie numer 6 wynosi więc
N
6
=−
103,0 kN
(Z3/1.46)
i równa się wartości wyznaczonej ze wzoru (Z3/1.23).
Pręty numer 2 i 6 są do siebie równoległe więc siłę normalną w pręcie numer 15 wyznaczymy z
równania sumy rzutów wszystkich sił działających na lewą część kratownicy płaskiej na oś pionową Y.
Równanie to ma postać
Y
=−
N
15
⋅
sin
−
25,0
43,25
=
0
.
(Z3/1.47)
Siła normalna w pręcie numer 15 wynosi więc
N
15
=40,81 kN
(Z3/1.48)
i równa się wartości wyznaczonej ze wzoru (Z3/1.22).
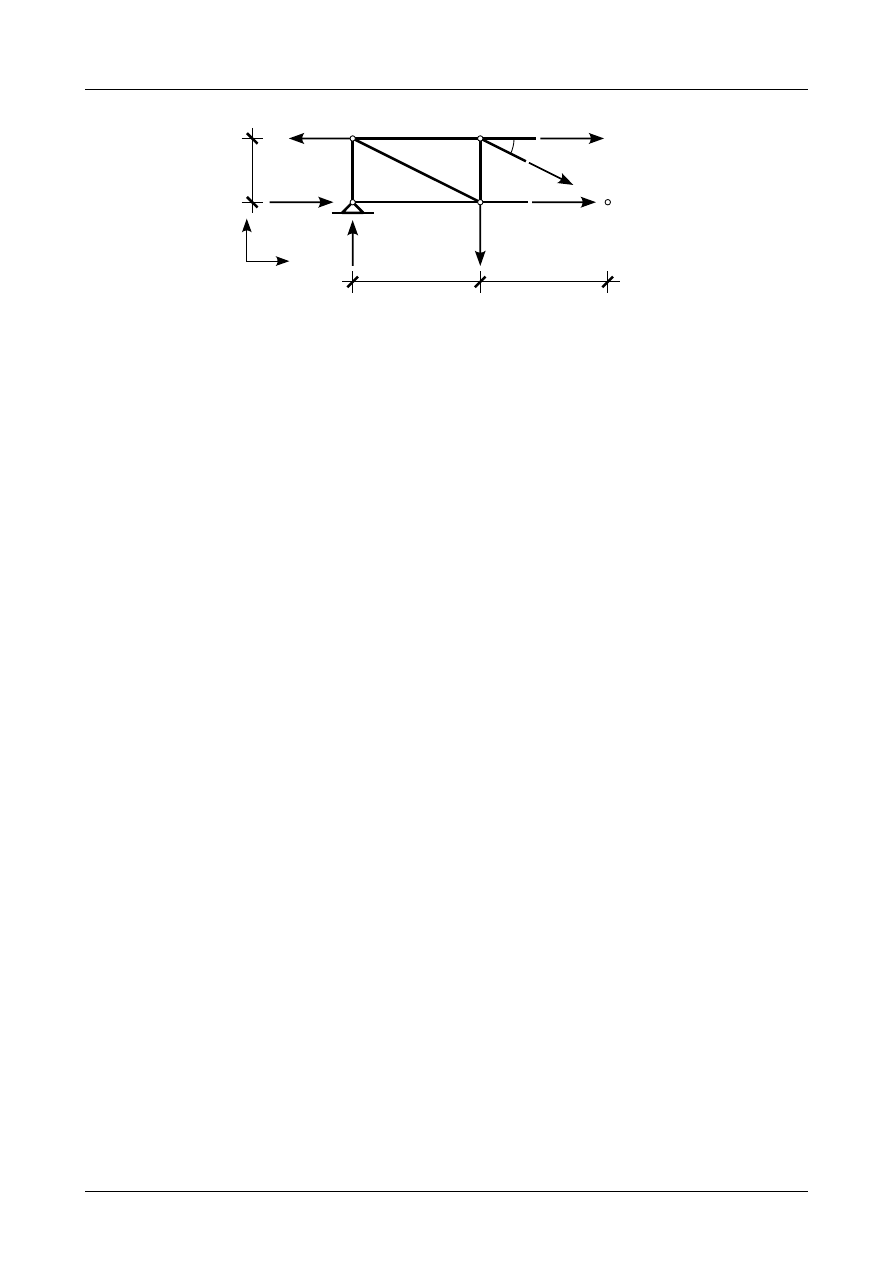
Aby wyznaczyć siłę normalną w pręcie numer 3 będziemy rozpatrywali równowagę prawej części
kratownicy płaskiej. Siły działające na tę część kratownicy płaskiej przedstawia rysunek Z3/1.19.
Punktem Rittera dla pręta numer 3 jest węzeł numer 8. Siłę normalną w tym pręcie wyznaczymy z
równania sumy momentów wszystkich sił działających na prawą część kratownicy płaskiej względem tego
punktu. Równanie to ma postać
M
8
=N
3
⋅3,0−40,75⋅6,0=0
.
(Z3/1.49)
Siła normalna w pręcie numer 3 wynosi więc
Dr inż. Janusz Dębiński
Zaoczni

MO
Z3/1. WYZNACZANIE SIŁ NORMALNYCH W KRATOWNICACH PŁASKICH
ZADANIE 1
12
30,0 kN
6,0
3,
0
[m]
3
4
7
8
12
13
16
17
8
10
7
9
40,75 kN
N
7
N
3
N
16
Rys. Z3/1.19. Siły działające na prawą część kratownicy płaskiej w przekroju B-B
N
3
=81,50 kN
(Z3/1.50)
i równa się wartości wyznaczonej ze wzoru (Z3/1.31).
Dr inż. Janusz Dębiński
Zaoczni
Document Outline
- Z3/1.1. Zadanie 1
- Z3/1.2. Analiza kinematyczna kratownicy płaskiej
- Z3/1.3. Wyznaczenie reakcji podporowych
- Z3/1.4. Wyznaczenie sił normalnych w prętach kratownicy płaskiej metodą zrównoważenia węzłów
- Z3/1.5. Wyznaczenie sił normalnych metodą Rittera
Wyszukiwarka
Podobne podstrony:
03 02 kratownice zadanie 02id 4 Nieznany (2)
04 01 belki i ramy zadanie 01id Nieznany (2)
04 03 belki i ramy zadanie 03id Nieznany (2)
[C] Badania Operacyjne Zadania (2009 03 01)
01 03 analiza kineamryczna zadanie 03
03 01 Wykopy doly rowy v1 1id 4 Nieznany (2)
e 03 2015 01 15 id 148697 Nieznany
probna 03 2008 rozszB zadania i Nieznany
02 01 podstawy statyki zadanie 01id 3499
2010 11 01 WIL Wyklad 01id 2717 Nieznany (2)
03 00 kratowniceid 4261 Nieznany (2)
02 03 podstawy statyki zadanie Nieznany (2)
312[01] 01 122 Arkusz egzaminac Nieznany (2)
04 18 belki i ramy zadanie 18id Nieznany (2)
01 Przygotowanie produkcji piek Nieznany (2)
więcej podobnych podstron