RADIACYJNA WYMIANA CIEPŁA

Natężenie promieniowania zostało zdefiniowane jako stosunek ilości wypromieniowanej energii, przez

elementarny wycinek powierzchni ciała, do pola powierzchni tego wycinka. W odniesieniu do

promieniowania jako nośnika energii cieplnej, natężeniu promieniowania odpowiada gęstości strumienia

cieplnego emitowanego przez ciało na drodze promieniowania:

𝑞

𝑟

=

𝑑𝑄

𝑑𝐹

𝑊

𝑚

2

,

gdzie:

dQ - strumień cieplny emitowany przez wycinek powierzchni ciała,

dF - wycinek powierzchni ciała który emituje strumień ciepła dQ.

Powierzchnie wszystkich ciał o temperaturze powyżej zera bezwzględnego są źródłami ciepła o natężeniu

zależnym od właściwości i temperatury powierzchni.

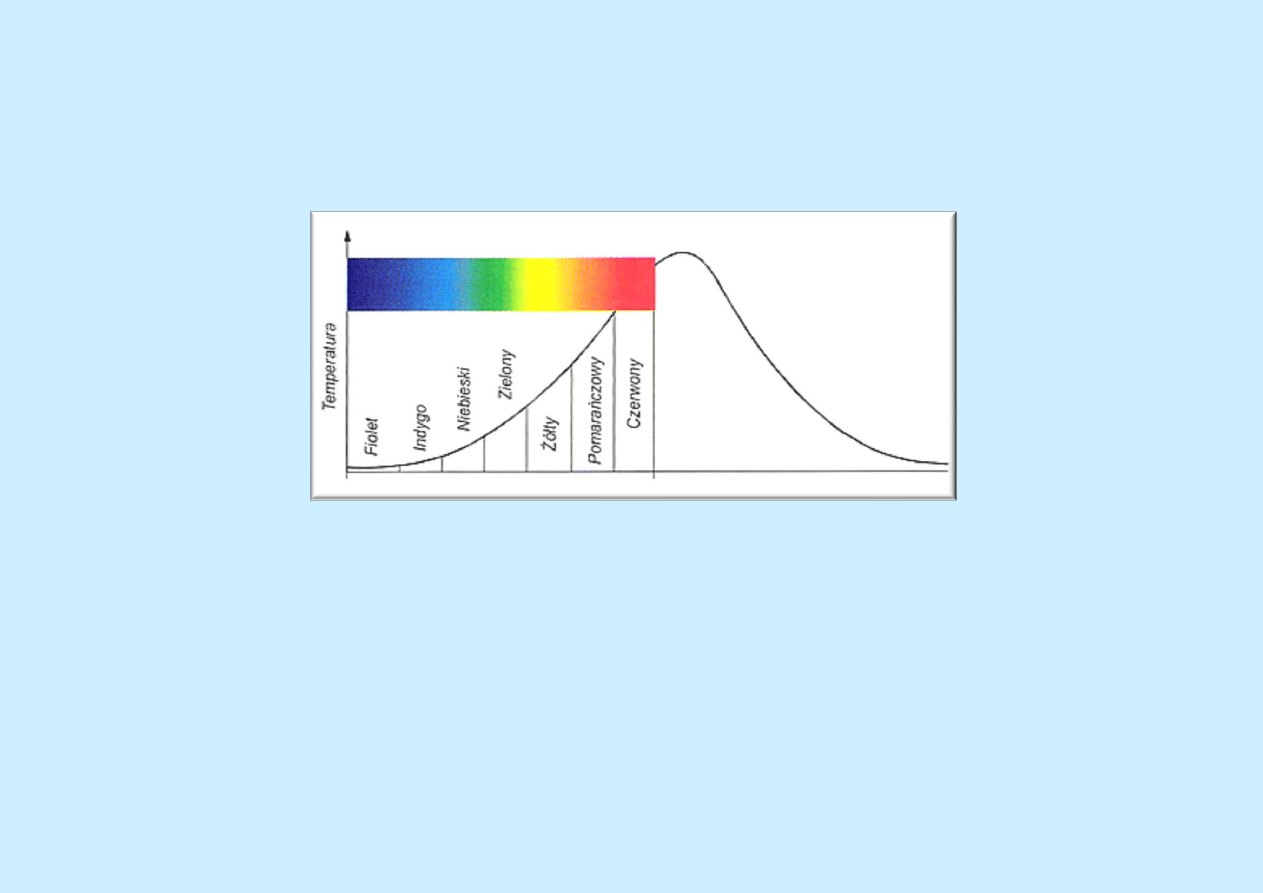
Można wykonać doświadczenie, które polega na rozproszeniu widma promieniowania słonecznego, przy

użyciu pryzmatu szklanego, i zbadaniu temperatur, przy użyciu czułych termometrów rtęciowych,

przypadających na poszczególne zakresy tego widma.

Rozkład temperatur przypadających na poszczególne widma promieniowania słonecznego.

Jak widać na powyższym wykresie, zakres widmowy promieniowania słonecznego wykracza poza zakres

widzialny. W związku z właściwościami tego promieniowania, nazywane jest ono promieniowaniem

cieplnym, bądź promieniowaniem podczerwonym w związku z tym, że jego spectrum leży bezpośrednio za

granicą czerwonego widma widzialnego.

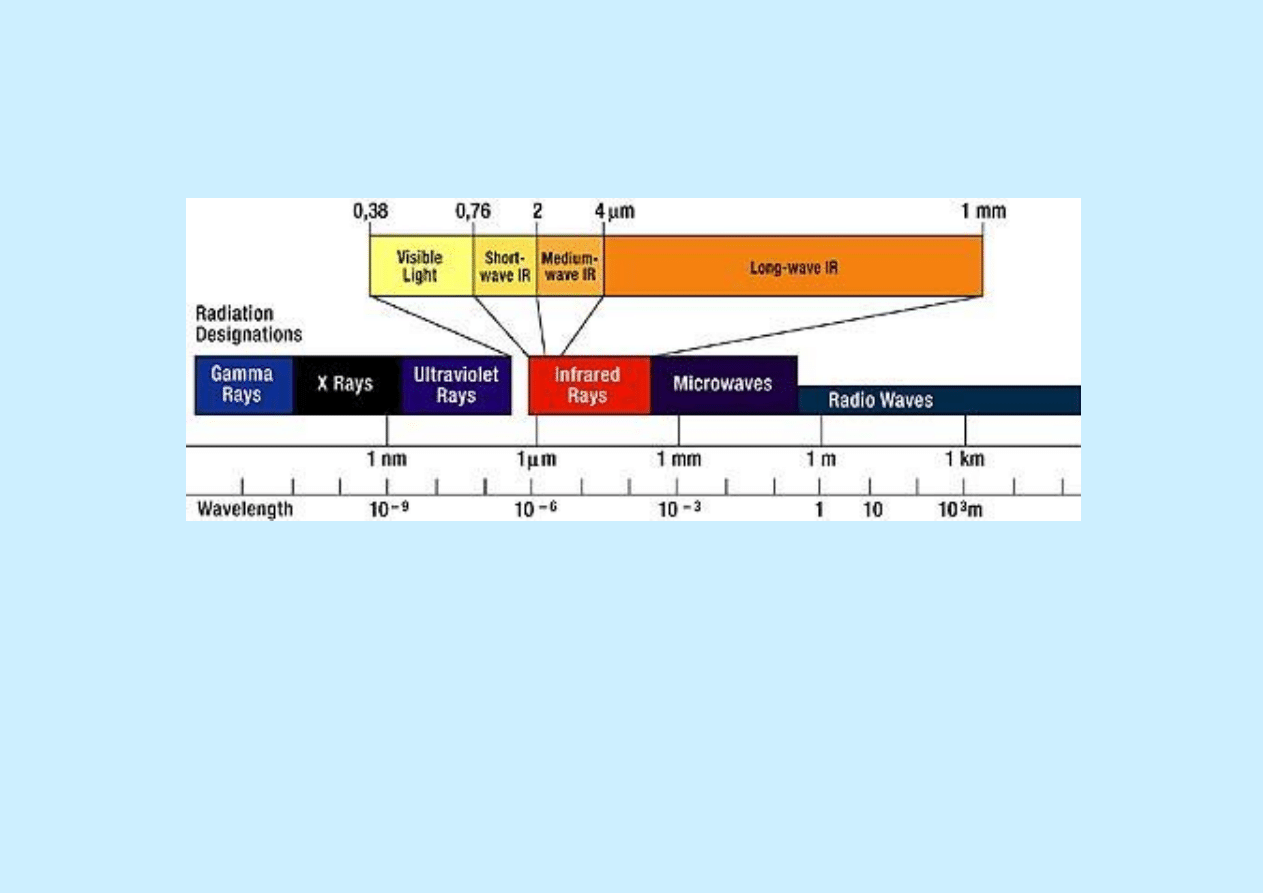
Przykładowy podział promieniowania występującego w przyrodzie, ze względu na długość fali λ, został

przedstawiony na poniższym rysunku.

Podział promieniowania występującego w przyrodzie ze względu na długość fali.

Natężenie promieniowania ciała czarnego dane jest wzorem:

𝐸

𝑜

= 𝐶

0

𝑇

100

4

gdzie:

C

o

- współczynnik promieniowania ciała czarnego, równy 5.67 W/m

2

K

4

,

T - temperatura bezwzględna powierzchni [ K ] .

W rzeczywistości mamy do czynienia z ciałami tzw. szarymi, to znaczy takimi które częściowo

promieniowanie cieplne pochłaniają , a częściowo odbijają. Współczynniki promieniowania i pochłaniania

dla promieniowania monochromatycznego są sobie równe (prawo Kirchoffa) i zawsze mniejsze od C

o

.

Związane są one ze współczynnikiem promieniowania ciała czarnego zależnością (prawo Stefana –

Boltzmanna):

C =



C

o

,

gdzie:

C - współczynnik promieniowania ciała szarego ,



- współczynnik emisji ( absorbcji) ciała szarego.

Współczynnik emisji, dalej zwany współczynnikiem absorbcji, zależy od długości fali promieniowania i kąta

padania promieniowania na daną powierzchnię. W fizyce budowli interesujemy się dwoma rodzajami

promieniowania:

- wysokotemperaturowym ( promieniowanie słoneczne odpowiadające temperaturze około 6000 K ),

- niskotemperaturowym ( promieniowanie od przegród i urządzeń grzejnych, odpowiadające

temperaturze w pobliżu 300 K ).

Należy zwrócić uwagę na fakt, że właściwości absorbcyjne materiałów mogą być całkowicie różne , w

zależności od zakresu temperatury źródła. Na przykład , w zakresie promieniowania

niskotemperaturowego aluminium matowe ( odpowiadające blasze stosowanej na przekrycia dachowe)

pochłania tylko 3,5% padającego promieniowania, podczas gdy azbesto-cement – 96% . Natomiast w

zakresie promieniowania wysokotemperaturowego właściwości obu materiałów są zbliżone ( dla

azbestocementu wsp. absorbcji wynosi 0.61 , a dla blachy aluminiowej 0.52). Oznacza to, że oba materiały

będą podobnie ogrzewać się od promieniowania słonecznego.

Wpływ dokładności określenia wartości emisyjności na ocenę intensywności radiacyjnej wymiany

ciepła

Eksperyment prezentujący wpływ emisyjności na wartość temperatury. Zdjęcie walca aluminiowego

wykonane za pomocą kamery termowizyjnej

Stosunek natężenia promieniowania odbitego od natężenia promieniowania padającego nazywamy

współczynnikiem odbicia „



” .

Współczynnik odbicia i absorbcji materiałów nieprzeźroczystych są związane zależnością:



+



= 1

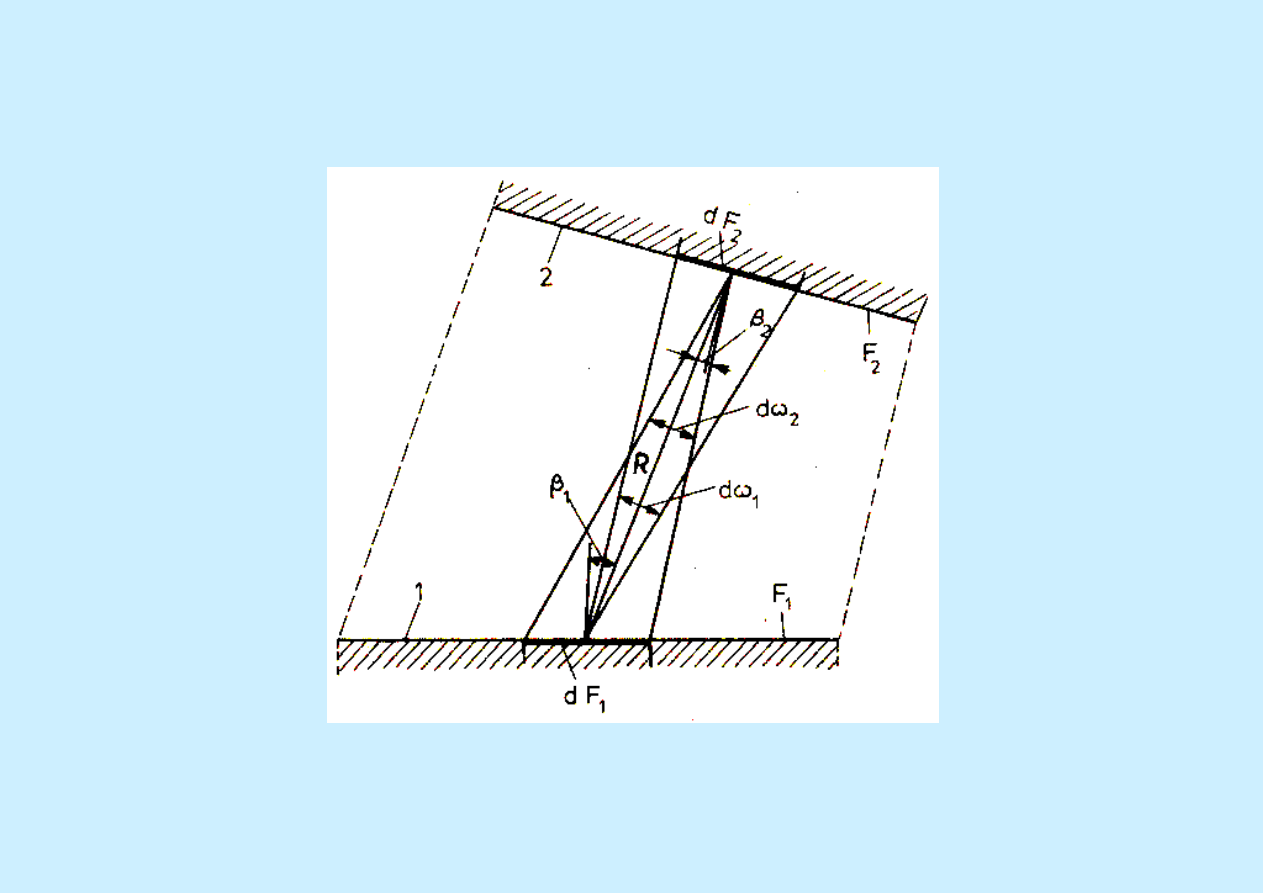
Rozpatrzmy teraz wymianę ciepła przez promieniowanie między dwoma powierzchniami F

1

i F

2

Rysunek 3.1 Wymiana ciepła przez promieniowanie między dwoma nieprzezroczystymi powierzchniami.

Na podstawie prawa Stefana – Boltzmanna dla ciał rzeczywistych, można sformułować zależności dla

strumieni ciepła, wymienianych między wycinkami dF

1

oraz dF

2

:

𝑑𝑞

1

= 𝜀

1

𝐶

0

𝑡

1

100

4

𝑑𝐹

1

,

𝑑𝑞

2

= 𝜀

2

𝐶

0

𝑡

2

100

4

𝑑𝐹

2

,

gdzie:

t

1

, t

2

- temperatura bezwzględna odpowiednich powierzchni.

Gęstość strumienia cieplnego wyemitowana, na drodze promieniowania, przez wycinek dF

1

i pochłaniana

przez wycinek dF

2

jest równa:

𝑑𝑞

1−2

= 𝜀

1

𝜀

2

𝐶

0

cos 𝛽

1

cos 𝛽

2

𝜋𝑅

2

𝑑𝐹

1

𝑑𝐹

2

𝑡

1

100

4

𝑑𝑞

2−1

= 𝜀

1

𝜀

2

𝐶

0

cos 𝛽

1

cos 𝛽

2

𝜋𝑅

2

𝑑𝐹

1

𝑑𝐹

2

𝑡

2

100

4

gdzie:

β

1

β

2

- kąty pomiędzy prostą łączącą punkty emitujące promieniowanie, a normalnymi do

powierzchni, odpowiednio 1 i 2.

Zaniedbując promieniowanie odbite, strumień ciepła wymieniany między powierzchniami dF

1

oraz dF

2

możemy zapisać jako różnicę strumieni ciepła emitowanych przez te powierzchnie:

𝑞

1−2

= 𝜀

1

𝜀

2

𝐶

0

cos 𝛽

1

cos 𝛽

2

𝜋𝑅

2

𝑑𝐹

1

𝑑𝐹

2

𝑡

1

100

4

−

𝑡

2

100

4

Powyższy wzór jest wzorem przybliżonym, gdyż zaniedbuje promieniowanie odbite wracające powrotem na

powierzchnię, która je wyemitowała. Ogólny wzór opisujący wymianę radiacyjną ciepła z powierzchni ciała

szarego F

1

do powierzchni ciała szarego F

2

ma postać:

𝑄

1−2

= 𝜀

1−2

𝐶

0

𝜑

1−2

𝐹

1

𝑡

1

100

4

−

𝑡

100

4

gdzie:

Q

1-2

- strumień ciepła wymieniany z powierzchni F

1

do F

2

,

ε

1-2

- emisyjność zastępcza,

φ

1-2

- współczynnik konfiguracji.

Emisyjność zastępcza

Wyznaczenie emisyjności zastępczej już dla przypadku dwu dowolnie usytuowanych wobec siebie

płaszczyzn jest skomplikowane i kłopotliwe w praktyce inżynierskiej. Istnieją jednak trzy przypadki, istotne

w praktyce inżynierskiej, dla których emisyjność zastępczą można określić w prosty sposób:

 dla bardzo małych powierzchni, znacznie od siebie oddalonych, i gdy współczynniki emisyjności tych

powierzchni są w przybliżeniu równe 1, powracającą część promieniowania, odbitą od drugiej

powierzchni można pominąć:

𝜀

1−2

= 𝜀

1

𝜀

2

 dla dwóch powierzchni równoległych, mało oddalonych od siebie i nie rozdzielonych gazem o dużym

współczynniku absorpcyjności, można przyjąć, że całe odbite promieniowanie wraca na powierzchnię,

która je wypromieniowała:

𝜀

1−2

=

1

1

𝜀

1

+

1

𝜀

2

− 1

 w przypadku gdy powierzchnia F

1

objęta jest ze wszystkich stron powierzchnią F

2

:

𝜀

1−2

=

1

1

𝜀

1

+

𝐹

1

𝐹

2

(

1

𝜀

2

− 1)

Podane wyżej wzory, aczkolwiek nie wyczerpują wszystkich możliwych przypadków, wystarczają do

oszacowania ilości ciepła wymienianej przez promieniowanie z dokładnością dostateczną dla

budownictwa.

Współczynnik konfiguracji

Współczynnik konfiguracji, zwany również kątowym, lub kierunkowym, określa jaka część ciepła

wypromieniowana przez powierzchnię F

1

pada na powierzchnię F

2

. W ogólnym przypadku określony jest

wzorem:

𝜑

1−2

=

1

𝐹

1

cos 𝛽

1

cos 𝛽

2

𝜋𝑅

2

𝑑𝐹

1

𝑑𝐹

2

W niektórych przypadkach powyższe wyrażenie znacznie się upraszcza.

Przy wymianie ciepła przez promieniowanie między dwiema nieograniczonymi (lub ograniczonymi, lecz

blisko położonymi) płaszczyznami:



1-2

=



2-1

= 1

Przy wymianie ciepła między powierzchnią, a wnętrzem nieograniczonej półkuli (co odpowiada wymianie

ciepła między płaskim dachem, a nieboskłonem):



1-2

= 1

Dla kilku innych charakterystycznych przypadków można skorzystać z wykresów zawartych w różnych

podręcznikach do Fizyki Budowli (np. „Fizyka Budowli, podstawy wymiany ciepła i masy”, J.A.

Pogorzelski ).

W celu uniwersalnego posługiwania się wykresami tego typu, stosujemy trzy reguły:

 Reguła zamkniętości – suma współczynników konfiguracji dla powierzchni A

1

wypromieniowującej

energię do wszystkich otaczających ją powierzchni jest równa 1:

𝜑

1−𝑖

𝑛

𝑖=1

= 1

 Reguła wzajemności – strumienie ciepła wymieniane między dwiema powierzchniami są sobie równe:

𝐹

1

𝜑

1−2

= 𝐹

2

𝜑

2−1

 Reguła rozdzielności – możliwość superponowania strumienia cieplnego, przy podziale powierzchni

F

1

i F

2

na m i n części:

𝐹

1

𝜑

1−2

= 𝐹

𝑚

𝜑

𝑚 −𝑛

𝑛

𝑚

Gęstość strumienia cieplnego

Zgodnie z definicją, gęstość strumienia cieplnego w radiacyjnej wymianie ciepła jest to stosunek

strumienia ciepła, emitowanego przez powierzchnię F

1

do powierzchni F

2

, do pola powierzchni F

1

:

𝑞

1−2

=

𝑄

1−2

𝐹

1

= 𝜀

1−2

𝐶

0

𝜑

1−2

𝑡

1

100

4

−

𝑡

2

100

4

𝑊

𝑚

2

Współczynnik przejmowania ciepła przez promieniowanie:

Analogicznie jak w konwekcyjnej wymianie ciepła, można określić wartość współczynnika przejmowania

ciepłą przez promieniowania:

𝛼

𝑟

=

𝑞

1−2

𝑡

1

− 𝑡

2

= 𝜀

1−2

𝐶

0

𝜑

1−2

𝑏

1−2

𝑊

𝑚

2

𝐾

gdzie:

b

1-2

- współczynnik temperaturowy,

𝑏

1−2

=

𝑡

1

100

4

−

𝑡

2

100

4

𝑡

1

− 𝑡

2

t

1

, t

2

- temperatury powierzchni wymieniających ciepło,

Temperatura słoneczna powietrza

Jest to hipotetyczna temperatura powietrza, przy której ilość ciepła przekazywanego przegrodzie przez

konwekcję byłaby równa ilości ciepła wymienianej między przegrodą, a powietrzem zewnętrznym, z

uwzględnieniem promieniowania słonecznego, padającego na tę przegrodę.

𝑡

𝑠

= 𝑡

𝑒

+

𝜀 𝐼
𝛼

𝑘

"

+ 𝑡

𝛼

𝑘

"

− 𝛼

𝑘

′

𝛼

𝑘

"

gdzie:

t

s

- temperatura słoneczna powietrza,

t

e

- temperatura powietrza zewnętrznego,

ε

- emisyjność promieniowania wysokotemperaturowego przegrody,

I

- natężenie promieniowania słonecznego,

α

k

”

- współczynnik przejmowania ciepła przez konwekcję dla temperatury powietrza

zewnętrznego t

s

,

α

k

’

- współczynnik przejmowania ciepła przez konwekcję dla realnej temperatury powietrza

zewnętrznego,

t

- temperatura powierzchni przegrody.

Temperatura nieboskłonu

Oprócz przejmowania ciepła na drodze konwekcji z powietrzem zewnętrznym, oraz na drodze

promieniowania wysokotemperaturowego ze słońcem, powierzchnia przegrody wymienia ciepło na drodze

promieniowania niskotemperaturowego z nieboskłonem.

𝑡

𝑛

= 𝑡

𝑒

0.526 + 0.075 𝑝

4

gdzie:

t

n

- bezwzględna temperatura nieboskłonu,

t

e

- bezwzględna temperatura powietrza,

p

- prężność cząstkowa pary wodnej w powietrzu [mm Hg].

Przy założeniu, że temperatura nieboskłonu t

n

jest niższa od temperatury powietrza zewnętrznego t

e

o pewną

wartość Δt, to dla powierzchni zewnętrznej można zapisać równanie bilansu cieplnego:

𝜀 𝐼 − 𝛼

𝑘

𝑡 − 𝑡

𝑒

− 𝛼

𝑟

𝑡 − 𝑡

𝑒

+ Δ𝑡 = 𝛼

𝑘

+ 𝛼

𝑟

𝑡

𝑠

− 𝑡

gdzie:

t

s

- skorygowana temperatura słoneczna.

Temperaturę słoneczną skorygowaną, można więc wyznaczyć z poniższej zależności:

𝑡

𝑠

= 𝑡

𝑒

+

𝐼 𝜀

𝛼

𝑒

−

𝛼

𝑟

Δ𝑡

𝛼

𝑒

gdzie współczynnik przejmowania ciepła w złożonej wymianie ciepła jest określony poniższym wzorem:

𝛼

𝑒

= 𝛼

𝑘

+ 𝛼

𝑟

gdzie:

α

r

- współczynnik przejmowania ciepła dla promieniowania niskotemperaturowego dla

wymiany ciepła między powierzchnią przegrody a nieboskłonem.