Laboratorium Automatyki. Instrukcja do ćwiczenia nr 1.

1

Ćwiczenie 1.

Roboty mobilne - DrRobot

Laboratorium Automatyki. Instrukcja do ćwiczenia nr 1.

2

1.Wstęp

Wykorzystywany w ćwiczeniu robot mobilny posiada dwa koła napędowe oraz jedno koło typu „castor”

zapewniające robotowi równowagę. Napęd robota stanowią dwa silniki prądu stałego z przekładniami redukcyjnymi.

Silniki zasilane są z układu mostkowego PWM. Napędy wyposażone są w pomiar położenia kół za pomocą enkoderów

o rozdzielczości 1200 impulsów na obróta. Robot wyposażony jest także w zestaw trzech czujników ultradźwiękowych,

w siedem czujników podczerwieni oraz dwa piroelektryczne czujniki podczerwieni umożliwiające wykrywanie ludzi

oraz ich ruch.

Ponadto robot wyposażony jest w kamerę, która może się poruszać dzięki serwomechanizmom. Robot

wyposażony jest w mikrofon i głośnik. Całość sterowana jest z nadrzędnego komputera klasy PC. Komunikacja między

robotem a komputerem odbywa się za pomocą sieci bezprzewodowej WIFI. Sterownik robota odpowiada tylko za

funkcje niskopoziomowe jak sterowanie silnikami, odczyt czujników itp. Główny program sterujący wykonywany jest

na komputerze PC. Tworzenie oprogramowania odbywa się w języku C/C++ z wykorzystaniem odpowiedniej kontrolki

ActiveX.

Położenie robota jest wyznaczane w sposób względny. Proces wyznaczania położenia opiera się na pomiarze

prędkości obrotowej kół, znajomości parametrów kinematycznych robota oraz założeniu braku poślizgu. Model

kinematyczny robota przyjmuje poniższą postać

(

)

(

) ( )

L

R

R

v

v

y

v

x

l

r

l

r

⋅

−

=

+

=

=

⋅

=

⋅

=

2

/

2

/

)

sin(

)

cos(

ϕ

ϕ

ω

ϕ

ϕ

ω

θ

θ

θ

&

&

&

&

&

&

&

(1)

gdzie R – promień kół, L – połowa odległości między kołami, φ – prędkości obrotowe kół. W ten sposób położenie

robota otrzymuje się całkując trzy pierwsze równania z uwzględnieniem warunków początkowych.

2. Obsługa stanowiska

Przystępując do ćwiczenia należy postępować zgodnie z poniższą procedurą.

1. Włączamy komputer i logujemy się.

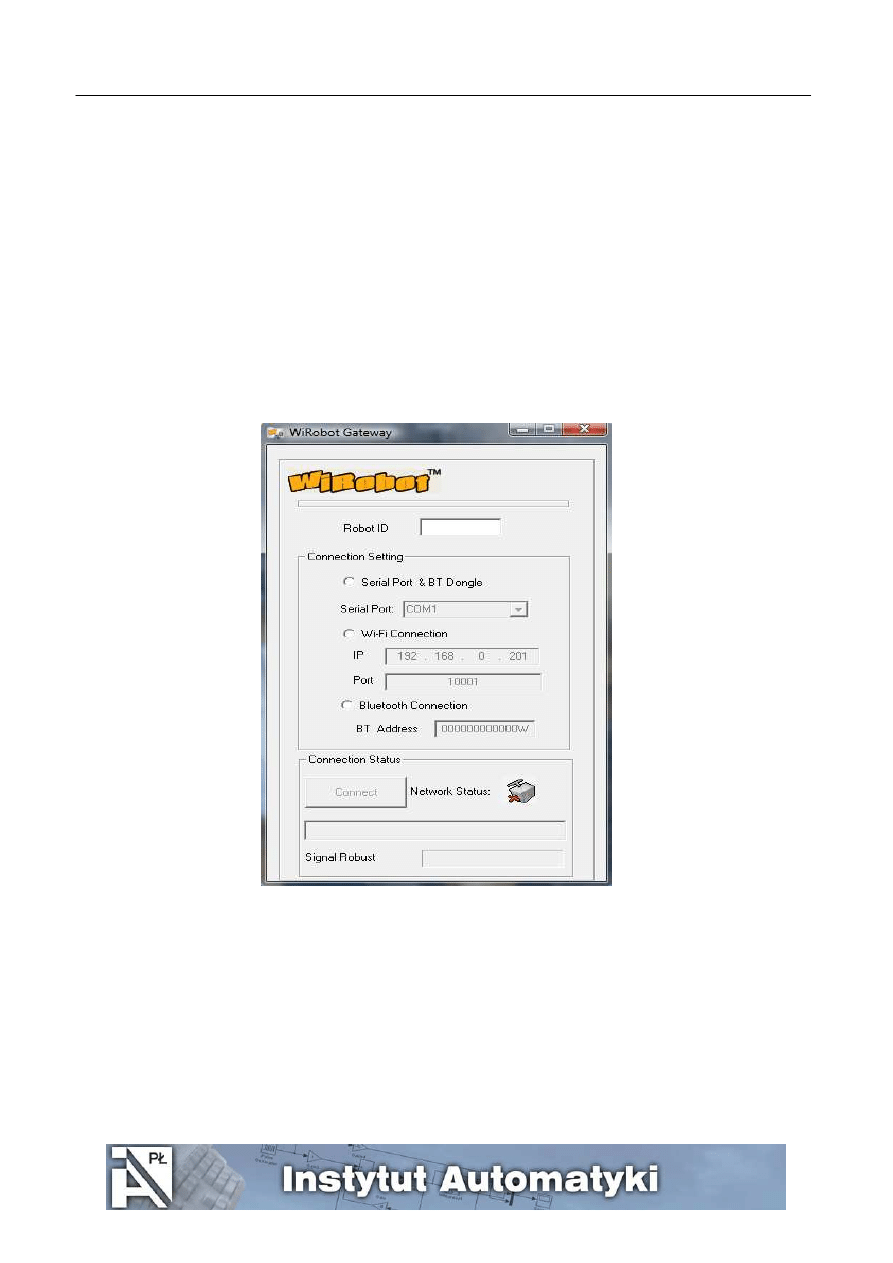
2. Uruchamiamy program WiRobot, do którego skrót znajduje się na pulpicie. Otwiera się okno pokazane na rys.

1. Po uruchomieniu programu w pole Robot ID wpisujemy motcom. Zaznaczamy opcje WiFi Connection, w

pola IP wpisujemy numer IP robota który jest umieszczony na spodzie robota a w pole Port liczbę 10001.

3. Po zakończeniu konfiguracji oprogramowania , włączamy robota wyłącznikiem umieszczonym na tylnej

ś

ciance. Po włączeniu robota wciskamy przycisk Connect. Następuje połączenie robota z komputerem

nadrzędnym.

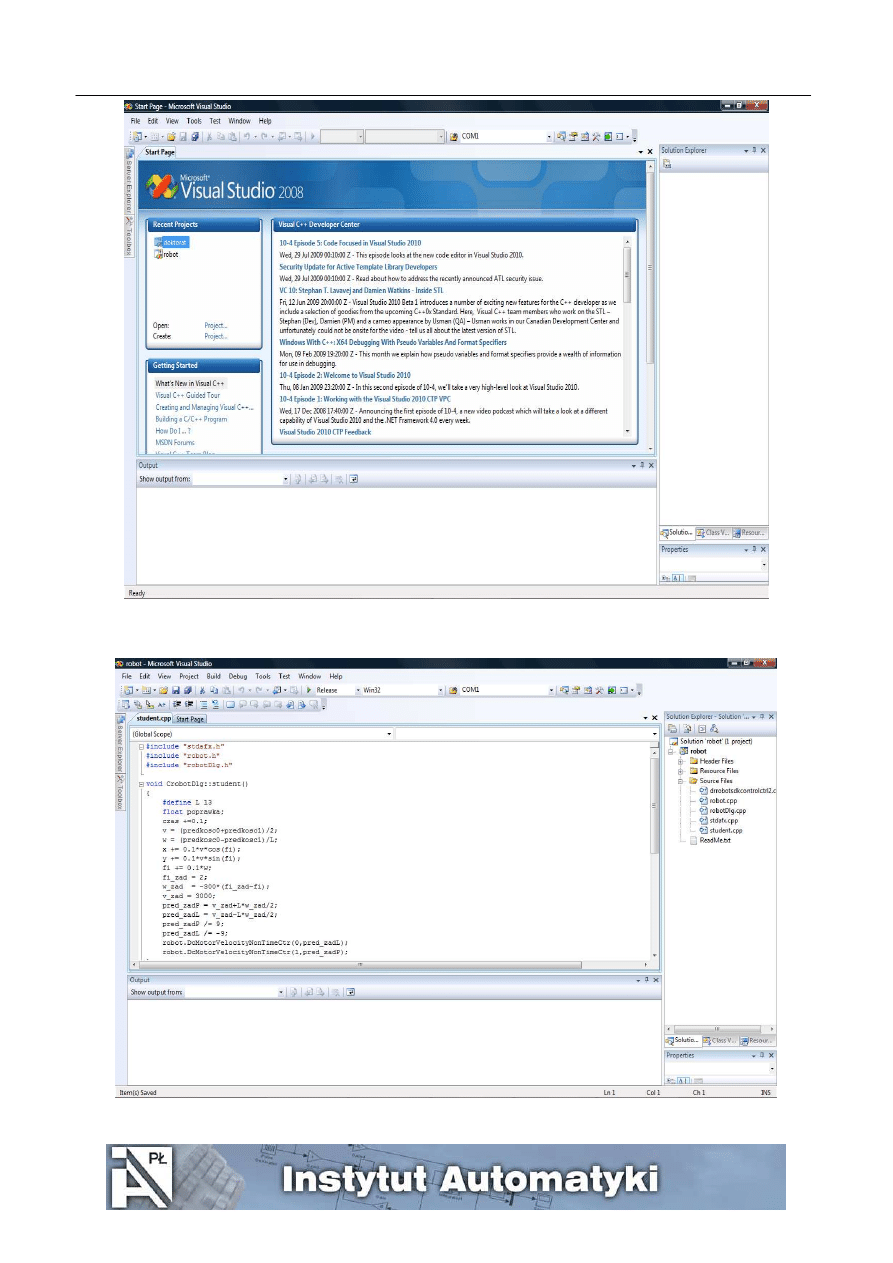
4. Uruchamiamy program Microsoft VisualStudio2008 skrótem na pulpicie o tej samej nazwie. Pojawia się okno

jak na rys. 2.

Laboratorium Automatyki. Instrukcja do ćwiczenia nr 1.

3

5. W zakładce Recent Projects klikamy nazwę Robot. Po kliknięciu w oknie Solution Explorer, które znajduje

się z prawej strony, rozwijamy menu klikając na krzyżyk obok nazwy robot, a następnie rozwijamy pole

Source Files.

6. Po rozwinięciu klikamy nazwę pliku student.cpp.

7. Otwiera się okno jak na rys. 3. W ciele funkcji student zamieszczamy modyfikacje programu wykonywane w

ramach programu ćwiczeń.

8. Postępując jak w p.6 w polu Header Files w pliku robotDlg.h umieszcza się deklaracje zmiennych

dodatkowych, których chcemy użyć w programie. Ich deklaracje umieszcza w miejscu po komentarzu

o następującej treści: „//tutaj umieszczamy deklaracje zmiennych wprowadzanych przez studentów”.

9. Po wprowadzeniu zmian kompilujemy i uruchamiamy program sterujący robotem za pomocą zielonej strzałki

lub klikamy najpierw F5 a potem F7. Jeśli nie popełniliśmy żadnych błędów składniowych języka C++

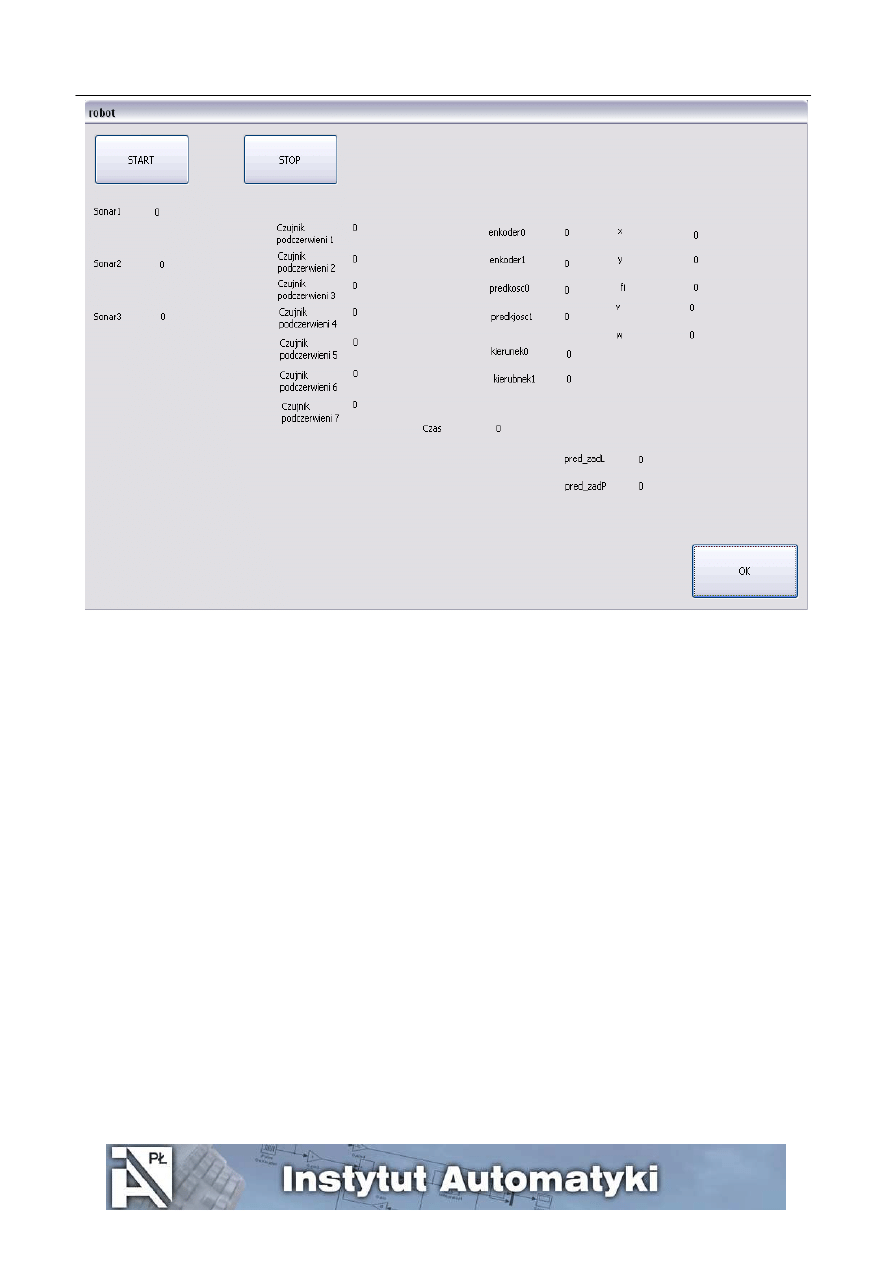
pojawia się okno programu sterującego robota pokazane na rys. 4.

Rys. 1 Okno konfiguracyjne bezprzewodowego połączenia robota

10. W razie wystąpienia błędów program poinformuje nas o tym. Błędy te należy poprawić. Ewentualne błędy

wraz z miejscami ich wystąpienia wyświetlane są w dolnej części okna z rys. 2 i 3, w zakładce Output.

Klikając na komunikacie o błędzie przenosimy się w miejsce jego wystąpienia.

11. Aby uruchomić pogram naciskamy przycisk Start aby zatrzymać przycisk Stop. Aby zamknąć okno

naciskamy przycisk Ok.

12. W oknie z rys. 4 widać na bieżąco wyświetlane są wartości interesujących nas zmiennych. Są one

automatycznie zapisywane do pliku o nazwie przebiegi.txt umieszczonego na dysku C.

Laboratorium Automatyki. Instrukcja do ćwiczenia nr 1.

4

Rys. 2.

Rys. 3

Laboratorium Automatyki. Instrukcja do ćwiczenia nr 1.

5

Rys. 4

Zmienne wykorzystywane w programie:

czas – zmienna typu float przechowująca informację o czasie jaki upłynął od wciśnięcia przycisku „START” wyrażona

w sekundach

x – zmienna typu float przechowująca współrzędną x robota, współrzędna względna liczona od położenia

początkowego po wciśnięciu przycisku „START” wyrażona w centymetrach

y – jak wyżej tylko współrzędna y

fi – zmienna typu float określająca aktualny kąt obrotu robota względem osi pionowej przechodzącej przez punkt

leżący pośrodku odcinka łączącego oba koła, liczona względnie od położenia początkowego wyrażona w radianach

v – prędkość liniowa robota (dokładniej punktu leżącego pośrodku odcinka łączącego oba koła) wyrażona w cm/s

w – prędkość kątowa robota wokół osi jak dla zmiennej fi wyrażona w rad/s

v_zad, w_zad – zmienne określające prędkości zadane odpowiednio prędkości liniowej i kątowej odpowiednio w cm/s

i rad/s

pred_zadL, pred_zadP – zmienne określające wartości zadane odpowiednio prędkości kątowej koła lewego i prawego

sonar1, sonar2, sonar3 – zmienne określające sygnały z czujników ultradźwiękowych

Laboratorium Automatyki. Instrukcja do ćwiczenia nr 1.

6

3. Część teoretyczna

3.1. Realizacja regulatora PID

Sygnał wyjściowy regulatora PID o transmitancji













+

+

=

D

I

p

sT

sT

k

s

G

1

1

)

(

(2)

opisany jest wzorem















+

+

=

∫

t

D

I

p

dt

t

de

T

d

e

T

t

e

k

t

u

0

)

(

)

(

1

)

(

)

(

τ

τ

(3)

W przypadku regulatora cyfrowego zastępujemy całkę sumowaniem i pochodną ilorazem różnicowym np. różnicą

wsteczną. Otrzymujemy wtedy wzór różnicowy:

(

)













−

−

+

−

+

=

∑

=

k

i

S

D

I

S

p

k

e

k

e

T

T

i

k

e

T

T

k

e

k

k

u

0

)

1

(

)

(

)

(

)

(

)

(

(4)

Wprowadzając

∑

=

−

=

−

k

i

i

k

e

k

S

1

)

(

)

1

(

(5)

otrzymujemy

(

)

(

)













−

−

+

−

+

+

=

)

1

(

)

(

)

1

(

)

(

)

(

)

(

k

e

k

e

T

T

k

S

k

e

T

T

k

e

k

k

u

S

D

I

S

p

(6)

3.2. Kształtowanie przebiegu prędkości zadanej

W najprostszym przypadku prędkość robota zadawana jest w postaci sygnału prostokątnego o amplitudzie V.

Oczywiście ze względu na ograniczenia (skończona wartość przyspieszenia) i dynamikę ruchu robot odtwarzać będzie

tak zadaną prędkość w sposób przybliżony. Wadą takiego sterowania jest bardzo duża wartość pochodnej prędkości

(robot „szarpie” ruszając i hamując). Aby tego uniknąć stosuje się stopniowe przyspieszanie/hamowanie robota, aby

kolejne pochodne prędkości nie przekraczały założonych wartości.

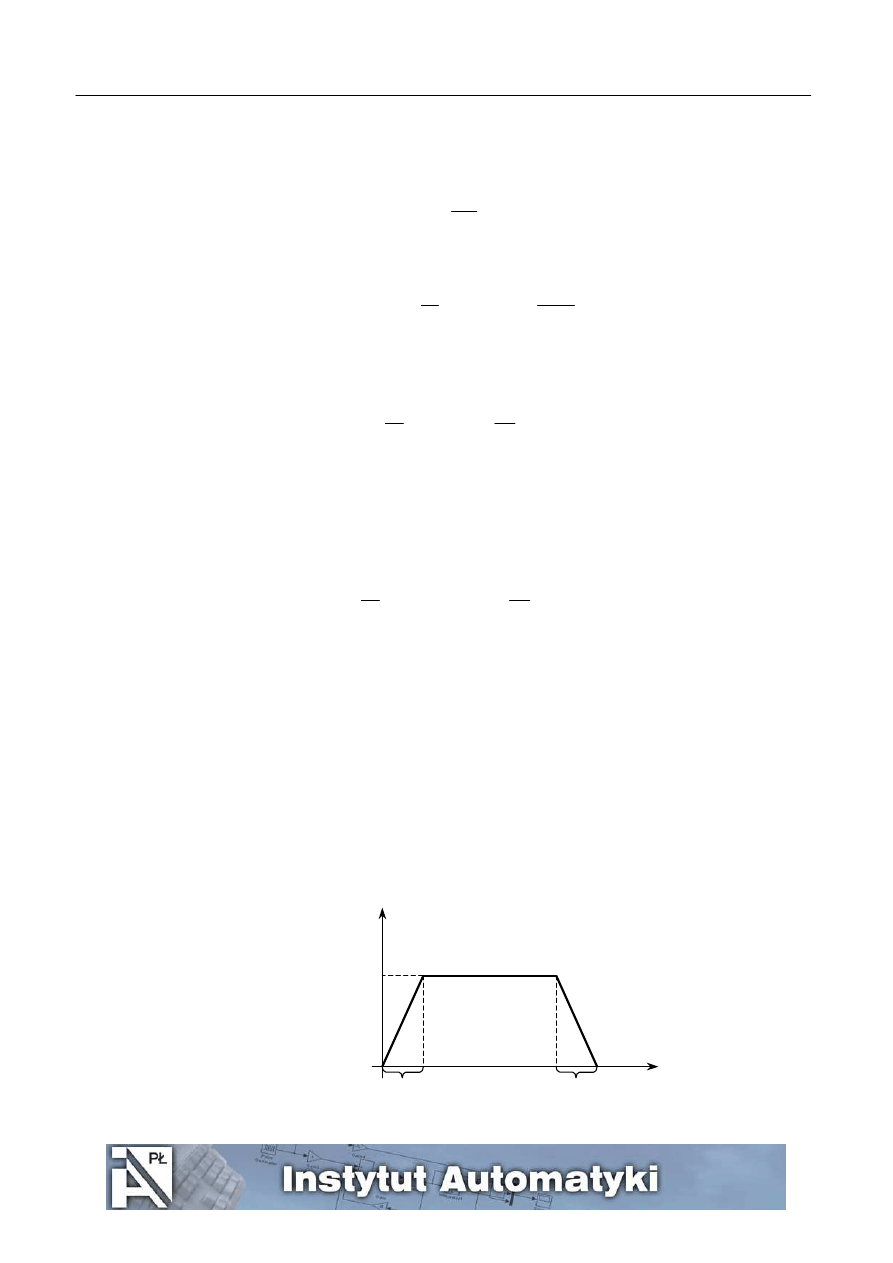
Pierwszym wariantem, który możemy zrealizować jest rozpędzanie robota ze stałym przyspieszeniem do założonej

prędkości, następnie ruch jednostajny i w końcu hamowanie ze stałym opóźnieniem. Aby ograniczyć ilość parametrów

przyjmiemy że czas przyspieszania i hamowania jest taki sam.

Rys. 5.

V

k

=a·T

1

V

t

T

T

T

Laboratorium Automatyki. Instrukcja do ćwiczenia nr 1.

7

Dla takiego kształtu prędkości zadanej na podstawie podstawowych zależności na drogę i prędkość, w celu uzyskania

przemieszczenia robota o założony odcinek S

k

musimy rozwiązać odpowiedni zestaw równań i nierówności po czasie T

k

otrzymujemy:

(

)

1

1

T

T

T

a

S

k

k

−

⋅

⋅

=

(7)

1

T

a

V

k

⋅

=

(8)

Ponadto mamy ograniczenia wynikające z możliwości napędu:

max

max

a

a

V

V

k

≤

≤

(9)

Z równania (7) wyznaczamy np. przyspieszenie:

(

)

1

1

T

T

T

S

a

k

k

−

⋅

=

(10)

Ze względu na prędkość maksymalną przyspieszenie nie może być większe niż:

1

max

T

V

a

=

(11)

I nie może przekraczać przyspieszenia dopuszczalnego a

max

.

0

0,5

1

1,5

2

2,5

3

3,5

4

0

0,5

1

1,5

2

2,5

Jak widać zadanie nie ma jednoznacznego rozwiązania. Otrzymaliśmy zbiór parametrów a i T

1

które spełniają

postawione zadanie.

3.3. Ruch po krzywej zadanej parametrycznie.

Krzywą na płaszczyźnie można przedstawić w postaci parametrycznej:

T

1 max

T

1 min

a

T

1

a

max

a

min

1

max

T

V

a

=

(

)

1

1

T

T

T

S

a

k

k

−

⋅

=

Laboratorium Automatyki. Instrukcja do ćwiczenia nr 1.

8







=

=

)

(

)

(

t

y

y

t

x

x

(12)

Przykładowo okrąg o promieniu R i środku w punkcie (0,0) przedstawiają poniższe wzory:
























⋅

⋅

=













⋅

⋅

=

t

T

R

t

y

t

T

R

t

x

π

π

2

sin

)

(

2

cos

)

(

(13)

gdzie T czas pokonywania jednego obrotu.

Większość algorytmów sterowania ze sprzężeniem zwrotnym wymaga znajomości chwilowej prędkości postępowej i

obrotowej. Dla takiego opisu prędkości te wynoszą:

2

2

2

2

)

(

y

x

x

y

y

x

y

x

V

V

a

V

a

V

V

V

t

v

+

⋅

−

⋅

=

+

=

ω

(14)

gdzie V

x

, V

y

oznaczają składowe prędkości, a

x

, a

y

składowe przyspieszenia i mogą zostać wyznaczone przez obliczenie

odpowiednich pochodnych po czasie, bądź analitycznie, bądź numerycznie.

4. Instrukcja wykonawcza

4.1. Podstawowe ruchy robota.

Napisać procedury ruchu robota bez warunków zatrzymania (zatrzymanie przy pomocy przycisku „STOP”):

•

Obrotu wokół jednego z kół (obrót „w przód” i „w tył”).

•

Obrót wokół osi robota (dwoma kołami).

•

Ruchu robota do przodu ze stałą prędkością.

Punkt startowy robota wybrać tak aby nie doszło do uderzenia robota w ograniczenia pola.

Widzimy, że robot w trakcie trzeciej procedury nie porusza się prostoliniowo. Przeanalizować przebiegi prędkości

silników, prądów silników, prędkości robota oraz kąta położenia robota.

4.2. Wprowadzenie korekcji toru ruchu robota.

Napisać procedury ruchu robota po linii prostej ze stałą prędkością z korekcją kąta polegającą na zmianie prędkości

zadanych siników:

•

Z regulatorem typu P

•

Z regulatorem typu PI

Porównać położenie i kąt robota z danymi uzyskanymi w poprzednim punkcie. Porównać odchyłki od kąta zadanego

dla obu regulatorów.

♦

Napisać procedury obrotu robota o założony kąt (np. 60

°

) z wykorzystaniem regulatora typu P i typu PI. Porównać

przebiegi kąta położenia robota dla obu typów regulatorów. Zwrócić szczególną uwagę na położenie końcowe robota.

Laboratorium Automatyki. Instrukcja do ćwiczenia nr 1.

9

4.3. Przejazd założonej odległości

•

Napisać procedurę realizującą przemieszczenie ze stałą prędkością o założoną odległość (np. 150 cm) pod

kątem 0, a następnie zatrzymanie robota.

•

Zmodyfikować procedurę aby robot pokonywał założoną odległość pod niezerowym kątem w stosunku

do położenia początkowego (jednoczesny ruch obrotowy i postępowy). Widzimy, że robot pokonuje tor

równoległy do założonego, odległość od toru zadanego zależy od zadanej prędkości.

•

Poprawić procedurę aby robot pokonywał założoną odległość pod dowolnym kątem jako sekwencję obrót

– jazda.

Porównać tory ruchu robota z regulatorem korygującym typu P i typu PI.

4.4. Ruch z ograniczonym przyspieszeniem

Zmodyfikować napisaną w poprzednim punkcie procedurę ruchu po linii prostej, tak aby prędkość zadana narastała

liniowo do wartości założonej i liniowo spadała do 0. Zaprojektować 3 różne przebiegi prędkości zadanej:

•

z przyspieszeniem bliskim ograniczeniu przyspieszenia (odczytanemu z przebiegów prędkości z

poprzedniego punktu).

•

z przyspieszeniem równym połowie tego ograniczenia.

•

z minimalnym przyspieszeniem zapewniającym przebycie założonej drogi w zadanym czasie.

Procedury powinny realizować ruch robota na tym samym dystansie.

4.5. Wykrywanie przeszkody przy pomocy czujników ultradźwiękowych

Zmodyfikować procedurę realizującą ruch po linii prostej ze stałą prędkością, tak aby robot po wykryciu przeszkody z

przodu zatrzymywał się. Usunięcie przeszkody ma powodować kontynuowanie ruchu robota.

4.6. Wykonywanie sekwencji ruchów.

Napisać procedurę realizującą ruch robota po torze zamkniętym jako sekwencję ruchów podstawowych obrót - jazda.

Sprawdzić czy robot wraca do położenia początkowego dla różnych regulatorów korygujących kąt ruchu.

4.7. Ruch robota po krzywej zadanej parametrycznie

•

Napisać procedurę ruchu robota po okręgu zadanym w postaci parametrycznej. Przeanalizować przebiegi

położenia robota w czasie, porównać jego położenie z trajektorią zadaną.

•

Zmodyfikować napisaną procedurę aby robot poruszał się po paraboli.

Uwaga! W ćwiczeniu tym należy zmienić parametry stanu początkowego robota (jego położenie x, y, oraz kąt) tak aby

odpowiadały one położeniu i kątowi wynikającemu z opisu parametrycznego trajektorii (położenie i orientacja w chwili

t=0).