1
Strop stalowy z płyt
ą
ż
elbetow
ą
Cz.2 – Stalowy podci
ą
g
Ć
WICZENIA I PROJEKTOWANIE
ZŁO
Ż
ONE KONSTRUKCJE
METALOWE
Strop stalowy z płyt
ą
ż
elbetow
ą
2
2.0 PODCI
Ą
G
2.1 SCHEMAT STATYCZNY
•
Schemat belki wolnopodpartej o rozpi
ę
to
ś
ci:
a
n
L
L
e
⋅
=
=
2.2 ZEBRANIE OBCI
ĄŻ
E
Ń
2.2.1 Obci
ąż
enie od ci
ęż
aru belek stropowych
•
obc. w postaci sił skupionych
→
obc. ci
ą
głe równomiernie rozło
ż
one:
2.2.2 Ci
ęż
ar własny podci
ą
gu
•
Ci
ęż
ar blachownicy spawanej:
a
R
bs
bs
⋅
=
2
g
85
.
0
)
100
700
(
g
⋅
⋅
+
=
L
bl
];
m
/
N
[
]
m
[
L
Strop stalowy z płyt
ą
ż
elbetow
ą
3
2.2.3 Warto
ść
charakterystyczna obci
ąż
enia podci
ą
gu ci
ęż
arem własnym stropu:
bl
k
bs
k
g
g
g
+
=
2.2.4 Warto
ść
charakterystyczna obci
ąż
enia u
ż
ytkowego podci
ą
gu:
2
kN/m
7,5
p
=
]
[kN/
p
b
p
k
m
⋅
=
wg. PN-EN 1991-1-1, obci
ąż
enie powierzchni kategorii E1
(powierzchnie do składowania i magazynowania)
Strop stalowy z płyt
ą
ż
elbetow
ą
4
2.2.5 Obci
ąż
enie obliczeniowe w stanie granicznym no
ś
no
ś
ci ULS:
zniszczenia lub nadmiernego odkształcenia konstrukcji (STR):
∑
∑
≥
≥
+
+
1
j
k,1
Q,1
j
k,
j
G,
j
1
j
k,1
0,1
Q,1
j
k,
j
G,
p
γ
g
γ
ξ
p
Ψ
γ
g
γ
gdzie:
0,85
ξ
0,7
Ψ
1,5
γ
1,35
γ
0,1
Q1
j
G,
=
=
=
=
q
max
Strop stalowy z płyt
ą
ż
elbetow
ą
5
2.3 WYZNACZENIE SIŁ WEWN
Ę
TRZNYCH:
y
0
Ed
y
M0
y
y
Rd
c,
Rd
c,
Ed
f
M
W
γ
f
W
M
1
M
M
M
γ
⋅
≥
→
⋅
=
≤
2.4 PRZYJ
Ę
CIE WYMIARÓW PRZEKROJU POPRZECZNEGO PODCI
Ą
GU
q
max
L
e
e
max
L
q
2
1
Strop stalowy z płyt
ą
ż
elbetow
ą
6
y
0
Ed
y
f
.
M
W
M
γ
≥
mm
6
t
min
w
=
w
y
w
t
W
1.1
h
⋅
≈
130
t
h
w
w
≥
w
w
h
2
a
h
⋅
≤
≤
6
h
t
h
W
A
w
w
w
y
f
⋅
−
=
40mm
b
A
t
f
f
f
≤
≈
(od 1000 do 3000mm co 250mm)
w
f
h
)
3
.
0
25
.
0
(
b
⋅
÷
≈
2
Strop stalowy z płyt
ą
ż
elbetow
ą
7
Ze wzgl
ę
du na technologi
ę
spawania zaleca si
ę
przyjmowanie spoin pachwinowych o wymiarach:
Przyj
ę
to wst
ę
pnie spoin
ę
o najmniejszej zalecanej grubo
ś
ci a = …. mm
)
t
,
t
min(
t
t
)
t
,
t
max(
t
t
f
w
min
1
f
w
max
2
=
=
=
=
mm
16
a
mm
3
t
0,7
a
t
0,2
1
2
≤
≤
⋅
≤
≤
⋅
gdzie:
Uwaga: PN-EN 1991-1-8 okre
ś
la tylko minimaln
ą
grubo
ść
spoiny pachwinowej a = 3 mm
Strop stalowy z płyt
ą
ż
elbetow
ą
8
2.5 WYZNACZENIE WIELKO
Ś
CI GEOMETRYCZNYCH ANALIZOWANEGO
PRZEKROJU POPRZECZNEGO:
•
A – pole przekroju poprzecznego
•
J
y
– moment bezwładno
ś
ci przekroju poprzecznego
•
W
y
– minimalny wska
ź
nik wytrzymało
ś
ci przekroju poprzecznego
2.6 STAN GRANICZNY NO
Ś
NO
Ś
CI
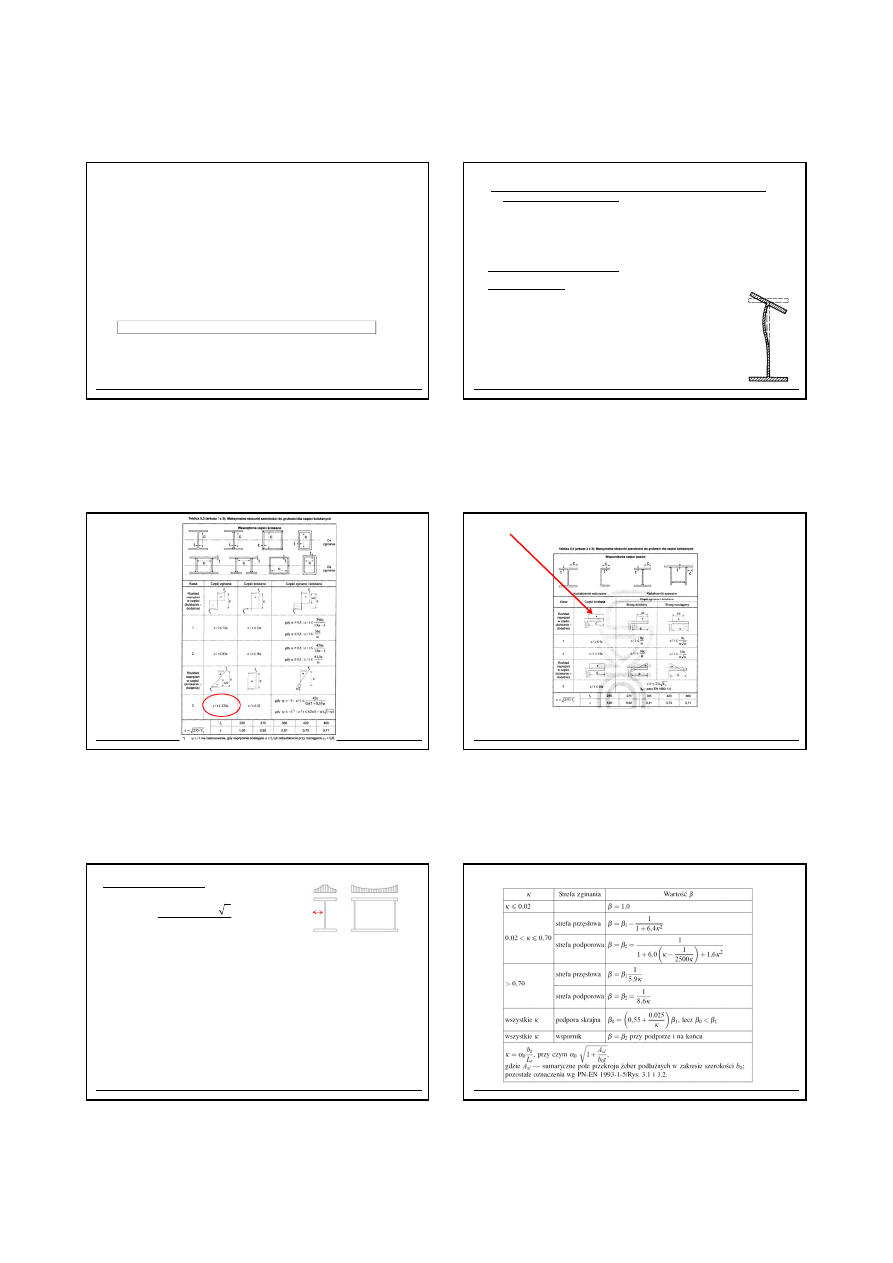
2.6.1 Klasa przekroju (PN-EN 1993-1-1, tabl.5.2 )
Klasa przekroju wyra
ż
a stopie
ń
odporno
ś
ci przekroju elementu na
miejscow
ą
utrat
ę
stateczno
ś
ci
ś
cianek (miejscowe wyboczenie) oraz
mo
ż
liwo
ść
wykorzystania zapasu no
ś
no
ś
ci przekroju wynikaj
ą
cego z
pozaspr
ęż
ystego zachowania si
ę
elementu.
•
Ś
cianki elementów konstrukcyjnych klas 1,2,3 nie trac
ą
stateczno
ś
ci
miejscowej.
• Przekroje klasy 4 s
ą
wra
ż
liwe na miejscow
ą
utrat
ę
stateczno
ś
ci i
ś
cianki takich elementów mog
ą
ulec miejscowemu wyboczeniu.
Strop stalowy z płyt
ą
ż
elbetow
ą
9
Strop stalowy z płyt
ą
ż
elbetow
ą
10
Strop stalowy z płyt
ą
ż
elbetow
ą
11
2.6.2 Efekt szerokiego pasa
b
0
2
2
2a
t
b
b
w
f
0
−
−
=
je
ż
eli b
0
≥
L
e
/
50, to nale
ż
y uwzgl
ę
dni
ć
efekt szerokiego pasa
0
eff
b
β
b
=
ββββ
wg tabl. 3.1 PN-EN 1993-1-5
z uwagi na brak
ż
eber podłu
ż
nych
α
0
=1,0
Szeroko
ść
efektywna b
eff
Strop stalowy z płyt
ą
ż
elbetow
ą
12
3
Strop stalowy z płyt
ą
ż
elbetow
ą
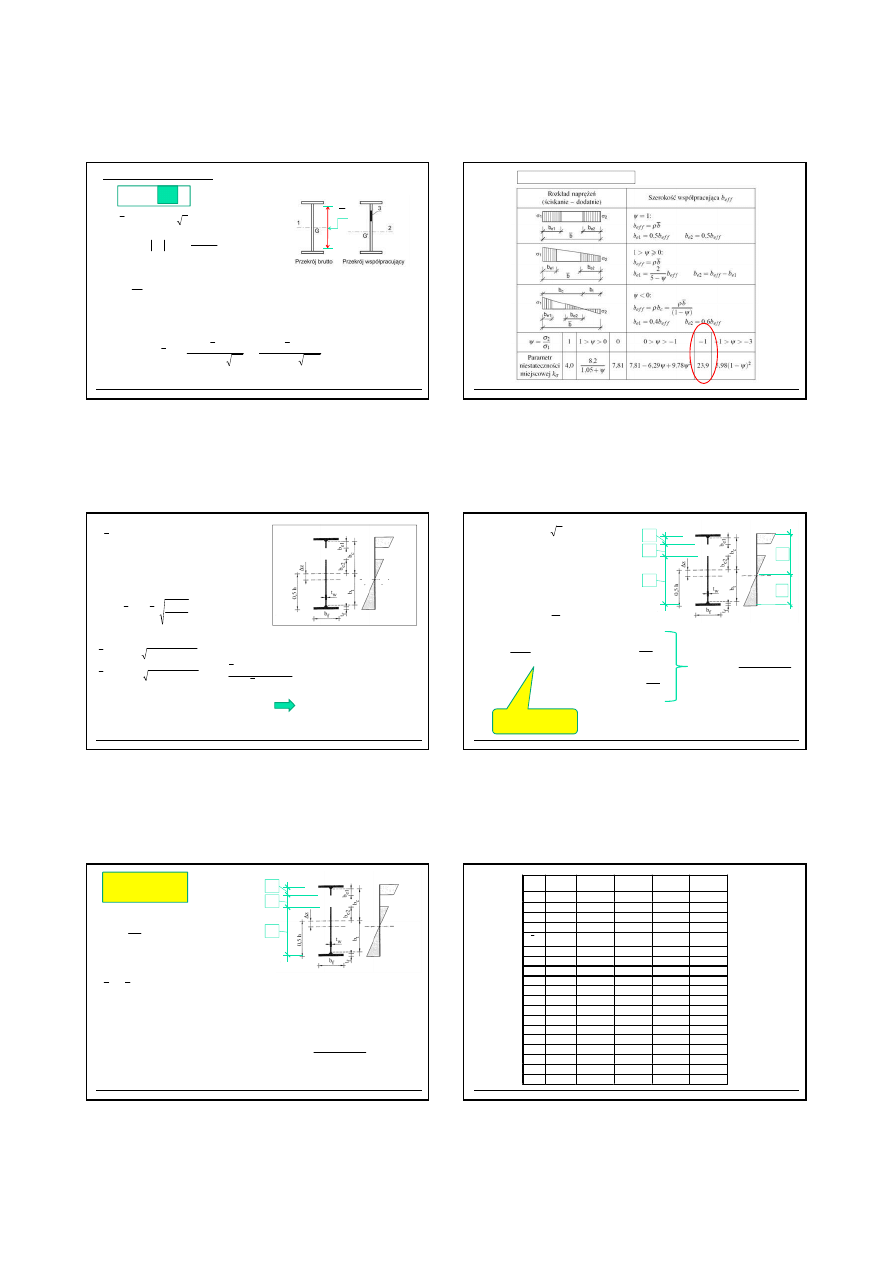
13
2.6.3 Przekrój współpracuj
ą
cy
wg PN-EN 1993-1-5, tabl.4.1
b
C
eff
ρb
b
=
2
a
2
h
b
w
−
=
1
y
Ed
1
2
Ed
com,
I
z
M
σ
σ
σ
⋅
=
=
=
23,9
k
4.1.
Tabl.
z
1
σ
σ
Ψ
σ
1
2
=
→
−
=
=
Smukło
ść
wzgl
ę
dna płytowa:
23,9
ε
28,4
/t
b
k
ε
28,4
/t
b
λ
p
⋅
⋅
=
⋅
⋅
=
σσσσ
Strop stalowy z płyt
ą
ż
elbetow
ą
14
Tabl.4.1 wg PN-EN 1993-1-5
Strop stalowy z płyt
ą
ż
elbetow
ą
15
2
red
p,
red
p,
red
p,
red
p,
λ
)
3
(
55
,
0
λ
to
0,005
-
0,085
0,5
λ
1,0
to
0,005
-
0,085
0,5
λ
ψ
ρ
ψ
ρ
ψ
+
−
=
+
>
=
+
≤
-
zredukowana smukło
ść
płytowa wg
PN-EN 1993-1-5, (4.4)
red
p,
λ
-
maksymalne obliczeniowe napr
ęż
enie
ś
ciskaj
ą
ce w
ś
ciance wyznaczone na
podstawie cech przekroju
współpracuj
ą
cego !!
Ed
com,
σ
eff
e2
eff
e1
c
eff
b
0,6
b
b
0,4
b
b
ρ
b
⋅
=
⋅
=
⋅
=
M0
y
Ed
com,
p
red
p,
/γ
f
σ
λ
λ
=
Strop stalowy z płyt
ą
ż
elbetow
ą
16
h
1
h
2
h
3
3
2
w
1
c
2
e1
3
h
h
h
h
b
ρ)
(1
h
2
a
b
h
−
−
=
⋅
−
=
+
=
)
h
(h
t
t
2b
A
2
w
w
f
f
eff
−
+
=
)
2
h
(b
t
h
S
2
e2
w
2
11
+
=
y
1
y
1
eff
11
A
S
Δz
=
y
2
y
2
t
y
eff
t,
c
y
eff
c,
y
z
I
W
z
I
W
I
2
2
2
=
=
→
→
M0
y
min
eff,
Rd
c,
γ
f
W
M
⋅
=
1 Iteracja
z
t
z
c
Strop stalowy z płyt
ą
ż
elbetow
ą
17
h
1
h
2
h
3
y
1
y
1
y
2
y
2
M0
y
min
eff,
Rd
c,
γ
f
W
M
2
⋅
=
2 Iteracja
σσσσ
1
σσσσ
2
3
y
eff
3
2
1
e2
e1
eff
red
p,
p
σ
1
2
I
Δz,
,
A
h
,
h
,
h
b
,
b
b
ρ
λ
,
λ
5)
-
1
-
1993
EN
-
PN
tabl.4.1
(z
k
1
σ
σ
Ψ
→
→
→
<
=
Strop stalowy z płyt
ą
ż
elbetow
ą
18
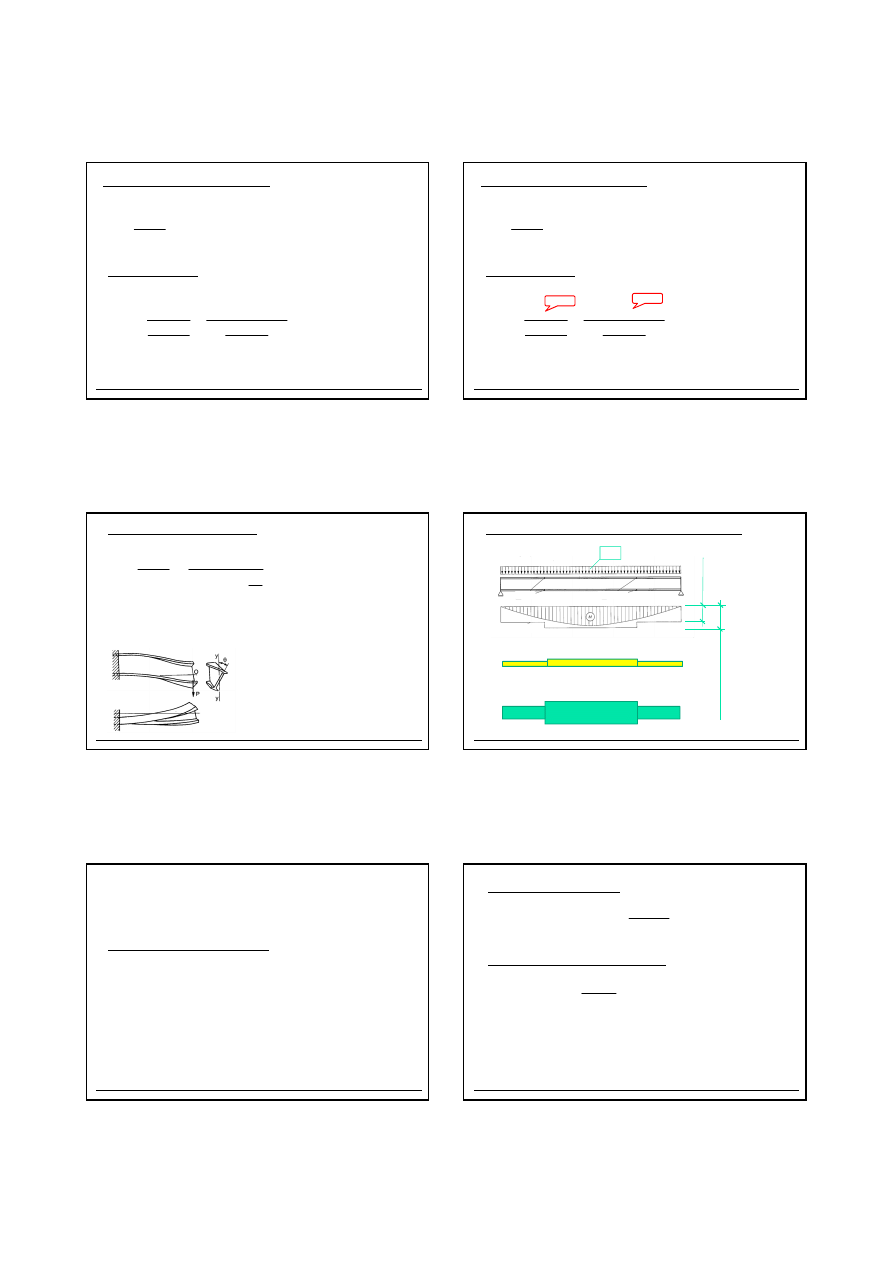
P ara-
metr
Jednost
ki
Iteracja 1
Iteracja 2
Iteracj a 3
It eracja 4
σ
σσ
σ
1
N/mm
2
σ
σσ
σ
2
N/mm
2
Ψ
Ψ
Ψ
Ψ
-
-1,00
k
σ
σσ
σ
-
23,9
p
λ
-
ρρρρ
-
b
eff
mm
b
e1
mm
b
e2
mm
h
1
mm
h
2
mm
h
3
mm
S
a-a
mm
3
A
eff
mm
2
Z
i +1
mm
I
y i+ 1
mm
4
W
eff ,t
mm
3
W
eff,c
mm
3
M
c,R d
Nmm
4
Strop stalowy z płyt
ą
ż
elbetow
ą
19
2.6.4 No
ś
no
ść
obliczeniowa przekroju klasy 4 przy jednokierunkowym zginaniu
wg PN-EN 1993-1-1, (6.12) i (6.15)
1
M
M
Rd
c,
Ed
≤
2.6.5 No
ś
no
ść
elementu przy
ś
ciskaniu i jednokierunkowym zginaniu
wg PN-EN 1993-1-5, (4.14)
1,0
γ
W
f
e
N
M
γ
A
f
N
η
M0
eff
y
N
Ed
Ed
M0
eff
y
Ed
1
≤
⋅
⋅
+
+
⋅
=
(4.14)
Strop stalowy z płyt
ą
ż
elbetow
ą
20
2.6.4 No
ś
no
ść
obliczeniowa przekroju klasy 4 przy jednokierunkowym zginaniu
wg PN-EN 1993-1-1, (6.12) i (6.15)
1
M
M
Rd
c,
Ed
≤
2.6.5 No
ś
no
ść
elementu przy
ś
ciskaniu i jednokierunkowym i zginaniu
wg PN-EN 1993-1-5, (4.14)
1,0
γ
W
f
e
N
M
γ
A
f
N
η
M0
eff
y
N
Ed
Ed
M0
eff
y
Ed
1
≤
⋅
⋅
+
+
⋅
=
= 0
= 0
Strop stalowy z płyt
ą
ż
elbetow
ą
21
2.6.6 No
ś
no
ś
ci elementu na zwichrzenie przy jednokierunkowym zginaniu
(wg PN-EN 1993-1-1, pkt.6.3.2.1)
Zwichrzenie – utrata stateczno
ś
ci ogólnej (utrata płaskiej postaci zginania)
χ
L
Τ
– współczynnik zwichrzenia
χ
L
Τ
= 1.0 (zgodnie z pkt. 6.3.2.1(2) )
1
W
χ
M
M
M
y
eff,
LT
Ed
Rd
b,
Ed
≤
⋅
=
M0
y
γ
f
Strop stalowy z płyt
ą
ż
elbetow
ą
22
2.7 WYZNACZENIE MIEJSC ZMIANY GRUBO
Ś
CI PASÓW PODCI
Ą
GU
q
max
M
1
=
W
1
f
y
/
γ
M
0
M
c
,R
d
=
W
e
ff
,m
in
f
y
/
γ
M
0
a) b
f
= const
b) t
f
= const
Strop stalowy z płyt
ą
ż
elbetow
ą
23
Zmniejszenie grubo
ś
ci półki – zalecenia konstrukcyjne:
•
dla gr. półki od 25 do 40 mm
→
pocienienie od 10 do 15 mm
•
dla gr. półki do 25mm
→
pocienienie od 5 do 10 mm
2.7.1 Wyznaczenie wielko
ś
ci geometrycznych dla analizowanego przekroju:
•
A
1
– pole przekroju poprzecznego
•
J
y
1
– moment bezwładno
ś
ci przekroju poprzecznego
•
W
y
1
– minimalny wska
ź
nik wytrzymało
ś
ci przekroju poprzecznego
M0
y
1
y
1
Rd
c,
/γ
f
W
M
⋅
=
Wst
ę
pnie przyj
ę
to:
Strop stalowy z płyt
ą
ż
elbetow
ą
24
2.7.2 Miejsce zmiany grubo
ś
ci pasa:
x
2
x
q
x
R
M
2
max
A
1
Rd
c,
⇒
⋅
−
⋅
=
)
m
3
x
(
≥
2.7.3 Siły wewn
ę
trzne w miejscu zmiany przekroju
2
x
q
x
R
M(x)
2
max
A
Ed
⋅
−
⋅
=
x
q
R
V(x)
max
A
Ed
⋅
−
=
5
Strop stalowy z płyt
ą
ż
elbetow
ą
25
2.8 SPRAWDZENIE WARUNKU NO
Ś
NO
Ś
CI PRZY ZGINANIU ZE
Ś
CINANIEM
2.8.1 No
ś
no
ść
obliczeniowa przekroju „1” przy jednokierunkowym zginaniu
1
Rd
c,
1
1
eff
1
M
,
Δz
,
b
,
ρ
1,0
M
M(x)
1
Rd
c,
Ed
≤
Strop stalowy z płyt
ą
ż
elbetow
ą
26
2.8.2 No
ś
no
ść
przekroju (przypodporowego) przy
ś
cinaniu
ś
rodnika u
ż
ebrowanego
(wg PN-EN 1993-1-5, pkt.5.1.(2) )
τ
w
w
k
ε
η
31
t
h
>
Je
ż
eli w
ś
rodnikach u
ż
ebrowanych :
to nale
ż
y sprawdzi
ć
niestateczno
ść
przy
ś
cinaniu
η
= 1,20 dla gatunków stali poni
ż
ej i ł
ą
cznie z S460
Strop stalowy z płyt
ą
ż
elbetow
ą
27
wg Zał
ą
cznika A3, PN-EN1993-1-5
ττs
2
w
τ
k
/a)
(h
4,00
5,34
k
+
⋅
+
=
dla a/h
w
≥
1
0
k
ττs
=
przy braku
ż
eber podłu
ż
nych:
No
ś
no
ść
obliczeniowa przekroju przy
ś
cinaniu:
Rd
w,
Rd
bf,
Rd
bw,
Rd
b,
V
V
V
V
≤
+
=
(5.1)
minimalny parametr niestateczno
ś
ci panelu
ś
rodnika przy
ś
cinaniu
k
τ
V
bw,Rd
– udział
ś
rodnika w no
ś
no
ś
ci obliczeniowej
V
bf,Rd
– udział pasów w no
ś
no
ś
ci obliczeniowej
V
w,Rd
– no
ś
no
ść
obliczeniowa
ś
rodnika przy uplastycznieniu
Strop stalowy z płyt
ą
ż
elbetow
ą
28
M1
w
w
yw
w
γ
3
t
h
f
χ
⋅
⋅
⋅
⋅
=
Rd
bw,
V
(5.2)
Wzgl
ę
dna smukło
ść
płytowa
ś
rodnika (gdy s
ą
ż
ebra po
ś
rednie i na podporach)
τ
w
w
w
k
ε
t
37,4
h
λ
⋅
⋅
⋅
=
(5.6)
Tablica 5.1. Współczynnik niestateczno
ś
ci przy
ś
cinaniu
ś
rodników
χχχχ
w
γ
M1
= 1,0
Strop stalowy z płyt
ą
ż
elbetow
ą
29
( )
−
⋅
⋅
⋅
=
2
Rd
f,
Ed
M1
yf
2
1
f
f
M
M
1
γ
c
f
t
b
Rd
bf,
V
(5.8)
( )
⋅
⋅
⋅
⋅
⋅
+
=
yw
2
w
yf
2
1
f
f
f
h
t
f
t
b
1,6
0,25
a
c
M
Ed
= 0
Wyznaczenie V
w,Rd
wg PN-EN 1993-1-1 (6.18)
M1
w
yw
Rd
w,
Rd
pl,
γ
3
t
h
f
η
V
V
⋅
⋅
⋅
⋅
=
=
Wyznaczenie V
b,Rd
i sprawdzenie warunku (5.1)
Strop stalowy z płyt
ą
ż
elbetow
ą
30
Je
ż
eli:
( )
0,5
V
x
V
η
Rd
bw,
Ed
3
>
=
2.8.3 Interakcyjny warunek no
ś
no
ś
ci
wg PN-EN 1993-1-5 pkt. 7.1
to nale
ż
y uwzgl
ę
dni
ć
interakcj
ę
sprawdzaj
ą
c warunek no
ś
no
ść
:
(
)
1,0
1
η
2
M
M
1
η
2
3
Rd
pl,
Rd
f,
1
≤
−
⋅
−
+
lecz
Rd
pl,
Rd
f,
1
M
M
η
≥
gdzie:
Rd
pl,
Ed
1
M
M(x)
η
=
(7.1)
Sprawdzenie warunku no
ś
no
ś
ci przekroju przypodporowego przy
ś
cinaniu
1,0
V
R
η
Rd
b,
A
3
≤
=
(5.10)
6
Strop stalowy z płyt
ą
ż
elbetow
ą
31
M
pl,Rd
- obliczeniowa no
ś
no
ść
plastyczna przy zginaniu przekroju zło
ż
onego
z efektywnych cz
ęś
ci pasów oraz w pełni efektywnego
ś
rodnika, niezale
ż
nie
od jego klasy przekroju:
M0
w
y,
w
2
w
f
y,
1
f
w
f
1
f
γ
f
t
2
h
f
)
t
(h
b
t
⋅
+
⋅
+
⋅
=
Rd
pl,
M
M
f,Rd
– obliczeniowa no
ś
no
ść
przy zginaniu przekroju zło
ż
onego wył
ą
cznie
z efektywnych cz
ęś
ci pasów:
M0
f
y,
1
f
w
f
1
f
Rd
f,
γ
)f
t
(h
b
t
M
+
=
Strop stalowy z płyt
ą
ż
elbetow
ą
32
2.9 SPOINA PACHWINOWA Ł
Ą
CZ
Ą
CA
Ś
RODNIK Z PASAMI PODCI
Ą
GU
Sprawdzenie no
ś
no
ś
ci wst
ę
pnie przyj
ę
tej spoiny a = …. mm
Rd
w,
Ed
w,
F
F
≤
Sprawdzenie warunku no
ś
no
ś
ci (wg PN-EN 1993-1-8, 4.5.3.3)
M2
w
u
d
vw,
Rd
w,
γ
β
3
a
f
a
f
F
⋅
⋅
⋅
=
=
∑
∑
ββββ
w
wg Tabl.4.1
γγγγ
M2
=1,25
(4.2)
(4.3)
(4.4)
Uwagi:
→
→
→
→
Strop stalowy z płyt
ą
ż
elbetow
ą
33
Je
ż
eli
M1
w
w
yw
w
Ed
γ
3
t
h
f
χ
V
⋅
≤
to spoiny wymiarujemy na nominalny strumie
ń
ś
cinania
V
=
V
Ed
/ h
w
M1
w
w
yw
w
Ed
γ
3
t
h
f
χ
V
⋅
>
Je
ż
eli
w
M0
w
w
yw
h
γ
3
t
h
f
η
V
⋅
⋅
=
to
Wg PN-EN 1993-1-5, pkt.9.3.5
Strop stalowy z płyt
ą
ż
elbetow
ą
34
2.10 STATECZNO
ŚĆ
PASA PRZY SMUKŁYM
Ś
RODNIKU
fc
w
yf
w
W
A
A
f
E
k
t
h
≤
Aby zapobiec wyboczeniu pasa
ś
ciskanego w płaszczy
ź
nie
ś
rodnika,
powinien spełniony by
ć
warunek:
A
fc
– efektywne pole przekroju pasa
K = 0,55 gdy przyjmuje si
ę
no
ś
no
ść
spr
ęż
yst
ą
przy zginaniu
(przekroje klasy 3. i 4.)
wg PN-EN 1993-1-5, pkt.8
(8.1)
Strop stalowy z płyt
ą
ż
elbetow
ą
35
2.11 STAN GRANICZNY U
Ż
YTKOWANIA
2.11.1 Maksymalne ugi
ę
cie podci
ą
gu (o zmiennym przekroju):
y
4
o
k
J
E
L
q
384
5.5
f
⋅
⋅
⋅
=
2.11.2 Dopuszczalne ugi
ę
cie podci
ą
gu (wg PN-EN 1993-1-1, NA.22):
2.11.3 Sprawdzenie warunku stanu granicznego u
ż
ytkowania:
gran
f
f
≤
350
L
f
0
gran
=
Strop stalowy z płyt
ą
ż
elbetow
ą
36
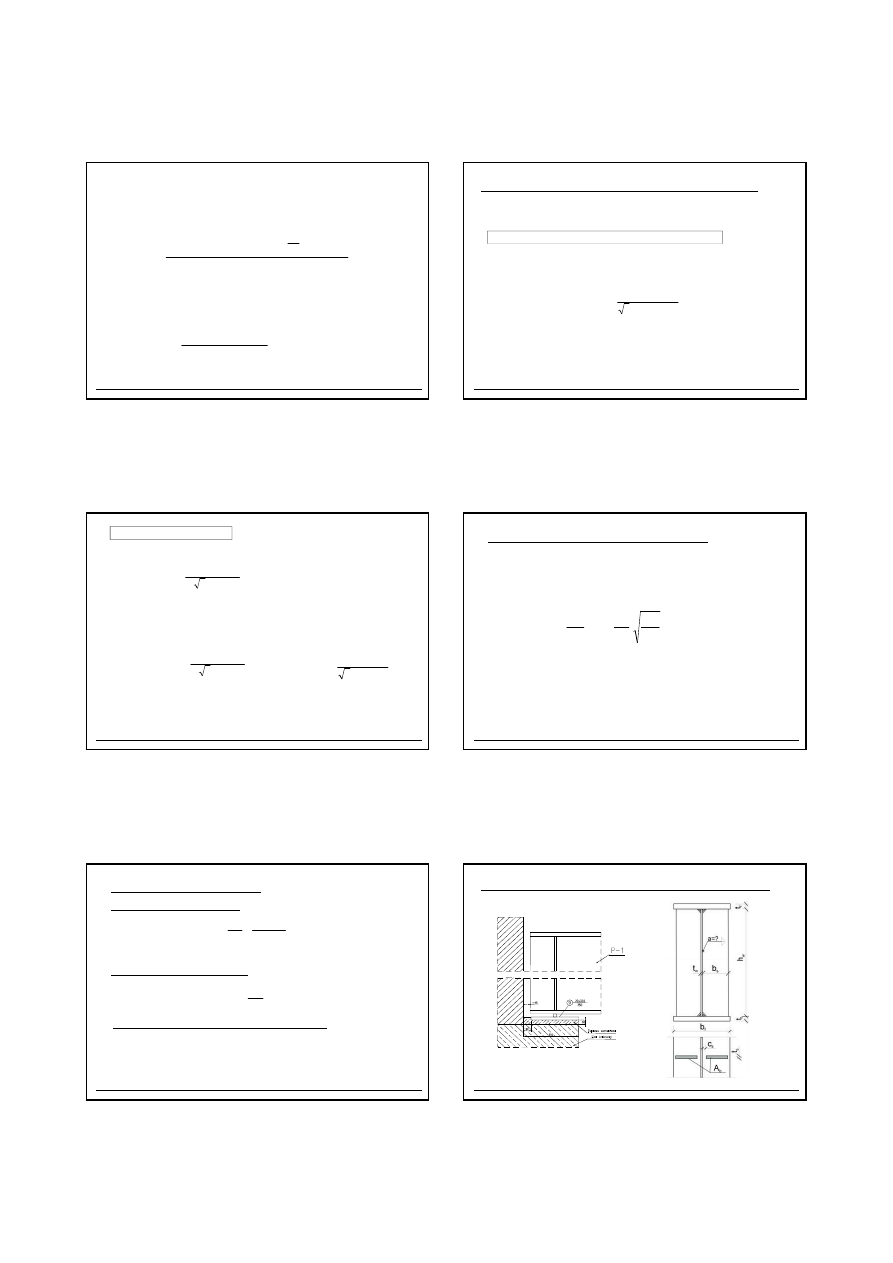
2.12
Ż
EBRO POPRZECZNE PODPOROWE. OPARCIE PODCI
Ą
GU NA
Ś
CIANIE
7
Strop stalowy z płyt
ą
ż
elbetow
ą
37
(
)
s
s
s
b
t
c
b
2
A
−
=
M0
y
b
Rd
b,
γ
f
A
F
=
2.12.1 Przyj
ę
cie grubo
ś
ci
ż
ebra podporowego t
s
mm
35
c
s
=
Ed
s
Ed,
V
N
=
t
s
Sprawdzenie klasy przekroju
ż
ebra
3
klasa
14ε
....
t
c
2
a
b
c
s
s
→
≤
=
−
=
1
F
N
Rd
b,
s
Ed,
≤
Strop stalowy z płyt
ą
ż
elbetow
ą
38
2.12.2 Sprawdzenie no
ś
no
ś
ci i stateczno
ś
ci
ż
ebra (wg PN-EN 1993-1-5, pkt. 9.4)
(
)
12
t
t
t
ε
30
2
t
b
b
t
12
b
t
2
I
3
w
s
w
2
w
s
s
s
3
s
s
st
+
+
+
+
=
b
s
t
s
(
)
w
t
w
s
s
st
t
t
t
ε
15
t
b
2
A
+
+
=
Mo
ż
na przyj
ąć
bez oblicze
ń
,
ż
e je
ż
eli
ś
rodnik jest klasy 4,
to jego cz
ęść
współpracuj
ą
ca
jest klasy 3.
st
st
st
A
I
i
=
w
cr
h
0,75
L
⋅
=
- przy zało
ż
eniu,
ż
e oba ko
ń
ce
ż
ebra (pasy)
s
ą
sztywno st
ęż
one w kierunku bocznym
Strop stalowy z płyt
ą
ż
elbetow
ą
39
1
st
cr
cr
y
λ
1
i
L
N
Af
λ
=
=
Smukło
ść
wzgl
ę
dna
λ
przy wyboczeniu gi
ę
tnym wg PN-EN 1993-1-1 (6.50)
je
ż
eli
λ ≤
0,2 to
χ
=1,0 - warunek stateczno
ś
ci sprowadza si
ę
do warunku no
ś
no
ś
ci elementu:
gdzie
λ
1
= 93,9
ε
1,0
N
N
Rd
c,
s
Ed,
≤
M0
y
st
Rd
c,
γ
f
A
N
gdzie
=
je
ż
eli
λ
>0,2 to:
- dla krzywej wyboczeniowej „c” parametr imperfekcji
α
= 0,49
(
)
[
]
1
χ
lecz
....
λ
Φ
Φ
1
χ
λ
0,2
λ
α
1
0,5
Φ
2
2
2
≤
=
−
+
=
+
−
+
=
Sprawdzamy warunek
stateczno
ś
ci (6.49)
Strop stalowy z płyt
ą
ż
elbetow
ą
40
2.12.3 Stateczno
ść
ż
ebra ze wzgl
ę
du na wyboczenie skr
ę
tne
wg PN-EN 1993-1-5,
pkt. 9.2.1(8)
E
f
5,3
I
I
y
p
T
≥
(9.3)
W przypadku
ż
eber dwustronnych mo
ż
na rozpatrywa
ć
tylko jedn
ą
cz
ęść
ż
ebra
3
s
s
T
t
b
3
1
I
=
Moment bezwładno
ś
ci przekroju
ż
ebra
przy skr
ę
caniu swobodnym (St. Venanta)
12
t
b
3
b
t
I
3
s
s
3
s
s
p
+
=
Biegunowy moment bezwładno
ś
ci
przekroju
ż
ebra wzgl
ę
dem punktu
styczno
ś
ci ze
ś
ciank
ą
Strop stalowy z płyt
ą
ż
elbetow
ą
41
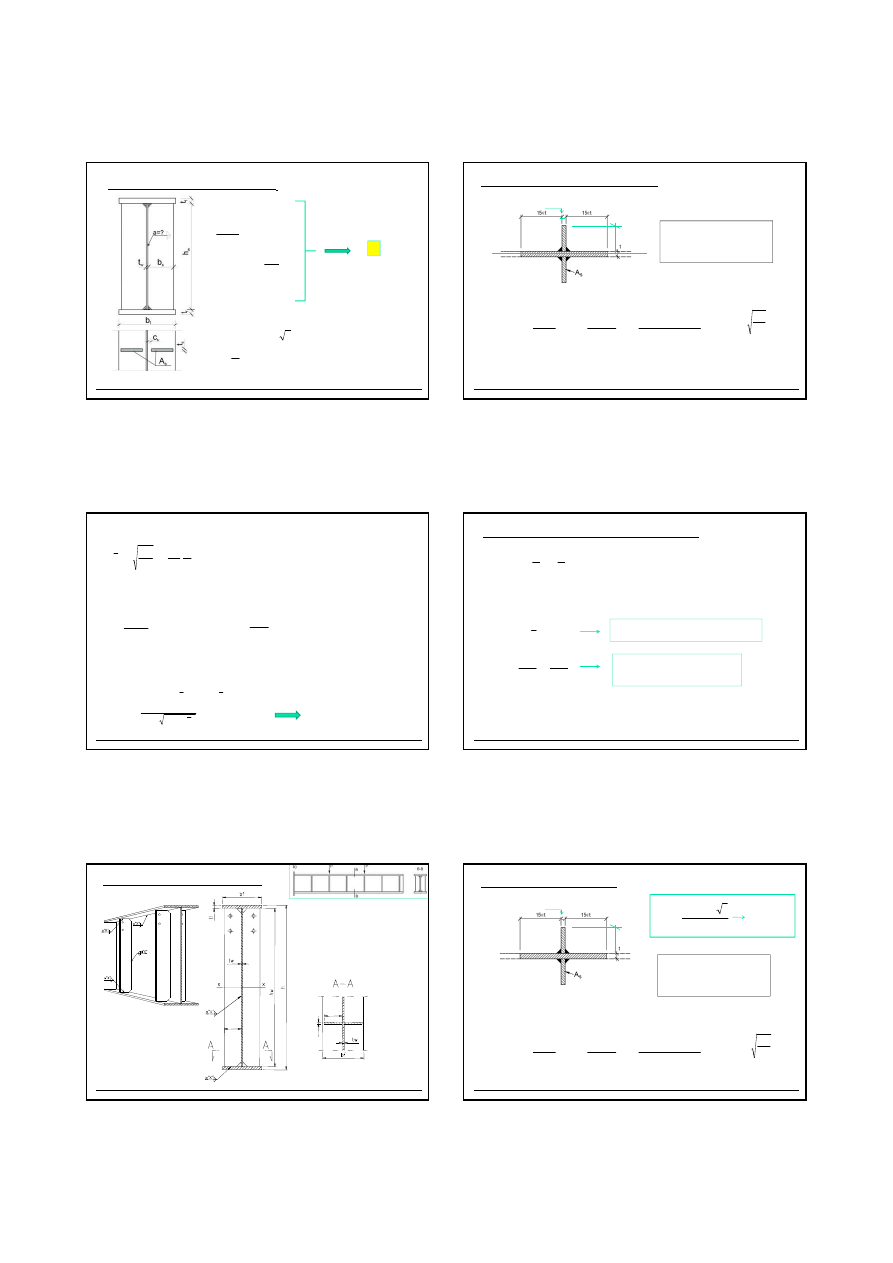
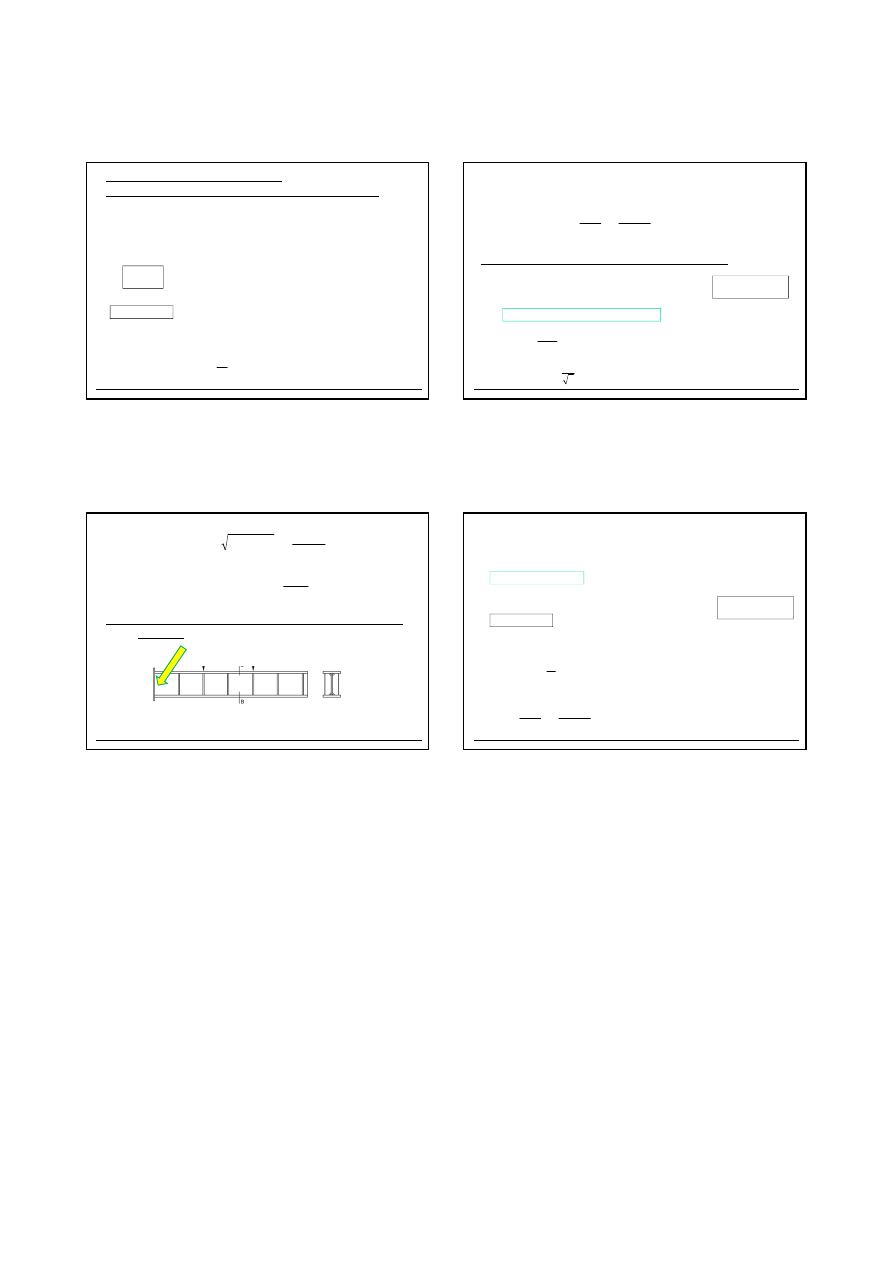
2.13
Ż
EBRO POPRZECZNE PO
Ś
REDNIE
b
s
b
s
t
s
Strop stalowy z płyt
ą
ż
elbetow
ą
42
2.13.1 Sprawdzenie sztywno
ś
ci
ż
ebra (wg PN-EN 1993-1-5, pkt. 9.3.3(3)):
b
s
ε
14
2
a
b
t
s
s
⋅
−
≥
t
s
(
)
w
t
w
s
s
st
t
t
t
ε
15
t
b
2
A
+
+
=
(klasa 3)
Mo
ż
na przyj
ąć
bez oblicze
ń
,
ż
e je
ż
eli
ś
rodnik jest klasy 4,
to jego cz
ęść
współpracuj
ą
ca
jest klasy 3.
st
st
st
A
I
i
=
(
)
12
t
t
t
ε
30
2
t
b
b
t
12
b
t
2
I
3
w
s
w
2
w
s
s
s
3
s
s
st
+
+
+
+
=
8
Strop stalowy z płyt
ą
ż
elbetow
ą
43
Ż
ebro po
ś
rednie mo
ż
na uzna
ć
za
sztywne
, gdy moment bezwładno
ś
ci
jego przekroju efektywnego I
st
spełnia warunki:
3
w
st
w
2
3
3
w
st
w
t
h
0,75
I
:
2
a/h
gdy
/a
t
h
1,5
I
:
2
a/h
gdy
≥
≥
≥
<
gdzie a - rozstaw
ż
eber
(9.6)
2.13.2 Sprawdzenie docisku
ż
ebra do pasa
gdzie N
Ed
=V
Ed
– siła poprzeczna w przekroju belki,
w którym usytuowane jest
ż
ebro
M0
y
b
Rd
b,
γ
f
A
F
=
1
F
N
Rd
b,
Ed
≤
(
)
s
s
s
b
t
c
b
2
A
−
=
Strop stalowy z płyt
ą
ż
elbetow
ą
44
2.13.3 Stateczno
ść
ż
ebra ze wzgl
ę
du na wyboczenie skr
ę
tne wg pkt. 9.2.1(8)
E
f
5,3
I
I
y
p
T
≥
(9.3)
W przypadku
ż
eber dwustronnych mo
ż
na rozpatrywa
ć
tylko jedn
ą
cz
ęść
ż
ebra
3
s
s
T
t
b
3
1
I
=
Moment bezwładno
ś
ci przekroju
ż
ebra
przy skr
ę
caniu swobodnym (St. Venanta)
12
t
b
3
b
t
I
3
s
s
3
s
s
p
+
=
Biegunowy moment bezwładno
ś
ci
przekroju
ż
ebra wzgl
ę
dem punktu
styczno
ś
ci ze
ś
cian
ą
Strop stalowy z płyt
ą
ż
elbetow
ą
45
2.13.4 No
ś
no
ść
sztywnego
ż
ebra poprzecznego
(metoda uproszczona – analiza spr
ęż
ysta I rz
ę
du)
F
N
s
Ed,
+
=
Ed
N
F = R
A
– reakcja z belki stropowej
N
Ed,s
– siła osiowa w
ż
ebrze po
ś
rednim
V
Ed
– maksymalna siła poprzeczna w s
ą
siednich panelach
M1
w
w
yw
2
w
Ed
s
Ed,
γ
3
t
h
f
λ
1
V
N
−
=
Wg PN-EN 1993-1-5 pkt. 9.1(3)
ż
ebro powinno przenie
ść
:
• obci
ąż
enie podłu
ż
ne N
Ed
:
(A)
Strop stalowy z płyt
ą
ż
elbetow
ą
46
• zast
ę
pcze obci
ąż
enie poprzeczne:
(
)
el
0
m
w
w
σ
4
π
q
+
=
(9.2)
w
el
– ugi
ę
cie spr
ęż
yste – mo
ż
na przyj
ąć
równe warto
ś
ci granicznej b/300
w
0
– wst
ę
pna imperfekcja (9.2.1(2))
pasów
rozstaw
osiowy
-
b
b)
,
a
,
(a
min
s
s/300
w
2
1
0
=
=
ż
ebro
+
=
2
1
max
Ed,
p
cr,
c
cr,
m
a
1
a
1
b
N
σ
σ
σ
Strop stalowy z płyt
ą
ż
elbetow
ą
47
E
p
σ,
p
cr,
σ
k
σ
⋅
=
σσσσ
cr,p
– spr
ęż
yste napr
ęż
enie krytyczne przy niestateczno
ś
ci typu płytowego
(dla
ś
cianek nieu
ż
ebrowanych podłu
ż
nie)
]
[N/mm
b
t
190000
b
)
ν
(1
12
t
E
π
σ
2
2
w
2
2
2
w
2
E
=
−
=
]
[N/mm
a
t
190000
a
)
ν
(1
12
t
E
π
σ
2
2
w
2
2
2
w
2
c
cr,
=
−
=
σσσσ
cr,c
- spr
ęż
yste napr
ęż
enie krytyczne przy niestateczno
ś
ci typu pr
ę
towego
Tabl.4.1
wg
k
k
σ
σ,p
=
Strop stalowy z płyt
ą
ż
elbetow
ą
48
N
Ed
– nie mo
ż
e by
ć
mniejsze od iloczynu napr
ęż
enia maksymalnego
i połowy pola przekroju współpracuj
ą
cego strefy
ś
ciskanej panelu
1
w
eff
Ed
σ
t
b
0,5
N
=
=
(B)
N
(A)
N
max
Ed
Ed
max
Ed,
N
(B)
Wyznaczamy:
σσσσ
m
(dla N
Ed,max
)
q
8
h
q
M
2
w
Ed
=
/2
t
b
I
W
w
s
st
st
+
=
M0
y
st
Ed
st
Ed
Ed
x,
γ
f
A
N
W
M
σ
≤
+
=
χχχχ
(6.42) wg PN-EN 1993-1-1
(A)
9
Strop stalowy z płyt
ą
ż
elbetow
ą
49
1
st
cr
cr
y
λ
1
i
L
N
Af
λ
=
=
Smukło
ść
wzgl
ę
dna
λ
przy wyboczeniu gi
ę
tnym wg PN-EN 1993-1-1 (6.50)
gdzie
λ
1
= 93,9
ε
dla krzywej wyboczeniowej „c” parametr imperfekcji
α
= 0,49
(
)
[
]
1
χ
lecz
....
λ
Φ
Φ
1
χ
λ
0,2
λ
α
1
0,5
Φ
2
2
2
≤
=
−
+
=
+
−
+
=
Sprawdzamy warunek
stateczno
ś
ci (6.46)
L
cr
=1,0 h
w
(6.49)
Je
ż
eli warto
ść
q jest bardzo mała, pomijamy zginanie
i sprawdzamy tyko no
ś
no
ść
na
ś
ciskanie
Strop stalowy z płyt
ą
ż
elbetow
ą
50
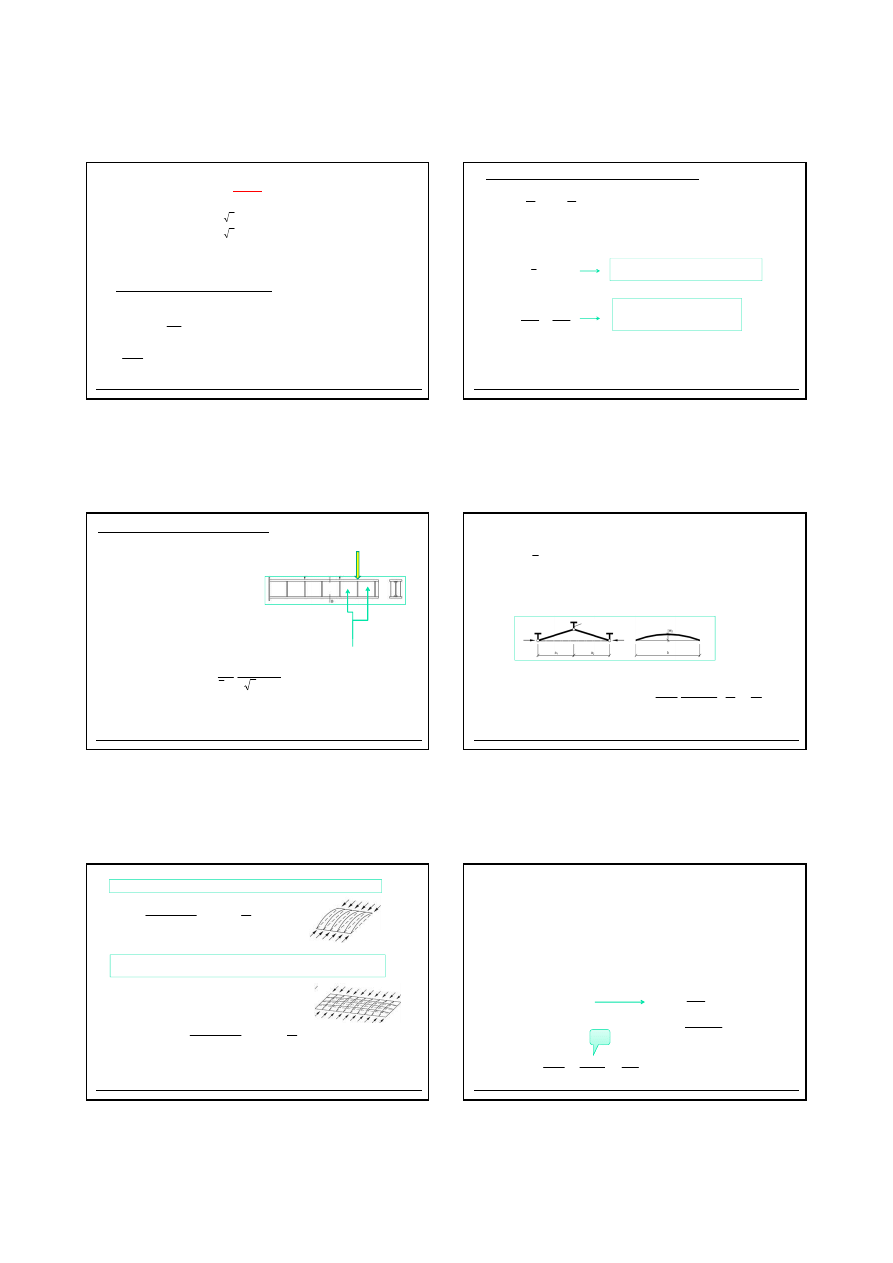
2.14
Ż
EBRO POPRZECZNE PODPOROWE. OPARCIE PODCI
Ą
GU NA SŁUPIE
b
s
b
s
A
b
s
s
b
t
b
A
=
t
s
Strop stalowy z płyt
ą
ż
elbetow
ą
51
2.14.1 Przyj
ę
cie grubo
ś
ci
ż
ebra podporowego t
s
t
s
Sprawdzenie klasy przekroju
ż
ebra:
3
klasa
14ε
....
t
c
b
c
s
s
→
≤
=
=
2
/
M0
y
b
Rd
b,
γ
f
A
F
=
Ed
s
Ed,
V
N
=
1
F
N
Rd
b,
s
Ed,
≤
Strop stalowy z płyt
ą
ż
elbetow
ą
52
12
b
t
I
3
s
s
st
⋅
=
b
s
t
s
2
w
s
s
st
t
15
t
b
A
ε
+
=
st
st
st
A
I
i
=
2.14.2 Sprawdzenie no
ś
no
ś
ci i stateczno
ś
ci
ż
ebra (wg PN-EN 1993-1-5, pkt. 9.4)
w
cr
h
0,75
L
⋅
=
- przy zało
ż
eniu,
ż
e oba ko
ń
ce
ż
ebra (pasy)
s
ą
sztywno st
ęż
one w kierunku bocznym
Strop stalowy z płyt
ą
ż
elbetow
ą
53
1
st
cr
cr
y
λ
1
i
L
N
Af
λ
=
=
Smukło
ść
wzgl
ę
dna przy wyboczeniu gi
ę
tnym wg PN-EN 1993-1-1 (6.50)
je
ż
eli
≤
0,2 to
χ
=1,0 - warunek stateczno
ś
ci sprowadza si
ę
do warunku no
ś
no
ś
ci elementu:
gdzie
λ
1
= 93,9
ε
1,0
N
N
Rd
c,
s
Ed,
≤
M0
y
st
Rd
c,
γ
f
A
N
gdzie
=
je
ż
eli
>0,2 to:
- dla krzywej wyboczeniowej „c” parametr imperfekcji
α
= 0,49
(
)
[
]
1
χ
lecz
....
λ
Φ
Φ
1
χ
λ
0,2
λ
α
1
0,5
Φ
2
2
2
≤
=
−
+
=
+
−
+
=
Sprawdzamy warunek
stateczno
ś
ci (6.49)
λλλλ
λλλλ
λλλλ
Strop stalowy z płyt
ą
ż
elbetow
ą
54
2.14.3 Stateczno
ść
ż
ebra ze wzgl
ę
du na wyboczenie skr
ę
tne
wg PN-EN 1993-1-5,
pkt. 9.2.1(8)
E
f
5,3
I
I
y
p
T
≥
(9.3)
3
s
s
T
t
b
3
1
I
=
Moment bezwładno
ś
ci przekroju
ż
ebra przy skr
ę
caniu swobodnym (St. Venanta)
3
t
b
12
b
t
I
3
s
s
3
s
s
p
+
=
Biegunowy moment bezwładno
ś
ci przekroju
ż
ebra wzgl
ę
dem punktu styczno
ś
ci ze
ś
ciank
ą
10
Strop stalowy z płyt
ą
ż
elbetow
ą
55
2.15.1 Pionowe spoiny pachwinowe ł
ą
cz
ą
ce
ż
ebra poprzeczne ze
ś
rodnikiem
a) Dobranie grubo
ś
ci spoiny:
b) Sprawdzenie warunku na długo
ść
obliczeniow
ą
spoiny (wg 4.5.1 (2) ):
35mm
2
h
l
w
i
⋅
−
=
2.15 SPOINY Ł
Ą
CZ
Ą
CE
Ż
EBRA Z PODCI
Ą
GIEM
wg PN-EN 1993-1-8
przyj
ę
to a = …. mm
l
i
≥
6a
l
i
≥
30mm
Wg pkt.4.11(4)
Długo
ść
spoiny pachwinowej ł
ą
cz
ą
cej
ż
ebro poprzeczne ze
ś
rodnikiem blachownicy
L
w
> 1,7 m, nale
ż
y zredukowa
ć
stosuj
ą
c współczynnik redukcyjny
ββββ
Lw.2
1,0
β
0,6
lecz
17
l
1,1
β
Lw.2
w
Lw.2
≤
≤
−
=
mm
16
a
mm
3
t
0,7
a
t
0,2
1
2
≤
≤
⋅
≤
≤
⋅
)
t
,
min(t
t
t
)
t
,
max(t
t
t
s
w
min
1
s
w
max
2
=
=
=
=
Strop stalowy z płyt
ą
ż
elbetow
ą
56
c) Sprawdzenie warunku no
ś
no
ś
ci spoiny - dla
ż
ebra podporowego i po
ś
redniego
(wg 4.5.3.2):
M2
w
u
i
Ed
II
γ
β
f
l
a
4
N
τ
≤
=
ββββ
w
wg Tabl.4.1
γγγγ
M2
=1,25
2.15.2 Poziome spoiny pachwinowe ł
ą
cz
ą
ce
ż
ebro z pasami podci
ą
gu
przyj
ę
to: a = …. mm, l
i
= b
s
-25 mm
l
i
≥
6a
30 mm
≤
l
i
≤
150mm
i
Ed
1
l
a
4
N
σ
=
1
σ
2
1
τ
σ
=
=
⊥
⊥
mm
16
a
mm
3
t
0,7
a
t
0,2
1
2
≤
≤
⋅
≤
≤
⋅
)
t
,
t
,
min(t
t
t
)
t
,
t
,
max(t
t
t
s
f
w
min
1
s
f
w
max
2
=
=
=
=
Strop stalowy z płyt
ą
ż
elbetow
ą
57
Warunki no
ś
no
ś
ci spoin:
M2
w
u
2
2
γ
β
f
3τ
σ
≤
+
⊥
⊥
M2
u
γ
f
0,9
σ
≤
⊥
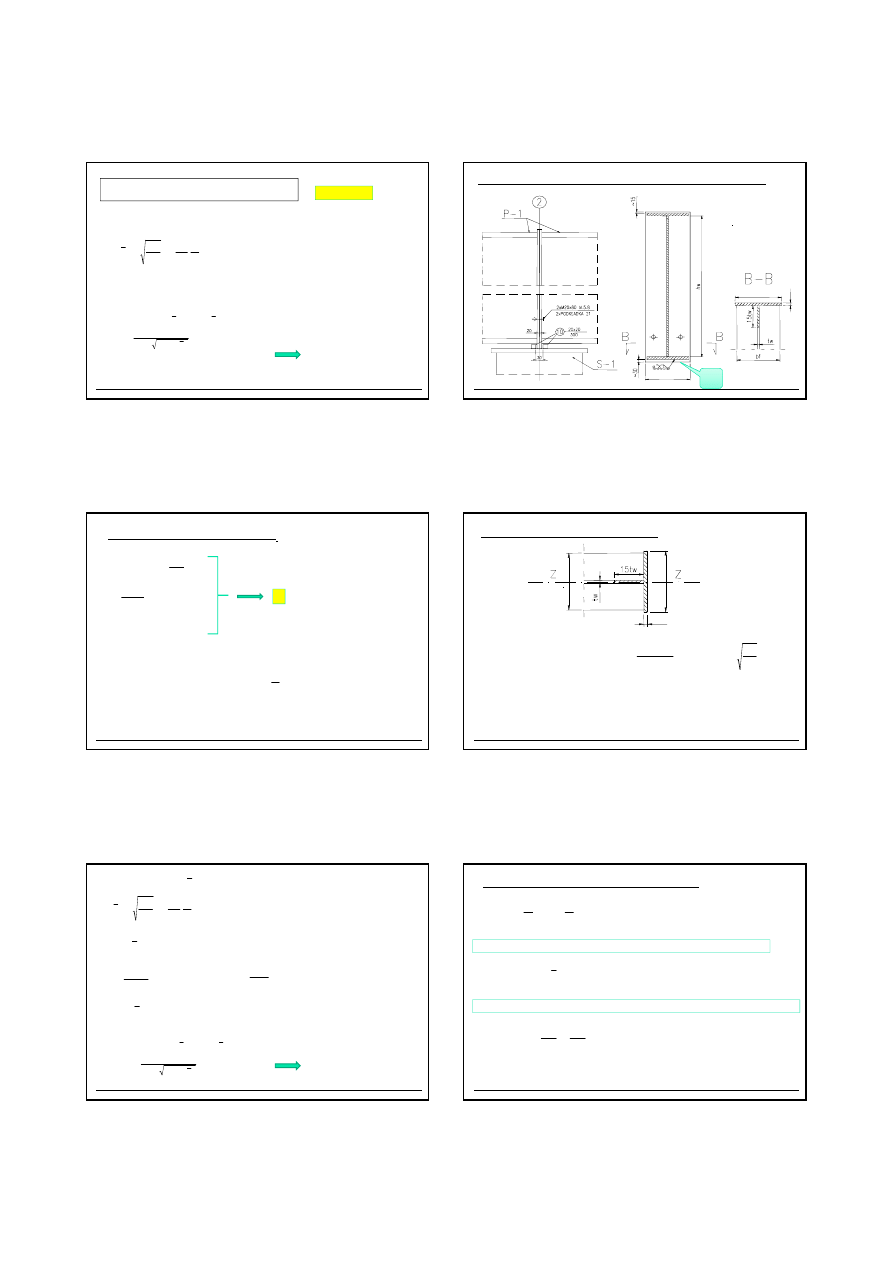
2.15.3 Pachwinowa spoina obwodowa ł
ą
cz
ą
ca blach
ę
czołow
ą
(
ż
ebro podporowe)
z podci
ą
giem.
Strop stalowy z płyt
ą
ż
elbetow
ą
58
b) Sprawdzenie warunku na długo
ść
obliczeniow
ą
spoiny:
w
i
h
l
=
przyj
ę
to: a = …. mm,
l
i
≥
6a
30 mm
≤
l
i
≤
150mm
mm
16
a
mm
3
t
0,7
a
t
0,2
1
2
≤
≤
⋅
≤
≤
⋅
)
t
,
t
,
min(t
t
t
)
t
,
t
,
max(t
t
t
s
f
w
min
1
s
f
w
max
2
=
=
=
=
a) Dobranie grubo
ś
ci spoiny:
Wg pkt.4.11(4)
1,0
β
0,6
lecz
17
l
1,1
β
Lw.2
w
Lw.2
≤
≤
−
=
Długo
ść
spoiny pachwinowej ł
ą
cz
ą
cej
ż
ebro poprzeczne ze
ś
rodnikiem blachownicy
L
w
> 1,7 m, nale
ż
y zredukowa
ć
stosuj
ą
c współczynnik redukcyjny
ββββ
Lw.2
M2
w
u
i
Ed
II
γ
β
f
l
a
2
N
τ
≤
=
ββββ
w
wg Tabl.4.1
γγγγ
M2
=1,25